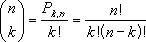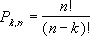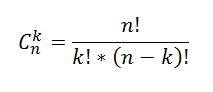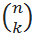Как посчитать количество комбинаций в excel

В этой статье описаны синтаксис формулы и использование функции ЧИСЛКОМБ в Microsoft Excel.

Описание

Возвращает количество комбинаций для заданного числа элементов. Функция ЧИСЛКОМБ используется для определения общего числа всех групп, которые можно составить из элементов данного множества.

Синтаксис

ЧИСЛКОМБ(число;число_выбранных)

Аргументы функции ЧИСЛКОМБ описаны ниже.

• Число    — обязательный аргумент. Количество элементов.

• Число_выбранных    — обязательный аргумент. Количество элементов в каждой комбинации.

Замечания

• Числовые аргументы усекаются до целых чисел.

• Если хотя бы один из аргументов не является числом, то #VALUE! значение ошибки #ЗНАЧ!.

• Если число < 0, number_chosen < 0 или < number_chosen, то #NUM! значение ошибки #ЗНАЧ!.

• Комбинацией считается любое множество или подмножество элементов независимо от их внутреннего порядка. Комбинации отличаются от перестановок, для которых порядок существен.

• Число комбинаций определяется по следующей формуле, где число = n, а число_выбранных = k:

  

  где

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ЧИСЛКОМБ(8;2)	Возможные команды по два человека, которые могут быть сформированы из восьми кандидатов.	28

Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).

Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примечание

: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.

Отличие Сочетаний от Размещений

В отличие от

Размещений

следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор

Сочетаний

включается только одна из этих комбинаций. Очевидно, что для тех же n и k число

Сочетаний

всегда меньше чем число

Размещений

(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.

Подсчет количества Сочетаний

Число всех

Сочетаний

из n элементов по k можно вычислить по формуле:

Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6}  равно 15=6!/(4!(6-4)!)

Примечание

:  Для

Сочетаний

из n элементов по k также используется и другая запись:

В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .

Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.

Примечание

: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье

Сочетания с повторениями: Комбинаторика в MS EXCEL

Вывод всех комбинаций Сочетаний

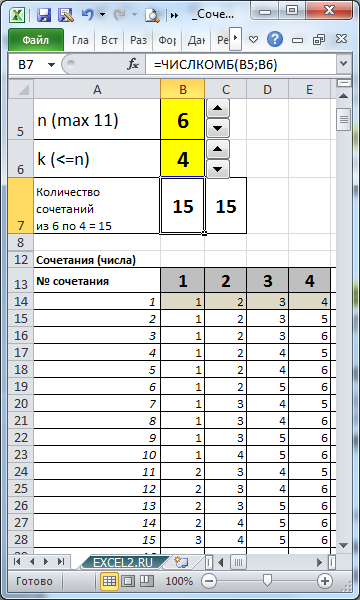
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью

элементов управления Счетчик

количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.

В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.

Задача

Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.

Нам нужно определить число

Сочетаний

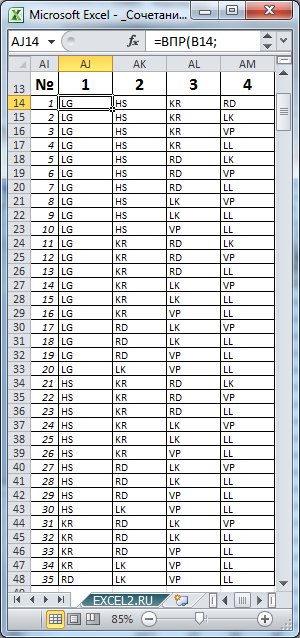
7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.

Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.

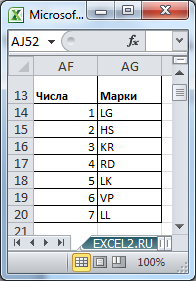
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Выставив в ячейках

В5

и

В6

значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).

Примечание

: О Перестановках можно прочитать в статье

Перестановки без повторений: Комбинаторика в MS EXCEL

, а о Размещениях в статье

Размещения без повторений: Комбинаторика в MS EXCEL

.

Функция ЧИСЛКОМБ возвращает количество комбинаций для заданного числа элементов.

Описание функции ЧИСЛКОМБ

Возвращает количество комбинаций для заданного числа элементов. Функция ЧИСЛКОМБ используется для определения общего числа всех групп, которые можно составить из элементов данного множества.

Синтаксис

=ЧИСЛКОМБ(число;число_выбранных)

Аргументы

Замечания

• Числовые аргументы усекаются до целых чисел.
• Если какой-либо из аргументов не является числом, функция ЧИСЛКОМБ возвращает значение ошибки #ЗНАЧ!.
• Если число < 0, число_выбранных < 0 или число < число_выбранных, то функция ЧИСЛКОМБ возвращает значение ошибки #ЧИСЛО!.
• Комбинацией считается любое множество или подмножество элементов независимо от их внутреннего порядка. Комбинации отличаются от перестановок, для которых порядок существен.
• Число комбинаций определяется по следующей формуле, где число = n, а число_выбранных = k:
  

Пример

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

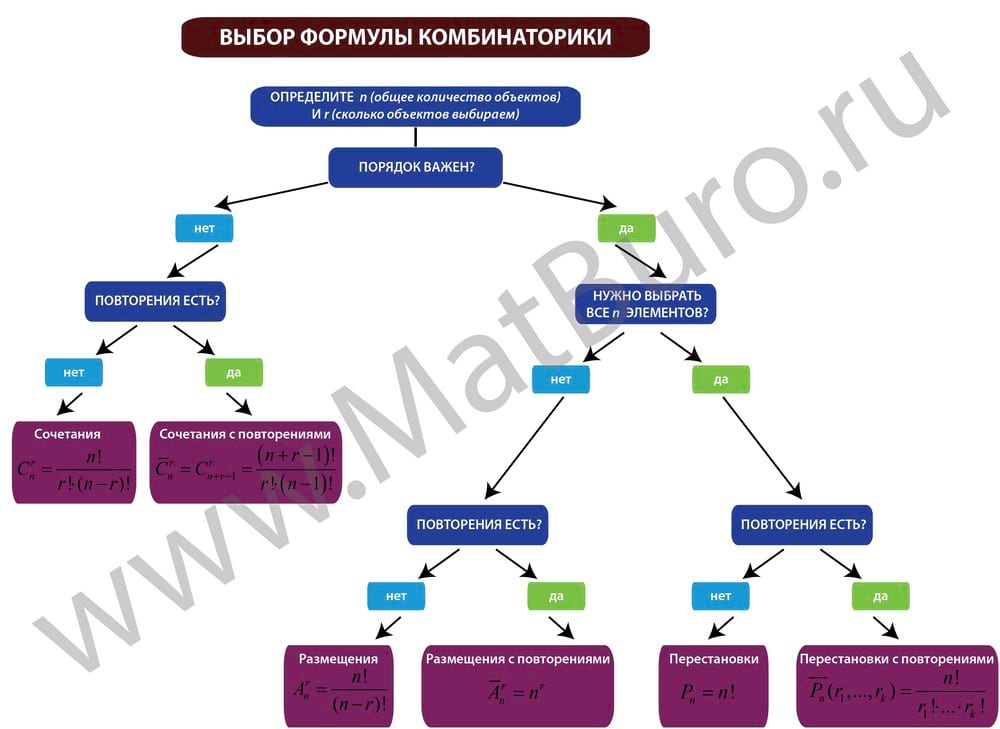
Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

• Сколько у нас есть объектов (число $n$)?
• Важен ли их порядок в комбинации?
• Могут ли встречаться повторяющиеся элементы?
• Нужно выбрать все элементы или только $klt n$?

Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

Схема выбора формул с примерами задач

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Подробнее: факториал в эксель.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.

Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$

Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).

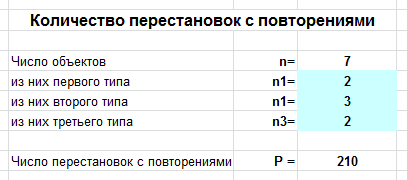
Задача. Сколько различных слов можно составить из букв слова «колокол»?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.

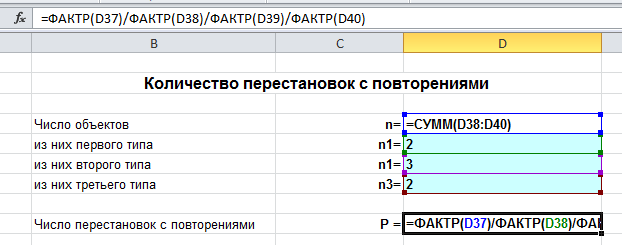
В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок c повторениями.

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.

Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

$$C_n^k=frac{n!}{(n-k)!cdot k!} $$

Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).

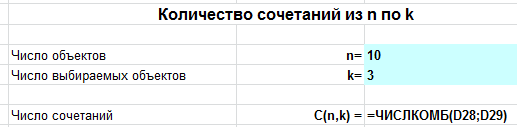
Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний.

Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Онлайн калькуляторы Онлайн учебник: Элементы комбинаторики Примеры решений

Как решать задачи по комбинаторике? Видеоуроки по комбинаторике Решение на заказ

Решебник задач по комбинаторике