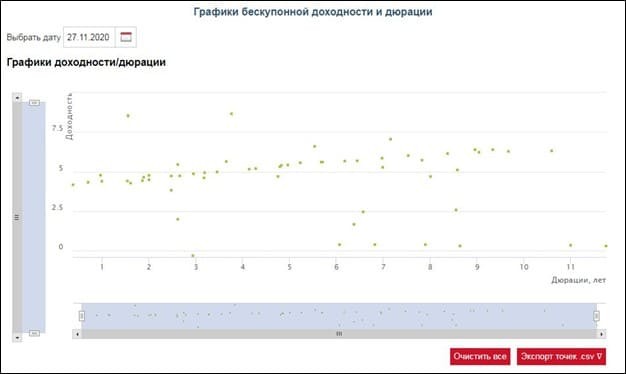
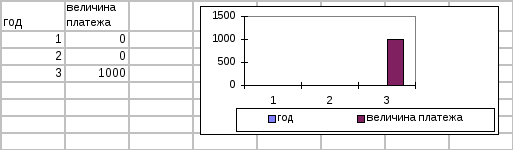
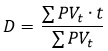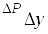Одной из важнейших характеристик, используемых в практических расчетах по денежным потокам, является дюрация, или продолжительность (duration). Дюрация представляет собой средневзвешенный срок по анализируемой последовательности платежей, где в качестве весов используется приведенная стоимость этих платежей (денежных потоков):
где PVt — платеж, относящийся ко времени t.
Скачать заметку в формате Word или pdf, примеры в формате Excel
Одним из важнейших свойств дюрации является то, что она представляет собой интегральную характеристику денежных потоков, рассроченных во времени, — средний срок выплаты или получения причитающихся сумм. Например, если у компании много обязательств и выплаты по ним предполагаются в разные периоды времени, то средневзвешенная дюрация обязательств компании может быть принята как оценка среднего срока погашения обязательств.[1]
Таким образом, условно заменим множество рассроченных во времени обязательств всего одним платежом со сроком, равным дюрации.
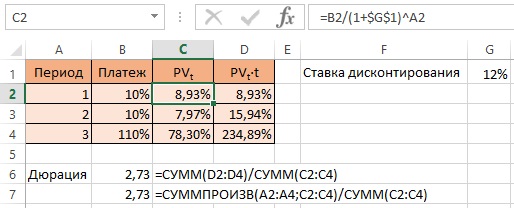
Рассмотрим пример. Корпоративная облигация выпущена на 3 года с купоном 10% в год и выплатой купонов раз в год. По окончании 3-го года она будет погашена по 100%-ной номинальной стоимости. Ставка дисконтирования – 12% годовых. Какова дюрация облигации?
Решение. Облигация генерирует последовательность платежей (денежных потоков):
1-й год = 10%;
2-й год = 10%;
3-й год = 100% + 10% (купон + погашение) = 110%.
Дюрация D:
Иногда в целях упрощения в качестве весов в этой формуле используют сами платежи, а не их приведенные стоимости, т.е. в нашем примере 10; 10; 110 вместо 8,93; 7,97 и 78,3. Это может быть оправданно, если ставка дисконтирования мало отличается от купона, а ее точное определение вызывает сложности теоретического или практического характера.
В нашем примере, дюрация рассчитанная таким образом составит:
Шаблон для расчета дюрации в Excel можно найти в прикрепленном файле.
Рис. 1. Расчет дюрации в Excel
[1] Это фрагмент из книги Михаил Лимитовский. Инвестиционные проекты и реальные опционы на развивающихся рынках
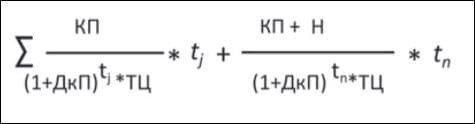
дюрации Маколея и используется для расчета изменения продолжительности облигации и цены на каждый процент изменения доходности к погашению.
Ключевые выводы
- Формула модифицированной дюрации показывает изменение стоимости облигации по отношению к изменению ее доходности к погашению.
- В Excel формула встроена в функцию MDURATION.
- Следуйте этому пошаговому примеру, чтобы заполнить формулу.
Вы можете использовать Microsoft Excel для расчета модифицированной дюрации облигации с учетом следующих параметров: дата расчета, дата погашения, купонная ставка, доходность к погашению и частота.
Что вам говорит измененная продолжительность
Модифицированная дюрация определяет изменение стоимости ценной бумаги с фиксированным доходом по отношению к изменению доходности к погашению. Формула, используемая для расчета модифицированной дюрации облигации, представляет собой дюрацию Маколея, деленную на 1, плюс доходность облигации к погашению, деленную на количество купонных периодов в году.
В Excel формула, используемая для расчета модифицированной дюрации облигации, встроена в функцию MDURATION. Эта функция возвращает измененную продолжительность Маколея для ценной бумаги, предполагая, что номинальная стоимость составляет 100 долларов США.
Пример расчета модифицированной продолжительности в Excel
Например, вы хотите рассчитать модифицированную дюрацию Маколея 10-летней облигации с датой погашения 1 января 2020 г., датой погашения 1 января 2030 г., годовой купонной ставкой 5% и годовой доходность к погашению 7%. Купон выплачивается ежеквартально.
Чтобы узнать измененную продолжительность, выполните следующие действия в Excel:
- Сначала щелкните правой кнопкой мыши столбцы A и B.
- Затем щелкните левой кнопкой мыши по ширине столбца и измените значение на 32 для каждого из столбцов, затем нажмите кнопку ОК. Введите «Описание облигации» в ячейку A1, затем выберите ячейку A1 и нажмите клавиши CTRL и B вместе, чтобы выделить заголовок жирным шрифтом. Затем введите «Данные облигации» в ячейку B1, затем выберите ячейку B1 и нажмите клавиши CTRL и B вместе, чтобы выделить заголовок жирным шрифтом.
- Введите «Дата погашения облигации» в ячейку A2 и «1 января 2020 года» в ячейку B2. Затем введите «Дата погашения облигации» в ячейку A3 и «1 января 2030 года» в ячейку B3. Затем введите «Годовая купонная ставка » в ячейку A4 и «5%» в ячейку B4. В ячейке A5 введите «Годовая доходность к погашению», а в ячейке B5 введите «7%». Поскольку купон выплачивается ежеквартально, частота составляет 4. Введите «Частота выплаты купона» в ячейку A6 и «4» в ячейку B6.
- Затем введите «Основа» в ячейку A7 и «3» в ячейку B8. В Excel базис не является обязательным, и выбранное значение рассчитывает измененную продолжительность с использованием фактических календарных дней для периода начисления и предполагает, что в году 365 дней.
- Теперь вы можете решить модифицированную дюрацию Маколея для облигации. Введите «Измененная продолжительность» в ячейку A8 и формулу «= MDURATION (B2, B3, B4, B5, B6, B7)» в ячейку B8. В результате модифицированная длительность составляет 7,59.
Формула, используемая для расчета процентного изменения цены облигации, представляет собой изменение доходности к погашению, умноженное на отрицательное значение модифицированной дюрации, умноженное на 100%. Следовательно, если процентные ставки увеличиваются на 1%, цена облигации, как ожидается, упадет на 7,59% = [0,01 * (-7,59) * 100%].
Экономика17 марта 2021 в 15:0019 575
Дюрация облигации
Как инвестор может рассчитать и использовать этот показатель
Понятие дюрации и её значение
Теоретические основы расчёта дюрации
Факторы, влияющие на дюрацию
Как рассчитать дюрацию с помощью специальных инструментов
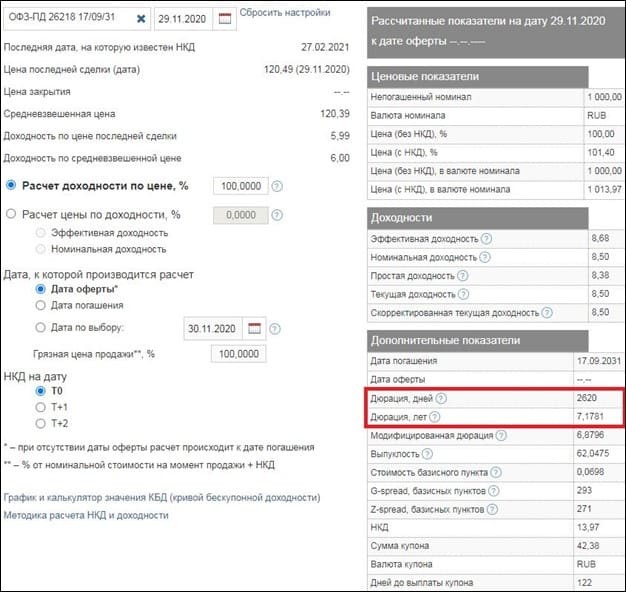
Рис. 2. Калькулятор для расчёта дюрации на Московской бирже (MOEX). Источник: сайт Московской биржи
Рис. 3. Чему равна дюрация для различных выпусков ОФЗ. Источник: сайт Московской биржи
Рис. 4. Аргументы функции «ДЛИТ» в Excel. Источник: сайт Microsoft
Ценовой риск.
Рыночная цена
облигации отличается от номинальной
цены в зависимости от изменения
доходности. Чем выше доходность, тем
ниже цена облигации. Инвестиции даже
в государственные облигации подвержены
риску
изменения процентной ставки.
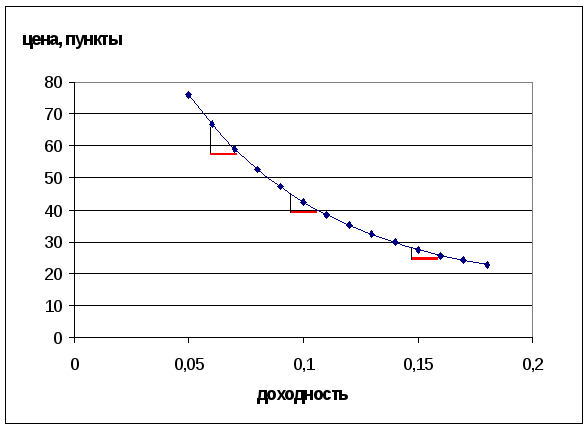
Рис.
3.6. На графике показана зависимость
цены облигации от ее доходности2.
Как видно из
графика для одной и той же величины
изменения доходности
изменение
цены
имеет
разное значение. Наклоны к касательных
уменьшаются с ростом доходности.
Величина
(3.16)
называется ценовым
риском. Цена в пунктах3
.
Ценовой риск измеряется на 1% изменения
доходности и отражает изменение цены
облигации по отношению к номиналу. При
малых изменениях доходности ценовой
риск равен
(3.17)
Дюрация.
Изменение цены
облигации при малых изменениях доходности
можно найти, если взять первую производную
от функции зависимости цены облигации.
Зависимость цены облигации от доходности
y
в общем виде можно записать, как
приведенную стоимость дисконтированного
потока наличности от облигации
. (3.18)
Заметим, что ставка
дисконтирования
постоянна
в течении всего времени «жизни» облигации
и вместо термина процентная ставка при
расчете дюрации используется термин
доходность. Доходность облигации,
рассчитанная для данного момента
времени является постоянной для всех
оставшихся периодов «жизни» облигации.
В то время, как процентная ставка
не является постоянной.
Первая
производная от цены облигации по r
равна
(3.19)
Разделим
обе части в выражении (3.19) на величину
цены Р.
Тогда получим
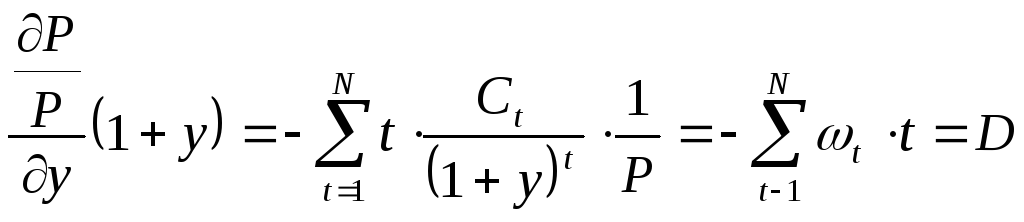
где
,
— величинаt
— го платежа в стоимости облигации. До
даты погашения — это купонные выплаты,
последняя выплата
это номинал плюс купон. Таким образом,
из выражения (3.20) для ценового риска
облигации получим
(3.21)
Это
выражения обычно записывают в виде
(3.22)
Величина D
называется дюрацией или продолжительностью
облигацией. Термин продолжительность
– это перевод слова duration.
В русскоязычной литературе используются
как термин дюрация, так и продолжительность.
Дюрация рассчитывается по формулам
,
,
, (3.23)
где
— доля приведенной стоимостиt
— го платежа
в стоимости облигации, деленной на
цену облигации P.
Дюрация измеряется в годах и отражает
изменение цен по отношению к «сегодняшней»
цене P
= PV
или приведенной стоимости инвестиции.
Чувствительность
цены облигации к изменению процентной
ставки у различных активов разная.
Краткосрочные активы имеют дюрацию
близкую к нулю. Среднесрочные более
чувствительны к изменению ставки
процента. Долгосрочные активы имеющие
высокую дюрацию и более чувствительны
к изменению доходности. Чувствительность
цены облигации к изменению процентной
ставки у различных активов разная.
Ценовой риск и
дюрация не равнозначны. По существу
ценовой риск это эластичность облигации.
Эластичность
— это проценты,
на которые возрастает текущая стоимость
облигации, если коэффициент дисконтирования
изменяется на 1%. При первичном размещении
выпуска облигаций ценовой риск и дюрация
близки. С течением “жизни” облигации
доходность выпуска отклоняется от
купонной ставки и ценовой риск и дюрация
расходятся в значениях.
Расчет дюрации.
Как было показано
выше, ценовой риск облигации при малых
значениях изменения процентной ставки
определяется дюрацией. Однако это не
единственный «ценовой» смысл дюрации.
Существует несколько определений
дюрациии, которые отражают способ ее
вычисления. Дюрация является средним
моментом, характеризующим структуру
потока платежа. Дюрация
средневзвешенный срок поступления
платежей в поток наличности (определения
Ф. Маколея). Весовым коэффициентом при
этом служат текущие стоимости этих
поступлений. Дюрация –
Существует
несколько определений «экономического»
смысла дюрации.
Дюрация
является средним моментом, характеризующим
структуру потока платежа.
Дюрация
— средневзвешенный срок поступления
платежей в поток наличности
это временная точка в будущем,
находясь в которой инвестор получит
половину своего первоначального вклада,
скорректированного с учетом временной
стоимости денег. Аналогом вышеприведенных
определений дюрации может служить
пример расчета центра тяжести невесомого
стрежня, на котором расположены на
одинаковом расстоянии равные по величине
грузики (купоны), за исключением
последнего (номинал). Положение центра
тяжести (дюрация) зависит от частоты
расположения этих грузиков (частота
выплаты купонов) от их величины (купон)
и груза в конце стрежня (номинал).
Пример
9.
Пусть имеется две облигации. Бескупонная
номиналом $1000 и сроком до погашения 3
года. Купонная облигация номиналом
$1000 и сроком погашения 4 года, купоном
10%. Доходность к погашению составляет
10%. Найти дюрацию облигаций.
Решение. Платежи
по облигациям распределены по времени
и величине, как показано ниже.
Рис. 3.7. Структура
потока платежей по бескупонной (а) и
купонной (б) облигациям.
По
формуле (3.23) найдем дюрацию бекупонной
облигации.
Стоимость облигации
равна
;.доля
;дюрация равна
.Дюрация бескупонной
облигации равна сроку до погашения,
т.е. 3 года.
Найдем дюрацию 4
– х летней купонной облигации.
Ниже приведен
расчет дюрации по формулам (3.23) в Excel.
|
Год t |
ежегодная выплата |
приведенная |
доля в общей |
доля в дюрации |
|
формулы |
|
|
|
|
|
1 |
100 |
89,29 |
0,095 |
0,095 |
|
2 |
100 |
79,72 |
0,085 |
0,170 |
|
3 |
100 |
71,18 |
0,076 |
0,227 |
|
4 |
1100 |
699,07 |
0,744 |
2,977 |
|
Приведенная |
939,25 |
1 |
|
Дюрацию можно
рассчитать для любого положительного
потока платежей при известной ставке
дисконтирования. Для расчета дюрации
в Excel
существует финансовая функция «ДЛИТ».
Пример10.
Вычислите дюрацию облигации, которая
продается по номиналу $1000. Срок до
погашения 6 лет, купон 7% с ежегодной
выплатой. Если доходность увеличится
до 8%, как изменится дюрация?
Решение. Рассчитаем
дюрацию, применяя финансовую функцию
«ДЛИТ» в Excel
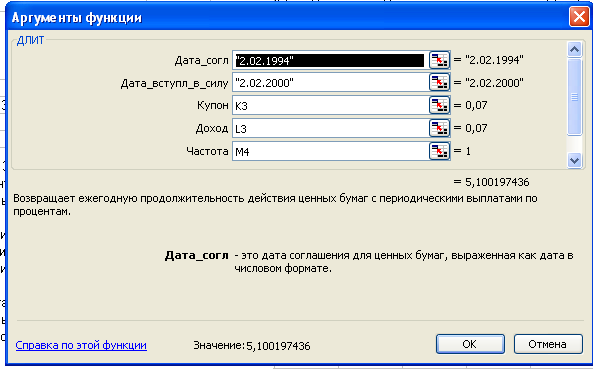
Рис. 3.7. Финансовая
функция «ДЛИТ».
Параметры функции
«ДЛИТ». Дата_согл – дата размещения
облигации. Обычно выражается в числовом
формате, дата преобразуется в числовой
формат с помощью функции ДАТА (см.гл.1).
Однако для решения задач, в которых не
важно точное количество дней, можно
воспользоваться форматом, показанном
на рисунке выше. Для получения правильного
результата важно, чтобы число лет между
Дата_согл
и Дата_вступл_в_силу
соответствовало сроку до погашения.
Дата_вступл_в_силу
– дата
погашения облигации.
Таблица
3. 3. Результаты расчета дюрации по
финансовой функции Excel.
-
FV
N
g
r
m
D
1000
6
0,07
0,07
1
5,10
0,08
1
5,08
Дюрация облигации
при 7% доходности равна 5,1. При 8% доходности
дюрация равна 5,08. С ростом доходности
дюрация уменьшается.
Для
дюрации можно получить аналитическое
выражение. Найдем первую производную
от стоимости
облигации по формуле (3.1)
—
. (3.24а)
Подставим в
выражение для дюрации (3.20).
.
Далее проведя
необходимые преобразования, получим
выражение для дюрации облигации с
числом купонных выплат N
(3.24)
Если облигация
бескупонная, то g
= 0, а отношение
=P,
следовательно, дюрация бескупонной
облигации равна сроку до погашения,
т.е. N.
Дюрация облигации,
приобретенной между выплатами купонных
платежей.
Пусть имеется
облигация с выплатой купонов два раза
в году. Если облигацию приобрели между
купонными выплатами, то надо учесть
время, прошедшее после последнего
платежа в этом случае дюрация
рассчитывается по формуле
, (3.25)
где f
– часть времени, прошедшая после
последнего купонного платежа, t
– количество полугодовых периодов
оставшихся до срока погашения облигации.
Например, если после выплаты последнего
купона прошло 3 месяца, то t
для такой облигации будут соответственно
равны 2/6 = 0,67; 1,67; 2,67 и т.д.,– полугодовая ставка доходности.
Факторы, влияющие
на дюрацию купонной облигации.
Рассмотрим факторы,
влияющие на дюрацию облигаций.
Зависимость
дюрации от величины купонной процентной
ставки.
Пусть доходность
до погашения составляет 7%. Сравним
дюрации облигаций с различными купонами
и одинаковыми сроками до погашения.
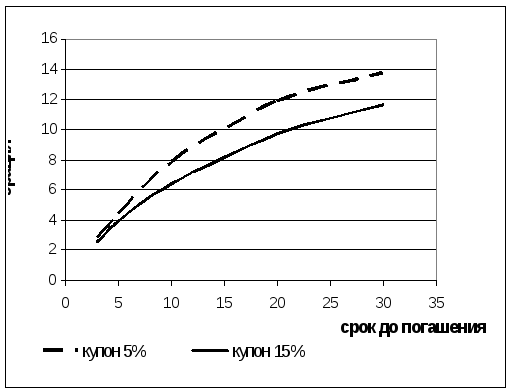
Таблица 3.4.
Зависимость дюрации купонной облигации
от купонной ставки.
|
срок до погашения |
купон 5% |
купон 15% |
|
|
3 |
2,817 |
2,57 |
|
|
5 |
4,457 |
3,88 |
|
|
10 |
7,798 |
6,39 |
|
|
20 |
11,87 |
9,66 |
|
|
30 |
13,73 |
11,67 |
Как видно из
расчетов и графика дюрация
и купонная процентная ставка обратно
пропорциональны.
При снижении купонной процентной
ставки, т.е. величины купонов дюрация
возрастает. Дюрация и купонная ставка
имеют отрицательную
корреляцию.
Высокая купонная ставка соответствует
более низкой дюрации. Облигации с более
высоким купоном дают большие поступления
в поток наличности до наступления срока
погашения. Доля номинала уменьшается.
Дисконтирование в меньшей степени
влияет на более ранние выплаты в поток
наличности, чем на отдаленные выплаты.
Зависимость
дюрации от доходности до погашения.
Сравним дюрации
облигаций с одинаковыми сроками до
погашения и различными купонными
процентными ставками.
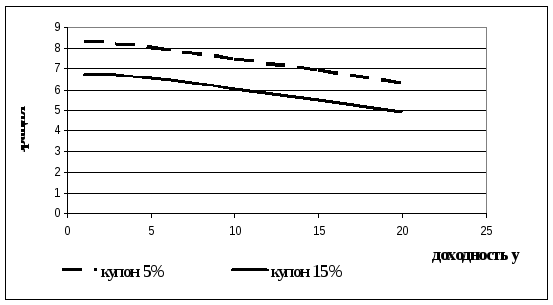
Таблица 3.5.
Зависимость дюрации от доходности.
|
Процентная |
купон 5% |
купон 15% |
|
|
1,00 |
8,33 |
6,72 |
|
|
5,0 |
7,99 |
6,61 |
|
|
10,0 |
7,49 |
6,05 |
|
|
15,0 |
6,93 |
5,48 |
|
|
20,0 |
6,32 |
4,93 |
Как видно из
расчетов и графика с ростом процентной
ставки дюрация обеих облигаций
уменьшается. Дюрация и доходность до
погашения обратно пропорциональны.
Зависимость
дюрации от времени оставшимся до
погашения облигации.
Существует
положительная
корреляция
между дюрацией и временем оставшимся
до погашения облигации. Для облигации
с нулевым купоном такая связь является
прямо пропорциональной. Такая зависимость
имеет две причины. Выплата номинала –
это самая большая доля в в общих
поступлениях от облигаций. Поступления
в поток наличности более растянутые
во времени увеличивают продолжительность.
Зависимость
дюрации от накопленных процентов.
Дюрация облигации
и величина накопленных процентов для
данной облигации
обратно пропорциональны.
В цене облигации учитываются выплаченные
(накопленные проценты). При вычислении
дюрации учитывается не котировочная,
а общая цена. Поэтому накопленные
проценты влияют на дюрацию. Накопленные
проценты — это инвестиции с нулевой
продолжительностью. Поэтому облигация
с большими накопленными процентами
имеет более низкую дюрацию, чем без
них. Выплата купона это уменьшение
срока до погашения. Так за день до
выплаты ежегодного купона дюрация 20 –
ти летней облигации с купоном в 7% и при
доходности в 10% равна 10 лет, а после
выплаты купона дюрация равна 9,84 года.
Купоны (проценты) являются денежной
инвестицией с нулевой продолжительностью,
чем больше их доля в общей цене, тем
меньше продолжительность.
Кроме рассмотренных
выше факторов на дюрацию облигации
влияют также отчисления в фонд погашения
(изменяется поток наличности), право
досрочного погашения, время, прошедшее
с момента эмиссии.
Можно выделить 7
основных факторов, влияющих на величину
дюрации:
-
срок до погашения;
-
купонная ставка;
-
накопленные
проценты; -
доходность до
погашения; -
отчисления в фонд
по гашения; -
право досрочного
погашения;
Модифицированная
дюрация.
Дюрация, рассчитанная
ранее по формуле (3.23), получила название
дюрацией Маколея. Для того чтобы в
полной мере дюрация могла бы быть
инструментом для измерения облигационного
риска она должна учитывать сложный
процент, т.е. должна учитывать дискретное
компаундирование.
(3.26)
Так, при 10% ставке
знаменатель в выражении (3.24) равен 1,10
для облигации с годовой выплатой
процентов, но для облигации с полугодовой
выплатой купонов знаменатель равен
1,05; 1,025 для облигации с квартальной
выплатой купонов. Только в случае
определения доходности облигации на
основе непрерывного компаундирования
никакой коррекции дюрации делать не
надо.
Модифицированная
дюрация равна
, (3.27)
где m
— частота начисления процента в год
(компаундирования), YTM
годовая доходность до погашения
облигации, выраженная в виде десятичной
дроби. Изменение цены облигации (3.22)
выраженное через модифицированную
дюрацию MD
имеет вид
(3.28)
Концепция
продолжительности была выведена для
облигаций без права досрочного отзыва.
Для облигаций с правом досрочного
отзыва (обычно это корпоративные
облигации) используется понятие
эффективной продолжительности.
Модифицированная
дюрация связана с ценовым риском
следующим соотношением
.
С увеличением
отклонения от уровня рыночной доходности
ошибка
в оценкерастет. При отклонении на 10 базисных
пунктов отошибок
практически нет, увеличение до 100
базисных пунктов ошибка составит
примерно 0,3 пункта. Прогнозируемая цена
облигации, рассчитанная на основе
дюрации равнане
выше реальной.
Если построить
график зависимости цены облигации от
доходности для купонной облигации и
провести касательную в точке,
соответствующей уровню рыночной
доходности
,
то наклон этой касательной является
линией модифицированной дюрации.
Модифицированная
дюрация учитывает сложный процент и
частоту выплаты купонов.
Модифицированная дюрация
является индикатором чувствительности
облигации к малым изменениям рыночной
процентной ставки. Модифицированная
дюрация является лучшей мерой рыночного
риска и по сравнению с такими индикаторами,
как срок до погашения и Маколеева
дюрация, поскольку учитывает сложный
процент (компаундирование).
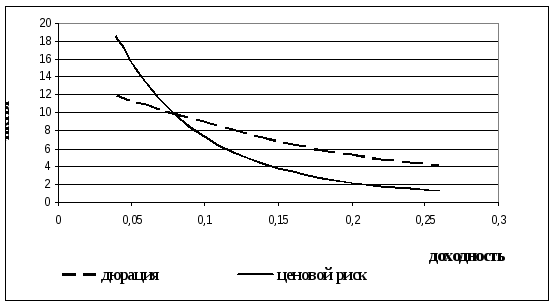
Рис. 3.8. Зависимость
модифицированной дюрации и ценового
риска (в пунктах) от доходности для 20
летней облигации с купоном в 8% и выплатой
купона два раза в год.
Значения
модифицированной дюрации и ценового
риска совпадают при доходности равной
купону.
Ограничения
применения концепции модифицированной
дюрации.
Применение
концепции модифицированной дюрации
справедливо при следующих условиях:
-
процентные ставки
изменяются мгновенно. Реально изменение
процентных ставок происходит медленно; -
при малых уровнях
изменения рыночной доходности не более
10 базисных пунктов; -
параллельное
изменение уровня рыночной доходности.
Процентные ставки
для разных временных периодов должны
изменятся на одну и ту же величину. Это
означает, что для всех облигаций с
разными сроками до погашения их
доходности изменились бы на одну и ту
же величину. Такое изменение более
сильно для краткосрочных облигаций,
чем для долгосрочных. Несмотря на
ограничения применения концепции
модифицированной дюрации, она является
одним из основных индикаторов рыночного
риска облигаций.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Добрый день. Подскажите пожалуйста, считая дюрацию по центробанку обратил внимание, что считая ее в ручную значения не сходятся, при этом использовав функцию МДЛИТ я вышел на искомые значения, сейчас у меня возникает вопрос , а как эта функция считает? вообще это как-то возможно узнать? как она оперирует с введеными аргументами? |
|
|
Sovereign Пользователь Сообщений: 155 |
Считает, как ДЛИТ делить на 1 + (доход/количество выплат за год) |
|
спасибо, ну да, я немного неверно сформулировал, тогда если копнуть глубже, как считается ДЛИТ(), есть определенные аргументы, дата начала, дата конца, база рассчета.и ставка и доходность, какие манипуляции с ними производит эксель при рассчете данной функции? |
|
|
1) в википедии формула совпадает с формулой используемой центробанком, на нее и опирался. |
|
|
к сожалению эта формула тоже содержит ДЛИТ() и не демострирует нам как оперирует с переменными. п.с. вообще формулы вшитые в функции являются секретом микрософта? |
|
|
R Dmitry Пользователь Сообщений: 3103 Excel,MSSQL,Oracle,Qlik |
#9 01.11.2011 13:02:17 {quote}{login=}{date=01.11.2011 10:20}{thema=Re: }{post}{quote}…вообще формулы вшитые в функции являются секретом микрософта?{/post}{/quote}
|
|
|
Serge Пользователь Сообщений: 11308 |
{quote}{login=}{date=01.11.2011 10:20}{thema=Re: }{post}формулы вшитые в функции являются секретом микрософта?{/post}{/quote}Нет конечно. Не Microsoft же их придумала http://otc.rbc.ru/bond_calc/help.jsp#f п.3.g http://birzhevik.net/forum/index.php?showtopic=5736 сразу под «Дюрация Маколея» |
|
мне ваши ответы понятны, но вопрос возник не на пустом месте, в том то и дело, что при рассчете по формулам, и при рассчете функцией длит получаются разные данные, да собственно и в рассчете данные разные используются. спасибо за ссылки) |
|
|
Узбек Гость |
#12 12.05.2012 13:13:05 Это ведь не сложно. Напишите мне на почту umid-13@mail.ru. Объясню |