17 авг. 2022 г.
читать 2 мин
Среднее абсолютное отклонение — это способ измерения дисперсии для набора значений данных.
Низкое значение среднего абсолютного отклонения указывает на то, что значения данных сконцентрированы близко друг к другу. Высокое значение среднего абсолютного отклонения указывает на то, что значения данных более разбросаны.
Формула для расчета среднего абсолютного отклонения выглядит следующим образом:
Среднее абсолютное отклонение = (Σ |x i – x |) / n
- Σ — просто причудливый символ, означающий «сумма»
- x i – i -е значение данных
- х – среднее значение
- n – размер выборки
Как рассчитать среднее абсолютное отклонение в Excel
Чтобы вычислить среднее абсолютное отклонение в Excel, мы можем выполнить следующие шаги:
Шаг 1: Введите данные.В этом примере мы введем 15 значений данных в ячейки A2: A16.
Шаг 2: Найдите среднее значение.В ячейке D1 введите следующую формулу: =СРЗНАЧ(A2:A16).Это вычисляет среднее значение для значений данных, которое оказывается равным 15,8 .
Шаг 3: Рассчитайте абсолютные отклонения. В ячейке B2 введите следующую формулу: =ABS(A2-$D$1).Это вычисляет абсолютное отклонение значения в ячейке A2 от среднего значения в наборе данных.
Затем щелкните ячейку B2. Затем наведите указатель мыши на правый нижний угол ячейки, пока не появится черный знак +.Дважды щелкните знак + , чтобы заполнить оставшиеся значения в столбце B.
Шаг 4: Рассчитайте среднее абсолютное отклонение.В ячейке B17 введите следующую формулу: =СРЗНАЧ(B2:B16).Это вычисляет среднее абсолютное отклонение для значений данных, которое оказывается равным 6,1866 .
Обратите внимание, что эти четыре шага можно использовать для вычисления среднего абсолютного отклонения для любого количества значений данных. В этом примере мы использовали 15 значений данных, но вы можете использовать эти точные шаги для вычисления среднего абсолютного отклонения для 5 значений данных или 5000 значений данных.
Другим распространенным способом измерения точности прогнозирования модели является MAPE — средняя абсолютная ошибка в процентах. О том, как посчитать MAPE в Excel, читайте здесь .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Содержание
- Как в офисе.
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Как рассчитать абсолютное отклонение в excel
- Как посчитать в Excel отклонение в процентах
- Простой расчёт отклонения
- Отклонение в процентах при отрицательных величинах
- Как не считать отклонение в процентах при отрицательных входных параметрах
- Как в офисе.
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Как легко рассчитать среднее абсолютное отклонение в Excel
- Как рассчитать среднее абсолютное отклонение в Excel
Как в офисе.
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Урок: Формула среднего квадратичного отклонения в Excel
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
Урок: Как посчитать среднее значение в Excel
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Источник
Как рассчитать абсолютное отклонение в excel
Как посчитать в Excel отклонение в процентах
Привет. Сегодняшняя статья – не совсем про Excel, но у меня так часто просят совета по этой теме, что я сдался. Поэтому, рассказываю, как в Экселе посчитать изменение в процентах. Не смотря на видимую простоту темы, здесь есть подводные камни, о которых расскажу.
Простой расчёт отклонения
Главное, что нужно знать – формула расчета такая:
Когда вы считаете это в Экселе, программа сама умножает число на 100%, когда для ячейки задан процентный формат. Вам умножать не нужно. Так, например, в Excel можно вычислить изменение прибыли от реализации товаров:
Это действительно просто и эффективно, пока в расчетах не появляются отрицательные составляющие.
Отклонение в процентах при отрицательных величинах
Что будет с изменением прибыли, если какие-то товары имеют отрицательное старое значение? Пусть в нашем примере в январе мы продавали в убыток и прибыль была негативной. А ведь это не такой уж и редкий случай!
Фактически, прибыль выросла, а по расчётам – нет. Исправим формулу, нужно знаменатель взять по модулю (отбросить знак минус). Это распространенный подход, многие его используют. Применим функцию ABS, которая возвращает модуль числа:
Проблема исправлена, этими результатами можно пользоваться. Однако, хочу вас предостеречь. Результаты могут быть недостаточно корректными. Взгляните на картинку еще раз. Прибыль от смартфонов выросла на 60 тысяч, и это 597%. А прибыль от телевизоров – на 110 тысяч, и это лишь 183%. Я использую такие результаты лишь для поверхностной оценки. Или можно не выводить отклонение для таких случаев.
Как не считать отклонение в процентах при отрицательных входных параметрах
Возможное решение описанной выше проблемы – отказаться от расчёта, когда попадаются негативные значения. Сделаем это с помощью функции ЕСЛИ:
Как в офисе.
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Урок: Формула среднего квадратичного отклонения в Excel
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
Урок: Как посчитать среднее значение в Excel
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Источник
Как легко рассчитать среднее абсолютное отклонение в Excel
Среднее абсолютное отклонение — это способ измерения дисперсии для набора значений данных.
Низкое значение среднего абсолютного отклонения указывает на то, что значения данных сконцентрированы близко друг к другу. Высокое значение среднего абсолютного отклонения указывает на то, что значения данных более разбросаны.
Формула для расчета среднего абсолютного отклонения выглядит следующим образом:
Среднее абсолютное отклонение = (Σ |x i – x |) / n
- Σ — просто причудливый символ, означающий «сумма»
- x i – i -е значение данных
- х – среднее значение
- n – размер выборки
Как рассчитать среднее абсолютное отклонение в Excel
Чтобы вычислить среднее абсолютное отклонение в Excel, мы можем выполнить следующие шаги:
Шаг 1: Введите данные.В этом примере мы введем 15 значений данных в ячейки A2: A16.
Шаг 2: Найдите среднее значение.В ячейке D1 введите следующую формулу: =СРЗНАЧ(A2:A16).Это вычисляет среднее значение для значений данных, которое оказывается равным 15,8 .
Шаг 3: Рассчитайте абсолютные отклонения. В ячейке B2 введите следующую формулу: =ABS(A2-$D$1).Это вычисляет абсолютное отклонение значения в ячейке A2 от среднего значения в наборе данных.
Затем щелкните ячейку B2. Затем наведите указатель мыши на правый нижний угол ячейки, пока не появится черный знак +.Дважды щелкните знак + , чтобы заполнить оставшиеся значения в столбце B.
Шаг 4: Рассчитайте среднее абсолютное отклонение.В ячейке B17 введите следующую формулу: =СРЗНАЧ(B2:B16).Это вычисляет среднее абсолютное отклонение для значений данных, которое оказывается равным 6,1866 .
Обратите внимание, что эти четыре шага можно использовать для вычисления среднего абсолютного отклонения для любого количества значений данных. В этом примере мы использовали 15 значений данных, но вы можете использовать эти точные шаги для вычисления среднего абсолютного отклонения для 5 значений данных или 5000 значений данных.
Другим распространенным способом измерения точности прогнозирования модели является MAPE — средняя абсолютная ошибка в процентах. О том, как посчитать MAPE в Excel, читайте здесь .
Источник
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Содержание
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
- Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
- Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
- В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.
Урок: Формула среднего квадратичного отклонения в Excel
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
- В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
- Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
- Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.
Урок: Как посчитать среднее значение в Excel
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
- Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
- Как видим, результат расчета выведен на экран.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
- После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
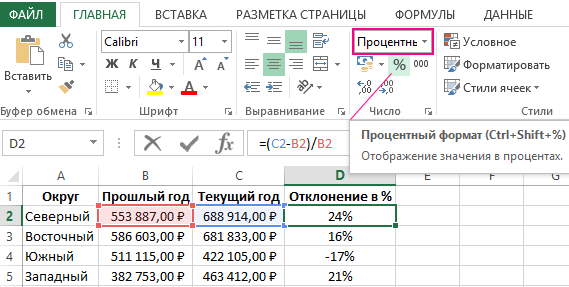
Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
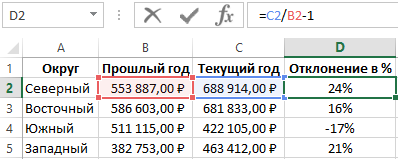
Альтернативная формула для вычисления процента отклонения в Excel
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
0
1 ответ:
4
0
Отклонение, это различие, разница между значениями.
Абсолютное отклонение вычислить очень просто, для этого понадобиться лишь вычесть одно значение из другого.
Если на примере, то выглядит это так:
В прошлом году налоги предприятия составили 100 000, а в этом году 120 000.
Абсолютное отклонения в этом случае будет 20 000, так как 120 000 — 100 000 = 20 000.
Что касается вычисления абсолютного отклонения в таблице Эксель, то для вычисления жмём клавишу «равно», затем левой кнопкой мышки на ячейку с одним значением, затем знак «минус» и снова левой кнопкой на второе значение во второй ячейке.
=F1-F2
Читайте также
Обратим внимание на то, что в качестве аргументов функции Найти используется диапазон ячеек, это даст ошибку #ЗНАЧ — неверное значение, следовательно это формула массива (ввод завершается CTRL+SHIFT+ENTER), в этом случае результатом будет массив значений, каждое значение будет соответствовать одной ячейке диапазона.
функция Левсимв находит для текста каждой ячейки, дополненного пробелом, символы от начала строки до пробела, получая массив текстовых значений.
Функция СУММ обрабатывает только числа, а текстовые значения из цифр вызовут ошибку.
(Пример: Результат выполнения формулы =СУММ( {«1»; «2»; «3»}) равен 0)
Знак минус не только меняет знак числа, начинающегося с цифры, но и выполняет преобразование текстовых цифр в число, а другой минус меняет отрицательное значение числа на противоположное.
двойной минус выполняет преобразование текстового значения в цифровое
(Пример: Результат выполнения формулы =СУММ( —{«1»; «2»; «3»}) равен 6)
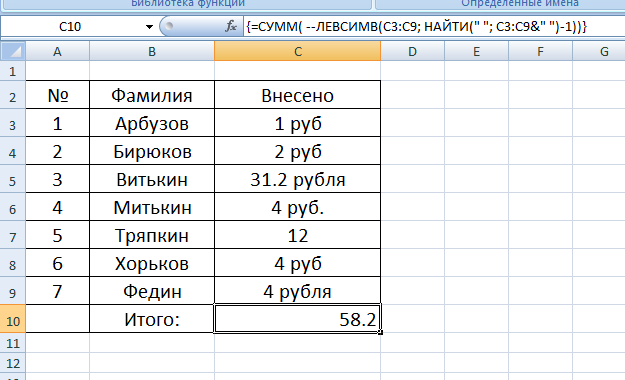
Формула
=СУММ( —ЛЕВСИМВ( C3:C9; НАЙТИ(» «; C3:C9&» «)-1))
суммирует написанные в ячейках цифры, даже если после цифры идет текст (пример: «10 руб.»), или формат ячейки текстовый.
Пример работы формулы:
Эту формулу можно было записать и так:
=СУММ( ЗНАЧЕН(ЛЕВСИМВ( C3:C9; НАЙТИ(» «; C3:C9&» «)-1)))
Ответ: приведенная формула является формулой массива (ввод завершается комбинацией клавиш CTRL+SHIFT+ENTER) и служит для суммирования чисел записанных в виде текста.
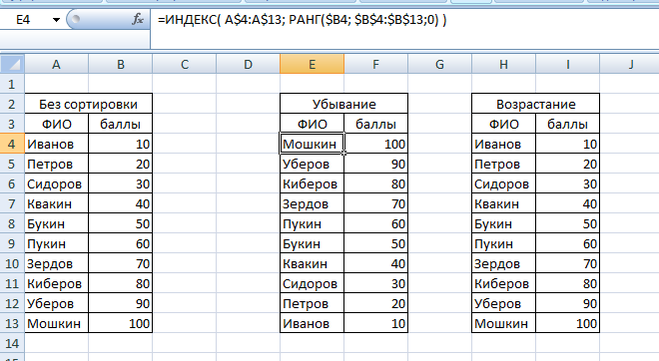
Сортировка формулами позволяет расположить на одном листе и таблицы, отсортированные по возрастанию и таблицы отсортированные, по убыванию рядом с исходной таблицей.
Алгоритм формулы:
- Составляем формулу для столбца по которому проходит сортировка (функции НАИБОЛЬШИЙ/НАИМЕНЬШИ<wbr />Й)
- Для каждой ячейки другого столбца находим соответствующие значение (функция ИНДЕКС)
Для сортировки столбца по которому проходит сортировка можно воспользоваться функцией РАНГ)
если данные находятся в диапазоне B4:B13
то номер ячейки в сортированной по убыванию таблице определим формулой:
=РАНГ( $B4 ; $B$4:$B$13 ; 0)
номер ячейки в сортированной по возрастанию таблице определим формулой:
=РАНГ( $B4 ; $B$4:$B$13 ; 1)
и затем растягиваем эту формулу на весь столбец
Формула сортировки по убыванию для ячейки B4 выглядит так:
=ИНДЕКС( A$4:A$13 ; РАНГ($B4; $B$4:$B$13 ;0) )
Формула сортировки по возрастанию для ячейки B4 выглядит так:
=ИНДЕКС( A$4:A$13 ; РАНГ($B4; $B$4:$B$13 ;1) )
Эта формула растягивается на весь диапазон таблицы.
Пример работы формулы:
- A$4:A$13 отображаемый столбец исходной таблицы
- $B4 текущая ячейка столбца, по которому проходит сортировка
- $B$4:$B$13 столбец, по которому проходит сортировка
Чтобы было понятно, проведём небольшую тренировку. Напишите в какой-либо ячейке формулу, например такую =(A1-C1)/B1. Теперь «встаньте в эту ячейку», нажмите клавишу F2 (включается режим редактирования формул непосредственно в ячейке). В ячейке появится формула и курсор (в виде палочки). Переместите курсор по ячейке так, чтобы он находился либо рядом с тем адресом, которым Вы хотите управлять (в данном случае B1), либо непосредственно внутри адреса, т.е. либо так =(A1-C1)/|B1, либо так (A1-C1)/B1|, либо так (A1-C1)/B|1.
Нажмите клавишу F4. Формула примет вид =(A1-C1)/$B$1.
Нажмите клавишу F4 ещё раз. Формула примет вид =(A1-C1)/B$1.
Нажмите клавишу F4 ещё раз. Формула примет вид =(A1-C1)/$B1.
Нажмите клавишу F4 ещё раз. Формула примет первоначальный вид =(A1-C1)/B1.
Нажмите клавишу F4 ещё раз. Формула примет вид =(A1-C1)/$B$1. И так далее по кругу.
Итак, имеется 4 представления адреса B1, $B$1, B$1, $B1. Значок доллара $ означает, что следующий за ним элемент адреса при копировании формулы не будет изменяться.
Если в формуле записано B1, то при копировании формулы могут изменяться и название столбца и номер строки.
Если записано $B$1, то при копировании формулы не будут изменяться ни название столбца ни номер строки.
Если записано B$1 то при копировании формулы название столбца будет изменяться, а номер строки изменяться не будет.
Если записано $B1 то при копировании формулы номер строки будет изменяться, а название столбца изменяться не будет.
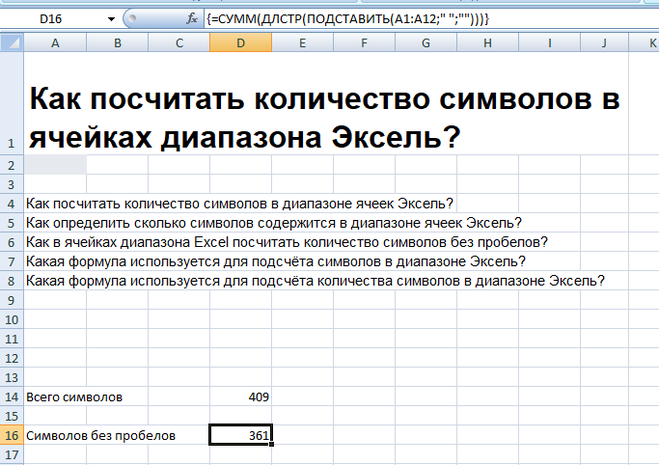
В Excel, чтобы определить количество символов в определённом диапазоне ячеек, придётся использовать формулу массива (вводится через CTRL+SHIFT+ENTER<wbr />).
Для диапазона ячеек A1:A12 формулы массива имеют вид:
найти количество символов: =СУММ(ДЛСТР( A1:A12 ))
найти количество символов без пробелов: =СУММ(ДЛСТР( ПОДСТАВИТЬ( A1:A12; » «; «»)))
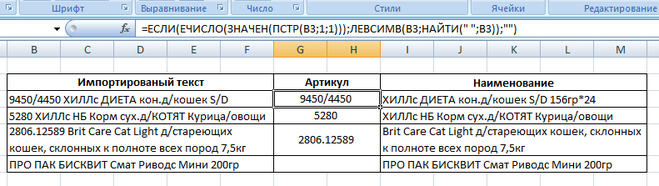
Допустим, что исходный текст записан в ячейке B3
Сначала надо проверить есть ли в начале текста артикул или условное цифровое обозначение, номер или код.
если текст начинается с цифры, то артикул есть
Формула для проверки (если есть артикул то результат ИСТИНА):
=ЕЧИСЛО( ЗНАЧЕН( ПСТР(B3;1;1) ))
Формула для столбца с цифрами:
=ЕСЛИ( ЕЧИСЛО( ЗНАЧЕН( ПСТР(B3;1;1) )) ; ЛЕВСИМВ( B3; НАЙТИ(» «; B3)) ; «»)
Формула для столбца с наименованием товара:
=ЕСЛИ( ЕЧИСЛО( ЗНАЧЕН( ПСТР( B3;1;1) )) ; ПРАВСИМВ( B3 ; ДЛСТР(B3)-НАЙТИ( » «;B3)) ; B3)
После копирования этих формул в свою таблицу надо заменить ячейку B3 на ту, в которой содержится текст, а потом растянуть на весь диапазон значений.