Как определить вид функций для excel

Содержание

  1. Как по графику определить функцию в excel
  2. Часть 10. Подбор формул по графику. Линия тренда
  3. Найти функцию по ее графику (аппроксимация)
  4. Решение
  5. Анализ функций, заданных таблично, с помощью EXCEL

Как по графику определить функцию в excel

Часть 10. Подбор формул по графику. Линия тренда

Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.

Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .

В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.

Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.

Excel предоставляет 5 видов аппроксимирующих функций:

1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.

2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.

3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.

4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.

5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.

Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).

В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:

Реклама (тыс. руб.) 1,5 2,5 3,5 4,5 5,5
Продажи (тыс. руб.)

Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.

Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.

Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):

В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.

После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).

После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.

Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.

В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.

Часть11. Контрольные задания

Найти функцию по ее графику (аппроксимация)

Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.

Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.

Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).

Помощь в написании контрольных, курсовых и дипломных работ здесь.

расчет.xlsx (15.9 Кб, 22 просмотров)

Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.

Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.

Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.

найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.

расчет (1).xlsx (16.1 Кб, 55 просмотров)

Сообщение было отмечено p1111 как решение

Решение

Как, оказывается, было просто.

Спасибо огромное, очень выручили.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.

Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.

Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.

Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.

Источник

Анализ функций, заданных таблично, с помощью EXCEL

Электронные таблицы EXCEL можно использовать при изучении многих разделов физики, математики и других предметов. Одной из данных тем является математическая тема: “Анализ элементарных функций”. Данная работа посвящена использованию электронных таблиц EXCEL в анализе элементарных функций.

На рис.1 представлена некоторая функция, заданная с помощью таблицы, построение которой приведено в Приложении 1.

Особенность анализа функций с помощью электронных таблиц заключается в том, что анализ проводится на дискретной информации. Действительно, количество значений исследуемой функции конечно и дано (как правило) с некоторым постоянным шагом по аргументу.

При анализе исходной функции необходимо решить следующие задачи:

  1. определение максимума (минимума) данной функции на заданном интервале,
  2. определение возрастания и/или убывания функции на заданном интервале,
  3. определение четности заданной функции,
  4. определение периодичности заданной функции,
  5. определение значения первой производной данной функции и наличия экстремумов.

Для решения этих задач потребуется построить таблицы ВводаИсходнойИнформации, таблицы ВыводаРезультатов, Расчетной таблицы для обработки информации и дополнительно построим Вспомогательную таблицу. Таблицу ВводаИсходнойИнформации и основу Расчетной таблицу построены при введении значений исследуемой функции в Приложении 1 и показанной на рис.1. Построим решения задач анализа.

Задача 1.
Для заданной функции на заданном интервале аргумента определить ее минимальное и максимальное значения.

Решение.
Для решения этой задачи построим таблицу ВыводаРезультатов в виде

D E
1 комментарии Значения
2 Макс f(X)
3 Мин f(X)

В мастере функций Excel имеются функции МАКС(…) и МИН(…), позволяющие решить нашу задачу. Для этого необходимо в ячейки Е2 и Е3 ввести соответственно формулы:

Примечание. Если “протяжка” велась до другой строки, то в интервале ссылок указать соответствующий номер строки.

Задача 2.
Определение возрастания и/или убывания функции на заданном интервале.

Решение.
Для решения данной задачи в расчетной таблице необходимо построить столбец D, в котором знак будет указывать на возрастание или убывание функции в данной точке. Для этого в ячейку D11 введем формулу

И там, где знак положительный, функция возрастает, а там, где знак отрицательный, функция – убывает.

Далее построим вспомогательную таблицу, в которой определим количество признаков возрастания и убывания функции

F G
1 КОММЕНТАРИИ ЗНАЧЕНИЯ
2 Признак возрастания
3 Признак убывания

Для этого в ячейки g2 и g3 соответственно вводим формулы:

G2 => [=СуммЕсли(d11:d50;”>0”)]
G3 => [=СуммЕсли(d11:d50;”

И для определения характера изменения заданной функции остается ввести в ячейку Е4 формулу:

E4 => [=ЕСЛИ(g2>0; ЕСЛИ(g3 [=f(b10) – f(-b10)]
и “протянуть” ее до строки №50.

Таблицу ВыводаРезультатов дополним строкой

D E
1 комментарии значения
2 Макс f(X) =МАКС(с10:с50)
3 Мин f(X) =МИН(с10:с50)
4 Возрастание/Убывание [=ЕСЛИ(g2>0; ЕСЛИ(g3

В ячейку Е4 таблицы ВыводаРезультатов вводим формулу.

Для данной задачи добавим в таблице ВводаИсходнойИнформации строку №6, в которой введем численное значение предполагаемого периода.

А В
1 КОММЕНТАРИИ ЗНАЧЕНИЯ
2 Xn
3 Xk
4 Shag
5 N
6 период

В ячейку В6 вводится число – предполагаемый период заданной функции.

Далее для решения данной задачи построим дополнительный столбец в расчетной таблице, для этого в ячейку F11 введем формулу

и “потягиваем” эту формулу до строки №50.

В таблице ВыводаРезультатов добавим строчку.

D E
1 комментарии значения
2 Макс f(X) =МАКС(с10:с50)
3 Мин f(X) =МИН(с10:с50)
4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3

В ячейке Е5 необходимо ввести формулу

и “протягиваем ее до строки с №50.

В результате получаем разностные приближенные значения первой производной заданной функции в заданных точках.

Для решения второй части задачи, то есть определения наличия и количества экстремумов на заданной функции в таблицу ВыводаРезультатов дополнить строкой.

Источник

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции ТИП в Microsoft Excel.

Описание

Возвращает тип значения. Функция ТИП используется, когда результаты вычисления другой функции зависят от типа значения в конкретной ячейке.

Синтаксис

ТИП(значение)

Аргументы функции ТИП описаны ниже.

  • Значение    Обязательный. Любое значение Microsoft Excel, например число, текст, логическое значение и т. д.

Тип значения

Функция ТИП возвращает

Число

1

Текст

2

Логическое значение

4

Значение ошибки

16

Массив

64

Составные данные

128

Замечания

  • Функция ТИП особенно удобна, когда используются такие функции, как АРГУМЕНТ и ВВОД, которые допускают данные различных типов. Функция ТИП позволяет выяснить, какой тип данных был возвращен функцией.

  • С помощью функции ТИП нельзя определить, содержится ли в ячейке формула. Эта функция только определяет тип результирующего (отображаемого) значения. Если аргумент «значение» является ссылкой на ячейку, содержащую формулу, функция ТИП возвращает тип результата вычисления формулы.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные

Климов

Формула

Описание

Результат

=ТИП(A2)

Возвращает тип значения в ячейке A2. Текстовый тип обозначается цифрой 2.

2

=ТИП(«г-н «&A2)

Возвращает тип значения «г-н Климов», которое является текстовым.

2

=ТИП(2+A2)

Возвращает тип формулы в C6, которая возвращает 16, тип сообщения об ошибке #VALUE! Сообщение об ошибке #ЗНАЧ! отображено в ячейке C7.

16

=(2+A2)

Значение ошибки, возвращаемое формулой =(2+A2), которая используется в ячейке C2.

#ЗНАЧ!

=ТИП({1;2:3;4})

Возвращает тип массива констант — 64.

64

Нужна дополнительная помощь?

Источник

Метод аппроксимации в Microsoft Excel

Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.

Выполнение аппроксимации

Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.

Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.

Но она может быть построена с применением одного из пяти видов аппроксимации:

  • Линейной;
  • Экспоненциальной;
  • Логарифмической;
  • Полиномиальной;
  • Степенной.

Рассмотрим каждый из вариантов более подробно в отдельности.

Способ 1: линейное сглаживание

Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.

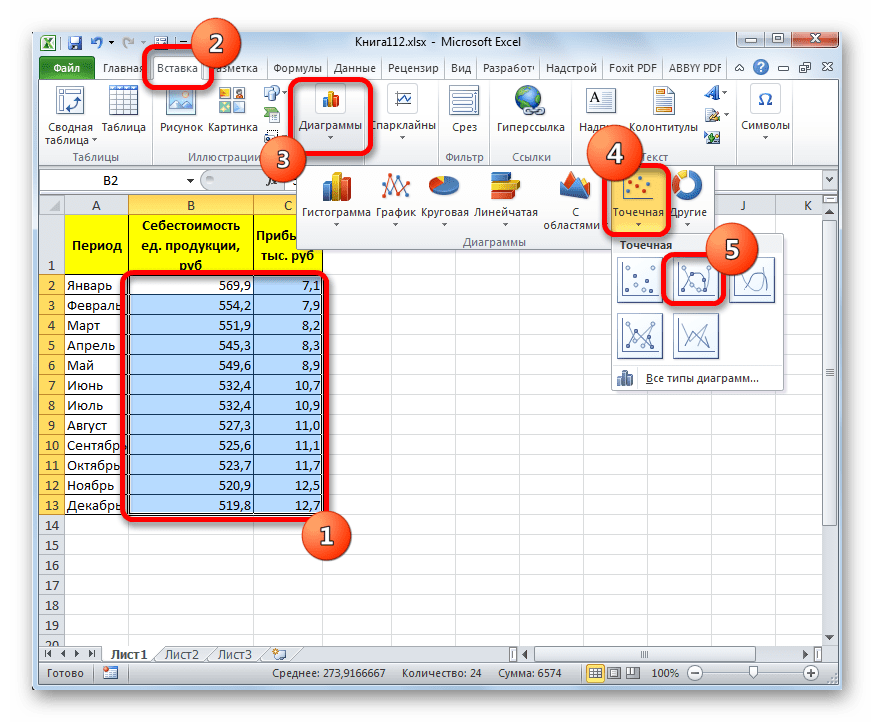
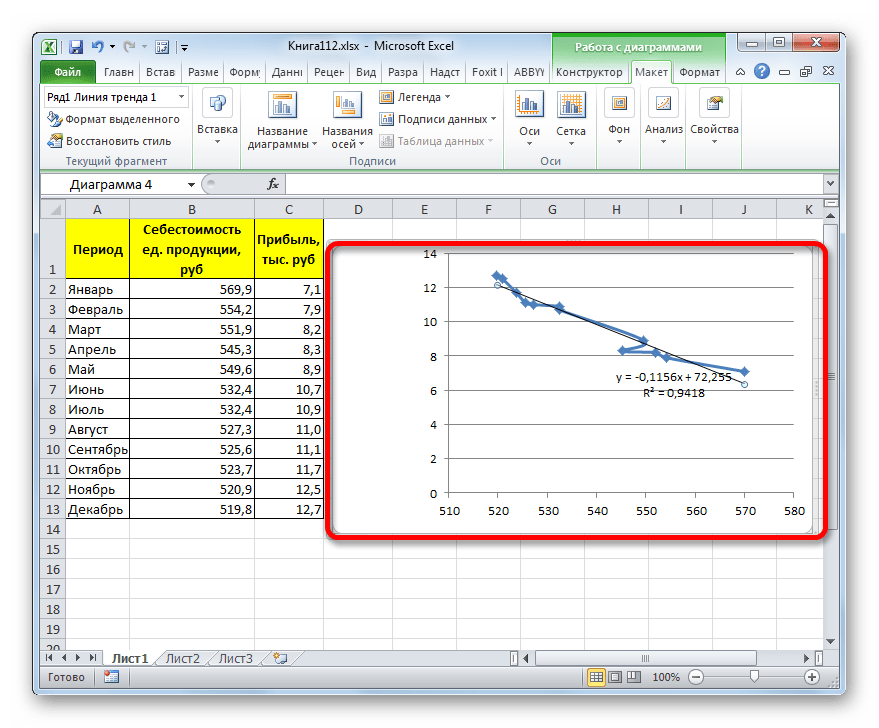
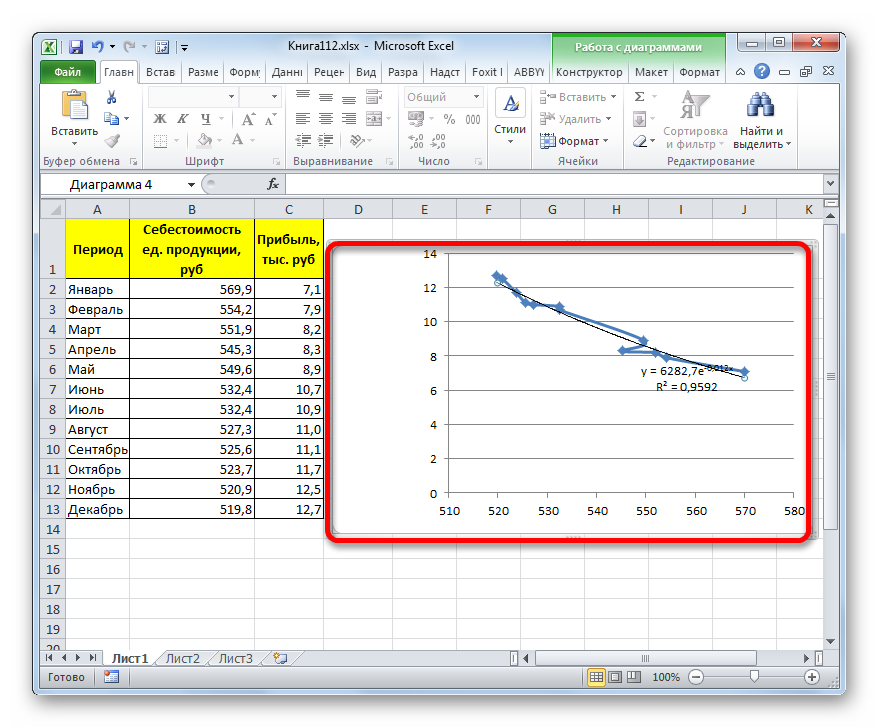
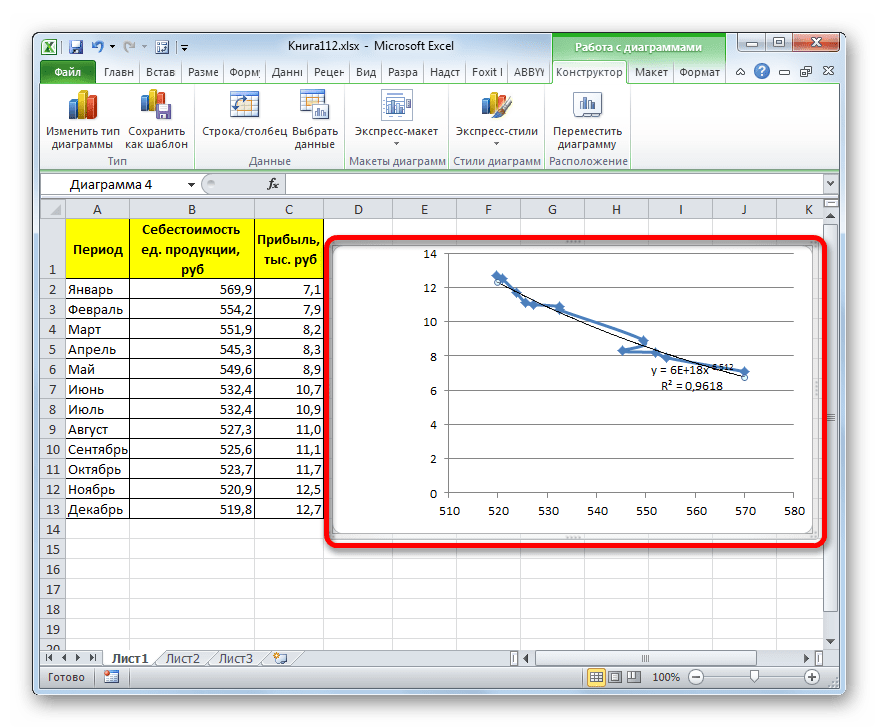
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.

    Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.

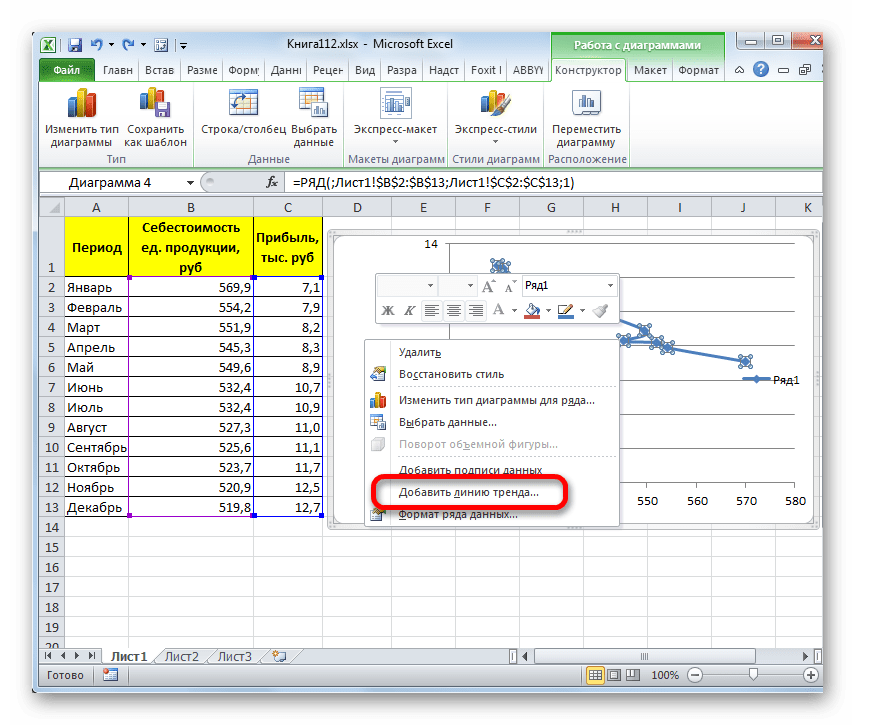
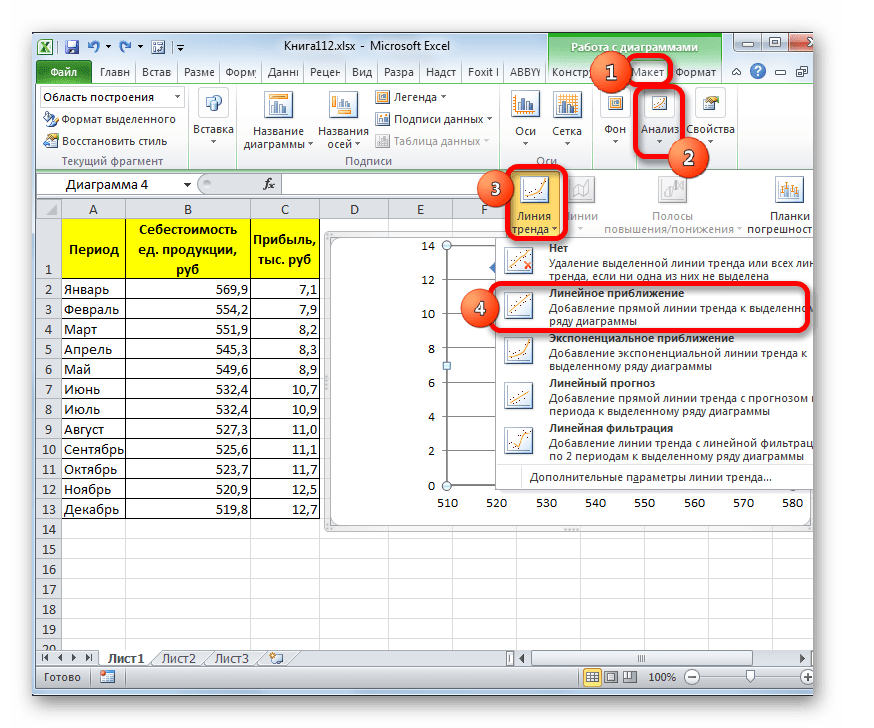
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».

Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.

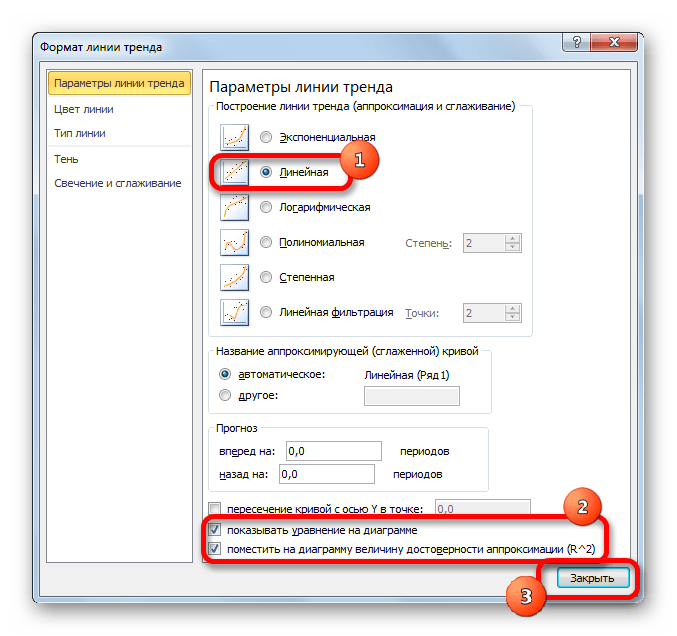
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.

Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.

После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.

  • Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.

    • Сглаживание, которое используется в данном случае, описывается следующей формулой:

    В конкретно нашем случае формула принимает такой вид:

    Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.

    Способ 2: экспоненциальная аппроксимация

    Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.

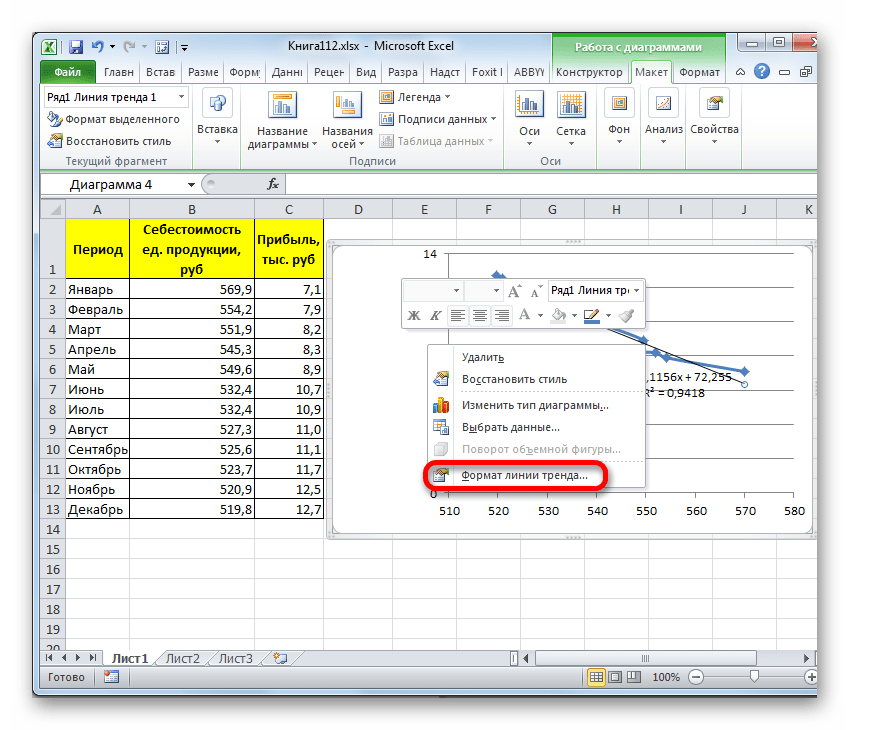
      Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».

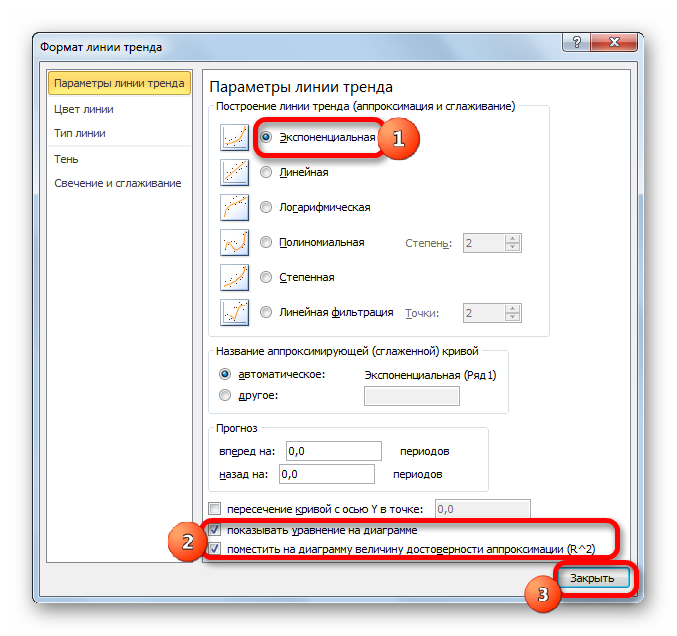
    После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».

    Общий вид функции сглаживания при этом такой:

    где e – это основание натурального логарифма.

    В конкретно нашем случае формула приняла следующую форму:

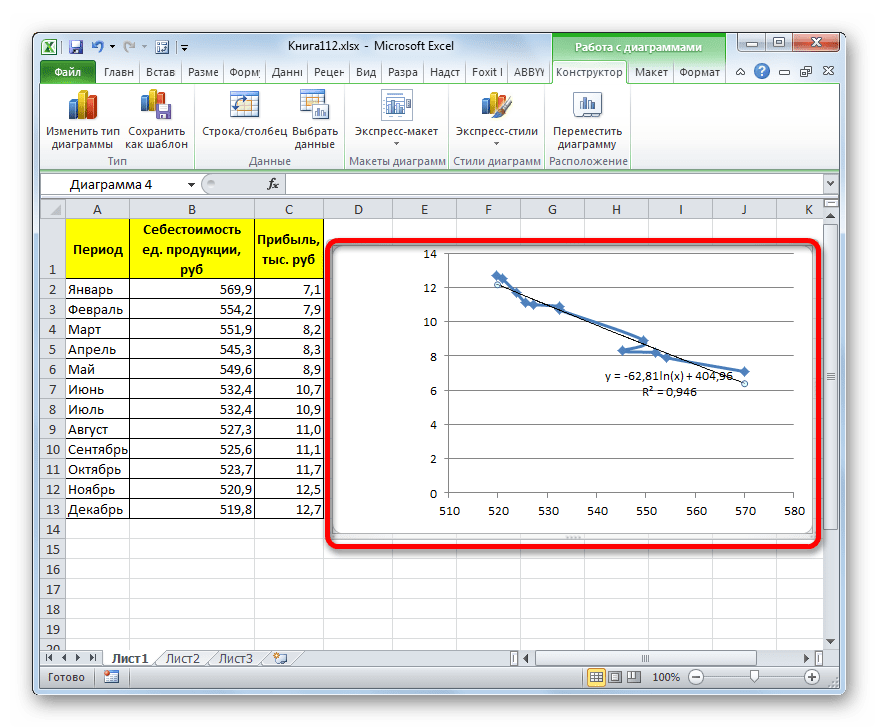
    Способ 3: логарифмическое сглаживание

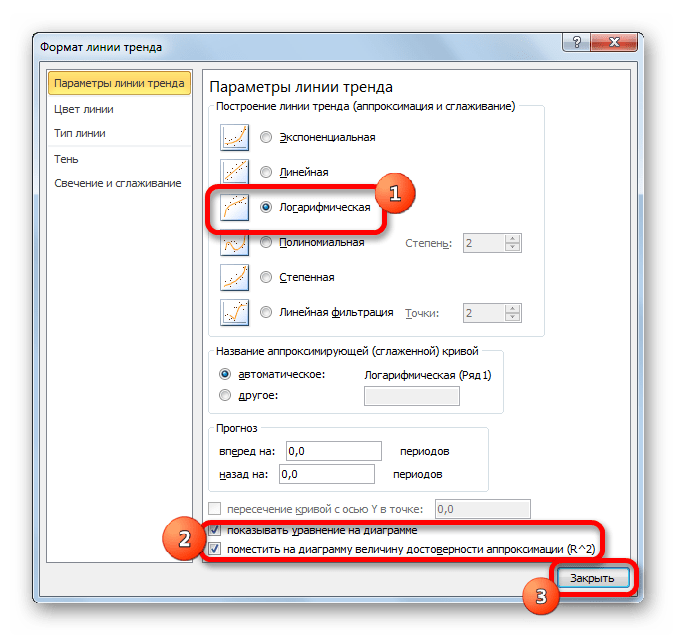
    Теперь настала очередь рассмотреть метод логарифмической аппроксимации.

      Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».

  • Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.

    • В общем виде формула сглаживания выглядит так:

    где ln – это величина натурального логарифма. Отсюда и наименование метода.

    В нашем случае формула принимает следующий вид:

    Способ 4: полиномиальное сглаживание

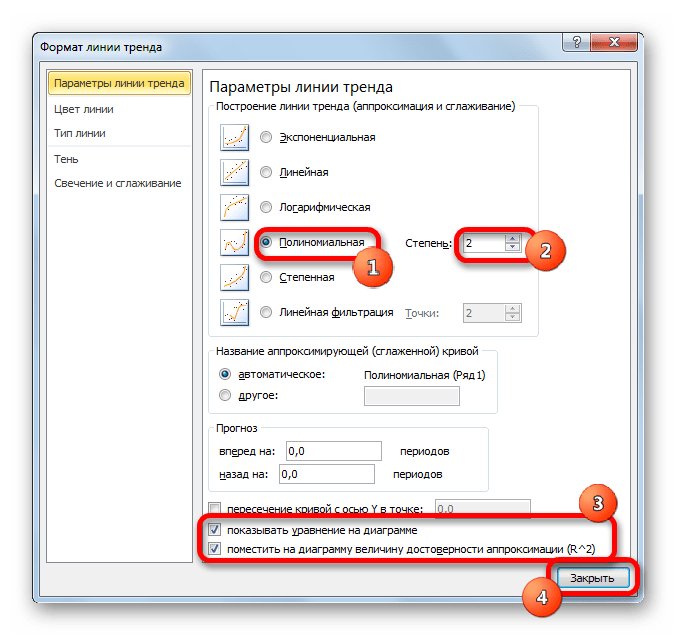
    Настал черед рассмотреть метод полиномиального сглаживания.

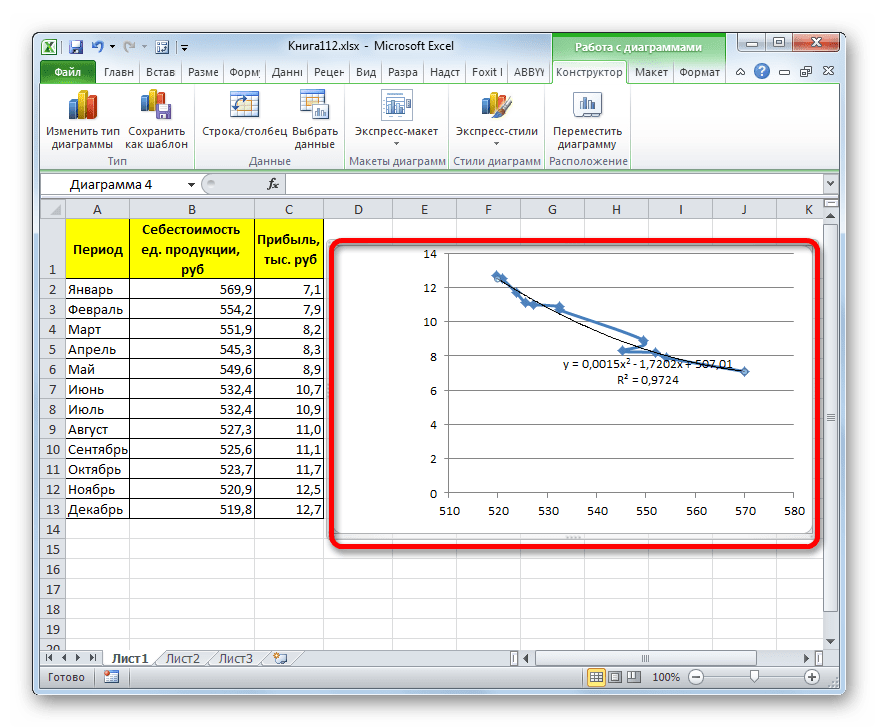
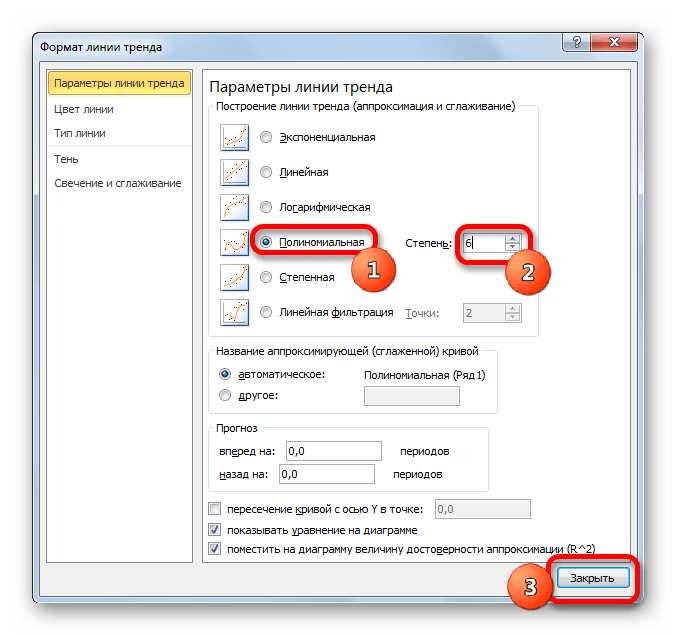
      Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».

    Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.

    Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:

    В нашем случае формула приняла такой вид:

    y=0,0015*x^2-1,7202*x+507,01
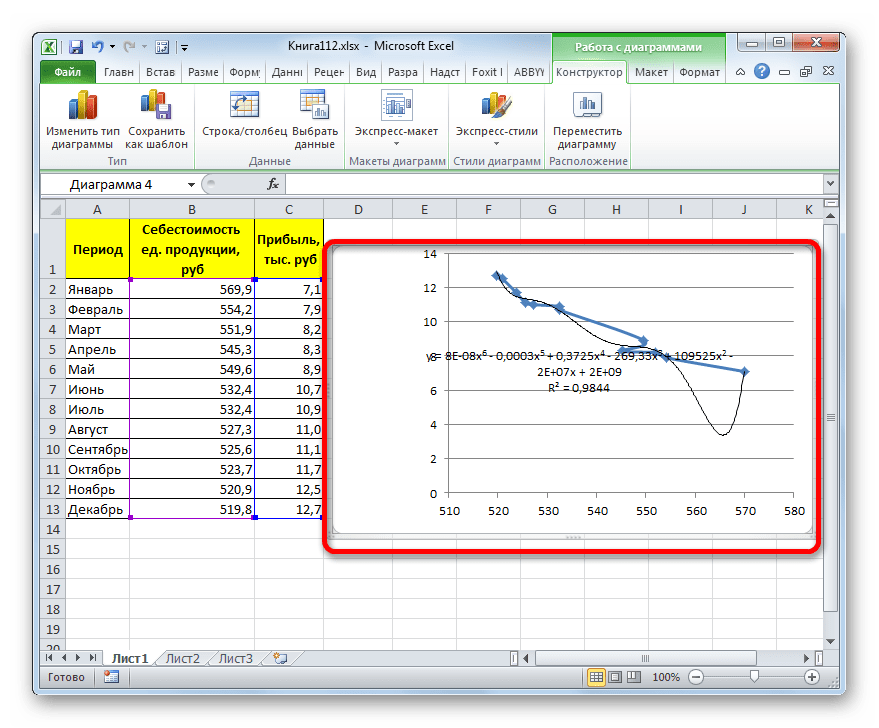
    Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.

  • Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.

    • Формула, которая описывает данный тип сглаживания, приняла следующий вид:

    Способ 5: степенное сглаживание

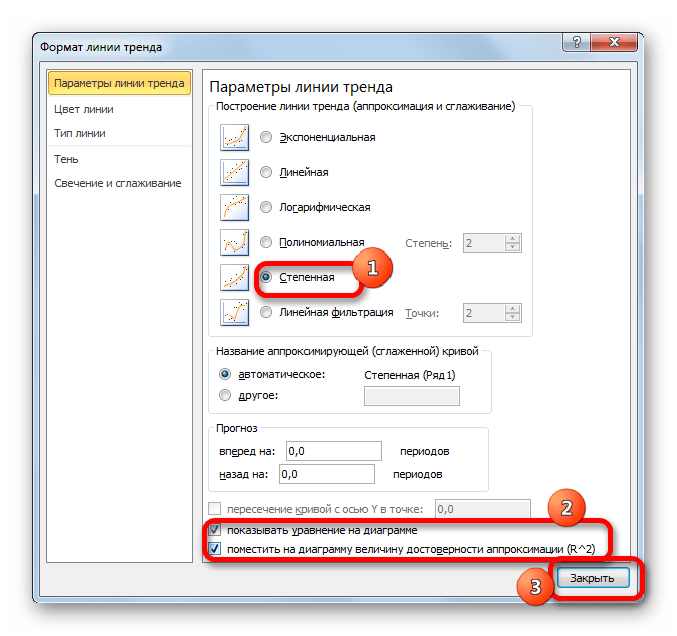
    В завершении рассмотрим метод степенной аппроксимации в Excel.

      Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».

  • Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.

    • Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.

    Общая формула, описывающая данный метод имеет такой вид:

    В конкретно нашем случае она выглядит так:

    Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.

    Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.

    Помимо этой статьи, на сайте еще 12683 инструкций.
    Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

    Отблагодарите автора, поделитесь статьей в социальных сетях.

    Как сделать линейную калибровочную кривую в Excel

    В Excel есть встроенные функции, которые вы можете использовать для отображения ваших данных калибровки и расчета линии наилучшего соответствия. Это может быть полезно, когда вы пишете отчет химической лаборатории или программируете поправочный коэффициент на единицу оборудования.

    В этой статье мы рассмотрим, как использовать Excel для создания диаграммы, построить линейную калибровочную кривую, отобразить формулу калибровочной кривой, а затем настроить простые формулы с помощью функций НАКЛОН и ПЕРЕКЛЮЧИТЬ, чтобы использовать уравнение калибровки в Excel.

    Что такое калибровочная кривая и как Excel полезен при ее создании?

    Чтобы выполнить калибровку, вы сравниваете показания устройства (например, температуру, отображаемую термометром) с известными значениями, называемыми стандартами (например, точки замерзания и кипения воды). Это позволяет вам создать серию пар данных, которые вы затем будете использовать для построения калибровочной кривой.

    Двухточечная калибровка термометра с использованием точек замерзания и кипения воды будет иметь две пары данных: одну с момента, когда термометр помещают в ледяную воду (32 ° F или 0 ° C), и одну в кипящую воду (212 ° F). или 100 ° С). Когда вы построите эти две пары данных в виде точек и проведете линию между ними (калибровочную кривую), а затем, предполагая, что реакция термометра является линейной, вы можете выбрать любую точку на линии, которая соответствует значению, которое отображает термометр, и вы мог найти соответствующую «истинную» температуру.

    Таким образом, линия, по сути, заполняет информацию между двумя известными для вас точками, так что вы можете быть достаточно уверенными при оценке фактической температуры, когда термометр показывает 57,2 градуса, но когда вы никогда не измеряли «стандарт», который соответствует это чтение.

    В Excel есть функции, которые позволяют графически отображать пары данных на графике, добавлять линию тренда (калибровочную кривую) и отображать уравнение калибровочной кривой на графике. Это полезно для визуального отображения, но вы также можете рассчитать формулу линии, используя функции Excel SLOPE и INTERCEPT. Когда вы введете эти значения в простые формулы, вы сможете автоматически рассчитать «истинное» значение на основе любого измерения.

    Давайте посмотрим на пример

    Для этого примера мы разработаем калибровочную кривую из серии из десяти пар данных, каждая из которых состоит из значения X и значения Y. Значения Х будут нашими «стандартами», и они могут представлять что угодно, от концентрации химического раствора, который мы измеряем с помощью научного прибора, до входной переменной программы, которая управляет пусковой машиной для мрамора.

    Значения Y будут «откликами», и они будут представлять собой показания прибора, полученные при измерении каждого химического раствора, или измеренное расстояние, на котором расстояние от пусковой установки, на которую упал мрамор, используя каждое входное значение.

    После того, как мы графически изобразим калибровочную кривую, мы будем использовать функции SLOPE и INTERCEPT, чтобы вычислить формулу калибровочной линии и определить концентрацию «неизвестного» химического раствора на основании показаний прибора или решить, какой ввод мы должны дать программе, чтобы мрамор приземляется на определенном расстоянии от пусковой установки.

    Шаг первый: создайте свою диаграмму

    Наш простой пример электронной таблицы состоит из двух столбцов: X-Value и Y-Value.

    Начнем с выбора данных для построения графика.

    Сначала выберите ячейки столбца «X-значение».

    Теперь нажмите клавишу Ctrl и затем щелкните ячейки столбца Y-значения.

    Перейдите на вкладку «Вставить».

    Перейдите в меню «Графики» и выберите первый вариант в раскрывающемся меню «Разброс».

    разброс» width=»314″ height=»250″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20314%20250’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-05.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.zXPKQgYC7-.png»/>

    Появится диаграмма, содержащая точки данных из двух столбцов.

    Выберите серию, нажав на одну из синих точек. После выбора Excel обрисовывает в общих чертах точки.

    Щелкните правой кнопкой мыши одну из точек и выберите опцию «Добавить линию тренда».

    На графике появится прямая линия.

    В правой части экрана появится меню «Format Trendline». Установите флажки рядом с «Показать уравнение на графике» и «Показать значение R-квадрат на графике». Значение R-квадрат является статистикой, которая говорит вам, насколько точно линия соответствует данным. Наилучшее значение R-квадрата равно 1.000, что означает, что каждая точка данных касается линии. По мере роста различий между точками данных и линией значение r-квадрата уменьшается, причем 0,000 является наименьшим возможным значением.

    Уравнение и R-квадрат статистики трендовой линии появятся на графике. Обратите внимание, что в нашем примере корреляция данных очень хорошая, значение R-квадрата равно 0,988.

    Уравнение имеет вид «Y = Mx + B», где M — наклон, а B — пересечение оси y прямой.

    Теперь, когда калибровка завершена, давайте поработаем над настройкой диаграммы, отредактировав заголовок и добавив заголовки осей.

    Чтобы изменить заголовок диаграммы, щелкните по нему, чтобы выделить текст.

    Теперь введите новый заголовок, который описывает диаграмму.

    Чтобы добавить заголовки к осям X и Y, сначала перейдите к «Инструменты диаграммы»> «Дизайн».

    дизайн» width=»650″ height=»225″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20225’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-14.png»/>

    Нажмите «Добавить элемент диаграммы».

    Теперь перейдите к Названия осей> Первичная горизонтальная.

    первичная горизонтальная» width=»650″ height=»500″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20500’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-16.png»/>

    Появится название оси.

    Чтобы переименовать заголовок оси, сначала выделите текст, а затем введите новый заголовок.

    Теперь перейдите к Названию осей> Первичная вертикаль.

    Появится название оси.

    Переименуйте этот заголовок, выделив текст и введя новый заголовок.

    Ваша диаграмма теперь завершена.

    Шаг второй: Рассчитать линейное уравнение и R-квадрат

    Теперь давайте вычислим линейное уравнение и R-квадрат, используя встроенные в Excel функции SLOPE, INTERCEPT и CORREL.

    К нашему листу (в строке 14) мы добавили заголовки для этих трех функций. Мы выполним фактические вычисления в ячейках под этими заголовками.

    Сначала рассчитаем НАКЛОН. Выберите ячейку A15.

    Перейдите к формулам> Дополнительные функции> Статистические> НАКЛОН.

    Дополнительные функции> Статистические> НАКЛОН» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-24.png»/>

    Откроется окно «Аргументы функции». В поле «Known_ys» выберите или введите ячейки столбца Y-значения.

    В поле «Known_xs» выберите или введите ячейки столбца X-Value. Порядок полей ‘Known_ys’ и ‘Known_xs’ имеет значение в функции SLOPE.

    Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:

    Обратите внимание, что значение, возвращаемое функцией SLOPE в ячейке A15, соответствует значению, отображенному на графике.

    Затем выберите ячейку B15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «ПЕРЕКРЫТЬ».

    Дополнительные функции> Статистические> INTERCEPT» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-28.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.6UWCgXDsRt.png»/>

    Откроется окно «Аргументы функции». Выберите или введите в ячейки столбца Y-значение для поля «Known_ys».

    Выберите или введите в ячейки столбца X-Value поле «Known_xs». Порядок полей «Known_ys» и «Known_xs» также имеет значение в функции INTERCEPT.

    Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:

    Обратите внимание, что значение, возвращаемое функцией INTERCEPT, соответствует точке пересечения y, отображаемой на диаграмме.

    Затем выберите ячейку C15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «CORREL».

    дополнительные функции> статистические> CORREL» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-32.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.n7KBBl00Uj.png»/>

    Откроется окно «Аргументы функции». Выберите или введите любой из двух диапазонов ячеек для поля «Массив1». В отличие от SLOPE и INTERCEPT, порядок не влияет на результат функции CORREL.

    Выберите или введите другой из двух диапазонов ячеек для поля «Array2».

    Нажмите «ОК». Формула должна выглядеть следующим образом на панели формул:

    Обратите внимание, что значение, возвращаемое функцией CORREL, не соответствует значению «r-квадрат» на графике. Функция CORREL возвращает «R», поэтому мы должны возвести ее в квадрат, чтобы вычислить «R-квадрат».

    Щелкните внутри панели функций и добавьте «^ 2» в конец формулы, чтобы возвести в квадрат значение, возвращаемое функцией CORREL. Заполненная формула теперь должна выглядеть так:

    После изменения формулы значение «R-квадрат» теперь соответствует значению, отображенному на графике.

    Шаг третий: настройка формул для быстрого расчета значений

    Теперь мы можем использовать эти значения в простых формулах, чтобы определить концентрацию этого «неизвестного» раствора или то, что мы должны ввести в код, чтобы шарик пролетел определенное расстояние.

    Эти шаги настроят формулы, необходимые для того, чтобы вы могли ввести значение X или значение Y и получить соответствующее значение на основе калибровочной кривой.

    Уравнение линии наилучшего соответствия имеет вид «Y-значение = НАКЛОН * X-значение + INTERCEPT», поэтому решение для «Y-значения» выполняется путем умножения значения X и SLOPE, а затем добавив ИНТЕРЦЕПТ.

    В качестве примера мы вводим ноль в качестве значения X. Возвращаемое значение Y должно быть равно ПЕРЕКЛЮЧЕНИЮ линии наилучшего соответствия. Это соответствует, поэтому мы знаем, что формула работает правильно.

    Решение для значения X на основе значения Y выполняется путем вычитания INTERCEPT из значения Y и деления результата на НАКЛОН:

    В качестве примера мы использовали INTERCEPT в качестве значения Y. Возвращаемое значение Х должно быть равно нулю, но возвращаемое значение равно 3.14934E-06. Возвращаемое значение не равно нулю, потому что мы непреднамеренно обрезали результат INTERCEPT при вводе значения. Однако формула работает правильно, потому что результат формулы равен 0,00000314934, что по существу равно нулю.

    Вы можете ввести любое значение X в первую ячейку с толстыми границами, и Excel автоматически вычислит соответствующее значение Y.

    Ввод любого значения Y во вторую ячейку с толстой рамкой даст соответствующее значение X. Эта формула используется для расчета концентрации этого раствора или того, что необходимо для запуска мрамора на определенном расстоянии.

    В этом случае прибор показывает «5», поэтому при калибровке будет предложена концентрация 4,94, или мы хотим, чтобы шарик прошел пять единиц расстояния, поэтому при калибровке предлагается ввести 4,94 в качестве входной переменной для программы, управляющей пусковой установкой мрамора. Мы можем быть достаточно уверены в этих результатах из-за высокого значения R-квадрата в этом примере.

    Как построить график в Excel по уравнению

    Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.

    Что это такое

    График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.

    А нужно ли это

    Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.

    Как построить график уравнения регрессии в Excel

    Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.

    Подготовительные работы

    Перед использованием функции активируйте Пакет анализа. Перейдите:
    Выберите раздел:
    Далее:
    Прокрутите окно вниз, выберите:
    Отметьте пункт:
    Открыв раздел «Данные», появится кнопка «Анализ».

    Как пользоваться

    Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите:
    Выберите:
    Отобразится окно настроек, где входной интервал:

    1. Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
    2. Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».

    Анализ

    Нажав кнопку «ОК», отобразится результат.
    Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.

    Как построить график квадратного уравнения в Excel

    График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].

    1. Составьте таблицу как на скриншоте;
    2. В третьей строке указываем коэффициенты и их значения;
    3. Пятая — диапазон значений;
    4. В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;

    Копируем её на весь диапазон значений аргумента вправо.
    При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
    Выделите диапазон значений по ним будем строить график. Перейдите:
    Поместите график в свободное место на листе.

    Как построить график линейного уравнения

    Функция имеет вид: y=kx+b. Построим в интервале [-4;4].

    1. В таблицу прописываем значение постоянных величин. Строка три;
    2. Строка 5. Вводим диапазон значений;
    3. Ячейка В6. Прописываем формулу.

    Выделите диапазон ячеек A5:J6. Далее:
    График — прямая линия.

    Вывод

    Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.

    источники:

    http://gadgetshelp.com/how-to/kak-sdelat-lineinuiu-kalibrovochnuiu-krivuiu-v-excel/

    http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/

    Источник

    Электронные таблицы EXCEL можно использовать при
    изучении многих разделов физики, математики и
    других предметов. Одной из данных тем является
    математическая тема: “Анализ элементарных
    функций”. Данная работа посвящена использованию
    электронных таблиц EXCEL в анализе элементарных
    функций.

    Рис. 1 (см. Приложение 2)

    На рис.1 представлена некоторая функция,
    заданная с помощью таблицы, построение которой
    приведено в Приложении 1.

    Особенность анализа функций с помощью
    электронных таблиц заключается в том, что анализ
    проводится на дискретной информации.
    Действительно, количество значений исследуемой
    функции конечно и дано (как правило) с некоторым
    постоянным шагом по аргументу.

    При анализе исходной функции необходимо решить
    следующие задачи:

    1. определение максимума (минимума) данной функции
      на заданном интервале,
    2. определение возрастания и/или убывания функции
      на заданном интервале,
    3. определение четности заданной функции,
    4. определение периодичности заданной функции,
    5. определение значения первой производной данной
      функции и наличия экстремумов.

    Для решения этих задач потребуется построить
    таблицы ВводаИсходнойИнформации, таблицы
    ВыводаРезультатов, Расчетной таблицы для
    обработки информации и дополнительно построим
    Вспомогательную таблицу. Таблицу
    ВводаИсходнойИнформации и основу Расчетной
    таблицу построены при введении значений
    исследуемой функции в Приложении 1 и показанной
    на рис.1. Построим решения задач анализа.

    Приложение 1

    Задача 1.
    Для заданной функции на заданном интервале
    аргумента определить ее минимальное и
    максимальное значения.

    Решение.
    Для решения этой задачи построим таблицу
    ВыводаРезультатов в виде

      D E
    1 комментарии Значения
    2 Макс f(X) <формула>
    3 Мин f(X) <формула>

    В мастере функций Excel имеются функции МАКС(…) и
    МИН(…), позволяющие решить нашу задачу. Для этого
    необходимо в ячейки Е2 и Е3 ввести соответственно
    формулы:

    E2 => [=МАКС(с10:с50)]
    и
    E3 => [=МИН(с10:с50)]

    Примечание. Если “протяжка” велась до
    другой строки, то в интервале ссылок указать
    соответствующий номер строки.

    ЗАДАЧА РЕШЕНА.

    Задача 2.
    Определение возрастания и/или убывания функции
    на заданном интервале.

    Решение.
    Для решения данной задачи в расчетной таблице
    необходимо построить столбец D, в котором знак
    будет указывать на возрастание или убывание
    функции в данной точке. Для этого в ячейку D11
    введем формулу

    D11 => [=ЕСЛИ(a11<>””;ЗНАК(D11-D10);””)]
    и “протянем” ее до строки №50.

    И там, где знак положительный, функция
    возрастает, а там, где знак отрицательный,
    функция – убывает.

    Далее построим вспомогательную таблицу, в
    которой определим количество признаков
    возрастания и убывания функции

      F G
    1 КОММЕНТАРИИ ЗНАЧЕНИЯ
    2 Признак возрастания <формула>
    3 Признак убывания <формула>

    Для этого в ячейки g2 и g3 соответственно вводим
    формулы:

    G2 => [=СуммЕсли(d11:d50;”>0”)]
    G3 => [=СуммЕсли(d11:d50;”<0”)]

    Таблицу ВыводаРезультатов дополним строкой

      D E
    1 комментарии значения
    2 Макс f(X) =МАКС(с10:с50)
    3 Мин f(X) =МИН(с10:с50)
    4 Возрастание/Убывание <формула>

    И для определения характера изменения заданной
    функции остается ввести в ячейку Е4 формулу:

    E4 => [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
    другое”;”возрастает”);”убывает”)

    ЗАДАЧА РЕШЕНА.

    Задача 3.
    Определение четности данной.

    Решение.
    Для решения данной задачи необходимо знание
    аналитического представления исходной функции,
    так как признаком четности функции является
    равенство f(X) = f(-X).

    Для решения данной задачи в расчетной таблице
    построим дополнительный столбец. В ячейку Е10
    введем формулу

    E10 => [=f(b10) – f(-b10)]
    и “протянуть” ее до строки №50.

    Таблицу ВыводаРезультатов дополним строкой

      D E
    1 комментарии значения
    2 Макс f(X) =МАКС(с10:с50)
    3 Мин f(X) =МИН(с10:с50)
    4 Возрастание/Убывание [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
    другое”;”возрастает”);”убывает”)
    5 четность <формула>

    В ячейку Е4 таблицы ВыводаРезультатов вводим
    формулу.

    E4 => [ЕСЛИ(ABS(СУММ(E10:E50))<0,000001; “ЧЕТНАЯ”;
    “НЕЧЕТНАЯ”)

    ЗАДАЧА РЕШЕНА.

    Задача 4.
    Определить является ли введенный период
    периодом заданной функции.

    Решение.
    Для решения данной задачи необходимо знание
    аналитического представления исходной функции,
    так как признаком периодичности функции
    является равенство f(Х) = f(X+<период>).

    Для данной задачи добавим в таблице
    ВводаИсходнойИнформации строку №6, в которой
    введем численное значение предполагаемого
    периода.

      А В
    1 КОММЕНТАРИИ ЗНАЧЕНИЯ
    2 Xn <значение>
    3 Xk <значение>
    4 Shag <значение>
    5 N <формула>
    6 период <значение>

    В ячейку В6 вводится число – предполагаемый
    период заданной функции.

    Далее для решения данной задачи построим
    дополнительный столбец в расчетной таблице, для
    этого в ячейку F11 введем формулу

    F10 => [=ЕСЛИ(a10<>””;f(b10)-f(b10+$b$6);””)]

    и “потягиваем” эту формулу до строки №50.

    В таблице ВыводаРезультатов добавим строчку.

      D E
    1 комментарии значения
    2 Макс f(X) =МАКС(с10:с50)
    3 Мин f(X) =МИН(с10:с50)
    4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
    другое”;”возрастает”);”убывает”)
    5 период <формула>

    В ячейке Е5 необходимо ввести формулу

    Е5 => [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;”не
    период”)]

    Если данное значение предполагаемого периода
    не подходит, то его можно изменить.

    ЗАДАЧА РЕШЕНА.

    Задача 5.
    Для заданной функции определить:

    • значения первой производной данной функции,
    • наличия и количество экстремумов.

    Решение.
    Для решения первой части задачи, то есть
    определения первой производной воспользуемся ее
    разностным определение.

    Построим столбец. Для этого в ячейку G11 вводим
    формулу:

    G11 => [= ЕСЛИ(a11<>””; ABS((c11-c10)/(b11-b10));””)]

    и “протягиваем ее до строки с №50.

    В результате получаем разностные приближенные
    значения первой производной заданной функции в
    заданных точках.

    Для решения второй части задачи, то есть
    определения наличия и количества экстремумов на
    заданной функции в таблицу ВыводаРезультатов
    дополнить строкой.

      D E
    1 комментарии значения
    2 Макс f(X) =МАКС(с10:с50)
    3 Мин f(X) =МИН(с10:с50)
    4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
    другое”;”возрастает”);”убывает”)
    5 период [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;
    ”не период”)]
    6 Количество Экстремумов. <формула>

    В ячейке Е6 необходимо ввести формулу

    E6 => [=СчетЕсли(g11:g50;”<0,05”)]

    ЗАДАЧА РЕШЕНА.

    Рис 2, см. Приложение 3

    На рис.2 приведена построенная таблица
    решения задач.

    Предложенные в данной работе задачи можно
    использовать на интегрированных уроках
    информатика-математика, на уроках информатики
    при изучении электронных таблиц, в частности, в
    теме: “Мастер функций”.

    Источник

    Как строить график функции в Экселе

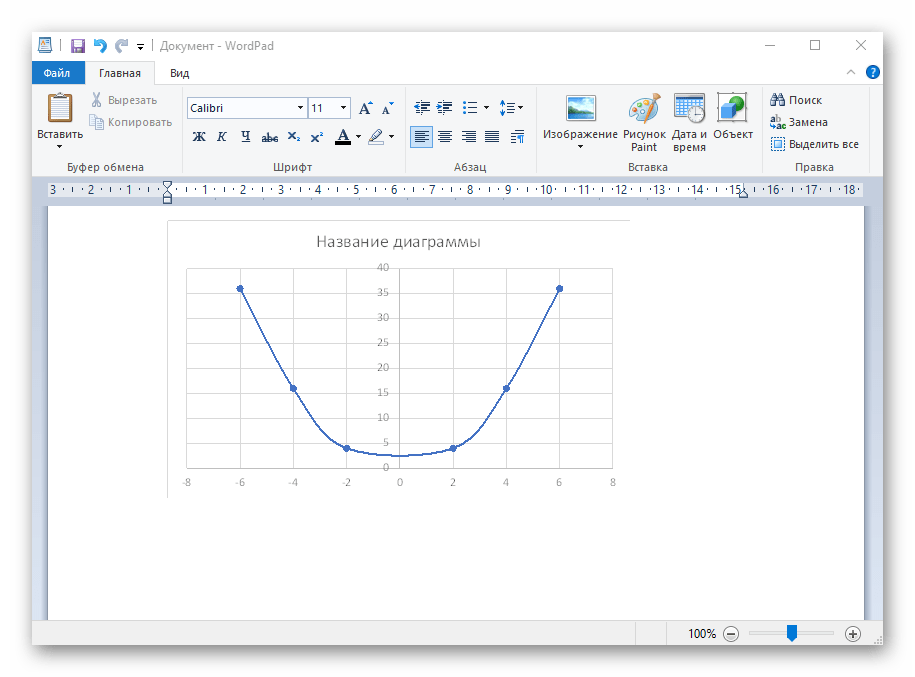
    Вариант 1: График функции X^2

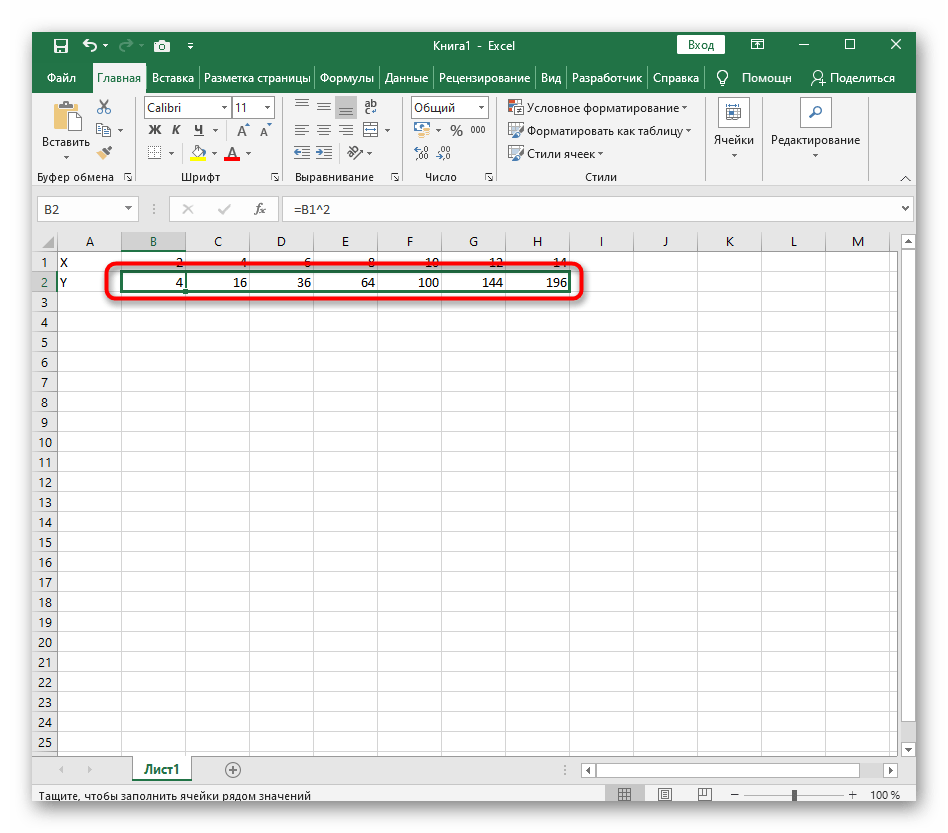
    В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

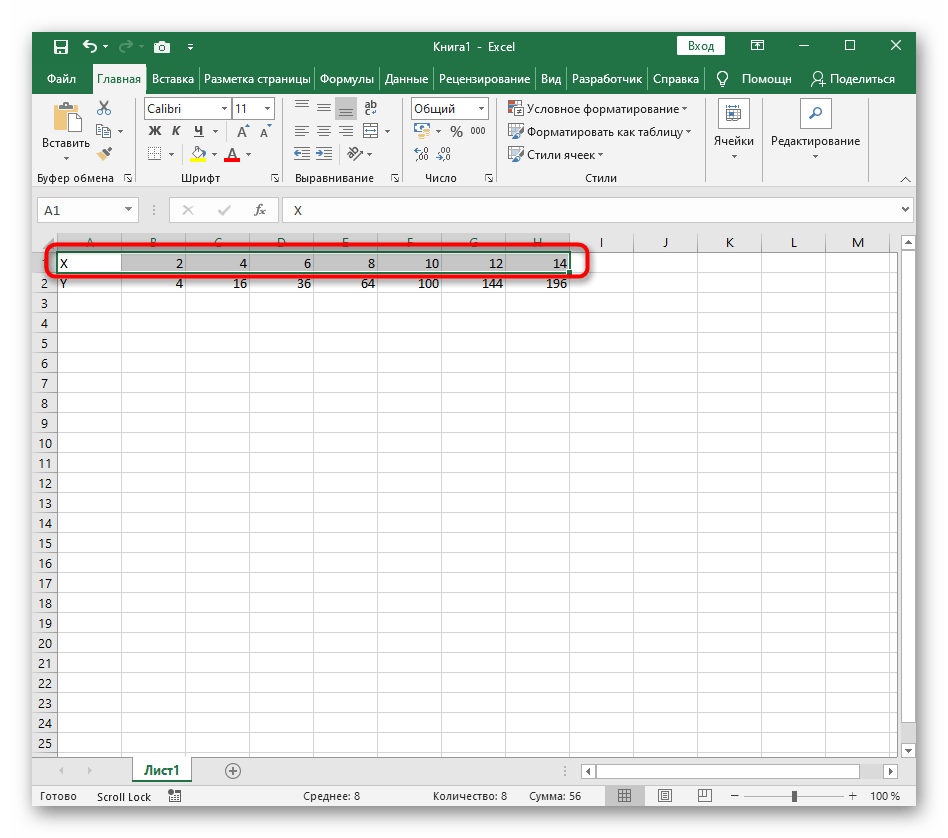
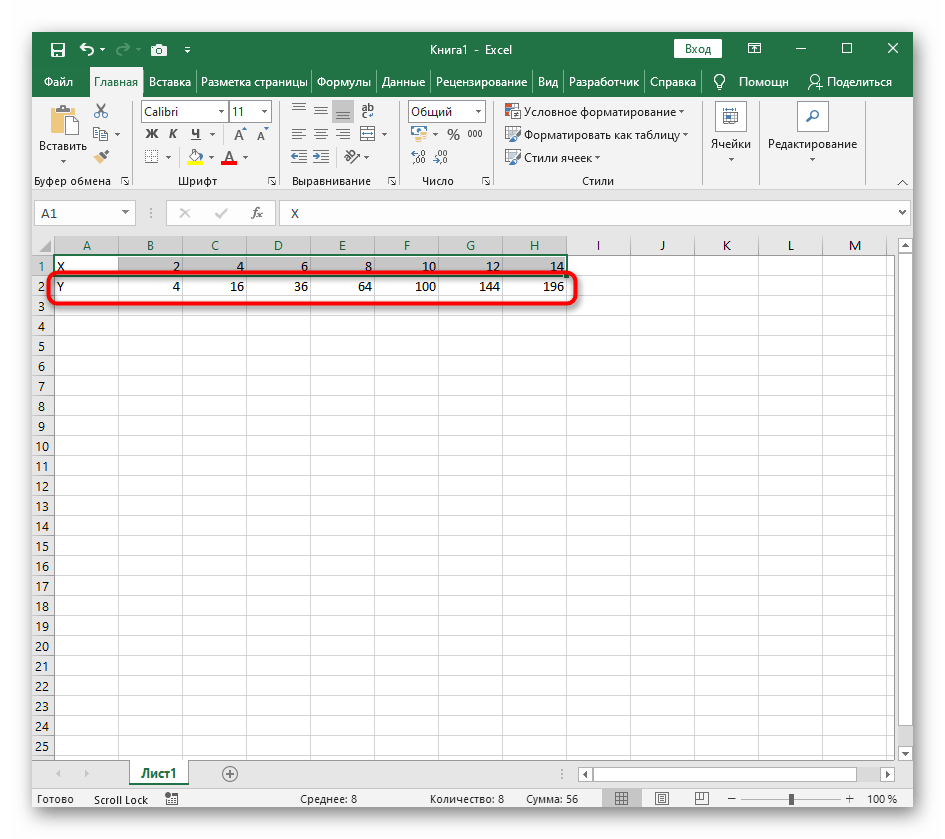
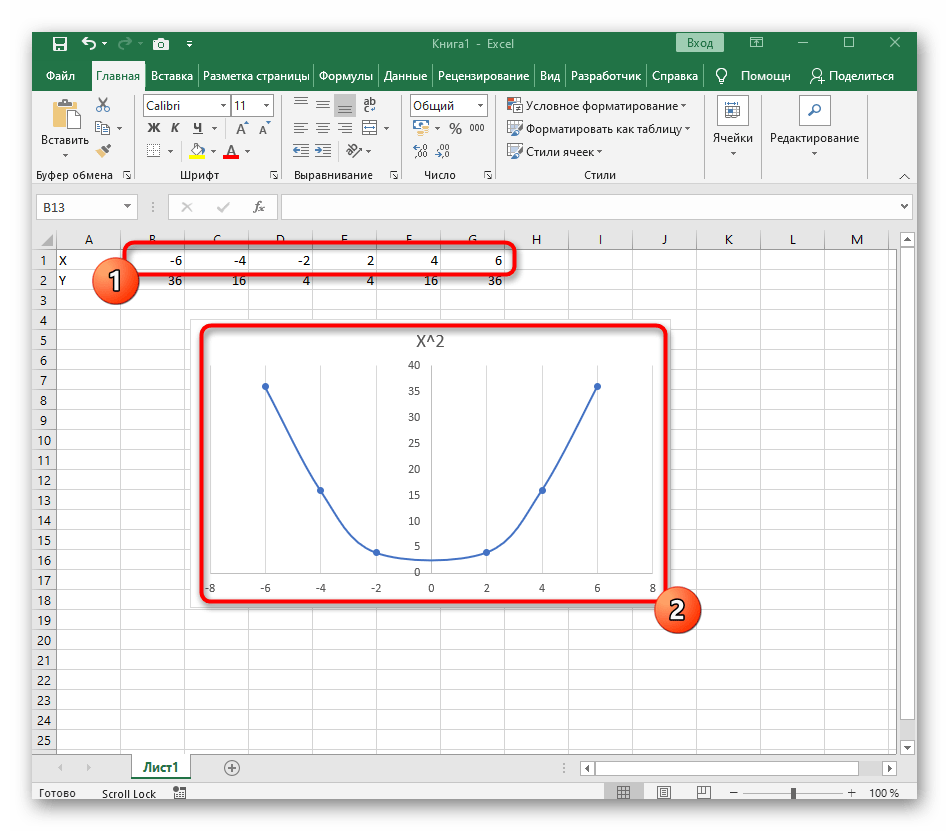
    1. Создайте строку X, где укажите необходимый диапазон чисел для графика функции.

      2. Создание первой строки для построения графика функции X^2 в Excel

    2. Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.

      3. Создание второй строки для построения графика функции X^2 в Excel

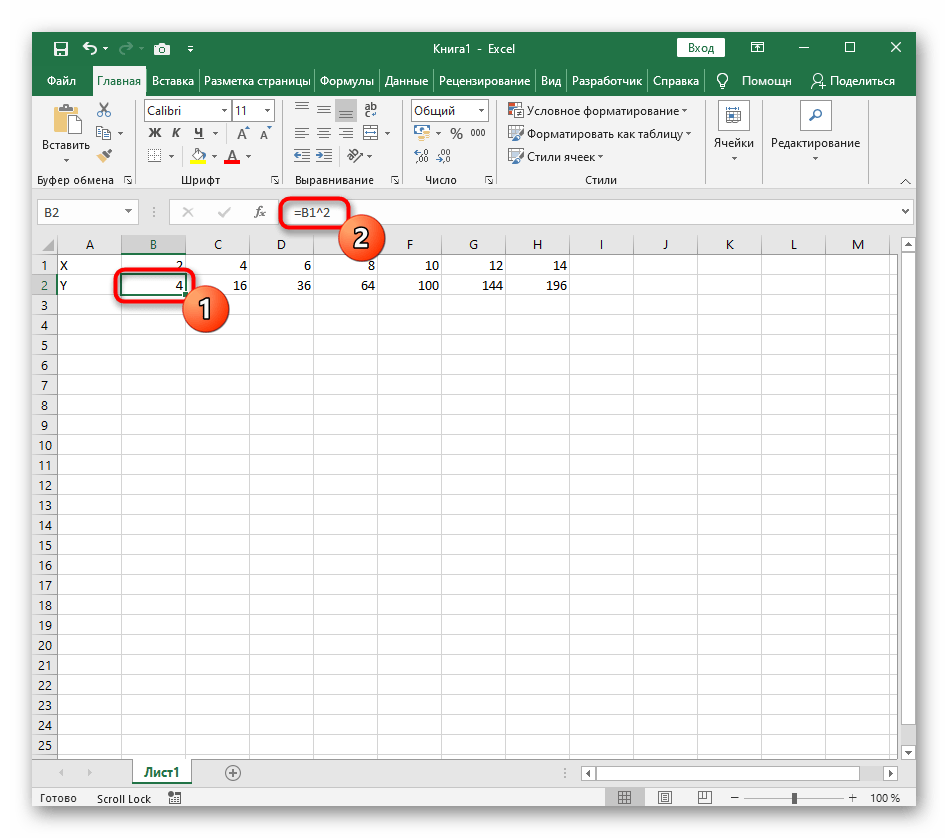
    3. Нажмите по первой ячейке и впишите =B1^2, что значит автоматическое возведение указанной ячейки в квадрат.

      4. Создание формулы для автоматического расчета значений при работе с графиком функции X^2 в Excel

    4. Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.

      5. Растягивание формулы перед создание графика функции X^2 в Excel

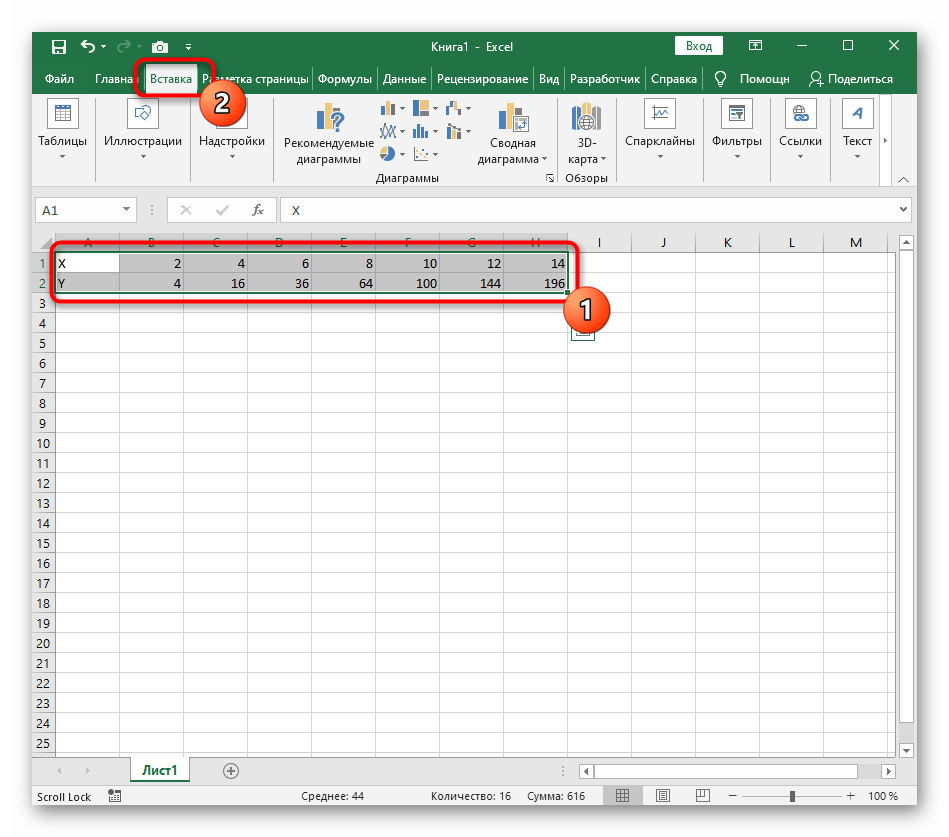
    5. Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».

      6. Выделение всего диапазона данных для создания графика функции X^2 в Excel

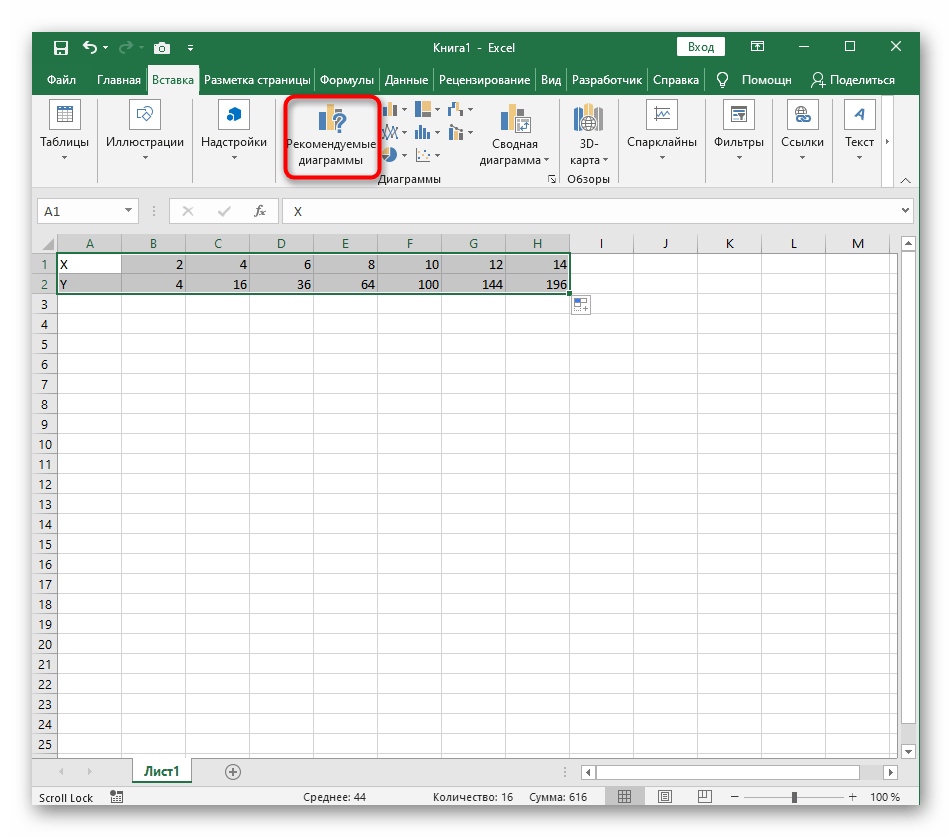
    6. На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».

      7. Переход в меню выбора диаграммы для создания графика функции X^2 в Excel

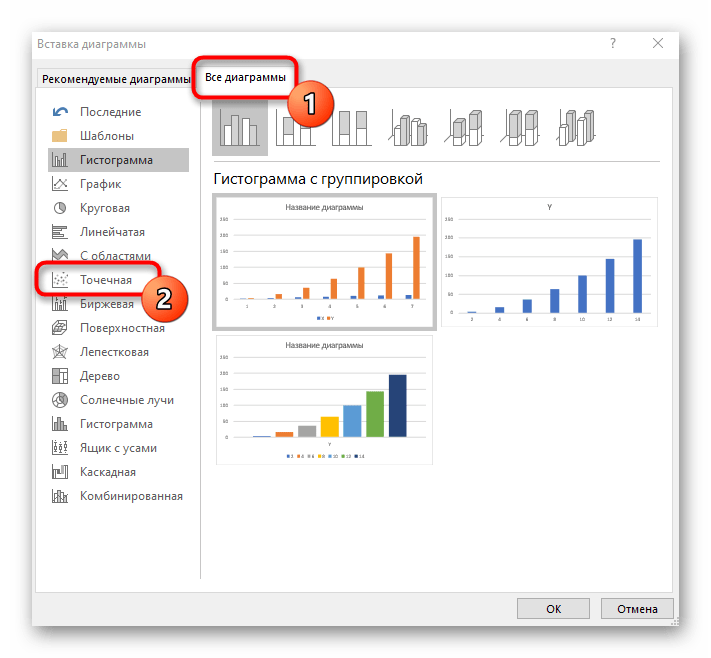
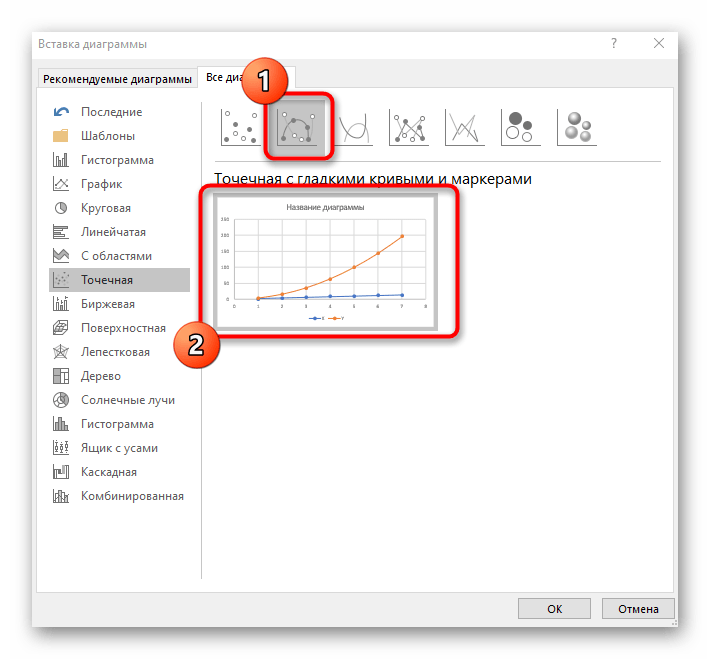
    7. В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».

      8. Выбор точечного графика для создания графика функции X^2 в Excel

    8. Подойдет вариант «Точечная с гладкими кривыми и маркерами».

      9. Добавление выбранного графика на лист для создания графика функции X^2 в Excel

    9. После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.

      10. Проверка созданного графика функции при работе с X^2 в Excel

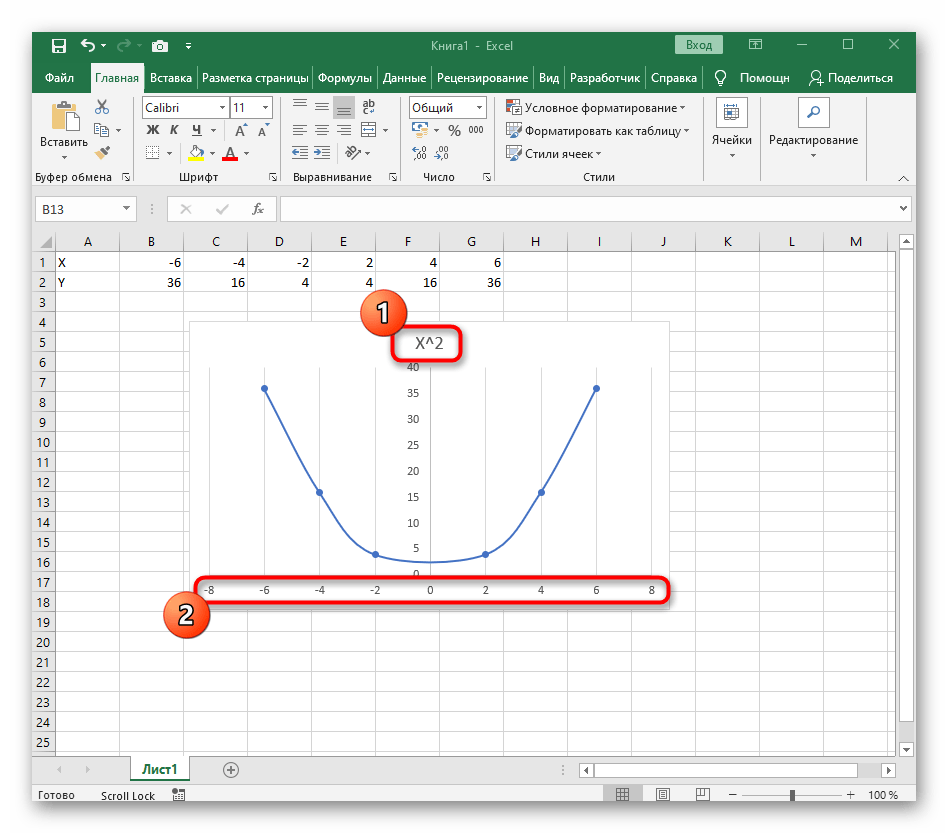
    10. Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.

      11. Редактирование графика функции X^2 в Excel после его добавления на лист

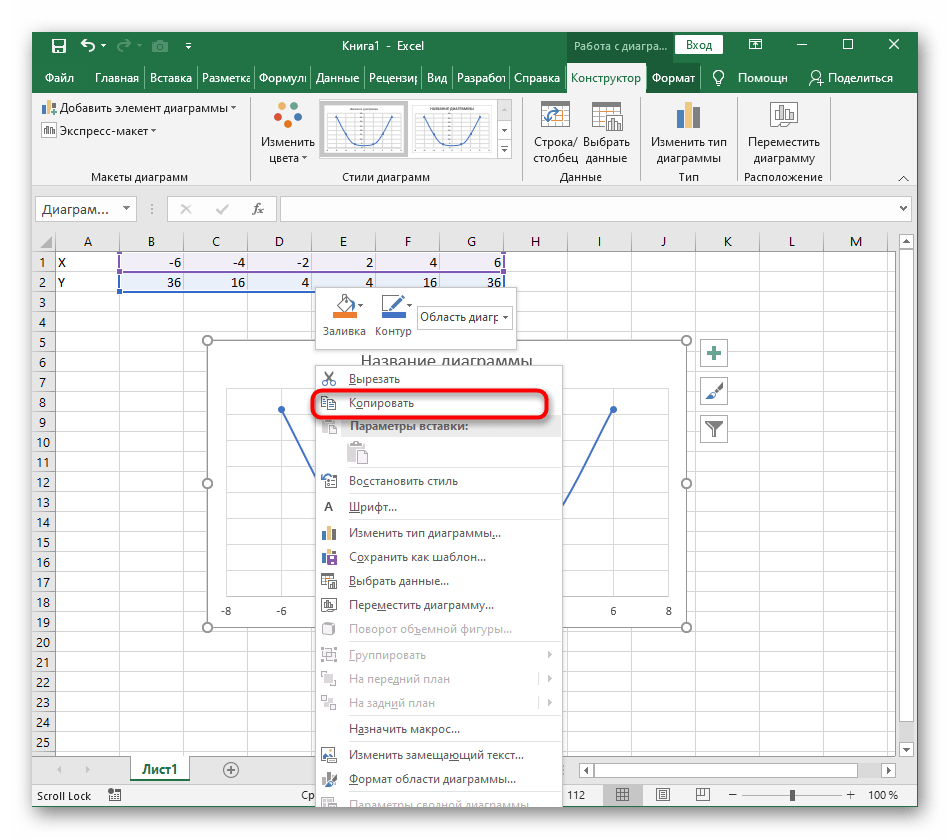
    11. Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».

      12. Кнопка для копирования созданного графика функции X^2 в Excel

    12. Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

      13. Успешная вставка построенного графика функции X^2 в Excel в текстовый редактор

    Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

    Вариант 2: График функции y=sin(x)

    Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

    Lumpics.ru

    1. Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.

      2. Добавление объяснений перед построением графика функции y=sin(x) в Excel

    2. Создайте сразу два столбца — X и Y, куда будете записывать данные.

      3. Добавление двух столбцов при построении графика функции y=sin(x) в Excel

    3. Запишите самостоятельно первые два или три значения с указанным шагом.

      4. Добавление первых значений для X при построении графика функции y=sin(x) в Excel

    4. Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.

      5. Растягивание значений при построении графика функции y=sin(x) в Excel

    5. Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.

      6. Добавление первого числа для формулы при расчете Y для построения графика функции y=sin(x) в Excel

    6. Сама функция автоматически высчитает синус заданного числа.

      7. Добавление первого числа для формулы при расчете Y для построения графика функции y=sin(x) в Excel

    7. Растяните столбец точно так же, как это было показано ранее.

      8. Растягивание формулы перед построением графика функции y=sin(x) в Excel

    8. Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.

      9. Удаление лишней разрядности перед построением графика функции y=sin(x) в Excel

    9. Выделите столбец с Y и перейдите на вкладку «Вставка».

      10. Выбор стандартного графика для построения графика функции y=sin(x) в Excel

    10. Создайте стандартный график, развернув выпадающее меню.

      11. Выбор диапазона данных для построения графика функции y=sin(x) в Excel

    11. График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

      12. Успешное построение графика функции y=sin(x) в Excel и его добавление на лист

    Еще статьи по данной теме:

    Помогла ли Вам статья?

    Источник

    Понравилась статья? Поделить с друзьями:
  • Как округлить целое число в excel до целого в большую сторону
  • Как определить версию файла excel
  • Как округлить формулу в excel до десятых
  • Как определить версию excel на компьютере
  • Как округлить формулу в excel до десятков