Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
Как построить диаграмму распределения в Excel
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
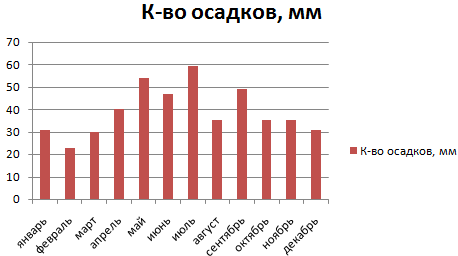
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
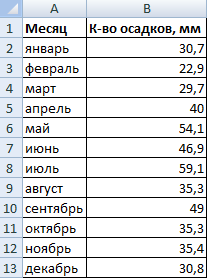
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
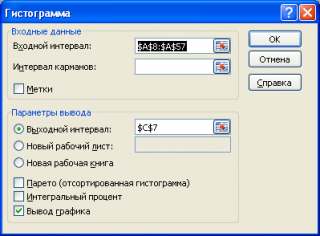
Выбираем «Гистограмма»:
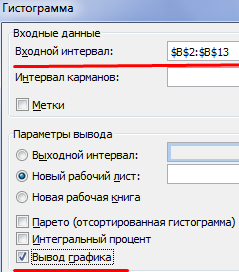
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
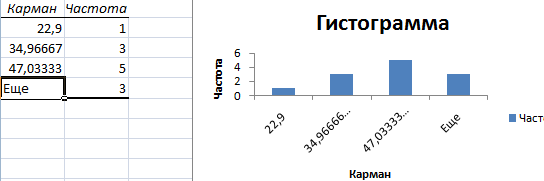
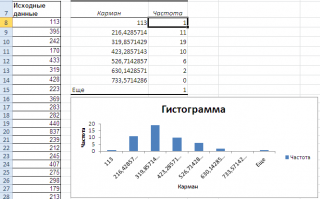
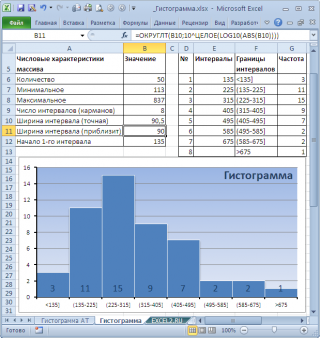
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
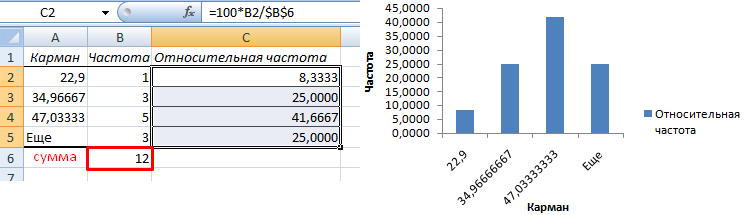
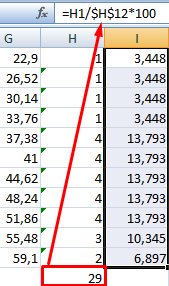
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
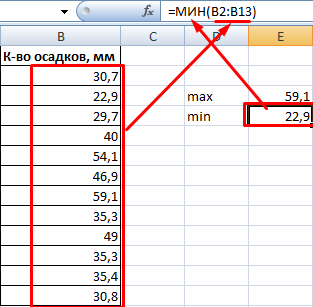
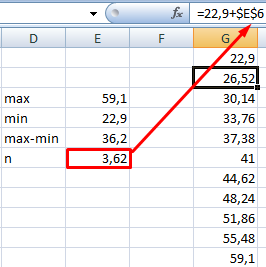
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
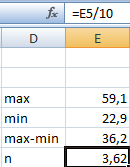
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
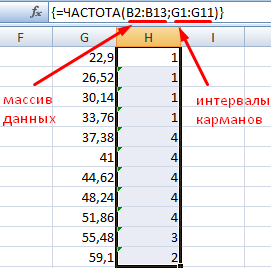
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
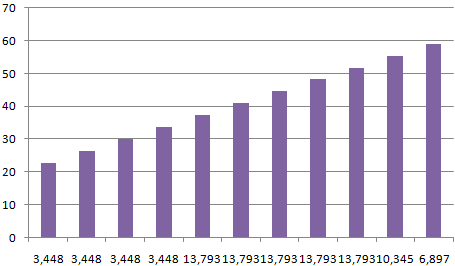
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
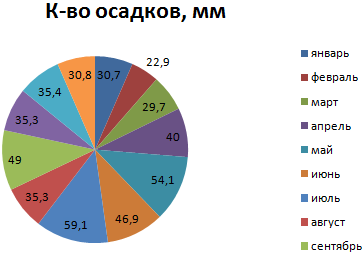
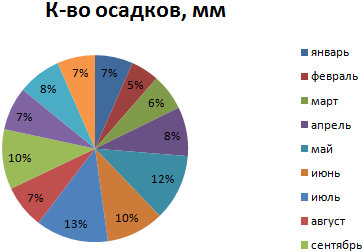
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Доля «каждого месяца» в общем количестве осадков за год:
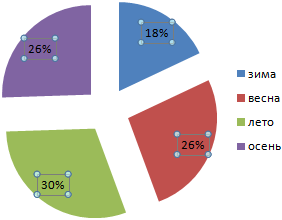
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
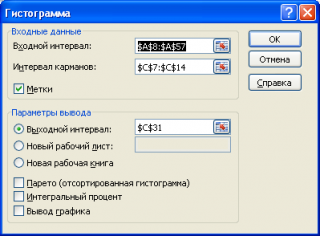
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
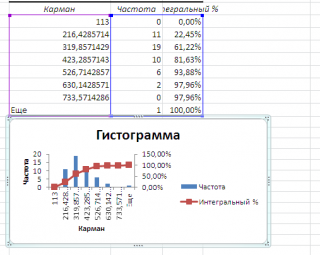
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
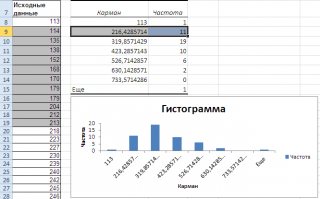
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
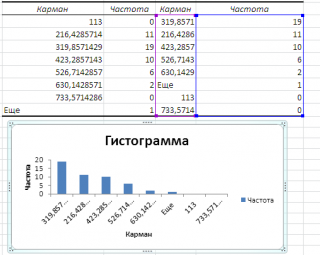
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
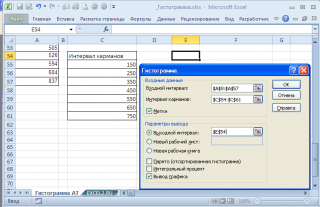
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
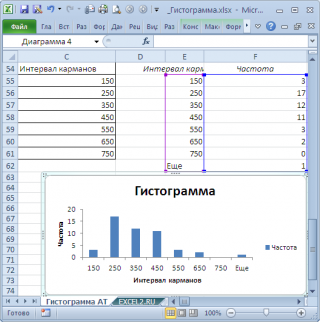
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
Одной из разновидностей гистограмм является
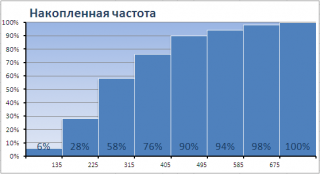
график накопленной частоты
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться ссылкой:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
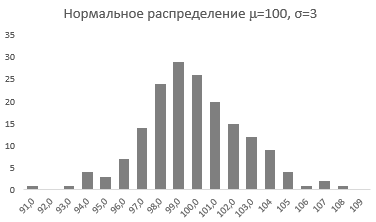
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
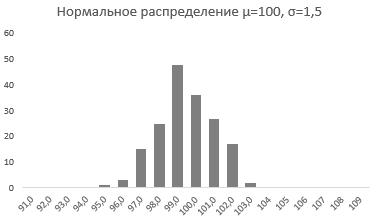
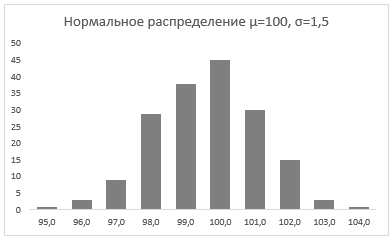
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
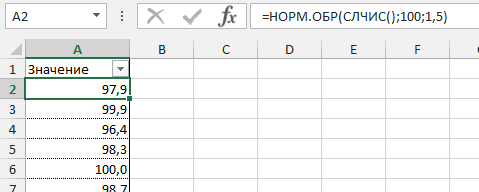
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
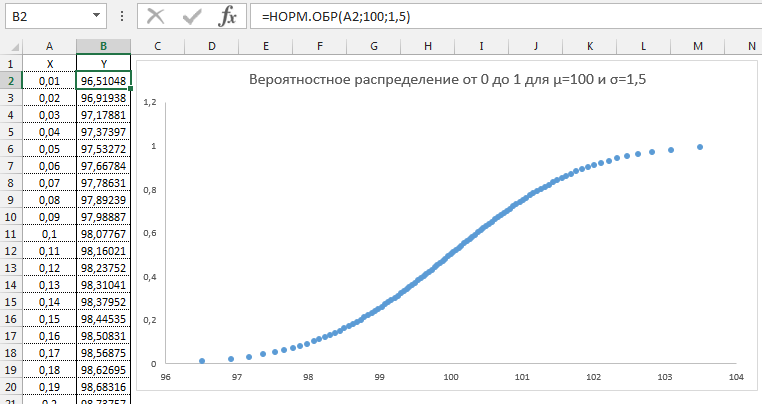
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
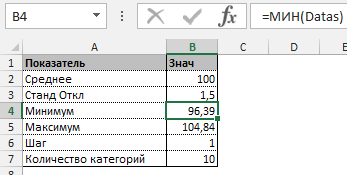
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
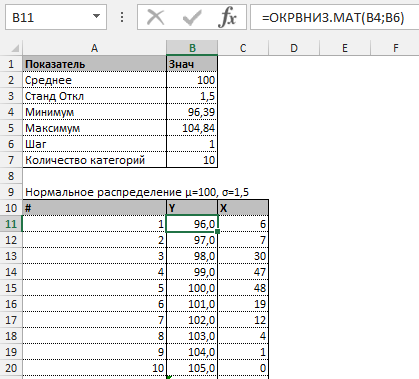
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
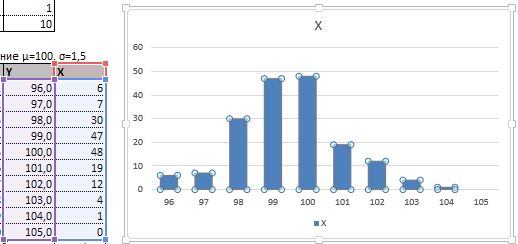
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
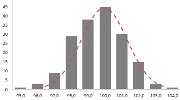
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
Выбираем «Гистограмма»:
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Доля «каждого месяца» в общем количестве осадков за год:
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
=ЧАСТОТА(tblData;C13:C22)=FREQUENCY(tblData,C13:C22)
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение:
17 авг. 2022 г.
читать 3 мин
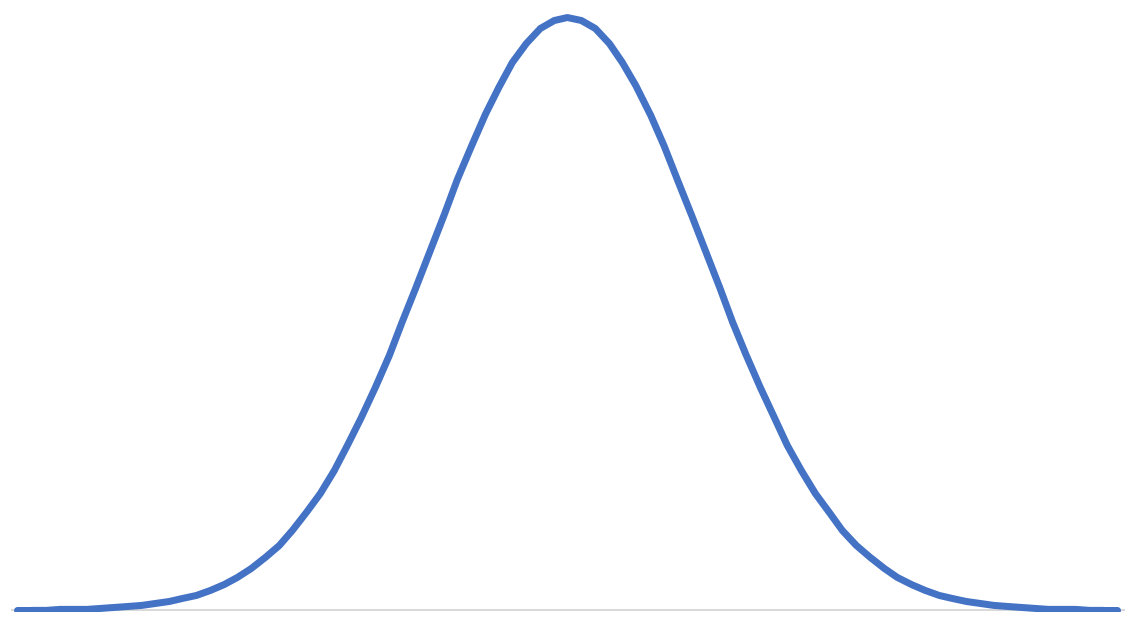
«Колокольная кривая» — это прозвище, данное форме нормального распределения , которая имеет отчетливую форму «колокола»:
В этом руководстве объясняется, как построить кривую нормального распределения в Excel для заданного среднего значения и стандартного отклонения, и даже предоставляется бесплатный загружаемый шаблон, который можно использовать для создания собственной кривой нормального распределения в Excel.
Пример: кривая нормального распределения в Excel
Используйте следующие шаги, чтобы сделать кривую колокола в Excel.
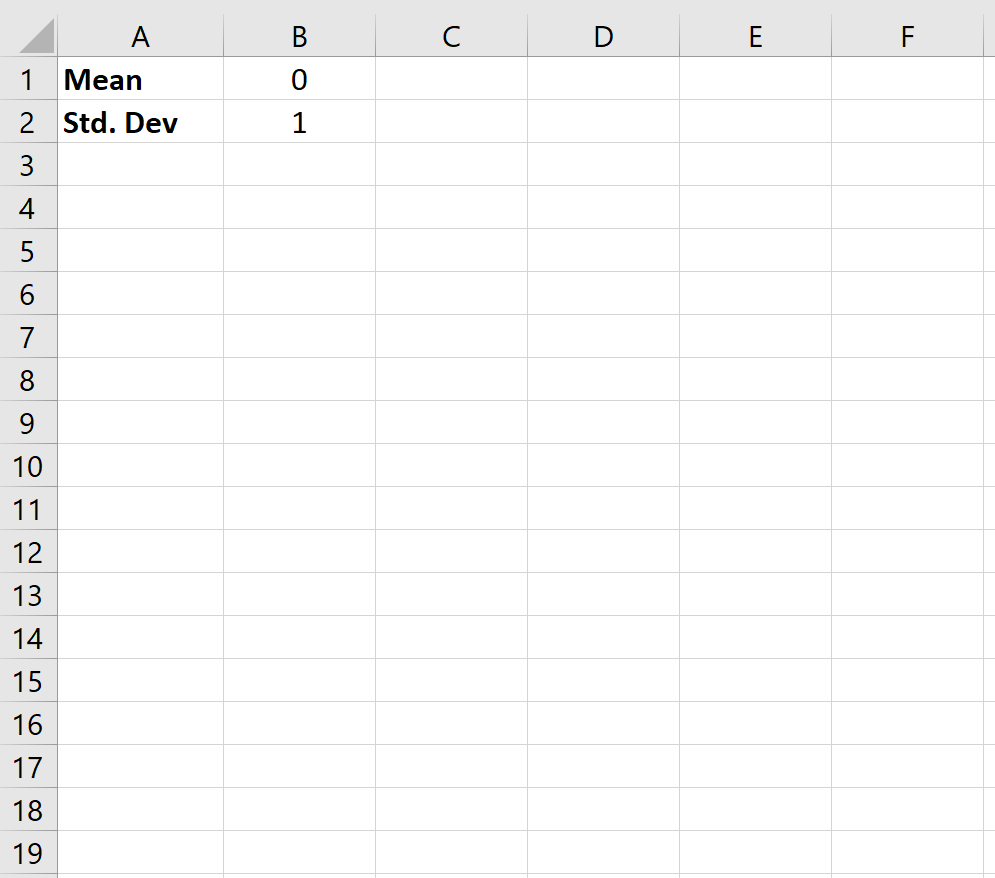
Шаг 1: Создайте ячейки для среднего значения и стандартного отклонения.
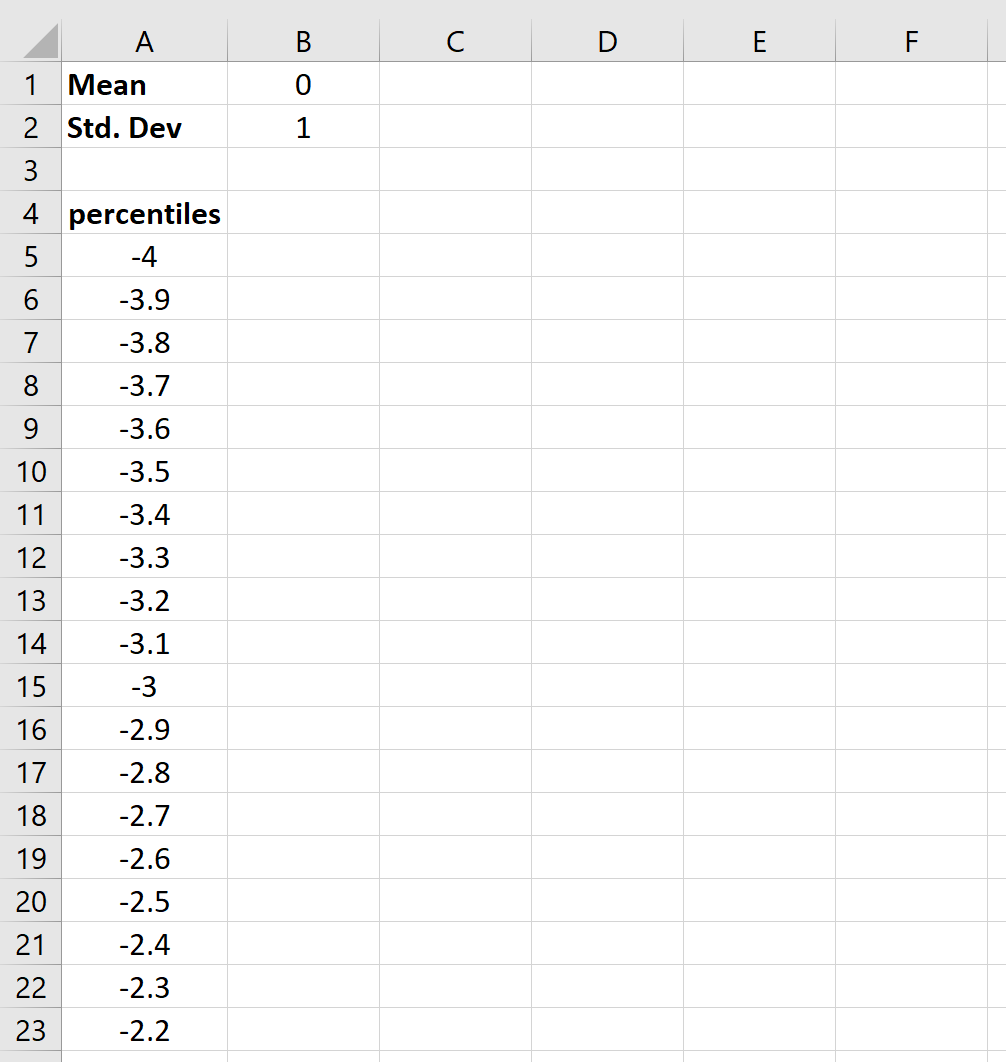
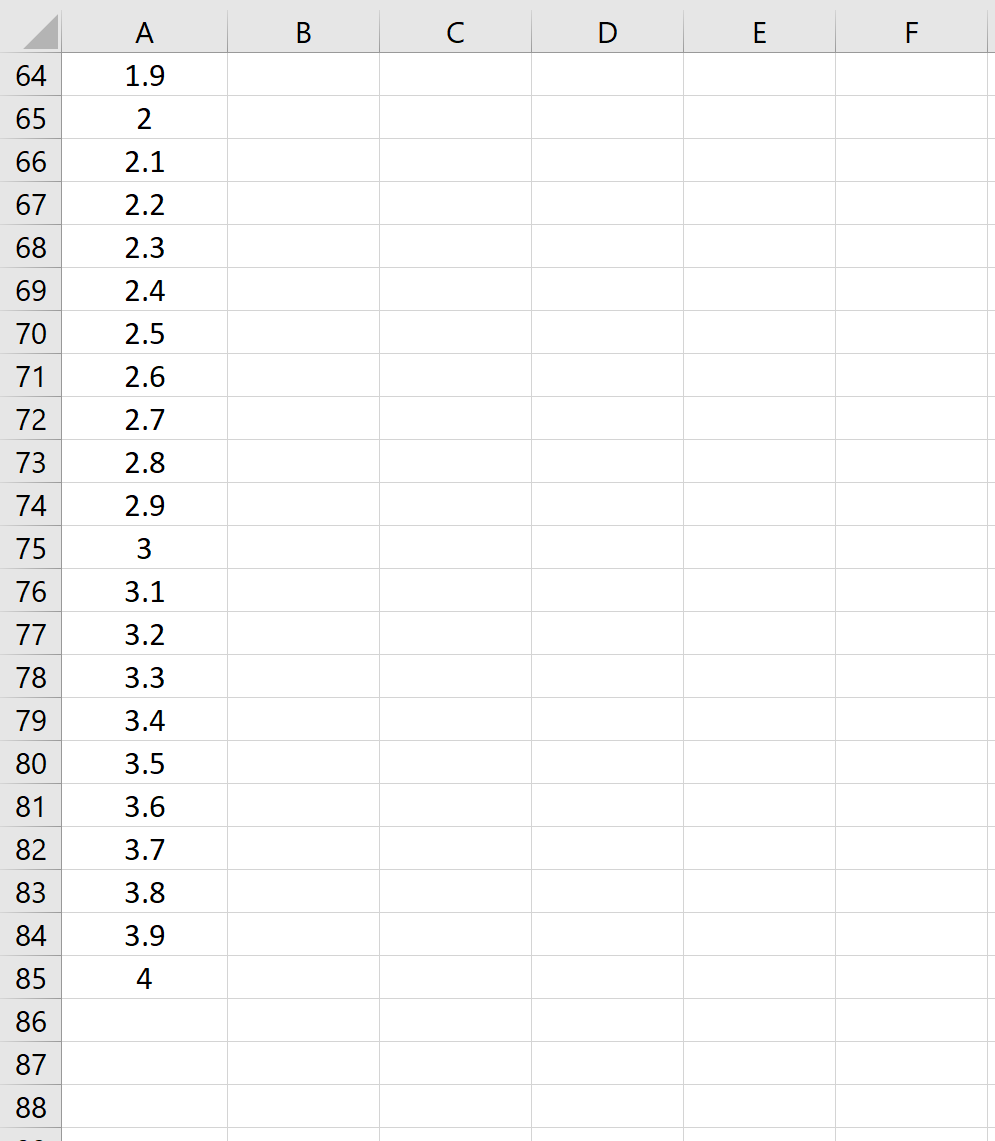
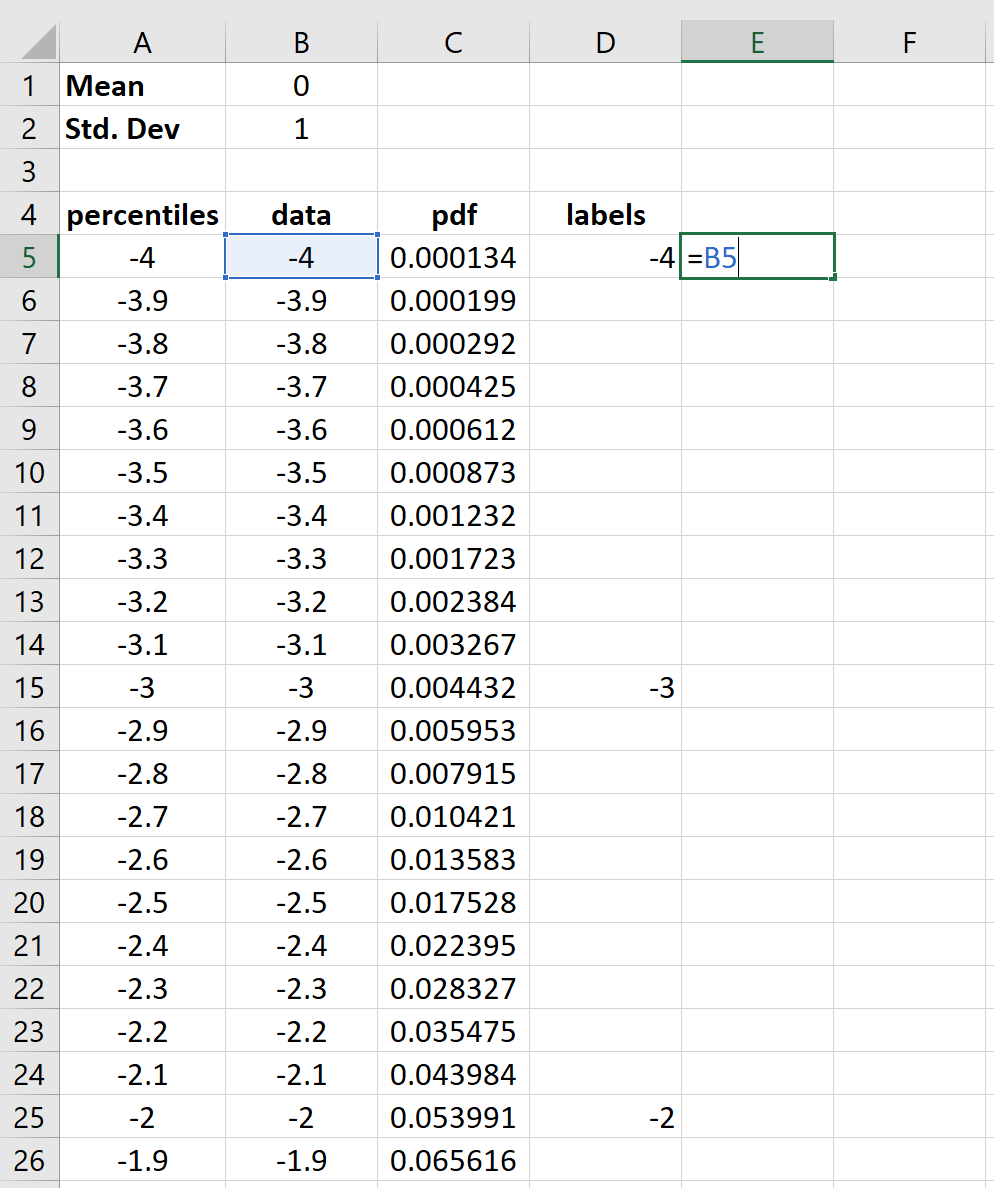
Шаг 2: Создайте ячейки для процентилей от -4 до 4 с шагом 0,1.
…
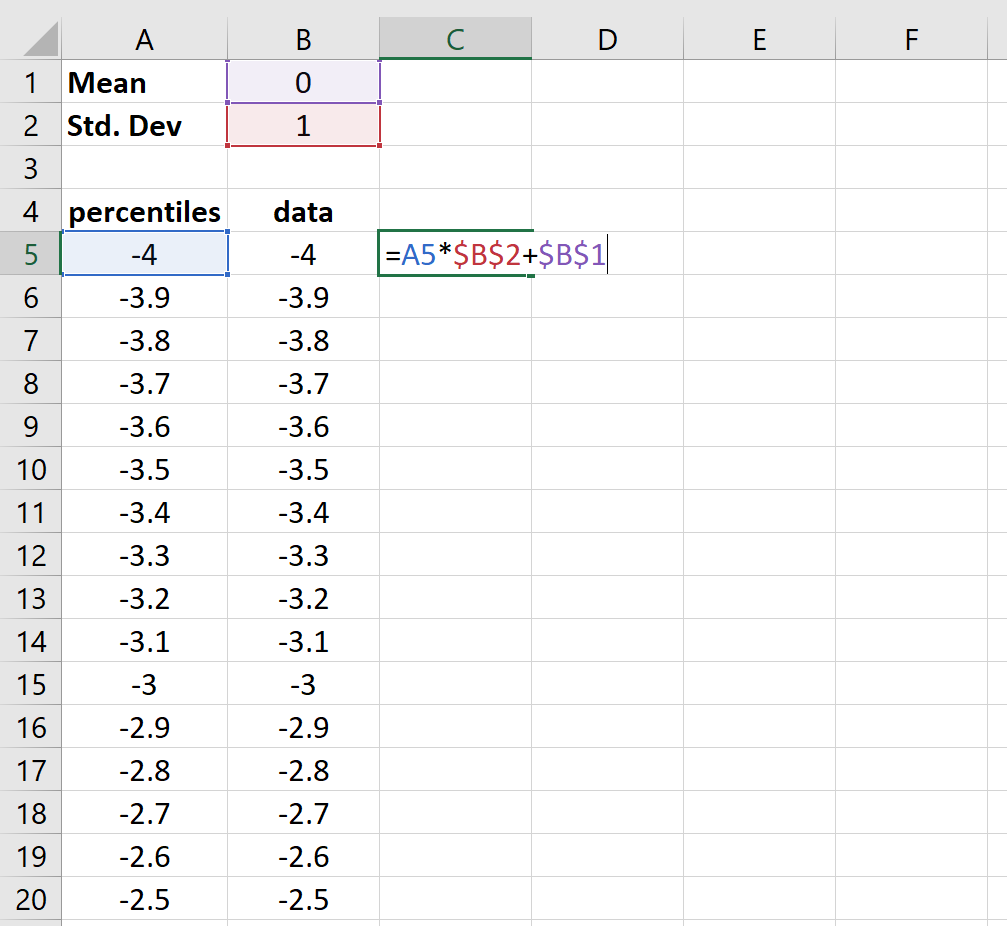
Шаг 3: Создайте столбец значений данных, которые будут использоваться на графике.
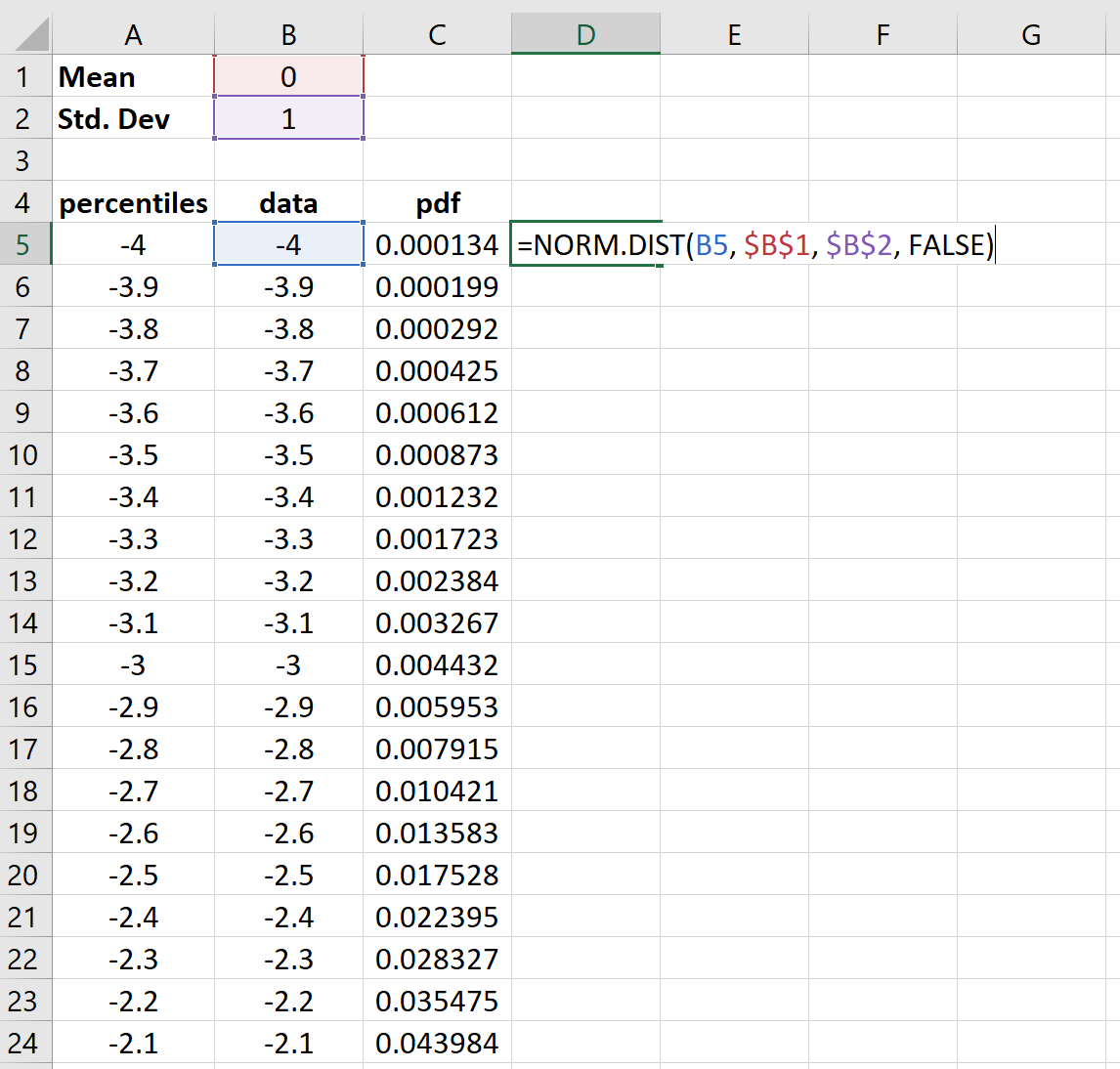
Шаг 4: Найдите значения для нормального распределения PDF.
Шаг 5: Создайте метки графика по оси X только для целочисленных процентилей.
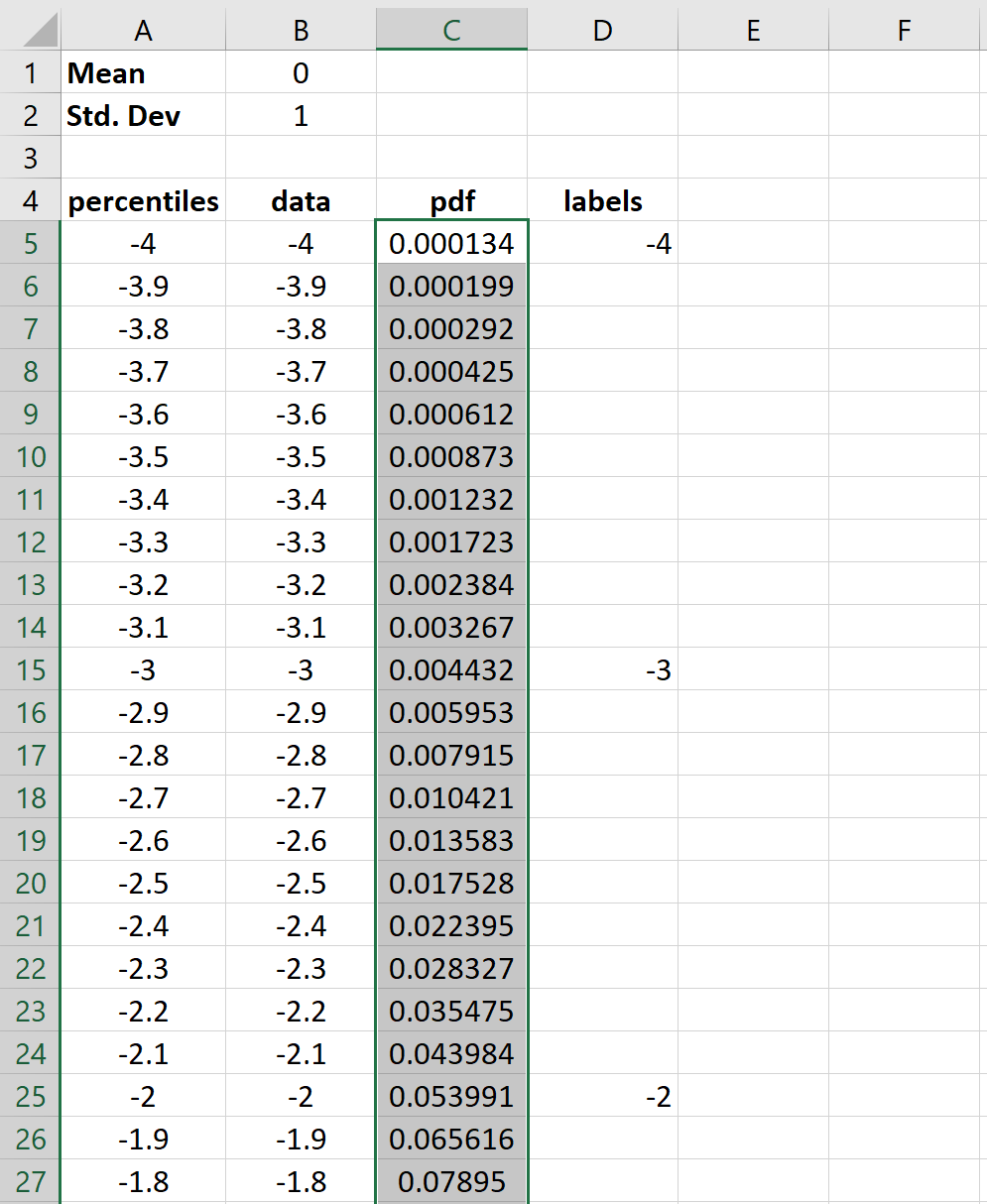
Шаг 6: Сделайте кривую колокола.
Сначала выделите все значения в столбце pdf :
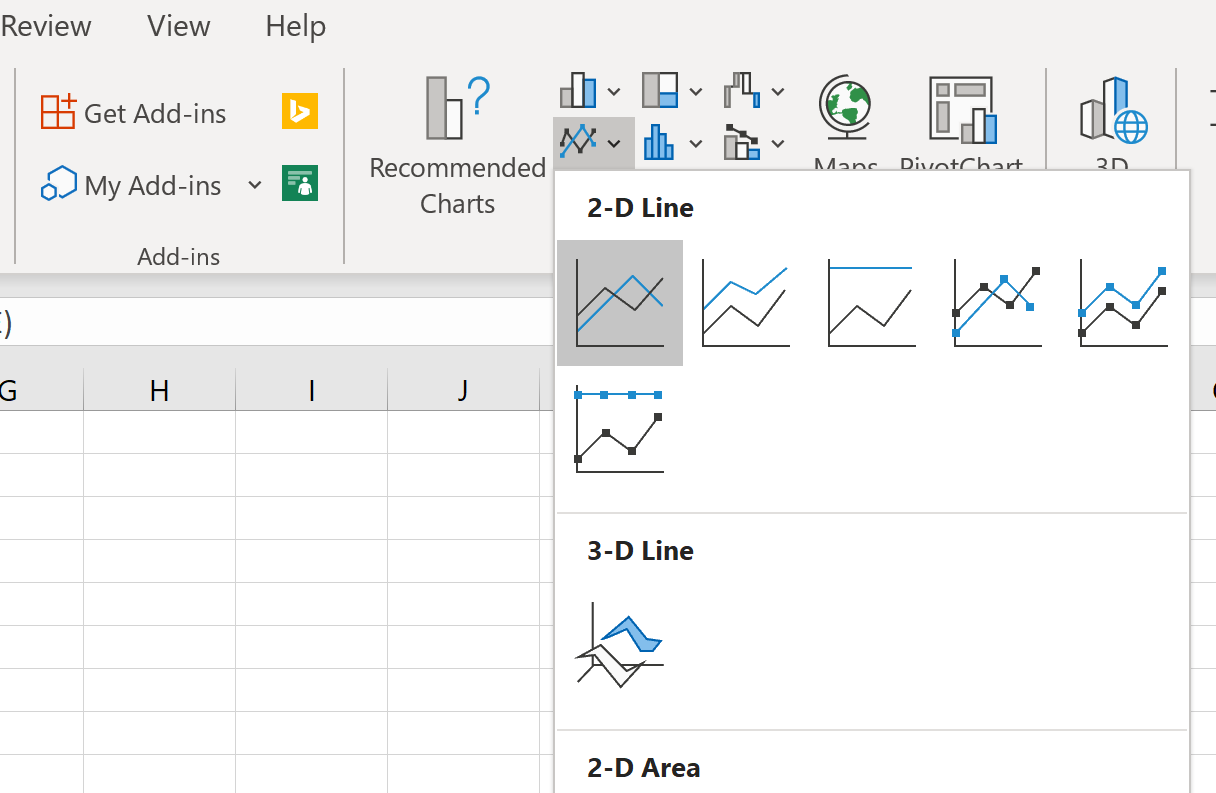
Затем в группе « Диаграммы » на вкладке « Вставка » щелкните первый параметр графика в категории « Вставить линию или диаграмму с областями»:
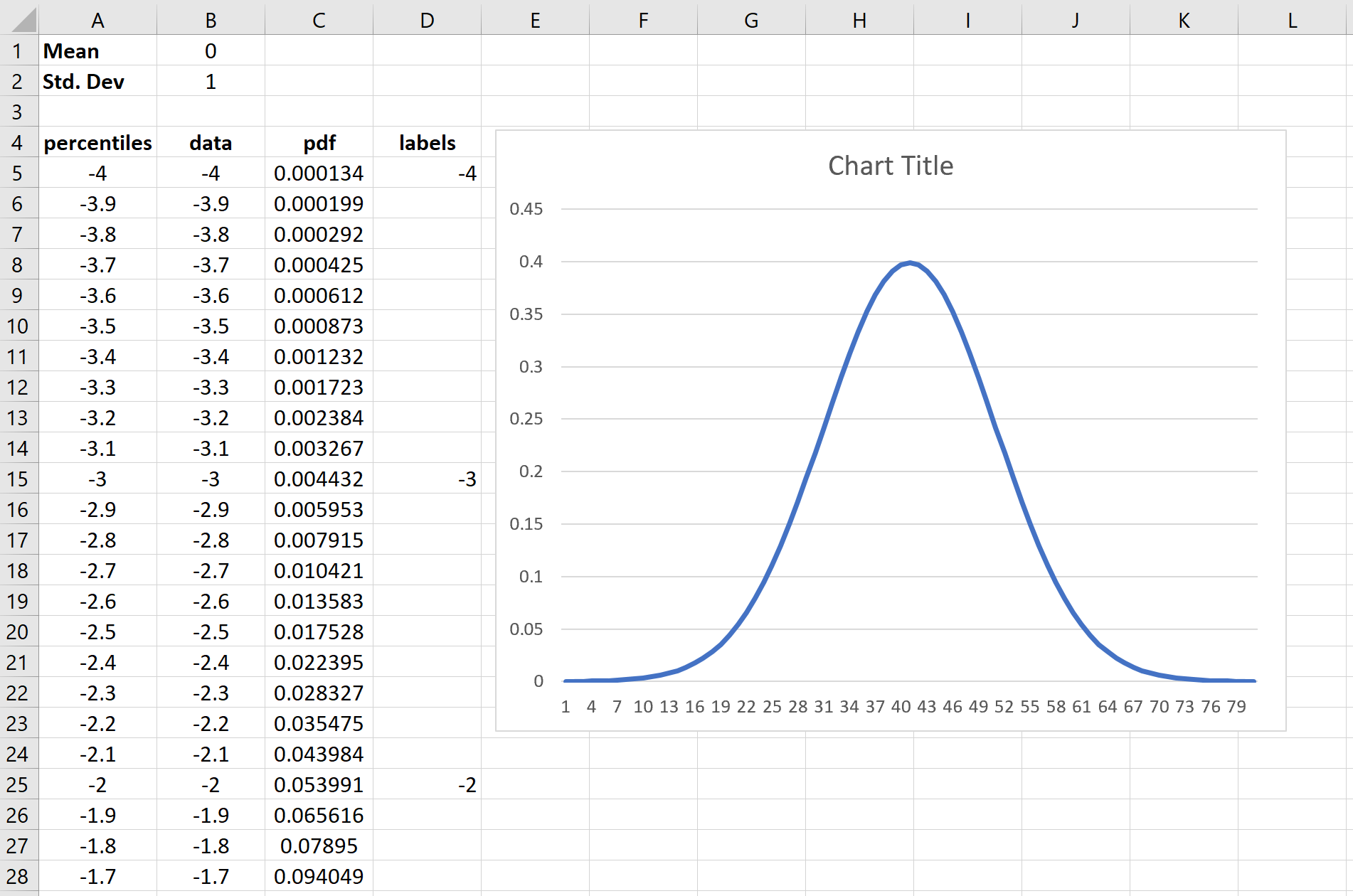
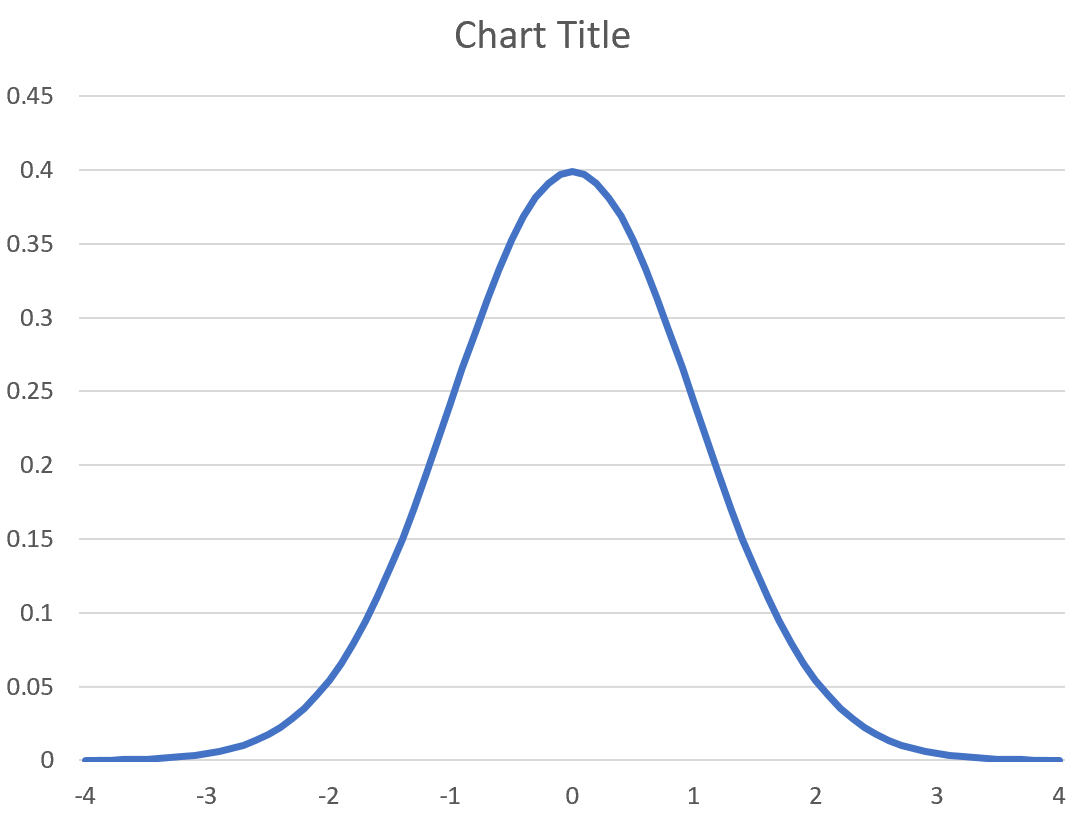
Автоматически появится кривая нормального распределения:
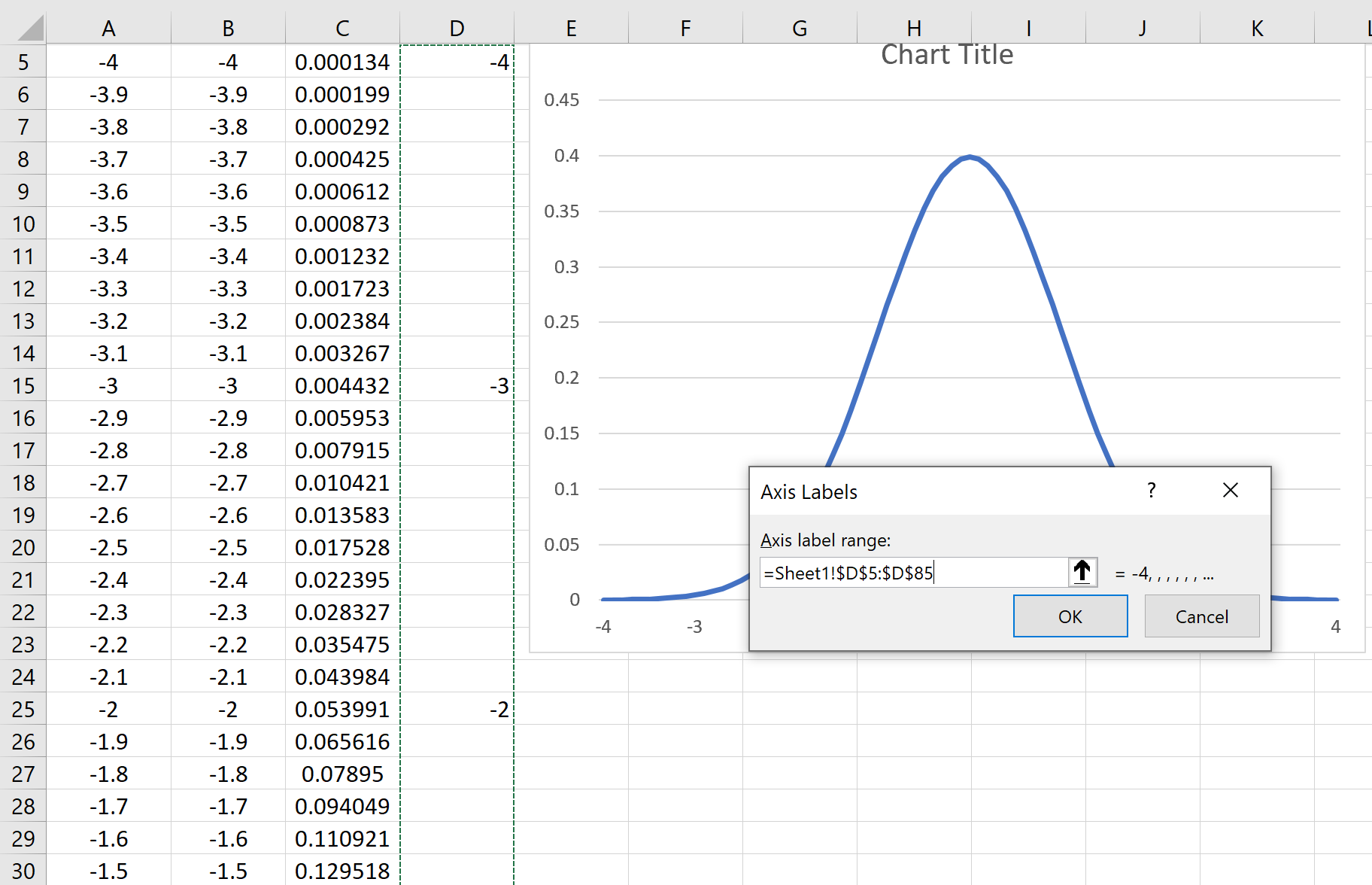
Шаг 7: Измените метки оси X.
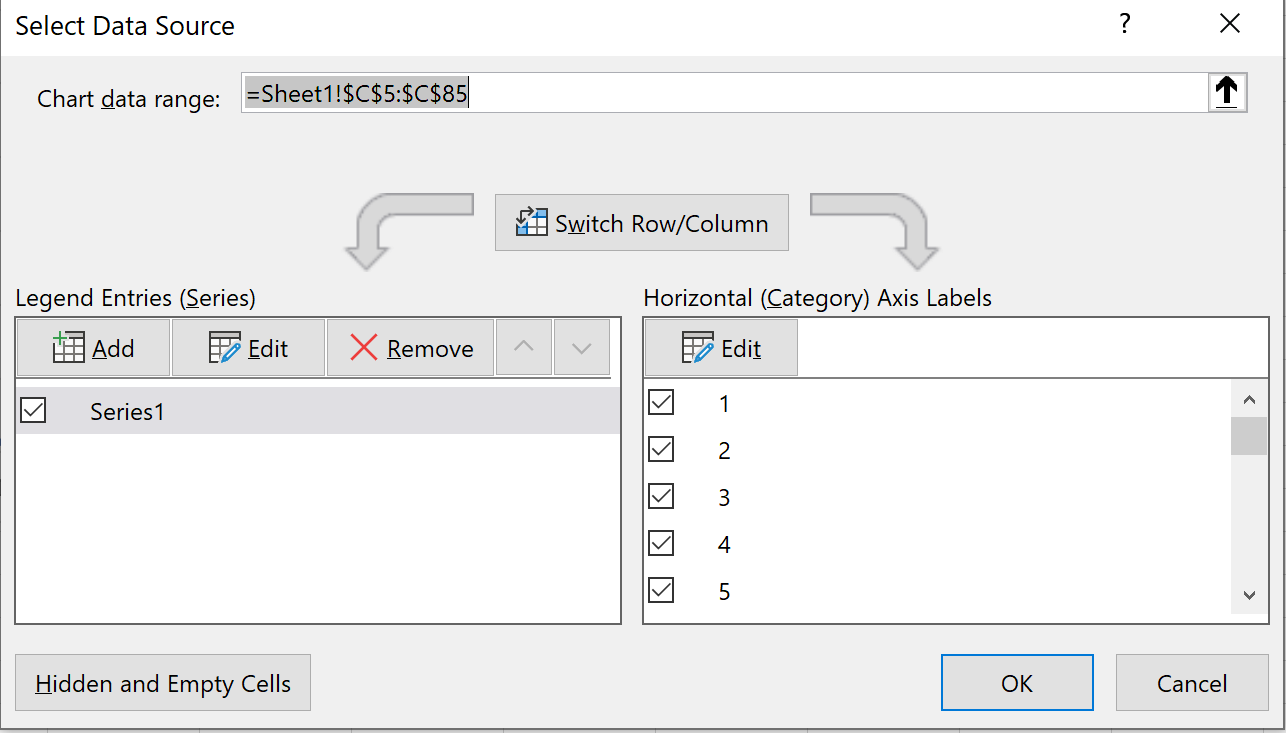
Щелкните правой кнопкой мыши в любом месте диаграммы и выберите Выбрать данные.Появится новое окно. Нажмите кнопку « Редактировать » в разделе «Метки горизонтальной оси»:
Выберите диапазон ячеек, в которых расположены метки оси X. В нашем случае это диапазон ячеек D5:D85.Затем нажмите ОК .
Метки оси X будут обновляться автоматически:
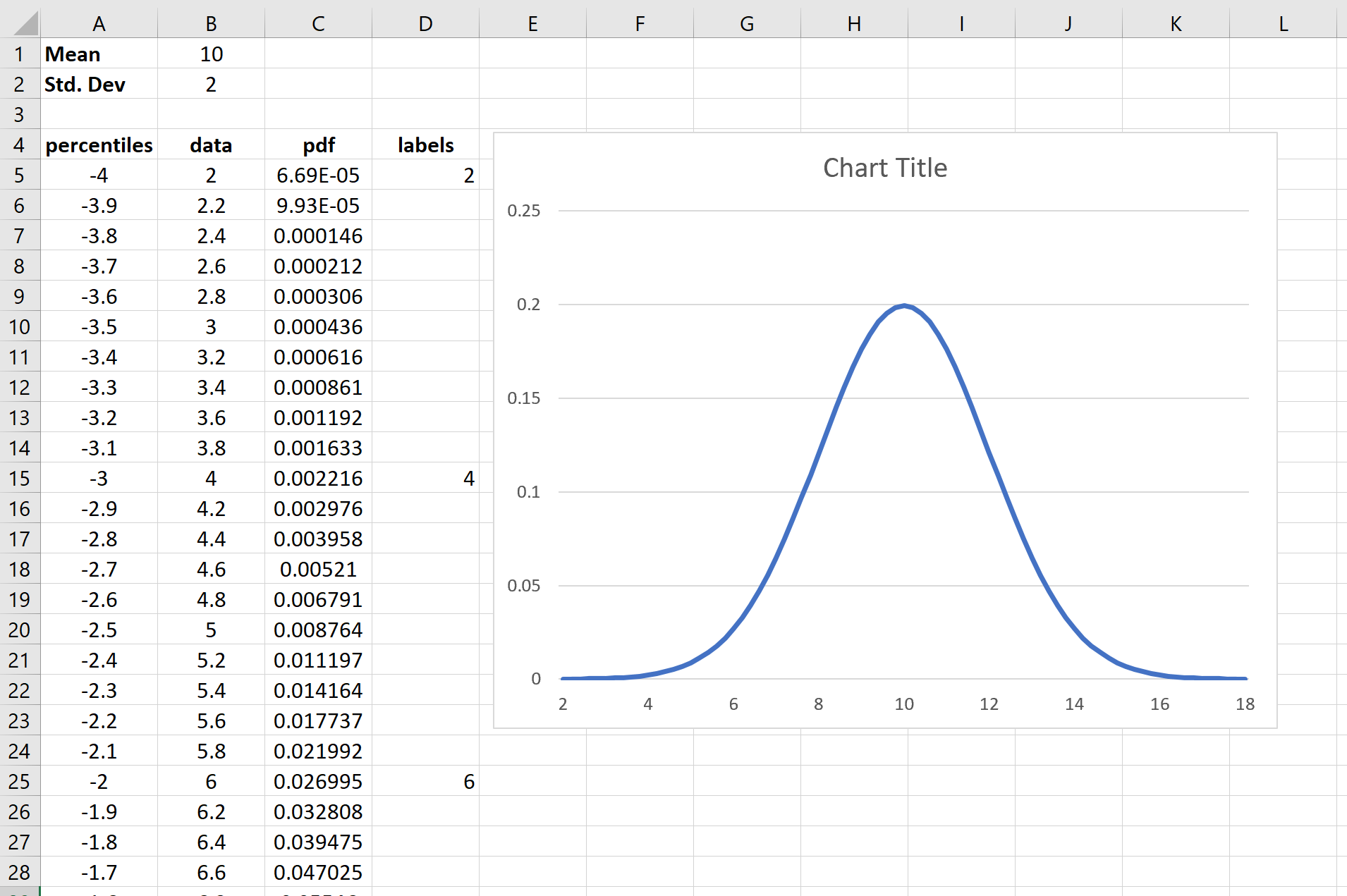
Вы заметите, что если вы измените среднее значение и стандартное отклонение, кривая нормального распределения обновится автоматически. Например, вот во что превращается кривая нормального распределения, если мы используем среднее значение = 10 и стандартное отклонение = 2:
Вы можете изменить заголовок диаграммы, добавить метки осей и изменить цвет, если хотите сделать диаграмму более эстетичной.
Бесплатный шаблон
Не стесняйтесь загружать этот бесплатный шаблон , который использовался для создания точной колоколообразной кривой в этом уроке.
Дополнительные ресурсы
Введение в нормальное распределение
Обычный калькулятор CDF
Как построить нормальное распределение в R
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.