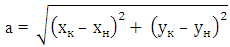Используйте функцию ПРОСМОТР, одну из функций поиска и работы со ссылками, когда нужно взять одну строку или столбец и найти значение, находящееся в той же позиции в другой строке или столбце.
Предположим, что вы знаете артикул детали автомобиля, но не знаете ее цену. Тогда, используя функцию ПРОСМОТР, вы сможете вернуть значение цены в ячейку H2 при вводе артикула в ячейку H1.

Используйте функцию ПРОСМОТР для поиска в одной строке или одном столбце. В приведенном выше примере рассматривается поиск цен в столбце D.
Советы: Рассмотрим одну из новых функций подстановки в зависимости от используемой версии.
-
Используйте функцию ВПР для поиска данных в одной строке или столбце, а также для поиска в нескольких строках и столбцах (например, в таблице). Это расширенная версия функции ПРОСМОТР. Посмотрите видеоролик о том, как использовать функцию ВПР.
-
Если вы используете Microsoft 365, используйте функцию XLOOKUP — это не только быстрее, но и в любом направлении (вверх, вниз, влево, вправо).
Функцию ПРОСМОТР можно использовать двумя способами: в векторной форме и в форме массива.
-
Векторная форма: используйте эту форму LOOKUP для поиска значения в одной строке или в одном столбце. Используйте векторную форму, если нужно указать диапазон, содержащий значения, которые необходимо сопоставить. Например, если вы хотите найти значение в столбце A, вниз до строки 6.
-
Форма массива. Мы настоятельно рекомендуем использовать ВПР или ГПР вместо формы массива. Посмотрите это видео об использовании ВПР. Форма массива предоставляется для совместимости с другими программами электронной таблицы, но ее функциональные возможности ограничены.
Массив — это набор значений в строках и столбцах (например, в таблице), в которых выполняется поиск. Например, если вам нужно найти значение в первых шести строках столбцов A и B, это и будет поиском с использованием массива. Функция ПРОСМОТР вернет наиболее близкое значение. Чтобы использовать форму массива, сначала необходимо отсортировать данные.
Векторная форма
При использовании векторной формы функции ПРОСМОТР выполняется поиск значения в пределах только одной строки или одного столбца (так называемый вектор) и возврат значения из той же позиции второго диапазона.
Синтаксис
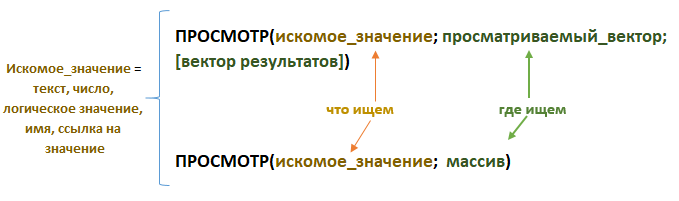
ПРОСМОТР(искомое_значение; просматриваемый_вектор; [вектор_результатов])
Функция ПРОСМОТР в векторной форме имеет аргументы, указанные ниже.
-
Искомое_значение. Обязательный аргумент. Значение, которое функция ПРОСМОТР ищет в первом векторе. Искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
-
Просматриваемый_вектор Обязательный аргумент. Диапазон, состоящий из одной строки или одного столбца. Значения в аргументе просматриваемый_вектор могут быть текстом, числами или логическими значениями.
Важно: Значения в аргументе просматриваемый_вектор должны быть расположены в порядке возрастания: …, -2, -1, 0, 1, 2, …, A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
-
result_vector Необязательный. Диапазон, содержащий только одну строку или столбец. Размер result_vector должен совпадать с размером lookup_vector. Он должен иметь одинаковый размер.
Замечания
-
Если функции ПРОСМОТР не удается найти искомое_значение, то в просматриваемом_векторе выбирается наибольшее значение, которое меньше искомого_значения или равно ему.
-
Если искомое_значение меньше, чем наименьшее значение в аргументе просматриваемый_вектор, функция ПРОСМОТР возвращает значение ошибки #Н/Д.
Примеры векторов
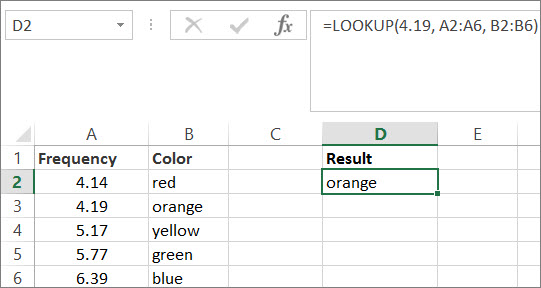
Чтобы лучше разобраться в работе функции ПРОСМОТР, вы можете сами опробовать рассмотренные примеры на практике. В первом примере у вас должна получиться электронная таблица, которая выглядит примерно так:
-
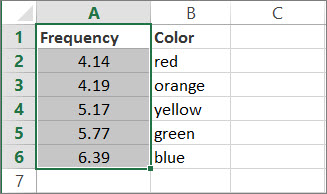
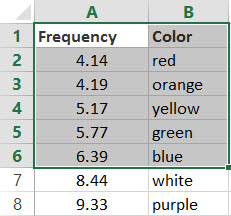
Скопируйте данные из таблицы ниже и вставьте их в новый лист Excel.
Скопируйте эти данные в столбец A
Скопируйте эти данные в столбец B
Частота
4,14
Цвет
красный
4,19
оранжевый
5,17
желтый
5,77
зеленый
6,39
синий
-
Теперь скопируйте формулы ПРОСМОТРА из приведенной ниже таблицы в столбец D своего листа.
Скопируйте эту формулу в столбец D
Ниже описано, что эта формула означает
Предполагаемый результат
Формула
=ПРОСМОТР(4,19; A2:A6; B2:B6)
Поиск значения 4,19 в столбце A и возврат значения из столбца B, находящегося в той же строке.
оранжевый
=ПРОСМОТР(5,75; A2:A6; B2:B6)
Поиск значения 5,75 в столбце A, соответствующего ближайшему наименьшему значению (5,17), и возврат значения из столбца B, находящегося в той же строке.
желтый
=ПРОСМОТР(7,66; A2:A6; B2:B6)
Поиск значения 7,66 в столбце A, соответствующего ближайшему наименьшему значению (6,39), и возврат значения из столбца B, находящегося в той же строке.
синий
=ПРОСМОТР(0; A2:A6; B2:B6)
Поиск значения 0 в столбце A и возврат значения ошибки, так как 0 меньше наименьшего значения (4,14) в столбце A.
#Н/Д
-
Чтобы эти формулы выводили результат, может потребоваться выделить их на листе Excel и нажать клавишу F2, а затем — ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Форма массива
Совет: Мы настоятельно рекомендуем использовать ВПР или ГПР вместо формы массива. См. это видео о функции ВПР. В нем приведены примеры. Форма поиска массива предоставляется для обеспечения совместимости с другими программами электронной таблицы, но ее функциональные возможности ограничены.
Форма массива функции ПРОСМОТР просматривает первую строку или первый столбец массив, находит указанное значение и возвращает значение из аналогичной позиции последней строки или столбца массива. Эта форма функции ПРОСМОТР используется, если сравниваемые значения находятся в первой строке или первом столбце массива.
Синтаксис
ПРОСМОТР(искомое_значение, массив)
Функция ПРОСМОТР в форме массива имеет аргументы, указанные ниже.
-
Искомое_значение. Обязательный аргумент. Значение, которое функция ПРОСМОТР ищет в массиве. Аргумент искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
-
Если функции ПРОСМОТР не удается найти искомое_значение, то в массиве выбирается наибольшее значение, которое меньше искомого_значения или равно ему.
-
Если искомое_значение меньше, чем наименьшее значение в первой строке или первом столбце (в зависимости от размерности массива), то функция ПРОСМОТР возвращает значение ошибки #Н/Д.
-
-
массив. Обязательный аргумент. Диапазон ячеек, содержащих текст, числа или логические значения, которые требуется сравнить с искомым значением.
Форма массива функции ПРОСМОТР очень похожа на функции ГПР и ВПР. Различие заключается в том, что функция ГПР ищет искомое_значение в первой строке, функция ВПР — в первом столбце, а функция ПРОСМОТР выполняет поиск в соответствии с размерностями массива.
-
Если ширина массива больше его высоты (т. е. есть массив имеет больше столбцов чем строк), то функция ПРОСМОТР ищет искомое_значение в первой строке.
-
Если высота массива больше его ширины (т. е. массив имеет больше строк, чем столбцов), то функция ПРОСМОТР выполняет поиск в первом столбце.
-
Используя функции ГПР и ВПР, можно указывать индекс по направлению вниз и вправо, а функция ПРОСМОТР всегда выбирает последнее значение в строке или столбце.
Важно: Значения в массиве должны быть расположены в порядке возрастания: …, -2, -1, 0, 1, 2, …, A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
-
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор
– это направленный отрезок прямой.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
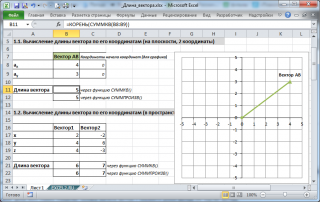
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a
x
и a
y
, то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение
=КОРЕНЬ(СУММКВ(B8:B9))
позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки
B8:B9
, см.
файл примера
).
Функция
СУММКВ()
возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =
B8*B8+B9*B9
.
В
файле примера
также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение
=КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9))
.
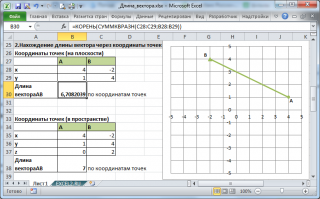
2. Нахождение длины вектора через координаты точек
Если вектор
задан через координаты точек его начала и конца, то формула будет другой
=КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны
C28:C29
и
B28:B29
соответственно.
Функция
СУММКВРАЗН()
в
озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
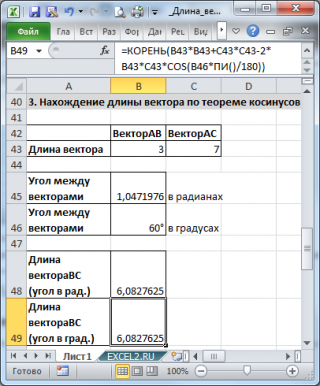
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу
=КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках
B43:B43
содержатся длины векторов а и b, а в ячейке
В45
— угол между ними в радианах (в долях числа
ПИ()
).
Если угол задан в градусах, то формула будет немного отличаться
=КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание
: для наглядности в ячейке со значением угла в градусах можно применить
пользовательский формат
, см. например, статью
Отображение широты и долготы в MS EXCEL
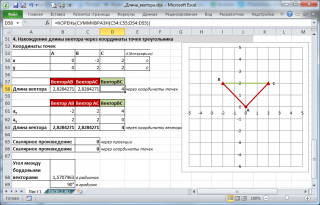
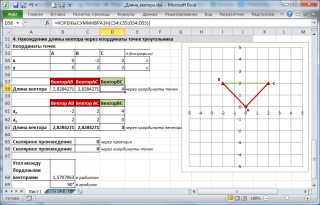
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле
=КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55))
.
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
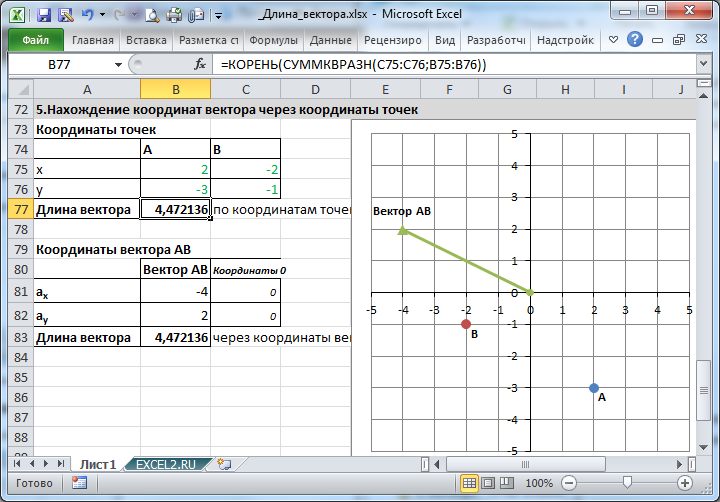
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
6.1. Векторы
В
- сложение — два вектора а и b с одинаковым числом компонент образуют новый вектор с:сi= ai+ bi ;
- умножение на число — каждая компонента вектора умножается на число, т.е. b = λа означает bi= λаi
здесь i — номер компоненты вектора.
Упражнение 6.1.1. Сложить два вектора:
- Ввести в первую строку вектор Х — (А1:Е1)
- Ввести во вторую строку вектор Y — (А2:Е2)
- Найти сумму векторов –
- выделить блок ячеек для результата в третьей строке ( А3:Е3 );
- ввести в строке формул =А1:Е1+А2:Е2
- нажать Ctrl+Shift+Enter.
Иллюстрация к примеру — рис. 14.

Рис. 14. Иллюстрация к упражнению 6.1.1.
Задача 6.1.1 . Умножить вектор на число.
Умножение вектор-столбца на вектор-строку.

1-й способ: записать в ячейку В2 формулу =$А2*В$1 и скопировать ее в остальные ячейки диапазона B2:D5.
2 -й способ (более экономный): выделить блок B2:D5. Запишем в него формулу массива <=А2:А5*B1:D1>.
А
Примечание. Если ввести формулу <=B1:D1* А2:А5>, то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомножителе должно равняться числу строк во втором сомножителе).
У
пражнение 6.1.3. Вычислить скалярное произведение двух векторов.
- У
становить курсор в ячейку, где нужен результат.
- Щёлкнуть кнопку автосуммы — .
- Выделить массив Х (А5:А12).
- Нажать знак умножить —*.
- Выделить массив Y (B5:B12).
- Нажать Ctrl + Shift + Enter.
Примечание. Тот же результат можно получить с помощью обычной функции: =СУММПРОИЗВ (А5:А12, В5:В12).
6.2. Матричные операции
Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.
Упражнение 6.2.1. Сложение матриц.
Задание. Сложить матрицы М и N, где
Решение.
M= 

1-й способ:
- Ввести матрицу М в блок А1:С2, а матрицу N в блок Е1:G2.
- В блок А4:С5 ввести табличную формулу <= А1:С2 + E1:G2>.
Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы.
Использование имен делает процедуру ввода табличной формулы намного проще:
- Задать диапазонам А1:С2 и E1:G2 имена М и N.
- В блок E4:G5 ввести табличную формулу < = М + N >.
Результат, естественно, тот же: M+N =
Упражнение 6.2.2 . Вычислить линейную комбинацию матриц 2*М — N (матрицы М.и N из упражнения 6.2.1.).
Решение. В блок А7:С8 ввести табличную формулу <= 2*М — N >.
Результат: 2*M — N =
Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложении матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сложение.
Д
МОБР — вычисление обратной матрицы;
МУМНОЖ — перемножение матриц;
Примечание. Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.
У
Решение. Разместить исходную матрицу в блоке А1 :СЗ.
- В ячейке Е2 поместить формулу для вычисления определителя = МОПРЕД (А1:СЗ).
- В блок А5:С7 ввести формулу для вычисления обратной матрицы:
- выделить блок А5:С7 (он имеет три строки и три столбца, как и исходная матрица).
- Ввести формулу <=МОБР (А1:СЗ)>.
Примечания:
- При использовании Мастера функций нужно завершать ввод нажатием комбинации клавиш Ctrl+Shift+Enter (вместо щелчка по кнопке «ОК»).
- Для удобства работы рекомендуется задавать имена исходной матрице и обратной матрице.
- Проверить правильность вычисления обратной матрицы умножением ее на исходную:
- задать имена исходной матрице — А и обратной матрице — АО;
- в блок D5:F7 ввести формулу .
- к
ак и следовало ожидать, получилась матрица, близкая к единичной.
Рис. 16. Иллюстрация к упражнению 6.2.3.
У
Решение:
пражнение 6.2.4. Вычислить абсолютные отклонения величин в матрицах.
В блок А9:С11 ввести табличную формулу <= abs (A-AО)>.

Пример вычисления определителя матрицы
А, введенной в формулу как массив констант: =МОПРЕД(<-73; 78; 24:
Задача 6.2.2 . При каком значении элемента а33 определитель матрицы А обратится в нуль.
Задача 6.2.3. Дана матрица S = 
Е — единичная матрица.
Задача 6.2.4. Вычислить обратную матрицу для
и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы.
Набор матричных операций в Excel беден.
Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive .
Вычисление длины (модуля) вектора в EXCEL
history 14 декабря 2015 г.
- Группы статей
- Пользовательский формат
- Векторы
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
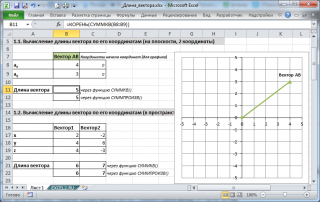
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
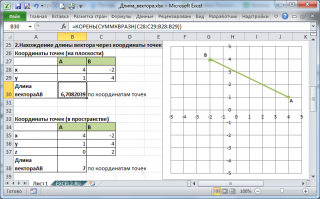
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
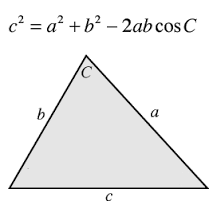
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
Векторы и матрицы в Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Векторы и матрицы в Excel
C овокупность n чисел 
Два n -мерных вектора 


Суммой двух n -мерных векторов 

Операция сложения векторов обладает свойствами коммутативности 

Вектор 
Вектор 

Операция вычитания векторов определяется как сложение с противоположным вектором 
Под произведением вектора 

Умножение вектора на число обладает свойством ассоциативности 

Модуль (норма, длина) вектора 
Пример вычисления модуля вектора 
Р
исунок 1 – Вычисление длины вектора
Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.
В общем случае скалярное произведение двух векторов 




Операция скалярного умножения векторов обладает следующими свойствами:

В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).
Векторным произведением вектора 







Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.
Р
исунок 2 – Определение скалярного произведения двух векторов
Значение векторного произведения определяется следующим образом:
На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов 
Р
исунок 4 – Вычисление векторного произведения векторов
Перейдем к рассмотрению основных операций матричного исчисления.
Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :
Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:
Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.
Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается
При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы 
Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:
Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:
Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица
называемая транспонированной по отношению к матрице А.
Если А=А Т , то такая матрица называется симметричной.
В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.
Р
исунок 5 – Вызов функции ТРАНСП
Пример. Имеем исходную матрицу

Из определения ясно, что транспонированной будет матрица А Т :

Решение задачи в Excel представлено на рисунке 6
Рисунок 6 – Транспонирование матрицы
Порядок решения следующий:
— определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);
— в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);
— выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;
— нажать Shit + Ctrl + Enter .
Суммой матриц А


Произведение матрицы на число — то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:
Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы 





В Excel для вычисления произведения матриц используется функция
= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).
Р
исунок 7 – Умножение матриц
Формула для расчета произведения матриц должна быть введена как формула массива!
Пусть даны матрицы
Вычислим их произведение в Excel (рисунок 8).
— шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);
— 
—
шаг 3 – выделить результирующий массив и нажать F2;
—
шаг 3 – нажать Shift+Ctrl+Enter.
Рисунок 8 – Вычисление произведения матриц
Действие умножения матрицы на матрицу обладает свойствами:
Отметим, что в общем случае
Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.
При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).
Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.
Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.
Для матрицы 2х2 определитель вычисляется как
Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:



Возможно разложение как по строкам, так и по столбцам.
В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).
Рисунок 9 – Расчет определителя матрицы
Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .
Детерминант треугольной матрицы равен произведению ее диагональных элементов
Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E
Обратную матрицу можно найти по следующей формуле:



Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).
Рисунок 10 – Расчет обратной матрицы
Заметим, что функция применяется к массиву как в ранее приведенных примерах.
Проверим выполнение условия А А -1 = E (рисунок 11)
Р
исунок 11- Произведение матрицы на обратную матрицу
Собственным числом квадратной матрицы
называется такое число 

Или, по-другому, собственными числами матрицы А являются корни уравнения 
Матрица 


Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:
Необходимо найти такие значения , при котором
Оформим лист Excel следующим образом (рисунок 12):
Рисунок 12 – Вычисление собственного числа матрицы
В ячейку B2 введено =2-F2; в ячейку С3 — =-6-F2; в ячейку D4 — =1-F2.
Из рисунка 12 видно, что при =0 определитель также равен 0, т.е. =0 есть первое собственное число матрицы.
Д
ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения , отображаемом в ячейке $F$2.
Рисунок 13 – Вычисление собственного числа матрицы
О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).
Рисунок 14 – Результат поиска решения
Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат =0.
П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):
Рисунок 15 – Ввод ограничения
В результате поиска получаем второе значение собственного числа: =3.
Повторим поиск при ограничении.
Если установить в ограничениях >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях
П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)
Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении
Рисунок 17 — Результат поиска третьего собственного числа
Собственным вектором соответствующим собственному числу λ называют такой вектор 
Найдем собственный вектор матрицы
Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.
1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).
2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.
3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.
4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор 
5. В ячейки (H2:H4) заносим умножение столбца 
6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).
7. В главном меню открываем Сервис — Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.
Нажать кнопку « Выполнить ».
В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).
Рисунок 18 – Определение собственного вектора матрицы
Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.
Задания для самостоятельной работы
Повторить решение всех примеров, приведенных в Лекции №5.
Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15
Определить длину векторов.
Вычислить сумму и разность векторов.
Определить скалярное произведение этих векторов.
Определить угол между векторами.
Определить векторное произведение двух векторов.
Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.
Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.
Получить транспонированные матрицы исходных матриц.
Проверить правильность решения путем умножения исходной матрицы на транспонированную.
Определить произведение исходных матриц.
Найти матрицу 3-го порядка для исходной квадратной матрицы.
Определить детерминант исходной квадратной матрицы.
источники:
http://excel2.ru/articles/vychislenie-dliny-modulya-vektora-v-ms-excel
http://infourok.ru/vektori-i-matrici-v-ecel-1119397.html
Функция ПРОСМОТР применяется, когда необходимо из одного столбца/строки найти соответствующее значение в той же позиции (то есть, напротив значения) из другого столбца/строки.
Практическая работа функции ПРОСМОТР в Excel
Как работает функция ПРОСМОТР? Синтаксис функции выглядит следующим образом:
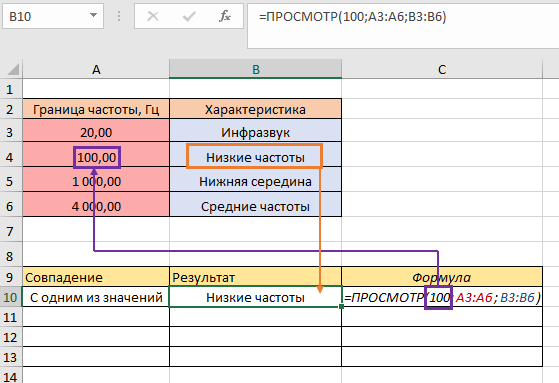
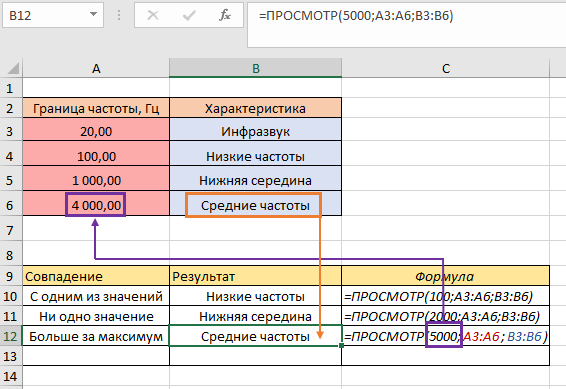
Первый аргумент «Искомое_значение» может быть любого типа в зависимости от данных таблицы и нужного результата. Аргумент «Вектор_результатов» является необязательным, он должен иметь размер, одинаковый с аргументом «Просматриваемый_вектор». Второй вариант синтаксиса используется не так часто и предназначен для совместимости з другими программами. Лучше всего вместо массива использовать функцию ВПР. На первом примере рассмотрим принцип работы ПРОСМОТР и все нюансы выполнения задачи. У нас есть таблица с данными о граничном значении частоты звука и его характеристике. Для начала выполним простейшее задание – нам нужно найти характеристику для частоты 100 Гц. Указываем число «100», затем выбираем диапазон А3:А6, в котором находится искомое значение. Последним этапом указываем В3:В6, из которого возвратим характеристику:
В результате получили характеристику «Низкие частоты», поскольку именно это находится на одной позиции с числом «100» и совпадение произошло с одним из значений. Теперь проверим как работает формула, когда ищет значение, которое не имеет совпадений из данных. Например, укажем искомое число 2000 среди диапазона:
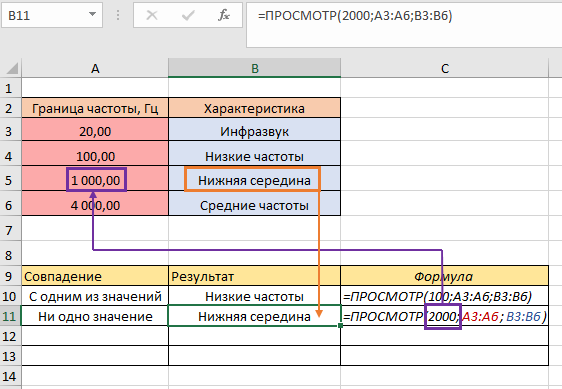
Результат мы все же получили. Формула сработала следующим образом – она нашла характеристику напротив ближайшего к числу «2000» значению в сторону уменьшения. То есть, «2000» попадает в диапазон «1000-4000», но «1000» меньше за «4000», поэтому возвратилось значение, соответствующее цифре «1000». Следующим шагом выберем число, больше за максимальное в столбце «Граница частоты, Гц», например, «5000»:
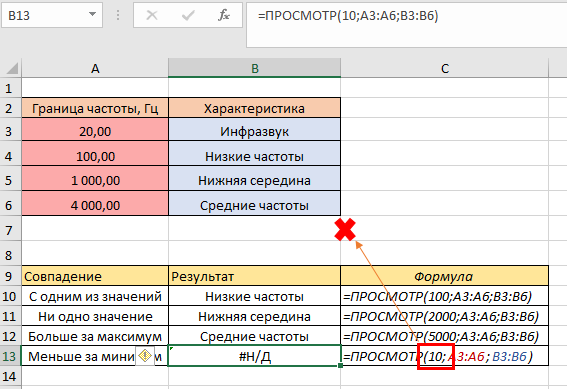
В ячейке В12 возвратилось «Средние частоты». Логика выполнения очень похожа на предыдущий пример – формула устремилась к меньшему ближайшему числу и выдала соответствующую характеристику. И последний пример – укажем число, которое будем искать, меньшее за минимальное, например, «10»:
Теперь у нас появилась ошибка, поскольку среди данных нет числа, меньшего за «10», формуле не на что опираться, и она возвратила ошибку.
Как использовать функцию ПРОСМОТР для разных задач
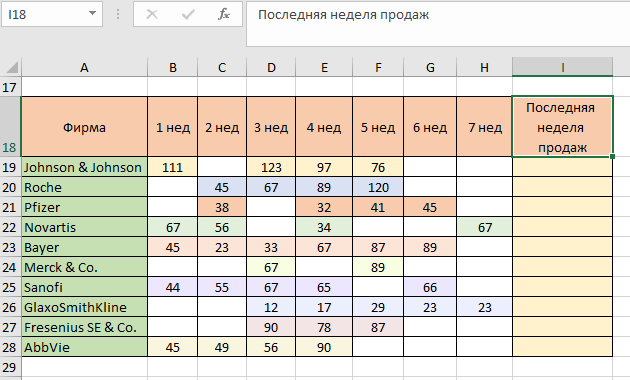
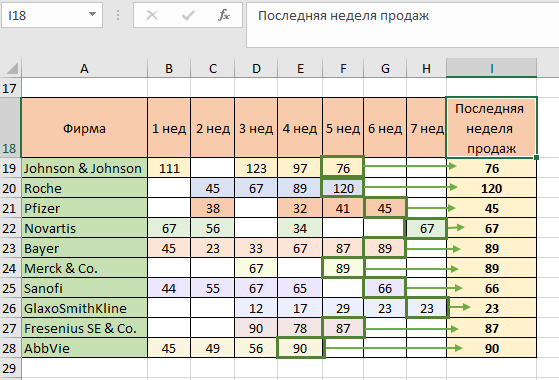
В следующем примере у нас будет таблица с продажами фирм в разные периоды. И будут также недели, в которые не было продаж, например, фирма Roche не имела продаж на 6 и 7 неделях:
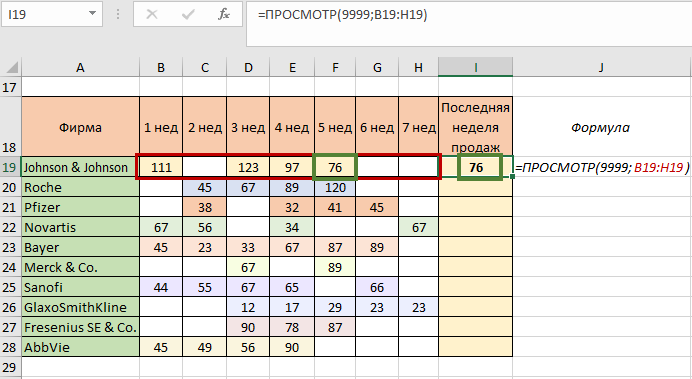
Наша задача состоит в том, чтобы извлечь те данные, которые были последними по каждой фирме. В случае, если бы таблица была полностью заполнена, информация по свежим продажам всегда была бы в столбце «7 нед». В этом примере работа фирм отличается. Из таблицы можем сделать вывод, что последние продажи фирмы Bayer были на 6 неделе, но фирм много, и для решения этой задачи воспользуемся функцией ПРОСМОТР. Искомое значение должно быть числом, которое будет больше любого имеющегося в таблице. Необязательно вычитывать, какое же число точно будет больше любого из таблицы, просто сразу укажем величину «9999». Затем для аргумента «Просматриваемый вектор» укажем диапазон «В19:Н19»:
Мы получили желаемое значение – информацию о самых свежих продажах, на 5 неделе были продажи объемом 76 условных единиц. Принцип работы формулы следующий: ПРОСМОТР просматривает содержимое каждой ячейки в диапазоне В19:Н19, сравнивая их с искомым значением. Если бы число из таблицы совпало с искомым, функция возвратила бы это число. Поскольку значение каждой следующей ячейки не совпадало идентично, ПРОСМОТР переходила от одной к следующей ячейке и возвратила значение последней проверяемой ячейки. Скопируем формулу до конца столбца и проверим, выполнили ли мы задание:
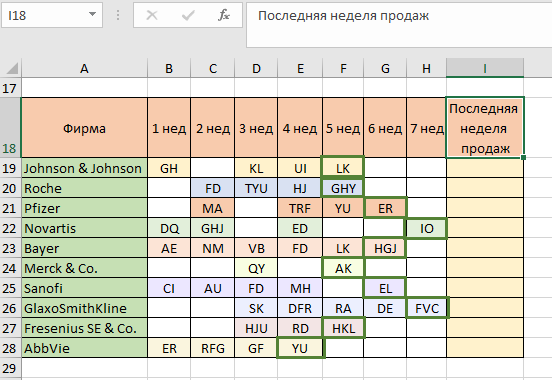
Как видим, по каждой фирме возвратились данные по последним продажам. Пусть вместо числовых значений у нас будут буквенные:
Принцип работы похожий, только теперь вместо очень большого числа нам нужно указать очень много букв – текст «яяяя». Дело в том, что «большой» текст – это код, который состоит из букв в следующем возрастании:
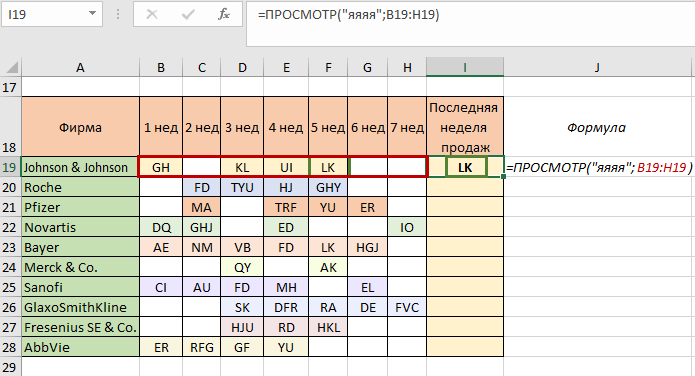
Заменяем искомый текст, оставляем тот же диапазон и смотрим результат:
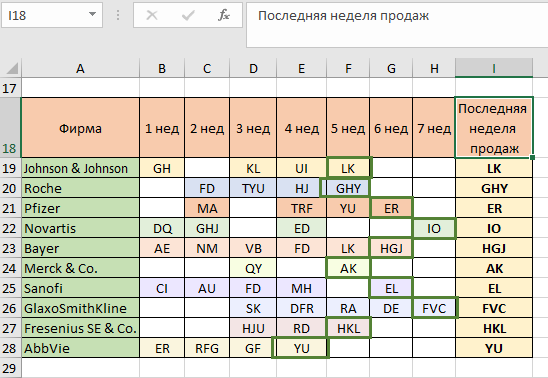
ПРОСМОТР так же отлично сработал на поиск последней заполненной ячейке по строке. Копируем формулу до конца столбца, чтобы выполнить задачу:
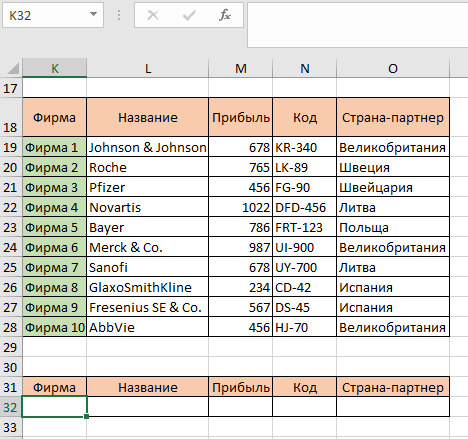
В следующем примере сделаем таблицу с выпадающим списком. У нас есть информация о фирмах. Нам нужно создать таблицу, в который мы выберем из списка нужную нам фирму и все данные по ней автоматически подтянутся:
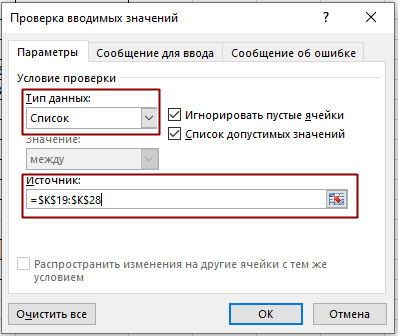
Первым этапом будет создание выпадающего списка из десяти фирм. Для начала убедитесь, что вы находитесь на нужной вам ячейке (клик по ячейке К32»). Переходим на вкладку «Данные», в группе «Работа с данными» выбираем «Проверка вводимых значений». Появится окно, в котором нужно среди элементов «Типа данных» выбрать список, а в «Источнике» указать диапазон. В нашем случае диапазоном будет список десяти фирм К19:К28:
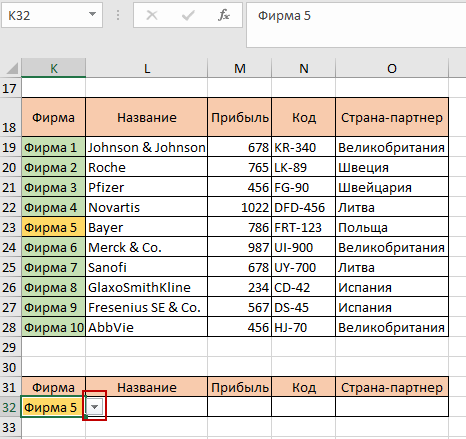
Сейчас возле ячейки К32 должен появиться указатель выпадающего списка, благодаря которому можно выбрать любую из десяти фирм:
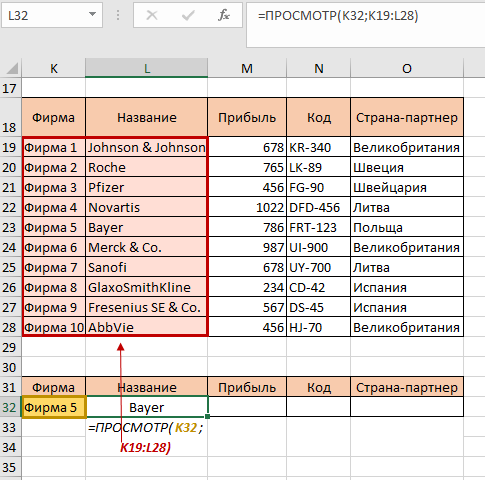
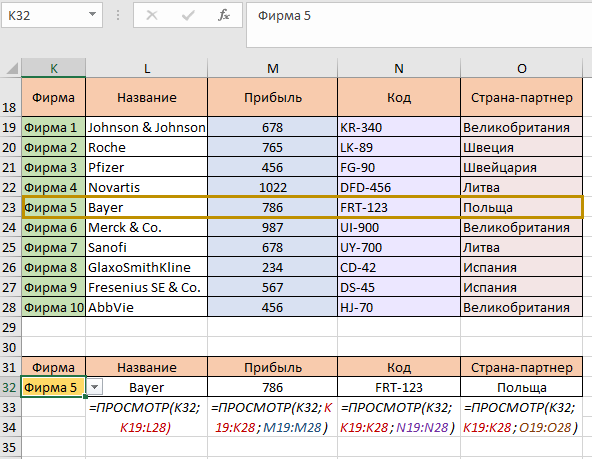
Теперь нам нужно организовать автоматическое подтягивание всех данных по выбранной фирме. В ячейке L32 пишем формулу ПРОСМОТР. В качестве искомого значения у нас будет ячейка К32, поскольку она будет меняться, и в зависимости от этих изменений будет меняться и совпадения «Фирма N = Название». Вторым аргументом будет диапазон К19:L28, в котором формула будет просматривать совпадения:
Сейчас видим результат Bayer, поскольку первая таблица содержит информацию, что Фирма 5 – это фирма с названием Bayer. Дальше так же мы строим формулы для прибыли, кода, и страны-партнера:
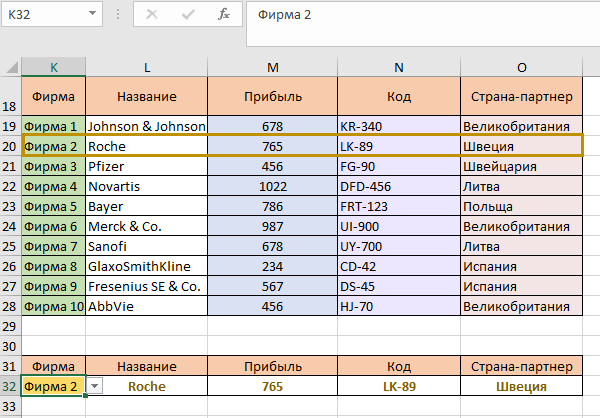
В формулах, где мы возвратим данные по прибыли, коду и стране-партнера второй аргумент разделится на два – просматриваемый вектор и вектор результатов. Первый будет неизменный – диапазон К19:К28, а второй – будет меняться в зависимости от столбца, из которого нужно возвратить данные. Как видим, по фирме 5 все получилось правильно – все элементы совпали. Теперь выберем любую другую фирму из списка, например, 2:
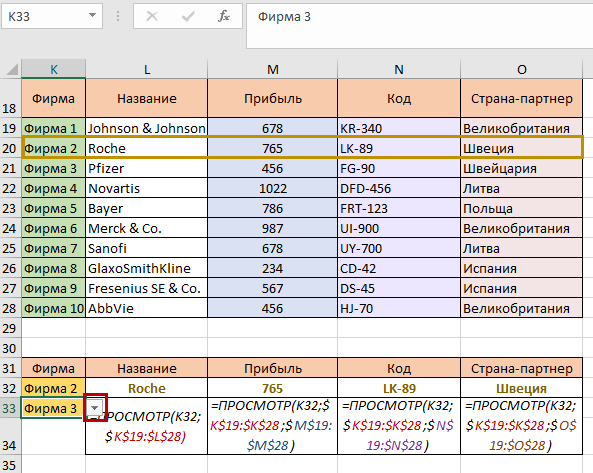
Сравниваем взглядом все совпадения. Наша таблица исправно выполняет работу. Так же мы можем немного расширить информацию во второй таблице. Пусть нам нужно сверять данные по двум фирмам одновременно. Для этого нам нужно, чтобы сразу две фирмы можно было выбирать и читать их характеристики. Сначала выполняем копирование ячейки К32 на один пункт вниз. Возле ячейки К33 так же должен быть указатель выпадающего списка. Затем копируем так же ячейки L32, M32, N32, O32. Однако, перед копированием нужно указать абсолютные ссылки для диапазонов, иначе формула съедет на одну позицию вниз и у нас будут ошибки:
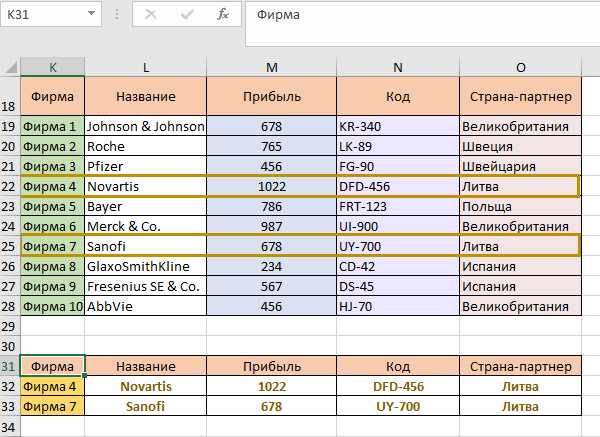
Теперь совершаем копирование и у нас есть два ряда с выпадающими списками фирм и информацией о них. Выберем фирму 4 и фирму 7:

Наша таблица полностью готова. Можно добавлять характеристики, количество фирм в обоих таблицах, все зависит от того, какая задача ждет выполнения.
history 19 декабря 2015 г.
- Группы статей
- Векторы
Найдем векторное произведение 2-х векторов с помощью функций MS EXCEL. Также создадим таблицу для проверки векторов на коллинеарность.
Сначала немного теории. Векторным произведением двух векторов а и b , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор c , что:
- он перпендикулярен обоим векторам а и b ;
- длина векторас равна произведению длин векторов а и b на синус угла между ними;
- вектор с направлен так, что тройка векторов а , b и с является правой ( с конца вектора с кратчайший поворот от вектора a к вектору b виден наблюдателю против часовой стрелки ).
Почему такое сложное определение? Дело в том, что результатом векторного произведения [ a х b ], в отличие от скалярного , является вектор. А для того, чтобы однозначно определить вектор нужно задать его длину (второй пункт определения) и направление (первый и третий пункты определения).
Векторное произведение двух векторов a = < a x ; a y ; a z > и b = < b x ; b y ; b z > в декартовой системе координат можно вычислить, используя формулы:
или в матричной форме:
Теперь вычислим векторное произведение в MS EXCEL. Встроенная функция к сожалению отсутствует. Кроме того, формула должна возвращать три значения, т.е. 3 координаты вектора. Это может быть реализовано только формулой массива (вариант, когда 3 координаты рассчитываются независимо, с использованием 3-х различных формул, очевиден, но не интересен, хотя и приведен файле примера ).
Пусть даны координаты векторов а и b , записанные в строках 8 и 9 (см. файл примера ).
Обратим внимание, что запись в матричной форме напоминает вычисление обратной матрицы методом алгебраических дополнений . Вместо единичных векторов i, j, k запишем вспомогательный вектор с координатами <1; 1; 1>и поместим его в строке 7 над векторами. Теперь у нас есть квадратная матрица А третьего порядка, для которой можно вычислить обратную матрицу.
Попробуем использовать функцию МОБР() для вычисления векторного произведения. Заметим, что три слагаемых из определения векторного произведения в матричной форме совпадают со значениями верхней строки матрицы алгебраических дополнений.
Примечание : Напомним, что алгебраическое дополнение A ij вычисляется по формуле A ij =(-1) i+j *М ij (где М — соответствующий минор, т.е. определитель, состоящий из элементов матрицы А за исключением всех элементов, расположенных на строке i и в столбце j).
Так как обратная матрица вычисляется по формуле:
то имея обратную матрицу, для вычисления верхней строки матрицы алгебраических дополнений и, соответственно, координат вектора с , необходимо ее транспонировать , а затем умножить ее на определитель матрицы А (той, что содержит координаты наших векторов а и b и единичный вектор).
Это реализовано с помощью формулы массива =ТРАНСП(МОБР(B7:D9))*МОПРЕД(B7:D9)
Коллинеарность векторов
Если два вектора коллинеарны, т.е. лежат на параллельных прямых, то их векторное произведение равно 0. В файле примеров приведена таблица для проверки векторов на коллинеарность.
Нахождение длины вектора с — результата векторного произведения
Из определения векторного произведения длина вектора с равна произведению длин векторов а и b на синус угла между ними.
Примечание : Как вычислить длины векторов по их координатам показано в статье Вычисление длины (модуля) вектора в MS EXCEL .
Синус угла найдем через тригонометрическую формулe sin 2 x+cos 2 x=1
Конечно, можно также сначала найти векторное произведение, а затем длину полученного вектора. Естественно, оба метода расчета дают одинаковые результаты.
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.
После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».
Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.
Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 11907 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

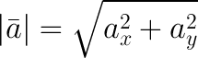
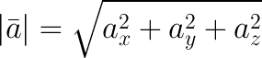



 становить курсор в ячейку, где нужен результат.
становить курсор в ячейку, где нужен результат.



 ак и следовало ожидать, получилась матрица, близкая к единичной.
ак и следовало ожидать, получилась матрица, близкая к единичной.