Как найти вариационный ряд в excel - Word и Excel - помощь в работе с программами

Как построить вариационный ряд в Excel

Вариационный ряд может быть:

— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).

— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.

Рассмотрим пример построения дискретного вариационного ряда.

Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения

Решение.

Алгоритм построения вариационного ряда:

1) Откроем таблицы Excel.

2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.

3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.

4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).

Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.

6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER

Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.

Построим полигон:

1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).

2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.

Рис.1.3. Пример 1. Построение полигона частот

Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel

Следующая тема: Построение интервального вариационного ряда в Excel.

Источник

Создание вариационного
ряда, вариационной кривой, определение среднего значения и среднеквадратичного
отклонения.

Для селекционера,
например, важно знать, сколько зерен содержит колос выведенного (выводимого) им
нового сорта пшеницы. В этой ситуации совершенно ясно, что подсчетом количества
зерен только в одном колосе не обойтись. Для определения числа зерен надо
воспользоваться достаточно большим количеством колосьев, скажем не менее сотни.
Приведем пример математической обработки результатов селекции.

Все поле
пшеницы, которое вырастил селекционер можно на математическом языке назвать
генеральной совокупностью. Подсчитать количество зерен в колосьях всей
генеральной совокупности, очевидно, не представляется возможным, но из всей
генеральной совокупности можно выбрать, скажем, сто колосьев и подсчитать
количество зерен в них. Эти сто колосьев будут называться выборкой из генеральной
совокупности, и они с определенной точностью будут отражать число зерен во всем
поле (генеральной совокупности). Чтобы по данным выборки иметь возможность
судить обо всей генеральной совокупности, она должна быть отобрана случайно.
Так в нашем случае селекционер ни в коем случае не должен отдавать предпочтение
тем или иным колосьям (по размерам, внешнему виду, месту произрастания на поле
и т.п.) в процессе их выборки. Наиболее целесообразно в данной ситуации
совершать выбор колосьев из непрозрачного мешка наугад. У всех выбранных
колосьев производится подсчет числа зерен, и результаты фиксируются в виде ряда
чисел, с которыми в дальнейшем и предстоит совершать математические действия. В
данном примере можно предложить следующую их последовательность.

2.1 Создание вариационного ряда.

Вариационным
рядом называется ранжированный в порядке возрастания или убывания ряд вариантов
с соответствующими им весами (частотами или частностями). Вариационный ряд
будет дискретным, если любые его варианты отличаются на постоянную величину, и
непрерывным, если варианты могут отличатся один от другого на сколь угодно
малую величину.

Иными словами в вариационном ряду
полученные значения располагаются в порядке их увеличения и, если значение
повторяется, то рядом записывается число его повторений. Т.е. в данном примере
по числу зерен в колосьях ряд может выглядеть так (таб. 2):

Таблица 2

Число зерен в колосе	17	18	19	20	21	22	23	24	25
Число колосьев	1	2	2	4	6	8	8	9	10
Число зерен в колосе	26	27	28	29	30	31	32	33	34
Число колосьев	9	9	9	8	6	4	3	1	1

Полученный вариационный ряд
позволяет выявить закономерности распределения колосьев по числу зерен в них.

2.2 Создание вариационной
кривой.

Закономерности распределения
можно представить более наглядно, создав вариационную кривую, называемую
полигоном (рис 3), или представить в виде столбчатой диаграммы, которая здесь
будет называться гистограммой (рис 4).

2ю1

2ю2

Из полученных схем уже можно наглядно судить о закономерностях
распределения.

Диаграммы
строятся при помощи «Excel»
так:

Ø Ввести в окно программы данные вариационного
ряда.

Ø Запустить «Мастер диаграмм», нажатием
кнопки .

Ø В графе «тип» выбирать или «гистограмма», или
«график».

Ø Нажать кнопку «Далее».

Ø В «шаге 2 из 4» найти строку с названием
«Диапазон» и щелкнуть по кнопке, расположенной справа от надписи и пустого
поля, при этом «Мастер диаграмм» несколько свернется.

Ø Выделить данные в окне программы (в примере это
значения в ячейках В1 – В18).

Ø Снова щелкнуть по кнопке в «Мастере диаграмм».
«Мастер» развернется. В окне «Мастера» появится эскиз гистограммы или полигона.

Ø В этом же шаге (2 из 4) щелкнуть по закладке с
надписью «Ряд».

Ø В открывшейся страничке найти строчку с надписью
«Подписи оси Х».

Ø Щелкнуть по кнопке справа от надписи и пустого
поля.

Ø Выделить значения в окне программы, которые
будут на диаграмме представляться в качестве данных оси Х. (в примере значения
в ячейках А1 – А18).

Ø Щелкнуть по кнопке в свернутом «Мастере».

Ø Щелкнуть по кнопке «Далее» (шаг 3 из 4).

Ø При необходимости, в графе «Заголовки» выполнить
подписи осей Х и Y, а
так же дать диаграмме название.

Ø Щелкнуть по кнопке далее, затем готово и в
результате получится готовая гистограмма или полигон (рис 3).

2.3 Определение среднего значения признака.

Среднее
значение ряда данных находится обычным образом. Суммируются все значения
признака и делятся на количество этих значений. Т.е. здесь общее число зерен в
100 колосках равно 2551, то среднее значение будет равно 2551/100 = 25.51.

Для определения
среднего значения признака с использованием «Excel» надо выполнить следующие шаги:

Ø Ввести в столбец А окна программы все значения
признака, в том числе и повторяющиеся. Т.е. здесь все 100 значений зерен в
колосках. Ввод можно осуществлять в любой последовательности – по возрастанию,
по убыванию или в разнобой. Введенный массив чисел лучше сохранить, так как он
пригодится для расчета отклонения.

Ø Щелкнуть в окне программы по любой пустой
ячейке. По окончании расчетов в ней появится соответствующее среднее значение.

Ø В меню «Вставка» выбрать «Функция».

Ø В появившемся списке функций выбрать функцию
«СРЗНАЧ».

Ø Щелкнуть по кнопке «ОК». Появится окно
«Аргументы функции».

Ø Щелкнуть по кнопке правее надписи «Число 1» и
поля (окно свернется).

Ø Выделить в окне программы весь числовой массив,
среднее значение которого необходимо определить.

Ø Щелчком по кнопке справа от поля с надписями
развернуть окно «Аргументы функции».

Ø Щелкнуть по кнопке «ОК». В выбранной
предварительно ячейке появится среднее значение массива чисел.

2.4 Определение среднего квадратического
отклонения.

Вариационная кривая имеет
определенную ширину. Нетрудно догадаться, что чем больше ширина вариационной
кривой, тем сильнее разброс значений относительно средней величины.

2ю3

2ю4

Как показано на рисунках 5 и 6 при
одном и том же среднем значении, равном 25.51, полигон первого рисунка шире
полигона второго.

Оценить
степень разброса данных относительно среднего значения можно рассчитав значение
дисперсии S²,
или среднее квадратическое отклонение S, равное корню квадратному из дисперсии. Дисперсией вариационного ряда называется
средняя арифметическая квадратов отклонений вариантов от их средней
арифметической. Значением среднего квадратического отклонения пользоваться
удобнее, так как оно выражается в тех же единицах, что и значение признака. Так
среднее квадратическое отклонение данных, представленных графически на первом
полигоне равно 3.70, а на втором полигоне 2.65. Видим, что отклонение первое
больше второго и это как раз и отражается на ширине полигона.

Алгоритм
расчета среднего квадратического отклонения
и дисперсии такой же, как и для расчета среднего арифметического
значения, только в списке функций надо выбрать «СТАНДОТКЛОН» для вычисления отклонения, или «ДИСП» для расчета дисперсии.

Источник

Построение рядов распределения

Любой ряд распределения характеризуется двумя элементами:

— варианта(х_i) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);

— частота (n_i) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.

— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).

Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:

где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле

При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:

— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.

— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.

Проиллюстрируем процесс первичной обработки данных на следующих примерах.

Пример 1.1. имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения

Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER

Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.

Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).

Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.

Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:

10,4	18,6	10,3	26,0	45,0	18,2	17,3	19,2	25,8	18,7
28,2	25,2	18,4	17,5	41,8	14,6	10,0	37,8	10,5	16,0
18,1	16,8	38,5	37,7	17,9	29,0	10,1	28,0	12,0	14,0
14,2	20,8	13,5	42,4	15,5	17,9	19,	10,8	12,1	12,4
12,9	12,6	16,8	19,7	18,3	36,8	15,0	37,0	13,0	19,5

Составить равноинтервальный ряд, построить гистограмму

Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).

Рис.1.4. Пример 2. Построение равноинтервального ряда

Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.

Рис.1.5. Пример 2. Построение равноинтервального ряда

Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.

Рис.1.6. Пример 2. Построение равноинтервального ряда

Мнение эксперта

Витальева Анжела, консультант по работе с офисными программами

Со всеми вопросами обращайтесь ко мне!

Задать вопрос эксперту

Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!

Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .

Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.

10,4	18,6	10,3	26,0	45,0	18,2	17,3	19,2	25,8	18,7
28,2	25,2	18,4	17,5	41,8	14,6	10,0	37,8	10,5	16,0
18,1	16,8	38,5	37,7	17,9	29,0	10,1	28,0	12,0	14,0
14,2	20,8	13,5	42,4	15,5	17,9	19,	10,8	12,1	12,4
12,9	12,6	16,8	19,7	18,3	36,8	15,0	37,0	13,0	19,5

Стиль и внешний вид гистограммы

После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:

добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:

Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:

Мнение эксперта

Витальева Анжела, консультант по работе с офисными программами

Со всеми вопросами обращайтесь ко мне!

Задать вопрос эксперту

Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!

Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).

Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО

автоматически рассчитаны интервалы значений (карманы);
подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.

Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.

Источник

Построим дискретный вариационный ряд
по затратам труда на 1 ц зерна.

Открываем лист Excel,
в ячейку А1 записываем условное обозначение
результативного признака – у, а в ячейки
А2:А31 значения затрат труда на 1 ц зерна.
В ячейки В2:В3 введём наименьшее и
следующее за ним значения признака 0,7
и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем
мышью правый нижний угол выделительной
рамки и потянем вниз до значения 1,5
(наибольшее значение признака). В ячейках
В2:В10 получим варианты признака в
ранжированном порядке. Для определения
частот проделаем следующие шаги:

1.Поставим курсор в ячейку С2.

2.Выберем Вставка,
Функция.

Выберем в категории
Статистические функции
функцию Частота и
нажмём ОК.

3.В поле данных
укажем ячейки А2:А31, а в поле интервалов
В2:В10.

4.Нажмём кнопку ОК.

5.Выделим ячейки
С2:С10.

6.Нажмём F2,
а затем комбинацию клавиш Shift+Ctrl+Enter.

В ячейках С2:С10 появятся
частоты.

Вычислим накопленные
частоты, которые потребуются для
дальнейших расчётов, путём последовательного
суммирования локальных частот (нарастающим
итогом). Так, первая плюс вторая частоты
дают накопленную частоту второго
варианта (1+2=3); прибавляя к ней третью
частоту, получим накопленную частоту
третьего варианта (3+4=7) и т.д.

Скопируем полученный
в Excel
вариационный ряд и построим таблицу.

Таблица 2

Дискретный вариационный ряд распределения
затрат труда на 1 ц зерна

Варианты	Частоты	Накопленные частоты
0,7	1	1
0,8	2	3
0,9	4	7
1,0	5	12
1,1	6	18
1,2	4	22
1,3	3	25
1,4	3	28
1,5	2	30

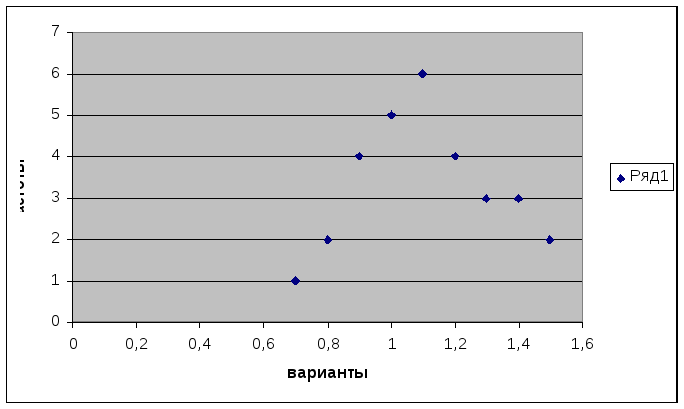
Построим
полигон распределения частот с помощью
Мастера
диаграмм.
Выберем точечную диаграмму, соединим
полученные точки отрезками, а крайние
точки с осью абсцисс в точках, отстоящих
от крайних на расстоянии шага.

Рис.
1. Полигон распределения сельскохозяйственных
предприятий по затратам труда на 1 ц
зерна

Рассмотрим
построение интервального вариационного
ряда.

Рис. 2. Построение интервального
вариационного ряда

На
листе Excel в ячейку А1 записываем условное
обозначение факторного признака – х,
в ячейки А2:А31 – значения факторного
признака – урожайности озимой пшеницы.
Произведём сортировку данных, для чего
выделяем диапазон данных, выбираем
Данные – Сортировка и в появившемся
окне «Сортировка диапазона» указываем
«по возрастанию», нажимаем ОК. Данные
в ячейках А2:А31 расположатся в ранжированном
порядке по возрастанию признака. По
формуле Стерджесса определяем количество
групп (интервалов). Для вычисления
десятичного логарифма lg30 выбираем
Мастер функций – Математические –
LOG10. В появившемся окне в поле Число
записываем число 30, десятичный логарифм
которого необходимо найти. Нажатием ОК
получаем этот логарифм 1,477121. . Подставляя
числовые данные в формулу (1), получим
число групп (интервалов) 5,9, округляем
до 6. По формуле (2) определяем величину
интервалов – шаг с такой же точностью,
с которой даны исходные данные (в данном
случае с точностью до десятых:
(30-20)/6≈1,7. Следовательно, совокупность
надо разбить на 6 интервалов. Получаем
шаг 1,7. Озаглавим следующие столбцы в
Excel словами «Интервалы», «Частоты»,
«Накопленные частоты», «Середины
интервалов». В ячейку В2 вписываем
минимальное значение признака Х_min=20,
в ячейку В3 формулу =В2+1,7, т.е. минимальное
значение плюс шаг. Копируем эту формулу
на 5 строк вниз. В результате в этих шести
строках (В3:В8) получим верхние границы
всех интервалов. Нижними границами
интервалов будут данные в соседних
верхних ячейках, т.е. для первого интервала
нижней границей будет содержание ячейки
В2, для второго В3 и для шестого В7.

Для
расчёта частот выберем Сервис — Анализ
данных – Гистограмма и нажмём ОК. В
появившемся окне «Гистограмма» в поле
«Входной интервал» копируем исходные
данные (ячейки А2:А31), в поле «Интервал
карманов» — верхние границы интервалов
(ячейки В3:В8), в поле «Выходной интервал»
ячейки частот (С3:С8), нажимаем ОК. В ячейки
D3:D8 будут записаны частоты для всех
шести интервалов. Накопленные частоты
подсчитываем нарастающим итогом.

Для
построения диаграммы необходимо найти
середины интервалов. Для этого вводим
формулу расчёта середины интервала:
,
рассчитаем середину первого интервала.
Копируем формулу для остальных пяти
групп.

Для
построения диаграммы выделяем массив
частот и середин интервалов.
Далее в
Мастере диаграмм выбираем вид диаграммы
— гистограмму определённого вида.
Нажимаем кнопку Далее. В появившемся
окне выбираем вкладку Ряд, удаляем ряд
1, а в поле «Подписи оси х» копируем
середины интервалов. Нажимаем далее, в
появившемся окне выбираем вкладку
Заголовки. В поле «ось х (категорий)»
вписываем название факторного признака
(в данном случае урожайность, ц/га), в
поле «Ось у (значений)» вписываем частоты.
Нажимаем Далее, Готово. Появится
диаграмма, состоящая из столбиков,
отделённых друг от друга некоторым
зазором. Щёлкаем правой кнопкой мыши
на одном из столбиков диаграммы. В
раскрывающемся списке элементов щёлкаем
по кнопке Формат рядов данных. В
появившемся диалоговом окне активизируем
вкладку Параметры и в поле Ширина зазора
устанавливаем значение 0. Нажимаем ОК,
в результате чего гистограмма принимает
стандартный вид.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

1. Построение вариационного ряда

Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»

2. Построение группировочного статистического ряда

Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:

а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)

b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.

с) выбрать функцию ЧАСТОТА

d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101

e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.

f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.

g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).

Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.

В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).

3. Построение гистограммы группировочного статистического ряда

Источник