Как найти угол зная косинус в excel

falconav Пользователь Сообщений: 2 Регистрация: 16.09.2016 Инженер	Прошу помочь по формуле — как получить значение угла в градусах /минутах от числового значения его косинуса?

Сергей Пользователь Сообщений: 11251 Регистрация: 01.01.1970	зайдите в эксель нажмите F1 почитайте справку по функциям там кажись в разделе математические функции что то подобное есть Лень двигатель прогресса, доказано!!!

Jack Famous Пользователь Сообщений: 10852 Регистрация: 07.11.2014 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome	falconav, интересный вопрос. =ГРАДУСЫ(ACOS(A1)) Тут табличка косинусов на всякий (можно, кстати, ВПРом неточно по табличке, искать и возвращать значение с шагом в 1 градус)   Изменено: Jack Famous — 16.09.2016 12:51:36 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄

falconav Пользователь Сообщений: 2 Регистрация: 16.09.2016 Инженер	#4 08.06.2018 07:32:36 Спасибо, Jack Famous , очень Вам благодарен.

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

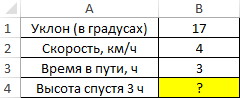
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

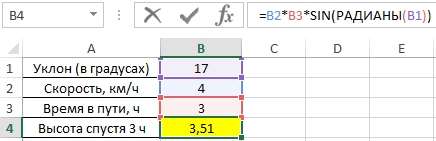
Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.



Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

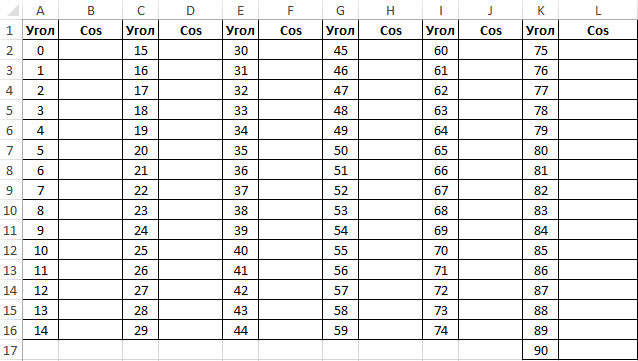
Заполним столбцы значениями углов в градусах:

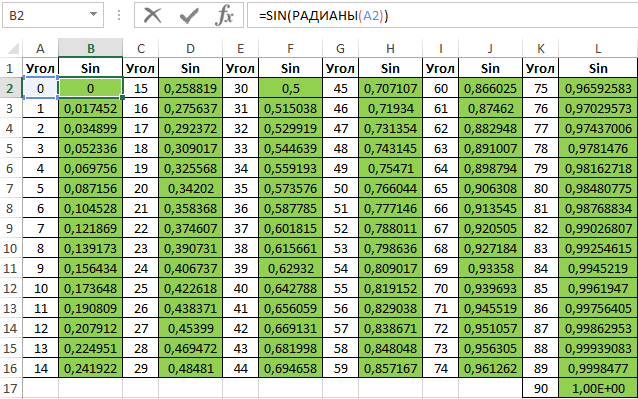
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

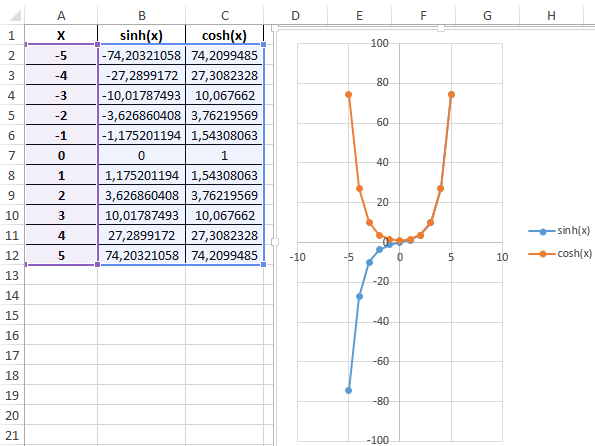
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Исходные данные:

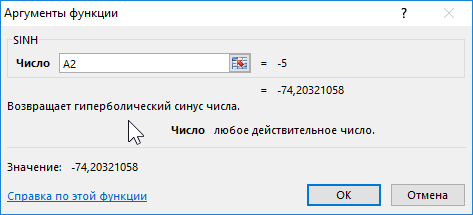
Формула для нахождения синусов гиперболических:

=SINH(A2:A12)

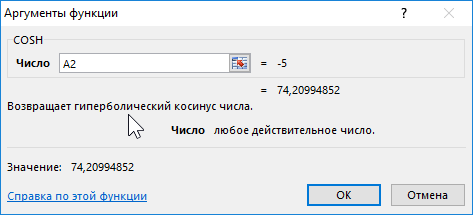
Формула для нахождения косинусов гиперболических:

=COSH(A2:A12)

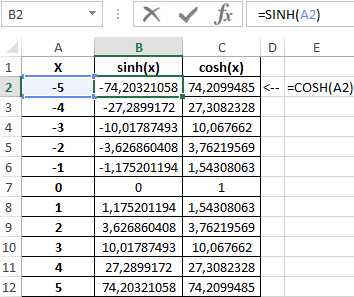
Таблица полученных значений:

Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Примечания 1:

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

Скачать примеры тригонометрических функций SIN и COS

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.

Описание

Возвращает косинус заданного угла.

Синтаксис

COS(число)

Аргументы функции COS описаны ниже.

• Число    — обязательный аргумент. Угол в радианах, для которого определяется косинус.

Замечания

Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=COS(1,047)	Косинус 1,047 радиан	0,5001711
=COS(60*ПИ()/180)	Косинус 60 градусов	0,5
=COS(РАДИАНЫ(60))	Косинус 60 градусов	0,5

If you’re working with any triangle with a right angle in it somewhere, it’s simple to find the tangent angle, so long as you know the length of two sides of the triangle.

Doing so is even easier in Microsoft Excel because there are built-in functions you can use.

What Is the Tangent Angle?

A tangent angle is an angle in the triangle where you know the length of the side opposite the angle and the side adjacent to it.

Imagine, for example, that your boss tells you to adjust a ladder at precisely 70 degrees from the ground. Unless you have some special tools, it would be complicated to measure whether the angle between the ladder and the ground is exactly 70 degrees.

However, if you have a measuring tape, you could measure the distance from the bottom of the ladder to the wall. Since the ladder against the wall forms a triangle, this would be the side that’s adjacent to the tangent angle you’re trying to calculate.

Next, you’d measure the distance from the bottom of the wall to where the top of the ladder touches it. This is the distance of the side that’s opposite from the tangent angle.

With the measurement of the opposite and adjacent sides, you can calculate the angle at the ladder base using the arctangent function.

If the wall (opposite) side is 10 feet, and the ground (adjacent) side is 5 feet, the formula for the tangent angle is the opposite side divided by the adjacent side. This is 10 divided by 5, or 0.5.

To find the value for the angle, you need to take the arctangent of 0.5.

Find the Tangent Angle With Excel

You could find a calculator that calculates the arctangent of a value, but Excel has a built-in function called ATAN that you can use.

The formula returns the angle in radians, which your boss probably won’t understand.

You’ll want to convert radians to degrees by multiplying it by 180/pi. Excel also has a PI function you can use for this purpose.

The answer, in this case, is 63.43 degrees. This means you’ll need to adjust one of the lengths until the angle is precisely 70 degrees.

Doing this is easy in Excel because you can change the opposite side’s value until the arctangent result is 70.

Using ASIN and ACOS in Excel

In this same scenario, let’s say you don’t have a tape measure long enough to measure the wall. You only know that the ladder is 15 feet and that it’s placed five feet from the wall.

Excel has two other functions that you can use to calculate the angle.

The ladder’s length is the hypotenuse of the triangle, and the ground distance is the adjacent side to the angle. So long as the triangle has one right (90 degree) angle, the information you have determines the formula you need to use.

• Cosine: Calculate the cosine angle if you know the length of the hypotenuse and the adjacent side.
• Sine: Calculate the sine angle if you know the length of the hypotenuse and the opposite side.

In this case, the angle is the arccosine of the adjacent side divided by the hypotenuse.

Since you know the adjacent side (the ground distance) is 5 feet, and the ladder length (hypotenuse) is 15 feet, the cosine of the angle is 5 divided by 15, or 0.333.

To calculate the angle, use the arccosine formula in Excel.

The result of the arccosine function is Excel is in radians, so you need to multiply it by 180/PI to convert it to degrees.

For a 15 foot ladder with its base 5 feet from the wall, the angle is 70.53 degrees.

If you knew that the height of the wall (the opposite side) is 10 feet, instead of the ground distance from the wall (the adjacent side), you’d use the arcsine formula in Excel.

In this case, the sine of the angle is the opposite side divided by the hypotenuse.

After converting to degrees, the angle, in this case, would be 48.12 degrees.

Why Use ATAN, ACOS, or ASIN?

Here are a few examples of situations where you may need to use one of these functions in Excel:

• In carpentry and construction, angles and lengths are used in all aspects of building houses and buildings.
• Photographers use angles to align lighting and their creative shots carefully.
• In sports, understanding angles can enhance skills and improve strategy.
• Ships and airplanes are located on radar using angles and distances.
• If you want to be sure furniture will fit right in your room, you’ll need to know how to calculate lengths and angles.

You may be able to accomplish these calculations on a scientific calculator. But if you don’t have one handy, Excel can help you make those calculations.

Thanks for letting us know!

Перейти к содержимому