Как найти сумму четных чисел в excel - Word и Excel - помощь в работе с программами

Как подсчитать / суммировать нечетные / четные числа или строки в Excel?

Если на вашем листе есть диапазон чисел, который содержит как нечетные, так и четные числа, но теперь вам нужно подсчитать или суммировать только нечетные или четные числа. Как можно быстро выполнить эту задачу на листе Excel?

Считайте четные или нечетные числа с помощью формул в Excel

Суммируйте нечетные или четные числа с формулами в Excel

Суммирование нечетных или четных строк с формулами в Excel

Подсчет/усреднение/сумма нечетных или четных строк с помощью Kutools for Excel

Считайте четные или нечетные числа с помощью формул в Excel

Чтобы подсчитать только четные или нечетные числа в диапазоне, вам могут помочь следующие формулы, выполните следующие действия:

1. Чтобы считать только нечетные числа, введите эту формулу = СУММПРОИЗВ ((MOD (A1: C8,2) <> 0) +0) в пустой ячейке, см. снимок экрана:

2, Затем нажмите Enter key, и вы получите количество нечетных значений в выбранном диапазоне.

Ноты:

1. Если вы хотите получить только количество четных значений, примените эту формулу = СУММПРОИЗВ ((МОД (A1: C8,2) = 0) +0).

2. В приведенных выше формулах A1: C8 — это диапазон, в котором вы хотите посчитать нечетные или четные числа, вы можете изменить его по своему усмотрению.

Суммируйте нечетные или четные числа с формулами в Excel

Если вам нужно сложить все нечетные или четные числа только в диапазоне, вы можете использовать следующие формулы: обычные формулы или формулы массива.

1. Нормальные формулы для суммирования нечетных / четных чисел в диапазоне:

Пожалуйста, введите эту формулу =SUMPRODUCT(—(MOD(A1:C8,2)=1),A1:C8) в пустую ячейку, см. снимок экрана:

Затем нажмите Enter key, все нечетные значения добавлены в диапазон.

Заметки： 1. Чтобы суммировать только четные числа, вы можете использовать следующую формулу: =SUMPRODUCT(—(MOD(A1:C8,2)=0),A1:C8).

2. В приведенных выше формулах A1: C8 — это диапазон, в котором вы хотите сложить нечетные / четные числа.

2. Формулы массива для суммирования четных и нечетных чисел в диапазоне

Следующие формулы массива также могут помочь вам справиться с этой проблемой.

В пустой ячейке введите эту формулу =SUM(IF(MOD($A$1:$C$8,2)=1,$A$1:$C$8)), Затем нажмите Ctrl + Shift + Enter ключи вместе. И вы получите сумму нечетных чисел.

Для суммирования четных чисел примените эту формулу массива =SUM(IF(MOD($A$1:$C$8,2)=0,$A$1:$C$8)), и не забудьте нажать Ctrl + Shift + Enter ключи.

Суммирование нечетных или четных строк с формулами в Excel

Иногда вам нужно суммировать диапазон ячеек, которые располагаются только в строках с четными или нечетными номерами. Вы также можете использовать формулы для ее решения.

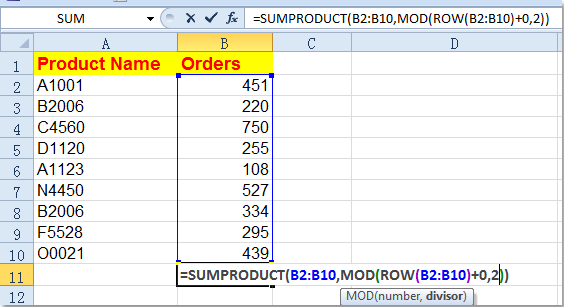
1. Предположим, у вас есть следующие данные, и теперь для суммирования нечетных строк в столбце B введите эту формулу =SUMPRODUCT(B2:B10,MOD(ROW(B2:B10)+0,2)) в пустую ячейку. Смотрите скриншот:

2, Затем введите Enter key, и все значения нечетных строк были добавлены.

Ноты:

1. Чтобы суммировать строки с четными номерами, используйте эту формулу =SUMPRODUCT(B2:B10,MOD(ROW(B2:B10)+1,2)).

2. В приведенных выше формулах B2: B10 — это диапазон, который вы хотите использовать, вы можете изменить его по своему усмотрению.

Подсчет/усреднение/сумма нечетных или четных строк с помощью Kutools for Excel

Если у вас есть Kutools for Excel После установки вы можете быстро выбрать нечетные или четные строки или столбцы, а затем просмотреть вычисления в строке состояния.

После бесплатная установка Kutools for Excel, пожалуйста, сделайте следующее:

1. Выберите весь диапазон строк и нажмите Кутулс > Выберите > Выберите интервальные строки и столбцы. Смотрите скриншот:

2. Затем в появившемся диалоговом окне отметьте Ряды or Колонны как вам нужно, и введите 1 в оба текстового поля, снимите флажок Выбрать целые строки. Смотрите скриншот:

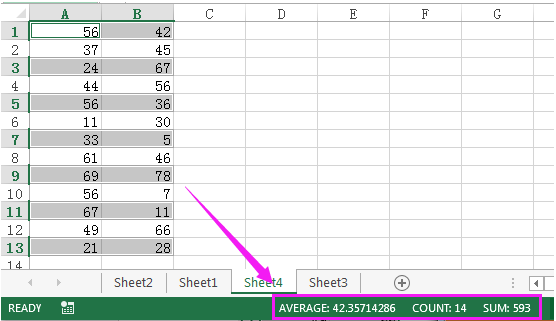
3. Нажмите Ok, теперь все нечетные строки выбраны, и вы перейдете в строку состояния, вы сможете просмотреть среднее значение, подсчет и суммирование результатов.

Наконечник: Если вы хотите подсчитать, усреднить или суммировать четные строки, просто выберите все строки, кроме первой, затем примените Выберите интервальные строки и столбцы.

Щелкните здесь, чтобы узнать подробнее о выборе интервальных строк и столбцов.

Связанная статья:

Как выделить четные или нечетные числа в Excel?

Лучшие инструменты для работы в офисе

Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%

Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.

Вкладка Office: интерфейс с вкладками в Office и упрощение работы

Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!

Источник

Содержание

Сумма четных и нечетных чисел в Excel
Стандартные функции
Пользовательская функция
Использование массива
Excel. Суммирование значений в четных (или кратных) строках (столбцах)
Как подсчитать / суммировать нечетные / четные числа или строки в Excel?
Подсчет нечетных или четных чисел с помощью формул в Excel
Суммирование нечетных или четных чисел с формулами в Excel
Суммирование нечетных или четных строк с формулами в Excel
Подсчет/усреднение/сумма нечетных или четных строк с помощью Kutools for Excel
Строки количества/суммы/среднего нечетного или события

Сумма четных и нечетных чисел в Excel

Высчитать сумму четных либо нечетных чисел в Excel можно несколькими способами:

Стандартные функции

Первый способ возможен при использовании стандартных функций приложения. Для этого необходимо создать два дополнительных столбца с формулами:

Четные числа – вставляем формулу «= ЕСЛИ ( ОСТАТ(число;2) =0;число;0)», которая вернет число, в случае если оно делится на 2 без остатка.
Нечетные числа – вставляем формулу «= ЕСЛИ ( ОСТАТ(число;2) =1;число;0)», которая вернет число, в случае если оно не делится на 2 без остатка.

Затем необходимо определит сумму по двум столбцам с помощью функции «=СУММ()».

Плюсы данного способа в том, что он будет понятен даже тем пользователям, которые профессионально не владею приложением.

Минусы способа – приходится добавлять лишние столбцы, что не всегда удобно.

Пользовательская функция

Второй способ, является более удобным, чем первый, т.к. в нем применяется пользовательская функция, написанная на VBA – sum_num(). Функция возвращает сумму чисел в виде целого числа. Суммируются либо четные числа, либо нечетные, в зависимости от значения ее второго аргумента.

Синтаксис функции: sum_num(rng;odd):

Аргумент rng – принимает диапазон ячеек, по которым необходимо произвести суммирование.
Аргумент odd – принимает логическое значение ИСТИНА для четных чисел или ЛОЖЬ для нечетных.

Важно: Четными и нечетными числа могут являться только целые числа, поэтому числа, которые не соответствуют определению целого числа, игнорируются. Также, если значением ячейки является срока, то данная строка не участвует в расчете.

Плюсы: нет нужны добавлять новые столбцы; лучший контроль над данными.

Минусы заключаются в необходимости перевода файла в формат .xlsm для версий Excel, начиная с версии 2007. Также функция будет работать только в той книге, в которой она присутствует.

Использование массива

Последний способ является самым удобным, т.к. не требует создания дополнительных столбцов и программирования.

Его решение схоже с первым вариантом — они используют одни и те же формулы, но данный способ, благодаря использованию массивов, производит подсчет в одной ячейке:

Для четных чисел — вставляем формулу «=СУММ( ЕСЛИ ( ОСТАТ(диапазон_ячеек;2) =0;диапазон_ячеек;0))». После ввода данных в строку формул нажимаем одновременно клавиши Ctrl + Shift + Enter, чем сообщаем приложению, что данные необходимо обрабатывать как массив, и оно заключит их в фигурные скобки;
Для нечетных чисел — повторяем действия, но изменяем формулу «=СУММ(ЕСЛИ( ОСТАТ(диапазон_ячеек;2) =1;диапазон_ячеек;0))».

Плюсом способа является то, что все рассчитывается в одной ячейке, без дополнительных столбцов и формул.

Минусом является лишь то, что неопытные пользователи могут не понять Ваших записей.

На рисунке видно,что все способы возвращают один и тот же результат, какой лучше, необходимо выбирать под конкретную задачу.

Источник

Excel. Суммирование значений в четных (или кратных) строках (столбцах)

Недавно у меня возникла задача просуммировать значения в каждом третьем столбце. Пример, о котором идет речь, мы рассмотрим позже в силу его сложности, а начнем с более простого случая – найдем сумму значений для всех четных / нечетных строк. Исходные данные представлены на рис. 1 (см. также лист «Пример1» Excel-файла).

Рис. 1. Данные о приходе / уходе [1]

Скачать заметку в формате Word или pdf, примеры в формате Excel

1-й способ. Суммирование четных строк. Более простой для понимания (на мой взгляд), но требующий дополнительной колонки для промежуточных вычислений. Введем в столбец Е формулу =ЕЧЁТН(СТРОКА()), возвращающую значение ИСТИНА, если строка четная, и ЛОЖЬ – если нечетная (рис. 2).

Рис. 2. Определение четности номера строки

После чего применим две формулы условного суммирования (рис. 3)

Рис. 3. Использование функции условного суммирования

Формула СУММЕСЛИ суммирует только те значения из диапазона D3:D46 (Диапазон_суммирования), для которых значение в столбце Е равно ЛОЖЬ. Аналогично для вычисления суммарного расхода в ячейке Н4 используется формула =СУММЕСЛИ(E3:E46;ИСТИНА;D3:D46).

Дополнение от 20.09.15. Еще проще с задачей справится формула =СУММЕСЛИ(C:C; » Приход » ;D:D), которая суммирует только те значения из столбца D, для которых значение в столбце С равно Приход.

2-й способ. Использование формулы массива. Если вы не знакомы с формулами массива, настоятельно рекомендую пройти по ссылке и почитать подробнее. На мой взгляд, работу формул массива кратко можно сформулировать так: формулы массива сначала выполняют действия, прописанные в них, над элементами массива, а потом суммируют эти действия для всех элементов массива (что-то наподобие формулы СУММПРОИЗВ – сумма произведений). Для того чтобы ввести в ячейку формулу массива, надо набрать формулу, а затем одновременно нажать CTRL+SHIFT+ВВОД. Это приведет к тому, что вокруг формулы (см. строку формул на рис. 4) появятся фигурные скобки: < и >. Не пытайтесь ввести скобки с клавиатуры; формула массива не возникнет! 🙂 После редактирования формулы массива (или если вы случайно встали курсором в ячейку с такой формулой), повторно нажмите CTRL+SHIFT+ВВОД.

Рис. 4. Использование формулы массива для суммирования значений в нечетных строках.

Рассмотрим, как действует формула массива в нашем случае (рис. 4):

СТРОКА(D3) – определяет номер строки для ячейки D3;
ЕНЕЧЁТ(СТРОКА(D3)) – определяет, является ли номер строки, содержащей ячейку D3, нечетным; если нечетный, возвращает значение ИСТИНА (или единица), если четный – ЛОЖЬ (или ноль);
ЕНЕЧЁТ(СТРОКА(D3))*D3 – умножает значение, хранящееся в ячейке D3 (536) на значение, полученное на предыдущем шаге;
<=СУММ(ЕНЕЧЁТ(СТРОКА(D3:D46))*(D3:D46))>– суммирует в диапазоне D3:D46, все значения, полученные на предыдущем шаге, то есть, ЕНЕЧЁТ(СТРОКА(D3))*D3 + ЕНЕЧЁТ(СТРОКА(D4))*D4 + … + ЕНЕЧЁТ(СТРОКА(D46))*D46

Для вычисления суммарного расхода в ячейке Е49 используется формула <=СУММ(ЕЧЁТН(СТРОКА(D3:D46))*(D3:D46))>, которая находит сумму значений в диапазоне D3:D46 только для четных строк.

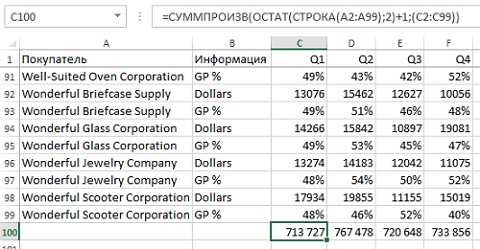
3-й способ. Подсмотрен у Билла Джелена в его книге Гуру Excel расширяют горизонты: делайте невозможное с Microsoft Excel (рис. 4а). Для подсчета значений в нечетных строках используйте формулу: =СУММПРОИЗВ(ОСТАТ(СТРОКА(A2:A99);2);(C2:C99)). Для полсчета значений в четных строках воспользуйтесь формулой: =СУММПРОИЗВ(ОСТАТ(СТРОКА(A2:A99);2)+1;(C2:C99))

Подробнее о том, как действует последняя формула:

СТРОКА(А2) – определяет номер строки для ячейки А2;
ОСТАТ(СТРОКА(A2;2) – определяет остаток от деления значения, полученного на предыдущем шаге, на двойку; понятно, что для четных строк ОСТАТОК() будет равен нулю, а для нечетных – единице;
ОСТАТ(СТРОКА(A2;2)+1 – прибавляет единицу к предыдущему результату; теперь для четных строк значение 1, а для нечетных – 0;
Далее значение 1 или 0 умножается на значение в ячейке С2; т.е., значения в четных строках столбца С равны сами себе, а в нечетных – нулю;
СУММПРОИЗВ() суммирует значения в столбце С только в четных строках.

Рис. 4а. Функция СУММПРОИЗВ для суммирования значений в четных строках

Для суммирования значений в четных строках также подойдут формулы (см. Excel-файл, лист «Рис. 4а»):

=СУММПРОИЗВ(ОСТАТ(СТРОКА(2:99);2)+1;(D2:D99)); не обязательно указывать буквы для вычисления номера строки;

=СУММПРОИЗВ( — — (ОСТАТ(СТРОКА(C2:C99);2)=0);(E2:E99)); если строка четная, то ОСТАТ()=0, т.е. этот фрагмент формулы вернет значение ИСТИНА, а операция минус минус, вернет значение 1;

=СУММПРОИЗВ(ОСТАТ(СТРОКА(A1:A98);2);(F2:F99)); вы просто сместили фрагмент формулы, определяющий 1/0, на строку выше.

Вернемся к более общей задаче – суммирование строк (столбцов) кратных n (рис. 5; см. также лист «Пример2» Excel-файла). Задача – найти сумму запасов, то есть сумму по строке 23 для всех столбцов с заголовком «Запасы».

Рис. 5. Суммирование значений в каждом третьем столбце

Рассмотрим, как работает формула массива во втором примере (рис. 5):

СТОЛБЕЦ(B23) – определяет номер столбца для ячейки В23;
ОСТАТ(СТОЛБЕЦ(B23);3) – определяет, остаток от деления номера столбца на 3;
ЕСЛИ(ОСТАТ(СТОЛБЕЦ(B23);3)=2;1;0) – если остаток равен двум, функция ЕСЛИ возвращает значение 1; если не равен – 0;
ЕСЛИ(ОСТАТ(СТОЛБЕЦ(B23);3)=2;1;0)*B23 – умножает значение, хранящееся в ячейке В23 (1) на значение, полученное на предыдущем шаге;
<=СУММ(ЕСЛИ(ОСТАТ(СТОЛБЕЦ(B23:BX23);3)=2;1;0)*B23:BX23)>– суммирует в диапазоне В23:ВХ23, все значения, полученные на предыдущем шаге, то есть, ЕСЛИ(ОСТАТ(СТОЛБЕЦ(B23);3)=2;1;0)*B23 + ЕСЛИ(ОСТАТ(СТОЛБЕЦ(С23);3)=2;1;0)*С23 + ЕСЛИ(ОСТАТ(СТОЛБЕЦ(D23);3)=2;1;0)*D23 + … + ЕСЛИ(ОСТАТ(СТОЛБЕЦ(BХ23);3)=2;1;0)*BХ23.

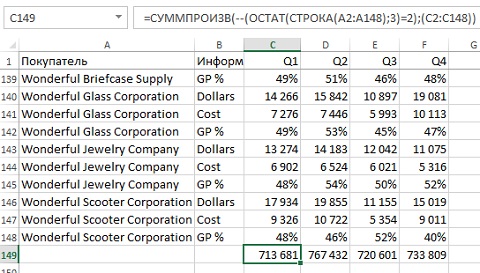
2-й способ. Также подсмотрен у Билла Джелена. Для суммирования значений в каждой третьей строке воспользуйтесь формулой: =СУММПРОИЗВ( — — (ОСТАТ(СТРОКА(A2:A148);3)=2);(C2:C148)).

Рис. 5а. Функция СУММПРОИЗВ для суммирования значений в каждой третьей строке

Подробнее о том, как действует эта формула:

СТРОКА(А2) – определяет номер строки для ячейки А2;
ОСТАТ(СТРОКА(A2);3) – определяет остаток от деления значения, полученного на предыдущем шаге, на тройку;
ОСТАТ(СТРОКА(A2);3)=2 – возвращает ИСТИНА, если остаток от деления равен 2 и ЛОЖЬ, если равен 0 или 1;
Операция минус минус конвертит логические значения ИСТИНА/ЛОЖЬ в числовые 1/0;
СУММПРОИЗВ() суммирует значения в столбце С только для тех строки, которые вернули значение 1 на предыдущем шаге.

[1] Данные оформлены весьма симпатично для их просмотра, но очень неудобно для дальнейшей обработки. По возможности оформляйте исходные данные в форме, приемлемой для последующей их обработки сводными таблицами. На эту тему рекомендую замечательную книгу: Билл Джелен, Майкл Александер «Сводные таблицы в Microsoft Excel 2010». Если бы данные были оформлены соответствующим образом, никаких ухищрений не понадобилось бы. Данные можно было бы обработать стандартными сводными таблицами.

Источник

Как подсчитать / суммировать нечетные / четные числа или строки в Excel?

Если на вашем листе есть диапазон чисел, который содержит как нечетные, так и четные числа, но теперь вам нужно подсчитать или суммировать только нечетные или четные числа. Как вы могли быстро выполнить эту задачу на листе Excel?

Подсчет нечетных или четных чисел с помощью формул в Excel

Суммировать нечетные или четные числа с формулами в Excel

Подсчет/усреднение/сумма нечетных или четных строк с помощью Kutools for Excel

Подсчет нечетных или четных чисел с помощью формул в Excel

Чтобы подсчитать только четные или нечетные числа в диапазоне, вам могут помочь следующие формулы:

1 . Чтобы подсчитать только нечетные числа, введите эту формулу = SUMPRODUCT ((MOD (A1: C8,2) 0) +0) в пустую ячейку, см. Снимок экрана:

2 . Затем нажмите клавишу Enter , и вы получите количество нечетных значений в выбранном диапазоне.

Примечания:

1. Если вы хотите получить только количество четных значений, примените эту формулу = СУММПРОИЗВ ((MOD (A1: C8,2) = 0) +0) .

2. В приведенных выше формулах A1: C8 – это диапазон, в котором вы хотите подсчитать нечетные или четные числа, вы можете изменить его по своему усмотрению.

Суммирование нечетных или четных чисел с формулами в Excel

Если вам нужно сложить все нечетные или четные числа только в диапазоне можно использовать следующие формулы: обычные формулы или формулы массива.

1. Обычные формулы для суммирования нечетных/четных чисел в диапазоне:

Введите эту формулу = СУММПРОИЗВ (- (MOD (A1: C8,2) = 1 ), A1: C8) в пустую ячейку, см. Снимок экрана:

А затем нажмите клавишу Enter , все нечетные значения были добавлены в диапазон.

= СУММПРОИЗВ (- (MOD (A1: C8,2) = 0), A1: C8) .

2. В приведенных выше формулах A1: C8 – это диапазон, в котором вы хотите сложить нечетные/четные числа.

2. Формулы массива для суммирования нечетных/четных чисел в диапазоне

Следующие формулы массива также могут помочь вам справиться с этой проблемой.

В пустом поле ячейку, введите эту формулу = SUM (IF (MOD ($ A $ 1: $ C $ 8,2) = 1, $ A $ 1: $ C $ 8)) , затем нажмите Ctrl + Shift + Enter вместе. И вы получите сумму нечетных чисел.

Для суммирования четных чисел примените эту формулу массива = SUM (IF (MOD ($ A $ 1: $ C $ 8,2) = 0, $ A $ 1: $ C $ 8)) и не забудьте нажать клавиши Ctrl + Shift + Enter .

Суммирование нечетных или четных строк с формулами в Excel

Иногда вам нужно суммировать диапазон ячейки, которые располагаются только в строках с четными или нечетными номерами. Вы также можете использовать формулы для ее решения.

1 . Предположим, у вас есть следующие данные, и теперь для суммирования нечетных строк в столбце B введите эту формулу = SUMPRODUCT (B2: B10, MOD (ROW (B2: B10) +0,2)) в пустую ячейку. См. Снимок экрана:

2 . Затем нажмите клавишу Enter , и все значения нечетных строк будут добавлены.

Примечания:

1. Чтобы суммировать строки с четными номерами, используйте эту формулу = СУММПРОИЗВ (B2: B10, MOD (ROW (B2: B10) +1,2)) .

2. В приведенных выше формулах B2: B10 – это диапазон, который вы хотите использовать, вы можете изменить его по своему усмотрению.

Подсчет/усреднение/сумма нечетных или четных строк с помощью Kutools for Excel

Если у вас есть Kutools for Excel , вы можете быстро выбрать нечетные или четные строки или столбцы, а затем просмотреть вычисления в строке состояния.

После бесплатной установки Kutools for Excel, сделайте следующее:

1. Выделите весь диапазон строк и нажмите Kutools > Выбрать > Выбрать интервальные строки и столбцы . См. Снимок экрана:

2. Затем в открывшемся диалоговом окне установите флажок Строки или Столбцы , как вам нужно, и введите 1 в оба текстовых поля, снимите флажок Выбрать целые строки . См. Снимок экрана:

3. Нажмите ОК , теперь все нечетные строки выделены, и перейдите в строку состояния, вы можете просмотреть среднее значение, подсчет и суммирование результатов.

Совет. Если вы хотите подсчитать, усреднить или суммировать четные строки, просто выберите все строки кроме первой строки, затем примените Выбрать строки и столбцы с интервалом .

Нажмите здесь, чтобы получить подробные сведения о выборе строк и столбцов с интервалом.

Строки количества/суммы/среднего нечетного или события

Как выделить нечетные или четные числа в Excel?

Источник

Adblock
detector

Kutools for Excel , с более чем 300 удобными функциями, облегчит вашу работу.

Источник

Стандартные функции

Четные числа – вставляем формулу «=
ЕСЛИ
(ОСТАТ(число;2)

=0;число;0)», которая вернет число, в случае если оно делится на 2 без остатка.
Нечетные числа – вставляем формулу «=
ЕСЛИ
(ОСТАТ(число;2)

=1;число;0)», которая вернет число, в случае если оно не делится на 2 без остатка.

Затем необходимо определит сумму по двум столбцам с помощью функции «=СУММ()».

Минусы способа – приходится добавлять лишние столбцы, что не всегда удобно.

Пользовательская функция

Синтаксис функции:
sum_num(rng;odd):

Аргумент rng – принимает диапазон ячеек, по которым необходимо произвести суммирование.
Аргумент odd – принимает логическое значение ИСТИНА для четных чисел или ЛОЖЬ для нечетных.

Важно:
Четными и нечетными числа могут являться только целые числа, поэтому числа, которые не соответствуют определению целого числа, игнорируются. Также, если значением ячейки является срока, то данная строка не участвует в расчете.

Плюсы: нет нужны добавлять новые столбцы; лучший контроль над данными.

Минусы заключаются в необходимости перевода файла в формат.xlsm для версий Excel, начиная с версии 2007. Также функция будет работать только в той книге, в которой она присутствует.

Использование массива

Для четных чисел — вставляем формулу «=СУММ
(ЕСЛИ
(ОСТАТ(диапазон_ячеек;2)

=0;диапазон_ячеек;0))». После ввода данных в строку формул нажимаем одновременно клавиши Ctrl + Shift + Enter, чем сообщаем приложению, что данные необходимо обрабатывать как массив, и оно заключит их в фигурные скобки;
Для нечетных чисел — повторяем действия, но изменяем формулу «=СУММ
(ЕСЛИ
(ОСТАТ(диапазон_ячеек;2)

=1;диапазон_ячеек;0))».

Плюсом способа является то, что все рассчитывается в одной ячейке, без дополнительных столбцов и формул.

Минусом является лишь то, что неопытные пользователи могут не понять Ваших записей.

Скачать файл
с описанными варианта можно по данной ссылке.

Немного теории

Среди олимпиадных задач для 5-6 классов обычно особую группу составляют такие, где требуется использовать свойства
чётности (нечётности) чисел. Простые и очевидные сами по себе эти свойства легко запоминаются или выводятся, и часто у школьников не возникает каких-либо сложностей при их изучении.
Но порой применить эти свойства и, главное, догадаться, что именно их надо применить для того или иного доказательства, бывает непросто. Перечислим здесь эти свойства.

Рассматривая с учениками задачи, в которых следует воспользоваться этими свойствами, нельзя не рассмотреть и такие, для решения
которых важно знать формулы чётного и нечётного чисел. Опыт преподавания этих формул пяти-шестиклассникам показывает, что многие из них даже не задумывались, что любое чётное число,
как и нечётное, можно выразить формулой. Методически бывает полезно озадачить ученика вопросом написать сначала формулу нечётного числа. Дело в том, что формула
чётного числа выглядит понятной и очевидной, а формула нечётного числа является своего рода следствием из формулы чётного числа. А если ученик в процессе изучения нового для себя материала задумался,
сделав паузу для этого, то он скорее запомнит обе формулы, чем если начинать с объяснение с формулы чётного числа. Так как чётное число — это то число, которое делится на 2, то его можно записать, как
2n, где n — целое число, а нечётное — соответственно как 2n+1.

Ниже приведены наиболее простые задачи на чётность/нечётность, которые бывает полезно рассматривать в виде лёгкой разминки.

Задачи

1) Докажите, что нельзя подобрать 5 нечётных чисел, сумма которых равна 100.

2) Имеется 9 листов бумаги. Некоторые из них разорвали на 3 или 5 частей. Некоторые из образовавшихся частей снова разорвали на 3 или 5 частей и так
несколько раз. Можно ли после нескольких шагов получить 100 частей?

3) Чётна или нечётна сумма всех натуральных чисел от 1 до 2019?

4) Докажите, что сумма двух последовательных нечетных чисел делится на 4.

5) Можно ли соединить 13 городов дорогами так, чтобы из каждого города выходило ровно 5 дорог?

6) Директор школы в своём отчёте написал, что в школе 788 учащихся, причём мальчиков на 225 больше, чем девочек. Но проверяющий инспектор сразу сообщил,
что в отчёте допущена ошибка. Как он рассуждал?

7) Записано четыре числа: 0; 0; 0; 1. За один ход разрешается прибавить 1 к любым двум из этих чисел. Можно ли за несколько
ходов получить 4 одинаковых числа?

Шахматный конь вышел из клетки a1 и через несколько ходов вернулся обратно. Докажите, что он сделал чётное число ходов.

9) Можно ли сложить замкнутую цепочку из 2017-ти квадратных плиток таким способом, как показано на рисунке?

10) Можно ли число 1 представить в виде суммы дробей

11) Докажите, что если сумма двух чисел есть число нечётное, то произведение этих чисел всегда будет числом чётным.

12) Числа a и b — целые. Известно, что a + b = 2018. Может ли сумма 7a + 5b равняться 7891?

13) В парламенте некоторой страны две палаты с равным количеством депутатов. В голосовании по важному вопросу приняли участие все
депутаты. По окончании голосования председатель парламента сказал, что предложение принято большинством в 23 голоса, причём воздержавшихся не было. После чего один из депутатов сказал, что результаты сфальсифицированы.
Как он догадался?

14) На прямой расположено несколько точек. Между двумя соседними точками поставили по точке. И так ставили точки дальше. После точки подсчитали.
Может ли количество точек быть равным 2018?

15) У Пети есть 100 рублей одной
купюрой, а у Андрея полные карманы монет по 2 и 5 рублей. Сколькими способами Андрей может
разменять купюру Пети?

16) Запишите в строчку пять чисел так, чтобы сумма любых двух соседних чисел была
нечётная, а сумма всех чисел была чётная.

17) Можно ли записать в строчку
шесть чисел так, чтобы сумма любых двух соседних чисел была чётная, а сумма всех чисел была бы нечёитная?

18) В секции фехтования мальчиков в 10 раз больше,
чем девочек, при этом всего в секции не более 20-ти человек. Смогут ли они разбиться на пары? Смогут ли они
разбиться на пары, если мальчиков будет в 9 раз больше, чем девочек? А если в 8 раз больше?

19) В десяти коробках лежат конфеты. В первой — 1, во второй — 2,
в третьей — 3, и т.д., в десятой — 10. Пете за один ход разрешается в любые две коробки добавлять по три конфеты.
Сможет ли Петя за несколько ходов уравнять количество конфет в коробках? Может ли Петя уравнять количество
конфет в коробках подкладывая в две коробки по три конфеты, если изначально коробок 11?

20) 25 мальчиков и 25 девочек сидят за круглым столом. Докажите, что
у кого-то из сидящих за столом оба соседа одного пола.

21) Маша и несколько пятиклассников
встали в круг, взявшись за руки. Оказалось, что каждый держит за руки либо двух мальчиков, либо двух девочек. Если в кругу стоит 10 мальчиков, то сколько там стоит девочек?

22) На плоскости расположено 11 шестеренок, соединенных по замкнутой цепочке, причём 11-я соединена с 1-й. Могут ли все шестеренки вращаться одновременно?

23) Докажите, что дробь
есть целое число при любом натуральном n.

24) На столе лежат 9 монет, причём одна
из них вверх олрлом, другие — вверх решкой. Можно ли все монеты положить вверх орлом, если разрешено одновременно
переворачивать две монеты?

25) Можно ли в таблице 5х5 расставить 25 натуральных чисел так,
чтобы во всех строках суммы были чётные, а во всех столбцах — нечётные?

26) Кузнечик прыгает по прямой: первый раз — на 1 см, второй раз на 2 см,
третий раз на 3 см и т.д. Может ли он через 25 прыжков вернуться на старое место?

27) Улитка ползает по плоскости с постоянной скоростью, каждые 15 минут поворачивая под прямым углом. Докажите, что вернуться
в исходную точку она сможет лишь через целое число часов.

28) В ряд выписаны числа от 1 до 2000. Можно ли меняя местами числа через одно, переставить их в обратном порядке?

29) На доске написаны 8 простых чисел, каждое из которых больше двух. Может ли их сумма равняться 79?

30) Маша и её друзья встали в круг. Оба соседа любого из детей — одного пола. Мальчиков 5, сколько девочек?

Четные числа — это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т.п.). Каждое такое число можно записать в виде 2K,
подобрав подходящее целое K (например, 4 = 2 х 2, 6 = 2 х 3, и т.д.).

Нечетные числа — это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т.п.). Каждое такое число можно записать в виде 2K + 1, подобрав подходящее целое K (например, 3 = 2 х 1 +
1, 5 = 2 х 2 + 1, и т.д.).

Сложение и вычитание:

- Ч
  ётное ±
  Ч
  ётное = Ч
  ётное
- Ч
  ётное ±
  Н
  ечётное = Н
  ечётное
- Н
  ечётное ±
  Ч
  ётное = Н
  ечётное
- Н
  ечётное ±
  Н
  ечётное = Ч
  ётное
Умножение:
- Ч
  ётное ×
  Ч
  ётное = Ч
  ётное
- Ч
  ётное ×
  Н
  ечётное = Ч
  ётное
- Н
  ечётное ×
  Н
  ечётное = Н
  ечётное
Деление:
- Ч
  ётное /
  Ч
  ётное — однозначно судить о чётности результата невозможно (если результат
  целое число
  
  ,
  то оно может быть как чётным, так и нечётным)
- Ч
  ётное /
  Н
  ечётное -— если результат
  целое число
  
  ,
  то оно Ч
  ётное
- Н
  ечётное /
  Ч
  ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н
  ечётное /
  Н
  ечётное —если результат
  целое число
  
  ,
  то оно Н
  ечётное

Сумма любого числа четных чисел –
четно.

Сумма нечетного
числа нечетных чисел – нечетно.

Сумма четного
числа нечетных чисел – четно.

Разность двух
чисел имеет ту же

четность, что и их сумма

.
(напр. 2+3=5 и 2-3=-1 оба нечетные)

Алгебраическая

(со знаками + или -) сумма целых чисел

имеет ту же

четность, что и их сумма

.
(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)

Идея
четности имеет много разных применений. Самые простые из них:

1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).

2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов,
если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу
переходов

между ними и наоборот !!!
)

2″. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны

, то периодов пребывания объекта в том или ином состоянии — четное

число, если исходное и конечное состояния совпадают — то нечетное

.
(переформулировка п.2)

3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.

3″. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли
начальное состояние с конечным. (переформулировка п.3)

4. Если предметы можно разбить на пары, то их количество четно.

5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой
предмет может быть не один (но их всегда нечетное число).

(!) Все эти соображения можно на олимпиаде
вставлять в текст решения задачи, как очевидные утверждения.

Примеры:

Задача 1.

На плоскости
расположено 9 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей… 9-я с первой). Могут ли они вращаться одновременно?

Решение:

Нет, не могут. Если бы
они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в
каком именно

направлении вращается первая шестеренка !
) Тогда всего должно быть
четное число шестеренок, а их 9 штук?! ч.и.т.д. (знак «?!» обозначает получение противоречия)

Задача 2.

В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки + и -, чтобы
получилось выражение, равное нулю?

Решение:

Нет, нельзя. Четность
полученного выражения всегда

будет совпадать с четностью суммы

1+2+…+10=55, т.е. сумма всегда будет нечетной

. А 0
— четное число?! ч.т.д.

Excel для Office 365

Excel для Office 365 для Mac

Excel для Интернета

Excel 2019

Excel 2016

Excel 2019 для Mac

Excel 2013

Excel 2010

Excel 2007

Excel 2016 для Mac

Excel для Mac 2011

Excel Starter 2010

Меньше

В этой статье описаны синтаксис формулы и использование функции ЕЧЁТН
в Microsoft Excel.

Описание

Возвращает значение ИСТИНА, если число четное, и значение ЛОЖЬ, если число нечетное.

Синтаксис

ЕЧЁТН(число)

Аргументы функции ЕЧЁТН описаны ниже.

Число
Обязательный. Проверяемое значение. Если число не является целым, оно усекается.

Замечания

Если значение аргумента «число» не является числом, функция ЕЧЁТН возвращает значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Когда нужно приготовить разного рода отчеты, иногда возникает потребность выделить все парные и непарные числа разными цветами. Для решения данной задачи наиболее рациональным способом является условное форматирование.

Как найти четные числа в Excel

Набор четных и нечетных чисел, которые следует автоматически выделить разными цветами:

Допустим парные числа нам нужно выделит зеленым цветом, а непарные – синим.

Две формулы отличаются только операторами сравнения перед значением 0. Закройте окно диспетчера правил нажав на кнопку ОК.

В результате у нас ячейки, которые содержат непарное число имеют синий цвет заливки, а ячейки с парными числами – зеленый.

Функция ОСТАТ в Excel для поиска четных и нечетных чисел

Функция =ОСТАТ() возвращает остаток от деления первого аргумента на второй. В первом аргументе мы указываем относительную ссылку, так как данные берутся из каждой ячейки выделенного диапазона. В первом правиле условного форматирования мы указываем оператор «равно» =0. Так как любое парное число, разделенное на 2 (второй оператор) имеет остаток от деления 0. Если в ячейке находится парное число формула возвращает значение ИСТИНА и присваивается соответствующий формат. В формуле второго правила мы используем оператор «неравно» 0. Таким образом выделяем синим цветом нечетные числа в Excel. То есть принцип работы второго правила действует обратно пропорционально первому правилу.

Источник

Сложение и вычитание:

- Ч
  ётное ±
  Ч
  ётное = Ч
  ётное
- Ч
  ётное ±
  Н
  ечётное = Н
  ечётное
- Н
  ечётное ±
  Ч
  ётное = Н
  ечётное
- Н
  ечётное ±
  Н
  ечётное = Ч
  ётное
Умножение:
- Ч
  ётное ×
  Ч
  ётное = Ч
  ётное
- Ч
  ётное ×
  Н
  ечётное = Ч
  ётное
- Н
  ечётное ×
  Н
  ечётное = Н
  ечётное
Деление:
- Ч
  ётное /
  Ч
  ётное — однозначно судить о чётности результата невозможно (если результат
  целое число
  
  ,
  то оно может быть как чётным, так и нечётным)
- Ч
  ётное /
  Н
  ечётное -— если результат
  целое число
  
  ,
  то оно Ч
  ётное
- Н
  ечётное /
  Ч
  ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н
  ечётное /
  Н
  ечётное —если результат
  целое число
  
  ,
  то оно Н
  ечётное

Сумма любого числа четных чисел –
четно.

Сумма нечетного
числа нечетных чисел – нечетно.

Сумма четного
числа нечетных чисел – четно.

Разность двух
чисел имеет ту же

четность, что и их сумма

.
(напр. 2+3=5 и 2-3=-1 оба нечетные)

Алгебраическая

(со знаками + или -) сумма целых чисел

имеет ту же

четность, что и их сумма

.
(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)

Идея
четности имеет много разных применений. Самые простые из них:

2″. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны

, то периодов пребывания объекта в том или ином состоянии — четное

число, если исходное и конечное состояния совпадают — то нечетное

.
(переформулировка п.2)

3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.

4. Если предметы можно разбить на пары, то их количество четно.

(!) Все эти соображения можно на олимпиаде
вставлять в текст решения задачи, как очевидные утверждения.

Примеры:

Задача 1.

Решение:

Задача 2.

Нет, нельзя. Четность
полученного выражения всегда

будет совпадать с четностью суммы

1+2+…+10=55, т.е. сумма всегда будет нечетной

. А 0
— четное число?! ч.т.д.

Excel для Office 365

Excel для Office 365 для Mac

Excel для Интернета

Excel 2019

Excel 2016

Excel 2019 для Mac

Excel 2013

Excel 2010

Excel 2007

Excel 2016 для Mac

Excel для Mac 2011

Excel Starter 2010

Меньше

В этой статье описаны синтаксис формулы и использование функции ЕЧЁТН
в Microsoft Excel.

Описание

Возвращает значение ИСТИНА, если число четное, и значение ЛОЖЬ, если число нечетное.

Синтаксис

ЕЧЁТН(число)

Аргументы функции ЕЧЁТН описаны ниже.

Число
Обязательный. Проверяемое значение. Если число не является целым, оно усекается.

Замечания

Если значение аргумента «число» не является числом, функция ЕЧЁТН возвращает значение ошибки #ЗНАЧ!.

Пример

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Задачи

1) Докажите, что нельзя подобрать 5 нечётных чисел, сумма которых равна 100.

3) Чётна или нечётна сумма всех натуральных чисел от 1 до 2019?

4) Докажите, что сумма двух последовательных нечетных чисел делится на 4.

5) Можно ли соединить 13 городов дорогами так, чтобы из каждого города выходило ровно 5 дорог?

9) Можно ли сложить замкнутую цепочку из 2017-ти квадратных плиток таким способом, как показано на рисунке?

10) Можно ли число 1 представить в виде суммы дробей

12) Числа a и b — целые. Известно, что a + b = 2018. Может ли сумма 7a + 5b равняться 7891?

23) Докажите, что дробь
есть целое число при любом натуральном n.

28) В ряд выписаны числа от 1 до 2000. Можно ли меняя местами числа через одно, переставить их в обратном порядке?

29) На доске написаны 8 простых чисел, каждое из которых больше двух. Может ли их сумма равняться 79?

30) Маша и её друзья встали в круг. Оба соседа любого из детей — одного пола. Мальчиков 5, сколько девочек?

Источник

Вычисление суммы значений четных и нечетных ячеек в столбцах

k987

Дата: Четверг, 29.03.2018, 20:55 |
Сообщение № 1

Группа: Пользователи

Ранг: Участник

Сообщений: 91

Репутация:
0
±

Замечаний:
0% ±

Добрый день! Помогите, пожалуйста с такой проблемой: есть файл, в котором нужно считать сумму в четных и сумму в нечетных ячейках (пример прилагаю). Написала формулу, по которой вроде бы должна считаться сумма всех ячеек четных столбцов. Формула в ячейке А2. Однако формула работает некорректно. Если же я выделяю ту часть формулы, которая отвечает за определение четной или нечетной ячейки и нажимаю F9, чтобы посмотреть результат вычисления, то значение меняется (ячейка 4А). Подскажите, в чем моя ошибка в итоговой формуле?

К сообщению приложен файл:

9186938.xlsx
(10.0 Kb)

Сообщение отредактировал k987 — Четверг, 29.03.2018, 20:56

Ответить

dude

Дата: Четверг, 29.03.2018, 21:06 |
Сообщение № 2

Группа: Проверенные

Ранг: Форумчанин

Сообщений: 193

Репутация:
28
±

Замечаний:
0% ±

2016

Код

=СУММПРОИЗВ((ОСТАТ(СТОЛБЕЦ(B2:U2);2)=0)*B2:U2)

Ответить

k987

Дата: Четверг, 29.03.2018, 21:13 |
Сообщение № 3

Группа: Пользователи

Ранг: Участник

Сообщений: 91

Репутация:
0
±

Замечаний:
0% ±

dude, спасибо большое. А как изменить формулу, если некоторые из ячеек пустые?

Ответить

AlexM

Дата: Четверг, 29.03.2018, 21:15 |
Сообщение № 4

Группа: Друзья

Ранг: Участник клуба

Сообщений: 4257

Репутация:
1046
±

Замечаний:
0% ±

Excel 2003

Почти также

Код

=СУММПРОИЗВ(ОСТАТ(СТОЛБЕЦ(B2:U2)+1;2)*B2:U2)

Код

=СУММПРОИЗВ(ОСТАТ(СТОЛБЕЦ(B4:U4);2)*B4:U4)

Номер мобильного модема (без голосовой связи)
9269171249 МегаФон, Московский регион.

Ответить

Karataev

Дата: Четверг, 29.03.2018, 21:15 |
Сообщение № 5

Группа: Проверенные

Ранг: Старожил

Сообщений: 1330

Репутация:
528
±

Замечаний:
0% ±

Excel

Формула массива — завершайте ввод формулы не клавишей Enter (как Вы это обычно делаете), а сочетанием клавиш Ctrl+Shift+Enter.

Код

=СУММ(ЕСЛИ(ЕЧЁТН(СТОЛБЕЦ(B2:U2));B2:U2))

Киви-кошелек: 9166309108

Сообщение отредактировал Karataev — Четверг, 29.03.2018, 21:16

Ответить

dude

Дата: Четверг, 29.03.2018, 21:16 |
Сообщение № 6

Группа: Проверенные

Ранг: Форумчанин

Сообщений: 193

Репутация:
28
±

Замечаний:
0% ±

2016

или

Ответить

k987

Дата: Четверг, 29.03.2018, 21:28 |
Сообщение № 7

Группа: Пользователи

Ранг: Участник

Сообщений: 91

Репутация:
0
±

Замечаний:
0% ±

Спасибо большое! Все получилось!

Ответить

Источник

pyus Пользователь Сообщений: 34 Регистрация: 01.01.1970	Подскажите, как можно подсчитать в строке нечетные и четные числа.

pyus Пользователь Сообщений: 34 Регистрация: 01.01.1970	{quote}{login=The_Prist}{date=03.03.2010 04:11}{thema=}{post}ЕЧЁТН и ЕНЕЧЁТ{/post}{/quote} Я извиняюсь то таких функций я не нашел в екселе, или что-то я не понял.

В Excel 2003 есть только ЕНЕЧЁТб да и то,если подключена надстройка пакета анализа. Поэтому если не Excel 2007, то без функций пакета анализа для первой строки 1:1 можно так

количество четных: =СУММПРОИЗВ(ЕЧИСЛО(1:1)*(ОСТАТ(1:1;2)=0))
количество нечетных: =СУММПРОИЗВ(ЕЧИСЛО(1:1)*(ОСТАТ(1:1;2)<>0))

сумма четных: =СУММПРОИЗВ(ЕЧИСЛО(1:1)*(ОСТАТ(1:1;2)=0);1:1)
сумма нечетных: =СУММПРОИЗВ(ЕЧИСЛО(1:1)*(ОСТАТ(1:1;2)<>0);1:1)

	Exel 2003 А так подойдет? 15 Кб

pyus

Пользователь

Сообщений: 34
Регистрация: 01.01.1970

{quote}{login=:)}{date=03.03.2010 04:29}{thema=}{post}В Excel 2003 есть только ЕНЕЧЁТб да и то,если подключена надстройка пакета анализа. Поэтому если не Excel 2007, то без функций пакета анализа для первой строки 1:1 можно так

сумма четных: =СУММПРОИЗВ(ЕЧИСЛО(1:1)*(ОСТАТ(1:1;2)=0);1:1)
сумма нечетных: =СУММПРОИЗВ(ЕЧИСЛО(1:1)*(ОСТАТ(1:1;2)<>0);1:1){/post}{/quote}

Большое спасибо разобрался, работает, подключил пакет анализа в 2003 что-то не работает функция =ЕЧЁТН(T11:X11)пишет #ЗНАЧ,

pyus

Пользователь

Сообщений: 34
Регистрация: 01.01.1970

{quote}{login=The_Prist}{date=03.03.2010 04:51}{thema=}{post}И парочка формул массива для подсчета все того же:

=СУММ(ЕСЛИ(($A$2:$A$50/2)=(ЦЕЛОЕ($A$2:$A$50/2));1)) — четные

=СУММ(ЕСЛИ(($A$2:$A$50/2)=(ЦЕЛОЕ($A$2:$A$50/2));1)) — нечетные{/post}{/quote}
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Чтот здесь нето

Большое спасибо мне подходит
=СУММПРОИЗВ(ЕЧИСЛО(T4:X4)*(ОСТАТ(T4:X4;2)=0))
=СУММПРОИЗВ(ЕЧИСЛО(T4:X4)*(ОСТАТ(T4:X4;2)<>0))

vikttur Пользователь Сообщений: 47199 Регистрация: 15.09.2012	Еще формулы массива: =СУММ(ОСТАТ(C1:C30;2)) =СУММ((1-ОСТАТ(C1:C30;2)))

	Большое спасибо! Нашол то, что искал)

	Скажите, если надо, например, по номеру месяца в одной ячейке получить номер квартала к которому этот месяц относится то как это делать?

vikttur Пользователь Сообщений: 47199 Регистрация: 15.09.2012	Вам нужно четный квартал или нечетный? Или четный месяц в нечетном квартале? Как Ваш вопрос согласуется с темой? По принципу «где открыл, там и наг… (опять не то) написал»?

{quote}{login=Кейт}{date=11.04.2011 03:21}{thema=Re: Re: Re: }{post}Скажите, если надо, например, по номеру месяца в одной ячейке получить номер квартала к которому этот месяц относится то как это делать?{/post}{/quote}

1) прочитать правила форума.
2) поступить в соответствии с правилами форума.

(конечно, если вас интересует результат)

	{quote}{login=Казанский}{date=11.04.2011 03:42}{thema=Кейт}{post}=ЦЕЛОЕ((A1-1)/3)+1{/post}{/quote} Месяц подкинуть и тады =ЦЕЛОЕ(МЕСЯЦ(A1-1)/3)+1…

MCH Пользователь Сообщений: 3875 Регистрация: 22.12.2012	{quote}{login=}{date=11.04.2011 03:55}{thema=Re: Кейт}{post}Месяц подкинуть и тады =ЦЕЛОЕ(МЕСЯЦ(A1-1)/3)+1…{/post}{/quote} лучше всетаки так: =ЦЕЛОЕ((МЕСЯЦ(A1)-1)/3)+1

	гы. профессионалы решают какие-то СВОИ задачи а у автора чётко написано — «по номеру месяца в одной ячейке». всем, кроме Казанского — незачёт.

Serge Пользователь Сообщений: 11308 Регистрация: 01.01.1970	ik, позволь остальным самим разобраться

	да я тоже с интересом наблюдаю за вариантами, да. самое интересное впереди — придёт Кейт (если придёт вообще) и окажется, что ему надо было нечто совсем другое

Serge Пользователь Сообщений: 11308 Регистрация: 01.01.1970

	нет, не «игрок», а «Кейт», задавший 11.04.2011 15:21 свой вопрос в чужой теме

	Друзья, подскажите почти блондинке, плиз: как в Excel задать формулу для подсчета четных (нечетных) строк? Заранее благодарна

MCH Пользователь Сообщений: 3875 Регистрация: 22.12.2012	так нужно? =СУММЕСЛИ($D$8:$D$261;$D262;E$8:E$261)

k61 Пользователь Сообщений: 2441 Регистрация: 21.12.2012	#22 15.02.2012 07:22:31 <EM><FONT color=#99000><STRONG>Солнышко, Ваш вопрос не удален только из уважения к отвечающим. Зачем разбрасывать свой вопрос по темам? Ответ дан в теме «Отдельная сумма четных и нечетных строк».</STRONG></FONT> — [<STRONG>МОДЕРАТОРЫ</STRONG>]</EM> Макрос наше всё. Прикрепленные файлы post_308211.xls (57.5 КБ)

Источник