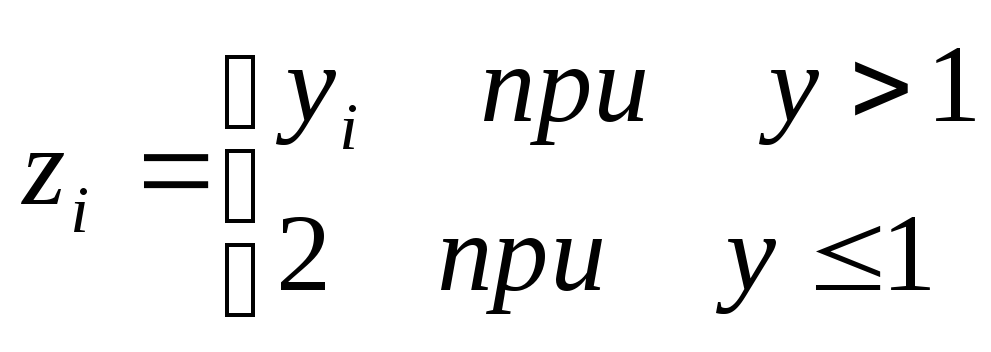Решение нелинейного уравнения в Excel
Разберём решение нелинейного уравнения в Excel вида:
y=4x 3 +2x–7
Ячейку A4 оставим пустой, а в ячейки B4 запишем формулу вида
Затем в Excel перейдём на вкладку Данные -> Поиск Решения
Открывается окно Параметры поиска решения. В поле оптимизировать целевую функцию выбираем ячейку B4, ставим Значения 0, ячейку переменной указываем A4, ставим галочку сделать переменные без ограничений неотрицательными, выбираем метод решения — поиск решения нелинейных задач методом ОПГ (обобщенного приведенного градиента) и жмем Найти решение
Получаем решение искомой задачи
x=1,06744215530327
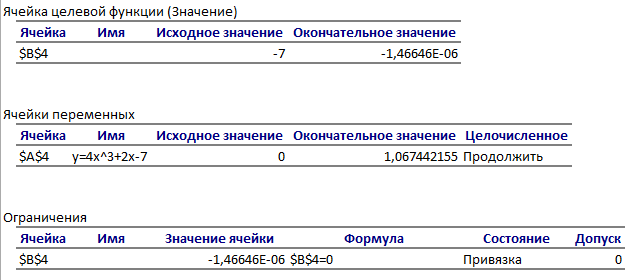
Отчет результатов вычисления в Excel
Решение уравнения с помощью инструмента «Поиск решения».
Практическая работа № 17.
Тема: Решение линейных и нелинейных уравнений с помощью MS Excel.
Цель: научиться решать линейные и нелинейные уравнения различными способами.
Теоретические сведения и задания:
Графический метод решения уравнения.
Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль.
Разберем графический метод решения уравнения на примере: пусть необходимо решить уравнение x 3 — 0,01x 2 — 0,7044x + 0,139104 = 0.
На листе 1 проведем табулирование нашей функции на интервале от -1 до 1 с шагом 0,2, для этого построим таблицу значений. Затем по таблице построим точечную диаграмму. Результаты вычислений приведены на рисунке, где в ячейку В2 была введена формула: = A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104. На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8] (можно получить более точное решение если выбрать шаг 0,1).
Лист 1 переименовать в Задание1 и сохранить работу в своей папке с именем Фамилия пр17.xls
Решение уравнения с помощью инструмента «Подбор параметра».
Перейти на лист 2.
Чтобы решить нелинейное уравнение можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.
Возьмем в качестве примера квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:
В ячейку С3 введем формулу для вычисления значения функции, стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.
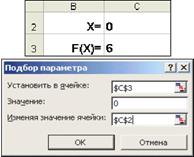
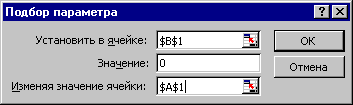
· В окне диалога Подбор параметра в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
· После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.
Вернемся к примеру. Возникает вопрос: как получить второй корень? Для того чтобы найти второй корень, достаточно в качестве начального приближения в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.
Лист 2 переименовать в Задание2.
Решение уравнения с помощью инструмента «Поиск решения».
Команда Подбор параметра является удобной для решения простых уравнений. Для более сложных задач следует использовать команду Поиск решения, доступ к которой реализован через пункт меню Сервис/Поиск решения. При решении уравнений с помощью Поиска решений можно учитывать различные дополнительные ограничения, например, ОДЗ (область допустимых значений).
Перейти на лист 3.
Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
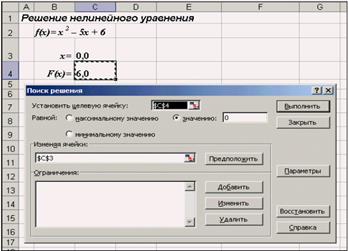
После открытия диалога Поиск решения необходимо выполнить следующие действия:
1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению, для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, как на рисунке. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.

Данную систему уравнений можно представить в матричной форме:




Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
Решить систему уравнений:

1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
источники:
http://megalektsii.ru/s18417t6.html
http://zf.bsut.by/it/fbo/zb1/lab2.htm
Решение нелинейного уравнения в Excel
Разберём решение нелинейного уравнения в Excel вида:
y=4x 3 +2x–7
Ячейку A4 оставим пустой, а в ячейки B4 запишем формулу вида
Затем в Excel перейдём на вкладку Данные -> Поиск Решения
Открывается окно Параметры поиска решения. В поле оптимизировать целевую функцию выбираем ячейку B4, ставим Значения 0, ячейку переменной указываем A4, ставим галочку сделать переменные без ограничений неотрицательными, выбираем метод решения — поиск решения нелинейных задач методом ОПГ (обобщенного приведенного градиента) и жмем Найти решение

Получаем решение искомой задачи
x=1,06744215530327
Отчет результатов вычисления в Excel
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.
Данную систему уравнений можно представить в матричной форме:


Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
Решить систему уравнений:
1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Кафедра прикладной математики и вычислительной техники
Решение нелинейных уравнений в Excel и Mathcad
к выполнению лабораторных работ
по дисциплине «Вычислительная математика»
Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.
Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».
Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.
Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.
Рецензент к. ф-м. н.
Ó , составление, 2012
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
1.2 Отделение корней
1.3 Уточнение корней стандартными средствами Excel и Mathcad
1.4 Метод деления отрезка пополам
1.6 Метод Ньютона (касательных)
1.7 Комбинированный метод
1.8 Метод итераций
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
2.2 Решение систем нелинейных уравнений методом Ньютона
2.3 Решение систем нелинейных уравнений методами итераций
3 Задания к лабораторным работам
Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения
Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения
Лабораторная № 3. Решение систем нелинейных уравнений
Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем
4 Вопросы и тесты для самоконтроля
Список рекомендуемой литературы
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.
В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.
Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).
1.2 Отделение корней
Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.
Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.
Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».
Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.
На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.
Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения
1.3 Уточнение корней стандартными средствами Excel и Mathcad
Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.
В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel
В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad
Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.
В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».
Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).
1.4 Метод деления отрезка пополам
В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.
Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.
Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.
На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.
Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.
Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad
1.5 Метод хорд
В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

1.6 Метод Ньютона (касательных)
Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.
Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.
Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.
Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.
Точность вычислений можно оценить из соотношения
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.
Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.
Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.
Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).
2.2 Решение систем нелинейных уравнений методом Ньютона
Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.
Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.
В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.
2.3 Решение систем нелинейных уравнений методами итераций
Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:
источники:
http://zf.bsut.by/it/fbo/zb1/lab2.htm
http://pandia.ru/text/78/157/38912.php
Нелинейные
уравнения – это уравнения вида f(x)=0,
где f(x)
– нелинейная функция. Решение уравнения
f(x)=0
сводится к поиску таких значений х*
(корней уравнения), которые превращают
уравнение в тождество. Различают
нелинейные алгебраические уравнения
и трансцендентные.
Например,
нелинейное алгебраическое уравнение
ax2
+
вx
+с =0
имеет два корня, которые могут быть
действительными или мнимыми. Например,
уравнение х2
+ 2=0 имеет два мнимых корня х1=
-2
и х2=
--2
.
В
дальнейшем будет идти речь о вычислении
только действительных корней.
Трансцендентным
называется
уравнение,
если в f(x)
входит хотя бы одна трансцендентная
функция. Например, sin(x)
–1=0;
Решение
нелинейных уравнений выполняют в два
этапа:
-
Этап
отделения
корней. -
Этап
уточнения
корней
, т.е. поиск коней с заданной точностью.
Этап
отделения корней
Для
этого построим график заданной функции
f(x)=0.
В столбце А располагаем изменение
аргумента, а в столбце В табулируемую
функцию. Строим график. На графике
выделяем границы корня и в этих границах
берем начальное приближение корня
(нарисовать график, выделить корни и
взять начальное приближение).
Этап
уточнение корня
Команда
Подбор
параметров
Порядок
уточнения:
1.
В ячейку A1
вводим
начальное приближение корня Х1.
2.
В ячейку В1
вводим
формулу с заданной функцией.
3.
Выполняем команды Сервис,
Подбор
параметра.
Появляется окно Подбор
параметра (рис.
7.7).
4.
В поле «Установить
в ячейке»
записать адрес первой формулы (можно
снять окно и щелкнуть ячейку В1,
затем восстановить окно).
5.
В поле «Значение»
установить 0.
6.
В поле «Изменяя
значение
ячейки«
установить адрес А1
(снять окно и щелкнуть А1).
7.
Щелкнуть ОК.
Появляется окно Результат
подбора параметра
(рис. 7.8), а в ячейке А1
будет уточненное значение корня.
Рис.
7.8
Рис.
7.7
7.5. Вычисления по итерационным формулам
Итерационной
называется формула типа yi+1
= f
(yi)
. Пример1.
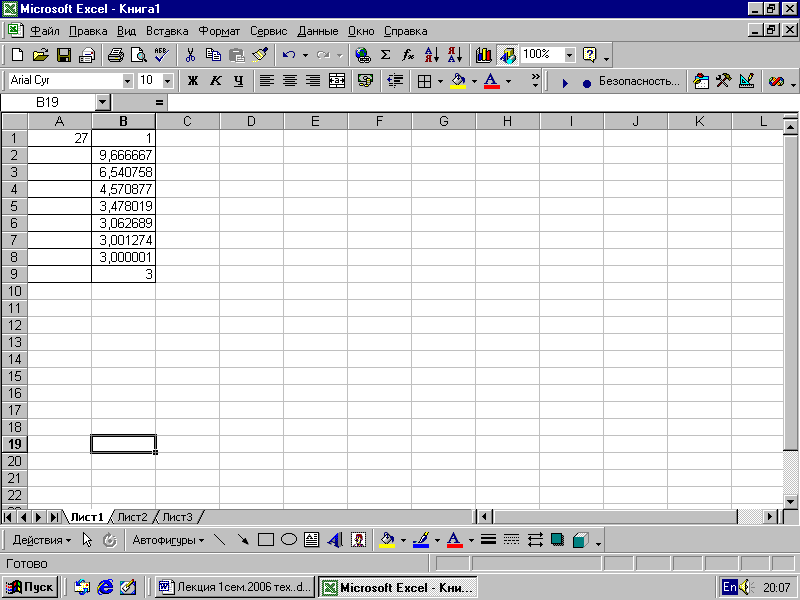
Вычисление
задано итерационной формулой yi+1=(x/yi2
+2yi)/3
Начальное
приближении у0=1
и значение х= 27.
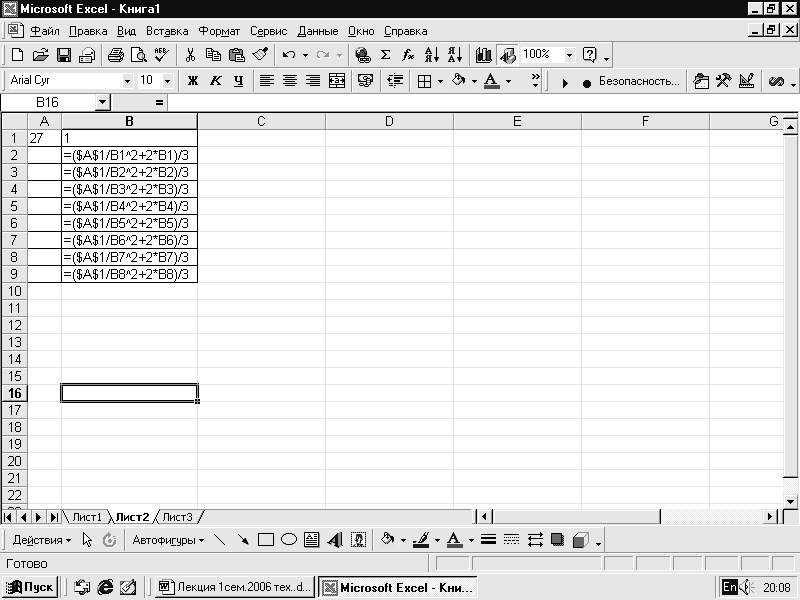
Составим
ЭТ для вычисления:
1.
В ячейку a2
запишем
значение х равное 27
(рис. 7.9).
2.
В ячейку b2
запишем
значение у0
равное 1.
3
Рис.
7.9
. В ячейку b3
запишем формулу =
($A$1/B1^2+2*B1)/3,
которую копируем вниз
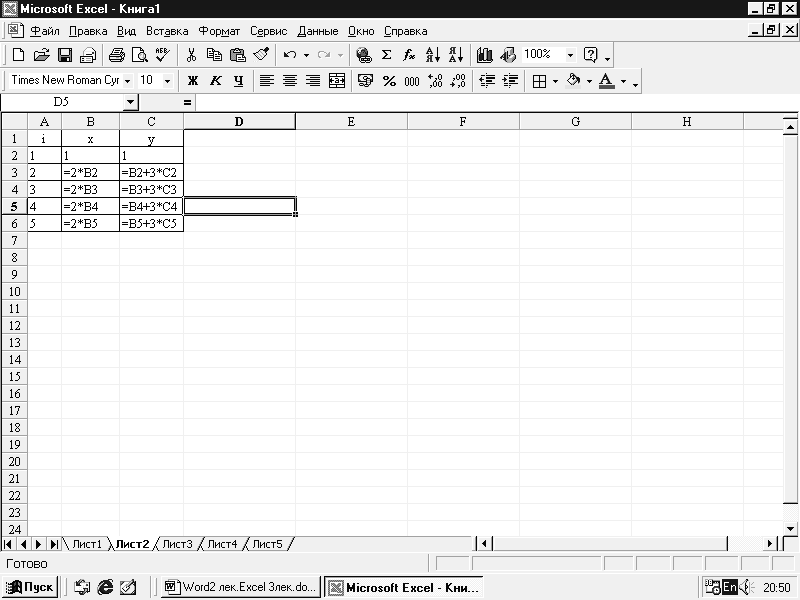
Пример
2. Заданы
итерационные формулы
x
i
=2xi-1
и yi=
xi-1
+ 3yi-1
при
изменении
i=2,3,4,5.
При
i=2
х2
= 2х1
и y2=
x1
+ 3y1
Начальные
значения x1=1
; y1=1
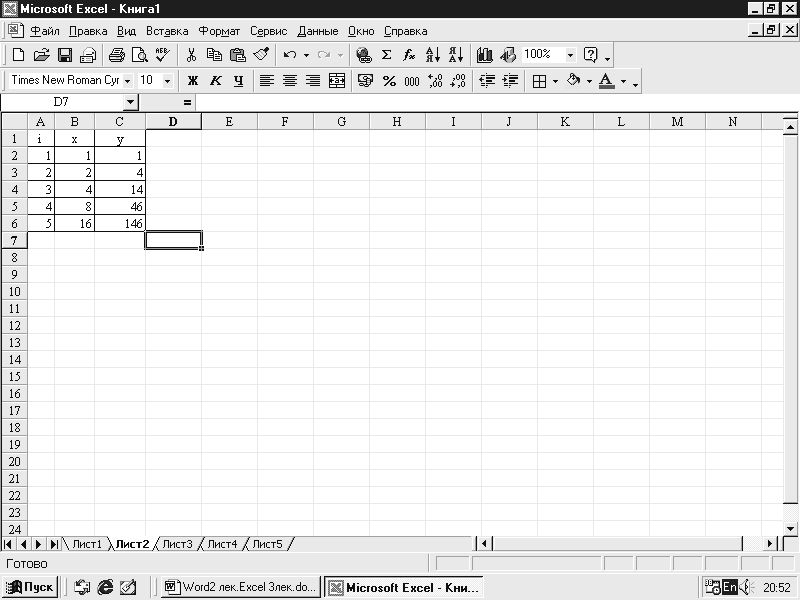
(рис. 7.10) запишем в В2 и С2 соответственно.
В ячейки В3 и С3 запишем формулы для х2
и у2
. Выделяем В3:С3 и копируем вниз до С6.
Результат вычисления на рис. 7.11.
Рис.
7.10
Рис.
7.11
Пример
3.
Решение
задач следующего типа:
Даны
действительные числа у1, у2,…у5, которые
записаны в В2:В6
Составить
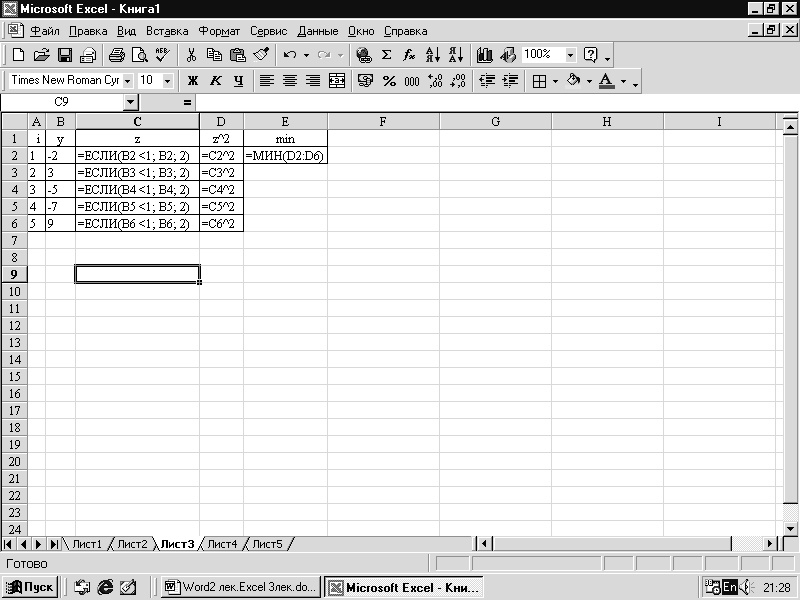
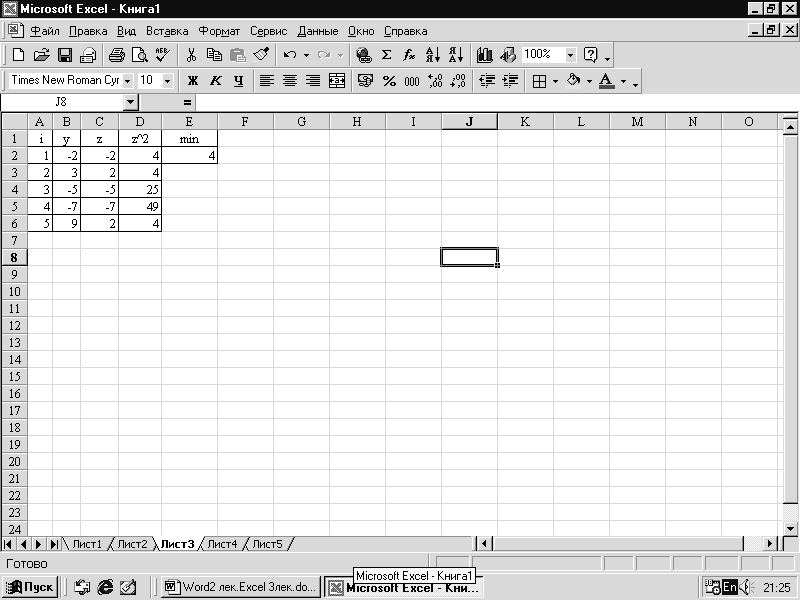
ЭТ для вычисления
и
определения min(z12,
z22,
…,z52)
при i=1,2,…,5
Рис.
7.12
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Разберём решение нелинейного уравнения в Excel вида:
y=4x3+2x–7
Ячейку A4 оставим пустой, а в ячейки B4 запишем формулу вида
=4*СТЕПЕНЬ(A4;3)+2*A4-7
Затем в Excel перейдём на вкладку Данные -> Поиск Решения
Открывается окно Параметры поиска решения. В поле оптимизировать целевую функцию выбираем ячейку B4, ставим Значения 0, ячейку переменной указываем A4, ставим галочку сделать переменные без ограничений неотрицательными, выбираем метод решения — поиск решения нелинейных задач методом ОПГ (обобщенного приведенного градиента) и жмем Найти решение
Получаем решение искомой задачи
x=1,06744215530327
Отчет результатов вычисления в Excel
5787
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
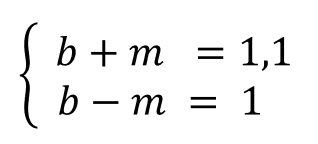
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
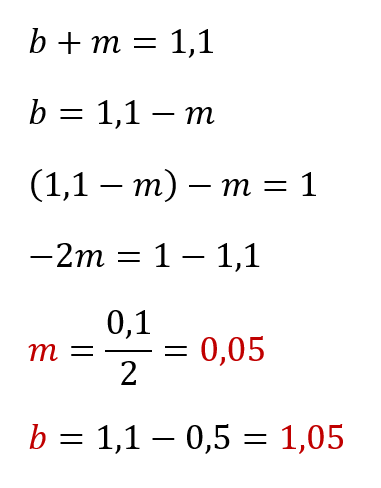
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
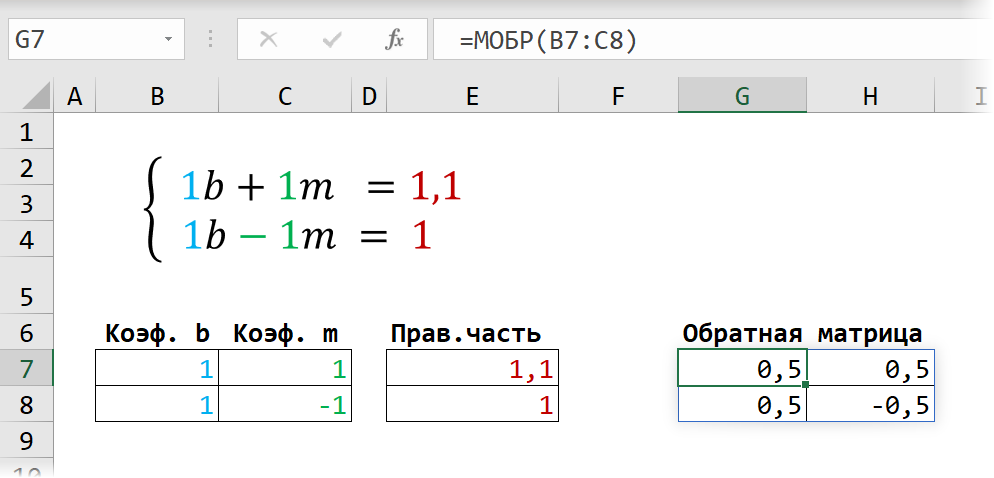
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
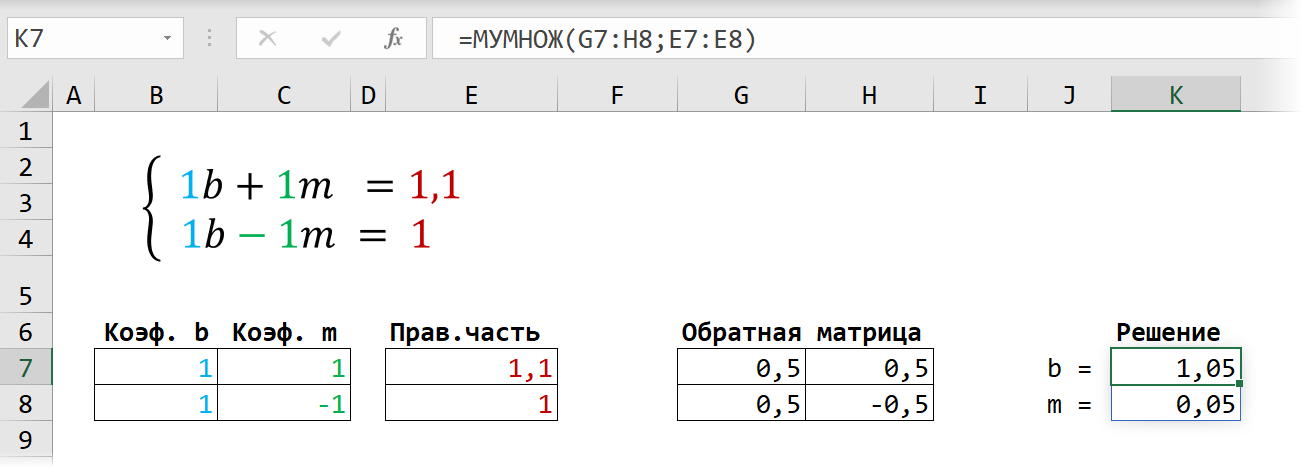
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
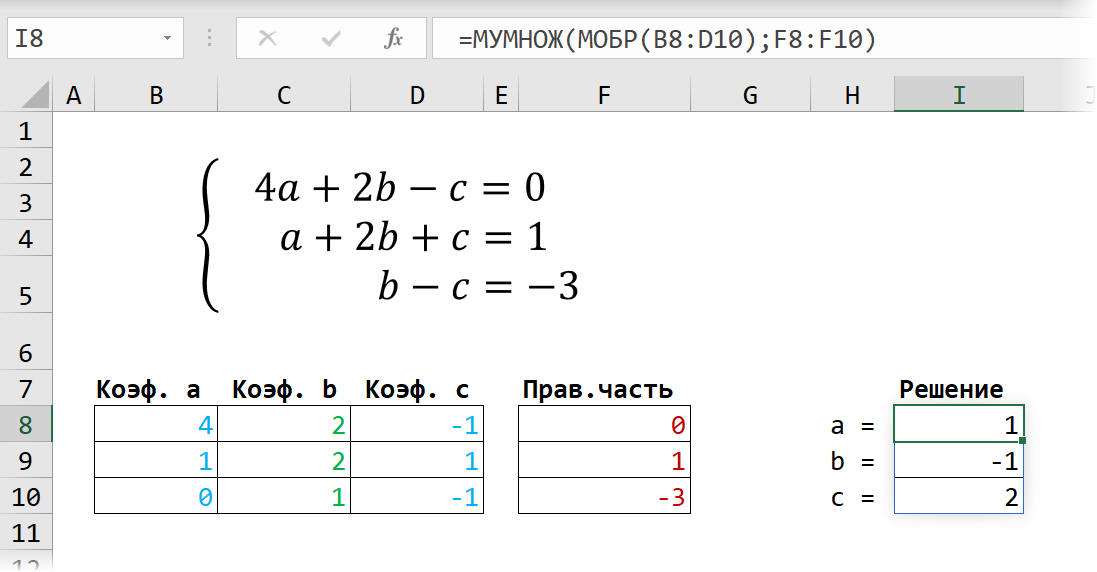
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
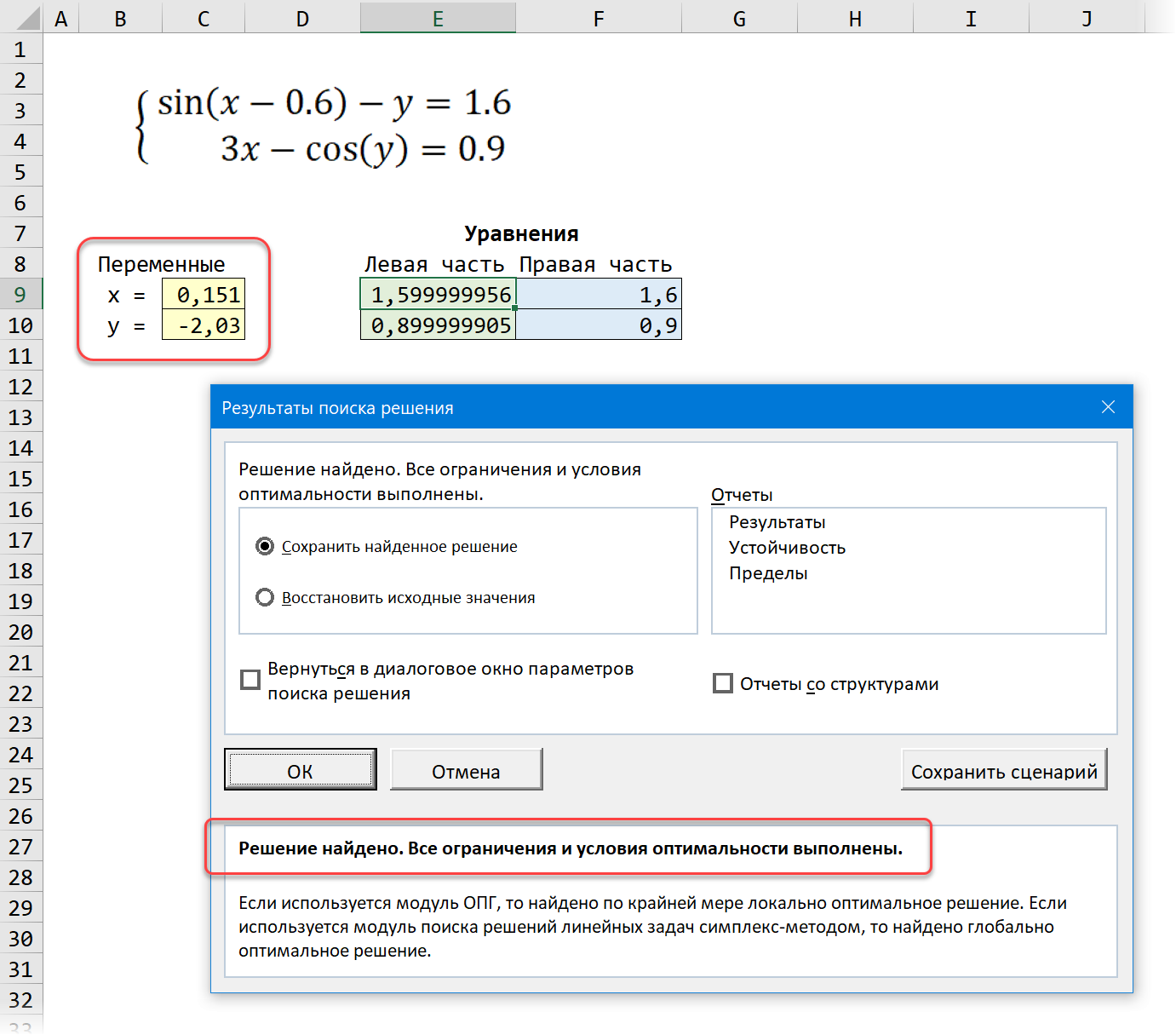
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
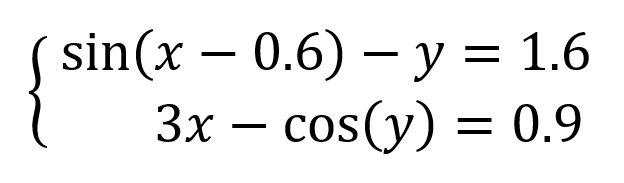
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
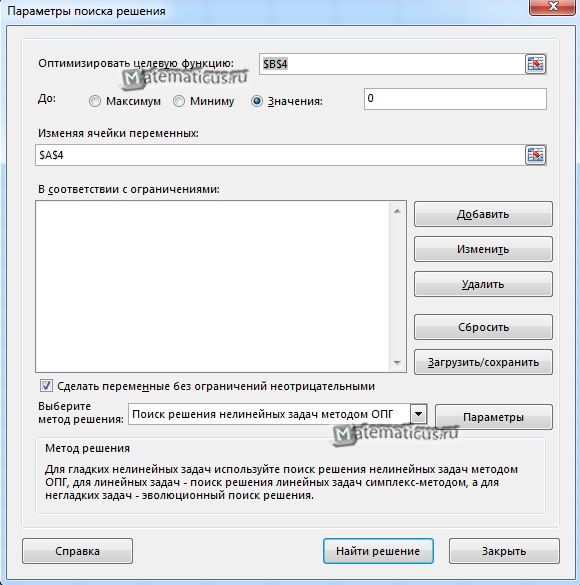
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
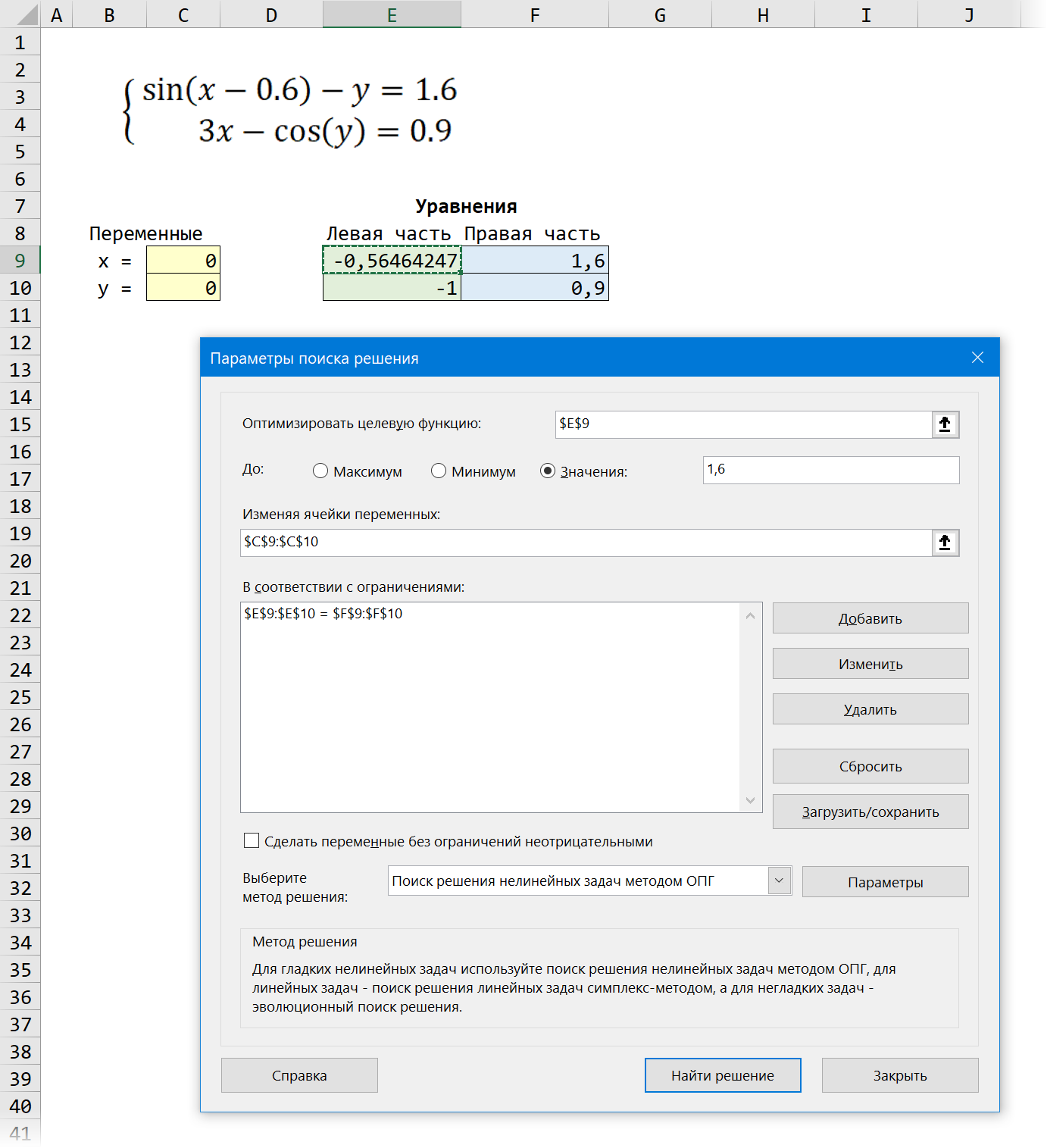
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).