Урок №12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц.
Уровень 1
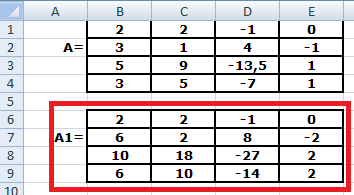
Задание 1. Найдите ранг матрицы А с помощью Excel.
 |
|
Ход решения.
- Первую строку оставляем без изменений. Скопируйте первую строку в ячейки B6:E6.
- Чтобы избежать появления дробей, умножим вторую, третью и четвертую строки на 2. Для этого введите в ячейку B7 формулу =2*B2. Скопируйте эту форму с помощью маркера заполнения в ячейки B7:E9 (Маркер заполнения — небольшой черный квадрат в правом нижнем углу ячейки. При наведении на него курсор принимает вид черного креста.). В результате должна получиться матрица А1 (рис.2).
Рисунок 2. 2-я,3-я,4-я строки умножены на 2.
- Первую строку оставим без изменения (скопируйте в ячейки B11:E11).
- В ячейку B12 внесите формулу =B7+B$6*(-$B7/$B$6). Скопируйте эту формулу в ячейки C12:E14 с помощью маркера заполнения. В итоге имеем матрицу А2 (рис.3)
Рисунок 3. Матрица А2
- Переходим к вычислению матрицы А3. Первую и вторую строки оставляем без изменения. Для этого выделите ячейки B11:E12, нажмите кнопку «Копировать», далее выделите ячейку B16 и в контекстном меню ячейки выберите «Специальная вставка». В открывшемся окне выберите пункт «значения» (рис.4) и нажмите ОК. В результате будут скопированы только значения ячеек, без формул.

Рисунок 4. Специальная вставка
- В ячейку С18 внесите формулу =C$12*(-$C13/$C$12)+C13. Скопируйте эту формулу в ячейки B18:E19 с помощью маркера заполнения. В итоге имеем матрицу А3 (рис.5)
Рисунок 5. Матрица А3
- Поменяйте местами третий и четвертый столбцы (используйте копирование и специальную ставку значений).
Рисунок 6. Матрица А4 — результирующая
Ответ: Базисный минор матрицы А4 стоит в первых трех столбцах и первых трех строках, . Следовательно, r(A)=3.
Рисунок 7. Общий вид листа вычисления
Рисунок 8. Для проверки формул
Уровень 2.
Задание 2. Найти первую норму матрицы А.
- Введите матрицу (рис.11)
Рисунок 11
- Далее нужно взять по модулю все значения матрицы. Для вычисления модуля в Excel используется функция ABS. Запишем результат в матрицу A1. Для этого в ячейку В5 внесите формулу =ABS(B1) и скопируйте ее в диапазон B5:C7 (рис.12)
Рисунок 12.
- Далее нужно вычислить сумму по столбцам. В ячейку B8 введите формулу =СУММ(B5:B7). Скопируйте ее в ячейку C8. В результате вы найдете сумму по двум столбцам (рис.13)
Рисунок 13. Сумма по столбцам
- Далее необходимо найти максимальный элемент из полученных. Для этого в ячейку B9 введите формулу =МАКС(B8:C8). Результат: норма матрицы = 19 (рис.14).
Рисунок 14. Результат
Задание 3: исправляя на листе вычислений, найдите норму матрицы А (рис.15)
Рисунок 15.
Ответ: норма равная 15.
Уровень 3.
Задание 4. Самостоятельно в Excel выполнить вычисления второй и третьей нормы матрицы А (рис.11).
Подсказка: для вычисления корня квадратного используется
Задание 5. Самостоятельно выполнить вычисление ранга матрицы А:

Рисунок 9. Матрица А
Самопроверка: Ответ: ранг матрицы равен 4.
Составитель: Салий Н.А.
учимся
программировать
Программированию нельзя научить, можно только научится
Главная » Уроки по Численным методам » Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц
Урок №12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц.
Уровень 1
Задание 1. Найдите ранг матрицы А с помощью Excel.
Рисунок 1. Исходная матрица
Ход решения.
- Первую строку оставляем без изменений. Скопируйте первую строку в ячейки B6:E6.
- Чтобы избежать появления дробей, умножим вторую, третью и четвертую строки на 2. Для этого введите в ячейку B7 формулу =2*B2. Скопируйте эту форму с помощью маркера заполнения в ячейки B7:E9 (Маркер заполнения — небольшой черный квадрат в правом нижнем углу ячейки. При наведении на него курсор принимает вид черного креста.). В результате должна получиться матрица А1 (рис.2).
Рисунок 2. 2-я,3-я,4-я строки умножены на 2.
- Первую строку оставим без изменения (скопируйте в ячейки B11:E11).
- В ячейку B12 внесите формулу =B7+B$6*(-$B7/$B$6). Скопируйте эту формулу в ячейки C12:E14 с помощью маркера заполнения. В итоге имеем матрицу А2 (рис.3)
Рисунок 3. Матрица А2
- Переходим к вычислению матрицы А3. Первую и вторую строки оставляем без изменения. Для этого выделите ячейки B11:E12, нажмите кнопку «Копировать», далее выделите ячейку B16 и в контекстном меню ячейки выберите «Специальная вставка». В открывшемся окне выберите пункт «значения» (рис.4) и нажмите ОК. В результате будут скопированы только значения ячеек, без формул.
Рисунок 4. Специальная вставка
- В ячейку С18 внесите формулу =C$12*(-$C13/$C$12)+C13. Скопируйте эту формулу в ячейки B18:E19 с помощью маркера заполнения. В итоге имеем матрицу А3 (рис.5)
Рисунок 5. Матрица А3
- Поменяйте местами третий и четвертый столбцы (используйте копирование и специальную ставку значений).
Рисунок 6. Матрица А4 — результирующая
Ответ: Базисный минор матрицы А4 стоит в первых трех столбцах и первых трех строках, 
Рисунок 7. Общий вид листа вычисления
Рисунок 8. Для проверки формул
Уровень 2.
Задание 2. Найти первую норму матрицы А.
- Введите матрицу (рис.11)
Рисунок 11
- Далее нужно взять по модулю все значения матрицы. Для вычисления модуля в Excel используется функция ABS. Запишем результат в матрицу A1. Для этого в ячейку В5 внесите формулу =ABS(B1) и скопируйте ее в диапазон B5:C7 (рис.12)
Рисунок 12.
- Далее нужно вычислить сумму по столбцам. В ячейку B8 введите формулу =СУММ(B5:B7). Скопируйте ее в ячейку C8. В результате вы найдете сумму по двум столбцам (рис.13)
Рисунок 13. Сумма по столбцам
- Далее необходимо найти максимальный элемент из полученных. Для этого в ячейку B9 введите формулу =МАКС(B8:C8). Результат: норма матрицы = 19 (рис.14).
Рисунок 14. Результат
Задание 3: исправляя на листе вычислений, найдите норму матрицы А (рис.15)
Рисунок 15.
Ответ: норма равная 15.
Уровень 3.
Задание 4. Самостоятельно в Excel выполнить вычисления второй и третьей нормы матрицы А (рис.11).
Подсказка: для вычисления корня квадратного используется
Задание 5. Самостоятельно выполнить вычисление ранга матрицы А:
Рисунок 9. Матрица А
Самопроверка: Ответ: ранг матрицы равен 4.
Число — число, для которого определяется ранг.
Ссылка — ссылка на список чисел (диапазон ячеек с числами). Напрямую массив задать нельзя, формула =РАНГ(10;) работать не будет. Но, если ввести формулу =РАНГ(B7;$A$7:$A$11) , то она будет работать (хотя ячейка B7 — вне списка с числами). Если в B7 содержится число вне списка с числами, то формула вернет ошибку #Н/Д.
Нечисловые значения в ссылке игнорируются. Числам, сохраненным в текстовом формате, ранг также не присваивается, функция воспринимает их как текст.
Порядок — число, определяющее способ упорядочения.
- Если порядок равен 0 (нулю) или опущен, то MS EXCEL присваивает ранг=1 максимальному числу, меньшим значениям присваиваются б о льшие ранги.
- Если порядок — любое ненулевое число, то то MS EXCEL присваивает ранг=1 минимальному числу, б о льшим значениям присваиваются б о льшие ранги.
Примечание : Начиная с MS EXCEL 2010 для вычисления ранга также используются функции РАНГ.СР() и РАНГ.РВ() . Последняя функция аналогична РАНГ() .
Определяем ранг в списке без повторов
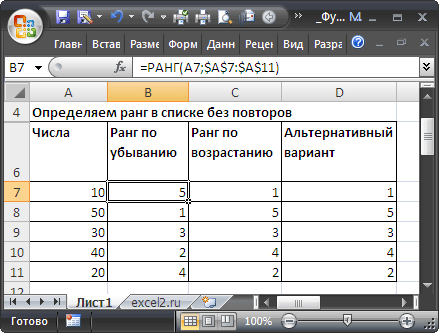
Если список чисел находится в диапазоне A7:A11 , то формула =РАНГ(A7;$A$7:$A$11) определит ранг числа из ячейки А7 (см. файл примера ).
Т.к. аргумент порядок опущен, то MS EXCEL присвоил ранг=1 максимальному числу (50), а максимальный ранг (5 = количеству значений в списке) — минимальному (10).
Альтернативный вариант: =СЧЁТЕСЛИ($A$7:$A$11;»>»&A7)+1
В столбце С приведена формула =РАНГ(A7;$A$7:$A$11;1) с рангом по возрастанию, ранг=1 присвоен минимальному числу. Альтернативный вариант: =СЧЁТЕСЛИ($A$7:$A$11;»
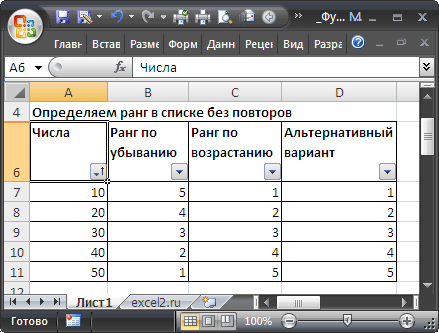
Если исходный список отсортировать , то ранг числа будет его позицией в списке.
Ранг по условию
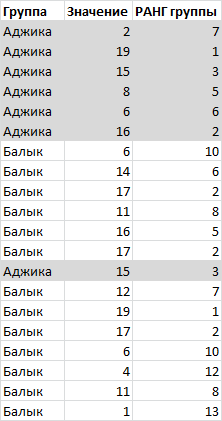
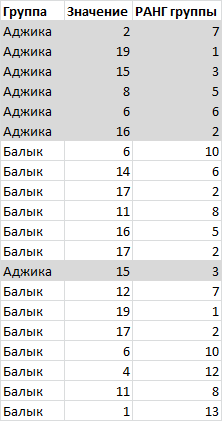
Если список состоит из значений, относящихся к разным группам (например, к разным маркам машин), то ранг можно вычислить не только относительно всей совокупности данных, но и относительно данных каждой отдельной группы.
В файле примера ранг по условию (условием является принадлежность значения к групп) вычислен с помощью формулы:
В столбце А содержатся названия группы, в столбце В — значения.
Связь функций НАИБОЛЬШИЙ() / НАИМЕНЬШИЙ() и РАНГ()
Функции НАИБОЛЬШИЙ() и РАНГ() являются взаимодополняющими в том смысле, что записав формулу =НАИБОЛЬШИЙ($A$7:$A$11;РАНГ(A7;$A$7:$A$11)) мы получим тот же исходный массив A7:A11 .
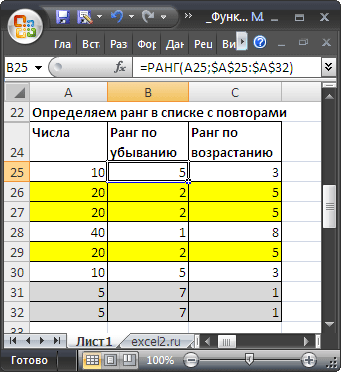
Определяем ранг в списке с повторами
Если список содержит повторы , то повторяющимся значениям (выделено цветом) будет присвоен одинаковый ранг (максимальный, если использована функция РАНГ() или РАНГ.РВ() ) или среднее значение, если РАНГ.СР() ). Наличие повторяющихся чисел влияет на ранги последующих чисел. Например, если в списке целых чисел, отсортированных по возрастанию, дважды встречается число 10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет иметь ранга 6).
Иногда это не удобно и требуется, чтобы ранги не повторялись (например, при определении призовых мест, когда нельзя занимать нескольким людям одно место).
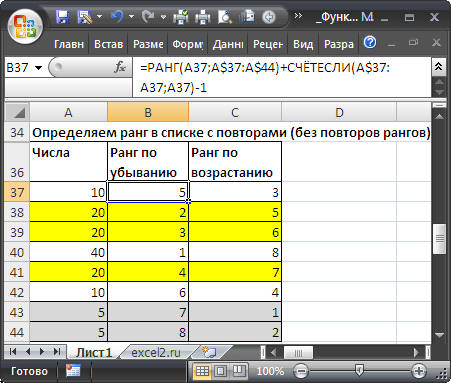
В этом нам поможет формула =РАНГ(A37;A$37:A$44)+СЧЁТЕСЛИ(A$37:A37;A37)-1
Предполагается, что исходный список с числами находится в диапазоне А37:А44 .
Примечание . В MS EXCEL 2010 добавилась функция РАНГ.РВ(число;ссылка;[порядок]) Если несколько значений имеют одинаковый ранг, возвращается наивысший ранг этого набора значений (присваивает повторяющимся числам одинаковые значения ранга). В файле примера дается пояснение работы этой функции. Также добавилась функция РАНГ.СР(число;ссылка;[порядок]) Если несколько значений имеют одинаковый ранг, возвращается среднее.
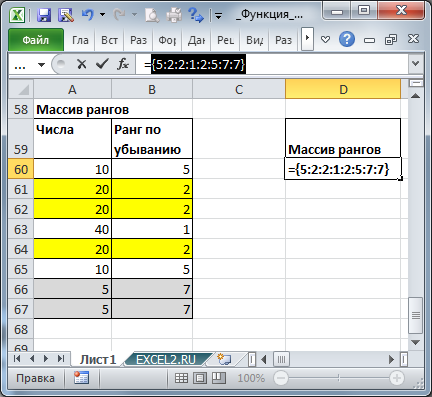
Массив рангов
Для построения некоторых сложных формул массива может потребоваться массив рангов, т.е. тот же набор рангов, но в одной ячейке.
Как видно из картинки выше, значения из диапазона В60:В67 и в ячейке D60 совпадают. Такой массив можно получить с помощью формулы =РАНГ(A60:A67;A60:A67) или с помощью формулы =СЧЁТЕСЛИ(A60:A67;»>»&A60:A67)+1
Ранги по возрастанию можно получить с помощью формулы =РАНГ(A60:A67;A60:A67;1) или =СЧЁТЕСЛИ(A60:A67;» .
Как найти ранг матрицы в excel
Регистрация на форуме тут, о проблемах пишите сюда — alarforum@yandex.ru, проверяйте папку спам! Обязательно пройдите восстановить пароль
| Поиск по форуму |
| Расширенный поиск |
Здравствуйте уважаемые форумчане.
Возникла пара вопросов следующего содержания:
1) Вычисление следа матрицы в Excel. След матрицы — это сумма всех диагональных элементов матрицы. Необходимо записать в ячейку формулу, которая будет считать след для больших матриц (100 на 100, к примеру).
2) Вычисление ранга матрицы. Ранг — это максимальное число линейно-независимых строкстолбцов.
Первое пытался сделать через СУММЕСЛИ, но так и не смог придумать, как задать условие равенства номера строки и столбца для значений матрицы.
К примеру, есть матрица 3 на 3, все нули, только по диагонали от А1 до C3 единицы. След должен давать значение A1+B2+C3=3.
Возможно я чего-то не понял в вашей формуле, для этой же матрицы делаю так: СУММ(A1:C3*(СТРОКА(A1:C3)=СТОЛБЕЦ(A 1:C3)), выдает ошибку.
Пробовал Вашу формулу видоизменять, полагая, что возможно Вы допустили опечатку, но так и не считает.
Всё считает как надо:
Посмотрите формулы в зеленых ячейказх:
__ Полезные надстройки для Excel. Парсинг сайтов и файлов. 
Рассмотрим
применение табличного процессора EXCEL
для работы с матрицами.
Процессор EXCEL
работает с числовыми матрицами и может
осуществлять следующие операции:
-
сложение (вычитание)
матриц, умножение матриц на число, -
преобразования
матрицы с целью получения нулей, -
вычисление
определителя матрицы, -
транспонирование
матрицы, -
нахождение обратной
матрицы.
Сложение матриц,
умножение матрицы на число, преобразование
матрицы осуществляются с помощью строки
формул. Для нахождения определителя
матрицы, транспонированной матрицы,
обратной матрицы, а также для умножения
матриц следует пользоваться соответствующими
встроенными функциями: МОПРЕД; ТРАНСП;
МОБР; МУМНОЖ. К сожалению, нет встроенной
функции для определения ранга матрицы.
Ранг придется находить переходом к
эквивалентной матрице. Такой же переход
полезен и для исследования линейных
систем.
Сложение матриц.
Рис.3
В ячейки
введена матрица
.
В ячейки
введена матрица
.
В ячейку
введена формула
и скопирована в диапазон
.
Умножение матрицы
на число.
Рис.4
В ячейки
введена матрица
,
В ячейку
введено число
.
В ячейку
введена формула
и скопирована в диапазон
.
Вычисление
определителя, транспонирование,
нахождение обратной матрицы.
Перечисленные
операции проводятся с помощью
соответствующих встроенных функций.
При выполнении операций транспонирования,
умножения матриц, нахождения обратной
матрицы необходимо предварительно
выделить диапазон ячеек для записи
результата. Результат получается
нажатием клавиш
(ввод
массива).
Рис.5
В ячейки
введена матрица
,
в ячейки— матрица
.
В ячейку
введем формулу
=МОПРЕД,
заполним поле значений аргумента,
получаем значение определителя матрицы.
Пример 16.
Вычислить обратную матрицу для
.
Выделим диапазон
ячеек
для записи обратной матрицы. Теперь
надо вызвать Мастер функций, выбрать
имя функции МОБР, ввести в поле значений
аргумента функциии нажать клавиши
(ввод
массива).
Пример 17.
Умножить матрицы
и
.
Определим размерность
матрицы
(результата
умножения):,
и выделим диапазондля записи этой матрицы.
Для умножения
надо вызвать Мастер функций, выбрать
имя функции МУМНОЖ, ввести в поле значений
1 аргумента функции первую матрицу, в
поле 2 – вторую матрицу, и нажать клавиши
(ввод
массива). В ячейках− результат умножения
.
Вычисление ранга
матрицы.
Будем последовательно
получать нули в первом, втором и т.д.
столбцах ниже диагональных элементов.
Рис.6
В ячейки
введем матрицу (пример 11).
Получим нули в
первом столбце матрицы
.
Для этого в ячейкувведем формулу
и скопируем ее в ячейки
,
в ячейкувведем формулу
и скопируем ее в ячейки
.
Аналогично получаем
нули во втором столбце. В ячейку
введем формулу
и скопируем ее в ячейку
.
В ячейкувведем формулу
и скопируем ее в ячейки
.
Дальше получаем
нули в третьем столбце. В ячейку
введем формулу
и скопируем ее в ячейку
.
В ячейкувведем формулу
и скопируем ее в ячейки
.
Получили полностью
нулевые строки. Ниже копированием
значений (специальная вставка) записана
преобразованная матрица (нули ниже
диагонали опущены). Следовательно, ранг
матрицы равен трем.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функция
РАНГ(
)
, английский вариант RANK(),
возвращает
ранг числа в списке чисел. Ранг числа — это его величина относительно других значений в списке. Например, в массиве {10;20;5} число 5 будет иметь ранг 1, т.к. это наименьшее число, число 10 — ранг 2, а 20 — ранг 3 (это ранг по возрастанию, когда наименьшему значению присваивается ранг 1). Если список отсортировать, то ранг числа будет его позицией (если нет повторов).
Синтаксис
РАНГ
(
число
;
ссылка
;порядок)
Число
— число, для которого определяется ранг.
Ссылка
— ссылка на список чисел (диапазон ячеек с числами). Напрямую массив задать нельзя, формула =РАНГ(10;{10:50:30:40:50}) работать не будет. Но, если ввести формулу
=РАНГ(B7;$A$7:$A$11)
, то она будет работать (хотя ячейка
B7
— вне списка с числами). Если в
B7
содержится число вне списка с числами, то формула вернет ошибку #Н/Д.
Нечисловые значения в ссылке игнорируются. Числам, сохраненным в текстовом формате, ранг также не присваивается, функция воспринимает их как текст.
Порядок
— число, определяющее способ упорядочения.
-
Если порядок равен 0 (нулю) или опущен, то MS EXCEL присваивает ранг=1 максимальному числу, меньшим значениям присваиваются б
о
льшие ранги. -
Если порядок — любое ненулевое число, то то MS EXCEL присваивает ранг=1 минимальному числу, б
о
льшим значениям присваиваются б
о
льшие ранги.
Примечание
: Начиная с MS EXCEL 2010 для вычисления ранга также используются функции
РАНГ.СР()
и
РАНГ.РВ()
. Последняя функция аналогична
РАНГ()
.
Определяем ранг в списке без повторов
Если список чисел находится в диапазоне
A7:A11
, то формула
=РАНГ(A7;$A$7:$A$11)
определит ранг числа из ячейки
А7
(см.
файл примера
).
Т.к. аргумент
порядок
опущен, то MS EXCEL присвоил ранг=1 максимальному числу (50), а максимальный ранг (5 = количеству значений в списке) — минимальному (10).
Альтернативный вариант:
=СЧЁТЕСЛИ($A$7:$A$11;»>»&A7)+1
В столбце
С
приведена формула
=РАНГ(A7;$A$7:$A$11;1)
с рангом по возрастанию, ранг=1 присвоен минимальному числу. Альтернативный вариант:
=СЧЁТЕСЛИ($A$7:$A$11;»<«&A7)+1
Если исходный список
отсортировать
, то ранг числа будет его позицией в списке.
Ранг по условию
Если список состоит из значений, относящихся к разным группам (например, к разным маркам машин), то ранг можно вычислить не только относительно всей совокупности данных, но и относительно данных каждой отдельной группы.
В
файле примера
ранг по условию (условием является принадлежность значения к групп) вычислен с помощью формулы:
=СЧЁТЕСЛИМН($A$3:$A$22;A3;$B$3:$B$22;»>»&B3)+1
В столбце А содержатся названия группы, в столбце В — значения.
Связь функций
НАИБОЛЬШИЙ()
/
НАИМЕНЬШИЙ()
и
РАНГ()
Функции
НАИБОЛЬШИЙ()
и
РАНГ()
являются взаимодополняющими в том смысле, что записав формулу
=НАИБОЛЬШИЙ($A$7:$A$11;РАНГ(A7;$A$7:$A$11))
мы получим тот же исходный массив
A7:A11
.
Определяем ранг в списке с повторами
Если список содержит
повторы
, то повторяющимся значениям (выделено цветом) будет присвоен одинаковый ранг (максимальный, если использована функция
РАНГ()
или
РАНГ.РВ()
) или среднее значение, если
РАНГ.СР()
). Наличие повторяющихся чисел влияет на ранги последующих чисел. Например, если в списке целых чисел, отсортированных по возрастанию, дважды встречается число 10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет иметь ранга 6).
Иногда это не удобно и требуется, чтобы ранги не повторялись (например, при определении призовых мест, когда нельзя занимать нескольким людям одно место).
В этом нам поможет формула
=РАНГ(A37;A$37:A$44)+СЧЁТЕСЛИ(A$37:A37;A37)-1
Предполагается, что исходный список с числами находится в диапазоне
А37:А44
.
Примечание
. В
MS EXCEL 2010
добавилась функция
РАНГ.РВ(число;ссылка;[порядок])
Если несколько значений имеют одинаковый ранг, возвращается наивысший ранг этого набора значений (присваивает повторяющимся числам одинаковые значения ранга). В
файле примера
дается пояснение работы этой функции. Также добавилась функция
РАНГ.СР(число;ссылка;[порядок])
Если несколько значений имеют одинаковый ранг, возвращается среднее.
Массив рангов
Для построения некоторых сложных
формул массива
может потребоваться
массив
рангов, т.е. тот же набор рангов, но в одной ячейке.
Как видно из картинки выше, значения из диапазона
В60:В67
и в ячейке
D60
совпадают. Такой массив можно получить с помощью формулы
=РАНГ(A60:A67;A60:A67)
или с помощью формулы
=СЧЁТЕСЛИ(A60:A67;»>»&A60:A67)+1
Ранги по возрастанию можно получить с помощью формулы
=РАНГ(A60:A67;A60:A67;1)
или
=СЧЁТЕСЛИ(A60:A67;»<«&A60:A67)+1
.
Такой подход использется в статьях
Отбор уникальных значений с сортировкой в MS EXCEL
и
Динамическая сортировка таблицы в MS EXCEL
.
MihailM писал(а):
Решил подойти еще более современно, попросил чатгпт
И вот результат… Вроде работает
Спасибо, но не работает.
Я скопировал эту программу в Excel-модуль и в качестве теста выдумал такую таблицу (матрицу):
[math]begin{pmatrix} 0 & 1 & 2 & 3 \ 0 & 0 & 1 & 2 \ 0 & 3 & 0 & 1 \ 1 & 4 & 3 & 0 end{pmatrix}[/math]
Определитель матрицы равен [math]-4 ne 0,[/math] это значит, что матрица невырожденная, и ее ранг должен быть равен 4.
Моя программа выдает ответ ранг = 3, а приведенная вами программа выдает ноль, чего вообще не бывает.
Вот текст моей программы:
Function MRang(Matrix) As Integer
Dim X, N As Integer, i As Integer, j As Integer, k As Integer, Mat() As Single, Zeile() As Single, Z As Byte, S As Byte
N = 0
For Each X In Matrix
N = N + 1
Next
N = Sqr(N)
ReDim Mat(1 To N, 1 To N) As Single, Zeile(N) As Singlek = 0
For Each X In Matrix ' Инициирует матрицу-----
k = k + 1
i = Int((k - 0.5) / N)
j = k - i * N
Mat(i + 1, j) = X
Next
' ----------------------------------- Приведение к треугольному виду ---------------------
For k = 1 To N ' Ведущая строка
For i = k To N ' текущая строка
X = Mat(i, k)
'-------------------------------- Перестановка строк -------------------------------------
If X = 0 And i < N Then ' поиск строки с X<>0
For Z = i To N: Zeile(Z) = Mat(i, Z): Next Z 'запомнить строку номер i
Z = i
Do 'поиск строки с X<>0
Z = Z + 1
X = Mat(Z, k)
Loop While X = 0 And Z < N
If Z < N Then
For S = i To N: Mat(i, S) = Mat(Z, S): Mat(Z, S) = Zeile(S): Next S ' собственно перестановка
End If
End If
'-------------------------------- конец перестановки -------------------------------------
X = Mat(i, k)
If X <> 0 And X <> 1 Then
For j = k To N
Mat(i, j) = Mat(i, j) / X 'Нормировка строк на первый ненулевой элемент
Next j
End If
Next iFor i = k + 1 To N ' Вычитаемая строка ( k-тая ), уменьшаемая строка (i-тая)
If Mat(i, k) <> 0 Then
For j = k To N ' элементы уменьшаемой строки
Mat(i, j) = Mat(i, j) - Mat(k, j)
Next j
End If
Next iNext k
'----------------------- вычисление ранга = число ненулевых элементов (равных 1) на главной диагонали --------------------
X = 0
For i = 1 To N
If Mat(i, i) <> 0 Then X = X + 1
Next i
MRang = X
End Function