Опубликовано 13 Янв 2016
Рубрика: Справочник Excel | 3 комментария

Если функция получена практическими измерениями и задана табличными значениями, то Excel может оказать в этом случае более существенную помощь при выполнении численного дифференцирования и последующей обработке и анализе результатов.
На практике задача вычисления производной методом численного дифференцирования может возникнуть и в механике (при определении скорости и ускорения объекта по имеющимся замерам пути и времени) и в теплотехнике (при расчете теплопередачи во времени). Это также может быть необходимо, например, при бурении скважин для анализа плотности проходимого буром слоя грунта, при решении целого ряда баллистических задач, и т. д.
Похожая ситуация имеет место при «обратной» задаче расчета сложно нагруженных балок, когда по прогибам возникает желание найти значения действующих нагрузок.
Во второй части статьи на «живом» примере рассмотрим вычисление производной по приближенной формуле численного дифференцирования с применением выражений в конечных разностях и разберемся в вопросе – можно ли используя приближения производных конечными разностями по прогибам балки определять действующие в сечениях нагрузки?
Минимум теории.
Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.
Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.
y’(x)=lim (Δy/Δx) при Δx→0
Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.
tg (α)=Δy/Δx
Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.
y’(x)i≈(Δy/Δx)i=(yi+1—yi-1)/(xi+1—xi-1)
Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.
В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.
Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
Дано:
На балку длиной 8 метров с шарнирными опорами по краям изготовленную из двух спаренных стальных (Ст3) двутавров 30М опираются 7 прогонов с шагом 1 метр. К центральной части балки крепится площадка с оборудованием. Предположительно усилие от покрытия, передаваемое через прогоны на балку, во всех точках одинаково и равно F1. Подвесная площадка имеет вес 2*F2 и крепится к балке в двух точках.
Предполагается, что балка до приложения нагрузок была абсолютно прямой, а после нагружения находится в зоне упругих деформаций.
На рисунке ниже показана расчетная схема задачи и общий вид эпюр.
На следующем скриншоте представлены исходные данные.
Расчетные исходные данные:
3. Погонная масса двутавра 30М:
γ=50,2 кг/м
Сечение балки составлено из двух двутавров:
n=2
Удельный вес балки:
q=γ*n*g=50,2*2*9,81/1000=0,985 Н/мм
5. Момент инерции сечения двутавра 30М:
Ix1=95 000 000 мм4
Момент инерции составного сечения балки:
Ix=Ix1*n=95 000 000*2=190 000 000 мм4
10. Так как балка нагружена симметрично относительно своей середины, то реакции обеих опор одинаковы и равны каждая половине суммарной нагрузки:
R=(q*zmax+8*F1+2*F2)/2=(0,985*8000+8*9000+2*50000)/2=85 440 Н
В расчете учитывается собственный вес балки!
Задача:
Найти значения изгибающего момента Mxi в сечениях балки аналитически по формулам сопротивления материалов и методом численного дифференцирования расчетной линии прогибов. Сравнить и проанализировать полученные результаты.
Решение:
Первое, что мы сделаем, это выполним расчет в Excel поперечных сил Qy, изгибающих моментов Mx, углов поворота Ux оси балки и прогибов Vx по классическим формулам сопромата во всех сечениях с шагом h. (Хотя, в принципе, значения сил и углов нам в дальнейшем не понадобятся.)
Результаты вычислений находятся в ячейках I5-L54. На скриншоте ниже показана половина таблицы, так как значения во второй ее части зеркальны или аналогичны представленным значениям.
Использованные в расчетах формулы можно посмотреть здесь.
Ссылка для скачивания файла с рассмотренным в статье примером: vychisleniye-proizvodnoy (xls 250,0KB).
Итак, нам известны точные значения моментов и прогибов.
Из теории мы знаем, что:
Угол поворота – это первая производная прогиба U=V’.
Момент – это вторая производная прогиба M=V’’.
Сила – это третья производная прогиба Q=V’’’.
Предположим, что столбец точных значений прогибов получен не аналитическими расчетами, а замерами на реальной балке и у нас больше нет никаких других данных. Вычислим вторые производные от точных значений прогибов, используя формулу (6) из таблицы предыдущего раздела статьи, и найдем значения моментов методом численного дифференцирования.
Mxi=Vy’’≈((Vi+1-2*Vi+Vi-1)/h2)*E*Ix
Итог расчетов мы видим в ячейках M5-M54.
Точные значения моментов, рассчитанные по аналитическим формулам сопромата с учетом веса самой балки, отличаются от найденных по приближенным формулам вычисления производных незначительно. Моменты определены весьма точно, судя по относительным погрешностям, рассчитанным в процентах в ячейках N5-N54.
ε=(Mx—Vy’’)/Mx*100%
Поставленная задача решена. Мы выполнили вычисление производной второго порядка по приближенной формуле с использованием центральных конечных разностей и получили отличный результат.
Зная точные значения прогибов можно методом численного дифференцирования с высокой точностью найти действующие в сечениях моменты и определить степень нагруженности балки!
Однако…
Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!
Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h, «устремляя его к нулю», хотя и это может не помочь избежать ошибок.
Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$…
Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i=4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε21=1,813%).
Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — аппроксимировать замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.
Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.
Вычисление производной численными методами всегда необходимо выполнять очень осторожно!
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
5.1. Вычисление производной функции одного переменного
Известно, что численными приближенными методами производная функции в заданной точке может быть вычислена с использованием формулы конечных разностей. Выражение для вычисления производной функции одного переменного, записанное в конечных разностях, имеет вид:
При достаточно малых приращениях х, можно с приемлемой точностью получить величину производной Для вычисления производной в MS Excel будем использовать приведенную зависимость. Рассмотрим методику вычисления производной на примере упражнения.
Пример 17. Найти производную функции Y= 2x 3 + x 2 в точке x= 3. Производная, вычисленная аналитическим методом, равна 60.
Решение:
1. Ведите в ячейку рабочего листа формулу правой части заданной функцио-нальной зависимости, например в ячейку В2, как показано на рисунке 27 , делая ссылку на ячейку, где будет находиться значение х, например А2: = 2*А2^3+A2^2 2. Определите окрестность точки х=3 достаточно малого размера, например значение слева Х k = 2,9999999, а справа Хk+1 = 3,00000001 и введите эти зна-чения в ячейку А2 и А3 соответственно.
3. В ячейку С2 введите формулу вычисления производной (см рис. 27):
= (В3-В2)/(A3-A2).
Рисунок 27
В результате в ячейке С2 будет вычислено приближенное значение производной заданной функции в точке х=3, величина которой равна 60, что соответствует результату, полученному аналитически.
Как делать производные в Excel
Microsoft Excel не имеет возможности генерировать производное уравнение по заданной формуле, но вы все равно можете использовать программу для вычисления значений как для формулы, так и для ее производной и построения их на графике. Это позволяет сравнивать формулу с ее производной, даже если вы не знаете самой производной. Поскольку Excel берет на себя все вычисления, вы можете использовать этот метод, даже если вы не знаете исчисления.
Введите нижнюю границу горизонтального диапазона, который вы хотите построить, в ячейке A1. Например, чтобы построить график от -2 до 2, введите «-2» в A1 (опуская кавычки здесь и на всех этапах).
Введите расстояние между точками графика в ячейку D1. Чем меньше расстояние, тем точнее будет выглядеть ваш график, но использование слишком большого количества точек может замедлить обработку. Для этого примера введите «0,1», что даст 41 точку графика из -2 и 2. Если вы используете меньший или больший диапазон, измените расстояние соответственно, чтобы получить как минимум несколько десятков точек, но не более нескольких тысяч. .
Введите формулу «= A1 + $ D $ 1» в ячейку A2. Перетащите маркер заполнения в углу ячейки вниз, чтобы повторить формулу для такого количества точек, которое необходимо для достижения желаемого верхнего диапазона.
Поместите исходную формулу в ячейку B1, начиная со знака равенства и заменив переменную на «A1». Например, чтобы использовать уравнение «y = 2x ^ 2», введите «= 2 * A1 ^ 2». Обратите внимание, что Excel не умножает смежные члены автоматически, поэтому для умножения необходимо ввести звездочку.
Дважды щелкните маркер заполнения в ячейке B1, чтобы заполнить все необходимые ячейки в столбце B.
Введите «= (B2-B1) / $ D $ 1» в ячейку C1. Это уравнение находит производную для вашей формулы в каждой точке, используя определение производной «dy / dx»: разница между каждой строкой в столбце B составляет «dy», а значение, которое вы выбрали для D1, представляет «dx». Дважды щелкните маркер заполнения в C1, чтобы заполнить столбец.
Прокрутите вниз и удалите последнее число в столбце C, чтобы избежать неточного значения для последней производной.
Щелкните и перетащите от заголовка столбца A к заголовку C, чтобы выделить первые три столбца. Откройте вкладку «Вставка» на ленте и нажмите «Диаграммы», «Точечная диаграмма», а затем «Точечная диаграмма с плавными линиями» или другой тип диаграммы разброса, если необходимо. Excel отобразит исходную формулу как «Серия 1», а производную — как «Серия 2».
Содержание
- Вычисление производной в Excel
- Минимум теории.
- Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
- Задача:
- Решение:
- Однако.
- Алгоритм нахождения производной
Вычисление производной в Excel

Если функция получена практическими измерениями и задана табличными значениями, то Excel может оказать в этом случае более существенную помощь при выполнении численного дифференцирования и последующей обработке и анализе результатов.
На практике задача вычисления производной методом численного дифференцирования может возникнуть и в механике (при определении скорости и ускорения объекта по имеющимся замерам пути и времени) и в теплотехнике (при расчете теплопередачи во времени). Это также может быть необходимо, например, при бурении скважин для анализа плотности проходимого буром слоя грунта, при решении целого ряда баллистических задач, и т. д.
Похожая ситуация имеет место при «обратной» задаче расчета сложно нагруженных балок, когда по прогибам возникает желание найти значения действующих нагрузок.
Во второй части статьи на «живом» примере рассмотрим вычисление производной по приближенной формуле численного дифференцирования с применением выражений в конечных разностях и разберемся в вопросе – можно ли используя приближения производных конечными разностями по прогибам балки определять действующие в сечениях нагрузки?
Минимум теории.
Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.
Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.
y’ ( x )=lim ( Δy / Δx ) при Δx →0
Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.
tg ( α )= Δy / Δx
Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.
Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.
В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.
Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
На балку длиной 8 метров с шарнирными опорами по краям изготовленную из двух спаренных стальных (Ст3) двутавров 30М опираются 7 прогонов с шагом 1 метр. К центральной части балки крепится площадка с оборудованием. Предположительно усилие от покрытия, передаваемое через прогоны на балку, во всех точках одинаково и равно F1 . Подвесная площадка имеет вес 2* F2 и крепится к балке в двух точках.
Предполагается, что балка до приложения нагрузок была абсолютно прямой, а после нагружения находится в зоне упругих деформаций.
На рисунке ниже показана расчетная схема задачи и общий вид эпюр.
На следующем скриншоте представлены исходные данные.
Расчетные исходные данные:
3. Погонная масса двутавра 30М:
γ =50,2 кг/м
Сечение балки составлено из двух двутавров:
n =2
Удельный вес балки:
q = γ * n * g =50,2*2*9,81/1000=0,985 Н/мм
5. Момент инерции сечения двутавра 30М:
Ix1 =95 000 000 мм 4
Момент инерции составного сечения балки:
Ix = Ix1 * n =95 000 000*2=190 000 000 мм 4
10. Так как балка нагружена симметрично относительно своей середины, то реакции обеих опор одинаковы и равны каждая половине суммарной нагрузки:
R =( q * zmax +8* F1 +2* F2 )/2=(0,985*8000+8*9000+2*50000)/2=85 440 Н
В расчете учитывается собственный вес балки!
Задача:
Найти значения изгибающего момента Mxi в сечениях балки аналитически по формулам сопротивления материалов и методом численного дифференцирования расчетной линии прогибов. Сравнить и проанализировать полученные результаты.
Решение:
Первое, что мы сделаем, это выполним расчет в Excel поперечных сил Qy , изгибающих моментов Mx , углов поворота Ux оси балки и прогибов Vx по классическим формулам сопромата во всех сечениях с шагом h . (Хотя, в принципе, значения сил и углов нам в дальнейшем не понадобятся.)
Результаты вычислений находятся в ячейках I5-L54. На скриншоте ниже показана половина таблицы, так как значения во второй ее части зеркальны или аналогичны представленным значениям.
Использованные в расчетах формулы можно посмотреть здесь.
Ссылка для скачивания файла с рассмотренным в статье примером: vychisleniye-proizvodnoy (xls 250,0KB).
Итак, нам известны точные значения моментов и прогибов.
Из теории мы знаем, что:
Угол поворота – это первая производная прогиба U = V’ .
Момент – это вторая производная прогиба M = V’’ .
Сила – это третья производная прогиба Q = V’’’ .
Предположим, что столбец точных значений прогибов получен не аналитическими расчетами, а замерами на реальной балке и у нас больше нет никаких других данных. Вычислим вторые производные от точных значений прогибов, используя формулу (6) из таблицы предыдущего раздела статьи, и найдем значения моментов методом численного дифференцирования.
Итог расчетов мы видим в ячейках M5-M54.
Точные значения моментов, рассчитанные по аналитическим формулам сопромата с учетом веса самой балки, отличаются от найденных по приближенным формулам вычисления производных незначительно. Моменты определены весьма точно, судя по относительным погрешностям, рассчитанным в процентах в ячейках N5-N54.
Поставленная задача решена. Мы выполнили вычисление производной второго порядка по приближенной формуле с использованием центральных конечных разностей и получили отличный результат.
Зная точные значения прогибов можно методом численного дифференцирования с высокой точностью найти действующие в сечениях моменты и определить степень нагруженности балки!
Однако.
Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!
Дело в том, что измерения прогибов требуется выполнять с точностью
1 мкм и стараться максимально уменьшать шаг замеров h , «устремляя его к нулю», хотя и это может не помочь избежать ошибок.
Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$.
Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i =4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении ( ε21 =1,813%).
Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — аппроксимировать замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.
Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.
Вычисление производной численными методами всегда необходимо выполнять очень осторожно!
Источник
Алгоритм нахождения производной
Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
Р.М.Магомедов, Е.В.Маевский
Приближенное вычисление производной функции в заданной точке ( Excel )
Учебно-методические рекомендации для проведения
семинара №5 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Москва 2017
Приближенное вычисление производной
Функции в заданной точке ( Excel )
Введение
Пусть функция 




Простейшими формулами для приближенного численного вычисления производной являются так называемые двухточечные формулы, которые можно получить непосредственно из определения производной: 
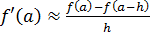
Если зафиксировать функцию и точку 


Более точная оценка получится, если использовать значения функции в трех точках: 



Еще более точными являются формулы, оценивающие производную по большему количеству точек (4 и более). Однако следует иметь в виду, что увеличение количества участвующих в формуле точек усложняет вычисление по формуле и увеличивает ошибку округления, возникающую при этом вычислении. Потому, хотя и возможно теоретически использовать для оценки производной в данной точке весь массив известных значений функции, но на практике этого никогда не делают.
Другой способ уточнения значения производной – уменьшение шага 
Задание 1. Вычислить в Excel приближенно производную функцию в заданной точке по следующему алгоритму.
Алгоритм нахождения производной
1. Составим таблицу значений функции 



1.1. Вводим в диапазон ячеек A3:A23 рабочего листа Excel числа от -10 до 10 с шагом 1, как показано на рисунке. В ячейку C1 вводим число 1. В ячейку B3 вводим формулу для нахождения значений функции 



1.2. Копируем формулу до ячейки B23.
2. В каждой точке 


2.1. В ячейку C3 водим формулу:
2.2. Копируем формулу до ячейки C23.
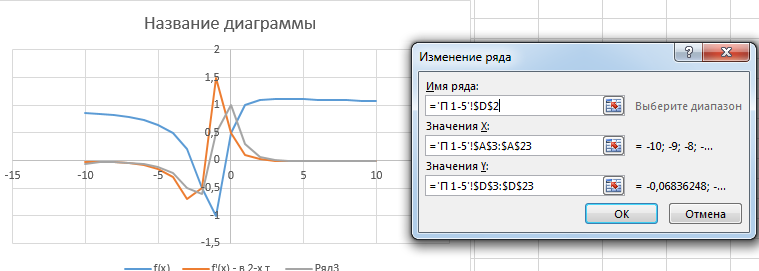
2.3. Для оформления и построения ломанной в ячейки A2, B2, C2 водим соответственно x, f(x), fᶦ(x) — в 2-х т., как показано на рисунке.
2.4. Выделяем диапазон ячеек A2:C23. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками., как показано на рисунке:
2.5. Нажимаем Ок.
2.6. В результате получиться ломанная как показано на рисунке выше.
3. В каждой точке 

3.1. В ячейку D3 водим формулу:
3.2. Копируем формулу до ячейки D23.
3.3. Для оформления и построения ломанной в ячейку D2 водим fᶦ(x) — в 3-х т., как показано на рисунке.
3.4. Выделяем диаграмму.
3.5. Из контекстного меню выбираем команду Выбрать данные.
3.6. В окне Выбор источника данных задаем команду Добавить.
3.7. Заполняем окно Изменение ряда как показано на рисунке:
3.8. В результате получиться ломанная как показано на рисунке выше.
4. Составим таблицу точных значений производной 

4.1. В ячейку E3 водим формулу:
4.2. Копируем формулу до ячейки E23.
4.3. Для оформления и построения ломанной в ячейку E2 водим fᶦ(x) точ, как показано на рисунке.
4.4. Как показано в пункте 3 в область диаграммы добавляем новые данные из диапазона E3:E23.
4.5. В результате должна получиться диаграмма как показано на рисунке:
5. Сравним точные значения производной с приближенными, построив три ломанные на одном графике.
5.1. Выделяем диапазон ячеек A2:A23, C2:E23, как показано на рисунке:
5.2. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:
6. Повторим вычисления пунктов 1-5, взяв величину шага 
6.1. Для этого на новом листе рабочей книги оформляем таблицу как показано на рисунке:
6.2. В ячейке B3 введена формула:
6.3. В ячейке C3 введена формула:
6.4. В ячейке D3 введена формула:
6.5. В ячейке E3 введена формула:
6.6. В ячейке F3 введена формула:
6.7. Выделяем диапазон ячеек A2:A23, D2:F23/
6.8. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:
7. Составим таблицу погрешностей двухточечной приближенной формулы, вычисляя разность 
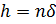


7.1. На новом листе рабочей книги Excel вводим в диапазон ячеек A4:A103 числа от -50, -49,…,-1,1,2,…,50 с шагом 1, как показано на рисунке (начало таблицы):
7.2. В ячейку C1 вводим число 0. В ячейку E1 вводим число 0,01.
7.3. В ячейку В4 вводим формулу:
7.4. В ячейку С4 вводим формулу:
8. Исследуем зависимость погрешности от 
8.1. Выделяем диапазон ячеек A3:A103, C3:C103.
8.2. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке (см. пункт 9).
9. Повторим шаги 7-8 для погрешности трехточечной формулы 
9.1. В ячейку D4 вводим формулу:
9.2. Выделяем диапазон ячеек A3:A103, C3:D103.
9.3. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:
Задание 2. Найти первую производную функции 
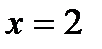

Из вышесказанного известно, что выражение для вычисления производной функции одной переменной в точке x, имеет вид:
где 

Примечание. Количество точек после запятой для выражения h зависить от того с какой заданной точностью нужно вычислить производную, если, например, производную нужно вычислить с точностью до 2 знаков после запятой, то достаточно взять h равной 0,0001.
Решение
Решим задачу двумя способами.
Способ 1
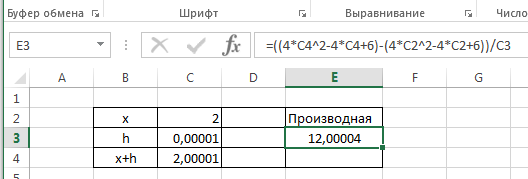
1. Вводим в ячейку C2 рабочего листа заданное значение аргумента, равное 2, в другой ячейке – C3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке C4 вычисляем сумму C3=C1+C2.
2. В ячейку E3 вводим формулу для вычисления производной:
3. После нажатия клавиши Enter получаем результат вычисления 12,00004 (см. рис.).
Способ 2
1. Зададим окрестность точки 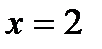

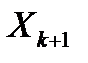
2. Вводим в ячейку рабочего листа формулу правой части заданной функциональной зависимости, например, в ячейку C3, как показано на рис., делая ссылку на ячейку B3, где находится значение х:
3. Копируем эту формулу в ячейку C4.
4. В ячейку E3 вводим формулу вычисления производной (рис.):
В результате вычисления в ячейке E3 будет выведено приближенное значение производной заданной функции в точке 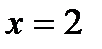
Задание 3. Найти первую производную функции 

Из вышесказанного известно, что выражение для вычисления первой производной функции одной переменной в точке x, имеет вид:
где 
Решение
1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное =3*пи()/4, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В3 вычисляем сумму В3=В1+В2.
2. В ячейку E3 вводим формулу для вычисления производной:
3. После нажатия клавиши Enter получаем результат вычисления 0,0000213 (см. рис.).
Задание 4. Найти вторую производную функции 
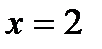
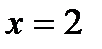
Из математики известно, что выражение для вычисления второй производной функции одной переменной в точке 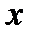
где 

Решение
1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное 2, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В4 вычисляем сумму В3=В1+В2.
2. В ячейку E3 вводим формулу для вычисления второй производной:
3. После нажатия клавиши Enter получаем результат вычисления 44,00003917 (см. рис.).
Источник
Содержание
- — Можете ли вы проводить расчеты в Excel?
- — Что такое производная формула?
- — Что такое производный символ?
- — Как мне вставить Quadf в Excel?
- — Что такое производный пример?
- — Каковы четыре основных производных правила?
Введите «= (B2-B1) / $ D $ 1» в ячейку C1. Это уравнение находит производную для вашей формулы в каждой точке, используя определение производной «dy / dx»: разница между каждой строкой в столбце B составляет «dy», а значение, которое вы выбрали для D1, представляет «dx». Дважды щелкните маркер заполнения в C1, чтобы заполнить столбец.
Программа электронных таблиц Microsoft Excel содержит множество математических функций, но имеет нет включить исчисление в стандартную версию. … Эти пакеты расширяют математические возможности Excel, позволяя использовать вычисления в электронных таблицах. Некоторые из этих функций работают с уравнениями; другие выполняют вычисления на числовых данных.
Что такое производная формула?
Производная помогает нам узнать, как меняются отношения между двумя переменными. Математически формула производной полезна для определения наклона линии, для определения наклона кривой и для определения изменения одного измерения по сравнению с другим измерением. Формула производной: ddx. хп = п. xn − 1 d d x.
Что такое производный символ?
Таблица математических символов для расчетов и анализа
| Условное обозначение | Название символа | Пример |
|---|---|---|
| DИкс у | производная | |
| DИкс2у | вторая производная | |
| частная производная | ∂ (х2+ y2) / ∂x = 2x | |
| ∫ | интеграл |
Как мне вставить Quadf в Excel?
Например, чтобы интегрировать формулу, хранящуюся в A1, относительно X1 между 1 и 2, вы используете функцию QUADF в формуле, как это: = QUADF (A1, X1,1,2). Фактически, чтобы интегрировать простую формулу, вы можете передать ее прямо следующим образом: = КВАДФ (X1 * КОРЕНЬ (X1); X1,1,2) .
Что такое производный пример?
Производный инструмент — это инструмент, стоимость которого определяется стоимостью одного или нескольких базовых инструментов, которыми могут быть товары, драгоценные металлы, валюта, облигации, акции, фондовые индексы и т. Д. Четыре наиболее распространенных примера производных инструментов: Форварды, фьючерсы, опционы и свопы.
Каковы четыре основных производных правила?
Это включает правило констант, правило мощности, правило множественных постоянных, правило сумм и правило разностей.
Интересные материалы:
Какой IP-адрес лучше всего подходит для Xbox Live?
Какой IP-адрес по умолчанию у маршрутизатора Edimax?
Какой IP-адрес у HP LaserJet P1102w?
Какой iPad лучше всего подходит для студентов?
Какой iPad может использовать сотовые данные?
Какой IQ у Григория Перельмана?
Какой ISO позволит снимать в помещении без вспышки?
Какой источник бензина?
Какой источник трафика лучше всего на YouTube?
Какой из благородных газов чаще всего используется в неоновых вывесках?
Несколько недель назад я писал о вычислении интеграла данных в Excel. На этой неделе я хочу изменить направление и показать, как вычислить производную в Excel. Как и при численном интегрировании, есть два способа выполнить это вычисление в Excel:
- Производные табличных данных на листе
- Производные от Функция с использованием VBA (или Visual Basic для приложений)
В этом посте я собираюсь сосредоточиться на вычислении производных табличных данных с сообщением о вычислении того же с использованием VBA более поздняя дата.
Это вид вычисления производной, который обычно выполняется на экспериментальных данных. Это может быть особенно полезно, когда вы не могли напрямую измерить интересующее количество, но смогли измерить его интегральную функцию.
[Примечание: хотите узнать больше о расширенных Методы Excel? Смотрите мое бесплатное обучение только для инженеров. В серии видео из трех частей я покажу вам, как легко решать инженерные задачи в Excel. Нажмите здесь, чтобы начать.]
Классическим примером, конечно же, являются положение и скорость:
Скажем, например, вы провели некоторый эксперимент, в котором было трудно получить скорость напрямую. Итак, вместо этого вы измеряли позицию в разное время, t . Вы можете импортировать данные в Excel и рассчитать скорость как производную от положения по времени.
Для выполнения этого вычисления в Excel используется метод конечных разностей.
Чтобы использовать метод конечных разностей в Excel, мы вычисляем изменение «y» между двумя точками данных и делим на изменение «x» между теми же самыми точками данных:

Это называется односторонней оценкой, потому что она учитывает только наклон данных на одном сторона точки интереса.
Более точной оценкой было бы вычисление среднего уклона в точке интереса путем усреднения наклона непосредственно до и после этой точки.
Итак, если мы хотим найти наклон в y 2 (z), мы могли бы использовать этот расчет:
Давайте посмотрим, как вычислить производную в Excel на примере. Мы можем использовать данные о положении, которые были рассчитаны путем интегрирования данных скорости в предыдущем посте, и использовать их для расчета скорости и ускорения. В качестве проверки мы сравним рассчитанные данные об ускорении с исходными данными об ускорении.
Чтобы упростить задачу, я спрятал старые данные об ускорении и скорости. В конце мы посмотрим, как они сравниваются.
Сначала я вычисляю скорость, используя уравнение конечных разностей выше. Поскольку нам нужны y3 и y1, я начинаю вычисление в ячейке E5 и заполняю ее.

[Примечание. Хотите узнать еще больше о передовых методах работы с Excel? Посмотрите мое бесплатное обучение только для инженеров. В серии из трех видео я покажу вам как легко решать инженерные задачи в Excel. Нажмите здесь, чтобы начать.]
Затем, используя вычисленную скорость, я могу рассчитать ускорение тем же методом. На этот раз расчет начинается в строке 6.

Теоретически, если мы дифференцируем данные, полученные путем интегрирования, тогда мы должны вернуться к исходным данным. Конечно, все численные методы вносят в данные какую-то ошибку.
Но насколько велика ошибка? Давайте сравним .

В этом случае мы видим небольшие отличия между исходными данными об ускорении и данными, полученными путем дифференцирования. Есть также некоторые незначительные различия в двух наборах данных о скорости. К счастью, ошибка численного дифференцирования n не является кумулятивным, в отличие от численного интегрирования.
Таблицы данных – не идеальный способ изучить эти данные, поэтому давайте посмотрим на графики:

Трудно увидеть, потому что две линии расположены друг над другом, но для всех практических целей скорости идентичны.
Как насчет разгона?

Здесь мы можем видеть, что во время периодов неуклонного увеличения или постоянного ускорения два набора данных очень похожи. Однако, когда в данных ускорения наблюдается разрыв (например, время 0,1, 0,45, 0,5, 0,7 и 0,75 с), ускорение, полученное дифференцированием (оранжевый), не соответствует исходным данным ускорения (синий).
Это связано с уравнением, которое мы использовали для выполнения дифференцирования. Помните, как мы получили производную в точке путем усреднения наклона по обе стороны от этой точки? Мы видим результаты здесь.
Если вы следовали инструкциям, поздравляем! Вы только что выполнили численное дифференцирование в Excel. Конечно, вычислить производную в Excel не так сложно, если вы знаете, как это сделать.
Использовали ли вы этот метод для некоторых данных? Расскажите мне об этом в комментариях ниже.
[Примечание: Хотите узнать еще больше о продвинутых методах Excel? Смотрите мое бесплатное обучение только для инженеров. В серии видео из трех частей я покажу вам, как легко решать инженерные задачи в Excel. Щелкните здесь, чтобы начать.]
RDF> ->