Как найти процентную ставку по кредиту в excel

Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа.

Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.

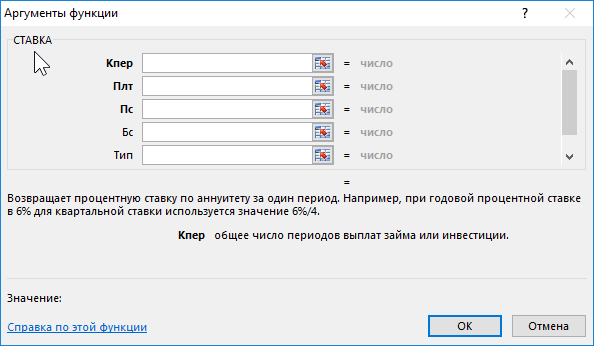
Для расчета процентной ставки в аннуитетной схеме используется функция

СТАВКА()

.

Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение])

возвращает процентную ставку по аннуитету.

Примечание

.

Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.

Вот что написано на сайте MS

: Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см.

обзорную статью о функциях аннуитета

).

Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути,

метод подбора

). Чтобы облегчить поиск Ставки методом итераций, используется аргумент

Предположение. Предположение

— это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение

Предположение

также полезно в случае

,

если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к

Предположению

.

Задача1 – Выплата кредита

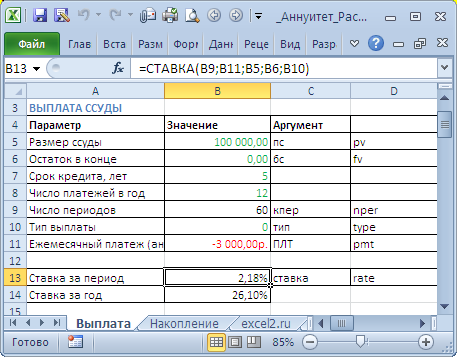
Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.

Примечание

. Аннуитетная схема погашения кредита подробно рассмотрена в статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)

.

В условии задачи содержится следующая информация:

• Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
• Проценты начисляются
  
  в конце
  
  каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0;
• В конце срока задолженность должна быть равна 0 (БС=0).

В результате формула для вычисления годовой ставки будет выглядеть так

=12*СТАВКА(12*5;-3000;100000;0;0)

или

=12*СТАВКА(12*5;-3000;100000)

Знак минус у регулярного платежа показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые

банк

дал

нам, -3000 – это деньги, которые мы

возвращаем банку

. Результат вычисления = 26,10%

Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в

файле примера на Листе Выплата

установить платеж =-1000).

Если задать платеж = 0 или того же знака, что и сумма кредита, то функция

СТАВКА()

вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.

Примечание

. С помощью

Подбора параметра

можно найти величину регулярного платежа, который бы обеспечил выплату кредита при заданной процентной ставке (обратная задача). Но, по большому счету, в этом нет необходимости – для этого существует функция

ПЛТ()

.

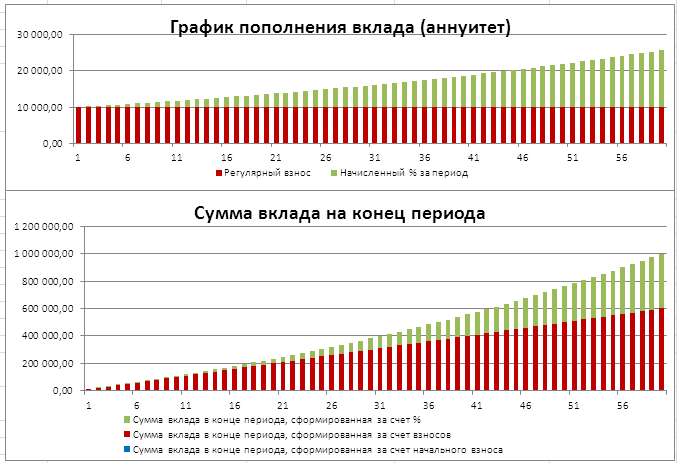
Задача2 – Накопление суммы вклада

Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см.

файл примера на Лист Накопление

)

Примечание

. Аннуитетная схема накопления целевой суммы подробно рассмотрена в статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад

.

Формула для вычисления годовой ставки будет выглядеть так

=12*СТАВКА(12*5;-10000;0;1000000)

=19,38%

Здесь ПС=0, т.е. начальная сумма вклада =0 (

Приведенная Стоимость

). Целевой вклад = 1000000 (БС –

Будущая Стоимость

).

Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.

Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция

СТАВКА()

вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.

Функция СТАВКА используется для определения процентной ставки по инвестиции либо денежному займу с аннуитетной структурой графика погашения для одного периода выплат (при условии, что будущая стоимость ценных бумаг, обеспечивающих инвестицию либо кредит является известной величиной) и возвращает полученное значение.

Если при заключении сделки процентная ставка не была установлена жестко, функция СТАВКА позволяет определить размер неявной ставки (то есть такой ставки, которая обеспечила бы получение эквивалентного дохода).

Примеры финансовых расчетов по функции СТАВКА в Excel

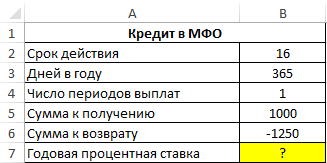
Пример 1. В МФО был взят кредит сроком на 16 дней, сумма которого составляет 1000 долларов. Сумма возврата составляет 1250 долларов. Определить годовую процентную ставку по указанным условиям займа.

Таблица данных:

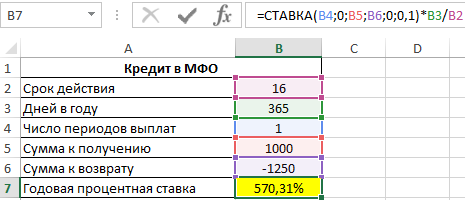
Для расчета в ячейку B7 введем следующую формулу:

=СТАВКА(B4;0;B5;B6;0;0,1)*B3/B2

Описание аргументов:

• B4 – число периодов выплат (в данном случае – 1);
• 0 – размер фиксированной выплаты (поскольку в данном примере только один период выплат, указано значение 0);
• B5 – тело кредита;
• B6 – сумма на момент погашения долга;
• 0 – характеризует тип выплат, при котором выплата производится в конце периода;
• 0,1 – предполагаемое значение процентной ставки (любое число из диапазона от 0 до 1);
• B3/2 – коэффициент для пересчета полученного значения ставки к годовой процентной ставке.

Результат вычислений:

Пи данных условиях микрокредитования сроком займа на 16 дней процентная ставка составляет 570,31% годовых! Несмотря на это, услуги по микрокредитованию сегодня продолжают набирать популярность.



Анализ пенсионных отчислений с использованием функции СТАВКА в Excel

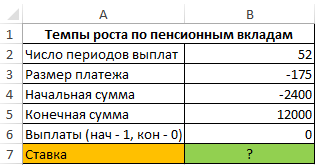
Пример 2. Определить темпы роста пенсионных отчислений (процентную ставку), если баланс средств на конец года составляет 12000 долларов, а в начале года – 2400 долларов. Еженедельные платежи на протяжении года составляли 150 долларов (то есть, количество периодов – 52).

Исходные данные:

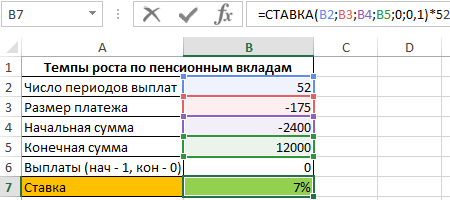
Формула для расчета:

=СТАВКА(B2;B3;B4;B5;0;0,1)*52

Описание аргументов:

• B2 – количество периодов выплат;
• B3 – сумма платежа (расходная операция, поэтому отрицательное значение);
• B4 – сумма средств до наступления первого периода выплат;
• B5 – сумма по окончанию последнего периода выплат;
• 0 – выплаты в конце периода;
• 0,1 – произвольное значение из интервала от 0 до 1;
• 52 – количество периода выплат для пересчета размера ставки в годовых.

Результат вычислений:

То есть, пенсионные отчисления выполняются под 7% годовых.

Определение реальной процентной ставки по кредиту

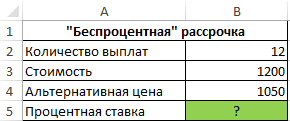
Пример 3. Ноутбук одной и той же модели можно приобрести за 1200 долларов в рассрочку (беспроцентную, судя по рекламе в первом магазине) или за 1050 долларов в другом магазине. Рассрочка выдается на 1 год с 12 периодами выплат. Определить реальный процент «беспроцентной» рассрочки платежей по кредиту.

Исходные данные:

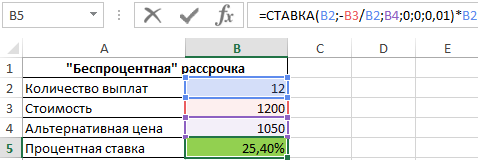
Формула для расчета:

=СТАВКА(B2;-B3/B2;B4;0;0;0,01)*B2

Описание аргументов:

• B2 – число периодов выплат;
• -B3/B2 – выражение для расчета размера ежемесячного платежа;
• B4 – реальная стоимость ноутбука (используется как начальная стоимость финансового инструмента, цена которого повысится до 1200 к окончанию последнего периода выплат);
• 0 – остаток по окончанию последнего периода выплат;
• 0 — выплаты в конце периода;
• 0,01 — произвольное значение предполагаемой ставки.

Результат расчетов:

То есть, фактически в первом магазине клиенту предложили кредит на ноутбук под 25,4% годовых.

Функция СТАВКА в Excel и особенности ее использования

Функция СТАВКА имеет следующий синтаксис:

= СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])

Описание аргументов:

• кпер – обязательный аргумент, характеризующий число периодов выплат по аннуитетной схеме.
• плт – обязательный аргумент, характеризующий фиксированное значение выплаты, производимой в каждый из периодов выплат. Сумма выплаты за каждый период включает две составляющие: тело и проценты без учета прочих комиссий и сборов. Если данный аргумент опущен, следующий аргумент должен быть указан явно.
• пс – обязательный аргумент, характеризующий текущую стоимость задолженности (либо вознаграждения), эквивалентную общей сумме последующих платежей на данный момент. Если значение неизвестно, необходимо явно указать значение 0 (нуль).
• [бс] – необязательный аргумент, характеризующий размер желаемого остатка средств после выполнения последней выплаты согласно графика платежей. Если явно не указан, по умолчанию используется значение 0 (нуль), а аргумент пс становится обязательным для заполнения.
• [прогноз] – необязательный аргумент, характеризующий предполагаемый размер процентной ставки. Если аргумент явно не указан, по умолчанию принимается значение 10%. Если полученное в результате вычислений значение не сходится с указанной прогнозной величиной, величину данного аргумента следует изменить. Рекомендуется выбирать значение для аргумента [прогноз] из диапазона от 0 до 1.
• [тип] – необязательный аргумент, принимающий значения 0 или 1:

1. Если введен 0, считается, что выплата производится в конце периода;
2. Если введен 1, считается, что выплата производится в начале периода.

Примечания:

1. Единицы измерения величин, указанных в качестве аргументов кпер и [прогноз], должны соответствовать друг другу. Например, при расчете ставки по займу, выданному на два года под 16% с ежемесячными выплатами необходимо, в качестве аргумента [прогноз] необходимо использовать значение 16%/12, а кпер – 2*12.
2. Если хотя бы в качестве одного из аргументов функции было передано текстовое значение, результатом выполнения функции будет являться код ошибки #ЗНАЧ!.
3. Аннуитетная схема выплаты вознаграждения либо погашения задолженности предполагает выплаты фиксированной суммы, включающей вознаграждение или тело кредита и дополнительных процентов (в зависимости от установленной процентной ставки) на протяжении установленного количества периодов выплат. В отличие от классической схемы, при которой проценты начисляются на остаток вознаграждения или задолженности, в аннуитетной схеме соотношение тело кредита/проценты является изменяющейся величиной.
4. При выполнении расчетов функция СТАВКА использует итерационный метод. Если после 20 итераций последующие результаты вычислений отличаются друг от друга более, чем на 10-7, результатом вычислений будет являться код ошибки #ЗНАЧ!.

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

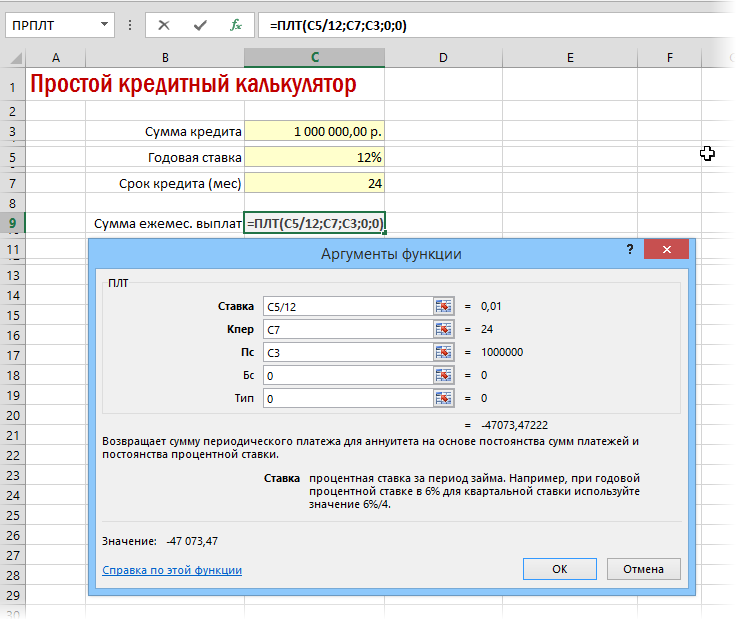
• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — начальный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0. 

Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

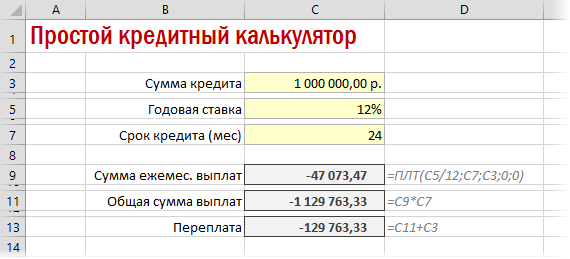
Вариант 2. Добавляем детализацию

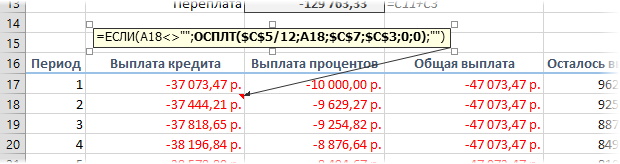
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

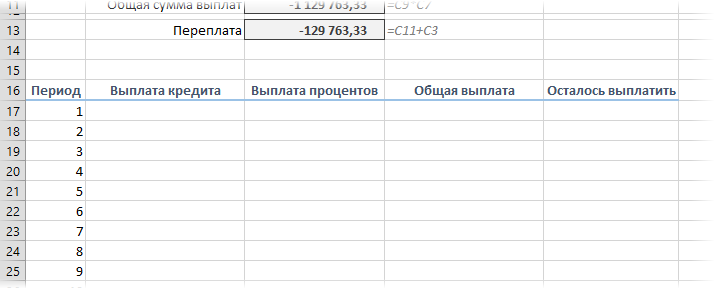
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

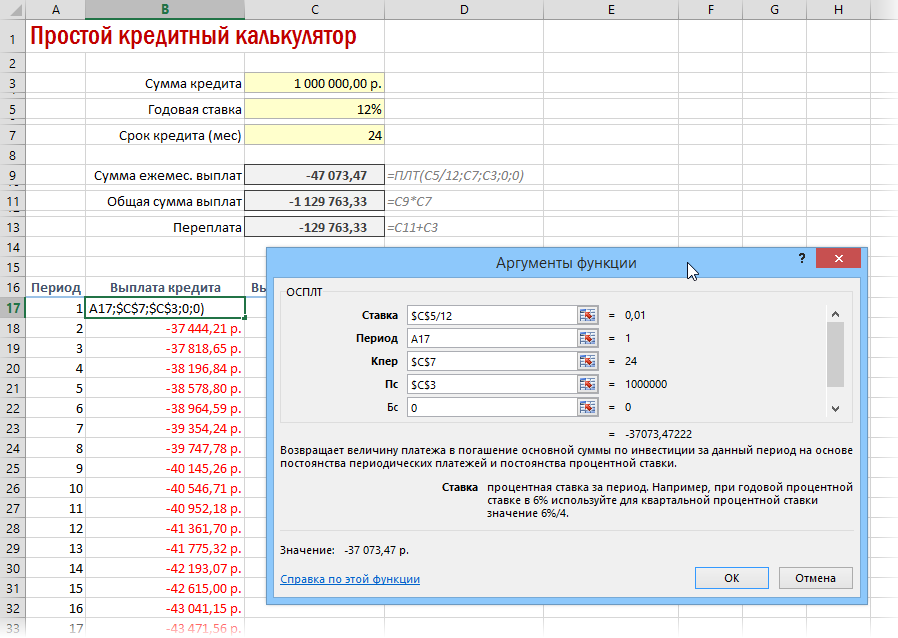
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

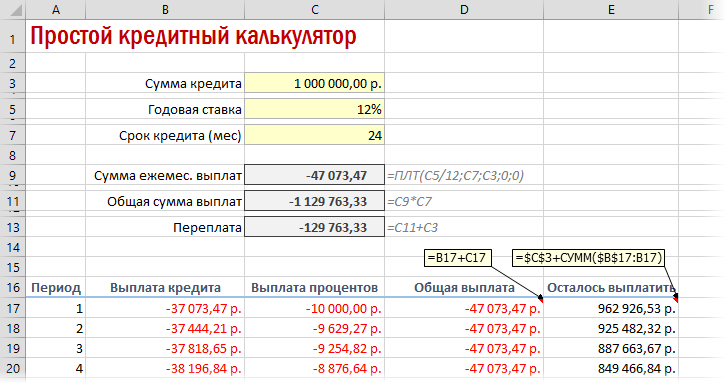
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;»»;A17+1)

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>»»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

Вариант 3. Досрочное погашение с уменьшением срока или выплаты

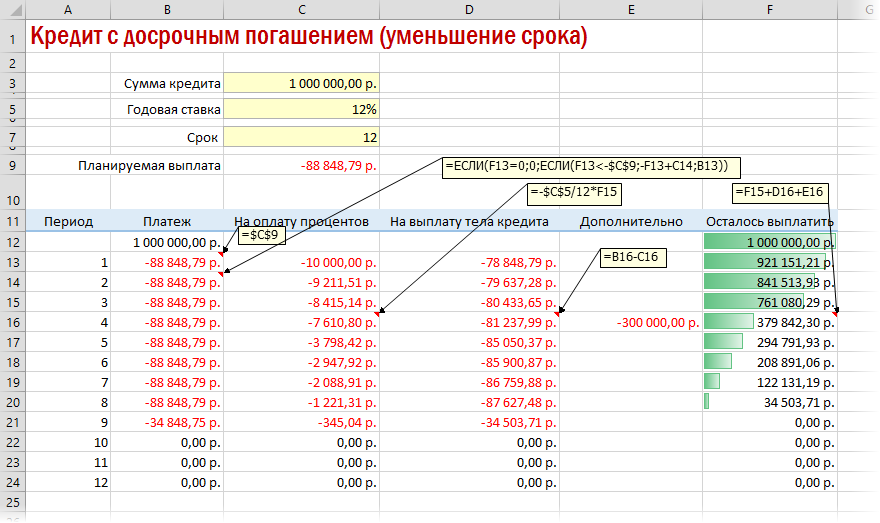
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

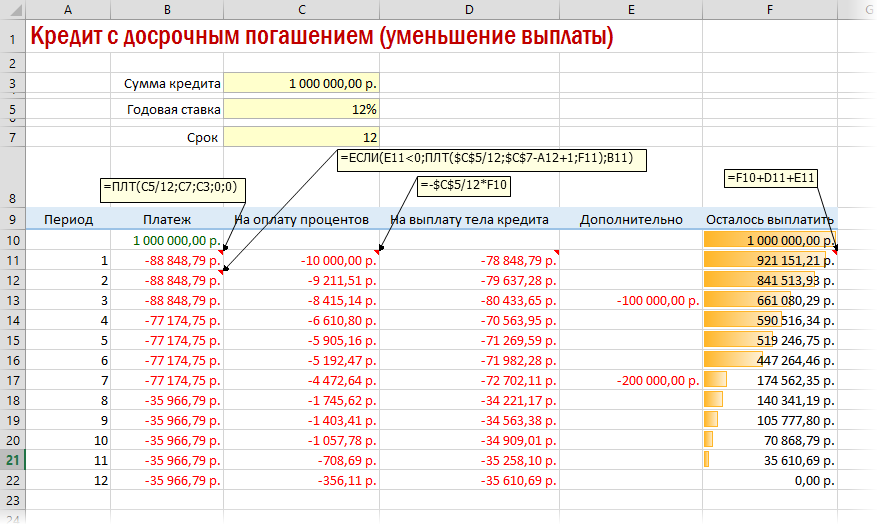
А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

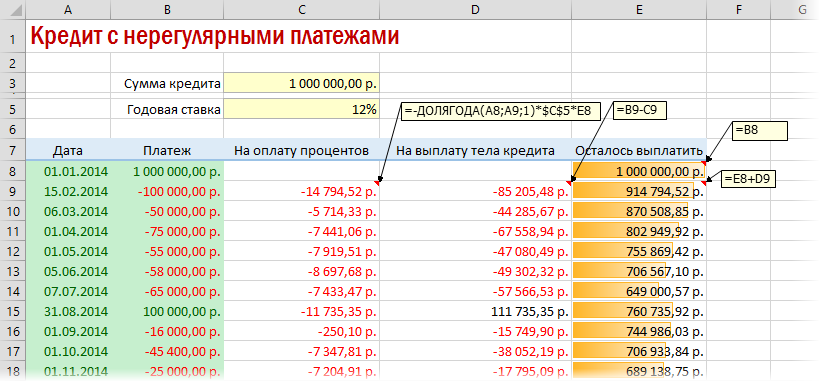
Предполагается что:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)

Функция СТАВКА вычисляет процентную ставку по займу или инвестиции, базируясь на величине будущей стоимости. В транзакциях, в которых процентная ставка не задана жестко, эта функция может быть использована для вычисления неявной ставки (ставки, по которой можно было бы получить такой же доход). Синтаксис функции следующий: СТАВКА(клер;ставка;пс;бс;тип;предположение).

Ставки краткосрочных займов

Краткосрочные займы обычно должны погашаться в течение 14 дней и, как правило, предполагают 15 долларов комиссии с каждых ста взятых взаймы долларов. Если вы взяли в кредит 200 долларов и согласились через 14 дней отдать 260 долларов, процентную ставку можно вычислить по следующей формуле: =СТАВКА(1;0;200;-260;0;,01)*365/14. Значение периода равно единице по той причине, что предполагается всего одна проплата. Этот единственный период охватывает 14 дней, поэтому результат нужно разделить на количество дней в году (365) и умножить на 14. Полученный результат (782%) такой большой потому, что заем краткосрочный (рис. 1).

Процентные ставки обычно опредёляются из расчета одного года, даже если срок займа больше или меньше года. Преобразование процентной ставки к годовой позволяет сравнить различные условия кредитных договоров. Если попытаться сравнить месячную процентную ставку с годовой, то первая будет выглядеть существенно меньшей, хотя на самом деле таковой не является.

Темпы роста

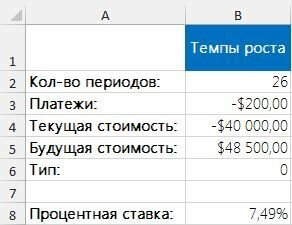
Чаще всего функцию СТАВКА используют для вычисления темпов роста на пенсионном счету. Предположим, что баланс на пенсионном счету составляет 40 тысяч долларов на начало года и 48,5 тысячи — на конец. В течение года с каждой получки (т.е. раз в две недели) вы клали на счет по 200 долларов (т.е. осуществили 26 платежей). Следующая формула показывает, как пополнялись ваши инвестиции (рис. 2): =СТАВКА(26;-200;-40000;48500;,01)*26.

В данном примере функция СТАВКА возвращает темпы роста за каждый период, поэтому для получения годовой процентной ставки следует умножить это число на 26. Результатом будет ставка 7,49%.

Беспроцентные займы

Беспроцентные займы на самом деле редко таковыми являются, так как интерес заимодателя уже учтен в стоимости товара. Предположим, что вы хотите купить кухню за 3 тысячи долларов и оформляете на нее беспроцентную рассрочку на 12 месяцев. Если бы у вас было достаточно наличных, вы смогли бы купить эту же кухню за 2500 долларов — фактически вы переплачиваете за рассрочку 500 долларов. Рассчитанная по следующей формуле приведенная процентная ставка составляет 35,07%: =СТАВКА(12;-3000/12;2500;0;0;,01)*12.

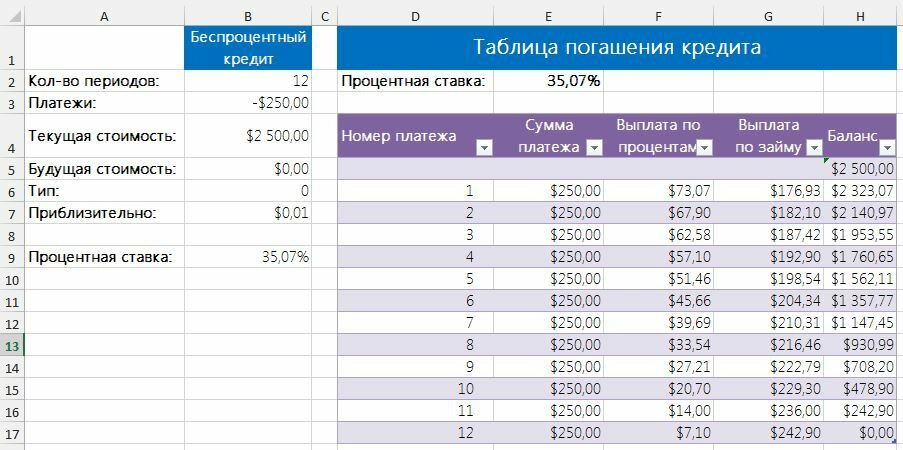
Проверить результаты функции СТАВКА можно, создав таблицу погашения кредита (рис. 3). Если баланс стремится к нулю, значит, процентная ставка вычислена правильно.