Хитрости »
14 Февраль 2017 25564 просмотров
Как быстро подобрать оптимальный вариант решения
Практически в любой компании в определенные периоды могут «высвобождаться» из оборота временно свободные денежные средства(ВСДС). Оставлять эти деньги просто так на счетах компании весьма нецелесообразно. Деньги должны делать деньги. Конечно, вложение денег в банковские депозиты может показаться не самым лучшим вариантом для инвестиций, но все же это хоть какой-то доход, который если и не будет колоссальным, то хотя бы частично покроет инфляционные потери.
И самое сложное это выбрать банк, программу депозита и срок для вложений таким образом, чтобы получить максимальную выгоду. Сделать это поможет один из самых мощных, но в тоже время малоиспользуемых инструментов Excel — надстройка Поиск решения(Solver).
Чтобы пошагово выполнять дальнейшие действия, описанные в статье рекомендую сразу скачать файл с моделью для Поиска решения:
Модель_расчета_ВСДС.xls (44,5 KiB, 1 466 скачиваний)
Надстройка Поиск решения хоть и устанавливается автоматически вместе с Excel(начиная с версий 2007 и выше), но по умолчанию отключена. Чтобы включить надстройку необходимо перейти в Файл(File) —Параметры(Options). В появившемся диалоговом окне выбрать слева пункт Надстройки(Add-ins). Далее справа внизу в выпадающем списке Управление выбрать —Надстройки Excel(Excel Add-ins) и нажать Перейти(Go):
В окне Надстройки(Add-ins) устанавливаем галочку напротив пункта Поиск решения(Solver), жмем ОК.
Поиск решения теперь будет доступен с вкладки Данные(Data) -группа Анализ(Analize):
Исходные данные
Для начала нам потребуется определить сумму временно свободных денежных средств и сроки, на которые мы хотим эти средства разместить в банке. Далее конечно же потребуется выбрать несколько банков (или конкретные предложения отдельного банка) с различными процентами годовых за размещение ДС. Но так же придется учесть и реалии: не стоит все средства размещать исключительно в одном банке и поэтому надо для банков/предложений определить лимит ДС, который нельзя превышать.
Т.е. наши исходные данные выглядят примерно так:
- период размещения ДС на депозите(скажем 14 дней, 28 дней, 62 дня и 91 день)
- сумма ДС, доступная на каждый период размещения
- процент за размещение ДС на каждый период для каждого типа размещения(срочный депозит, до востребования, овернайт и т.д.) или банка
- лимит на размещение средств по каждому типу депозита или для каждого банка(лимит определяется самой компанией)
Как работает Поиск решения
Поиск решения хорош тем, что он может быть применен практически к любой задаче. Что он делает? Он на основании заданных условий и ограничений перебирает все возможные варианты, которые подходят под условия и не выходят за рамки заданных ограничений, если они есть. И из всех подобранных вариантов выбирает самый оптимальный. В нашем случае будем подбирать наиболее выгодный для нас вариант размещения ВСДС.
А что считать наиболее выгодным? Конечно то, что принесет наибольший доход. При этом наша цель не просто выбрать депозит с самым большим процентом (это было бы слишком просто и для этого не нужен Поиск решения), а может даже совместить несколько вариантов размещения ВСДС на разных депозитах с разными ставками и разными периодами. Ведь для различных сумм или сроков и ставки могут быть разными.
И теперь останется определить какие у нас могут быть ограничения. По сути их два основных:
- Непосредственно сумма ВСДС – мы не должны при расчете максимального дохода выходить за рамки общей суммы доступных ВСДС
- Лимит по депозиту для размещения – как упоминалось выше, могут быть установлены лимиты на размещение средств в том или ином банке на усмотрение компании. Конечно, любой банк заинтересован в большей сумме, но не стоит рисковать и вкладывать всю сумму в один банк
Исходные данные определены, ограничения тоже. Осталось записать все это в удобную таблицу(приложена к статье), в которой при необходимости сможем изменять эти исходные данные и ограничения:
Для большей наглядности блоки таблицы разделены цветами:
- Синий и голубой – заполняемые вручную данные: суммы ВСДС, сроки ВСДС, лимиты размещения ВСДС в банках, процент по каждому банку/размещению
- Зеленый – расчетные поля. Их не надо изменять вручную
- Красный – поля, заполняемые автоматически Поиском решения или формулами. Их не надо изменять вручную
- Так же серый шрифт – это «служебные» ячейки, которые не влияют на расчеты непосредственно в таблице, но которые потребуются нам для корректной работы Поиска решения для учета ограничений
После заполнения таблицы исходными данными можно приступать к определению максимального выгодного вложения ВСДС.
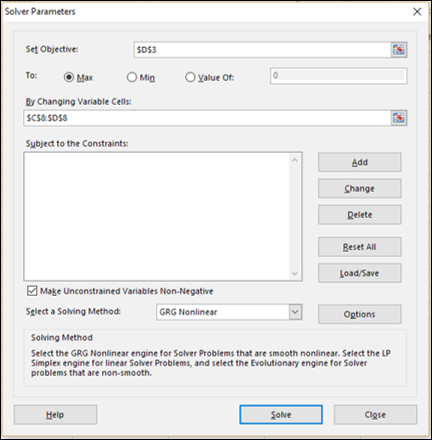
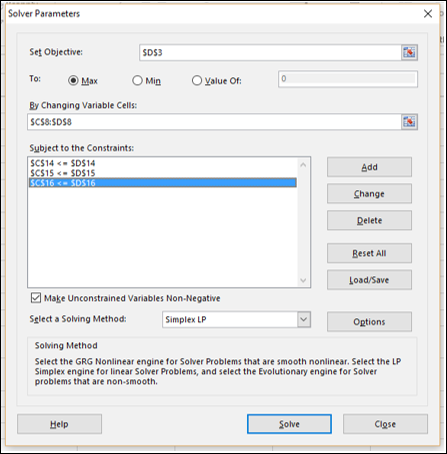
Переходим на вкладку Данные(Data) -группа Анализ(Analize) —Поиск решения(Solver). В появившемся окне указываем следующие данные:
- Оптимизировать целевую функцию(Set Objective) – указываем ячейку H18, в которой у нас подводится сумма общего дохода от вложений
- До(To) – выбираем Максимум(Max), т.к. нам нужен максимально возможный доход
- Изменяя ячейки переменных(By Changing Variable Cells) – указываем H9:K14. В эти ячейки Поиск решения будет подставлять суммы к размещению и вычисляя от этого возможный доход. Собственно, заполненные здесь данные нам и нужны в итоге
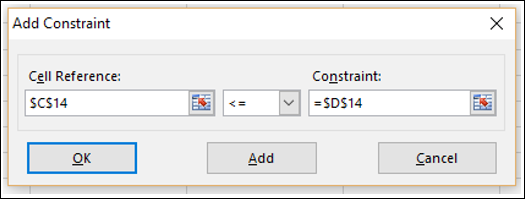
- В соответствии с ограничениями(Subject to the Constraints) – здесь мы сами добавляем ограничения, которые необходимо учитывать при расчете дохода. Нам потребуется добавить два ограничения(на скрине выше они уже добавлены, но в любом случае необходимо знать как их создавать). Нажимаем справа кнопку Добавить(Add), появится окно добавления ограничения:
В данном случае я хочу добавить ограничение, что суммы в ячейках с лимитом размещения в банке должны быть больше или равны общей сумме размещенных ВСДС. Эта сумма у нас подводится в ячейках L9:L14. Таким образом нам в левой части надо выбрать ячейки с суммами заданных лимитов (C9:C14), а в правой суммы всех вложений – L9:L14. В выпадающем списке между двумя этими полями можно выбрать тип сравнения. В нашем случае ячейки слева (лимиты ДС) должны быть больше или равны(>=) общей сумме вложений по данному типу – ячейки справа.
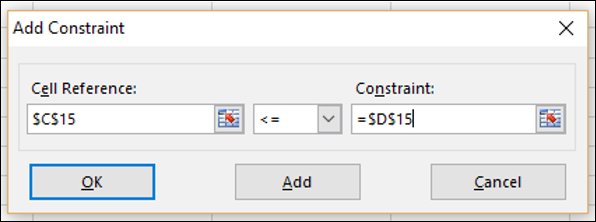
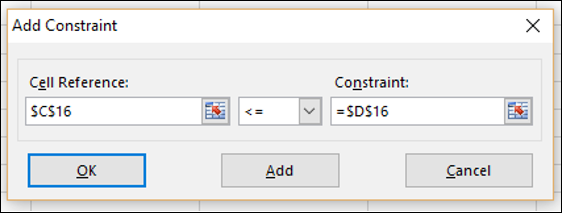
Аналогично добавляем второе ограничение – суммы доступных ВСДС не должны превышать суммы, которые Поиск решения предложит разместить. Доступные суммы у нас указаны в ячейках D7:G7, а общие суммы предложенных к размещению Поиском решения – в ячейках H16:K16(в этих ячейках записаны формулы, суммирующие данные сумм по каждому периоду в ячейках H9:K14) - Так же лучше установить галочку Сделать переменные без ограничений неотрицательными(Make Unconstrained Variables Non-Negative), чтобы Поиск решения не стал подбирать отрицательные суммы для выполнения условий
В рассматриваемой задаче это маловероятно, но при использовании Поиска решения в других задачах этому пункту советую уделять особое внимание, т.к. иногда оптимальным решением для достижения заданного результата с точки зрения Поиска решения будет добавление отрицательного значения среди заполняемых ячеек
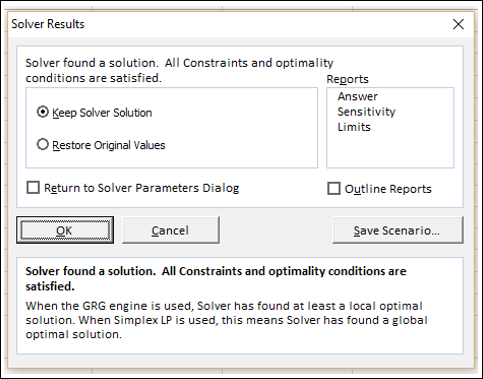
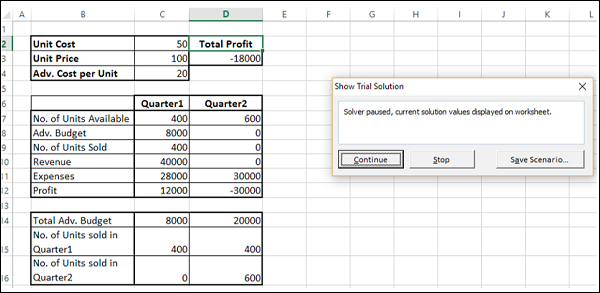
Нажимаем Найти решение(Solve). Если все условия заданы правильно и ограничения выполнимы, то Поиск решения заполнит ячейки суммами и выдаст сообщение о том, что решение найдено и предложит сохранить найденные значения или восстановить предыдущие. В нашем случае надо оставить пункт Сохранить найденное решение(Keep Solver Solution) и нажать Ок.
После этого мы сможем более детально изучить предложенное решение:
При необходимости изменить какие-то исходные данные и запустить поиск решения заново. Все ранее указанные ограничения и условия сохраняются и создавать их заново не придется.
В приложенном к статье файле все ограничения и условия уже созданы и для их просмотра и правки достаточно просто запустить Поиск решения
Осталось понять Как работает вся эта таблица в Поиске решения
В блоке Доход в зависимости от срока размещения, руб(M9:P14) записаны формулы, которые определяют сумму дохода в зависимости от вложенной суммы и срока размещения. При этом рассчитываются они из сумм, записанных в ячейках красного блока (Суммы к размещению на соответствующие сроки – H9:K14) и от сроков, указанных в исходных данных(D8:G8). В ячейке Итого доходность(H18) подводится сумма этих ячеек. Т.е. мы определяем общий доход от вложений. Все, что остается делать Поиску решения – это изменять значения ячеек Суммы к размещению на соответствующие сроки (H9:K14) до тех пор, пока сумма всех доходов (Итого доходность — H18) не достигнет максимального значения из всех возможных вариантов при всех существующих ограничениях. Суммы в ячейках H9:K14 и будут являться оптимальным решением.
При этом если мы захотим исключить какой-либо банк/тип депозита из просчета, достаточно будет установить в ячейках C7:C14 для этого типа значение 0. Тогда он не будет учитываться для размещения Поиском решения и не надо будет удалять/добавлять строки и переопределять ограничения.
Проверка результатов
Надстройка Поиск решения реализована при помощи весьма сложных алгоритмов и, пожалуй, является самой непредсказуемой надстройкой в Excel. Поэтому рекомендуется тщательно перепроверять результаты вручную, прежде чем полностью на них положиться. Сверяйте полученные результаты, чтобы убедиться, что ограничения не нарушены и главное, что результат отвечает ожиданиям (хотя бы примерно).
Так же следует учитывать, что надстройка может при одинаковых условиях и исходных данных выдавать различные результаты при многократном запуске. Это так же обусловлено сложностью заложенных алгоритмов. Т.е. теоретически, запустив Поиск решения пять раз есть вероятность, что все пять раз решение будет разным. Хотя в большинстве случаев я наблюдал ситуации, когда при одинаковых исходных данных решение было одинаковым.
Скачать пример:

Подбор под сумму через Поиск решения
И еще один пример применения Поиска решения. Предположим, что у нас есть таблица с начислениями НДС за первый квартал. И есть некая итоговая сумма, которая должна быть отчислена за первый квартал. Проблема в том, что не все строки из таблицы были использованы для отчисления общего налога за первый квартал. Задача отобрать из всех сумм только те, которые при сложении дадут именно нужную итоговую сумму отчислений. Данный прием я решил не описывать текстом, а записать видео для большей наглядности:
Скачать файл из видео:

Так же см.:
План-фактный анализ в Excel при помощи Power Query
Автообновляемая сводная таблица
Статья помогла? Поделись ссылкой с друзьями!
Видеоуроки
Поиск по меткам
Access
apple watch
Multex
Power Query и Power BI
VBA управление кодами
Бесплатные надстройки
Дата и время
Записки
ИП
Надстройки
Печать
Политика Конфиденциальности
Почта
Программы
Работа с приложениями
Разработка приложений
Росстат
Тренинги и вебинары
Финансовые
Форматирование
Функции Excel
акции MulTEx
ссылки
статистика
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
В этой статье обсуждается использование надстройки Microsoft Excel «Решение», которая позволяет анализировать «что если» для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
-
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
-
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
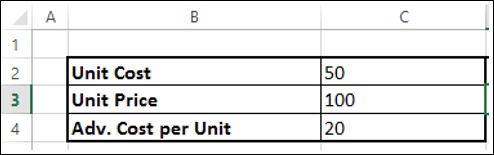
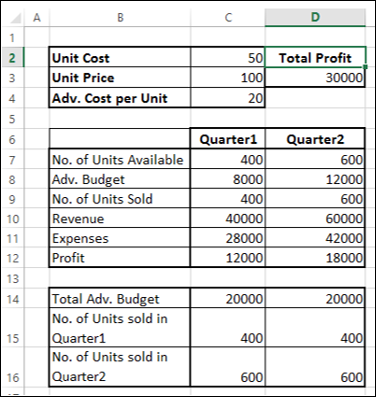
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
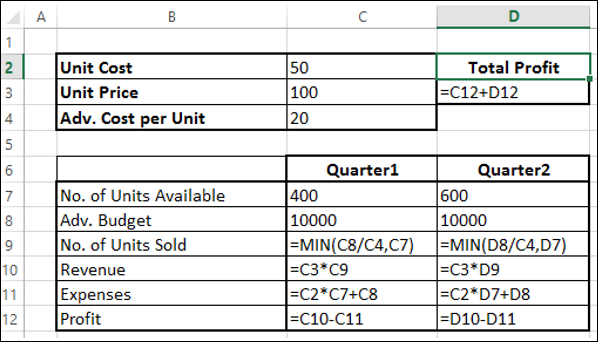
Если бы нам не было известно ничего о надстройке Excel «Решение», мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, «Поиск решения» — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+
(Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + …
(Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
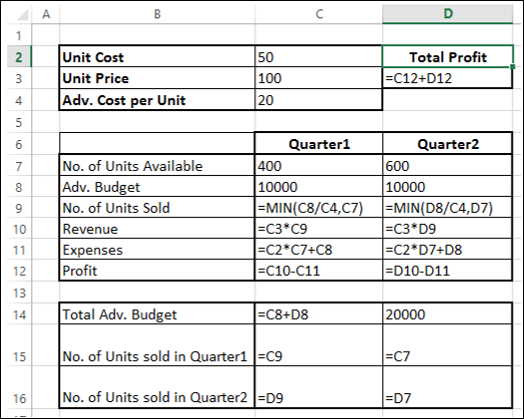
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
-
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
-
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
-
Ограничения. В этом примере есть следующие ограничения:
-
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
-
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в «Найти решение». Все, что вам нужно сделать, — это нажать кнопку «Найти решение», чтобы найти набор товаров, который максимально увеличить прибыль!
Для начала на вкладке «Данные» в группе «Анализ» нажмите кнопку «Найти решение».
Примечание: Как объяснялось в главе 26 «Введение в оптимизацию с помощью надстройки Excel «Решение», надстройка «Решение» устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке «Управление» щелкните «Надстройки Excel», выберите поле «Найти решение» и нажмите кнопку «ОК».
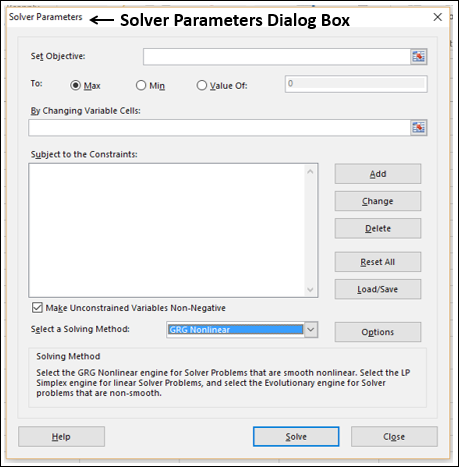
Появится диалоговое окно «Параметры решения», как показано на рисунке 27–2.
Щелкните поле «Установить целевую ячейку» и выберите ячейку прибыли (ячейка D12). Щелкните поле «Изменяя ячейки», а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как «Рисунок 27-3».
Теперь можно добавить ограничения в модель. Нажмите кнопку «Добавить». На рисунке 27–4 показано диалоговое окно «Добавить ограничение».
Чтобы добавить ограничения использования ресурсов, щелкните поле «Ссылка на ячейку» и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле ограничения, а затем выберите диапазон ячеев F14:F15. Диалоговое окно «Добавить ограничение» должно выглядеть так: «Рисунок 27-5».
Теперь, когда «Найти решение» пытается использовать другие значения для изменяющихся ячеек, будут учитываться только сочетания, которые удовлетворяют как D14<=F14 (трудоемка меньше или равна доступной работе), так и D15<=F15 (используемый необработаный материал меньше или равен доступному неоцененному). Нажмите кнопку «Добавить», чтобы ввести ограничения по запросу. Заполните поле в диалоговом окне «Добавить ограничение», как показано на рисунке 27–6.
Добавление этих ограничений гарантирует, что при попытках «Найти решение» для изменяемого значения ячейки будут учитываться только сочетания, которые удовлетворяют следующим параметрам:
-
D2<=D8 (количество произведенного средства 1 не превышает потребность в этом средстве)
-
E2<=E8 (количество произведенного средства 2 не превышает или равно запросу на доступ к более 2).
-
F2<=F8 (количество произведенного средства 3 не превышает потребность в этом средстве)
-
G2<=G8 (количество произведенного средства 4 не превышает или равно запросу на доступ к наркотиками 4)
-
H2<=H8 (количество произведенного средства 5 не превышает или равно запросу на доступ к более 5).
-
I2<=I8 (количество произведенного средства 6 не превышает потребность в этом средстве)
В диалоговом окне «Добавить ограничение» нажмите кнопку «ОК». Окно «Решение» должно выглядеть так: «Рисунок 27-7».
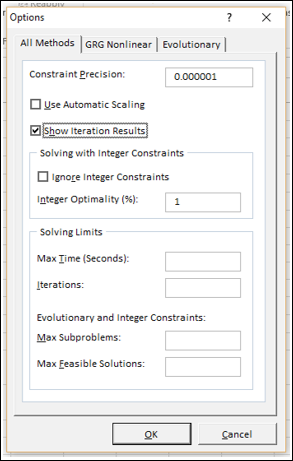
В диалоговом окне «Параметры решения» введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку «Параметры» в диалоговом окне «Параметры решения». Проверьте окне «Предполагаемая линейная модель» и «Нео отрицательная», как показано на рисунке 27–8 на следующей странице. Нажмите кнопку «ОК».
При проверке значения «Предположим, неохожим» над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле «Предполагаемая линейная модель», так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель «Поиск решения» является линейной в следующих условиях:
-
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
-
Каждое ограничение соответствует «требованиям к линейной модели». Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема «Поиск решения» линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мыed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1)<=(Потребность в наркотиками 1)
(От 2 досье 2)<=(Потребность в наркотиками 2)
§
(от 6 досье 6)<=(Потребность в наркотиками 6)
Каждое ограничение запроса также соответствует требованию к линейной модели, поскольку каждое из них вычисляется путем свести вместе условия формы (изменяемая ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
-
Если модель «Поиск решения» является линейной и выбран вариант «Предположим, линейный режим», «Поиск решения» гарантирован, что будет найдено оптимальное решение для модели «Поиск решения». Если модель «Поиск решения» не линейный, «Поиск решения» может не найти оптимальное решение.
-
Если модель «Поиск решения» является линейной и выбран вариант «Предполагаемая линейная модель», то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель «Поиск решения» является линейной и не выбран вариант «Предполагаемая линейная модель», «Поиск решения» использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
После нажатия кнопки «ОК» в диалоговом окне «Параметры решения» вернимся в главное диалоговое окно «Решение», показанное ранее на рисунке 27–7. При нажатии кнопки «Поиск решения» «Поиск решения» вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
-
Мы выпускаем больше 5, чем за него требуются.
-
Мы используем больше трудоемких ресурсов, чем доступно.
-
Мы используем больше необработанных материалов, чем доступно.
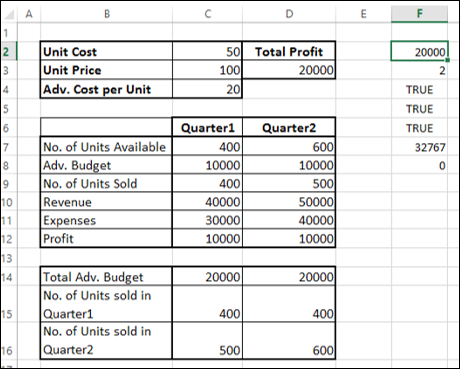
Нажав кнопку «Поиск решения», «Поиск решения» быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать «Сохранить решение для решения проблемы», чтобы сохранить оптимальные значения решения на работе.
Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу «Нет реального решения» в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте «Решение», выберите ограничение D2:I2<=D8:I8 и нажмите кнопку «Изменить». Появится диалоговое окно «Изменение ограничения», показанное на рисунке 27–12.
Выберите >=, а затем нажмите кнопку «ОК». Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки «Найти решение» отобразилось сообщение «Поиск решения не удалось найти целесообразное решение». Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка «Решение» просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области «Набор значений не сходится» на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте «Поиск решения», нажмите кнопку «Параметры» и откроем поле «Неохритимые». В диалоговом окне «Параметры решения» выберите ограничение запроса D2:I2<=D8:I8, а затем нажмите кнопку «Удалить», чтобы удалить это ограничение. При нажатии кнопки «Найти решение» возвращается сообщение «Установить значение ячейки не сходится». Это сообщение означает, что если нужно развернуть целевую ячейку (как в нашем примере), существуют допустимые решения, в том числе и для суммарных значений целевых ячеок. (Если целевая ячейка должна быть свернута, сообщение «Установить значения ячейки не сходятся» означает, что существуют возможные решения с небольших целевых значений, заверяемого в третейском деле.) В нашем случае, разрешив негативное производство в случае злоупотреблений, мы фактически создадим ресурсы, которые можно использовать для вывода в произвольное количество других средств. С учетом нашего неограниченного запроса это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечно. Если вы видите сообщение «Установить значения не сходятся», это означает, что в модели есть ошибка.
-
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
-
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта («Товары 1», «2» и «3»). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Продукт
Специалист А
Специалист Б
Специалист C
Специалист Д
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый специалист может работать до 120 часов в месяц. Как изготовитель микросхем может максимально увеличить ежемесячную прибыль? Предположим, что можно получить лишь дробное количество единиц.
-
Компьютерный завод производит мыши, клавиатуры и игровые joysticks. Доход за единицу, за единицу трудоемких ресурсов, ежемесячная потребность и за единицу машинного времени даются в следующей таблице:
Мыши
Клавиатуры
Joysticks
Прибыль/единица
8 $
11 $
9 $
Использование трудов и единицы
0,2 часа
0,3 часа
0,24 часа
Машинное время/единица
0,04 ч
0,055 ч.
0,04 ч
Ежемесячный запрос
15 000
27,000
11,000
-
Каждый месяц доступно 13 000 часов труда и 3000 часов машинного времени. Как изготовитель может максимально увеличить ежемесячный взнос в прибыль от растения?
-
Допустим, необходимо устранить проблему с этой проблемой при условии, что должны быть выполнены минимальные требования к 200 единицам для каждого из них.
-
Он делает ромбовидные ромбои, окаймлы и затейные. Он хочет работать не более 160 часов в месяц. У него 800 ромбов. Ниже дается прибыль, время труда и количество ромбов, необходимых для получения каждого товара. Если потребность в каждом продукте не ограничена, как Максим может увеличить прибыль?
Продукт
Прибыль за единицу
Трудоемкие часы на единицу
Ромбы на единицу
Лексема
300р.
.35
1,2
Кулигов
200 ₽
.15
.75
Кулигов
100р.
0,05
.5
Лабораторная
работа Часть 1. Подбор параметра
Создайте таблицу
(цена и объем выбрать можете произвольно), а остальные столбцы рассчитайте по
формулам:
|
Курс |
55 |
|||
|
Наименование |
Цена в $ |
Объем заказа |
Сумма в $ |
Сумма в руб. |
|
оргтехника |
||||
|
ПК |
89 |
6 |
534 |
29 370,00 ₽ |
|
Ноутбуки |
69 |
10 |
690 |
37 950,00 ₽ |
|
Принтеры |
57 |
13 |
741 |
40 755,00 ₽ |
|
Ксероксы |
83 |
5 |
415 |
22 825,00 ₽ |
|
сканеры |
77 |
9 |
693 |
38 115,00 ₽ |
|
ИТОГО |
375 |
43 |
3073 |
169 015,00 ₽ |
Эта
таблица, в которой объемы заказов являются желаемыми. Видно, что итоговая сумма
169015,00 руб. Допустим у нас ограниченный бюджет на закупку оргтехники в
размере 150 000 руб. Возникает вопрос в том, что объем заказа нужно
сокращать.
Например, мы считаем
что для нас допустимым является уменьшить число принтеров. Чтобы автоматически
найти до какого количества можно сократить число принтеров, воспользуемся
«подбором» параметра.
Выделите ячейку с
объемом принтеров. Найдите функцию «подбор параметра» на вкладке «данные». Если
его нет, то через кнопку «Офис» и «параметры эксель» найдите эту функцию и
добавьте ее:
Далее запустив данную функцию увидите окно:
В котором нужно указать ячейку где
рассчитывается стоимость всего заказа. В поле «значение» установите значение
равное 150 000 (это помним ограничение по бюджету). Изменяемой ячейкой
естественно должна быть ячейка в которой указывает объем заказыаемых принтеров.
Нажмите Ок.
В итоге:
Видим, что число заказываемых принтеров 6.9,
следовательно не более 6 целых принтеров мы можем заказать , чтобы уложиться в
бюджет.
Задания. Теперь выполните подбор параметра для «курса валюты» при котором бы все
заявленные объемы могли быть приобретены в рамках данного бюджета в
150 000 руб. Также выполните подбор параметра для ячейки «цена ПК» при
которой можно было бы уложиться в указанный бюджет в размере 145 000 руб,
не изменяя исходных объемов заказа.
Часть
2. Расчет оптимальных значений (поиск оптимальных значений).
Необходимо решить задачу оптимизации. Возьмем
задачу линейного программирования, в которой есть целевая функция (критерий) Z, и три ограничения.
Условие
задачи: Завод производит два вида продукции:
велосипеды и мотоциклы. При этом цех по сборке велосипедов имеет мощность 100
тыс. штук в год, цех по сборке мотоциклов – 30 тыс. Одна группа механических
цехов завода может производить либо детали для 120 тыс. велосипедов, либо
детали для 40 тыс. мотоциклов, либо другую комбинацию деталей, ограниченную
этими данными. Другая группа механических цехов может выпускать детали либо для
80 тыс. велосипедов, либо для 60 тыс. мотоциклов, либо любую допустимую их
комбинацию. В результате реализации каждой тысячи велосипедов завод получает
прибыль в 2 тыс. рублей, а каждой тысячи мотоциклов – 3 тыс. рублей.
Математический
вид задачи:
,
.
В
качестве переменных задачи естественно взять количества велосипедов и
мотоциклов, выпускаемых заводом в год (в тыс. штук): и
.
В
екселе решение задачи будет выглядеть так:
В
итоге необходимо решить данную задачу средствами ексель. Воспользуемся
«надстройкой» называемой «поиск решения». «Поиск решения» должна быть во
вкладке «данные». Если ее нет. Установите ее, через кнопку «офис»-«параметры Ексель»-«надстройки». Здесь поиск решения будет
отображаться среди неактивных настроек:
Выберите ее и нажмите «перейти». Получим:
Выбираем «поиск решения». Ставим галочку и
нажимаем ОК. Далее происходит установка этой надстройки. Подождите.
Затем на вкладке данные появится возможность
вызвать данную функцию:
Запустите ее. Видим:
Здесь укажите тип задачи (максимизация или
минимизация) в нашем случае – максимизация примбыли, а в целевой ячейке,
укажите ячейку в которой рассчитывается целевая функция Z.
Это в нашем примере ячейка D1. В ней должна быть формула
для расчета целевой функции (обратите внимание, что она соответствует
математической записи задачи):
Где B4 и В5 это ячейки
для значений переменных х1 и х2:
Эти две ячейки (B4 и В5)
нужно указать здесь:
Далее в поле «Ограничение» указываем ячейки в
которых рассчитываются ограничения:
Формулы для ячеек с ограничениями:
Т.е. при добавлении ограничения, видим:
Где указыается ячейка для ограничения и
значение (число) чем значение ограничивается, в нашем случае 1 (см.
математическую запись задачи).
После того, как все ограничения введены
получим решения нажав «выполнить»
Видим:
Максимум прибыли равно 163.333. При этом нужно
выпускать 66.6 велосипедов, и 10 мотоциклов.
Решить задачи самостоятельно в ексель:
1. ,

Ответ:
2. ,

Ответ:
3. ,

Ответ:
4. ,

.
5. ,

Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
После нажатия кнопки
Поиск решения
в группе
Анализ,
откроется его диалоговое окно
.
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
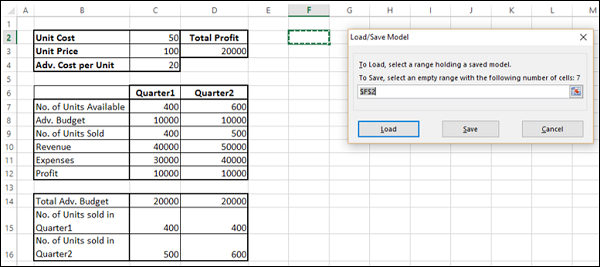
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
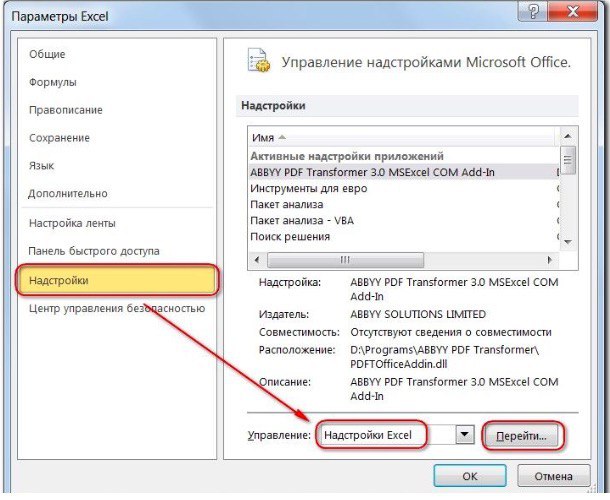
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.
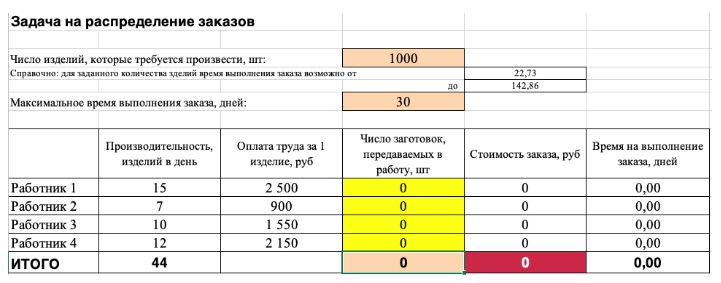
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
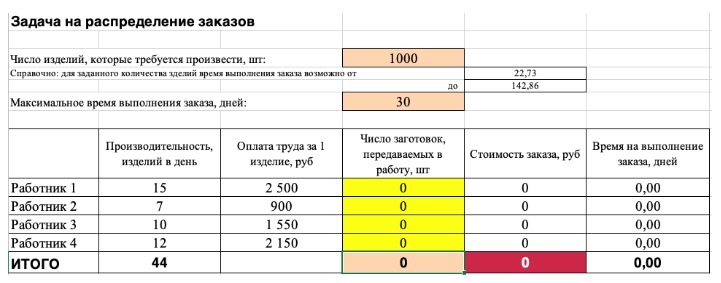
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).
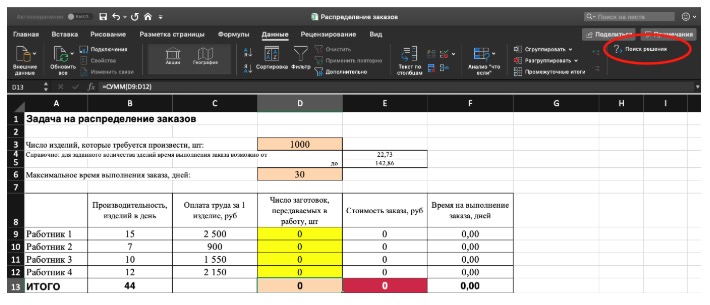
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).
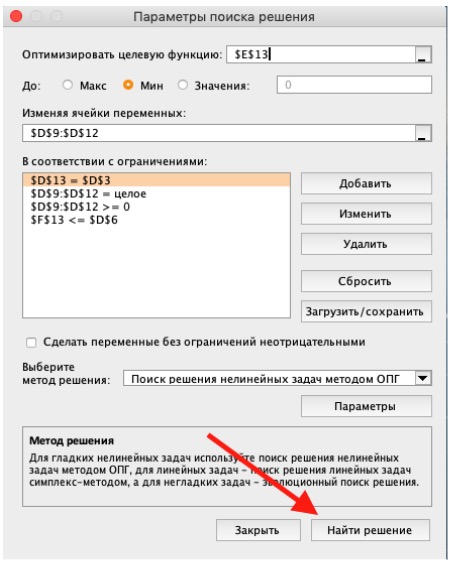
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.
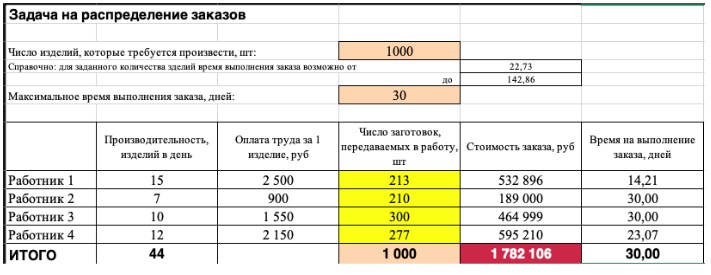
Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
Подбор слагаемых для нужной суммы


В реальной жизни эта задача может выглядеть по-разному.
- Например, мы выгрузили из интернет-банка все платежи, которые поступили на наш счет за последний месяц. Один из клиентов разбивает сумму своего платежа на несколько отдельных счетов и платит частями. Мы знаем общую сумму оплаты и количество счетов, но не знаем их сумм. Надо подобрать те суммы в истории платежей, которые дадут в общем заданное значение.
- У нас есть несколько рулонов стали (линолеума, бумаги…), из которых надо подобрать под заказ те, что дадут заданную длину.
- Блэкджек или в народе «очко». Надо набрать карты суммарной стоимостью максимально близкой к 21 баллу, но не превысить этот порог.
В некоторых случаях может быть известна разрешенная погрешность допуска. Она может быть как нулевой (в случае подбора счетов), так и ненулевой (в случае подбора рулонов), или ограниченной снизу или сверху (в случае блэкджека).
Давайте рассмотрим несколько способов решения такой задачи в Excel.
Способ 1. Надстройка Поиск решения (Solver)
Эта надстройка входит в стандартный набор пакета Microsoft Office вместе с Excel и предназначена, в общем случае, для решения линейных и нелинейных задач оптимизации при наличии списка ограничений. Чтобы ее подключить, необходимо:
- в Excel 2007 и новее зайти Файл — Параметры Excel — Надстройки — Перейти (File — Excel Options — Add-ins — Go)
- в Excel 2003 и старше — открыть меню Сервис — Надстройки (Tools — Add-ins)
и установить соответствующий флажок. Тогда на вкладке или в меню Данные (Data) появится нужная нам команда.
Чтобы использовать надстройку Поиск решения для нашей задачи необходимо будет слегка модернизировать наш пример, добавив к списку подбираемых сумм несколько вспомогательных ячеек и формул:
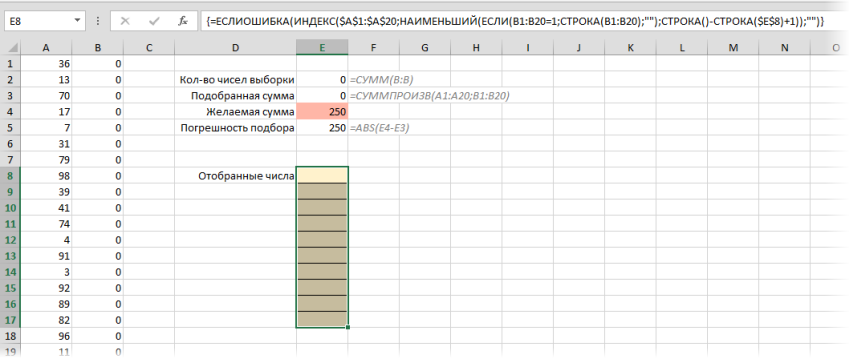
- Диапазон A1:A20 содержит наши числа, из которых мы будем выбирать нужные, чтобы «вписаться» в заданную сумму.
- Диапазон В1:B20 будет своего рода набором переключателей, т.е. будет содержать нули или единички, показывая, отбираем мы данное число в выборку или нет.
- В ячейке E2 стоит обычная автосумма всех единичек по столбцу B, подсчитывающая кол-во выбранных чисел.
- В ячейке E3 с помощью функции СУММПРОИЗВ (SUMPRODUCT) считается сумма попарных произведений ячеек из столбцов А и B (то есть A1*B1+A2*B2+A3*B3+…). Фактически, здесь подсчитывается сумма чисел из столбца А, отобранных единичками из столбца В.
- В розовую ячейку E4 пользователь вводит желаемую сумму для подбора.
- В ячейке E5 вычисляется абсолютное по модулю значение погрешности подбора с целью ее будущей минимизации.
- Все желтых ячейках Е8:E17 хотелось бы получить список отобранных чисел, т.е. тех чисел из столбца А, напротив которых в столбце В есть единички. Для этого необходимо выделить сразу все (!) желтые ячейки и в них ввести вот такую формулу массива:
=ЕСЛИОШИБКА(ИНДЕКС($A$1:$A$20;НАИМЕНЬШИЙ(ЕСЛИ(B1:B20=1;СТРОКА(B1:B20);»»);СТРОКА()-СТРОКА($E$8)+1));»»)
=IFERROR(INDEX($A$1:$A$20;SMALL(IF(B1:B20=1;ROW(B1:B20);»»);ROW()-ROW($E$8)+1));»»)
После ввода формулы ее необходимо ввести не как обычную формулу, а как формулу массива, т.е. нажать не Enter, а Ctrl+Shift+Enter. Похожая формула используется в примере о ВПР, выдающей сразу все найденные значения (а не только первое).
Теперь перейдем на вкладку (или в меню) Данные и запустим инструмент Поиск решения (Data — Solver):
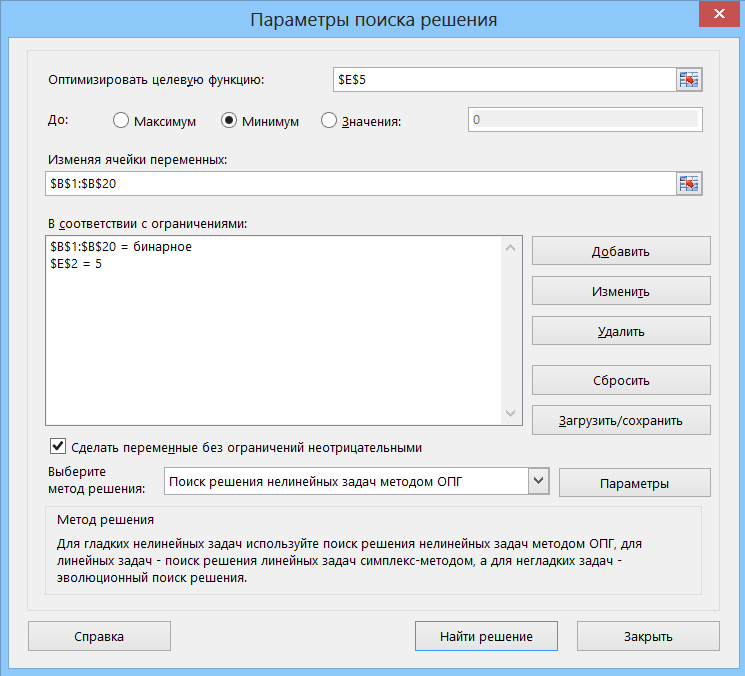
В открывшемся окне необходимо:
- Задать как целевую функцию (Target Cell) — ячейку вычисления погрешности подбора E5. Чуть ниже выбрать опцию — Минимум, т.к. мы хотим подобрать числа под заданную сумму с минимальной (а лучше даже нулевой) погрешностью.
- В качестве изменяемых ячеек переменных (Changing cells) задать диапазон столбца переключателей B1:B20.
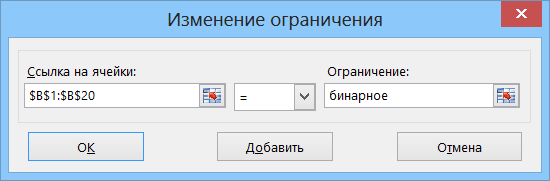
- С помощью кнопки Добавить (Add) создать дополнительное условие на то, что ячейки диапазона B1:B20 должны быть бинарными (т.е. содержать только 0 или 1):
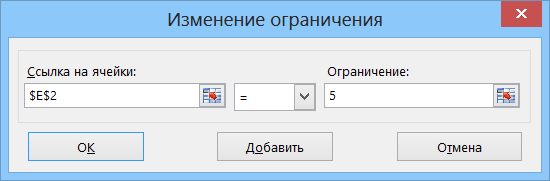
- С помощью той же кнопки, при необходимости, создать ограничение на количество чисел в выборке. Например, если мы знаем, что сумма была разбита на 5 счетов, то:
После ввода всех параметров и ограничений запускаем процесс подбора кнопкой Найти решение (Solve). Процесс подбора занимает от нескольких секунд до нескольких минут (в тяжелых случаях) и заканчивается появлением следующего окна:
Теперь можно либо оставить найденное решение подбора (Сохранить найденное решение), либо откатиться к прежним значениям (Восстановить исходные значения).
Необходимо отметить, что для такого класса задач существует не одно, а целое множество решений, особенно, если не приравнивать жестко погрешность к нулю. Поэтому запуск Поиска решения с разными начальными данными (т.е. разными комбинациями 0 и 1 в столбце В) может приводить к разным наборам чисел в выборках в пределах заданных ограничений. Так что имеет смысл прогнать эту процедуру несколько раз, произвольно изменяя переключатели в столбце В.
Найденные комбинации можно сохранять виде сценариев (кнопка Сохранить сценарий), чтобы вернуться к нем позднее с помощью команды Данные — Анализ «что-если» — Диспетчер сценариев (Data — What-If Analysis — Scenario Manager):
И весьма удобно будет вывести все найденные решения, сохраненные в виде сценариев, в одной сравнительной таблице с помощью кнопки Отчет (Summary):
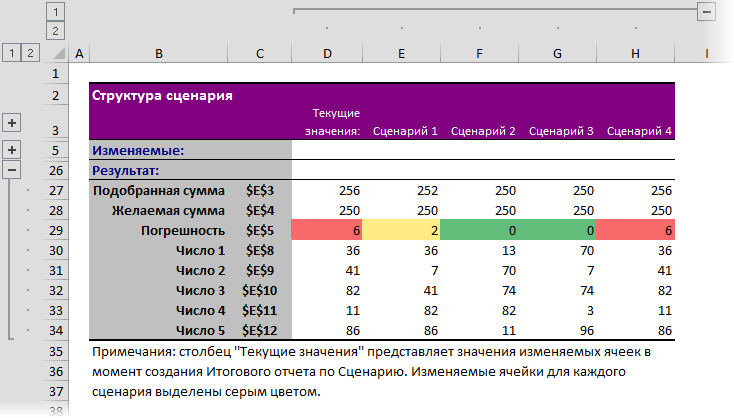
Способ 2. Макрос подбора
В этом способе всю работу делает макрос, который тупо перебирает случайные комбинации чисел, пока не наткнется на нужную сумму в пределах разрешенной погрешности. Добавлять столбец с нулями и единичками и формулы в этом случае не нужно.
Для использования макроса нажмите сочетание Alt+F11, в открывшемся окне редактора Visual Basic вставьте новый модуль через меню Insert — Module и скопируйте туда этот код:
Sub Combinator()
Dim Data() As Variant, Selected() As Variant
Dim goal As Double, sel_count As Integer, prec As Double
Const LIMIT = 1000000
prec = Range("D5").Value
sel_count = Range("D2").Value
goal = Range("D4").Value
Set OutRange = Range("D8")
Set InputRange = Range("A1", Range("A1").End(xlDown))
input_count = InputRange.Cells.Count
Data = InputRange.Value
ReDim Selected(1 To sel_count) As Variant
NewTry:
For j = 1 To sel_count
Start:
RandomIndex = Int(Rnd * input_count + 1)
RandomValue = Data(RandomIndex, 1)
'начиная со второго элемента дополнительно проверяем, чтобы такой уже не был выбран
If j > 1 Then
For k = 1 To j - 1
If Selected(k) = RandomValue Then GoTo Start
Next k
End If
Selected(j) = RandomValue
Next j
If Abs(WorksheetFunction.Sum(Selected) - goal) <= prec Then
Range("D3").Value = WorksheetFunction.Sum(Selected)
MsgBox "Подбор завершен. Необходимая точность достигнута."
Range(OutRange, OutRange.End(xlDown)).ClearContents
OutRange.Resize(sel_count, 1).Value = Application.Transpose(Selected)
Exit Sub
Else
iterations = iterations + 1
If iterations > LIMIT Then
MsgBox "Достигнут лимит попыток. Решение не найдено."
Exit Sub
Else
GoTo NewTry
End If
End If
End Sub
Аналогично первому способу, запуская макрос несколько раз, можно получать разные наборы подходящих чисел.
P.S. Сейчас набегут энтузиасты с мехмата МГУ с криками «Тупой перебор — это неэстетично!» Да, я в курсе, что прямой перебор вариантов — это не самый оптимальный способ поиска. Да, существует много умных алгоритмов поиска решения таких задач, которые сокращают время поиска и находят нужную комбинацию заметно быстрее. Могу даже рассказать про парочку. Но мне на данном этапе существующей скорости «тупого перебора» вполне достаточно — обработка массива из 1000 ячеек идет меньше секунды. Готов подождать 
Ссылки по теме
- Оптимизация бизнес-модели с помощью надстройки Поиск решения (Solver)
- Что такое макросы, куда и как вставлять код макросов на VBA
Solver is a Microsoft Excel add-in program you can use for optimization in what-if analysis.
According to O’Brien and Marakas, optimization analysis is a more complex extension of goal-seeking analysis. Instead of setting a specific target value for a variable, the goal is to find the optimum value for one or more target variables, under certain constraints. Then, one or more other variables are changed repeatedly, subject to the specified constraints, until you discover the best values for the target variables.
In Excel, you can use Solver to find an optimal value (maximum or minimum, or a certain value) for a formula in one cell called the objective cell, subject to certain constraints or limits, on the values of other formula cells on the worksheet.
This means that the Solver works with a group of cells called decision variables that are used in computing the formulas in the objective and constraint cells. Solver adjusts the values in the decision variable cells to satisfy the limits on constraint cells and produce the result you want for the objective cell.
You can use Solver to find optimal solutions for diverse problems such as −
-
Determining the monthly product mix for a drug manufacturing unit that maximizes the profitability.
-
Scheduling workforce in an organization.
-
Solving transportation problems.
-
Financial planning and budgeting.
Activating Solver Add-in
Before you proceed with finding solution for a problem with Solver, ensure that the Solver Add-in is activated in Excel as follows −
- Click the DATA tab on the Ribbon. The Solver command should appear in the Analysis group as shown below.
In case you do not find the Solver command, activate it as follows −
- Click the FILE tab.
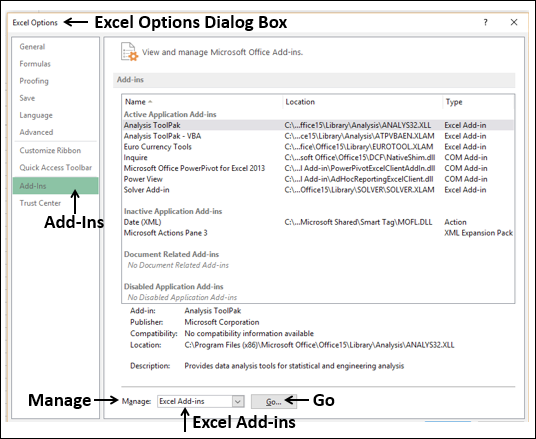
- Click Options in the left pane. Excel Options dialog box appears.
- Click Add-Ins in the left pane.
- Select Excel Add-Ins in the Manage box and click Go.
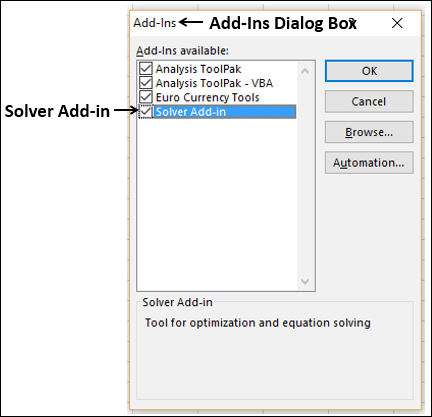
The Add-Ins dialog box appears. Check Solver Add-in and click Ok. Now, you should be able to find the Solver command on the Ribbon under the DATA tab.
Solving Methods used by Solver
You can choose one of the following three solving methods that Excel Solver supports, based on the type of problem −
LP Simplex
Used for linear problems. A Solver model is linear under the following conditions −
-
The target cell is computed by adding together the terms of the (changing cell)*(constant) form.
-
Each constraint satisfies the linear model requirement. This means that each constraint is evaluated by adding together the terms of the (changing cell)*(constant) form and comparing the sums to a constant.
Generalized Reduced Gradient (GRG) Nonlinear
Used for smooth nonlinear problems. If your target cell, any of your constraints, or both contain references to changing cells that are not of the (changing cell)*(constant) form, you have a nonlinear model.
Evolutionary
Used for smooth nonlinear problems. If your target cell, any of your constraints, or both contain references to changing cells that are not of the (changing cell)*(constant) form, you have a nonlinear model.
Understanding Solver Evaluation
The Solver requires the following parameters −
- Decision Variable Cells
- Constraint Cells
- Objective Cells
- Solving Method
Solver evaluation is based on the following −
-
The values in the decision variable cells are restricted by the values in the constraint cells.
-
The calculation of the value in the objective cell includes the values in the decision variable cells.
-
Solver uses the chosen Solving Method to result in the optimal value in the objective cell.
Defining a Problem
Suppose you are analyzing the profits made by a company that manufactures and sells a certain product. You are asked to find the amount that can be spent on advertising in the next two quarters subject to a maximum of 20,000. The level of advertising in each quarter affects the following −
- The number of units sold, indirectly determining the amount of sales revenue.
- The associated expenses, and
- The profit.
You can proceed to define the problem as −
- Find Unit Cost.
- Find the advertising cost per Unit.
- Find Unit Price.
Next, set the cells for the required calculations as given below.
As you can observe, the calculations are done for Quarter1 and Quarter2 that are in consideration are −
-
No. of units available for sale in Quarter1 is 400 and in Quarter2 is 600 (cells – C7 and D7).
-
The initial values for advertising budget are set as 10000 per Quarter (Cells – C8 and D8).
-
No. of units sold is dependent on the advertising cost per unit and hence is budget for the quarter / Adv. Cost per unit. Note that we have used the Min function to take care to see that the no. of units sold in <= no. of units available. (Cells – C9 and D9).
-
Revenue is calculated as Unit Price * No. of Units sold (Cells – C10 and D10).
-
Expenses is calculated as Unit Cost * No. of Units Available + Adv. Cost for that quarter (Cells – C11 and D12).
-
Profit is Revenue – Expenses (Cells C12 and D12).
-
Total Profit is Profit in Quarter1 + Profit in Quarter2 (Cell – D3).
Next, you can set the parameters for Solver as given below −
As you can observe, the parameters for Solver are −
-
Objective cell is D3 that contains Total Profit, which you want to maximize.
-
Decision Variable cells are C8 and D8 that contain the budgets for the two quarters – Quarter1 and Quarter2.
-
There are three Constraint cells — C14, C15 and C16.
-
Cell C14 that contains total budget is to set the constraint of 20000 (cell D14).
-
Cell C15 that contains the no. of units sold in Quarter1 is to set the constraint of <= no. of units available in Quarter1 (cell D15).
-
Cell C16 that contains the no. of units sold in Quarter2 is to set the constraint of <= no. of units available in Quarter2 (cell D16).
-
Solving the Problem
The next step is to use Solver to find the solution as follows −
Step 1 − Go to DATA > Analysis > Solver on the Ribbon. The Solver Parameters dialog box appears.
Step 2 − In the Set Objective box, select the cell D3.
Step 3 − Select Max.
Step 4 − Select range C8:D8 in the By Changing Variable Cells box.
Step 5 − Next, click the Add button to add the three constraints that you have identified.
Step 6 − The Add Constraint dialog box appears. Set the constraint for total budget as given below and click Add.
Step 7 − Set the constraint for total no. of units sold in Quarter1 as given below and click Add.
Step 8 − Set the constraint for total no. of units sold in Quarter2 as given below and click OK.
The Solver Parameters dialog box appears with the three constraints added in box –Subject to the Constraints.
Step 9 − In the Select a Solving Method box, select Simplex LP.
Step 10 − Click the Solve button. The Solver Results dialog box appears. Select Keep Solver Solution and click OK.
The results will appear in your worksheet.
As you can observe, the optimal solution that produces maximum total profit, subject to the given constraints, is found to be the following −
- Total Profit – 30000.
- Adv. Budget for Quarter1 – 8000.
- Adv. Budget for Quarter2 – 12000.
Stepping through Solver Trial Solutions
You can step through the Solver trial solutions, looking at the iteration results.
Step 1 − Click the Options button in the Solver Parameters dialog box.
The Options dialog box appears.
Step 2 − Select the Show Iteration Results box and click OK.
Step 3 − The Solver Parameters dialog box appears. Click Solve.
Step 4 − The Show Trial Solution dialog box appears, displaying the message — Solver paused, current solution values displayed on worksheet.
As you can observe, the current iteration values are displayed in your working cells. You can either stop the Solver accepting the current results or continue with the Solver from finding solution in further steps.
Step 5 − Click Continue.
The Show Trial Solution dialog box appears at every step and finally after the optimal solution is found, Solver Results dialog box appears. Your worksheet is updated at every step, finally showing the result values.
Saving Solver Selections
You have the following saving options for the problems that you solve with Solver −
-
You can save the last selections in the Solver Parameters dialog box with a worksheet by saving the workbook.
-
Each worksheet in a workbook can have its own Solver selections, and all of them will be saved when you save the workbook.
-
You can also define more than one problem in a worksheet, each with its own Solver selections. In such a case, you can load and save problems individually with the Load/Save in the Solver Parameters dialog box.
-
Click the Load/Save button. The Load/Save dialog box appears.
-
To save a problem model, enter the reference for the first cell of a vertical range of empty cells in which you want to place the problem model. Click Save.
-
-
The problem model (the Solver Parameters set) appears starting at the cell that you have given as the reference.
-
To load a problem model, enter the reference for the entire range of cells that contains the problem model. Then, click on the Load button.





















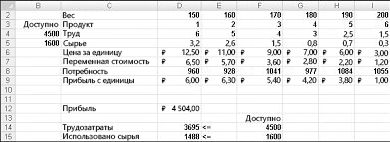
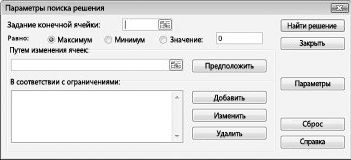
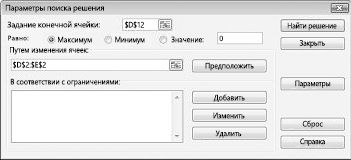
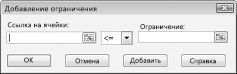
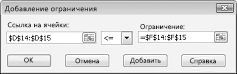
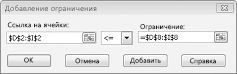
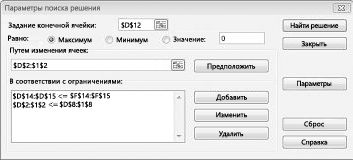
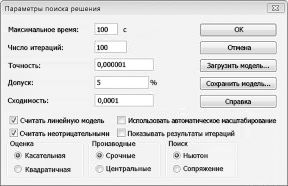
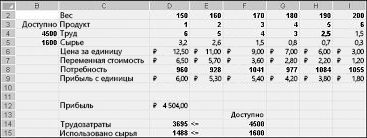
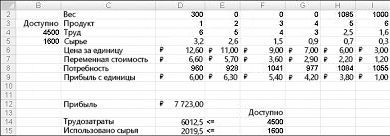

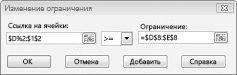















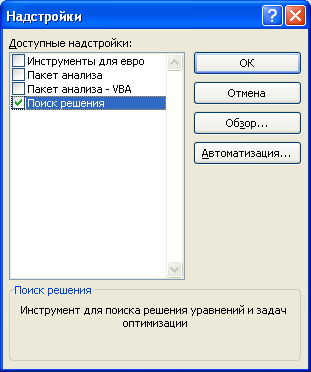
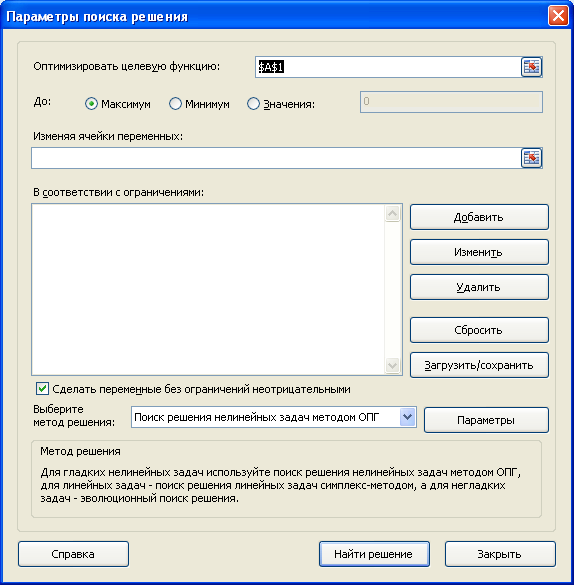
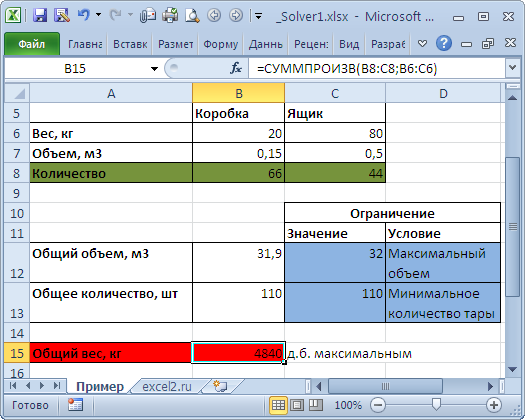
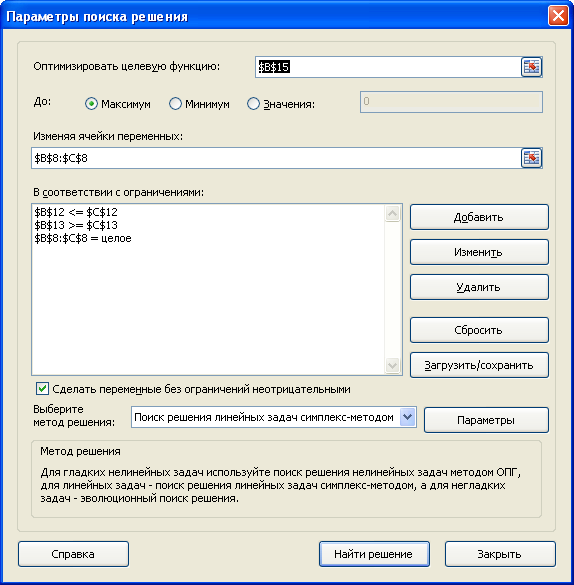
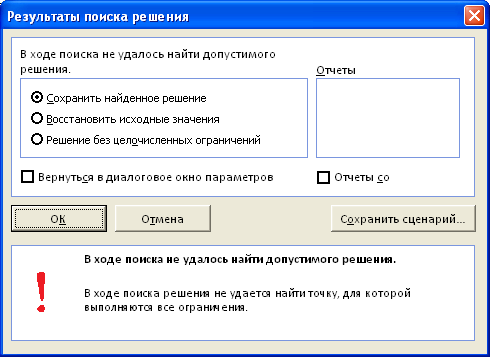
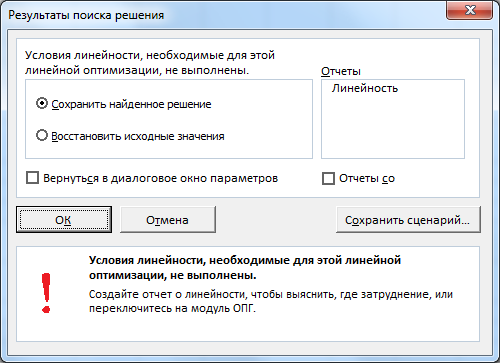
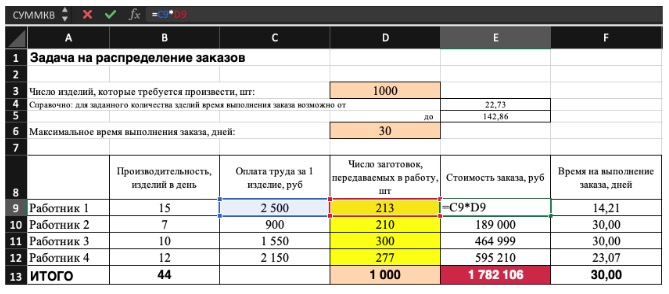
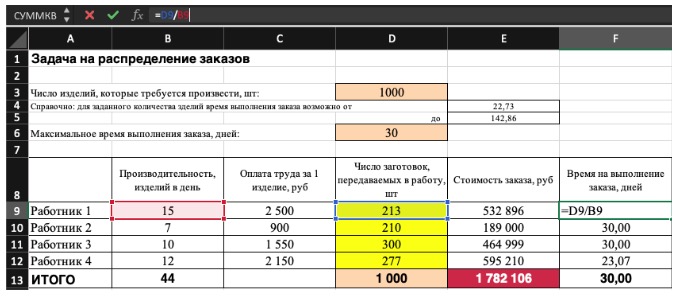
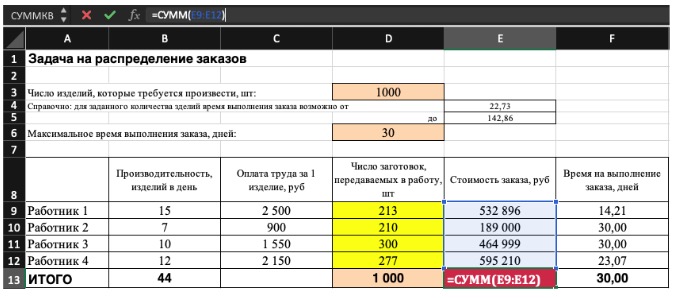
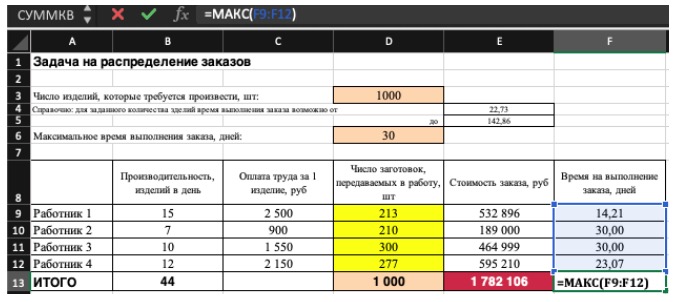













 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.