«Подбор параметра» — ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».
В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.
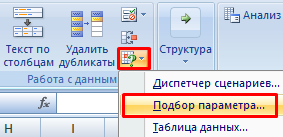
Где находится «Подбор параметра» в Excel
Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.
Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.
Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.
Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» — «Анализ «Что-Если»» — «Подбор параметра».
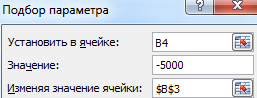
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» — абсолютная ссылка на ячейку с искомым параметром ($B$3).
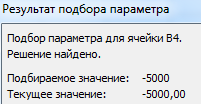
После нажатия ОК на экране появится окно результата.
Чтобы сохранить, нажимаем ОК или ВВОД.
Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.
Решение уравнений методом «Подбора параметров» в Excel
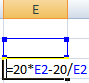
Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.
В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.
А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.
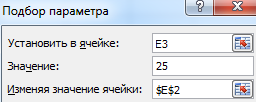
Запускам инструмент и заполняем поля:
«Установить в ячейке» — Е3 (ячейка с формулой);
«Значение» — 25 (результат уравнения);
«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).
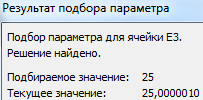
Результат функции:
Найденный аргумент отобразится в зарезервированной для него ячейке.
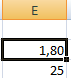
Решение уравнения: х = 1,80.
Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.
Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.
Примеры подбора параметра в Excel
Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.
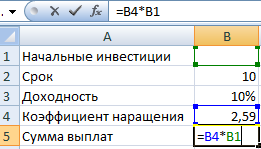
Пример 1. Метод подбора начальной суммы инвестиций (вклада).
Известные параметры:
- срок – 10 лет;
- доходность – 10%;
- коэффициент наращения – расчетная величина;
- сумма выплат в конце срока – желаемая цифра (500 000 рублей).
Внесем входные данные в таблицу:
Начальные инвестиции – искомая величина. В ячейке В4 (коэффициент наращения) – формула =(1+B3)^B2.
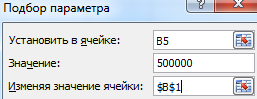
Вызываем окно команды «Подбор параметра». Заполняем поля:
После выполнения команды Excel выдает результат:
Чтобы через 10 лет получить 500 000 рублей при 10% годовых, требуется внести 192 772 рубля.
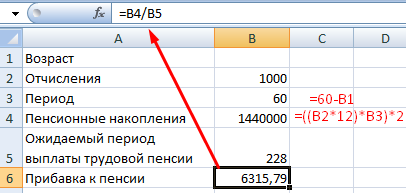
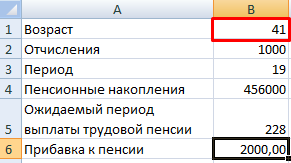
Пример 2. Рассчитаем возможную прибавку к пенсии по старости за счет участия в государственной программе софинансирования.
Входные данные:
- ежемесячные отчисления – 1000 руб.;
- период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
- пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза);
- ожидаемый период выплаты трудовой пенсии – 228 мес.;
- желаемая прибавка к пенсии – 2000 руб.
С какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей:
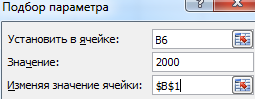
- Ячейка с формулой расчета прибавки к пенсии активна – вызываем команду «Подбор параметра». Заполняем поля в открывшемся меню.
- Нажимаем ОК – получаем результат подбора.
Чтобы получить прибавку в 2000 руб., необходимо ежемесячно переводить на накопительную часть пенсии по 1000 рублей с 41 года.
Функция «Подбор параметра» работает правильно, если:
- значение желаемого результата выражено формулой;
- все формулы написаны полностью и без ошибок.
Поиск значений в списке данных
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Предположим, что вы хотите найти расширение телефона сотрудника, используя его номер эмблемы или правильную ставку комиссионных за объем продаж. Вы можете искать данные для быстрого и эффективного поиска определенных данных в списке, а также для автоматической проверки правильности данных. После поиска данных можно выполнить вычисления или отобразить результаты с возвращаемой величиной. Существует несколько способов поиска значений в списке данных и отображения результатов.
Что необходимо сделать
-
Точное совпадение значений по вертикали в списке
-
Подыыывка значений по вертикали в списке с помощью приблизительного совпадения
-
Подстановка значений по вертикали в списке неизвестного размера с использованием точного совпадения
-
Точное совпадение значений по горизонтали в списке
-
Подыыывка значений по горизонтали в списке с использованием приблизительного совпадения
-
Создание формулы подступа с помощью мастера подметок (только в Excel 2007)
Точное совпадение значений по вертикали в списке
Для этого можно использовать функцию ВLOOKUP или сочетание функций ИНДЕКС и НАЙТИПОЗ.
Примеры ВРОТ

Дополнительные сведения см. в этой информации.
Примеры индексов и совпадений
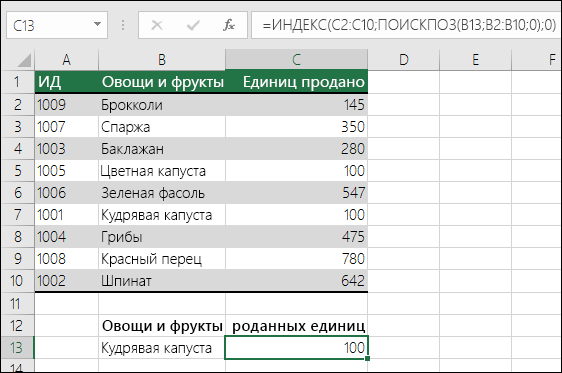
Что означает:
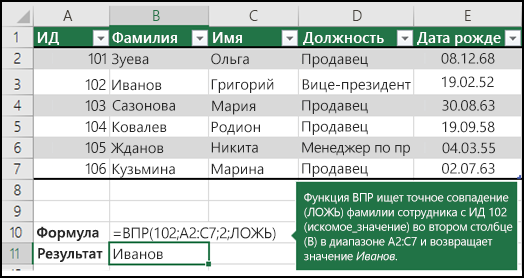
=ИНДЕКС(нужно вернуть значение из C2:C10, которое будет соответствовать ПОИСКПОЗ(первое значение «Капуста» в массиве B2:B10))
Формула ищет в C2:C10 первое значение, соответствующее значению «Ольга» (в B7), и возвращает значение в C7(100),которое является первым значением, которое соответствует значению «Ольга».
Дополнительные сведения см. в функциях ИНДЕКС иФУНКЦИЯ MATCH.
К началу страницы
Подыыывка значений по вертикали в списке с помощью приблизительного совпадения
Для этого используйте функцию ВЛВП.
Важно: Убедитесь, что значения в первой строке отсортировали в порядке возрастания.
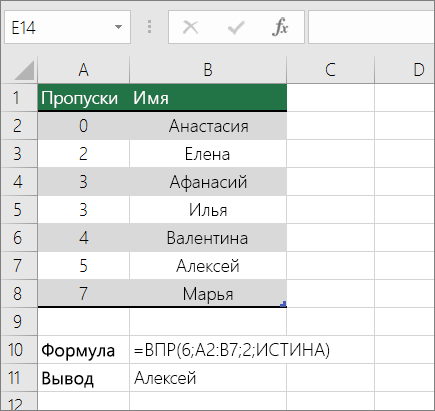
В примере выше ВРОТ ищет имя учащегося, у которого 6 просмотров в диапазоне A2:B7. В таблице нет записи для 6 просмотров, поэтому ВРОТ ищет следующее самое высокое совпадение меньше 6 и находит значение 5, связанное с именем Виктор,и таким образом возвращает Его.
Дополнительные сведения см. в этой информации.
К началу страницы
Подстановка значений по вертикали в списке неизвестного размера с использованием точного совпадения
Для этого используйте функции СМЕЩЕНИЕ и НАЙТИВМЕСЯК.
Примечание: Используйте этот подход, если данные в диапазоне внешних данных обновляются каждый день. Вы знаете, что цена находится в столбце B, но вы не знаете, сколько строк данных возвращает сервер, а первый столбец не отсортировали по алфавиту.
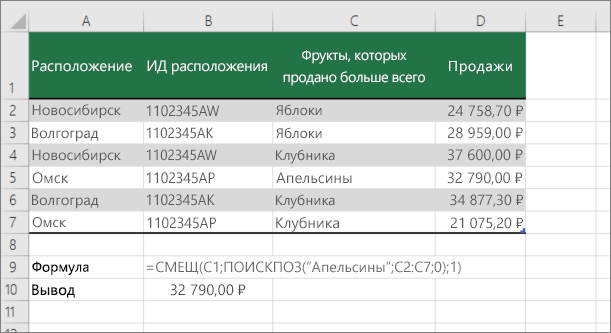
C1 — это левые верхние ячейки диапазона (также называемые начальной).
MATCH(«Оранжевая»;C2:C7;0) ищет «Оранжевые» в диапазоне C2:C7. В диапазон не следует включать запускаемую ячейку.
1 — количество столбцов справа от начальной ячейки, из которых должно быть возвращено значение. В нашем примере возвращается значение из столбца D, Sales.
К началу страницы
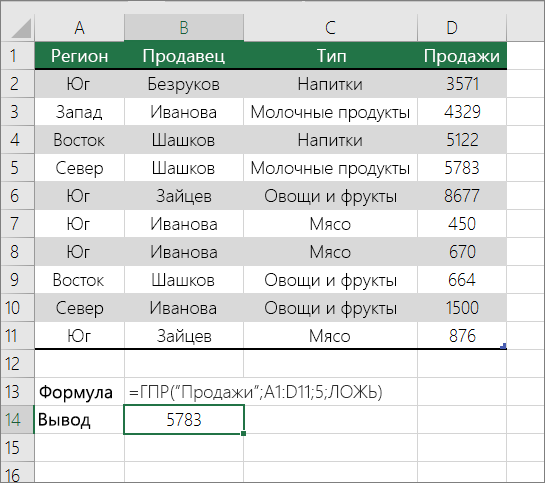
Точное совпадение значений по горизонтали в списке
Для этого используйте функцию ГГПУ. См. пример ниже.
Г ПРОСМОТР ищет столбец «Продажи» и возвращает значение из строки 5 в указанном диапазоне.
Дополнительные сведения см. в сведениях о функции Г ПРОСМОТР.
К началу страницы
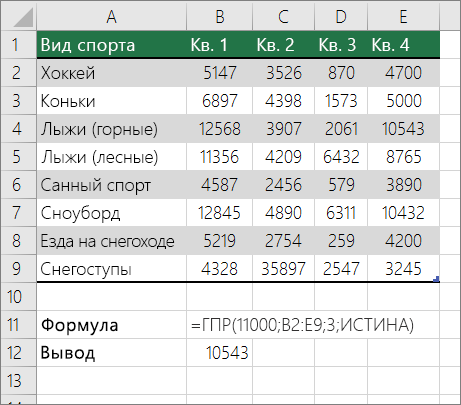
Подыыывка значений по горизонтали в списке с использованием приблизительного совпадения
Для этого используйте функцию ГГПУ.
Важно: Убедитесь, что значения в первой строке отсортировали в порядке возрастания.
В примере выше ГЛЕБ ищет значение 11000 в строке 3 указанного диапазона. Она не находит 11000, поэтому ищет следующее наибольшее значение меньше 1100 и возвращает значение 10543.
Дополнительные сведения см. в сведениях о функции Г ПРОСМОТР.
К началу страницы
Создание формулы подступа с помощью мастера подметок (толькоExcel 2007 )
Примечание: В Excel 2010 больше не будет надстройки #x0. Эта функция была заменена мастером функций и доступными функциями подменю и справки (справка).
В Excel 2007 создается формула подытов на основе данных на основе данных на основе строк и столбцов. Если вы знаете значение в одном столбце и наоборот, мастер под поисков помогает находить другие значения в строке. В формулах, которые он создает, используются индекс и MATCH.
-
Щелкните ячейку в диапазоне.
-
На вкладке Формулы в группе Решения нажмите кнопку Под поиск.
-
Если команда Подытов недоступна, вам необходимо загрузить мастер под надстройка подытогов.
Загрузка надстройки «Мастер подстройок»
-
Нажмите кнопку Microsoft Office
, выберите Параметры Excel и щелкните категорию Надстройки.
-
В поле Управление выберите элемент Надстройки Excel и нажмите кнопку Перейти.
-
В диалоговом окне Доступные надстройки щелкните рядом с полем Мастер подстрок инажмите кнопку ОК.
-
Следуйте инструкциям мастера.
К началу страницы
Нужна дополнительная помощь?
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12704 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Ищем оптимальное решение задачи с неизвестными параметрами в Excel
«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
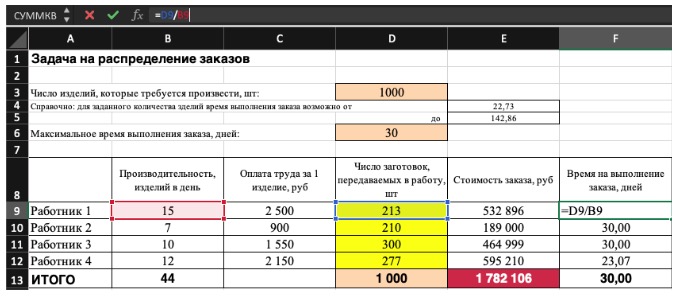
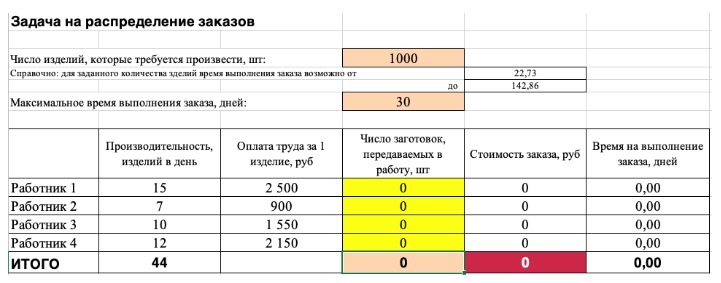
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.
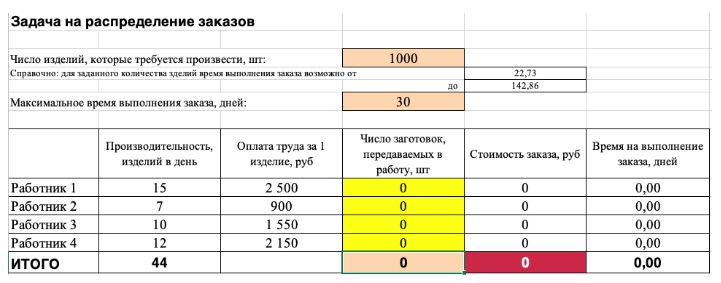
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
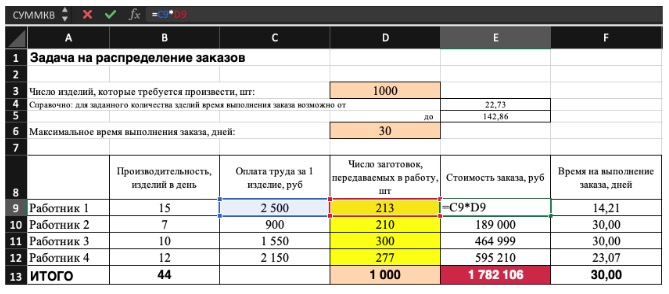
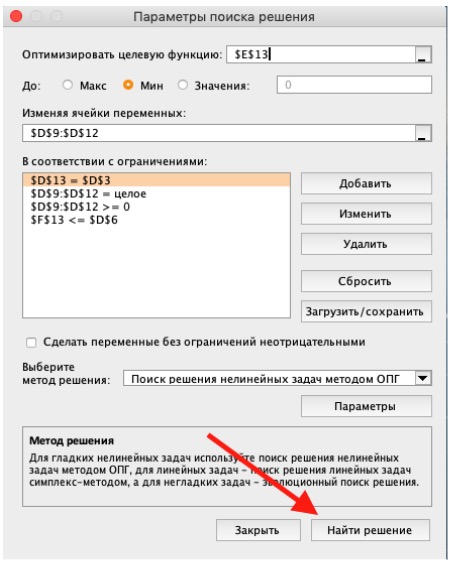
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).
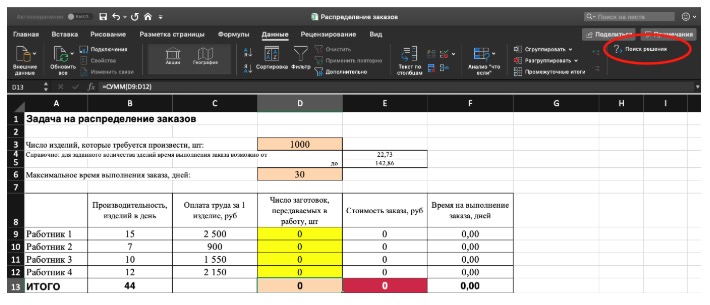
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
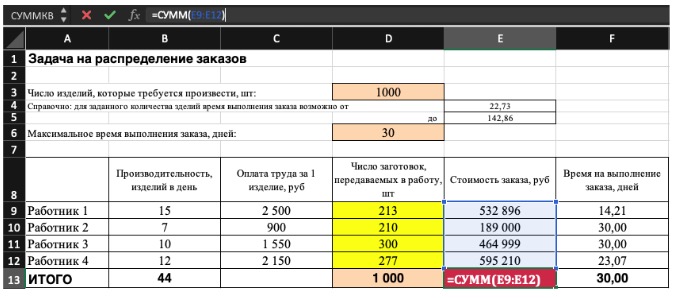
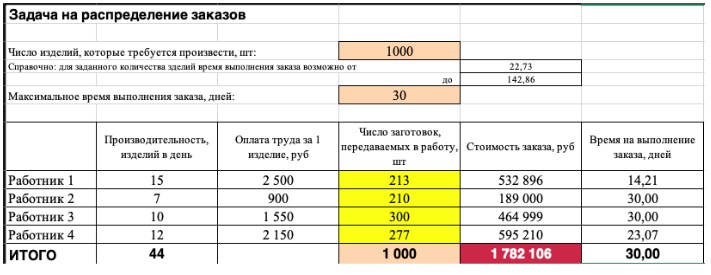
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.
Подписаться на карьерную рассылку
Подписывайтесь на рассылку и получайте карьерные советы — от выбора индустрии и компании до лайфхаков по самоорганизации и развитию коммуникативных навыков.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://changellenge.com/article/ishchem-optimalnoe-reshenie-zadachi-s-neizvestnymi-parametrami-v-excel-/
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
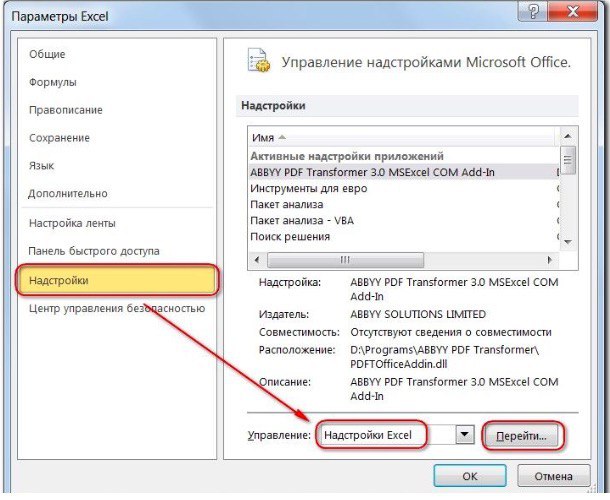
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
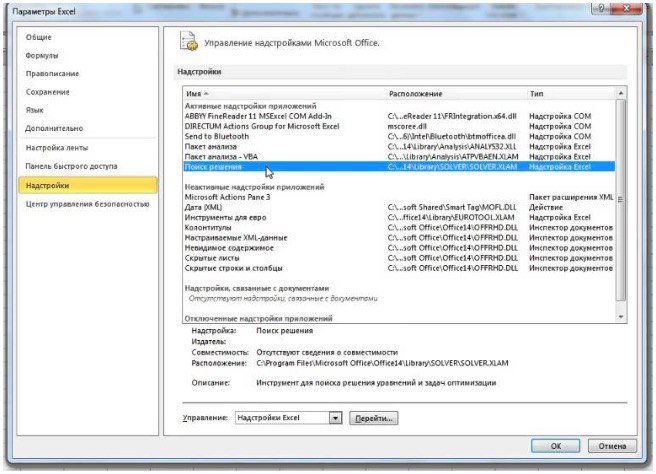
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
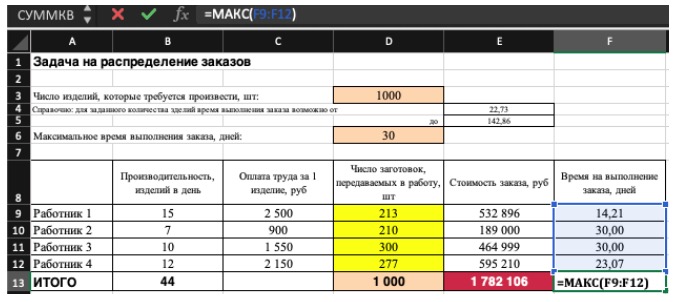
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.
Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
«Подбор параметра» является удобной надстройкой «Поиска решения» в Excel, однако имеет некоторые функциональные ограничения. Он используется, как правило, в частных случаях и подходит для быстрого поиска нужных параметров.
Что за функция, зачем нужна?
Метод предназначен для случаев, когда нужно найти неизвестное значение в одиночной формуле, исходя из уже известного результата. То есть все составные части формулы (результат и входные данные) известны, при этом решение не может быть сформулировано полностью из-за отсутствия одного из входных параметров.
Функционал по поиску решений подобного рода задач встроен в программу Excel в качестве стандартного расширения, поэтому пользователю не нужно использовать сторонние библиотеки. Достаточно будет сделать несколько кликов по кнопкам расположенным на главной панели и программа сама определит недостающий элемент.
Использование функции
В Microsoft Excel подобные задачи решаются с помощью стандартного меню. Подбор параметра в Excel 2007, 2010, 2013 и новее находится во вкладке «Данные», в группе «Работы с данными».
Следующий шаг – заполнение полей в появившемся окне. Первое поле предназначено для заданной формулы, второе для целевого значения, в третье для адреса элемента вывода (более подробно это будет разобрано далее на конкретных примерах).
Третий шаг это подтверждение операции и вывод результата.
Пример использования функции
Для большей наглядности функцию подбора параметров в Экселе лучше сразу рассматривать на примере.
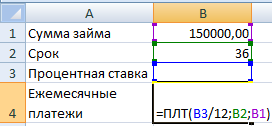
Определить — какая будет процентная ставка (по займу). Входными данными являются срок (36) и сумма (150000). Для начала их нужно отобразить в табличном представлении.
Не определена только процентная ставка. Чтобы посчитать ежемесячный, платеж следует воспользоваться функцией подбора параметров. После внесения всех данных задачи в таблицу, нужно переключиться во вкладку, отвечающую за работу с данными. Затем найти группу инструментов по работе с данными и в выпадающем списке «Анализ “что если”» выбрать опцию соответствующую подбору параметра.
Во всплывающем окошке в поле «Установить в ячейке» должна быть указана ссылка ячейки, в которой содержится основная формула (B4). В текстовое поле «Значение» необходимо ввести предположительную сумму ежемесячного платежа. К примеру, -5 000 (знак «минус» обозначает, что денежная сумма будет отдана). В третьем поле «Изменяя значение ячейки» – следует списать ссылку табличного элемента, в которой будет выведен искомый параметр ($B$3).
После клика по кнопке «ОК» в новом окне отобразится результат подсчета.
Для подтверждения операции следует кликнуть по соответствующей кнопке.
Функция подбора неизвестного параметра будет перебирать значение искомого элемента до момента получения результата формулы. Команда выдаст только одно решение.
Решение уравнений
Подбор параметра также используют, если нужно найти какое-либо из значений в заданном уравнении. В качестве примера воспользуемся следующим выражением: 2*а+3*b=x, где x=21, а=3, неизвестная переменная — b.
Для начала нужно заполнить таблицу.
Параметры а и b следует вводить в ячейки B2 и B3 соответственно. Табличный элемент B4 отведен для формулы =2*B2+3*B3. Переменная x в ячейке B5 указана в качестве примечания.
Необходимо выделить ячейку, в которой вписана формула (B4) и вызвать целевую функцию по определению параметра (инструкция вызова подробно изложена в предыдущем примере).
Затем вписать во второе поле (значение) результат (21), а в третье адрес ячейки B3, поскольку именно она будет изменяться.
Подтвердить действие кликом по соответствующей кнопке.
В результате выполнения команды переменной b подобралось значение 5.
Конечно, искомый параметр можно определить в ручном режиме, путем последовательного ввода в ячейку B3 значений до момента пока оно не совпадет с целевым. Однако зачастую формулы имеют более сложную структуру, поэтому решить уравнение не используя автоматический подбор, будет сложно.
Для закрепления материала решим еще одно уравнение – 15*x+18*x=46. Для начала нужно записать формулу в ячейку B2. Вместо x необходимо указать ссылку на табличный элемент, где будет отображен результат, в данном случае A2.
Затем нужно запустить команду по высчитыванию параметра тем методом, который уже был описан ранее.
Во всплывающем окне, в первом верхнем текстовом поле нужно вписать ссылку ячейки, содержащей формулу (B2). Во втором поле — число из уравнения после знака равно, то есть 46. В третьем поле должна быть ссылка на ячейку со значением x, в данном случае это A2.
После того как все поля заполнены, нужно подтвердить операцию. На экране в новом всплывающем окне отобразиться правильное решение уравнения. Значение x будет равно 1,39393939393939.
После изучения функциональных преимуществ и способов применения функции подбора параметра, пользователю программы Excel будет очень просто определять недостающие элементы. С помощью этой функции можно производить как табличные вычисления, так и решать уравнения с одним неизвестным.


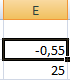

 , выберите Параметры Excel и щелкните категорию Надстройки.
, выберите Параметры Excel и щелкните категорию Надстройки.