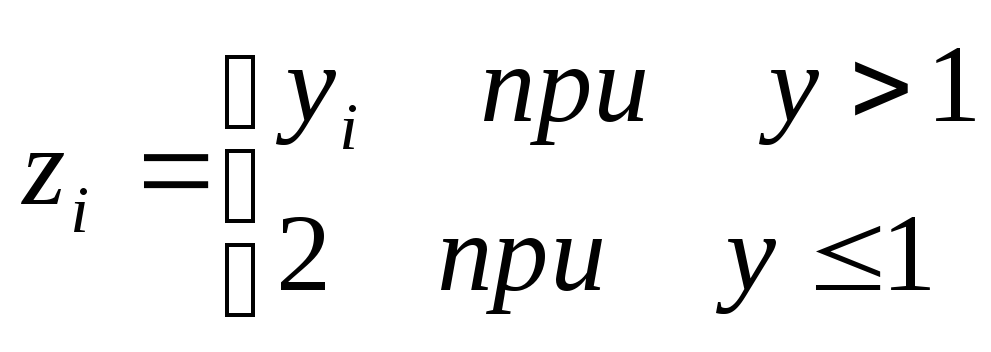Как найти корни трансцендентного уравнения в excel - Word и Excel

Трансцендентные уравнения? «Подбор параметра» в Excel!

Нелинейные, трансцендентные уравнения функции одной переменной – это уравнения вида f (x) = 0, в которых нельзя найти алгебраическими методами корни. Функция f (x) – это, как правило, достаточно сложная и громоздкая функция, содержащая в своем составе.

. тригонометрические, логарифмические, степенные и иные нелинейные функции с различной глубиной вложенности. Например: f (x) = sin (3,14^x) + cos (x) = 0. Уравнения такого вида решаются численными методами.

В этой статье я постараюсь доступно и кратко рассказать и показать на примерах, как и когда такие задачи возникают и как их сегодня быстро и просто можно решать в Excel.

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили.

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.

Трансцендентные уравнения. Два метода решения в Excel.

Если у вас на компьютере нет программы MS Excel, то расчеты можно выполнить в программе OOo Calc из бесплатного пакета Open Office.

Задач, которые требуют для получения ответа составления и решения трансцендентных уравнений, вокруг нас очень много. Это — задачи и физики, и теплотехники, и астрономии, и элементарной геометрии в обычной жизни… Инженерам-конструкторам и программистам в повседневной работе необходимо уметь составлять и быстро решать численными методами нелинейные уравнения. На мой взгляд — это один из критериев профессионализма. Более того, уравнения, которые решаются аналитически, сегодня иногда гораздо проще и быстрее при наличии вычислительной техники решить численными методами, поэтому нужно уметь это делать.

Вычисление угла зацепления зубчатой передачи методом Ньютона (методом касательных)

Рассмотрим пример из статьи «Расчет геометрии зубчатой передачи». Необходимо найти угол зацепления зубчатой передачи atw . Я обещал в той статье рассказать, как это делается. Выполняю обещание.

Если расстояние между центрами колеса и шестерни не задано, то угол зацепления можно вычислить путем решения трансцендентного уравнения:

inv ( atw )=tg ( atw ) — atw =2* xs *tg ( a )/( z2 + T * z1 )+ tg ( at ) — at

Подставив данные из примера, рассмотренного в вышеупомянутой статье, получим после преобразований следующее уравнение:

inv ( atw )=0,020910

f ( atw )=tg ( atw )— atw -0,020910=0

Используем метод Ньютона, потому что взять производную представленной выше функции элементарно просто, а итерационная формула очень проста и компактна:

f’( atw )=1/(cos ( atw ))^2—1

atw (i+1) = atw i — f ( atw ) i/ f’( atw ) i

Открываем файл Excel и начинаем работу.

Исходные данные будем традиционно писать в ячейки со светло-бирюзовой заливкой. Результаты расчетов будем считывать в ячейках со светло-желтой заливкой.

1. Инволюту угла зацепления inv( atw ) заносим

в ячейку D3: 0,020910

2. Значение угла зацепления в нулевом приближении atw 0 в радианах записываем

3. Итерационную формулу atw (i+1)= atw i— f( atw )i/ f’( atw )i заносим

в D5: =D4- (TAN (D4) -D4-$D$3)/(1/(COS (D4))^2-1) =0,591706

atw 1= atw 0- (tg ( atw 0) — atw 0- inv ( atw ))/(1/(cos ( atw 0))^2-1)

и копируем в ячейки D6… D14

4. Видим, что уже после шестой итерации угол зацепления atw в радианах вычислен с нулевой абсолютной и относительной ошибкой:

atw =D13- (TAN (D13) -D13-$D$3)/(1/(COS (D13))^2-1) =0,389140

Решение найдено, расчет в Excel завершен!

Решение задачи ландшафтного дизайна с помощью сервиса «Подбор параметра» в Excel

Задача:

Вдоль отмостки стены дома длиной 14 метров необходимо разбить цветник в виде сегмента круга площадью ровно 16 квадратных метров. На сколько метров цветник будет отстоять от края отмостки по центру стены? Каким радиусом необходимо выполнить границу цветника?

1. Длину отмостки стены дома — хорды сегмента круга x в метрах записываем

в ячейку D17: 14,000

2. Площадь цветника – сегмента круга S в квадратных метрах вписываем

в D18: 16,000

3. Предположительное произвольное (не нулевое) значение центрального угла сегмента a в радианах пишем

Трансцендентное уравнение a / sin( a /2 ) -2*cos ( a /2) — (8* S / x ^2) *sin( a /2)=0 вводим

в объединенную ячейку E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2)

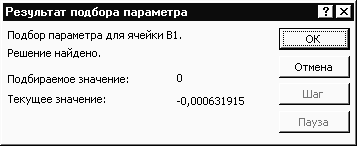
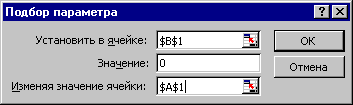
Включаем сервис «Подбор параметра» в Excel: «Сервис» – «Подбор параметра». Пишем в появившемся окне все как на рисунке слева и нажимаем кнопку OK.

В появившемся новом окне видим, что решение найдено, снова нажимаем на кнопку OK.

Считываем искомое значение центрального угла сегмента a в радианах

в D19: 0,950057

При этом видим, что значение трансцендентного уравнения равно нулю; считываем

в объединенной ячейке E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2) =0

4. Радиус наружной границы цветника – радиус сегмента круга r в метрах рассчитывается

в D20: =D17/2/SIN (D19/2) =15,305

r = x /2/sin( a /2)

5. Максимальная ширина цветника – высота сегмента круга h в метрах рассчитывается

в ячейке D21: =D20*(1-COS (D19/2)) =1.695

h = r *(1- cos( a /2))

Ответы получены, вторая задача успешно решена!

Я не приводил вывода использованных формул потому, что это не по теме поста, и, думаю, с геометрией и тригонометрией вы легко разберетесь. Будут вопросы – обращайтесь.

Чтобы получать информацию о выходе новых статей вам нужно подписаться на анонсы в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей». С этого момента к вам на почтовый ящик будет приходить небольшое уведомление о появлении на моем блоге новой статьи.

Краткие выводы

1. Итерационными численными методами удобно и быстро можно решать трансцендентные уравнения и громоздкие нелинейные алгебраические.

2. При написании расчетных модулей программ в Excel, если нежелательны лишние остановки по ходу вычислений, можно использовать вставки блоков с классическими методами решения нелинейных уравнений или макросов с вызовом инструмента «Подбор параметра».

3. Использование инструмента «Подбор параметра» в Excel является сегодня, безусловно, наиболее оптимальным и эффективным методом решения нелинейных, трансцендентных уравнений функций одной переменной, а также проведения анализа типа «Что будет? Если…».

Умение применять в работе сервис «Подбор параметра» существенно повышает ваш уровень, как специалиста вообще, так и как пользователя Excel – в частности.

Буду очень рад увидеть ваши комментарии к статье, уважаемые читатели!

Решение алгебраических и трансцендентных уравнений в среде Microsoft Excel

Презентация к уроку

Загрузить презентацию (641 кБ)

В общем случае процесс решения задачи с использованием ЭВМ состоит из следующих этапов:

1. Постановка задачи и построение математической модели (этап моделирования);

2. Выбор метода и разработка алгоритма (этап алгоритмизации);

3. Запись алгоритма на языке, понятном ЭВМ (этап программирования);

4. Отладка и использования программы на ЭВМ (этап реализации);

5. Анализ полученных результатов (этап интерпретации).

В данной работе показано решение алгебраических и трансцендентных уравнений в среде Microsoft Excel. Уточнения корня производилось различными методами: методом бисекции; методом итераций; методом секущих; методом Ньютона.

Самый простейший из методов уточнения корня является метод половинного деления и используется во многих стандартных программных средствах.
Метод хорд в отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения. Он требует, чтобы один конец отрезка, на котором ищется корень был не подвижен. Берется один из концов отрезка. Метод является двухточечным, его сходимость монотонная и односторонняя. Метод хорд использует пропорциональное деление интервала.

В методе касательных в отличие от методов дихотомии и хорд задается не начальный интервал местонахождения корня, а его начальное приближение.

У метода хорд и у метода Ньютона имеется общий недостаток: на каждом шаге проверяется точность значения.

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

источники:

http://urok.1sept.ru/articles/674326

http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/

Источник

В общем случае процесс решения задачи с использованием ЭВМ состоит из следующих этапов:

1. Постановка задачи и построение математической модели (этап моделирования);

2. Выбор метода и разработка алгоритма (этап алгоритмизации);

3. Запись алгоритма на языке, понятном ЭВМ (этап программирования);

4. Отладка и использования программы на ЭВМ (этап реализации);

5. Анализ полученных результатов (этап интерпретации).

У метода хорд и у метода Ньютона имеется общий недостаток: на каждом шаге проверяется точность значения.

Источник

Лабораторная работа

Решение нелинейных
алгебраических и трансцендентных уравнений в «Excel» и «MathCAD»

Решение многих
задач приводит к исследованию сложных математических моделей. При этом в
большинстве случаев не удается получить точных аналитических решений. Тогда
используют численные методы. Решение, полученное численными методами, обычно является
приближенным, т.е. содержит некоторую погрешность. Ее источниками являются:
неполное соответствие математической модели реальной задаче: погрешность исходных
данных; погрешность самих численных методов; погрешности округления.

Цель и содержание

Целью данной
лабораторной работы является овладение практическими навыками решения
нелинейных уравнений численными методами средствами программ MS Excel и MathCAD.

Аппаратура и материалы

Лабораторная работа проводится в
компьютерном классе на IBM-совместимых персональных ЭВМ
с использованием программ MS Excel и MathCAD.

Указания по технике
безопасности

Для выполнения лабораторной работы
студент должен:

1.
Перед включением ПЭВМ подготовить рабочее место, убрать ненужные
для работы предметы; обо всех замеченных технических неисправностях сообщить
преподавателю. Запрещается включать устройства при неисправных заземлении или
кабелях питания; пользоваться поврежденными розетками, рубильниками и другими
электроустановочными приборами.

2.
После получения разрешения преподавателя включить ПЭВМ и
приступить к работе. Запрещается производить подключение или отключение
различных периферийных устройств. Запрещается работать, если при прикосновении
к корпусам оборудования ощущается действие электрического тока.

3.
После выполнения задания и получения разрешения преподавателя
необходимо закрыть активные приложения, корректно завершить работу ПЭВМ и
отключить питание.

4.
Привести в порядок рабочее место, и после получения разрешения
преподавателя покинуть помещение.

Теоретическое обоснование

Нелинейные
уравнения можно разделить на 2 класса – алгебраические и трансцендентные. Алгебраическими
уравнениями называют уравнения, содержащие только алгебраические функции
(целые, рациональные, иррациональные). В частности, многочлен является целой
алгебраической функцией. Уравнения, содержащие другие функции
(тригонометрические, показательные, логарифмические и другие) называются трансцендентными.

Часто возникающей
задачей при решении нелинейных уравнений является поиск приближенных значений
корней. Многие уравнение, например трансцендентные,
не имеют аналитических решений. Однако они могут решаться численными методами.

Пусть дано
уравнение

f(x)=0, (1)

где функция f(x) –
некоторая заданная функция.

Решить уравнение
(1) значит установить, имеет ли оно корни, сколько корней и найти значения
корней.

Методика и порядок выполнения работы

Прежде чем начать
выполнение лабораторной работы, внимательно прочтите задание на лабораторную
работу и просмотрите примеры выполнения работы. После этого запустите сначала
программу MathCAD, выполните все вычисления, необходимые для
выполнения лабораторной работы, и сохраните файл с вычислениями. Затем запустите программу MS Excel, выполните все
вычисления, необходимые для выполнения лабораторной работы, и также сохраните
файл с вычислениями. После того, как студент выполнил все вычисления, он может
приступить к формированию отчета по лабораторной работе.

Задание. Согласно данному преподавателем варианту необходимо:

1. Решить заданное
уравнение с помощью графического
метода в программе MathCAD.

2. Решить заданное
уравнение с помощью вычислительного
блока Given/Find в программе MathCAD.

3. Решить заданное уравнение с помощью метода подбора параметра в программе MS Excel.

Методика выполнения задания

Графический
метод. Рассмотрим в MathCAD графический метод, используемый для поиска приближенных значений корней нелинейных уравнений.

В качестве примера возьмем уравнение

. (2)

Чтобы определить, сколько корней оно имеет, проведем локализацию корней данного уравнения, т.е.
определим и выделим отрезки, на
каждом из которых уравнение имеет ровно один корень. Один из способов
решения данной проблемы – построение графика функции F(x), т.е.
графический метод. Для большей наглядности вводится две функции f(x)=4(1-х²) и g(x)=е^х, и строятся графики этих функций (рисунок 1).

Рисунок 1 – Графики
функций f(x) и g(x)

Из графика, представленного на рисунке 1,
видно, что графики функций f(x) и g(x) пересекаются в двух точках, расположенных внутри интервалов [–2;0] и [0;2]. На каждом из этих отрезков
корень можно найти, воспользовавшись опцией root(f(x)-g(x),x,a,b), где
а и b – начальная и
конечная точки отрезка локализации.

Окончательно, результат решения нелинейного уравнения с помощью
графического метода представлен на рисунке 2.

Рисунок 2 – Графическое
определение отрезков локализации и поиск корней уравнения с помощью
графического метода

Таким образом, корнями нелинейного уравнения
(2) являются два корня: и .

Рассмотрим также вычислительный блок Given/Find, используемый для решения нелинейного уравнения.

Вычислительный блок Given/Find. При использовании вычислительного блока Given/Find неизвестному значению
необходимо присвоить начальное значение. Неизвестной является значение
переменной х, поэтому именно она является аргументом встроенной функции Find(х), решающей нелинейное уравнение. После этого, чтобы численным
методом решить нелинейное уравнение, следует после ключевого слова Given записать нелинейное уравнение. Затем необходимо
записать функцию Find(х), поставить
знак «=», после чего на экране появится значение корня нелинейного уравнения.

Решим уравнение (2), задав начальное значение х₀>0, например . Для
этого обозначим блок решения словом Given, введем уравнение с помощью булевского
оператора «=» и найдем корень уравнения с помощью опции Find (рисунок 3).

Рисунок 3 – Поиск положительного корня уравнения с помощью функции Find

Второй корень уравнения можно получить,
выбрав отрицательное начальное значение х₀ , например (рисунок 4).

Рисунок 4 – Поиск отрицательного корня
уравнения с помощью функции Find

Метод
подбора параметра. Рассмотрим, как на рабочем листе при помощи подбора параметра
в MS Excel можно находить корни нелинейного уравнения с одним аргументом. В
качестве базового примера рассмотрим следующее уравнение:

Для нахождения
корней их первоначально надо локализовать, т.е. найти интервалы, на которых эти
корни существуют. Такими интервалами локализации корней могут служить
промежутки, на концах которых функция имеет противоположный знак. С целью
нахождения интервалов, на концах которых функция изменяет знак, необходимо
построить ее график или ее протабулировать. Например, протабулируем наш полином
на интервале [–2; 2] с шагом 0,4. С этой целью:

1.
Введите в
ячейку А2 значение -2, а в ячейку A3 – значение -1,6.

2.
Выберите
диапазон А2:АЗ, расположите указатель мыши на маркере заполнения этого
диапазона и протяните его на диапазон А4:А12. Аргумент протабулирован.

3.
В ячейку
В2 введите формулу: =4*(1–А2^2)–2,72^А2.

4.
Выберите
ячейку В2. Расположите указатель мыши на маркере заполнения этой ячейки и
протяните его на диапазон В3:В12. Функция также протабулирована.

Результаты табуляции представлены на рисунке 5.

На рисунке 6
видно, что функция меняет знак на интервалах [–1; –0,8] и [0,5; 1], и поэтому
на каждом из этих интервалов имеется свой корень. Так как квадратное уравнение
имеет не более двух корней, то они все локализованы.

Рисунок
5 – Результаты табуляции

Рисунок 6 – График функции

Прежде чем
приступить к нахождению корней при помощи подбора параметра, необходимо
выполнить некоторую подготовительную работу:

1. установите точность, с
которой находится корень. Корень при помощи подбора параметра находится методом
последовательных приближений. Для этого выберите команду Сервис→Параметры
и на вкладке Вычисления диалогового окна Параметры задайте
относительную погрешность и предельное число итераций равными 0,00001 и 1000,
соответственно.

2. Отведите на рабочем листе ячейку под
искомый корень, например, С2. Эта ячейка будет играть двойную роль. До
применения подбора параметра в ней находится начальное приближение к корню
уравнения, а после применения – найденное приближенное значение корня.

Корень при помощи
подбора параметра находим методом последовательных приближений, поэтому в
ячейку С2 надо ввести значение, являющееся приближением к искомому корню. В
нашем случае первым отрезком локализации корня является [-1; -0,8].
Следовательно, за начальное приближение к корню разумно взять среднюю точку
этого отрезка -0.9.

Отведите ячейку,
например, D2, под функцию, для которой ведется поиск корня. Причем, вместо
неизвестного, у этой функции должна указываться ссылка на ячейку, отведенную
под искомый корень. Таким образом, в ячейку D2 введите формулу
=4*(1-C2^2)-2,72^C2.

Аналогично надо
поступить с другим искомым корнем:

Отвести ячейку СЗ
под второй корень, ввести в нее начальное приближение 0,6. а в ячейку D3 ввести
следующую формулу =4*(1-C3^2)-2,72^C3.

Теперь можно
переходить к нахождению первого корня уравнения:

1. Выберите команду Сервис→Подбор
параметра. На экране отобразится диалоговое окно Подбор параметра.

2. В поле Установить в ячейке
введите ссылку на ячейку D2 (рисунок 7). В этом поле дается ссылка на ячейку, в
которой введена формула, вычисляющая значение левой части уравнения. Для
нахождения корня с помощью подбора параметра уравнение надо представить в таком
виде, чтобы его правая часть не содержала переменную.

3. В поле Значение
введите 0. Здесь указывается значение из правой части уравнения.

4. В поле Изменяя значение
ячейки введите С2. В данном поле приводится ссылка на ячейку, отведенную
под переменную.

Рисунок 7 – Локализация
корней уравнения и диалоговое окно

Подбор параметра

5. Нажмите кнопку ОК.

На экране
отображается окно Результат подбора параметра (рисунок с результатами
работы команды Подбор параметра. Кроме того, рассматриваемое средство
помещает найденное приближенное значение корня в ячейку С2. В данном случае оно
равно -0,950483819.

Затем необходимо
провести все операции для поиска второго корня. На экране отображается окно Результат
подбора параметра (рисунок 9) с результатами работы команды Подбор
параметра. Кроме того, рассматриваемое средство помещает найденное
приближенное значение корня в ячейку С3. В данном случае оно равно 0,703322024.

Окончательно,
результат решения нелинейного уравнения с помощью метода подбора параметра
представлен на рисунке 10.

Таким образом, корнями нелинейного уравнения
(2) являются два корня: и .

Рисунок 8 –Диалоговое окно
Результат подбора параметра

после успешного завершения
поиска первого корня

Рисунок 9 –Диалоговое окно
Результат подбора параметра

после успешного завершения
поиска второго корня

Рисунок 10 – Результат
решения нелинейного уравнения с помощью

метода подбора параметра

Варианты
заданий для самостоятельного выполнения

№ варианта	Уравнение f(x)=0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Вопросы для защиты работы

1. Какие бывают нелинейные
уравнения? Дать определения.

2. В чем заключается графический
метод вычисления нелинейных уравнений?

3. Как решается нелинейное
уравнение с помощью вычислительного блока Given/Find?

4.
Как можно
найти корни нелинейного уравнения при помощи подбора параметра?

Список литературы

1.
Васильев
А.Н. MathCAD 13 на примерах. – СПб.:
БХВ-Петербург, 2006. – 528 с.: ил.

2.
Гурский
Д., Турбина Е. MathCAD для студентов и школьников.
Популярный самоучитель. – СПб.: Питер, 2005. – 400 с.: ил. – (Серия «Популярный
самоучитель»)

3.
Поршнев
С.В., Беленкова
И.В. Численные методы на базе MathCAD. –
СПб.: БХВ-Петербург, 2005. – 464 с.: ил.

4.
Семененко
М.Г. Математическое моделирование в MathCAD. – М.: Альтекс-А, 2003. – 208 с.

5.
Численные
методы и инженерные расчеты в Excel.
Методические указания к выполнению лабораторных работ. – СПб.: СЗЗГТУ, 2001г.

6.
Официальный
образовательный математический сайт: http://exponenta.ru/index.php

Источник

Нелинейные
уравнения – это уравнения вида f(x)=0,
где f(x)
– нелинейная функция. Решение уравнения
f(x)=0
сводится к поиску таких значений х^*
(корней уравнения), которые превращают
уравнение в тождество. Различают
нелинейные алгебраические уравнения
и трансцендентные.

Например,
нелинейное алгебраическое уравнение
ax²+
вx
+с =0
имеет два корня, которые могут быть
действительными или мнимыми. Например,
уравнение х²
+ 2=0 имеет два мнимых корня х₁=
-2
и х₂=
--2
.

В
дальнейшем будет идти речь о вычислении
только действительных корней.

Трансцендентным
называется
уравнение,

если в f(x)

входит хотя бы одна трансцендентная
функция. Например, sin(x)
–1=0;

Решение
нелинейных уравнений выполняют в два
этапа:

Этап
отделения
корней.
Этап
уточнения
корней
, т.е. поиск коней с заданной точностью.

Этап
отделения корней

Для
этого построим график заданной функции
f(x)=0.
В столбце А располагаем изменение
аргумента, а в столбце В табулируемую
функцию. Строим график. На графике
выделяем границы корня и в этих границах
берем начальное приближение корня
(нарисовать график, выделить корни и
взять начальное приближение).

Этап
уточнение корня

Команда
Подбор
параметров

Порядок
уточнения:

1.
В ячейку A1
вводим
начальное приближение корня Х₁.

2.
В ячейку В1
вводим
формулу с заданной функцией.

3.
Выполняем команды Сервис,

Подбор
параметра.
Появляется окно Подбор
параметра (рис.
7.7).

4.
В поле «Установить
в ячейке»
записать адрес первой формулы (можно
снять окно и щелкнуть ячейку В1,
затем восстановить окно).

5.
В поле «Значение»
установить 0.

6.
В поле «Изменяя
значение
ячейки«
установить адрес А1
(снять окно и щелкнуть А1).

7.
Щелкнуть ОК.
Появляется окно Результат
подбора параметра
(рис. 7.8), а в ячейке А1
будет уточненное значение корня.

Рис.
7.8

Рис.
7.7

7.5. Вычисления по итерационным формулам

Итерационной
называется формула типа y_i₊₁
= f
(y_i)
. Пример1.
Вычисление

задано итерационной формулой y_i₊₁=(x/y_i²
+2y_i)/3

Начальное
приближении у₀=1
и значение х= 27.

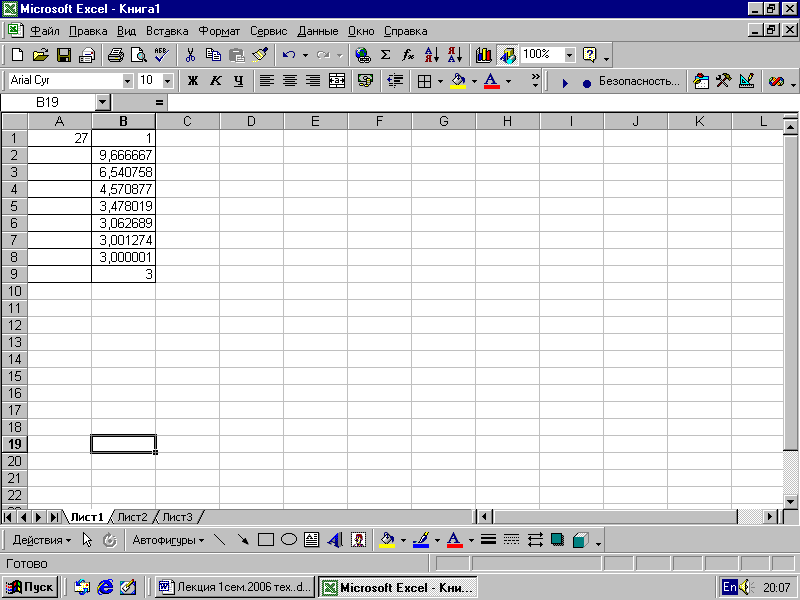
Составим
ЭТ для вычисления:

1.
В ячейку a2
запишем
значение х равное 27
(рис. 7.9).

2.
В ячейку b2
запишем
значение у₀равное 1.

Рис.
7.9

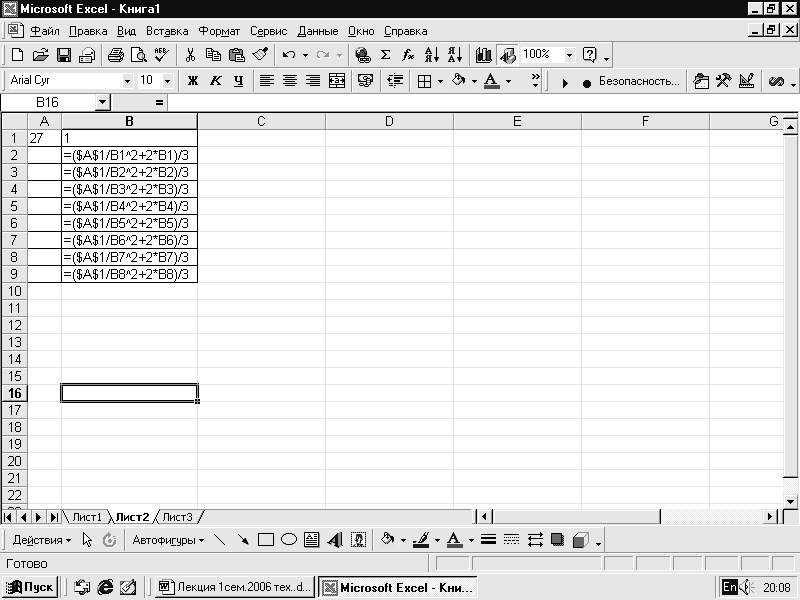
. В ячейку b3
запишем формулу =
($A$1/B1^2+2*B1)/3,
которую копируем вниз

Пример
2. Заданы
итерационные формулы

x_i
=2x_i_-1
и y_i=
x_i_-1
+ 3y_i_-1
при
изменении
i=2,3,4,5.

При
i=2
х₂= 2х₁
и y₂=
x₁
+ 3y₁

Начальные
значения x₁=1
; y₁=1
(рис. 7.10) запишем в В2 и С2 соответственно.
В ячейки В3 и С3 запишем формулы для х₂
и у₂
. Выделяем В3:С3 и копируем вниз до С6.
Результат вычисления на рис. 7.11.

Рис.
7.10

Рис.
7.11

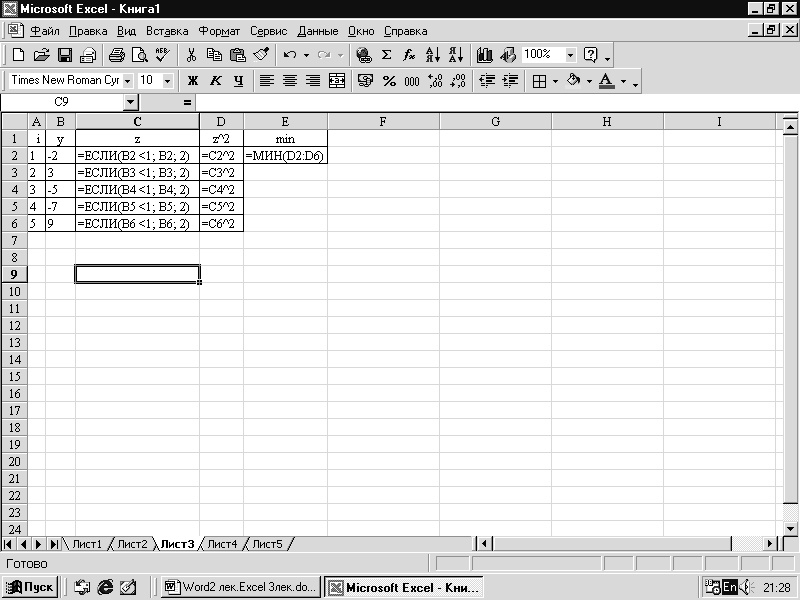
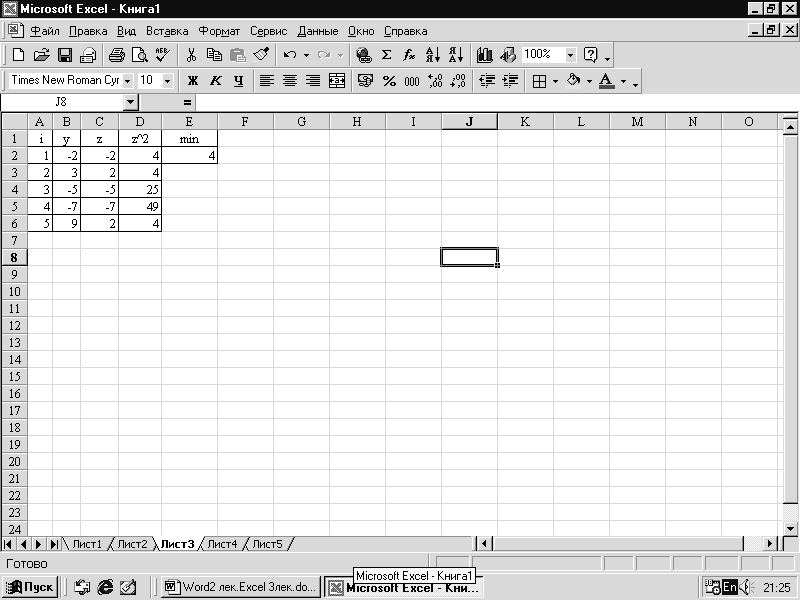
Пример
3.

Решение
задач следующего типа:

Даны
действительные числа у1, у2,…у5, которые
записаны в В2:В6

Составить
ЭТ для вычисления

и
определения min(z1²,
z2²,
…,z5²)
при i=1,2,…,5

Рис.
7.12

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Привет тому, кто попал на моу тему! Как уже понятно из заголовка темы проблему нужно решить в экселе. Перехожу к сути. Так вот, дано трансцендентное уравнение, известна область его определения (два целых числа и неважно каких), в одну ячейку ввёл среднее этих двух чисел, в другую, в ту что правее — ввёл формулу с подстановкой вместо неизвестной переменной этого значения, выделил правую ячейку, вызвал «Подбор параметра», заполнил окно как надо (вроде) и получил то, что в ячейке с формулой (правая) вместо возращения значения «0» получил, то что получил, тогда как в изменяемой ячейке (соответственно в левой) возвращено искомое значение (см. скрин), файл с этой белибердой тоже приложу. Заранее спасибо!

Источник