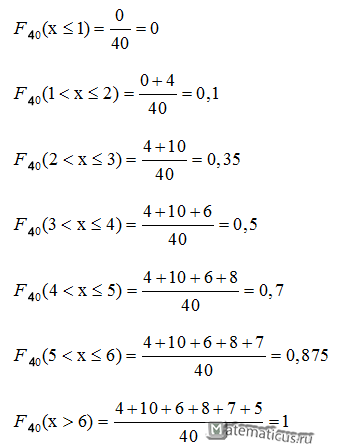Как найти эмпирическую функцию распределения в excel

2.1.2. Эмпирическая функция распределения

Это статистический аналог функции распределения из теорвера. Данная функция определяется, как отношение:
, где – количество вариант СТРОГО МЕНЬШИХ, чем ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.

Построим эмпирическую функцию распределения для нашей задачи. Чтобы было нагляднее, отложу варианты и их количество на числовой оси:

На интервале – по той причине, что левее ЛЮБОЙ точки этого интервала вариант нет. Кроме того, функция равна нулю ещё и в точке . Почему? Потому, что значение определяет количество вариант (см. определение), которые СТРОГО меньше двух, а это количество равно нулю.

На промежутке – и опять обратите внимание, что значение не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению).

На промежутке – и далее процесс продолжается по принципу накопления частот:
– если , то ;
– если , то ;
– и, наконец, если , то – и в самом деле, для ЛЮБОГО «икс» из интервала ВСЕ частоты расположены СТРОГО левее этого значения «икс» (см. чертёж выше).

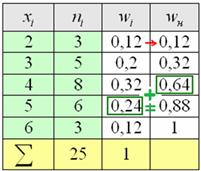
Накопленные относительные частоты удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева частоту (красная стрелка), и каждое следующее значение получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения):

Вот ещё, кстати, один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.

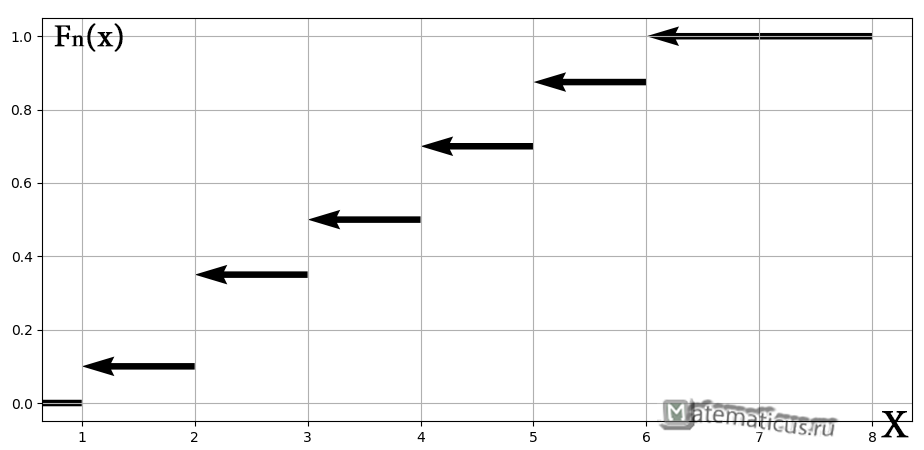
Построенную функцию принято записывать в кусочном виде:

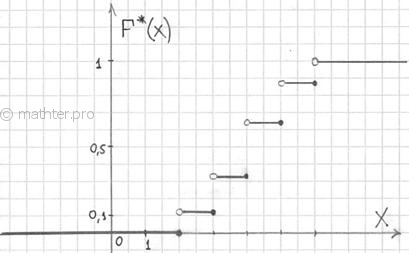
а её график представляет собой ступенчатую фигуру:

Эмпирическая функция распределения не убывает и принимает значения лишь из промежутка , и если у вас вдруг получится что-то не так, то ищите ошибку.

Теперь смотрим видео, о том, как построить эту функцию в Экселе (Ютуб).

И, конечно, вспомним основной метод математической статистики. Эмпирическая функция распределения строится по выборке и приближает теоретическую функцию распределения . Легко догадаться, что последняя появляется в результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была репрезентативна, дабы приближение было хорошим.

Миниатюрное задание для закрепления материала:

Пример 5

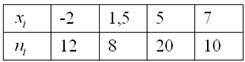
Дано статистическое распределение совокупности:

Составить эмпирическую функцию распределения, выполнить чертёж

Решаем самостоятельно – все числа уже в Экселе! Свериться с образцом можно в конце книги. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.

Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки

Эмпирическая функция распределения имеет вид

Построим график кусочно-постоянной эмпирической функции распределения

таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.

2 комментария

У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.

Построить эмпирическое распределение результатов тестирования в баллах для следующей выборки: 69, 85, 78, 85, 83, 81, 95, 88, 97, 92, 74, 83, 89, 77, 93.

В ячейку А1 введите слова Результаты, в диапазон А2:А16 – результаты тестирования.

Выберите ширину интервала 5 баллов. Тогда при крайних результатах 69 и 97 баллов, получится 7 интервалов. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.

Введите заголовки создаваемой таблицы: в ячейку D1 – Абсолютные частоты, в ячейку Е1 – Относительные частоты, в F1 – Накопленные частоты.

Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек D2:D8, вызовите Мастер функций, категория – Статистические, функция – Частота, в поле Массив данных введите диапазон данных тестирования А2:А16, в поле Массив интервалов введите диапазон интервалов С2:С8, нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D8 появится массив абсолютных частот.

В ячейке D9 найдите общее количество результатов тестирования, с помощью Автосумма.

Заполните столбец относительных частот. В ячейку Е2 введите формулу =$D2/$D$9 .

Протягиванием скопируйте полученное значение в диапазон Е3:Е8. Получим массив относительных частот.

Заполните столбец накопленных частот. В ячейку F2 скопируйте значение относительной частоты из ячейки Е2. В ячейку F3 введите формулу =F2+E3. Протягиванием скопируйте полученное значение в диапазон F4:F8. Получим массив накопленных частот.

В результате получим таблицу, представленную на рисунке 1.

Пусть Nх — число наблюдений, при которых значение при­знака Х меньше Х. При объеме выборки, равном П, относитель­ная частота события Х XK.

Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х 6. Напишем формулу искомой эмпирической функции:

4. Рассмотрим любой из критериев оценки качеств педагога-профессионала, например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку такого измерения, необходимо увеличить число возможных ответов на конкретный критериальный вопрос. В табл. 1 представлены возможные варианты ответов.

Обозначим этот параметр через х. Тогда в процессе ответа на вопрос величина х примет дискретное значение х, принадлежащее определенному интервалу значений. Поставим в соответствие каждому из ответов определенное числовое значение параметра х (см. табл. 1).

Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неиз­вестных параметров. В частности, невозможно
рассчитать точное значение соот­ветствующих вероятностей, так как нельзя
определить количество общих и благо­приятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в ко­торых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.

Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой со­бытия
и его вероятностью.

Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов). 

Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
чис­ла на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.

По
найденным относительным час­тотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.

Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того  интервала
включительно, для которого определяется накопленная частота.

В Excel для построения выборочных функций распределения
используются спе­циальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интер­валах
значений и выводит их как массив цифр, где

•     
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;

•     
двоичный_массив
— это массив интервалов, по
ко­торым группируются значения выборки.

Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:

•     
Входной диапазон — диапазон исследуемых данных
(выборка);

•     
Интервал карманов — диа­пазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в воз­растающем порядке. Если
диапазон карманов не был введен, то набор интерва­лов, равномерно распределенных между минимальным и
максимальным зна­чениями данных, будет создан
автоматически.

•     
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.

•     
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму гра­фика интегральных
процентов.

•     
переключатель
Вывод графика позволяет установить режим автоматическо­го создания встроенной диаграммы на листе, содержащем
выходной диапа­зон.

Пример 1. Построить эмпирическое распределение веса
студентов в килограм­мах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.

Решение

1.  В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).

2.        
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения ин­тервалов (40, 45,
50, 55, 60, 65, 70).

3.        
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные час­тоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накоплен­ные частоты.(см. рис. 1).

4.        
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
па­нели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появив­шемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться мас­сив абсолютных частот (см. рис.1).

5.        
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Ав­тосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.

6.        
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.

7.        
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение от­носительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.

                     Рис. 1. Результат вычислений из
примера 1

8.   
Постройте диаграмму относительных и накопленных частот. Щелчком ука­зателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаг­раммы График/гистограмма. После 
редактирования диаграмма будет иметь такой вид, как на рис. 2.

Рис. 2
Диаграмма относительных и накопленных частот из примера 1

Задания для самостоятельной работы

1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.

2.  Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.

3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).

4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.

Обозначим 
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).

Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания

При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.

Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).

Таблица 2.
Результаты опроса ста учителей

Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=

где

W(x) – относительная частота наступления события;

          — стандартное
отклонение;

          =3,14.

Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.

При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.

При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.

Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.

Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.

Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет гене­ральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).

Элементами выборки (x₁ х₂, . х_п) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).

Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.

Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.

Пример 2.1.

Известны следующие данные о результатах сдачи студентами экзамена (в баллах):

18	16	20	17	19	20	17
17	12	15	20	18	19	18
18	16	18	14	14	17	19
16	14	19	12	15	16	20

Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.

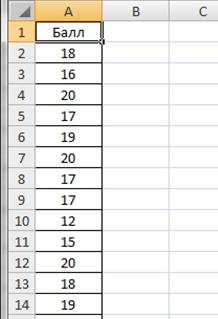
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).

Рисунок 2.6. Баллы успеваемости студентов

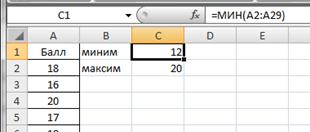
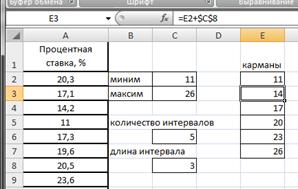
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).

Рисунок 2.7. Минимальный и максимальный балл

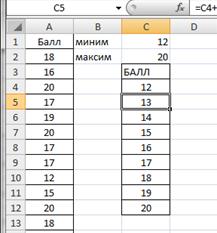
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.

Рисунок 2.8. Значения признака

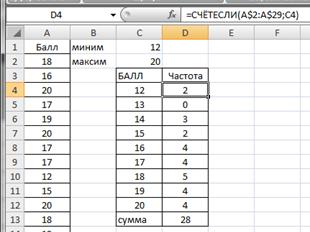
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).

Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.

Рис.2.9. Частоты вариационного ряда

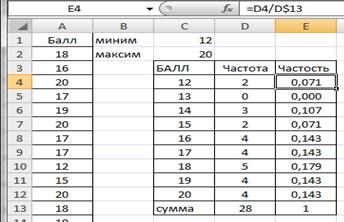
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).

Рисунок 2.10. Частости ряда распределения

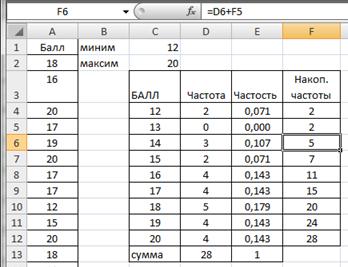
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).

Рисунок 2.11. Накопленные частоты ряда

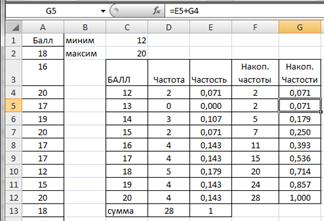
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.

Рисунок 2.12. Накопленные частости ряда

Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.

Рисунок 2.13. Полигон распределения частот

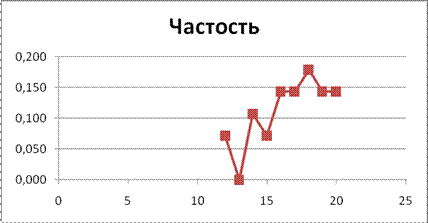
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.

Рисунок 2.14. Полигон распределения частостей

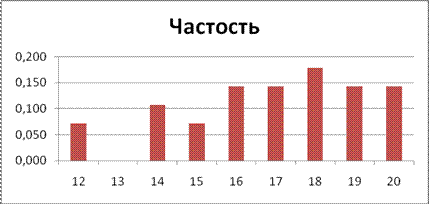
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» – «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).

Рисунок 2.15. Гистограмма распределения частостей

Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.

Рисунок 2.16. Кумулята

Пример 2.2.

В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.

Банковские процентные ставки

№ Банка	Процентная ставка, %
1	20,3
2	17,1
3	14,2
4	11,0
5	17,3
6	19,6
7	20,5
8	23,6
9	14,6
10	17,5
11	20,8
12	13,6
13	24,0
14	17,5
15	15,0
16	21,1
17	17,6
18	15,8
19	18,8
20	22,4
21	16,1
22	17,9
23	21,7
24	18,0
25	16,4
26	26,0
27	18,4
28	16,7
29	12,2
30	13,9

Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.

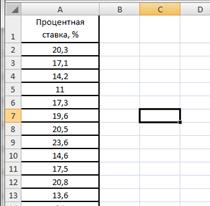
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).

Рисунок 2.17. Процентные ставки банков

Рисунок 2.18. Число интервалов

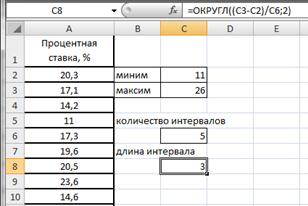
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).

Рисунок 2.19. Длина интервала

Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).

Рисунок 2.20. Границы интервалов

Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.

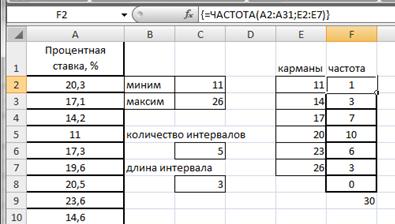
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.

Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).

Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.

Рисунок 2.21. Частоты значений признака

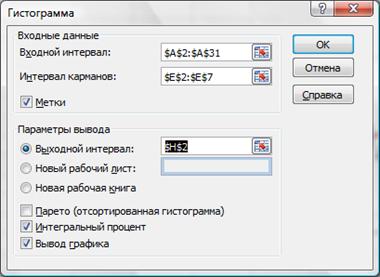
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).

Рисунок 2.22. Построение гистограммы

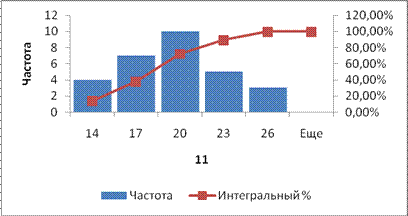
Полученная гистограмма представлена на рис.2.23.

Рис.2.23. Гистограмма частот

Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.

Дата добавления: 2018-11-12 ; просмотров: 1065 | Нарушение авторских прав

Вариационный ряд может быть:

– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).

– интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.

Рассмотрим пример построения дискретного вариационного ряда.

Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения

Решение .

Алгоритм построения вариационного ряда:

1) Откроем таблицы Excel.

2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.

3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.

4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).

Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.

6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER

Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.

Построим полигон:

1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа – в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).

2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.

Рис.1.3. Пример 1. Построение полигона частот

В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).

Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.

После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).

Размахом вариации называется число

где х_тах — наибольший вариант;

x min — наименьший вариант.

Сумма всех частот равна определенному числу л, которое называется объемом совокупности:

Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:

Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).

Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.

Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.

Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.

В результате получим дискретный вариационный ряд (табл. 3.10).

Ранжированный ряд успеваемости

Число студентов, л,

Относительная частота, А

В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).

Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).

Рис. 3.13. Контекстное меню строки состояния

Рассмотрим два варианта подсчета частот:

• 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
• 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.

Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»

В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).

Рис. 3.15. Результаты применения инструмента «Гистограмма)

Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).

В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.

Постановка
задачи.

Построить
график эмпирической функции распределения
с подогнанной ожидаемой функцией
распределения.

Теоретические
основы.

См.
стр. 31-32 пособия [4].

Вычисления.

Если
попытаться построить ЭФР средствами
Excel,
упорядочив сначала данные и сопоставив
затем каждому упорядоченному значению
x_(k)
значение
,
то вместо горизонтальных получим
наклонные ступеньки. Чтобы избежать
этого недостатка, можно каждое значение
вариационного ряда повторить дважды,
при этом первому из этих значений
сопоставить ЭФР,
а второму
.

Вычисление нормальной функции
распределения описано ниже в главе
“Встроенные функции Excel”.
Здесь кратко только скажем, что для
этого можно использовать функцииНОРМРАСПиНОРМСТРАСПиз
категории “Статистические”.

Функция
распределения экспоненциального закона
вычисляется с помощью простой функции
EXP.

Кроме того,
предполагается, что уже вычислены
среднее значение и дисперсия выборки
(задание 1).

Пример.

Рис.
2

 Порядок
вычислений.

1. Скопировать
   исходные данные в буфер обмена;

2. перейти
   на лист “ЭФР”
   и, установив курсор в ячейку A3,
   вставить данные из буфера обмена;

3. повторить
   процесс восстановления данных, начиная
   с ячейки A104

• установить
  курсор в ячейку A104;

• вставить данные
  из буфера обмена

1. – всего
   получится 202
   значения с 3-й
   по 204-ю
   ячейки;

1. упорядочить
   значения в столбце A

• кликнуть
  мышкой по кнопке
  ;

1. ввести
   в ячейку B3
   формулу

• =(СТРОКА(B3)-1)/202-1/101

1. – функция
   «СТРОКА»
   возвращает номер строки указанного
   аргумента, то есть в данном случае в
   ячейке B3
   получится значение (3-1)/202-1/101
   = 0;

1. ввести
   в ячейку B4
   формулу

• =(СТРОКА(B3)-1)/202

1. – получится
   значение (3-1)/202
   = 1/101;

1. выделить
   обе ячейки B3
   и B4
   и скопировать их параллельно всем
   данным до ячейки B204

1. – в
   последней ячейке должно получиться
   значение 1;

1. добавить
   в ячейку A2
   значение, на единицу меньшее значения
   ячейки A3
   и сопоставить ему значение 0
   в ячейке B2;

2. добавить
   в ячейку A205
   значение, на единицу большее значения
   ячейки A204
   и сопоставить ему значение 1
   в ячейке B205.

Ввести формулы
вычисления нормального распределения:

1. в
   ячейки F4,
   F5
   (те, которые скрыты графиком) скопировать
   среднее и стандартное отклонение,
   соответственно

• =МОМЕНТЫ!B4

• =МОМЕНТЫ!B6

1. в
   ячейку C2
   ввести формулу нормального распределения

• =НОРМРАСП(A2;$F$4;$F$5;1)

1. в
   ячейку D2
   ввести формулу вычисления расхождения
   между ЭФР и ожидаемой функцией
   распределения

• =ABS(C2-B2)

1. скопировать
   обе ячейки C2
   и D2
   вплоть до 205-й строки;

2. вычислить
   максимальное расхождение, например, в
   ячейке F6

• =МАКС(D2:D205)

Теперь уже можно
рисовать графики:

1. выделить
   все значения в ячейках A2:C205;

2. вызвать
   “Мастера
   Диаграмм”;

3. выбрать
   «Точечную»
   диаграмму – без маркеров со сглаживающей
   линией (третья по порядку среди точечных
   диаграмм);

4. при
   выборе представления диаграммы, после
   двух нажатий кнопки
   ,
   удалить “Легенду”
   и добавить “Заголовок
   по
   оси Х”:

• МАКСИМАЛЬНОЕ
  РАСХОЖДЕНИЕ D=…

1. (указав
   здесь полученное значение Δ из ячейки
   F6);

1. ;

2. установить
   параметры диаграммы, как в примере.

Замечание.
Если бы параметры нормальной модели
не оценивались по выборочным данным, а
были бы в точности равны этим оценкам,
то при полученном здесь расхождении
Δ=0,097 гипотезу нормальности следовало
бы принять с критическим уровнем
значимости > 0,20 (см. таблицу 6.2 сборника
таблиц [1]). Это надо воспринимать как
хороший знак и не более того. Если
неизвестные значения параметров
оцениваются по выборке, то критический
уровень значимости становится зависящим
от неизвестных параметров и трудно
ожидать, что даже в предположениях
гипотезы критерий будет иметь приемлемый
размер.

Контрольные
вопросы.

1. Сформулируйте
   статистическую задачу.

2. Что такое
   вариационный ряд?

   1. 31.

3. Дайте определение
   эмпирической функции распределения?

   1. 31.

4. Почему
   некоторые ступеньки ЭФР высокие, а
   некоторые низкие?

   1. 31.

5. Почему одни
   ступеньки ЭФР длинные, а другие короткие?

   1. 31.

6. Постройте
   ЭФР по следующим данным: 1; 2; 1; 3; 1; 5; 1; 3.

7. Выпишите
   формулу для функции распределения
   нормального закона (равномерного,
   экспоненциального).

   1. 16-21.

8. Можно
   ли утверждать, что ЭФР является
   состоятельной оценкой истинной функции
   распределения? Что сие означает?

   1. 31.

9. Можно
   ли утверждать, что ЭФР является
   несмещенной оценкой истинной функции
   распределения? Что сие означает?

   1. 31.

10. Докажите
    несмещенность ЭФР.

11. Можно
    ли по значению максимального расхождения
    между ЭФР и ожидаемой функцией
    распределения принять или отвергнуть
    гипотезу о виде истинной функции
    распределения?

    1. 32.

Соседние файлы в папке Матстат

• #
• #