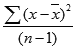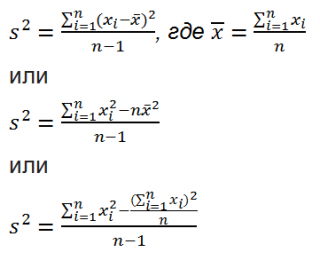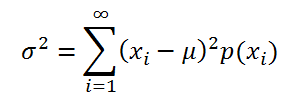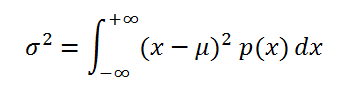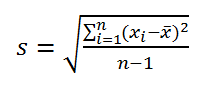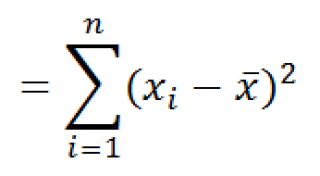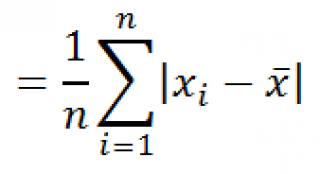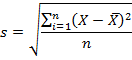Содержание
- Вычисление дисперсии
- Способ 1: расчет по генеральной совокупности
- Способ 2: расчет по выборке
- Вопросы и ответы
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Вычисление дисперсии
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:
=ДИСП.Г(Число1;Число2;…)
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
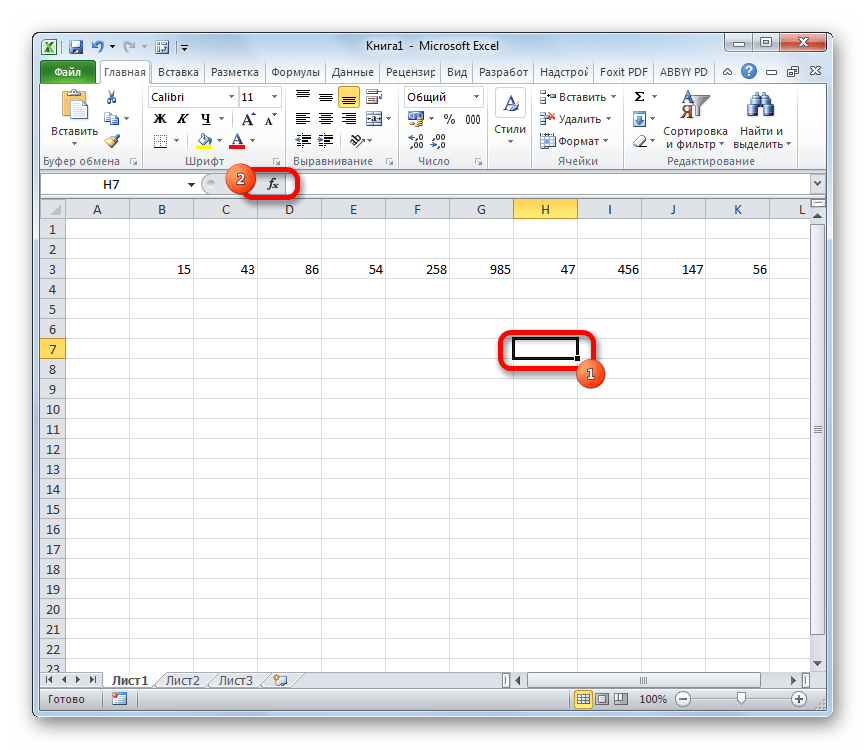
- Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.
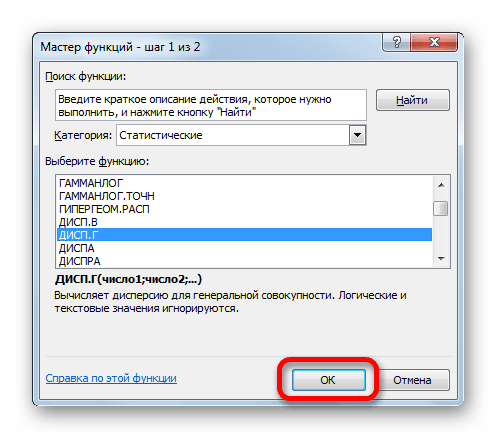
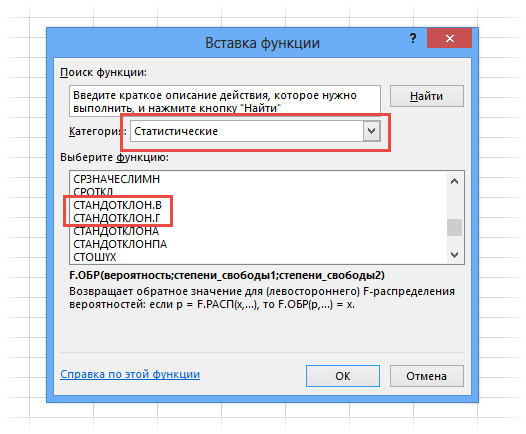
- Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».
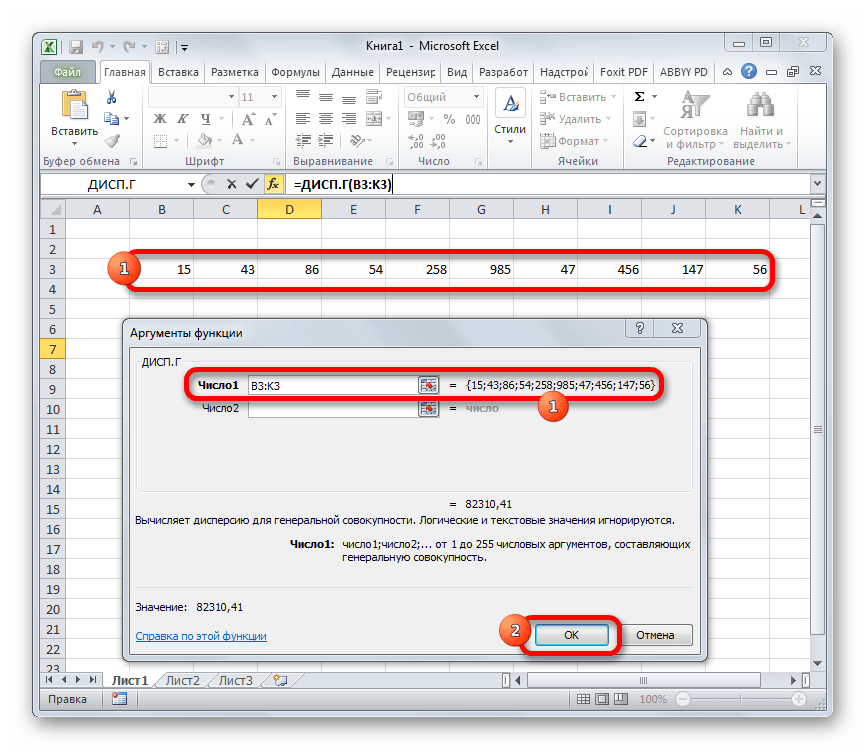
- Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».
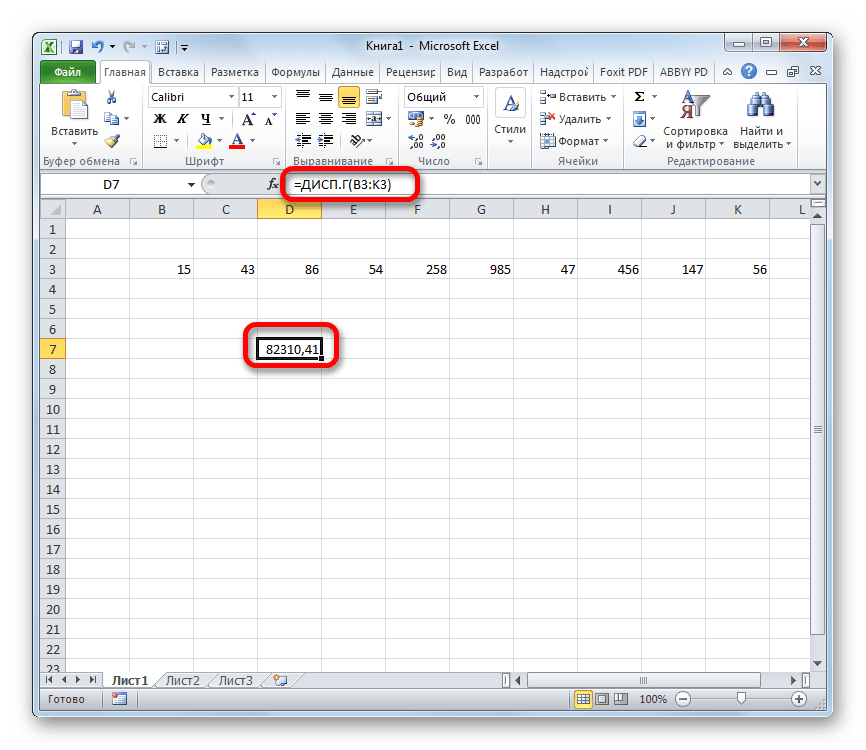
- Как видим, после этих действий производится расчет. Итог вычисления величины дисперсии по генеральной совокупности выводится в предварительно указанную ячейку. Это именно та ячейка, в которой непосредственно находится формула ДИСП.Г.
Урок: Мастер функций в Эксель
Способ 2: расчет по выборке
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
=ДИСП.В(Число1;Число2;…)
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
- Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.
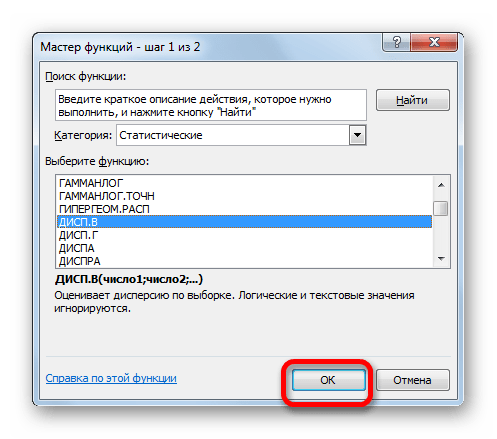
- В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».
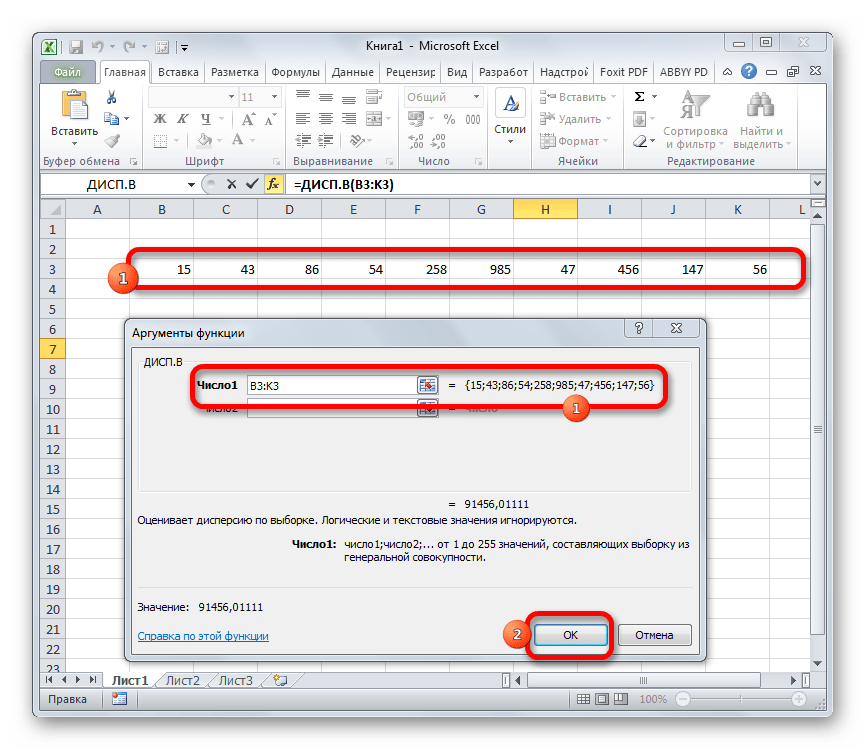
- Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».
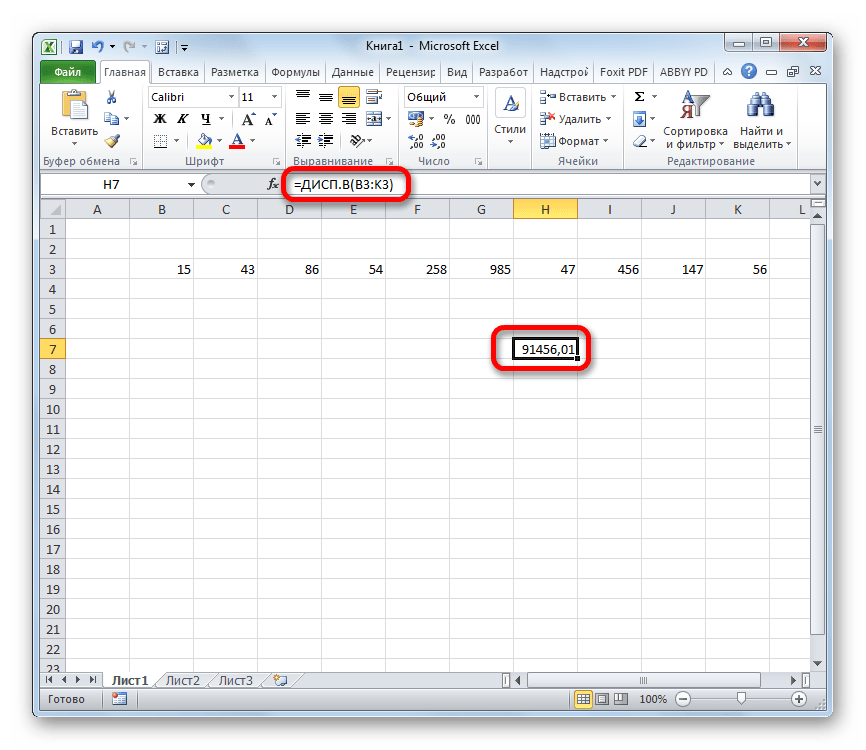
- Результат вычисления будет выведен в отдельную ячейку.
Урок: Другие статистические функции в Эксель
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Синтаксис
ДИСП(число1;[число2];…)
Аргументы функции ДИСП описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Замечания
-
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
-
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание |
Результат |
|
=ДИСП(A2:A11) |
Дисперсия предела прочности для всех протестированных инструментов. |
754,2667 |
Нужна дополнительная помощь?
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
— это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) — отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
Variance is an important metric in statistics, and it can help you calculate like the risk of an investment. In this guide, we’re going to show you how to calculate variance in Excel.
Download Workbook
What is variance?
Variance is the average of the squared differences from the average or mean. You can calculate the variance of a data by taking the differences between each number in the data set and the average, then squaring the differences (which makes them positive), and finally dividing the sum of the squares by the number of values in the data set.
The formula is as follows:
- σ²: variance
- x: mean (average) of data
- x ̅: data
- n: data size
A large variance value shows that numbers are far from the mean and each other. A small one, on the other hand, means an opposite correlation. Zero variance means that all numbers in the data set are identical.
Sample variance
If the data set does not represent the entire population, but a number of items from it is sample variance. A common example for this is an election poll.
The formula of a sample variance is almost the same except for the data size. Instead of using exact an data size, use minus 1.
How to calculate variance in Excel
Although, you can calculate variance in Excel by creating the same formula as above, there are built in functions that can make this even easier. The following table shows the formulas and properties that distinguish them.
| Function | Variance type | Excel Version | Text and logical values |
| VAR.S | Sample | 2010 | Ignored |
| VARA | Sample | 2000 | Evaluated |
| VAR | Sample | 2000 | Ignored |
| VAR.P | Population | 2010 | Ignored |
| VARPA | Population | 2000 | Evaluated |
| VARP | Population | 2000 | Ignored |
Each function uses the same syntax. You can provide data as references or static values. Aside from the sample versus population choice, you need to decide whether you want text and logical values to be evaluated as numbers. VARA and VARPA functions evaluate text and FALSE logical value to zero (0) and TRUE to 1.
VAR.S(number1,[number2],…)
VARA(number1,[number2],…)
VAR(number1,[number2],…)
VAR.P(number1,[number2],…)
VARPA(number1,[number2],…)
VARP(number1,[number2],…)
The following example shows what each function returns for the same data set. The data set is at B5:B10 under the name “data”.
Please note that VAR and VARP functions have been updated with VAR.S and VAR.P functions in Excel 2010. Although Microsoft continues to support these functions for backwards compatibility, they encourage using VAR.S and VAR.P instead.
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
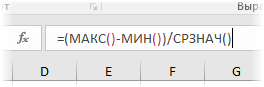
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях: