Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование комплексного
в Microsoft Excel.
Описание
Преобразует коэффициенты при вещественной и мнимой частях комплексного числа в комплексное число в форме x + yi или x + yj.
Синтаксис
КОМПЛЕКСН(действительная_часть;мнимая_часть;[мнимая_единица])
Аргументы функции КОМПЛЕКСН описаны ниже.
-
Действительная_часть — обязательный аргумент. Действительная часть комплексного числа.
-
Мнимая_часть — обязательный аргумент. Мнимая часть комплексного числа.
-
Мнимая_единица — необязательный аргумент. Обозначение мнимой единицы в комплексном числе. Если аргумент «мнимая_единица» опущен, используется суффикс «i».
Примечание: Все функции с комплексными числами принимают суффиксы «i» и «j», но не «I» и «J». Использование верхнего регистра результатов в #VALUE! значение ошибки #ЗНАЧ!. Для всех функций, которые принимают два или более сложных числа, требуется, чтобы все суффиксы совпадали.
Замечания
-
Если real_num не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
-
Если i_num не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
-
Если суффикс не является ни «i», ни «j», то #VALUE! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=КОМПЛЕКСН(3;4) |
Комплексное число с действительным и мнимым коэффициентами 3 и 4 соответственно |
3+4i |
|
=КОМПЛЕКСН(3;4;»j») |
Комплексное число с действительным и мнимым коэффициентами 3 и 4 соответственно и мнимой единицей j |
3+4j |
|
=КОМПЛЕКСН(0;1) |
Комплексное число с действительным и мнимым коэффициентами 0 и 1 соответственно |
i |
|
=КОМПЛЕКСН(1;0) |
Комплексное число с действительным и мнимым коэффициентами 1 и 0 соответственно |
1 |
Нужна дополнительная помощь?
Наблюдения и советы этой статьи мы подготовили на основании опыта команды IMAGINARY Функция возвращает мнимый коэффициент заданного комплексного числа в виде x + yi или x + yj.
Примечание: Комплексное число состоит из действительного коэффициента и мнимого коэффициента. Вы можете применить КОМПЛЕКСНАЯ функция для преобразования действительных и мнимых коэффициентов в комплексное число вида x + yi или x + yj.
Синтаксис
IMAGINARY(inumber)
аргументы
- номер (обязательно): Комплексное число, для которого вы хотите вернуть мнимый коэффициент.
Замечания
1. Аргумент может быть представлен как любой из следующих:
— Вещественное число, мнимая часть которого равна 0, например, 1 является комплексным числом 1+0i; Или чисто мнимое число, действительная часть которого равна 0, например, i — комплексное число 0 + 1i;
— Ссылка на ячейку, которая относится к комплексному числу;
— Комплексное число, заключенное в двойные кавычки.
2. #СТОИМОСТЬ! ошибка возникает, если «число» является логическим значением.
3. #NUM! ошибка возникает, если «inumber» не может быть распознан как комплексное число.
Возвращаемое значение
Возвращает числовое значение.
Пример
В следующей таблице приведен список комплексных чисел. Чтобы получить мнимые коэффициенты этих комплексных чисел, вы можете применить функцию IMAGINARY следующим образом.
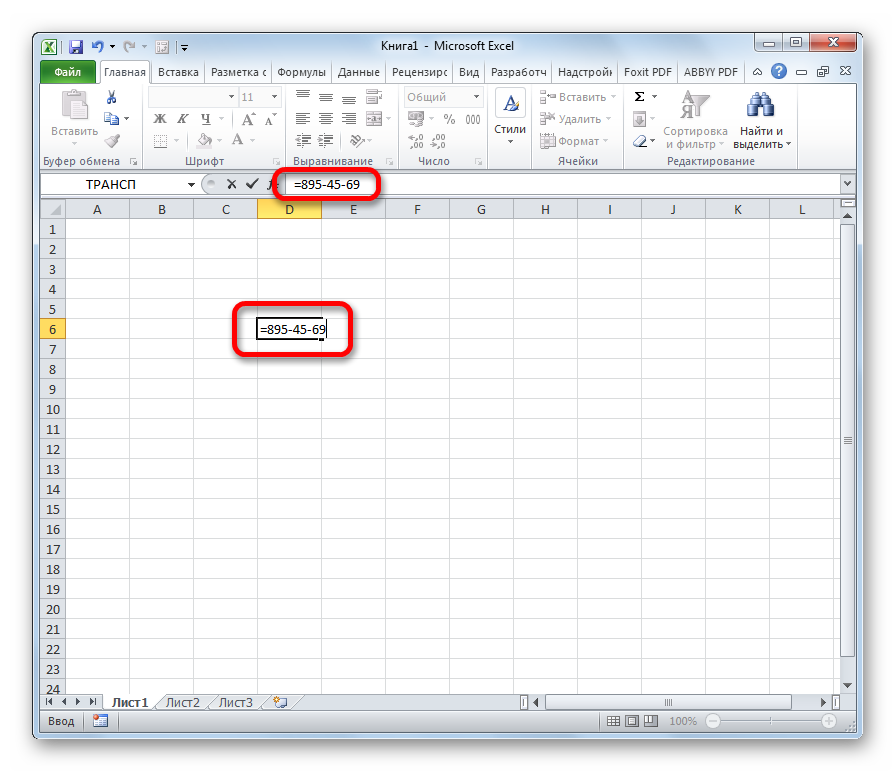
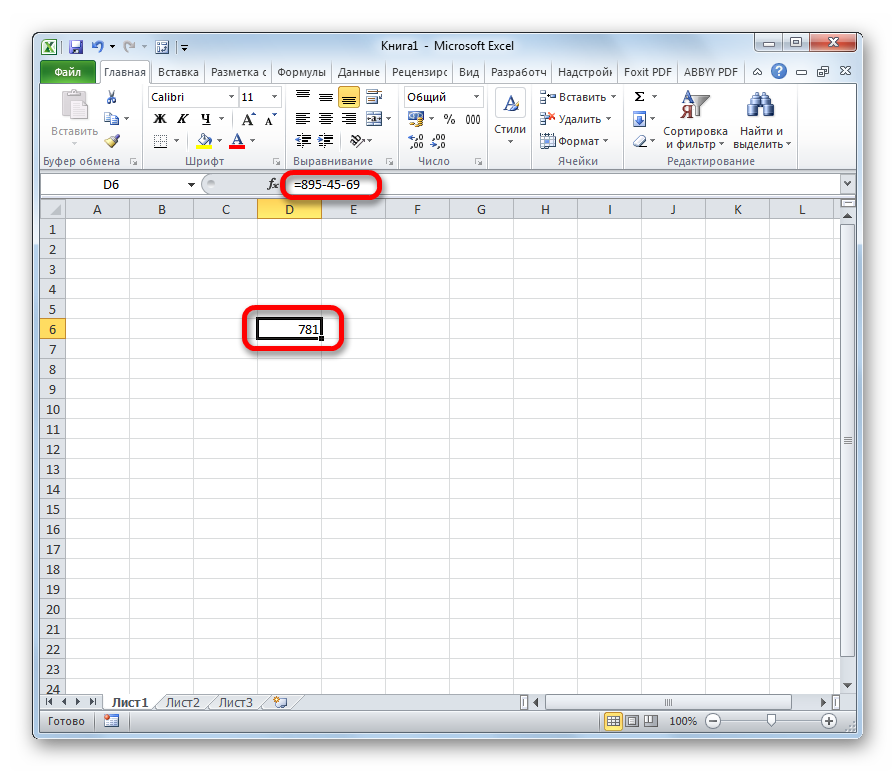
Выберите ячейку (в данном случае D6), введите приведенную ниже формулу и нажмите кнопку Enter ключ, чтобы получить первый мнимый коэффициент. Выберите эту ячейку результата, а затем перетащите ее маркер автозаполнения вниз, чтобы получить другие результаты.
=IMAGINARY(B6)
Ноты:
1) Комплексное число может быть введено непосредственно в формулу и должно быть заключено в двойные кавычки. Таким образом, формулу в D6 можно изменить на:
=IMAGINARY(«4+2i»)
2) Функция IMAGINARY принимает только строчные буквы «i» и «j».
Связанные функции
Excel КОМПЛЕКС функция
Функция КОМПЛЕКС преобразует действительные и мнимые коэффициенты в комплексное число вида x + yi или x + yj.
Функция Excel IMABS
Функция IMABS получает абсолютное значение комплексного числа в форме x + yi или x + yj.
Функция усиления Excel
Функция IMPOWER возвращает комплексное число, возведенное в заданную степень.
Функция Excel improduct
Функция ИМПРОИЗВ возвращает произведение комплексных чисел от 1 до 255 в текстовом формате x + yi или x + yj.
Функция Excel БИТАНД
Функция IMREAL возвращает действительный коэффициент комплексного числа в виде x + yi или x + yj.
Функция Excel IMSUB
Функция IMSUB возвращает разность двух комплексных чисел в текстовом формате x + yi или x + yj.
Функция Excel ИМСУММ
Функция IMSUM возвращает сумму двух или более комплексных чисел в текстовом формате x + yi или x + yj.
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!
Операции с комплексными числами в MS Excel Санина Алёна
Представление комплексных чисел Комплексным числом называется выражения вида: z=x+iy, где х и у – действительные числа, i — мнимая единица Представление комплексного числа в таком виде является алгебраической формой комплексного числа
ПРИМЕЧАНИЕ. Все функции работы с комплексными числами допускают для мнимой единицы обозначение «i» или «j», но не «I» или «J». Использование верхнего регистра приводит к ошибке #ЗНАЧ!. Все функции, в которых используются два и более комплексных числа, требуют, чтобы обозначение мнимой единицы было идентичным.
Существуют также тригонометрическая и показательная формы. Тригонометрическая форма Показательная форма
Сопряженные комплексные числа Числа z=x+iy и z=x-iy называются сопряженными Два комплексных числа называются равными, если равны их действительные и мнимые части.
Функции МНИМ. ВЕЩ(компл_число) и МНИМ. ЧАСТЬ(компл_число) определяют, соответственно, вещественную и мнимую части комплексного числа компл_число, представленного в алгебраической форме и записанного в одну ячейку в формате x+yi
Функции МНИМ. ABS(компл_число) и МНИМ. АРГУМЕНТ(компл_число) вычисляют, значения модуля и аргумента комплексного числа, представленного в алгебраической форме в формате x+yi
Функция МНИМ. СОПРЯЖ (компл_число) вычисляет сопряженное комплексное число для комплексного числа, представленного в алгебраической в формате x+yi
Использование функции КОМПЛЕКСН(действительная_часть, мнимая_часть, [мнимая_единица]) Преобразует коэффициенты при вещественной и мнимой частях комплексного числа в комплексное число в форме x + yi или x — yj.
Аргументы функции КОМПЛЕКСН Действительная_часть — обязательный аргумент. Действительная часть комплексного числа. Мнимая_часть — обязательный аргумент. Мнимая часть комплексного числа. Мнимая_единица — необязательный аргумент. Обозначение мнимой единицы в комплексном числе. Если аргумент «мнимая_единица» опущен, используется суффикс «i».
Замечания Если действительная_часть не является числом, функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!. Если мнимая_единица не является ни «i», ни «j», функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
Арифметические операции 1. Сумма(разность) комплексных чисел: 2. Произведение комплексных чисел:
Арифметические операции 3. Деление дух комплексных чисел: 4. Возведение комплексного числа в натуральную степень n: 5. Извлечение корня из комплексного числа:
В MS Excel для выполнения арифметических операций с комплексным числами предназначены функции МНИМ. СУММ, МНИМ. РАЗН, МНИМ. ПРОИЗВЕД, МНИМ. ДЕЛ, МНИМ. СТЕПЕНЬ, и МНИМ. КОРЕНЬ.
Функуции МНИМ. СУММ(компл_число 1; компл_число 2; …) и МНИМ. ПРОИЗВЕД(компл_число 1; компл_число 2; …) предназначены для вычисление суммы и произведения, соответственно, до 29 комплексных чисел (компл_число 1; компл_число 2; …), представленных в алгебраической форме.
Функуции МНИМ. РАЗН (компл_число 1; компл_число 2; …) и МНИМ. ДЕЛ(компл_число 1; компл_число 2; …) предназначены для вычисления разности и частного от деления двух комплексных чисел (компл_число 1; компл_число 2; …), представленных в алгебраической форме;
Функции МНИМ. СТЕПЕНЬ(компл_число; Число) и МНИМ. КОРЕНЬ(компл_число; число 2) вычисляют целую или дробную степень (число) комплексного числа (компл_число) и квадратный корень из комплексного числа (компл_число), представленного в алгебраической форме.
Функции комплексной переменной Функция w=f(z), где z=x+iy и w=u+iv, определена, если известны две функции от двух действительных переменных: u=u(x, y), v=v(x, y)
Из большого числа функций комплексной переменной в Excel реализованы несколько функций, наиболее часто используемых на практике. 1. Экспоненциальная функция комплексной переменной реализованная в функции Excel-МНИМ. ЕХР 2. Функция натурального логарифма которой соответствует функция МНИМ. LN
3. Функция десятичного логарифма осуществляет функция МНИМ. LOG 10 4. Функция логарифма по основанию 2 осуществляется функцией МНИМ. LOG 2.
5. Функции синуса и косинуса МНИМ. SIN соответственно МНИМ. COS Здесь shy и chy — гиперболические функции синуса и косинуса:
Все специальные функции Excel, реализующие названные функции комплексной переменной имеют единственный параметр — компл_число. Компл_число — это комплексное число в алгебраической форме, которое является переменной z для соответствующей функции. Результатом вычислений также является комплексное число в алгебраической форме.
Функция КОМПЛЕКСН как и большинство функций категории «Инженерные», работает начиная с 2007-й версии Excel.
Описание функции КОМПЛЕКСН
Преобразует коэффициенты при вещественной и мнимой частях комплексного числа в комплексное число в форме x + yi или x + yj.
Внимание! Все функции работы с комплексными числами допускают для мнимой единицы обозначение «i» или «j», но не «I» или «J». Использование верхнего регистра приводит к ошибке #ЗНАЧ!. Все функции, в которых используются два и более комплексных числа, требуют, чтобы обозначение мнимой единицы было идентичным.
Синтаксис
=КОМПЛЕКСН(действительная_часть; мнимая_часть; [мнимая_единица])Аргументы
действительная_частьмнимая_частьмнимая_единица
Обязательный аргумент. Действительная часть комплексного числа.
Обязательный аргумент. Мнимая часть комплексного числа.
Необязательный аргумент. Обозначение мнимой единицы в комплексном числе. Если аргумент «мнимая_единица» опущен, используется суффикс «i».
Замечания
- Если действительная_часть не является числом, функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
- Если мнимая_часть не является числом, функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
- Если мнимая_единица не является ни «i», ни «j», функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
Пример
В этом учебном материале вы узнаете, как использовать Excel функцию КОМПЛЕКСН с синтаксисом и примерами.
Описание
Microsoft Excel функция КОМПЛЕКСН преобразует коэффициенты (действительные и мнимые) в комплексные числа. Комплексное число может быть в любой форме: x + yi или x + yj. КОМПЛЕКСН функция — это встроенная в Excel функция, которая относится к категории инженерных функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию КОМПЛЕКСН можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции КОМПЛЕКСН в Microsoft Excel:
КОМПЛЕКСН(действительная_часть;мнимая_часть;[мнимая_единица])
Аргументы или параметры
- действительная_часть
- Реальный коэффициент комплексного числа.
- мнимая_часть
- Мнимый коэффициент комплексного числа.
- мнимая_единица
- Необязательно. Это либо «i», либо «j», которое должно представлять суффикс мнимой составляющей комплексного числа.
Еслимнимая_единицаопущен, предполагается, чтомнимая_единицаравен «i».
Возвращаемое значение
Функция КОМПЛЕКСН возвращает строковое/текстовое значение.
Если действительная_часть не является числовым значением, функция КОМПЛЕКСН вернет ошибку #ЗНАЧ!.
Если мнимая_часть не является числовым значением, функция КОМПЛЕКСН вернет ошибку #ЗНАЧ!.
Если мнимая_единица не является ни «i», ни «j», функция КОМПЛЕКСН вернет ошибку #ЗНАЧ!.
Если мнимая_единица введен в верхнем регистре (например, «I» или «J» вместо «i» или «j»), функция КОМПЛЕКСН вернет ошибку #ЗНАЧ!.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции КОМПЛЕКСН, чтобы понять, как использовать Excel функцию КОМПЛЕКСН в качестве функции рабочего листа в Microsoft Excel:
На основании, приведенной выше электронной таблицы Excel могут быть возвращены следующие примеры КОМПЛЕКСН функций:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
=КОМПЛЕКСН(A2;B2) Результат: «3+5i» =КОМПЛЕКСН(A2;B2;«i») Результат: «3+5i» =КОМПЛЕКСН(A2;B2;«j») Результат: «3+5j» =КОМПЛЕКСН(A3;B3) Результат: «2+i» =КОМПЛЕКСН(A3;B3;«i») Результат: «2+i» =КОМПЛЕКСН(A3;B3;«j») Результат: «2+j» |
Сервис для работы с таблицами Microsoft Excel часто используется для систематизации данных в числовом формате и проведения вычислений с ними. Вычитание – одно из основных математических действий, без него не обходится ни одно сложное вычисление. Есть несколько способов внедрить в таблицу ячейки с вычитанием, каждый из которых будет подробно разобран ниже.
Содержание
- Как в Экселе сделать функцию вычитания
- Процедура вычитания
- Пример 1: разность конкретных чисел
- Пример 2: вычитание числа из ячейки
- Пример 3: разность между числами в ячейках
- Пример 4: вычитание одного столбца из другого
- Пример 5: вычитание конкретного числа из столбца
- Вычитание чисел в интервалах
- Функция IMSUBTR
- Заключение
Как в Экселе сделать функцию вычитания
Вычитание в таблице происходит так же, как и на бумаге. Выражение должно состоять из уменьшаемого, вычитаемого и знака «-» между ними. Можно вписать уменьшаемое и вычитаемое вручную или выбрать ячейки с этими данными.
Обратите внимание! Существует одно условие, отличающее вычитание в Excel от обычного действия. Любая функция в этой программе начинается со знака равенства. Если не поставить этот знак перед составленным выражением, результат не появится в ячейке автоматически. Программа воспримет написанное как текст. По этой причине важно всегда ставить в начале знак «=».
Необходимо составить формулу со знаком «-», проверить правильность выбора ячеек или записи чисел и нажать «Enter». В ячейке, где была написана формула, немедленно появится разность двух или большего количества чисел. К сожалению, в Менеджере функций нет готовой формулы вычитания, поэтому придется пойти другими путями. Воспользоваться каталогом формул получится только для более сложных вычислений, например, тех, где используются комплексные числа. Рассмотрим все работающие способы далее.
Процедура вычитания
Сначала, как и говорилось, необходимо написать в сроке функций или в самой ячейке знак равенства. Это показывает, что значение ячейки равно результату математического действия. Далее в выражении должно появится уменьшаемое – число, которое станет меньше в результате расчета. Второе число – это вычитаемое, на него становится меньше первое. Между числами ставится минус. Не нужно делать тире из дефиса, иначе действие не сработает. Исследуем пять способов вычитания в таблицах Excel. Каждый пользователь сможет выбрать для себя удобный метод из этого списка.
Пример 1: разность конкретных чисел
Таблица составлена, ячейки заполнены, но теперь нужно вычесть один показатель из другого. Попробуем вычесть одно известное число из другого.
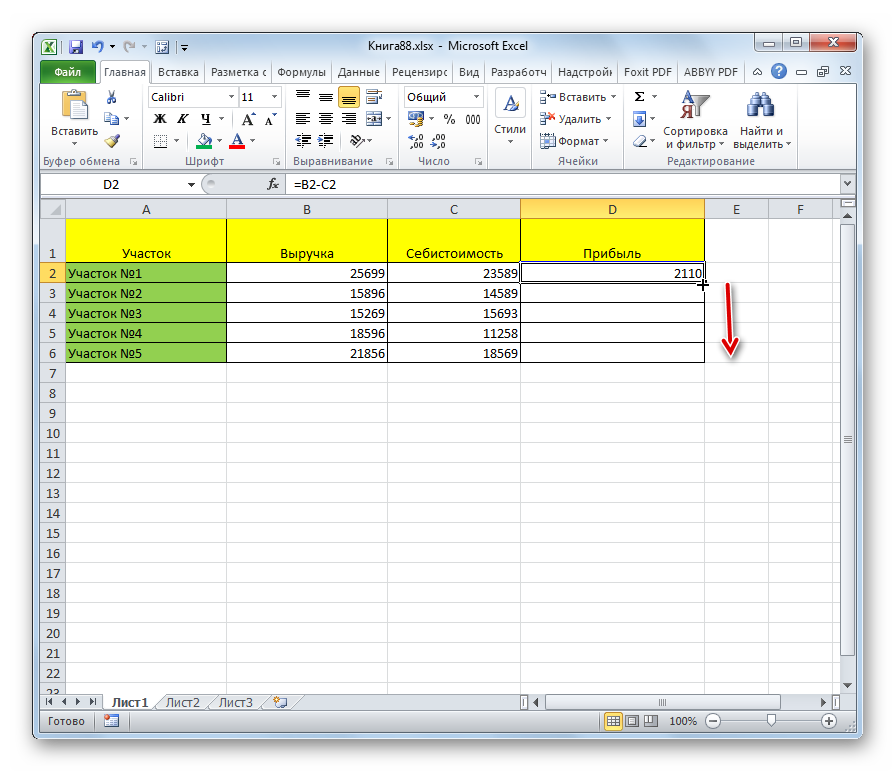
- Для начала необходимо выбрать ячейку, в которой окажется результат вычисления. Если на листе составлена таблица, и в ней есть колонка для таких значений, следует остановиться на одной из ячеек в этой колонке. В примере мы рассмотрим вычитание в случайной ячейке.
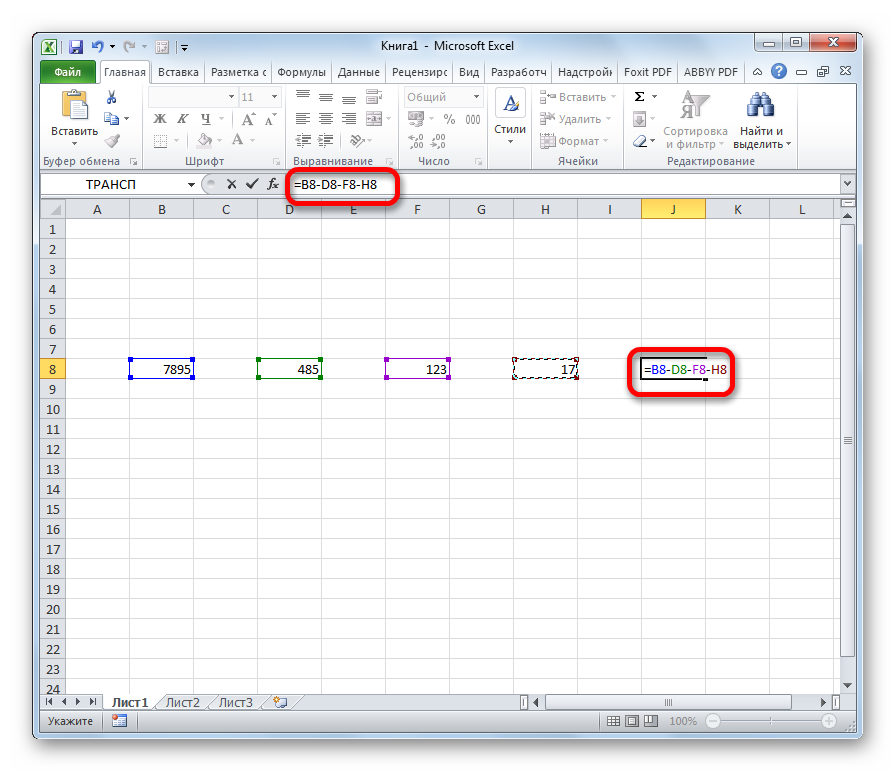
- Кликните по ней дважды, чтобы внутри появилось поле для заполнения. В это поле нужно вписать выражение по форме, которая была описана ранее: знак «=», уменьшаемое, знак минус и вычитаемое. Писать выражение можно и в строке функций, которая расположена над листом. Результат всех этих действий выглядит так:
Обратите внимание! Вычитаемых может быть сколько угодно, это зависит от цели вычисления. Перед каждым из них необходим минус, иначе расчеты не будут проведены правильно.
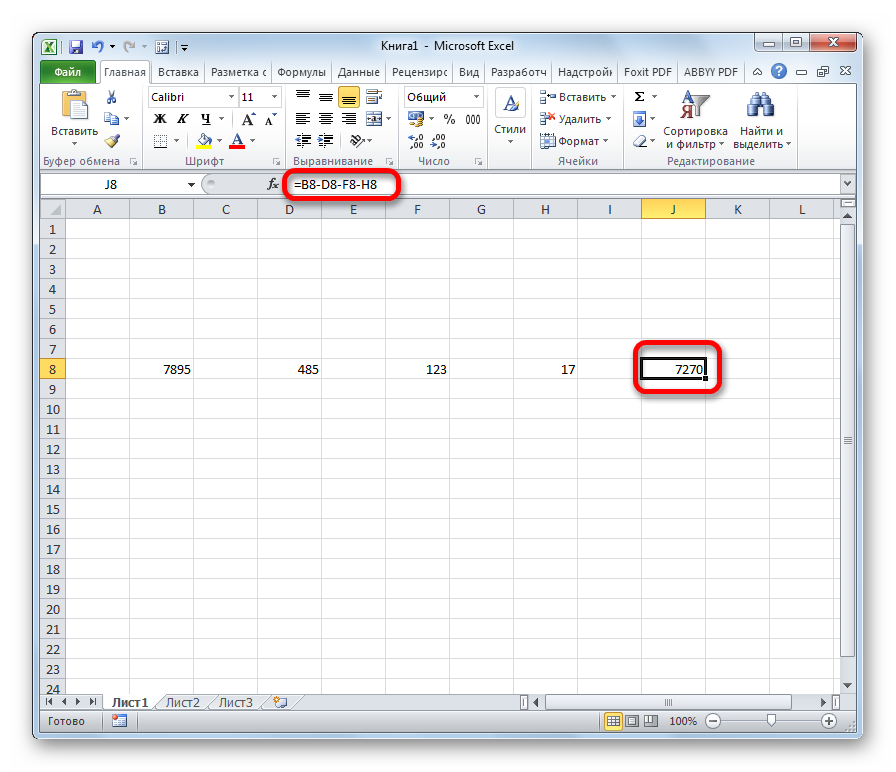
- Если числа в выражении и прочие его части записаны верно, следует нажать клавишу «Enter» на клавиатуре. В выбранной ячейке тут же появится разность, а в строке функций можно будет просмотреть записанное выражение и проверить его на ошибки. После проведения автоматических вычислений экран выглядит так:
Табличный процессор Microsoft Excel предназначен в том числе для удобного проведения расчетов, поэтому он работает с положительными и отрицательными числами. Не обязательно, чтобы уменьшаемым было большее число, но тогда результат будет меньше нуля.
Пример 2: вычитание числа из ячейки
Работа с ячейками таблиц – главная задача Эксель, поэтому с ними можно проводить самые разные действия. Например, можно составить математическое выражение, где уменьшаемым будет ячейка, а вычитаемым – число или наоборот.
- Первым действием снова выбираем ячейку для формулы и ставим в ней знак равенства.
- Далее нужно действовать иначе, чем в первом способе – необходимо найти в таблице ячейку со значением, которое уменьшится в результате вычитания, и кликнуть по ней. Вокруг этой ячейки образуется подвижный пунктирный контур, а в формуле появится ее обозначение в виде буквы и числа.
- Далее ставим знак «-», а после него вручную записываем в формулу вычитаемое. Должно получиться выражение такого вида:
- Чтобы запустить расчет, нужно нажать клавишу «Enter». Во время вычислений программа вычтет число из содержимого ячейки. Точно так же в ячейке с формулой появится результат. Пример результата:
Пример 3: разность между числами в ячейках
Не обязательно, чтобы в выражении было даже одно конкретное число – все действия можно совершать только с ячейками. Это удобно, когда в таблице много столбцов, и нужно быстро подсчитать итоговый результат с помощью вычитания.
- Расчет начинается с постановки знака равенства в выбранной ячейке.
- После этого необходимо найти ячейку, в которой содержится уменьшаемое. Важно не перепутать части таблицы между собой, потому что вычитание отличается от сложения строгим порядком записи выражения.
- После клика по ней в функции окажется название в виде обозначений строки и столбца, например, A2, C12 и прочее. Ставим минус и находим в таблице ячейку с вычитаемым.
- По ней тоже нужно кликнуть, и выражение станет законченным – в него автоматически попадет обозначение вычитаемого. Можно добавить сколько угодно вычитаемых и действий – программа все автоматически вычислит. Взгляните на то, как выглядит финальное выражение:
- Жмем клавишу «Enter» и получаем разность содержимого нескольких ячеек без лишних действий в виде копирования или повторного ручного введения чисел.
Важно! Главное правило использования этого способа – следить, чтобы ячейки в выражении оказались на своих местах.
Пример 4: вычитание одного столбца из другого
Возникают случаи, когда нужно вычесть содержимое ячеек одного столбца из ячеек другого. Пользователи нередко начинают прописывать отдельные формулы для каждой строки, но это очень трудоемкий процесс. Чтобы сэкономить время, которое тратится на составление нескольких десятков выражений, можно вычесть один столбец из другого одной функцией.
Причины воспользоваться этим методом могут быть разными, но одна из самых распространенных – необходимость высчитать прибыль. Для этого нужно вычесть из суммы дохода себестоимость сбытой продукции. Рассмотрим способ вычитания на таком примере:
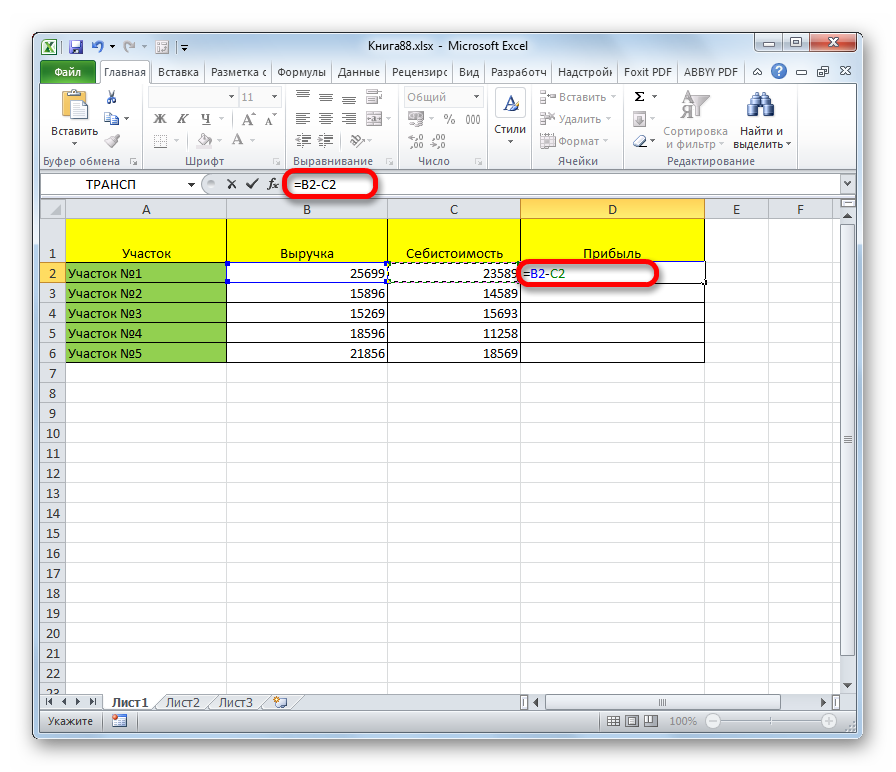
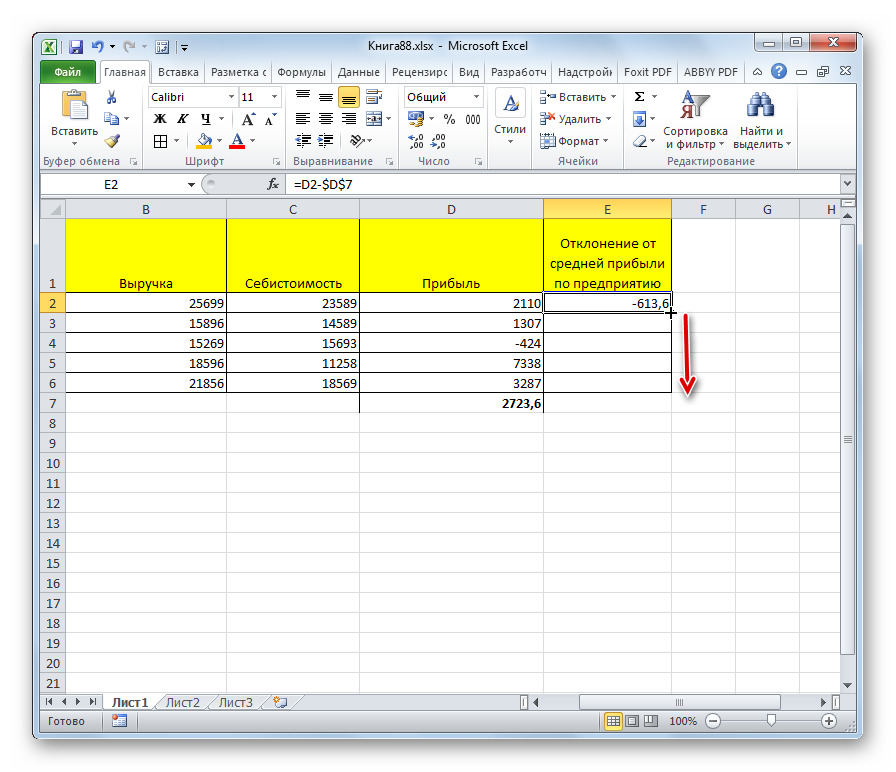
- Необходимо дважды кликнуть по верхней ячейке пустого столбца, вписать знак «=».
- Далее нужно составить формулу: выделяем ячейку с выручкой, ставим после ее обозначения в функции минус и нажимаем на ячейку с себестоимостью.
Внимание! Если ячейки выбраны правильно, не стоит нажимать на другие элементы листа. Легко не заметить, что уменьшаемое или вычитаемое случайно изменилось из-за такой ошибки.
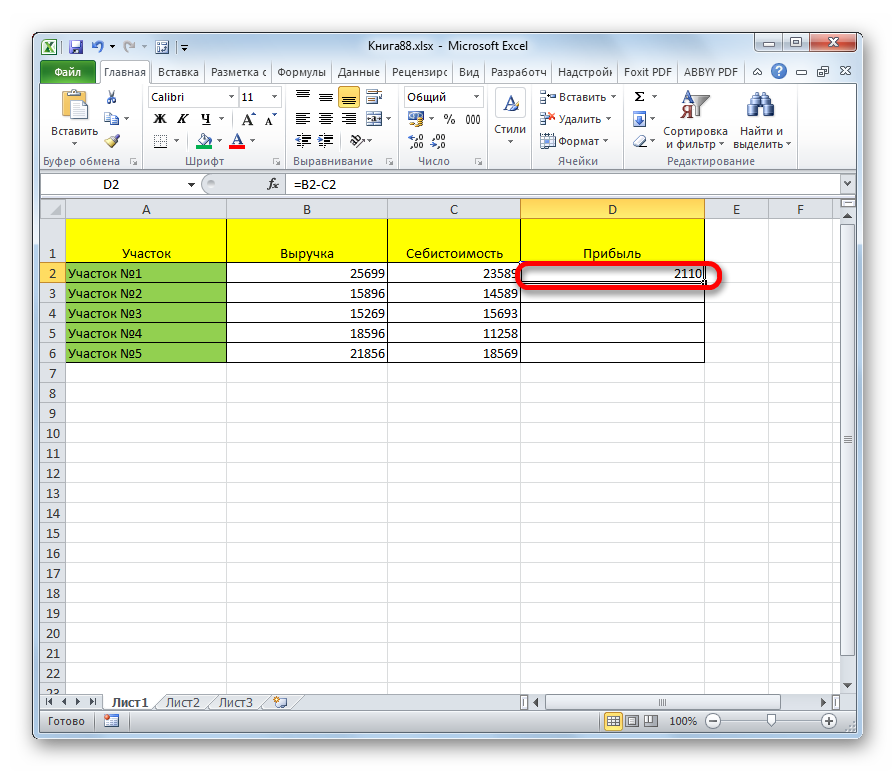
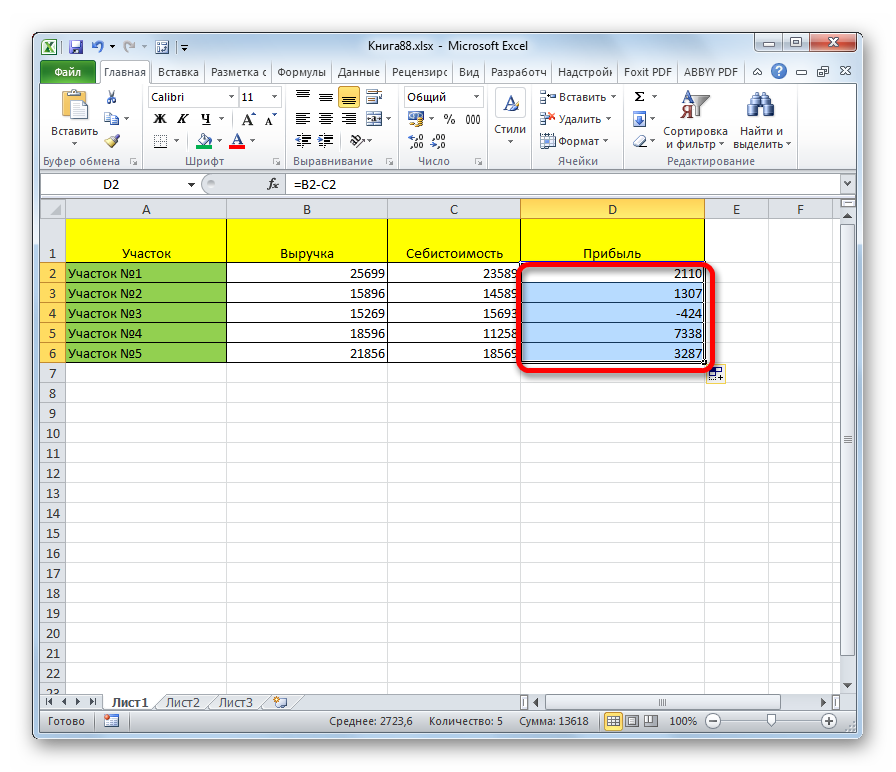
- Разность появится в ячейке после нажатия клавиши «Enter». Перед тем, как выполнять остальные шаги, нужно запустить вычисление.
- Взгляните на правый нижний угол выбранной ячейки – там находится маленький квадрат. При наведении на него курсора стрелка превращается в черный крест — это маркер заполнения. Теперь нужно зажать курсором правый нижний угол ячейки и потянуть вниз до последней ячейки, входящей в таблицу.
Важно! Выделение нижних ячеек после зажатия контура верхней ячейки в других местах не приведет к переносу формулы на строки ниже.
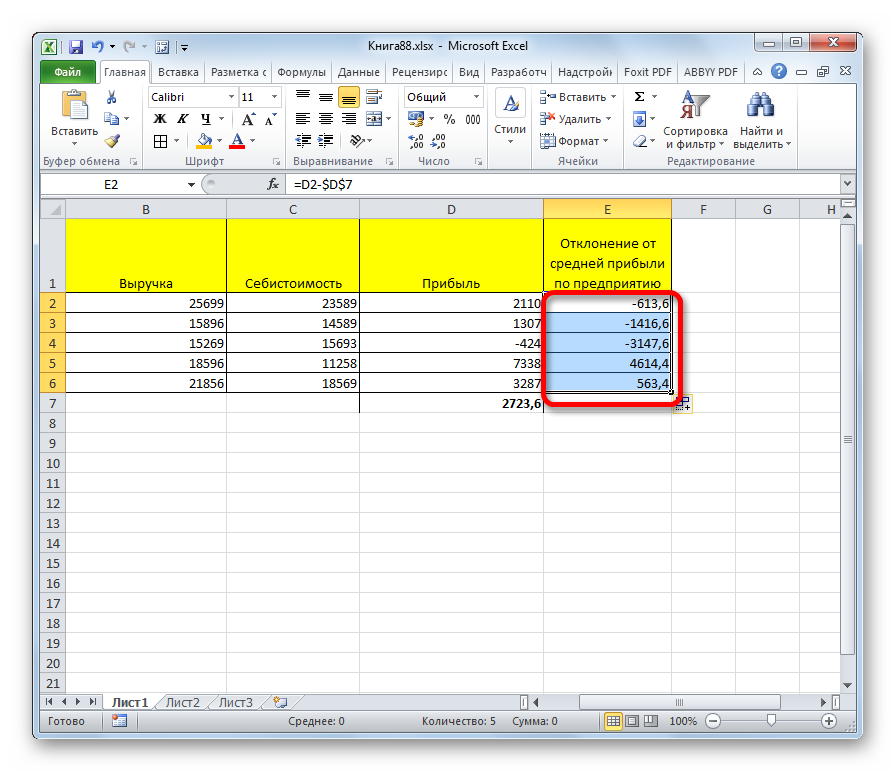
- Формула вычитания переместится в каждую ячейку столбца с заменой уменьшаемого и вычитаемого на соответствующие строке обозначения. Вот, как это выглядит:
Пример 5: вычитание конкретного числа из столбца
Иногда пользователям необходимо, чтобы при копировании происходило только частичное смещение, то есть, чтобы одна ячейка в функции оставалась неизменной. Такое тоже возможно благодаря табличному процессору Microsoft Excel.
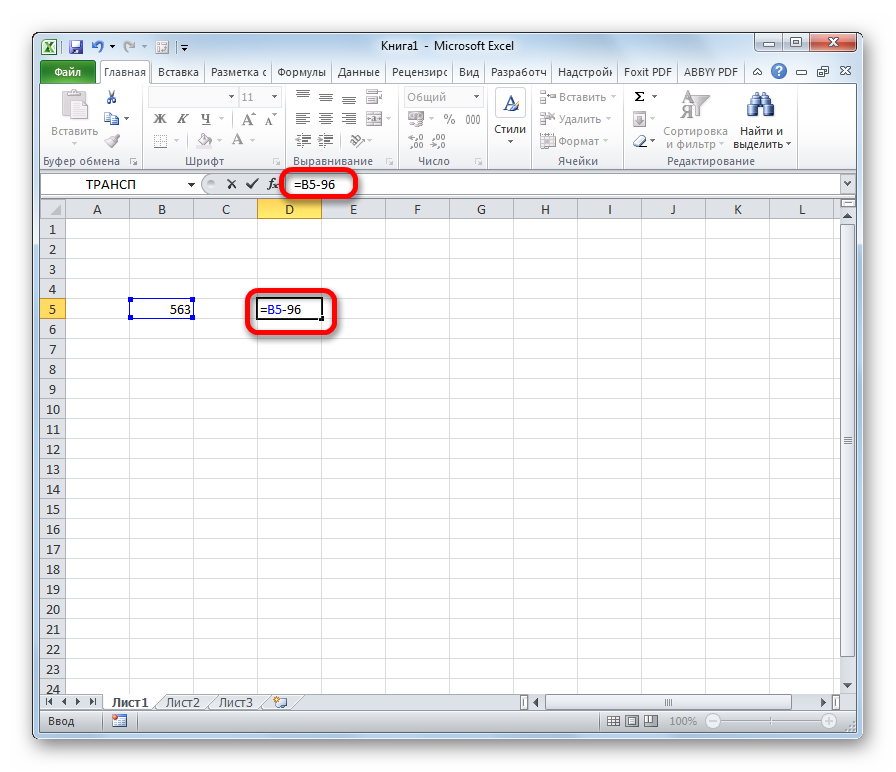
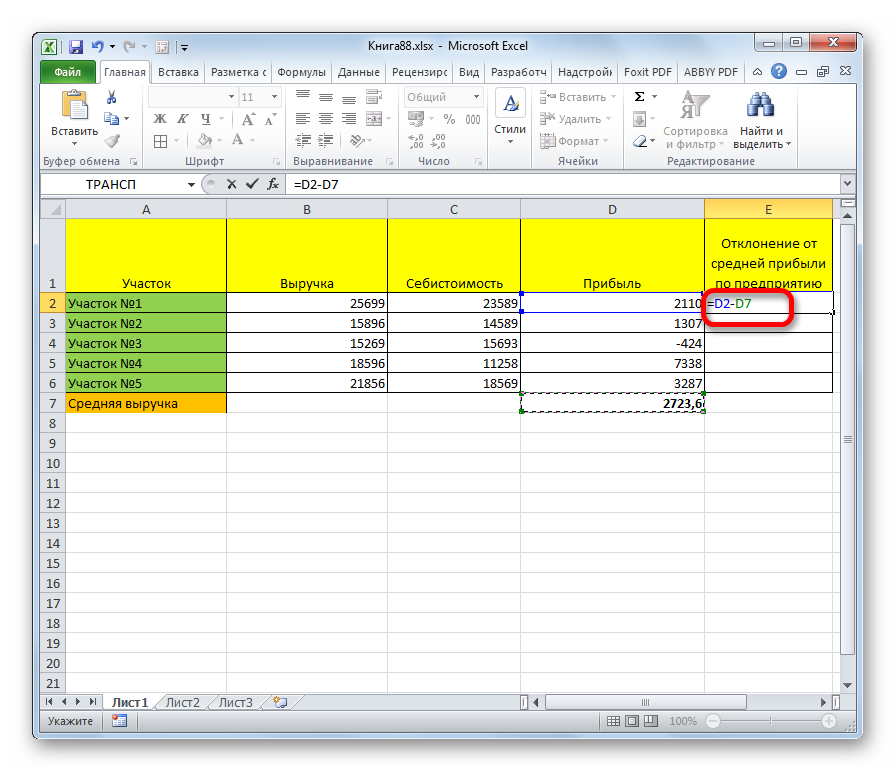
- Начать снова следует с выбора свободной ячейки и элементов выражения, постановки знаков «=» и «-». Представим, что в конкретном случае вычитаемое должно оставаться неизменным. Формула приобретает стандартный вид:
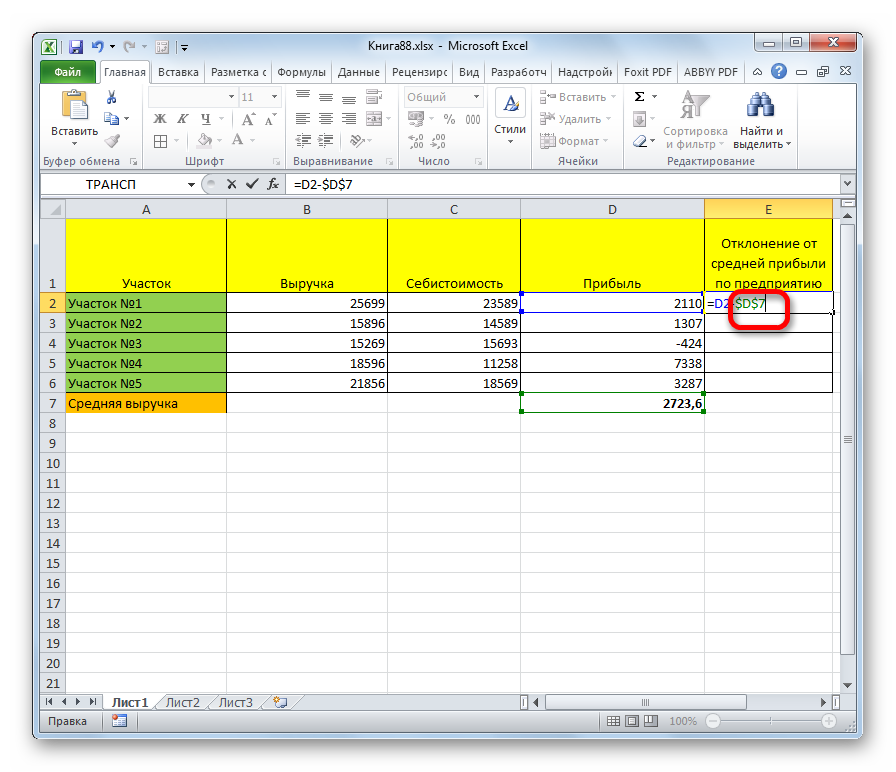
- Перед обозначениями ячейки вычитаемого, буквой и цифрой нужно поставить знаки доллара. Это закрепит вычитаемое в формуле, не позволит ячейке изменяться.
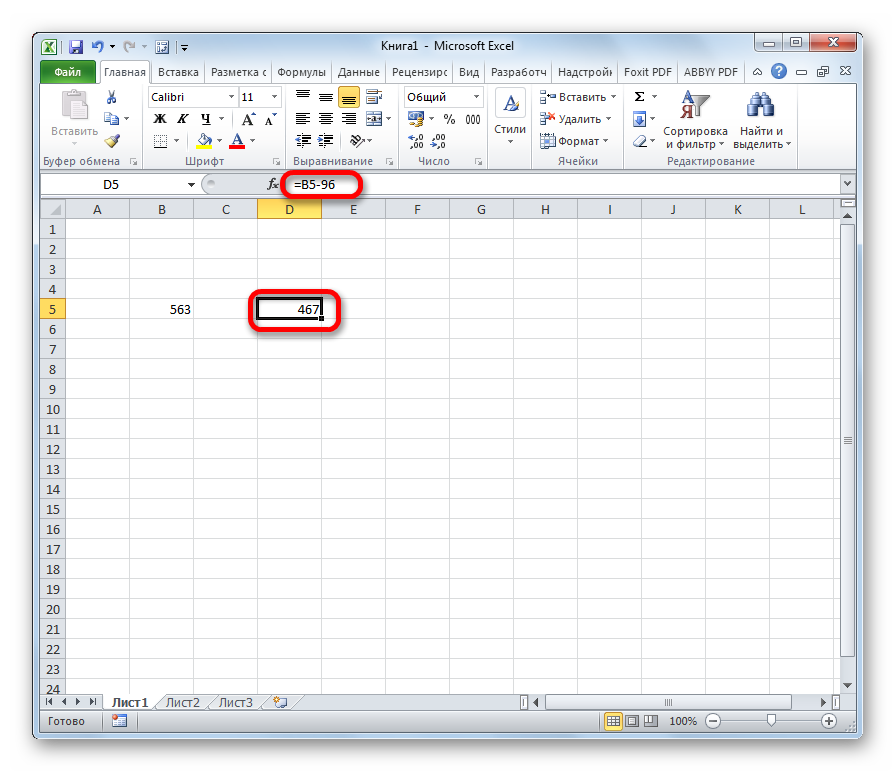
- Запустим расчет кликом по клавише «Enter», в первой строке столбца появится новое значение.
- Теперь можно заполнить весь столбец. Необходимо зажать маркер в правом нижнем углу первой ячейки и выделить оставшиеся части столбца.
- Проведется вычисление со всеми нужными ячейками, при этом вычитаемое не изменится. Проверить это можно кликом на одну из выделенных ячеек – в строке функций появится выражение, которым она заполнена. Итоговый вариант таблицы выглядит так:
Бессменной ячейкой может стать и уменьшаемое – зависит от того, где поставить знаки «$». Показанный пример – это частный случай, не всегда формула должна выглядеть именно так. Количество компонентов выражения может быть любым.
Вычитание чисел в интервалах
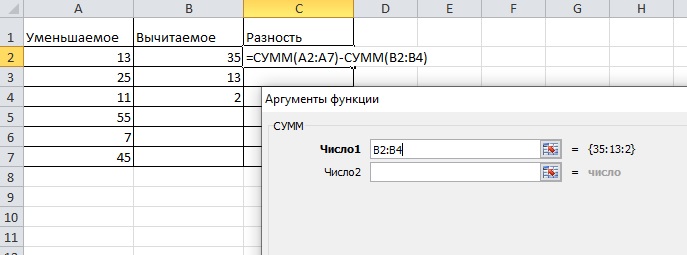
Вычесть одно число из содержимого столбца можно с помощью функции СУММ.
- Выберем свободную ячейку и откроем «Менеджер функций».
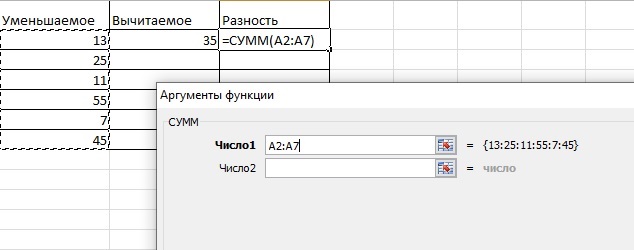
- Необходимо найти функцию СУММ и выбрать ее. Появится окно для заполнения функции значениями.
- Выделяем все ячейки строки уменьшаемого, где есть значения, интервал попадет в строку «Число 1», следующую строку заполнять не нужно.
- После нажатия на кнопку «ОК» в окне выбора чисел в ячейке появится сумма всех ячеек уменьшаемого, но это еще не конец – нужно провести вычитание.
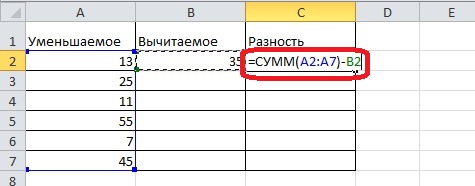
- Дважды кликаем на ячейку с формулой и добавляем после закрывающей скобки минус.
- Далее нужно выбрать ячейку-вычитаемое. В итоге формула должна выглядеть так:
- Теперь можно нажать «Enter», и в ячейке появится нужный результат.
- Вычитаемым может стать еще один интервал, для этого нужно еще раз использовать функцию СУММ после минуса. В итоге один интервал вычитается из другого. Немного дополним таблицу значениями в столбце вычитаемого для наглядности:
Функция IMSUBTR
На русском эта функция называется МНИМ.РАЗН. Это одна из инженерных функций, с ее помощью можно вычислить разность комплексных чисел. Комплексное число состоит из действительных и мнимых единиц. Несмотря на то, что между единицами стоит плюс, эта запись является единым числом, а не выражением. В реальности представить такое явление невозможно, оно является сугубо математическим. Комплексные числа можно изобразить на плоскости в виде точек.
Мнимая разность – это сочетание разностей действительных и мнимых частей комплексного числа. Результат вычитания вне таблицы:
(10+2i)-(7+10i) = 3-8i
10-7=3
2i-10i= -8i
- Чтобы провести вычисления, выберем пустую ячейку, откроем «Менеджер функций» и найдем там функцию МНИМ.РАЗН. Она находится в разделе «Инженерные».
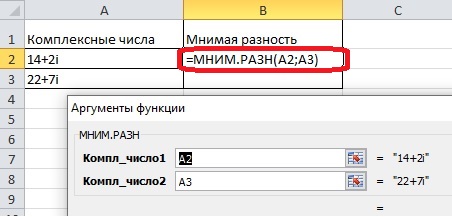
- В окне выбора чисел нужно заполнить обе строки – в каждой должно быть по одному комплексному числу. Для этого необходимо кликнуть по первой строке, а потом – по первой ячейке с числом, то же сделать со второй строкой и ячейкой. Итоговая формула выглядит так:
- Далее нажимаем «Enter» и получаем результат. В формуле не бывает больше одного вычитаемого, можно рассчитать мнимую разность только двух ячеек.
Заключение
Благодаря инструментам Excel вычитание превращается в легкую математическую операцию. Программа позволяет выполнять как самые простые действия со знаком «минус», так и заниматься узконаправленными вычислениями с использованием комплексных чисел. Пользуясь описанными выше методами, можно успеть намного больше во время работы с таблицами.
Оцените качество статьи. Нам важно ваше мнение:
Комплексные числа
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
Комплексно сопряженные числа
Два комплексных числа z = x + iy и у которых вещественные части одинаковые, а мнимые части отличаются знаком, называются комплексно сопряжёнными числами .
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
[expert_bq id=»1570″]Ввести формулу, в которой каждым множителем будет адрес ячейки причем они могут располагаться в любых местах, даже на разных листах или в отдельных книгах. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Использовать автосумму лучше тогда, когда диапазон суммирования является неразрывным, и ячейка для суммирования находится снизу или справа от диапазона суммирования. Иначе придется вручную поправлять диапазон, что не есть большая проблема.
Умножение в Эксель: 7 способов, формулы |
Выше были приведены примеры арифметических последовательностей. Некоторые другие виды последовательностей можно также сформировать формулами. Например, последовательность n2+1 ((n в степени 2) +1) создадим формулой =(СТРОКА()-СТРОКА($A200))^2+1 начиная с ячейки А2 .
















![Использование функции КОМПЛЕКСН(действительная_часть, мнимая_часть, [мнимая_единица]) Преобразует коэффициенты при вещественной и мнимой частях комплексного числа Использование функции КОМПЛЕКСН(действительная_часть, мнимая_часть, [мнимая_единица]) Преобразует коэффициенты при вещественной и мнимой частях комплексного числа](https://present5.com/presentation/117017419_107953049/image-11.jpg)