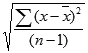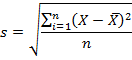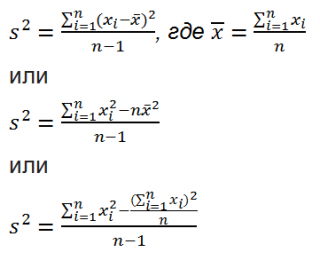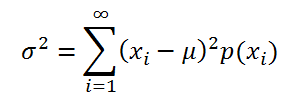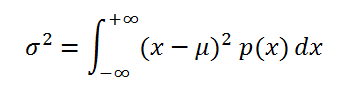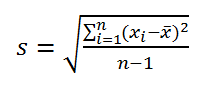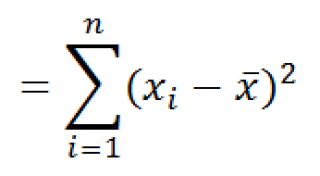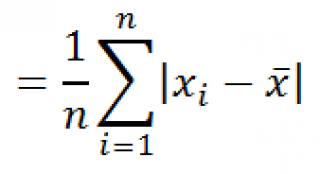Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции Функция СТАНДОТКЛОН.В.
Синтаксис
СТАНДОТКЛОН(число1;[число2];…)
Аргументы функции СТАНДОТКЛОН описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОНА.
-
Функция СТАНДОТКЛОН вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОН(A3:A12) |
Стандартное отклонение предела прочности (27,46392) |
27,46392 |
Нужна дополнительная помощь?
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
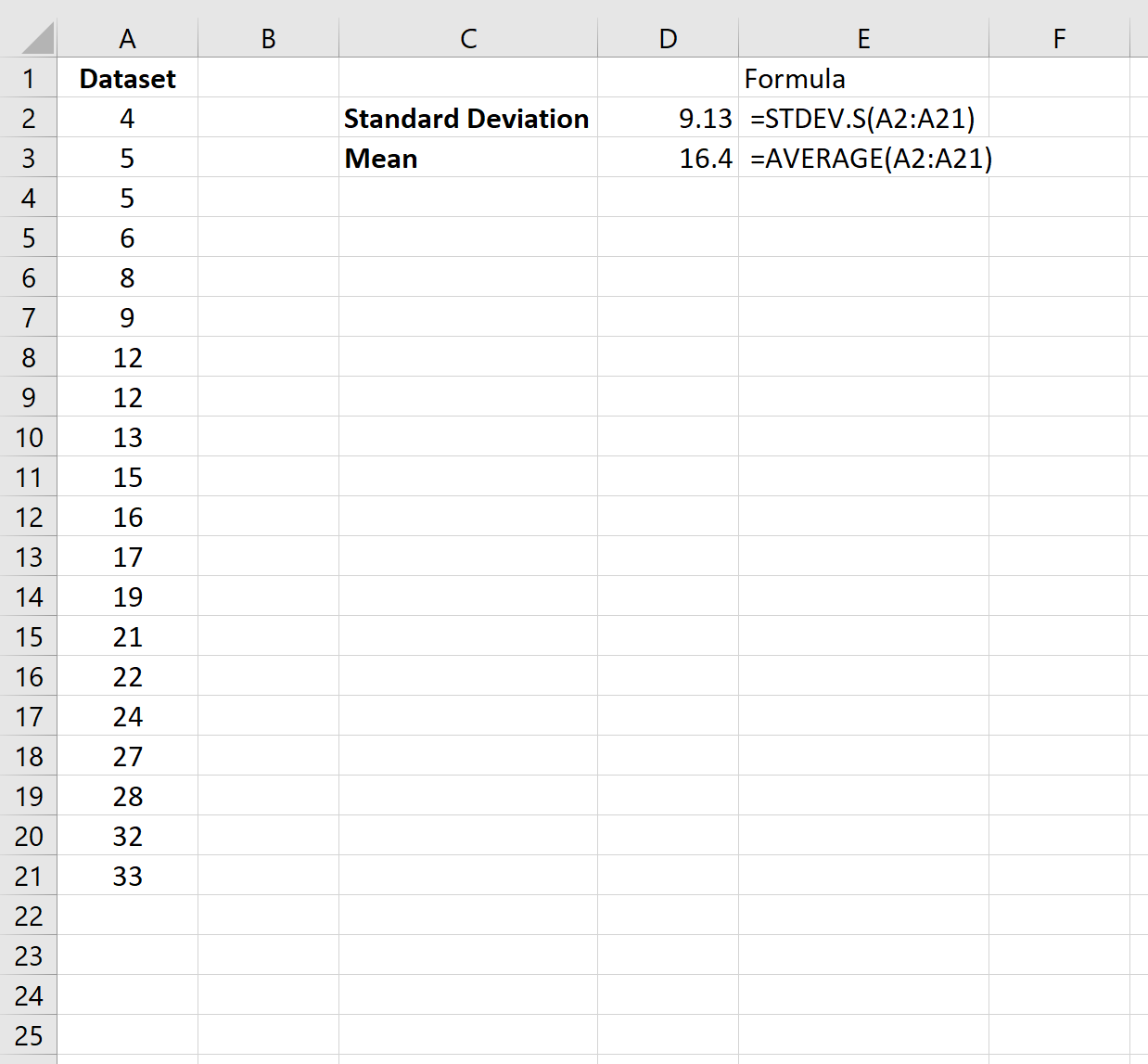
Пример 1: Среднее и стандартное отклонение одного набора данных
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
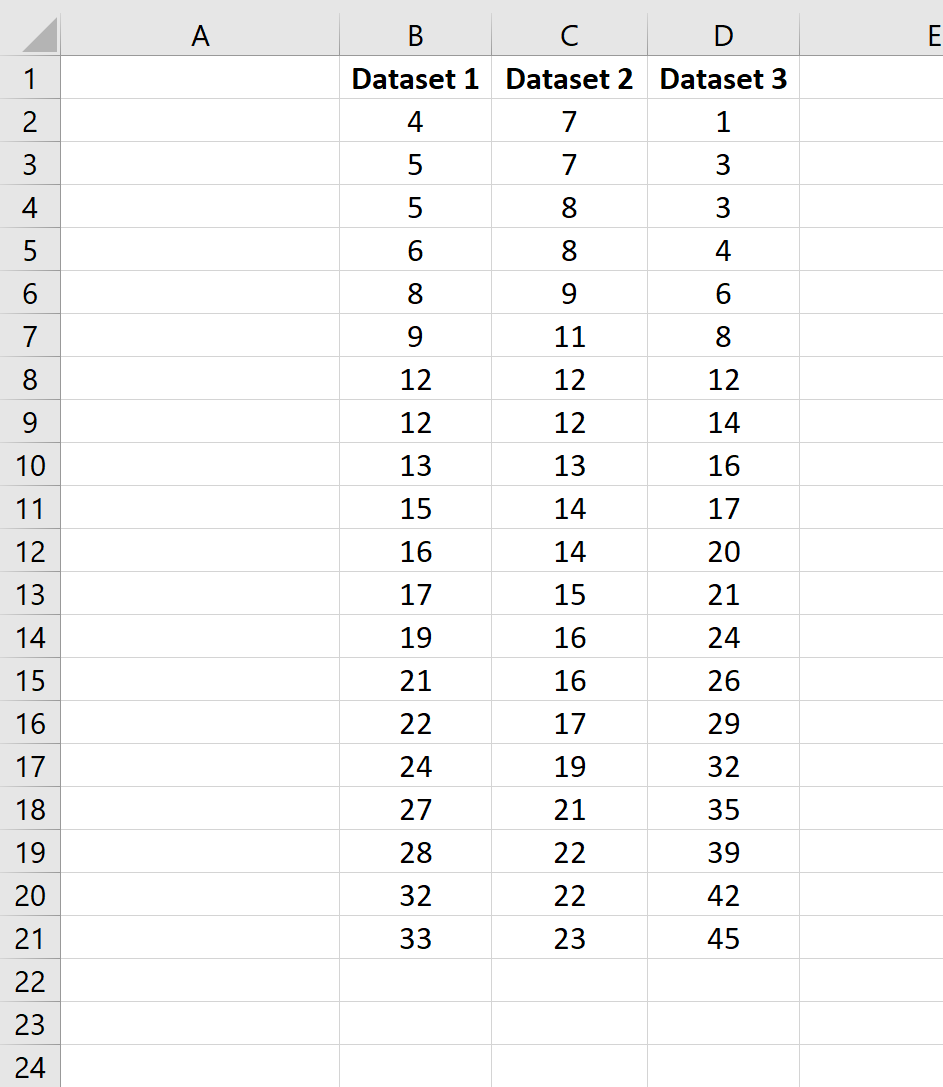
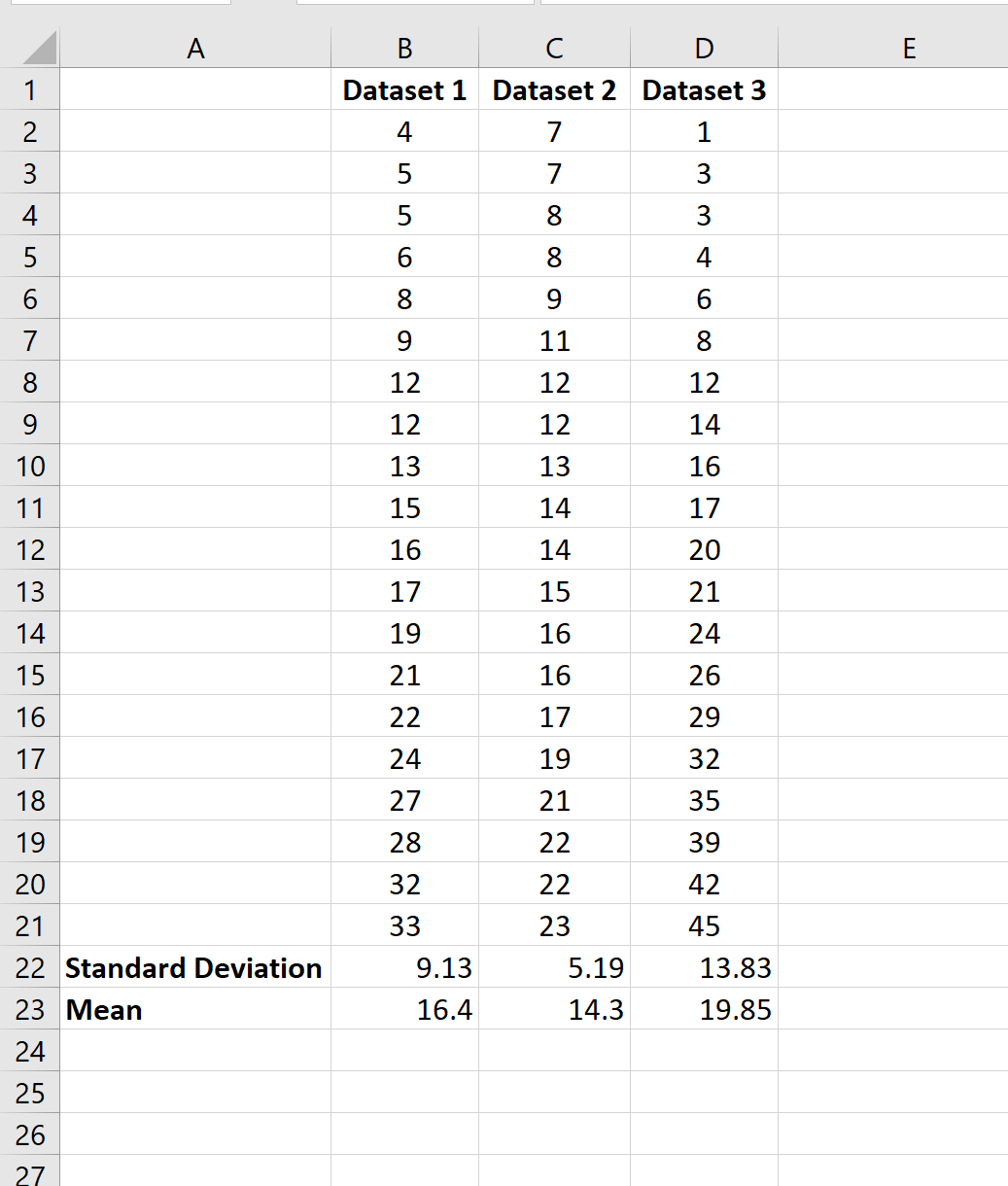
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
Предположим, у нас есть несколько наборов данных в Excel:
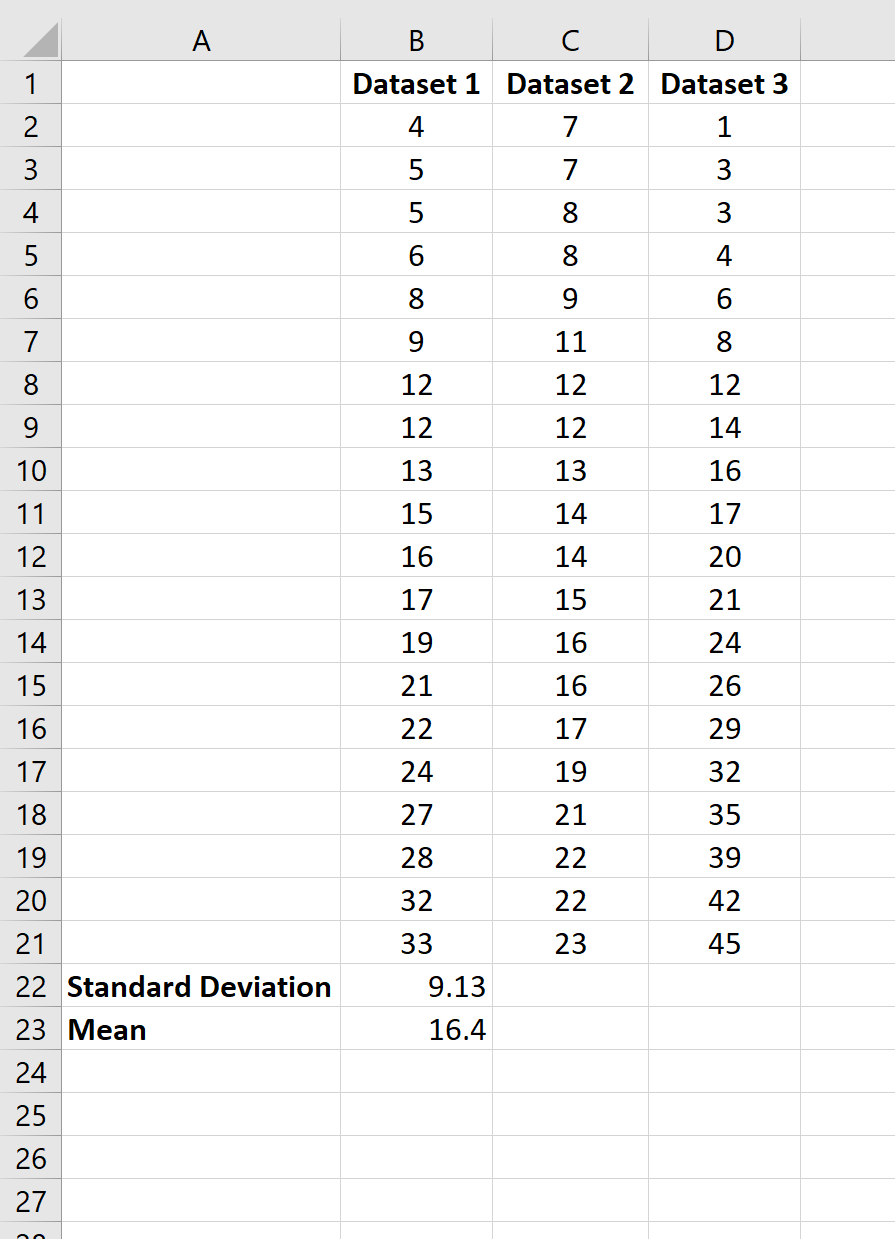
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Содержание
- Определение среднего квадратичного отклонения
- Расчет в Excel
- Способ 1: мастер функций
- Способ 2: вкладка «Формулы»
- Способ 3: ручной ввод формулы
- Вопросы и ответы
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
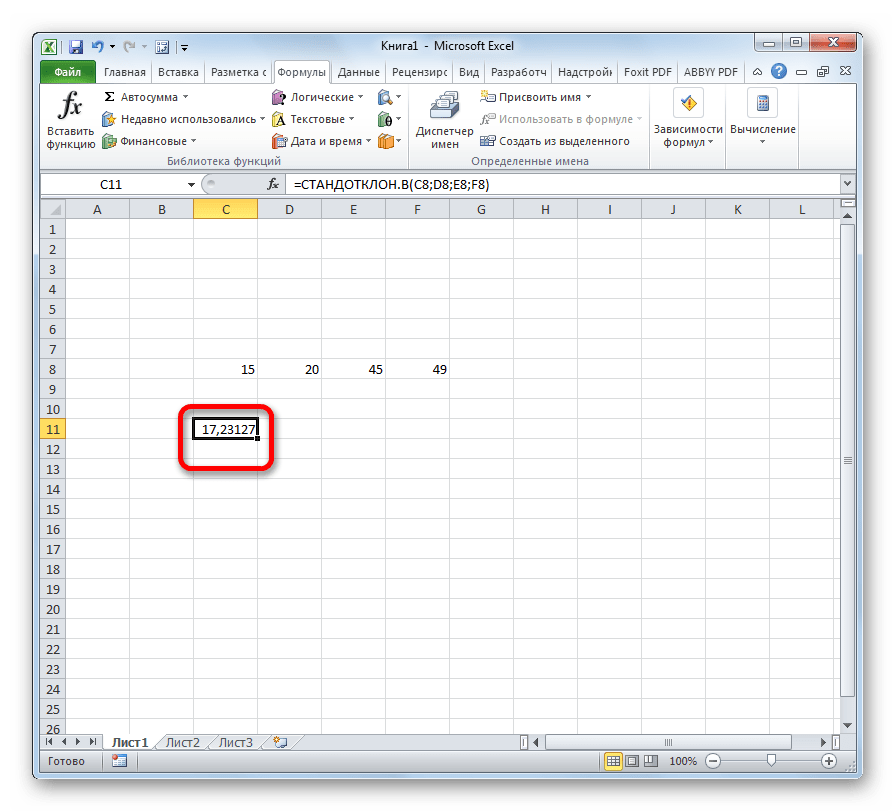
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
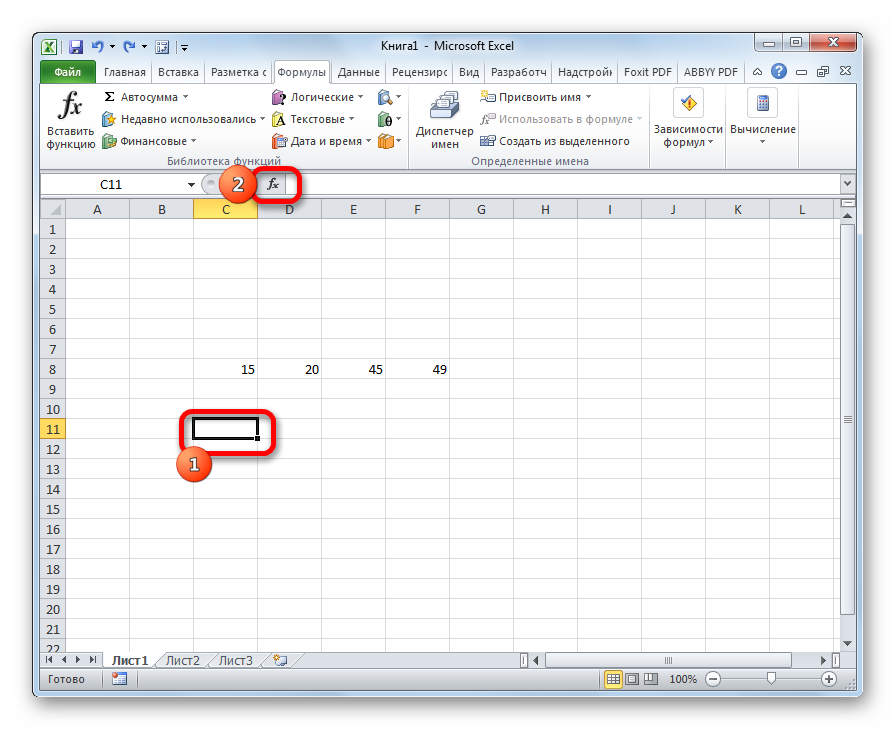
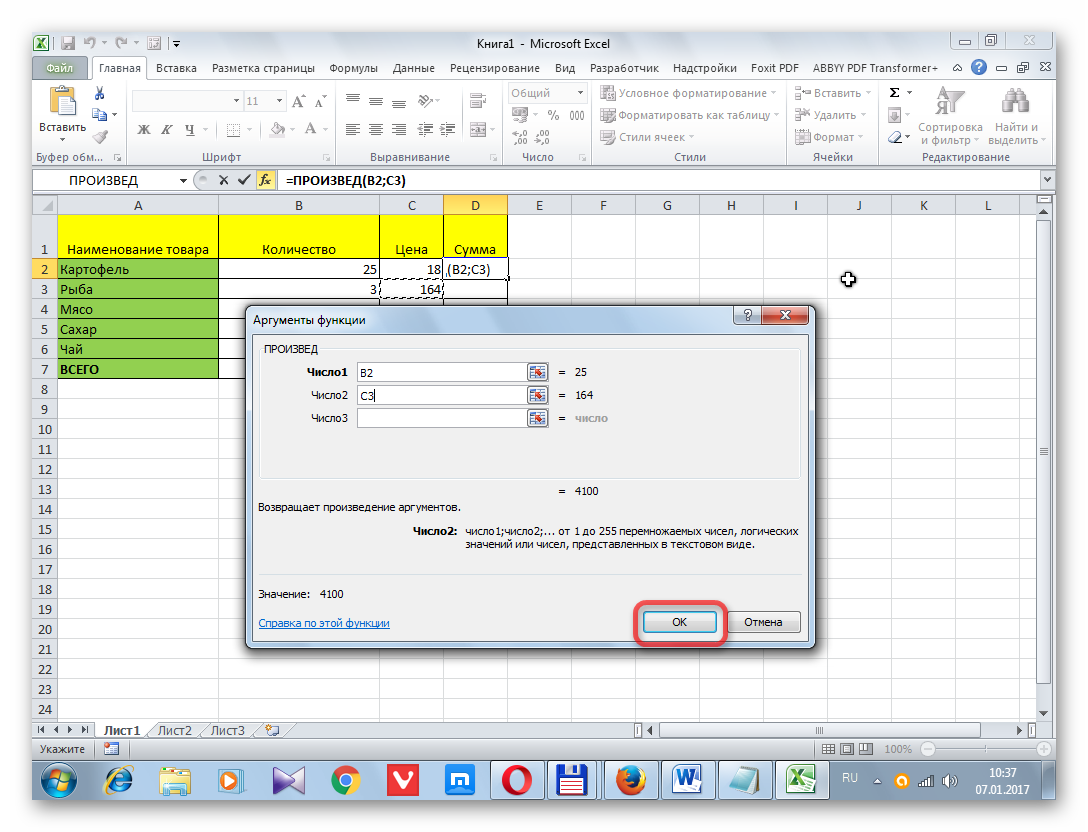
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
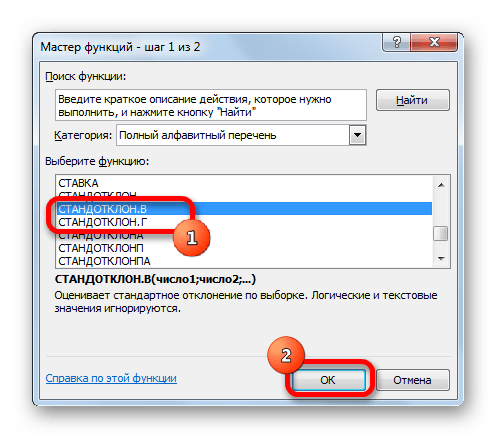
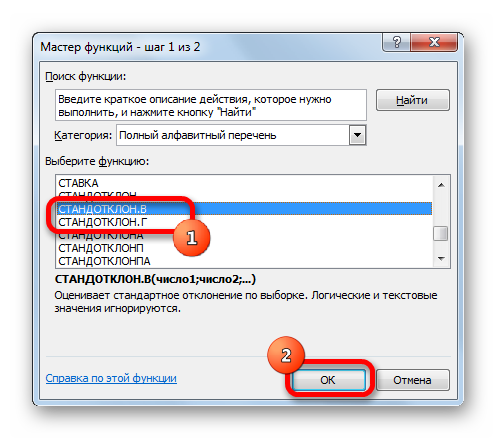
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
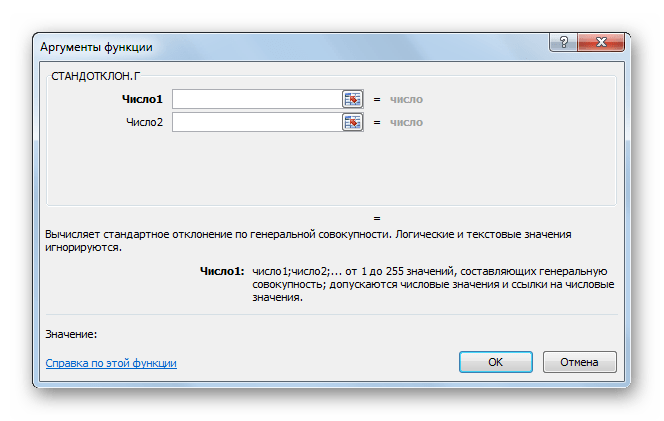
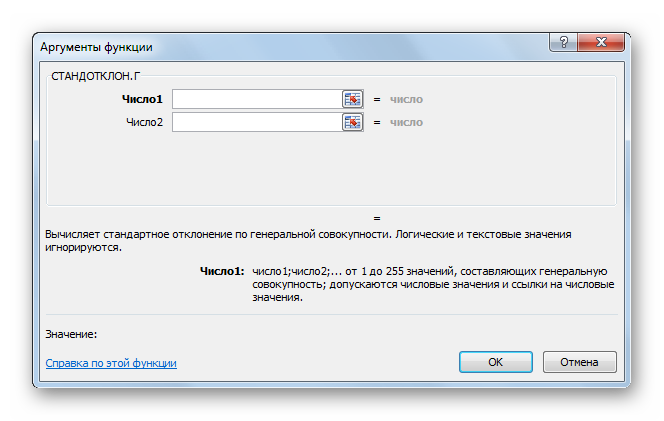
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
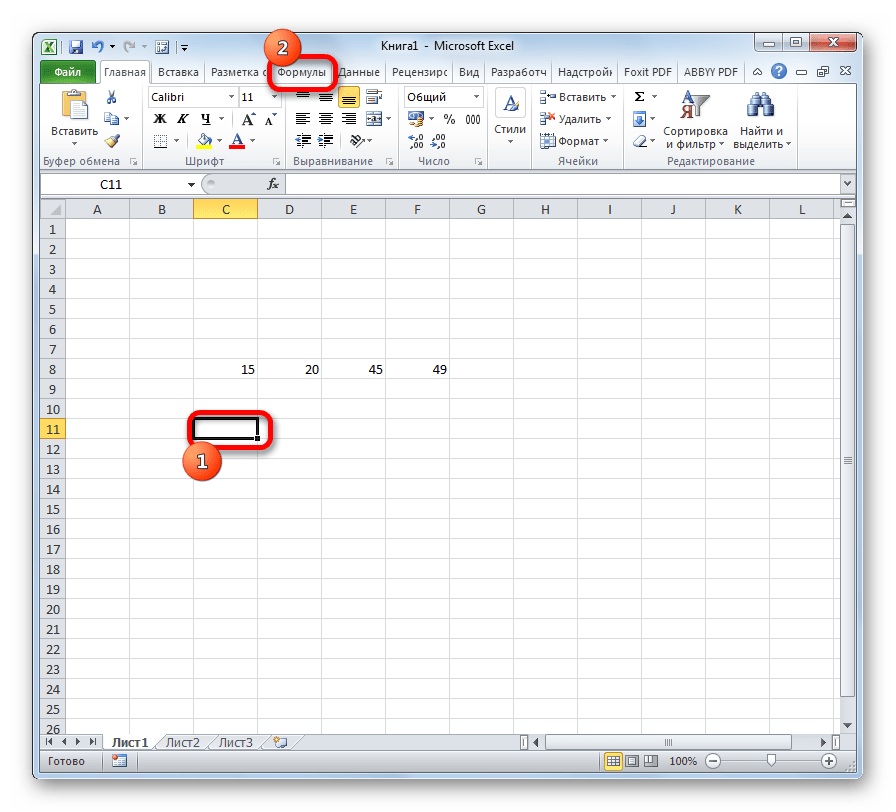
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
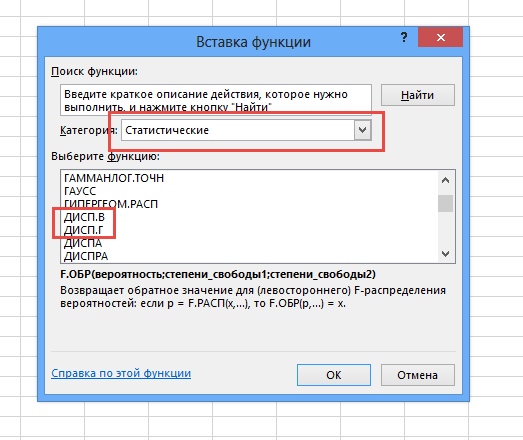
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
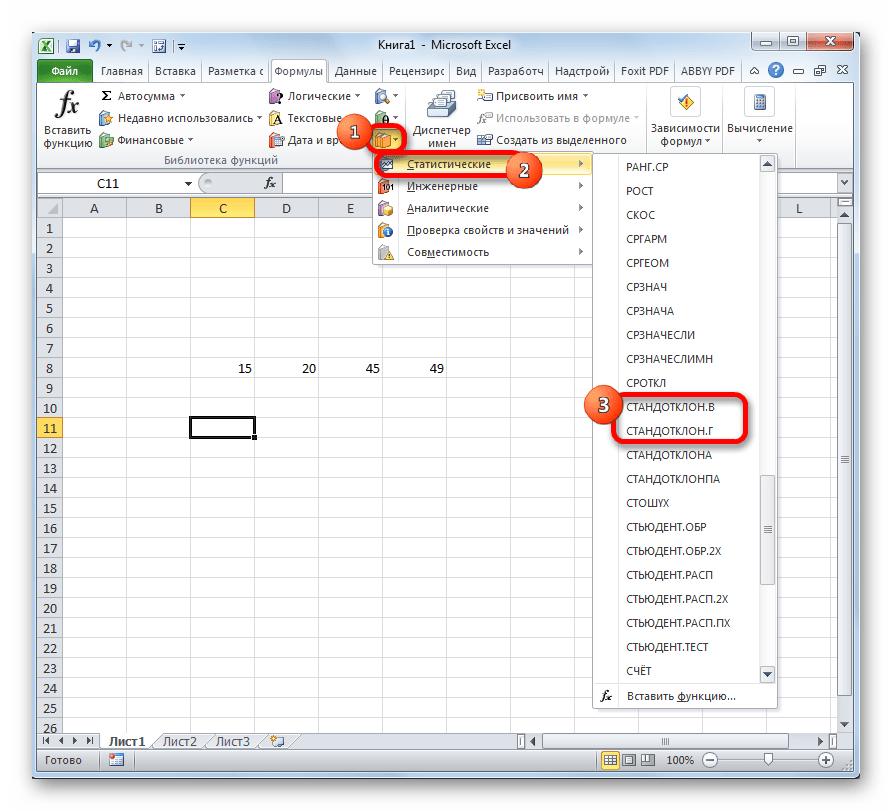
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
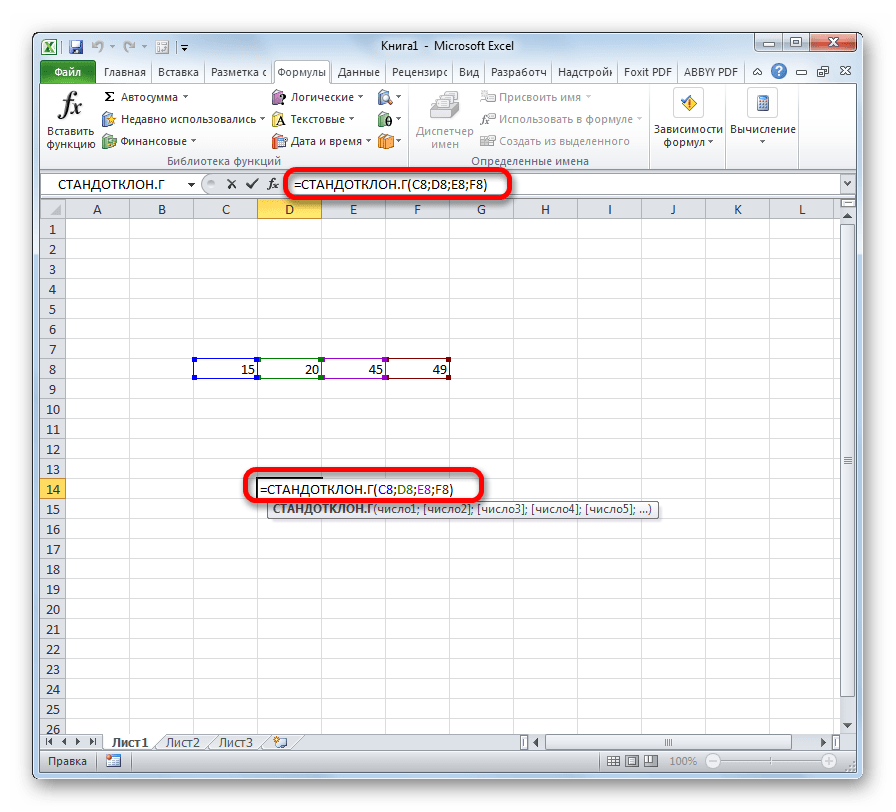
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
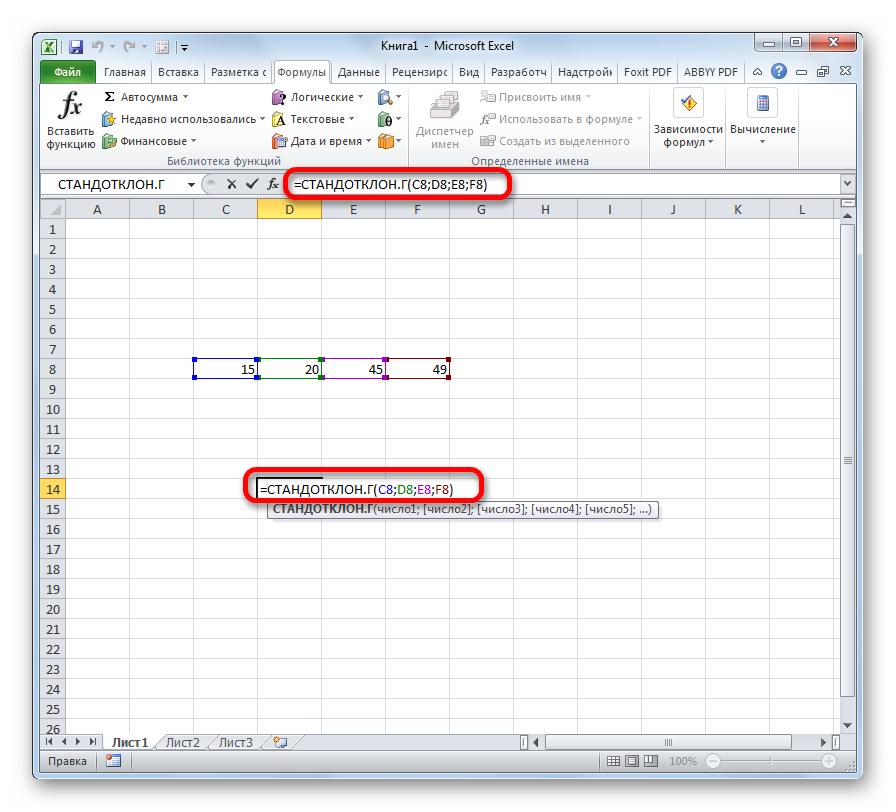
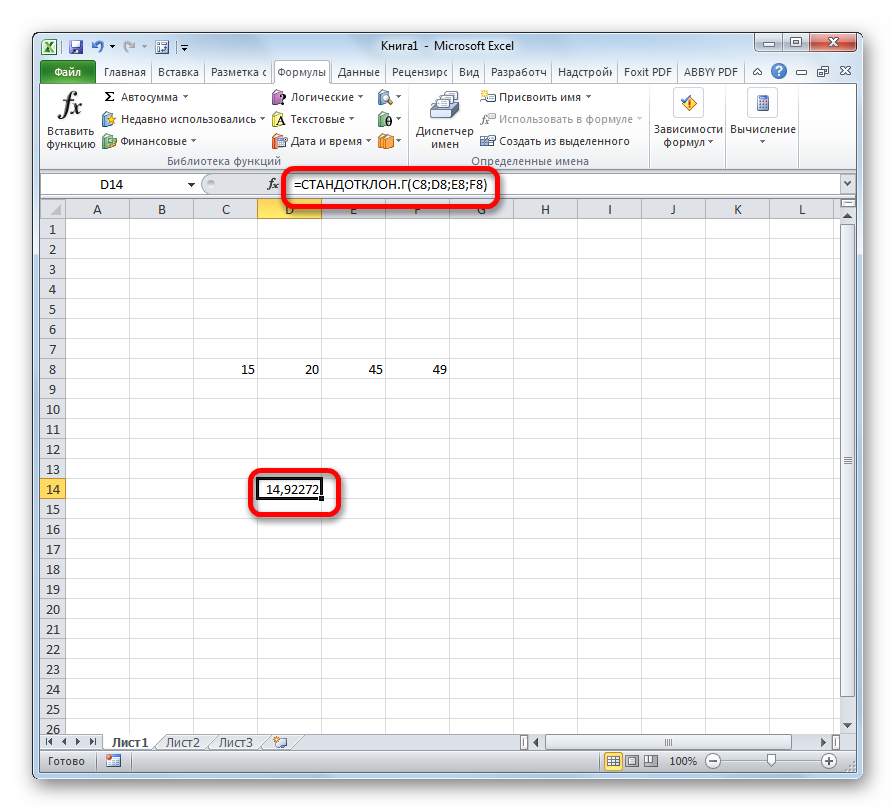
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
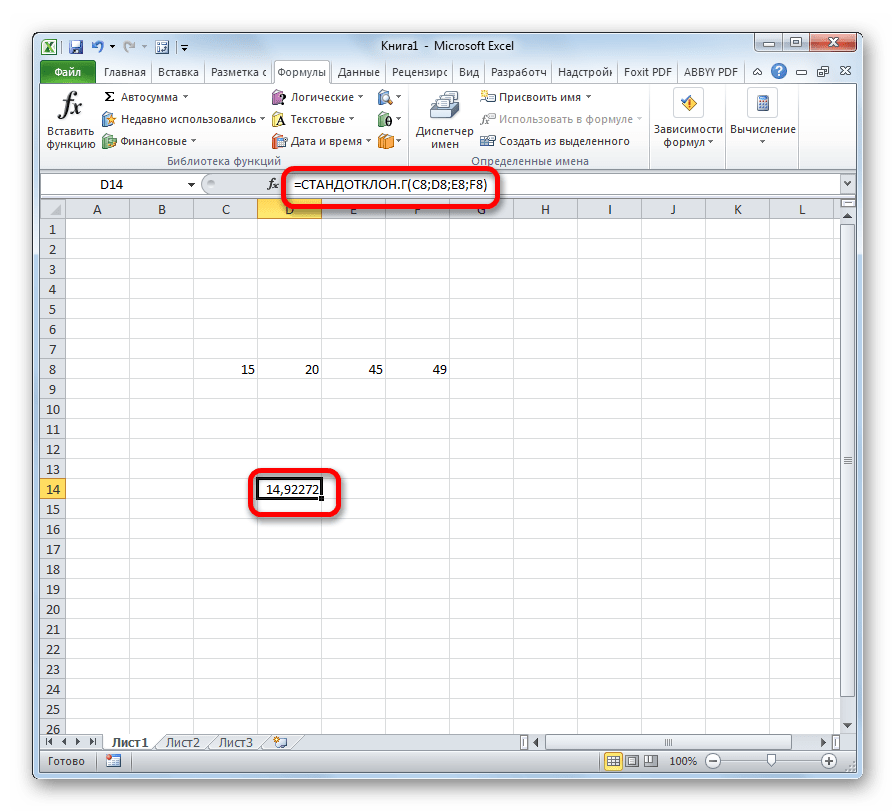
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Еще статьи по данной теме:
Помогла ли Вам статья?
Шаги
-
1
Запустите Microsoft Excel. Дважды щелкните по значку в виде белой буквы «X» на зеленом фоне. Как правило, он находится на рабочем столе или на панели задач. Откроется начальная страница Excel.
- Если у вас есть готовая таблица Excel с нужными данными, дважды щелкните по файлу, чтобы открыть его в Excel, а затем перейдите к шагу «Щелкните по пустой ячейке».
-
2
Нажмите Новая книга. Эта опция находится в верхней левой части начальной страницы Excel.
-
3
Введите данные. Выберите столбец, а затем введите нужные данные в ячейки этого столбца.
- Например, если вы выбрали столбец «A», введите числа в ячейки «A1», «A2», «A3» и так далее.
-
4
Щелкните по пустой ячейке. Это ячейка, в которой отобразится значение стандартного отклонения. Так вы выберете ячейку.
-
5
Введите формулу для вычисления стандартного отклонения. В пустой ячейке введите =СТАНДОТКЛОН.Г(), где «Г» — генеральная совокупность. Стандартное отклонение по генеральной совокупности учитывает все данные (N).[1]
- Чтобы найти стандартное отклонение по выборке, введите =СТАНДОТКЛОН.В(). В этом случае учитывается (N-1) данных.
-
6
Введите диапазон значений. Внутри круглых скобок введите букву и номер ячейки с первым числом, потом введите двоеточие (:), а затем введите букву и номер ячейки с посленим числом.
- Например, если вы ввели числа в столбце «A» в строках с 1 по 10, формула должна выглядеть так: =СТАНДОТКЛОН.Г(A1:A10).
- Чтобы посчитать стандартное отклонение нескольких чисел, которые, например, находятся в ячейках A1, B3 и C5, введите адреса ячеек через запятые (например, =СТАНДОТКЛОН.В(A1,B3,C5)).
-
7
Нажмите ↵ Enter. Формула будет выполнена, а в ячейке с формулой отобразится стандартное отклонение выбранных данных.
Реклама
Советы
- В большинстве случаев вычисляется стандартное отклонение по генеральной совокупности, чтобы учесть все данные.
Реклама
Предупреждения
- Старая формула =СТАНДОТКЛОН() не работает в версиях Excel старше 2007 года.
Реклама
Об этой статье
Эту страницу просматривали 115 468 раз.
Была ли эта статья полезной?
На чтение 5 мин Опубликовано 15.01.2021
Для вычисления среднеквадратического отклонения в Microsoft Office Excel используется специальная формула, которой можно пользоваться несколькими способами. О них пойдет речь в данной статье.
Содержание
- Как вычислить среднее квадратическое отклонение в Excel
- Способ 1. С помощью Мастера функций
- Способ 2. Расчет стандартного отклонения в разделе «Формулы»
- Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
- Способ 4. Ручной подсчет
- Заключение
Как вычислить среднее квадратическое отклонение в Excel
Это один из показателей вариации. В теории вероятностей этот показатель рассчитывается по формуле:
В Эксель пользователю не нужно будет вручную рассчитывать среднеквадратичное отклонение. Существует ряд способов, позволяющих найти эту величину в кратчайшие сроки с помощью встроенных в Excel инструментов. Далее будут рассмотрены самые распространенные из них.
Способ 1. С помощью Мастера функций
Данный метод расчета стандартного отклонения в Excel занимает минимальное количество времени. Вычисление производится следующим образом:
- Левой клавишей манипулятора на рабочем листе программы выделить ячейку, в которой будет отображаться результат вычисления.
- Кликнуть по кнопке «Вставка функции», расположенной с левой стороны от строки ввода.
- После выполнения предыдущего действия откроется окошко Мастера функций. Здесь пользователю потребуется найти строку «СТАНДОТКЛОН.В», выделить ее ЛКМ и нажать на «ОК» внизу меню. В списке функций также есть записи «СТАНДОТКЛОН.Г» и просто «СТАНДОТКЛОН». На них нажимать не нужно!
- В следующем окне аргументов функции необходимо прописать числа совокупности в каждом поле. Если эти значения уже написаны на рабочем листе Excel, то можно указать координаты соответствующих ячеек.
- Нажать на «ОК» внизу меню «Аргументы функции», когда все строчки будут заполнены.
- Проверить результат. В выделенной на первом этапе ячейке будет прописано число. Это и есть среднее квадратичное отклонение.
Обратите внимание! Если после выполнения вышеуказанных манипуляций в ячейке будут отображаться знаки «###», то значит результатом является большое число, и ячейку нужно растянуть.
Способ 2. Расчет стандартного отклонения в разделе «Формулы»
Через вкладку «Формулы» в программе Excel также возможно рассчитать стандартное отклонение. Алгоритм вычисления состоит из следующих шагов:
- По аналогичной схеме выделить любую свободную ячейку на рабочем листе. В этот элемент в дальнейшем будет выводиться результат.
- В графе инструментов сверху главного меню программы найти слово «Формулы» и щелкнуть по нему ЛКМ.
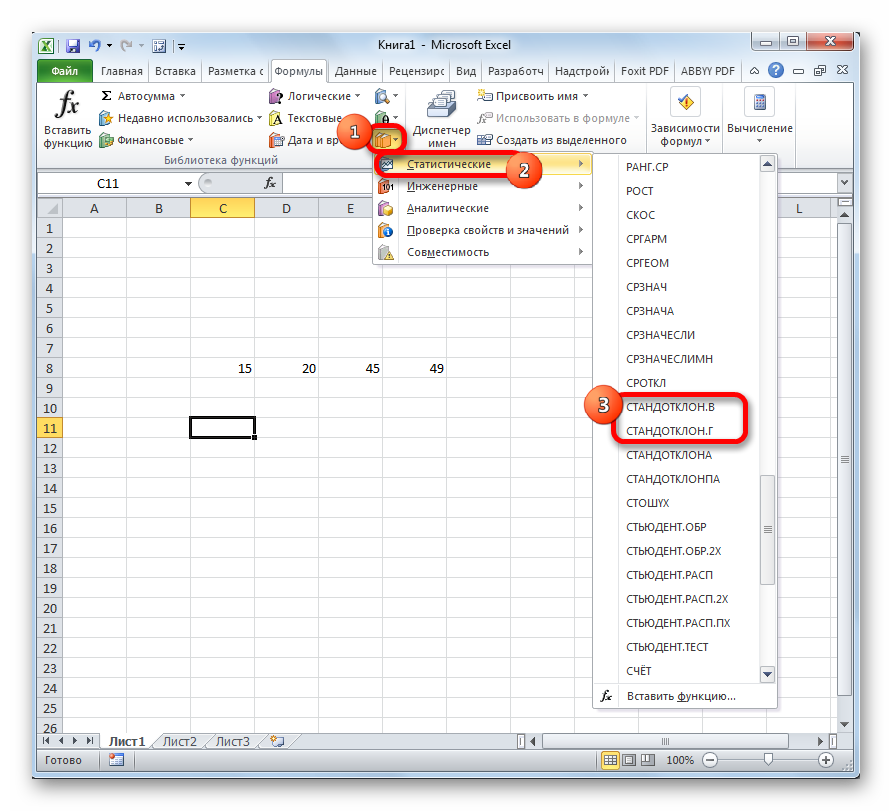
- В открывшейся области найти подраздел «Библиотека функций, а затем развернуть вкладку «Другие функции».
- В контекстном меню выбрать тип «Статистические» и поставить курсор мышки на это слово.
- Развернется дополнительное контекстное окно, в котором пользователю необходимо щелкнуть по строчке «СТАНДОТКЛОН.В».
- В запустившемся окне «Аргументы функции» надо заполнить два поля, указав координаты соответствующих ячеек на рабочем листе или в табличном массиве. Нужные значения также можно прописать вручную.
- После выполнения этих манипуляций нажать на «ОК».
- Удостовериться, что в указанной ранее ячейке отобразился результат работы формулы – число, характеризующее среднеквадратичное отклонение.
Важно! Если необходимо посчитать стандартное отклонение у нескольких параметров, то исходную формулу можно растянуть на оставшиеся ячейки табличного массива.
Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
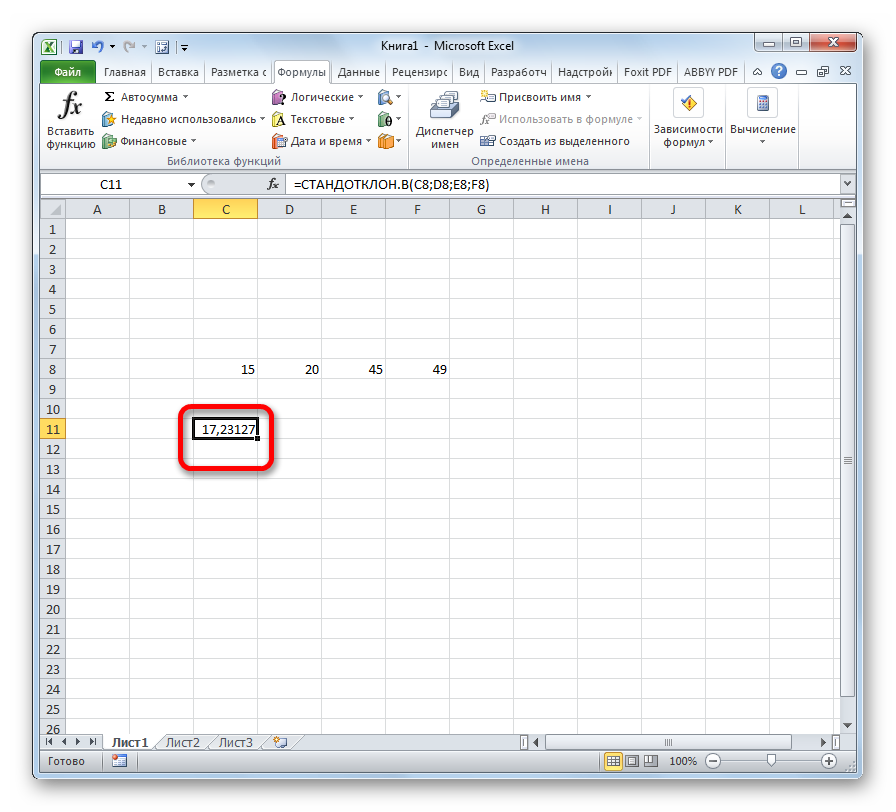
Чтобы рассчитать стандартное отклонение в Microsoft Office Excel, можно ввести специальную формулу с клавиатуры, результат будет одинаковым. Такой метод вычисления заключается в выполнении следующих этапов:
- Поставить курсор мыши в ячейку, куда будет выводиться результат.
- В выделенный элемент ввести с клавиатуры формулу «=СТАНДОТКЛОН.В(а,b,c,d)». Вместо букв в скобках нужно указать соответствующие аргументы. Это числа из табличного массива данных.
- Нажать на «Enter» для завершения процедуры.
- Проверить результат. В итоге в ячейке должно отобразиться конкретное значение среднеквадратичного отклонения.
Дополнительная информация! Также для расчета можно использовать формулу «СТАНОТКЛОН.Г()». Получится идентичный результат. Данный метод будет работать независимо от версии программного обеспечения.
Способ 4. Ручной подсчет
Такую операцию в Microsoft Office Excel нецелесообразно выполнять. Данный метод основан на применении обычного калькулятора, который также присутствует в Эксель. Для ручного счета необходимо проделать следующие действия по алгоритму:
- Левой клавишей манипулятора выделить ячейку табличного массива, в которую будет выводиться результат.
- Поставить знак «=» и с клавиатуры компьютера прописать числовые значения для расчета среднеквадратичного отклонения, указывая координаты соответствующих ячеек из таблички. Здесь надо подставлять параметры в формулу из первого рисунка.
- После написания формулы нажать на «Enter» и убедиться, что в ячейке отобразился результат стандартного отклонения.
Обратите внимание! Формулу для вычисления среднеквадратичного отклонения, написанную вручную в Excel, также можно растянуть на оставшиеся ячейки для их автоматического заполнения.
Заключение
Таким образом, стандартное отклонение в Microsoft Office Excel рассчитывается с помощью формулы или выбора соответствующей функции. Основные методы вычисления данного параметра были рассмотрены выше.
Оцените качество статьи. Нам важно ваше мнение:
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
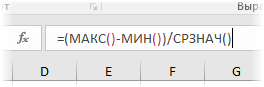
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Download Article
Step-by-step tutorial for the STDEV functions
Download Article
This wikiHow shows you how to find the standard deviation of a dataset in Microsoft Excel. Whether you’re studying for statistics, analyzing data at work, or just researching something for fun, calculating a standard deviation is essential. And, it’s pretty easy to do in Excel! There are built-in functions for calculating the standard deviation.
Things You Should Know
- There are four functions for calculating standard deviation.
- STDEV.P and STDEV.S cover most situations. Use STDEV.P for populations and STDEV.S for samples.
- The function will calculate the standard deviation for a selected range of cells.
Steps
-
1
Enter the values you want to use. Pick a column in which you want to enter your data, then type each data value into individual cells in that column. Using Excel is a great way to organize and analyze your data.
- For example, if you select column «A» as the area in which to enter your data, you might type a number into cell A1, cell A2, cell A3, and so on.
- If needed, you can move columns in your spreadsheet to organize your data.
-
2
Note this information about the different functions. There are four functions in Excel for calculating standard deviation. The functions differ in two ways:[1]
- The selected function will either calculate the standard deviation for a sample (using n — 1) or a population (using n), where n is the sample size.
- The selected function will include or exclude logical values (TRUE and FALSE) and text (numbers represented as text). TRUE is interpreted as a 1, while FALSE is 0.
Advertisement
-
3
Choose a standard deviation function. Here are the four options for calculating standard deviation:
- STDEV.P — Finds the standard deviation of a population. This function doesn’t include logical values or text.[2]
- STDEV.S — Finds the standard deviation of a sample. This function doesn’t include logical values or text.[3]
- STDEVA — Finds the standard deviation of a sample. This function does include logical values or text.[4]
- STDEVPA — Finds the standard deviation of a population. This function does include logical values or text.[5]
- There are also two outdated functions that have been replaced by the above functions. They are still present in Excel for backward compatibility reasons, but may be phased out in future versions.
- STDEV — This function was replaced by STDEV.S. Finds the standard deviation of a sample. This function doesn’t include logical values or text.[6]
- STDEVP — This function was replaced by STDEV.P. Finds the standard deviation of a population. This function doesn’t include logical values or text.[7]
- STDEV — This function was replaced by STDEV.S. Finds the standard deviation of a sample. This function doesn’t include logical values or text.[6]
- STDEV.P — Finds the standard deviation of a population. This function doesn’t include logical values or text.[2]
-
4
Click a blank cell. This should be the cell in which you want to display the standard deviation value. Doing so selects the cell.
-
5
Type in the standard deviation function. In the cell you selected, enter the standard deviation function you want to use. Here is STDEV.S() as an example:
- =STDEV.S()
-
6
Add your value range. To do so:
- In between the parentheses, type the letter and number of the cell containing your first data value.
- Type a colon (:)
- Type the letter and number of the last cell.
- For example, if you entered your data in column «A» from rows 1 through 10, you would have =STDEV.S(A1:A10) typed here.
- If you just want to display the standard deviation of the value of a few scattered cells such as A1, B3, and C5, you can type the cell names separated by commas (e.g., =STDEV.S(A1,B3,C5)).
-
7
Press ↵ Enter. This will prompt Excel to run the formula, displaying the standard deviation of the selected cells in the formula’s cell.
- If you want to check your work, you can calculate the standard deviation by hand.
Advertisement
Add New Question
-
Question
How do I use Excel to calculate 2 standard deviations?
Use =STDEV(), and put your range of values in the parentheses. This can be 2 cells or 2 values (numbers).
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Advertisement
-
The old =STDEV( ) formula doesn’t work in versions of Excel older than 2007.
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 444,078 times.
Is this article up to date?
wikiHow Tech Help:
Tech troubles got you down? We’ve got the tips you need
Subscribe
You’re all set!
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
— это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) — отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
Функция СТАНДОТКЛОН.В возвращает значение стандартного отклонения, рассчитанного для определенного диапазона числовых значений.
Функция СТАНДОТКЛ.Г используется для определения стандартного отклонения генеральной совокупности числовых значений и возвращает величину стандартного отклонения с учетом, что переданные значения являются всей генеральной совокупностью, а не выборкой.
Функция СТАНДОТКЛОНА возвращает значение стандартного отклонения для некоторого диапазона чисел, которые являются выборкой, а не всей генеральной совокупностью.
Функция СТАНДОТЛОНПА возвращает значение стандартного отклонения для всей генеральной совокупности, переданной в качестве ее аргументов.
Примеры использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
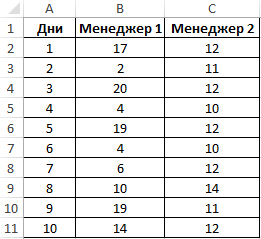
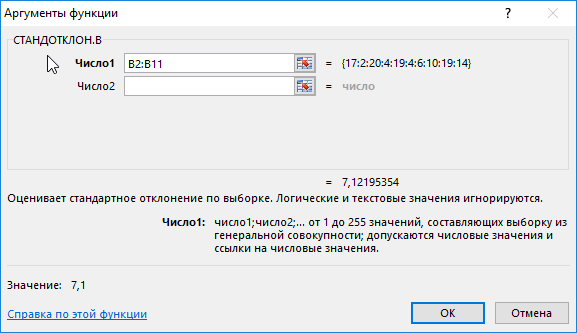
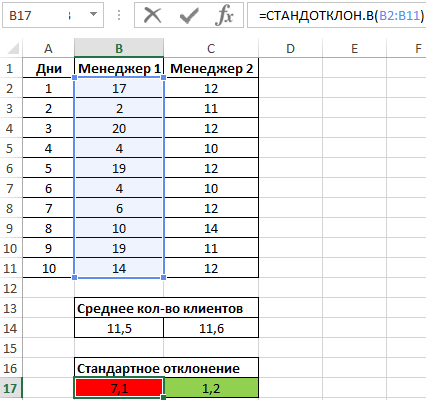
Пример 1. На предприятии работают два менеджера по привлечению клиентов. Данные о количестве обслуженных клиентов в день каждым менеджером фиксируются в таблице Excel. Определить, какой из двух сотрудников работает эффективнее.
Таблица исходных данных:
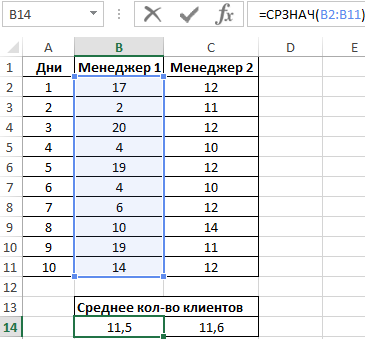
Вначале рассчитаем среднее количество клиентов, с которыми работали менеджеры ежедневно:
=СРЗНАЧ(B2:B11)
Данная функция выполняет расчет среднего арифметического значения для диапазона B2:B11, содержащего данные о количестве клиентов, принимаемых ежедневно первым менеджером. Аналогично рассчитаем среднее количество клиентов за день у второго менеджера. Получим:
На основе полученных значений создается впечатление, что оба менеджера работают примерно одинаково эффективно. Однако визуально виден сильный разброс значений числа клиентов у первого менеджера. Произведем расчет стандартного отклонения по формуле:
=СТАНДОТКЛОН.В(B2:B11)
B2:B11 – диапазон исследуемых значений. Аналогично определим стандартное отклонение для второго менеджера и получим следующие результаты:
Как видно, показатели работы первого менеджера отличаются высокой вариабельностью (разбросом) значений, в связи с чем среднее арифметическое значение абсолютно не отражает реальную картину эффективности работы. Отклонение 1,2 свидетельствует о более стабильной, а, значит, и эффективной работе второго менеджера.
Пример использования функции СТАНДОТКЛОНА в Excel
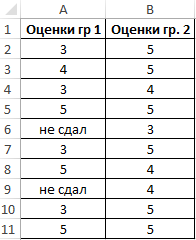
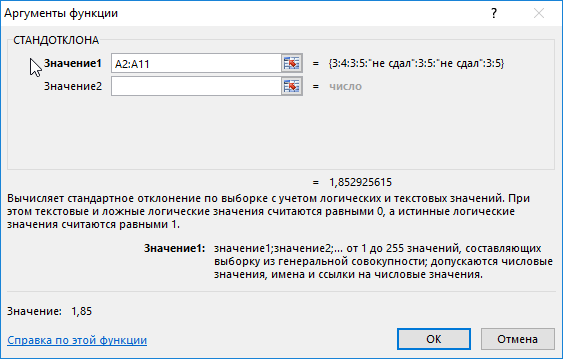
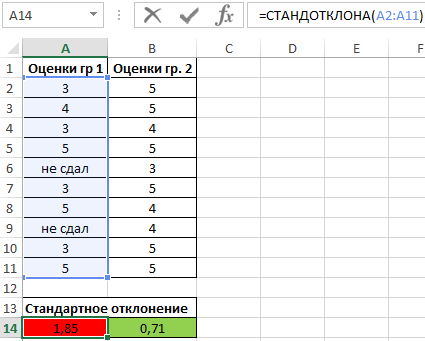
Пример 2. В двух различных группах студентов колледжа проводился экзамен по одной и той же дисциплине. Оценить успеваемость студентов.
Таблица исходных данных:
Определим стандартное отклонение значений для первой группы по формуле:
=СТАНДОТКЛОНА(A2:A11)
Аналогичный расчет произведем для второй группы. В результате получим:
Полученные значения свидетельствуют о том, что студенты второй группы намного лучше подготовились к экзамену, поскольку разброс значений оценок относительно небольшой. Обратите внимание на то, что функция СТАНДОТКЛОНА преобразует текстовое значение «не сдал» в числовое значение 0 (нуль) и учитывает его в расчетах.
Пример функции СТАНДОТКЛОН.Г в Excel
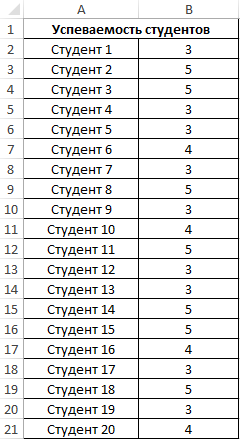
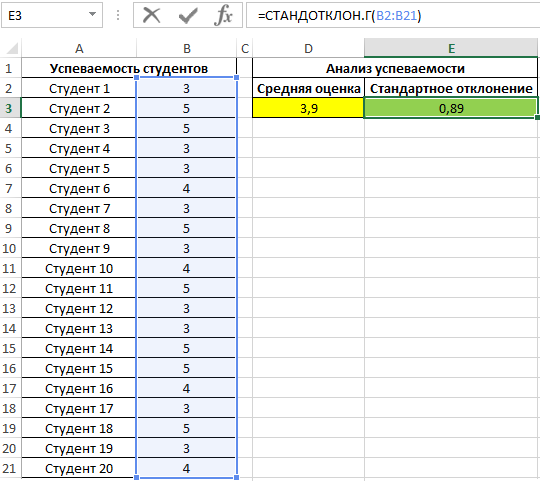
Пример 3. Определить эффективность подготовки студентов к экзамену для всех групп университета.
Примечание: в отличие от предыдущего примера, будет анализироваться не выборка (несколько групп), а все число студентов – генеральная совокупность. Студенты, не сдавшие экзамен, не учтены.
Заполним таблицу данных:
Для оценки эффективности будем оперировать двумя показателями: средняя оценка и разброс значений. Для определения среднего арифметического используем функцию:
=СРЗНАЧ(B2:B21)
Для определения отклонения введем формулу:
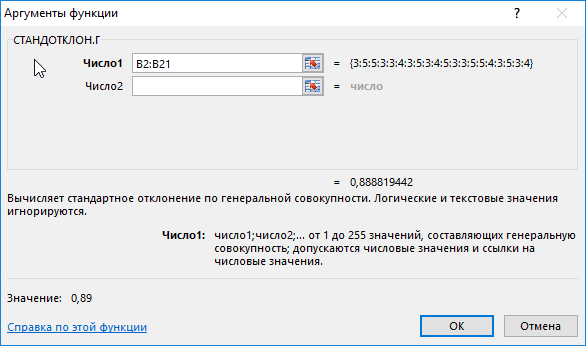
=СТАНДОТКЛОН.Г(B2:B21)
В результате получим:
Полученные данные свидетельствует об успеваемости немного ниже среднего (<4), величина разброса характеризует довольно большое количество студентов, получивших 5 и 3 соответственно (учитывая, что анализировались только данные из диапазона от 3 до 5).
Пример функции СТАНДОТКЛОНПА в Excel
Пример 4. Проанализировать успеваемость студентов по результатам сдачи экзамена с учетом тех студентов, которым не удалось сдать этот экзамен.
Таблица данных:
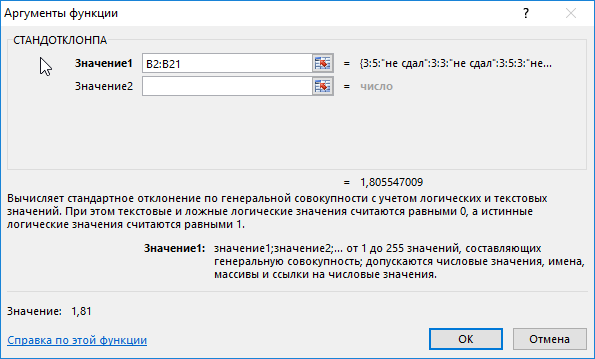
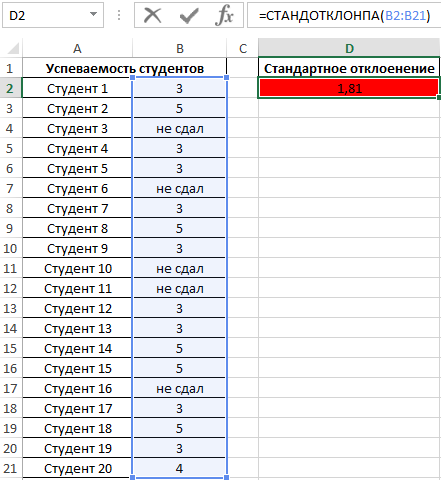
В данном примере также анализируем генеральную совокупность, однако некоторые поля данных содержат текстовые значения. Для определения стандартного отклонения используем функцию:
=СТАНДОТКЛОНПА(B2:B21)
В результате получим:
Высокий разброс значений в последовательности свидетельствует о большом числе не сдавших экзамен студентов.
Особенности использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
Функции СТАНДОТКЛОНА И СТАНДОТКЛОНПА имеют идентичную синтаксическую запись типа:
=ФУНКЦИЯ (значение1; [значение2];…)
Описание:
- ФУНКЦИЯ – одна из двух рассмотренных выше функций;
- значение1 – обязательный аргумент, характеризующий одно из значений выборки (либо генеральной совокупности);
- [значени2] – необязательный аргумент, характеризующий второе значение исследуемого диапазона.
Примечания:
- В качестве аргументов функций могут быть переданы имена, числовые значения, массивы, ссылки на диапазоны числовых данных, логические значения и ссылки на них.
- Обе функции игнорируют пустые значения и текстовые данные, содержащиеся в диапазоне переданных данных.
- Функции возвращают код ошибки #ЗНАЧ!, если в качестве аргументов были переданы значения ошибок или текстовые данные, которые не могут быть преобразованы в числовые значения.
Функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г имеют следующую синтаксическую запись:
=ФУНКЦИЯ(число1;[число2];…)
Описание:
- ФУНКЦИЯ – любая из функций СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г;
- число1 – обязательный аргумент, характеризующий числовое значение, взятое из выборки или всей генеральной совокупности;
- число2 – необязательный аргумент, характеризующий второе числовое значение исследуемого диапазона.
Примечание: обе функции не включают в процесс вычисления числа, представленные в виде текстовых данных, а также логические значения ИСТИНА и ЛОЖЬ.
Примечания:
- Стандартное отклонение широко используется в статистических расчетах, когда нахождение среднего значения диапазона величин не дает верное представление о распределении данных. Оно демонстрирует принцип распределения величин относительно среднего значения в конкретной выборке или всей последовательности целиком. В Примере 1 будет наглядно рассмотрено практическое применение данного статистического параметра.
- Функции СТАНДОТКЛОНА и СТАНДОТКЛОН.В следует использовать для анализа только части генеральной совокупности и производят расчет по первой формуле, а СТАНДОТКЛОН.Г и СТАНДОТКЛОНПА должны принимать на вход данные о всей генеральной совокупности и производят расчет по второй формуле.
- В Excel содержатся встроенные функции СТАНДОТКЛОН и СТАНДОТКЛОНП, оставленные для совместимости с более старыми версиями Microsoft Office. Они могут быть не включены в более поздние версии программы, поэтому их использование не рекомендуется.
- Для нахождения стандартного отклонения используются две распространенные формулы: S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/(n-1)) и S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/n), где:
- S – искомое значение стандартного отклонения;
- n – рассматриваемый диапазон значений (выборка);
- x_i – отдельно взятое значение из выборки;
- x_ср – среднее арифметическое значение для рассматриваемого диапазона.