Как excel называется средство применяемое для решения задач оптимального планирования

Сегодня на уроке мы с вами заканчиваем
изучение теоретических основ «Информационного моделирования». На прошлом уроке
мы занимались моделированием корреляционных зависимостей. И узнали, что
существует два вида зависимостей. Уже хорошо знакомая функциональная
зависимость (когда определённому значению независимой переменной
соответствует строго определённое значение зависимой переменной) и корреляционная.

Корреляционная зависимость
– это такая зависимость, когда данному значению одной величины соответствует
целый ряд значений другой, причём при изменении данной величины меняются и
другие значения, а также и его среднее. То есть зависимость между величинами,
каждая из которых подвергается неконтролируемому разбросу.

При изучении корреляционных зависимостей
мы рассмотрели два вида задач.

Первый вид –
Оказывает ли фактор В какое-либо заметное постоянное влияние на фактор А?

Второй – Какие из
факторов B,
C или D
оказывают наибольшее влияние на фактор А?

Так же мы узнали, что раздел
математической статистики, который исследует корреляционные зависимости,
называется корреляционным анализом.

Затем, рассмотрев пример корреляционной
зависимости, мы пришли к тому, что оценку корреляции величин начинают с
высказывания гипотезы о возможном характере зависимости между их значениями.

Чаще всего считают, что это линейная
зависимость. Тогда мера корреляционной зависимости – это величина, которая
называется коэффициентом корреляции.

 Коэффициент корреляции (обычно
обозначают греческой буквой ƍ) характеризует величину, отражающую степень
взаимосвязи двух переменных между собой. ƍ может изменяться в пределах от
-1 до +1. То есть в зависимости от того к чему будет ближе коэффициент
корреляции к нулю, к плюс или минус единице, зависимость может быть
соответственно сильной или отсутствовать вообще.

Но существуют задачи другого типа.

На прошлом уроке мы рассмотрели
зависимость производительности труда рабочего на предприятии от
энерговооружённости данного предприятия, то есть от условий работы, которые
предприятие создаёт для своего рабочего.

Но для того чтобы предприятие развивалось
и модернизировалось нужно научиться оптимально использовать ресурсы при
производственном планировании. Например, научиться находить оптимальные
комбинации различных видов продукции для хранения на складах. А также
минимизировать транспортные расходы, при перевозке продукции.

Сегодня на уроке мы свами будем
разбираться со следующими вопросами:

·                  
Что
такое оптимальное планирование и в чём состоит задача оптимального
планирования.

·                  
Что
такое плановые показатели, ресурсы и цели.

·                  
А
также, какое программирование называется математическим, а какое линейным.

Объектом планирования
может стать любая система: от детского сада до предприятия-гиганта, любая
отрасль промышленности или сельского хозяйства, любой регион и, наконец,
государство.

При постановке задачи учитывают следующее:

·                  
Имеющиеся
плановые показатели: икс, игрек и другие:

·                  
Имеющиеся
ресурсы: R1, R2
и другие. За счёт ресурсов достигаются плановые показатели. Но ресурсы
практически всегда ограничены.

·                  
И
стратегическая цель. Цель зависит от значений плановых показателей и на
неё ориентируются при планировании.

Тогда оптимальным планом называется
значение плановых показателей при достижении стратегической цели, с учётом
ограниченности ресурсов.

Рассмотрим примеры.

Пусть объектом планирования
является транспортная компания, которая занимается доставкой товаров из
нескольких предприятий, нескольким потребителям.

Основными ресурсами
транспортной компании будут транспортные средства, необходимые для перевозки
товаров, а также расходы на перевозку.  Стратегической целью данной
компании будет планирование маршрута так, чтобы расходы на перевозку были
минимальными.

Или другой пример: Пусть объектом
моделирования является средняя общеобразовательная школа.

Плановыми показателями
здесь могут выступить, например, количество учителей и учащихся. Основными
ресурсами деятельности школы являются объём финансирования, оснащённость
учебных кабинетов средствами обучения, например, учебными стендами, плакатами,
интерактивной доской и компьютерами.  Естественно в школе стратегической
целью является образование и воспитание школьников. А количественной
мерой будет повышение среднего балла успеваемости.

На уроках информатики логично, для решения
задач использовать компьютер. Следовательно, нужно информационную модель
преобразовать в математическую, то есть представить в виде формул, уравнений и
других средств математики.

Давайте рассмотрим пример решения задачи
оптимального планирования с помощью компьютера.

На рыбоводческом комплексе занимаются
разведением карпов и толстолобиков. Для обеспечения нормальных условий их
выращивания используется три вида кормов. Количество корма каждого вида,
которое должны ежедневно получать карпы и толстолобики, приведено в таблице. В
ней же указаны общее количество корма каждого вида, которое может быть
использовано комплексом, а также прибыль от реализации рыбы.

Нужно определить, сколько карпов и
толстолобиков следует выращивать на рыбоводческом комплексе, чтобы прибыль от
их реализации максимальной.

Естественно, что это чисто учебный пример.
Вряд ли существует такой рыбоводческий комплекс, который занимается разведением
всего двух видов рыб, да и наибольшая выручка – это не единственная цель его
работы.

Итак, здесь плановыми показателями
являются:

Икс штук – карпов и игрек штук –
толстолобиков.

Ресурсами
в этом примере можно назвать количество корма каждого вида, которое должны
ежедневно получать карпы и толстолобики.

Для упрощения решения задачи, будем
считать, что другие ресурсы, например, электроэнергия, не ограничены.

Из условия задачи известно, что для
обеспечения нормальных условий выращивания карпов и толстолобиков используются
три вида кормов. Также известно количество корма каждого вида, которое должны
ежедневно получать карпы и толстолобики, и общее количество корма каждого вида,
которое может быть использовано рыбоводческим комплексом. Составим систему неравенств.

Итак, для первого корма. Ежедневно карпы
должны получать 2 единицы первого корма, а толстолобики 3 единицы, но в месяц
количество потребления первого корма рыбами не должно превышать 150-ти единиц.

Аналогично составим неравенства для
второго и третьего корма.

К трём полученным неравенствам нужно
добавить условия положительности значений величин икс и игрек, так как не может
быть отрицательное число карпов и толстолобиков. В итоге получим следующую
систему неравенств.

Теперь сформулируем стратегическую цель.
Нам нужно определить, сколько карпов и толстолобиков следует выращивать на
рыбоводческом комплексе, чтобы прибыль от реализации рыбы была максимальной.

По условию мы знаем, что прибыль от
реализации одного карпа равна 16 условным единицам, а толстолобика – 12 у.е.,
тогда сумма 16x+12y должна стремиться к максимуму.

Цель рыбоводческого комплекса
– получение максимальной выручки от продажи рыбы.

Рассмотрим записанное выражение как
функцию от x, y.

То есть f_xy,
игрек равно 16x +
12y.

Такая функция называется целевой
функцией.

Следовательно, получение оптимального
плана свелось к следующей математической задаче:

Требуется найти значения плановых
показателей x и y,
которые будут удовлетворять данной системе неравенств и придавать максимальное
значение целевой функции.

Итак, мы построили математическую модель
задачи оптимального планирования для рыбоводческого комплекса.

Решить данную задачу нам помогут средства,
реализованные в табличном процессоре Excel.

Математическое программирование —
это раздел математики, содержащий методы решения задач оптимального
планирования.

Так как в целевую функцию f_xy
игрек
величины икс и игрек входят линейно, то есть они в первой степени, то нашу
задачу можно отнести к разделу этой науки, который называется линейное
программирование.

Линейное программирование – это
раздел математического программирования, решающий задачи оптимального
планирования с линейной целевой функцией.

Для решения задачи в MS Excel, создадим
таблицу с исходными данными.

Ячейки В7 и С7 оставим соответственно для
значений х (количество выращиваемых карпов) и у (количество выращиваемых
толстолобиков).

В ячейки В2:С2 введём коэффициенты в
ограничениях по первому корму, то есть 2 и 3 соответственно. В ячейки В3:С3 по
второму корму. И в В4:С4 по третьему. Далее В диапазон ячеек Д2:Д4 запишем
общее количество корма каждого вида, которое может быть использовано
комплексом.

В ячейки В6 и С6 запишем коэффициенты
целевой функции, в нашем случае это 16 и 12.

Далее в ячейку В8 введём формулу целевой
функции. Будем использовать встроенную функцию СУММПРОИЗВ.

Данная функция перемножает
соответствующие элементы заданных списков, а затем складывает полученные
произведения.

Аргументами
функции СУММПРОИЗВ являются диапазоны ячеек, причём все диапазоны должны иметь
одинаковые размерности.

Встроенная функция СУММПРОИЗВ
будет записываться следующим образом: равно СУММПРОИЗВ, далее в круглых скобках
нужно указать два диапазона ячеек, которые нужно перемножить и затем сложить
произведения. В нашей задаче целевая функция записана следующим образом:
шестнадцать икс плюс двенадцать игрек, то есть нам нужно найти сумму
произведений коэффициентов целевой функции и переменных. Указываем первый
диапазон В6:С6 точка с запятой и второй диапазон В7:С7.

Функция СУММПРОИЗВ
перемножит соответствующие ячейки диапазона, то есть В6 умножит на В7, а С6
умножит на С7. Затем полученные произведения суммирует.

В ячейку Е2 введём ограничения. Снова
будем использовать встроенную функцию СУММПРОИЗВ. Здесь первый диапазон ячеек –
это коэффициенты в ограничениях для первого корма, а второй – переменные.
Аналогично заполним ограничения для второго и третьего корма.

Теперь необходимо вызвать программу
оптимизации и сообщить ей, где расположены данные. Для этого необходимо сначала
загрузить её.

Откроим вкладку Файл и выберем пункт
Параметры. Далее выбираем команду Надстройки, а затем в окне Управление
выбираем пункт Надстройки Excel. Нажимаем кнопку Перейти. Теперь в окне
Доступные надстройки установим флажок Поиск решения и нажимаем кнопку ОК.

После загрузки надстройки «Поиск решения»
на вкладки Данные в группе Анализ становится доступна команда Поиск решения.
Выбираем её, после чего перед нами открывается соответствующая форма.

Далее необходимо выполнить следующий
алгоритм:

 Ввести координату ячейки с целевой
функцией. В нашем случае это В8. (Заметим, что если перед этим установить
курсор на ячейку В8, то ввод произойдёт автоматически).

Поставить отметку «максимальному
значению», то есть сообщить программе, что нас интересует нахождение максимума
целевой функции.

В поле «Изменяя ячейки переменных» ввести
В7:С7, то есть сообщить, какое место отведено под значения переменных-плановых
показателей.

В поле «Ограничения» надо ввести
информацию о неравенствах-ограничениях следующим образом: щёлкнуть по кнопке
«Добавить».

Итак, первое неравенство имеет вид 150
больше либо равно два икс плюс три игрек. Теперь в появившемся диалоговом окне
«Добавление ограничения» ввести ссылку на ячейку Д2, выбрать из меню знак
неравенства больше либо равно и ввести ссылку на ячейку Е2; снова щёлкнуть по
кнопке «добавить» и аналогично ввести второе ограничение Д3 больше либо равно
Е3 и так далее. В конце нажимаем ОК.

Закрываем диалоговое окно «Добавление
ограничения». Снова появится форма «Поиск решения». После завершения ввода всех
ограничений и параметров нажимаем «Найти решение» и получаем искомое решение
задачи.

То есть в результате применения
инструмента Поиск решения получен следующий оптимальный план разведения
карпов и толстолобиков на рыбоводческом комплексе: нужно вырастить 57 карпов
и 12 толстолобиков.

Решение данной задачи может быть
представлено и в дробных числах, но так как у нас в задаче надо найти
количество рыб, а оно не может быть дробным числом, мы числа округляем до
целых.

Представим систему полученных нами
неравенств на координатной плоскости.

То есть нам нужно изобразить пять прямых,
соответствующих следующим линейным уравнениям:

В результате мы получим четырёхугольник ABCD.
Любая точка четырёхугольника является решением нашей системы неравенств. Если
икс равно 57, а игрек равно 12, то в этой точке значение целевой функции Эф от
пятидесяти семи и двенадцати равно 1056. Если один карп стоит 16 условных
единиц, а толстолобик 12, то полученная выручка составит 1056 условных единиц.
Этой точке соответствует точка Бэ на нашем графике.

Итак, сегодня на уроке мы с вами построили
модель оптимального планирования на рыбоводческом комплексе.

А теперь давайте повторим всё, что мы
узнали сегодня на уроке:

Оптимальное планирование
— это определение значений плановых показателей с учётом ограниченности
ресурсов при условии достижения заданной цели.

Ограниченность ресурсов может описываться
с помощью:

·                  
системы
неравенств;

·                  
системы
равенств;

·                  
смешанной
системы.

Цель описывается
функцией, для которой требуется найти минимум или максимум.

Microsoft Excel имеет специальное средство
Поиск решения для решения задач оптимального планирования.

Урок
№___

Тема: Практическая
работа №18

«Решение задач оптимального
планирования в Microsoft Excel»

Тип урока: практическая работа

Цели:

·       
Получение представления о построении оптимального плана методом
линейного программирования;

·       
Практическое освоение раздела Microsoft
Excel «Поиск
решения» для построения оптимального плана;

·       
Формирование навыка по работе в MS Excel;

·       
Развитие системного мышления, позволяющего выделять
в окружающей действительности системы, элементы систем, адекватные поставленной
задаче;

·       
Формирование профессиональных навыков работы.

Оборудование:

·       
ПК;

·       
Интерактивная доска;

·       
MS Excel

Ход
урока:

I. Организационный момент (5 мин.)

Приветствие.
Сообщение темы.

II. Актуализация
знаний (5 мин.)

Проверка
домашнего задания.

III. Практическая
работа (30 мин.)

Практическая работа

Справочная информация

Средство,
которое используется в данной работе, называется Поиск решения.
Соответствующая команда находится в меню Сервис. Поиск решения —
одно из самых мощных средств табличного процессора Excel.
Покажем на простейшем примере («пирожки и пирожные», см. учебник, § 39), как
воспользоваться указанным средством.

Задание 1

Реализовать
поиск оптимального решения для задачи планирования работы школьного
кондитерского цеха, описанной в § 39 учебника.

1. Подготовить таблицу к решению задачи
оптимального планирования.

В
режиме отображения формул таблица показана на рисунке. Ячейки В5 и С5
зарезервированы соответственно для значений х (план по
изготовлению пирожков) и у (план по изготовлению
пирожных). Ниже представлена система неравенств, определяющая ограничения на
искомые решения. Неравенства разделены на левую часть (столбец В) и правую
часть (столбец D).
Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая
функция занесена в ячейку В15.

	А	В	С	D
1	Оптимальное планирование
2
3	Плановые показатели
4		X (пирожки)	У (пирожные)
5
6
7	Ограничения
8
9		Левая часть	Знак	Правая часть
10	Время производства:	1000	<=	1000
11	Общее количество:	700	<=	700
12	Положительность X:	600	>=	0
13	Положительность Y:	100	>=	0
14
15	Целевая функция	=B5+2*C5

2.
Вызвать программу оптимизации и сообщить ей, где расположены данные. Для этого
выполнить следующие действия:

1.    
Перейти на вкладку Данные

2.    
В группе Анализ щелкнуть на
кнопку Поиск решений

На
экране откроется соответствующая форма:

3.
Выполнить следующий алгоритм:

1.     ввести
адрес ячейки с целевой функцией. В нашем случае это $В$15 (заметим, что если
перед этим установить указатель мыши на ячейку В15, то ввод произойдет
автоматически);

2.     поставить
отметку максимальному значению, т. е. сообщить программе, что нас
интересует нахождение максимума целевой функции;

3.     в
поле Изменяя ячейки ввести $В$5:$С$5, т. е. сообщить, какое место
отведено под значения переменных — плановых показателей;

4.     в
поле Ограничения ввести неравенства-ограничения, которые имеют вид: B10<=D10;
B11<=D11;
B12>=D12;
B13>=D13.
Огра­ничения вводятся следующим образом:

a.      щелкнуть
на кнопке Добавить;

b.     в
появившемся диалоговом окне Добавление ограничения ввести ссылку на
ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10;

c.      снова
щелкнуть на кнопке Добавить и аналогично ввести второе ограничение B11<=D11
и т. д.

d.     в
конце щелкнуть на кнопке ОК.

5.     закрыть
диалоговое окно Добавление ограничения. Перед нами снова форма Поиск
решения:

6.     указать,
что задача является линейной (это многократно облегчит программе ее решение).
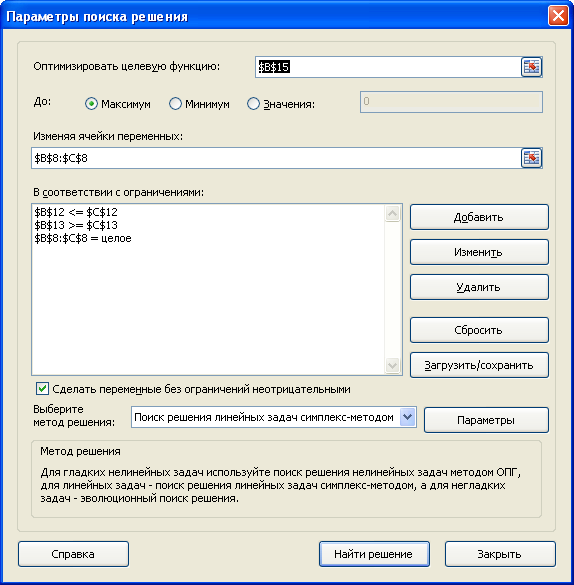
Для этого щелкнуть на кнопке Параметры, после чего открывается форма Параметры
поиска решения:

7.    
установить флажок линейная
модель. Остальная информация на форме Параметры поиска решения чисто
служебная, автоматически устанавливаемые значения нас устраивают, и вникать в
их смысл не будем. Щелкнуть на кнопке ОК. Снова откроется форма Поиск
решения.

8.     щелкнуть
на кнопке Выполнить — в ячейках В5 и С5 появляется оптимальное решение:

Справочная
информация

В
результате применения инструмента Поиск решения, получен следующий
оптимальный план дневного производства кондитерского цеха: нужно выпускать 600
пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис.
6.9 в учебнике. В этой точке значение целевой функции f(600,
100) = 800. Если один пирожок стоит 5 руб., то полученная выручка составит 4000
руб.

Задание
2

Требуется
решить задачу поиска оптимального плана производства школьного кондитерского
цеха с измененными условиями.

Представьте
себе, что в школе учатся неисправимые сладкоежки. И, кроме всех прочих
ограничений, перед кондитерским цехом ставится обязательное условие: число
пирожных должны быть не меньше числа пирожков. При такой постановке задачи
система неравенств (см. § 39) примет вид:

1.        
Внести соответствующие изменения в
электронную таблицу, построенную при выполнении предыдущего задания.

2.        
Получить оптимальный план с помощью
средства Поиск решения.

Проанализировать
полученные результаты. Сопоставить их с результатами задания 1.

Задание для самостоятельного выполнения по теме

«Оптимальное
планирование»

Задание

Составить
оптимальный план проведения экскурсионных поездок школьников во время каникул в
следующей ситуации. Областной департамент образования может профинансировать
поездки школьников из пяти районов области (районы будем обозначать номерами) в
три города (назовем эти города X, У и Z).

Количество
учащихся, которых следует отправить в поездки, таково:

Экскурсионное
бюро может в данные каникулы обеспечить поездку следующего количества учащихся
в каждый из трех городов:

Стоимость
поездки (в рублях) приведена в следующей таблице.

Город	Номер района
1	2	3	4	5
X	500	700	750	1000	1100
Y	700	600	400	500	800
Z	1200	1000	800	600	500

Смысл
чисел в таблице таков: если в ячейке Y2
стоит 600, то это значит, что поездка одного учащегося из района 2 в город У
обходится в 600 рублей.

Необходимо составить такой план экскурсий,
который бы:

·       
позволил каждому из намеченных к
поездке учащихся побывать на экскурсии;

·       
удовлетворил условию об общем числе
экскурсантов в каждый из городов;

·       
обеспечил максимально низкие
суммарные расходы финансирующей стороны.

Поскольку
эта задача непроста, поможем вам с ее математической фор­мулировкой.

План
перевозок, который нам надлежит составить, будет отражен в следующей таблице:

Величины,
стоящие в этой таблице, и являются объектами поиска. Так, X₃
есть число учащихся из района № 3, которые
по разрабатываемому плану поедут в город X.

Первое
условие (ограничение задачи) состоит в том, что все учащиеся из каждого района
поедут на экскурсию. Математически оно выражается следующими уравнениями:

                     (1)

Второе
условие — в каждый город поедут столько учащихся, сколько этот город в
состоянии принять:

                          (2)

Кроме
того, искомые величины, разумеется, неотрицательны:

 
           (3)

Теперь
запишем общую стоимость расходов на экскурсии. Поскольку привести, например, на
экскурсию X₁
учащихся в целом стоит X₁*500
рублей (см. таблицу стоимости поездки), то общие
расходы составят:

(4)

Теперь
имеется все для полной математической формулировки задачи: требуется найти
наименьшее значение функции (4) при
условии, что входящие в нее переменные удовлетворяют системам уравнений (1) и
(2)
и неравенств (3).

Это
весьма непростая задача. Однако ее решение (как и задач, существенно более
сложных) вполне «по плечу» программе Excel
с помощью средства Поиск решений, которым вам и надлежит воспользоваться.

Приведем результат решения задачи:

X1	X2	X3	X4	X5	Y1	Y2	Y3	Y4	Y5	Z1	Z2	Z3	Z4	Z5
300	100	0	0	0	0	100	400	0	0	0	50	0	350	200

Итог:
в город X поедут
на экскурсию 300 учащихся из района №1 и 100 учащихся из района № 2, в город У —
100 учащихся из района № 2 и 400 из района № 3, в город Z
— 50 учащихся из района № 2, 350 — из
района № 4 и 200 — из района № 5.

Полученный
результат можно сформулировать следующим образом: все учащиеся из района №1
уедут в город X, учащиеся из района № 2 поделятся между городами X, У и
Z
(соответственно 100, 100 и 5), все
учащиеся из района № 3 уедут в город У, а все учащиеся из районов № 4 и № 5
поедут в город Z.
Такое неочевидное, на первый взгляд,
разделение обеспечивает в данном случае наибольшую экономию средств.

IV. Итог урока (2 мин.) Объявляются оценки.

V.
Домашнее задание (3 мин.) Подготовка к к/р. Подготовка
докладов по § 40-43

В программу Excel встроены возмож­ности
решения задач математического
программирования.

Средство «Поиск решения» реализовано
в форме надстройки. Соответствующая
команда находится в меню Сервис (MS
Excel 97-2003) или в группе
Анализ вкладки Данные.

Замечание. Средство поиска решения
является надстройкой — вспомогательной
программой, служащая для добавления в
Microsoft Office специальных команд или
возможностей. Чтобы использовать эту
надстройку в Excel, необходимо сначала
загрузить ее. Для этого в MS
Excel 7 нажмите кнопку MS
Office

,
а затем щелкните Параметры Excel.
Выберите команду Надстройки, а затем
в окне Управление выберите пункт
Надстройки Excel. Нажмите кнопку
Перейти. В окне Доступные надстройки
установите флажок Поиск решения и
нажмите кнопку ОК.

В случае появления сообщения о том, что
надстройка для поиска решения не
установлена на компьютере, нажмите
кнопку Да, чтобы установить ее.

Покажем на рассмотренном нами простейшем
примере («пирожки и пирожные»), как
воспользоваться средством Поиск Решения.

Вначале надо подготовить электронную
таблицу к решению задачи оптимального
планирования. В режиме отображения
формул таблица показана на рис. 2.20.
Ячейки В5 и С5 зарезервированы соответственно
для значений х (план по изготовлению
пирожков) и у (план по изготовлению
пирожных). Ниже этих ячеек представлена
система неравенств (а), определяющая
ограничения на искомые решения.
Неравенства разделены на левую часть
(столбец В) и правую часть (столбец D).
Знаки неравенств в столбце С имеют чисто
оформительское значение. Целевая функция
(p) занесена в ячейку В15.

	А	В	С	D
1	Оптимальное планирование
2
3	Плановые показатели
4		X (пирожки)	У (пирожные)^
5
6
7	Ограничения
8
9		Левая часть	Знак	Правая часть
10	Время производства:	=В5+4*С5	<=	1000
11	Общее количество:	=В5+С5	<=	700
12	Положительность X:	=В5	>=	0
13	Положительность Y:	=С5	>=	0
14
15	Целевая функция	=В5+2*С5
16

Рис. 2.20. Таблица, подготовленная к
вычислению оптимального плана

Теперь следует вызвать программу
оптимизации «Поиск решения» и сообщить
ей, где расположены данные. Для это­го
надо выполнить команду => Сервис =>
Поиск решения. На экране откроется
соответствующая форма (рис. 2.21).

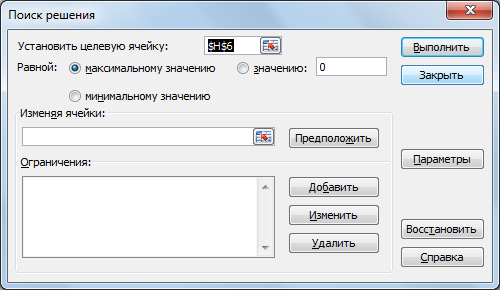
Рис. 2.21. Начальное состояние формы «Поиск
решения»

Далее надо выполнить следующий алгоритм:

Ввести координату ячейки с целевой
функцией. В нашем случае это В15. (Заметим,
что если перед этим установить курсор
на ячейку В15, то ввод произойдет
автоматически).

Поставить отметку «максимальному
значению», то есть сообщить программе,
что нас интересует нахождение максимума
целевой функции.

В поле «Изменяя ячейки» ввести В5:С5, то
есть сообщить, какое место отведено под
значения переменных — плановых показателей.

В поле «Ограничения» надо ввести
информацию о неравенствах-ограничениях,
которые имеют вид B10<=D10;

B1K=D11;

B12>=D12;

B13>=D13.

Ограничения вводятся следующим образом:

=> щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление
ограничения» ввести ссылку на ячейку
В10, выбрать из меню знак неравенства <=
и ввести ссылку на ячейку D10; снова
щелкнуть по кнопке «добавить» и аналогично
ввести второе ограничение B11<=D11 и так
далее. В конце надо щелкнуть на кнопке
ОК.

Закрыть диалоговое окно «Добавление
ограничения».Снова появится форма
«Поиск решения» (рис. 2.22).

Теперь надо дать последние указания:
задача является линейной (это многократно
облегчит программе ее реше­ние). Для
этого следует щелкнуть по кнопке
«Параметры» — появится форма «Параметры
поиска решения» (рис. 2.23).

Рис. 2.23. Форма «Параметры поиска решения»

Надо выставить флажок на переключателе
«Линейная модель» Остальная информация
в форме «Параметры поиска решения»
служебная, автоматически устанавливаемые
значения нас устраивают . Следует
щелкнуть по кнопке ОК, что возвратит
нас в форму «Поиск решения».

Вся информация введена. Далее надо
щелкнуть по кнопке «Выполнить» —
мгновенно в ячейках В5 и С5 появится
оптимальное решение (числа 600 и 100), а
также число 800 в ячейке В15 — максимальное
значение целевой функции (рис. 2.24).

	А	В	С	D
1	Оптимальное планирование
2
3	Плановые показатели
4		X (пирожки)	Y (пирожные)
5		600	100
в
7	Ограничения
8
9		Левая часть	Знак	Правая часть
10	Время производства:	1000	<=	1000
11	Общее количество:	700	<=	700
12	Положительность X:	600	>=	0
13	Положительность Y:	100	>=	0
14
15	Целевая функция	800
16

Рис. 2.24. Результаты решения задачи

Кроме того, на экране появилась еще одна
форма — «Результаты поиска решения».

На первом этапе освоения возможностей
программы на эту форму можно не обращать
внимания (хотя в принципе в ней может
оказаться очень полезная информация).

Итак, в результате применения инструмента
«Поиск решения», мы получим следующий
оптимальный план дневного производства
кондитерского цеха: нужно выпускать
600 пирожков и 100 пирожных. В этой точке
значение целевой функции f(600,100)
= 800. Если один пирожок стоит 2 рубля, то
полученная выручка составит 1600 рублей.

Решение, которое мы получили, вполне
разумно как с экономической точки
зрения, так и с медицинской. Много
сладкого — вредно для здоровья, а пирожки
и сытнее и полезнее.

Полученная электронная таблица и
настроенная на нее сервисная функция
«Поиск решения» являются средством, с
помощью которого можно решать задачу
оптимального планирования при меняющихся
условиях. Например, может измениться
длина рабочего дня. Тогда надо внести
новое значение в ячейку D10 и оптимальный
план автоматически пересчитается. Так
же может измениться допустимое суммарное
число изделий в ячейке D11.

Представьте себе, что в вашей школе
учатся неисправи­мые сладкоежки. И,
кроме всех прочих ограничений, перед
кондитерским цехом ставится обязательное
условие: число пирожных должно быть не
меньше числа пирожков. При такой
постановке задачи система неравенств
(а) примет вид:

х + 4у < 1000;

х + у < 700;

х >0; у>х.

Соответствующее изменение легко внести
в электронную таблицу. Для этого
достаточно в ячейке D13 вместо 0 запи­сать
В5. Результаты поиска решения будут
следующими: х = 200, у = 200, f(x,y) = 600. Таким
планом вряд ли будет доволен директор
кондитерского цеха, поскольку потери
прибыли окажутся очень существенными.

Следует иметь в виду, что при решении
подобных задач могут возникнуть проблемы,
о которых мы здесь не говори­ли.
Например, искомого оптимального решения
может вовсе не существовать — тогда
программа об этом сообщит

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Поиск решения — это надстройка Microsoft Excel, с помощью которой  можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.

Поиск решения будем рассматривать в

MS EXCEL 2010

(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в

MS EXCEL 2007)

. В этой статье рассмотрим:

• создание оптимизационной модели на листе MS EXCEL
• настройку
  
  Поиска решения;
  
• простой пример (линейная модель).

Установка Поиска решения

Команда

Поиск решения

находится в группе

Анализ

на вкладке

Данные

.

Если команда

Поиск решения

в группе

Анализ

недоступна, то необходимо включить одноименную надстройку. Для этого:

• На вкладке
  
  Файл
  
  выберите команду
  
  Параметры
  
  , а затем — категорию
  
  Надстройки
  
  ;
• В поле
  
  Управление
  
  выберите значение
  
  Надстройки Excel
  
  и нажмите кнопку
  
  Перейти;
  
• В поле
  
  Доступные надстройки
  
  установите флажок рядом с пунктом
  
  Поиск решения
  
  и нажмите кнопку ОК.

Примечание

. Окно

Надстройки

также доступно на вкладке

Разработчик

. Как включить эту вкладку

читайте здесь

.

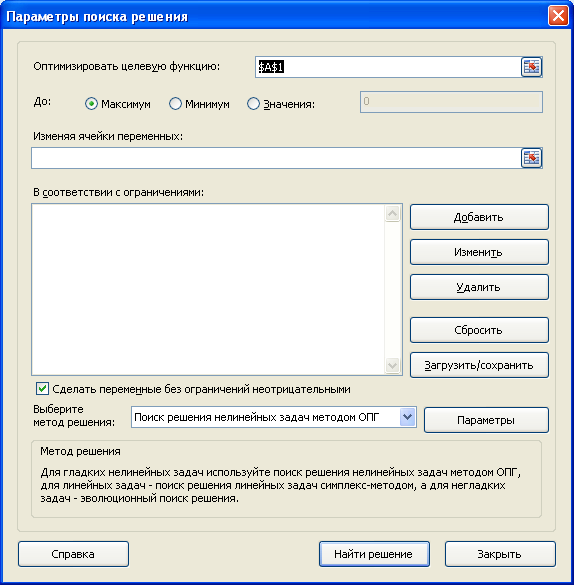
После нажатия кнопки

Поиск решения

в группе

Анализ,

откроется его диалоговое окно

.

При частом использовании

Поиска решения

его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт

Добавить на панель быстрого доступа

.

О моделях

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет

. Перед использованием

Поиска решения

настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка

Поиск решения

помогает определить

лучший способ

сделать

что-то

:

• «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
• «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

• Определить

  план производства

  , при котором доход от реализации произведенной продукции максимальный;

• Определить

  схему перевозок

  , при которой общие затраты на перевозку были бы минимальными;

• Найти

  распределение нескольких станков по разным видам работ

  , чтобы общие затраты на производство продукции были бы минимальными;

• Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется

Поиском решения

только по одному показателю

(этот оптимизируемый показатель называется

целевой функцией

). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.

Поиск решения

подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание

. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента

Подбор параметра

. Перед первым знакомством с

Поиском решения

имеет смысл сначала детально разобраться с родственным ему инструментом

Подбор параметра

. Основные отличия

Подбора параметра

от

Поиска решения

:

• 
  Подбор параметра
  
  работает только с моделями с одной переменной;
• в нем невозможно задать ограничения для переменных;
• определяется не максимум или минимум целевой функции, а ее равенство некому значению;
• эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Подготовка оптимизационной модели в MS EXCEL

Поиск решения

оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне

Поиска решения

возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.

Совет

. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки

Поиска решения

(см. ниже).

Приведем алгоритм работы с

Поиском решения

, который советуют сами разработчики (

]]>
www.solver.com

]]> ):

• Определите ячейки с переменными модели (decision variables);
• Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
• Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
• С помощью диалогового окна
  
  Поиск решения
  
  введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
• Запустите
  
  Поиск решения
  
  для нахождения оптимального решения.

Проделаем все эти шаги на простом примере.

Простой пример использования

Поиска решения

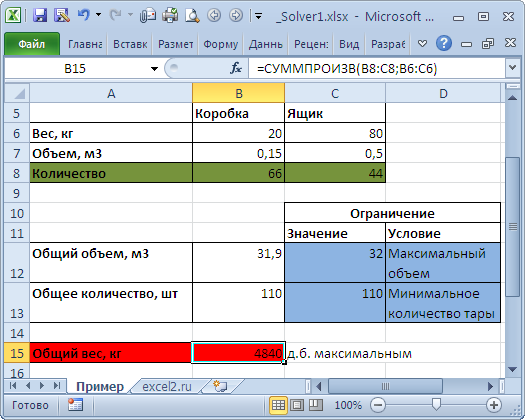
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см.

файл примера

).

Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле

=СУММПРОИЗВ(B8:C8;B6:C6)

– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —

=СУММПРОИЗВ(B7:C7;B8:C8)

. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары

=СУММ(B8:C8)

. Теперь с помощью диалогового окна

Поиск решения

введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.

После нажатия кнопки

Найти решение

будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.

Совет

: в статье »

Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями

» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.

Резюме

На самом деле, основной проблемой при решении оптимизационных задач с помощью

Поиска решения

является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью

Поиска решения

. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью

Поиска решения

рассмотрено

в этом разделе

.

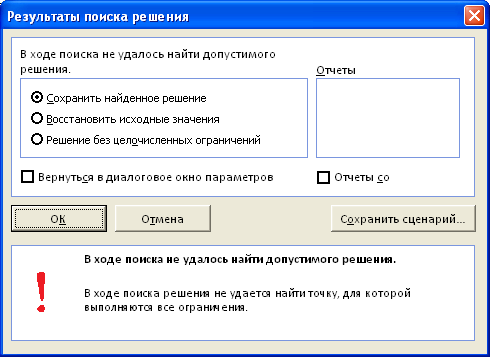
Поиску решения не удалось найти решения (Solver could not find a feasible solution)

Это сообщение появляется, когда

Поиск решения

не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете

Симплекс метод решения линейных задач

, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите

Поиск решения

с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и

Поиск решения

не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,

Поиск решения

может найти решение (если оно действительно существует).

Примечание

. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи

Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства

.

В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,

Поиск решения

не найдет решения.

При ограничении 17 м3

Поиск решения

найдет решение.

Некоторые настройки

Поиска решения

Метод решения

Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения

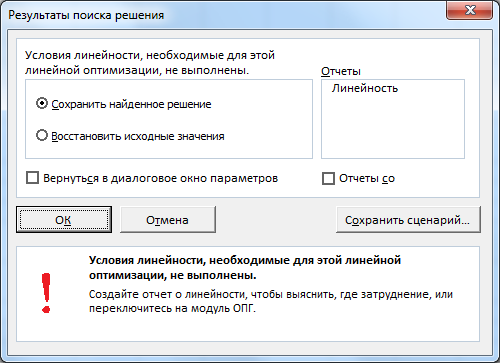
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:

В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.

Кнопки Добавить, Изменить, Удалить

Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.

Кнопка Сбросить

Чтобы удалить все настройки

Поиска решения

нажмите кнопку

Сбросить

– диалоговое окно очистится.

Сохранение и загрузка модели

Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка

Загрузить/ Сохранить,

далее нажмите кнопку

Сохранить

) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку

Параметры

). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку

Загрузить/ Сохранить

, затем, в появившемся диалоговом окне кнопку

Загрузить

, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.

Точность

При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание

ограниченную точность

вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.