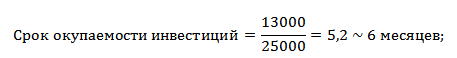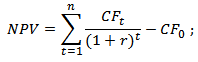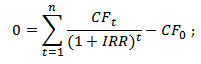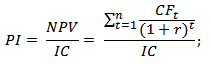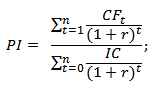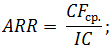In this article, we’ll calculate ARR in Excel. Accounting Rate of Return is one of the calculation percentages of the rate of return, particularly relevant in long-term investments. If you are planning to invest in a long-term project, then it’s necessary to check out the possibilities of the return from this benchmark percent.
So, it’s the best concept for computing the potential of the possibility of getting the percentage of return in this challenging financial environment.
In simple terms, it’s the return of investment and the way to whether to accept or not. Calculating the ARR in Excel is an easy task, with the help of Salvage Value, we can find out whether the project is to be accepted or not meaning the product/commodity is worth investing in or not. Besides this, we also need to have an Average EADT, NCO for calculating the ARR in Excel.
ARR is the combination of an Average Annual Profit by Average Investment. Symbolically,
ARR = Average EADT/ (NCO + Salvage Value/2)
Using the spreadsheet it’s easy to track out the easy changes in the ARR. So, check out the steps to keep on calculating the ARR in Excel.
1. Creating the Year Date
At 1st, we need to create the date of a specific year. Also, you can assume the date for some years. Here we have assumed the time to be 6 years from cell A6:A11.
Assuming the data up to certain years gives an idea about coping with the challenges and rate of return from that investment.
2. Create CFAT Data
After assuming the project for a defined year, enter the CFAT Value of each year. Here for Year 0, we have entered the CFAT Value of (100000).
Enter the CFAT Value for all the assuming years. We have entered the value for all the years assumed.
3. Create EADT
Assume the different values for different years in EADT Column. Earnings After Depreciation and Taxes (EADT) for each year. Since Year 0 cannot earn any return, we’ve placed an empty value.
Enter an assuming or given EADT value for each year. We have entered the EADT value for all except the Base Year (Year 0) and Final Year (Year 6).
4. Calculate an Average EADT
To calculate the average of EADT, choose a cell for the result, here we have chosen another column cell to calculate an average.
Enter the syntax of Average, and select the EADT Column cells. It’s =AVERAGE(C6:C11).
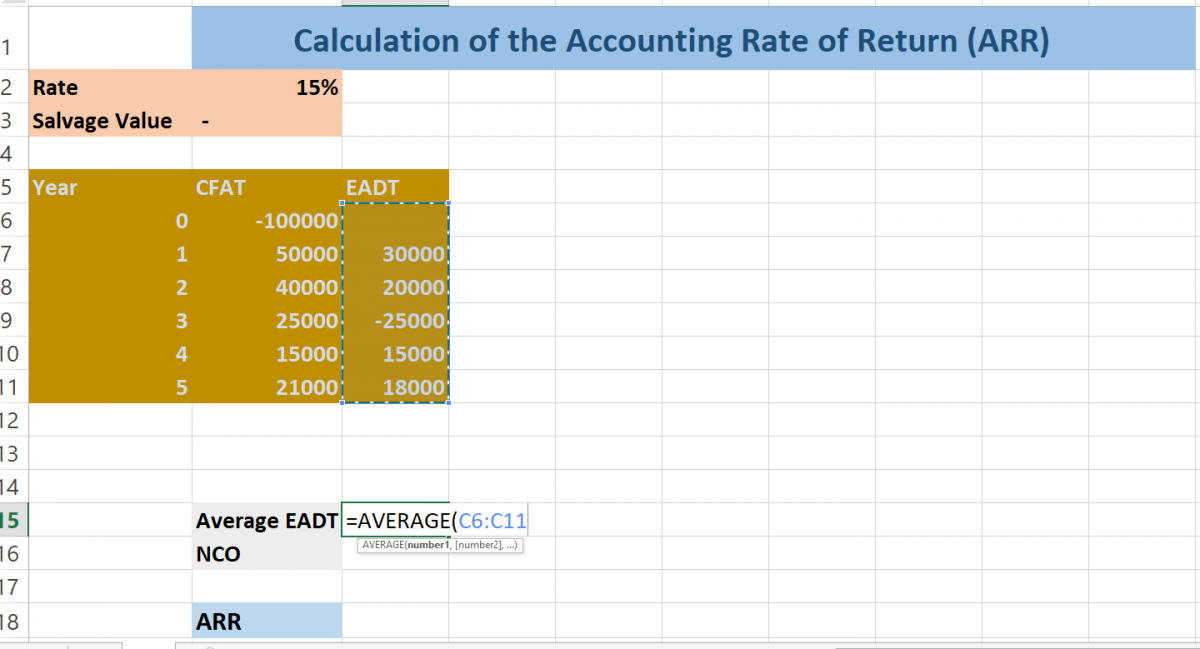
Here you will get an Average EADT.
5. Calculation of NCO Value
Type, =SUMIF(range,criteria,(sum_range)
Select the range, it’s the CFAT Value. So, after SUMIF( select the CFAT(Cash Flow After Taxes) value. In our case, the CFAT Values are from B6:B11, which we enter in the function, followed by a comma.
In the criteria, we have to include the condition. Here in our case Year 1 has a negative value, so we’ve to enter the criteria. Here we enter this again followed by a comma.
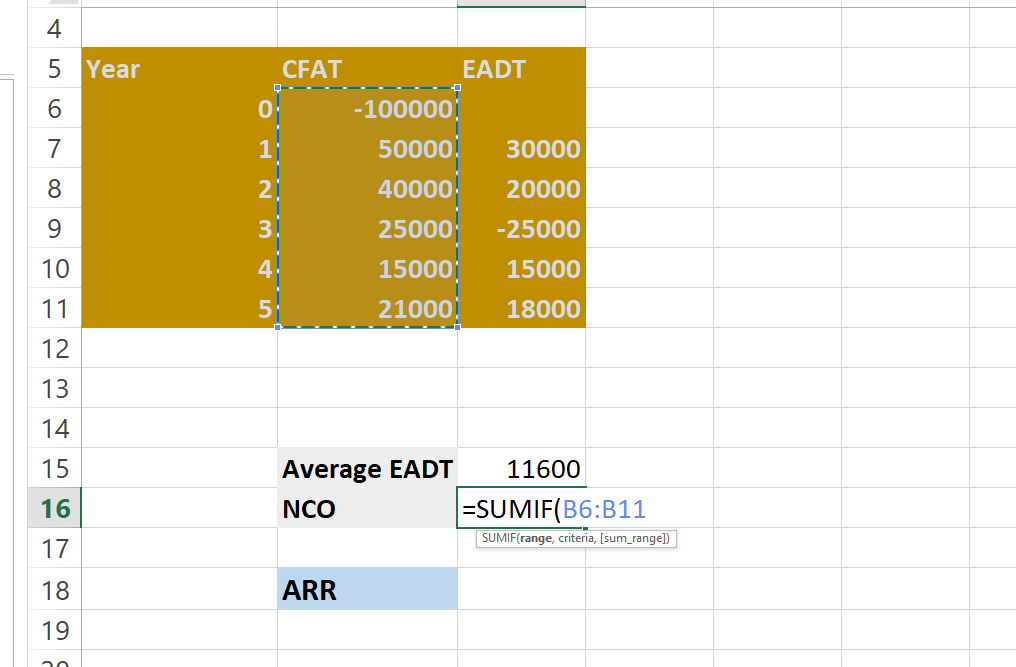
For a sum_range parameter, again select the CFAT Values. Here in our example, from B6:B11. After this, hit enter and see the NCO Result. It’s 100000 in our assumption calculation. Here we used for NCO, =SUMIF(B6:B11,”<“&0,B6:B11)
Final Calculation Using Formula
Go to ARR Cells, here we are going to calculate the ARR forecast.
Select the Average EADT, like =C15. Here are our EADT Lies in Column C15. So, you have to select the average EADT Cell. After selecting the Average EADT, input the Divide sign (/).
After the divide sign, open a bracket and select the NCO value. If the NCO is negative, then you have to enter the ABS Function.
In our case, it’s negative. So, we enter the ABS before NCO. Like this, =C15/((ABS(C16)+.
Now Select the Salvage Value, it’s in B3 in our worksheet. Like this, =C15/((ABS(C16)+B3)/
Divide the value by 2 and close the bracket. It’s =C15/((ABS(C16)+B3)/2
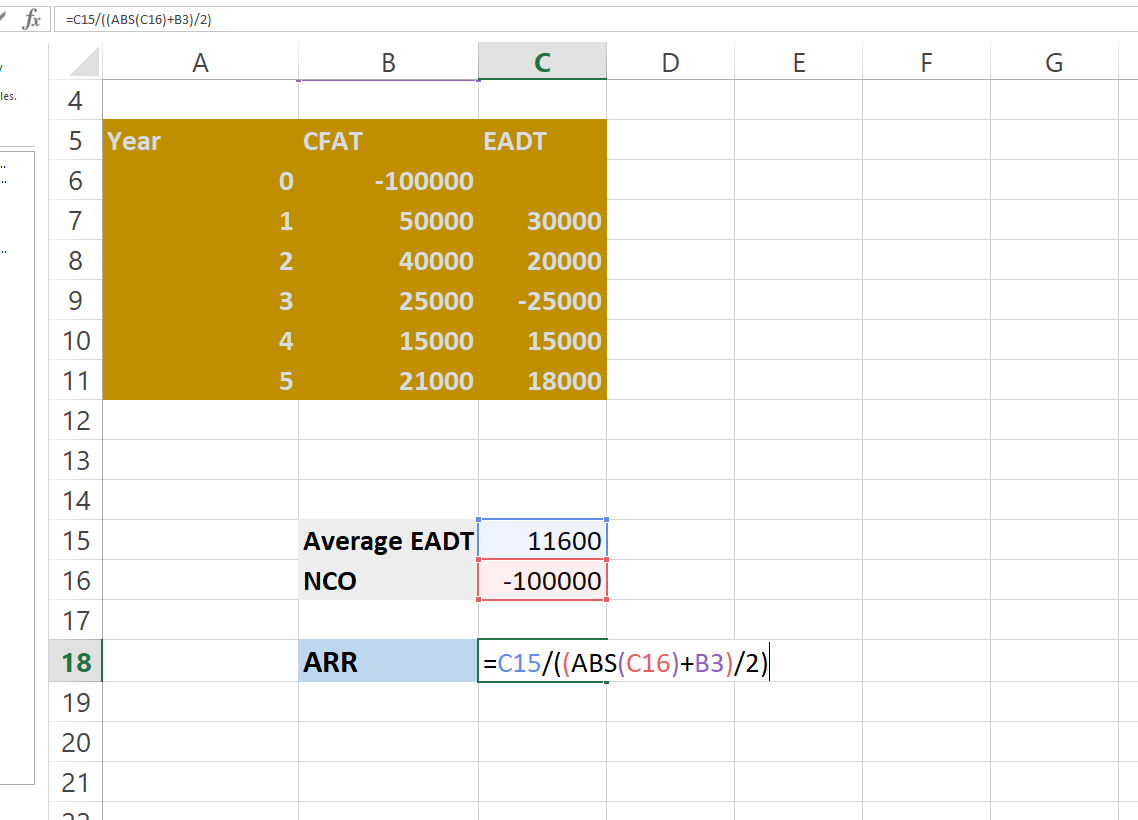
ARR = Average EADT/ (NCO + Salvage Value/2)
In Above Example =C15/((ABS(C16)+B3)/2)
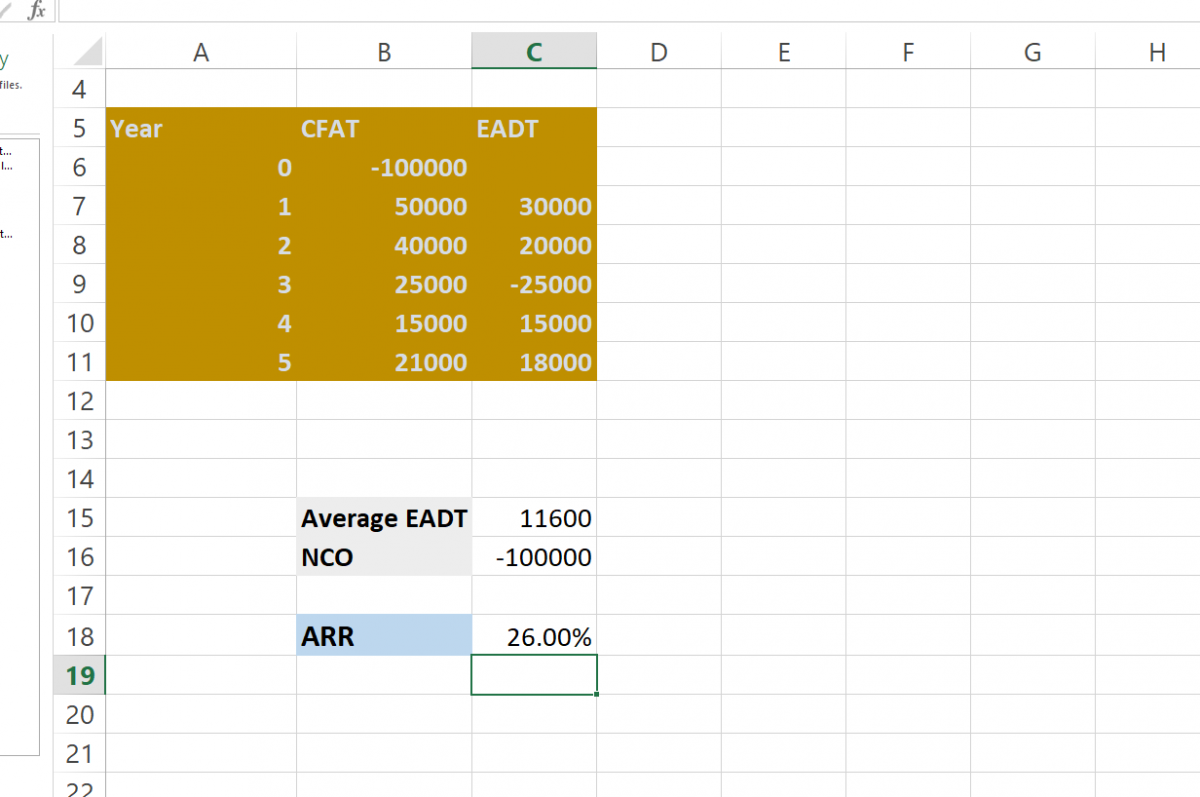
As per this calculation, we can make the decision whether to go for an investment or not.
Conclusion
That’s the end of the tutorial. Hope you have learned about ARR (Accounting Rate of Return) and how to calculate ARR in Excel and now can implement it yourself well to forecast an investment opportunity.
Главная » ⚡ Инвестиционный анализ » 6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI
На чтение 14 мин Просмотров 275к.
Рассмотрим 6 методов оценки эффективности инвестиций, дам различные формулы расчета инвестиционных коэффициентов, методику (алгоритм) расчета их в Excel. Данные методы будут полезны инвесторам, финансовым аналитикам, бизнес-аналитикам и экономистам. Сразу следует отметить, что под инвестициями будем понимать различные инвестиционные проекты, объекты вложения и активы. То есть данные методы могут быть широко использованы в оценочной деятельности любого предприятия/компании.
Все методы оценки эффективности инвестиционных проектов можно разделить на две большие группы:
- Статистические методы оценки инвестиционных проектов
- Срок окупаемости инвестиционного проекта (PP, Payback Period)
- Рентабельность инвестиционного проекта (ARR, Accounting Rate of Return)
- Динамические методы оценки инвестиционных проектов
- Чистый дисконтированный доход (NPV, Net Present Value)
- Внутренняя норма прибыл (IRR, Internal Rate of Return)
- Индекс прибыльности (PI, Profitability index)
- Дисконтированный срок окупаемости (DPP, Discounted Payback Period)
Содержание
- Статистические методы оценки эффективности инвестиций/инвестиционных проектов
- Срок окупаемости инвестиций (Payback Period)
- Формула расчета срока окупаемости инвестиций (инвестиционного проекта)
- Пример расчета срока окупаемости инвестиционного проекта в Excel
- Направления использования срока окупаемости инвестиций (инвестиционных проектов)
- Достоинства и недостатки показателя срока окупаемости инвестиций
- Коэффициент рентабельности инвестиций (Accounting Rate of Return)
- Формула расчета коэффициента рентабельности инвестиций
- Пример расчета коэффициента рентабельности инвестиций (инвестиционного проекта) в Excel
- Цели использования коэффициента рентабельности инвестиционного проекта
- Достоинства и недостатки коэффициента рентабельности инвестиций
- Динамические методы оценки эффективности инвестиций/инвестиционных проектов. Как рассчитать эффективность проекта
- Чистый дисконтированный доход (Net Present Value)
- Формула чистого дисконтированного дохода
- Оценка проекта на основе критерия NPV
- Пример расчета чистого дисконтированного дохода в Excel
- Мастер-класс: «Как рассчитать чистый дисконтированный доход для бизнес плана»
- Внутренняя норма прибыли инвестиционного проекта
- Формула расчета внутренней нормы прибыли инвестиционного проекта
- Пример расчета IRR инвестиционного проекта в Excel
- Достоинства и недостатки внутренней нормы доходности IRR
- Мастер-класс: «Как рассчитать внутреннюю норму доходности для бизнес плана»
- Индекс прибыльности инвестиций (Profitability index)
- Формула расчета индекса прибыльности инвестиций
- Разновидность формулы индекса прибыльности инвестиций
- Оценка проекта на основе критерия PI
- Пример расчета индекса прибыльности проекта в Excel
- Дисконтированный срок окупаемости инвестиций
- Формула расчета дисконтированного срока окупаемости инвестиций
- Пример расчета дисконтированного срока окупаемости инвестиций в Excel
- Достоинства и недостатки дисконтированного срока окупаемости
- Мастер-класс: «Как рассчитать срок окупаемости для бизнес плана: инструкция»
- Выбор инвестиции на основе коэффициентов оценки эффективности
Статистические методы оценки эффективности инвестиций/инвестиционных проектов
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Статистические методы оценки являются самым простым классом подходов к анализу инвестиций и инвестиционных проектов. Несмотря на свою кажущуюся простоту расчета и использования, они позволяют сделать выводы по качеству объектов инвестиций, сравнить их между собой и отсеять неэффективные.
Срок окупаемости инвестиций (Payback Period)
Срок окупаемости инвестиций или инвестиционного проекта (англ. Payback Period, PP, период окупаемости) – данный коэффициент показывает период, за который окупятся первоначальные инвестиции (затраты) в инвестиционный проект. Экономический смысл данного показателя заключается в том, что бы показать срок, за который инвестор вернет обратно свои вложенные деньги (капитал).
Формула расчета срока окупаемости инвестиций (инвестиционного проекта)
где:
IC (Invest Capital) – инвестиционный капитал, первоначальные затраты инвестора в объект вложения. В формуле в иностранной практике иногда используют понятие не инвестиционный капитал, а затраты на капитал (Cost of Capital, CC), что по сути несет аналогичный смысл;
CF (Cash Flow) – денежный поток, который создается объектом инвестиций. Под денежным потоком иногда в формулах подразумевают чистую прибыль (NP, Net Profit).
Формулу расчета срока/период окупаемости можно расписать по-другому, такой вариант тоже часто встречается в отечественной литературе по финансам:
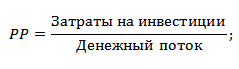
Пример расчета срока окупаемости инвестиционного проекта в Excel
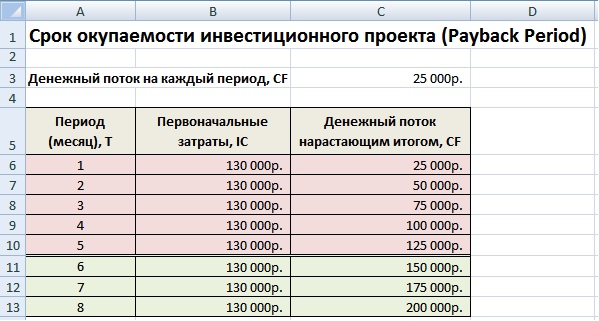
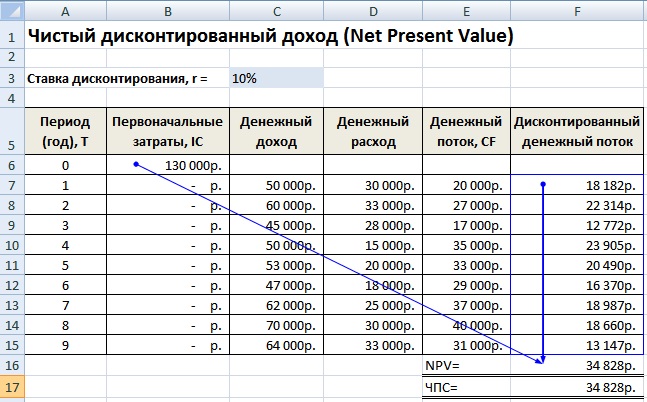
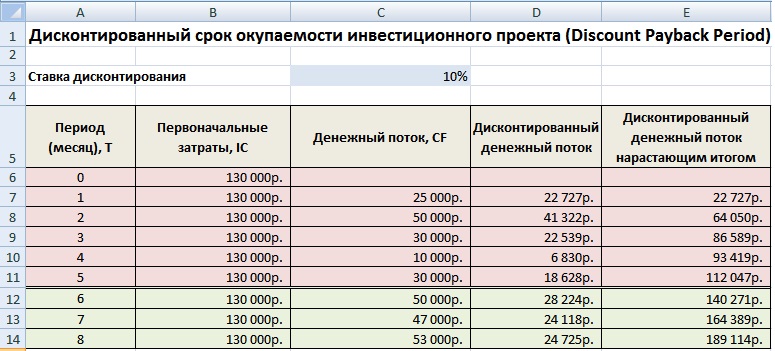
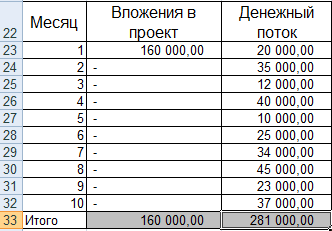
На рисунке ниже показан пример расчета срока окупаемости инвестиционного проекта. У нас имеются исходные данные, что стоимость первоначальных затрат составили 130000 руб., ежемесячно денежный поток от инвестиций составлял 25000 руб. В начале необходимо рассчитать денежный поток нарастающим итогом, для этого использовалась следующая простая формула:
Денежный поток нарастающим итогом рассчитывается в колонке С, C7=C6+$C$3
Если рассчитать срок окупаемости по формуле, то получится следующее:
Так как мы у нас период дискретный, то необходимо округлить этот период до 6 месяцев.
Направления использования срока окупаемости инвестиций (инвестиционных проектов)
Показатель периода окупаемости инвестиций использует как сравнительный показатель для оценки эффективности альтернативных инвестиционных проектов. Тот проект, у которого быстрее период окупаемости тот эффективнее. Данный коэффициент используют, как правило, всегда в совокупности с другими показателям, которые мы разберем ниже.
Достоинства и недостатки показателя срока окупаемости инвестиций
Достоинства показателя его скорость и простота расчета. Недостаток данного коэффициента очевиден – в его расчете используется постоянный денежный поток. В реальных условиях достаточно сложно спрогнозировать устойчивые будущие денежные поступления, поэтому период окупаемости может существенно измениться. Для того чтобы снизить возможные отклонения от плана окупаемости следует обеспечить надежность источников поступления денежного потока инвестиционного проекта. К тому же показатель не учитывает влияние инфляции на изменение стоимости денег во времени. Срок окупаемости инвестиций как может быть использован как критерий отсева на первом этапе оценки и отбора «тяжелых» инвестиционных проектов.
Коэффициент рентабельности инвестиций (Accounting Rate of Return)
Коэффициент рентабельности инвестиций или инвестиционного проекта (англ. Accounting Rate of Return, ARR, ROI, учетная норма прибыли, рентабельность инвестиций) – показатель отражающий прибыльность объекта инвестиций без учета дисконтирования.
Формула расчета коэффициента рентабельности инвестиций
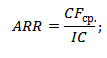
CFср – средний денежный поток (чистая прибыль) объекта инвестиций за рассматриваемый период (месяц, год);
IC (Invest Capital) – инвестиционный капитал, первоначальные затраты инвестора в объект вложения.
Существует также следующая разновидность формулы рентабельности инвестиций отражающая случай, когда в объект/проект в течение рассматриваемого периода вносят дополнительные инвестиционные вложения. Поэтому берется средняя стоимость капитала за период. Формула при этом имеет вид:
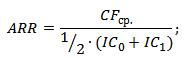
IC0, IC1 – стоимость инвестиций (затраченного капитала) на начало и конец отчетного периода.
Пример расчета коэффициента рентабельности инвестиций (инвестиционного проекта) в Excel
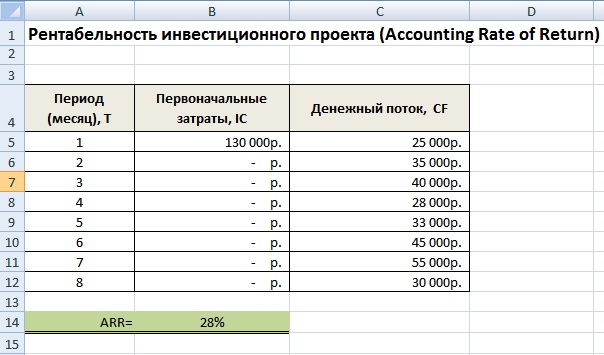
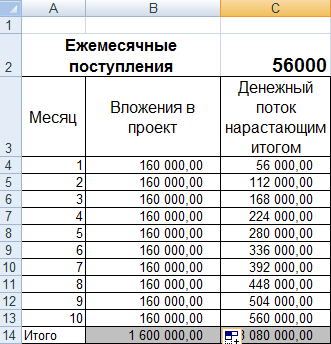
Для того чтобы лучше понять экономический смысл и алгоритм расчета воспользуемся программой Excel. Затраты, которые понес инвестор были только в первом периоде и составили 130000 руб., денежные поступления от инвестиций изменялись ежемесячно, поэтому мы рассчитываем средние поступления по месяцам. За расчетный период может браться любой временной отрезок, квартал, год. В нашем случае мы получаем месячную рентабельность инвестиционного проекта. Формула расчета в Excel следующая:
В14=СРЗНАЧ(C5:C12)/B5
Цели использования коэффициента рентабельности инвестиционного проекта
Данный показатель используется для сравнения различных альтернативных инвестиционных проектов. Чем выше ARR, тем выше привлекательность данного проекта для инвестора. Как правило, данный показатель используется для оценки уже существующих проектов, где можно проследить и статистически оценить эффективность создания денежного потока данной инвестиций.
Достоинства и недостатки коэффициента рентабельности инвестиций
Достоинства коэффициента в его простоте расчета и получения и на этом его достоинства заканчиваются. К недостаткам данного коэффициента можно отнести сложность прогнозирования будущих денежных поступлений/доходов от проекта. К тому же если проект венчурный, то данный показатель может сильно исказить картину восприятия проекта. ARR как правило используется для внешней демонстрации успешного того или иного проекта. Показатель в своей формуле не учитывает изменения стоимости денег во времени. Данный показатель может быть использован на первом этапе оценки и отбора инвестиционных проектов.
Динамические методы оценки эффективности инвестиций/инвестиционных проектов. Как рассчитать эффективность проекта
Рассмотрим ряд динамических методов оценки инвестиционных проектов, данные показатели используют дисконтирование, что является несомненным преимуществом по отношению к статистическим методам.
Чистый дисконтированный доход (Net Present Value)
Чистый дисконтированный доход (англ. Net Present Value, NPV, чистая текущая стоимость, чистый приведенный доход, текущая стоимость) – показатель, отражающий изменение денежных потоков и показывает разность между дисконтированными денежными доходами и расходами.
Чистый дисконтированный доход используют для того чтобы отобрать наиболее инвестиционно привлекательный проект.
Формула чистого дисконтированного дохода
где:
NPV – чистый дисконтированный доход проекта;
CFt – денежный поток в период времени t;
CF0 – денежный поток в первоначальный момент. Первоначальный денежный поток равняется инвестиционному капиталу (CF0 = IC);
r – ставка дисконтирования (барьерная ставка).
Оценка проекта на основе критерия NPV
| Критерий оценки NPV | Заключение по проекту |
| NPV<0 | Инвестиционный проект, имеющий отрицательное значение NPV следует исключить из рассмотрения |
| NPV=0 | Инвестиционный проект обеспечит уровень безубыточности, когда все доходы равны расходам |
| NPV>0 | Инвестиционный проект привлекателен для вложения |
| NPV1>NPV2* | Сравнение NPV одного проекта с NPV* другого, показывает большую инвестиционную привлекательность первого |
Пример расчета чистого дисконтированного дохода в Excel
Рассмотрим пример расчета чистого дисконтированного дохода в программе Excel. В программе есть удобная функция ЧПС (чистая приведенная стоимость), которая позволяет использовать ставку дисконтирования в расчетах. Рассчитаем ниже в двух вариантах NPV.
Вариант №1
Итак, разберем алгоритм последовательного расчета всех показателей NPV.
- Расчет денежного потока по годам: E7=C7-D7
- Дисконтирование денежного потока по времени: F7=E7/(1+$C$3)^A7
- Суммирование всех дисконтированных денежных поступлений по инвестиционному проекту и вычитание первоначальных капитальных затрат: F16 =СУММ(F7:F15)-B6
Вариант №2
Расчет с использованием встроенной формулы ЧПС. Следует заметить, что необходимо вычесть первоначальные капитальные затраты (В6).
=ЧПС($C$3;E7;E8;E9;E10;E11;E12;E13;E14;E15)-B6
Результаты в обоих методах подсчета NPV, как мы видим, совпадают.
Мастер-класс: «Как рассчитать чистый дисконтированный доход для бизнес плана»
Внутренняя норма прибыли инвестиционного проекта
Внутренняя норма прибыли (англ. Internal Rate of Return, IRR, внутренняя норма дисконта, внутренняя норма прибыли, внутренний коэффициент эффективности) – показывает такую ставку дисконтирования, при которой чистый дисконтированный доход равняется нулю.
Формула расчета внутренней нормы прибыли инвестиционного проекта
где:
CF (Cash Flow) – денежный поток, который создается объектом инвестиций;
IRR – внутренняя норма прибыли;
CF0 – денежный поток в первоначальный момент. В первом периоде, как правило, денежный поток равняется инвестиционному капиталу (CF0 = IC).
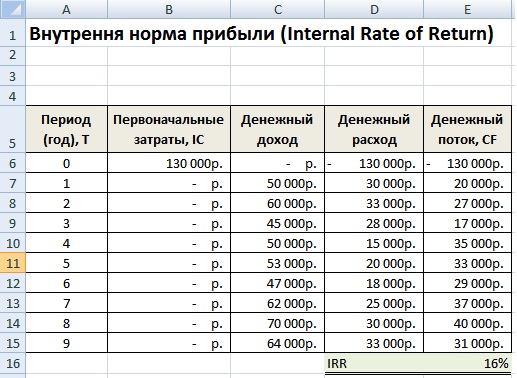
Пример расчета IRR инвестиционного проекта в Excel
Рассмотрим пример расчета внутренней нормы прибыли в Excel, в программе есть хорошая функция ВСД (внутренняя ставка доходности), которая позволяет быстро рассчитать IRR. Данную функцию корректно использовать в том случае если есть хотя бы один положительный и отрицательный денежный поток.
E16 =ВСД(E6:E15)
Достоинства и недостатки внутренней нормы доходности IRR
+ ) возможность сравнения инвестиционных проектов между собой, имеющих разный горизонт инвестирования;
+ )возможность сравнения не только проектов, но и альтернативных инвестиций, например банковский вклад. Если IRR проекта составляет 25%, а банковский вклад равен 15%, то проект более инвестиционно привлекателен.
+ ) экспресс-оценка проекта на его целесообразность дальнейшего развития.
Внутреннюю норму прибыли оценивают со средневзвешенной стоимостью привлеченного капитала, что позволяет сделать оценку целесообразности дальнейшего развития проекта.
| Оценка значений коэффициента IRR | Заключение по проекту |
| IRR > WACC | Вложенный в инвестиционный проект капитал будет создавать доходность выше, чем стоимость вложенного капитала. Такой проект инвестиционно привлекателен |
| IRR = WACC | Проект не принесет ни убытков, ни дохода в будущем периоде и такой проект не является привлекательным |
| IRR < WACC | Такой проект будет создавать отрицательный дисконтированный денежный поток в будущем |
— ) не отражен абсолютный рост стоимости инвестиционного проекта;
— ) денежные потоки часто имеют не систематическую структуру, что затрудняет правильный расчет данного показателя.
Мастер-класс: «Как рассчитать внутреннюю норму доходности для бизнес плана»
Индекс прибыльности инвестиций (Profitability index)
Индекс прибыльность инвестиций (англ. Profitability index, PI, индекс доходности, индекс рентабельности) – показатель эффективности инвестиций, показывающий отдачу (доходность) вложенного капитала. Индекс прибыли представляет собой отношение дисконтированной стоимости будущих денежных потоков к стоимости первоначальных инвестиций. Экономический смысл данного коэффициента – это оценка дополнительной ценности на каждый вложенный рубль.
Формула расчета индекса прибыльности инвестиций
где:
NPV – чистый дисконтированный доход;
n – срок реализации проекта;
r – ставка дисконтирования (%);
IC – вложенный (затраченный) инвестиционный капитал.
Разновидность формулы индекса прибыльности инвестиций
Если вложения в проект осуществляются не единовременно, а на протяжении всего времени реализации, то необходимо инвестиционный капитал (IC) привести к единой стоимости, т.е. дисконтировать его. Формула в этом случае станет иметь следующий вид:
Чем выше коэффициент прибыльности инвестиций, тем большую отдачу на вложенный капитал приносит данная инвестиция. Данный критерий используется для сравнения между собой нескольких инвестиционных проектов. На практике большой индекс прибыли не всегда показывает эффективность проекта, ведь в таком случае оценка будущих доходов могла быть завышена или периодичность их получения не правильно оценена.
Оценка проекта на основе критерия PI
| Критерий оценки PI | Заключение по выбору проекта |
| PI<1 | Инвестиционный проект не сможет возместить в полном размере вложенные в него капитальные затраты |
| PI=1 | Инвестиционный проект имеет доходность равную выбранной ставки дисконтирования |
| PI>1 | Проект инвестиционно привлекателен для вложения, так как сможет обеспечить дополнительную отдачу капитала. |
| PI1>PI2* | Сравнение между собой инвестиционной привлекательности нескольких проектов. Первый проект имеет большую рентабельность, поэтому второй будет отброшен |
Пример расчета индекса прибыльности проекта в Excel
Рассмотрим на примере вычисление индекса прибыльности. На рисунке ниже показан расчет PI в ячейке F18.
- Расчет столбца F – Дисконтированного денежного потока =E7/(1+$C$3)^A7
- Расчет чистого дисконтированного дохода NPV в ячейке F16 =СУММ(F7:F15)-B6
- Оценка прибыльности инвестиций в ячейке F18 =F16/B6
Если бы инвестиционные затраты были каждый год, то необходимо было индекс прибыльности рассчитывать по второй формуле и приводить их к настоящему времени (дисконтировать).
Дисконтированный срок окупаемости инвестиций
Дисконтированный срок окупаемости (англ. Discounted Payback Period, DPP) – показатель отражающий период, через который окупятся первоначальные инвестиционные затраты. Формула расчета коэффициента аналогична формуле оценки периода окупаемости инвестиций, только используется дисконтирование
Формула расчета дисконтированного срока окупаемости инвестиций

IC (Invest Capital)– инвестиционный капитал, первоначальные затраты инвестора в объект вложения;
CF (Cash Flow) – денежный поток, который создается объектом инвестиций;
r – ставка дисконтирования;
t –период оценки получаемого денежного потока.
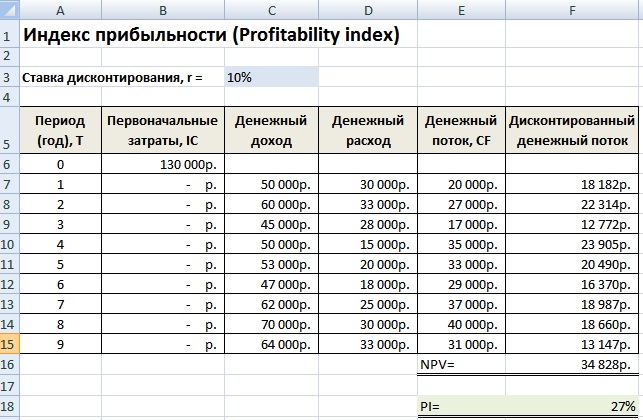
Пример расчета дисконтированного срока окупаемости инвестиций в Excel
Рассчитаем коэффициент дисконтированного срока окупаемости инвестиций в Excel. На рисунке ниже показан пример расчета. Для этого необходимо выполнить следующие операции:
- Рассчитать дисконтированный денежный поток в колонке D =C7/(1+$C$3)^A7
- Посчитать нарастающим итогом прирост капитала в колоне E =E7+D8
- Оценить в какой период вложенные инвестиции (IC) окупились полностью.
Как мы видим окупаемость всех затрат дисконтированным денежным потоком произошла на 6 месяц. Чем меньше период окупаемости инвестиционного проекта, тем более привлекательны данные проекты.
Достоинства и недостатки дисконтированного срока окупаемости
Достоинством коэффициента является возможность использовать в формуле свойство денег изменять свою стоимость со временем за счет инфляционных процессов. Это повышает точность оценки периода возврата вложенного капитала. Сложность использования данного коэффициента заключаются в точном определении будущих денежных поступлений от инвестиции и оценке ставки дисконтирования. Ставка может изменяться на всем жизненном цикле инвестиции из-за действия различных экономических, политических, производственных факторов.
Мастер-класс: «Как рассчитать срок окупаемости для бизнес плана: инструкция»
Выбор инвестиции на основе коэффициентов оценки эффективности
На рисунке ниже показана таблица критериев выбора инвестиционного проекта/инвестиции на основе рассмотренных коэффициентов. Данные показатели позволяют дать экспресс-оценку привлекательности проекта. Следует заметить, что данные показатели плохо применяются для оценки венчурных проектов, потому что сложно спрогнозировать какие будут продажи, доходы и спрос в этом проекте. Показатели хорошо себя зарекомендовали в оценке уже реализованных проектов с четко выстроенными бизнес процессами.
| Показатель | Критерий выбора инвестиции |
| Статистические методы оценки эффективности инвестиций | |
| Период окупаемости | PP -> min |
| Рентабельность инвестиционного капитала | ARR>0 |
| Динамические методы оценки эффективности инвестиций | |
| Чистый дисконтированный доход | NPV>0 |
| Внутренняя норма прибыли | IRR>WACC |
| Индекс прибыльности | PI>1 |
| Дисконтированный период окупаемости | DPP -> min |
Резюме
Использование коэффициентов оценки инвестиционных проектов позволяет сделать выбрать наиболее привлекательные объекты для вложения. Мы рассмотрели как статистические, так и динамические методы оценки, на практике, первые подходят для отражения общей характеристики объекта, тогда как динамические позволяют более точно оценить параметры инвестиции. В современной экономике, во времена кризисов, использование данных показателей эффективно на сравнительно не большой горизонт инвестирования. Помимо внешних факторов, на оценку влияют внутренние – сложность точного определения будущих денежных поступлений от проекта. Показатели дают в большей степени финансовое описание жизни инвестиции и не раскрывают причинно-следственных связей с получаемыми доходами (сложно оценить венчурные проекты и стартапы ). В тоже время, простота расчетов коэффициентов позволяет уже на первом этапе анализа исключить не рентабельные проекты. На этом описание коэффициентов оценки эффективности инвестиций завершено. Изучайте инвестиционный анализ, в следующих статьях я расскажу про более сложные методы оценки проектов, спасибо за внимание, с вами были Иван Жданов.
Автор: к.э.н. Жданов Иван Юрьевич
На чтение 24 мин. Просмотров 90.8k.

Дональд Кнут
Список настолько же силен, как и его самое слабое звено
В таблице ниже краткая справка по использованию массивов в VBA. В статье постарался замахнуться на звание самого подробного руководства, которое вы найдете о массивах VBA.
Содержание
- Краткое руководство по массивам VBA
- Введение
- Быстрые заметки
- Что такое массивы и зачем они нужны?
- Типы массивов VBA
- Объявление массива
- Присвоение значений массиву
- Использование функций Array и Split
- Использование циклов с массивами
- Использование Erase
- ReDim с Preserve
- Сортировка массива
- Передача массива в Sub или функцию
- Возвращение массива из функции
- Двумерные массивы
- Чтение из диапазона ячеек в массив
- Как заставить ваши макросы работать на суперскорости
- Заключение
Краткое руководство по массивам VBA
| Задача | Статический массив |
Динамический массив |
| Объявление | Dim arr(0 To 5) As Long |
Dim arr() As Long Dim arr As Variant |
| Установить размер | Dim arr(0 To 5) As Long |
ReDim arr(0 To 5)As Variant |
| Увеличить размер (сохранить существующие данные) |
Только динамический |
ReDim Preserve arr(0 To 6) |
| Установить значения |
arr(1) = 22 | arr(1) = 22 |
| Получить значения | total = arr(1) | total = arr(1) |
| Первая позиция | LBound(arr) | LBound(arr) |
| Последняя позиция | Ubound(arr) | Ubound(arr) |
| Читать все записи (1D) | For i = LBound(arr) To UBound(arr) Next i Or For i = LBound(arr,1) To UBound(arr,1) Next i |
For i = LBound(arr) To UBound(arr) Next i Or For i = LBound(arr,1) To UBound(arr,1) Next i |
| Читать все записи (2D) | For i = LBound(arr,1) To UBound(arr,1) For j = LBound(arr,2) To UBound(arr,2) Next j Next i |
For i = LBound(arr,1) To UBound(arr,1) For j = LBound(arr,2) To UBound(arr,2) Next j Next i |
| Читать все записи | Dim item As Variant For Each item In arr Next item |
Dim item As Variant For Each item In arr Next item |
| Перейти на Sub | Sub MySub(ByRef arr() As String) | Sub MySub(ByRef arr() As String) |
| Возврат из функции | Function GetArray() As Long() Dim arr(0 To 5) As Long GetArray = arr End Function |
Function GetArray() As Long() Dim arr() As Long GetArray = arr End Function |
| Получить от функции |
Только динамический |
Dim arr() As Long Arr = GetArray() |
| Стереть массив | Erase arr *Сбрасывает все значения по умолчанию |
Erase arr *Удаляет массив |
| Строка в массив | Только динамический |
Dim arr As Variant arr = Split(«James:Earl:Jones»,»:») |
| Массив в строку | Dim sName As String sName = Join(arr, «:») |
Dim sName As String sName = Join(arr, «:») |
| Заполните значениями |
Только динамический |
Dim arr As Variant arr = Array(«John», «Hazel», «Fred») |
| Диапазон в массив | Только динамический |
Dim arr As Variant arr = Range(«A1:D2») |
| Массив в диапазон | Так же, как в динамическом |
Dim arr As Variant Range(«A5:D6») = arr |
Введение
В этой статье подробно рассматриваются массивы на языке программирования Excel VBA. Она охватывает важные моменты, такие как:
- Зачем вам массивы
- Когда вы должны их использовать
- Два типа массивов
- Использование более одного измерения
- Объявление массивов
- Добавление значений
- Просмотр всех предметов
- Супер эффективный способ чтения Range в массив
В первом разделе мы рассмотрим, что такое массивы и зачем они нужны. Вы можете не понимать часть кода в первом разделе. Это нормально. Я буду разбивать на простые термины в следующих разделах статьи.
Быстрые заметки
Иногда коллекции лучше, чем массивы. Вы можете прочитать о коллекциях здесь.
Массивы и циклы идут рука об руку. Наиболее распространенными циклами, которые вы используете с массивами, являются циклы For i и For Each.
Что такое массивы и зачем они нужны?
Массив VBA — это тип переменной. Используется для хранения списков данных одного типа. Примером может быть сохранение списка стран или списка итогов за неделю.
В VBA обычная переменная может хранить только одно значение за раз.
В следующем примере показана переменная, используемая для хранения оценок ученика.
' Может хранить только 1 значение за раз Dim Student1 As Integer Student1 = 55
Если мы хотим сохранить оценки другого ученика, нам нужно создать вторую переменную.
В следующем примере у нас есть оценки пяти студентов
Мы собираемся прочитать эти отметки и записать их в Immediate Window.
Примечание. Функция Debug.Print записывает значения в Immediate Window. Для просмотра этого окна выберите View-> Immediate Window из меню (сочетание клавиш Ctrl + G).
Как видите в следующем примере, мы пишем один и тот же код пять раз — по одному для каждого учащегося.
Public Sub StudentMarks()
With ThisWorkbook.Worksheets("Лист1")
' Объявите переменную для каждого студента
Dim Student1 As Integer
Dim Student2 As Integer
Dim Student3 As Integer
Dim Student4 As Integer
Dim Student5 As Integer
' Читайте оценки студентов из ячейки
Student1 = .Range("C2").Offset(1)
Student2 = .Range("C2").Offset(2)
Student3 = .Range("C2").Offset(3)
Student4 = .Range("C2").Offset(4)
Student5 = .Range("C2").Offset(5)
' Печать студенческих оценок
Debug.Print "Оценки студентов"
Debug.Print Student1
Debug.Print Student2
Debug.Print Student3
Debug.Print Student4
Debug.Print Student5
End With
End Sub
Ниже приведен вывод из примера
Проблема с использованием одной переменной для каждого учащегося заключается в том, что вам необходимо добавить код для каждого учащегося. Поэтому, если в приведенном выше примере у вас будет тысяча студентов, вам понадобится три тысячи строк кода!
К счастью, у нас есть массивы, чтобы сделать нашу жизнь проще. Массивы позволяют нам хранить список элементов данных в одной структуре.
Следующий код показывает приведенный выше пример с использованием массива.
Public Sub StudentMarksArr()
With ThisWorkbook.Worksheets("Лист1")
' Объявите массив для хранения оценок для 5 студентов
Dim Students(1 To 5) As Integer
' Читайте оценки учеников из ячеек C3: C7 в массив
Dim i As Integer
For i = 1 To 5
Students(i) = .Range("C2").Offset(i)
Next i
' Распечатывать оценки студентов из массива
Debug.Print "Оценки студентов"
For i = LBound(Students) To UBound(Students)
Debug.Print Students(i)
Next i
End With
End Sub
Преимущество этого кода в том, что он будет работать для любого количества студентов. Если нам нужно изменить этот код для работы с 1000 студентами, нам нужно всего лишь изменить (от 1 до 5) на (от 1 до 1000) в декларации. В предыдущем примере нам нужно было добавить примерно пять тысяч строк кода.
Давайте проведем быстрое сравнение переменных и массивов. Сначала мы сравним процесс объявления.
' Объявляем переменные
Dim Student As Integer
Dim Country As String
' Объявляем массивы
Dim Students(1 To 3) As Integer
Dim Countries(1 To 3) As String
Далее мы сравниваем присвоение значения
' присвоить значение переменной
Student1 = .Cells(1, 1)
' присваивать значение первому элементу в массиве
Students(1) = .Cells(1, 1)
Наконец, мы смотрим на запись значений
' Вывести значение переменной
Debug.Print Student1
' Вывести значение первого студента в массиве
Debug.Print Students(1)
Как видите, использование переменных и массивов очень похоже.
Важным является тот факт, что массивы используют индекс (также называемый нижним индексом) для доступа к каждому элементу. Это означает, что мы можем легко получить доступ ко всем элементам в массиве, используя цикл For.
Теперь, когда у вас есть представление о том, почему массивы полезны, давайте пройдемся по ним шаг за шагом.
Типы массивов VBA
В VBA есть два типа массивов:
- Статический — массив фиксированного размера.
- Динамический — массив, в котором размер задается во время выполнения
Разница между этими массивами в основном в том, как они создаются. Доступ к значениям в обоих типах массивов абсолютно одинаков. В следующих разделах мы рассмотрим оба типа.
Объявление массива
Статический массив объявляется следующим образом
Public Sub DecArrayStatic()
' Создать массив с местоположениями 0,1,2,3
Dim arrMarks1(0 To 3) As Long
' По умолчанию от 0 до 3, то есть местоположения 0,1,2,3
Dim arrMarks2(3) As Long
' Создать массив с местоположениями 1,2,3,4,5
Dim arrMarks1(1 To 5) As Long
' Создать массив с местоположениями 2,3,4 'Это редко используется
Dim arrMarks3(2 To 4) As Long
End Sub
Как видите, размер указывается при объявлении статического массива. Проблема в том, что вы никогда не можете быть заранее уверены, какой размер вам нужен. Каждый раз, когда вы запускаете макрос, у вас могут быть разные требования к размеру.
Если вы не используете все расположения массива, ресурсы тратятся впустую. Если вам нужно больше места, вы можете использовать ReDim, но это по сути создает новый статический массив.
Динамический массив не имеет таких проблем. Вы не указываете размер, когда объявляете. Поэтому вы можете увеличиваться и уменьшаться по мере необходимости.
Public Sub DecArrayDynamic()
' Объявить динамический массив
Dim arrMarks() As Long
' Установите размер массива, когда вы будете готовы
ReDim arrMarks(0 To 5)
End Sub
Динамический массив не выделяется, пока вы не используете оператор ReDim. Преимущество в том, что вы можете подождать, пока не узнаете количество элементов, прежде чем устанавливать размер массива. Со статическим массивом вы должны указать размер заранее.
Присвоение значений массиву
Чтобы присвоить значения массиву, вы используете номер местоположения (пересечении строки и столбца). Вы присваиваете значение для обоих типов массивов одинаково.
Public Sub AssignValue()
' Объявить массив с местоположениями 0,1,2,3
Dim arrMarks(0 To 3) As Long
' Установите значение позиции 0
arrMarks(0) = 5
' становите значение позиции 3
arrMarks(3) = 46
' Это ошибка, так как нет местоположения 4
arrMarks(4) = 99
End Sub
Номер места называется индексом. Последняя строка в примере выдаст ошибку «Индекс вне диапазона», так как в примере массива нет местоположения 4.
Использование функций Array и Split
Вы можете использовать функцию Array для заполнения массива списком элементов. Вы должны объявить массив как тип Variant. Следующий код показывает, как использовать эту функцию.
Dim arr1 As Variant
arr1 = Array("Апельсин", "Персик","Груша")
Dim arr2 As Variant
arr2 = Array(5, 6, 7, 8, 12)
Массив, созданный функцией Array, начнется с нулевого индекса, если вы не используете Option Base 1 в верхней части вашего модуля. Затем он начнется с первого индекса. В программировании, как правило, считается плохой практикой иметь ваши реальные данные в коде. Однако иногда это полезно, когда вам нужно быстро протестировать некоторый код. Функция Split используется для разделения строки на массив на основе разделителя. Разделитель — это символ, такой как запятая или пробел, который разделяет элементы.
Следующий код разделит строку на массив из трех элементов.
Dim s As String
s = "Красный,Желтый,Зеленый,Синий"
Dim arr() As String
arr = Split(s, ",")
Функция Split обычно используется, когда вы читаете из cvs или txt-файла, разделенного запятыми, или из другого источника, который предоставляет список элементов, разделенных одним и тем же символом.
Использование циклов с массивами
Использование цикла For обеспечивает быстрый доступ ко всем элементам массива. Вот где сила использования массивов становится очевидной. Мы можем читать массивы с десятью значениями или десятью тысячами значений, используя те же несколько строк кода. В VBA есть две функции: LBound и UBound. Эти функции возвращают самый маленький и самый большой индекс в массиве. В массиве arrMarks (от 0 до 3) LBound вернет 0, а UBound вернет 3.
В следующем примере случайные числа присваиваются массиву с помощью цикла. Затем он печатает эти числа, используя второй цикл.
Public Sub ArrayLoops()
' Объявить массив
Dim arrMarks(0 To 5) As Long
' Заполните массив случайными числами
Dim i As Long
For i = LBound(arrMarks) To UBound(arrMarks)
arrMarks(i) = 5 * Rnd
Next i
' Распечатайте значения в массиве
Debug.Print "Место нахождения", "Значение"
For i = LBound(arrMarks) To UBound(arrMarks)
Debug.Print i, arrMarks(i)
Next i
End Sub
Функции LBound и UBound очень полезны. Их использование означает, что наши циклы будут работать правильно с любым размером массива. Реальное преимущество заключается в том, что если размер массива изменяется, нам не нужно менять код для печати значений. Цикл будет работать для массива любого размера, пока вы используете эти функции.
Использование цикла For Each
Вы можете использовать цикл For Each с массивами. Важно помнить, что он доступен только для чтения. Это означает, что вы не можете изменить значение в массиве.
В следующем коде значение метки изменяется, но оно не меняет значение в массиве.
For Each mark In arrMarks
' Не изменит значение массива
mark = 5 * Rnd
Next mark
Цикл For Each отлично подходит для чтения массива. Как видите, лучше писать специально для двумерного массива.
Dim mark As Variant
For Each mark In arrMarks
Debug.Print mark
Next mark
Использование Erase
Функция Erase может использоваться для массивов, но она работает по-разному в зависимости от типа массива.
Для статического массива функция Erase сбрасывает все значения по умолчанию. Если массив состоит из целых чисел, то все значения устанавливаются в ноль. Если массив состоит из строк, то все строки устанавливаются в «» и так далее.
Для динамического массива функция удаления стирает память. То есть она удаляет массив. Если вы хотите использовать его снова, вы должны использовать ReDim для выделения памяти.
Давайте рассмотрим пример статического массива. Этот пример аналогичен примеру ArrayLoops в последнем разделе с одним отличием — мы используем Erase после установки значений. Когда значение будет распечатано, все они будут равны нулю.
Public Sub EraseStatic()
' Объявить массив
Dim arrMarks(0 To 3) As Long
' Заполните массив случайными числами
Dim i As Long
For i = LBound(arrMarks) To UBound(arrMarks)
arrMarks(i) = 5 * Rnd
Next i
' ВСЕ ЗНАЧЕНИЯ УСТАНОВЛЕНЫ НА НОЛЬ
Erase arrMarks
' Распечатайте значения - там все теперь ноль
Debug.Print "Место нахождения", "Значение"
For i = LBound(arrMarks) To UBound(arrMarks)
Debug.Print i, arrMarks(i)
Next i
End Sub
Теперь мы попробуем тот же пример с динамикой. После того, как мы используем Erase, все места в массиве были удалены. Нам нужно использовать ReDim, если мы хотим использовать массив снова.
Если мы попытаемся получить доступ к членам этого массива, мы получим ошибку «Индекс вне диапазона».
Public Sub EraseDynamic()
' Объявить массив
Dim arrMarks() As Long
ReDim arrMarks(0 To 3)
' Заполните массив случайными числами
Dim i As Long
For i = LBound(arrMarks) To UBound(arrMarks)
arrMarks(i) = 5 * Rnd
Next i
' arrMarks теперь освобожден. Места не существуют.
Erase arrMarks
End Sub
ReDim с Preserve
Если мы используем ReDim для существующего массива, то массив и его содержимое будут удалены.
В следующем примере второй оператор ReDim создаст совершенно новый массив. Исходный массив и его содержимое будут удалены.
Sub UsingRedim()
Dim arr() As String
' Установить массив в слоты от 0 до 2
ReDim arr(0 To 2)
arr(0) = "Яблоко"
' Массив с яблоком теперь удален
ReDim arr(0 To 3)
End Sub
Если мы хотим расширить размер массива без потери содержимого, мы можем использовать ключевое слово Preserve.
Когда мы используем Redim Preserve, новый массив должен начинаться с того же начального размера, например мы не можем сохранить от (0 до 2) до (от 1 до 3) или до (от 2 до 10), поскольку они являются различными начальными размерами.
В следующем коде мы создаем массив с использованием ReDim, а затем заполняем массив типами фруктов.
Затем мы используем Preserve для увеличения размера массива, чтобы не потерять оригинальное содержимое.
Sub UsingRedimPreserve()
Dim arr() As String
' Установить массив в слоты от 0 до 1
ReDim arr(0 To 2)
arr(0) = "Яблоко"
arr(1) = "Апельсин"
arr(2) = "Груша"
' Изменение размера и сохранение исходного содержимого
ReDim Preserve arr(0 To 5)
End Sub
Из приведенных ниже снимков экрана видно, что исходное содержимое массива было «сохранено».
Предостережение: в большинстве случаев вам не нужно изменять размер массива, как мы делали в этом разделе. Если вы изменяете размер массива несколько раз, то вам захочется рассмотреть возможность использования коллекции.
Использование Preserve с 2-мерными массивами
Preserve работает только с верхней границей массива.
Например, если у вас есть двумерный массив, вы можете сохранить только второе измерение, как показано в следующем примере:
Sub Preserve2D()
Dim arr() As Long
' Установите начальный размер
ReDim arr(1 To 2, 1 To 5)
' Изменить размер верхнего измерения
ReDim Preserve arr(1 To 2, 1 To 10)
End Sub
Если мы попытаемся использовать Preserve на нижней границе, мы получим ошибку «Индекс вне диапазона».
В следующем коде мы используем Preserve для первого измерения. Запуск этого кода приведет к ошибке «Индекс вне диапазона»:
Sub Preserve2DError()
Dim arr() As Long
' Установите начальный размер
ReDim arr(1 To 2, 1 To 5)
' Ошибка «Вне диапазона»
ReDim Preserve arr(1 To 5, 1 To 5)
End Sub
Когда мы читаем из диапазона в массив, он автоматически создает двумерный массив, даже если у нас есть только один столбец.
Применяются те же правила сохранения. Мы можем использовать Preserve только на верхней границе, как показано в следующем примере:
Sub Preserve2DRange()
Dim arr As Variant
' Назначить диапазон массиву
arr = Sheet1.Range("A1:A5").Value
' Preserve будет работать только на верхней границе
ReDim Preserve arr(1 To 5, 1 To 7)
End Sub
Сортировка массива
В VBA нет функции для сортировки массива. Мы можем отсортировать ячейки листа, но это медленно, если данных много.
Функция быстрой сортировки ниже может использоваться для сортировки массива.
Sub QuickSort(arr As Variant, first As Long, last As Long)
Dim vCentreVal As Variant, vTemp As Variant
Dim lTempLow As Long
Dim lTempHi As Long
lTempLow = first
lTempHi = last
vCentreVal = arr((first + last) / 2)
Do While lTempLow <= lTempHi
Do While arr(lTempLow) < vCentreVal And lTempLow < last
lTempLow = lTempLow + 1
Loop
Do While vCentreVal < arr(lTempHi) And lTempHi > first
lTempHi = lTempHi - 1
Loop
If lTempLow <= lTempHi Then
' Поменять значения
vTemp = arr(lTempLow)
arr(lTempLow) = arr(lTempHi)
arr(lTempHi) = vTemp
' Перейти к следующим позициям
lTempLow = lTempLow + 1
lTempHi = lTempHi - 1
End If
Loop
If first < lTempHi Then QuickSort arr, first, lTempHi
If lTempLow < last Then QuickSort arr, lTempLow, last
End Sub
Вы можете использовать эту функцию так:
Sub TestSort()
' Создать временный массив
Dim arr() As Variant
arr = Array("Банан", "Дыня", "Персик", "Слива", "Яблоко")
' Сортировать массив
QuickSort arr, LBound(arr), UBound(arr)
' Печать массива в Immediate Window(Ctrl + G)
Dim i As Long
For i = LBound(arr) To UBound(arr)
Debug.Print arr(i)
Next i
End Sub
Передача массива в Sub или функцию
Иногда вам нужно будет передать массив в процедуру. Вы объявляете параметр, используя круглые скобки, аналогично тому, как вы объявляете динамический массив.
Переход к процедуре с использованием ByRef означает, что вы передаете ссылку на массив. Таким образом, если вы измените массив в процедуре, он будет изменен, когда вы вернетесь.
Примечание. Когда вы используете массив в качестве параметра, он не может использовать ByVal, он должен использовать ByRef. Вы можете передать массив с помощью ByVal, сделав параметр вариантом.
' Передает массив в функцию
Public Sub PassToProc()
Dim arr(0 To 5) As String
' Передать массив в функцию
UseArray arr
End Sub
Public Function UseArray(ByRef arr() As String)
' Использовать массив
Debug.Print UBound(arr)
End Function
Возвращение массива из функции
Важно помнить следующее. Если вы хотите изменить существующий массив в процедуре, вы должны передать его как параметр, используя ByRef (см. Последний раздел). Вам не нужно возвращать массив из процедуры.
Основная причина возврата массива — это когда вы используете процедуру для создания нового. В этом случае вы присваиваете возвращаемый массив массиву в вызывающей программе. Этот массив не может быть уже выделен. Другими словами, вы должны использовать динамический массив, который не был выделен.
Следующие примеры показывают это:
Public Sub TestArray()
' Объявить динамический массив - не выделен
Dim arr() As String
' Возврат нового массива
arr = GetArray
End Sub
Public Function GetArray() As String()
' Создать и выделить новый массив
Dim arr(0 To 5) As String
' Возвращаемый массив
GetArray = arr
End Function
Двумерные массивы
Массивы, на которые мы смотрели до сих пор, были одномерными. Это означает, что массивы представляют собой один список элементов.
Двумерный массив — это список списков. Если вы думаете об одной строке электронной таблицы как об одном измерении, то более одного столбца является двухмерным. На самом деле электронная таблица является эквивалентом двумерного массива. Он имеет два измерения — строки и столбцы.
Следует отметить одну маленькую вещь: Excel обрабатывает одномерный массив как строку, если вы записываете его в электронную таблицу. Другими словами, массив arr (от 1 до 5) эквивалентен arr (от 1 до 1, от 1 до 5) при записи значений в электронную таблицу.
На следующем рисунке показаны две группы данных. Первый — это одномерный массив, а второй — двухмерный.
Чтобы получить доступ к элементу в первом наборе данных (одномерном), все, что вам нужно сделать, это дать строку, например. 1,2, 3 или 4.
Для второго набора данных (двумерного) вам нужно указать строку И столбец. Таким образом, вы можете думать, что 1-мерное — это несколько столбцов, а одна строка и двухмерное — это несколько строк и несколько столбцов.
Примечание. В массиве может быть более двух измерений. Это редко требуется. Если вы решаете проблему с помощью 3+-мерного массива, то, вероятно, есть лучший способ сделать это.
Вы объявляете двумерный массив следующим образом:
Dim ArrayMarks(0 To 2, 0 To 3) As Long
В следующем примере создается случайное значение для каждого элемента в массиве и печатается значение в Immediate Window.
Public Sub TwoDimArray()
' Объявить двумерный массив
Dim arrMarks(0 To 3, 0 To 2) As String
' Заполните массив текстом, состоящим из значений i и j
Dim i As Long, j As Long
For i = LBound(arrMarks) To UBound(arrMarks)
For j = LBound(arrMarks, 2) To UBound(arrMarks, 2)
arrMarks(i, j) = CStr(i) & ":" & CStr(j)
Next j
Next i
' Вывести значения в массиве в Immediate Window
Debug.Print "i", "j", "Знаечние"
For i = LBound(arrMarks) To UBound(arrMarks)
For j = LBound(arrMarks, 2) To UBound(arrMarks, 2)
Debug.Print i, j, arrMarks(i, j)
Next j
Next i
End Sub
Видите, что мы используем второй цикл For внутри первого цикла, чтобы получить доступ ко всем элементам.
Результат примера выглядит следующим образом:
Этот макрос работает следующим образом:
- Входит в цикл i
- i установлен на 0
- цикл Enters j
- j установлен на 0
- j установлен в 1
- j установлен на 2
- Выход из цикла j
- i установлен в 1
- j установлен на 0
- j установлен в 1
- j установлен на 2
- И так до тех пор, пока i = 3 и j = 2
Заметьте, что LBound и UBound имеют второй аргумент 2. Это указывает, что это верхняя или нижняя граница второго измерения. Это начальное и конечное местоположение для j. Значение по умолчанию 1, поэтому нам не нужно указывать его для цикла i.
Использование цикла For Each
Использование For Each лучше использовать при чтении из массива.
Давайте возьмем код сверху, который выписывает двумерный массив.
' Для цикла For необходимо два цикла
Debug.Print "i", "j", "Значение"
For i = LBound(arrMarks) To UBound(arrMarks)
For j = LBound(arrMarks, 2) To UBound(arrMarks, 2)
Debug.Print i, j, arrMarks(i, j)
Next j
Next i
Теперь давайте перепишем его, используя цикл For Each. Как видите, нам нужен только один цикл, и поэтому гораздо проще написать:
' Использование For Each требует только одного цикла
Debug.Print "Значение"
Dim mark As Variant
For Each mark In arrMarks
Debug.Print mark
Next mark
Использование цикла For Each дает нам массив только в одном порядке — от LBound до UBound. В большинстве случаев это все, что вам нужно.
Чтение из диапазона ячеек в массив
Если вы читали мою статью о ячейках и диапазонах, то вы знаете, что VBA имеет чрезвычайно эффективный способ чтения из диапазона ячеек в массив и наоборот.
Public Sub ReadToArray()
' Объявить динамический массив
Dim StudentMarks As Variant
' Считать значения в массив из первой строки
StudentMarks = Range("A1:Z1").Value
' Запишите значения обратно в третий ряд
Range("A3:Z3").Value = StudentMarks
End Sub
Динамический массив, созданный в этом примере, будет двухмерным массивом. Как видите, мы можем прочитать весь диапазон ячеек в массив всего за одну строку.
В следующем примере будут считаны примеры данных студента ниже из C3: E6 Лист1 и распечатаны в Immediate Window.
Public Sub ReadAndDisplay()
' Получить диапазон
Dim rg As Range
Set rg = ThisWorkbook.Worksheets("Лист1").Range("C3:E6")
' Создать динамический массив
Dim StudentMarks As Variant
' Считать значения в массив из листа 1
StudentMarks = rg.Value
' Вывести значения массива
Debug.Print "i", "j", "Значение"
Dim i As Long, j As Long
For i = LBound(StudentMarks) To UBound(StudentMarks)
For j = LBound(StudentMarks, 2) To UBound(StudentMarks, 2)
Debug.Print i, j, StudentMarks(i, j)
Next j
Next i
End Sub
Как видите, первое измерение (доступное через i) массива — это строка, а второе — столбец. Чтобы продемонстрировать это, взглянем на значение 44 в Е4 данных образца. Это значение находится в строке 2 столбца 3 наших данных. Вы можете видеть, что 44 хранится в массиве в StudentMarks (2,3).
Как заставить ваши макросы работать на суперскорости
Если ваши макросы работают очень медленно, этот раздел будет очень полезным. Особенно, если вы имеете дело с большими объемами данных. В VBA это держится в секрете.
Обновление значений в массивах происходит экспоненциально быстрее, чем обновление значений в ячейках.
В последнем разделе вы увидели, как мы можем легко читать из группы ячеек в массив и наоборот. Если мы обновляем много значений, то мы можем сделать следующее
- Скопируйте данные из ячеек в массив.
- Измените данные в массиве.
- Скопируйте обновленные данные из массива обратно в ячейки.
Например, следующий код будет намного быстрее, чем код ниже:
Public Sub ReadToArray()
' Считать значения в массив из первой строки
Dim StudentMarks As Variant
StudentMarks = Range("A1:Z20000").Value
Dim i As Long
For i = LBound(StudentMarks) To UBound(StudentMarks)
' Обновление отметок здесь
StudentMarks(i, 1) = StudentMarks(i, 1) * 2
'...
Next i
' Запишите новые значения обратно на лист
Range("A1:Z20000").Value = StudentMarks
End Sub
Sub UsingCellsToUpdate()
Dim c As Variant
For Each c In Range("A1:Z20000")
c.Value = ' Обновите значения здесь
Next c
End Sub
Назначение из одного набора ячеек в другой также намного быстрее, чем с помощью копирования и вставки.
' Назначение - быстрее
Range("A1:A10").Value = Range("B1:B10").Value
' Копировать Вставить - медленнее
Range("B1:B1").Copy Destination:=Range("A1:A10")
Заключение
Ниже приводится краткое изложение основных моментов этой статьи.
- Массивы — это эффективный способ хранения списка элементов одного типа.
- Вы можете получить доступ к элементу массива напрямую, используя номер местоположения, который известен как индекс.
- Распространенная ошибка «Индекс вне диапазона» вызвана доступом к несуществующему местоположению.
- Существует два типа массивов: статический и динамический.
- Статический используется, когда размер массива всегда одинаков.
- Динамические массивы позволяют вам определять размер массива во время выполнения.
- LBound и UBound обеспечивают безопасный способ поиска самых маленьких и самых больших подписок массива.
- Основной массив является одномерным. Есть еще многомерные массивы.
- Чтобы только передать массив в процедуру, используйте ByRef. Вы делаете это так: ByRef arr() as long.
- Вы можете вернуть массив из функции, но массив, которому он назначен, не должен быть выделен в данный момент.
- Рабочий лист с его строками и столбцами по сути является двумерным массивом.
- Вы можете читать непосредственно из диапазона листа в двухмерный массив всего за одну строку кода.
- Вы также можете записать из двумерного массива в диапазон всего за одну строку кода.
Массивы в VBA Excel: одномерные, многомерные и динамические. Объявление и использование массивов. Операторы Public, Dim и ReDim. Функции Array, LBound, UBound.
Массивы – это множества однотипных элементов, имеющих одно имя и отличающиеся друг от друга индексами. Они могут быть одномерными (линейными), многомерными и динамическими. Массивы в VBA Excel, как и другие переменные, объявляются с помощью операторов Dim и Public. Для изменения размерности динамических массивов используется оператор ReDim. Массивы с заранее объявленной размерностью называют статическими.
Одномерные массивы
Объявление одномерных (линейных) статических массивов в VBA Excel:
|
Public Massiv1(9) As Integer Dim Massiv2(1 To 9) As String |
В первом случае публичный массив содержит 10 элементов от 0 до 9 (нижний индекс по умолчанию — 0, верхний индекс — 9), а во втором случае локальный массив содержит 9 элементов от 1 до 9.
По умолчанию VBA Excel считает в массивах нижним индексом нуль, но, при желании, можно сделать нижним индексом по умолчанию единицу, добавив в самом начале модуля объявление «Option Base 1».
Многомерные массивы
Объявление многомерных статических массивов в VBA Excel аналогично объявлению одномерных массивов, но с добавлением размерностей дополнительных измерений через запятую:
|
‘Массив двухмерный Public Massiv1(3, 6) As Integer ‘Массив трехмерный Dim Massiv2(1 To 6, 1 To 8, 1 To 5) As String ‘Массив четырехмерный Dim Massiv3(9, 9, 9, 9) As Date |
Третий массив состоит из 10000 элементов — 10×10×10×10.
Динамические массивы
Динамические массивы в VBA Excel, в отличие от статических, объявляются без указания размерности:
|
Public Massiv1() As Integer Dim Massiv2() As String |
Такие массивы используются, когда заранее неизвестна размерность, которая определяется в процессе выполнения программы. Когда нужная размерность массива становится известна, она в VBA Excel переопределяется с помощью оператора ReDim:
|
Public Massiv1() As Integer Dim Massiv2() As String ReDim Massiv1(1 To 20) ReDim Massiv2(3, 5, 4) |
При переопределении размерности массива вместо верхнего индекса можно использовать переменную:
|
Dim Massiv1() as Variant, x As Integer x = 20 ReDim Massiv1(1 To x) |
Переопределять размерность динамических массивов в процессе работы программы можно неоднократно, как по количеству измерений, так и по количеству элементов в измерении.
С помощью оператора ReDim невозможно изменить обычный массив, объявленный с заранее заданной размерностью. Попытка переопределить размерность такого массива вызовет ошибку компиляции с сообщением: Array already dimensioned (Массив уже измерен).
При переопределении размерности динамических массивов в VBA Excel теряются значения их элементов. Чтобы сохранить значения, используйте оператор Preserve:
|
Dim Massiv1() As String ——— операторы ——— ReDim Massiv1(5, 2, 3) ——— операторы ——— ReDim Preserve Massiv1(5, 2, 7) |
Обратите внимание!
Переопределить с оператором Preserve можно только последнюю размерность динамического массива. Это недоработка разработчиков, которая сохранилась и в VBA Excel 2016. Без оператора Preserve можно переопределить все размерности.
Максимальный размер
Размер массива – это произведение длин всех его измерений. Он представляет собой общее количество элементов, содержащихся в данный момент в массиве.
По информации с сайта разработчиков, максимальный размер массивов зависит от операционной системы и доступного объема памяти. Использование массивов, размер которых превышает объем доступной оперативной памяти компьютера, приводит к снижению скорости, поскольку системе необходимо выполнять запись данных и чтение с диска.
Использование массивов
Приведу два примера, где не обойтись без массивов.
1. Как известно, функция Split возвращает одномерный массив подстрок, извлеченных из первоначальной строки с разделителями. Эти данные присваиваются заранее объявленному строковому (As String) одномерному динамическому массиву. Размерность устанавливается автоматически в зависимости от количества подстрок.
2. Данные в массивах обрабатываются значительно быстрее, чем в ячейках рабочего листа. Построчную обработку информации в таблице Excel можно наблюдать визуально по мерцаниям экрана, если его обновление (Application.ScreenUpdating) не отключено. Чтобы ускорить работу кода, можно значения из диапазона ячеек предварительно загрузить в динамический массив с помощью оператора присваивания (=). Размерность массива установится автоматически. После обработки данных в массиве кодом VBA полученные результаты выгружаются обратно на рабочий лист Excel. Обратите внимание, что загрузить значения в диапазон ячеек рабочего листа через оператор присваивания (=) можно только из двумерного массива.
Функции Array, LBound, UBound
Функция Array
Функция Array возвращает массив элементов типа Variant из первоначального списка элементов, перечисленных через запятую. Нумерация элементов в массиве начинается с нуля. Обратиться к элементу массива можно, указав в скобках его номер (индекс).
|
Sub Test1() Dim a() As Variant a = Array(«text», 25, «solo», 35.62, «stop») MsgBox a(0) & vbNewLine & a(1) & vbNewLine _ & a(2) & vbNewLine & a(3) & vbNewLine & a(4) End Sub |
Скопируйте код в модуль VBA Excel и запустите его на выполнение. Информационное сообщение MsgBox покажет значения массива, извлеченные по индексу.
Функция LBound
Функция LBound возвращает значение типа Long, равное наименьшему (нижнему) доступному индексу в указанном измерении массива.
Синтаксис:
LBound (arrayname[, dimension])
- arrayname — это имя переменной массива, является обязательным аргументом;
- dimension — это номер измерения массива, необязательный аргумент, по умолчанию принимает значение 1.
Наименьший индекс по-умолчанию может быть равен 0 или 1 в зависимости от настроек оператора Option Base. Нижняя граница архива, полученного с помощью функции Array, всегда равна 0.
При объявлении переменных массивов или переопределении их размерности наименьшие индексы могут быть любыми целыми числами, в том числе отрицательными.
Функция UBound
Функция UBound возвращает значение типа Long, равное наибольшему (верхнему) доступному индексу в указанном измерении массива.
Синтаксис:
UBound( arrayname[, dimension])
- arrayname — это имя переменной массива, является обязательным аргументом;
- dimension — это номер измерения массива, необязательный аргумент, по умолчанию принимает значение 1.
Функция UBound используется вместе с функцией LBound для определения размера массива.
|
Sub Test2() Dim a(—2 To 53) As String MsgBox «Наименьший индекс = « & LBound(a) & _ vbNewLine & «Наибольший индекс = « & UBound(a) End Sub |
Скопируйте код в модуль VBA Excel и запустите его на выполнение. Информационное сообщение MsgBox покажет значения наименьшего и наибольшего индекса переменной массива a.
Обход массива циклом
Обход одномерного массива циклом For… Next, в котором для определения границ массива используются функции UBound и LBound:
|
Sub Test3() Dim a() As Variant, i As Long a = Array(«text», 25, «solo», 35.62, «stop») For i = LBound(a) To UBound(a) Debug.Print «a(« & i & «) = « & a(i) Next End Sub |
Результат работы цикла вы увидите в окне Immediate.
Очистка (обнуление) массивов
Первый способ
Очистить любой массив, статический или динамический, без использования цикла можно с помощью оператора Erase. Термин «обнуление» можно применить только к массиву числового типа.
|
Dim Massiv1(4, 3) As String, Massiv2() As Variant ——— операторы ——— ‘переопределяем динамический массив ReDim Massiv2(2, 5, 3) ——— операторы ——— ‘очищаем массивы Erase Massiv1 Erase Massiv2 |
Обратите внимание, что оба массива при таком способе очистки будут возвращены в исходное состояние, которое они имели сразу после объявления:
- статический Massiv1 сохранит размерность (4, 3);
- динамический Massiv2 не сохранит размерность ().
Второй способ
Динамический массив можно очистить (обнулить) без использования цикла с помощью оператора ReDim. Просто переопределите его с той же размерностью.
|
Dim Massiv() As Double ——— операторы ——— ‘переопределяем массив ReDim Massiv(5, 6, 8) ——— операторы ——— ‘очищаем массив ReDim Massiv(5, 6, 8) |
В данной статье подробно рассматриваются массивы на языке программирования Excel VBA. Рассматриваются различные вопросы и схемы применения, такие как:
- Зачем нужны массивы
- Когда нужно применять массивы
- Типы массивов
- Использования многомерных массивов
- Объявление массивов
- Добавление значений
- Просмотр всех элементов
- Эффективный способ чтения диапазонов (Range) в массив
| Задача | Статический массив | Динамический массив |
|---|---|---|
| Объявление | Dim arr(0 To 5) As Long | Dim arr() As Long Dim arr As Variant |
| Задать размер | см. выше | ReDim arr(0 To 5)As Variant |
| Получить размер(количество элементов) | см. функцию ArraySize . | см. функцию ArraySize |
| Увеличить размер (с сохранением данных) | Только динамический массив | ReDim Preserve arr(0 To 6) |
| Задать значение | arr(1) = 22 | arr(1) = 22 |
| Получить значение | total = arr(1) | total = arr(1) |
| Первый элемент | LBound(arr) | LBound(arr) |
| Последний элемент | Ubound(arr) | Ubound(arr) |
| Прочитать все элементы(1D) | For i = LBound(arr) To UBound(arr) Next i Or For i = LBound(arr,1) To UBound(arr,1) Next i |
For i = LBound(arr) To UBound(arr) Next i Or For i = LBound(arr,1) To UBound(arr,1) Next i |
| Прочитать все элементы(2D) | For i = LBound(arr,1) To UBound(arr,1) For j = LBound(arr,2) To UBound(arr,2) Next j Next i |
For i = LBound(arr,1) To UBound(arr,1) For j = LBound(arr,2) To UBound(arr,2) Next j Next i |
| Прочитать все элементы | Dim item As Variant For Each item In arr Next item |
Dim item As Variant For Each item In arr Next item |
| Передать в процедуру | Sub MySub(ByRef arr() As String) | Sub MySub(ByRef arr() As String) |
| Вернуть из функции | Function GetArray() As Long() Dim arr(0 To 5) As Long GetArray = arr End Function |
Function GetArray() As Long() Dim arr() As Long GetArray = arr End Function |
| Получить из функции | Только динамические массивы | Dim arr() As Long Arr = GetArray() |
| Стереть массив | Erase arr *сбрасывает все значения по умолчанию |
Erase arr *удаляет массив |
| Строку в массив | Только динамические массивы | Dim arr As Variant arr = Split(“James:Earl:Jones”,”:”) |
| Массив в строку | Dim sName As String sName = Join(arr, “:”) |
Dim sName As String sName = Join(arr, “:”) |
| Заполнить значениями | Только динамические массивы | Dim arr As Variant arr = Array(“Значение1”, “Значение2”, “Значение3”) |
| Диапазон в массив | Только динамические массивы | Dim arr As Variant arr = Range(“A1:D2”) |
| Массив в диапазон | также как в динамическом массиве | Dim arr As Variant Range(“A5:D6”) = arr |
В VBA есть два типа массивов:
Статический – массив фиксированного размера.
Динамический – массив, в котором размер задается во время выполнения.
Разница между этими массивами в основном в том, как они создаются. Доступ к значениям в обоих типах массивов абсолютно одинаков. В следующих разделах мы рассмотрим оба типа.
Объявление массива
Статический массив объявляется следующим образом
Public Sub DecArrayStatic()
' создаем массив с элементами 0,1,2,3
Dim arrMarks1(0 To 3) As Long
' массив с элементами 0,1,2,3
Dim arrMarks2(3) As Long
' массив с элементами 1,2,3,4,5
Dim arrMarks3(1 To 5) As Long
' массив с элементами 2,3,4 ' редко используется
Dim arrMarks4(2 To 4) As Long
End Sub
Как видите, при объявлении статического массива указывается его размер. Но проблема в том, что вы никогда не можете заранее знать, какой размер вам нужен. Каждый раз при запуске макроса у вас могут быть разные требования к размеру массива
Если вы не используете все элементы массива, ресурсы памяти расходуются в пустую. Если нужно добавить больше элементов можно использовать метод ReDim, но по сути это создает новый статический массив
Динамические массивы не имеют таких проблем. Размер массивы не указывается при объявлении. Поэтому его размер может расти и уменьшаться по мере необходимости
Public Sub DecArrayDynamic()
' Объявление динамического массива
Dim arrMarks() As Long
' Устанавливаем размер массива
ReDim arrMarks(0 To 5)
End Sub
Динамический массив не создается, пока вы не используете оператор ReDim. Преимущество в том, что вы можете подождать, пока не узнаете количество элементов, прежде чем устанавливать размер массива. Со статическим массивом вы должны указать размер заранее.
Чтение из диапазона ячеек в массив
VBA имеет очень эффективный способ чтения из диапазона ячеек в массив и наоборот
Public Sub ReadToArray()
' Объявляем динамический массив
Dim StudentMarks As Variant
' Считываем данные в массив из первой строки
StudentMarks = Range("A1:Z1").Value
' Записываем значения назад в третью строку
Range("A3:Z3").Value = StudentMarks
End Sub
Динамический массив, созданный в этом примере, будет двухмерным массивом. Как видите, мы можем прочитать весь диапазон ячеек в массив всего за одну строку.
В следующем примере будут считаны данные из диапазона C3: E6 листа Sheet1 и отображены в окне Immediate Window.
Public Sub ReadAndDisplay()
' Получаем диапазон
Dim rg As Range
Set rg = ThisWorkbook.Worksheets("Sheet1").Range("C3:E6")
' Создаем динамический массив
Dim StudentMarks As Variant
' Записываем данные в массив
StudentMarks = rg.Value
' Печатаем данные из массива
Debug.Print "i", "j", "Value"
Dim i As Long, j As Long
For i = LBound(StudentMarks) To UBound(StudentMarks)
For j = LBound(StudentMarks, 2) To UBound(StudentMarks, 2)
Debug.Print i, j, StudentMarks(i, j)
Next j
Next i
End Sub
Как сделать выполнение ваших макросов супер скоростным
Если ваши макросы работают очень медленно, этот метод может оказаться очень полезным. Особенно если вы имеете дело с большими объемами данных.
Обновление значений в массивах происходит гораздо быстрее, чем обновление значений в ячейках.
В последнем разделе вы увидели, как мы можем легко читать из группы ячеек в массив и наоборот. Если мы обновляем много значений, мы можем сделать следующее
- Копируем данные из ячеек в массив.
- Изменяем данные в массиве.
- Копируем обновленные данные из массива обратно в ячейки.
Например, следующий код будет намного быстрее, чем код ниже
Public Sub ReadToArray()
' Считываем данные в массив
Dim StudentMarks As Variant
StudentMarks = Range("A1:Z20000").Value
Dim i As Long
For i = LBound(StudentMarks) To UBound(StudentMarks)
' Update marks here
StudentMarks(i, 1) = StudentMarks(i, 1) * 2
'...
Next i
' Записываем новые значения на лист
Range("A1:Z20000").Value = StudentMarks
End Sub
Sub UsingCellsToUpdate()
Dim c As Variant
For Each c In Range("A1:Z20000")
c.Value = ' Обновляем значения
Next c
End Sub
Назначение из одного множества ячеек в другой также намного быстрее, чем с помощью копирования и вставки
' Ассоциирование диапазона- это быстро
Range("A1:A10").Value = Range("B1:B10").Value
' Копировать вставить - медленно
Range("B1:B1").Copy Destination:=Range("A1:A10")
Пример с динамическим диапазоном
Sub ReadingRange()
Dim arr As Variant
arr = shData.Range("A1").CurrentRegion
Dim i as long
For i = LBound(arr,1) + 1 to UBound(arr,1)
arr(i,5) = arr(i,5) - 100
next i
shData.Range("H1").CurrentRegion.ClearContents
Dim rowCount as Long, columnCount as Long
rowCount - UBound(arr,1)
columnCount = UBound(arr,2)
shData.Range("H1".Resize(rowCount, columnCount).Value = arr
End Sub
Любой инвестиционный проект имеет несколько важных условий: первоначальные вложения, определенный срок работы проекта и полученная прибыль за этот период. IRR демонстрирует ставку кредита, при значении которой инвестиция не приведет к убыткам. То есть, тот уровень прибыли в процентах, на котором вложения вернутся и проект окупится, но ничего не принесет дополнительно.


Рассчитав IRR, инвестор получает верхнюю планку допустимой стоимости заемного капитала, который вкладывается. Если цена капитала выше, чем IRR, проект убыточен. Если для компании стоимость капитала ниже найденного IRR проекта, компания сможет существовать за разницу между процентами банковского займа и прибыльностью вложений.
Пример 1: срочный вклад в «Сбербанке»

В нашем примере проценты планируется снимать в конце года, поэтому капитализации не будет и получится 9% в год – сумма получается 6 000 000 х 0.09 = 540 000 дохода в год. По завершении третьего года можно будет снять проценты за него и основную сумму, закрыв депозит.
Вклад в банке считается инвестиционным проектом, для него можно рассчитать IRR. IRR для инвестиции в депозит равна процентной ставке депозита – 9%. И если 6 000 000 рублей были накоплены или остались в наследство, их можно вкладывать (ведь стоимость капитала – 0). Если же деньги планируется взять в кредит в банке и вложить в другой, то процентная ставка заемных средств должна быть ниже 9%, если выше – проект не окупится.
Пример 2: покупка квартиры с целью заработка на сдаче ее в аренду

IRR проекта при условии покупки и сдачи в аренду квартиры в течение 3 лет, а потом продажи, равна 6%. То есть, если брать заемные средства на реализацию проекта, процент должен быть меньше 6%, чтобы получать прибыль. И на протяжении 10, 15 лет IRR меняться не будет, исключением является лишь ситуация с подорожанием квартиры.
Внутренняя норма доходности – важный и интересный показатель, который при правильном использовании можно применять достаточно эффективно для просчета прибыльности разных инвестиционных проектов, особенно когда речь идет об их сравнении и выборе наиболее доходного.
Как считать доходность?
Почему большинство инвесторов часто имеют неправильное представление о том, какова настоящая результативность их инвестиций.
Сложность заключается в том, что большинство подходов к расчету доходности подразумевают простую формулу:
$$ R =frac{A}{B}$$
А – полученный доход
В – стартовые инвестиции
Представим себе жизненную ситуацию, когда человек в январе инвестировал 10 000 р, а в декабре – 90 000 р. К концу года на инвестиционном счете оказалось 110 000 р (ценные бумаги выросли в цене). Какова доходность инвестиций? Что на что делить? Если мы возьмем доход в 10 000 р и разделим на сумму всех инвестиций – 100 000 р, то получим очень сложно интерпретируемый результат – 10%. Ведь большую часть срока на счете находилось всего 10 000 р, а остаток добавлен только за месяц до конца года …
Или еще более интересный пример. В январе инвестор положил на брокерский счет 100 000 р, а в декабре забрал с него 90 000 р. К концу года на брокерском счете фигурировала сумма 15 000 р. Если просто сложить пополнения и изъятия получится что суммарная инвестиция равна 100 000 – 90 000 = 10 000 р. Разделив доход на суммарные инвестиции, получим слишком оптимистичные 50%. Очевидно, что так делать нельзя …
Более подробно о теме расчетов доходности без пополнений и изъятий читайте в статье: Правильный расчет среднегодовой доходности в инвестициях
Внутренняя норма доходности – IRR
Внутренняя норма доходности (англ. Internal Rate of Return, IRR), известная также как внутренняя ставка доходности, является ставкой дисконтирования, при которой чистая приведенная стоимость (англ. Net Present Value, NPV) проекта равна нолю.
Другими словами, настоящая стоимость всех ожидаемых денежных потоков проекта равна величине первоначальных инвестиций.
В основе метода IRR лежит методика дисконтированных денежных потоков, а сам показатель получил широкое использование в бюджетировании капитальных вложений и при принятии инвестиционных решений в качестве критерия отбора проектов и инвестиций.
Формула IRR
Чтобы рассчитать внутреннюю норму доходности проекта необходимо решить следующее уравнение, приравняв NPV проекта к нолю.
Критерий отбора проектов
Правило принятия решений при отборе проектов можно сформулировать следующим образом:
- Внутренняя норма доходности должна превышать средневзвешенную стоимость капитала (англ. Weighted Average Cost of Capital, WACC), привлеченного для реализации проекта, в противном случае его следует отклонить.
- Если несколько независимых проектов соответствуют указанному выше критерию, все они должны быть приняты. Если они являются взаимоисключающими, то принять следует тот из них, у которого наблюдается максимальный IRR.
Пример расчета внутренней нормы доходности
Предположим, что существует два проекта с одинаковым уровнем риска, первоначальными инвестициями и общей суммой ожидаемых денежных потоков. Для более наглядной иллюстрации концепции стоимости денег во времени, поступление денежных потоков по Проекту А ожидается несколько раньше, чем по Проекту Б.
Подставим представленные в таблице данные в уравнение.
Для решения этих уравнений можно воспользоваться функцией «ВСД» Microsoft Excel, как это показано на рисунке ниже.
- Выберите ячейку вывода I4.
- Нажмите кнопку fx, выберите категорию «Финансовые», а затем функцию «ВСД» из списка.
- В поле «Значение» выберите диапазон данных C4:H4, оставьте пустым поле «Предположение» и нажмите кнопку OK.
Таким образом, внутренняя ставка доходности Проекта А составляет 20,27%, а Проекта Б 12,01%. Схема дисконтированных денежных потоков представлена на рисунке ниже.
Предположим, что средневзвешенная стоимость капитала для обеих проектов составляет 9,5% (поскольку они обладают одним уровнем риска). Если они являются независимыми, то их следует принять, поскольку IRR выше WACC. Если бы они являлись взаимоисключающими, то принять следует Проект А из-за более высокого значения IRR.
Преимущества и недостатки метода IRR
Использование метода внутренней нормы доходности имеет три существенных недостатка.
- Предположение, что все положительные чистые денежные потоки будут реинвестированы по ставке IRR проекта. В действительности такой сценарий маловероятен, особенно для проектов с ее высокими значениями.
- Если хотя бы одно из значений ожидаемых чистых денежных потоков будет отрицательным, приведенное выше уравнение может иметь несколько корней. Эта ситуация известна как проблема множественности IRR.
- Конфликт между методами NPV и IRR может возникнуть при оценке взаимоисключающих проектов. В этом случае у одного проекта будет более высокая чистая приведенная стоимость, но более низкая внутренняя норма доходности, а у другого наоборот. В такой ситуации следует отдавать предпочтение проекту с более высокой чистой приведенной стоимостью.
Рассмотрим конфликт NPV и IRR на следующем примере.
Для каждого проекта была рассчитана чистая приведенная стоимость для диапазона ставок дисконтирования от 1% до 30%. На основании полученных значений NPV построен следующий график.
При стоимости капитала от 1% до 13,092% реализация Проекта А является более предпочтительной, поскольку его чистая приведенная стоимость выше, чем у Проекта Б. Стоимость капитала 13,092% является точкой безразличия, поскольку оба проекта обладают одинаковой чистой приведенной стоимостью. При стоимости капитала более 13,092% предпочтительной уже является реализация Проекта Б.
С точки зрения IRR, как единственного критерия отбора, Проект Б является более предпочтительным. Однако, как можно убедиться на графике, такой вывод является ложным при стоимости капитала менее 13,092%. Таким образом, внутреннюю норму доходности целесообразно использовать в качестве дополнительного критерия отбора при оценке нескольких взаимоисключающих проектов.
- ← Индекс рентабельности, PI
- Проблема множественности IRR →
Формула расчета IRR
Поскольку IRR представляет собой ставку дисконтирования в ситуации, когда NPV равно нулю, то для расчета показателя применяется та же формула, что и для определения чистой приведенной стоимости.
В приведенной формуле присутствуют такие показатели, как:
- CF – суммарный денежный поток за период t;
- t – порядковый номер периода;
- i – ставка дисконтирования денежного потока (ставка приведения);
- IC – сумма первоначальных инвестиций.
Если известно, что NPV равен нулю, то получится сложное уравнение, в котором внутренняя норма доходности должна быть извлечена из-под корня со степенью. В связи с этим IRR невозможно точно рассчитать вручную.
Для расчета можно воспользоваться финансовым калькулятором. Однако даже в этом случае расчеты окажутся громоздкими.
Ранее для расчета внутренней ставки доходности использовали графический метод: рассчитывали для каждого из проектов NPV и строили их линейные графики. В точках пересечения графиков с осью абсцисс (ось Х) и находилось значение IRR. Однако такой метод неточен и носит демонстрационный характер.
Справка!
В финансовой математике применяется метод подбора, который позволяет с использованием логарифмических расчетов выявить зависимость между NPV и ВНД. Такой способ не менее сложен и требует умения проводить действия с логарифмами.
В связи с этим наиболее простым, удобным и точным способом расчета IRR выступает использование финансовой функции ВСД табличного редактора Excel
Примеры
Пример1
Пример задачи
Задача «Купить или арендовать»
Вы осмысливаете покупку или аренду, скажем, грузовика, который будет приносить вам прибыль (предположим, вы транспортная компания). Купить грузовик вы можете за 2,5 миллиона рублей (цифры взяты с потолка), аренда обойдется вам в 600 тысяч рублей/год. Вы знаете, что срок полезного использования грузовика — пять лет, после чего он обладает остаточной стоимостью, скажем, 400 тысяч. После аренды грузовик остается у арендодателя. Предположим, что оплата производится авансом на год вперед. Свободных средств на покупку у вас нет, но есть возможность привлечь финансирование под 18% годовых. Что выгоднее?
Экономическая наука изучает вопросы снижения затрат на при реализации проекта и получение максимальной прибыли. При этом основной акцент ставится на прибыль.
В финансовом анализе предложено множество систем, позволяющих оценить эффективность проектов, но в большинстве случаев используется система показателей приведенных денежных потоков. Одним из них является показатель IRR (норма внутренней доходности). Именно особенности данного показателя разберем в статье.
Особенности использования функции ЧПС
Ввести одномоментно 254 значения в одну ячейку бывает весьма утомительно.
Лучше заранее заполнить численными значениями некоторый диапазон, а затем подставлять в формулу ЧПС ссылки на входящие в диапазон ячейки.
Такой подход позволит легко комбинировать данные и исправлять возможные ошибки.
Следует помнить, что для расчета функции ЧПС важен ПОРЯДОК, в котором следуют значения P1, P2, …, Pn. Изменение этого порядка приведет к разным значениям нашей функции.
Предполагается также, что расчет производится для случая, когда выплаты или поступления отстоят друг от друга на один и тот же период (неделя, месяц, год и т.д.), то есть имеет место равномерное распределение денежных потоков во времени.
Все аргументы должны иметь численный формат. Ошибочно введенные в формулу ЧПС буквенные значения или символы при расчетах будут проигнорированы.
Функция ВСД в Excel и пример как посчитать IRR
Для расчета внутренней ставки доходности (внутренней нормы доходности, IRR) в Excel используется функция ВСД. Ее особенности, синтаксис, примеры рассмотрим в статье.
Один из методов оценки инвестиционных проектов – внутренняя норма доходности. Расчет в автоматическом режиме можно произвести с помощью функции ВСД в Excel. Она находит внутреннюю ставку доходности для ряда потоков денежных средств. Финансовые показатели должны быть представлены числовыми значениями.
Суммы внутри потоков могут колебаться. Но поступления регулярные (каждый месяц, квартал или год). Это обязательное условие для корректного расчета.
Внутренняя ставка доходности (IRR, внутренняя норма доходности) – процентная ставка инвестиционного проекта, при которой приведенная стоимость денежных потоков равняется нулю.
При данной ставке инвестор вернет вложенные первоначально средства.
Инвестиции состоят из платежей (суммы со знаком «–») и доходов (со знаком «+»), которые происходят в одинаковые по продолжительности временные промежутки.
Аргументы функции ВСД в Excel:
- Значения. Диапазон ячеек, в которых содержатся числовые выражения денежных средств. Для данных сумм нужно посчитать внутреннюю норму доходности.
- Предположение. Цифра, которая предположительно близка к результату. Аргумент необязательный.
Секреты работы функции ВСД (IRR):
- В диапазоне с денежными суммами должно содержаться хотя бы одно положительное и одно отрицательное значение.
- Для функции ВСД важен порядок выплат или поступлений. То есть денежные потоки должны вводится в таблицу в соответствии со временем их возникновения.
- Текстовые или логические значения, пустые ячейки при расчете игнорируются.
- В программе Excel для подсчета внутренней ставки доходности используется метод итераций (подбора). Формула производит циклические вычисления с того значения, которое указано в аргументе «Предположение». Если аргумент опущен, со значения 0,1 (10%).
При расчете ВСД в Excel может возникнуть ошибка #ЧИСЛО!. Почему? Используя метод итераций при расчете, функция находит результат с точностью 0,00001%. Если после 20 попыток не удается получить результат, ВСД вернет значение ошибки.
Когда функция показывает ошибку #ЧИСЛО!, повторите расчет с другим значением аргумента «Предположение».
Расчет внутренней нормы рентабельности рассмотрим на элементарном примере. Имеются следующие входные данные:
Заходим на вкладку «Формулы». В категории «Финансовые» находим функцию ВСД. Заполняем аргументы.
Значения – диапазон с суммами денежных потоков, по которым необходимо рассчитать внутреннюю норму рентабельности. Предположение – опустим.
Искомая IRR (внутренняя норма доходности) анализируемого проекта – значение 0,209040417. Если перевести десятичное выражение величины в проценты, то получим ставку 20,90%.
Еще один показатель эффективности инвестиционного проекта – NPV (чистый дисконтированный доход). NPV и IRR связаны: IRR определяет ставку дисконтирования, при которой NPV = 0 (то есть затраты на проект равны доходам).
Для расчета NPV в Excel применяется функция ЧПС. Чтобы найти внутреннюю ставку доходности графическим методом, нужно построить график изменения NPV. Для этого в формулу расчета NPV будем подставлять разные значения ставок дисконта.
На основании полученных данных построим график изменения NPV.
Пересечение графика с осью Х (когда чистый дисконтированный доход проекта равняется нулю) дает показатель IRR для данного проекта. Графический метод показал результат ВСД, аналогичный найденному в Excel.
Как пользоваться показателем ВСД:
Если значение IRR проекта выше стоимости капитала для предприятия, то данный инвестиционный проект нужно принять.
То есть если ставка кредита меньше внутренней нормы рентабельности, то заемные средства принесут прибыль. Так как в при реализации проекта мы получим больший процент дохода, чем величина капитала.
Скачать пример функций ВСД IRR и ЧПС NPV в Excel.
Вернемся к нашему примеру. Допустим, для запуска проекта брался кредит в банке под 15% годовых. Расчет показал, что внутренняя норма доходности составила 20,9%. На таком проекте можно заработать.
Как рассчитать правильно показатель IRR
Разобравшись с тем, что такое IRR инвестиционного проекта, стоит рассмотреть, как его можно посчитать. Методов расчета существует несколько – с использованием формулы или таблицы Excel, а также графический способ. Можно найти в Интернете и специальные калькуляторы, в которые просто нужно внести значения и получить искомый показатель.
Формула и пример расчета в экономике
Для расчета IRR формула исходная представлена в виде уравнения:
Тут:
- NPV – это чистая приведенная стоимость рассматриваемого проекта.
- N – число расчетных периодов (лет чаще всего).
- T – номер конкретного расчетного периода.
- IS – расходы на проект первоначальные (стартовые инвестиции) и последующие.
- IRR – внутренняя норма доходности.
Предельно низкая ВСД равна значению NPV, соответствующему нулю. То есть, текущая стоимость, посчитанная по ставке прибыльности IRR, должна быть равной самоокупаемости. Благодаря преобразованиям формулы можно отыскать минимальный показатель IRR:
Тут:
- IRRmin – минимальное значение
- N – число расчетных периодов.
- IST – величина инвестиций каждого периода.
- IS – общее число инвестиций.
Расчет в таблице Excel
Когда рассчитывается внутренняя норма доходности, формула используется далеко не всегда. Посчитать внутреннюю норму рентабельности можно и в Excel, где есть встроенная функция ВСД.
Как рассчитывается средняя норма рентабельности в Excel:
- Вход в программу.
- Создание книги с указанием таблицы денежных потоков, дат. Одно значение должно иметь отрицательный показатель (это сумма вложений). Таблица может включать информацию про множество проектов, если их нужно сравнить.
- Далее осуществляется выбор функции IRR (русский интерфейс обозначает его как ВСД либо ВНД), потом нужно нажать fx.
- Отметка участка нужного столбца со всеми данными, которые планируется проанализировать. В строке должно появиться что-то типа IRR(B4:В:15.2, 7.1%). Нажать на «ОК».
Графический метод определения IRR
Для поиска показателя используется не только формула расчета, но и графический метод. Он более наглядный, но и менее точный. Чтобы построить диаграмму, нужно выполнить определенные вычисления, но тут требования по точности гораздо ниже. Да и исходные данные могут давать погрешность.
Суть метода заключается в определении величины предельного значения IRR в виде точки пересечения линия графика и оси координат (нулевой отметкой доходности). Обычно графики зависимости приведенной стоимости от показателя ставки дисконтирования чертят вручную либо же с применением функции диаграммы в Excel.
Графиков может быть несколько и расшифровка их заключается в поиске более предпочтительного инвестиционного проекта – того, значение предельной прибыльности инвестиции которого окажется расположенным дальше от нулевой точки.
Правила применения данного показателя

- Для определения нормы доходности по инвестиционному проекту. Участники принимают решение о том, есть ли потребность привлекать заемные средства;
- Для оценки решений по инвестиционным проектам. В этом случае полученные результаты соотносятся с оптимальными значениями для данной отрасли экономики;
- Для расчета устойчивости проекта. Для этого меняются условия, при которых будет реализоваться проекты.
Применение IRR при расчете доходности инвестиционного проекта имеет ряд недостатков и преимуществ
.
К положительным сторонам
относится возможность сравнения инвестиционных проектов по длительности и масштабам их деятельности. Но главным достоинством применения IRR является возможность расчета рентабельности инвестиционных потоков.
Недостатком
считается при изменении знака денежного потока расчет нескольких значений IRR, что может дать ложную информацию. Рассчитывая данный показатель, эксперт придерживается мнения, что средства реинвестируются под тот процент, который получился. Но по факту, это не всегда соответствует реальности.
Основываясь на критериях поступлений денежных средств в проект, следует отметить, что применять IRR метод следует только при условии чистых поступлений при реализации инвестиционного проекта.
Порядок расчета показателя приведенной стоимости (NPV) в Excel рассмотрен в следующем видео сюжете:
Если Вы еще не зарегистрировали организацию, то проще всего
это сделать с помощью онлайн сервисов, которые помогут бесплатно сформировать все необходимые документы:
Если у Вас уже есть организация, и Вы думаете над тем, как облегчить и автоматизировать бухгалтерский учет и отчетность, то на помощь приходят следующие онлайн-сервисы, которые полностью заменят бухгалтера на Вашем предприятии и сэкономят много денег и времени. Вся отчетность формируется автоматически, подписывается электронной подписью и отправляется автоматически онлайн.
Он идеально подходит для ИП или ООО на УСН , ЕНВД , ПСН , ТС , ОСНО.
Все происходит в несколько кликов, без очередей и стрессов. Попробуйте и Вы удивитесь
, как это стало просто!
IRR или Внутренняя норма доходности (ВНД)
Одним из самых простых и распространенных способов измерить результативность инвестиций является расчет IRR (Internal Rate of Return, Внутренняя норма доходности). IRR – это не совсем доходность. Формально IRR или – это процентная ставка, при которой приведённая стоимость денежных поступлений (списаний) равна размеру исходных инвестиций. IRR очень распространен в бизнесе и финансах. При помощи этой величины считается, например, рентабельность проектов в бизнесе. Аналогично считается доходности к погашению для облигаций. IRR можно считать это своего рода стандартом при измерении результативности.
Еще одно важное преимущество – IRR легко считается в EXCEL и других электронных таблицах.
Если IRR меньше ставки по депозитам в Сбербанке, то надо задуматься, все ли нормально с инвестиционной стратегией.
Задача на нахождение NPV
Пример. Первоначальные инвестиции в проект A составляют 10000 рублей. Ежегодная процентная ставка – 10 %. Динамика поступлений с 1-го по 10-ый годы представлена в нижеследующей таблице:
| Период | Притоки | Оттоки |
| 10000 | ||
| 1 | 1100 | |
| 2 | 1200 | |
| 3 | 1300 | |
| 4 | 1450 | |
| 5 | 1600 | |
| 6 | 1720 | |
| 7 | 1860 | |
| 8 | 2200 | |
| 9 | 2500 | |
| 10 | 3600 |
Для наглядности cответствующие данные можно представить графически:
Рисунок 1. Графическое представление исходных данных для расчета NPV
Необходимо рассчитать показатель NPV.
Стандартное решение. Для решения задачи будем использовать уже известную нам формулу NPV:
Просто подставляем в нее известные значения, которые затем суммируем. Для этих вычислений нам пригодится калькулятор:
NPV = -10000/1,1 + 1100/1,11 + 1200/1,12 + 1300/1,13 + 1450/1,14 + 1600/1,15 + 1720/1,16 + 1860/1,17 + 2200/1,18 + 2500/1,19 + 3600/1,110 = 352,1738 рублей.
Синтаксис
ВСД(значения; )
Аргументы функции ВСД описаны ниже.
Значения
– обязательный аргумент. Массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности.
Значения должны содержать по крайней мере одно положительное и одно отрицательное значение.
В функции ВСД для интерпретации порядка денежных выплат или поступлений используется порядок значений. Убедитесь, что значения выплат и поступлений введены в нужном порядке.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, такие значения игнорируются.
Предположение
– необязательный аргумент. Величина, предположительно близкая к результату ВСД.
В Microsoft Excel используется итеративный метод расчета ВСД. Начиная с предположения, ВСД циклически перейдет к вычислению, пока результат не станет точным в 0,00001%. Если функция ВСД не может найти результат, который работает после 20 попыток, #NUM! возвращено значение ошибки.
В большинстве случаев для вычислений с помощью функции ВСД нет необходимости задавать аргумент “предположение”. Если он опущен, предполагается значение 0,1 (10%).
Если функция ВСД возвращает значение ошибки #ЧИСЛО! или результат далек от ожидаемого, попробуйте повторить вычисление с другим значением аргумента “предположение”.
Функция ВСД в Excel и пример как посчитать IRR
Для расчета внутренней ставки доходности (внутренней нормы доходности, IRR) в Excel используется функция ВСД. Ее особенности, синтаксис, примеры рассмотрим в статье.
Один из методов оценки инвестиционных проектов – внутренняя норма доходности. Расчет в автоматическом режиме можно произвести с помощью функции ВСД в Excel. Она находит внутреннюю ставку доходности для ряда потоков денежных средств. Финансовые показатели должны быть представлены числовыми значениями.
Суммы внутри потоков могут колебаться. Но поступления регулярные (каждый месяц, квартал или год). Это обязательное условие для корректного расчета.
Внутренняя ставка доходности (IRR, внутренняя норма доходности) – процентная ставка инвестиционного проекта, при которой приведенная стоимость денежных потоков равняется нулю.
При данной ставке инвестор вернет вложенные первоначально средства.
Инвестиции состоят из платежей (суммы со знаком «–») и доходов (со знаком «+»), которые происходят в одинаковые по продолжительности временные промежутки.
Аргументы функции ВСД в Excel:
- Значения. Диапазон ячеек, в которых содержатся числовые выражения денежных средств. Для данных сумм нужно посчитать внутреннюю норму доходности.
- Предположение. Цифра, которая предположительно близка к результату. Аргумент необязательный.
Секреты работы функции ВСД (IRR):
- В диапазоне с денежными суммами должно содержаться хотя бы одно положительное и одно отрицательное значение.
- Для функции ВСД важен порядок выплат или поступлений. То есть денежные потоки должны вводится в таблицу в соответствии со временем их возникновения.
- Текстовые или логические значения, пустые ячейки при расчете игнорируются.
- В программе Excel для подсчета внутренней ставки доходности используется метод итераций (подбора). Формула производит циклические вычисления с того значения, которое указано в аргументе «Предположение». Если аргумент опущен, со значения 0,1 (10%).
При расчете ВСД в Excel может возникнуть ошибка #ЧИСЛО!. Почему? Используя метод итераций при расчете, функция находит результат с точностью 0,00001%. Если после 20 попыток не удается получить результат, ВСД вернет значение ошибки.
Когда функция показывает ошибку #ЧИСЛО!, повторите расчет с другим значением аргумента «Предположение».
Расчет внутренней нормы рентабельности рассмотрим на элементарном примере. Имеются следующие входные данные:
Заходим на вкладку «Формулы». В категории «Финансовые» находим функцию ВСД. Заполняем аргументы.
Значения – диапазон с суммами денежных потоков, по которым необходимо рассчитать внутреннюю норму рентабельности. Предположение – опустим.
Искомая IRR (внутренняя норма доходности) анализируемого проекта – значение 0,209040417. Если перевести десятичное выражение величины в проценты, то получим ставку 20,90%.
Еще один показатель эффективности инвестиционного проекта – NPV (чистый дисконтированный доход). NPV и IRR связаны: IRR определяет ставку дисконтирования, при которой NPV = 0 (то есть затраты на проект равны доходам).
Для расчета NPV в Excel применяется функция ЧПС. Чтобы найти внутреннюю ставку доходности графическим методом, нужно построить график изменения NPV. Для этого в формулу расчета NPV будем подставлять разные значения ставок дисконта.
На основании полученных данных построим график изменения NPV.
Пересечение графика с осью Х (когда чистый дисконтированный доход проекта равняется нулю) дает показатель IRR для данного проекта. Графический метод показал результат ВСД, аналогичный найденному в Excel.
Как пользоваться показателем ВСД:
Если значение IRR проекта выше стоимости капитала для предприятия, то данный инвестиционный проект нужно принять.
То есть если ставка кредита меньше внутренней нормы рентабельности, то заемные средства принесут прибыль. Так как в при реализации проекта мы получим больший процент дохода, чем величина капитала.
Скачать пример функций ВСД IRR и ЧПС NPV в Excel.
Вернемся к нашему примеру. Допустим, для запуска проекта брался кредит в банке под 15% годовых. Расчет показал, что внутренняя норма доходности составила 20,9%. На таком проекте можно заработать.
Применение внутренней нормы рентабельности
Главным направлением использования ВНД служит ранжирование проектов по степени их привлекательности вне зависимости от размера первоначальных инвестиций и отрасли. Существуют и иные варианты применения показателя нормы рентабельности:
- оценка прибыльности проектных решений;
- определение стабильности направлений инвестирования;
- выявление максимально возможной стоимости привлекаемых ресурсов.
Важный момент!
Эксперты обращают внимание на такие недостатки показателя, как отсутствие возможности учета реинвестиций и дохода в абсолютных величинах, зависимость от того, насколько правильно оценены потоки денежных средств. В этой статье описаны синтаксис формулы и использование функции ВСД
в Microsoft Excel
В этой статье описаны синтаксис формулы и использование функции ВСД
в Microsoft Excel.
Зачем нужен расчет?
Экономический смысл показателя состоит в том, что он характеризует следующие моменты:
Прибыльность возможного вложения
. Когда предприятие выбирает, в какой проект произвести инвестиции, оно ориентируется на величину этого показателя. Чем больше размер ВНД, тем выше рентабельность вложений.
Оптимальная ставка кредита
. ВНД – это максимальная цена, при которой вложение остаётся безубыточным
Если компания планирует получить кредит на осуществление этой инвестиции, то следует обратить внимание на ставку годовых. Если процент по кредиту больше, чем полученное значение, то проект будет приносить убыток.
При использовании показателя для оценки будущих вложений нужно учитывать преимущества и недостатки этого метода.
К положительным моментам применения ВНД относятся:
- Сравнение возможных вложений между собой по эффективности использования капитала. Предприятие предпочтёт выбрать ту инвестицию, у которой при равной процентной ставке показатель больше.
- Сравнение проектов с разным горизонтом инвестирования, то есть временным периодом, на который осуществляется вложение. В данном случае при сопоставлении ВНД разных возможных вкладов выявляется тот, который будет приносить наибольшие доходы в долгосрочной перспективе.
К основным недостаткам и отрицательным чертам относят:
- Сложность прогнозирования выплат. С помощью расчёта данной величины нельзя предсказать, каков будет размер следующего поступления по вкладу. На размер прибыли влияет множество различных факторов, рисков, ситуаций на микро и макроэкономическом уровне, которые не учитываются при вычислении.
- Невозможно определить абсолютную величину притока денег. ВНД – относительный показатель, он уточняет только тот процент, при котором вклад всё ещё остаётся безубыточным.
- Не учитывается реинвестирование. Некоторые вклады предполагают включение в состав процентных отчислений. То есть происходит процесс наращивания суммы инвестиции за счёт прибыли с неё. Расчёт ВНД не предусматривает такую возможность, поэтому показатель не отражает реальную доходность этих затрат.
Пример расчета чистой приведенной стоимости
Не смею больше испытывать ваше терпение и предлагаю немедля окунуться в завораживающий мир расчета чистой приведенной стоимости с помощью функции ЧПС.
Итак, обещанный пример. Внимательно смотрим на иллюстрацию ниже:
Организуйте на листе вашей таблицы Excel размещение данных, аналогичных вышеприведенным.
Здесь важно заполнить ячейки A1, A2, A3, A4 и A5 конкретными числовыми данными, а в ячейку A7 поместить (важен каждый символ) выражение =ЧПС(A1; A2; A3; A4; A5). Значение ячейки A7 как раз и будет содержать результат вычисления чистой приведенной стоимости ряда A2:A5
Значение ячейки A7 как раз и будет содержать результат вычисления чистой приведенной стоимости ряда A2:A5.
Соответствующий диапазон, естественно, вы можете расширить или сузить, как вам заблагорассудится, а результирующее значение поместить в любую другую удобную для вас ячейку.
Здесь главное — понять принцип.
Обратите внимание, что значение в ячейке A3 имеет отрицательное значение (-5350). Это означает, что имеет место выплата денежных средств (что в данном случае соответствует размеру первоначальных инвестиций)
Это означает, что имеет место выплата денежных средств (что в данном случае соответствует размеру первоначальных инвестиций).
Значения всех следующих аргументов являются положительными, так как мы имеем дело с поступлениями, символизирующими отдачу от наших инвестиций.
Заметим также, что наша функция в ячейке A7 может иметь и более краткий вид: =ЧПС(A1; A2:A5).
Такая запись соответствует синтаксическим стандартам Excel и позволяет сэкономить в ряде случаев и время, и нервы…
Итоговое значение (4110,00р) в денежном формате отображено во все той же ячейке A7.
Обязательно ВРУЧНУЮ проработайте приведенный выше пример.
Вы получите очень важный навык расчета реального финансового показателя – чистой приведенной стоимости — с помощью таблиц Excel.
Если вы планируете серьезно погрузиться в мир инвестиций, вам придется кое-что уметь и кое в чем разбираться.
Умение считать не на бумажке, а с использованием современного программного обеспечения – один из таких навыков.
Удачных инвестиций!
This post provides an in-depth look at the VBA array which is a very important part of the Excel VBA programming language. It covers everything you need to know about the VBA array.
We will start by seeing what exactly is the VBA Array is and why you need it.
Below you will see a quick reference guide to using the VBA Array. Refer to it anytime you need a quick reminder of the VBA Array syntax.
The rest of the post provides the most complete guide you will find on the VBA array.
Related Links for the VBA Array
Loops are used for reading through the VBA Array:
For Loop
For Each Loop
Other data structures in VBA:
VBA Collection – Good when you want to keep inserting items as it automatically resizes.
VBA ArrayList – This has more functionality than the Collection.
VBA Dictionary – Allows storing a KeyValue pair. Very useful in many applications.
The Microsoft guide for VBA Arrays can be found here.
A Quick Guide to the VBA Array
| Task | Static Array | Dynamic Array |
|---|---|---|
| Declare | Dim arr(0 To 5) As Long | Dim arr() As Long Dim arr As Variant |
| Set Size | See Declare above | ReDim arr(0 To 5)As Variant |
| Get Size(number of items) | See ArraySize function below. | See ArraySize function below. |
| Increase size (keep existing data) | Dynamic Only | ReDim Preserve arr(0 To 6) |
| Set values | arr(1) = 22 | arr(1) = 22 |
| Receive values | total = arr(1) | total = arr(1) |
| First position | LBound(arr) | LBound(arr) |
| Last position | Ubound(arr) | Ubound(arr) |
| Read all items(1D) | For i = LBound(arr) To UBound(arr) Next i Or For i = LBound(arr,1) To UBound(arr,1) Next i |
For i = LBound(arr) To UBound(arr) Next i Or For i = LBound(arr,1) To UBound(arr,1) Next i |
| Read all items(2D) | For i = LBound(arr,1) To UBound(arr,1) For j = LBound(arr,2) To UBound(arr,2) Next j Next i |
For i = LBound(arr,1) To UBound(arr,1) For j = LBound(arr,2) To UBound(arr,2) Next j Next i |
| Read all items | Dim item As Variant For Each item In arr Next item |
Dim item As Variant For Each item In arr Next item |
| Pass to Sub | Sub MySub(ByRef arr() As String) | Sub MySub(ByRef arr() As String) |
| Return from Function | Function GetArray() As Long() Dim arr(0 To 5) As Long GetArray = arr End Function |
Function GetArray() As Long() Dim arr() As Long GetArray = arr End Function |
| Receive from Function | Dynamic only | Dim arr() As Long Arr = GetArray() |
| Erase array | Erase arr *Resets all values to default |
Erase arr *Deletes array |
| String to array | Dynamic only | Dim arr As Variant arr = Split(«James:Earl:Jones»,»:») |
| Array to string | Dim sName As String sName = Join(arr, «:») |
Dim sName As String sName = Join(arr, «:») |
| Fill with values | Dynamic only | Dim arr As Variant arr = Array(«John», «Hazel», «Fred») |
| Range to Array | Dynamic only | Dim arr As Variant arr = Range(«A1:D2») |
| Array to Range | Same as dynamic | Dim arr As Variant Range(«A5:D6») = arr |
Download the Source Code and Data
Please click on the button below to get the fully documented source code for this article.
What is the VBA Array and Why do You Need It?
A VBA array is a type of variable. It is used to store lists of data of the same type. An example would be storing a list of countries or a list of weekly totals.
In VBA a normal variable can store only one value at a time.
In the following example we use a variable to store the marks of a student:
' Can only store 1 value at a time Dim Student1 As Long Student1 = 55
If we wish to store the marks of another student then we need to create a second variable.
In the following example, we have the marks of five students:
Student Marks
We are going to read these marks and write them to the Immediate Window.
Note: The function Debug.Print writes values to the Immediate Window. To view this window select View->Immediate Window from the menu( Shortcut is Ctrl + G)
As you can see in the following example we are writing the same code five times – once for each student:
' https://excelmacromastery.com/ Public Sub StudentMarks() ' Get the worksheet called "Marks" Dim sh As Worksheet Set sh = ThisWorkbook.Worksheets("Marks") ' Declare variable for each student Dim Student1 As Long Dim Student2 As Long Dim Student3 As Long Dim Student4 As Long Dim Student5 As Long ' Read student marks from cell Student1 = sh.Range("C" & 3).Value Student2 = sh.Range("C" & 4).Value Student3 = sh.Range("C" & 5).Value Student4 = sh.Range("C" & 6).Value Student5 = sh.Range("C" & 7).Value ' Print student marks Debug.Print "Students Marks" Debug.Print Student1 Debug.Print Student2 Debug.Print Student3 Debug.Print Student4 Debug.Print Student5 End Sub
The following is the output from the example:
Output
The problem with using one variable per student is that you need to add code for each student. Therefore if you had a thousand students in the above example you would need three thousand lines of code!
Luckily we have arrays to make our life easier. Arrays allow us to store a list of data items in one structure.
The following code shows the above student example using an array:
' ExcelMacroMastery.com ' https://excelmacromastery.com/excel-vba-array/ ' Author: Paul Kelly ' Description: Reads marks to an Array and write ' the array to the Immediate Window(Ctrl + G) ' TO RUN: Click in the sub and press F5 Public Sub StudentMarksArr() ' Get the worksheet called "Marks" Dim sh As Worksheet Set sh = ThisWorkbook.Worksheets("Marks") ' Declare an array to hold marks for 5 students Dim Students(1 To 5) As Long ' Read student marks from cells C3:C7 into array ' Offset counts rows from cell C2. ' e.g. i=1 is C2 plus 1 row which is C3 ' i=2 is C2 plus 2 rows which is C4 Dim i As Long For i = 1 To 5 Students(i) = sh.Range("C2").Offset(i).Value Next i ' Print student marks from the array to the Immediate Window Debug.Print "Students Marks" For i = LBound(Students) To UBound(Students) Debug.Print Students(i) Next i End Sub
The advantage of this code is that it will work for any number of students. If we have to change this code to deal with 1000 students we only need to change the (1 To 5) to (1 To 1000) in the declaration. In the prior example we would need to add approximately five thousand lines of code.
Let’s have a quick comparison of variables and arrays. First we compare the declaration:
' Variable Dim Student As Long Dim Country As String ' Array Dim Students(1 To 3) As Long Dim Countries(1 To 3) As String
Next we compare assigning a value:
' assign value to variable Student1 = .Cells(1, 1) ' assign value to first item in array Students(1) = .Cells(1, 1)
Finally we look at writing the values:
' Print variable value Debug.Print Student1 ' Print value of first student in array Debug.Print Students(1)
As you can see, using variables and arrays is quite similar.
The fact that arrays use an index(also called a subscript) to access each item is important. It means we can easily access all the items in an array using a For Loop.
Now that you have some background on why arrays are useful let’s go through them step by step.
Two Types of VBA Arrays
There are two types of VBA arrays:
- Static – an array of fixed length.
- Dynamic(not to be confused with the Excel Dynamic Array) – an array where the length is set at run time.
The difference between these types is mostly in how they are created. Accessing values in both array types is exactly the same. In the following sections we will cover both of these types.
VBA Array Initialization
A static array is initialized as follows:
' https://excelmacromastery.com/ Public Sub DecArrayStatic() ' Create array with locations 0,1,2,3 Dim arrMarks1(0 To 3) As Long ' Defaults as 0 to 3 i.e. locations 0,1,2,3 Dim arrMarks2(3) As Long ' Create array with locations 1,2,3,4,5 Dim arrMarks3(1 To 5) As Long ' Create array with locations 2,3,4 ' This is rarely used Dim arrMarks4(2 To 4) As Long End Sub
An Array of 0 to 3
As you can see the length is specified when you declare a static array. The problem with this is that you can never be sure in advance the length you need. Each time you run the Macro you may have different length requirements.
If you do not use all the array locations then the resources are being wasted. So if you need more locations you can use ReDim but this is essentially creating a new static array.
The dynamic array does not have such problems. You do not specify the length when you declare it. Therefore you can then grow and shrink as required:
' https://excelmacromastery.com/ Public Sub DecArrayDynamic() ' Declare dynamic array Dim arrMarks() As Long ' Set the length of the array when you are ready ReDim arrMarks(0 To 5) End Sub
The dynamic array is not allocated until you use the ReDim statement. The advantage is you can wait until you know the number of items before setting the array length. With a static array you have to state the length upfront.
To give an example. Imagine you were reading worksheets of student marks. With a dynamic array you can count the students on the worksheet and set an array to that length. With a static array you must set the length to the largest possible number of students.
Assigning Values to VBA Array
To assign values to an array you use the number of the location. You assign the value for both array types the same way:
' https://excelmacromastery.com/ Public Sub AssignValue() ' Declare array with locations 0,1,2,3 Dim arrMarks(0 To 3) As Long ' Set the value of position 0 arrMarks(0) = 5 ' Set the value of position 3 arrMarks(3) = 46 ' This is an error as there is no location 4 arrMarks(4) = 99 End Sub
The array with values assigned
The number of the location is called the subscript or index. The last line in the example will give a “Subscript out of Range” error as there is no location 4 in the array example.
VBA Array Length
There is no native function for getting the number of items in an array. I created the ArrayLength function below to return the number of items in any array no matter how many dimensions:
' https://excelmacromastery.com/ Function ArrayLength(arr As Variant) As Long On Error Goto eh ' Loop is used for multidimensional arrays. The Loop will terminate when a ' "Subscript out of Range" error occurs i.e. there are no more dimensions. Dim i As Long, length As Long length = 1 ' Loop until no more dimensions Do While True i = i + 1 ' If the array has no items then this line will throw an error Length = Length * (UBound(arr, i) - LBound(arr, i) + 1) ' Set ArrayLength here to avoid returing 1 for an empty array ArrayLength = Length Loop Done: Exit Function eh: If Err.Number = 13 Then ' Type Mismatch Error Err.Raise vbObjectError, "ArrayLength" _ , "The argument passed to the ArrayLength function is not an array." End If End Function
You can use it like this:
' Name: TEST_ArrayLength ' Author: Paul Kelly, ExcelMacroMastery.com ' Description: Tests the ArrayLength functions and writes ' the results to the Immediate Window(Ctrl + G) Sub TEST_ArrayLength() ' 0 items Dim arr1() As Long Debug.Print ArrayLength(arr1) ' 10 items Dim arr2(0 To 9) As Long Debug.Print ArrayLength(arr2) ' 18 items Dim arr3(0 To 5, 1 To 3) As Long Debug.Print ArrayLength(arr3) ' Option base 0: 144 items ' Option base 1: 50 items Dim arr4(1, 5, 5, 0 To 1) As Long Debug.Print ArrayLength(arr4) End Sub
Using the Array and Split function
You can use the Array function to populate an array with a list of items. You must declare the array as a type Variant. The following code shows you how to use this function.
Dim arr1 As Variant arr1 = Array("Orange", "Peach","Pear") Dim arr2 As Variant arr2 = Array(5, 6, 7, 8, 12)
Contents of arr1 after using the Array function
The array created by the Array Function will start at index zero unless you use Option Base 1 at the top of your module. Then it will start at index one. In programming, it is generally considered poor practice to have your actual data in the code. However, sometimes it is useful when you need to test some code quickly.
The Split function is used to split a string into an array based on a delimiter. A delimiter is a character such as a comma or space that separates the items.
The following code will split the string into an array of four elements:
Dim s As String s = "Red,Yellow,Green,Blue" Dim arr() As String arr = Split(s, ",")
The array after using Split
The Split function is normally used when you read from a comma-separated file or another source that provides a list of items separated by the same character.
Using Loops With the VBA Array
Using a For Loop allows quick access to all items in an array. This is where the power of using arrays becomes apparent. We can read arrays with ten values or ten thousand values using the same few lines of code. There are two functions in VBA called LBound and UBound. These functions return the smallest and largest subscript in an array. In an array arrMarks(0 to 3) the LBound will return 0 and UBound will return 3.
The following example assigns random numbers to an array using a loop. It then prints out these numbers using a second loop.
' https://excelmacromastery.com/ Public Sub ArrayLoops() ' Declare array Dim arrMarks(0 To 5) As Long ' Fill the array with random numbers Dim i As Long For i = LBound(arrMarks) To UBound(arrMarks) arrMarks(i) = 5 * Rnd Next i ' Print out the values in the array Debug.Print "Location", "Value" For i = LBound(arrMarks) To UBound(arrMarks) Debug.Print i, arrMarks(i) Next i End Sub
The functions LBound and UBound are very useful. Using them means our loops will work correctly with any array length. The real benefit is that if the length of the array changes we do not have to change the code for printing the values. A loop will work for an array of any length as long as you use these functions.
Using the For Each Loop with the VBA Array
You can use the For Each loop with arrays. The important thing to keep in mind is that it is Read-Only. This means that you cannot change the value in the array.
In the following code the value of mark changes but it does not change the value in the array.
For Each mark In arrMarks ' Will not change the array value mark = 5 * Rnd Next mark
The For Each is loop is fine to use for reading an array. It is neater to write especially for a Two-Dimensional array as we will see.
Dim mark As Variant For Each mark In arrMarks Debug.Print mark Next mark
Using Erase with the VBA Array
The Erase function can be used on arrays but performs differently depending on the array type.
For a static Array the Erase function resets all the values to the default. If the array is made up of long integers(i.e type Long) then all the values are set to zero. If the array is of strings then all the strings are set to “” and so on.
For a Dynamic Array the Erase function DeAllocates memory. That is, it deletes the array. If you want to use it again you must use ReDim to Allocate memory.
Let’s have a look an example for the static array. This example is the same as the ArrayLoops example in the last section with one difference – we use Erase after setting the values. When the value are printed out they will all be zero:
' https://excelmacromastery.com/ Public Sub EraseStatic() ' Declare array Dim arrMarks(0 To 3) As Long ' Fill the array with random numbers Dim i As Long For i = LBound(arrMarks) To UBound(arrMarks) arrMarks(i) = 5 * Rnd Next i ' ALL VALUES SET TO ZERO Erase arrMarks ' Print out the values - there are all now zero Debug.Print "Location", "Value" For i = LBound(arrMarks) To UBound(arrMarks) Debug.Print i, arrMarks(i) Next i End Sub
We will now try the same example with a dynamic. After we use Erase all the locations in the array have been deleted. We need to use ReDim if we wish to use the array again.
If we try to access members of this array we will get a “Subscript out of Range” error:
' https://excelmacromastery.com/ Public Sub EraseDynamic() ' Declare array Dim arrMarks() As Long ReDim arrMarks(0 To 3) ' Fill the array with random numbers Dim i As Long For i = LBound(arrMarks) To UBound(arrMarks) arrMarks(i) = 5 * Rnd Next i ' arrMarks is now deallocated. No locations exist. Erase arrMarks End Sub
Increasing the length of the VBA Array
If we use ReDim on an existing array, then the array and its contents will be deleted.
In the following example, the second ReDim statement will create a completely new array. The original array and its contents will be deleted.
' https://excelmacromastery.com/ Sub UsingRedim() Dim arr() As String ' Set array to be slots 0 to 2 ReDim arr(0 To 2) arr(0) = "Apple" ' Array with apple is now deleted ReDim arr(0 To 3) End Sub
If we want to extend the length of an array without losing the contents, we can use the Preserve keyword.
When we use Redim Preserve the new array must start at the same starting dimension e.g.
We cannot Preserve from (0 to 2) to (1 to 3) or to (2 to 10) as they are different starting dimensions.
In the following code we create an array using ReDim and then fill the array with types of fruit.
We then use Preserve to extend the length of the array so we don’t lose the original contents:
' https://excelmacromastery.com/ Sub UsingRedimPreserve() Dim arr() As String ' Set array to be slots 0 to 1 ReDim arr(0 To 2) arr(0) = "Apple" arr(1) = "Orange" arr(2) = "Pear" ' Reset the length and keep original contents ReDim Preserve arr(0 To 5) End Sub
You can see from the screenshots below, that the original contents of the array have been “Preserved”.
Before ReDim Preserve
After ReDim Preserve
Word of Caution: In most cases, you shouldn’t need to resize an array like we have done in this section. If you are resizing an array multiple times then you may want to consider using a Collection.
Using Preserve with Two-Dimensional Arrays
Preserve only works with the upper bound of an array.
For example, if you have a two-dimensional array you can only preserve the second dimension as this example shows:
' https://excelmacromastery.com/ Sub Preserve2D() Dim arr() As Long ' Set the starting length ReDim arr(1 To 2, 1 To 5) ' Change the length of the upper dimension ReDim Preserve arr(1 To 2, 1 To 10) End Sub
If we try to use Preserve on a lower bound we will get the “Subscript out of range” error.
In the following code we use Preserve on the first dimension. Running this code will give the “Subscript out of range” error:
' https://excelmacromastery.com/ Sub Preserve2DError() Dim arr() As Long ' Set the starting length ReDim arr(1 To 2, 1 To 5) ' "Subscript out of Range" error ReDim Preserve arr(1 To 5, 1 To 5) End Sub
When we read from a range to an array, it automatically creates a two-dimensional array, even if we have only one column.
The same Preserve rules apply. We can only use Preserve on the upper bound as this example shows:
' https://excelmacromastery.com/ Sub Preserve2DRange() Dim arr As Variant ' Assign a range to an array arr = Sheet1.Range("A1:A5").Value ' Preserve will work on the upper bound only ReDim Preserve arr(1 To 5, 1 To 7) End Sub
Sorting the VBA Array
There is no function in VBA for sorting an array. We can sort the worksheet cells but this could be slow if there is a lot of data.
The QuickSort function below can be used to sort an array.
' https://excelmacromastery.com/ Sub QuickSort(arr As Variant, first As Long, last As Long) Dim vCentreVal As Variant, vTemp As Variant Dim lTempLow As Long Dim lTempHi As Long lTempLow = first lTempHi = last vCentreVal = arr((first + last) 2) Do While lTempLow <= lTempHi Do While arr(lTempLow) < vCentreVal And lTempLow < last lTempLow = lTempLow + 1 Loop Do While vCentreVal < arr(lTempHi) And lTempHi > first lTempHi = lTempHi - 1 Loop If lTempLow <= lTempHi Then ' Swap values vTemp = arr(lTempLow) arr(lTempLow) = arr(lTempHi) arr(lTempHi) = vTemp ' Move to next positions lTempLow = lTempLow + 1 lTempHi = lTempHi - 1 End If Loop If first < lTempHi Then QuickSort arr, first, lTempHi If lTempLow < last Then QuickSort arr, lTempLow, last End Sub
You can use this function like this:
' https://excelmacromastery.com/ Sub TestSort() ' Create temp array Dim arr() As Variant arr = Array("Banana", "Melon", "Peach", "Plum", "Apple") ' Sort array QuickSort arr, LBound(arr), UBound(arr) ' Print arr to Immediate Window(Ctrl + G) Dim i As Long For i = LBound(arr) To UBound(arr) Debug.Print arr(i) Next i End Sub
Passing the VBA Array to a Sub
Sometimes you will need to pass an array to a procedure. You declare the parameter using parenthesis similar to how you declare a dynamic array.
Passing to the procedure using ByRef means you are passing a reference of the array. So if you change the array in the procedure it will be changed when you return.
Note: When you use an array as a parameter it cannot use ByVal, it must use ByRef. You can pass the array using ByVal making the parameter a variant.
' https://excelmacromastery.com/ ' Passes array to a Function Public Sub PassToProc() Dim arr(0 To 5) As String ' Pass the array to function UseArray arr End Sub Public Function UseArray(ByRef arr() As String) ' Use array Debug.Print UBound(arr) End Function
Returning the VBA Array from a Function
It is important to keep the following in mind. If you want to change an existing array in a procedure then you should pass it as a parameter using ByRef(see last section). You do not need to return the array from the procedure.
The main reason for returning an array is when you use the procedure to create a new one. In this case you assign the return array to an array in the caller. This array cannot be already allocated. In other words you must use a dynamic array that has not been allocated.
The following examples show this
' https://excelmacromastery.com/ Public Sub TestArray() ' Declare dynamic array - not allocated Dim arr() As String ' Return new array arr = GetArray End Sub Public Function GetArray() As String() ' Create and allocate new array Dim arr(0 To 5) As String ' Return array GetArray = arr End Function
Using a Two-Dimensional VBA Array
The arrays we have been looking at so far have been one-dimensional arrays. This means the arrays are one list of items.
A two-dimensional array is essentially a list of lists. If you think of a single spreadsheet row as a single dimension then more than one column is two dimensional. In fact a spreadsheet is the equivalent of a two-dimensional array. It has two dimensions – rows and columns.
One small thing to note is that Excel treats a one-dimensional array as a row if you write it to a spreadsheet. In other words, the array arr(1 to 5) is equivalent to arr(1 to 1, 1 to 5) when writing values to the spreadsheet.
The following image shows two groups of data. The first is a one-dimensional layout and the second is two dimensional.
To access an item in the first set of data(1 dimensional) all you need to do is give the row e.g. 1,2, 3 or 4.
For the second set of data (two-dimensional), you need to give the row AND the column. So you can think of 1 dimensional being multiple columns and one row and two-dimensional as being multiple rows and multiple columns.
Note: It is possible to have more than two dimensions in an array. It is rarely required. If you are solving a problem using a 3+ dimensional array then there probably is a better way to do it.
You declare a two-dimensional array as follows:
Dim ArrayMarks(0 To 2,0 To 3) As Long
The following example creates a random value for each item in the array and the prints the values to the Immediate Window:
' https://excelmacromastery.com/ Public Sub TwoDimArray() ' Declare a two dimensional array Dim arrMarks(0 To 3, 0 To 2) As String ' Fill the array with text made up of i and j values Dim i As Long, j As Long For i = LBound(arrMarks) To UBound(arrMarks) For j = LBound(arrMarks, 2) To UBound(arrMarks, 2) arrMarks(i, j) = CStr(i) & ":" & CStr(j) Next j Next i ' Print the values in the array to the Immediate Window Debug.Print "i", "j", "Value" For i = LBound(arrMarks) To UBound(arrMarks) For j = LBound(arrMarks, 2) To UBound(arrMarks, 2) Debug.Print i, j, arrMarks(i, j) Next j Next i End Sub
You can see that we use a second For loop inside the first loop to access all the items.
The output of the example looks like this:
How this Macro works is as follows:
- Enters the i loop
- i is set to 0
- Entersj loop
- j is set to 0
- j is set to 1
- j is set to 2
- Exit j loop
- i is set to 1
- j is set to 0
- j is set to 1
- j is set to 2
- And so on until i=3 and j=2
You may notice that LBound and UBound have a second argument with the value 2. This specifies that it is the upper or lower bound of the second dimension. That is the start and end location for j. The default value 1 which is why we do not need to specify it for the i loop.
Using the For Each Loop
Using a For Each is neater to use when reading from an array.
Let’s take the code from above that writes out the two-dimensional array
' Using For loop needs two loops Debug.Print "i", "j", "Value" For i = LBound(arrMarks) To UBound(arrMarks) For j = LBound(arrMarks, 2) To UBound(arrMarks, 2) Debug.Print i, j, arrMarks(i, j) Next j Next i
Now let’s rewrite it using a For each loop. You can see we only need one loop and so it is much easier to write:
' Using For Each requires only one loop Debug.Print "Value" Dim mark As Variant For Each mark In arrMarks Debug.Print mark Next mark
Using the For Each loop gives us the array in one order only – from LBound to UBound. Most of the time this is all you need.
Reading from a Range to the VBA Array
If you have read my previous post on Cells and Ranges then you will know that VBA has an extremely efficient way of reading from a Range of Cells to an Array and vice versa
' https://excelmacromastery.com/ Public Sub ReadToArray() ' Declare dynamic array Dim StudentMarks As Variant ' Read values into array from first row StudentMarks = Range("A1:Z1").Value ' Write the values back to the third row Range("A3:Z3").Value = StudentMarks End Sub
The dynamic array created in this example will be a two dimensional array. As you can see we can read from an entire range of cells to an array in just one line.
The next example will read the sample student data below from C3:E6 of Sheet1 and print them to the Immediate Window:
' https://excelmacromastery.com/ Public Sub ReadAndDisplay() ' Get Range Dim rg As Range Set rg = ThisWorkbook.Worksheets("Sheet1").Range("C3:E6") ' Create dynamic array Dim StudentMarks As Variant ' Read values into array from sheet1 StudentMarks = rg.Value ' Print the array values Debug.Print "i", "j", "Value" Dim i As Long, j As Long For i = LBound(StudentMarks) To UBound(StudentMarks) For j = LBound(StudentMarks, 2) To UBound(StudentMarks, 2) Debug.Print i, j, StudentMarks(i, j) Next j Next i End Sub
Sample Student data
Output from sample data
As you can see the first dimension(accessed using i) of the array is a row and the second is a column. To demonstrate this take a look at the value 44 in E4 of the sample data. This value is in row 2 column 3 of our data. You can see that 44 is stored in the array at StudentMarks(2,3).
You can see more about using arrays with ranges in this YouTube video
How To Make Your Macros Run at Super Speed
If your macros are running very slow then you may find this section very helpful. Especially if you are dealing with large amounts of data. The following is a very well-kept secret in VBA
Updating values in arrays is exponentially faster than updating values in cells.
In the last section, you saw how we can easily read from a group of cells to an array and vice versa. If we are updating a lot of values then we can do the following:
1. Copy the data from the cells to an array.
2. Change the data in the array.
3. Copy the updated data from the array back to the cells.
For example, the following code would be much faster than the code below it:
' https://excelmacromastery.com/ Public Sub ReadToArray() ' Read values into array from first row Dim StudentMarks As Variant StudentMarks = Range("A1:Z20000").Value Dim i As Long For i = LBound(StudentMarks) To UBound(StudentMarks) ' Update marks here StudentMarks(i, 1) = StudentMarks(i, 1) * 2 '... Next i ' Write the new values back to the worksheet Range("A1:Z20000").Value = StudentMarks End Sub
' https://excelmacromastery.com/ Sub UsingCellsToUpdate() Dim c As Variant For Each c In Range("A1:Z20000") c.Value = ' Update values here Next c End Sub
Assigning from one set of cells to another is also much faster than using Copy and Paste:
' Assigning - this is faster Range("A1:A10").Value = Range("B1:B10").Value ' Copy Paste - this is slower Range("B1:B1").Copy Destination:=Range("A1:A10")
The following comments are from two readers who used arrays to speed up their macros
“A couple of my projects have gone from almost impossible and long to run into almost too easy and a reduction in time to run from 10:1.” – Dane
“One report I did took nearly 3 hours to run when accessing the cells directly — 5 minutes with arrays” – Jim
You can see more about the speed of Arrays compared to other methods in this YouTube video.
To see a comparison between Find, Match and Arrays it is worth checking out this post by Charles Williams.
Conclusion
The following is a summary of the main points of this post
- Arrays are an efficient way of storing a list of items of the same type.
- You can access an array item directly using the number of the location which is known as the subscript or index.
- The common error “Subscript out of Range” is caused by accessing a location that does not exist.
- There are two types of arrays: Static and Dynamic.
- Static is used when the length of the array is always the same.
- Dynamic arrays allow you to determine the length of an array at run time.
- LBound and UBound provide a safe way of find the smallest and largest subscripts of the array.
- The basic array is one dimensional. You can also have multidimensional arrays.
- You can only pass an array to a procedure using ByRef. You do this like this: ByRef arr() as long.
- You can return an array from a function but the array, it is assigned to, must not be currently allocated.
- A worksheet with its rows and columns is essentially a two-dimensional array.
- You can read directly from a worksheet range into a two-dimensional array in just one line of code.
- You can also write from a two-dimensional array to a range in just one line of code.
What’s Next?
Free VBA Tutorial If you are new to VBA or you want to sharpen your existing VBA skills then why not try The Ultimate VBA Tutorial.
Related Training: Get full access to the Excel VBA training webinars.
(NOTE: Planning to build or manage a VBA Application? Learn how to build 10 Excel VBA applications from scratch.)
Хитрости »
27 Июль 2013 307116 просмотров
Полагаю не совру когда скажу, что все кто программирует в VBA очень часто в своих кодах общаются к ячейкам листов. Ведь это чуть ли не основное предназначение VBA в Excel. В принципе ничего сложного в этом нет. Например, чтобы записать в ячейку A1 слово Привет необходимо выполнить код:
Range("A1").Value = "Привет"
Тоже самое можно сделать сразу для нескольких ячеек:
Range("A1:C10").Value = "Привет"
Если необходимо обратиться к именованному диапазону:
Range("Диапазон1").Select
Диапазон1 — это имя диапазона/ячейки, к которому надо обратиться в коде. Указывается в кавычках, как и адреса ячеек.
Но в VBA есть и альтернативный метод записи значений в ячейке — через объект Cells:
Cells(1, 1).Value = "Привет"
Синтаксис объекта Range:
Range(Cell1, Cell2)
- Cell1 — первая ячейка диапазона. Может быть ссылкой на ячейку или диапазон ячеек, текстовым представлением адреса или имени диапазона/ячейки. Допускается указание несвязанных диапазонов(A1,B10), пересечений(A1 B10).
- Cell2 — последняя ячейка диапазона. Необязательна к указанию. Допускается указание ссылки на ячейку, столбец или строку.
Синтаксис объекта Cells:
Cells(Rowindex, Columnindex)
- Rowindex — номер строки
- Columnindex — номер столбца
Исходя из этого несложно предположить, что к диапазону можно обратиться, используя Cells и Range:
'выделяем диапазон "A1:B10" на активном листе Range(Cells(1,1), Cells(10,2)).Select
и для чего? Ведь можно гораздо короче:
Иногда обращение посредством Cells куда удобнее. Например для цикла по столбцам(да еще и с шагом 3) совершенно неудобно было бы использовать буквенное обозначение столбцов.
Объект Cells так же можно использовать для указания ячеек внутри непосредственно указанного диапазона. Например, Вам необходимо выделить ячейку в 3 строке и 2 столбце диапазона «D5:F56». Можно пройтись по листу и посмотреть, отсчитать нужное количество строк и столбцов и понять, что это будет «E7». А можно сделать проще:
Range("D5:F56").Cells(3, 2).Select
Согласитесь, это гораздо удобнее, чем отсчитывать каждый раз. Особенно, если придется оперировать смещением не на 2-3 ячейки, а на 20 и более. Конечно, можно было бы применить Offset. Но данное свойство именно смещает диапазон на указанное количество строк и столбцов и придется уменьшать на 1 смещение каждого параметра для получения нужной ячейки. Да и смещает на указанное количество строк и столбцов весь диапазон, а не одну ячейку. Это, конечно, тоже не проблема — можно вдобавок к этому использовать метод Resize — но запись получится несколько длиннее и менее наглядной:
Range("D5:F56").Offset(2, 1).Resize(1, 1).Select
И неплохо бы теперь понять, как значение диапазона присвоить переменной. Для начала переменная должна быть объявлена с типом Range. А т.к. Range относится к глобальному типу Object, то присвоение значения такой переменной должно быть обязательно с применением оператора Set:
Dim rR as Range Set rR = Range("D5")
если оператор Set не применять, то в лучшем случае получите ошибку, а в худшем(он возможен, если переменной rR не назначать тип) переменной будет назначено значение Null или значение ячейки по умолчанию. Почему это хуже? Потому что в таком случае код продолжит выполняться, но логика кода будет неверной, т.к. эта самая переменная будет содержать значение неверного типа и применение её в коде в дальнейшем все равно приведет к ошибке. Только ошибку эту отловить будет уже сложнее.
Использовать же такую переменную в дальнейшем можно так же, как и прямое обращение к диапазону:
Вроде бы на этом можно было завершить, но…Это как раз только начало. То, что я написал выше знает практически каждый, кто пишет в VBA. Основной же целью этой статьи было пояснить некоторые нюансы обращения к диапазонам. Итак, поехали.
Обычно макрорекордер при обращении к диапазону(да и любым другим объектам) сначала его выделяет, а потом уже изменяет свойство или вызывает некий метод:
'так выглядит запись слова Test в ячейку А1 Range("A1").Select Selection.Value = "Test"
Но как правило выделение — действие лишнее. Можно записать значение и без него:
'запишем слово Test в ячейку A1 на активном листе Range("A1").Value = "Test"
Теперь чуть подробнее разберем, как обратиться к диапазону не выделяя его и при этом сделать все правильно. Диапазон и ячейка — это объекты листа. У каждого объекта есть родитель — грубо говоря это другой объект, который является управляющим для дочернего объекта. Для ячейки родительский объект — Лист, для Листа — Книга, для Книги — Приложение Excel. Если смотреть на иерархию зависимости объектов, то от старшего к младшему получится так:
Applicaton => Workbooks => Sheets => Range
По умолчанию для всех диапазонов и ячеек родительским объектом является текущий(активный) лист. Т.е. если для диапазона(ячейки) не указать явно лист, к которому он относится, в качестве родительского листа для него будет использован текущий — ActiveSheet:
'запишем слово Test в ячейку A1 на активном листе Range("A1").Value = "Test"
Т.е. если в данный момент активен Лист1 — то слово Test будет записано в ячейку А1 Лист1. Если активен Лист3 — в А1 Лист3. Иначе говоря такая запись равносильна записи:
ActiveSheet.Range("A1").Value = "Test"
Поэтому выхода два — либо активировать сначала нужный лист, либо записать без активации.
'активируем Лист2 Worksheets("Лист2").Select 'записываем слово Test в ячейку A1 Range("A1").Value = "Test"
Чтобы не активируя другой лист записать в него данные, необходимо явно указать принадлежность объекта Range именно этому листу:
'запишем слово Test в ячейку A1 на Лист2 независимо от того, какой лист активен Worksheets("Лист2").Range("A1").Value = "Test"
Таким же образом происходит считывание данных с ячеек — если не указывать лист, данные ячеек которого необходимо считать — считаны будут данные с ячейки активного листа. Чтобы считать данные с Лист2 независимо от того, какой лист активен применяется такой код:
'считываем значение ячейки A1 с Лист2 независимо от того, какой лист активен MsgBox Worksheets("Лист2").Range("A1").Value
Т.к. ячейка является частью листа, то лист в свою очередь является частью книги. Исходя из того легко сделать вывод, что при открытых двух и более книгах мы так же можем обратиться к ячейкам любого листа любой открытой книги не активируя при этом ни книгу, ни лист:
'запишем слово Test в ячейку A1 на Лист2 книги Книга2.xlsx независимо от того, какая книга и какой лист активен Workbooks("Книга2.xlsx").Worksheets("Лист2").Range("A1").Value = "Test" 'считываем значение ячейки A1 с Лист2 книги Книга3.xlsx независимо от того, какой лист активен MsgBox Workbooks("Книга3.xlsx").Worksheets("Лист2").Range("A1").Value
Важный момент: лучше всегда указать имя книги вместе с расширением(.xlsx, xlsm, .xls и т.д.). Если в настройках ОС Windows(Панель управления —Параметры папок -вкладка Вид —Скрывать расширения для зарегистрированных типов файлов) указано скрывать расширения — то указывать расширение не обязательно — Workbooks(«Книга2»). Но и ошибки не будет, если его указать. Однако, если пункт «Скрывать расширения для зарегистрированных типов файлов» отключен, то указание Workbooks(«Книга2») обязательно приведет к ошибке.
Очень часто ошибки обращения к ячейкам листов и книг делают начинающие, особенно в циклах по листам. Вот пример неправильного цикла:
Dim wsSh As Worksheet For Each wsSh In ActiveWorkbook.Worksheets Range("A1").Value = wsSh.Name 'записываем в ячейку А1 имя листа MsgBox Range("A1").Value 'проверяем, то ли имя записалось Next wsSh
MsgBox будет выдавать правильные значения, но сами имена листов будут записываться не на каждый лист, а последовательно в ячейку активного листа. Поэтому на активном листе в ячейке А1 будет имя последнего листа.
А вот так выглядит правильный цикл:
Вариант 1 — активация листа(медленный)
Dim wsSh As Worksheet For Each wsSh In ActiveWorkbook.Worksheets wsSh.Activate 'активируем каждый лист Range("A1").Value = wsSh.Name 'записываем в ячейку А1 имя листа MsgBox Range("A1").Value 'проверяем, то ли имя записалось Next wsSh
Вариант 2 — без активации листа(быстрый и более правильный)
Dim wsSh As Worksheet For Each wsSh In ActiveWorkbook.Worksheets wsSh.Range("A1").Value = wsSh.Name 'записываем в ячейку А1 имя листа MsgBox wsSh.Range("A1").Value 'проверяем, то ли имя записалось Next wsSh
Важно: если код записан в модуле листа(правая кнопка мыши на листе-Исходный текст) и для объекта Range или Cells родитель явно не указан(т.е. нет имени листа и книги) — тогда в качестве родителя будет использован именно тот лист, в котором записан код, независимо от того какой лист активный. Иными словами — если в модуле листа записать обращение вроде Range(«A1»).Value = «привет», то слово привет всегда будет записывать в ячейку A1 именно того листа, в котором записан сам код. Это следует учитывать, когда располагаете свои коды внутри модулей листов.
В конструкциях типа Range(Cells(,),Cells(,)) Range является контейнером, в котором указываются ссылки на объекты, из которых и будет создана ссылка на непосредственно конечный объект.
Предположим, что активен «Лист1», а код запущен с листа «Итог».
Если запись будет вида
Sheets("Итог").Range(Cells(1, 1), Cells(10, 1))
это вызовет ошибку «Run-time error ‘1004’: Application-defined or object-defined error». А ошибка появляется потому, что контейнер и объекты внутри него не могут располагаться на разных листах, равно как и:
Sheets("Итог").Range(Cells(1, 1), Sheets("Итог").Cells(10, 1)) 'запись ниже так же неверна Range(Cells(1, 1), Sheets("Итог").Cells(10, 1))
т.к. ссылки на объекты внутри контейнера относятся к разным листам. Cells(1, 1) — к активному листу, а Sheets(«Итог»).Cells(10, 1) — к листу Итог.
А вот такие записи будут правильными:
Sheets("Итог").Range(Sheets("Итог").Cells(1, 1), Sheets("Итог").Cells(10, 1)) Range(Sheets("Итог").Cells(1, 1), Sheets("Итог").Cells(10, 1))
Вторая запись не содержит ссылки на родителя для Range, но ошибки это в большинстве случаев не вызовет — т.к. если для контейнера ссылка не указана, а для двух объектов внутри контейнера родитель один — он будет применен и для самого контейнера. Однако лучше делать как в первой строке — т.е. с обязательным указанием родителя для контейнера и для его составляющих. Т.к. при определенных обстоятельствах(например, если в момент обращения к диапазону активной является книга, открытая в режиме защищенного просмотра) обращение к Range без родителя может вызывать ошибку выполнения.
Если запись будет вида Range(«A1″,»A10»), то указывать ссылку на родителя внутри Range не обязательно — достаточно будет указать эту ссылку перед самим Range — Sheets(«Итог»).Range(«A1″,»A10»), т.к. текстовое представление адреса внутри Range не является объектом(у которого может быть какой-то родительский объект), что обязывает создать ссылку именно на родителя контейнера.
Разберем пример, приближенный к жизненной ситуации. Необходимо на лист Итог занести формулу вычитания, начиная с ячейки А2 и до последней заполненной. На момент записи активен Лист1. Очень часто начинающие записывают так:
Sheets("Итог").Range("A2:A" & Cells(Rows.Count, 1).End(xlUp).Row) _ .FormulaR1C1 = "=RC2-RC11"
Запись смешанная — и текстовое представление адреса ячейки(«A2:A») и ссылка на объект Cells. В данном случае явную ошибку код не вызовет, но и работать будет не всегда так, как хотелось бы. А это самое плохое, что может случиться при разработке.
Sheets(«Итог»).Range(«A2:A» — создается ссылка на столбец "A" листа Итог. Но далее идет вычисление последней строки первого столбца. И вот как раз это вычисление происходит на основе объекта Cells, который не содержит в себе ссылки на родительский объект. А значит он будет вычислять последнюю строку исключительно для текущего листа(если код записан в стандартном модуле, а не модуле листа) — т.е. для Лист1. Правильно было бы записать так:
Sheets("Итог").Range("A2:A" & Sheets("Итог").Cells(Rows.Count, 1).End(xlUp).Row) _ .FormulaR1C1 = "=RC2-RC11"
Но и здесь неверное обращение с диапазоном может сыграть злую шутку. Например, надо получить последнюю заполненную ячейку в конкретной книге:
lLastRow = Workbooks("Книга3.xls").Sheets("Лист1").Cells(Rows.Count, 1).End(xlUp).Row
с виду все нормально, но есть нюанс. Rows.Count по умолчанию будет относится к активной книге, если записано в стандартном модуле. Приведенный выше код должен работать с книгой формата 97-2003 и вычислить последнюю заполненную ячейку на листе1. В книгах формата Excel 97-2003(.xls) всего 65536 строк. Если в момент выполнения приведенной строки активна книга формата 2007 и выше(форматы .xlsx, .xlsm, .xlsb и пр) — то Rows.Count вернет 1048576, т.к. именно такое количество строк в листах книг версий Excel, начиная с 2007. И т.к. в книге, в которой мы пытаемся вычислить последнюю строку всего 65536 строк — получим ошибку 1004, т.к. не может быть номера строки 1048576 на листе с количеством строк 65536. Поэтому имеет смысл указывать явно откуда считывать Rows.Count:
lLastRow = Workbooks("Книга3.xls").Sheets("Лист1").Cells(Workbooks("Книга3.xls").Sheets("Лист1").Rows.Count, 1).End(xlUp).Row
или применить конструкцию With
With Workbooks("Книга3.xls").Sheets("Лист1") lLastRow = .Cells(.Rows.Count, 1).End(xlUp).Row End With
Также не мешало бы упомянуть возможность выделения несмежного диапазона(часто его называют «рваным»). Это диапазон, который обычно привыкли выделять на листе при помощи зажатой клавиши Ctrl. Что это дает? Это дает возможность выделить одновременно ячейки A1 и B10 и записать значения только в них. Для этого есть несколько способов. Самый очевидный и описанный в справке — метод Union:
Union(Range("A1"), Range("B10")).Value = "Привет"
Однако существует и другой метод:
Range("A1,B10").Value = "Привет"
В чем отличие(я бы даже сказал преимущество) Union: можно применять в цикле по условию. Например, выделить в диапазоне A1:F50 только те ячейки, значение которых больше 10 и меньше 20:
Sub SelOne() Dim rCell As Range, rSel As Range For Each rCell In Range("A1:F50") If rCell.Value > 10 And rCell.Value < 20 Then If rSel Is Nothing Then Set rSel = rCell Else Set rSel = Union(rSel, rCell) End If End If Next rCell If Not rSel Is Nothing Then rSel.Select End Sub
Конечно, можно и просто в Range через запятую передать все эти ячейки, сформировав предварительно строку. Но в случае со строкой действует ограничение: длина строки не должна превышать 255 символов.
Надеюсь, что после прочтения данной статьи проблем с обращением к диапазонам и ячейкам у Вас будет гораздо меньше.
Также см.:
Как определить последнюю ячейку на листе через VBA?
Как определить первую заполненную ячейку на листе?
Как из Excel обратиться к другому приложению
Статья помогла? Поделись ссылкой с друзьями!
Видеоуроки
Поиск по меткам
Access
apple watch
Multex
Power Query и Power BI
VBA управление кодами
Бесплатные надстройки
Дата и время
Записки
ИП
Надстройки
Печать
Политика Конфиденциальности
Почта
Программы
Работа с приложениями
Разработка приложений
Росстат
Тренинги и вебинары
Финансовые
Форматирование
Функции Excel
акции MulTEx
ссылки
статистика
Одной из важнейших задач для руководителя проектов является правильная оценка экономической эффективности предлагаемого проекта. Эта оценка очень важны как на начальном этапе для определения более выгодного варианта среди альтернатив, а так же на стадии завершения для оценки суммарного экономического эффекта для проектного офиса. Не смотря на то, что существуют специализированные программные продукты помогающие производить подобные расчеты, все это по силам сделать и стандартными средствами таблиц Excel. В статье, мы кратко коснемся основных расчетных коэффициентов, их экономической сути и кратенько отобразим наглядные примеры, то как это можно выполнить в Excel-таблицах.
Все методы оценки эффективности инвестиционных проектов можно разделить на две большие группы:
-
Статистические методы оценки инвестиционных проектов
- Срок окупаемости инвестиционного проекта (PP, Payback Period)
- Рентабельность инвестиционного проекта (ARR, Accounting Rate of Return)
-
Динамические методы оценки инвестиционных проектов
- Чистый дисконтированный доход (NPV, Net Present Value)
- Внутренняя норма прибыл (IRR, Internal Rate of Return)
- Индекс прибыльности (PI, Profitability index)
- Дисконтированный срок окупаемости (DPP, Discounted Payback Period)
СТАТИСТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИЙ/ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
Статистические методы оценки являются самым простым классом подходов к анализу инвестиций и инвестиционных проектов. Несмотря на свою кажущуюся простоту расчета и использования, они позволяют сделать выводы по качеству объектов инвестиций, сравнить их между собой и отсеять неэффективные.
СРОК ОКУПАЕМОСТИ ИНВЕСТИЦИЙ (PAYBACK PERIOD)
Срок окупаемости инвестиций или инвестиционного проекта (англ. Payback Period, PP, период окупаемости) – данный коэффициент показывает период, за который окупятся первоначальные инвестиции (затраты) в инвестиционный проект. Экономический смысл данного показателя заключается в том, что бы показать срок, за который инвестор вернет обратно свои вложенные деньги (капитал).
ФОРМУЛА РАСЧЕТА СРОКА ОКУПАЕМОСТИ ИНВЕСТИЦИЙ (ИНВЕСТИЦИОННОГО ПРОЕКТА)
где:
IC (Invest Capital) – инвестиционный капитал, первоначальные затраты инвестора в объект вложения. В формуле в иностранной практике иногда используют понятие не инвестиционный капитал, а затраты на капитал (Cost ofCapital, CC), что по сути несет аналогичный смысл;
CF (Cash Flow) – денежный поток, который создается объектом инвестиций. Под денежным потоком иногда в формулах подразумевают чистую прибыль (NP, Net Profit).
Формулу расчета срока/период окупаемости можно расписать по-другому, такой вариант тоже часто встречается в отечественной литературе по финансам:
Следует отметить, что затраты на инвестиции представляют собой все издержки инвестора при вложении в инвестиционный проект. Денежный поток необходимо учитывать за определенные периоды (день, неделя, месяц, год). В результате период окупаемости инвестиций будет иметь аналогичную шкалу измерения.
ПРИМЕР РАСЧЕТА СРОКА ОКУПАЕМОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА В EXCEL
На рисунке ниже показан пример расчета срока окупаемости инвестиционного проекта. У нас имеются исходные данные, что стоимость первоначальных затрат составили 130000 руб., ежемесячно денежный поток от инвестиций составлял 25000 руб. В начале необходимо рассчитать денежный поток нарастающим итогом, для этого использовалась следующая простая формула:
Денежный поток нарастающим итогом рассчитывается в колонке С, C7=C6+$C$3
Если рассчитать срок окупаемости по формуле, то получится следующее:
Так как мы у нас период дискретный, то необходимо округлить этот период до 6 месяцев.
НАПРАВЛЕНИЯ ИСПОЛЬЗОВАНИЯ СРОКА ОКУПАЕМОСТИ ИНВЕСТИЦИЙ (ИНВЕСТИЦИОННЫХ ПРОЕКТОВ)
Показатель периода окупаемости инвестиций использует как сравнительный показатель для оценки эффективности альтернативных инвестиционных проектов. Тот проект, у которого быстрее период окупаемости тот эффективнее. Данный коэффициент используют, как правило, всегда в совокупности с другими показателям, которые мы разберем ниже.
ДОСТОИНСТВА И НЕДОСТАТКИ ПОКАЗАТЕЛЯ СРОКА ОКУПАЕМОСТИ ИНВЕСТИЦИЙ
Достоинства показателя его скорость и простота расчета. Недостаток данного коэффициента очевиден – в его расчете используется постоянный денежный поток. В реальных условиях достаточно сложно спрогнозировать устойчивые будущие денежные поступления, поэтому период окупаемости может существенно измениться. Для того чтобы снизить возможные отклонения от плана окупаемости следует обеспечить надежность источников поступления денежного потока инвестиционного проекта. К тому же показатель не учитывает влияние инфляции на изменение стоимости денег во времени. Срок окупаемости инвестиций как может быть использован как критерий отсева на первом этапе оценки и отбора «тяжелых» инвестиционных проектов.
КОЭФФИЦИЕНТ РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИЙ (ACCOUNTING RATE OF RETURN)
Коэффициент рентабельности инвестиций или инвестиционного проекта (англ. Accounting Rate of Return, ARR, ROI, учетная норма прибыли, рентабельность инвестиций) – показатель отражающий прибыльность объекта инвестиций без учета дисконтирования.
ФОРМУЛА РАСЧЕТА КОЭФФИЦИЕНТА РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИЙ
где:
CFср – средний денежный поток (чистая прибыль) объекта инвестиций за рассматриваемый период (месяц, год);
IC (Invest Capital) – инвестиционный капитал, первоначальные затраты инвестора в объект вложения.
Существует также следующая разновидность формулы рентабельности инвестиций отражающая случай, когда в объект/проект в течение рассматриваемого периода вносят дополнительные инвестиционные вложения. Поэтому берется средняя стоимость капитала за период. Формула при этом имеет вид:
где:
IC0, IC1 – стоимость инвестиций (затраченного капитала) на начало и конец отчетного периода.
ПРИМЕР РАСЧЕТА КОЭФФИЦИЕНТА РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИЙ (ИНВЕСТИЦИОННОГО ПРОЕКТА) В EXCEL
Для того чтобы лучше понять экономический смысл и алгоритм расчета воспользуемся программой Excel. Затраты, которые понес инвестор были только в первом периоде и составили 130000 руб., денежные поступления от инвестиций изменялись ежемесячно, поэтому мы рассчитываем средние поступления по месяцам. За расчетный период может браться любой временной отрезок, квартал, год. В нашем случае мы получаем месячную рентабельность инвестиционного проекта. Формула расчета в Excel следующая:
В14=СРЗНАЧ(C5:C12)/B5
ЦЕЛИ ИСПОЛЬЗОВАНИЯ КОЭФФИЦИЕНТА РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА
Данный показатель используется для сравнения различных альтернативных инвестиционных проектов. Чем выше ARR, тем выше привлекательность данного проекта для инвестора. Как правило, данный показатель используется для оценки уже существующих проектов, где можно проследить и статистически оценить эффективность создания денежного потока данной инвестиций.
ДОСТОИНСТВА И НЕДОСТАТКИ КОЭФФИЦИЕНТА РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИЙ
Достоинства коэффициента в его простоте расчета и получения и на этом его достоинства заканчиваются. К недостаткам данного коэффициента можно отнести сложность прогнозирования будущих денежных поступлений/доходов от проекта. К тому же если проект венчурный, то данный показатель может сильно исказить картину восприятия проекта. ARR как правило используется для внешней демонстрации успешного того или иного проекта. Показатель в своей формуле не учитывает изменения стоимости денег во времени. Данный показатель может быть использован на первом этапе оценки и отбора инвестиционных проектов.
ДИНАМИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИЙ/ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
Рассмотрим ряд динамических методов оценки инвестиционных проектов, данные показатели используют дисконтирование, что является несомненным преимуществом по отношению к статистическим методам.
ЧИСТЫЙ ДИСКОНТИРОВАННЫЙ ДОХОД (NET PRESENT VALUE)
Чистый дисконтированный доход (англ. Net Present Value, NPV, чистая текущая стоимость, чистый приведенный доход, текущая стоимость) – показатель, отражающий изменение денежных потоков и показывает разность между дисконтированными денежными доходами и расходами.
Чистый дисконтированный доход используют для того чтобы отобрать наиболее инвестиционно привлекательный проект.
ФОРМУЛА ЧИСТОГО ДИСКОНТИРОВАННОГО ДОХОДА
где:
NPV – чистый дисконтированный доход проекта;
CFt – денежный поток в период времени t;
CF0 – денежный поток в первоначальный момент. Первоначальный денежный поток равняется инвестиционному капиталу (CF0 = IC);
r – ставка дисконтирования (барьерная ставка).
ОЦЕНКА ПРОЕКТА НА ОСНОВЕ КРИТЕРИЯ NPV
| Критерий оценки NPV | Заключение по проекту |
| NPV<0 | Инвестиционный проект, имеющий отрицательное значение NPV следует исключить из рассмотрения |
| NPV=0 | Инвестиционный проект обеспечит уровень безубыточности, когда все доходы равны расходам |
| NPV>0 | Инвестиционный проект привлекателен для вложения |
| NPV1>NPV2* | Сравнение NPV одного проекта с NPV* другого, показывает большую инвестиционную привлекательность первого |
ПРИМЕР РАСЧЕТА ЧИСТОГО ДИСКОНТИРОВАННОГО ДОХОДА В EXCEL
Рассмотрим пример расчета чистого дисконтированного дохода в программе Excel. В программе есть удобная функция ЧПС (чистая приведенная стоимость), которая позволяет использовать ставку дисконтирования в расчетах. Рассчитаем ниже в двух вариантах NPV.
Вариант №1
Итак, разберем алгоритм последовательного расчета всех показателей NPV.
- Расчет денежного потока по годам: E7=C7-D7
- Дисконтирование денежного потока по времени: F7=E7/(1+$C$3)^A7
- Суммирование всех дисконтированных денежных поступлений по инвестиционному проекту и вычитание первоначальных капитальных затрат: F16 =СУММ(F7:F15)-B6
Вариант №2
Расчет с использованием встроенной формулы ЧПС. Следует заметить, что необходимо вычесть первоначальные капитальные затраты (В6).
=ЧПС($C$3;E7;E8;E9;E10;E11;E12;E13;E14;E15)-B6
Результаты в обоих методах подсчета NPV, как мы видим, совпадают.
ВНУТРЕННЯЯ НОРМА ПРИБЫЛИ ИНВЕСТИЦИОННОГО ПРОЕКТА
Внутренняя норма прибыли (англ. Internal Rate of Return, IRR, внутренняя норма дисконта, внутренняя норма прибыли, внутренний коэффициент эффективности) – показывает такую ставку дисконтирования, при которой чистый дисконтированный доход равняется нулю.
ФОРМУЛА РАСЧЕТА ВНУТРЕННЕЙ НОРМЫ ПРИБЫЛИ ИНВЕСТИЦИОННОГО ПРОЕКТА
где:
CF (Cash Flow) – денежный поток, который создается объектом инвестиций;
IRR – внутренняя норма прибыли;
CF0 – денежный поток в первоначальный момент. В первом периоде, как правило, денежный поток равняется инвестиционному капиталу (CF0 = IC).
ПРИМЕР РАСЧЕТА IRR ИНВЕСТИЦИОННОГО ПРОЕКТА В EXCEL
Рассмотрим пример расчета внутренней нормы прибыли в Excel, в программе есть хорошая функция ВСД (внутренняя ставка доходности), которая позволяет быстро рассчитать IRR. Данную функцию корректно использовать в том случае если есть хотя бы один положительный и отрицательный денежный поток.
E16 =ВСД(E6:E15)
ДОСТОИНСТВА И НЕДОСТАТКИ ВНУТРЕННЕЙ НОРМЫ ДОХОДНОСТИ IRR
+ ) возможность сравнения инвестиционных проектов между собой, имеющих разный горизонт инвестирования;
+ )возможность сравнения не только проектов, но и альтернативных инвестиций, например банковский вклад. Если IRR проекта составляет 25%, а банковский вклад равен 15%, то проект более инвестиционно привлекателен.
+ ) экспресс-оценка проекта на его целесообразность дальнейшего развития.
Внутреннюю норму прибыли оценивают со средневзвешенной стоимостью привлеченного капитала, что позволяет сделать оценку целесообразности дальнейшего развития проекта.
| Оценка значений коэффициента IRR | Заключение по проекту |
| IRR > WACC | Вложенный в инвестиционный проект капитал будет создавать доходность выше, чем стоимость вложенного капитала. Такой проект инвестиционно привлекателен |
| IRR = WACC | Проект не принесет ни убытков, ни дохода в будущем периоде и такой проект не является привлекательным |
| IRR < WACC | Такой проект будет создавать отрицательный дисконтированный денежный поток в будущем |
— ) не отражен абсолютный рост стоимости инвестиционного проекта;
— ) денежные потоки часто имеют не систематическую структуру, что затрудняет правильный расчет данного показателя.
ИНДЕКС ПРИБЫЛЬНОСТИ ИНВЕСТИЦИЙ (PROFITABILITY INDEX)
Индекс прибыльность инвестиций (англ. Profitability index, PI, индекс доходности, индекс рентабельности) – показатель эффективности инвестиций, показывающий отдачу (доходность) вложенного капитала. Индекс прибыли представляет собой отношение дисконтированной стоимости будущих денежных потоков к стоимости первоначальных инвестиций. Экономический смысл данного коэффициента – это оценка дополнительной ценности на каждый вложенный рубль.
ФОРМУЛА РАСЧЕТА ИНДЕКСА ПРИБЫЛЬНОСТИ ИНВЕСТИЦИЙ
где:
NPV – чистый дисконтированный доход;
n – срок реализации проекта;
r – ставка дисконтирования (%);
IC – вложенный (затраченный) инвестиционный капитал.
РАЗНОВИДНОСТЬ ФОРМУЛЫ ИНДЕКСА ПРИБЫЛЬНОСТИ ИНВЕСТИЦИЙ
Если вложения в проект осуществляются не единовременно, а на протяжении всего времени реализации, то необходимо инвестиционный капитал (IC) привести к единой стоимости, т.е. дисконтировать его. Формула в этом случае станет иметь следующий вид:
Чем выше коэффициент прибыльности инвестиций, тем большую отдачу на вложенный капитал приносит данная инвестиция. Данный критерий используется для сравнения между собой нескольких инвестиционных проектов. На практике большой индекс прибыли не всегда показывает эффективность проекта, ведь в таком случае оценка будущих доходов могла быть завышена или периодичность их получения не правильно оценена.
ОЦЕНКА ПРОЕКТА НА ОСНОВЕ КРИТЕРИЯ PI
| Критерий оценки PI | Заключение по выбору проекта |
| PI<1 | Инвестиционный проект не сможет возместить в полном размере вложенные в него капитальные затраты |
| PI=1 | Инвестиционный проект имеет доходность равную выбранной ставки дисконтирования |
| PI>1 | Проект инвестиционно привлекателен для вложения, так как сможет обеспечить дополнительную отдачу капитала. |
| PI1>PI2* | Сравнение между собой инвестиционной привлекательности нескольких проектов. Первый проект имеет большую рентабельность, поэтому второй будет отброшен |
ПРИМЕР РАСЧЕТА ИНДЕКСА ПРИБЫЛЬНОСТИ ПРОЕКТА В EXCEL
Рассмотрим на примере вычисление индекса прибыльности. На рисунке ниже показан расчет PI в ячейке F18.
- Расчет столбца F – Дисконтированного денежного потока =E7/(1+$C$3)^A7
- Расчет чистого дисконтированного дохода NPV в ячейке F16 =СУММ(F7:F15)-B6
- Оценка прибыльности инвестиций в ячейке F18 =F16/B6
Если бы инвестиционные затраты были каждый год, то необходимо было индекс прибыльности рассчитывать по второй формуле и приводить их к настоящему времени (дисконтировать).
ДИСКОНТИРОВАННЫЙ СРОК ОКУПАЕМОСТИ ИНВЕСТИЦИЙ
Дисконтированный срок окупаемости (англ. Discounted Payback Period, DPP) – показатель отражающий период, через который окупятся первоначальные инвестиционные затраты. Формула расчета коэффициента аналогична формуле оценки периода окупаемости инвестиций, только используется дисконтирование
ФОРМУЛА РАСЧЕТА ДИСКОНТИРОВАННОГО СРОКА ОКУПАЕМОСТИ ИНВЕСТИЦИЙ
где:
IC (Invest Capital)– инвестиционный капитал, первоначальные затраты инвестора в объект вложения;
CF (Cash Flow) – денежный поток, который создается объектом инвестиций;
r – ставка дисконтирования;
t –период оценки получаемого денежного потока.
ПРИМЕР РАСЧЕТА ДИСКОНТИРОВАННОГО СРОКА ОКУПАЕМОСТИ ИНВЕСТИЦИЙ В EXCEL
Рассчитаем коэффициент дисконтированного срока окупаемости инвестиций в Excel. На рисунке ниже показан пример расчета. Для этого необходимо выполнить следующие операции:
- Рассчитать дисконтированный денежный поток в колонке D =C7/(1+$C$3)^A7
- Посчитать нарастающим итогом прирост капитала в колоне E =E7+D8
- Оценить в какой период вложенные инвестиции (IC) окупились полностью.
Как мы видим окупаемость всех затрат дисконтированным денежным потоком произошла на 6 месяц. Чем меньше период окупаемости инвестиционного проекта, тем более привлекательны данные проекты.
ДОСТОИНСТВА И НЕДОСТАТКИ ДИСКОНТИРОВАННОГО СРОКА ОКУПАЕМОСТИ
Достоинством коэффициента является возможность использовать в формуле свойство денег изменять свою стоимость со временем за счет инфляционных процессов. Это повышает точность оценки периода возврата вложенного капитала. Сложность использования данного коэффициента заключаются в точном определении будущих денежных поступлений от инвестиции и оценке ставки дисконтирования. Ставка может изменяться на всем жизненном цикле инвестиции из-за действия различных экономических, политических, производственных факторов.
На рисунке ниже показана таблица критериев выбора инвестиционного проекта/инвестиции на основе рассмотренных коэффициентов. Данные показатели позволяют дать экспресс-оценку привлекательности проекта. Следует заметить, что данные показатели плохо применяются для оценки венчурных проектов, потому что сложно спрогнозировать какие будут продажи, доходы и спрос в этом проекте. Показатели хорошо себя зарекомендовали в оценке уже реализованных проектов с четко выстроенными бизнес процессами.
| Показатель | Критерий выбора инвестиции |
| Статистические методы оценки эффективности инвестиций | |
| Период окупаемости | PP -> min |
| Рентабельность инвестиционного капитала | ARR>0 |
| Динамические методы оценки эффективности инвестиций | |
| Чистый дисконтированный доход | NPV>0 |
| Внутренняя норма прибыли | IRR>WACC |
| Индекс прибыльности | PI>1 |
| Дисконтированный период окупаемости | DPP -> min |
Резюме
Использование коэффициентов оценки инвестиционных проектов позволяет сделать выбрать наиболее привлекательные объекты для вложения. Мы рассмотрели как статистические, так и динамические методы оценки, на практике, первые подходят для отражения общей характеристики объекта, тогда как динамические позволяют более точно оценить параметры инвестиции.Помимо внешних факторов, на оценку влияют внутренние – сложность точного определения будущих денежных поступлений от проекта. Показатели дают в большей степени финансовое описание жизни инвестиции и не раскрывают причинно-следственных связей с получаемыми доходами (сложно оценить венчурные проекты и стартапы ).
За материалы спасибо Жданов Иван
Для привлечения и вложения средств в какое-либо дело инвестору необходимо тщательно изучить внешний и внутренний рынок.
На основании полученных данных составить смету проекта, инвестиционный план, спрогнозировать выручку, сформировать отчет о движении денежных средств. Наиболее полно всю нужную информацию можно представить в виде финансовой модели.
Финансовая модель инвестиционного проекта в Excel
Составляется на прогнозируемый период окупаемости.
Основные компоненты:
- описание макроэкономического окружения (темпы инфляции, проценты по налогам и сборам, требуемая норма доходности);
- прогнозируемый объем продаж;
- прогнозируемые затраты на привлечение и обучение персонала, аренду площадей, закупку сырья и материалов и т.п.;
- анализ оборотного капитала, активов и основных средств;
- источники финансирования;
- анализ рисков;
- прогнозные отчеты (окупаемость, ликвидность, платежеспособность, финансовая устойчивость и т.д.).
Чтобы проект вызывал доверие, все данные должны быть подтверждены. Если у предприятия несколько статей доходов, то прогноз составляется отдельно по каждой.
Финансовая модель – это план снижения рисков при инвестировании. Детализация и реалистичность – обязательные условия. При составлении проекта в программе Microsoft Excel соблюдают правила:
- исходные данные, расчеты и результаты находятся на разных листах;
- структура расчетов логичная и «прозрачная» (никаких скрытых формул, ячеек, цикличных ссылок, ограниченное количество имен массивов);
- столбцы соответствуют друг другу;
- в одной строке – однотипные формулы.
Расчет экономической эффективности инвестиционного проекта в Excel
Для оценки эффективности инвестиций применяются две группы методов:
- статистические (PP, ARR);
- динамические (NPV, IRR, PI, DPP).
Срок окупаемости:
Коэффициент PP (период окупаемости) показывает временной отрезок, за который окупятся первоначальные вложения в проект (когда вернутся инвестированные деньги).
Экономическая формула расчета срока окупаемости:
где IC – первоначальные вложения инвестора (все издержки),
CF – денежный поток, или чистая прибыль (за определенный период).
Расчет окупаемости инвестиционного проекта в Excel:
- Составим таблицу с исходными данными. Стоимость первоначальных инвестиций – 160000 рублей. Ежемесячно поступает 56000 рублей. Для расчета денежного потока нарастающим итогом была использована формула: =C4+$C$2.
- Рассчитаем срок окупаемости инвестированных средств. Использовали формулу: =B4/C2 (сумма первоначальных инвестиций / сумма ежемесячных поступлений).
Так как у нас дискретный период, то срок окупаемости составит 3 месяца.
Данная формула позволяет быстро найти показатель срока окупаемости проекта. Но использовать ее крайне сложно, т.к. ежемесячные денежные поступления в реальной жизни редко являются равными суммами. Более того, не учитывается инфляция. Поэтому показатель применяется вкупе с другими критериями оценки эффективности.
Рентабельность инвестиций
ARR, ROI – коэффициенты рентабельности, показывающие прибыльность проекта без учета дисконтирования.
Формула расчета:
где CFср. – средний показатель чистой прибыли за определенный период;
IC – первоначальные вложения инвестора.
Пример расчета в Excel:
- Изменим входные данные. Первоначальные вложения в размере 160 000 рублей вносятся только один раз, на старте проекта. Ежемесячные платежи – разные суммы.
- Рассчитаем средние поступления по месяцам и найдем рентабельность проекта. Используем формулу: =СРЗНАЧ(C23:C32)/B23. Формат ячейки с результатом процентный.
Чем выше коэффициент рентабельности, тем привлекательнее проект. Главный недостаток данной формулы – сложно спрогнозировать будущие поступления. Поэтому показатель часто применяется для анализа существующего предприятия.
Примеры инвестиционне6ого проекта с расчетами в Excel:
- скачать полный инвестиционный проект
- скачать сокращенный вариант в Excel
Статистические методы не учитывают дисконтирование. Зато позволяют быстро и просто найти необходимые показатели.