Итерационный метод решения матричных игр excel

Решим, используя надстройку
«Поиск решения» Excel игру, заданную
матрицей

.

Нижняя
и верхняя цены игры:

=
max(l;3)
= 3;

не совпадают, поэтому применяем смешанные
стратегии.

Для
нахождения оптимальной стратегии
первого игрока решаем задачу линейного
программирования: найти
минимальное значение функциипри ограничениях

,

;

,.

Здесь
,

где
вероятность выбора первой строкивероятность выбора второй строки,цена игры.

Для
ее решения на рабочем листе Excel выполним
указанный выше алгоритм. Вводим исходные
данные в виде таблицы

	A	B	C	D
1	u1	u2	L
2
3	1	1
4	1	6		1
5	9	3		1

Вводим зависимости для целевой функции
и системы ограничений. Для этого в ячейку
С2 вводим формулу =СУММПРОИЗВ(A2:B2;A3:B3). В
ячейки С4 и С5 соответственно формулы:
=СУММПРОИЗВ(A2:B2;A4:B4) и =СУММПРОИЗВ(A2:B2;A5:B5).
В результате получаем таблицу.

	A	B	C	D
1	u1	u2	L
2			0
3	1	1
4	1	6	0	1
5	9	3	0	1

Запускаем команду «Поиск решения» и
заполняем появившееся окно Поиск
решения следующим образом. В поле
«Оптимизировать целевую функцию» вводим
ячейку С2. Выбираем оптимизации значения
целевой ячейки «Минимум».

В поле «Изменяя ячейки переменных»
вводим изменяемые ячейки A2:B2. В поле «В
соответствии с ограничениями» вводим
заданные ограничения с помощью кнопки
«Добавить». Ссылки на ячейку $C$4:$C$5
Ссылки на ограничения =$D$4:$D$5 между ними
знак => затем кнопку «ОК».

Ставим флажок в поле «Сделать переменные
без ограничений неотрицательными».
Выбрать метод решения «Поиск решения
линейных задач симплекс-методом».

Нажатием кнопки «Найти решение»
запускается процесс решения задачи. В
итоге появляется диалоговое окно
«Результаты поиска решения» и исходная
таблица с заполненными ячейками для
значений переменных и оптимальным
значением целевой функции.

	A	B	C	D
1	u1	u2	L
2	0,058824	0,156863	0,215686
3	1	1
4	1	6	1	1
5	9	3	1	1

В диалоговом окне «Результаты поиска
решения» сохраняем результат u1=0,058824,
u2=0,156863,
L=0,215686-равный
минимальному значению целевой функции.
Заметим, что нужное количество знаков
после запятой можно ввести, выбрав
команду Формат ячеек.

Так
как
и,,
то находим, что=4,63637,=0,2727280,27,=0,7272740,73
с такими вероятностями первый игрок
должен выбирать первую и вторую строки.

Находим
оптимальную стратегию второго игрока,
т.е. находим наибольшее
значение функции
и соответствующие значения
неотрицательных переменных
,,
если выполняются
неравенства:

Здесь
,

где
вероятность выбора первогостолбцавероятность выбора второго столбца,цена игры.

Решение этой задачи с использованием
надстройки «Поиск решения» Excel дано в
таблице

	A	B	C	D
1	t1	t2	L
2	0,117647	0,098039	0,215686
3	1	1
4	1	9	1	1
5	6	3	1	1

Так
как
и,,
то находим, что=4,63637,=0,5454550,55,=0,4545460,45
с такими вероятностями второй игрок
должен выбирать первый столбец и второй.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Найдиготовую курсовую работувыполненное домашнее заданиерешённую задачуготовую лабораторную работунаписанный рефератподготовленный докладготовую ВКРготовую диссертациюготовую НИРготовый отчёт по практикеответы и шпаргалкиполные лекцииполные семинарызаполненную рабочую тетрадьподготовленную презентациюпереведённый текстнаписанное изложениенаписанное сочинениеготовую статью

Ответы на популярные вопросы

Отзывы студентов

Добавляйте материалы
и зарабатывайте!

Продажи идут автоматически

Обучение Подробнее

Решение систем линейных алгебраических уравнений в Excel

1. Метод обратной матрицы (решение в Excel)

Если дано уравнение:
A*X = B, где A — квадратная матрица, X,B — вектора;
причем B — известный вектор (т е столбец чисел), X — неизвестный вектор,
то решение X можно записать в виде:
X = A -1 *B, где A -1 — обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы (или матрица на вектор) — функцией МУМНОЖ().

Имеются «тонкости» использования этих матричных действий в Excel. Так, чтобы вычислить обратную матрицу от матрицы А, нужно: Чтобы умножить матрицу на вектор: Есть и другой спососб, при котором используется кнопка построителя функции Excel.

Пример СЛАУ 4-го порядка

Скачать документ Excel, в котором этот пример решён различными методами.

2. Метод Гаусса

Краткое описание.

1. Решаю систему уравнений: A*X=B, где A — квадратная матрица n-го порядка, X,B — вектора
2. К матрице A справа приписываю вектор B. Получаю расширенную матрицу A
3. В дальнейшем A обозначает расширенную матрицу (n строк, n+1 столбец)
4. Aij — обозначает элемент матрицы, находящийся на i-й строке и j-м столбце
5. Делю 1-ю строку на A11, т е A’1j = A1j/A11 (j = 1..n+1). В результате A’11 = 1. A’ обозначает преобразованную строку
6. Преобразую остальные строки по формуле: A’ij = Aij — A’1j*Ai1 (i = 2..n; j = 1..n+1)
7. В результате 1-й столбец в строках 2..n заполнится нулями
8. Отметим, что все эти преобразования не нарушают правильность уравнений
9. Аналогичные действия проводим для обнуления 2-го столбца в строках 3..n, то есть:
10. Делю 2-ю строку на A’22, т е A»2j = A’2j/A’22 (j = 2..n+1). В результате A»22 = 1. A» обозначает резельтат 2-го преобразования строки
11. Преобразую остальные строки по формуле: A»ij = A’ij — A»2j*A’i2 (i = 3..n; j = 2..n+1)
12. В результате 2-й столбец в строках 3..n заполнится нулями
13. Аналогичные действия проводим далее
14. В результате левые n столбцов матрицы A превращаютс в верхнюю треугольную матрицу, т е ниже главной диагонали находятся только нули (а на главной диагонали — единицы) — см Рис 1. На этом рисунке вектор B — слева, S — номер шага
15. Затем выполняется «обратный ход», начиная с нижней строки, из которой можно вычислить Xn = Bn/Ann, например: Х4 = 9,55741/68,6388 = 0,13924 (рис. 1)
16. Затем можно вычислить X3 = (0,9065 — 2,40919*0,13924) = 0,57059
17. Затем из второй строки: X2 + 2,83562*X3 + 8,17808*X4 = 2,47945 вычисляю X2, и т д

3. Метод Якоби (метод простых итераций)

Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.

Далее номер в скобках означает номер строки. Новую первую строку получаю сложением старой первой строки с другими строками, умноженными на специально подобранные коэффициенты. Записываю это в виде формулы:

Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:

Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид :

А вектор В2:


Скачать

Решение линейных уравнений методом простой итерации c помощью программы Microsoft Excel

Страницы работы

Содержание работы

Министерство общего образования

Уральский государственный технический университет-УПИ

филиал в г.Краснотурьинске

Кафедра вычислительной техники

По численным методам

Решение линейных уравнений методом простой итерации

c помощью программы Microsoft Excel

Руководитель Кузьмина Н.В.

Студент Нигматзянов Т.Р.

Тема: «Нахождение с заданной точностью корня уравнения F(x)=0 на промежутке [a;b] методом простой итерации».

Контрольный пример: 0,25-х+sinx=0

Условия задачи: для заданной функции F(x) на интервале [0,5;2] найти корень уравнения F(x)=0 методом простой итерации.

Корень вычислить дважды(с помощью автоматического и ручного расчета).

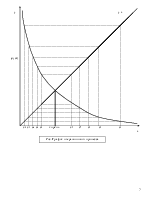
Предусмотреть построение графика функции на заданном интервале.

1.Теоретическая часть 5

2.Описание хода работы 7

3.Входные и выходные данные 8

Библиографический список 12

В ходе данной работы мне необходимо ознакомиться с различными методами решения уравнения и найти корень нелинейного уравнения 0,25-х+sin(x)=0 численным методом – методом простой итерации. Для проверки правильности нахождения корня необходимо решить уравнение графически ,найти приближенное значение и сравнить его с полученным результатом.

Метод простой итерации.

Итерационный процесс состоит в последовательном уточнении начального приближения х0 (корня уравнения). Каждый такой шаг называется итерацией.

Для использования этого метода исходное нелинейное уравнение записывается в виде: х=j(х), т.е. выделяется х; j(х) – непрерывна и дифференцируема на интервале (а; в). Обычно это можно сделать несколькими способами:

arcsin(2x+1)-x 2 =0 (f(x)=0)

x=0.5(sinx 2 -1) (x=j(x))

x=x+arcsin(2x+1)-x 2 (x=j(x))

x= 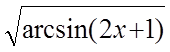(x=j(x)),знак берется в зависимости от интервала [а;b].

Преобразование должно быть таким, чтобы ½j(x)

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Решение систем линейных уравнений методом итераций в экселе

Найдем корень нелинейного уравнения в табличном процессоре Excel методом итерации с использованием циклических ссылок. Для включения режима циклических вычислений в Excel 2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле «Включить итеративные вычисления».

M – максимальное значение производной на промежутке (по модулю). Найдем М, для этого вычислим

Т. к. значение производных Меню сайта

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)