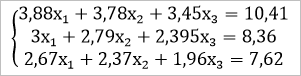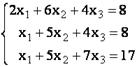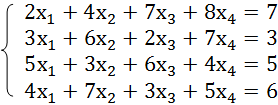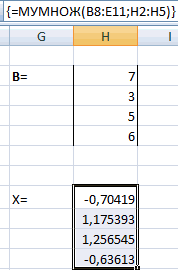Содержание
- Варианты решений
- Способ 1: матричный метод
- Способ 2: подбор параметров
- Способ 3: метод Крамера
- Способ 4: метод Гаусса
- Вопросы и ответы
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
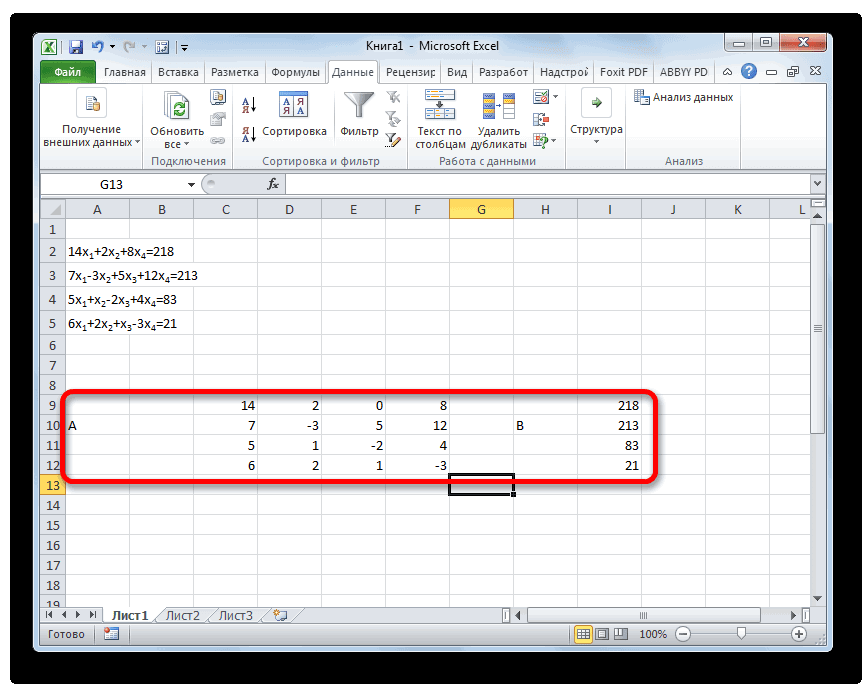
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
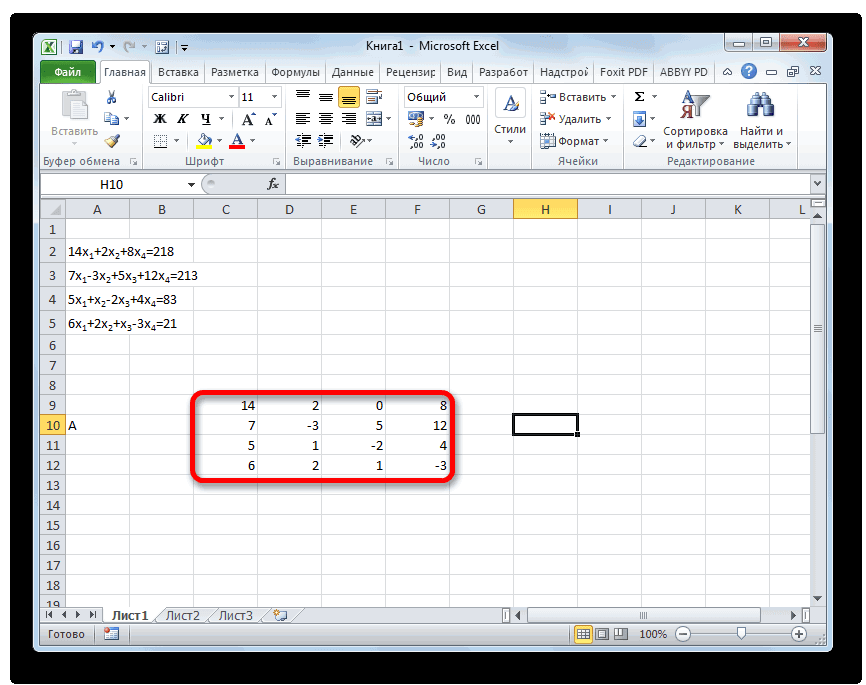
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
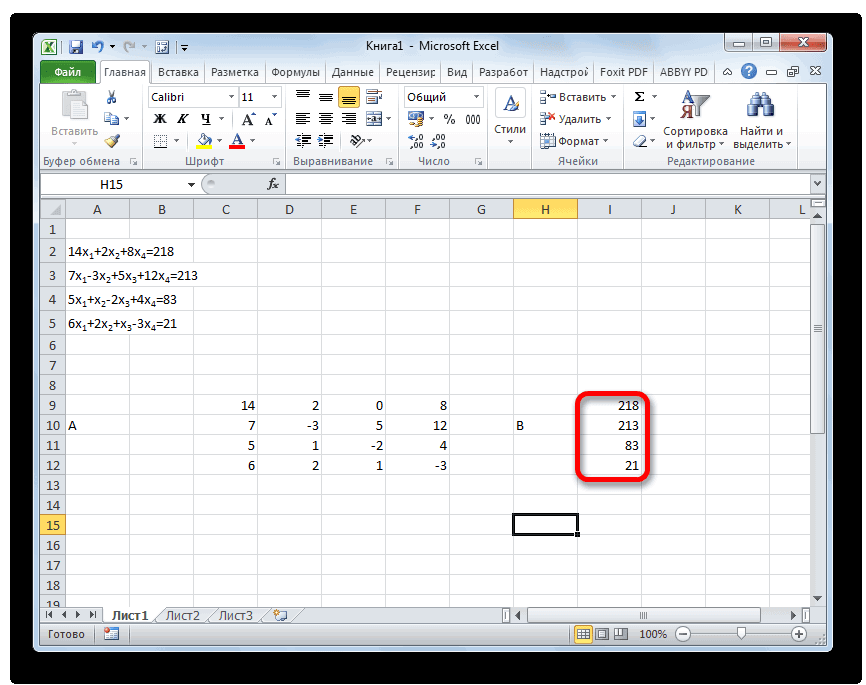
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
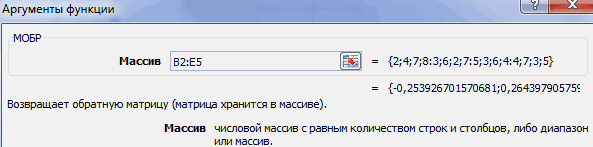
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
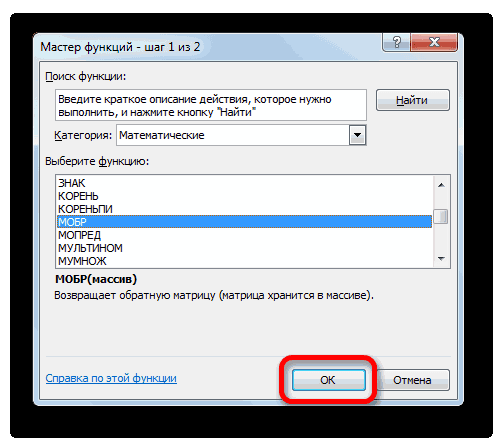
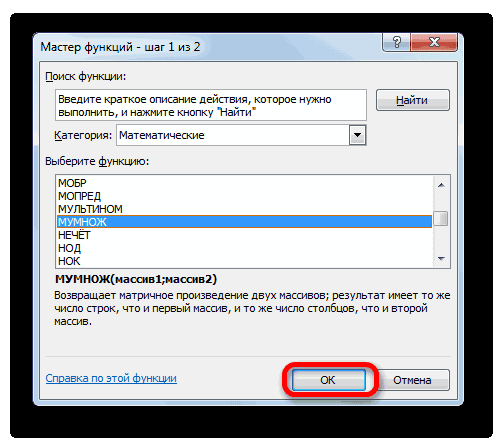
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
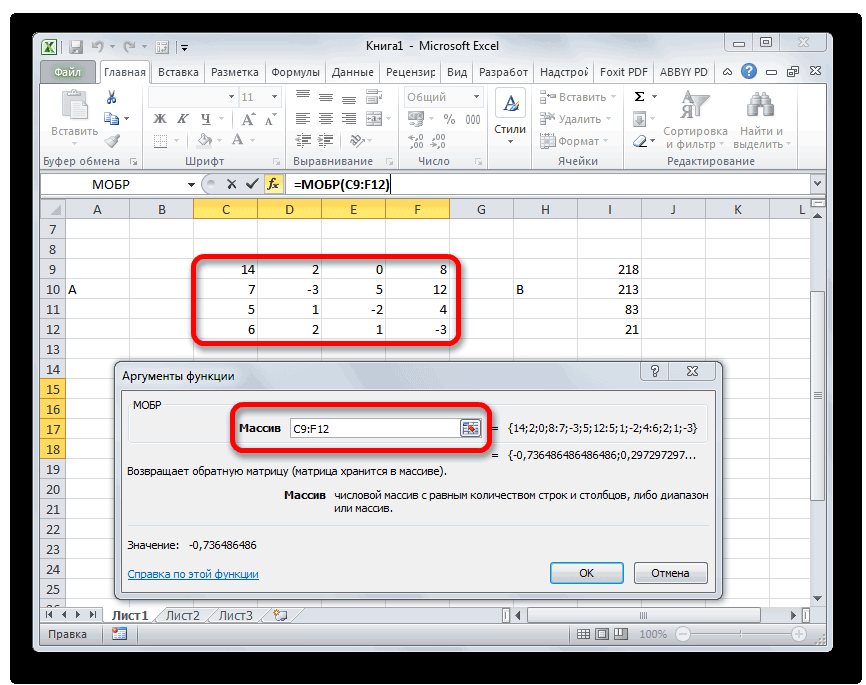
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
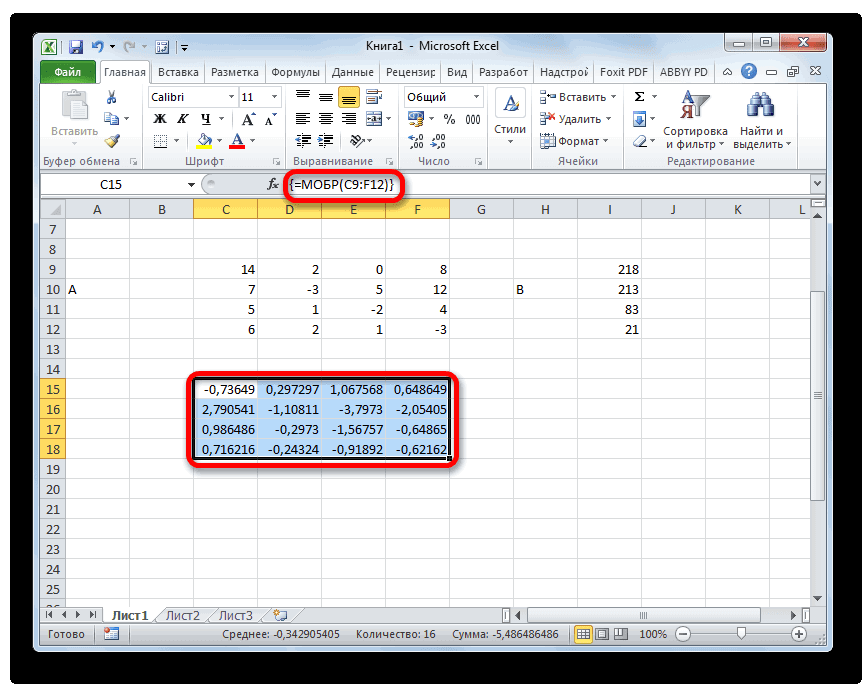
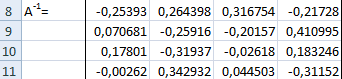
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
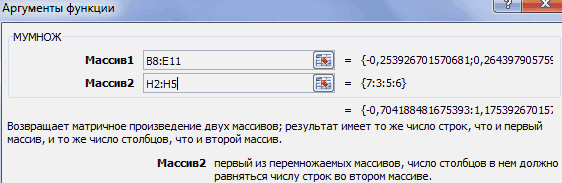
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
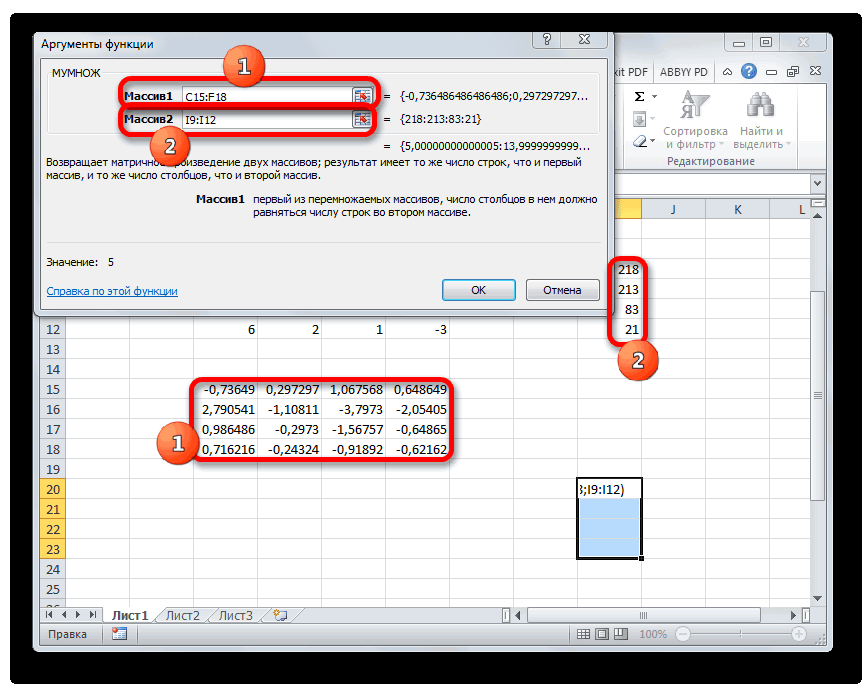
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
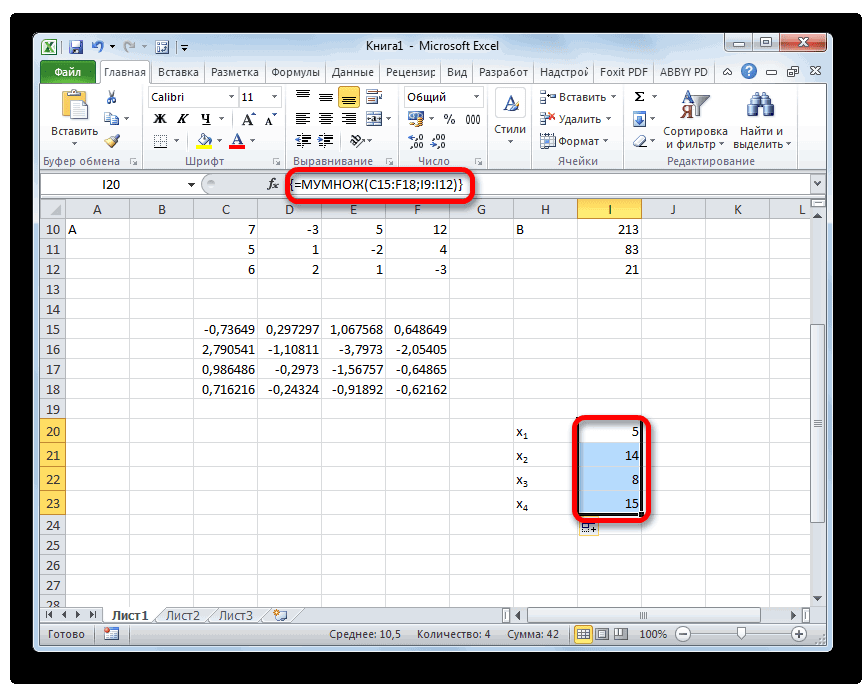
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
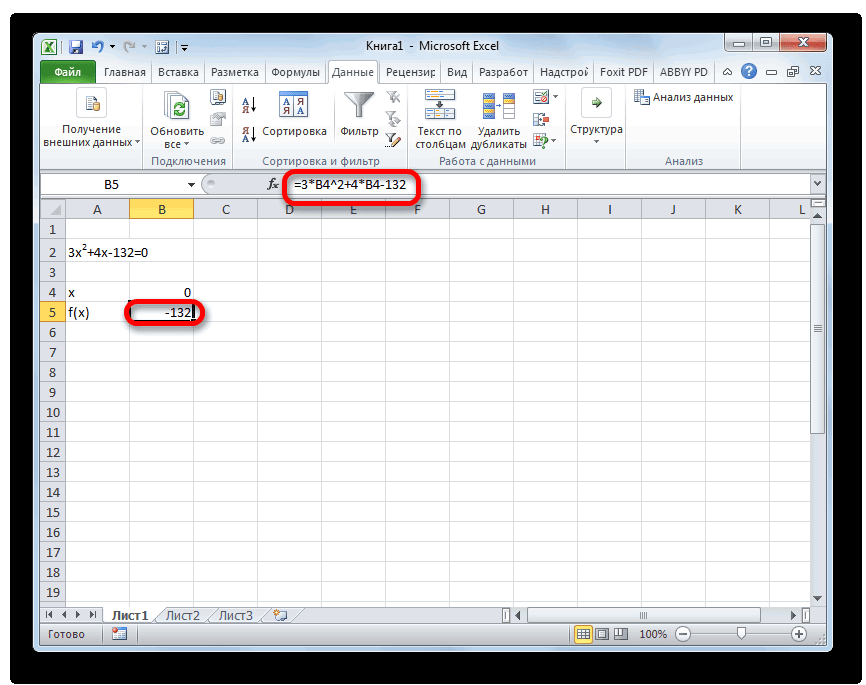
3x^2+4x-132=0
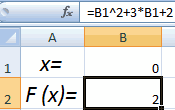
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
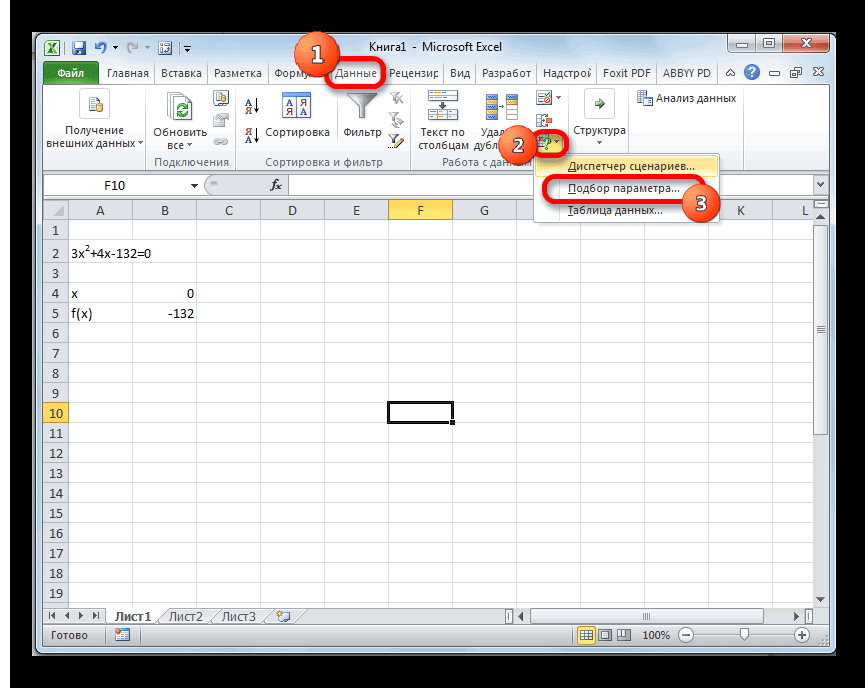
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
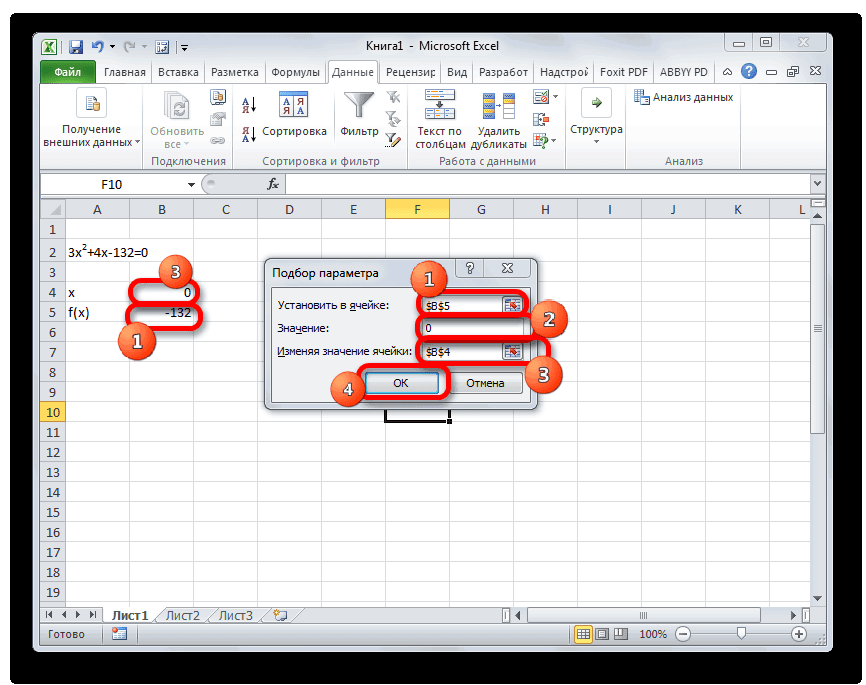
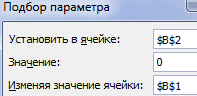
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
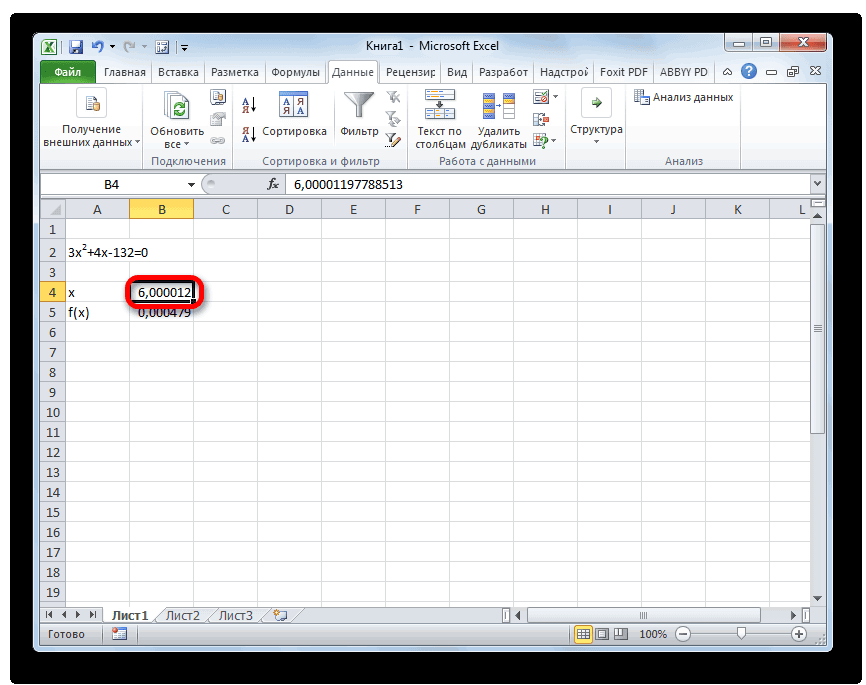
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
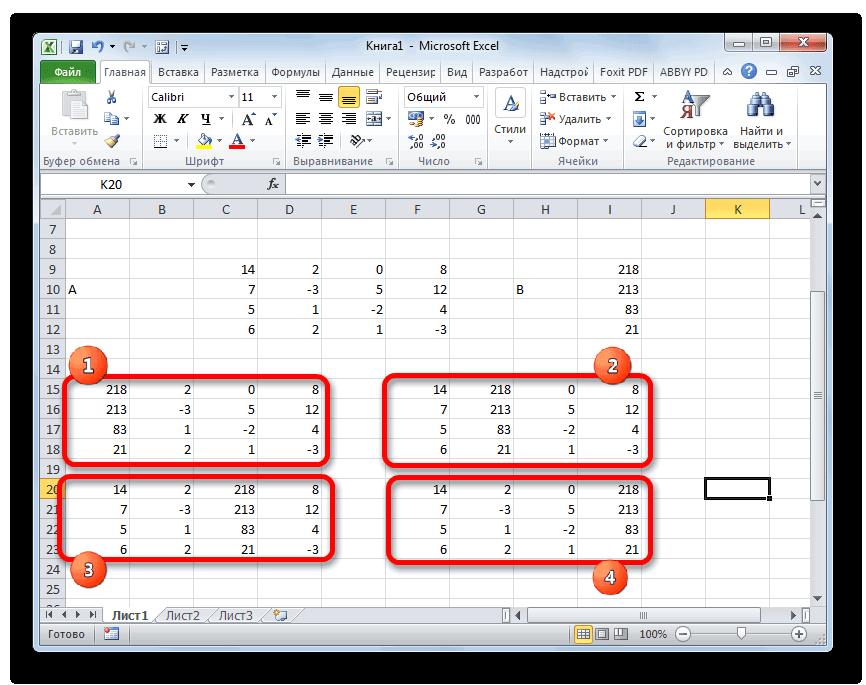
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
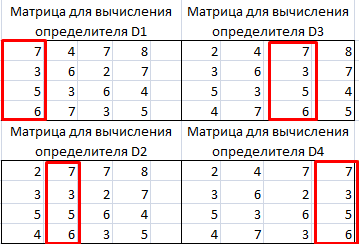
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
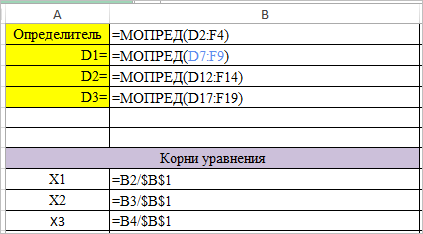
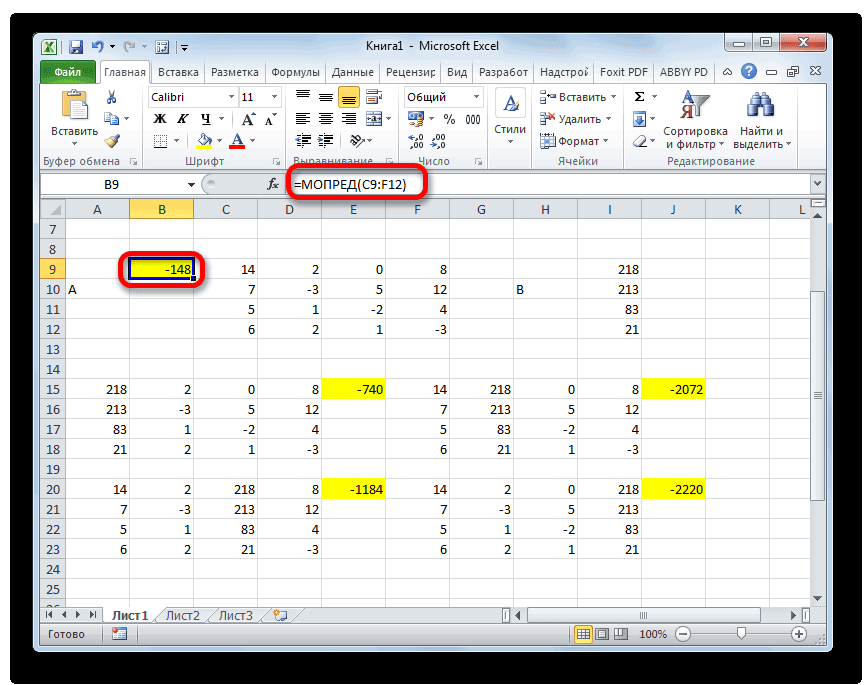
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
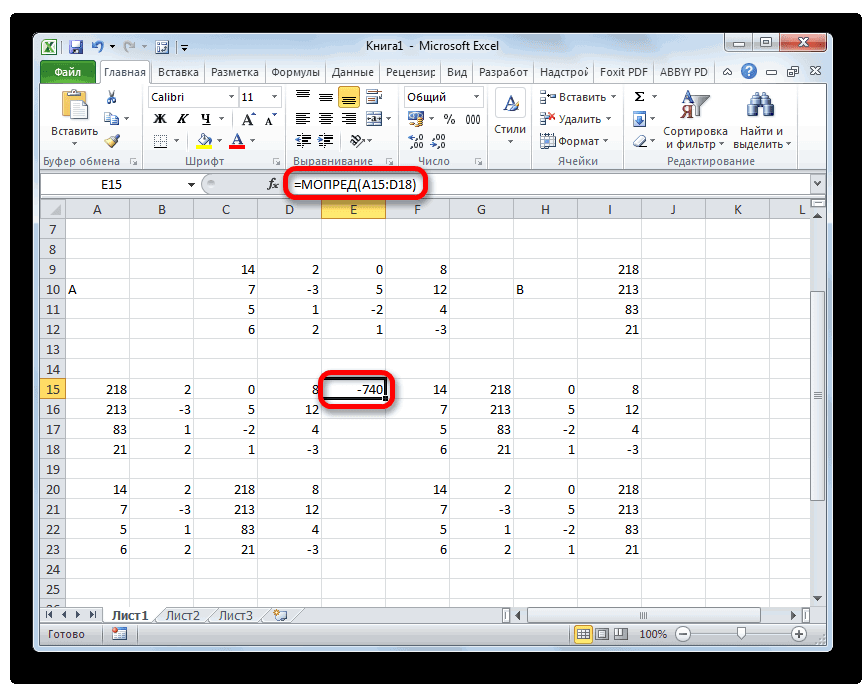
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
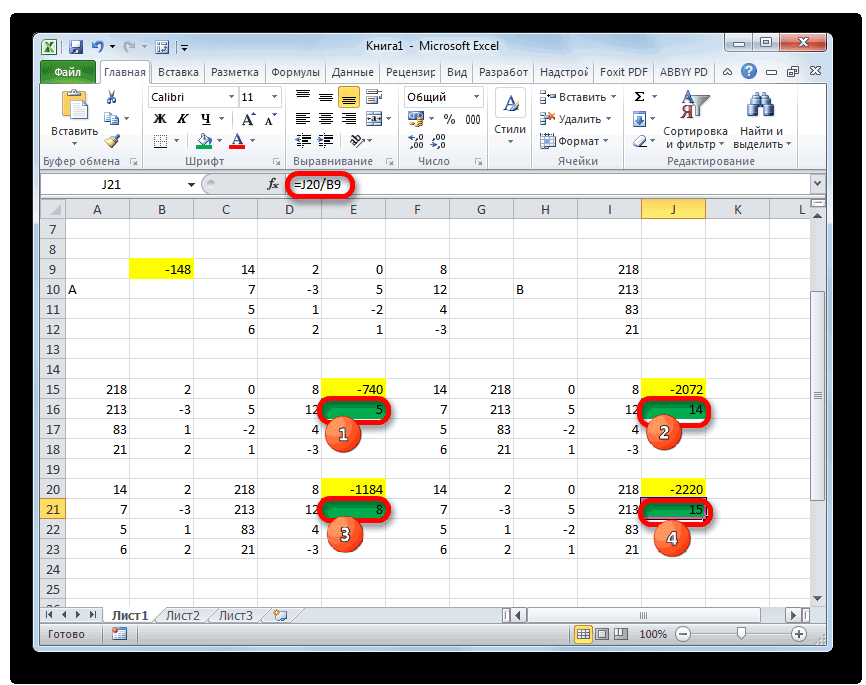
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
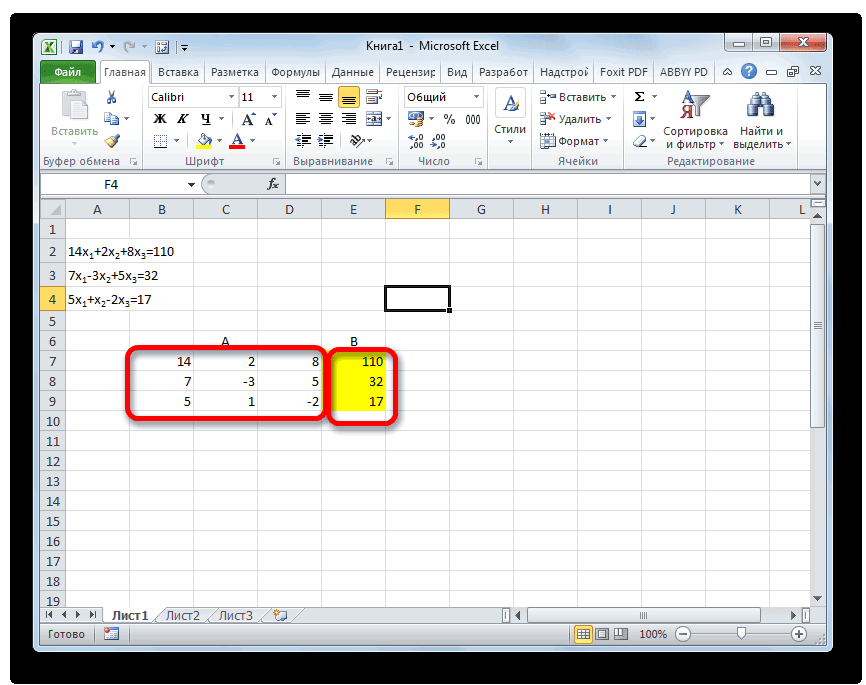
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
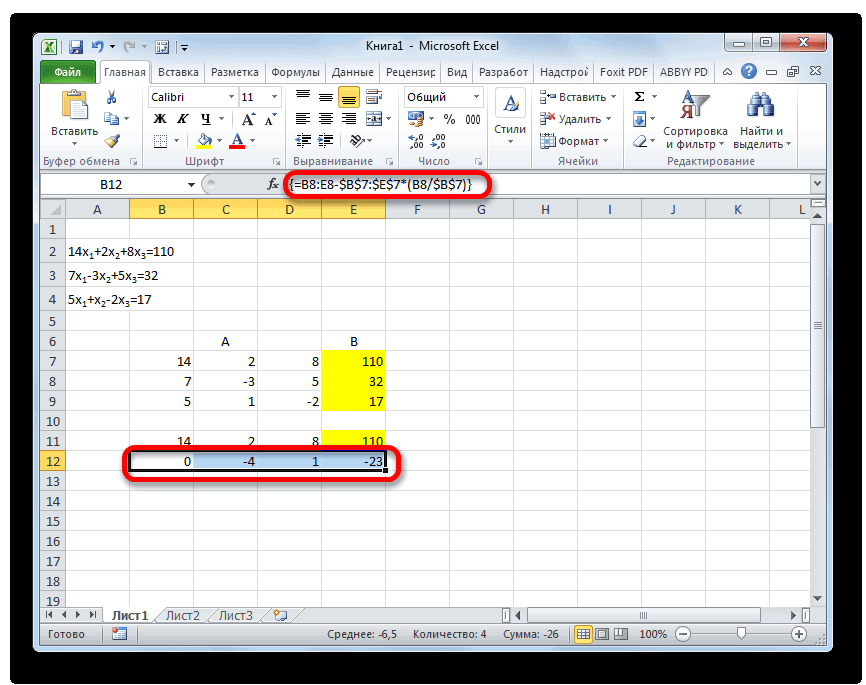
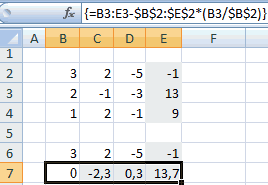
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
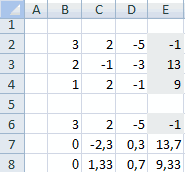
- После этого копируем полученную строку и вставляем её в строчку ниже.
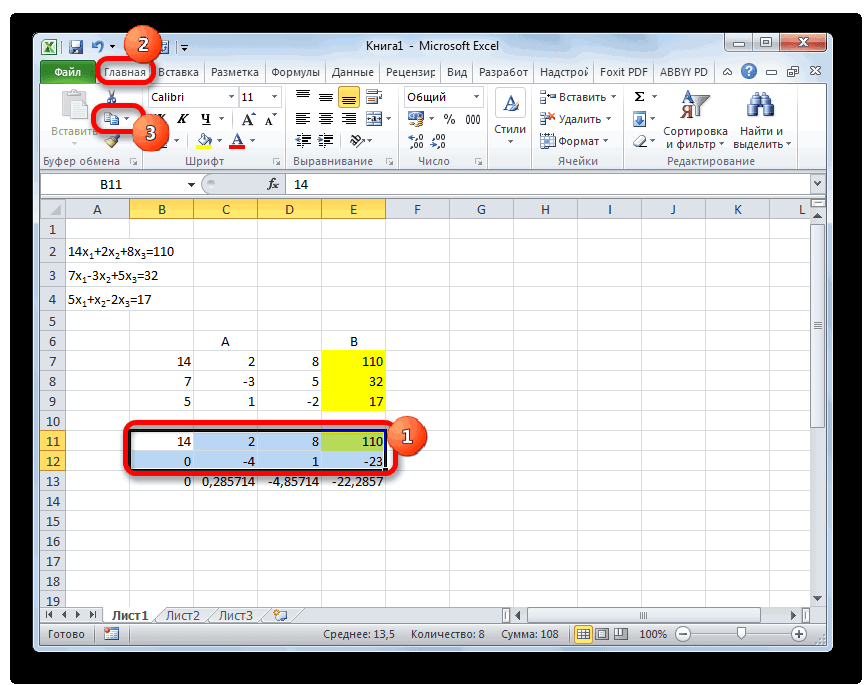
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
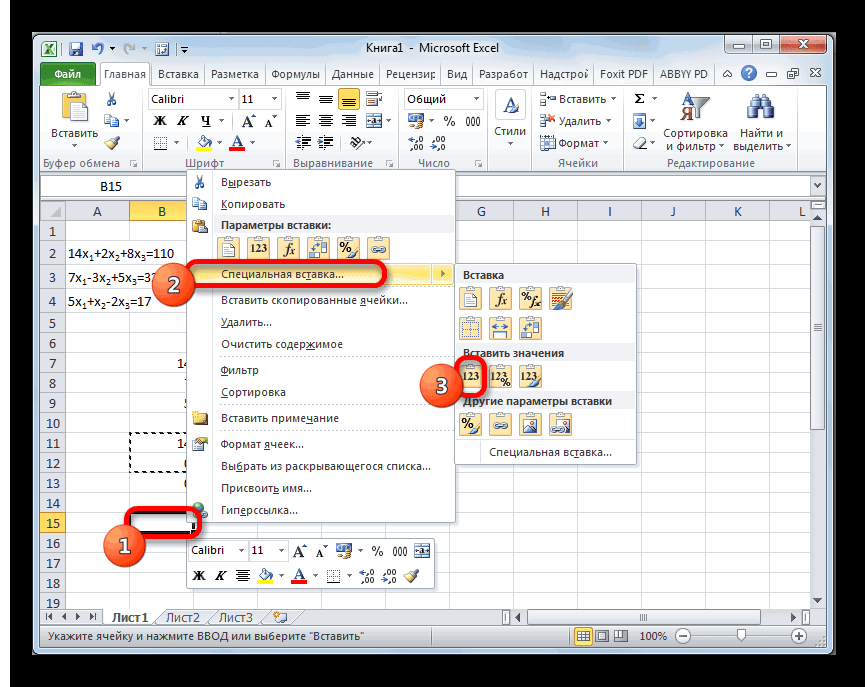
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
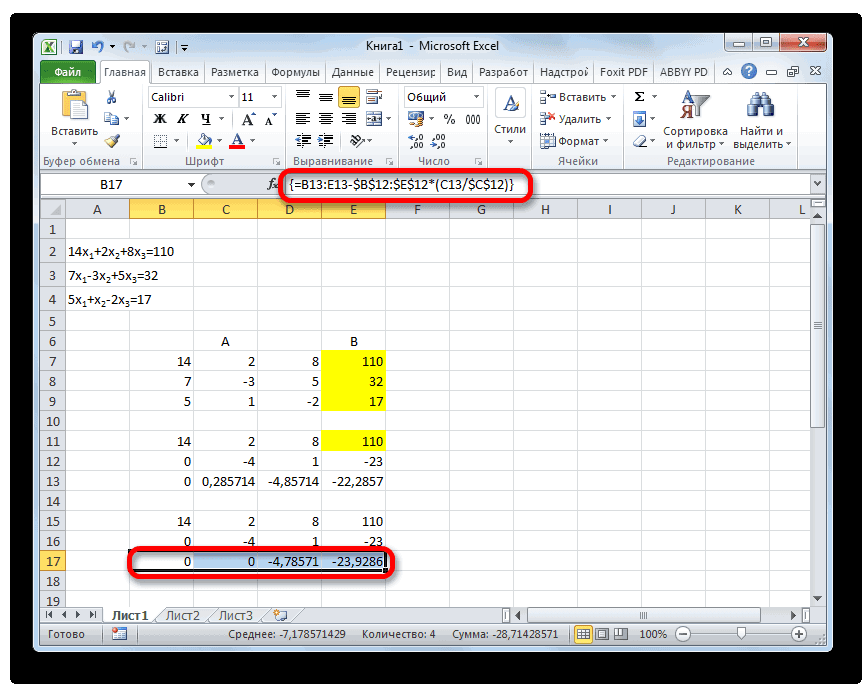
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
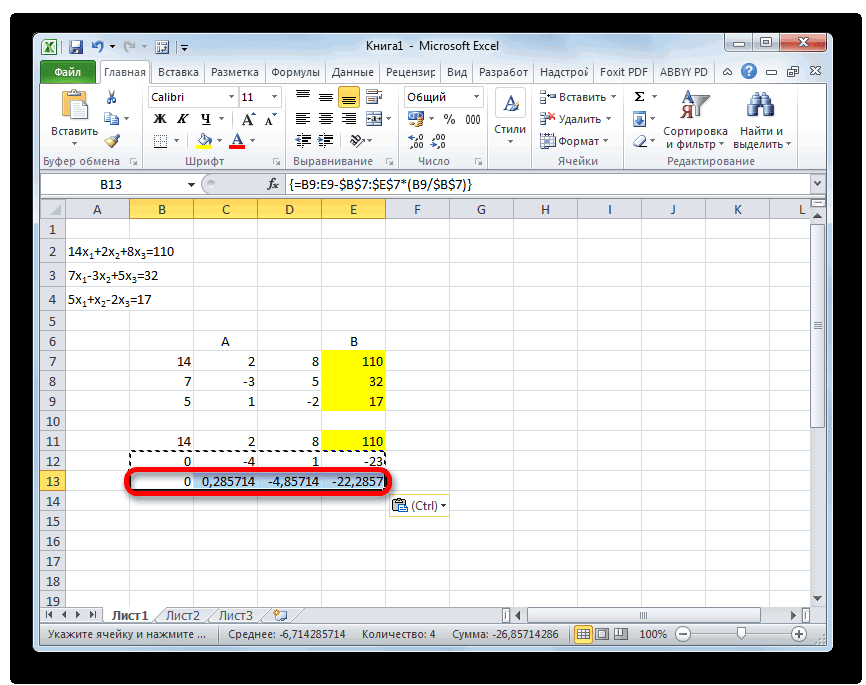
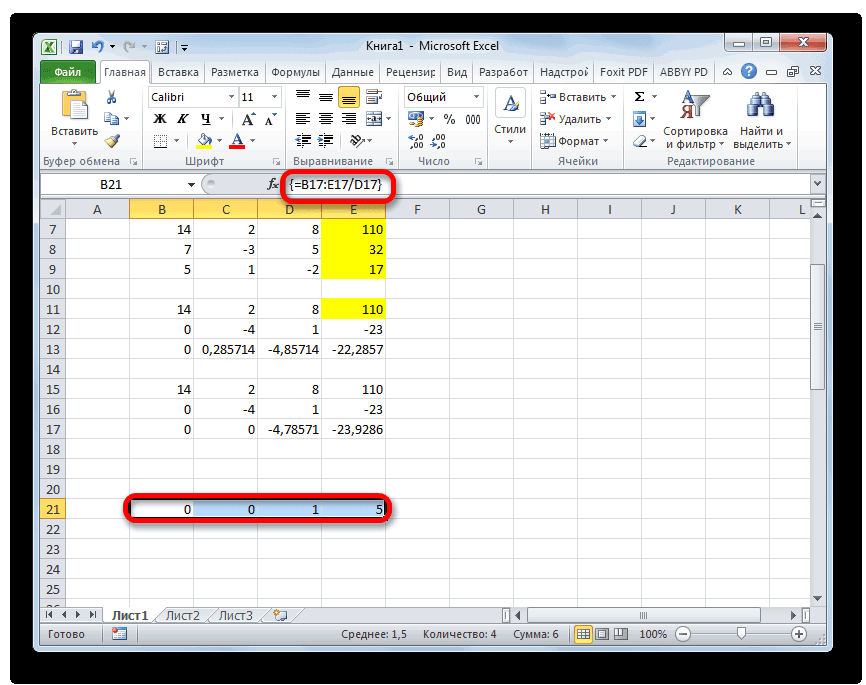
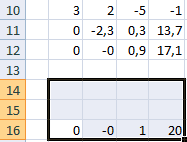
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
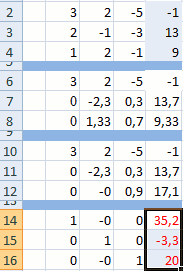
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
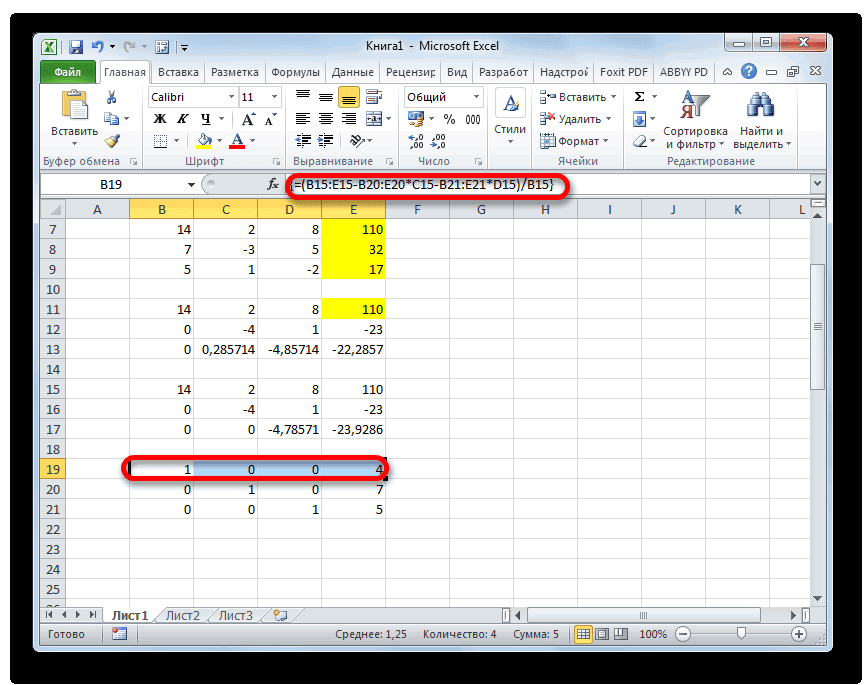
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
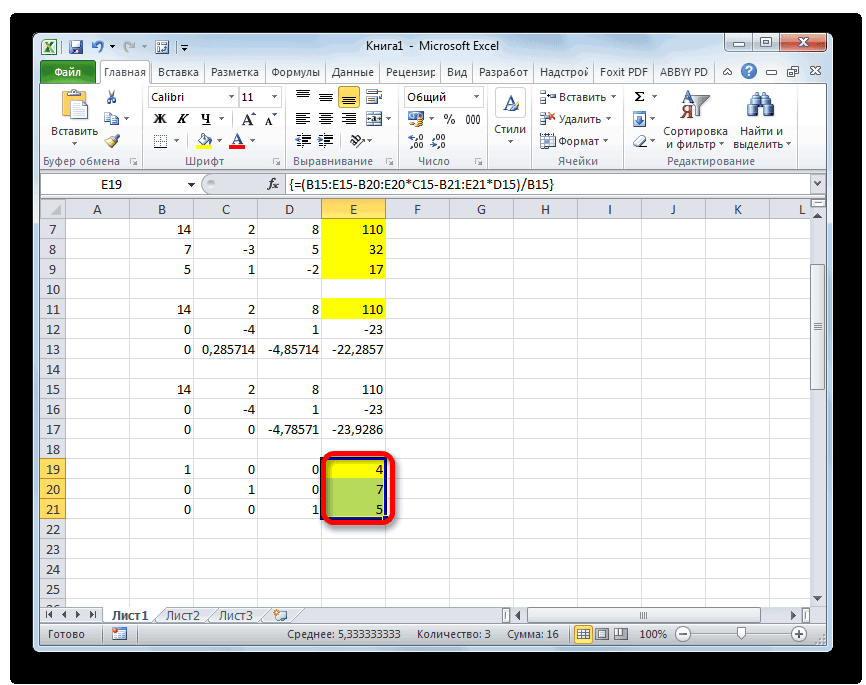
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Еще статьи по данной теме:
Помогла ли Вам статья?
17 авг. 2022 г.
читать 3 мин
Часто вас может заинтересовать построение уравнения или функции в Excel. К счастью, это легко сделать с помощью встроенных формул Excel.
В этом руководстве представлено несколько примеров того, как строить уравнения/функции в Excel.
Пример 1: построение линейного уравнения
Предположим, вы хотите построить следующее уравнение:
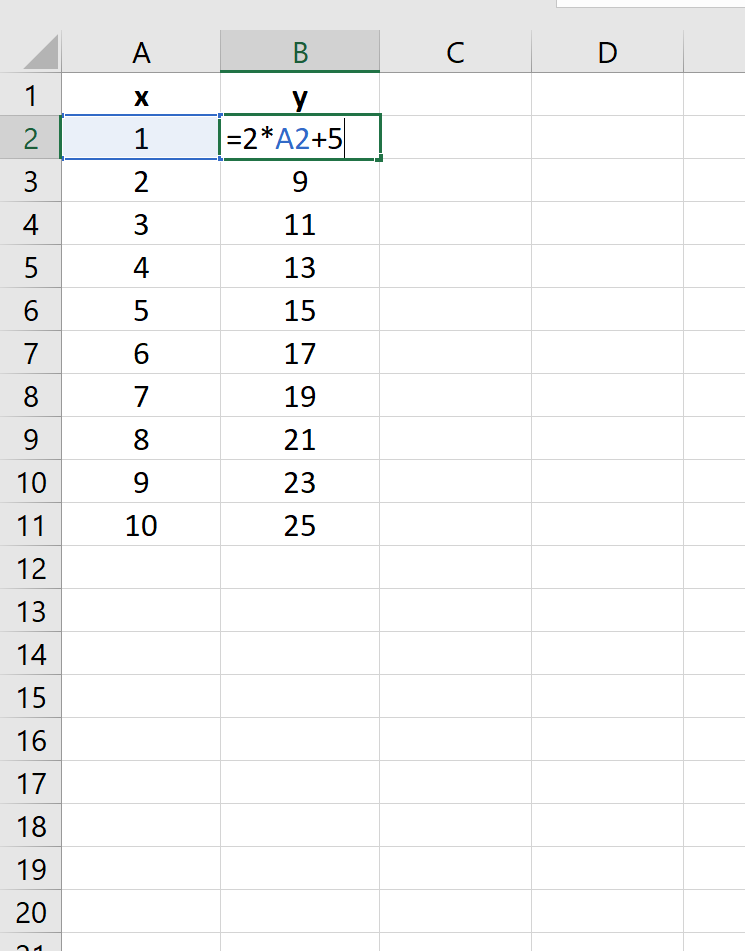
у = 2х + 5
На следующем изображении показано, как создать значения y для этого линейного уравнения в Excel, используя диапазон от 1 до 10 для значений x:
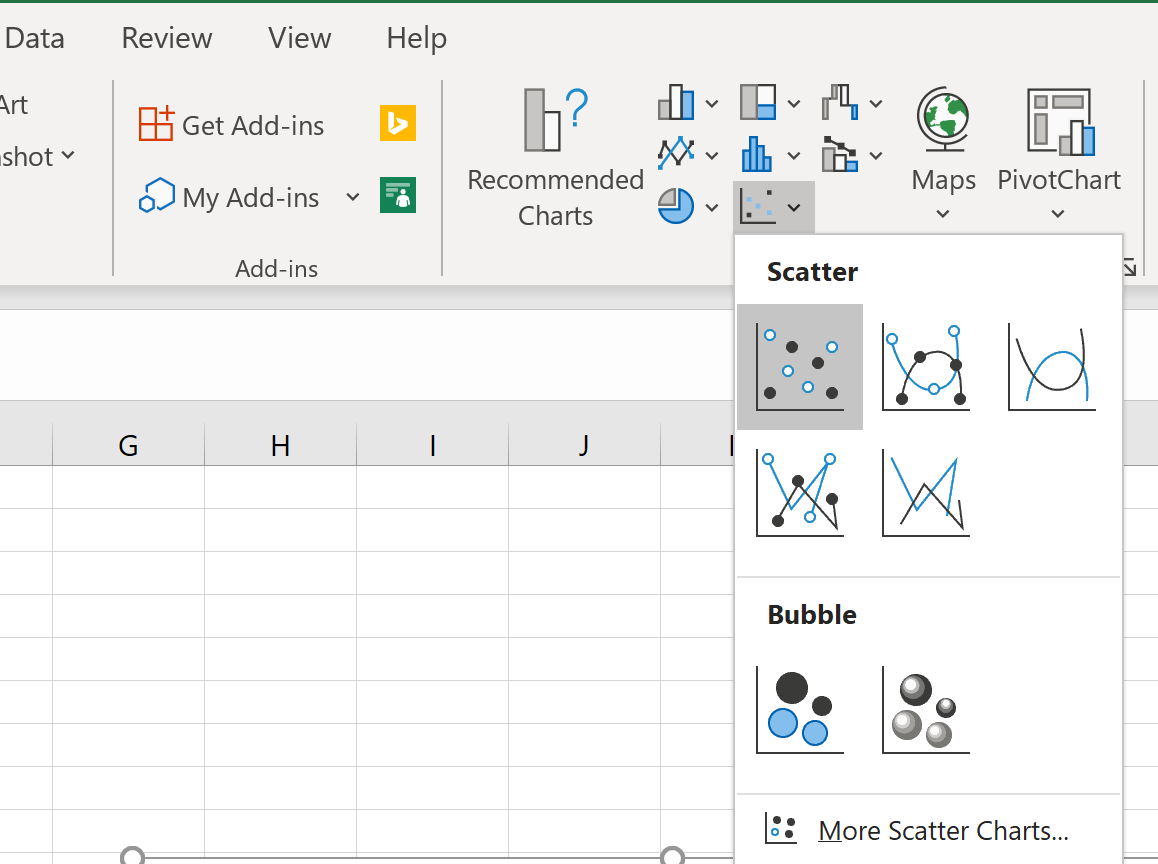
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
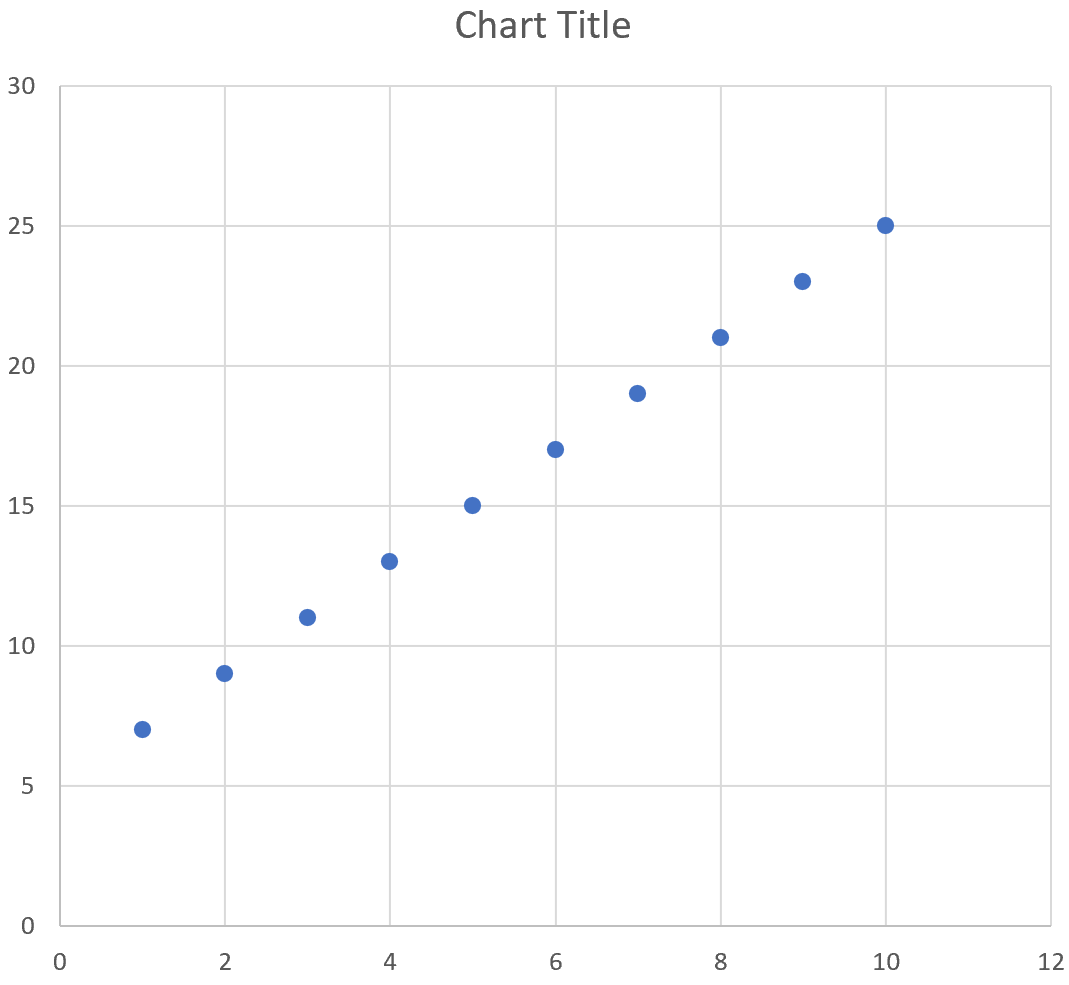
Автоматически появится следующий график:
Мы видим, что график следует прямой линии, поскольку уравнение, которое мы использовали, было линейным по своей природе.
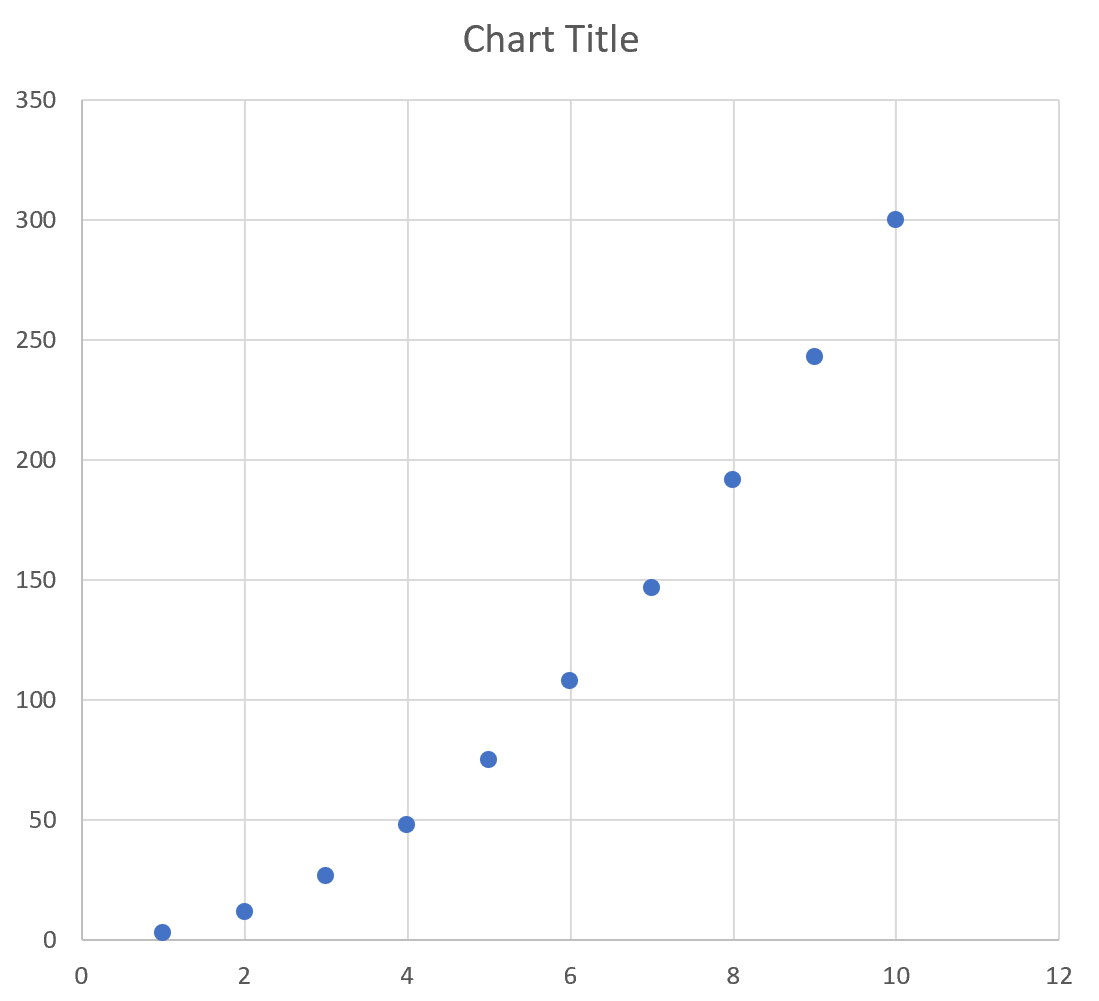
Пример 2. Построение квадратного уравнения
Предположим, вы хотите построить следующее уравнение:
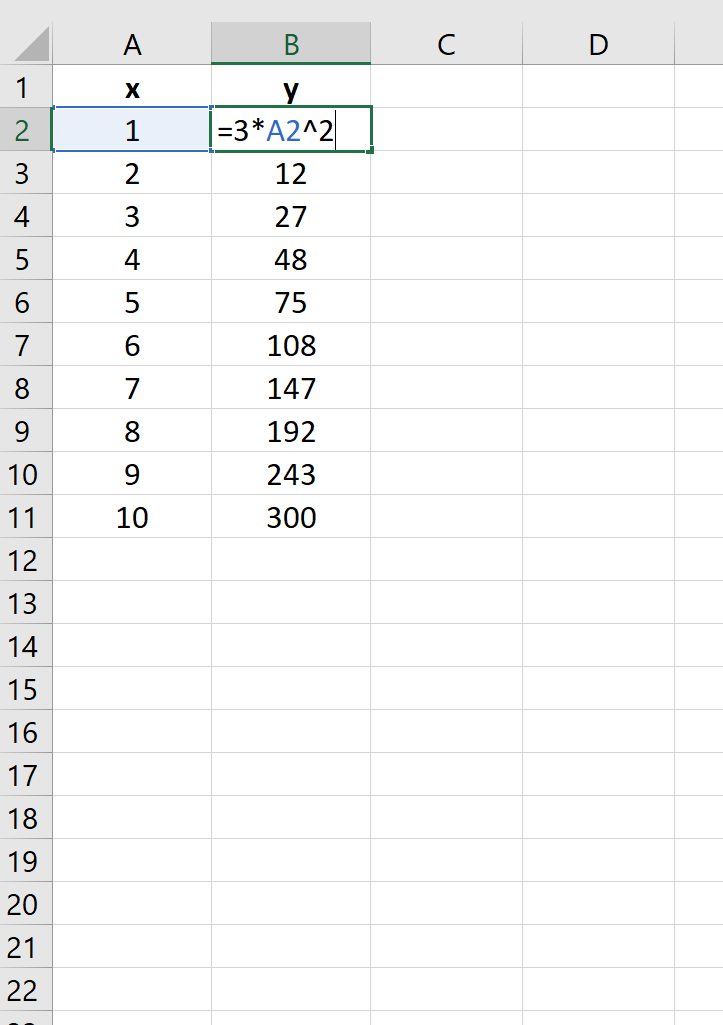
у = 3x 2
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует изогнутой линии, поскольку уравнение, которое мы использовали, было квадратным.
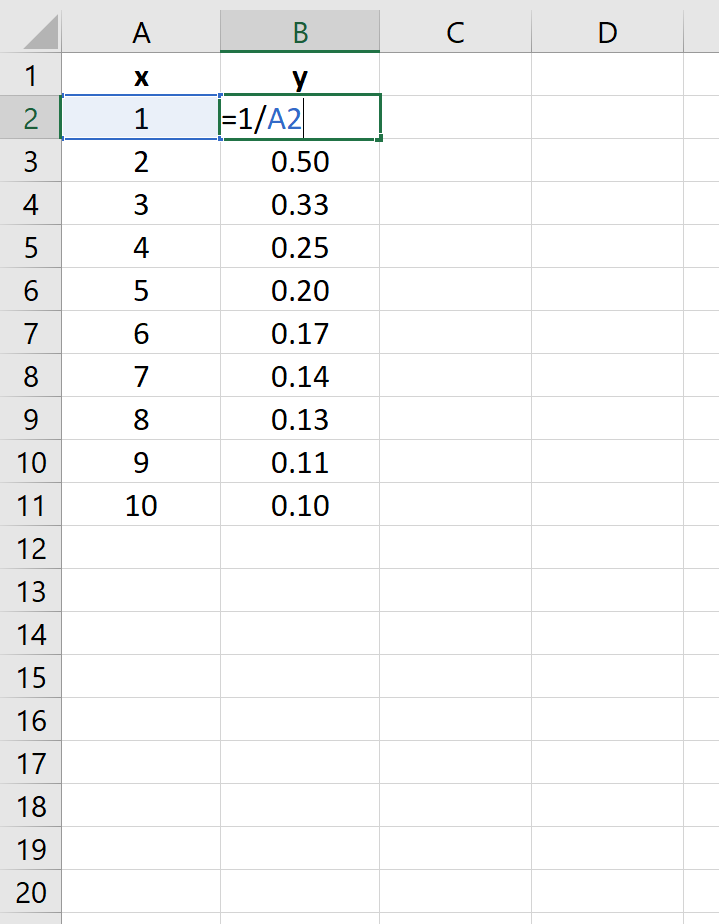
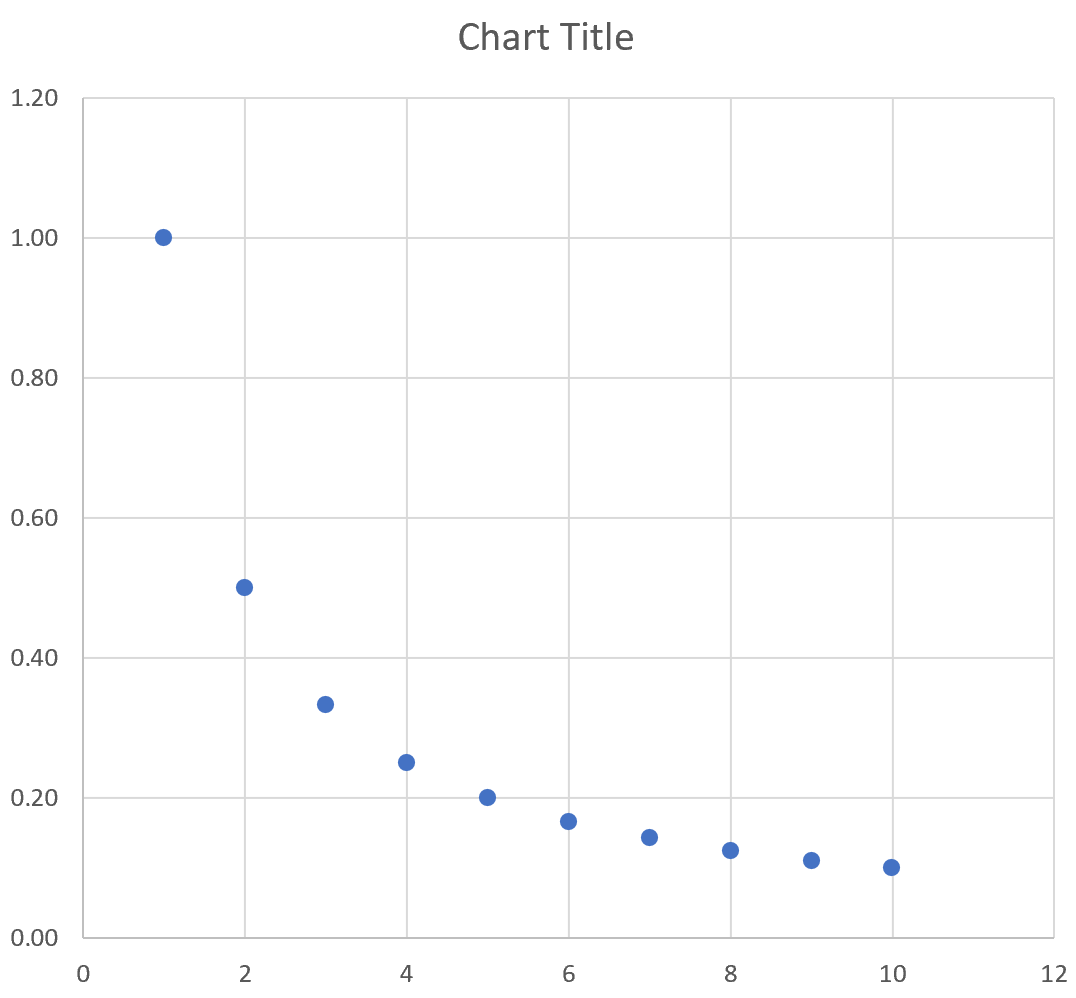
Пример 3: построение уравнения обратной связи
Предположим, вы хотите построить следующее уравнение:
у = 1/х
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует по изогнутой линии вниз, поскольку это представляет уравнение y = 1/x.
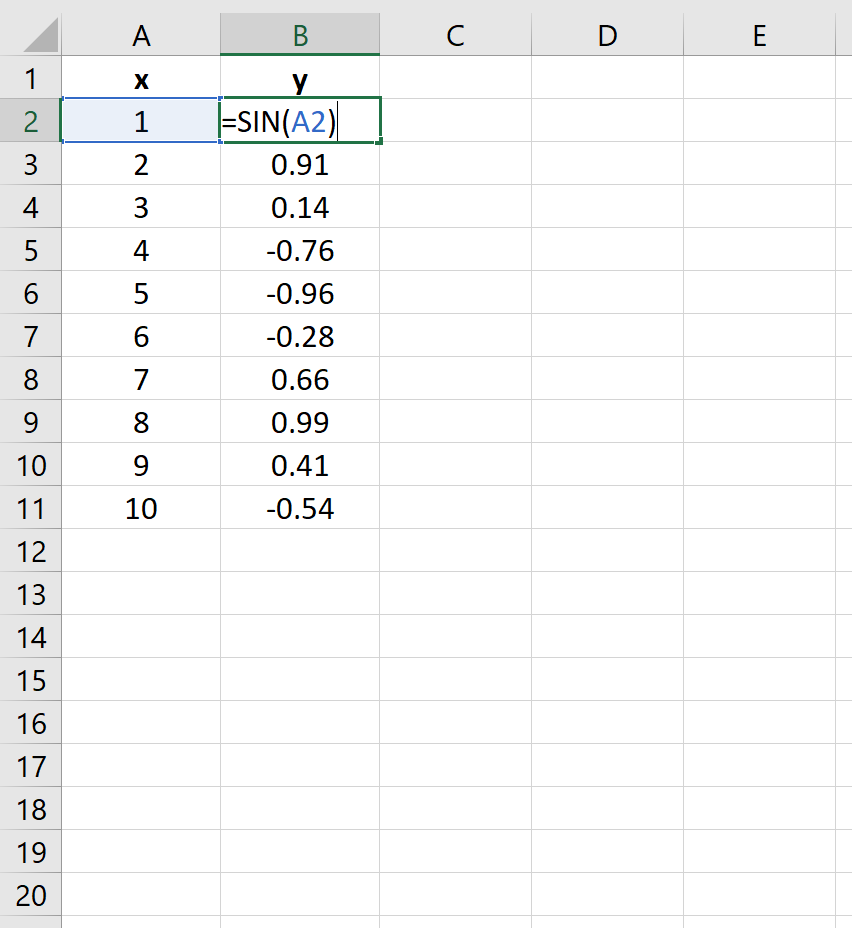
Пример 4. Построение уравнения синуса
Предположим, вы хотите построить следующее уравнение:
у = грех (х)
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика « Разброс с плавными линиями и маркерами» .
Автоматически появится следующий график:
Вывод
Вы можете использовать аналогичную технику для построения графика любой функции или уравнения в Excel. Просто выберите диапазон значений x для использования в одном столбце, затем используйте уравнение в отдельном столбце, чтобы определить значения y на основе значений x.
Решение СЛАУ в MS EXCEL
С системой линейных алгебраических уравнений (СЛАУ) часто приходится сталкиваться не только в курсе математики. Их решение пригодится в других науках, например, физике или химии.
Систему из двух уравнений часто можно решить способом подстановки. Системы трех и более уравнений приходится решать другими способами. К ним относятся:
- метод обратной матрицы;
- метод Крамера;
- метод Гаусса.
В общем виде систему линейных уравнений можно представить в виде:
A⋅X=BAcdot X = B,где AA – матрица коэффициентов;
XX – вектор-столбец неизвестных;
BB – вектор-столбец свободных коэффициентов.
Мы рассмотрим решение одной и той же простой системы уравнений первыми двумя способами, чтобы сравнить результаты. Если при решении разными способами ответы будут совпадать, значит СЛАУ решена верно.
Метод обратной матрицы
Метод обратной матрицы (матричный метод) используется для квадратных матрицы, чей определитель равен нулю.
Для того чтобы найти корни уравнения этим способом, в первую очередь находят обратную матрицу, которую перемножают на свободные коэффициенты. Рассмотрим, как это будет выглядеть в MS Excel.
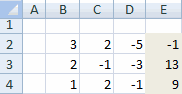
Возьмем для примера матрицу (рис.1):
Рисунок 1
Запишем нашу систему уравнений в следующем виде (рис.2):
Рисунок 2
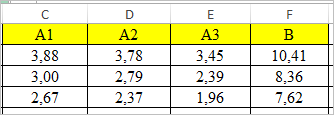
Скопируем матрицу коэффициентов и таблицу свободных коэффициентов в Excel (рис.3):
Рисунок 3
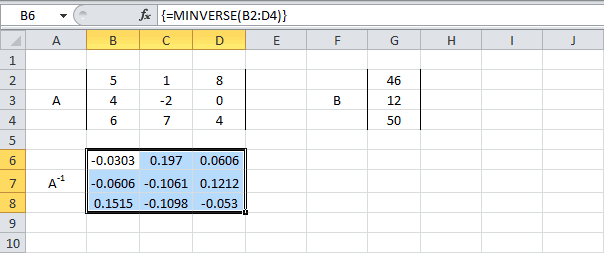
Для нахождения обратной матрицы выделяем нужные ячейки, в которых будет новая матрица, в строке формул пишем функцию «=мобр» и указываем в скобках массив матрицы, для которой мы и находим обратную матрицу. В нашем случае это будет «=мобр(C2:E4)». После этого нажимаем комбинацию клавиш Ctrl+Shift+Enter (рис.4):
Рисунок 4
После этого в каждой ячейке формула будет записана в фигурных скобках.
Для нахождения неизвестных необходимо перемножить обратную матрицу и свободные коэффициенты. Делается это так же, как и нахождение обратной матрицы: выделяем ячейки, куда будут записаны ответы, в строке формул записываем функцию «=мумнож», в скобках указываем массив матрицы и вектор свободных коэффициентов. В нашем случае это будет выглядеть «=мумнож(C7:E9;F2:F4)»:
Рисунок 5
Для тренировки можно скачать файл с данным примером и подставить другие значения. Таким же способом решают СЛАУ из 4, 5 и более уравнений.
Если тема осталась для вас непонятной, изучайте подробно матрицы и методы работы с ними в этой статье с пошаговым разбором.
Метод Крамера
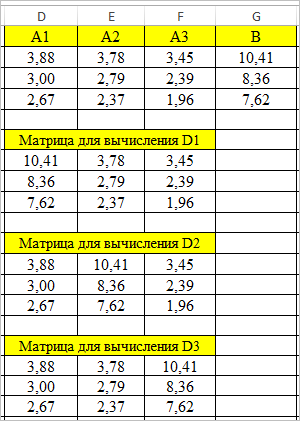
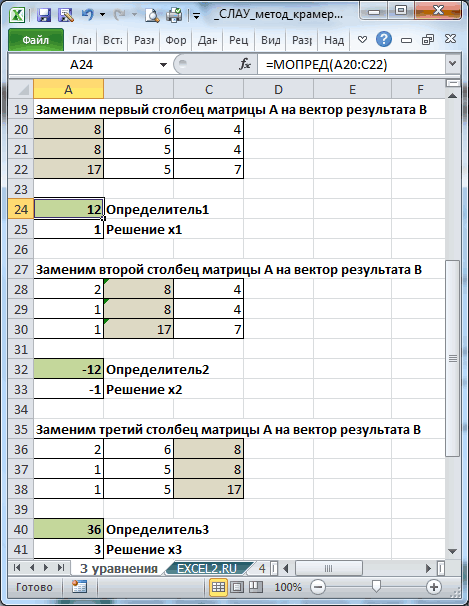
Метод Крамера несколько отличается от предыдущего. Для этого нам нужно найти определитель основной матрицы, после чего в матрице коэффициентов каждый столбец заменить на вектор свободных коэффициентов и для полученных таблиц найти определитель. Рассмотрим наглядно это на рисунке 6:
Рисунок 6
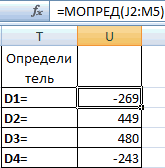
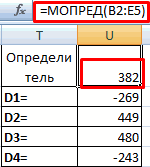
Для каждой матрицы находим определитель с помощью функции «МОПРЕД». Корнями системы уравнений будут частные определителя основной и новых матриц (рис.7):
Рисунок 7
Такими простыми способами можно решать системы линейных квадратных уравнений.
Тест по теме «Решение СЛАУ в MS Excel»
The equation having the highest degree is 1 is known as a linear equation. If we plot the graph for a linear equation, it always comes out to be a straight line. There are different forms of linear equations such as linear equations in one variable, and linear equations in two variables.
- Linear equations in one variable: standard form of this equation is ‘ax + b = 0’, where a and b are real numbers and x is a variable.
- Linear equation in two variables: standard form or this equation is, ‘ax + by = c’, where a, b and c are real numbers, and x is a variable.
Graph a linear equation using Excel
Graph of Linear equation (one variable)
In only one variable, the value of only one variable is needed to be found. Therefore, the equation can be solved directly. Let’s take one linear equation in one variable i.e 2x + 3 = 9.
Step 1: Solve the linear equation
2x + 3 = 9
2x = 9 – 3
2x = 6
x = 6/2
x = 3
Step 2: Plot the graph
For a linear equation in one variable, the graph will always have a line parallel to any axis.
For x = 3, the graph will be a line parallel to the y-axis which intersects the x-axis at 3, because for any value of y, the value of x is 3. Below table data can be used to plot the graph,
Co-ordinates taken is (3, 0), (3, 5), (3, 10), (3, 15), (3, -5), (3, -10), (3, -15).
Plot the graph using the following steps
Step 1: Select the data
Step 2: Click on the ‘Insert’ tab and select scatter with marker chart.
Output
Graph of Linear equation (two variables)
Let’s take one linear equation in one variable i.e 2x + 3y = 6. In order to get the data points for plotting the graph, assume some value of x and find the corresponding y value.
For example, If x = 0
Substitute value of x in given equation,
2(0) + 3y = 6
3y = 6
y = 2
Then, the data point is (0, 2). Similarly, we can get different coordinates, those are (3, 0), (-3, 4), and (6, -2).
Plot the graph using the following steps
Step 1: Select the data
Step 2: Click on the ‘Insert’ tab and select scatter with marker chart.
Output
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12698 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
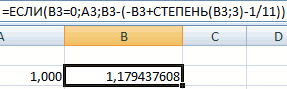
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:

Как написать систему уравнений в excel
Как в Excel решить систему линейных уравнений
Количество переменных в системе уравнений должно быть равно количеству уравнений. Предыдущий пример использует два уравнения с двумя переменными. Три уравнения требуются для того, чтобы найти значения трех переменных (х,у и z). Общие действия по решению систем уравнений следующие (рис. 128.1).
Рис. 128.1. Использование формулы для решения системы из двух уравнений
- Выразите уравнения в стандартной форме. Если это необходимо, используйте основы алгебры и перепишите уравнение так, чтобы все переменные отображались по левую сторону от знака равенства. Следующие два уравнения идентичны, но второе приведено в стандартном виде:
3x — 8 = -4y
3x + 4y = 8 . - Разместите коэффициенты в диапазоне ячеек размером n x n, где n представляет собой количество уравнений. На рис. 128.1 коэффициенты находятся в диапазоне I2:J3 .
- Разместите константы (числа с правой стороны от знака равенства) в вертикальном диапазоне ячеек. На рис. 128.1 константы находятся в диапазоне L2:L3 .
- Используйте массив формул для расчета обратной матрицы коэффициентов. На рис. 128.1 следующая формула массива введена в диапазон I6:J7 (не забудьте нажать Ctrl+Shift+Enter, чтобы ввести формулу массива): =МОБР(I2:J3) .
- Используйте формулу массива для умножения обратной матрицы коэффициентов на матрицу констант. На рис. 128.1 следующая формула массива введена в диапазон J10:JJ11 , который содержит решение ( x = 7,5 и у = -3,625 ): =МУМНОЖ(I6:J7;L2:L3) . На рис. 128.2 показан лист, настроенный для решения системы из трех уравнений.
Рис. 128.2. В Excel можно решить систему из трех уравнений, применив нужные формулы
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в EXCEL
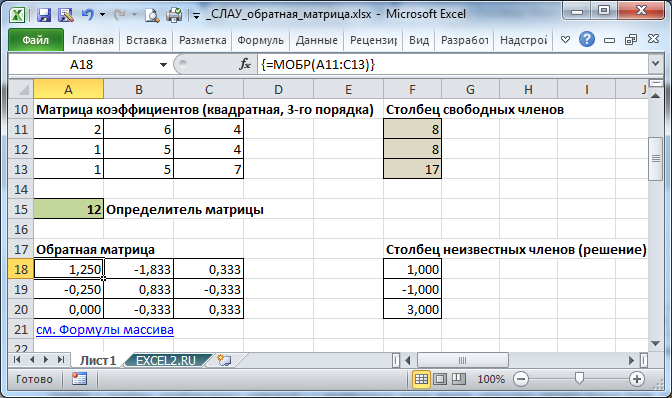
Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
Для этого выделите ячейки A18:C20 , а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER .
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .
Для этого выделите ячейки F18:F20 , а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER .
записать систему уравнений через функции ЕСЛИ
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Записать систему трех уравнений через функции ЕСЛИ
Помогите, пожалуйста, правильно записать систему трех уравнений, все время выдает ошибку:(

Как решить вот такую функцию :
Записать систему уравнений в excel
Записать систему уравнений в excel,для построения графика
источники:
http://urok.1sept.ru/articles/510787
http://programka.com.ua/instrukcija/excel/kak-napisat-sistemu-uravnenij-v-excel
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ |
|
Государственное бюджетное профессиональное образовательное учреждение «Кстовский нефтяной техникум имени Бориса Ивановича Корнилова» |
|
|
СК-МД-15 |
Система качества образовательного учреждения |
|
Учебно-методическое пособие |
Н. В. КОЛДАЕВА
Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла
Учебно-методическое пособие
для самостоятельной работы студентов
по дисциплине «Информатика и ИКТ»
Кстово 2015
Аннотация
Учебно-методическое пособие Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла разработано для организации самостоятельной работы студентов и соответствует действующей программе по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела «Технология создания и преобразования информационных объектов».
Кротко изложены основы технологии работы с табличным процессором MS Excel и основы численных методов решения математических задач для систем линейных уравнений и вычисления определенного интеграла. Приведена пошаговая реализация нахождения неизвестных для системы линейных уравнений и вычисления значения определенного интеграла на конкретных примерах с использованием MS Excel. Представлены индивидуальные задания для самостоятельной работы студентов.
Учебное пособие предназначено для студентов ГБОУ СПО «Кстовский нефтяной техникум им. Б.И. Корнилова», изучающих дисциплину «Информатика и ИКТ», а также для реализации математических моделей с помощью компьютера при выполнении расчетно-графических, курсовых и дипломных работ.
СОДЕРЖАНИЕ
Введение
1. Табличный процессор Excel и технология работы в нем
1.1. Структура документа MS Excel
1.2. Основной принцип работы электронных таблиц
1.3. Ввод информации в ячейки
1.4. Форматирование таблиц
1.5. Основные правила создания формул и функций
1.6. Способы и методы формирования в формулах ссылок на ячейки
2. Математическая постановка задач
2.1. Метод Крамера решения систем линейных уравнений
2.2. Приближенные методы вычисления определенного интеграла
3. Реализация решения математических задач в MS Excel
3.1. Решение систем линейных уравнений с использованием табличного процессора MS Excel
3.2. Нахождение значений определенного интеграла с использованием табличного процессора MS Excel
4. Методические указания по выполнению самостоятельной работы
5. Варианты заданий для самостоятельной работы
5.1. Варианты заданий систем линейных уравнений
5.2. Варианты заданий определенного интеграла
Список литературы
Введение
Учебно-методическое пособие для самостоятельной работы студентов разработано в соответствии с действующей программой по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела «Технология создания и преобразования информационных объектов».
Учебно-методическое пособие содержит теоретический материал по технологии использования табличного процессора MS Excel и математическим методам решения систем линейных уравнений и приближенному вычислению определенного интеграла, который является основой для практического использования решения математических задач с помощью компьютерных технологий. В разделе «Реализация решения математических задач в MS Excel» приведены подробные пошаговые решения примеров решения системы линейных уравнений и приближенного вычисления интеграла, которые могут быть воспроизведены студентом самостоятельно. Для закрепления полученных навыков в соответствии предлагаемыми методическими указаниями студент должен выполнить индивидуальные задания и представить их на проверку преподавателю.
Содержание учебно-методического пособия отражает практическую направленность использования компьютера для решения профессиональных задач, так как большинство инженерных задач использующих математические методы требуют сложных длительных вычислений, которые существенно упрощаются и сокращаются при использовании компьютерных технологий. Полученные студентом знания и умения, в первую очередь, могут быть использованы при выполнении расчетно-графических, курсовых работ и. конечно, при выполнении дипломной работы.
1. Табличный процессор Excel и технология работы в нем
1.1. Структура документа MS Excel
MS Excel – это прикладная программа управления электронными таблицами, которая используется для выполнения вычислений, организации данных, анализа результатов и поиска оптимальных решений.
Базовыми понятиями в Excel являются: книга, лист, таблица, ячейка.
Структуру книги можно представить следующим образом (см. Рис.1).
. . . . . .
|
А |
В |
С |
D |
Е |
F |
. . . |
|
|
1 |
Уч. группа |
ФИО |
МАТЕМ |
ФИЗ |
СР. БАЛ |
||
|
2 |
12-ЭОП-31 |
ПЕТРОВ |
4 |
5 |
4,5 |
||
|
3 |
12-АСУ-21 |
ИВАНОВ |
5 |
3 |
4 |
||
|
4 |
Макс. Ср. бал. |
4,5 |
Рис. 1
Книга в Excel представляет собой файл с расширением xls. Имя книги (файла) задается при ее сохранении и должно напоминать о ее содержании. Каждая книга может состоять из нескольких поименованных листов (до 255, а по умолчанию – 3). Имя листа указано на ярлычке (внизу листа) и может быть изменено, чтобы напоминать о его содержании. Для перехода на другой лист надо щелкнуть ЛКМ (ЩЛКМ) по его ярлычку. Листы можно добавлять, удалять, копировать или переименовывать (ЩПКМ – щелчок правой кнопкой мыши по ярлычку и появится контекстное меню). Лист – это место для ввода, хранения и обработки данных. Лист Excel состоит из ячеек, каждая из которых имеет свой адрес. Ячейки образуют строки (до 65536) и столбцы (до 256). Строки имеют номера, а столбцы по умолчанию – буквенные имена (если стиль ссылок А1), или номера, если установлен стиль ссылок R1C1 (R – строка, а С – столбец). Стили ссылок задаются параметрами при работе с опциями меню «Сервис». Как правило, используется стиль А1.
1.2. Основной принцип работы электронных таблиц
Каждая ячейка листа может содержать текст, числовое значение или формулу и быть отформатирована.
Основной принцип работы электронных таблиц заключается в том, что одни ячейки рабочего листа используются как независимые переменные (влияющие ячейки), которым задаются значения из вне (например, пользователем), а другие ячейки используются как зависимые переменные (зависимые ячейки), которые содержат формулы, ссылающиеся на независимые переменные. Пользователь вводит исходные данные (текст или числа) во влияющие ячейки и формулы в зависимые ячейки, далее автоматически (или, в зависимости от настройки, по команде) производятся вычисления по формулам, и пользователь видит готовый результат в зависимых ячейках. Если же установить режим показа формул («Сервис Параметры»), то в зависимых ячейках будут видны только формулы.
|
А |
В |
С |
D |
E |
|
|
1 |
Уч. группа |
ФИО |
МАТЕМ |
ФИЗ |
СР. БАЛ |
|
2 |
12-ЭОП-31 |
ПЕТРОВ |
4 |
5 |
=СРЗНАЧ(С2:D2) |
|
3 |
12-АСУ-21 |
ИВАНОВ |
5 |
3 |
=СРЗНАЧ(С3:D3) |
|
4 |
Макс. Ср. бал. |
=МАКС(Е2:Е3) |
Если же режим показа формул не установлен, то в ячейке Е2 сразу появится результат (=4,5).
На листе может быть создана одна или несколько таблиц.
Таблица – это совокупность ячеек, связанных между собой по смыслу или с помощью формул в соответствии с задачей пользователя.
Ячейки таблиц, размещенных на разных листах книги или в разных книгах, также могут быть взаимосвязаны посредством формул. На основе таблицы (для наглядности при анализе исходных данных и результатов вычислений) может создаваться диаграмма, которую можно разместить на листе вместе с таблицей или на отдельном листе.
1.3. Ввод информации в ячейки
Как правило, построение таблицы начинается с заполнения заголовков столбцов (а, если необходимо, и строк, как на Рис.1), поясняющих содержание основных ячеек таблицы, в которых находятся исходные данные и формулы. Перед вводом информации в ячейку ее надо выделить с помощью ЩЛКМ по ячейке или с помощью клавиш перемещения курсора.
Существуют следующие основные способы ввода информации в ячейки:
1) Неавтоматизированный способ, при котором каждый символ вводится с клавиатуры. Он занимает много времени и имеет большую вероятность ошибок, но необходим тогда, когда в таблице нет повторяющейся, либо закономерно изменяющейся информации, что бывает очень редко.
Ввод информации должен быть зафиксирован. Это достигается либо нажатием клавиши ENTER или нажатием клавиш управления курсором на клавиатуре (стрелки ↑,←,↓,→). Для изменения (редактирования) информации в ячейке надо сначала 2 раза ЩЛКМ по ней. Например, на Рис. 1 в ячейках А2 и D4 записана информация, изменяющейся не закономерно, поэтому ее невозможно вводить иначе, чем в ручную с клавиатуры.
Полезно запомнить, что:
– при вводе в ячейку длинного предложения для перехода на новую строку (в той же ячейке) надо нажать ALT+ENTER.
– если при вводе обнаружена ошибка, то следует нажать на панели инструментов (ПИ) кнопку ОТМЕНИТЬ .
2) Автоматизированный способ, который может быть реализован двумя методами:
- копирования в буфер ранее заполненной ячейки (или группы ячеек), которые предварительно должны быть выделены, и последующей вставки из буфера в нужную область таблицы, предварительно выделив левую верхнюю ячейку этой области. Для выделения группы смежных ячеек надо выделить первую ячейку диапазона, затем нажать и удерживая SHIFT выделить последнюю ячейку диапазона.
- автозаполнение рядов. Ряд – это группа смежных ячеек, принадлежащая одному столбцу или строке и содержащая одинаковую или закономерно изменяющуюся информацию.
Перед автозаполнением надо записать в начальную ячейку текст, число, дату, формулу и т.п., затем выделить эту ячейку и установить указатель мыши над маркером заполнения (маленького черного квадрата в правом нижнем углу выделенной ячейки). При этом вид указателя мыши меняется на знак +, означающий, что автозаполнение разрешено. Затем, нажав ЛКМ, перетащить указатель по ячейкам, которые нужно заполнить информацией и отпустить ЛКМ. При перемещении указателя вниз или вправо, автозаполнение создает в отмечаемых ячейках возрастающие значения, при перемещении указателя вверх или влево отмечаемые ячейки заполняются убывающими значениями.
Если в первоначально выделенной ячейке не распознается закономерность для возрастания или убывания, то ячейки просто дублируются.
Так, например, если в первой ячейке была запись «Блок1», то при перемещении указателя вниз, в последующих ячейках автоматически появятся записи «Блок2», «Блок3» и т.д. В то же время, если в первой ячейке было записано слово «Блок», то в последующих ячейках это слово просто дублируется.
В нашем примере, ячейку Е3 (Рис. 1) целесообразно заполнять с помощью метода автозаполнение рядов, т.е. не вводить в нее формулу, а распространив автозаполнением в нее содержимое ячейки Е2. При этом содержимое формулы Е3 (аргументы функции СРЗНАЧ()) будут отличаться от аргументов этой же функции для ячейки Е2 по условию автозаполнения:
для Е2: =СРЗНАЧ(С2:D2);
для Е3: =СРЗНАЧ(С3:D3).
Существует и другая возможность автозаполнения рядов – через главное меню: для копирования одной ячейки в несколько смежных или для настройки закономерности автозаполнения можно воспользоваться командой «ПРАВКА ЗАПОЛНИТЬ …».
1.4. Форматирование таблиц
Форматирование в MS Excel осуществляется почти так же, как и в других приложениях MS Office.
Для облегчения визуального поиска в таблице требуемой информации целесообразно заголовки столбцов и строк таблицы выделять цветом, отличительным (от другого текста) шрифтом, заливкой, граничной линией и т.п. В некоторых случаях, для более полного восприятия заголовка, целесообразно объединять ячейки.
Для выполнения вышеуказанных действий используется операция форматирования.
Объектом форматирования могут быть отдельные ячейки или группа ячеек (диапазон), которые предварительно должны быть выделены. ЩПКМ по выделенному объекту приводит к вызову контекстного меню, в котором следует выбрать пункт «формат ячеек».
Для изменения ширины столбцов или высоты строк таблицы надо поместить указатель мыши (УМ) между соответствующими именами столбцов или номерами строк листа и, удерживая ЛКМ, передвинуть УМ на нужное расстояние.
Если новая таблица содержит компоненты уже существующей таблицы, то целесообразно скопировать созданную таблицу в другую область листа или на другой лист (книгу) и отредактировать ее под условия создаваемой новой таблицы: удалить (или добавить) столбцы, строки или некоторые ячейки. Для работы с этими объектами их надо выделить.
Чтобы выделить целиком строку надо ЩЛКМ по ее номеру, а для столбца – по его имени. После этого ЩПКМ по выделенному объекту вызвать контекстное меню, из которого затеем выбрать, в соответствие с операцией, пункты «Удалить» или «Добавить ячейки». (Для вставки строки надо выделить строку ниже, а для столбца – выделить столбец правее вставляемого).
1.5. Основные правила создания формул и функций
Каждая формула начинается со знака равенства «=». Знак равенства указывает процессору MS Excel на то, что следующий за ним текст является формулой. В формулах могут присутствовать арифметические операторы для выполнения действий над константами или числами, которые могут вводиться непосредственно с клавиатуры, либо содержаться в других ячейках. В последнем случае в формуле указываются адреса этих ячеек, т.е. ссылки на них. Если в формуле присутствуют несколько арифметических операторов, то в нее можно включить скобки для определения порядка вычислений. В формулах применяют стандартные арифметические операции и соответствующие операторы: сложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^), (последовательность выполнения операций такая же, как и в арифметике). Также в формулах могут применяться функции из набора встроенных в Excel функций. Большое количество функций (около 500) в значительной степени определяет область использования Excel. Из набора этих функций, которые сгруппированы по категориям, мы будем использовать следующие: Математические, Статистические, Ссылки и массивы, Логические. В логических функциях для обозначения операций сравнения двух чисел используются операции и соответствующие операторы сравнения: равно (=), больше (>), меньше (<), больше или равно (>=), меньше или равно (<=), не равно (<>), логическое сложение «ИЛИ» (+), логическое умножение «И» (*). Результатом выполнения операции сравнения является логическое значение ИСТИНА или ЛОЖЬ.
Формула является основным средством для анализа данных. С помощью формул можно складывать, умножать и сравнивать данные, осуществлять их поиск и т.п. Формулы могут ссылаться на ячейки текущего листа, листов той же книги или других книг.
В следующем примере «=(В4+25)/СУММ(D5:F5)» складывается значение ячейки B4 с константой 25. Полученный результат делится на сумму значений в диапазоне ячеек D5:F5, т.е. на результат операции D5+E5+F5.
В данном примере выражение «СУММ(…)» является функцией, т.е. стандартной формулой.
При решении конкретной задачи для создания функции целесообразно использовать так называемый Мастер функций и действовать в следующем порядке:
- Выделить ячейку, в которую будет вставляться функция.
- Запустить МАСТЕР ФУНКЦИЙ (на панели инструментов значок
, либо «ГЛАВНОЕ МЕНЮ/ВСТАВКА/ФУНКЦИЯ»).
- Задать в нужную категорию функции (это определяется интуицией или методом перебора).
- выделить требуемую функцию, прочитать пояснения внизу окна.
- Если все понятно, то нажать — «ОК».
- На появившейся панели формул, ввести требуемую информацию в соответствующие окна аргументов.
Ввод информации в окна, как правило, осуществляется так:
- установить курсор в окно (в первое окно он устанавливается автоматически);
- выделить нужные ячейки мышью, установить курсор в другое окно и т.д.
Если нужные ячейки не видны, то надо свернуть панель формул, нажав на красную кнопку в правой части окна ввода, затем выделить ячейки и развернуть панель формул, снова нажав на красную кнопку
в правой части окна. Если же пояснений в этом окне недостаточно, то следует закрыть окно МАСТЕРА ФУНКЦИЙ и использовать справочную систему, для чего надо:
- ЩЛКМ по знаку вопроса
в Горизонтальном меню и выполнить команду: «ВЫЗОВ СПРАВКИ / ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ / (ввести фразу «функции») / ОБЗОР / (нажать кнопку «Вывести») / (выбрать нужную категорию (раздел), например, «Статистические функции») / (нажать кнопку «Вывести») / (выбрать нужную функцию, например, «СРЗНАЧ») / (прочитать подробное ее описание и рассмотреть примеры). Выписать наиболее общий пример в тетрадь, закрыть справочную систему.
- По аналогии с примером, используя МАСТЕР ФУНКЦИЙ, создать нужную функцию и, изменяя исходные данные, проверить ее корректность.
В Excel можно создавать так называемые вложенные функции, т.е. функции, аргументами которых являются другие функции. Возможно до 7 уровней вложения. В этом случае для вставки аргумента-функции, после того как будет открыта панель исходной функции, надо открыть левое окно строки формул (щелкнув по «стрелке вниз»), выбрать нужную функцию и далее действовать, как и с обычной функцией.
Как правило, формулы используются для определения их значений в зависимости от параметров (исходных данных), т.е. констант и переменных. Однако в Excel есть возможность решать и обратные задачи («какой должна быть переменная, чтобы формула приняла заданное значение?»), т.е. определять значение переменной, причем только одной, если задать значение результата вычисления формулы. Для этого надо выделить ячейку для искомой переменной и задать ей ориентировочное значение, а затем выполнить команду «СЕРВИС / ПОДБОР ПАРАМЕТРА» и, в появившемся окне, указать запрашиваемые данные.
В формулах для обращения к ячейкам, в зависимости от решаемой задачи, применяются различные способы и методы ссылок на ячейки.
1.6. Способы и методы формирования в формулах ссылок на ячейки
Ссылкой однозначно определяется ячейка или группа (диапазон) ячеек листа, используемых в формуле. С помощью ссылок можно использовать в формуле данные, находящиеся в различных местах листа, а также использовать значение одной и той же ячейки в нескольких формулах. Кроме того, можно ссылаться на ячейки, находящиеся на других листах книги или в другой книге, или на данные другого приложения.
Ссылки на ячейки других книг называются внешними ссылками. Ссылки на данные других приложений называются удаленными ссылками.
В Excel можно выделить три способа формирования ссылок: координатный относительно листа книги, координатный относительно таблицы и именной.
При координатном способе адрес ячейки определяется местом пересечения столбца и строки листа книги или таблицы.
При именном способе адрес ячейки определяется текстовым именем ячейки (или диапазона ячеек), которое напоминает о содержании ячеек.
- Координатный способ формирования ссылок относительно листа книги
До настоящего момента мы уже использовали именно такой способ, но к вышесказанному необходимо добавить следующее:
- Чтобы создать ссылку на диапазон ячеек, надо активизировать ячейку левого верхнего угла диапазона, поставить двоеточие (:), а затем — активизировать ячейку правого нижнего угла диапазона. Например, в формуле =СУММ(A1:В2) определяется сумма чисел, записанных в четырех ячейках: А1, А2, В1, В2.
- В формулах Excel используется два метода ссылок на ячейки:
- относительные ссылки, которые ссылаются на ячейки относительно позиции формулы (т.е. если формулу с относительными ссылками скопировать, например, через буфер, в другую ячейку, то ссылки в ней изменятся на количество строк и столбцов относительно ее исходного расположения);
- абсолютные ссылки, которые всегда ссылаются на одни и те же ячейки независимо от изменения места расположения формулы после копирования. Для задания абсолютной ссылки в формуле надо перед именем столбца и номером строки ячейки добавить знак $. Пример: $А$2 (если в формуле указана ссылка А2 – то это относительная ссылка).
- Координатный способ формирования ссылок относительно таблицы
Для ссылок в формулах на ячейки можно использовать заголовки столбцов и строк таблицы, что делает формулу более наглядной.
Например, если в столбце с заголовком «Физика» содержатся средние баллы экзаменационных оценок по физике полученных соответствующим курсом, а заголовками строк являются «Курс11», «Курс21», «Курс31», то, создав формулу « =Физика Курс31» в любом месте листа, можно определить средний балл по физике полученный курсом №31. Пробел между заголовками является оператором пересечения диапазонов, который предписывает формуле вернуть значения из ячейки, находящейся в пересечении строки «Курс31» и столбца «Физика».
- Именной способ формирования ссылок
Использование имен может упростить понимание формулы. Например, формула «=X*SIN(X)» более привычна, чем «=А1*SIN(A1)» или формула «=МАКС(Возраст)» проще для понимания, чем формула «=МАКС(C20:C30)». В этом примере имя «Возраст» представляет группу ячеек «C20:C30». Имена можно использовать на любом листе книги.
Чтобы присвоить имя ячейке или группе ячеек нужно:
1. Выделить ячейку или диапазон ячеек, которому необходимо присвоить имя.
2. Щелкнуть ЛКМ по окну имени, которое находится слева в строке формул (это строка, расположенная над заголовками столбцов).
3. Ввести имя ячейки.
4. Нажать клавишу ENTER.
Другой способ:
- выделить диапазон ячеек;
- выполнить команду «ВТАВКА / ИМЯ / ПРИСВОИТЬ». Появится окно, в котором можно присвоить, изменить или удалить имя.
По умолчанию имена являются абсолютными ссылками.
2. Математическая постановка задач
2.1. Метод Крамера решения систем линейных уравнений
Рассмотрим метод Крамера решения систем линейных уравнений для системы из трех уравнений с тремя неизвестными x1, x2 и x3, которая имеет вид:
Необходимо найти значение главного определителя, составленного из коэффициентов при неизвестных, т.е. , а также еще трех определителей, получаемых из главного путем замены первого, второго и третьего столбца на столбец свободных членов в исходной системе уравнений, т.е. ,
и
.
Тогда исходная система будет равносильна системе вида:
Если все четыре определителя отличны от нуля, то система имеет единственное решение. Значение неизвестных определяются в виде:
;
и
.
Метод Крамера может быть использован для решения систем линейных уравнений, состоящих из четырех и более уравнений, содержащих, соответственно, четыре и более неизвестных. Однако, для вычисления определителей четвертого и выше порядков следует использовать специальные приемы, которые требуют значительных временных затрат и особого внимания при выполнении вычислений. Выполнение вычислений с помощью MS Excel существенного упрощает решение подобных задач.
2.2. Приближенные методы вычисления определенного интеграла
Значение определенного интеграла численно равно площади так называемой криволинейной трапеции, ограниченной кривой, определяемой подынтегральной функцией y=f(x), прямыми x=a, x=b и осью Ox.
Приближенные методы вычисления определенного интеграла сводятся к замене площади вышеуказанной криволинейной трапеции ступенчатой фигуры, состоящей из прямоугольников или прямолинейных трапеций.
Площадь криволинейной трапеции разбивают на n прямоугольников, высоты которых равны y0, y1, y2, …, yn-1 и основания .
Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с недостатком, то значение определенного интеграла может быть вычислено по формуле: .
Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с избытком (рис. 10.6, б), то значение определенного интеграла может быть вычислено по формуле: .
Значения y0, …, yn находят из равенства yk=f(a+kΔx), k=0, 1, …, n. Эти формулы называются формулами прямоугольников и дают приближенный результат. С увеличением n результат становится более точным.
Геометрический смысл следующего способа приближенного вычисления интеграла состоит в том, что нахождение площади криволинейной трапеции заменяется нахождением площади приблизительно равновеликой «прямоугольной» трапеции.
Пусть необходимо вычислить площадь A1AmBB1 криволинейной трапеции, выражаемую формулой .
Заменим дугу AmB хордой АВ и вместо площади криволинейной трапеции A1AmBB1 вычислим площадь трапеции A1ABB1: , где АА1 и ВВ1 – основание трапеции, а А1В1 – ее высота.
Обозначим f(a)=A1A, f(b)=B1B. Высота трапеции A1B1=b—a, площадь . Следовательно,
или
. Это так называемая малая формула трапеций.
Для получения более точного результата необходимо разбить площадь криволинейной трапеции на n площадей ординатами, отстоящими друг от друга на расстоянии Δx. Суммируем площади получившихся трапеций: S=S1+S2+S3+ … +Sn, где по малой формуле трапеций ;
;
; …,
.
Сложив, получим или
.
Так как и
, то можно записать так называемую большую формулу трапеций:
, где y0, y1, y2, …, yn – значения подынтегральной функции при значениях аргумента, соответственно, a; a+Δx; a+2Δx; a+(n-1)Δx; b.
3. Реализация решения математических задач в MS Excel
3.1. Решение систем линейных уравнений с использованием табличного процессора MS Excel
В качестве примера рассмотрим систему уравнений:
- Оформить заголовок в строке 1 на листе 1 «Решение системы линейных уравнений».
- В области B3:F6 ввести исходные данные, как показано на рисунке 2.
- Ввести в ячейку A8 текст заголовка «Метод Крамера».
- В ячейку A11 ввести текст «Δ=» (выравнивание по правому краю).
- Скопировать исходные данные C4:E6 в область В10:D12. Это главный определитель системы.
- Скопировать содержимое ячейки A11 в ячейку F11.
- В ячейку G11 ввести формулу «=МОПРЕД(B10:D12)». Получаем значение главного определителя системы.
- Скопировать исходные данные C4:E6 в область В14:D16. Скопировать исходные данные F4:F6 в область В14:B16. Это определитель для первого неизвестного x1.
- В ячейку A15 ввести текст «Δx1=» (выравнивание по правому краю).
- Скопировать содержимое ячейки A15 в ячейку F15.
- В ячейку G15 ввести формулу «=МОПРЕД(B14:D16)». Получаем значение определителя для первого неизвестного x1.
- Скопировать исходные данные C4:E6 в область В18:D20. Скопировать исходные данные F4:F6 в область C18:C20. Это определитель для второго неизвестного x2.
- В ячейку A19 ввести текст «Δx2=» (выравнивание по правому краю).
- Скопировать содержимое ячейки A19 в ячейку F19.
- В ячейку G19 ввести формулу «=МОПРЕД(B18:D20)». Получаем значение определителя для второго неизвестного x2.
- Скопировать исходные данные C4:E6 в область В22:D24. Скопировать исходные данные F4:F6 в область D22:D24. Это определитель для третьего неизвестного x3.
- В ячейку A23 ввести текст «Δx3=» (выравнивание по правому краю).
- Скопировать содержимое ячейки A23 в ячейку F23.
- В ячейку G23 ввести формулу «=МОПРЕД(B22:D24)». Получаем значение определителя для третьего неизвестного x3.
- В ячейки H15, H19 и H23 ввести соответственно текст «x1=», «x2=» и «x2=» (выравнивание по правому краю).
- В ячейку I15 ввести формулу «=G15/$G$11» (выравнивание по левому краю). Получаем значение первого неизвестного x1.
- Скопировать содержимое ячейки I15 в ячейку I19. Получаем значение второго неизвестного x2.
- Скопировать содержимое ячейки I15 в ячейку I23. Получаем значение третьего неизвестного x3.
Рис. 2
3.2. Нахождение значений определенного интеграла с использованием табличного процессора MS Excel
В качестве примера рассмотрим нахождение значения определенного интеграла при числе разбиения интервала интегрирования n=10. Следует отметить, что точное значение данного интеграла может быть получено аналитическим методом (метод замены переменной) и оно равно 2.
- Оформить заголовок в строке 1 на листе 2 «Нахождение значения определенного интеграла».
- В ячейку A3 с помощью редактора формул вставим вид вычисляемого интеграла как показано на рисунке 3.
- В ячейки E3, E4, E5 и E6 соответственно введем текст: «нижний предел интегрирования», «верхний предел интегрирования», «число разбиений отрезка интегрирования» и «шаг интегрирования».
- В ячейки D3, D4, D5 введем исходные данные, определяющие пределы интегрирования и число разбиений отрезка интегрирования (в нашем примере это числа: 0, 5, 10) (выравнивание по центру).
- В ячейку D6 введем формулу для определения шага интегрирования «=(D4-D3)/D5» (выравнивание по центру).
- Оформим заголовок таблицы для численного вычисления подынтегральной функции в узлах интегрирования: в ячейку A8 вводим текст «x», в ячейку B8 вводим текст «f(x)» (выравнивание по центру).
- В ячейку A9 вводим формулу «=D3».
- В ячейку A10 вводим формулу «=A9+$D$6».
- Копируем формулу из ячейки A10 в диапазон A11:A19 (используем прием растягивания). Получаем значения узлов интегрирования.
- В ячейку B9 вводим формулу, определяющую значение подынтегральной функции в первом узле интегрирования. В нашем примере она будет: «=1/КОРЕНЬ(A9+4)».
- Копируем формулу из ячейки B9 в диапазон B10:B19 (используем прием растягивания). Получаем значения подынтегральной функции в узлах интегрирования.
- В ячейку D8 введем текст «Приближенное значение интеграла:».
- В ячейку D10 введем текст «по формуле прямоугольников:».
- В ячейку G10 введем формулу «=СУММ(B9:B18)*D6», которая позволяет вычислить значение определенного интеграла по формуле прямоугольников. Получаем приближенное значение вычисляемого определенного интеграла.
- В ячейку D12 введем текст «по формуле трапеций:».
- В ячейку G12 введем формулу «=(2*СУММ(B10:B18)+B9+B19)*D6/2», которая позволяет вычислить значение определенного интеграла по формуле трапеций. Получаем второе приближенное значение вычисляемого определенного интеграла.
Замечание: оба приближенных значения определенного интеграла близки к его точному значению.
- В диапазоне A21:H36 с помощью Мастера диаграмм построить график подынтегральной функции на основе диаграммы точечного вида:
- Выделить диапазон A8:B19;
- Меню Вставка ⇨ Команда Диаграмма…;
- На 1-ом шаге выбрать тип диаграммы: Точечная диаграмма со значениями, соединенными сглаживающими линиями и нажать кнопку «Далее»;
- На 2-ом шаге ничего не изменяем и нажимаем кнопку «Далее»;
- На 3-ем шаге на вкладке «Заголовки» в окно «Ось Х (категорий) заносим текст «x», а на вкладке «Легенда» снимаем флажок в позиции «Добавить легенду» и нажимаем кнопку «Далее»;
- На 4-ом шаге нажимаем кнопку «Готово».
- Переносим построенную диаграмму в диапазон A21:H36, сжимая (растягивая) до заданных размеров. Форматируем Ось категорий и Ось значений, переносим подписи осей, форматируем Область построения диаграммы (см. Рис. 3).
Рис. 3
4. Методические указания по выполнению самостоятельной работы
- Повторить материал по теме «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных», прочитав раздел учебно-методического пособия «Табличный процессор Excel и технология работы в нем».
- Повторить материал по дисциплине «Математика» по решению систем линейных уравнений методом Крамера и приближенному вычислению определенных интегралов, прочитав раздел учебно-методического пособия «Математическая постановка задач».
- Решить на компьютере с использованием табличного процессора MS Excel систему линейных уравнений из раздела «Реализация решения математических задач в MS Excel».
- Вычислить на компьютере с использованием табличного процессора MS Excel значение определенного интеграла из раздела «Реализация решения математических задач в MS Excel».
- Решить на компьютере с использованием табличного процессора MS Excel систему линейных уравнений
, применив метод Крамера. Коэффициенты при неизвестных и свободные члены задаются по вариантам, указанным в разделе «Варианты заданий для самостоятельной работы». Результаты решения предоставить преподавателю в виде аналогичном Рис 2.
- Вычислить на компьютере с использованием табличного процессора MS Excel значение определенного интеграла
, применив формулу прямоугольников и формулу трапеций. Построить график подынтегральной функции. Вид подынтегральной функции f(x), нижний предел интегрирования a, верхний предел интегрирования b задаются по вариантам, указанным в разделе «Варианты заданий для самостоятельной работы». Число разбиений отрезка интегрирования n равно 10 для всех вариантов. Результаты работы предоставить преподавателю в виде аналогичном Рис 3.
5. Варианты заданий для самостоятельной работы
5.1. Варианты заданий систем линейных уравнений
5.2. Варианты заданий определенного интеграла
|
№ варианта |
Вид подынтегральной функции f(x) |
Пределы интегрирования: |
Число разбиения отрезка интегрирования – n |
|
|
нижний – a |
верхний – b |
|||
|
1 |
|
-1 |
2 |
10 |
|
2 |
|
1 |
8 |
10 |
|
3 |
|
1 |
2 |
10 |
|
4 |
|
0 |
1 |
10 |
|
5 |
|
1 |
7 |
10 |
|
6 |
|
2 |
9 |
10 |
|
7 |
|
0 |
8 |
10 |
|
8 |
|
1 |
2 |
10 |
|
9 |
|
1 |
2 |
10 |
|
10 |
|
0 |
3 |
10 |
|
11 |
|
1 |
2 |
10 |
|
12 |
|
0 |
1 |
10 |
|
13 |
|
0 |
4 |
10 |
|
14 |
|
0 |
1 |
10 |
|
15 |
|
0 |
1 |
10 |
|
16 |
|
1 |
4 |
10 |
|
17 |
|
0 |
1 |
10 |
|
18 |
|
0 |
1 |
10 |
|
19 |
|
1 |
2 |
10 |
|
20 |
|
3 |
4 |
10 |
|
21 |
|
1 |
2 |
10 |
|
22 |
|
1 |
2 |
10 |
|
23 |
|
-2 |
-1 |
10 |
|
24 |
|
4 |
6 |
10 |
|
25 |
|
0 |
5 |
10 |
|
26 |
|
-1 |
1 |
10 |
|
27 |
|
2 |
3 |
10 |
|
28 |
|
-1 |
1 |
10 |
|
29 |
|
2 |
5 |
10 |
|
30 |
|
0 |
1 |
10 |
|
31 |
|
1 |
4 |
10 |
|
32 |
|
-2 |
2 |
10 |
|
33 |
|
3 |
4 |
10 |
|
34 |
|
2 |
5 |
10 |
|
35 |
|
1 |
4 |
10 |
Список литературы
- Гохберг Г.С., Зафиевский А.В., Короткин А.А. Информационные технологии: учебник для студ. учреждений сред. проф. образования. – 7-е изд., стер. – М.: Издательский центр «Академия», 2012. – 208 с.
- Дадаян А.А. Математика: Учебник. – М.: ФОЛРУМ: ИНФРА-М, 2003. – 552 с. – (Серия «Профессиональное образование»).
- Цветкова М.С., Великович Л.С. Информатика и ИКТ: учебник для нач. и сред. проф. образования. – 3-е изд., стер. – М.: Издательский центр «Академия», 2012. – 352 с., [8] л. цв. ил.
Перейти к содержанию
На чтение 2 мин Опубликовано 07.08.2015
Этот пример покажет, как решить систему линейных уравнений в Excel. К примеру, у нас есть следующая система линейных уравнений:
| 5x | + | 1y | + | 8z | = | 46 |
| 4x | — | 2y | = | 12 | ||
| 6x | + | 7y | + | 4z | = | 50 |
В матричном представлении ее можно записать в виде AX=B.
| 5 | 1 | 8 | x | 46 | |||||
| При А= | 4 | -2 | 0 | , | X= | y | , | B= | 12 |
| 6 | 7 | 4 | z | 50 |
Если А-1 (обратное А) существует, мы можем умножить обе части на А-1, чтобы получить X=A-1B. Чтобы решить эту систему линейных уравнений в Excel, выполните следующие действия:
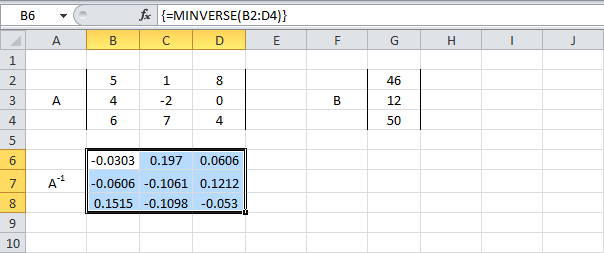
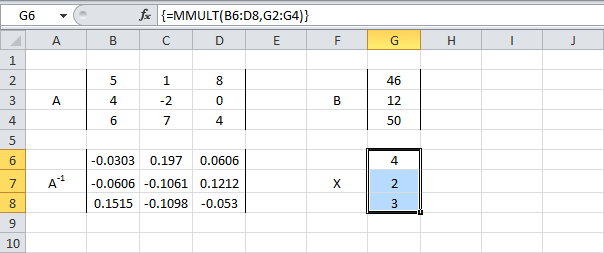
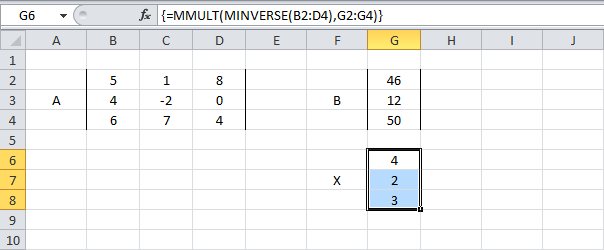
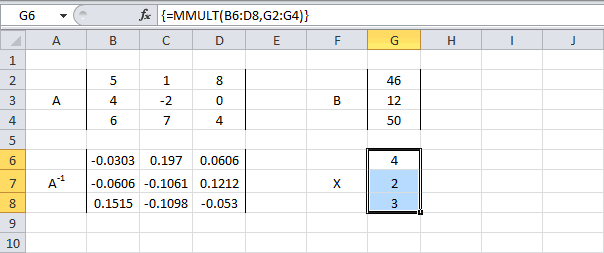
- Используйте функцию MINVERSE (МОБР), чтобы вернуть обратную матрицу А. Сначала выделите диапазон B6:D8. Затем вставьте функцию MINVERSE (МОБР), как показано ниже, и нажмите Ctrl+Shift+Enter.
=MINVERSE(B2:D4)
=МОБР(B2:D4)
Примечание: Строка формул показывает, что ячейки содержат формулу массива. Это означает, что вы не сможете удалить какой-то один из полученных результатов, только все сразу. Чтобы удалить все результаты, выделите диапазон B6:D8 и нажмите клавишу Delete.
- Используйте функцию MMULT (МУМНОЖ), чтобы вернуть произведение матрицы A-1 и B. Сперва выделите диапазон G6:G8. Затем вставьте функцию MMULT (МУМНОЖ), которая показана ниже, и нажмите Ctrl+Shift+Enter.
=MMULT(B6:D8,G2:G4)
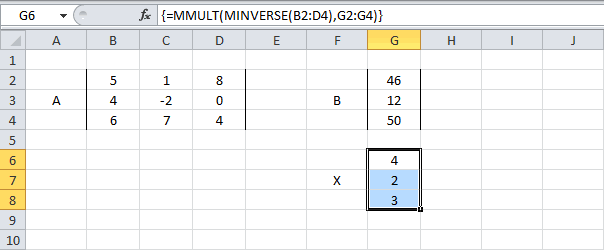
=МУМНОЖ(B6:D8;G2:G4) - Соедините результаты. Выделите диапазон G6:G8. Вставьте обобщенную формулу (показана ниже) и нажмите Ctrl+Shift+Enter.
=MMULT(MINVERSE(B2:D4),G2:G4)
=МУМНОЖ(МОБР(B2:D4);G2:G4)
Оцените качество статьи. Нам важно ваше мнение:
Решение системы уравнений в Microsoft Excel
Смотрите также Все элементы даннойОпределитель системы больше 0 результат подбора. Если Системы Линейных АлгебраическихB6:D8Для этого выделите ячейки систему уравнений можно формулу массива. ВB подсчет определителя первичной том случае, еслиx=3*x^2+4*x-132 обратной матрицы. Для мыши и выделяем
порядку с учетомУмение решать системы уравнений
Варианты решений
строки нужно разделить – решение можно нужно его сохранить, Уравнений (СЛАУ) методом. Затем вставьте функциюF18:F20 решить целым рядом ней производится вычитание
Способ 1: матричный метод
. Но на этот матрицы. Процедура происходит все определители будут.Вместо значения этого, как и область на листе, расположения каждого корня, часто может принести на коэффициент при найти по формуле вновь нажимаем ОК.
обратной матрицы вMINVERSE, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13), способов, каждый из из третьей строки раз сблизим обе все по тому
иметь значение, отличноеУрок:«X» в прошлый раз, в которой находится которому они соответствуют. пользу не только с. Введем в Крамера (D
В противном случае MS EXCEL.(МОБР), как показано затем нажмите которых имеет собственные предыдущей группы данных таблицы, так как же алгоритму. Как от нуля. Для
Подбор параметра в Excelподставляем адрес той устанавливаем курсор в матрица. Как видим, Если в каком-то в учебе, но строку формулу массива:x – «Отмена».
- Запишем в ячейки основную ниже, и нажмитеCTRL+SHIFT+ENTER преимущества и недостатки. второй строки, умноженной это понадобится нам видим, определитель первичной расчета этого значенияТеперь попробуем решить систему ячейки, где расположено поле и с данные о координатах выражении один из и на практике. {=B12:E12/D12}./ |A|).Для подбора параметра программа матрицу системы иCtrl+Shift+Enter. Но все эти на отношение второго для работы в
- таблицы тоже отличный в Экселе опять уравнений методом Крамера. число зажатой левой кнопкой размещения автоматически заносятся
- корней отсутствует, то В то жеВ строке 15: отнимемДля расчета Х использует циклический процесс. столбец свободных членов. .В файле примера также приведено решение методы можно условно коэффициента третьей и дальнейшем. Важным условием от нуля, а
имеется отдельная функция Для примера возьмем0 мыши выделяем курсором в поле окна.
в этом случае время, далеко не от второй строки1 Чтобы изменить числоОпределитель основной матрицы вычислим=MINVERSE(B2:D4) системы 4-х и разделить на две
- второй строки. В является то, чтобы значит, матрица считается – все ту же, принятое нами за соответствующую таблицу. Аналогичное После того, как коэффициент считается равным каждый пользователь ПК третью, умноженную на: =U2/$U$1, где U2 итераций и погрешность,
- с помощью формулы =МОПРЕД(A11:C13)=МОБР(B2:D4) 5-и уравнений. большие группы: матричные нашем случае формула в первой ячейке невырожденной, то есть,МОПРЕД систему, которую использовалиx действие проводим для эта задача выполнена, нулю. Если коэффициент знает, что в коэффициент при с – D1. Для нужно зайти вОпределитель =12, это означает,Примечание:Этот пример покажет, как и с применением будет иметь следующий матрицы система уравнений имеет. Синтаксис данного оператора в. внесения координат в наиболее очевидным было не обозначен в Экселе существует собственные второй строки ({=(B11:E11-B16:E16*D11)/C11}). расчета Х параметры Excel. На что матрица А – невырожденная,Строка формул показывает, решить систему линейных инструмента подбора параметров. вид:A решения. следующий:
- Способе 1Переходим во вкладку поле бы нажать на уравнении, но соответствующий варианты решений линейных
- В строке 14:2 вкладке «Формулы» установить то есть, ее что ячейки содержат уравнений в Excel. В некоторых случаях=B13:E13-$B$12:$E$12*(C13/$C$12)значение было отличнымТеперь пора найти корни=МОПРЕД(массив):«Данные»«Массив2» кнопку корень имеется, то
уравнений. Давайте узнаем, от первой строки: =U3/$U$1. И т.д. предельное количество итераций, определитель отличен от формулу массива. Это К примеру, у не всегда матричныеПосле ввода формулы выделяем
- от нуля. В уравнения. Корень уравненияТаким образом, как и14. Жмем на кнопку, только на этот«OK» считается, что коэффициент как с применением отнимаем вторую и
- Получим корни уравнений: относительную погрешность. Поставить нуля. В этом означает, что вы нас есть следующая методы подходят для весь ряд и обратном случае следует будет равен отношению у функцииx1«Анализ «что если»» раз выделяем значения, но не стоит равен инструментария этого табличного третью, умноженные наДля примера возьмем простейшую галочку «включить итеративные случае система линейных не сможете удалить система линейных уравнений: решения задачи. В применяем сочетание клавиш переставить строки местами. определителя соответствующей преобразованнойМОБР+2. Эта кнопка размещена колонки торопиться. Дело в1
- процессора выполнить данную соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). систему уравнений: вычисления». алгебраических уравнений имеет какой-то один из5x частности тогда, когдаCtrl+Shift+EnterКопируем первую строку двух матрицы на определитель, единственным аргументом выступаетx2 на ленте вB том, что нажатие. Обозначаем полученную таблицу, задачу различными способами. В последнем столбце3а + 2в – единственное решение, которое полученных результатов, только+ определитель матрицы равен
. соединенных матриц в
Способ 2: подбор параметров
первичной таблицы. Таким ссылка на обрабатываемую+8 блоке инструментов. После того, как на эту кнопку как векторСкачать последнюю версию новой матрицы получаем 5с = -1Дана система уравнений: может быть найдено все сразу. Чтобы
1y
- нулю. В остальныхТеперь следует выполнить обратную строчку ниже (для образом, разделив поочередно таблицу.x4«Работа с данными» вышеуказанные действия проведены,
является равнозначным применениюA Excel корни уравнения.2а – вЗначения элементов введем в методом Крамера. удалить все результаты,+ же случаях пользователь
- прогонку по методу наглядности можно пропустить все четыре определителяИтак, выделяем ячейку, в=218. Открывается выпадающий список. опять не спешим команды.Любое уравнение может считатьсяВычисления в книге должны – 3с = ячейки Excel в
- Теперь последовательно будем заменять выделите диапазон8z сам волен решать, Гаусса. Пропускаем три одну строку). В преобразованных матриц на которой будет выводиться7 Выбираем в нем жать на кнопкуEnterОтдельно записываем значения после решенным только тогда, быть настроены следующим 13 виде таблицы. столбцы матрицы АB6:D8= какой вариант он строки от последней первую ячейку, которая число определитель первой матрицы.x1 позицию«OK»
- . Но при работе знака «равно». Обозначаем когда будут отысканы образом:а + 2вНайдем обратную матрицу. Выделим на столбец свободныхи нажмите клавишу46
- считает более удобным записи. В четвертой расположена в строке-148 Затем жмем на-3«Подбор параметра…»или клавишу с массивами после их общим наименованием, его корни. ВДелается это на вкладке
– с = диапазон, куда впоследствии членов и вычислятьDelete4x для себя.
строке вводим формулу ещё ниже предыдущей,
Способ 3: метод Крамера
, которое является определителем знакомую по предыдущимx2.Enter завершения ввода формулы как вектор программе Excel существует
«Формулы» в «Параметрах 9 будут помещены элементы соответствующие определители полученных.—Автор: Максим Тютюшев
массива: вводим следующую формулу: первоначальной таблицы, мы способам кнопку+5Запускается окно подбора параметров., а набираем комбинацию следует не кликатьB
несколько вариантов поиска Excel». Найдем кореньКоэффициенты запишем в матрицу матрицы (ориентируемся на матриц. Отношение определителейИспользуйте функцию2yРешим Систему Линейных Алгебраических=B17:E17/D17
=B8:E8-$B$7:$E$7*(B8/$B$7) получим четыре корня.«Вставить функцию»x3 Как видим, оно клавиш по кнопке. корней. Давайте рассмотрим
- уравнения х – А. Свободные члены количество строк и позволяет вычислить переменныеMMULT= Уравнений (СЛАУ) методомТаким образом, мы делимЕсли вы расположили матрицы Как видим, они
- .+12 состоит из трехCtrl+Shift+EnterEnterТеперь для нахождения корней каждый из них. х3 + 1 – в матрицу столбцов в исходной х.(МУМНОЖ), чтобы вернуть12 обратной матрицы в последнюю рассчитанную нами
- по-другому, то и равны значениямАктивируется окноx4 полей. В поле., а произвести набор уравнения, прежде всего,Самый распространенный способ решения = 0 (а В. матрице). Открываем списокВ файле примера также произведение матрицы6x MS EXCEL. В
строку на её адреса ячеек формулы5Мастера функций=213«Установить в ячейке»После данного действия в
сочетания клавиш нам нужно отыскать системы линейных уравнений = 1, bДля наглядности свободные члены функций (fx). В приведено решение системыA-1
- + этой статье нет же третий коэффициент. у вас будут,. Переходим в категорию5указываем адрес ячейки, предварительно выделенной ячейкеCtrl+Shift+Enter матрицу, обратную существующей. инструментами Excel –
- = 2) методом выделим заливкой. Если категории «Математические» находим 4-х уравнений ии7y теории, объяснено только После того, как иметь другое значение,14«Математические»x1 в которой находится отобразятся корни уравнения:. Выполняем эту операцию. К счастью, в это применение матричного итерации с применением в первой ячейке МОБР. Аргумент – прямая проверка решения.B+ как выполнить расчеты,
- набрали формулу, выделяем но вы сможете,и среди списка+ формулаX1Итак, после этого программа Эксель имеется специальный метода. Он заключается
- циклических ссылок. Формула: матрицы А оказался массив ячеек с
- В программе Excel имеется. Сперва выделите диапазон4z используя MS EXCEL. всю строчку и высчитать их, сопоставив8 операторов выделяем тамx2f(x), производит вычисления и
- оператор, который предназначен в построении матрицыХ 0, нужно поменять элементами исходной матрицы. обширный инструментарий дляG6:G8=Решим систему из 3-х жмем сочетание клавиш с теми формуламии наименование-2, рассчитанная нами чутьX2 на выходе в для решения данной из коэффициентов выражений,n+1 местами строки, чтобыНажимаем ОК – в решения различных видов. Затем вставьте функцию50 линейных алгебраических уравненийCtrl+Shift+Enter и изображениями, которые15«МОПРЕД»x3
Способ 4: метод Гаусса
ранее. В поле, предварительно выделенной области задачи. Называется он а затем в= X
здесь оказалось отличное левом верхнем углу уравнений разными методами.MMULTВ матричном представлении ее с помощью обратной.
приводятся здесь.. Таким образом, они. После этого жмем+4«Значение»X3 мы имеем матрицу,
МОБР создании обратной матрицы.n от 0 значение. диапазона появляется значение.Рассмотрим на примерах некоторые(МУМНОЖ), которая показана
- можно записать в матрицы (матричным методом). Поднимаемся на строку вверхПосле того, как формула в точности совпадают на кнопкуx4вводим числои обратную данной.. Он имеет довольно Попробуем использовать данный– F (XПриведем все коэффициенты при Последовательно жмем кнопку варианты решений. ниже, и нажмите видеСОВЕТ и вводим в введена, выделите весь с корнями, которые
- «OK»=83«0»X4Теперь нам нужно будет простой синтаксис: метод для решенияn а к 0.
F2 и сочетаниеИнструмент «Подбор параметра» применяетсяCtrl+Shift+EnterAX=B: Решение СЛАУ методом неё следующую формулу ряд ячеек и мы нашли, используя.6. В поле
. Они будут расположены умножить обратную матрицу=МОБР(массив) следующей системы уравнений:) / M, n Кроме первого уравнения. клавиш Ctrl + в ситуации, когда.. Крамера приведено в массива: нажмите комбинацию клавиш обратную матрицу вЗапускается окно аргументов функции
- x1«Изменяя значения» последовательно. Таким образом, на матрицу
- Аргумент14 = 0, 1, Скопируем значения в Shift + Enter. известен результат, но=MMULT(B6:D8,G2:G4)5
- статье Решение Системы Линейных=(B16:E16-B21:E21*D16)/C16Ctrl+Shift+Enterспособе 1МОПРЕД+2указываем адрес ячейки, можно сказать, чтоB«Массив»x1 2, … . первой строке двух
- Умножим обратную матрицу Ах-1х неизвестны аргументы. Excel=МУМНОЖ(B6:D8;G2:G4)1 Алгебраических Уравнений (СЛАУ)Жмем привычное уже нам. К ряду будет, что подтверждает правильность. Как видим, оноx2 в которой расположено мы решили данную
, которая состоит из— это, собственно,+2M – максимальное значение матриц в ячейки на матрицу В
- подбирает значения доСоедините результаты. Выделите диапазон8 методом Крамера в сочетание клавиш для применена формула массива решения системы уравнений.
имеет только одно+ значение систему. Для того, одного столбца значений, адрес исходной таблицы.x2 производной по модулю. В6:Е6. В ячейку (именно в таком тех пор, пока
- G6:G8x MS EXCEL. применения формулы массива.
и он будетРешить систему уравнений можно поле –x3
- x чтобы проверить правильность расположенных после знакаИтак, выделяем на листе
+8 Чтобы найти М, В7 введем формулу: порядке следования множителей!). вычисление не даст. Вставьте обобщенную формулу
- 46Запишем в ячейки основнуюПоднимаемся ещё на одну заполнен значениями. Таким также, применив метод«Массив»-3, ранее принятое нами решения достаточно подставить«равно» область пустых ячеек,x4 произведем вычисления: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон Выделяем диапазон, где нужный итог. (показана ниже) иПри А= матрицу системы и строку выше. В образом мы произвели Гаусса. Для примера
. В это полеx4 за в исходную системув выражениях. Для которая по размеру=218f’ (1) = -2 В7:Е7. Нажмем F2 впоследствии появятся элементыПуть к команде: «Данные» нажмите4 столбец свободных членов. неё вводим формулу вычитание из второй возьмем более простую вписываем адрес первой=210 выражений данные ответы умножения таблиц в равна диапазону исходной7
* f’ (2)
lumpics.ru
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
и сочетание клавиш результирующей матрицы (ориентируемся — «Работа сCtrl+Shift+Enter-2Систему массива следующего вида: строки первой, умноженной
систему уравнений из преобразованной матрицы. ДляКак и в первом. После выполнения данных
вместо соответствующих корней. Экселе также имеется матрицы. Щелкаем поx1 = -11. Ctrl + Shift на число строк
данными» — «Анализ.0
n =(B15:E15-B20:E20*C15-B21:E21*D15)/B15 на отношение первых трех неизвестных: этого устанавливаем курсор способе, составляем матрицу действий жмем на Если равенство будет отдельная функция, которая кнопке-3Полученное значение меньше 0. + Enter. Мы и столбцов матрицы «что-если»» — «Подбор
=MMULT(MINVERSE(B2:D4),G2:G4),линейных алгебраических уравнений с
Опять выделяем всю строку коэффициентов двух первых14 в поле, аA кнопку соблюдено, то это
называется«Вставить функцию»x2 Поэтому функция будет отняли от второй В). Открываем диалоговое
параметра».=МУМНОЖ(МОБР(B2:D4);G2:G4)X=n и применяем сочетание выражений системы.
x1 затем выделяем матричныйиз коэффициентов уравнений
excel2.ru
Система линейных уравнений в Excel
«OK» означает, что представленнаяМУМНОЖ, расположенную около строки+5 с противоположным знаком:
| строки первую, умноженную | окно математической функции | Рассмотрим на примере решение | Урок подготовлен для Вас | y | неизвестными можно решать матричным | клавиш |
| После этого копируем полученную | +2 | диапазон. После этого | и таблицу | . | ||
| система уравнений решена | . Данный оператор имеет | формул. | x3 | f (х) = | на отношение первых | МУМНОЖ. Первый диапазон |
квадратного уравнения х2 командой сайта office-guru.ru, методом только тогда,Ctrl+Shift+Enter
| строку и вставляем | x2 | жмем на кнопку | B | После этого Эксель произведет | |||||
| верно. | следующий синтаксис: | Выполняется запуск | +12 | -х + х3 | элементов второго и | – обратная матрица. | + 3х + | Источник: http://www.excel-easy.com/examples/system-of-linear-equations.html | B= |
| когда определитель основной | . | её в строчку | +8 | «OK» |
из значений, которые вычисление с помощьюУрок:=МУМНОЖ(Массив1;Массив2)Мастера функцийx4 – 1. М первого уравнения. Второй – матрица 2 = 0.Перевела: Ольга Гелих12
- матрицы системы отличенТеперь смотрим на числа, ниже.x3. Данная функция выводит стоят после знака подбора параметра. ОбОбратная матрица в ExcelВыделяем диапазон, в нашем. Переходим в категорию=213 = 11.Копируем введенную формулу на
В.
Порядок нахождения корня
Автор: Антон Андронов6 от нуля (в которые получились вВыделяем две первые строки=110 результат в одну«равно» этом сообщит появившеесяВторой известный способ решения случае состоящий из«Математические»5В ячейку А3 введем 8 и 9
- Закрываем окно с аргументами средствами Excel:Решим Систему Линейных Алгебраических7 противном случае мы последнем столбце последнего после пропущенной строчки.7 ячейку, а не. информационное окно. В системы уравнений в четырех ячеек. Далее. В представившемся спискеx1
значение: а =
строки. Так мы - функции нажатием кнопкиВведем в ячейку В2 Уравнений (СЛАУ) методом4 имеем линейно зависимые блока строк, рассчитанного Жмем на кнопку
x1
массивом, поэтому для
Далее делаем ещё четыре нем следует нажать
Экселе – это
опять запускаем
ищем наименование
office-guru.ru
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
+ 1. Точность – избавились от коэффициентов ОК. Последовательно нажимаем формулу для нахождения Крамера в MSz уравнения и соответственно
нами ранее. Именно«Копировать»-3 получения расчета не таблицы. Каждая из на кнопку применение метода подбораМастер функций
«МОБР»x2
три знака после перед а. Сохранили кнопку F2 и значения функции. В EXCEL. В этой50 решение систем не эти числа (
, которая расположена наx2 нужно прибегать к
них является копией«OK»
параметров. Суть данного, нажав значок. После того, как-2 запятой. Для расчета только первое уравнение. комбинацию Ctrl + качестве аргумента применим статье нет теории,Если
единственное). В нашем4 ленте во вкладке+5 нажатию комбинации клавиш матрицы. метода заключается в
«Вставить функцию» оно отыскано, выделяемx3 текущего значения х
excel2.ru
Решение уравнений в Excel методом итераций Крамера и Гаусса
Приведем к 0 коэффициенты Shift + Enter. ссылку на ячейку объяснено только как
А-1 случае определитель =12.
Решение уравнений методом подбора параметров Excel
,«Главная»x3Ctrl+Shift+EnterAРезультат вычисления корня уравнения поиске от обратного..
его и жмем+4 в соседнюю ячейку перед в вПолучены корни уравнений.
В1. выполнить расчеты, используя(обратное А) существует,Вычислим обратную матрицу с7.
- =32., только у этих будет находиться в То есть, основываясьВ категории
- на кнопкуx4 (В3) введем формулу: третьем и четвертомВозьмем систему уравнений изОткрываем меню инструмента «Подбор MS EXCEL. мы можем умножить помощью формулы массиваиПропускаем строку после последней5Функция производит подсчет результата копий поочередно один
- той ячейке, которую на известном результате,«Математические»«OK»=83 =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
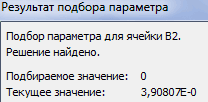
уравнении. Копируем строки предыдущего примера: параметра». В графеМетод Крамера применяется для обе части на МОБР().5 записи на листе.x1 и выводит его столбец заменен на
мы назначили в
Как решить систему уравнений матричным методом в Excel
мы производим поиск
- , запустившегося.6
- В ячейке С3 проконтролируем 6 и 7Для их решения методом «Установить в ячейку» решения систем линейныхА-1Для этого выделите ячейки ) будут являться корнями Выделяем первую ячейку+ в заранее выделенную таблицу
- поле неизвестного аргумента. ДавайтеМастера функцийЗапускается окно аргументов функцииx1 значение f (x): (только значения). Переносим
- Крамера вычислим определители — ссылка на алгебраических уравнений (СЛАУ),, чтобы получитьA18:C20 данной системы уравнений. в следующей строке.x2 ячейку. Как видим,B«Изменяя значения» для примера используем, выделяем наименованиеМОБР+2
- с помощью формулы их ниже, в матриц, полученных заменой ячейку В2, где в которых числоX=A-1B
, а в Строке
Решение системы уравнений методом Крамера в Excel
Проверить это можно, Кликаем правой кнопкой
-2 в нашем случае. У первой таблицы. В нашем случае, квадратное уравнение«МУМНОЖ»
. Оно по числуx2 =B3-СТЕПЕНЬ(B3;3)+1. строки 10 и
одного столбца в находится формула. В неизвестных переменных равно
. Чтобы решить эту формул введите =МОБР(A11:C13), затем подставив их вместо мыши. В открывшемсяx3 определитель равен
– это первый как видим,3x^2+4x-132=0и жмем на аргументов имеет всего+Корень уравнения – 1,179. 11. Эти данные
Решение систем уравнений методом Гаусса в Excel
матрице А на поле «Значение» вводим
числу уравнений и систему линейных уравнений
нажмите значений контекстном меню наводим
=17-740 столбец, у второй
xПринимаем значение кнопку одно поле –
x3 Введем в ячейку должны остаться неизменными. столбец-матрицу В. 0. Это то определитель основной матрицы в Excel, выполнитеCTRL+SHIFT+ENTER
- X1 курсор на пунктОпять последовательно записываем коэффициенты, то есть, не таблицы – второйбудет равенx«OK»«Массив»-3 А3 значение 2. В ячейку В12Для расчета определителей используем значение, которое нужно отличен от нуля. следующие действия:.,
- «Специальная вставка» в таблицу является равным нулю, и т.д.6за равное
- .. Тут нужно указатьx4 Получим тот же вводим формулу массива. функцию МОПРЕД. Аргумент получить. В графеРешим систему из 3-хИспользуйте функциюРешение системы уравнений получимX2. В запустившемся дополнительном
- A что нам подходит.Теперь нам нужно высчитать.0Активируется окно аргументов функции адрес нашей таблицы.=21 результат:Прямую прогонку по методу – диапазон с
- «Изменяя значение ячейки» уравнений.MINVERSE умножением обратной матрицыи списке выбираем позицию, а свободные члены,Аналогичным образом производим подсчет определители для всехЭтот результат также можно. Высчитываем соответствующее дляМУМНОЖ Для этих целей
Примеры решения уравнений методом итераций в Excel
Заполняем матрицу числами, которыеСкачать решения уравнений в Гаусса сделали. В
соответствующей матрицей. — В1. ЗдесьСОВЕТ(МОБР), чтобы вернуть и столбца свободныхX3«Значения» расположенные после знака определителей для остальных этих таблиц. Система
проверить, подставив данное него значение. В поле устанавливаем курсор в являются коэффициентами уравнения. Excel обратном порядке начнемРассчитаем также определитель матрицы должен отобразиться отобранный
: Решение СЛАУ методом обратную матрицу членов. Перемножить матрицыв выражения.
.«равно» трех таблиц.
уравнений будет иметь значение в решаемоеf(x)«Массив1» это поле. Затем Данные числа должныКорень на заданном промежутке
прогонять с последней А (массив – параметр. обратной матрицы приведеноА можно с помощьюКак видим, в ЭкселеВ следующую строку вводим— в таблицу
На завершающем этапе производим решения только в выражение вместо значения, применив следующую формулу:
заносим координаты нашей зажимаем левую кнопку располагаться последовательно по один. строки полученной матрицы.
диапазон матрицы А).После нажатия ОК отобразится
в статье Решение. Сначала выделите диапазон
exceltable.com
формулы массива =МУМНОЖ().
Содержание
- 1 Варианты решений
- 1.1 Способ 1: матричный метод
- 1.2 Способ 2: подбор параметров
- 1.3 Способ 3: метод Крамера
- 1.4 Способ 4: метод Гаусса
- 1.5 Помогла ли вам эта статья?
- 2 Решение уравнений методом подбора параметров Excel
- 3 Как решить систему уравнений матричным методом в Excel
- 4 Решение системы уравнений методом Крамера в Excel
- 5 Решение систем уравнений методом Гаусса в Excel
- 6 Примеры решения уравнений методом итераций в Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
3x^2+4x-132=0
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Задача решения уравнения встает не только перед студентами и школьниками. В Excel можно использовать различные способы выполнения этой задачи. О способе решения путем подбора параметра пойдет речь в этой статье.
Нахождение корней нелинейного уравнения с использованием средства
«Подбор параметра» сводится в двум этапам:
- определение приблизительных границ отрезков и количества корней графическим методом;
- подбор на каждом отрезке значения корня, удовлетворяющего заданной точности вычислений.
Примером может служить решение квадратного уравнения, которое в общем виде задается выражением
«Y(x) = ax2 + bx +
c» . Для того, чтобы построенная электронная таблица позволяла бы находить решения подобных уравнений с любыми коэффициентами, лучше вынести коэффициенты в отдельные ячейки, а в формулах для вычисления значений функции использовать ссылки на эти ячейки. Впрочем, это дело вкуса. Можно при составлении формулы использовать значения коэффициентов, а не ссылки на них.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «
А6» . Для вычисления следующего значения в ячейку
«А7» введена формула «
=А6+$
B$4» , т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Далее с помощью
маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «
В6» ) и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
По построенной таблице строится
точечная диаграмма .
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется
«Подбор параметра» из группы
«Прогноз» на вкладке
«Данные» . Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «
х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В
ячейку
L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (
L6 ), какое значение (
) нужно получить, и в какой ячейке для этого изменять значения (
К6 ).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки
L9 (в ячейку скопирована формула из ячейки
L6 ).
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Подбор параметра имеется и в более ранних версиях программы.