Использование графических возможностей excel при решении статистических задач

Министерство образования и науки Астраханской области

ГАПОУ АО «Астраханский социально-педагогический колледж»

Специальность: 39.02.01 «Социальная работа»

Сообщение.

По дисциплине: «Статистика»

Тема: Использование графических возможностей Excel при решении статистических задач.

Выполнила: Студентка группы 2 «С» ___________Рюминой Д.А. Проверила: Преподаватель ___________ Коржова А.П.

г. Астрахань, 2023

В современном обществе к статистическим методам проявляется повышенный интерес как к одному из важнейших аналитических инструментариев в сфере поддержки процессов принятия решений. Статистикой пользуются все- от политиков, желающих предсказать исход выборов, до предпринимателей, стремящихся оптимизировать прибыль при тех или иных вложениях капитала. Большим шагом вперёд к развитию статистической науки послужило применение экономико-математических методов и использование компьютерной техники в анализе социально-экономических явлений.

Программа обработки электронных таблиц MS Excel- мощная и достаточно простая в использовании программа, предназначенная для решения широкого круга планово-экономических, учетно-статистических, научно-технических и других задач, в которых числовая, текстовая или графическая информация с некоторой регулярной, повторяющейся структурой представлена в табличном виде.

Программа MS Excel предоставляет богатые возможности создания и изменения таблиц, которые могут содержать числа, тексты, даты, денежные единицы, графику, а также математические и иные формулы для выполнения вычислений.

Предусмотрены средства представления числовых данных в виде диаграммы, создания, сортировки и фильтрации списков, статического анализа данных и решения оптимизационных задач.

В данной работе я постараюсь показать, какие возможности для обработки статистических данных имеет программа MS Excel.

Объектом исследования данной работы являются возможности табличного процессора.

Предметом исследования является применение программы MS Excel для решения статистических задач.

Актуальность работы обусловлена недостаточной реализацией возможностей MS Excel для решения статистических задач.

Цель настоящего исследования заключается в формировании устойчивых знаний о возможностях MS Excel для решения статистических задач.

Для достижения поставленной цели потребовалось решить следующие задачи:

1. Раскрыть сущность возможностей MS Excel.

2. Определить способы применения этих возможностей при решении задач статистики.

В качестве гипотезы выдвигается следующее:

Использование возможностей программы MS Excel облегчает и ускоряет решения задач статистики.

Глава 1. Применение Microsoft Excel для решения

статистических задач.

Работа с данными

В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде.

Графические изображения используются, прежде всего, для наглядного представления статистических данных, благодаря ним существенно облегчается их восприятие и понимание. Существенна их роль и тогда, когда речь идет о контроле полноты и достоверности исходного статистического материала, используемого для обработки и анализа.

Статистические данные приводятся в виде длинных и сложных статистических таблиц, поэтому бывает весьма трудно обнаружить в них имеющиеся неточности и ошибки.

В процессе анализа данных, как правило, присутствуют следующие основные этапы:

1. Ввод данных

Введенные данные обычно отражаются в форме электронной таблицы или матрицы данных, где столбцы представляют различные переменные (например, рост, вес), а строки — измерение значений этих переменных, произведенные в различных условиях, в различное время, у различных объектов и т.п.

2. Преобразование данных

Данные в электронной таблице можно просмотреть и скорректировать методами ручного редактирования или же полуавтоматического преобразования к виду, адекватному выбранному методу анализа. Здесь может быть использован широкий набор алгебраических, матричных, структурных преобразований, а также комбинирование этих операций в требуемой последовательности.

3. Визуализация данных

На данные обязательно следует просто посмотреть, чтобы составить общее (в том числе и интуитивное) представление о характере их изменения, специфических особенностях и закономерностях, что очень важно при выборе стратегии и тактики дальнейшего анализа. Для этого можно использовать как исходное числовое представление, так и различные формы графического изображения.

4. Статистический анализ

Собственно выбор метода, анализ данных и интерпретация результатов.

5. Представление результатов

Для наглядности производимых выводов полученные результаты желательно представлять в виде адекватных, убедительных и эффектных графиков.

Для успешного применения процедур анализа необходимы начальные знания в области статистических и инженерных расчетов, для которых эти инструменты были разработаны

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и дисперсионного анализа.

При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов, вычисление параметров применяемых математических функций является быстро выполняемой счетной операцией.

Возможность использования формул и функций является одним из важнейших свойств программы обработки электронных таблиц. Это, в частности, позволяет проводить статистический анализ числовых значений в таблице.

Текст формулы, которая вводится в ячейку таблицы, должен начинаться со знака равенства (=), чтобы программа Excel могла отличить формулу от текста. После знака равенства в ячейку записывается математическое выражение, содержащее аргументы, арифметические операции и функции.

В качества аргументов в формуле обычно используются числа и адреса ячеек. Для обозначения арифметических операций могут использоваться следующие символы: + (сложение); — (вычитание); * (умножение); / (деление).

Формула может содержать ссылки на ячейки, которые расположены на другом рабочем листе или даже в таблице другого файла. Однажды введенная формула может быть в любое время модифицирована. Встроенный Менеджер формул помогает пользователю найти ошибку или неправильную ссылку в большой таблице.

Кроме этого, программа Excel позволяет работать со сложными формулами, содержащими несколько операций. Для наглядности можно включить текстовый режим, тогда программа Excel будет выводить в ячейку не результат вычисления формулы, а собственно формулу.

Программа Excel интерпретирует вводимые данные либо как текст (выравнивается по левому краю), либо как числовое значение (выравнивается по правому краю). Для ввода формулы необходимо ввести алгебраическое выражение, которому должен предшествовать знак равенства (=). [7]

Ввод формул можно существенно упростить, используя маленький трюк. После ввода знака равенства следует просто щелкнуть мышью по первой ячейке, затем ввести операцию деления и щелкнуть по второй ячейке.

Инструменты пакета анализа в Microsoft Excel

Дисперсионный анализ

Пакет анализа включает в себя три средства дисперсионного анализа. Выбор конкретного инструмента определяется числом факторов и числом выборок в исследуемой совокупности данных. [6]

Однофакторный дисперсионный анализ

Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности. Этот метод распространяется также на тесты для двух средних (к которым относится, например, t-критерий).

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ И
ПРОГНОЗИРОВАНИЕ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ.

Цель занятия. Изучение информационной технологии использования
возможностей Excel для статистических расчетов, графического представления
данных и прогнозирования.
Инструментарий. ПЭВМ IBM PC, программа MS Excel.

Литература.
1. Информационные
технологии в профессиональной деятельности: учебное пособие/ Елена
Викторовна Михеева. – М.: Образовательно-издательский центр «Академия», 2004.

ЗАДАНИЯ

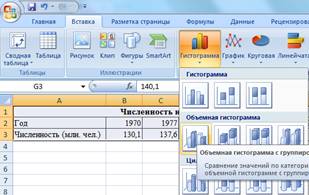
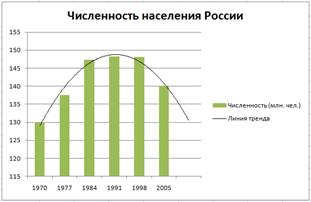
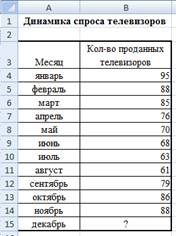
Задание 1. С помощью диаграммы (обычная гистограмма)
отобразить данные о численности населения России (млн. чел.) за 1970- 2005 гг.

Исходные данные представлены на рис.1, результаты работы на рис.3

Рис.1.

Порядок работы.

1. Откройте редактор электронных таблиц Microsoft Excel и создайте новую
электронную книгу (при стандартной установке MS Office выполните Пуск/Все
программы/ Microsoft Excel).

2. Создайте на листе 1 таблицу численности населения по образцу (рис.1). Для
ввода значений лет создайте ряд чисел с интервалом в 7 лет (введите первые два
значения даты — 1970 и 1977, выделите обе ячейки и протяните вправо за маркер
автозаполнения до нужной конечной даты).

3. Постройте диаграмму (обычная гистограмма) по данным таблицы. Для этого
выделите интервал ячеек с данными численности населения А3:G3 и выберите
команду Вставка/Диаграмма. На первом шаге работы с Мастером диаграмм
выберите тип диаграммы – гистограмма обычная; на втором шаге на вкладке Ряд в
окошке Подписи оси Х укажите интервал ячеек с годами В2: G2 (рис.2).
Далее введите название диаграммы и подписи осей; дальнейшие шаги построения
диаграммы осуществляется по подсказкам мастера.

Рис.2.

Задание 2. Осуществить прогноз численности населения России на 2012
г. добавлением линии тренда к ряду данных графика.

Краткая справка.

Для наглядного показа тенденции изменения некоторой
переменной целесообразно на график вывести линию тренда. Это возможно не для
всех типов диаграмм, а только для гистограмм, линейчатых диаграмм, диаграмм с
областями, графиков. Введенная линия тренда сохраняет связь с исходным рядом,
т.е. при изменении данных соответственно изменяется линия тренда. Линию тренда
можно использовать для прогноза данных.

Порядок работы.

1. Добавьте линию тренда к диаграмме, построенной в Задании 1. Для этого
сделайте диаграмму активной щелком мыши по ней и в меню Диаграмма выберите
команду Добавить линию тренда.

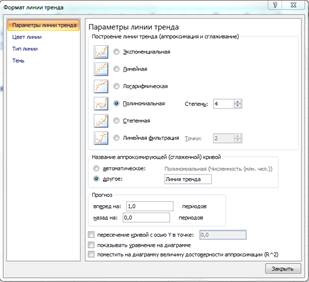
2. В открывшемся окне Линия тренда (рис.3) на вкладке Тип выберите
вид тренда полиномиальный 4-й степени;

Рис.3

3. Для осуществления прогноза на вкладке Параметры введите название
кривой «Линия тренда» и установите параметр прогноза — вперед на один период
(рис.4).

Рис.4

4. На диаграмме будет показана линия тренда и прогноз на один период вперед
(рис.5).

Рис.5

5. Добавьте линии сетки на диаграмме (Диаграмма/ Параметры диаграммы/ Линии
сетки).

Измените цену одного деления оси Y с 5 на 1 (Выполните двойной щелчок по оси и
на вкладке «Шкала» задайте новые значения).

Средствами рисования проведите линию красного цвета (на ось Y) для определения
значения прогноза на 2012 г.

Если вы все сделали правильно, то прогноз численности населения России по линии
тренда составит 131 млн.чел.

Внесите численное значение прогноза на 2012
г. в исходную таблицу.

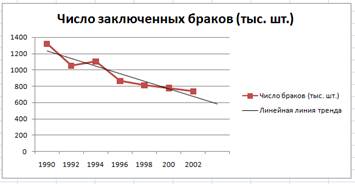
Задание 3. Построить график о числе заключенных браков населением
России. Добавить линейную линию тренда и составить прогноз на три периода
вперед.

Исходные данные представлены на рис. 6, результаты работы на рис. 7.

Рис. 6

Рис. 7

Тема: Графическое
изображение статистических данных и прогнозирование в Microsoft Excel.

Цель
занятия:
Изучение информационных технологий использования возможностей Microsoft excel для
статистических расчетов графического представления данных и прогнозирования.

Задание
1. С
помощью диаграммы (обычная гистограмма) отобразите данные о численности
населения России (млн. чел.) за 1970-2005 гг.

Исходные данные представлены на рис.1,
результаты работы на рис. 3.

Порядок работы

1.     Откройте редактор
электронных таблиц Microsoft Excel и создайте новую
электронную книгу (при стандартной установке Microsoft Office выполните Пуск
– Все программы-Microsoft Office – Microsoft Office Excel).

Рисунок 1 – Исходные данные для задания 1

2.    
Создайте
на листе 1 таблицу численности населения по образцу (см. рис.1). Для ввода
значений лет создайте ряд чисел с интервалом в 7 лет (введите первые два
значения даты – 1970 и 1977 г., выделите обе ячейки и протяните вправо за
маркер автозаполнения до нужной конечной даты).

3.    
Постройте
диаграмму (обычная гистограмма) по данным таблицы. Для этого выделите интервал
ячеек с данными численности населения A3:G3 и выберите
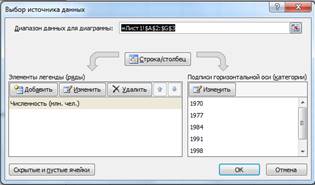
команду Вставка – Гистограмма – Обычная гистограмма. Щелкните правой
кнопкой мыши по построенной диаграмме и выберите команду Выбрать
данные… в открывшемся диалоговом окне измените данные так как показано на
рисунке 3 и нажмите ОК.

Рисунок 2 – Выбор типа диаграммы

Рисунок 3 – Второй этап построения диаграммы

Задание
2. Осуществить
прогноз численности населения России на 2012 г. Добавлением линии тренда к ряду
данных графика.

Краткая справка. Для наглядного
показа тенденции изменения некоторой переменной целесообразно на график вывести
линию тренда. Это возможно не для всех типов диаграмм, а только для гистограмм,
линейчатых диаграмм, диаграмм с областями, графиков. Введенная линия тренда
сохраняет связь с исходным рядом, т. е. при изменении данных соответственно
изменяется линия тренда. Линию тренда можно использовать для прогноза данных.

Порядок работы

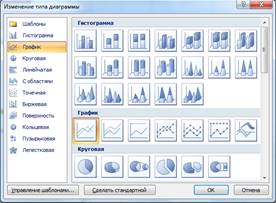
1. Добавьте линию тренда к диаграмме, построенной в
   задании 1. Для этого сделайте диаграмму активной, затем щелкните правой
   кнопкой мыши по диаграмме и выберите команду Изменить тип диаграммы. Измените,
   тип диаграммы выберите График.

Рисунок
4 – Изменения типа тиаграммы

Затем перейдите на
вкладку Макет – Линия тренда – Дополнительные параметры линии тренда… — в
диалоговом окне Формат линии тренда выберите Полиномиальная 4-й
степени затем Закрыть.

Рисунок
5 – Формат линии тренда

Далее измените тип
диаграммы на обычную гистограмму.

1. Для осуществления прогноза в области Название
   аппроксимирующей (сглаженной) кривой выберите Другое и введите
   с клавиатуры Линия тренда.
2. На диаграмме будет показана линия тренда и
   прогноз на один период вперед (рис. 6).

Рисунок 6 – конечный вид диаграммы и линии тренда
задания 1

1. Внесите численное значение прогноза на 2012 г. в
   исходную таблицу. Если вы все сделали правильно, то прогноз численности
   населения России по линии тренда составит 131 млн. чел.

Задание
3. Построить
график о числе заключенных населением России браков. Добавить линию тренда и
составить прогноз на три периода вперед.

Исходные данные представлены на рис. 7,
результаты работы на рис. 8.

Рисунок 7 – Исходные данные для задания 3

Рисунок 8 – Конечный вид графика и линии тренда
задания 3

Задание
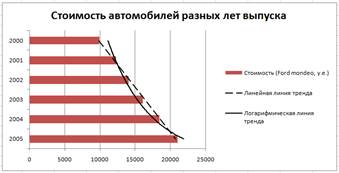
4. Построить
линейчатую диаграмму изменения стоимости автомобилей в зависимости от года
выпуска. Добавить линейную и логарифмическую линии тренда. Определить, какой
вид линии тренда дает более реальный прогноз. Определить примерную стоимость
автомобилей 1998 и 1997 гг. выпуска.

Исходные данные представлены на рис. 9,
результаты работы на рис. 10.

Рисунок 9 – Исходные данные для задания 4

Рисунок 10 – Конечный вид диаграммы и линий тренда
задания 4

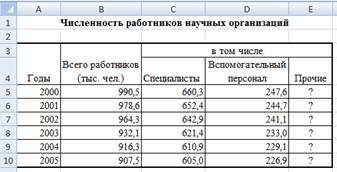
Задание
5. По
данным о численности работников научных организаций (тыс. чел.) в России за
2000-2005 гг. произвести расчеты и построить графики численности работников по
категориям

Формула для расчета столбца «Прочие»:

Прочие = Всего работников — Специалисты –
Вспомогательный персонал.

Добавить линию тренда и составить прогноз
изменений численности специалистов на три года вперед.

Исходные данные представлены на рис. 11.

Рисунок 11 – Исходные данные для
задания 5

Задание 6. Произвести
прогнозирование спроса товаров народного потребления торгового центра на
декабрь текущего года добавлением к графику полиномиальной линии тренда

Исходные данные представлены на рис. 12.

Рисунок 12 – Исходные данные для
задания 6

Лабораторная работа
№1

Цель работы:
Получить навыки построения диаграмм
распределений в среде электронных
таблиц MS
Excel.

Задачи работы:
Изучить основные методы графического
представления статистических данных.
Изучить возможности построения графиков
в среде Excel.
По данным выборочной совокупности
построить полигон частот, гистограмму
и сглаженную кумулятивную кривую
распределения с использованием
электронных таблиц MS
Excel.

Теоретические сведения

Большинство
экономических задач, где требуется
обработка большого количества данных,
решается с помощью методов математической
статистики. Практически любая обработка
данных начинается с ее графического
анализа. Использование графиков в
статистике насчитывает более двухсот
лет. Однако, прежде чем рассмотреть
графические методы анализа, необходимо
ознакомиться с основными понятиями
одного из главного раздела теории
статистики, получившей название
описательной статистики, в рамках
которой и изучаются методы построения
различных видов диаграмм и графиков.

Описательная
статистика позволяет
описывать, подытоживать и воспроизводить
в виде таблиц или графиков данные того
или иного распределения,
вычислять среднее
для данного распределения и его размах
и дисперсию.
Все эти параметры часто называют
описательными статистиками основными
числовыми характеристиками выборки
(совокупности) или мерами центральной
тенденции. Описательная статистика
включает в себя табулирование,
представление и описание совокупностей
данных, которые могут быть как
количественные (например, измерение
роста, веса и т.д.), так и качественные
(например, пол или тип личности).

Одна из задач описательной
статистики состоит в том, чтобы
анализировать данные, полученные на
части популяции, с целью сделать выводы
относительно популяции в целом.

Популяция или
генеральная совокупность в
статистике не обязательно означает
какую-либо группу людей или естественное
сообщество; этот термин относится ко
всем существам или предметам, образующим
общую изучаемую совокупность, будь то
атомы или студенты, посещающие то или
иное кафе.

Выборка или
выборочная совокупность
— это небольшое количество элементов,
отобранных с помощью научных методов
так, чтобы она была репрезентативной,
т.е. отражала популяцию в целом.

Другими словами, выборка
– это совокупность случайно отобранных
объектов, а генеральная совокупность
– это совокупность объектов, из которых
производится выборка.

Объемом совокупности
(выборочной или генеральной) называют
число объектов этой совокупности.
Например, из 1000 человек для исследования
отобрано 100 людей, то объем генеральной
совокупности

,
а объем выборки

.

Генеральная совокупность
часто содержит конечное число объектов.
Однако если это число достаточно велико,
то иногда в целях упрощения вычислений,
или для облегчения теоретических
выводов, допускают, что генеральная
совокупность состоит из бесчисленного
множества объектов. Такое допущение
оправдывается тем, что увеличение объема
генеральной совокупности (достаточно
большого объема) практически не
сказывается на результатах обработки
данных выборки.

Пусть из генеральной
совокупности извлечена выборка, причем

наблюдалось

раз,

—

раз,

—

раз и

— объем выборки. Наблюдаемые значения

называют вариантами,
а последовательность вариант, записанных
в возрастающем порядке – вариационным
рядом. Числа
наблюдений называют частотами,
а их отношения к объему выборки

— относительными частотами.

Статистическим
распределением выборки
называют перечень вариант и соответствующих
им частот или относительных частот.
Статистическое распределение можно
также задать в виде последовательности
интервалов и соответствующих им частот
(в качестве частоты, соответствующей
интервалу, принимаю сумму частот,
попавших в этот интервал).

Для оценки статистического
распределения вводится понятие функции
распределения, которая находится
эмпирическим (опытным) путем и называется
эмпирической.

Эмпирической функцией
распределения (функцией распределения
выборки) называют функцию

,
определяющую для каждого значения

относительную
частоту события

:

,

где

— число вариант, меньших

;

— объем выборки.

В отличие от эмпирической
функции распределения выборки функцию
распределения

генеральной совокупности называют
теоретической функцией распределения.
Различия между эмпирической и теоретической
функцией распределения состоит в том,
что теоретическая функция

определяет вероятность события

,
а эмпирическая функция

определяет частоту этого же события.

В большинстве случаев
при решении реальных задач закон
распределения и его параметры неизвестны.
Поэтому для определения вида закона
распределения и его параметров необходимо
выполнять ряд действий по анализу
полученных исходных данных.

Таким образом,
описательная статистика позволяет
обобщать первичные результаты, полученные
при наблюдении или в эксперименте.
Процедуры здесь сводятся к группировке
данных по их значениям, построению
распределения их частот, выявлению
центральных тенденций распределения
(например, средней арифметической) и,
наконец, к оценке разброса данных по
отношению к найденной центральной
тенденции.

Построение распределения
— это разделение первичных данных,
полученных на выборке, на классы или
категории с целью получить обобщенную
упорядоченную картину, позволяющую их
анализировать.

Для наглядности строят
различные графики статистического
распределения, в частности, полигон
распределения, гистограмму или сглаженную
кумулятивную кривую.

Полигоном частот
называют ломаную, отрезки которой
соединяют точки

,

,
…,

.
Для построения полигона часто на оси
абсцисс откладывают варианты

,
а на оси ординат – соответствующие им
частоты

.
Точки

соединяют
отрезками прямых и получают полигон
частот.

Полигоном относительных
частот называют
ломаную, отрезки которой соединяют
точки

,

,
…,

.
Для построения полигона часто на оси
абсцисс откладывают варианты

,
а на оси ординат – соответствующие им
относительные частоты

.
Точки

соединяют
отрезками прямых и получают полигон
относительных частот.

На рис. 1 показан полигон
относительных частот для следующего
распределения:

Варианта (значение признака),	12	14	16	18	20
Частота,	0,1	0,2	0,4	0,2	0,1

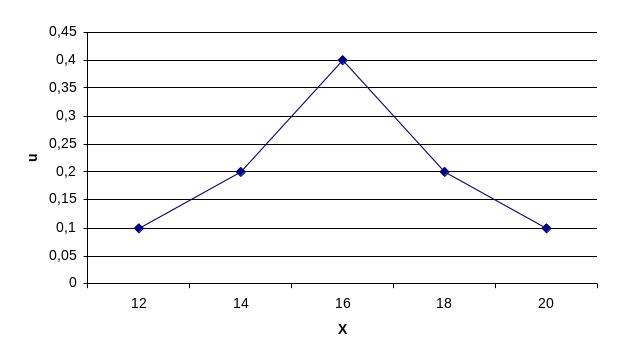
Рис. 1 – Полигон
относительных частот

Гистограммой частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною

,
а высоты равны отношению

(плотность частоты).

Для построения
гистограммы частот на оси абсцисс
откладывают частичные интервалы, а над
ними проводят отрезки, параллельные
оси абсцисс на расстоянии

.
Площадь

-го
частичного прямоугольника равна

— сумме частот вариант

-го
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, т.е. объему выборки.

Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною

,
а высоты равны отношению

(плотность относительной частоты).

Для построения
гистограммы частот на оси абсцисс
откладывают частичные интервалы, а над
ними проводят отрезки, параллельные
оси абсцисс на расстоянии

.
Площадь

-го
частичного прямоугольника равна

— относительной частоте вариант, попавших
в

-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, т.е.
единице.

На рис. 2 приведен пример
гистограммы для данных, отображенных
в таблице 1.

Таблица 1

Исходное распределение

Показатель	Номер интервала
1	2	3	4	5
Частичный интервал ( )	100-199	200-299	300-399	400-499	500-600
Частота интервала,	9	4	2	2	3
Плотность частоты,	0,09	0,04	0,02	0,02	0,03

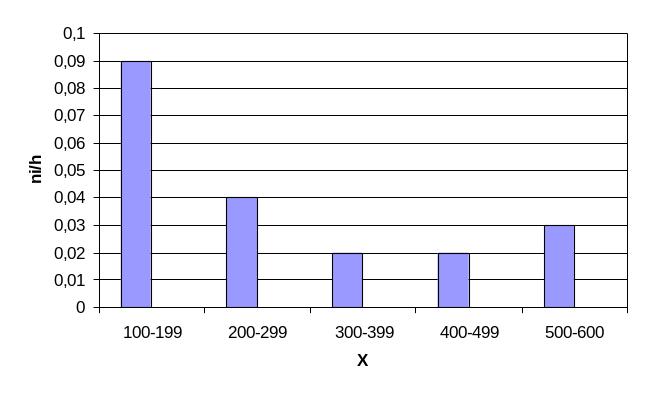
Рис. 2 – Гистограмма
частот распределения

Для некоторых целей
более полезным в сравнении с простыми
графиками распределения частот является
сглаженная кривая
накопленных (кумулятивных) частот.
При построении такой кривой частоты,
которые соответствуют интервалам,
накапливаются, начиная с одного из
концов распределения, т.е. накопленные
частоты к любой
заданной оценке представляют собой
суммарное количество частот на этой
оценке или ниже ее. Обычно, такая
сглаженная кривая отображает относительные
накопленные частоты в процентах, а не
в относительных единицах. На рис. 3
приведен пример кривой накопленных
частот для данных, приведенных в таблице
1.

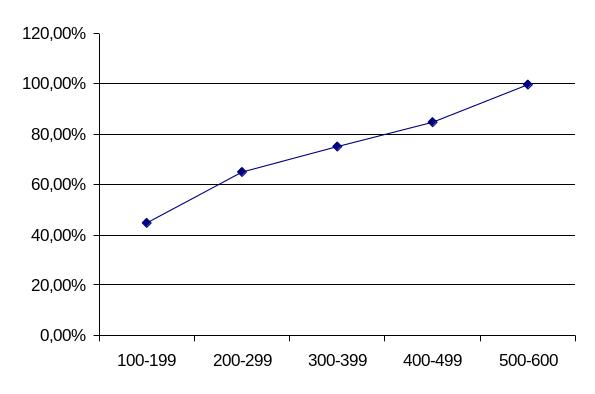
Рис. 3 – Сглаженная
накопленная кривая

Рассмотрим для примера
задачу анализа чистой прибыли предприятия
с помощью электронных таблиц MS
Excel.
На рис. 4 приведена электронная копия
экрана с примером исходных данных по
некоторому предприятию за 11 лет.

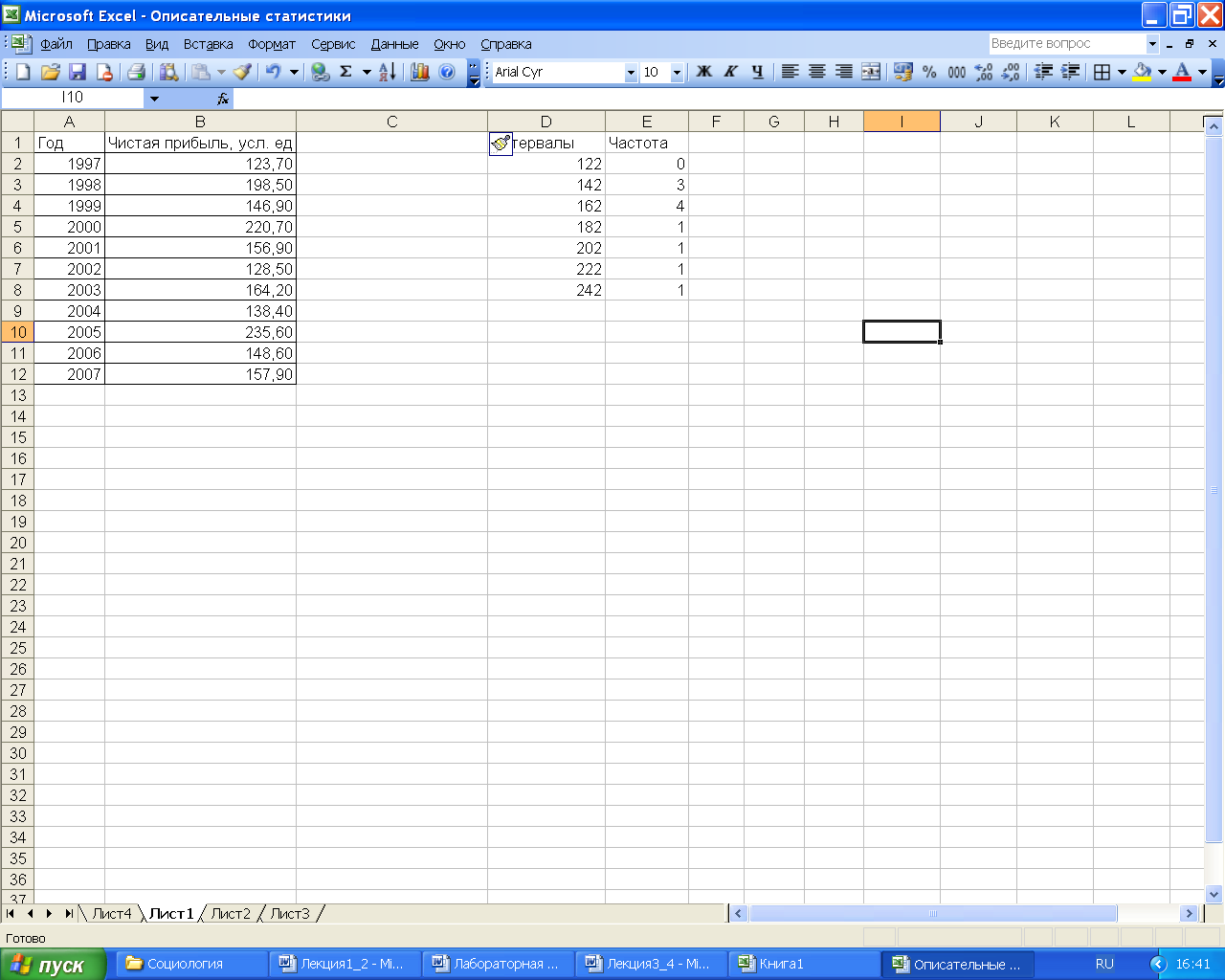
Рис. 4 – Исходные данные
по предприятию

На первом этапе
необходимо задать интервалы, в которых
планируется определить частоты появления
случайной величины. Выберем ширину
интервала длиной в 20 единиц и поместим
границы в столбец С (рис. 5). В данном
случае значение левой границы интервального
ряда составляет 122, а правой 242, поскольку
значение чистой прибыли не меньше 123,7
усл. ед., и не больше 235,6 усл. ед.

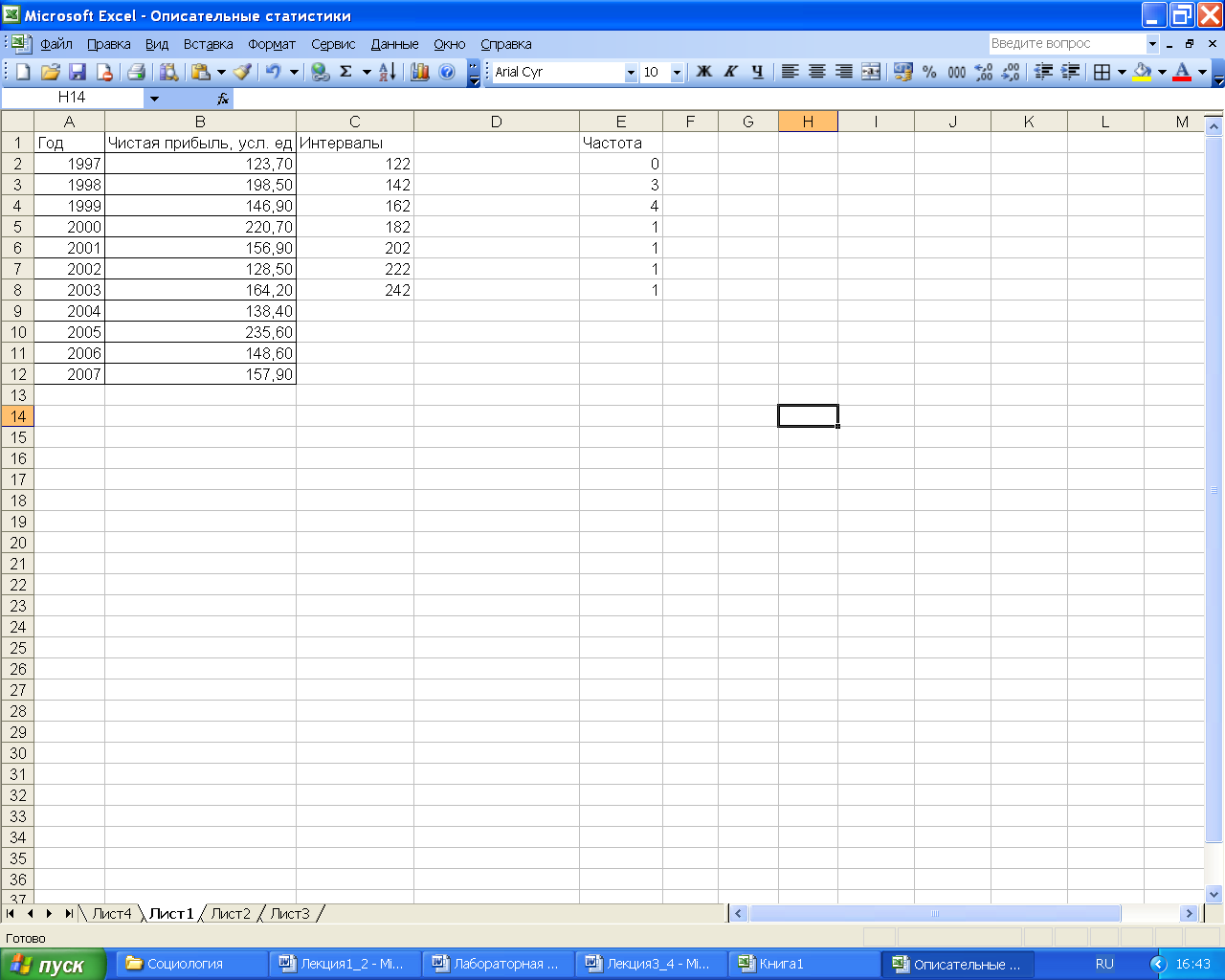
Рис. 5 – Задание границ
интервалов

Для расчета частот,
соответствующих данным интервалам,
необходимо выделить диапазон ячеек
D2:D9,
а в строке формул ввести следующую
функцию: «=ЧАСТОТА(B2:B12;C2:C8)» и закончить
ввод нажатием комбинации клавиш
[Ctrl]+[Shift]+[Enter].
MS
Excel
автоматически заключит введенную
формулу в фигурные скобки: {
=ЧАСТОТА(B2:B12;C2:C8)}. Такой
способ ввода применен в связи с тем, что
функция ЧАСТОТА возвращает массив
значений и ее необходимо вводить как
формулу массива. При этом, количество
элементов в возвращаемом массиве будет
на единицу больше числа элементов в
массиве интервалов.
В результате в ячейки диапазона D2:D9
будут помещены частоты, соответствующие
интервалам (рис. 6).

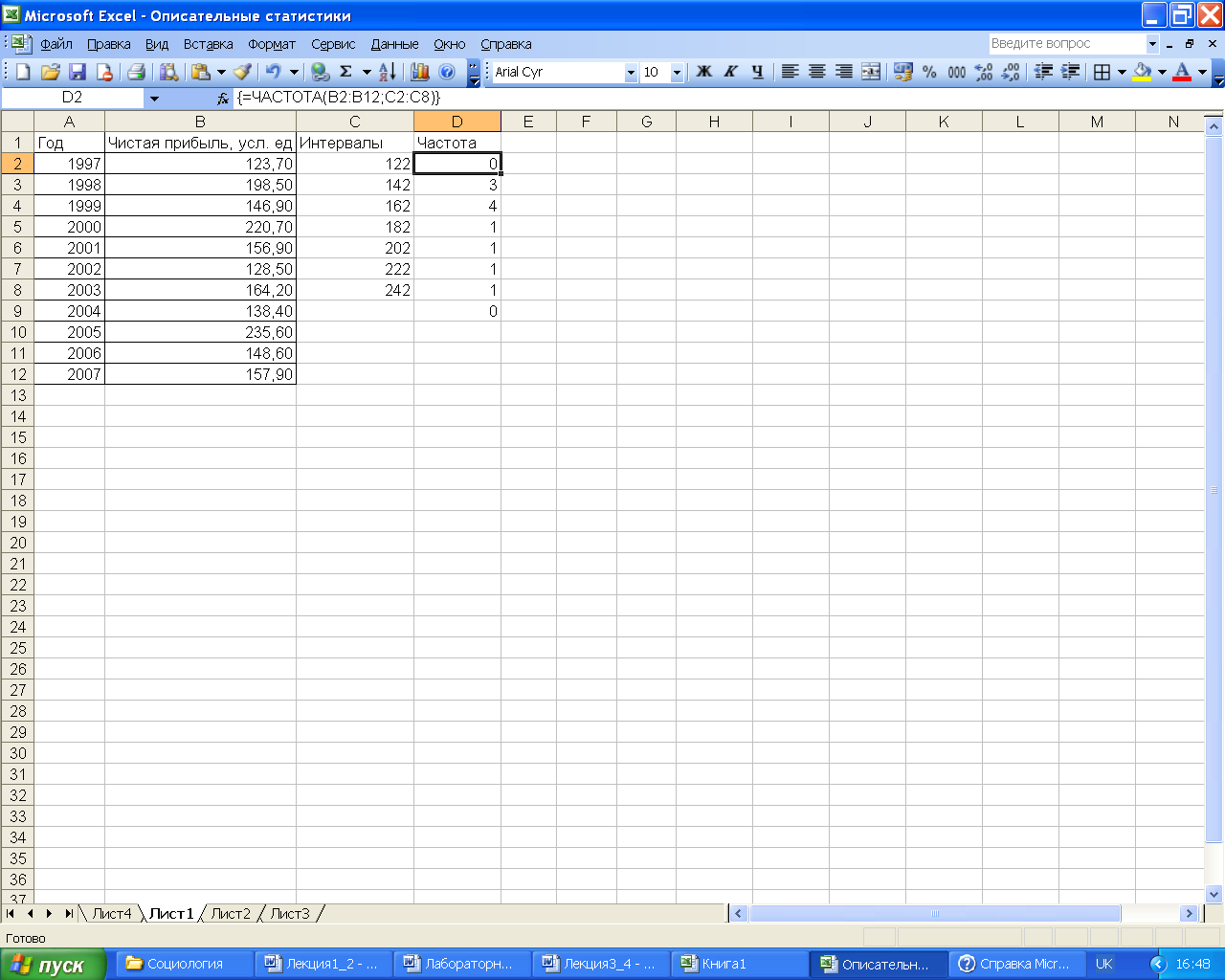
Рис. 6 – Размещение
частот

Теперь с помощью мастера
диаграмм можно построить соответствующий
график: гистограмму или полигон частот
(рис. 7).

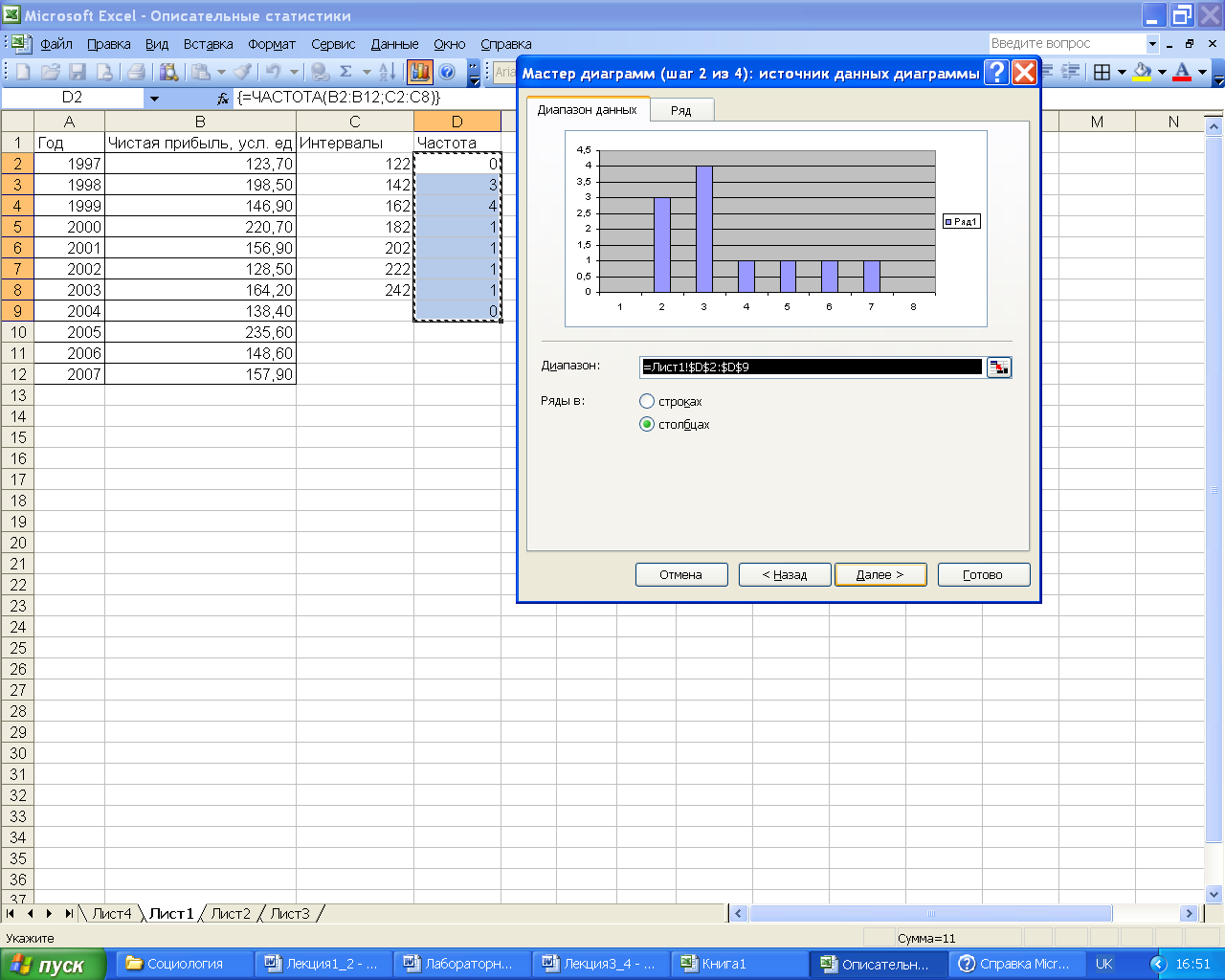
Рис. 7 – Построение
гистограммы распределения

Аналогичное построение
гистограммы можно выполнить с помощью
функции, имеющейся в пакете Анализ
данных. Для этого
в меню последовательно выбирается
Сервис,
Анализ данных.
Появившемся окне (рис. выбирается
Гистограмма.
Затем в следующем окне (рис. 9) необходимо
задать исходные данные для построения
гистограммы.

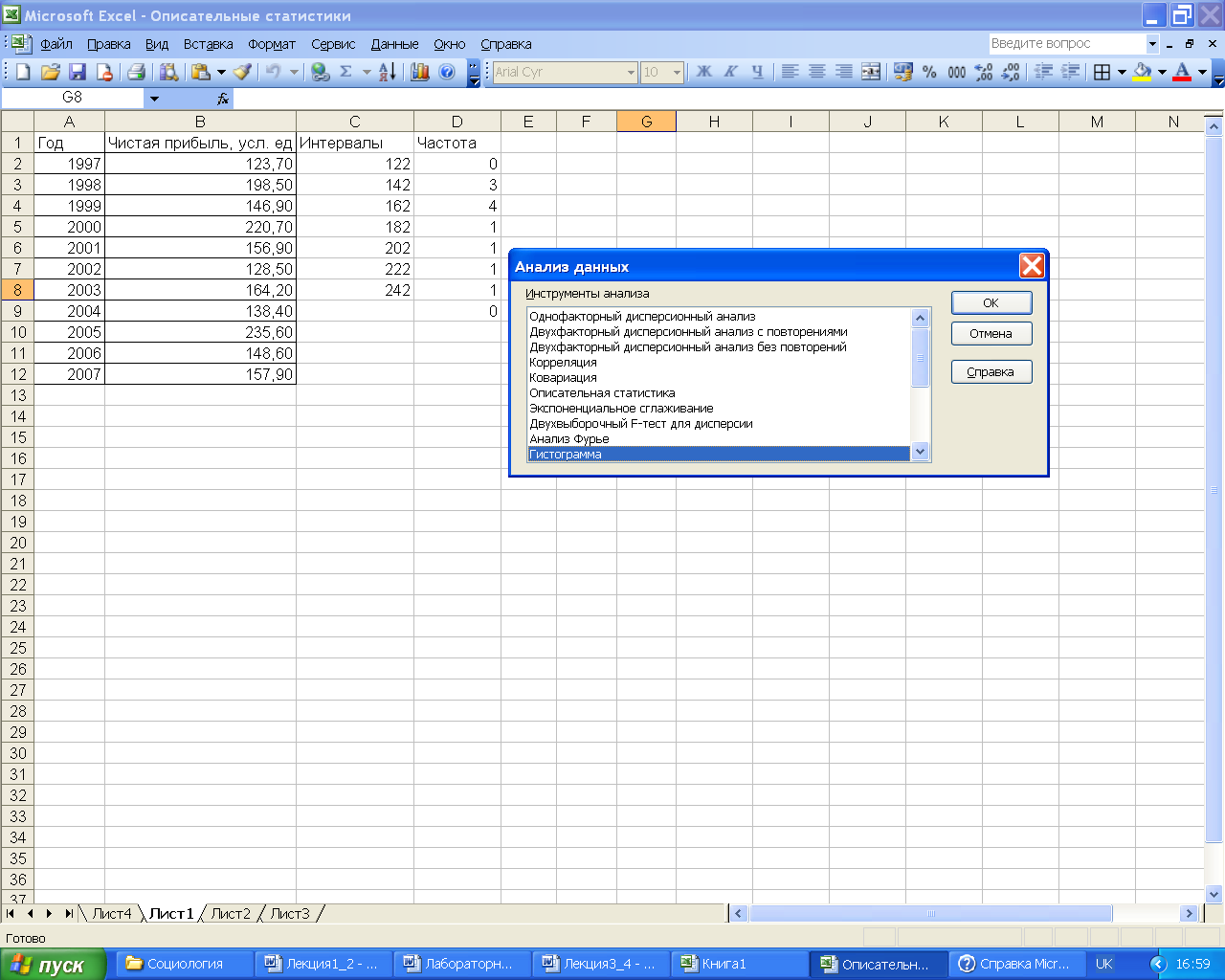
Рис. 8 – Окно выбора
функции

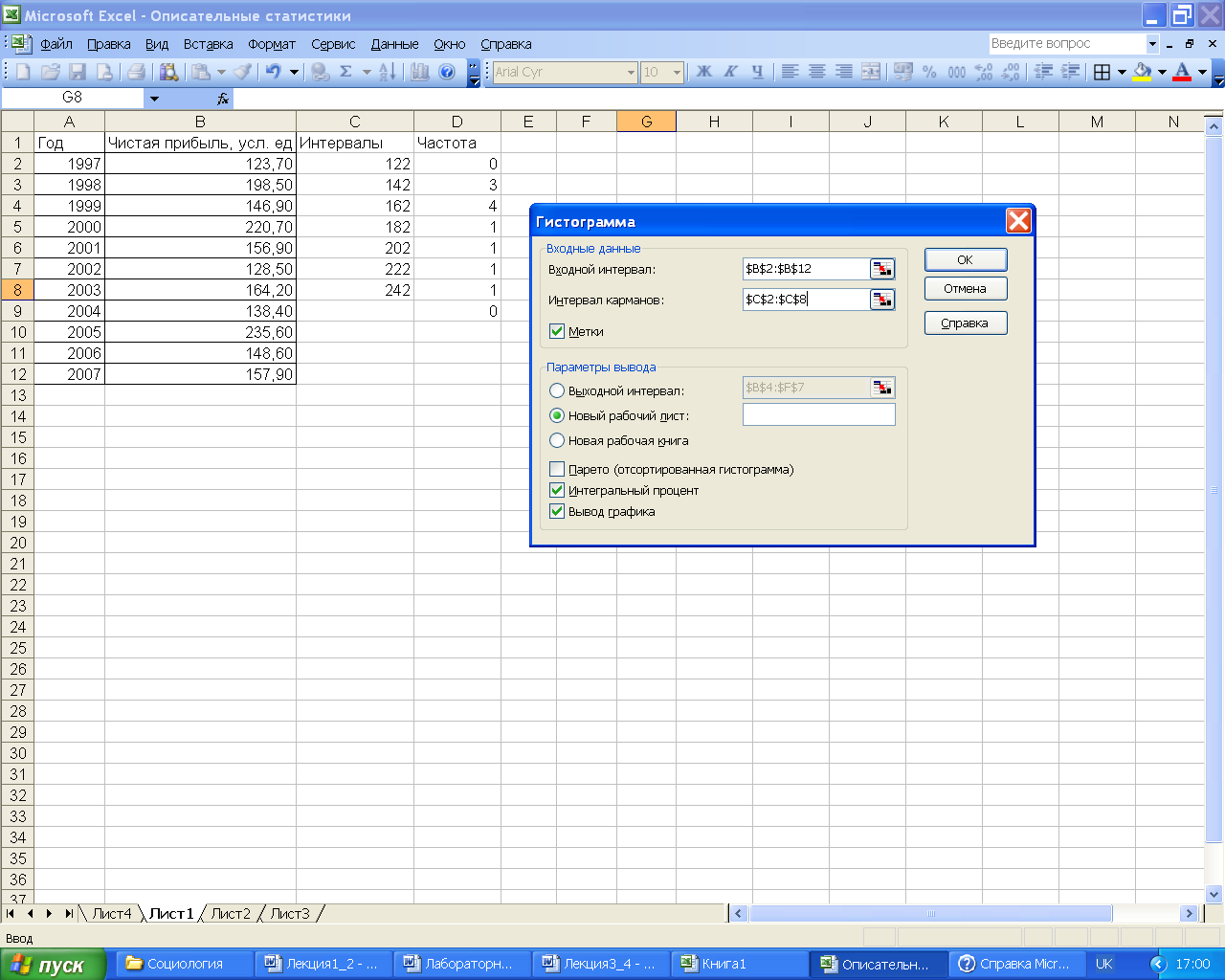
Рис. 9 – Окно задания
исходных данных для построения гистограммы

Назначение параметров
диалогового окна Гистограмма
приведены в таблице 2.

Таблица 2

Параметры диалогового
окна Гистограмма

Параметр	Назначение
Входной диапазон	В этом окне задается ссылка на диапазон ячеек, в которых находится исходные данные. Исходные данные должны представлять собой перечень значений, а не частоты!
Интервал карманов (необязательный)	В поле вводится диапазон ячеек и необязательный набор граничных значений, определяющих отрезки интервалов (карманы). Эти значения должны быть введены в возрастающем порядке. В Microsoft Excel вычисляется число попаданий данных между текущим началом отрезка и соединим большим по порядку, если такой есть. При этом включаются значения на нижней границе отрезка и не включаются значения на верхней границе. Если диапазон карманов не был введён, то набор отрезков, равномерно распределённых между минимальным и максимальным значениями данных, будет создан автоматически.
Метки	Ставится отметка, если первая строка или первый столбец входного интервала содержит заголовки. Если таковые отсутствуют, названия для данных выходного диапазона создаются автоматически.
Выходной диапазон	Вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер последнего будет определён автоматически и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.
Новый рабочий лист	Переключатель устанавливается в том случае, если требуется открыть новый лист в книге и вставить результаты анализа, начиная с ячейки А1.
Новая рабочая книга	Переключатель устанавливается в том случае, если требуется открыть новую рабочую книгу и вставить результаты анализа в ячейку А1.
Парето (отсортированная диаграмма)	При выборе этой возможности данные предоставляются в порядке убывания частоты. В математической статистике такая форма гистограммы не используется.
Интегральный процент	Рассчитываются значения и строится график накопленной частоты, т.е. строится сглаженная кривая кумулятивных частот.
Вывод графика	Устанавливается флажок для автоматического создания встроенной диаграммы. Внимание! Если вы хотите построить график, то обязательно нужно задать значения Новый рабочий лист или Новая книга.

Результаты построения
диаграммы с помощью пакета Анализа
данных приведены на рис. 10.

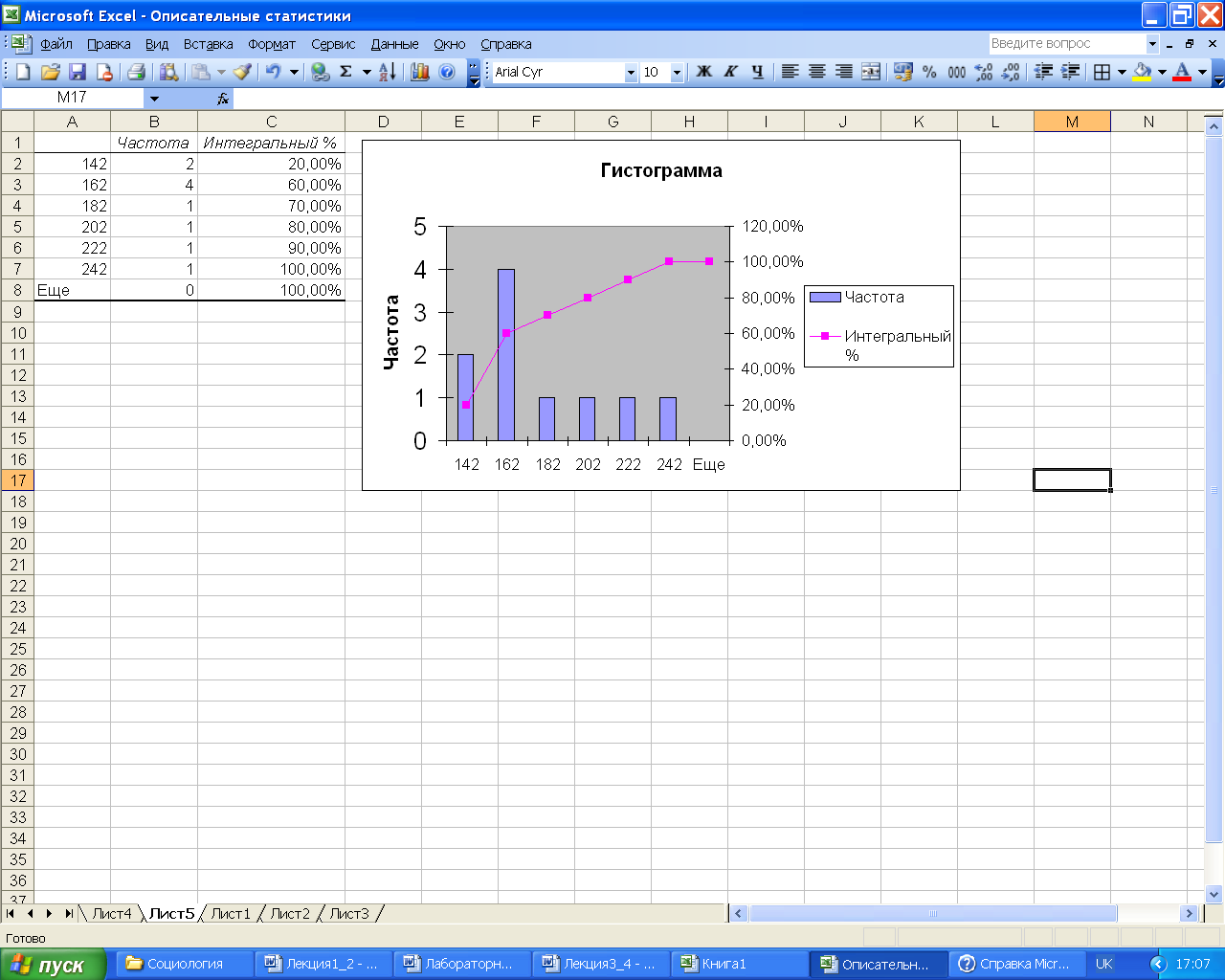
Рис. 10 – Результат
построения гистограммы

Следует отметить, что
ни один из графиков, рассмотренных выше,
не является универсальным. Гистограмма
– наиболее легкая для восприятия форма,
поэтому ее обычно предпочитают, если
изображается не более одного распределения.
Но если необходимо сравнить два или
более распределений, то для этой цели
лучше всего подходит полигон частот
(или полигон относительных частот).
Сглаженные кривые накопленных частот
имеют много преимуществ, которыми не
обладают другие представления. Например,
можно оценить с высокой степенью точности
различные параметры распределений или
сравнивать несколько групп данных на
одном графике.

Существуют и другие
формы представления статистических
данных, например круговые диаграммы,
диаграммы с областями, лепестковые или
поверхностные диаграммы и другие,
подробно о которых можно узнать в
[1,2,3].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Цели урока:

1. Ввести понятие диаграммы, объяснить необходимость ее
   использования; познакомить обучающихся с типами диаграмм; формирование
   навыков анализа данных с помощью диаграмм различных типов.
2. Развитие творческих способностей, логического и
   аналитического мышления.
3. Нравственное воспитание личности, формирование
   целеустремленности, аккуратности при работе за ЭВМ

Подготовка к уроку:

1. На доске – текст домашнего задания
2. Презентация для демонстрации во время объяснения нового
   материала (Приложение 3).
3. Для контроля знаний, полученных на предыдущем занятии:

1. Тест, созданный средствами Excel (Приложение
   1).
2. Карточки с готовыми заданиями (Приложение
   2).

1. Для закрепления материала на рабочих столах каждой ЭВМ
   разместить файл в формате Excel с готовыми текстами заданий (Приложение
   4).

Ход урока

I. Повторение изученного материала.

Группа обучающихся по усмотрению преподавателя условно
делится на 3 подгруппы: обучающиеся первой подгруппы выполняют компьютерное
тестирование (Приложение 1), обучающиеся второй
подгруппы определяют значение формулы, образованной копированием по карточкам (Приложение
2).

С оставшимися обучающимися проводится фронтальный опрос:

1. Назначение и запуск приложения Excel.
2. Типы данных, используемые в Excel.
3. Понятие относительных и абсолютных ссылок.
4. Понятие функции. Виды функций (привести примеры).

II. Активизация знаний.

Объяснение материала ведется с использованием презентации (Приложение
3).

После того, как рабочая таблица на листе построена, можно с
ней работать. И хотя в таблице сразу выводится результат после ввода в нее
данных, вычисления обычно на этом не заканчиваются. Далее, как правило,
начинается анализ результатов, оценка иных вариантов ситуации, т.е. рассуждения
на тему «А что было бы, если бы…» («… что было бы, если бы ананасов завезли на
20 кг меньше, а рыбы – на 100 больше?»).

Такой подход – перебор вариантов решения задачи – очень
полезен. Для многих задач это единственный способ нахождения приемлемого
варианта решения задачи. Для этих целей Excel незаменим: быстро меняем данные –
мгновенно получаем результат.

С развитием компьютерных технологий развилась одна из
областей применения ЭВМ – визуализация информации. Существует несколько
направлений в этой области: инженерная графика, деловая графика и ряд других.
Построение диаграмм с помощью ЭВМ – одно из основных средств деловой графики.

III. Объяснение нового материала.

Диаграмма – это условное изображение числовых величин
или их соотношений графическим способом Примером диаграммы, ее частным случаем
является всем известный график функции.

В деловой, финансовой, экономической сферах роль диаграмм
очень велика. Сколько же времени должен затратить экономист фирмы, впиваясь
взглядом в таблицу, выискивая в ней максимальные и минимальные значения
различных показателей, выявляя соотношения этих значений для различных
подразделений! Естественно, что подобный анализ многократно упрощается при
наличии диаграмм. Иногда достаточно одного-двух взглядов на диаграмму для
получения нужной информации.

Диаграммы MS Excel дают возможность графического
представления различных числовых данных. Выбрав тип, макет и стиль диаграммы,
которые в новой версии Office Excel 2007 всегда доступны на ленте, каждую
диаграмму можно быстро и профессионально обработать.

В Excel можно строить два типа диаграмм: внедренные
и диаграммы на отдельных листах. Внедренные создаются на рабочих листах
рядом с таблицами, данными и текстом и используются при создании отчетов.
Диаграммы на отдельном листе удобны для подготовки слайдов или для вывода на
печать.

Excel предлагает различные типы диаграмм и предусматривает
широкий спектр возможностей для их изменения (типа диаграммы, надписей, легенды
и т.д.) и для форматирования всех объектов диаграммы.

Для создания диаграмм в MS Excel прежде всего следует
подготовить данные для построения диаграмм и определить ее тип. Построение
диаграммы выполняется с помощью Мастера диаграмм. Это программа с большими
возможностями. Для решения задачи необходимо выделить в таблице диапазон ячеек,
значения которых следует представить в виде диаграммы, и уяснить для себя:
данные какого столбца (строки) следует откладывать по оси Х (т.е. рассматривать
как категории), а каких столбцов (строк) – по оси Y (рассматривать как
значения).

Количество рядов данных (У) должно быть меньше, чем категория
(Х). Исходя из этого, определяется расположение рядов (в строках или столбцах)
если диаграмма строится для диапазона ячеек, имеющего больше столбцов, чем
строк, или равное их число, то рядами данных считают строки. Если диапазон ячеек
имеет больше строк, то рядами данных считают столбцы. Excel предполагает, что
названия, связанные с рядами данных, считаются их именами и составляют легенду
диаграммы. Данные, интерпретируемые как категории, считаются названиями
категорий и выводятся вдоль оси Х.

Excel 2007 поддерживает различные типы диаграмм, помогая
пользователям отображать данные понятным для конкретной аудитории способом. При
создании или изменении существующей диаграммы можно выбрать один из множества
доступных подтипов диаграмм каждого типа.

Гистограммы. Данные, которые расположены в столбцах
или строках, можно изобразить в виде гистограммы. Гистограммы используются для
демонстрации изменений данных за определенный период времени или для
иллюстрирования сравнения объектов. В гистограммах категории обычно формируются
по горизонтальной оси, а значения — по вертикальной.

Линейчатые диаграммы. Похожи на гистограммы (отличие –
повернуты на 90⁰ по часовой стрелке). Используются для сопоставления
отдельных значений в определенный момент времени, не дают представления об
изменении объектов во времени. Горизонтальное расположение полос позволяет
подчеркнуть положительные или отрицательные отклонения от некоторой величины.

Линейчатые диаграммы можно использовать для отображения
отклонений по разным статьям бюджета в определенный момент времени. Можно
перетаскивать точки в любое положение. Линейчатые диаграммы иллюстрируют
сравнение отдельных элементов.

Графики. Графики позволяют изображать зависимость
данных (ось У) от величины, которая меняется с постоянным шагом (ось Х). Метки
оси категорий должны располагаться по возрастанию или убыванию.

Графики чаще используют для коммерческих или финансовых
данных, равномерно распределенных по времени (отображение непрерывных данных),
или таких категорий, как продажи, цены и т.п.

Может возникнуть необходимость использовать графики для
отображения равномерно распределенных значений, например, месяцев, кварталов или
финансовых лет. Это особенно важно при наличии нескольких рядов — для одного
ряда можно использовать ось категорий. Также графики можно использовать при
наличии нескольких равномерно распределенных числовых меток, особенно лет. Если
числовых меток больше десяти, вместо графика лучше использовать точечную
диаграмму.

Круговые диаграммы. Данные, которые расположены в
одном столбце или строке, можно изобразить в виде круговой диаграммы. Круговая
диаграмма демонстрирует размер элементов одного ряда данных пропорционально
сумме элементов. Точки данных  на круговой диаграмме выводятся в виде
процентов от всего круга. Эти диаграммы можно использовать, когда компоненты в
сумме составляют 100%.

Точечные диаграммы. Точечная диаграмма показывает
отношения между численными значениями в нескольких рядах данных или отображает
две группы чисел как один ряд координат x и y.

Точечная диаграмма имеет две оси значений, при этом один
набор значений выводится вдоль горизонтальной оси (оси X), а другой — вдоль
вертикальной оси (оси Y). На точечной диаграмме эти значения объединяются в одну
точку данных и выводятся с неравными интервалами, или кластерами. Точечные
диаграммы обычно используются для представления и сравнения числовых значений,
например, научных, статистических или инженерных данных. Для вывода данных
таблицы в виде точечной диаграммы следует поместить данные по оси X в одну
строку или столбец, а соответствующие данные по оси Y — в соседние строки или
столбцы.

Диаграммы с областями. Диаграммы с областями
иллюстрируют величину изменений в зависимости от времени и могут использоваться
для привлечения внимания к суммарному значению в соответствии с трендом.

Например, данные, отражающие прибыль в зависимости от
времени, можно отобразить в диаграмме с областями, чтобы обратить внимание на
общую прибыль.

Отображая сумму значений рядов, такая диаграмма наглядно
показывает вклад каждого ряда.

Поверхностные диаграммы. Поверхностная диаграмма
используется, когда требуется найти оптимальные комбинации в двух наборах
данных. Как на топографической карте, цвета и штриховки выделяют зоны одинаковых
диапазонов значений. Поверхностные диаграммы можно использовать для иллюстрации
категорий и наборов данных, представляющих собой числовые значения.

Кольцевые диаграммы. Как и круговая диаграмма,
кольцевая диаграмма отображает отношение частей к целому, но может содержать
более одного ряда

Создание диаграмм в приложении Excel. Чтобы создать в
Excel базовую диаграмму, которую впоследствии можно изменять и форматировать,
сначала введите на лист данные для этой диаграммы. Затем просто выделите эти
данные и выберите нужный тип диаграммы на ленте (вкладка Вставка, группа
Диаграммы).

Изменение диаграмм. Создав диаграмму, можно вносить в
нее изменения. Например, можно изменить вид осей, добавить название диаграммы,
переместить или скрыть легенду, а также добавить дополнительные элементы
диаграммы.

Имеются следующие возможности изменения диаграммы:

1. Изменение вида осей диаграммы. Можно указать масштаб
   осей и изменить промежутки между значениями или категориями.
2. Добавление к диаграмме названия и подписи. Для пояснения
   отображенных на диаграмме данных можно добавить название диаграммы, названия
   осей и подписи.
3. Добавление легенды и таблицы данных. Можно отобразить
   или скрыть легенду либо изменить ее расположение. В некоторых
   диаграммах также можно отобразить таблицу данных и значения,
   представленные на диаграмме.

Эффектный формат диаграмм. Помимо применения
встроенного стиля диаграммы можно легко изменить форматирование ее отдельных
элементов, например, маркеров данных, области диаграммы, области построения,
чисел и текста в названиях и подписях, что привлечет внимание и сделает
диаграмму оригинальной.

Имеются следующие возможности форматирования диаграммы:

1. Заливка элементов диаграммы. Для привлечения внимания к
   определенным элементам диаграммы можно залить их цветом, текстурой, рисунком
   или применить градиентную заливку.
2. Изменение контуров элементов диаграммы. Для выделения
   элементов диаграммы можно изменить их цвет, стиль или толщину линий.
3. Добавление специальных эффектов к элементам
   диаграммы. Для придания диаграмме завершенности к ее элементам можно
   применить специальные эффекты, например, тень, отражение, свечение,
   сглаживание, рельеф или объемное вращение.
4. Форматирование текста и чисел. Текст и числа в
   названиях, подписях и надписях на диаграмме можно форматировать так же, как
   текст и числа на листе. Чтобы выделить текст или число, можно также
   применять стили WordArt.

Изменение типа существующей диаграммы. Для большинства
плоских диаграмм можно изменить тип всей диаграммы, придав ей совершенно другой
вид, или выбрать другой тип диаграммы для любого одиночного ряда данных,
превратив диаграмму в смешанную диаграмму.

IV. Физкультурная минутка.

V. Закрепление полученных знаний.

Для создания диаграмм на рабочих столах имеются файлы
приложения Excel с готовыми заданиями (Приложение 4).

При выполнении задания 1 обучающиеся определяют выделяемый
диапазон ячеек, объясняют тип диаграммы, дополняют диаграмму подписями,
заголовками. Готовую диаграмму форматируют. Анализируя данные диаграммы,
обучающиеся должны ответить на вопрос: чем объясняется спад объема продаж в 90-х
гг.

Задание 2 выполняется самостоятельно. Обучающиеся создают
таблицу значений аргументов, вводят формулы и копируют их для вычисления
значений функции. По имеющимся данным создают график, форматируют его.
Определяют значения аргумента, при которых функция имеет отрицательные значения.

Задание 3 также выполняется обучающимися самостоятельно.
Необходимо составить диаграмму, отражающую долю стоимости устройств компьютера в
общей его стоимости. Заметно ли подорожает компьютер при приобретении более
производительных схем процессора и оперативной памяти?

VI. Блиц-опрос.

1. Что такое диаграмма?
2. В каких случаях возникает необходимость исследовать или отобразить
   данные с помощью диаграмм?
3. Когда используют внедренные диаграммы?
4. Когда создают диаграммы на отдельных листах?
5. С чего начать построение диаграммы?
6. Что такое категории и значения?
7. Какие типы диаграмм вам известны?
8. Что вы знаете о гистограмме?
9. Когда используют линейчатые диаграммы?
10. Что изображают графики?
11. Если данные расположены в одном столбце или строке – используют…
12. Перечислите еще известные вам типы диаграмм.
13. Как создать диаграмму по имеющимся данным?
14. Какие способы форматирования диаграмм вы знаете?

VII. Задание на дом.

Создать таблицу зависимости средней температуры воздуха в
зависимости от времени года (разбить по кварталам). Использовать данные,
полученные на уроках биологии. Проанализировать результаты прогноза с помощью
диаграмм.

VIII. Выставление оценок.

Во время записи домашнего задания выставить оценки по результатам
тестирования, проверить карточки, оценить работы за ЭВМ. Дать качественную
оценку работ.

IX. Подведение итогов урока.

Обобщение материала. Устранение пробелов знаниях.

Работа добавлена на сайт samzan.net: 2015-07-05

Задание по Excel №1 «Простейшие вычисления и использование графических возможностей Excel»

Цель работы:

1.  Исследование основных приемов построения формул Excel.
2.  Использование основных статистических функций Excel.
3.  Исследование основных приемов форматирования ячеек.
4.  Исследование графических возможностей Excel.

Задание:

1.  На первом листе книги создать таблицу, содержащую не менее 10 строк.
   1.  Применить в расчетах статистические функции Excel (вкладка «Формулы»/ группа «Библиотека функций»/ Автосумма).
   2.  На основе полученных в таблице расчетов создать гистограмму с полным форматированием (цветовое оформление, подписи осей, название диаграммы). Для этого выделить исходные данные диаграммы, вкладка «Вставка»/ группа «Диаграмма»/ Гистограмма.
2.  На втором листе книги построить графическое решение уравнения.
   1.  Для этого построить числовые ряды данных, например, для уравнения

«Вставка»/ группа «Диаграмма»/ Точечная.

1.  Если графическое решение существует, найти решение аналитическое методом.

Если известен результат, который требуется вычислить при помощи формулы, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством «Подбор параметра». В нашем случае необходимо найти такое значение х, при котором функция обратится в ноль.

1.  Для вызова диалогового окна «Подбор параметра» добавьте нужную пиктограмму на панель быстрого доступа: кнопка «Офис»/ Параметры Excel / Настройка / Выбрать команды из: / вкладка «Данные» /Подбор параметра / кнопка «Добавить».

Общие требования:

•  Применить цветовое оформление к таблице расчетов, используя либо пользовательское форматирование, либо готовые стили (вкладка «Главная» / группа «Стили»).
•  Использовать отображение всего текста ячейки в несколько строк .

Вкладка «Главная»/ группа «Выравнивание»/ кнопка «Перенос текста».

•  Уметь использовать автоподбор ширины ячейки;
•  Применить к ячейкам нужный формат (числовой, денежный, процентный и т.д.).
•  Данные, общие для всех строк вынести за пределы таблицы.

Уметь:

•  Строить несколько графиков на одном изображении.
•  Для копирования оформления, уметь пользоваться форматом по образцу .
•  Уметь копировать, перемещать, удалять значение ячейки; вставлять и удалять столбцы и строки.
•  Знать определение относительных и абсолютных ссылок.

Вариант 1

1.  Группа студентов из 10 человек получила стипендию за январь в размере 120 руб и единовременное пособие в размере 12 % от стипендии. Вычислить сколько денег получил каждый студент и общую сумму денег, выданную на группу.
2.  На втором листе книги графически и методом подбора решить уравнение arctg(x)=1/3x^3

Вариант 2

Бригада токарей вытачивает детали 5-ти видов. Каждая деталь оплачивается по-разному. Ежемесячная премия составляет  500 руб. Вычислить количество денег, выдаваемых на бригаду из 7 человек. Вычислить  минимальное, максимальное и среднее значение зарплат рабочих. Данные расположить в виде двумерной таблицы.

1.  На втором листе книги графически и методом подбора решить уравнение tg(x)=2x.

Вариант 3

Имеется группа товаров с определенной оптовой ценой. Вычислить розничную цену каждого товара, учтя транспортные издержки и магазинную наценку. Определить общую цену всех товаров. Найти минимальную, максимальную и среднюю стоимость товаров.

1.  На втором листе книги графически и методом подбора решить уравнение sin(x)=0,5x.

Вариант 4

Продаются автомобили, имеющие определенную заводскую цену. Транспортные издержки составляют 10% от заводской цены. Предпродажная подготовка 13 % от заводской цены. Вычислить итоговую стоимость каждого автомобиля и общую выручку от продаж всех машин. Найти минимальную, максимальную и среднюю стоимость машин.

1.  На втором листе книги графически и методом подбора решить уравнение x^3-18x^2+6=0.

Вариант 5

Задан угол 0 до 180 градусов с шагом 5 градусов. Вычислить значение синуса и косинуса в градусах и радианах. Найти минимальное, максимальное и среднее значение синусов и произведение и  среднее геометрическое значений косинуса.

1.   На втором листе книги графически и методом подбора решить уравнение 3^x=3x+2.

Вариант 6

Бригада из 10 человек работает по основному рабочему тарифу 10 руб/час. Отработанное время  у каждого рабочего разное. Вычислить размер заработной платы, если уральский коэффициент составляет 12%, налог 15 %. Рассчитать общую сумму денег.

1.  На втором листе книги графически и методом подбора решить уравнение 2sin(x)=0,5x^2-1.

Вариант 7

Вычислить по схеме Горнера:

Разложить вычисления по ячейкам. Вычислить  минимальное, максимальное и среднее значение коэффициентов полинома.

1.  На втором листе книги графически и методом подбора решить уравнение arctg(x-1)+2x=0

Вариант 8

Вычислить

Разложить вычисления по ячейкам. Вычислить  минимальное, максимальное и среднее значение ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение x^2cos(2x)=—1.

Вариант 9

Задается последовательность из 45 случайных чисел .Вычислить

Разложить вычисления по ячейкам. Вычислить  минимальное, максимальное и среднее значение коэффициентов полинома .

1.  На втором листе книги графически и методом подбора решить уравнение 0,5^x-3=—(x+1)^2.

Вариант 10

Вычислить

Разложить вычисления по ячейкам. Вычислить  минимальное, максимальное и среднее геометрическое значение ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение (x-2)^2=1-2^x.

Вариант 11

Вычислить факториал  20!, используя  встроенную функцию Excel и собственный алгоритм. Разложить вычисления по ячейкам. Вычислить  минимальное, максимальное и среднее значение и сумму ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение 5sin(x)=x.

Вариант 12

Рассчитать плату за электроэнергию. На каждый месяц задаются два числа, характеризующих показания счетчика на начало и конец месяца. Причем второе число предыдущего месяца должно равняться первому числу следующего месяца. Стоимость одного кВатта 24 коп. Вычислить плату за год.

Вычислить  минимальное, максимальное и среднее значение ежемесячных показаний.

1.  На втором листе книги графически и методом подбора решить уравнение 6sin(x^2)=x^2.

Вариант 13

Составить таблицу значений функции .  Х меняется на диапазоне от –4 до 6 с шагом 0.4.

Вычислить  минимальное, максимальное и среднее значение коэффициентов полинома.

1.  На втором листе книги графически и методом подбора решить уравнение x^2=20sin(x).

Вариант 14

Продавец берет на оптовой базе группу товаров. Наценка на каждый товар составляет 12 %. Налог 7 %. Вычислить чистую прибыль продавца.

1.  Вычислить  минимальное, максимальное и среднее значение стоимости товаров.
2.  На втором листе книги графически и методом подбора решить уравнение 3^(x-1)+4—x=0.

Вариант 15

Составить таблицу значений функции , х меняется от 1 до 21 с шагом 1.

Разложить вычисления по ячейкам. Вычислить сумму, произведение, минимальное, максимальное и среднее значение ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение 2*lg(x)=x/2+1.

Вариант 16

Вычислить сумму  с шагом 2.

Разложить вычисления по ячейкам. Вычислить минимальное, максимальное и среднее значение ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение (x-3)cos(x)=1.

Вариант 17

Задана функция  y=a*(cos(x)-b)- b*(sin(x)-a). a,b =коэффициенты; x – параметр функции, изменяющийся от –10 до 10 с шагом 0.5. Найти разницу между максимальным и минимальным значением функции.

1.  На втором листе книги графически и методом подбора решить уравнение 3^x+2-x=0.

Вариант 18

Заданы числа от 50 до 200 с шагом  1, представляющие  собой температуру в градусах Фаренгейта. Получить для каждого числа соответствующую температуру в градусах Цельсия по формуле  Цел=3/5*(Фар — 32).

1.  На втором листе книги графически и методом подбора решить уравнение 2x^2-0,5^x=2.

Вариант 19

Вычислить по схеме Горнера

Разложить вычисления по ячейкам. Вычислить минимальное, максимальное и среднее значение ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение cos(x+0,3)=x^2.

Вариант 20

Решить задачу про репку. Каждый подход к репке оплачивается  по 30 руб. У деда 6 подходов. У каждого последующего тянущего на 1 меньше. Каждый участник получает премию в размере 50 %  от заработанных денег. Вычислить зарплату каждого и общее количество денег, выдаваемых на бригаду.

1.  На втором листе книги графически и методом подбора решить уравнение sin(x-0,5)=x-0,5.

Вариант 21

Запрограммировать таблицу, т.е. подобрать такие числа в верхней строке и в крайнем левом столбце, чтобы на пересечении получились нужные цифры. В остальных ячейках таблицы использовать универсальные формулы.

?	?	?	?	?	?	?	?	…	?
?	9	8	7	6	5	4	3		0
?	19	18	17	16	15	14	13		10
?	29	28	27	26	25	24	23		20
?	39	38	37	36	35	34	33		30
?	49	48	47	46	45	44	43		40
…
?	99	98	97	96	95	94	93		90

1.  На втором листе книги графически и методом подбора решить уравнение x*lg(x+1)=1.

Вариант 22

Задано число n. Вычислить y=(2*n-1)! , используя  встроенную функцию Excel и собственный алгоритм. Разложить вычисления по ячейкам. Вычислить  минимальное, максимальное и среднее значение и сумму ячеек.

1.  На втором листе книги графически и методом подбора решить уравнение 2ar5ctg(x)-3x=2.

Вариант 23

Запрограммировать таблицу, т.е. подобрать такие числа в верхней строке и в крайнем левом столбце, чтобы на пересечении получились нужные цифры. В остальных ячейках таблицы использовать универсальные формулы.

?	?	?	?	?	?	?	?	…	?
?	99	98	97	96	95	94	93		90
?	89	88	87	86	85	84	83		80
?	79	78	77	76	75	74	73		70
?	69	68	67	66	65	64	63		60
?	59	58	57	56	55	54	53		50
…
?	9	8	7	6	5	4	3		0

1.  На втором листе книги графически и методом подбора решить уравнение 2e^x=2x-3.

Вариант 24