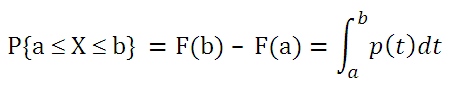Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
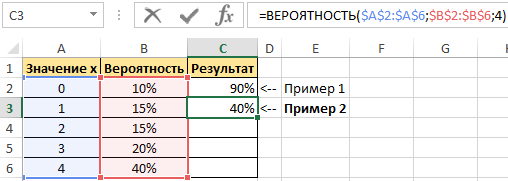
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
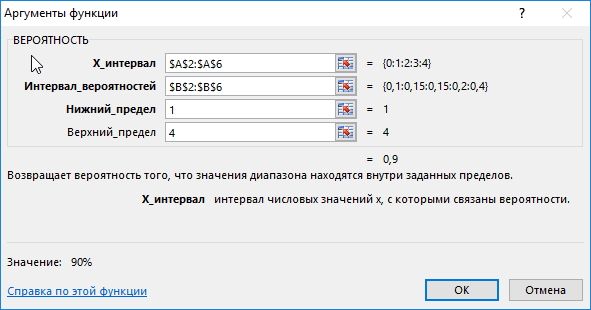
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
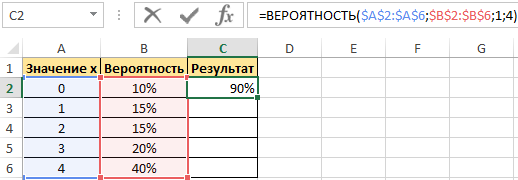
В результате выполненных вычислений получим:
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
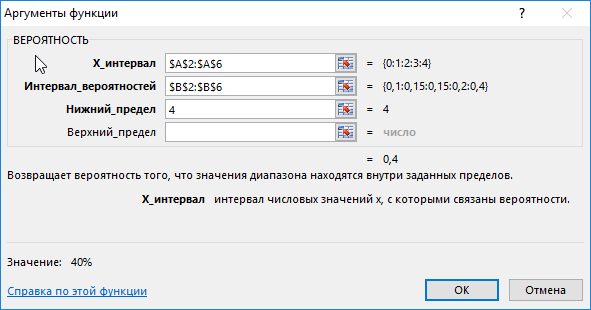
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Спасибо за ваши закладки и рекомендации
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
| ЧИСЛКОМБ / COMBIN |
Возвращает количество сочетаний без повторений. |
| ФАКТР / FACT |
Вычисляет факториал числа. |
| СЛЧИС / RAND |
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное). |
| СЛУЧМЕЖДУ / RANDBETVEEN |
Выдает случайное число в заданном интервале. |
| БИНОМРАСП / BINOMDIST |
Вычисляет отдельное значение биномиального распределения. |
| ГИПЕРГЕОМЕТ / HYRGEOMDIST |
Определяет гипергеометрическое распределение. |
| НОРМРАСП / NORMDIST |
Вычисляет значение нормальной функции распределения. |
| НОРМОБР / NORMINV |
Выдает обратное нормальное распределение. |
| НОРМСТРАСП / NORMSDIST |
Выдает стандартное нормальное интегральное распределение. |
| НОРМСТОБР / NORMSINV |
Выдает обратное значение стандартного нормального распределения. |
| ПЕРЕСТ / PERMUT |
Находит количество размещений без повторений |
| ВЕРОЯТНОСТЬ / PROB |
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов. |
Подробнее: Формулы комбинаторики в Excel.
Подробно решим ваши задачи по теории вероятностей
Математическая статистика
При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):
Обработка выборки: формулы Excel
| СРОТКЛ / AVEDEV |
Вычисляет среднее абсолютных значений отклонений точек данных от среднего. |
| СРЗНАЧ / AVERAGE |
Вычисляет среднее арифметическое аргументов. |
| СРГЕОМ / GEOMEAN |
Вычисляет среднее геометрическое. |
| СРГАРМ / HARMEAN |
Вычисляет среднее гармоническое. |
| ЭКСЦЕСС / KURT |
Определяет эксцесс множества данных. |
| МЕДИАНА / MEDIAN |
Находит медиану заданных чисел. |
| МОДА / MODE |
Определяет значение моды множества данных. |
| КВАРТИЛЬ / QUARTILE |
Определяет квартиль множества данных. |
| СКОС / SKEW |
Определяет асимметрию распределения. |
| СТАНДОТКЛОН / STDEV |
Оценивает стандартное отклонение по выборке. |
| ДИСП / VAR |
Оценивает дисперсию по выборке. |
Законы распределений: формулы Excel
| БЕТАРАСП / BETADIST |
Определяет интегральную функцию плотности бета-вероятности. |
| БЕТАОБР / BETAINV |
Определяет обратную функцию к интегральной функции плотности бета-вероятности. |
| ХИ2РАСП / CHIDIST |
Вычисляет одностороннюю вероятность распределения хи-квадрат. |
| ХИ2ОБР / CHIINV |
Вычисляет обратное значение односторонней вероятности распределения хи-квадрат. |
| ЭКСПРАСП / EXPONDIST |
Находит экспоненциальное распределение. |
| FРАСП / FDIST |
Находит F-распределение вероятности. |
| FРАСПОБР / FINV |
Определяет обратное значение для F-распределения вероятности. |
| ФИШЕР / FISHER |
Находит преобразование Фишера. |
| ФИШЕРОБР / FISHERINV |
Находит обратное преобразование Фишера. |
| ГАММАРАСП / GAMMADIST |
Находит гамма-распределение. |
| ГАММАОБР / GAMMAINV |
Находит обратное гамма-распределение. |
| ПУАССОН / POISSON |
Выдает распределение Пуассона. |
| СТЬЮДРАСП / TDIST |
Выдает t-распределение Стьюдента. |
| СТЬЮДРАСПОБР / TINV |
Выдает обратное t-распределение Стьюдента. |
| ВЕЙБУЛЛ / WEIBULL |
Выдает распределение Вейбулла. |
Другое (корреляция, регрессия и т.п.)
| ДОВЕРИТ / CONFIDENCE |
Определяет доверительный интервал для среднего значения по генеральной совокупности. |
| КОРРЕЛ / CORREL |
Находит коэффициент корреляции между двумя множествами данных. |
| СЧЁТ / COUNT |
Подсчитывает количество чисел в списке аргументов. |
| СЧЁТЕСЛИ / COUNTIF |
Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона. |
| КОВАР / COVAR |
Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек. |
| ПРЕДСКАЗ / FORECAST |
Вычисляет значение линейного тренда. |
| ЛИНЕЙН / LINEST |
Находит параметры линейного тренда. |
| ПИРСОН / PEARSON |
Определяет коэффициент корреляции Пирсона. |
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Полезные ссылки
|
|
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
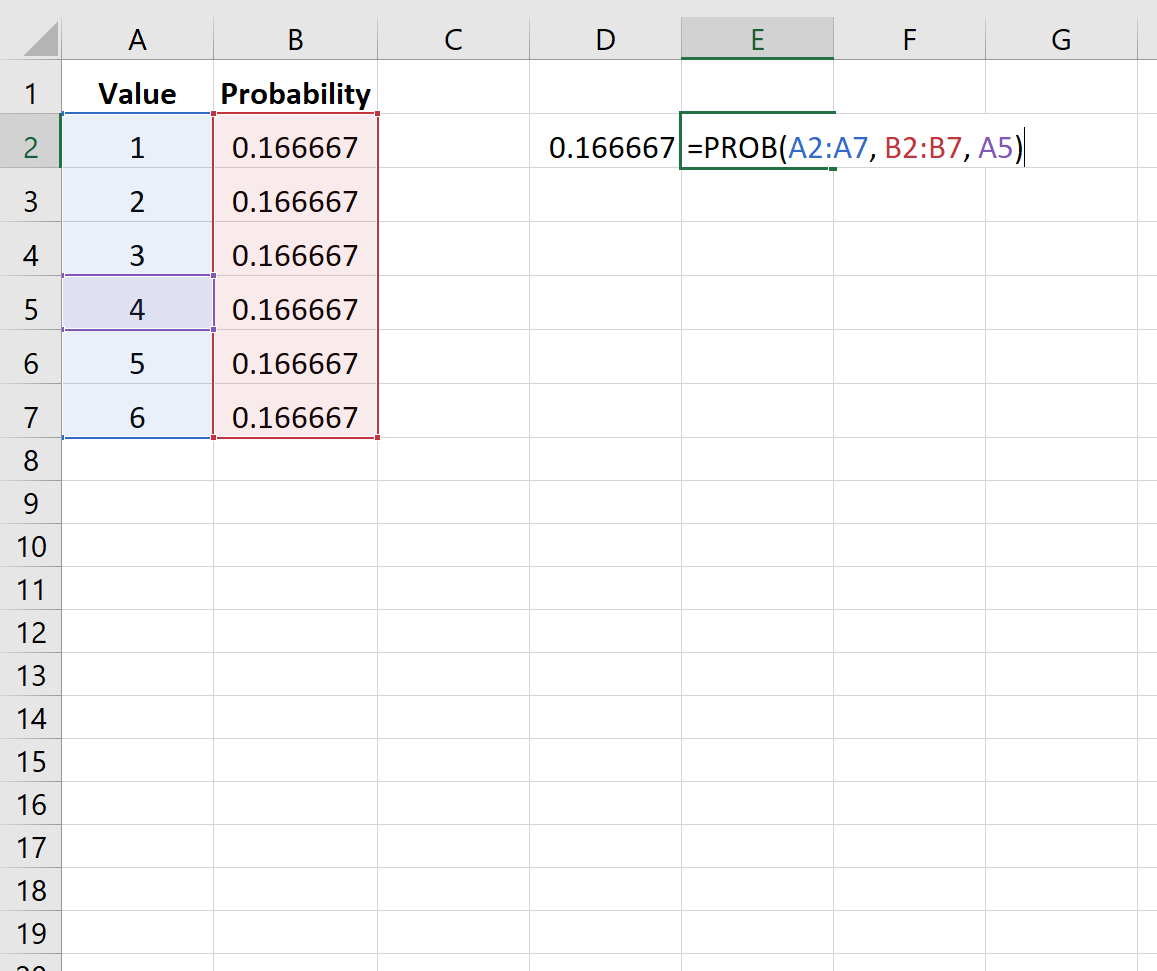
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
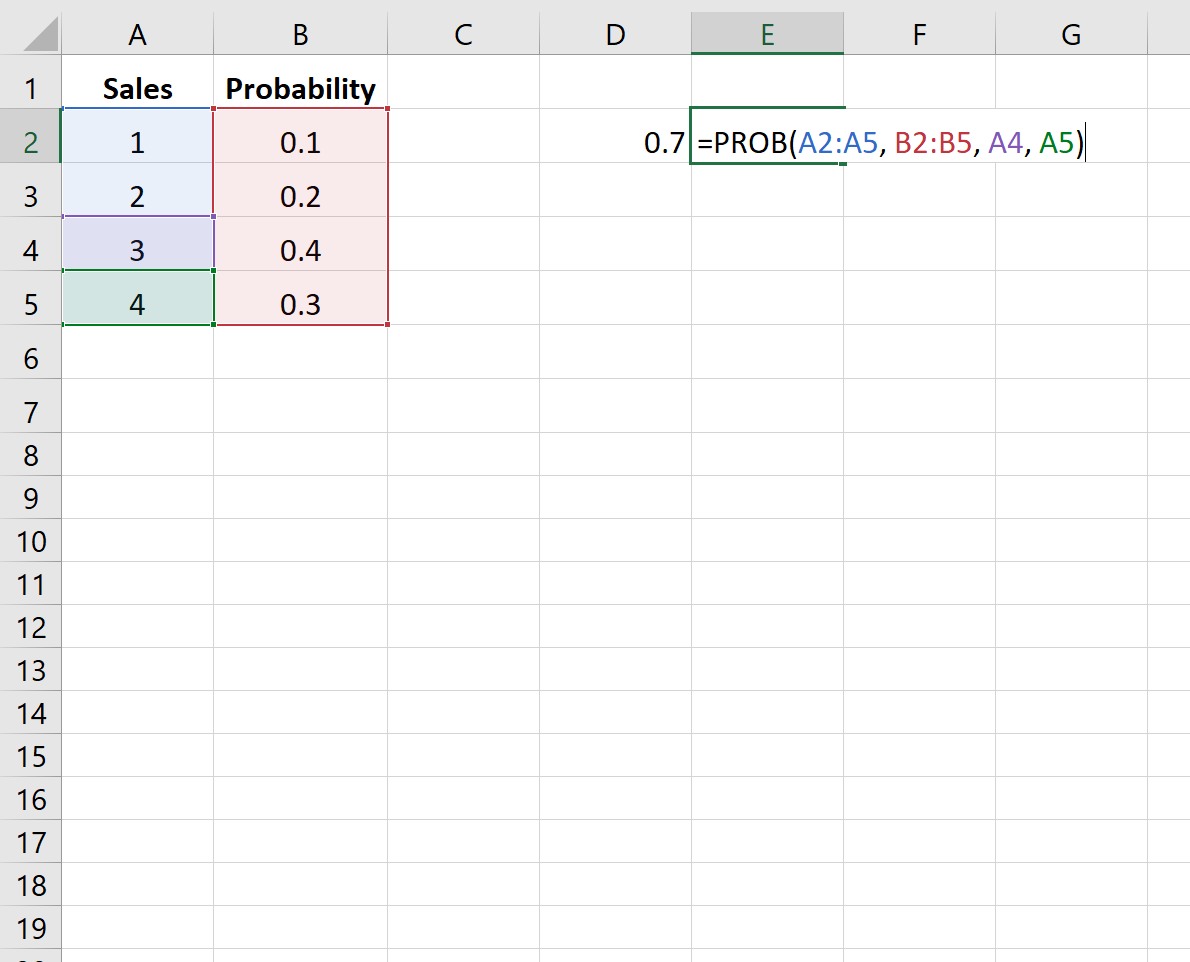
Пример 2: Вероятность продаж
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Содержание
- Формула Бернулли в Excel
- Схема независимых испытаний
- Формула Бернулли в Эксель
- Примеры решений задач
- Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
- Примеры использования функции вероятность для расчетов в Excel
- Вычисление процента вероятности события в Excel
- Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
- Решение задач на вычисление вероятности в Excel
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
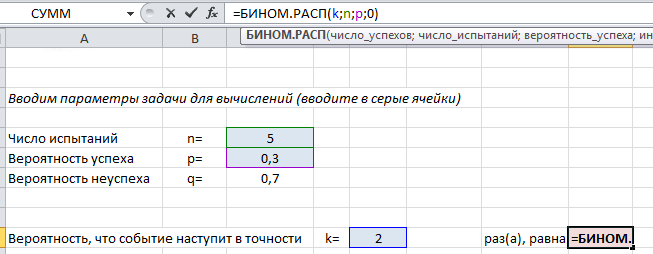
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
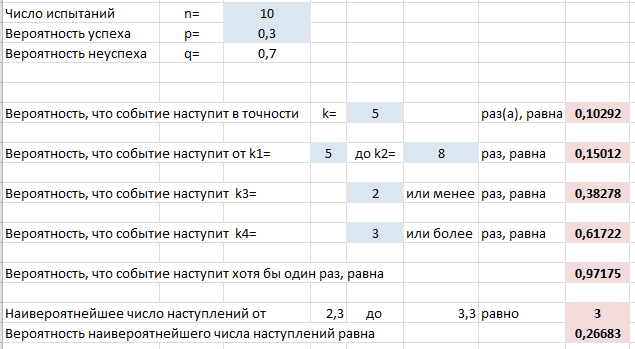
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Источник
Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
В результате выполненных вычислений получим:
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Источник
Решение задач на вычисление вероятности в Excel
Пример 4. В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.
Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.
Искомую вероятность можно рассчитать с помощью функции = ГИПЕРГЕОМЕТ (1; 4; 5; 20), которая дает значение 0,4696.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.
Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: 
Для нахождения наиболее вероятного числа успехов k 0 по заданным n и р можно воспользоваться неравенствами np – q £ k 0£ np + p или правилом: если число np + p не целое, то k 0 равно целой части этого числа.
В случае, если n велико, р мало, а 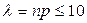

Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1- р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна 
Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.
Решение. Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р 400(5)» 
В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


Имеются таблицы, в которых помещены значения функции 
Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла 

Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 


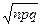

Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. Воспользуемся интегральной формулой Лапласа: n = 400; k 1 = 70; k 2 = 100; р = 0,2; q = 0,8; 

Для вычисления в Excel используем формулу нормального распределения = НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.
Источник
В обучении высшей математике в вузе весьма актуальной задачей является обеспечение доступности усвоения новых математических идей, понятий, методов, в частности, желательно чтобы вычислительная (количественная) сторона не заслоняла содержательной (качественной) стороны изучаемого материала. В решении этой задачи обучения важную роль играют средства обучения математике.
Общеизвестно, что для оптимизации и управления процессом обучения должны использоваться такие средства обучения, как приборы и модели, печатные средства, экранные средства, контрольно-обучающие устройства и технические средства обучения.
Специфика обучения математики такова, что основным средством обучения служат задачи и упражнения, которые выступают не только как носители математического содержания, но и как носители математической деятельности, составляющей математический стиль мышления. Для формирования как содержательной, так и процессуальной оставляющей теории вероятностей и математической статистики, необходимо решить достаточное количество задач и упражнений. Только в этом случае представления, понятия, методы, алгоритмы станут инструментами мышления обучаемого.
При изучении таких разделов высшей математики, как теория вероятностей и математическая статистика вычислительная сторона задач отнимает у студентов столько сил и времени, что на осознание содержательной стороны нового учебного материала их уже не хватает. Это обнаруживается, например, при изучении таких тем, как элементы комбинаторики, теорема умножения вероятностей и ее следствия, дискретные случайные величины, проверка статистических гипотез, линейная корреляция и т.п. Объемные вычисления не позволяют в ограниченное несколькими часами время рассмотреть достаточное количество задач для формирования требуемого уровня знаний и умений по конкретной теме у всех студентов, слабые остаются за бортом.
Приведем примеры некоторых задач.
Задача 1. Студент Козлов плохо подготовился к экзамену по математике, но не отчаивается, т.к. рассчитывает получить подсказки от своих друзей: Иванова, Петрова и Сидорова. Первый, второй и третий могут подсказать правильный ответ с вероятностями 3/10, 2/5 и 1/2 соответственно. Если Козлов получит три подсказки, то он сдаст экзамен наверняка. Если он получит две, одну и ни одной подсказки, то сдаст экзамен с вероятностями 3/5, 1/4 и 1/10 соответственно. Козлов сдал экзамен. Какова вероятность того, что он получил одну подсказку? Ответ: искомая вероятность равна 0,30137.
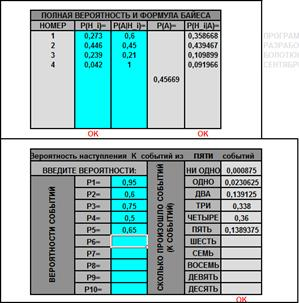
Задача 2. Пять студентов пересдают экзамен. Вероятность пересдачи для каждого из них равна соответственно 0,95; 0,60; 0,75; 0,5 и 0,65. Найти закон распределения числа студентов, успешно пересдавших экзамен, математическое ожидание, дисперсию, начальные и центральные моменты до четвертого порядка включительно. Ответ: см. второй рисунок.
Задача 3. Дана выборка из ста чисел: 44,73; 49,87; 5,00; 34,02; 22,26; 50,33; 63,24; 68,95; 56,52; 49,19; 56,08;52,41; 50,26; 46,67; 61,10; 52,39; 43,22; 60,31; 42,34; 44,15; 49,55; 31,33; 53,88; 60,66; 58,07; 51,44; 30,28; 27,86; 54,47; 52,31; 58,82; 63,32; 24,85; 47,03; 49,67; 44,29; 50,44; 62,19; 19,26; 36,32; 22,61; 41,76; 64,22; 28,50; 44,18; 31,68; 43,25; 54,81; 41,11; 43,46; 78,26; 70,63; 33,25; 50,92; 100; 52,66; 61,19; 57,53; 48,35; 76,06; 41,11; 52,37; 69,26; 69,70; 24,68; 36,33; 39,85; 37,13; 60,70; 61,19; 34,37; 54,20; 45,94; 77,31; 49,94; 74,89; 49,07; 67,92; 21,02; 29,33; 46,40; 52,36; 34,81; 55,96; 29,96; 39,80; 55,93; 72,00; 23,63; 54,72; 65,32; 61,70; 55,05; 49,77; 48,19; 35,27; 23,17; 78,75; 55,82; 66,37. Проверить гипотезу о нормальном распределении с помощью критерия Пирсона при уровне значимости 0,05. Ответ: см. последний рисунок.
Если студентов в первой или второй задаче будет шесть или больше, то их решения займет больше времени. В третьей задаче значений непрерывного количественного признака может быть больше, например, 200, 300, 1000. Если указанные в первых двух задачах вероятности были равны, то применялась бы формула Бернулли. В указанных условиях требуется применить теоремы сложения и умножения вероятностей, что для 4,5 и более событий ведет к громоздким вычислениям. В задаче 2 обработка статистического ряда и вычисление его числовых характеристик также занимает много времени.
Компенсировать вычислительную сложность задач можно с помощью компьютера и табличного процессора Excel. Эффективность применения компьютеров обусловлена следующими факторами: быстрота и надежность обработки любого вида информации; возможность представления информации в графической форме; хранение и быстрота подачи больших объемов информации; возможность моделирования с помощью компьютера разнообразных процессов; активизация содержательной, операционной и мотивационной сторон процесса обучения; оперативное управление учебной деятельностью учащихся; возможность оптимально дифференцировать учебную деятельность школьников в зависимости от уровня подготовки, познавательных интересов и т.д.; организация оперативного контроля и помощи учащимся со стороны учителя; возможность проводить различные математические эксперименты.
Ясно, что при первоначальном знакомстве с теоремами сложения и умножения вероятностей, числовыми характеристиками статистического ряда, алгоритмом проверки статистических гипотез студентам обязательно нужно осознанно прорешать ряд упражнений вручную. Применение калькулятора или компьютера на начальном этапе изучения новой формулы или алгоритма принесет больше вреда, чем пользы, т.к. важно понять как и почему работают и применяются в данной ситуации конкретные формулы и алгоритмы.
Конечно, для профессиональной статистической обработки результатов экспериментов есть специализированные программные средства, а для написания контрольно-обучающих программ есть более подходящие средства, чем Excel, однако последний можно с успехом использовать не только для этой цели.
Во-первых, преподаватель может использовать Excel для подготовки к занятиям. Для составления необходимого задачного материала, например, можно применить генераторы псевдослучайных чисел, в частности, с помощью «генератора задач» достаточно просто выполнить проверку решения или подбор «хороших» ответов.
Во-вторых, подачу массивов статистических данных, динамических иллюстраций, экспериментов, использующих генераторы случайных чисел, преподаватель может осуществлять с помощью Excel.
В-третьих, Excel можно использовать как средство изучения материала теории вероятностей и математической статистики. Студент может разработать как свою собственную Excel-программу для вычисления вероятностей, обработки статистических данных и их наглядного представления, так и воспользоваться готовой программой, например, разработанной преподавателем. Данная программа может использоваться для решения задач типового расчета. Если же студенту необходимо указать полное решение, то он может использовать Excel для проверки правильности решения задач, перед тем как сдавать их на проверку преподавателю.
Для подобного использования компьютера при обучении теории вероятностей и математической статистике автором статьи разработана Excel-программа, которая может быть использована и студентами, и преподавателями.
Программа содержит 15 листов: комбинаторика, формула Байеса, формула Муавра-Лапласа, ДСВ-1, ДСВ-2, генератор «выборка 100», расчет «выборка 100», расчет статистического ряда, расчет «выборка 10 000», перерасчет «выборка 10 000», выборка 10 000, генератор корреляционных таблиц 5 на 5, расчет корреляционных таблиц 5 на 5, расчет корреляционных таблиц 20 на 20, черновик.
На листе «Комбинаторика» можно посчитать перестановки, размещения и сочетания с повторениями и без них. Для перестановок с повторениями количество повторяющихся элементов не должно превосходить 10 (для практических нужд достаточно). Программой проверяется правильность вводимых в формулу аргументов. В случае небольших чисел студент может проверить правильность вычислений на бумаге, а в случае больших аргументов удается сэкономить время для решения других задач.
На листе «формула Муавра-Лапласа» можно проводить вычисления по локальной и интегральной формулам Муавра-Лапласа, формуле Бернулли. Необходимые промежуточные значения вычисляются автоматически.

На листе «ДСВ-2» можно получить статистические ряды биномиального и геометрического законов распределения, задаваемые числом испытаний и вероятностью успеха (получается копируемая таблица, которую можно вставить на лист «ДСВ-1»).
На листе «Генератор «выборка 100» можно получить 100 значений равномерно, нормально или показательно распределенного количественного признака в заданных пользователем пределах. На этом же листе автоматически рассчитывается таблица с группированными данными: концы интервалов, их середины, частота и частость, компоненты среднего и среднее, компоненты дисперсии и дисперсия, теоретические частоты и частости, компоненты критерия согласия Пирсона, теоретическое значение (по заданному пользователем уровню значимости) и наблюдаемое его значение. Кроме указанных значений рассчитываются доверительные интервалы для математического ожидания и среднего квадратического отклонения нормально распределенного количественного признака, начальные и центральные моменты до четвертого порядка включительно, асимметрия и эксцесс. Делается вывод о принятии нулевой или альтернативной гипотезы о виде закона распределения. Строится гистограмма.
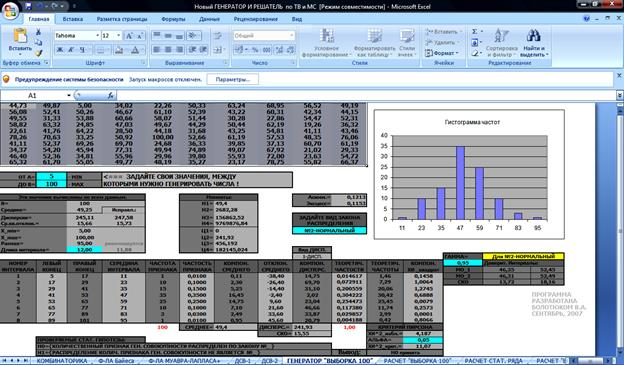
На листе «Расчет статистического ряда» производятся вычисления аналогичные вычислениям предыдущего листа, но исходные данные вводятся не в виде выборки, а в виде статистического ряда из восьми элементов (соответствует объему выборки в 100 элементов). Строится гистограмма.
Негибкость вычислений предыдущих листов компенсируется листами «Выборка 10 000» и «Расчет выборки 10 000». Содержимое этих двух листов позволяет проводить вычисления полностью аналогичные вычислениям листа «Расчет «выборка 100», но для выборок с количеством элементов до 10 000. Имеется возможность выбора равномерного, нормального или показательного закона для проверки гипотезы о виде закона распределения. Строится гистограмма.
На листе «Перерасчет «выборка 10 000» можно скорректировать длину интервала группирования и их количество, остальные данные автоматически копируются с листа «Расчет «выборка 10 000». Строится гистограмма. Этот лист позволяет наглядно продемонстрировать, к чему ведут ошибки при вычислении длины интервала или их количества.
На листе «Генератор корреляционных таблиц 5 на 5» можно получить случайную корреляционную таблицу с результатами расчетов по ней: необходимые суммы, коэффициент корреляции, уравнения линейной регрессии. Осуществляется проверка гипотезы о значимости коэффициента корреляции, уровень значимости задается пользователем.
На листе «Расчет корреляционных таблиц» производятся вычисления полностью аналогичные вычислениям предыдущего листа, но исходные данные вводятся пользователем.
На листе «Расчет корреляционных таблиц 20 на 20» можно обрабатывать корреляционные таблицы, не превосходящие указанного в заголовке размера. Вычисляются необходимые суммы, коэффициент корреляции, уравнения линейной регрессии. Осуществляется проверка гипотезы о значимости коэффициента корреляции, уровень значимости задается пользователем.
Некоторые «несовершенные» листы, допускающие негибкость в вычислениях, оставлены после усовершенствования программы по той причине, что с ними легко работать тем, кто не гонится за универсальностью, а желает преподнести студентам сам метод вычислений.
Например, при обучении соответствующим темам курса теории вероятностей и математической статистики после разбора основных задач можно выдать студентам домашнее задание на составление программы в Excel, которая помогла бы решить большинство задач рассмотренных на занятии. Примеры составления и работы такой программы преподаватель может разобрать на конкретной задаче. Компьютер есть у многих студентов, но компьютерный класс (идеальный вариант), который можно использовать для проведения лабораторных и практических занятий по теории вероятностей и математической статистике, к сожалению, имеется не во всех вузах.
Таким образом, преподаватель, располагая компьютером и подобной программой, сможет продуктивнее выполнять подготовку к практическим занятиям по теории вероятностей и математической статистике. Например, автор использовал данную программу для написания учебного пособия по математической статистике, подготовки задач типового расчета, подбора «хороших» ответов в задачах для самостоятельного решения, при проверке задач контрольных работ заочников. Студенты же, умея пользоваться этой или аналогичной (возможно собственноручно составленной) программой, смогут осознаннее усваивать материал курса, не обременяя себя, где это возможно громоздкими вычислениями, разовьют логическое и алгоритмическое мышление, повысят компьютерную грамотность при работе с офисными программами.
Основные термины (генерируются автоматически): математическая статистика, лист, задача, студент, вычисление, статистический ряд, уровень значимости, предыдущий лист, проверка гипотезы, теория вероятностей.
Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x1, x2, … xn образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p1, p2,… pn. (pn должны быть
положительны и в сумме давать единицу).
В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.
1 Биномиальное распределение
Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.
Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требуется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.
В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.
Функция использует следующие
параметры:
БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где
число_успехов — это количество успешных
испытаний;
число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);
вероятность_ успеха — это вероятность успеха
каждого испытания;
интегральный — это логическое значение,
определяющее форму функции.
Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);
если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).
Пример 1. Какова вероятность того,
что трое из четырех новорожденных будут мальчиками?
Решение:
1. Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.
2. Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).
3. В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Категория указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.
Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вводим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.
В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероятностью 0,25.
Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.
Задания для самостоятельной работы
1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)
2.
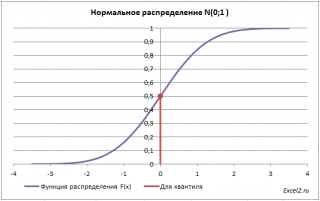
Нормальное распределение
Нормальное распределение — это совокупность объектов, в которой крайние значения
некоторого признака — наименьшее и наибольшее — появляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближается
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.
Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Медиана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен
.
В Excel для вычисления значений
нормального распределения используются функция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:
х — значения выборки, для
которых строится распределение;
среднее — среднее арифметическое
выборки;
стандартное_откл — стандартное отклонение
распределения;
интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интегральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.
Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стандартное
нормальное распределение.
Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и
=1,5.
Решение
1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ функции
плотности вероятности — f(x).
2. Вводим в диапазон А2:А21
значения х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).
3. Устанавливаем табличный курсор в ячейку В2 и
для получения значения вероятности воспользуемся специальной функцией —
нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.
4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математического ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В рабочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.
5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.
6. По полученным данным строим искомую диаграмму
нормальной функции распределения. Щелчком указателя мыши на кнопке на панели
инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово.
Рис. 1 График нормальной функции распределения
Получен приближенный график
нормальной функции плотности распределения (см. рис.1).
Задания для самостоятельной работы
1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при
= 3.
3. Генерация случайных величин
Еще одним аспектом
использования законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимо
получить последовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятностей.
Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или нескольких распределений.
В MS Excel для генерации СВ используются функции из категории Математические:
СЛЧИС () – выводит на экран равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;
СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между произвольными заданными
значениями.
В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
заполнить следующие поля:
— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;
— число случайных чисел
вводится число случайных значений, которое необходимо вывести для
каждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены;
— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:
1. равномерное — характеризуется
верxней и нижней границами. Переменные извлекаются с одной и
той же вероятностью для всех значений интервала.
2. нормальное
— характеризуется средним значением и стандартным отклонением. Обычно для
этого распределения используют среднее значение
0 и стандартное отклонение 1.
3. биномиальное
— характеризуется вероятностью успеха (величина р) для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;
4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержащего значения, и правого, содержащего
вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть
равна 1;
5. распределения Бернулли, Пуассона
и Модельное.
— в поле случайное рассеивание
вводится произвольное значение, для которого необходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.
— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на экран будет выведено сообщение в случае
возможного наложения выходного диапазона на исходные
данные.
Рассмотрим пример.
Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.
Решение
1.
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
2.
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
3.
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.
4.
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.
Задание для
самостоятельной работы
1. Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
2. Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
3. Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
4. Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.
5. Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта
www.excel2.ru
. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL
.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется
генеральная совокупность
(population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения
генеральная совокупность
представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является
случайной величиной
. По определению, любая
случайная величина
имеет
функцию распределения
, которая обычно обозначается F(x).
Функция распределения
Функцией распределения
вероятностей
случайной величины
Х называют функцию F(x), значение которой в точке х равно вероятности события X
F(x) = P(X
Поясним на примере нашего станка. Хотя предполагается, что наш станок производит только один тип деталей, но, очевидно, что вес изготовленных деталей будет слегка отличаться друг от друга. Это возможно из-за того, что при изготовлении мог быть использован разный материал, а условия обработки также могли слегка различаться и пр. Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая — 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 200 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.
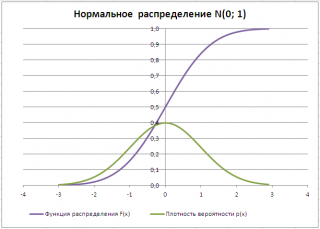
Типичный график
Функции распределения
для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см.
файл примера
):
В справке MS EXCEL
Функцию распределения
называют
Интегральной
функцией распределения
(
Cumulative
Distribution
Function
,
CDF
).
Приведем некоторые свойства
Функции распределения:
Функция распределения
F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
Функция распределения
– неубывающая функция;-
Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x
1
<=X
2)=F(x
2
)-F(x
1
).
Существует 2 типа распределений:
непрерывные распределения
и
дискретные распределения
.
Дискретные распределения
Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется
дискретным
. Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см.
схему Бернулли
). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
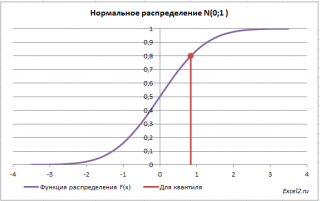
Непрерывные распределения и плотность вероятности
В случае
непрерывного распределения
случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для
непрерывной случайной величины
равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой
функции плотности распределения p(x)
. Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение
функции распределения
на этом интервале:
Как видно из формулы выше
плотность распределения
р(х) представляет собой производную
функции распределения
F(x), т.е. р(х) = F’(x).
Типичный график
функции плотности распределения
для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
В литературе
Функция плотности распределения
непрерывной случайной величины может называться:
Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF)
.
Чтобы все усложнить, термин
Распределение
(в литературе на английском языке —
Probability
Distribution
Function
или просто
Distribution
)
в зависимости от контекста может относиться как
Интегральной
функции распределения,
так и кее
Плотности распределения.
Из определения
функции плотности распределения
следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от
Функции распределения,
больше 1. Например, для
непрерывной равномерной величины
, распределенной на интервале [0; 0,5]
плотность вероятности
равна 1/(0,5-0)=2. А для
экспоненциального распределения
с параметром
лямбда
=5, значение
плотности вероятности
в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что
плотность распределения
является производной от
функции распределения
, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что
плотность распределения
>1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере
экспоненциального распределения
).
Примечание
: Площадь, целиком заключенная под всей кривой, изображающей
плотность распределения
, равна 1.
Примечание
: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL
интегральной функцией распределения
. Этот термин присутствует в параметрах функций, например в
НОРМ.РАСП
(x; среднее; стандартное_откл;
интегральная
). Если функция MS EXCEL должна вернуть
Функцию распределения,
то параметр
интегральная
, д.б. установлен ИСТИНА. Если требуется вычислить
плотность вероятности
, то параметр
интегральная
, д.б. ЛОЖЬ.
Примечание
: Для
дискретного распределения
вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL
плотность вероятности
может называть даже «функция вероятностной меры» (см. функцию
БИНОМ.РАСП()
).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить
плотность вероятности
для определенного значения случайной величины, нужно знать ее распределение.
Найдем
плотность вероятности
для
стандартного нормального распределения
N(0;1) при x=2. Для этого необходимо записать формулу
=НОРМ.СТ.РАСП(2;ЛОЖЬ)
=0,054 или
=НОРМ.РАСП(2;0;1;ЛОЖЬ)
.
Напомним, что
вероятность
того, что
непрерывная случайная величина
примет конкретное значение x равна 0. Для
непрерывной случайной величины
Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
(см. картинку выше), приняла положительное значение. Согласно свойству
Функции распределения
вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)
=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
, приняла отрицательное значение. Согласно определения
Функции распределения,
вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(0;ИСТИНА)
=0,5.
3) Найдем вероятность того, что случайная величина, распределенная по
стандартному нормальному распределению
, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу
=НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА)
.
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по
стандартному нормальному закону
N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье
Распределения случайной величины в MS EXCEL
приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
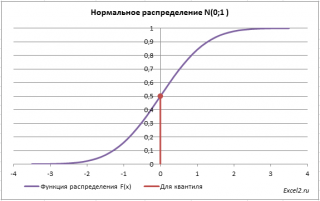
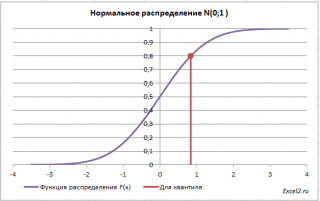
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела:
Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение
медиану
или 50-ю
процентиль
).
Для этого необходимо на графике
функции распределения
найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение <0, равна 0,5.
В MS EXCEL используйте формулу
=НОРМ.СТ.ОБР(0,5)
=0.
Однозначно вычислить значение
случайной величины
позволяет свойство монотонности
функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно
функцию распределения
, а не
плотность распределения
. Поэтому, в аргументах функции
НОРМ.СТ.ОБР()
отсутствует параметр
интегральная
, который подразумевается. Подробнее про функцию
НОРМ.СТ.ОБР()
см. статью про
нормальное распределение
.
Обратная функция распределения
вычисляет
квантили распределения
, которые используются, например, при
построении доверительных интервалов
. Т.е. в нашем случае число 0 является 0,5-квантилем
нормального распределения
. В
файле примера
можно вычислить и другой
квантиль
этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе
обратная функция распределения
часто называется как Percent Point Function (PPF).
Примечание
: При вычислении
квантилей
в MS EXCEL используются функции:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Цели и задачи:
Образовательные: закрепить такие
понятия теории вероятности как: среднее
арифметическое, размах, мода и медиана рядов
чисел; систематизировать знания по пройденной
теме, формировать умение учащихся применять
знания к решению практических задач, контроль,
оценка и проверка знаний учащихся, закрепить
знание способов ввода данных в ячейки и порядок
создания формул с использованием встроенных
функций в табличном процессоре MS Excel. Показать
важность межпредметных связей
Развивающие: развитие
познавательной активности, творческих
способностей учащихся, умения сопоставлять,
анализировать, развить навыки ввода данных в
ячейки с использованием автозаполнения и
вычисления итоговых значений с помощью
статистических функций табличного процессора MS
Excel;
Воспитательные: способствовать
воспитанию у учащихся аккуратности, усидчивости,
навыков учебного труда, интереса к предмету.
Ход урока
-
Организационный момент.
-
Актуализация опорных знаний. Опрос.
- Как определить среднее арифметическое ряда?
- Что называется модой ряда?
- Как определить размах ряда?
- Что называется медианой ряда?
- Что такое адрес ячейки и из чего он состоит?
- Чем абсолютный адрес отличается от
относительного? - Что такое автозаполнение и как им пользоваться?
- Что такое функция Excel?
-
Решить задачу:
- Администрация школы решила проверить
математическую подготовку учащихся 8 класса. С
этой целью был составлен тест, содержащий 9
заданий. Работу выполняли 40 учащихся школы. При
проверке каждой работы учитель отмечал число
верно выполненных заданий. В результате был
составлен такой ряд чисел:
- Определить сколько заданий в среднем выполнил
каждый ученик верно? - Найти разницу в числе верно выполненных заданий
между учащимися. - Чему равна мода и медиана данного ряда?
-
Закрепление материала
6,5,4,0,4,5,7,9,1,6,8,7,9,5,8,6,7,2,5,7,6,3,4,4,5,6,8,6.7,7,4,3.5,9,6,7,8,6,9,8.
Задача разбирается вместе с учителем
для постановки проблемной ситуации, в разрешении
которой помогает использование электронных
таблиц.
Чтобы ответить на вопросы задачи
необходимо упорядочить ряд данных, а при
нахождении статистических характеристик ряда
нам помогут на доске записанные статистические
функции Excel, которые используются для нахождения
среднего арифметического, размаха, моды и
медианы рядов чисел:
=МЕДИАНА(аргументы) – медиана
ряда;
=СРЗНАЧ(аргументы) – среднее
арифметическое ряда;
=МОДА(аргументы) – мода ряда;
=МАКС(аргументы)-МИН(аргументы)
– размах ряда.
Учащиеся получают листки с задачами,
рассаживаются за компьютеры и решают их с
помощью Excel. Для решения задач необходим файл
(Приложение1)
Задачи для закрепления
- Найдите среднее арифметическое, размах, моду и
медиану рядов чисел; - За четверть Люда получила по алгебре пять двоек,
четыре четверки и две пятерки. Ее мама считает,
что за четверть Люде надо ставить двойку, папа
считает, что надо ставить тройку, а сама Люда
считает, что надо ставить четверку. Попробуйте
привести аргументы в пользу каждой точки зрения
(какие статистические характеристики вычисляет
каждый член семьи?). Какую бы оценку вы поставили
Люде? - В таблице представлены результаты опроса 100
человек. - Света, Люда и Женя договорились в течение трех
дней по-очереди поливать в классе цветы. Сколько
у них есть способов установить порядок
дежурства? - 8 детей делят пирожки. Все пирожки имеют разную
начинку. Один из них с морковью. Сколько
существует способов разделить пирожки (каждому
по штуке) так, чтобы пирожок с морковью не
достался ребенку, который не любит такую начинку?
| Количество опрошенных | Зарплата |
| 10 | 500 |
| 30 | 1000 |
| 50 | 1500 |
| 10 | 3000 |
а) сколько денег, в среднем, получает один
человек из этой группы (найдите среднее
арифметическое ряда данных)?
б) сколько денег получает ежемесячно
“средний” человек из этой группы (найдите
медиану этих данных)?
в) какой заработок наиболее распространен у
членов этой группы (найдите моду этих данных)?
-
Подведение итогов (выставление оценок)
Приложение
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>
ight)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>
ight)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)= = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>==left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1
ight)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, 4,5 le m le 5,5, m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта ]]> www.excel2.ru ]]> . Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной. По определению, любая случайная величина имеет функцию распределения, которая обычно обозначается F(x).
Функция распределения
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):
В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения (Cumulative Distribution Function, CDF).
Приведем некоторые свойства Функции распределения:
- Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
- Функция распределения – неубывающая функция;
- Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x1 Примечание: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL.
Непрерывные распределения и плотность вероятности
В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1.
Выходом из этой ситуации является введение так называемой функции плотности распределения p(x). Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:
Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).
Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL.
В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF).
Чтобы все усложнить, термин Распределение (в литературе на английском языке — Probability Distribution Function или просто Distribution) в зависимости от контекста может относиться как Интегральной функции распределения, так и кее Плотности распределения.
Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины, распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда=5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что плотность распределения является производной от функции распределения, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения).
Примечание: Площадь, целиком заключенная под всей кривой, изображающей плотность распределения, равна 1.
Примечание: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения. Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная, д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности, то параметр интегральная, д.б. ЛОЖЬ.
Примечание: Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже «функция вероятностной меры» (см. функцию БИНОМ.РАСП() ).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.
Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .
Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5.
Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.
3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.
Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения, а не плотность распределения. Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная, который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение.
Обратная функция распределения вычисляет квантили распределения, которые используются, например, при построении доверительных интервалов. Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения. В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).
Примечание: При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL.
События, характеризующие данные, могут носить случайный характер и появляться с разной вероятностью.
Вероятность события p есть отношение числа благоприятных исходов m к числу всех возможных исходов n этого события: p=m/n. Например, вероятность появления туза в наугад выбранной карте из колоды в 52 карты равна 4/52=0.0769, так как m=4, а n=52.
Если известно соответствие между появлениями (величинами) x1, x2, …, xn случайного события (переменной) X и соответствующими вероятностями их реализации p1, p2, …, pn, то говорят, что известен закон распределения случайной величины F(x). Большинство встречающихся на практике распределений вероятностей реализовано в Excel.
Распределения вероятностей имеют числовые характеристики.
Функции Excel для вычисления числовых характеристик распределения вероятностей. Они входят в группу Статистические. При вычислении функций в качестве случайных величин используйте следующие значения:
Математическое ожидание случайной величины (среднее арифметическое), характеризующее центр распределения вероятностей, вычисляется функцией СРЗНАЧ. СРЗНАЧ(A1:A7) = 9.
Дисперсия, характеризует разброс случайной величины относительно центра распределения вероятностей и вычисляется функцией ДИСПР. ДИСПР(A1:A7) = 4.857.
Среднеквадратичное отклонение есть квадратный корень из дисперсии, характеризует разброс случайной величины в единицах случайной величины и вычисляется функцией СТАНДОТКЛОНП. СТАНДОТКЛОНП(A1:A7) = 2.203893.
Квантиль случайной величины с законом распределения F(x) есть значение случайной величины x при заданной вероятности p., т.е. есть решение уравнения F(x)=p. Медиана есть квантиль с вероятностью p=0.5.
Excel, вместо квантилей содержит функции вычисления х для определенных уровней р: квартили (кварта – четверть), децили (дециль – десятая часть), персентили (персент – процент). Различают нижний квартиль с вероятностью p=0.25 и верхний квартиль с вероятностью p=0.75. Децили это квантили с вероятностью 0.1, 0.2, …, 0.9.
Функцию КВАРТИЛЬ используют, чтобы разбить данные на группы. В качестве второго аргумента указывают уровень (четверть), для которого нужно вернуть решение: 0 – минимальное значение распределения, 1 – первый, нижний квартиль, 2 – медиана, 3 – третий, верхний квартиль, 4 – максимальное значение. Например, КВАРТИЛЬ(A1:A7;3) = 10, т.е. 75% всех значений меньше 10, КВАРТИЛЬ(A1:A7;2) = 9.
Функция ПЕРСЕНТИЛЬ вычисляет квантиль указанного уровня вероятности и используется для определения порога приемлемости значений. В качестве второго аргумента указывают уровень 0.1, 0.2, …, 0.9. ПЕРСЕНТИЛЬ(A1:A7;0,9) = 11.8, т.е. 90% всех значений меньше 11.8.
Excel содержит инструмент Ранг и персентиль, который на основе набора данных формирует выходную таблицу, содержащую порядковый и процентный ранги для каждого значения в наборе данных. См. справку по F1. Ниже приведен пример установки надстройки Пактет анализа
Распределения вероятностей, реализованные в Excel.
Каждый закон распределения описывает процессы разной вероятностной природы и характеризуется специфическими параметрами:
равномерное распределение – n случайных чисел выпадает с одной и той же вероятностью p=1/n; характеризуется нижней и верхней границей; примером является появление чисел 1, 2, …, 6 при бросании игральной кости (p=1/6);
биномиальное распределение моделирует взаимосвязь числа успешных испытаний m и вероятностей успеха каждого испытания p при общем количестве испытаний n — функции БИНОМРАСП и КРИТБИНОМ;
нормальное (гауссово) распределение описывает процессы, в которых на результат воздействует большое число независимых случайных факторов, среди которых нет сильно выделяющихся – функции НОРМРАСП, НОРМСТРАСП, НОРМОБР, НОРМСТОБР и НОРМАЛИЗАЦИЯ;
распределение Пуассона, предсказывает число случайных событий на определенном отрезке времени или на определенном пространстве, позволяет аппроксимировать биномиальное распределение – функция ПУАССОН;
экспоненциальное (показательное) распределение, моделирует временные задержки между событиями, описывает процессы в задачах массового обслуживания и в задачах с «временем жизни» — ЭКСПРАСП;
распределение хи-квадрат, связано с нормальным, возвращает одностороннюю вероятность распределения и используется для сравнения предполагаемых и наблюдаемых значений – функция ХИ2РАСП;
распределение Стьюдента, связано с нормальным, возвращает вероятность для t-распределения Стьюдента и используется для проверки гипотез при малом объеме выборки – функция СТЬЮДРАСП;
F-распределение (Фишера), связано с нормальным и может быть использовано в F-тесте, который сравнивает степени разброса двух множеств данных – fраспобр;
гамма-распределение используется для изучения случайных величин, имеющих асимметричное распределение, в теории очередей – функция ГАММАРАСП;
а также другие распределения – функции БЕТАРАСП, ВЕЙБУЛЛ, ОТРБИНОМРАСП, ГИПЕРГЕОМЕТ, ЛОГНОРМРАСП и др.
Биномиальное распределение характеризуется числом успешных испытаний m, вероятностью успеха каждого испытания p и общим количеством испытаний n. Классическим примером использования биномиального распределения является выборочный контроль качества больших партий товара, изделий в торговле, на производстве, когда сплошная проверка невозможна. Из партии выбирают n образцов и регистрируют число бракованных m. Бракованными могут быть 1, 2, … , n образцов, но вероятности реального числа бракованных будут различными. Если контрольная вероятность брака ниже допустимой вероятности, то можно гарантировать достаточное качество всей партии.
В Excel функция БИНОМРАСП вычисляет вероятность отдельного значения распределения по заданным m, n и р, а функция КРИТБИНОМ – случайное число по заданной вероятности. Обычно функция КРИТБИНОМ используется для определения наибольшего допустимого числа брака.
В качестве примера построим график плотности вероятности биномиального распределения для n=10 (1, 2, …, 10) и p=0.2. Введите исходные данные, как показано на рисунке:
Далее в ячейку В4 введите статистическую функцию БИНОМРАСП и заполните ее параметры как показано на рисунке:
Здесь параметр Число_s есть число успешных испытаний m, Испытания – число независимых испытаний n, Вероятность_s – вероятность успеха каждого испытания p. Параметр Интегральный равен 0, если требуется получить плотность распределения (вероятность для значения m), и равен 1, если требуется получить вероятность с накоплением (вероятность того, что число успешных испытаний не меньше значения аргумента Число_s).
Формулу из В4 размножьте в ячейки В5:В13. Ниже показан результат:
В колонке В вычислены вероятности успешных испытаний m=1, 2, …, 10. Теперь по диапазону В4:В13 постройте график или гистограмму биномиальной функции плотности распределения – результат на рисунке. Поэкспериментируйте, изменяя значение вероятности в ячейке В1: 0.3, 0.4, 0.8, проследите за изменениями формы графика.
Для иллюстрации функции КРИТБИНОМ используем предыдущий пример – необходимо найти число m, для которого вероятность интегрального распределения больше или равна 0.75. Вызовите функцию КРИТБИНОМ и заполните параметры. Вы должны получить значение 3. Это означает, что при вероятности интегрального распределения >= 0.75 будет не менее трех (m>=3) успешных испытаний.
Нормальное распределение характеризуется средним арифметическим (математическим ожиданием) m и стандартным (среднеквадратичным) отклонением r. Дисперсия равна r 2 . Краткое обозначение распределения N(m,r 2 ). График нормального распределения симметричен относительно центра распределения (точки m), чем меньше r, тем больше вероятность появления случайной величины. В пределы [m—r,m+r] нормально распределенная случайная величина попадает с вероятностью 0,683 в пределы [m-2r,m+2r] — с вероятностью 0,955 и т.д.
При m=0 и r=1 нормальное распределение называется стандартным или нормированным – N(0,1).
Нормальное распределение имеет очень широкий круг приложений. В качестве примера построим график плотности вероятностей нормального распределения при m=15 и r=1,5 в диапазоне [m-3r,m+3r] c шагом 0,5. Результат показан на рисунке.
Выполните следующие действия:
в ячейку А4 введите формулу =B1-3*B2, в ячейку А5 формулу =A4+B$3 и размножьте ее по ячейку А22;
в ячейку В4 введите функцию НОРМРАСП из группы Статистические – параметры заполните как на рисунке;
размножьте формулу из ячейки В4 по ячейку В22 и по диапазону В4:В22 постройте график; на 2-ом шаге мастера диаграмм в закладке Ряд введите подписи к оси х из диапазона А4:А22.
Функция ВЕРОЯТНОСТЬ возвращает вероятность того, что значение из интервала находится внутри заданных пределов.
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
В результате выполненных вычислений получим:
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:

Источник: http://exceltable.com/funkcii-excel/primer-funkcii-veroyatnost
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
| ЧИСЛКОМБ / COMBIN |
Возвращает количество сочетаний без повторений. |
| ФАКТР / FACT |
Вычисляет факториал числа. |
| СЛЧИС / RAND |
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное). |
| СЛУЧМЕЖДУ / RANDBETVEEN |
Выдает случайное число в заданном интервале. |
| БИНОМРАСП / BINOMDIST |
Вычисляет отдельное значение биномиального распределения. |
| ГИПЕРГЕОМЕТ / HYRGEOMDIST |
Определяет гипергеометрическое распределение. |
| НОРМРАСП / NORMDIST |
Вычисляет значение нормальной функции распределения. |
| НОРМОБР / NORMINV |
Выдает обратное нормальное распределение. |
| НОРМСТРАСП / NORMSDIST |
Выдает стандартное нормальное интегральное распределение. |
| НОРМСТОБР / NORMSINV |
Выдает обратное значение стандартного нормального распределения. |
| ПЕРЕСТ / PERMUT |
Находит количество размещений без повторений |
| ВЕРОЯТНОСТЬ / PROB |
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов. |
Подробнее: Формулы комбинаторики в Excel.
Подробно решим ваши задачи по теории вероятностей
Источник: http://MatBuro.ru/tvart_sub.php?p=excel_form
Задания для самостоятельной работы
1. Какова вероятность того, что восемь из десяти студентов,сдающих зачет, получат «незачет». (0,04)
Источник: http://sites.google.com/site/ktnoscience/Home/lab/lab2w
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Источник: http://exceltable.com/funkcii-excel/primer-funkcii-veroyatnost
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) – соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены – мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет – ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Источник: http://dudom.ru/kompjutery/formula-bernulli-v-excel/
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Источник: http://MatBuro.ru/tvart_sub.php?p=excel_form
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Значение x |
Вероятность |
|
|
0,2 |
||
|
1 |
0,3 |
|
|
2 |
0,1 |
|
|
3 |
0,4 |
|
|
Формула |
Описание |
Результат |
|
=ВЕРОЯТНОСТЬ(A3:A6;B3:B6;2) |
Вероятность того, что x является числом 2. |
0,1 |
|
=ВЕРОЯТНОСТЬ(A3:A6;B3:B6;1;3) |
Вероятность того, что x находится в интервале от 1 до 3. |
0,8 |
Нужна дополнительная помощь?
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C-9ac30561-c81c-4259-8253-34f0a238fc49
Полезные ссылки
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
Источник: http://MatBuro.ru/tvart_sub.php?p=excel_form
3. Генерация случайных величин
Еще одним аспектомиспользования законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимополучить последовательность случайных чисел. Это, в частности, требуется длямоделирования объектов, имеющих случайную природу, по известному распределениювероятностей.
Процедура генерациислучайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными изодного или нескольких распределений.
В MSExcel для генерации СВ используются функции из категории Математические:
СЛЧИС () – выводит на экран равномернораспределенные случайные числа больше или равные 0 и меньшие 1;
СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экранслучайное число, лежащее между произвольными заданнымизначениями.
В случае использованияпроцедуры Генерация случайных чисел из пакета Анализа необходимозаполнить следующие поля:
– число переменныхвводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то всестолбцы в выходном диапазоне будут заполнены;
– число случайных чиселвводится число случайных значений, которое необходимо вывести длякаждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены;
– в поле распределение необходимо выбрать тип распределения,которое следует использовать для генерации случайных переменных:
1. равномерное – характеризуетсяверxней и нижней границами. Переменные извлекаются с одной итой же вероятностью для всех значений интервала.
2. нормальное— характеризуется средним значением и стандартным отклонением. Обычно дляэтого распределения используют среднее значение0 и стандартное отклонение 1.
3. биномиальное— характеризуется вероятностью успеха (величина р) для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайнойпеременной;
4. дискретное— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,содержащего значения, и правого, содержащеговероятности, связанные со значением в данной строке. Сумма вероятностей должна бытьравна 1;
5. распределения Бернулли, Пуассонаи Модельное.
– в поле случайное рассеиваниевводится произвольное значение, для которого необходимогенерировать случайные числа. Впоследствии можно снова использовать этозначение для получения тех же самых случайных чисел.
– выходной диапазонвводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, ина экран будет выведено сообщение в случаевозможного наложения выходного диапазона на исходныеданные.
Рассмотрим пример.
Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобыпервые блюда чередовались в случайном порядке.
Решение
1. Пронумеруем первыеблюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
2. Укажем желаемую вероятность появлениякаждого первого блюда. Пусть все блюда будутравновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
3. В меню Сервисвыбираем пункт Анализ данных и далее указываем строку Генерацияслучайных чисел. В появившемся диалоговом окне указываем Числопеременных — 1, Число случайных чисел — 30 (количестводней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входнойинтервал значений и вероятностейвводим (мышью) диапазон, содержащий номера супов и ихвероятности. – А2:В5.
4. Указываем выходнойдиапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,4.
Источник: http://sites.google.com/site/ktnoscience/Home/lab/lab2w