Использование excel в логистике

  1. Лыкова Н.П.

    Российский государственный гуманитарный университет

NovaInfo 7, скачать PDF
Опубликовано 13 октября 2011
Раздел: Технические науки
Просмотров за месяц: 87

Аннотация

Одним из важнейших на данный момент разделом логистики, является транспортная логистика. Которая представляет собой систему по организации доставки, а именно по перемещению каких-либо материальных предметов, веществ и прочего из одной точки в другую по оптимальному маршруту.

Ключевые слова

MS EXCEL, РЕШЕНИЕ, ЛОГИЧЕСКИЕ ЗАДАЧИ

Текст научной работы

Одним из важнейших на данный момент разделом логистики, является транспортная логистика. Которая представляет собой систему по организации доставки, а именно по перемещению каких-либо материальных предметов, веществ и прочего из одной точки в другую по оптимальному маршруту.

Оптимальным считается маршрут, по которому возможно доставить логистический объект, в кратчайшие сроки (или предусмотренные сроки) с минимальными затратами, а также с минимальным вредом для объекта доставки.

Одним из способов нахождения такого оптимального маршрута может служить решение транспортных задач в MS Excel.

Транспортная задача является частным типом задачи линейного программирования и формулируется следующим образом: имеется m пунктов отправления (или пунктов производства) А_i,dots,А_m, в которых сосредоточены запасы однородных продуктов в количестве a_1,dots,а_m единиц. Имеется n пунктов назначения (или пунктов потребления) В_1,dots,В_m, потребность которых в указанных продуктах составляет b_1,dots,b_n единиц. Известны также транспортные расходы Сij, связанные с перевозкой единицы продукта из пункта Ai в пункт Вj, i=1,dots,m; j=1,dots,n.

Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А_1,А_2,dots,А_n в n пунктов назначения В_1,В_2,dots,В_n.

В качестве критерия оптимальности (целевая функция) обычно задается минимальная суммарная стоимость перевозок всего груза или минимальная суммарная транспортная работа по доставке грузов, которая может быть пропорциональна времени доставки грузов потребителям или расстоянию между поставщиками и потребителями. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная суммарная стоимость перевозок всего груза.

Обозначим Cij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через ai — запасы груза в i -ом пункте отправления, через bj — потребности в грузе в j-ом пункте назначения, а через xi — количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая модель транспортной задачи состоит в определении минимального значения функции:

F=sum_{i=1}^msum_{j=1}^nc_{ij}x_{ij}rightarrow min, (1)

при условиях

sum_{i=1}^mx_{ij}=b_j, j = 1,2,…,n, (2)

sum_{j=1}^nx_{ij}=a_i, i = 1,2,…,m (3)

x_{ij}geq0, i=1,2,dots,m, j=1,2,dots,n. (4)

Поскольку переменные x_{ij}geq0, i=1,2,dots,m, j=1,2,dots,n. удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза в каждой из пунктов назначения, вывоз всего имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Суммарное количество груза у поставщиков равно sum_{i=1}^ma_i суммарная потребность в грузе в пунктах назначения равна sum_{j=1}^nb_j. Если суммарная потребность в грузе в пунктах назначения равна суммарному запасу груза в пунктах отправления, т. е.

sum_{i=1}^ma_i=sum_{j=1}^nb_j, (5)

то такая транспортная задача называется закрытой или сбалансированной. В противном случае — открытой или несбалансированной.

В случае превышения суммарного запаса над суммарной потребностью, т.е. если

sum_{i=1}^ma_i>sum_{j=1}^nb_j,

вводится фиктивный n+1-й потребитель (или пункт назначения) с потребностью, равной:

b_{n+1}=sum_{i=1}^ma_i-sum_{j=1}^nb_j

а соответствующие транспортные тарифы от всех поставщиков до фиктивного потребителя полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5).

В случае превышения суммарной потребности в грузе над суммарными запасами поставщиков, т. е. если

sum_{i=1}^ma_i<sum_{j=1}^nb_j

вводится фиктивный m+l-й пункт отправления с запасом груза в нем, равным:

a_{m+1}=sum_{i=1}^ma_i-sum_{j=1}^nb_j

а соответствующие транспортные тарифы от фиктивного поставщика до всех потребителей полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5)

Предположим, что sum_{i=1}^ma_i=sum_{j=1}^nb_j, т. е. общий объем производства равен общему объему потребления. Требуется составить такой план перевозок (откуда, куда и сколько единиц продукта везти), чтобы удовлетворить спрос всех пунктов потребления за счет реализации всего продукта, произведенного всеми пунктами производства, при минимальной общей стоимости всех перевозок.

Рассмотрим алгоритм решения таких задач на конкретном примере:

Продукты, находящиеся на четырех складах — С1, С2, С3, С4 необходимо развезти по пяти магазинам — Ml, М2, МЗ, М4 и М5. Потребности этих магазинов в продуктах равны соответственно 15, 14, 25, 5 и 9 ед. Запасы продуктов на складах С1, С2, СЗ, С4 составляют соответственно 23, 15, 45, 15 ед. Тарифы по доставке продуктов (руб./ед. груза) приведены в таблице:

Таблица 1. Тарифы по доставке продуктов (руб./ед. груза)

Склады

Магазины

М1

М2

М3

М4

М5

С1

10

3

4

5

6

С2

2

1

11

14

3

С3

4

13

3

2

8

С4

5

13

4

12

7

Составьте план перевозок продуктов, при котором суммарные расходы по их доставке будут минимальными.

Так как данная задача относится к задачам линейного программирования, то решение начинается с построения математической модели:

begin{cases}x_{11}+x_{12}+x_{13}+x_{14}=23 \ x_{21}+x_{22}+x_{23}+x_{24}=15 \ x_{31}+x_{32}+x_{33}+x_{34}=45 \ x_{41}+x_{42}+x_{43}+x_{44}=15 \ x_{11}+x_{12}+x_{13}+x_{14}=15 \ x_{21}+x_{22}+x_{23}+x_{24}=14 \ x_{31}+x_{32}+x_{33}+x_{34}=25 \ x_{41}+x_{42}+x_{43}+x_{44}=5 \ x_{51}+x_{52}+x_{53}+x_{54}=9 \ xijgeq0,i=1,2,3,4,j=1,2,3,4,5end{cases}

При данном плане перевозок суммарная их стоимость составит (целевая функция):

F=10x_{11}+3x_{12}+4x_{13}+5x_{14}+6x_{15}+

+2x_{21}+1x_{22}+11x_{23}+14x_{24}+3x_{25}+

+4x_{31}+13x_{32}+3x_{33}+2x_{34}+8x_{35}+

+5x_{41}+13x_{42}+4x_{43}+12x_{44}+7x_{45}+

+0x_{51}+0x_{52}+0x_{53}+0x_{54}+0x_{55}rightarrow min

Дальнейшее решение задачи ведётся в MS Excel.

Составляется таблица с исходными данными (рис. 1)

Исходные данные

Рисунок 1. Исходные данные

Затем заполняем столбец с ограничениями, при помощи функции СУММ (для ячейки Н4 =СУММ (В4:F4)), а формулу СУММПРОИЗВ мы вводим в строке с целевой функцией (=СУММПРОИЗВ (B4:F8;B15:F19)).

После введения всех данных и формул, мы ставим курсор на ячейку с формулой целевой функции и вызываем программу Поиск решения.

В поле изменяя ячейки выбираем ячейки с неизвестными переменными (B4:F8), а поле ограничения вводим наложенные нами ограничения.

Далее во вкладке параметры выбираем значения: линейная модель, неотрицательные значения и автоматическое масштабирование.

После чего получаем ответ к задаче (рис. 2)

Результаты поиска решений

Рисунок 2. Результаты поиска решений

Решив математическую модель, пришли к выводу, что

из пункта 1-го необходимо поставлять 8 ед. продукции на 2-й склад, из 2-го необходимо 6 ед. на 2-й и 9 на 5-й, из 3-го 15 ед. на 1-й, 25 на 3-й, 5 на 4-й, из 4-го продукции не требуется, при этом затраты на перевозку составят 202 ден. ед.

Как видно из примера, решение задачи с помощью MS Excel быстрое и удобное, так как:

  • создав один раз таблицу, её можно применять для задач такого же типа изменяя только исходные данные;
  • практически все необходимые для решения задачи формулы уже представлены в MS Excel;
  • решение задачи занимает в несколько раз меньше времени, нежели её же решение вручную;
  • точность решения гораздо выше, чем вручную, а погрешности сведены к минимуму.

Читайте также

  • Принятие управленческих решений в образовательном процессе

    1. Половнева М.В.
    NovaInfo 58, с.130-133, 30 января 2017, Технические науки

  • Табличная имитация алгоритмов искусственного интеллекта в MS Excel

    1. Любивая Т.Г.
    NovaInfo 56, с.251-256, 15 декабря 2016, Экономические науки

  • К вопросу о практическом применении RFM-анализа клиентской базы (на примере магазина «Подарки»)

    1. Генералов И.Г.
    2. Жавронович М.Ю.
    3. Суслов С.А.
    NovaInfo 49, с.251-255, 2 августа 2016, Экономические науки

  • Практическое применение информационных технологий в изучении экономики АПК

    1. Петрова Л.В.
    NovaInfo 41, с.77-80, 27 февраля 2016, Экономические науки

  • Разбор и анализ таблиц Excel с помощью MS XML в TestComplete

    1. Долганов А.А.
    NovaInfo 2, 13 июля 2010, Технические науки

Список литературы

  1. Акулич И.Л. Математическое программирование в примерах и задачах: учебное пособие для ВУЗов. — М.: Высшая школа, 2004
  2. Красс М. Математика для экономических специальностей. Учебник. 3-е изд., перераб и доп. М, Экономист, 2004.

Цитировать

Князева, А.А. Применение MS Excel в решение логистических задач / А.А. Князева, Н.П. Лыкова. — Текст : электронный // NovaInfo, 2011. — № 7. — URL: https://novainfo.ru/article/1364 (дата обращения: 15.04.2023).

Поделиться

Источник

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

  • в виде схемы;
  • в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

  • открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
  • закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.



Пример решения транспортной задачи в Excel

Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

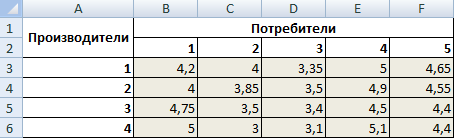
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители Потребители Объем производства
В1 В2 В3 В4 В5
А1 4,2 4 3,35 5 4,65 246
А2 4 3,85 3,5 4,9 4,55 186
А3 4,75 3,5 3,4 4,5 4,4 196
А4 5 3 3,1 5,1 4,4 197
Объем потребления 136 171 71 261 186

Задача: минимизировать транспортные расходы по перевозке продукции.

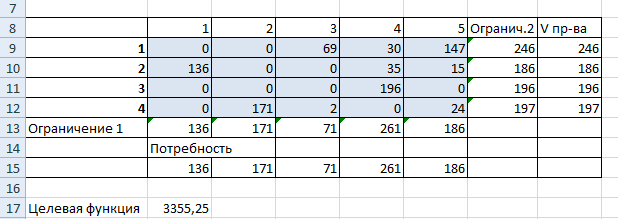
  1. Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
  2. Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
  3. Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.

    4. Стоимость перевозки.

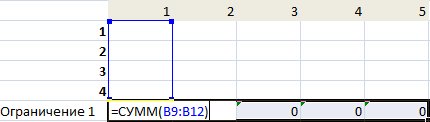
  4. Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.

    5. Формулы потребности.

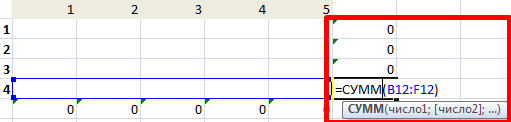
  5. Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.

    6. Формулы производства.

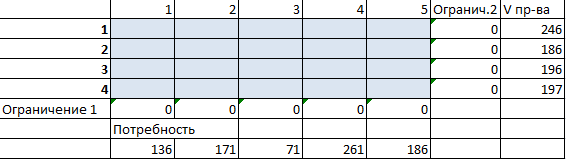
  6. Вносим известные значения потребности в товаре и объема производства.

    7. Значения.

  7. Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
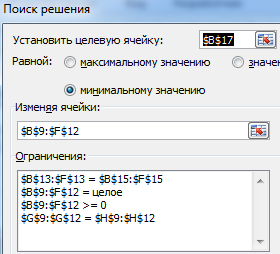
  8. Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.

    9. Поиск решения.

  9. Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Пример.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

  • суммарный объем производства превышает суммарную потребность в товаре;
  • суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.

Источник

1. Решение логистических задач

в Excel

2. Задачи  транспортной логистики

Задачи транспортной логистики
• создание транспортных систем;
• совместное планирование транспортных
процессов на разных видах транспорта;
• обеспечение единства транспортноскладского процесса;
• выбор способа транспортировки и
транспортного средства;
• определение рациональных маршрутов
доставки.

3. Виды транспортировки:

По назначению различают :
• внешнюю — снабжение – сбыт;
• внутреннюю (внутрипроизводственную)
транспортировку.
Оба вида транспортировки взаимосвязаны
между собой и образуют транспортную
систему предприятия.

4. Роль транспортировки

• Ключевая роль транспортировки в
логистике объясняется большим удельным
весом транспортных расходов в
логистических издержках, которые
составляют до 50% суммы общих затрат на
логистику.

5. Выбор вида транспорта

Основой выбора вида
транспорта, оптимального для
конкретной перевозки, служит
информация о характерных
особенностях различных видов
транспорта.

6. Существуют следующие виды транспорта:

железнодорожный;
морской;
внутренний водный (речной);
автомобильный;
воздушный;
трубопроводный.

7. Сравнительная характеристика основных видов транспорта

Вид
транспорта
Железнодорожный
Достоинства
Недостатки
Высокая провозная и пропускная Ограниченное число
способности.
перевозчиков.
Высокая регулярность перевозок. Большие капитальные
Относительно низкие тарифы.
вложения в
Значительные скидки для
производственнотранзитных отправок.
техническую базу.
Высокая скорость доставки грузов Высокая материалоемкость и
на большие расстояния
энергоемкость перевозок.
Низкая доступность к
конечным точкам продаж.
Недостаточно высокая
сохранность грузов

8. Сравнительная характеристика основных видов транспорта

Автомобильный
Высокая доступность.
Низкая
Возможность доставки
производительность.
груза «от двери до
Зависимость от
двери».
погодных и
Высокая маневренность.
дорожных условий.
Высокая скорость доставки. Относительно высокая
Возможность использования себестоимость
различных маршрутов и
перевозок на
схем доставки.
большие расстояния.
Возможность отправки
Недостаточная
груза малыми партиями
экологическая
чистота

9. Выделяют шесть факторов, влияющих на выбор вида транспорта:

• время доставки,
• частота отправлений груза,
• надежность соблюдения графика доставки,
• способность перевозить разные грузы,
• способность доставить груз в любую точку,
• стоимость перевозки.
При выборе транспортного средства в первую
очередь принимают во внимание: надежность
соблюдения графика доставки; время доставки;
стоимость перевозки.

10. Организация и планирование перевозок

Организация работы внутреннего транспорта
включает:
• выбор системы планирования перевозок,
• осуществление соответствующих
подготовительных работ,
• установление определенного порядка работы
транспортных средств,
• выполнения погрузо-разгрузочных работ.

11. Виды системы планирования перевозок

• по стандартным расписаниям применяется при достаточно
мощных и стабильных
грузопотоках,
• по заявкам – при эпизодической
потребности в транспортных
средствах.

12. Виды маршрутов

• Маятниковый маршрут — транспортное средство
осуществляет перевозку грузов между двумя
определенными пунктами.
• Веерный маршрут – перевозка грузов
осуществляется из нескольких пунктов в один или
из одного пункта в несколько.
• Кольцевой маршрут — при последовательном
обслуживании транспортным средством в течение
цикла нескольких пунктов отправления и
получения грузов.

13. Планирование перевозок состоит из трех этапов:

• Технико-экономическое планирование составление календарных годовых или
квартальных планов перевозок.
Эти планы включают в себя план перевозок,
грузооборот, объем погрузо-разгрузочных
работ, необходимое количество
транспортных средств и механизмов,
численность транспортных рабочих.

14. Планирование перевозок состоит из трех этапов:

• Календарные планы перевозок — на более
короткие периоды: смену, сутки, месяц.
Они охватывают погрузо-разгрузочные
работы, ремонт транспортных средств и
путей сообщения.
Основным оперативным плановым документом
является расписание движения транспортных
средств.

15. Планирование перевозок состоит из трех этапов:

• Оперативное руководство ходом
транспортных работ — диспетчирование:
контроль за соблюдением расписаний
движения транспортных средств и сменносуточных планов, организация выполнения
плановых работ.
Оперативный учет ведется на основе суточных
рапортов о работе транспортных
подразделений

16. Транспортные тарифы

Расчеты за услуги, оказываемые транспортными
организациями, осуществляются с
помощью транспортных тарифов.
Тарифы включают в себя:
• плату, взыскиваемую за перевозку грузов;
• сборы за дополнительные операции,
связанные с перевозкой грузов;
• правила исчисления платы и сборов.

17. Системы тарифов

• Общие тарифы – это основной вид тарифов.
С их помощью определяется стоимость
перевозки основной массы грузов.
• Исключительными тарифами называются
тарифы, которые устанавливаются с
отклонением от общих тарифов в виде
специальных надбавок или скидок. Эти
тарифы могут быть повышенными или
пониженными.

18. Системы тарифов

• Льготные тарифы применяются при
перевозке грузов для определенных целей, а
также грузов для самих железных дорог.
• Местные тарифы включают в себя размеры
плат за перевозку грузов и ставки различных
сборов, действующие в пределах данной
железной дороги.

19. Системы тарифов: особенности

На железнодорожном транспорте используют общие,
исключительные, льготные и местные тарифы.
На автомобильном транспорте используют следующие
виды тарифов:
• сдельные на перевозку грузов;
• на повременное пользование грузовыми автомобилями;
• за перегон подвижного состава;
• договорные и др.

20. Факторы:

На стоимость перевозки автомобильным
транспортом оказывают влияние такие
факторы:
• расстояние перевозки,
• масса и объемный вес груза,
• грузоподъемность и тип автомобиля,
• время использования автомобиля.

21. Транспортная задача (ТЗ).

Постановка ТЗ: некоторый груз у m
поставщиков в количестве Ai (i = 1…m)
единиц, нужно доставить n потребителям в
количестве Вj (j=1…n) ед.
• Сij — стоимость перевозки единицы груза от
i – го поставщика j- му потребителю.
• Составить план перевозок, позволяющий
вывезти все грузы, удовлетворить
потребности потребителя и иметь
минимальную стоимость.

22. Математическая модель ТЗ:

• Хij — количество ед груза, запланированных к
перевозке от i – го поставщика j- му
потребителю.
• Стоимость одной перевозки составит:
Сij* Хij
• Стоимость всего плана перевозки:
m
n
Cil * X ij — целевая функция
Z =
i 1 j 1

23. Система ограничений:

• Все грузы нужно перевезти –
• Потребности потребителя нужно
удовлетворить Вj
Ai

24. Цель:

• найти минимальное значение целевой
функции Z =
при ограничениях
Ai ,
Вj
• Хij 0
• При этом суммарные запасы груза равны
суммарным потребностям: – такая задача
называется закрытой моделью, в
противном случае – открытой.

25. Понятия:

• Транспортная задача имеет n+m
уравнений с n*m неизвестными.
• Матрица X = (Xij)m,n – план перевозок.
План, при котором целевая функция
(ЦФ) минимальна – называется
оптимальным.

26. Определение оптимального срока  замены ТС

Определение оптимального
срока замены ТС
• Транспортные расходы, в том числе
расходы на содержание транспортных
средств, в структуре затрат на логистику
занимают свыше 40%.
Сократить эту статью расходов позволяет
своевременная замена транспортного
средства.

27. Определение оптимального срока  замены ТС

Определение оптимального
срока замены ТС
При массовом характере сборки нет двух
одинаковых автомобилей. Каждый из них
имеет свой срок службы даже при
одинаковых условиях эксплуатации.
• Проблема в том, что чем больше «возраст»
автомобиля, тем больше затраты на его
содержание и поддержание в рабочем
состоянии, и, в то же время, тем меньше цена
его возможной реализации.

28. Точка замены ТС

Определяется:
• минимальными общими затратами F(l),
складывающимися из затрат на ремонт fp(l),
приходящихся на единицу выполненной
работы l (пробег автомобиля), и величиной
потребленного капитала fk(l) на единицу
работы.

29. Точка замены ТС: график

Для построения графика fp(l) необходимо
определить:
• затраты на ремонт Zi к концу каждого i-го
года эксплуатации;
• суммарный пробег автомобиля li к концу
каждого года эксплуатации.
i
р
i
Z
f (l )
l

30. Точка замены ТС: график

Для построения графика fp(l) необходимо
определить:
• величину необходимого капитала к концу
каждого периода эксплуатации, как разницу
между первоначальной стоимостью
транспортного средства и его стоимостью на
конец i-го периода: Кi = C0 — Ci
• величину необходимого капитала в расчете
на 1 км пробега

31. Точка замены ТС: график

Для построения графика fp(l) необходимо
определить:
• величину необходимого капитала в расчете
на 1 км пробега:
Ki
f k (l )
Li
• Тогда суммарные капитальные затраты
составят:
F (l ) f p (l ) f k (l )

Источник

Excel –  очень функциональная программа. Она может использоваться для решения огромного пласта задач, с которыми приходится сталкиваться в бизнесе. Одна из самых распространённых –  транспортная задача. Представим, что нам нужно понять, какой способ перевозки от производителя к конечному покупателю самый оптимальный по затратам времени, денег и других ресурсов. Эта проблема довольно популярная, независимо от того, в какой сфере работает бизнес. Поэтому давайте более подробно разберемся, как её реализовать с помощью Excel.

Содержание

  1. Описание транспортной задачи
  2. Как включить функцию “Поиск решения” в Excel
  3. Пример решения транспортной задачи в Excel
  4. Условия задачи
  5. Решение – пошаговый алгоритм
  6. Заключение

Описание транспортной задачи

Итак, у нас есть два контрагента, которые постоянно взаимодействуют друг с другом. В нашем случае это  покупатель и продавец. Нам нужно посчитать, как перевозить товары таким образом, чтобы издержки были минимальны. Для этого нужно представить все данные в схематической или матричной форме. В Эксель используем последний вариант. В целом, выделяют два типа транспортных задач:

  1. Закрытые. В этом случае спрос и предложение находятся в балансе.
  2. Открытые. Здесь нет равенства между спросом и предложением. Чтобы получить решение этой задачи, нужно сперва ее привести к первому типу, уравняв спрос и предложение. Для этого нужно ввести дополнительный показатель – наличие условного покупателя или продавца. Кроме этого, нужно внести определенные изменения в таблицу издержек.

Как включить функцию “Поиск решения” в Excel

Для решения транспортных задач в Excel существует специальная функция, которая называется «Поиск решения». Она не активирована по умолчанию, поэтому нужно сделать следующие шаги:

  1. Открыть меню «Файл», которое находится в левом верхнем углу окна программы. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
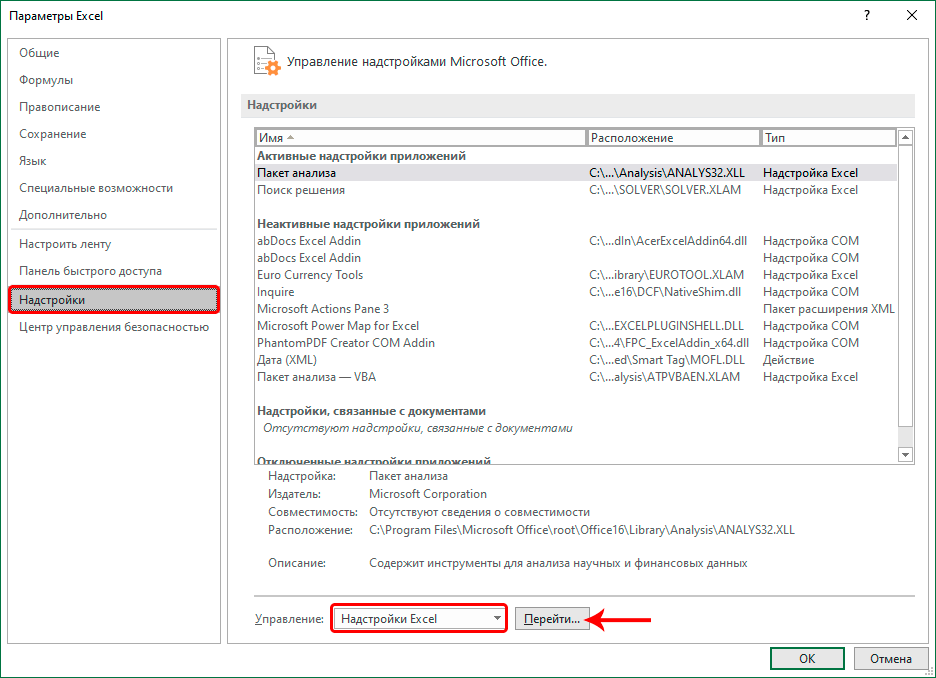
  2. После этого нажимаем на кнопку с параметрами. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
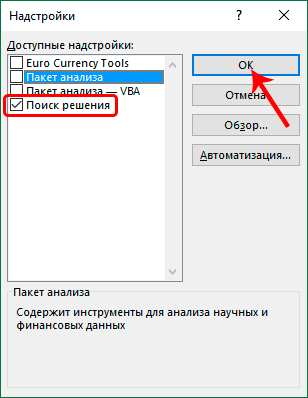
  3. Далее находим подраздел «Настройки» и переходим в меню управления надстройками. Это маленькие программы, которые выполняются в рамках среды Microsoft Excel. Видим, что сначала мы нажали на меню «Надстройки», а потом в правой части внизу выставили пункт «Надстройки Excel» и нажали на кнопку «Перейти». Все нужные действия выделены красными прямоугольниками и стрелочками. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
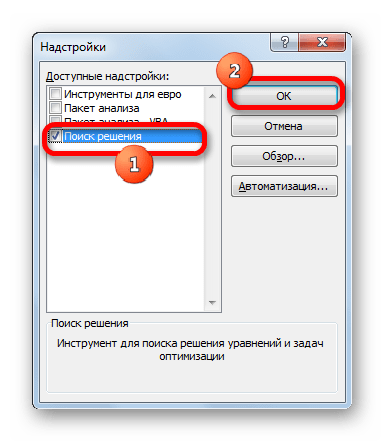
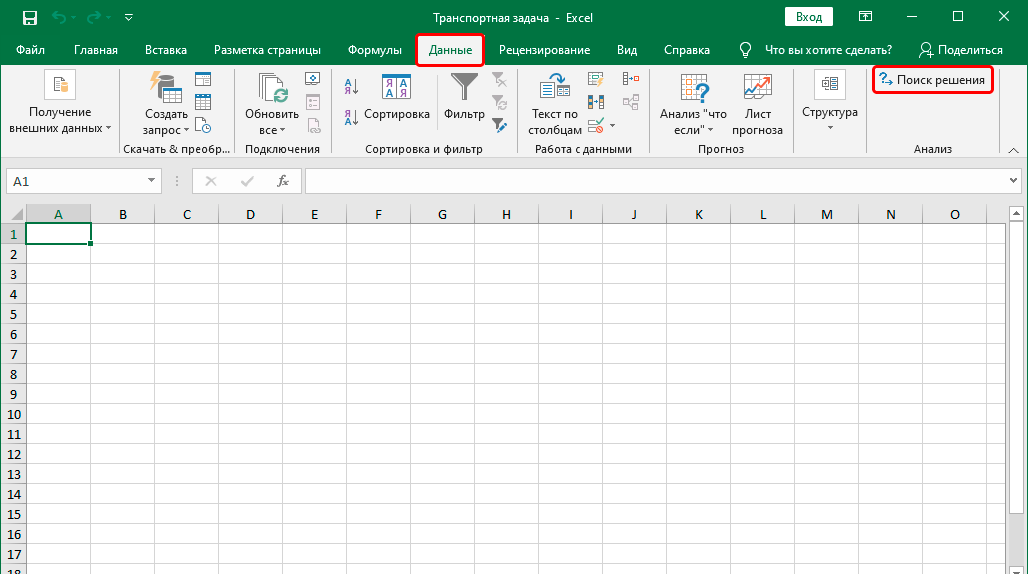
  4. Далее включаем надстройку «Поиск решения», после чего подтверждаем свои действия нажатием клавиши ОК. Исходя из описания настройки, мы видим, что она предназначена для анализа сложных данных, таких как научные и финансовые. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
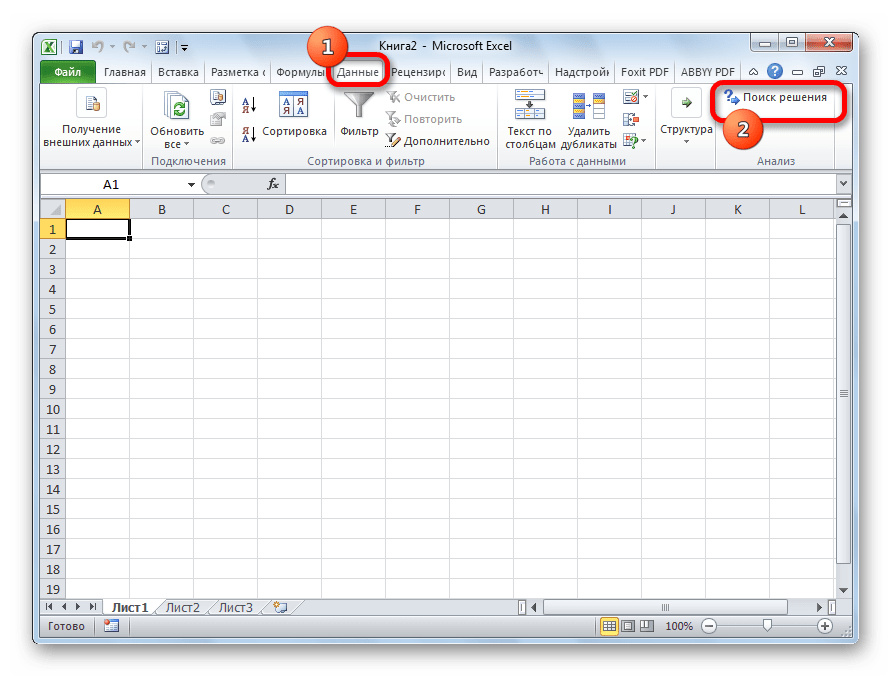
  5. После этого переходим во вкладку «Данные», где видим новую кнопку, которая называется так же, как и надстройка. Ее можно найти в группе инструментов «Анализ».Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

Осталось только кликнуть по этой кнопке, и мы переходим к решению транспортной задачи. Но перед этим следует немного подробнее поговорить про инструмент «Поиск решения» в Excel. Это специальное дополнение Эксель, которое дает возможность находить самое быстрое решение задачи. Характерная особенность – учет ограничений, которые пользователь задает на этапе подготовки. Если говорить простым языком, это подпрограмма, дающая возможность определить самый лучший способ достижения определенной задачи. К таким задачам могут относиться следующие:

  1. Инвестирование, загрузка склада или любая другая подобная деятельность. В том числе, и доставка товара.
  2. Лучший способ. Сюда входят такие задачи, как достижение максимальной прибыли при минимальных издержках, способы достижения самого лучшего качества при имеющихся ресурсах и так далее.

Кроме транспортных задач, эта надстройка используется и для таких целей:

  1. Разработка плана производства. То есть, сколько нужно выработать единиц товара, чтобы достичь максимального дохода.
  2. Найти распределение рабочих сил по разным видам работ, чтобы суммарные затраты на производство товара или услуг были самыми маленькими.
  3. Установить, сколько минимально времени понадобится на то, чтобы выполнить все работы.

Как видим, задачи бывают самыми разными. Универсальное правило применения этой надстройки – необходимо перед решением задачи создать модель, которая бы соответствовала ключевым характеристикам поставленной проблемы. Моделью является совокупность функций, которые используют переменные в качестве своих аргументов. То есть, значения, которые могут изменяться.

Важно учесть, что оптимизация набора значений осуществляется исключительно по одному показателю, который называется целевой функцией.

Надстройка «Поиск решения» осуществляет перебор разных значений переменных, которые передаются целевой функции таким образом, чтобы она была максимальной, минимальной или равной определенному значению (именно это и является ограничением). Есть еще одна функция, которая несколько похожая по своему принципу действия, и какую нередко путают с «Поиском решения». Называется она «Подбор параметра». Но если копнуть более глубоко, то разница между ними колоссальная:

  1. Функция «Подбор параметра» не работает больше, чем с одной переменной.
  2. Она не предусматривает возможности задавать ограничения для переменных.
  3. Способна определять только равенство целевой функции определенному значению, но не дает возможности находить максимум и минимум. Поэтому для нашей задачи она не подходит.
  4. Способна эффективно вычислять лишь если модельно линейного типа. Если модель нелинейная, то она находит значение, которое наиболее близкое к изначальному.

Транспортная задача по своей структуре значительно сложнее, поэтому надстройки «Подбор параметра» для этого недостаточно. Давайте разберемся более детально, как реализовать на практике функцию «Поиск решения» на примере транспортной задачи.

Пример решения транспортной задачи в Excel

Для того, чтобы наглядно продемонстрировать, как на практике решать транспортные задачи в Excel, давайте приведем пример.

Условия задачи

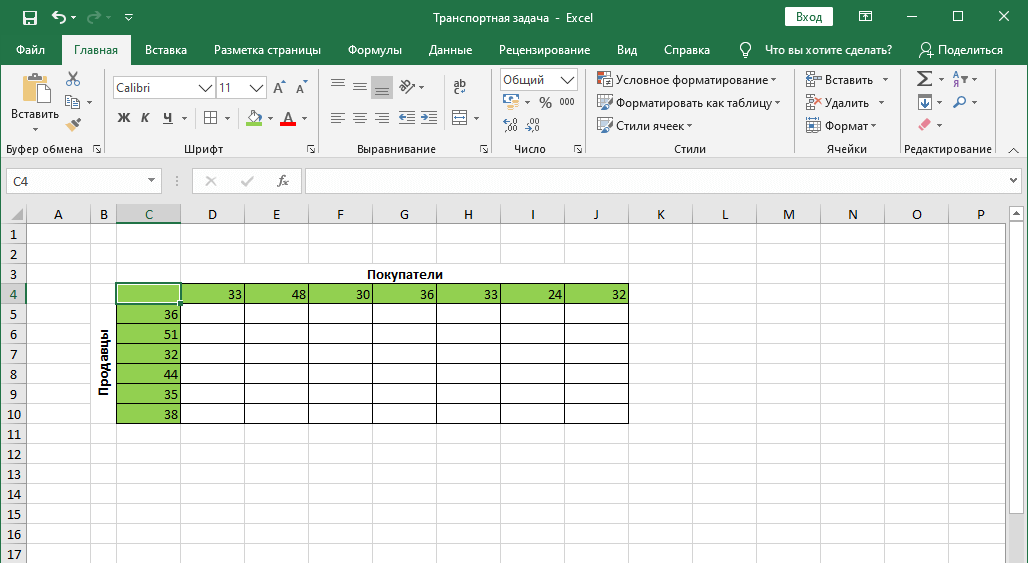
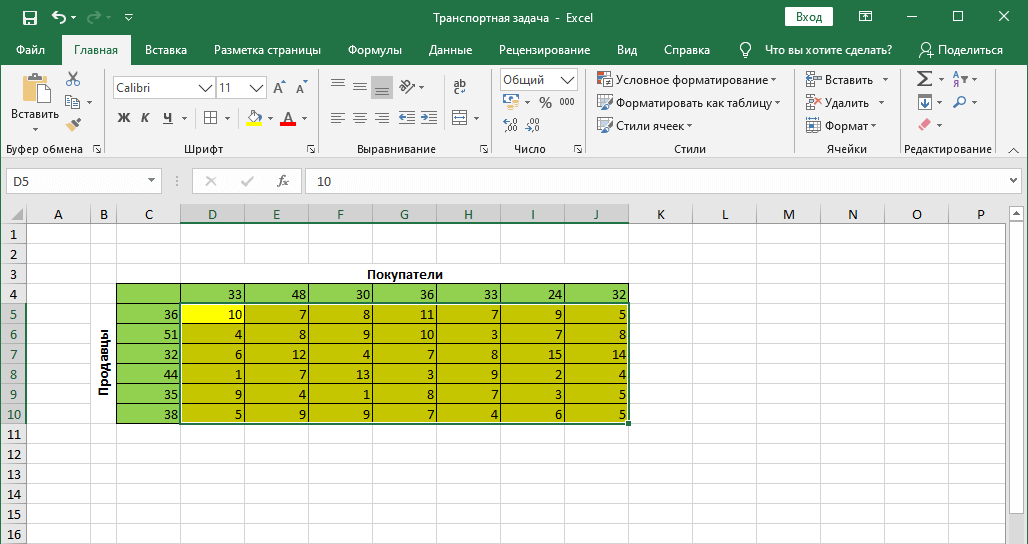
Предположим, у нас есть 6 продавцов и 7 покупателей. Спрос и предложение между ними распространяется соответственно следующим способом: 36, 51, 32, 44, 35 и 38 единиц – продавцы и 33, 48, 30, 36, 33, 24 и 32 единицы – покупатели. Если просуммировать все эти значения, то обнаружится, что спрос и предложение находятся в балансе. Следовательно, эта задача закрытого типа, которая решается очень просто.

Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

Кроме этого, у нас есть информация о том, сколько нужно потратить на перевозку из пункта А в пункт Б (они на примере выделены желтыми ячейками). Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

Решение – пошаговый алгоритм

Теперь, после того, как мы ознакомились с таблицами с исходными данными, можем воспользоваться следующим алгоритмом, чтобы решить эту задачу:

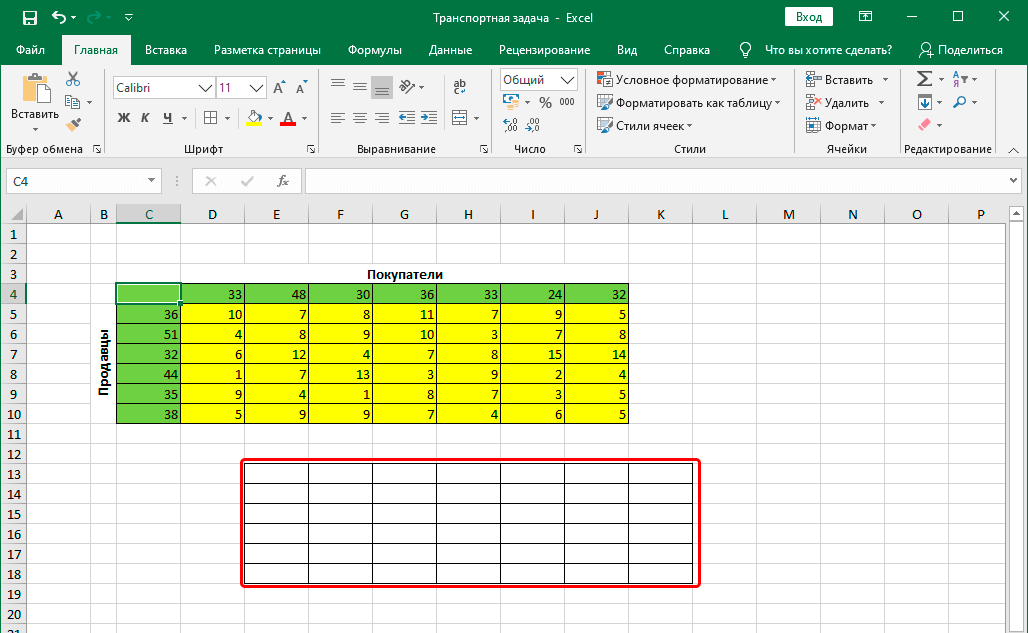
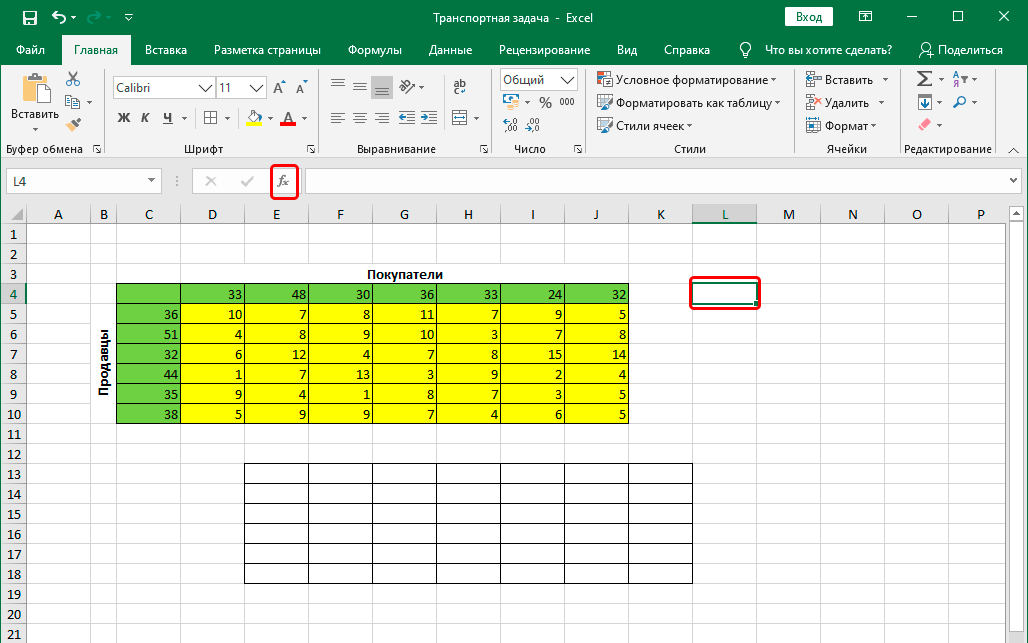
  1. Сперва делаем таблицу, состоящую из 6 строк и 7 колонок. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
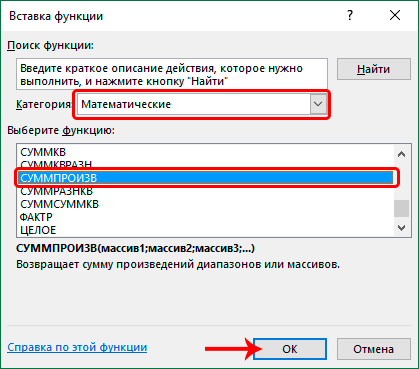
  2. После этого переходим в какую-угодно ячейку, не содержащую никаких значений и при этом лежащую за пределами новосозданной таблицы и вставляем функцию. Для этого нажимаем на кнопку fx, которая находится слева от строки ввода функции. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
  3. У нас появляется окно, в котором нам нужно выбрать категорию «Математические». А какая функция нас интересует? Та, которая выделена на этом скриншоте. Функция СУММИПРОИЗВ умножает диапазоны или массивы между собой и суммирует их. Как раз то, что нам нужно. После этого нажимаем клавишу ОК.Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
  4. Далее на экране появится окно, в котором необходимо указать параметры функции. Они следующие:
    1. Массив 1. Это первый аргумент, в котором записываем тот диапазон, который выделен жёлтым  цветом. Задать параметры функции можно как используя клавиатуру, так и выделив соответствующую область с помощью левой кнопки мыши.
    2. Массив 2. Это второй аргумент, в качестве которого выступает новосозданная таблица. Действия выполняются аналогичным образом.

Подтверждаем свое действие нажатием клавиши ОК. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

  1. После этого делаем левый клик мыши по той ячейке, которая служит верхней левой в новосозданной таблице. Теперь снова нажимаем кнопку вставки функции. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
  2. Выбираем ту же категорию, что и в предыдущем случае. Но на этот раз нас интересует функция СУММ. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
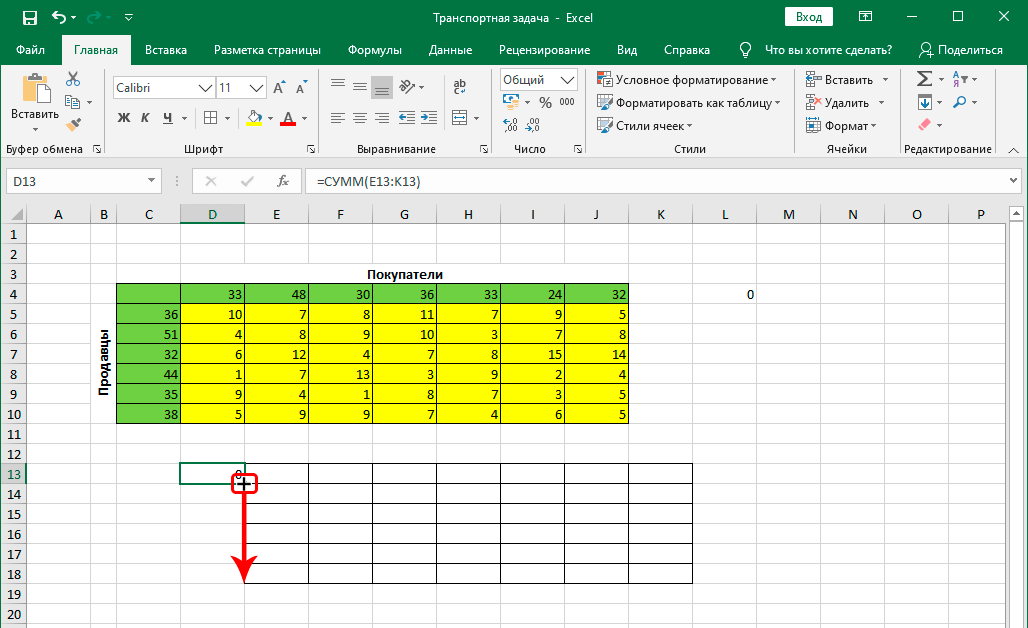
  3. Теперь наступил этап заполнения аргументов. В качестве первого аргумента записываем верхнюю строку таблицы, которую мы создали в начале. Точно так же, как и раньше, это можно сделать путем выделения этих ячеек на листе, так и вручную. Подтверждаем свои действия нажатием клавиши ОК. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
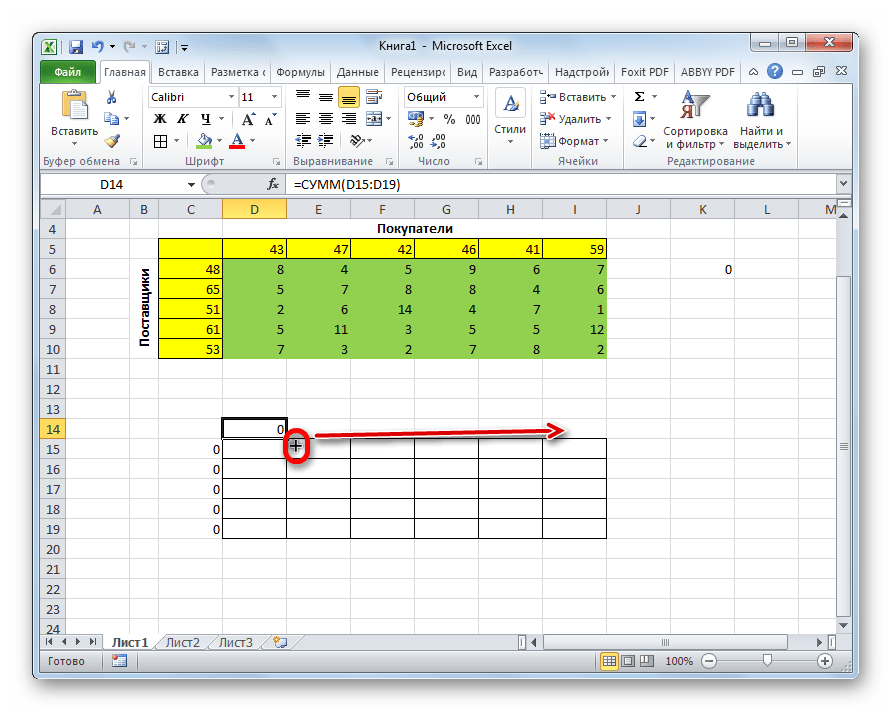
  4. Увидим результаты в ячейке с функцией. В данном случае это ноль. Далее переносим курсор в правый нижний угол, после чего появится маркер автозаполнения. Выглядит он, как маленький чёрный плюсик. Если он появился, зажимаем левую кнопку мыши и перемещаем курсор до последней ячейки в нашей таблице. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
  5. Это дает нам возможность перенести формулу во все остальные ячейки и получить правильные результаты без необходимости выполнения дополнительных расчетов.
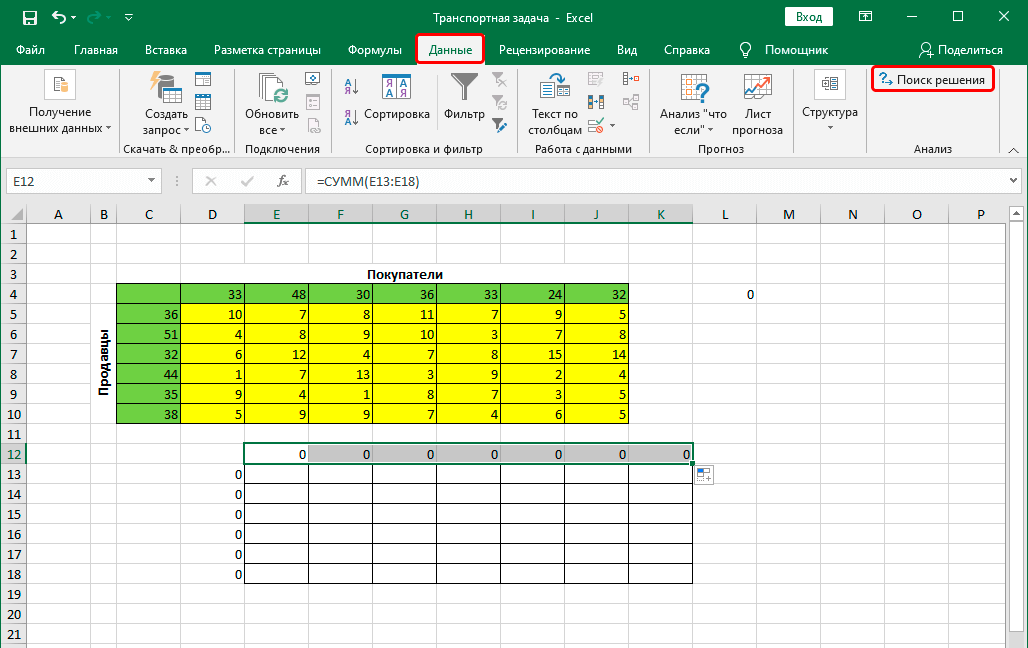
  6. Следующий шаг – выбор левой верхней ячейки и вставка функции СУММ в нее. После этого заносим аргументы и с помощью маркера автозаполнения заполняем все оставшиеся ячейки.
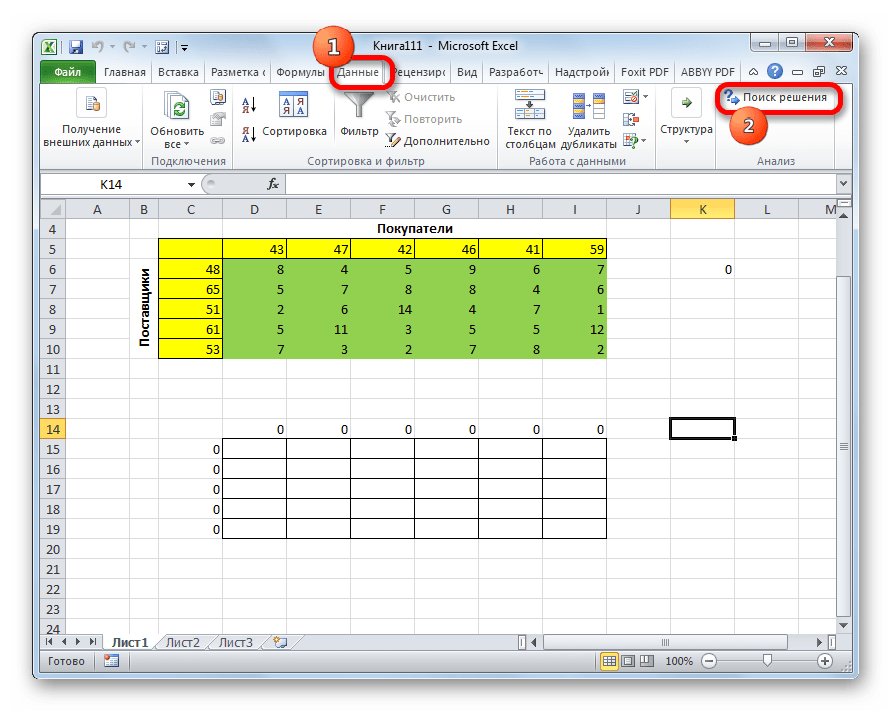
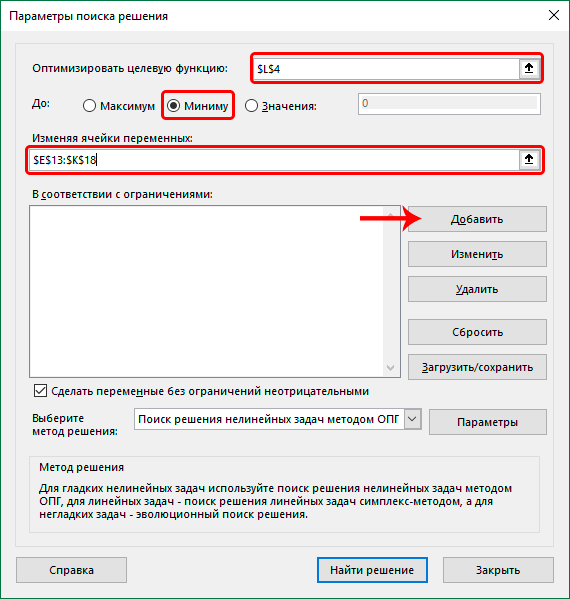
  7. После этого приступаем непосредственно к решению задачи. Для этого воспользуемся дополнением, которое мы включили ранее. Переходим на вкладку «Данные», и там находим инструмент «Поиск решения». Нажимаем по этой кнопке. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
  8. Теперь перед нашим взором появилось окошко, через которое можно настроить параметры нашего дополнения. Давайте каждый из этих параметров разберем:
    1. Оптимизировать целевую функцию. Здесь нам нужно выбрать ячейку, содержащую функцию СУММПРОИЗВ. Видим, что эта опция дает возможность выбрать функцию, для которой будет осуществляться поиск решения.
    2. До. Здесь выставляем опцию «Минимум».
    3. Изменяя ячейки переменных. Здесь указываем диапазон, соответствующий той таблице, которую мы создавали в самом начале (за исключением суммирующей строки и столбца).
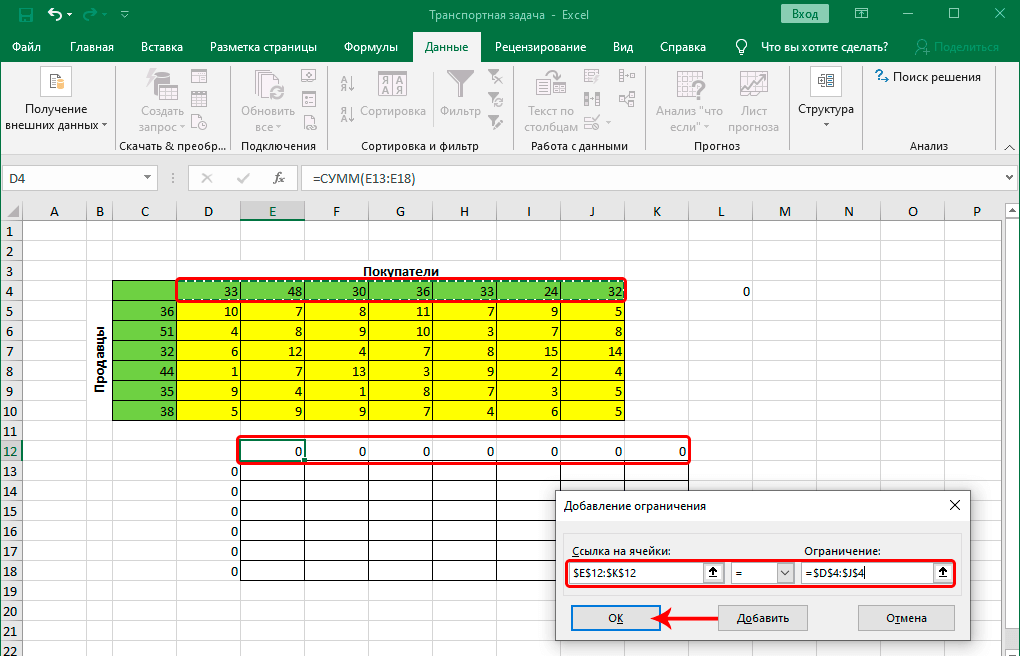
    4. В соответствии с ограничениями. Здесь нам нужно добавить ограничения, нажав кнопку «Добавить». Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю
    5. Мы помним, какое ограничение нам нужно создать – сумма значений спросов покупателей и предложений продавцов должны быть одинаковыми.
  9. Задача ограничений осуществляется следующим образом:
    1. Ссылка на ячейки. Здесь заносим диапазон таблицы для расчётов.
    2. Условия. Это математическая операция на предмет соответствия которой проверяется диапазон, заданный в первом поле ввода.
    3. Значение условия или ограничение. Сюда заносим подходящую колонку в исходной таблице.
    4. После того, как все действия будут выполнены, нажимаем кнопку ОК, тем самым подтверждая наши действия.

Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

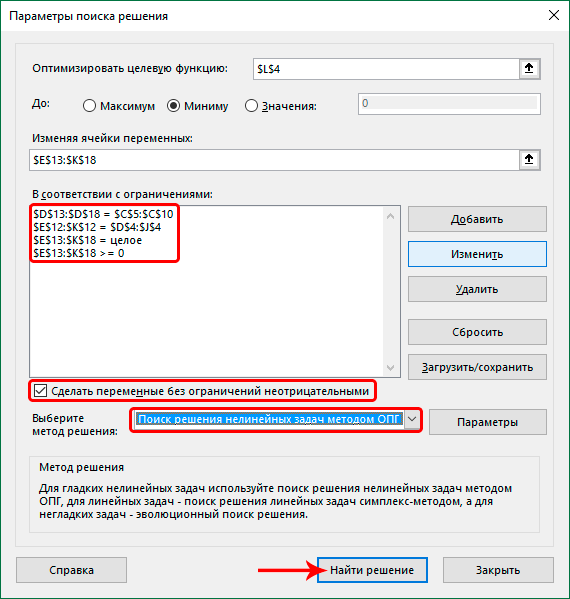
Точно такие же операции производим для верхних строк, задавая следующее условие: они должны быть равны. Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

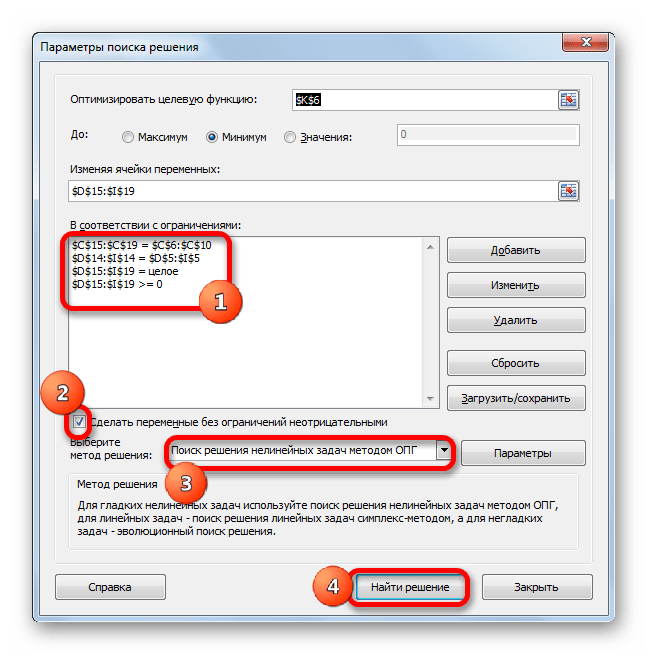
Следующий этап – задание условий. Нам необходимо установить следующие критерии для суммы ячеек в таблице – больше или равно нулю, целое число. В результате у нас появляется такой перечень условий, при которых задача решается. Здесь нужно убедиться, что поставлен флажок возле опции «Сделать переменные без ограничений неотрицательными». Также в нашей ситуации требуется, чтобы был выбран метод решения задачи – «Поиск решения нелинейных задач методов ОПГ». Теперь можно смело говорить, что настройка осуществлена. Поэтому осталось только выполнить расчеты. Для этого нажимаем на кнопку «Найти решение». 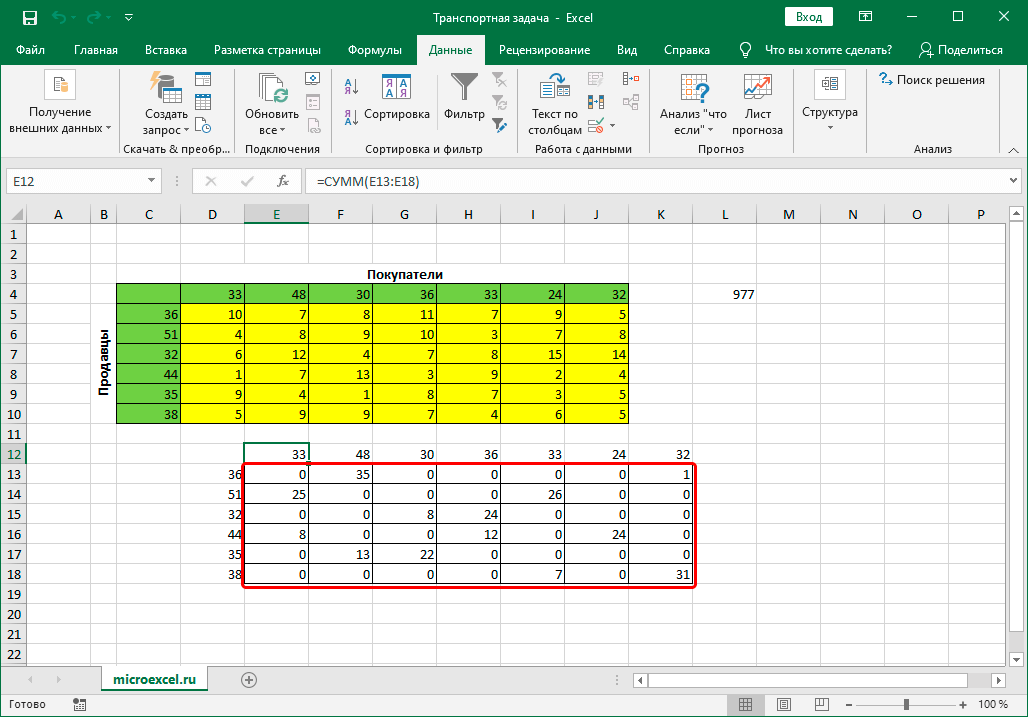Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

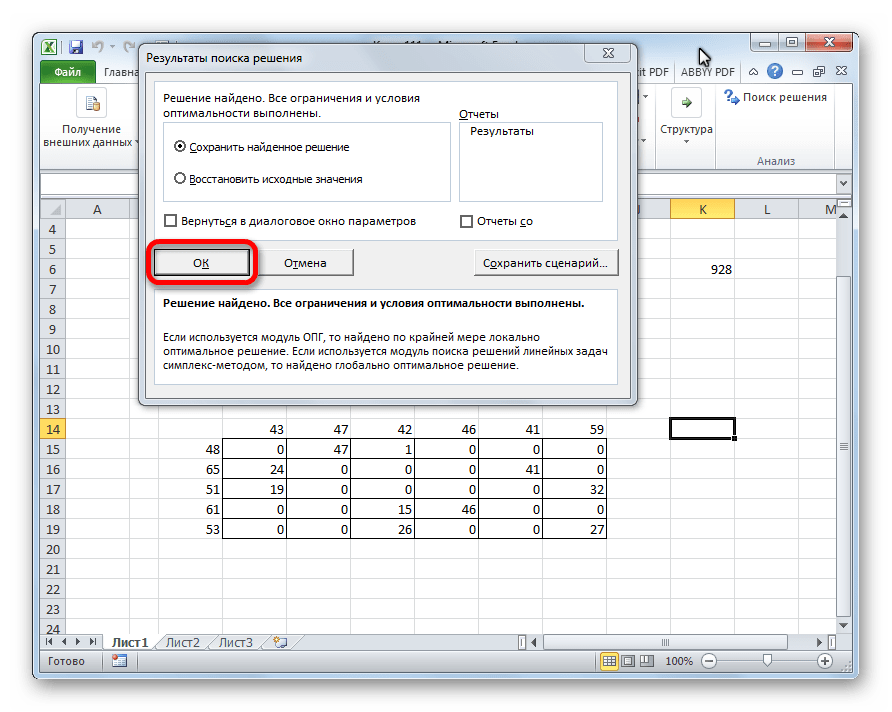
После этого все данные будут рассчитаны автоматически, а потом Эксель покажет окно с результатами. Оно необходимо для того, чтобы перепроверить работу компьютера, поскольку возможны ошибки, если условия ранее были заданы неверно. Если все правильно, то нажимаем кнопку «ОК» и видим готовую таблицу.

Транспортная задача в Excel. Нахождение лучшего способа перевозки от продавца покупателю

Если же оказывается, что у нас задача стала открытого типа, то это плохо, поскольку нужно отредактировать исходную таблицу так, чтобы задача превратилась в закрытую. Тем не менее, когда это сделать, оставшийся алгоритм будет такой же.

Заключение

Как видим, Excel может использоваться и для очень сложных вычислений, которые на первый взгляд не доступны простой компьютерной программе, которая установлена почти у каждого. Тем не менее, это так. Сегодня мы уже рассмотрели продвинутый уровень использования. Данная тема не такая простая, но как говорится, дорогу осилит идущий. Главное – следовать плану действий, и точно выполнять все действия, указанные выше. Тогда ошибок не возникнет, а программа самостоятельно выполнит все необходимые расчеты. Не нужно будет думать, какую функцию использовать и так далее.

Оцените качество статьи. Нам важно ваше мнение:

Источник
Опытный руководитель, читая заголовок статьи, наверняка скажет:«Такого не может быть, у нас работают опытные люди, они занимаются планированием уже многие годы. Не могу представить, что мы где-то теряли деньги при доставке!»

Давайте разберемся, как устроен процесс планирования в компаниях, и докажем на примере, что:

Если сотрудники ведут планирование в Excel, даже самый эффективный отдел логистики не может быть на 100% уверен, что компания не теряет деньги.

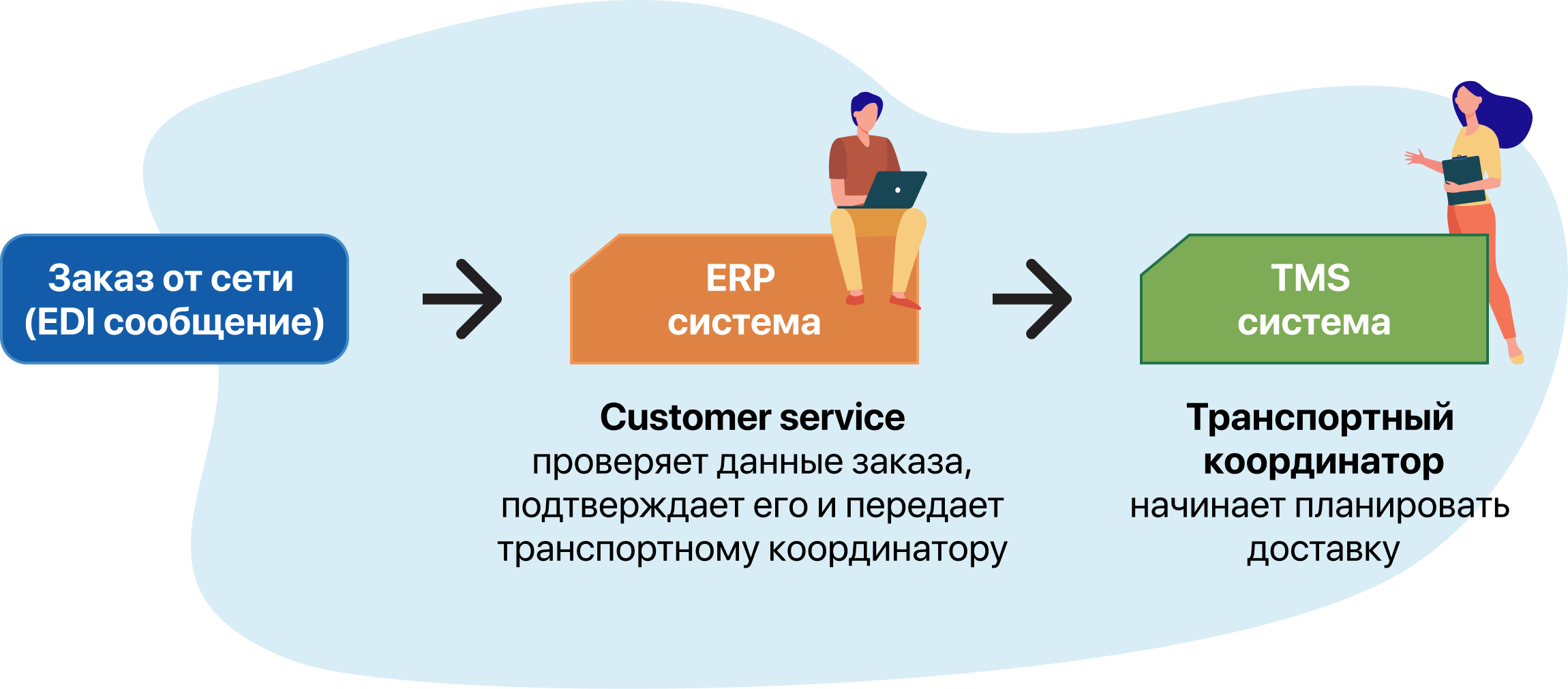
Типичный процесс планирования выглядит следующим образом. Сотрудники customer service получают заказы от торговых сетей, обрабатывают, подтверждают и передают транспортному менеджеру для планирования доставки.

Получив заказы, транспортный координатор должен ответить на два ключевых вопроса:

  1. Как мы доставим товар?
  2. Кто выполнит перевозку?

Специфика работы с торговыми сетями заключается в том, что заказы приходят регулярно и доставляются по определенному графику на РЦ торговой сети. При этом размер заказа может значительно варьироваться от недели к неделе и от РЦ к РЦ. Например, на популярные РЦ сеть может заказывать полную фуру товара, а на удаленные (допустим, Мурманск) – всего несколько паллет. То есть от недели к неделе логист получает новый набор заказов со своими параметрами и должен оперативно решить, как их везти.

Тут-то и становится понятно, что выбор оптимального способа доставки и перевозчика для каждого заказа — весьма нетривиальная задача. Вот лишь несколько вопросов, на которые должен ответить логист, решая эту задачу:

  • Дешевле отвезти полной фурой или отдать в сборку?

  • Если везем фурой, то какие заказы можно объединить, чтобы максимально утилизировать машину?

  • Если везем сборкой, то есть ли подходящий график у 3PL-операторов для доставки, и можно ли воспользоваться пулингом, чтобы сэкономить?

  • Можно ли в одну фуру положить заказы для двух разных РЦ по пути ее следования, или есть риск, что машина застрянет на первой точке?

  • Можно ли доложить в фуру заказ от другого поставщика, который едет на тот же РЦ, и тем самым сэкономить на доставке?

  • Как выбрать перевозчика на рейс? Самого дешевого? Или закрепленного в рамках тендера? Или вообще отдать рейс на торги?

Отвечая на эти вопросы, логист должен держать в голове следующие параметры:

  • Информация по заказу: количество паллет, объемно-весовые характеристики, даты доставки, время авизации;

  • Доступные графики 3PL-операторов;
  • Уровень набора пулинга для того или иного направления;
  • Тарифы на фуру и на паллетную доставку от каждого перевозчика;
  • Сравнение стоимости паллетной доставки по сравнению с FTL по каждому направлению и перевозчику. Например, для одного направления 23 паллеты дешевле отправить полной фурой, а для другого – паллетной доставкой;
  • Правила назначения перевозчиков на рейс. В частности, закрепление перевозчиков за определенными направлениями, распределение заявок по квотам и так далее;
  • Лид-таймы доставки по каждому направлению и для каждого перевозчика;
  • Особенности клиентов (допустим, регулярные простои на определенном РЦ сети или строгие требования ко времени доставки, нарушение которых ведет к штрафу от сети).

Связаться с нами

Безусловно, на рынке уже не осталось компаний, не научившихся решать эти задачи в том или ином виде. Чаще всего в разговорах с транспортными менеджерами мы слышим:«У меня есть Excel-таблица с макросом, в котором я все планирую, поэтому TMS-система мне не нужна!»


Но у такого подхода есть ряд минусов:

  1. Чаще всего макрос автоматизирует не всю задачу целиком, а только ее часть. Остальные решения логист по-прежнему принимает вручную. Простой пример – маршрутизация. Есть 2 заказа: на РЦ «Тандер» и РЦ «Перекресток» в Екатеринбурге, один с доставкой в 10:00, другой – с доставкой в 22:00. Логист помнит, что год назад на РЦ «Тандер» был долгий простой. И теперь опасается объединять этот заказ с другими, чтобы не попасть на штраф на второй точке. Хотя простой был всего один раз, ситуация уже давно изменилась и, объединив заказ со вторым, можно было бы заказать на одну фуру меньше;
  2. Это ненадежно. Вся информация хранится в одном файле у сотрудника. Если он заболеет или уволится, а файл потеряется, то информация пропадет вместе с ним;
  3. Велик риск ошибки из-за человеческого фактора. Если неправильно скопировать формулу, забыть обновить тарифы или случайно удалить значение в ячейке, компания может понести финансовые потери. Распространенная ошибка: компания провела тендер и обновила тарифы, а логист по инерции еще несколько месяцев ориентируется на старые. Например: при старых тарифах FTL на Новосибирск было выгодно использовать от 25 паллет в заказе, а при новых – уже от 23 паллет. Логист по старинке для 23 заказывает паллетную доставку, и компания теряет деньги. Еще один пример: в апреле стало тепло, а сотрудник по-прежнему продолжает заказывать рефрижераторные перевозки;
  4. Это непрозрачно. Как работает макрос по планированию? Учитывает ли он все параметры или только часть из них? Кто может подтвердить, что макрос корректно выбирает оптимальный способ доставки? Как убедиться, что рейсы распределяются между перевозчиками согласно политике компании и без сговора? Допустим, если логист работает в Excel, то руководитель никогда не сможет поднять исторические данные по рейсу и понять, почему для него назначили определенного перевозчика;
  5. Это требует времени. Логист должен получить заказы от customer service, загрузить их в файл с макросом, проверить результат, выгрузить обратно и передать транспортной компании. Все эти действия занимают время и растягивают срок обработки заказов до момента передачи перевозчику. Ситуация усугубляется в случае увольнения человека и его замены на менее опытного: процессы заказа транспорта просядут на несколько месяцев, пока новый сотрудник не обучится работе с файлом.

Внедряя TMS-систему, компания получает ряд важных преимуществ

Во-первых, упрощается процесс взаимодействия customer service и транспортного координатора. Подтвержденные заказы поступают в TMS-систему, транспортный координатор моментально их видит. По каждому заказу система автоматически подгружает все мастер-данные, и заказы готовы к планированию.

Во-вторых, после получения заказов транспортному координатору остается лишь запустить алгоритм планирования, использующий все мастер-данные, тарифы перевозчиков и правила распределения заявок между ними. Алгоритм сформирует предложение по вариантам доставки, и логисту останется лишь утвердить его или скорректировать.

В-третьих, TMS-система позволяет систематизировать большие объемы информации и учитывать их при принятии решений.

Все решения принимаются на основе объективной статистики, а не субъективного мнения

Таким образом, компания получает следующие преимущества:

  1. Сокращается ручной труд. Транспортный координатор тратит значительно меньше времени на обработку и планирование заказов. В некоторых случаях функционал планирования доставки даже может быть передан сотрудникам customer service;
  2. Ускоряются процессы. С момента получения заказов от сети до передачи перевозчику на планирование уходят минуты, а не часы;
  3. Сокращаются затраты на доставку. Автоматический алгоритм позволяет подобрать самый рациональный способ доставки. В отдельных случаях экономия может достигать 10-20%;
  4. Повышается надежность процессов: руководитель всегда знает, что планирование доставки происходит в соответствии с алгоритмом и не зависит от человека, который этим занимается. Исключена ситуация, когда, например, в Новосибирск уедет фура с 5 паллетами, потому что новый сотрудник не нашел более оптимального решения;
  5. Исключен человеческий фактор при выборе перевозчика: руководитель на 100% уверен, что рейсы распределяются между перевозчиками в соответствии с результатами тендера.

Безусловно, для любого транспортного менеджера при планировании доставки нет более удобного и простого в использовании инструмента, чем Excel.

Но только решив использовать TMS-систему, руководитель может быть на 100% уверен, что компания не теряет деньги на доставке

В следующей статье мы расскажем о том, почему все больше компаний переходят на электронный обмен информацией с перевозчиками, и какие преимущества получают от этого.

Если вы после прочтения статьи и решили внедрить TMS-систему, мы рады предложить вам наше решение. Pooling Plus – это облачная TMS-система, обеспечивающая управление доставкой на всех этапах.

Связаться с нами

Источник

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Содержание

  1. Транспортная задача: описание
  2. Подготовительный этап: включение функции “Поиск решения”
  3. Пример задачи и ее решение
    • Условия
    • Алгоритм решения
  4. Заключение

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

  • Закрытая – совокупное предложение продавца равняется общему спросу.
  • Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

  1. Открываем меню “Файл”.Переход в меню Файл в Эксель
  2. В перечне слева выбираем пункт “Параметры”.Переход к параметрам Эксель
  3. В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.Переход к надстройкам Excel
  4. В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.Включение надстройки Поиск решения в Эксель
  5. В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.Поиск решения во вкладке Данные в Excel

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Исходные данные транспортной задачи для решения в Эксель

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Исходные данные транспортной задачи для решения в Excel

Алгоритм решения

Итак, приступи к решению нашей задачи:

  1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.Создание новой таблицы для решения транспортной задачи в Эксель
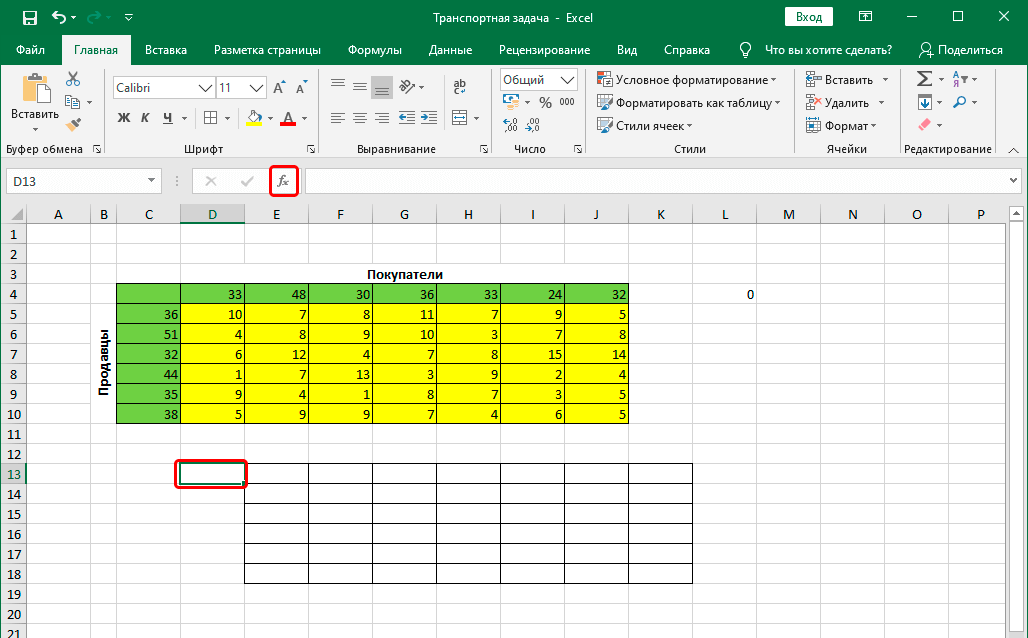
  2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).Вставка функции в ячейку Excel
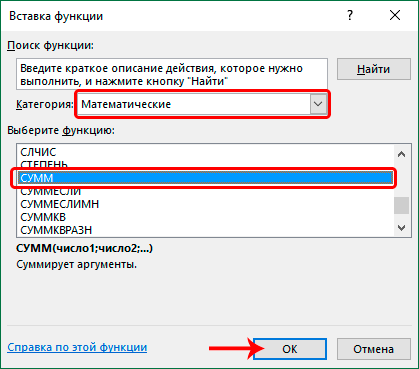
  3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.Выбор функции СУММПРОИЗВ в Эксель
  4. На экране отобразится окно, в котором нужно заполнить аргументы:
    • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
    • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
    • по готовности жмем OK.Заполнение аргументов функции СУММПРОИЗВ в Эксель
  5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.Вставка функции в ячейку таблицы Excel
  6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.Выбор функции СУММ в Эксель
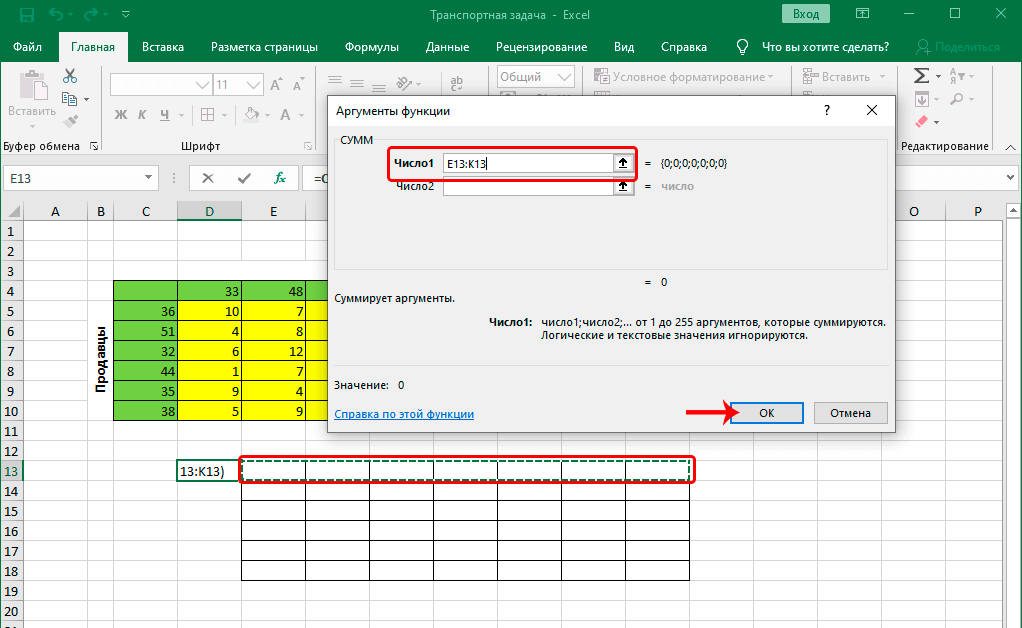
  7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.Заполнение аргументов функции СУММ в Excel
  8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.Копирование формулы с помощью Маркера заполнения в Эксель
  9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.Результат копирования формулы в другие ячейки столбца в Эксель
  10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.Вставка функции СУММ в ячейку таблицы Эксель
  11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.Заполнение аргументов функции СУММ в Эксель
  12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.Результат копирования формулы в другие ячейки строки в Эксель
  13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).Функция Поиск решения в Эксель
  14. Перед нами появится окно с параметрами функции:
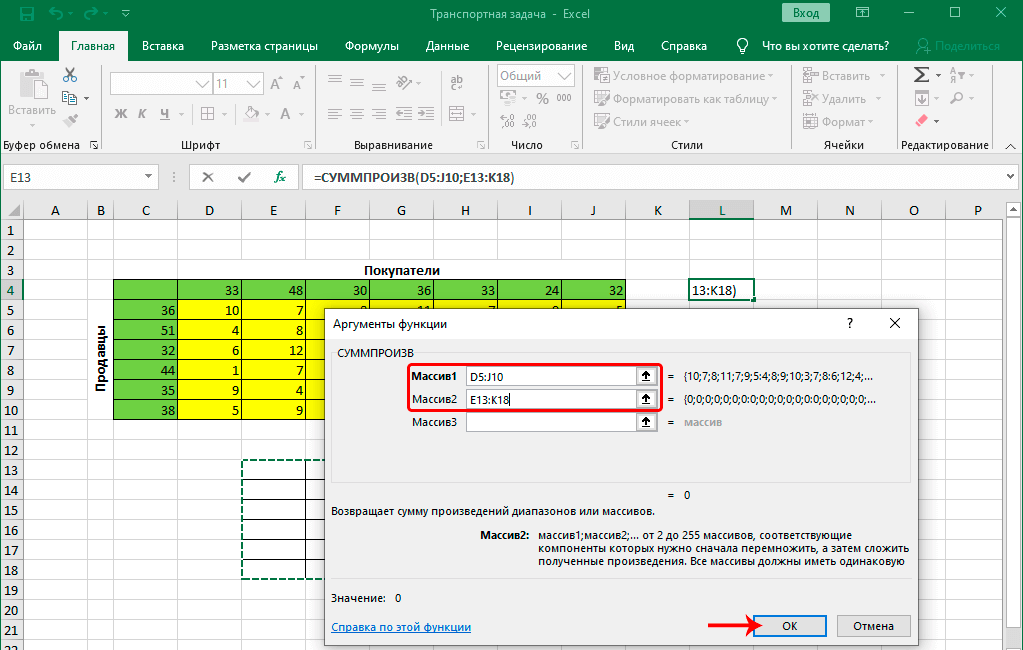
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.Заполнение параметров функции Поиск решения в Эксель
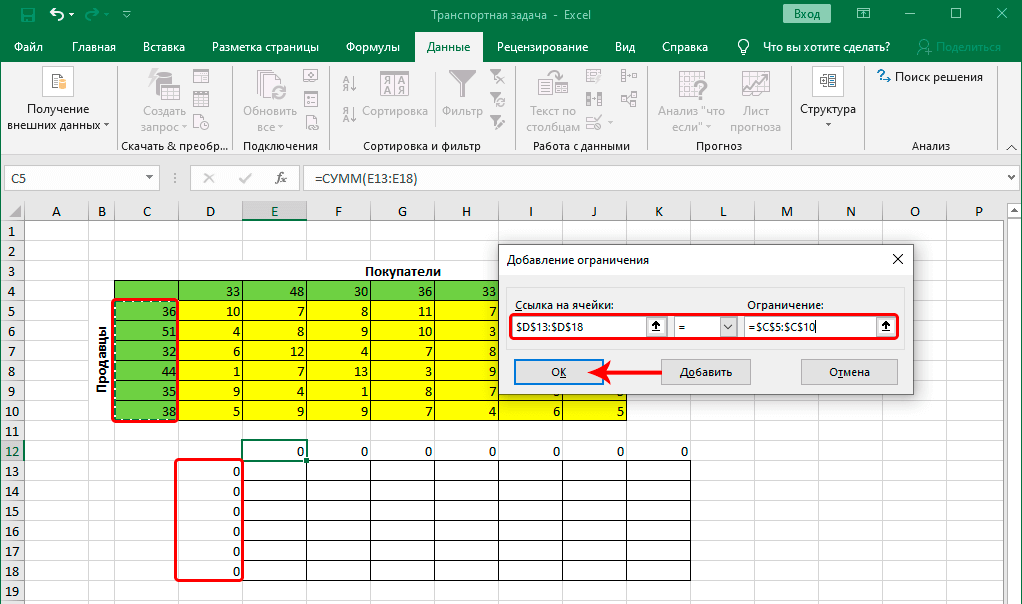
  15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.Добавление ограничения в параметры функции Поиск решения в Excel
  16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.Добавление ограничения в параметры функции Поиск решения в Эксель
  17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
  18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.Запуск функции Поиск решения в Эксель
  19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.Результат работы функции Поиск решения в Excel
  20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.Решенная транспортная задача в Эксель

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Источник

Содержание

  1. Транспортная задача в Microsoft Excel
  2. Общее описание транспортной задачи
  3. Инструменты для решения транспортной задачи в Эксель
  4. Пример решения транспортной задачи в Excel
  5. Условия задачи
  6. Решение задачи
  7. Решение транспортной задачи в Excel с примером и описанием
  8. Виды транспортных задач
  9. Пример решения транспортной задачи в Excel
  10. Решение открытой транспортной задачи в Excel
  11. Как решить транспортную задачу в Excel
  12. Транспортная задача: описание
  13. Подготовительный этап: включение функции “Поиск решения”
  14. Пример задачи и ее решение
  15. Условия задачи
  16. Алгоритм решения
  17. Заключение

Транспортная задача в Microsoft Excel

Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.

Общее описание транспортной задачи

Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.

Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.

Инструменты для решения транспортной задачи в Эксель

Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.

  1. Делаем перемещение во вкладку «Файл».
  2. Кликаем по подразделу «Параметры».

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

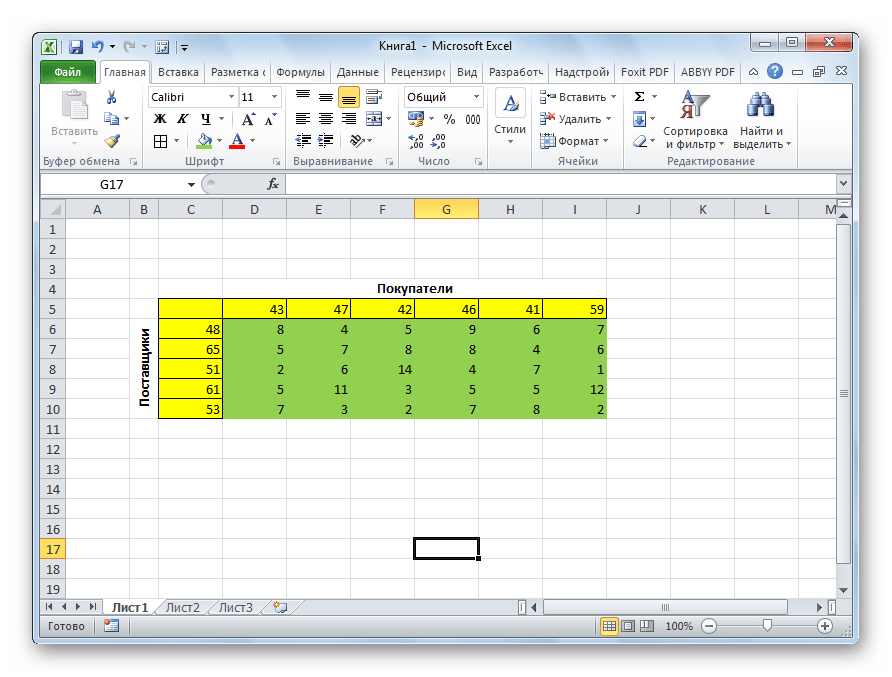
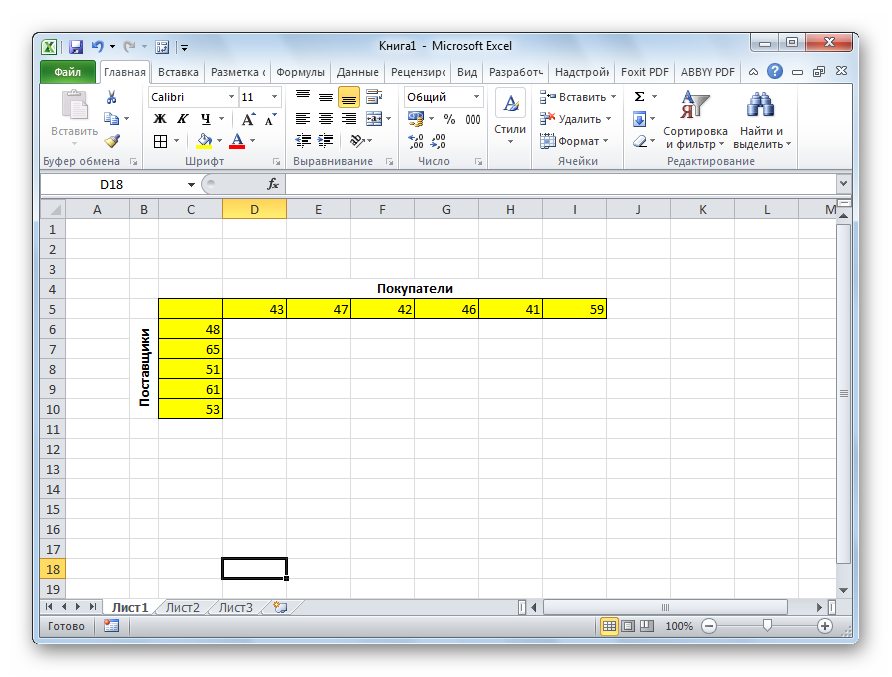
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

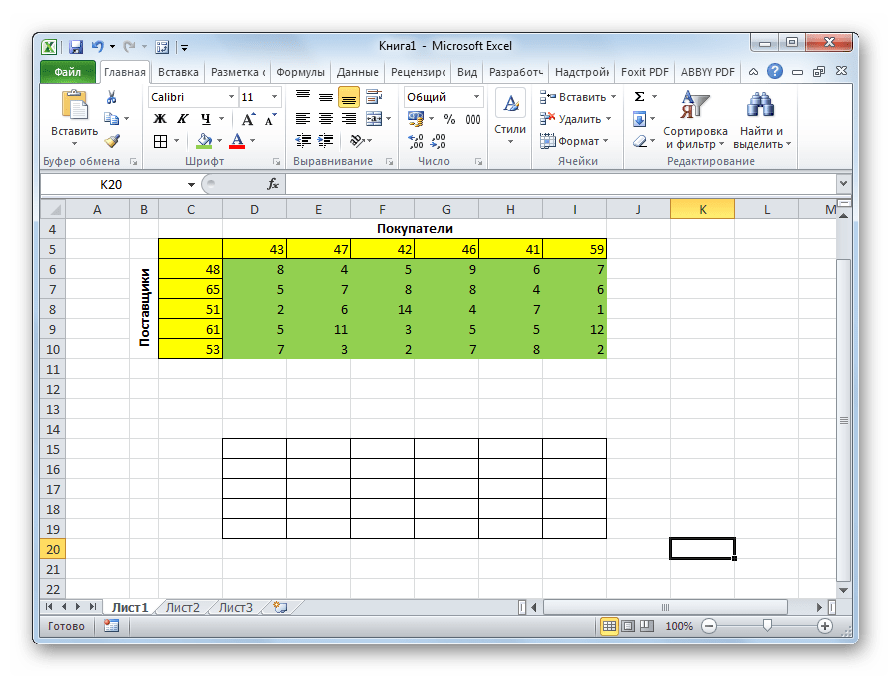
  1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
  2. Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
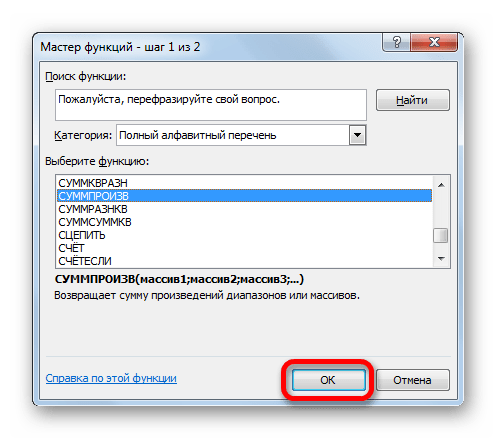
  3. Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
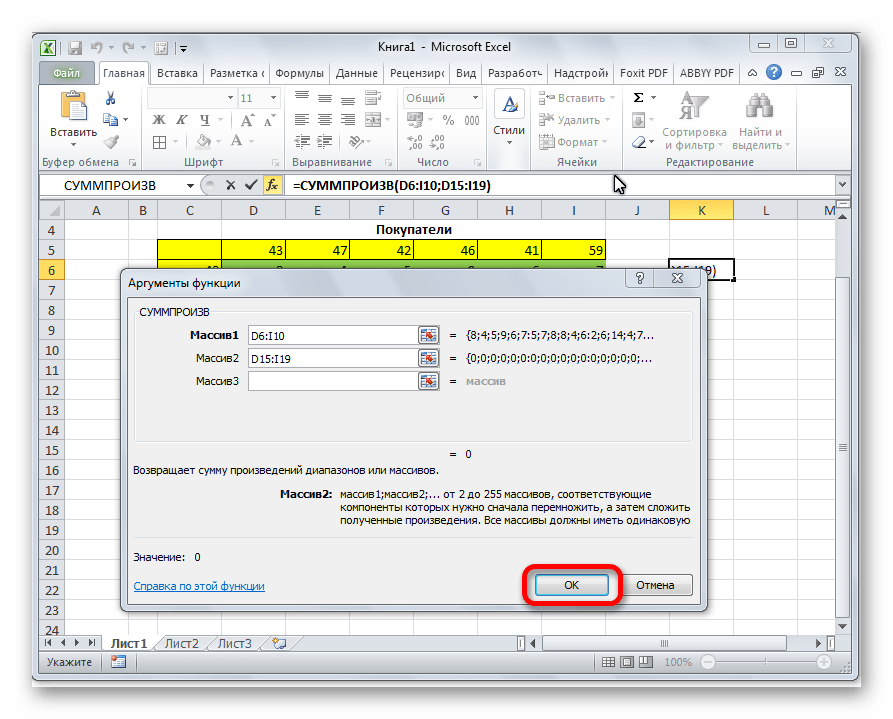
  4. Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
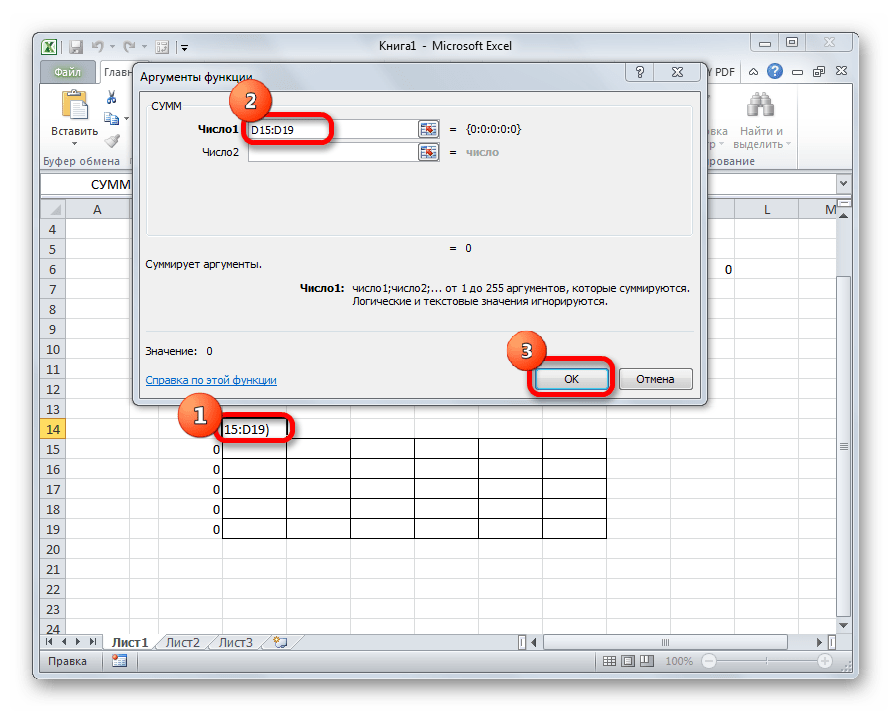
  5. Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
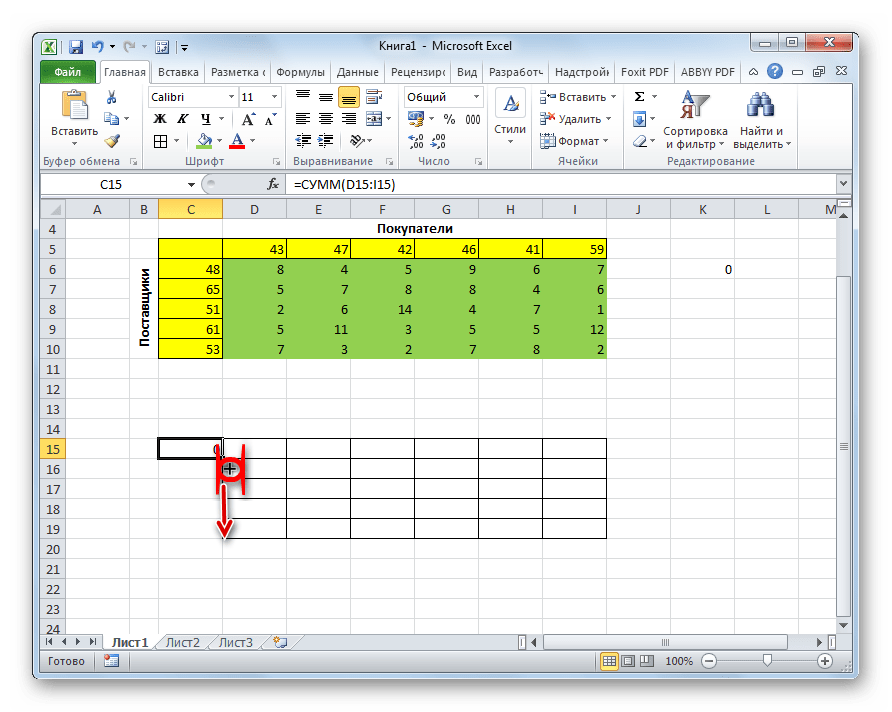
  6. Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
  7. Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
  8. Копируем маркером заполнения формулу на всю строку.
  9. Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
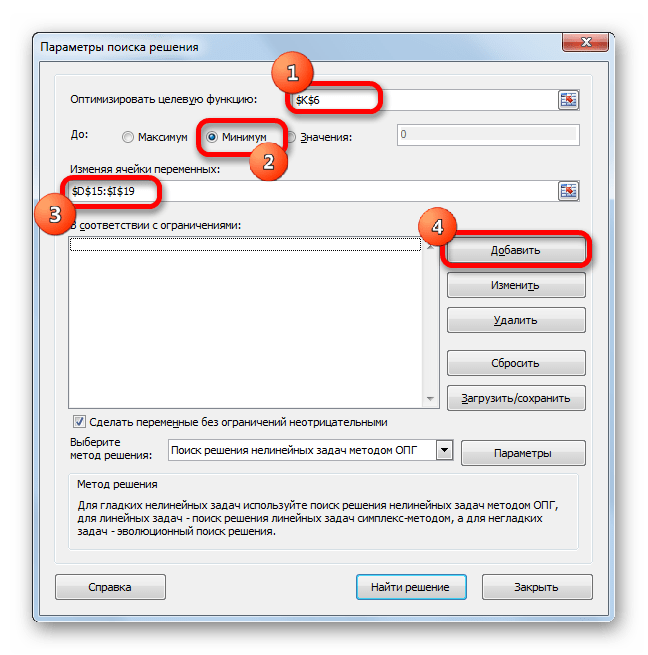
  10. Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
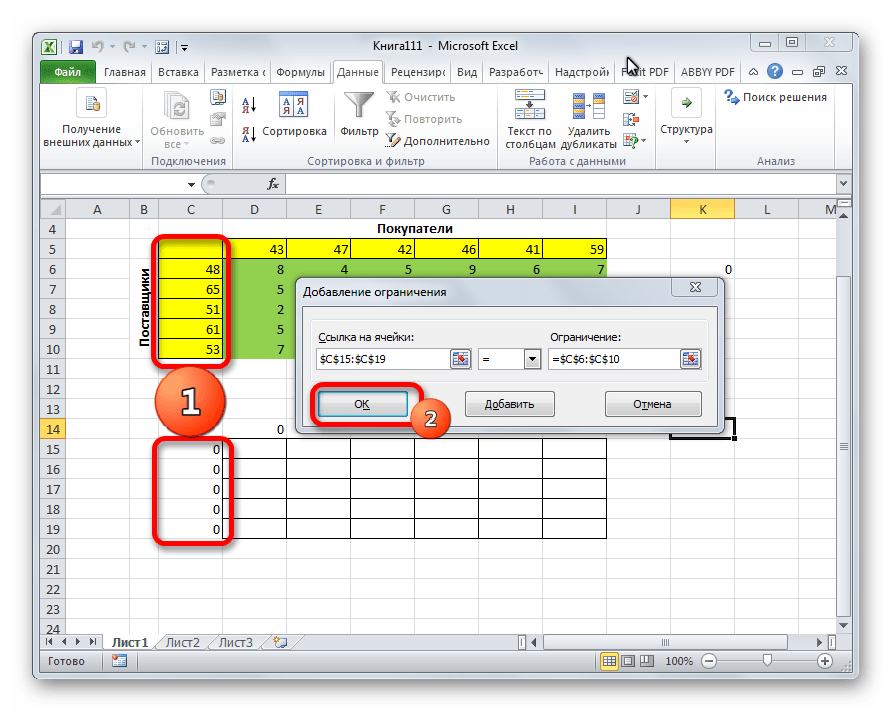
  11. Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
  12. Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
  13. После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Источник

Решение транспортной задачи в Excel с примером и описанием

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

  • открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
  • закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.

Пример решения транспортной задачи в Excel

Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители Потребители Объем производства
В1 В2 В3 В4 В5
А1 4,2 4 3,35 5 4,65 246
А2 4 3,85 3,5 4,9 4,55 186
А3 4,75 3,5 3,4 4,5 4,4 196
А4 5 3 3,1 5,1 4,4 197
Объем потребления 136 171 71 261 186

Задача: минимизировать транспортные расходы по перевозке продукции.

  1. Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
  2. Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
  3. Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
  4. Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
  5. Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
  6. Вносим известные значения потребности в товаре и объема производства.
  7. Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
  8. Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
  9. Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

  • суммарный объем производства превышает суммарную потребность в товаре;
  • суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Источник

Как решить транспортную задачу в Excel

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

  • Закрытая – совокупное предложение продавца равняется общему спросу.
  • Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

  1. Открываем меню “Файл”.
  2. В перечне слева выбираем пункт “Параметры”.
  3. В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
  4. В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
  5. В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

  1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
  2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
  3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
  4. На экране отобразится окно, в котором нужно заполнить аргументы:
    • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
    • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
    • по готовности жмем OK.
  5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
  6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
  7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
  8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
  9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
  10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
  11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
  12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
  13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
  14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
  15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
  16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
  17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
  18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
  19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
  20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Источник

Источник

Содержание

  • Общее описание транспортной задачи
  • Инструменты для решения транспортной задачи в Эксель
  • Пример решения транспортной задачи в Excel
    • Условия задачи
    • Решение задачи
  • Вопросы и ответы

Транспортная задача в Microsoft Excel

Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.

Общее описание транспортной задачи

Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.

Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.

Инструменты для решения транспортной задачи в Эксель

Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.

  1. Делаем перемещение во вкладку «Файл».

    2. Переход в раздел Файл в Microsoft Excel

  2. Кликаем по подразделу «Параметры».

    3. Переход в параметры в программе Microsoft Excel

  3. В новом окне переходим по надписи «Надстройки».

    4. Переход в надстройки в Microsoft Excel

  4. В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».

    5. Переход в надстройки Excel в Microsoft Excel

  5. Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».

    6. Активация инструмента Поиск решения в Microsoft Excel

  6. Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.

Поиск решения в приложении Microsoft Excel

Урок: функция «Поиск решения» в Экселе

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Таблица объемов спроса и предложения в Microsoft Excel

Lumpics.ru

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Матрица затрат в Microsoft Excel

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

  1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.

    2. Макет таблицы для решения задачи в Microsoft Excel

  2. Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.

    3. Переход к Мастеру функций в Microsoft Excel

  3. Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».

    4. Мастер функций программы Microsoft Excel

  4. Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».

    5. Аргументы функции СУММПРОИЗВ в Microsoft Excel

  5. Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».

    6. Аргументы функции СУММ в Microsoft Excel

  6. Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.

    7. Копирование формулы маркером заполнения в Microsoft Excel

  7. Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».

    8. Аргументы функции СУММ в Microsoft Excel

  8. Копируем маркером заполнения формулу на всю строку.

    9. Копирование формулы маркером заполнения в строку в Microsoft Excel

  9. Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».

    10. Переход в Поиск решения в Microsoft Excel

  10. Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.

    11. Параметры поиска решения в Microsoft Excel

  11. Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».

    12. Добавление ограничения в Microsoft Excel

  12. Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».

    13. Параметры Поиска решений в Microsoft Excel

  13. После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Результаты поиска решения транспортной задачи в Microsoft Excel

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Понравилась статья? Поделить с друзьями:
  • Использование excel в качестве базы данных
  • Использование excel в быту
  • Использование excel в банке
  • Использование checkbox в excel
  • Исполняемая программа для word