На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.
В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.
Для удобства восприятия материала сгруппируем эти функции в три блока:
1. Функционал расчетных формул в Excel.
2. Функционал Excel для обработки табличных данных.
3. Инструменты Excel для моделирования и анализа экономических данных.
ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL
Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.
Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.
Решение экономической задачи с помощью формулы ЕСЛИ
Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.
С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.
Запись расчетной формулы в заданной ячейке в общем виде выглядит так:
=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),
где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);
значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;
значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.
Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.
Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.
Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).
Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).
В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.
Решение экономической задачи с помощью формулы СУММЕСЛИ
Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.
Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.
Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.
Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).
Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.
Результат решения задачи — в табл. 2.
Решение экономической задачи с помощью формул ВПР и ГПР
Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:
- ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
- ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.
Формулы прописывают в общем виде следующим образом:
=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);
=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).
Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.
Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:
- продажи в натуральном измерении;
- продажи в суммовом измерении;
- средняя цена реализации единицы продукции в рублях.
Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.
Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.
Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).
Пояснения к формуле:
В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;
Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;
3 — номер столбца, по которому нужно выбрать данные;
ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.
Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.
Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).
Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.
В результате выполненных действий появился искомый отчет о продажах (табл. 3).
На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.
Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.
Решение экономической задачи с помощью формулы СУММПРОИЗВ
Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).
Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.
Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).
Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).
Выполнив указанные действия, получим искомое решение задачи в табл. 4.
Решение экономической задачи с помощью формулы СЧЕТЕСЛИ
Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.
Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.
Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.
Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:
- выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
- в меню редактора выбираем путь: Данные → Проверка данных;
- в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
- в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
- в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».
Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).
ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ
Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.
Решение экономической задачи с применением функции сортировки данных
Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.
Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.
Сортировку данных выполнить просто:
- выделяем курсором столбцы таблицы;
- заходим в меню редактора: Данные → Сортировка;
- выбираем нужные параметры сортировки и получаем новый вид табличных данных.
Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.
Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).
Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.
Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.
Решение экономической задачи с использованием функционала Автофильтр
Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.
В табличном редакторе Excel есть два вида фильтров:
- автофильтр — используют для фильтрации данных по простым критериям;
- расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.
Автофильтр работает следующим образом:
- выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
- заходим в меню редактора: Данные → Фильтр → Автофильтр;
- выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.
Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.
Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.
Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».
Чтобы организовать «Диапазон условий», следует выполнить следующие действия:
- в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
- под каждым из заголовков задаем условие отбора данных.
Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».
Порядок работы с функционалом консолидации данных
Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.
Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:
- макеты всех консолидируемых таблиц одинаковые;
- названия столбцов во всех консолидируемых таблицах идентичные;
- в консолидируемых таблицах нет пустых столбцов и строк.
Работа с функционалом консолидации включает ряд последовательных действий:
1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;
2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;
3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;
4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);
5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);
6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;
7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.
Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета
Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.
Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.
В появившемся диалоговом окне формируем параметры будущей таблицы:
- указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
- указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
- в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.
Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.
ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ
Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.
Решение экономической задачи с помощью надстройки «Поиск решения»
Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.
Такими экономическими задачами могут быть:
- расчет оптимального объема выпуска продукции при ограниченности сырья;
- минимизация транспортных расходов на доставку продукции покупателям;
- решение по оптимизации фонда оплаты труда.
Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:
- в меню Excel выбрать путь: Файл → Параметры → Надстройки;
- в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
- вернуться в меню Excel и выбрать: Данные → Поиск решения.
Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:
1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).
2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).
3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).
Исходные данные, размещенные таким образом, показаны в табл. 8.1.
Далее приступаем к подготовке поиска решения.
1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.
2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).
3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):
- оптимизировать целевую функцию — ячейка J4;
- цель оптимизации — до минимума;
- изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
- ограничения поиска решения:
– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);
– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);
– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);
– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).
Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).
При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.
Пакет расширенного анализа данных
Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.
Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).
Специализированные надстройки для финансово-экономической работы
В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.
Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.
Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.
Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:
- финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
- работа с формулами;
- работа с текстом;
- работа с книгами и листами Excel;
- работа с ячейками Excel;
- поиск дубликатов и сравнение диапазонов данных;
- вставка дат и примечаний к диапазонам данных;
- загрузка курсов валют;
- создание выпадающих списков.
Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:
- кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
- депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
- вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
- набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.
Статья опубликована в журнале «Планово-экономический отдел» № 10, 2020.
Возможности табличного процессора Excel широко применяются в экономике. С помощью офисной программы можно обрабатывать и анализировать данные, составлять отчеты, бизнес-модели, прогнозировать, определять ценность клиентов и т.д.
В рамках данной статьи рассмотрим использование функции ВПР для решения экономических задач.
Описание и синтаксис функции
ВПР – функция просмотра. Формула находит нужное значение в пределах заданного диапазона. Поиск ведется в вертикальном направлении и начинается в первом столбце рабочей области.
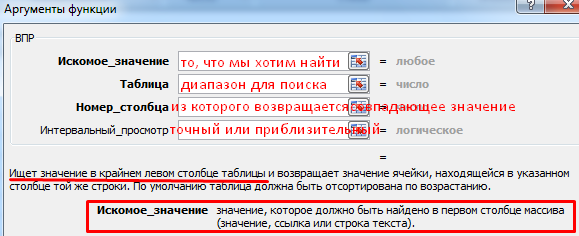
Синтаксис функции:
Аргумент «Интервальный просмотр» необязательный. Если указано значение «ИСТИНА» или аргумент опущен, то функция возвращает точное или приблизительное совпадение (меньше искомого, наибольшее в диапазоне).
Для правильной работы функции значения в первом столбце нужно отсортировать по возрастанию.
ВПР в Excel и примеры по экономике
Составим формулу для подбора стоимости в зависимости от даты реализации продукта.
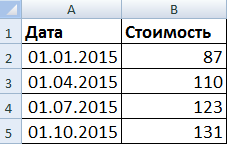
Изменения стоимостного показателя во времени представлены в таблице вида:
Нужно найти, сколько стоил продукт в следующие даты.
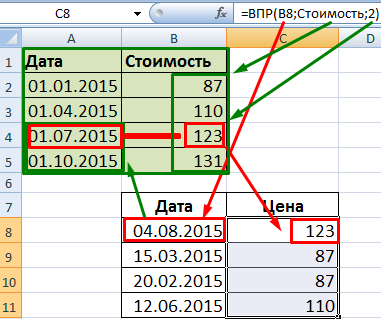
Назовем исходную таблицу с данными «Стоимость». В первую ячейку колонки «Цена» введем формулу: =ВПР(B8;Стоимость;2). Размножим на весь столбец.
Функция вертикального просмотра сопоставляет даты из первого столбца с датами таблицы «Стоимость». Для дат между 01.01.2015 и 01.04.2015 формула останавливает поиск на 01.01.2015 и возвращает значение из второго столбца той же строки. То есть 87. И так прорабатывается каждая дата.
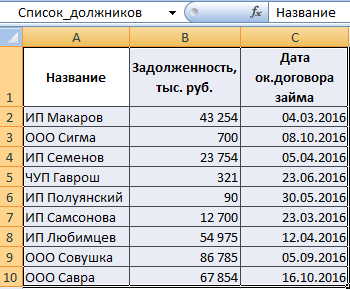
Составим формулу для нахождения имени должника с максимальной задолженностью.
В таблице – список должников с данными о задолженности и дате окончания договора займа:
Чтобы решить задачу, применим следующую схему:
- Для нахождения максимальной задолженности используем функцию МАКС (=МАКС(B2:B10)). Аргумент – столбец с суммой долга.
- Так как функция вертикально просматривает крайний левый столбец диапазона (а суммы находятся во втором столбце), добавим в исходную таблицу столбец с нумерацией.
- Чтобы найти номер предприятия с максимальной задолженностью, применим функцию ПОИСКПОЗ (=ПОИСКПОЗ(C12;C2:C10;0)). Тип сопоставления – 0, т.к. к столбцу с долгами не применялась сортировка.
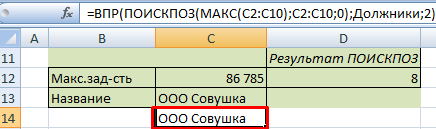
- Чтобы вывести имя должника, применим функцию: =ВПР(D12;Должники;2).
Сделаем из трех формул одну: =ВПР (ПОИСКПОЗ (МАКС (C2:C10); C2:C10;0); Должники;2). Она нам выдаст тот же результат.
Функция ВПР в экономических расчетах полезна, когда нужно извлечь определенное значение из огромного диапазона данных. Причем это значение нужно найти по другому значению (цену по идентификатору продукта, налоговую ставку по уровню дохода и т.п.).
Использование Excel в экономике не ограничивается функциями просмотра. Табличный процессор предлагает пользователю возможности и побогаче.
Вычислительные функции — это сердцевина Excel и то, что, по-сути, отличает программу от обычного калькулятора. Функций в программе довольно много — более 400. Часть из них дублируется, но тем не менее, возможности для экономических расчетов в программе огромные.
С помощью формул можно безошибочно рассчитать себестоимость товара, подготовить аналитические отчеты, свести планы. Решить как простые экономические задачи учета, так и составить полный баланс предприятия. Подборку инструментов Excel для бухгалтера мы уже делали. Настал черед рассмотреть основные функции Excel для экономиста, которые упростят работу с данными и большими таблицами.
Что такое функции Excel и где они находятся
Функции в Excel — это команды, которые помогают в считанные минуты откорректировать данные в ячейках, рассчитать значения по определенным критериям, изъять нужную информацию из огромного массива. Функции часто используют в формулах, чтобы их упростить и сделать более гибкими.
Как мы уже говорили, в программе функций много — около 10 категорий: есть математические, логические, текстовые. И специальные функции — финансовые, статистические и пр. Все функции лежат во вкладке «Формулы». Перейдя в нее, нужно нажать на кнопку «Вставить функцию» на панели инструментов, после чего запустится «Мастер функций».
Останется выбрать в «Категориях» нужную функцию для вычислений и заполнить данные по структуре в выпадающем окошке.
Если вы знаете, какая функция вам нужна, просто введите ее в строке формул, начиная со знака «=». Как только ввели, нажмите «Enter» для вычисления.
Запоминать, что делает каждая функция не нужно. В Excel есть удобные подсказки, зачем нужна та или иная формула, и как ее использовать.
Ниже рассмотрим основные и часто используемые формулы в Excel для экономистов: ЕСЛИ, СУММЕСЛИ, ВПР, СУММПРОИЗВ, СЧЁТ, СРЗНАЧ и МАКС/МИН.
Функция ЕСЛИ для сравнения данных
Самая популярная логическая функция, которая полезна экономистам, бухгалтерам. С ее помощью можно сравнить числовые и текстовые значения по определенным критериям. Например, рассчитать амортизацию, скидки, наценку или убрать ошибки из расчетов. Иногда используется встроенная функция ЕСЛИ в статистических, текстовых и математических формулах, что наделяет их способностью «принимать решения».
Функция ЕСЛИ помогает точно сравнить значения и получить результат, в зависимости от того, истинно сравнение или нет.
Так выглядит формула:
=ЕСЛИ(лог_выражение;[значение_если_истина];[значение_если_ложь])
- Лог_выражение — это то, что нужно проверить или сравнить (числовые или текстовые данные в ячейках)
- Значение_если_истина — это то, что появится в ячейке, если сравнение будет верным.
- Значение_если_ложь — то, что появится в ячейке при неверном сравнении.
Например, магазин торгует аксессуарами для мужчин и женщин. В текущем месяце на все женские товары скидка 20%. Отсортировать акционные позиции можно с помощью функции ЕСЛИ для текстовых значений.
Пропишем формулу в столбце «Скидка» так:
=ЕСЛИ(B2=»женский»;20%;0)
И применим ко всем строкам. В ячейках, где равенство выполняется, увидим товары по скидке.
Так применяется функция ЕСЛИ для текстовых значений с одним условием
Функции СУММЕСЛИ и СУММЕСЛИМН
Еще одна полезная функция СУММЕСЛИ, которая позволяет просуммировать несколько числовых данных по определенному критерию. Состоит формула из 2-х частей:
- СУММ — математическая функция сложения числовых значений. Записывается как =СУММ(ячейка/диапазон 1; ячейка/диапазон 2; …).
- и функция ЕСЛИ, которую рассмотрели выше.
Например, вам нужно просчитать общую сумму начисленной заработной платы менеджерам, а в отчете указаны данные по всем сотрудникам предприятия.
В формуле нужно прописать такие аргументы:
- Выделить диапазон всех должностей сотрудников — в нашем случае B2:B10.
- Прописываем критерий выбора через точку с запятой — “менеджер”.
- Диапазон суммирования — это заработные платы. Указываем C2:C10.
И получаем в один клик общую сумму заработной платы менеджеров:
С помощью СУММЕСЛИ можно просуммировать ячейки, которые соответствуют определенному критерию
Важно! Функция СУММЕСЛИ чувствительна к правильности и точности написания критериев. Малейшая опечатка может дать неправильный результат. Это также касается названий ячеек. Формула выдаст ошибку, если написать диапазон ячеек кириллицей, а не латиницей.
Более сложный вариант этой формулы — функция СУММЕСЛИМН. По-сути, это выборочное суммирование данных, отобранных по нескольким критериям. В отличие от СУММЕСЛИ, можно использовать до 127 критериев отбора данных. Например, с помощью этой формулы легко рассчитать суммарную прибыль от поставок разных товаров сразу в несколько стран.
В функции СУММЕСЛИМН можно работать с подстановочными символами, использовать операторы для вычислений типа «больше», «меньше» и «равно». Для удобства работы с функцией лучше применять абсолютные ссылки в Excel — они не меняются при копировании и позволяют автоматически пересчитать формулу, если данные в ячейке изменились.
Функции ВПР и ГПР — поиск данных в большом диапазоне
Экономистам часто приходится обрабатывать огромные таблицы, чтобы получить необходимые данные для анализа. Или сводить две таблицы в одну, что тоже не редкость. Функция ВПР или, как ее еще называют, вертикальный просмотр (англ. вариант VLOOKUP) позволяет быстро найти и извлечь нужные данные в столбцах. Либо перенести данные из одной таблицы в соответствующие ячейки другой.
Синтаксис самой простой функции ВПР выглядит так:
= ВПР(искомое_значение; таблица; номер_столбца; [интервальный просмотр]).
Например, вам нужно быстро извлечь наименование товара по номеру в списке. С помощью функции ВПР это сделать очень просто:
Функция ВПР позволяет быстро найти нужные данные и перенести их в выделенную ячейку.
В ячейке С1 мы указали номер товара. Потом выделили диапазон ячеек, где его искать (A1:B10) и написали номер столбца «2», в котором нужно взять данные. Нажали Enter и получили нужный товар в выделенной ячейке.
Есть менее популярная функция ГПР. Она работает также, как ВПР, но ищет данные в горизонтальных списках.
Важно! Чтобы увеличить область применения этой функции, можно задать данные с помощью подстановочных знаков.
Одна из задач этой функции — упростить подготовку исходных данных для аналитических и сводных таблиц. Как подготовить такую таблицу можете почитать бесплатно в книге Сводные таблицы в Excel.
Функция СУММПРОИЗВ в Excel
Четвертая функция нашего списка — СУММПРОИЗВ или суммирование произведений. Поможет быстро справиться с любой экономической задачей, где есть массивы. Включает в себя возможности предыдущих формул ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, а также позволяет провести расчеты в 255 массивах. Ее любят бухгалтеры и часто используют при расчетах заработной платы и других расходов.
Что в данном случае может быть произведениями? Как заданные диапазоны, так и целые массивы данных. Чтобы задать количество массивов, их нужно перечислить через точку с запятой, потом перемножить, а затем просуммировать. При этом, есть одно условие — массивы должны быть одинаковые по типу и длине.
Например, у вас есть месячный отчет по продажам в магазине, из которого нужно узнать, на какую сумму продали футболок размера «М».
Для этого используем функцию СУММПРОИЗВ и указываем 2 условия. Каждое из них берем в скобки, а между ними ставим «звездочку», которая в Excel читается как союз «и».
Запишем команду так: =СУММПРОИЗВ((A5:A11=A13)*(B5:B11=B13)*C5:C11), где
- первое условие A5:A11=A13— диапазон поиска и наименование нужного товара
- второе условие B5:B11=B13 — диапазон поиска и размер
- C5:C11 — массив, из которого берется итоговая сумма
С помощью функции СУММПРОИЗВ мы узнали за пару минут, что в магазине за месяц продали футболок М-размера на 100 у.е.
Чтобы узнать продажи по другому товару и размеру, нужно просто заменить данные в ячейках A13 и B13.
Данный пример слишком прост, по сравнению с тем, с какими объемами данных приходится работать экономистам. Но зная, что умеет данная формула, уже не так страшны таблицы в миллионы строк и сотни столбцов, а нужные данные находятся за считанные минуты.
Как применить МАКС, ВПР и ПОИСКПОЗ для решения задач
Функции МИН и МАКС помогают найти наименьшее или наибольшее значение данных. Функция ПОИСКПОЗ помогает найти номер указанного элемента в выделенном диапазоне. А формула ВПР, напомним, позволяет извлечь нужные данные из столбцов в указанные ячейки.
Рассмотрим комбинацию этих функций на примере решения задачи в Excel для экономистов. Составим комбинированную формулу, чтобы найти компанию с наибольшей суммой задолженности.
Для начала составим список должников, укажем сумму их задолженности и выставим дату окончания кредитного договора.
Для решения задачи, можно применить функции последовательно:
- Найти самый крупный долг поможет функция МАКС (=МАКС(B2:B10)), где B2:B10 — столбец с данными по задолженности.
- Чтобы найти номер компании-должника в списке, нужно в таблицу добавить столбец с нумерацией. Так как функция ПОИСКПОЗ ищет данные только в крайнем левом столбце выделенного диапазона.
Составляем функцию по формуле:
ПОИСКПОЗ(искомое_значение;просматриваемый_массив;[тип_сопоставления])
В нашем случае это будет =ПОИСКПОЗ(14569;C2:C10;0), где искомое — максимальная сумма долга. Тип сопоставления будет “0”, потому что к столбцу с долгами мы не применяли сортировку.
- Чтобы узнать название компании-должника, применим знакомую функцию ВПР.
Выглядеть она будет так =ВПР(D14;A2:B10;2), где D4 — искомое, A2:B10 — таблица или выделенный диапазон с названиями компаний и нумерацией, а “2” — номер столбца с должниками.
Этот же результат можно было получить, собрав одну формулу из 3-х:
=ВПР (ПОИСКПОЗ (МАКС (C2:C10); C2:C10;0); A2:B10;2).
В экономических расчетах функция ВПР помогает быстро извлечь нужное значение из огромного диапазона данных. Причем значение можно найти по разным критериям отбора. Например, цену товара можно извлечь по идентификатору, налоговую ставку — по уровню дохода и пр.
Кроме вышеупомянутых функций, экономисты часто используют формулу СРЗНАЧ, например, для расчета средней заработной платы. Функцию СЧЁТ, когда нужно рассчитать количество отгрузок в разрезе клиентов или стоимости товара за определенный период. Кстати, на примере отгрузок, формула МИН/МАКС поможет отследить диапазон, в котором изменялась стоимость товара.
Существует еще сотня математических и финансовых функций в Ехсеl, с помощью которых можно решить экономические задачи разной сложности. Например, обрабатывать заказы, планировать загрузку производства, рассчитывать налоги, вести кадровый учет и управлять сбытом. Но для решения подобных задач, подсказок в Excel будет уже недостаточно. Тут необходимо глубже погружаться в программу и учиться работать с разными ее инструментами: от функций и сводных таблиц, до диаграмм и макросов.
Цветные диаграммы лучше покажут вашу работу с данными, чем сетка Excel!
Освойте программу Power BI, создавайте визуальные отчеты в пару кликов после курса «ACPM: Бизнес-анализ данных в финансах»!
Насколько уверенно вы владеете Excel?
Всем известна востребованность экономических
знаний сегодня. Самостоятельность в принятии
решений, эффективный анализ проблемы,
отстаивание собственной точки зрения – эти
качества приобретёт каждый, работая в одной
команде над решением экономической задачи.
В данном уроке представлены задачи
оптимального планирования производства и оценки
эффективности денежных вложений с помощью
финансовых функций MS Excel.
Урок проводится в 11 классе при изучении
технологий обработки числовой информации (по
учебнику «Информатика. 11 класс», под ред. Семакина
И.Г.). Учащиеся владеют основными экономическими
понятиями и терминами из изучаемого курса
экономики.
Тема: Математическое моделирование в
планировании и управлении.
Тема урока: Использование MS Excel для решения
экономических задач (2 часа).
Цели урока:
1.Общеобразовательные:
– повторение и обобщение
изученного материала по темам: текстовый
редактор, математическое моделирование,
электронные таблицы, относительная и абсолютная
адресация, встроенные функции Excel .
2. Познавательные:
– формирование учебного
действия «подведение под понятие»;
– формирование учебного действия по выведению
следствия из факта принадлежности объекта
понятию;
– формирование умений применять имеющиеся
математические знания и знания из курса
информатики к решению практических задач;
– развитие внимания, познавательной активности,
творческих способностей, логического мышления.
3. Воспитательные:
– воспитание интереса к предмету;
– самостоятельности в принятии решения;
– формирование культуры общения.
Методы обучения:
– частично-поисковый;
– проблемный.
Тип урока: Урок повторения и обобщения
знаний, умений и навыков учащихся.
Дидактическое и методическое оснащение урока:
– дидактические материалы.
Подготовка к уроку: Занятия проводятся в
группе по 12-15 человек. Учащиеся заранее делятся
на 2 группы примерно с равным уровнем знаний.
План урока:
1. Мотивационно-ориентировочный этап:
разъяснение учащимся целей учебной
деятельности, задач и хода урока.
2. Подготовительный этап: актуализация опорных
знаний учащихся.
3. Основной этап: работа в группах.
4. Заключительный этап: выводы по уроку и
подведение итогов.
Ход урока:
1. Сегодня мы проведём
несколько необычный урок. Каждый из вас на уроке
попытается стать предпринимателем, открыть своё
дело.
Несколько лет назад, когда открылась возможность для создания
собственного бизнеса, каждый гражданин получил
возможность открыть своё дело.
Многие начинающие предприниматели не вполне
представляют, какими должны быть их первые шаги в
бизнесе, какие ресурсы необходимо привлечь на
пути становления своего предприятия и какие
задачи придётся решать в первую очередь.
Уильям А. Уард однажды сказал: “Четыре шага к
достижению: целеустремлённый план, тщательная
набожная подготовка, положительные действия,
постоянная настойчивость”. Воспользуемся его
советом, переложим его слова применительно к
нашему времени и попробуем составить бизнес-план
вашего будущего предприятия. Это будет ваша задача на сегодняшний
урок.
С какими же проблемами мы
можем столкнуться при создании собственного
предприятия? Какие два самых важных вопроса
встанут перед вами?
– 1) Что это будет за предприятие?
– 2) Сколько средств
необходимо вложить в своё дело на начальном
этапе и в будущем?
На втором этапе нужно хорошо представлять, на
что и куда пойдут эти средства. Давайте же
попытаемся выяснить, на что могут быть потрачены
первоначально вложенные деньги.
– Стоимость оборудования;
– Аренда (покупка) помещения;
– Оплата энергетических ресурсов;
– Регулярные отчисления (налоги, выплаты);
– Покупка средств передвижения (машины).
Затем перед нами встанет задача оптимального
планирования производства. Как организовать
работу своего предприятия так, чтобы оно было
прибыльным?
Итак, давайте начнём с выбора производства. Как
вы думаете, от чего зависит выбор производства?
– Как правило, от
первоначально вложенного капиталла.
Высокотехнологичные производства требуют
больших затрат. Мы же остановимся на маленьких
затратах, и, как следствие, на маленьком
производстве, и откроем небольшой кондитерский
цех по производству булочек и пирожных.
Мы разделимся на две группы. Каждая группа
попытается составить свой бизнес-план создания
и развития своего предприятия. Каждая группа
получит полный список документов, которые
необходимо представить для открытия и
регистрации своего предприятия. И вы в группе
сами распределите, кто каким видом деятельности
будет заниматься. По окончании урока вы сдаёте
полный пакет документов на рассмотрение учителя.
В ходе подготовки необходимых документов вы
можете воспользоваться любыми программными
средствами MS Windows и MS Office2000.
2. Рассмотрим подробнее
первый пакет необходимых документов.
Пакет № 1. Должен содержать титульный лист с
названием и полной характеристикой вашего
предприятия и рекламный проспект вашего
предприятия.
Пакет № 2. Необходимо представить полное
решение и оформление следующих задач:
1) Из какой суммы
необходимо исходить для того, чтобы выгодно
начать своё дело (чтобы прибыль составляла 100%)?
2) Какова должна быть
себестоимость выбранной вами продукции?
Расчёты представить для 1-й рабочей смены (8 часов)
в цеху и для 2 видов продукции в количестве 700
штук.
В отчёте отразить следующее:
| Вид продукции | Пирожки | Булочки |
| Производительность труда | ||
| Отпускная цена продукции | ||
| Сумма реализации | ||
| Затраты: | ||
| – на производство продукции | ||
| – на оборудование | ||
| – на аренду помещения | ||
| – зар. плата рабочим | ||
| – электроэнергия | ||
| – налоги | ||
| Итого затрат | ||
| Прибыль | ||
| Чистая прибыль=Сумма реализации – Расходы |
||
| Всего затраты | ||
| Себестоимость продукции |
Подумайте, где лучше оформить данную таблицу,
оцените необходимость использования тех или
иных средств.
Следующая важная проблема, с которой вы
сталкиваетесь, – проблема оптимального
планирования производства. Это очень важная
проблема, и от её правильного решения зависит
прибыльность вашего производства.
Действительно, в этом случае справедлив так
называемый закон Букера: “Даже маленькая
практика стоит большой теории”. Вам придётся
очень хорошо подумать над решением данной
задачи. Она представлена вам в пакете № 3.
Пакет № 3.
Дневной план производства.
Задача: Школьный кондитерский цех производит
булочки и пирожные. В силу ограниченности
ёмкости склада за день можно приготовить в
совокупности не более 700 изделий. Рабочий день в
кондитерском цехе длится 8 часов. Если выпускать
только пирожные, за день можно произвести не
более 250 штук, булочек же можно произвести 1000,
если не выпускать пирожных. Себестоимость
продукции известна (из предыдущего пакета №2).
Требуется составить дневной план производства,
обеспечивающий кондитерскому цеху наибольшую
выручку.
Какими средствами вы воспользуетесь для
решения данной задачи?
– Средствами
математического моделирования.
Необходимо составить математическую модель
данной задачи. Составить целевую функцию.
И к какой новой задаче мы должны прийти?
– Найти значения плановых
показателей х и у, при которых целевая функция
принимает максимальные значения.
Пакет № 4.Регулярные выплаты.
Вы знаете, что каждое предприятие ежемесячно отчисляет n-сумму средств.
Что же входит в понятие регулярных выплат?
– выплаты по ссуде;
– техобслуживание;
– арендная плата;
– зар. плата.
Какую функцию предоставляет Excel для работы с регулярными выплатами?
– БЗ();
– ПЗ();
– ППЛАТ().
Выберите, какую из функций вы будете
использовать при решении
следующей задачи:
Определите сколько денег должно быть в бюджете
компании в начале года, чтобы она имела
возможность ежемесячно выплачивать 600$ за
оборудование, если бюджетные деньги
обеспечивают компании прибыль по эффективной
годовой ставке 5%?
Пакет № 5. Экономические альтернативы.
Для нужд вашего предприятия необходим
грузовик. На каких условиях лучше купить
грузовик, стоимостью 15000$: взять ссуду под 1,5%
годовых или купить его со скидкой 1500$, выплачивая
более высокие проценты по ссуде?
Здесь вы подошли к серьёзному испытанию –
выбору наиболее благоприятного варианта. Вам
придётся сделать свой выбор. Как лучше заключить
сделку? Как выгоднее оформить ссуду? Вы должны
обосновать правильность сделанного выбора.
Итак, что лучше?
1) Выплачивать полную стоимость ссуды, однако
при этом будут начисляться низкие проценты по
ссуде.
2) Выплачивать стандартную процентную ставку (9%
годовых, начисляемых ежемесячно), получая при
этом скидку.
Другая задача: Холодильник
можно купить, воспользовавшись одним из таких
вариантов:
– Холодильник стоит
60000$ и срок его эксплуатации в среднем составляет
10 лет: на техобслуживание такого холодильника
придётся тратить 2200$ в год, а его ликвидационная
стоимость составляет 12000$.
– Холодильник стоит 32000$ и в среднем имеет
пятилетний срок эксплуатации; на
техобслуживание такого холодильника придется
затрачивать 2600$ в год, а его ликвидационная
стоимость равна 0.
Какая сделка выгоднее?
1) Покупка дорого оборудования, требующего
небольших затрат на техобслуживание и
обладающего более длительным сроком
эксплуатации.
2) Приобретение более дешевого оборудования,
техобслуживание которого будет стоить дороже, а
эксплуатация продлится меньше.
Для ответа на эти вопросы необходимо привести
все денежные суммы к одному и тому же моменту
времени, к текущему моменту. И найти величину
ежемесячных выплат в каждом случае.
Подумайте, какую функцию вы будете
использовать в данном случае?
– ППЛАТ().
3. Учащиеся приступили к
решению задач и оформлению необходимых
документов.
Приводим решение некоторых задач.
Задача из пакета №3.
Составим математическую модель задачи.
Плановыми показателями являются:
Х – дневной план выпуска булочек, У – дневной
план выпуска пирожных. Для определённости будем
считать, что стоимость пирожного вдвое больше,
чем булочки (учащиеся возьмут свои, получившиеся
в пакете №2, показатели себестоимости продукции).
Из условия задачи следует, что на изготовление
одного пирожного затрачивается в 4 раза больше
времени, чем на изготовление одной булочки. Если
обозначить время изготовления булочки – t
мин, то время изготовления
пирожного будет равно 4t мин.
Значит, суммарное время на изготовление х
булочек и у пирожных равно tх + 4tу = (х+4у)t.
Но это время не может быть больше длительности
рабочего дня. Отсюда следует неравенство: (х+4у)t<=8*60 или
(х+4у)t<=480. Можно вычислить t – время
изготовления одной булочки. Т.к. за рабочий день
их может быть изготовлено 1000 штук, то на одну
булочку затрачивается 480/1000=0,48 мин. Подставляя
это значение в неравенство, получим: (х+4у)0,48<=480.
Отсюда: х+4у<=1000. Ограничение на общее число
изделий даёт неравенство: х+4у<=700. К двум
полученным неравенствам следует добавить
условие положительности значений величин х и у
(не может быть отрицательного числа булочек и
пирожных). В итоге мы получаем систему
неравенств:
х+4у<=1000;
х+у<=700;
х>=0;
у>=0.
Выручка – это стоимость всей проданной
продукции. Пусть цена одной булочки – r рублей. По условию задачи, цена
пирожного 2r рублей. Отсюда
стоимость всей произведённой за день продукции
равна rх + 2rу=r(х+2у). Будем рассматривать
записанное выражение как функцию от х и у.
Получили целевую функцию: f(x,y)= r(х+2у). Т.к. r –
константа, то максимальное значение функции
будет достигнуто при максимальной величине
выражения (х+2у). Поэтому в качестве целевой
функции можно принять f(x,y)=х+2у.
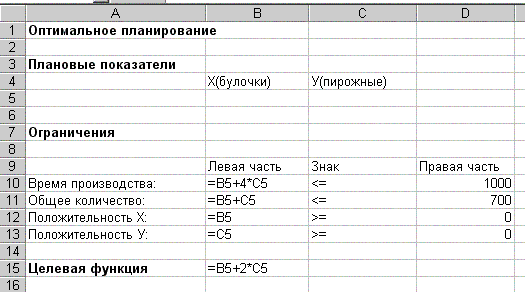
Теперь подготовим электронную таблицу к
решению задачи оптимального планирования: рис. 1.
Выполним поиск решения.
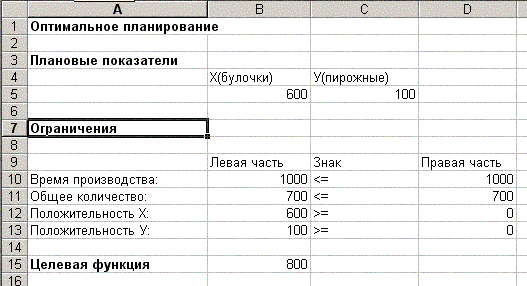
Результаты решения задачи: рис. 2.
Получили следующий оптимальный план дневного
производства: нужно выпускать 600 булочек и 100
пирожных. При этом достигается получение
максимальной прибыли – 1600 рублей.
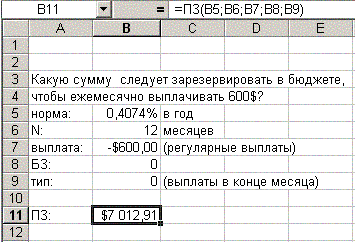
Задача из пакета № 4.
В данном примере указано количество регулярных
выплат. Нужно определить, какую сумму следует
зарезервировать в бюджете на нулевой момент
времени, чтобы оплатить все счета за
оборудование. Для ответа на этот вопрос
используем функцию ПЗ().
Эффективную годовую ставку (5%) нужно
преобразовать в периодическую ежемесячную
процентную ставку. Это две величины связаны
между собой таким уравнением:
где
in – периодическая
процентная ставка,
iэ – эффективная годовая
процентная ставка,
N – количество периодов
начисления процентов за год.
Подставив в формулу, получим, что эффективная
годовая процентная ставка, равная 5%,
эквивалентна ежемесячной процентной ставке 0,4074%:
in= 0,004074, или 0,4074% в месяц.
Сумму, которую нужно оставить в бюджете на
выплату счетов за оборудование, находим с
помощью функции ПЗ().
Так как на сумму, которая находится в бюджете,
начисляются проценты, на выплату всех двенадцати
ежемесячных платежей в начале года достаточно
будет отложить чуть больше 7000$.
Задача из пакета № 5.
Найдём величину ежемесячных выплат в каждом из
описанных случаев.
1) Годовая процентная ставка составляет 1,5% (в
ячейке В3 содержится формула В3:=1,5%/12, или 0,125% в
месяц), количество месяцев равно 48. Принимая во
внимание, что приведенная стоимость автомобиля
– 15000$, находим ежемесячные выплаты: ППЛАТ=$322,16.
Или:
2) Годовая процентная ставка составляет 9% (в
ячейке В3 содержится формула В3:=9%/12, или 0,750% в
месяц ), количество месяцев равно 48. Принимая во
внимание, что приведённая стоимость автомобиля
со скидкой – 135000$, находим ежемесячные выплаты:
ППЛАТ=$335,95.
Ссуда, предоставляемая по годовой процентной
ставке, равной 1,5%, обеспечивает более низкие
выплаты, хотя разница очень мала. В данной задаче
первый вариант предпочтительнее, хотя при
увеличении суммы скидки ситуация может
измениться.
4. Подготовленные документы
сдаются на рассмотрение учителю.
(Выставляется общая оценка группе, ошибки и
недостатки работ подробно разбираются на
следующем занятии)
Пройдёт совсем немного времени, и вы выйдете в
большую взрослую жизнь. Я думаю, вам нечего
бояться предстоящих трудностей, вы справитесь с
ними так же, как и с предложенными вам сегодня
задачами. Упорство, вооруженное знаниями,
высокая работоспособность, я верю, приведут вас к
победе. Успехов вам!
Муниципальное образовательное учреждение
Октябрьская средняя общеобразовательная школа
Радищевского района Ульяновской области
Реферат на тему:
«Решение прикладных (экономических) задач
в Excel»
Работу выполнил:
Учащийся 11 класса
Чахоян Каруш
Руководитель:
Учитель информатики
Юдахина Т. М.
П. Октябрьский. 2007 г
Оглавление:
1. Введение. Обоснование выбора темы реферата…………………………….3
2. Решение прикладных задач в Excel………….…………………………………3
3. Задачи оптимизации …………………………………………………………..6
4. Прогнозирование ……………………………………………………………..11
5. Заключение. Актуальность выбранной темы……………………………….13
6. Используемая литература………………………………….…………………14
7. ПРИЛОЖЕНИЕ (файлы таблицы Excel) ……………………………………..…… 15
- ВВЕДЕНИЕ
Обоснование выбора темы реферата.
Целью данной работы является использование функций Excel для решения экономических задач. Данные задачи будут решаться с помощью программ табличного процессора Excel. Microsoft Excel средство для работы с электронными таблицами, намного превышающее по своим возможностям существующие редакторы таблиц, первая версия данного продукта была разработана фирмой Microsoft в 1985 году. Табличные процессоры — удобный инструмент для экономистов, бухгалтеров, инженеров, научных работников — всех тех, кому приходится работать с большими массивами числовой информации. Эти программы позволяют создавать таблицы, которые являются динамическими, т. е. содержат так называемые вычисляемые поля, значения которых автоматически пересчитываются по заданным формулам при изменении значений исходных данных, содержащихся в других полях. В дальнейшем ее можно просматривать, изменять, записывать на магнитный диск для хранения, печатать на принтере. Microsoft Excel – это программа управления электронных таблицами общего назначения, которая используется для вычислений, организации и анализа деловых данных. Многие фирмы разработчики программного обеспечения для ПК создали свои версии табличных процессоров. Из них наибольшую известность приобрели Lotus 1-2-3 фирмы Lotus Development, Supercalc фирмы Computer Associates.
Excel — очень мощный инструмент для решения задач, имеющих дело с массивами разнообразных данных, поэтому область его применения обширна, начиная от бухгалтерских и складских задач и заканчивая расчетами энергетики спутниковых линий. В Excel удобно решать задачи линейной алгебры, такие как работа с матрицами и др. Также есть все возможности по полноценной работе (сортировка, выборка, сводные таблицы, анализ) с базами данных. Благодаря наличию языка программирования в Excel возможно создание различных пользовательских программ, которые автоматизируют специфические стандартные задачи.
Мне интересна данная тема именно в использовании электронной таблицы в ведении бухгалтерии. Я собираюсь связать свою профессию с экономикой. Наша семья имеет частный магазин. Поэтому я взялся за данную тему. Я уже сейчас занимаюсь экономическими и бухгалтерскими расчетами, помогая отцу в содержании магазина и организации его эффективной работы. Использование компьютера очень помогает мне быстро и правильно производить расчеты и строить перспективы на дальнейшую работу.
2. Решение прикладных задач в Excel
В данном разделе вы убедитесь, что Excel позволяет не только производить расчеты, но и решать сложные задачи в различных сферах деятельности, такие как решение уравнений, задачи оптимизации, прогнозирования. Решение этих задач может быть существенно облегчено с помощью инструмента Поиск решения (Solver в английских версиях Excel).
Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Поэтому решение задачи необходимо начинать с построения соответствующей модели.
Если надстройка Поиск решения (Solver) не была установлена при первоначальной установке Excel, то следует запустить процесс установки повторно и выбрать только эту настройку.
Для того чтобы надстройка Поиск решения (Solver) загружалось сразу при запуске Excel:
-выберите команду Сервис, Надстройки;
-в диалоговом окне Надстройки в списке надстроек установите флажок напротив надстройки Поиск решения. Если в списке нет элемента Поиск решения, то нажмите кнопку Обзор, чтобы самостоятельно найти файл Solver.XLA.
Виды математических моделей.
При решении оптимизационных задач с помощью надстройки Поиск решения необходимо различать линейные и нелинейные модели. Под линейными понимаются модели, в которых связь между входными значениями переменных и результирующими значениями описывается линейными функциями. Например:
Y=A*X1+B*X2+C*X3+…
В этом выражении А,В,С — константы, Х1,Х2,Х3-переменные, Y-результат.
Если выражение для целевой величины и выражение для ограничений являются линейными, то можно применять быстрые и надежные методы поиска решения. Для использования именно линейных методов следует установить параметр Линейная модель в окне Параметры поиска решения. Если этот параметр не установить, то даже для линейной задачи будут использоваться общие, более медленные методы.
Ограничения в задачах.
Под ограничениями понимаются соотношения типа A1>=B1, A2=B2, A3>0.
По крайней мере, одна из ячеек в соотношении, определяющем ограничение, должна зависеть от переменных задачи, в противном случае это ограничение не может влиять на процесс решения. Часто ограничения записываются сразу для групп ячеек, например:
A1:A10<=B1:B10 или A1:E1>=0.
Правильная формулировка ограничений является наиболее ответственной частью при формировании модели для поиска решения.
В одних случаях ограничения просты и очевидны, например ограничения на количество сырья. Другие ограничения менее очевидны и могут быть указаны неверно или , хуже того, оказаться пропущенными.
Решение уравнений.
Часто при решении практических задач возникают ситуации, когда необходимо достичь какой-то конкретной цели. Например, необходимо, чтобы себестоимость продукции составляло 20 у. е.
Специфика таких задач состоит в том, что в вашем распоряжении есть математическая модель исследуемого процесса, например закон ценообразования, но вы не знаете, при каком значении входящего в нее параметра можно достичь поставленной цели.
Решение таких задач можно искать методом перебора, однако на это уходит много времени (в лучшем случае).
Можно предложить другие способы решения. В Excel они реализованы как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.
Эта процедуру используют для поиска такого значения ячейки, при котором значение другой ячейки, вычисляемая по формуле, заранее задано. В формуле должна быть ссылка на ячейку, значение которой ищут. Ограничения на искомое значение ячейки не налагают.
Познакомимся с этой процедурой на примере составления штатного расписания.
Задача 1. Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 у. е. Необходимо определить, какими должны быть оклады сотрудников больницы.
Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальное оклады будем вычислять, исходя из него: во сколько-то раз или на сколько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: Ai*C+Bi, где С- оклад санитарки; Ai и Bi-коэффициенты, которые для каждой должности определяются следующим образом:
-медсестра получает в 1,5 раза больше санитарки (А2=1,5; В2=0);
-врач в 3раза больше санитарки (А3=3;В3=0);
-заведующий отделением –на 30у.е. больше, чем врач (А4=3;В4=30);
-заведующий аптекой- в 2 раза больше санитарки (А5=2;В5=0);
-заведующий хозяйством – на 40 у. е. больше медсестры (А6=1,5; В6=40);
-главный врач — в 4 раза больше санитарки (А7=4; В7=0);
-заведующий больницей — на 20 у.е больше главного врача (А8=4;В8=20).
Зная количество человек на каждой должности, нашу модель можно записать как уравнение:
N1*A1*C+N2(A2*C+B2)+…+N8*(A8*C+B8)=10000, где N1-число санитарок, N2-число медсестер и т. д.
В этом уравнений нам известны А1…А8, В1…В8 и N1…N8, а С неизвестно.
Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С.
Решим его.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствии с образцом в таблице (файл hospital.xls) cм Приложения
В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D2 формула расчета имеет вид =B2*$G$2+C2.Затем заполните вниз.
В столбце F вычислите заработную плату всех работающих на данной должности. Например, для ячейки F2 формула расчета имеет вид =D2*Е2. Затем заполните вниз.
В ячейке F10 вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже: (файл hospital 1.xls) cм Приложения
Как видите, взяв оклад санитарки за 150, мы превысили месячный фонд зарплаты. Определите оклад санитарки так, чтобы расчетный фонд был равен заданному. Для этого:
-активизируйте команду Подбор параметра из меню Сервис;
-в поле «Установить в ячейке» появившегося окна введите ссылку на ячейку F10, содержащую формулу;
-в поле «Значение» наберите искомый результат 10000.
В поле «Изменяя значение ячейки» введите ссылку на изменяемую ячейку G2 и щелкните кнопкой ОК. Таблица будет выглядеть следующим образом: (Таблица сохранена в каталоге Приложения под именем hospital2.xls.)
Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако благодаря этому простому примеру стало очевидно, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, — это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решить любые уравнения с одной переменной.
3.Задачи оптимизации
Иногда интересует не конкретный результат, а минимально или максимально возможный. Например, как минимизировать затраты на содержание персонала или максимизировать прибыли от реализации продукции?
Такие задачи в Excel также решаются с помощью Поиска решения.
Если математическая модель исследуемого процесса и ограничения на значения ее параметров линейны, то задача достижения цели является задачей линейного программирования.
Познакомимся с решением этих задач на следующем примере.
Задача 2. Составление штатного расписания.
Усложним рассмотренную ранее задачу. Пусть известно, что для нормальной работы больницы необходимо 5-7 санитарок, 8-10 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты должен быть минимален, Необходимо определить, какими должны быть оклады сотрудников больницы, при условии, что оклад санитарки не должен быть меньше прожиточного минимума — 80у.е.
В качестве модели решения этой задачи возьмем, как и раньше, линейную. Запишем ее так:
N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8)=Минимум.
В этом уравнений нам не известно число санитарок (N1), медсестер (N2), врачей (N3) и оклад санитарки (C).
Используя Поиск решения, найдем их.
Откройте созданный в предыдущей задаче (файл hospital 1.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения.
В окне установить целевую ячейку укажите ячейку F10, содержащую модель.
Поскольку необходимо минимизировать общий месячный фонд зарплаты, то активизируйте радиокнопку Минимальному значению.
Используя кнопку Добавить, опишите ограничения задачи.
$E$2<=7
$E$2>=5
$E$3<=10
$E$3>=8
$G$2>=80
Щелкните кнопкой ОК, затем — Выполнить.
Решение приведено ниже: (файл hospital3.xls) см Приложения
Оно тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы.
Задача 3. План выгодного производства
Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у. е., «В»-10 у. е., «С»-16 у.е.
Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализаций была максимальной.
Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже.
|
Сырье |
Нормы расхода |
Запас |
||
|
А |
B |
C |
||
|
Какао |
18 |
15 |
12 |
360 |
|
сахар |
6 |
4 |
8 |
192 |
|
наполнитель |
5 |
3 |
3 |
180 |
|
прибыль |
9 |
10 |
16 |
Решение.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствии с данными задачи (таблица файл konfetki.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
$A$10<=360
$B$10<=192
$B$3>=0
$B$4>=0
$B$5>=0
$C$10<=180.
Не забудьте указать, что изменяются ячейки $B$3:$B$5 и в Параметрах на Линейность модели.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано в таблице (файл konfetki 1.xls) см. Приложения
Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет «В» и 20 кг конфет «С». Конфеты «А» производить не стоит. Полученная вами прибыль составит 400 у. е.
Задача 4. Ваше предприятие выпускает изделия 1, изделия 2, изделия 3, используя общий склад комплектующих. Каждое изделие состоит из деталей, имеющихся на складе. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Прибыль, получаемая от каждого изделия, равна соответственно 47,32; 31,55; 22,08. Число деталей, идущих на каждое изделие, указано в таблице.
|
Наличие на складе |
Изделие1 |
Изделие 2 |
Изделие 3 |
|
|
Деталь 1 |
450 |
1 |
1 |
0 |
|
Деталь 2 |
250 |
1 |
0 |
0 |
|
Деталь 3 |
800 |
2 |
2 |
1 |
|
Деталь 4 |
450 |
1 |
1 |
0 |
|
Деталь 5 |
600 |
2 |
1 |
1 |
Решение.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствий с образцом: (файл detali.xls) см Приложения
В ячейках D4:F8 указывается, из какого числа деталей состоит каждое изделие.
В ячейках D2:F2 указываем примером количество изделий, которые собирается выпускать.
В ячейках В4:В8 указывается число деталей на складе.
В ячейках С4:С8 подсчитываем число деталей, взятых со склада для изготовления изделий.
В ячейках D11:G11 подсчитываем прибыль, полученную от изготовления каждого изделия, и общую прибыль.
В меню Сервис активизируйте команду Поиск решения и опешите его ограничения, как указано ниже:
$B$4:$B$8>=$C$4:$C$8
$D$2:$F$2>=0.
Самостоятельно укажите изменяемые ячейки.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано в таблице (файл detali1.xls) cм. Приложения
Задача 5. Найти оптимальный объём перевозок товаров с 3 заводов на 5 региональных складов. То есть минимизировать затраты на перевозку грузов от заводов – производителей на торговые склады.
Производительность каждого завода и затраты на перевозку от завода на каждый склад приведены в таблице:
|
Заводы |
Поставки |
затраты |
||||
|
Склад 1 |
Склад 2 |
Склад3 |
Склад4 |
Склад5 |
||
|
Завод1 |
310 |
10 |
8 |
6 |
5 |
4 |
|
Завод2 |
260 |
6 |
5 |
4 |
3 |
6 |
|
6Завод3 |
280 |
3 |
4 |
5 |
5 |
9 |
Решение
Технология работы:
-Запустите табличный процессор Excel.
Заполните таблицу в соответствии с образцом: (файл sklad.xls) см Приложения
Допускаем, что от каждого завода на каждый склад перевозиться единица продукций. Ячейки $C$6:$G$6.
В меню Сервис активизируйте команду Поиск решения и опешите его ограничения, как указано ниже:
$B$2:$B$4>=$B$10:$B$12 Количество перевезенных грузов не может превышать производственных возможностей заводов.
$C$6:$G$6>=$C$8:$G$8 Количество доставляемых грузов не должно быть меньше потребностей складов. То есть производство должно быть не меньше потребностей.
$C$2:$G$4>=0 Число перевозок не может быть отрицательным.
Целевая ячейка $B$14. Изменяемые ячейки $C$2:$G$4.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл sklad1.xls) см Приложения
Обратите внимание, что с первого завода вывезена не вся изготовленная продукция, а склады заполнены полностью. Измените потребности складов, затраты на перевозку от заводов к складу, и вы получите другое решение.
Задача 6. Парк отдыха обслуживается семью группами сотрудников. (Группы обозначены А, Б, В, Г, Д, Е, Ж..) Каждая группа имеет разные выходные дни. Выходных дней для каждой группы должно быть не менее двух, выходные следуют подряд. Один сотрудник входит только в одну группу. Известна потребность в сотрудниках в каждый из дней. Все сотрудники имеют одинаковый размер недельной оплаты, который не зависит от графика работы. Необходимо подобрать такую численность сотрудников в каждой группе, чтобы добиться минимизации затрат на оплату труда при выполнении требования по числу сотрудников на каждый день. Дневная зарплата сотрудников 40 у. е.
Решение
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствии с образцом (файл sоtrudniki.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
$C$2:$C$8>=0 Количество сотрудников в группе не может быть отрицательным.
$C$2:$C$8= целое. Число сотрудников должно быть целым.
$D$10:$J$10>=$D$12:$J$12. Число ежедневно занятых сотрудников не должно быть меньше ежедневной потребности.
Целевая ячейка $C$15. Изменяемые ячейки $C$2:$C$8.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл sоtrudniki1.xls) см Приложения
Вот тут-то и начинается самое интересное!
Важной особенностью этой задачи является наличие нескольких оптимальных решений, каждое из которых обеспечивает достижение целевой функций при выполнений всех ограничений.
Вызовите диалоговое окно Поиск решения и вновь выполните расчет. Вы получите новое оптимальное решение. Но общее число сотрудников в любом из решении равно 25. Таким образом, можно найти все оптимальные решения и выбрать наиболее подходящее с точки зрения дополнительных критериев.
Задача7. В нескольких пунктах (пункты отправки) скопились транспортные средства (ТС). Эти ТС необходимо перегнать в другие пункты (пункты приемки). Необходимо составить такой план перегона, чтобы общая стоимость перегона была минимальной.
В этой задаче мы имеем следующие значимые факторы:
-число ТС, имеющихся на каждом из трех пунктов отправки:
|
Пункты |
Скопилось ТС |
|
А1 |
120 |
|
А2 |
110 |
|
А3 |
130 |
-необходимые количества ТС для каждого из пяти пунктов приема:
|
Пункты приема |
В1 |
В2 |
В3 |
В4 |
В5 |
|
Требуется ТС |
80 |
60 |
70 |
100 |
50 |
-стоимость перегона одного ТС по каждому из пятнадцати маршрутов:
|
Пункты отправки |
В1 |
В2 |
В3 |
В4 |
В5 |
|
А1 |
2 |
4 |
1 |
6 |
7 |
|
А2 |
3 |
10 |
5 |
4 |
2 |
|
А3 |
8 |
9 |
8 |
3 |
4 |
Решение.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствий с образцом: (файл transport.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
$B$6:$F$6=$B$11:$F$11 Исходные данные – требуемое число ТС по каждому маршруту и число принятых ТС должно быть одинаковым.
$B$8:$F$10>=0 и $B$8:$F$10=целое. Изменяемые данные должны быть целыми и положительными.
$G#3:$G$5=$G$8:$G$10 Исходные данные – количество ТС, скопившихся в каждом из пунктов отравления и отправляемых из этого пункта.
Целевая ячейка $G$16. Изменяемые ячейки $B$8:$F$10.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл transport1.xls) см Приложения
В заключение отметим, что при некоторых исходных данных задача может иметь несколько оптимальных решений.
Задача 8. Для некоторого технологического процесса требуется использование угля с определенным содержанием фосфора и пепла. Доступны три сорта угля – А, В, С. Как их следует смешать, чтобы удовлетворить ограничения на примеси и минимизировать цену? Характеристики каждого угля приведены в таблице:
|
Сорт угля |
Содержание примеси фосфора, % |
Содержание примеси пепла, % |
Цена |
|
А |
0,06 |
2,00 |
30,00 |
|
В |
0,04 |
4,00 |
30,00 |
|
С |
0,02 |
3,00 |
45,00 |
Смесь угля должна иметь следующие характеристики:
|
Содержание примеси фосфора в смеси не более, % |
0,03 |
|
Содержание примеси пепла в смеси не более, % |
3,25 |
Технология работы:
Запустите табличный процессор Excel.
Заполните таблицу в соответствии с образцом: (файл ugol.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
Целевая ячейка $E$11. Изменяемые ячейки: $B$8:$B$10.
Ограничения:
$B$11=1 Сумма долей угля от разных поставщиков равна единице.
$C$11<=$E$1 Суммарные доли примесей фосфора не должны быть больше предельно допустимых.
$D$11<=$E2 Суммарные доли примесей пепла не должны быть больше предельно допустимых.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл ugol1.xls) см Приложения
Попробуйте выяснить, несколько дешевым должен стать уголь сорта «А», чтобы стало целесообразным его покупать.
Задача 9. Задача о рюкзаке.
Имеется 4 предмета, каждый из которых характеризуется весом и ценой. Нужно выбрать из них такие и столько, чтобы их общий вес не превышал 83, а суммарная цена была максимальной.
Решение.
Введите исходные данные и формулы в электронную таблицу, как указано ниже (в режиме просмотра формул): (файл rukzak.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
Целевая ячейка $G$7. Находим максимальное значение.
Изменяемые ячейки: $E$3:$E$6.
Ограничения:
$E$3:$E$6>=0 Количество предметов не может быть отрицательным.
$E$3:$E$6= целое Предметы не разделяются.
$F$7<=B$1 общий вес не должен превышать предельно допустимый.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл rukzak1.xls) см Приложения
4. Прогнозирование
Иногда нам хочется знать, «что будет», заранее. Это облегчает принятие предстоящих решений в свою пользу. Как принято говорить, мы хотим «подстелить соломку».
В науке предвидения называют прогнозированием. Основой прогнозирования являются наблюдения. Точнее, не сами наблюдения, а числовые значения неких состояний наблюдаемого явления. Например, курс ценных бумаг. Фиксируя значения курса во времени, мы получим табличное описание процесса изменения курса. Понятно, что если описать аналитический этот процесс, то есть поставить ему в соответствие некую функциональную зависимость:
ПРОГНОЗ=f(x), где х – некий момент времени, то ПРОГНОЗ будет не чем иным, как значением f(x) в некоторой наперед заданный момент времени х.
Аппроксимация позволяет описать наблюдаемые результаты аналитической функцией.
Продемонстрируем возможность прогнозирования на примере определения зависимости высоты от времени свободного падения тела.
Заполните данными рабочий лист электронной таблицы, как показано ниже:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
|
1 |
Время |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
Высота |
5.1 |
19.4 |
45.2 |
78.4 |
122.8 |
176.3 |
238.6 |
312.9 |
396.9 |
499.6 |
Постройте диаграмму зависимости высоты от времени свободного падения.
Аппроксимируйте полученную кривую с помощью степенной зависимости. Для этого:
-выделите данные диаграммы, установив курсор на графике и щелкнув правой кнопкой мыши;
-выберите из меню команду Формат линий тренда. На экране появится окно выбора линий тренда.
Сделайте настройку линий тренда:
-выберите на вкладе «Тип» степенную аппроксимацию;
-выберите на вкладе «Параметры» «Показать уравнение на диаграмме»;
-щелкните кнопкой ОК.
Результат аппроксимации показан на рисунке (файл prognoz.xls) см Приложения
Как видно, получена следующая аппроксимирующая функция: y=5,0118x 1,9895
Если бы мы не знали из школьного курса физики, что точная зависимость y=gx2/2, то по полученной с помощью Excel зависимости можно было бы предсказать, например, что за время х=20с тело пролетит 1962 м.
Это же можно проверить и с помощью Excel, выбрав на вкладе «Параметры» «Прогноз вперед на … периодов».
Таким образом, как показывает рассмотренный пример, Excel позволяет не только определить аналитические выражение зависимости таблично представляемых данных, но и предсказать тенденцию их изменения.
Заключение.
Актуальность выбранной темы:
Данная тема актуальна потому, что табличные редакторы на сегодняшний день — одни из самых распространенных программных продуктов, используемых во всем мире. Они без специальных навыков позволяют создавать достаточно сложные приложения, которые удовлетворяют до 90% запросов средних пользователей.
Я выбрал эту тему из-за того, что мне нравится использовать сложные формулы в Excel и решать экономические задачи, не прилагая больших усилий и не требуя обширных знаний в области экономики.
Надеюсь, что данная работа заинтересует, поможет разобраться в решении достаточно сложных задач. А главное — даст возможность убедиться, что Excel – одна из самых интересных и полезных программ, используемых пользователями разного уровня!
Список литературы
1. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов.-М.: Высш. шк., 1986.
2. Microsoft Excel. Руководство пользователя. — Корпорация Microsoft, 1993.
3. Гусева О.Л., Миронова Н. Н. Excel для Windows. Практические работы //Информатика и образование. 1996 №3.
4. Электронные учебники по Excel.