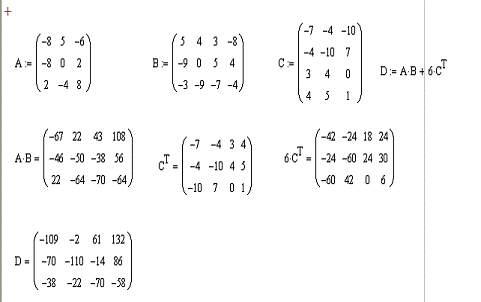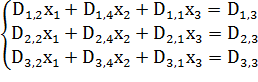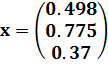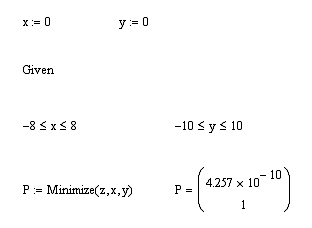Содержание
- Использование табличного процессора Excel для реализации численных методов в инженерных и экономических расчетах
- С. П. Никитенкова, н. Я. Николаев
- Научный редактор н.С. Петрухин
- Введение
- Использование программы MS Excel в решении инженерных задач
- информатика.docx
- Обработка эксперимента по определению приведенного модуля объемной упругости жидкости
- Постановка задачи:
- Последовательность выполнения
Использование табличного процессора Excel для реализации численных методов в инженерных и экономических расчетах
по курсу «Информатика»
для студентов всех форм обучения
Нижний Новгород 2000
Составители: В. Ф. Билюба, В. Н. Ершов, С. Н. Митяков, О. И. Митякова,
С. П. Никитенкова, н. Я. Николаев
Использование табличного процессора Excel для реализации численных методов в инженерных и экономических расчетах: Метод. разработка по курсу «Информатика» для студентов всех форм обучения / НГТУ;
Сост.: В. Ф. Билюба, В. Н. Ершов, С. Н. Митяков, О. И. Митякова,
С. П. Никитенкова, Н. Я. Николаев. Нижний Новгород, 2000. 37 с.
Изложены элементы численных методов в инженерных и экономических расчетах. Приведены примеры их реализации с использованием табличного процессора Microsoft Excel.
Научный редактор н.С. Петрухин
Редактор Е. В. Комарова
Подп. 22.06.2000. Формат 60х84 1 /16. Бумага газетная. Печать офсетная.
Печ. л. 2,3. Уч. -изд. л. 2,1. Тираж 300 экз. Заказ 410.
Нижегородский государственный технический университет.
Типография НГТУ. 603600, Н. Новгород, ул. Минина, 24.
технический университет, 2000
Введение
При решении многочисленных инженерных и экономических задач обычно реальное явление заменяется математической моделью. Модель является упрощенным представлением реальности и обычно содержит некоторое количество уравнений. Главной задачей моделирования является максимальное приближение к реальности при достаточной простоте модели. В ряде случаев удается найти аналитическое решение задачи. Однако в большинстве своем приходится использовать численные методы. Эти методы предполагают применение ЭВМ и сводятся к некоторым действиям над числами. При этом в большинстве случаев решение является приближенным.
Существуют различные подходы к реализации численных методов. Традиционный подход предполагает построение алгоритма метода с последующим программированием на языке высокого уровня. В последнее время широко используются специализированные программные продукты — математические пакеты типа MathCad, которые существенно упрощают процесс составления алгоритма и обладают встроенными библиотеками и графическими возможностями. В данной работе описан еще один подход, позволяющий в ряде случаев существенно ускорить процесс решения задачи. Он основан на использовании табличного процессора Excel, широко распространенного среди пользователей. Вместе с тем, применение данного программного продукта для реализации численных методов до сих пор не нашло соответствующего отражения в литературе.
Методическая разработка содержит краткое описание некоторых численных методов, примеры инженерных и экономических задач и технологию их решения с использованием пакета Excel. Предполагается наличие у студентов основных навыков работы с электронными таблицами типа Excel.
Источник
Использование программы MS Excel в решении инженерных задач
Автор работы: Пользователь скрыл имя, 19 Июня 2012 в 22:02, курсовая работа
Описание
Программы цикла Microsoft Office давно уже прочно вошли в различные области техники, анализа, быта и сферы услуг. Они используются в различных отчетах, подсчетах, вычислениях, базах данных, презентациях и во многом другом.
Содержание
Введение……………………………………………………………….3
ОБРАБОТКА ЭКСПЕРИМЕНТА ПО ОПРЕДЕЛЕНИЮ
ПРИВЕДЕННОГО МОДУЛЯ ОБЪЕМНОЙ УПРУГОСТИ ЖИДКОСТИ……. 5
ОБРАБОТКА ДАННЫХ ЭКСТРЕМАЛЬНЫХ ЭКСПЕРИМЕНТОВ
НА ПРИМЕРЕ ИССЛЕДОВАНИЯ ОПЕРАЦИИ ВЫТЯЖКИ
Работа состоит из 1 файл
информатика.docx
НИМБ, Дмитриев И.С.
Нижегородский институт менеджмента и бизнеса
Реферат на тему:
«Использование программы MS Excel в решении инженерных задач»
Выполнил студент Дмитриев И.С.
г. Нижний Новгород,2012
ПРИВЕДЕННОГО МОДУЛЯ ОБЪЕМНОЙ УПРУГОСТИ ЖИДКОСТИ……. 5
- ОБРАБОТКА ДАННЫХ ЭКСТРЕМАЛЬНЫХ ЭКСПЕРИМЕНТОВ
НА ПРИМЕРЕ ИССЛЕДОВАНИЯ ОПЕРАЦИИ ВЫТЯЖКИ
Программы цикла Microsoft Office давно уже прочно вошли в различные области техники, анализа, быта и сферы услуг. Они используются в различных отчетах, подсчетах, вычислениях, базах данных, презентациях и во многом другом. Остановимся подробнее на одной программе из цикла Microsoft Office, а именно Microsoft Exсel.
Табличный процессор Excel является наиболее популярным на сегодняшний день табличный редактор. Он позволяет легко оперировать с цифровыми данными, обладает удобным интерфейсом — это как компьютер «ведет диалог» с пользователем, позволяет юзеру посредством различных инструментов проводить построение различных графиков, множества диаграмм, которые способствуют более наглядному способу представления информации и усвоения материала.
Microsoft Excel — это много функциональная программа, позволяющая производить различные операции с большими объемами информации, представленных в виде текстовой информации, чисел и др.
Табличный процессор обеспечивает работу с масштабными числовыми таблицами.
Табличный процессор — программное средство для проектирования электронных таблиц, поэтому они дают возможность не только создавать разнообразные таблицы, но и автоматически обрабатывать табличные данные с помощью языка формул.
Сталкиваясь с необходимостью обработки и анализа большого объема данных, будь то описания, названия, цифры, где нужны несложные, циклически повторяемые операции предпочтительно задействать Excel. С помощью данной программы возможно не просто выполнять математические действия, но и структурировать данные, размещая их в отдельные строки, столбцы и ячейки таблиц Microsoft Excel. Информация в форме электронных таблиц вполне предназначена для анализа.
Обработка эксперимента по определению приведенного модуля объемной упругости жидкости
Постановка задачи:
Создать электронную таблицу для обработки данных эксперимента по определению приведенного модуля объемной упругости жидкости.
Последовательность выполнения опыта:
- Аккумулятор винтового пресса-молота заряжается до начального давления 25 МПА.
- Открывается вентиль, через который жидкость (минеральное масло) начинает вытекать в мерный объем (мензурку)
- Фиксируется объем вытекшего масла через определенные промежутки текущего давления в аккумуляторе.
- Опыт повторяется 3 раза
Модуль объемной упругости жидкости определяли путем обработки результатов эксперимента по следующему алгоритму:
- Определяется объем вытекшего масла на каждом интервале замеров давления:
- i=1,2,3 — число точек фиксации объема вытекшего масла pi=20,15,10,5,4,3,2,1,0 [МПа] — давления, при которых фиксируется объем масла Vi — объем вытекшего масла, соответствующий i-му давлению в аккумуляторе DVi=Vi+1-Vi, (1) при i=18, V9=0
- Вычисления по п1 выполняют для каждого из трех опытов
- Вычисляют среднее значение изменения объема на каждом интервале:
- Vсрi= (V1, i+V2, i+V3, i) /3, (2) где индексы 1, i 2, i 3, i соответствуют номеру опыта и номеру интервала
- Вычисляют среднее значение объема масла в точках фиксации давления по результатам трех опытов:
- Vсрi= Vсрi+1+Vi ( 3) при i=8¼1, Vср9=0
- Строится график P=f (Vср) и визуально определяют точку n перехода от нелинейного начального к линейному конечному участку графика
- Результаты соответствующие точкам i=1¼n аппроксимируют прямой p=b0+b1*Vср (4)
- Определяют приведенный модуль объемной упругости жидкости по формуле:
- k=V0* dp/dVср (5) где V0=1,1577*10 4 см 3 — объем аккумулятора dp/dVср=tana= b1, a — угол наклона прямой, аппроксимирующей линейный участок зависимости P=f (Vср)
Последовательность выполнения
- Запустить EXCEL
- Создать таблицу с исходными данными эксперимента и поясняющими надписями в соответствие с прилагаемой ниже таблицей. Обратить внимание, что текст, целиком не помещающийся в ячейку вводится в ячейку, номер которой соответствует началу текста. Например, весь текст «Экспериментальное определение модуля объемной упругости» вводится в ячейку А1
При заполнении, там где это целесообразно, пользуйтесь методами автозаполнения и копирования, изученными на предыдущем занятии
Символы DV в тексте пояснений в таблице заменяют символы в V формулах
Экспериментальное определение модуля объемной упругости
Данные для построение графика результатов эксперимента
Построение линейной регрессии
Приведенный модуль объемной упругости
- Занести в ячейку С7 формулу (1), которая будет иметь вид =D4-C4 и распространить ее на диапазон C7: J9.
- Занести в ячейку С10 формулу для определения среднего значения изменения объема Vсрi Для этого можно воспользоваться встроенной функцией СРЗНАЧ. Рассмотрим порядок ввода формул с использованием встроенных функций на этом примере:
- установить курсор в ячейку C10
- нажать на кнопку (Мастер функции или Вставить функцию) на стандартной панели инструментов
- в открывшемся окне выбрать Категория: Математические, Функция: СРЗНАЧ и щелкните по кнопке ОК (для Excel97) или Шаг> (для Excel5.0,7.0)
- в открывшемся окне диалога в пункте Число1 вместо предложенного мастером функций диапазона занесите диапазон ячеек, для которых вы вычисляете среднее значение C7: C9 и щелкните по экранной кнопке OK (Закончить) Ввод диапазона можно осуществлять как вручную (обратите внимание на то, что клавиатура должна находиться в латинском регистре), так и мышью — что более предпочтительно.
- Для ввода диапазона с помощью мыши необходимо просто выделить мышью нужный вам диапазон в таблице (если нужный диапазон закрыт окном диалога, то окно можно передвинуть в другое место экрана методом Drag and Drop)
- Распространить формулу в ячейке С10 на диапазон
- Для того, чтобы увидеть точное значение вычисленных величин (если Excel округлил их до целых), выделите диапазон С10: J10 и несколько раз нажмите кнопку (Увеличить разрядность) на панели инструментов Форматирование.
- В ячейку J12 внести формулу (3), которая будет иметь вид=K12+J10 и распространить ее на диапазон J12: C12. Если это необходимо, то увеличьте разрядность отображения величин.
- В ячейки C14 и C15 занесите формулы для определения максимальной и минимальной погрешности вычисления объема, которые будут иметь вид:таблица
- для C14: =МАКС (С7: C9) — C10 для C15: =C10-МИН (C7: C9) Функции МИН и МАКС находятся в категории Статистические мастера функций.
- Распространите формулы из диапазона C13: C14 на диапазон C13: K14
- Построить график зависимости P=f (Vср):
- выделите диапазон ячеек B12: K13, на основании которого вы будете строить диаграмму.
- щелкните по кнопке Мастер диаграмм стандартной панели инструментов (в зависимости от версии Excel она имеет различный внешний вид, поэтому найдите ее сами с помощью всплывающих подсказок) либо воспользуйтесь командой меню Вставка-Диаграмма.
- следуйте указаниям Мастера диаграмм в каждом диалоговом окне, возникающим последовательно после нажатия экранных кнопок Далее> (или Шаг> для ранних версий). Ниже приведена последовательность действий для Excel97 (для ранних версий Excel последовательность и содержание окон несколько другое, но получаемый результат будет идентичен). Если Вас что-то не устраивает в построенной диаграмме, то в последующем ее можно изменить:
- Шаг1: Щелчком мыши выберите тип диаграммы Точечная, а вид — со значениями, соединенными сглаживающими линиями. Нажмите кнопку Далее.
- Шаг2: Если диапазон данных в окне ввода Диапазон указан верно, а вид диаграммы тот, который вы ожидаете, нажмите кнопку Далее. В противном случае в окне Диапазон введите нужный диапазон данных
- Шаг3: В окно Название диаграммы сотрите содержащиеся там данные; в окне Ось X введите: V, см3; в окне Ось Y введите: p, МПа. Нажмите кнопку Далее.
- Шаг4: В окне Поместить диаграмму на листе выберите пункт Имеющемся, рядом с которым выберите в открывающемся списке пункт Лист2. Нажмите кнопку Готово.
- Как правило, вид созданной диаграммы мастером диаграмм бывает неудовлетворительным, поэтому диаграмму следует отформатировать. Выполните форматирование диаграммы в соответствие со следующими указаниями:
- Щелкните мышью по области диаграммы. Область диаграммы выделится черной рамкой, по углам которой и в середине сторон имеются черные квадратики — размерные маркеры. Кроме того в меню Excel добавится пункт Диаграмма Для изменения размеров диаграммы необходимо буксировать размерные маркеры. Перед буксировкой необходимо навести указатель мыши на один из размерных маркеров. Указатель мыши при этом примет вид двунаправленной стрелки. После чего необходимо нажать левую клавишу мыши и перемещать (буксировать) маркер. Буксировка маркера, расположенного в середине стороны, позволяет изменять горизонтальные и вертикальные размеры диаграммы. Буксировка углового маркера позволяет изменять одновременно вертикальные и горизонтальные размеры.
- Для перемещения диаграммы необходимо навести указатель мыши на область диаграммы (указатель примет вид белой стрелки, направленной под углом влево-вверх) и отбуксировать ее на новое место
- Отбуксируйте диаграмму в левый верхний угол листа, а затем измените ее размеры так, чтобы она занимала примерно ¾ пространства листа.
- Диаграмма состоит из нескольких элементов. К ним, в частности, относятся:
- область диаграммы (весь чертеж)
- область построения диаграммы
- легенда
- ряды данных
- названия осей и т.п.
Для редактирования элемента его необходимо выделить. Это можно сделать нажатием стрелок перемещения курсора ↑ ↓ на клавиатуре, либо одиночным щелчком левой клавиши мыши по соответствующему элементу. При выделении в поле имени (крайнее левое поле в строке формул) появляется название элемента. Выделенный элемент отмечается размерными маркерами.
Редактирование выделенного элемент осуществляется через меню Формат, в котором появляется пункт для редактирования соответствующего элемента, либо нажатием клавиатурной комбинации Ctrl-1, которая позволяет произвести форматирование текущей ячейки, диапазона, элемента диаграммы или объекта.
Выделенный элемент можно перемещать, менять его размеры методом буксировки, а также удалять, нажав клавишу Del.
- Выделите диаграмму, щелкнув по области диаграммы
- Последовательно нажимая клавишу ↑ на клавиатуре обратите внимание на элементы диаграммы, присутствующие в построенной вами диаграмме.
- Удалите легенду
- Отбуксируйте название оси X (категорий) в правый нижний угол области диаграммы
- Измените размеры области построения диаграммы так, чтобы она занимала максимальный размер внутри области диаграммы. Выберите подходящий цвет заливки области построения (по нашему мнению для черно-белых принтеров наиболее целесообразно применять прозрачную заливку).
- Отобразите на диаграмме погрешности вычисления. Для этого выделите кривую (она имеет название Ряд «p, МПа»), нажмите клавиатурную комбинацию Ctrl-1. Затем в окне Формат ряда данных выберите вкладку X-погрешности, в который выберите вид показа — обе планки погрешностей, величина погрешностей — пользовательская, в графе «+» введите диапазон положительной погрешности, вычисленной Вами =Лист1! $C$14: $K$14 (это можно сделать и мышью, выделяя соответствующий диапазон в таблице), а в графе «-«=Лист1! $C$15: $K$15
- Добавьте (если их нет) линии сетки для значений по оси X. Для этого в меню Диаграмма выберите пункт Параметры диаграммы и на вкладке Линии сетки щелкните по пункту Ось X — основные линии, после чего нажмите кнопку OK
- Отформатируйте осьY так, чтобы график занимал всю область построения диаграммы. Для этого после выделения оси и перехода в окно редактирования одним из указанных выше способов (например с помощью клавиатурной комбинации Ctrl-1) выберите вкладку Шкала и в графе Максимальное значение поставьте максимальное значение давления в исходной таблице — 20. Посмотрите другие вкладки в окне форматирования оси. Возможно Вы захотите изменить и другие параметры и внешний вид элементов оси.
- Измените название оси категорий так, чтобы размерность объема была поставлена правильно: не см3, а см 3 . Для это выделите название оси, затем выделите цифру 3 в размерности, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта щелкните мышью по пункту Верхний индекс раздела Эффекты.
Источник
Министерство образования Российской
Федерации
Нижегородский
государственный технический университет
Кафедра «Прикладная математика»
Методическая
разработка
по
курсу «Информатика»
для
студентов всех форм обучения
Нижний
Новгород 2000
Составители: В. Ф. Билюба, В. Н. Ершов,
С. Н. Митяков, О. И. Митякова,
С. П. Никитенкова, н. Я. Николаев
УДК 651. 3. 06
Использование
табличного процессора Excel
для реализации численных методов в
инженерных и экономических расчетах:
Метод. разработка по курсу «Информатика»
для студентов всех форм обучения / НГТУ;
Сост.: В. Ф.
Билюба, В. Н. Ершов, С. Н. Митяков, О. И.
Митякова,
С.
П. Никитенкова, Н. Я. Николаев. Нижний
Новгород, 2000. 37 с.
Изложены элементы численных методов в
инженерных и экономических расчетах.
Приведены примеры их реализации с
использованием табличного процессора
Microsoft Excel.
Научный редактор н.С. Петрухин
Редактор
Е. В. Комарова
Подп.
22.06.2000. Формат 60х841/16.
Бумага газетная. Печать офсетная.
Печ.
л. 2,3. Уч. -изд. л. 2,1. Тираж 300 экз. Заказ
410.
_______________________________________________
Нижегородский
государственный технический университет.
Типография
НГТУ. 603600, Н. Новгород, ул. Минина, 24.
©
Нижегородский государственный
технический
университет,
2000
Введение
При
решении многочисленных инженерных и
экономических задач обычно реальное
явление заменяется математической
моделью. Модель является упрощенным
представлением реальности и обычно
содержит некоторое количество
уравнений. Главной задачей моделирования
является максимальное приближение
к реальности при достаточной простоте
модели. В ряде случаев удается найти
аналитическое решение задачи. Однако
в большинстве своем приходится
использовать численные методы. Эти
методы предполагают применение ЭВМ и
сводятся к некоторым действиям над
числами. При этом в большинстве случаев
решение является приближенным.
Существуют
различные подходы к реализации численных
методов. Традиционный подход
предполагает построение алгоритма
метода с последующим программированием
на языке высокого уровня. В последнее
время широко используются
специализированные программные продукты
— математические пакеты типа MathCad,
которые существенно упрощают процесс
составления алгоритма и обладают
встроенными библиотеками и графическими
возможностями. В данной работе описан
еще один подход, позволяющий в ряде
случаев существенно ускорить процесс
решения задачи. Он основан на использовании
табличного процессора Excel, широко
распространенного среди пользователей.
Вместе с тем, применение данного
программного продукта для реализации
численных методов до сих пор не нашло
соответствующего отражения в литературе.
Методическая
разработка содержит краткое описание
некоторых численных методов, примеры
инженерных и экономических задач и
технологию их решения с использованием
пакета Excel. Предполагается наличие у
студентов основных навыков работы с
электронными таблицами типа Excel.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение инженерных задач с помощью программ Excel и Mathcad
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РФ
БРЯНСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «
Информатика и программное обеспечение»
КУРСОВАЯ
РАБОТА
по курсу «Информатика»
Тема: «Решение инженерных задач с помощью
программ Excel и Mathcad»
Выполнил: Коротков Д.И.
Проверил: к.т.н. доц. Азарченков А.A.
БРЯНСК
2012
Оглавление
Введение
.
Задание №1
1.1 Условие задания
.2 Решение
2.
Задание №2
2.1 Условие задания
.2 Решение
3.
Задание №3
3.1 Условие задания
.2 Решение
4.
Задание №4
4.1 Условие задания
.2 Решение
5.
Задание №5
5.1 Условие задания
.2 Решение
Заключение
Список
использованной литературы
Введение
Мы все являемся свидетелями того, как компьютеры на глазах изменяют нашу
жизнь.
Автоматические и научно-технические расчеты являются важной сферой
применения персональных компьютеров. Часто они выполняются с помощью программ.—
универсальный математический пакет, предназначенный для выполнения инженерных и
научных расчетов. Основное преимущество пакета — естественный математический
язык, на котором формируются решаемые задачи. Объединение текстового редактора
с возможностью использования общепринятого математического языка позволяет
пользователю получить готовый итоговый документ. Пакет обладает широкими
графическими возможностями, расширяемыми от версии к версии. Практическое
применение пакета существенно повышает эффективность интеллектуального труда.
Если же говорить об EXCEL, которая является одной из наиболее известных
программ обработки электронных таблиц, то без преувеличения можно утверждать,
что ее возможности практически неисчерпаемы. Лично я считаю, что такие
программы на сегодняшний день представляют собой один из наиболее мощных и
гибких инструментов, созданных для компьютера.
Возможности EXCEL очень высоки. Обработка текста , управление базами
данных — программа настолько мощна, что во многих случаях превосходит
специализированные программы — редакторы или программы баз данных. Такое
многообразие функций может поначалу запутать , нежели заставить применять их на
практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что
границ возможностей EXCEL тяжело достичь.
1. Задание №1
.1 Условие задания
Дана нелинейная функция f(x) согласно варианту. Требуется:
. Решить нелинейное уравнение вида f(x)=0 с помощью программы
Excel. Для этого необходимо выполнить следующие действия.
· Провести табулирование функции f(x) на заданном интервале.
Шаг табуляции h=0.2. Оформить таблицу (рамки, названия столбцов и т.п.).
· Построить график функции f(x).
· По графику определить приближенные значения корней уравнения
f(x)=0 и точек экстремума функции. Этот этап называется «локализация корней и
экстремумов». На нем необходимо обязательно задавать начальное приближение того
значения аргумента, вблизи которого имеется корень или экстремум. В ходе
последующего использования имеющихся процедур осуществляется уточнение значения
аргумента (соответствующего нужному корню или экстремуму). Поэтому для каждого
корня или экстремума обязательно должно быть задано свое начальное приближение.
· С помощью процедуры «Подбор параметра» определить уточненные
значения корней уравнения f(x)=0. Точность реализации этого этапа можно
настроить, используя меню «Параметры». Результат записать с точностью 5 знаков
после запятой.
. С помощью надстройки «Поиск решения» Excel найти экстремумы
функции f(x). Выделить в таблице цветом точки корней и экстремумов или привести
в соответствующих строках подписи рядом с таблицей («Корень 1», «Корень 2»,
«Максимум 1», «Минимум 2» и т.п.). Результат записать с точностью 5 знаков
после запятой.
. Решить это же нелинейное уравнение с помощью программы Mathcad.
Для этого необходимо выполнить следующие действия.
· Построить график функции f(x).
· По графику определить начальные приближения корней уравнения
f(x).
· Для каждого приближения определить уточненные значения корней
уравнения. Для этих целей могут быть использованы соответствующие функции
Mathcad: «root», «find» и т.п. Результат записать с точностью 5 знаков после
запятой.
. С помощью символьных вычислений в Mathcad найти производную
функции f(x). Найти экстремумы функции f(x) путем решения уравнения f'(x)=0
аналогично пункту 3. Результат записать с точностью 5 знаков после запятой.
. Провести сравнение полученных результатов и сделать выводы об
эффективности Excel и Mathcad при решении задач нахождения корней нелинейного
уравнения и поиска экстремумов функции.
1.2 Решение
Дана
функция: на интервале [-5;10] c шагом 0.2. На
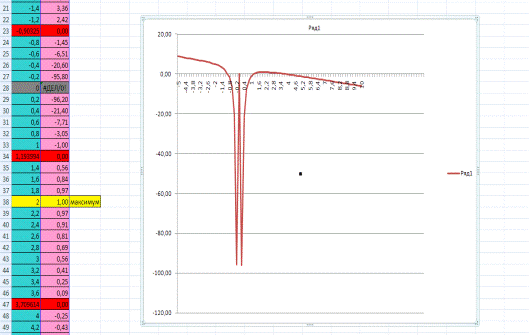
основе полученной таблицы табуляции строим график функции f(x)(рис. 1).
Рис.
1. Табуляция функции и построение графика в Excel
. На полученном графике определяем приближенные значения корней
уравнения. Данные корни будут находиться в точках пересечения графика функции с
осью абсцисс, а также их приближенные значения можно определить по таблице
табуляции в строках, где значения в столбце y меняют свой знак. Получаем
следующие приближенные значения корней уравнения:0.85,1.2,4.0.
. С помощью процедуры «Подбор параметра» определяем точное
значение корня для каждого приближенного значения. Получаем следующие значения
корней уравнения: x1=-0.903.x2=1.194,
x3=3.709.
3. Найдем
в Excel экстремумы функции f(x). По графику видно, что данная функция имеет
одну точку экстремума (максимума) в районе x=2. Для нахождения этого экстремума
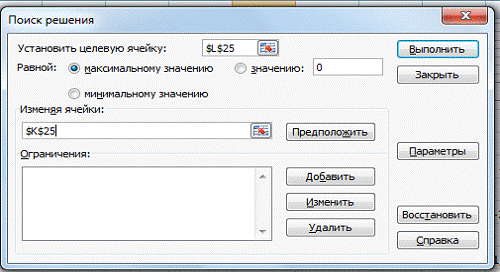
воспользуемся надстройкой «Поиск решения» и настроим её согласно рис.2. Для
функций такого типа (с разрывами) обязательно нужно добавлять ограничения
нижнего и верхнего значения аргумента, чтобы в решении не оказалось бесконечное
число, соответствующее точке разрыва(рис. 2).
Рис.
2. Настройка формы «Поиск решений» для точки максимума
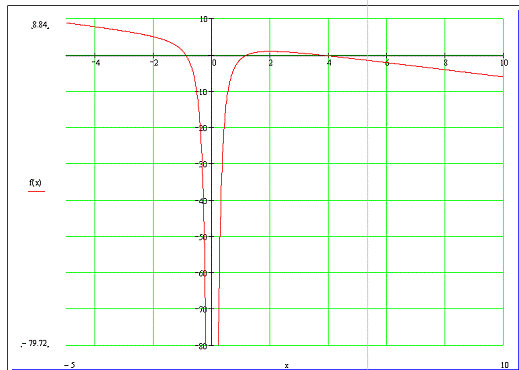
4. С
помощью программы Mathcad построим график функции (рис. 3). По графику определяем приближенные значения
корней уравнения:0.85,1.2,4.0.
Рис.
3. График функции f(x) построенный в Mathcad
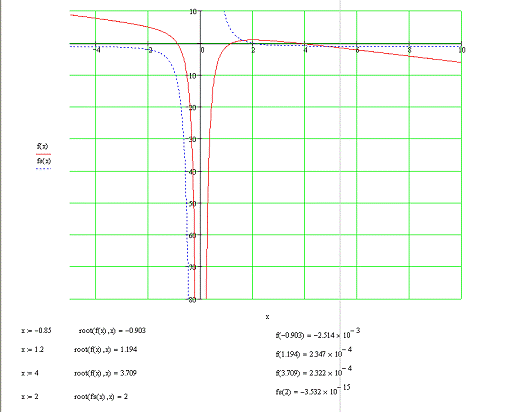
. С помощью функции root
находим точные значения корней уравнения:x1=-0.903,x2=1.194,x3=3.709
2. Используя символьные вычисления Mathcad, найдем производную
3. Построим
график производной функции f(x). По графику определяем приближенное значение корня .С помощью функции root также
находим точное значение корней уравнения(рис. 4).
Рис.
4. Нахождение корней уравнения и экстремумов функции с помощью Mathcad
2. Задание №2
нелинейный
уравнение экстремум двухмерный
2.1 Условие задания
Даны матрицы A, B и С. Вычислить матрицу D по формуле . Задание выполнить
в Excel и Mathcad.
.2 Решение
Даны
матрицы A, B, и С. Вычислить матрицу D по формуле.
Используя коэффициенты полученной матрицы D решить систему
уравнений(рис. 5).
Рис.
5. Вычисление матрицы D в Mathcad
1. С
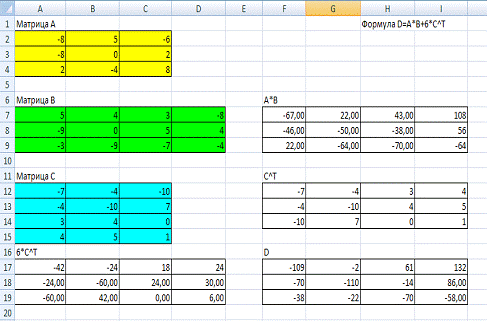
помощью Excel произведем расчеты матрицы D (рис. 6).
Рис.
6. Вычисление матрицы D в Excel
3.2 Решение
1. Решим
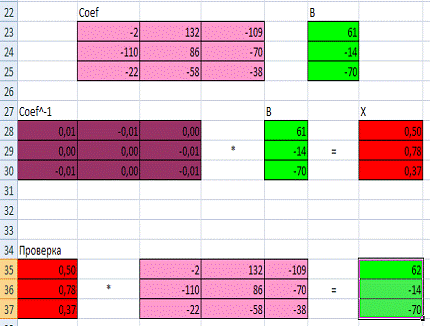
полученную систему уравнений в Excel с помощью обратной матрицы (рис. 7). В результате
получим вектор решения:
Рис.
7. Решение системы линейных уравнений с помощью Excel
Проведем
расчет матрицы D средствами Mathcad. Заполним матрицу коэффициентов
системы уравнений и найдем ее решение (рис. 
Рис.
8. Решение системы линейных уравнений с помощью Mathcad
4. Задание №4
.1 Условие задания
Дана таблично заданная функция — пары точек (xi,yi), для которых
необходимо сделать следующее:
С помощью программы Mathcad провести кусочно-линейную интерполяцию и
найти значения y.
Используя опцию “Добавить линию тренда” Excel, выполнить аппроксимацию
заданных точек, подобрав подходящие формы аппроксимирующих кривых по виду
графика.
4.2 Решение
Решим задачу с использованием Mathcad.
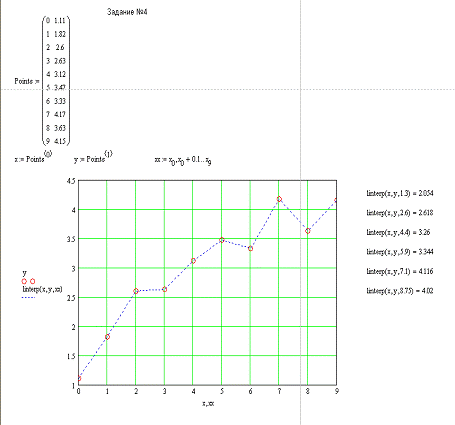
1. Проведем
кусочно-линейную интерполяцию для заданных точек (xi,yi) и определяем значение
функции для указанных значений аргумента (рис. 9):
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
y |
1.11 |
1.82 |
2.6 |
2.63 |
3.12 |
3.47 |
3.33 |
4.17 |
3.63 |
4.15 |
Рис.
9. Кусочно-линейная интерполяция в Mathcad
Рис.
10. Добавление на график аппроксимирующей линии(линии тренда)
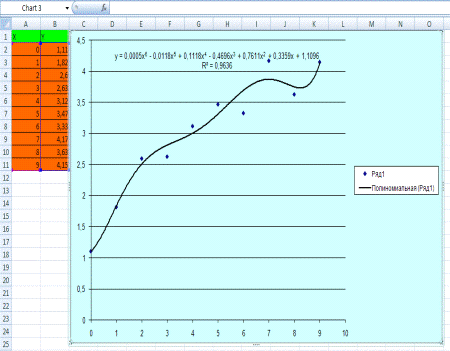
2. Проведем
аппроксимацию точек с помощью Excel. Для этого сначала заполним исходную
таблицу точек и отметим эти точки на координатной плоскости(рис. 10)(рис. 11).
Рис.
11. Наилучшая аппроксимирующая линия(линии тренда)
5. Задание №5
.1 Условие задания
Найти экстремум функции двух переменных в Excel и Mathcad. Построить
график двухмерной поверхности в Excel и Mathcad. Сравнить результаты и сделать
выводы.
.2 Решение
Рассмотрим функцию
1. Построим
график функции в Mathcad (рис. 12).
. По
графику определяем, что функция z имеет точку минимума.
. Воспользуемся
блоком решения Mathcad и функцией Minimize. За начальное приближение точки
минимума возьмем x=0 и y=0. В качестве ограничений укажем интервалы для x[-8;8]
и y[-10;10].
. Получили
решение x=4,257*10^-10; y=1-наименьшее значение в заданной области определения
(рис. 13).
Рис.
12. Построение поверхности в Mathcad
Рис.
13. Наименьшее значение в заданной области определения
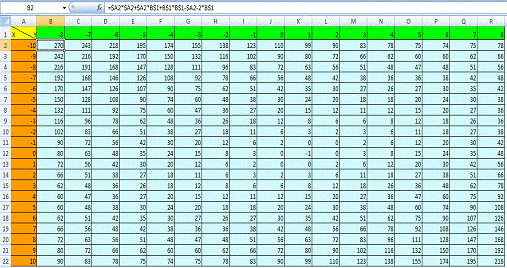
5. Теперь
выполним это же задания в Excel. Для этого сначала проведем табуляцию функции
на интервале по x [-8;8] и y[-10;10] (рис. 14).
Рис.
14. Табулирование функции 2-х переменных в Excel
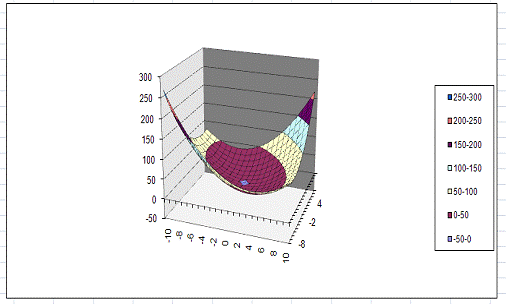
На
основе полученной таблицы строим поверхность (рис. 15).
Рис.
15. График функции двух переменных в Excel
Заключение
Данная курсовая работа позволила мне более близко познакомиться с
программами MathCAD и MS Excel. Мной были рассмотрены способы
решения инженерных задач с использованием данных программ.
Задачи исследования были максимально реализованы т.к. в курсовой работе
были описаны все функции, используемые в системе MathCAD и MS Excel, и рассмотрена работа некоторых из
них на конкретных примерах.
Список использованной литературы
1. Бидасюк Ю.М. Mathsoft MathCAD 11. Самоучитель. — СПб: Диалектика, 2004. — 224 с.
2. Бутенков
С.А. Методические указания к использованию системы MathCad в практических занятиях по курсу высшей математики. —
Таганрог : ТРТУ, 1995. — 450 с.
. Гмурман
В.Е. Теория вероятностей и математическая статистика. Учебное пособие для
ВУЗов. — М.: Высшая школа, 1972. — 368 с.
. Кудрявцев
В.М. MathCAD 8. — М.: ДМК, 2000. — 320 с.
. Плис
А.И. MathCAD 2000: Математический практикум для
экономистов/ А.И.Плис, Н.А.Сливина. — М.: Финансы и статистика, 2000. — 656 с.
. Шушкевич
Г.Ч. Введение в MathCAD 2000:
Учебное пособие / Г.Ч. Шушкевич, С.В. Шушкевич. — Гродно: ГрГУ, 2001. — 138 с.
7. MathCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95./Перевод с англ. — М.:
Информационно-издательский дом «Филин», 1996. — 712 с.
Пособие содержит четыре взаимосвязанных раздела: простейшие вычисления в таблицах, использование стандартных формул, построение графиков; работа с массивами данных, построение сводных таблиц данных, поиск решений, анализ «Что — если», решение оптимизационных задач; использование макрокоманд и основы программирования в VBA; разработка приложений с использованием визуальных компонентов, создание собственных интерфейсов. Рассмотрены основные режимы работы в MS Excel для решения специальных задач, возникающих в практической деятельности инженеров и научных работников. Теоретический материал иллюстрирован примерами решения задач различной сложности с подробными комментариями. Подробно изложены основы разработки приложений в среде VBA, программирование элементов интерфейса. Предназначено для студентов, обучающихся по техническим направлениям подготовки высшего образования.
Название: Методы MS Excel для решения инженерных задач
Автор: Бильфельд Н. В., Фелькер М. Н.
Издательство: Лань
Год: 2020
Страниц: 164
Формат: pdf, rtf
Язык: русский
Размер: 16,65 Мб
Скачать Бильфельд Н.В., Фелькер М.Н. Методы MS Excel для решения инженерных задач
НИМБ,
Дмитриев И.С.
Нижегородский
институт менеджмента и бизнеса
Реферат на тему:
«Использование
программы MS Excel в решении инженерных
задач»
Выполнил студент
Дмитриев И.С.
Проверил
…………………
г. Нижний Новгород,2012
Содержание
- Введение……………………………………………………………….3
- ОБРАБОТКА ЭКСПЕРИМЕНТА ПО ОПРЕДЕЛЕНИЮ
ПРИВЕДЕННОГО
МОДУЛЯ ОБЪЕМНОЙ УПРУГОСТИ ЖИДКОСТИ………..5
- ОБРАБОТКА ДАННЫХ ЭКСТРЕМАЛЬНЫХ ЭКСПЕРИМЕНТОВ
НА ПРИМЕРЕ
ИССЛЕДОВАНИЯ ОПЕРАЦИИ ВЫТЯЖКИ
ЛИСТОВЫХ ОБРАЗЦОВ……………………………………………….…………13
- Исследование операции обжима………………………………….21
- Заключение…………………………………………………………..25
- Список литературы………………………………………………….26
Введение
Программы
цикла Microsoft Office давно уже прочно вошли
в различные области техники, анализа,
быта и сферы услуг. Они используются в
различных отчетах, подсчетах, вычислениях,
базах данных, презентациях и во многом
другом. Остановимся подробнее на одной
программе из цикла Microsoft Office, а именно
Microsoft Exсel.
Табличный
процессор Excel является наиболее популярным
на сегодняшний день табличный редактор.
Он позволяет легко оперировать с цифровыми
данными, обладает удобным интерфейсом
— это как компьютер «ведет диалог»
с пользователем, позволяет юзеру посредством
различных инструментов проводить построение
различных графиков, множества диаграмм,
которые способствуют более наглядному
способу представления информации и
усвоения материала.
Microsoft Excel — это много функциональная программа,
позволяющая производить различные операции
с большими объемами информации, представленных
в виде текстовой информации, чисел и
др.
Табличный процессор
обеспечивает работу с масштабными числовыми
таблицами.
Табличный процессор — программное средство
для проектирования электронных таблиц,
поэтому они дают возможность не только
создавать разнообразные таблицы, но и
автоматически обрабатывать табличные
данные с помощью языка формул.
Сталкиваясь с
необходимостью обработки и анализа
большого объема данных, будь то описания,
названия, цифры, где нужны несложные,
циклически повторяемые операции предпочтительно
задействать Excel. С помощью данной программы
возможно не просто выполнять математические
действия, но и структурировать данные,
размещая их в отдельные строки, столбцы
и ячейки таблиц Microsoft Excel. Информация
в форме электронных таблиц вполне предназначена
для анализа.
Обработка эксперимента
по определению приведенного модуля объемной
упругости жидкости
Постановка задачи:
Создать электронную таблицу для обработки
данных эксперимента по определению приведенного
модуля объемной упругости жидкости.
Последовательность выполнения опыта:
- Аккумулятор винтового пресса-молота заряжается до начального давления 25 МПА.
- Открывается вентиль, через который жидкость (минеральное масло) начинает вытекать в мерный объем (мензурку)
- Фиксируется объем вытекшего масла через определенные промежутки текущего давления в аккумуляторе.
- Опыт повторяется 3 раза
Модуль объемной упругости жидкости
определяли путем обработки результатов
эксперимента по следующему алгоритму:
- Определяется объем вытекшего масла на каждом интервале замеров давления:
- i=1,2,3 — число точек фиксации объема вытекшего масла pi=20,15,10,5,4,3,2,1,0 [МПа] — давления, при которых фиксируется объем масла Vi — объем вытекшего масла, соответствующий i-му давлению в аккумуляторе DVi=Vi+1-Vi, (1) при i=18, V9=0
- Вычисления по п1 выполняют для каждого из трех опытов
- Вычисляют среднее значение изменения объема на каждом интервале:
- Vсрi= (V1, i+V2, i+V3, i) /3, (2) где индексы 1, i 2, i 3, i соответствуют номеру опыта и номеру интервала
- Вычисляют среднее значение объема масла в точках фиксации давления по результатам трех опытов:
- Vсрi= Vсрi+1+Vi
(
3) при i=8¼1, Vср9=0 - Строится график P=f (Vср) и визуально определяют точку n перехода от нелинейного начального к линейному конечному участку графика
- Результаты соответствующие точкам i=1¼n аппроксимируют прямой p=b0+b1*Vср (4)
- Определяют приведенный модуль объемной упругости жидкости по формуле:
- k=V0* dp/dVср (5) где V0=1,1577*104 см3 — объем аккумулятора dp/dVср=tana= b1, a — угол наклона прямой, аппроксимирующей линейный участок зависимости P=f (Vср)
Последовательность выполнения
- Запустить EXCEL
- Создать таблицу с исходными данными эксперимента и поясняющими надписями в соответствие с прилагаемой ниже таблицей. Обратить внимание, что текст, целиком не помещающийся в ячейку вводится в ячейку, номер которой соответствует началу текста. Например, весь текст «Экспериментальное определение модуля объемной упругости» вводится в ячейку А1
При заполнении, там где это целесообразно,
пользуйтесь методами автозаполнения
и копирования, изученными на предыдущем
занятии
Символы DV в тексте пояснений в таблице
заменяют символы в V формулах
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
|
1 |
Экспериментальное |
||||||||||
|
2 |
Величина |
№экс |
Экспериментальные |
||||||||
|
3 |
p, |
20 |
15 |
10 |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
4 |
DV, |
1 |
116 |
155 |
190 |
228 |
233 |
245 |
250 |
268 |
280 |
|
5 |
DV, |
2 |
130 |
164 |
202 |
235 |
243 |
251 |
260 |
272 |
290 |
|
6 |
DV, |
3 |
110 |
146 |
179 |
215 |
224 |
228 |
240 |
248 |
270 |
|
7 |
DV, |
1 |
0 |
||||||||
|
8 |
DV, |
2 |
0 |
||||||||
|
9 |
DV, |
3 |
0 |
||||||||
|
10 |
DVср, |
0 |
|||||||||
|
11 |
Данные |
||||||||||
|
12 |
Vср, |
0 |
|||||||||
|
13 |
p, |
20 |
15 |
10 |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
14 |
погрешность |
max |
|||||||||
|
15 |
min |
||||||||||
|
16 |
Построение |
||||||||||
|
17 |
коэффициенты |
m1 |
b |
||||||||
|
18 |
|||||||||||
|
19 |
Линейная |
||||||||||
|
20 |
p, |
||||||||||
|
21 |
Объем |
||||||||||
|
22 |
1,1577E4 |
V0, |
|||||||||
|
23 |
Приведенный |
||||||||||
|
24 |
МПа |
- Занести в ячейку С7 формулу (1), которая будет иметь вид =D4-C4 и распространить ее на диапазон C7: J9.
- Занести в ячейку С10 формулу для определения среднего значения изменения объема Vсрi Для этого можно воспользоваться встроенной функцией СРЗНАЧ. Рассмотрим порядок ввода формул с использованием встроенных функций на этом примере:
- установить курсор в ячейку C10
- нажать на кнопку
(Мастер функции или Вставить функцию) на стандартной панели инструментов - в открывшемся окне выбрать Категория: Математические, Функция: СРЗНАЧ и щелкните по кнопке ОК (для Excel97) или Шаг> (для Excel5.0,7.0)
- в открывшемся окне диалога в пункте Число1 вместо предложенного мастером функций диапазона занесите диапазон ячеек, для которых вы вычисляете среднее значение C7: C9 и щелкните по экранной кнопке OK (Закончить) Ввод диапазона можно осуществлять как вручную (обратите внимание на то, что клавиатура должна находиться в латинском регистре), так и мышью — что более предпочтительно.
- Для ввода диапазона с помощью мыши необходимо просто выделить мышью нужный вам диапазон в таблице (если нужный диапазон закрыт окном диалога, то окно можно передвинуть в другое место экрана методом Drag and Drop)
- Распространить формулу в ячейке С10 на диапазон
- Для того, чтобы увидеть точное значение вычисленных величин (если Excel округлил их до целых), выделите диапазон С10: J10 и несколько раз нажмите кнопку
(Увеличить разрядность) на панели инструментов Форматирование. - В ячейку J12 внести формулу (3), которая будет иметь вид=K12+J10 и распространить ее на диапазон J12: C12. Если это необходимо, то увеличьте разрядность отображения величин.
- В ячейки C14 и C15 занесите формулы для определения максимальной и минимальной погрешности вычисления объема, которые будут иметь вид:таблица
- для C14: =МАКС (С7: C9) — C10 для C15: =C10-МИН (C7: C9) Функции МИН и МАКС находятся в категории Статистические мастера функций.
- Распространите формулы из диапазона C13: C14 на диапазон C13: K14
- Построить график зависимости P=f (Vср):
- выделите диапазон ячеек B12: K13, на основании которого вы будете строить диаграмму.
- щелкните по кнопке Мастер диаграмм стандартной панели инструментов (в зависимости от версии Excel она имеет различный внешний вид, поэтому найдите ее сами с помощью всплывающих подсказок) либо воспользуйтесь командой меню Вставка-Диаграмма.
- следуйте указаниям Мастера диаграмм в каждом диалоговом окне, возникающим последовательно после нажатия экранных кнопок Далее> (или Шаг> для ранних версий). Ниже приведена последовательность действий для Excel97 (для ранних версий Excel последовательность и содержание окон несколько другое, но получаемый результат будет идентичен). Если Вас что-то не устраивает в построенной диаграмме, то в последующем ее можно изменить:
- Шаг1: Щелчком мыши выберите тип диаграммы Точечная, а вид — со значениями, соединенными сглаживающими линиями. Нажмите кнопку Далее.
- Шаг2: Если диапазон данных в окне ввода Диапазон указан верно, а вид диаграммы тот, который вы ожидаете, нажмите кнопку Далее. В противном случае в окне Диапазон введите нужный диапазон данных
- Шаг3: В окно Название диаграммы сотрите содержащиеся там данные; в окне Ось X введите: V, см3; в окне Ось Y введите: p, МПа. Нажмите кнопку Далее.
- Шаг4: В окне Поместить диаграмму на листе выберите пункт Имеющемся, рядом с которым выберите в открывающемся списке пункт Лист2. Нажмите кнопку Готово.
- Как правило, вид созданной диаграммы мастером диаграмм бывает неудовлетворительным, поэтому диаграмму следует отформатировать. Выполните форматирование диаграммы в соответствие со следующими указаниями:
- Щелкните мышью по области диаграммы. Область диаграммы выделится черной рамкой, по углам которой и в середине сторон имеются черные квадратики — размерные маркеры. Кроме того в меню Excel добавится пункт Диаграмма Для изменения размеров диаграммы необходимо буксировать размерные маркеры. Перед буксировкой необходимо навести указатель мыши на один из размерных маркеров. Указатель мыши при этом примет вид двунаправленной стрелки. После чего необходимо нажать левую клавишу мыши и перемещать (буксировать) маркер. Буксировка маркера, расположенного в середине стороны, позволяет изменять горизонтальные и вертикальные размеры диаграммы. Буксировка углового маркера позволяет изменять одновременно вертикальные и горизонтальные размеры.
- Для перемещения диаграммы необходимо навести указатель мыши на область диаграммы (указатель примет вид белой стрелки, направленной под углом влево-вверх) и отбуксировать ее на новое место
- Отбуксируйте диаграмму в левый верхний угол листа, а затем измените ее размеры так, чтобы она занимала примерно ¾ пространства листа.
- Диаграмма состоит из нескольких элементов. К ним, в частности, относятся:
- область диаграммы (весь чертеж)
- область построения диаграммы
- легенда
- ряды данных
- названия осей и т.п.
Для редактирования элемента его необходимо
выделить. Это можно сделать нажатием
стрелок перемещения курсора ↑ ↓ на клавиатуре,
либо одиночным щелчком левой клавиши
мыши по соответствующему элементу. При
выделении в поле имени (крайнее левое
поле в строке формул) появляется название
элемента. Выделенный элемент отмечается
размерными маркерами.
Редактирование выделенного элемент
осуществляется через меню Формат, в котором появляется пункт для редактирования
соответствующего элемента, либо нажатием
клавиатурной комбинации Ctrl-1, которая
позволяет произвести форматирование
текущей ячейки, диапазона, элемента диаграммы
или объекта.
Выделенный элемент можно перемещать,
менять его размеры методом буксировки,
а также удалять, нажав клавишу Del.
- Выделите диаграмму, щелкнув по области диаграммы
- Последовательно нажимая клавишу ↑ на клавиатуре обратите внимание на элементы диаграммы, присутствующие в построенной вами диаграмме.
- Удалите легенду
- Отбуксируйте название оси X (категорий) в правый нижний угол области диаграммы
- Измените размеры области построения диаграммы так, чтобы она занимала максимальный размер внутри области диаграммы. Выберите подходящий цвет заливки области построения (по нашему мнению для черно-белых принтеров наиболее целесообразно применять прозрачную заливку).
- Отобразите на диаграмме погрешности вычисления. Для этого выделите кривую (она имеет название Ряд «p, МПа»), нажмите клавиатурную комбинацию Ctrl-1. Затем в окне Формат ряда данных выберите вкладку X-погрешности, в который выберите вид показа — обе планки погрешностей, величина погрешностей — пользовательская, в графе «+» введите диапазон положительной погрешности, вычисленной Вами =Лист1! $C$14: $K$14 (это можно сделать и мышью, выделяя соответствующий диапазон в таблице), а в графе «-«=Лист1! $C$15: $K$15
- Добавьте (если их нет) линии сетки для значений по оси X. Для этого в меню Диаграмма выберите пункт Параметры диаграммы и на вкладке Линии сетки щелкните по пункту Ось X — основные линии, после чего нажмите кнопку OK
- Отформатируйте осьY так, чтобы график занимал всю область построения диаграммы. Для этого после выделения оси и перехода в окно редактирования одним из указанных выше способов (например с помощью клавиатурной комбинации Ctrl-1) выберите вкладку Шкала и в графе Максимальное значение поставьте максимальное значение давления в исходной таблице — 20. Посмотрите другие вкладки в окне форматирования оси. Возможно Вы захотите изменить и другие параметры и внешний вид элементов оси.
- Измените название оси категорий так, чтобы размерность объема была поставлена правильно: не см3, а см3. Для это выделите название оси, затем выделите цифру 3 в размерности, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта щелкните мышью по пункту Верхний индекс раздела Эффекты.
- Проанализируйте, начиная с какой точки график изменения объема становится линейным. По-видимому это будет точка, соответствующая давлению 4 МПа. Определите параметры прямой, которой можно аппроксимировать кривую изменения давления на линейном участке. Для этого следует воспользоваться встроенной функцией ЛИНЕЙН, позволяющей построить функцию вида y=b+m1*x1+mi*xi на основе некоторого массива исходных данных методом наименьших квадратов. Функция ЛИНЕЙН относится к категории статистических. В данном случае воспользуемся «ручным» набором, без использования мастера функций.
Синтаксис функции
ЛИНЕЙН (известные_значения_y; известные_значения_x;
константа; статистика)
- Константа — это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА (1), то b вычисляется обычным образом.
- Статистика — это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если статистика имеет значение ЛОЖЬ (0), то функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
- Выделите диапазон ячеек C18: D18, затем в строке формул наберите следующую формулу =ЛИНЕЙН (C13: G13; C12: G12; 1; 0) и нажмите клавиатурную комбинацию Ctrl-Shift-Enter (по этой клавиатурной комбинации вводится единая формула для всего массива). Обратите внимание, что после ввода клавиатурной комбинации Ctrl-Shift-Enter набранная формула заключается в фигурные скобки, что означает, что это формула массива, а не одной ячейки, а в ячейках C18: D18 появляются значения.
- Постройте прямую, аппроксимирующую график на линейном участке, на той же диаграмме. Для этого сначала необходимо сформировать массив данных, а затем изменить диаграмму.
- В ячейку C20 введите формулу =$D$18+$C$18*C12 (вспомните, что для превращения относительной ссылки в абсолютную не обязательно вручную вводить знаки $ — достаточно нажать клавишу F4)
- Распространите формулу из ячейки C20 на диапазон C20: K20
- Выделите диаграмму на Листе2, затем в меню Диаграмма выберите пункт Добавить данные
- Для ввода в окно Диапазон нового ряда данных щелкните по закладке Лист1, в нем курсором мыши выделите диапазон C20: J20 и нажмите кнопку OK — на диаграмме появится график прямой.
- Вычислите приведенный модуль объемной упругости рабочей жидкости, для чего в ячейку A24 введите формулу (5), которая будет иметь вид =A22*C18
- Отформатируйте таблицу.
- Расположите заголовке по центру диапазона столбцов. Для этого выделите нужный диапазон столбцов и нажмите кнопку
(Центрировать по выделению) на панели инструментов Форматирование. Проделайте это для диапазонов A1: K1; C2: K2; A11: K11; A19: K19
- В необходимых местах добавьте линии границ ячеек. Выделите ячейки A2: K10, нажмите клавиатурную комбинацию Ctrl-1, выберите вкладку Границы, отметьте Все внешние и внутренние границы. Для ячеек K5,K8 уберите верхнюю и нижнюю границу (выделите ячейки, Ctrl-1, убрать границы). Аналогично оформите таблицы в диапазонах A12: K15; A17: D18; B20: K20.
- Измените формат показателей степени в размерностях см3. Для это нужной ячейке выделите цифру 3 в размерности, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта щелкните мышью по пункту Верхний индекс раздела Эффекты. Повторите это для ячеек A5, A8, B12, B22.
- В ячейках A8, A10 измените символы DV на V. Для этого выделите D в соответствующих ячейках, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта выберите шрифт Symbol в окне Шрифт
- Посмотрите, поместится ли созданная Вами таблица на один лист при печати. Для этого нажмите кнопку
(Предварительный просмотр) на стандартной панели инструментов. Измените ширину столбцов A-K таким образом, чтобы все столбцы поместились на одной странице, и при этом все данные и надписи в столбцах были бы видны. Для плавного изменения ширины столбца достаточно щелкнуть по букве столбца мышью (выделить весь столбец), навести указатель курсора на границу столбца (указатель примет вид двунаправленной стрелки) и отбуксировать границу в нужное место.
- Проверьте себя: приблизительный внешний вид таблиц и диаграммы приведен в приложении
- Завершить работу, сохранив ее в файле work2. xls.
Обработка данных
экстремальных экспериментов на примере
исследования операции вытяжки листовых
образцов
Постановка задачи 1:
Рассматривается задача отыскания максимального
коэффициента вытяжки цилиндрического
стаканчика из листовой заготовки с использованием
метода крутого восхождения Бокса-Уилсона.
Напомним, что коэффициентом вытяжки
k=D/d, где D — диаметр исходной заготовки,
d — диаметр вытянутого из этой заготовки
стаканчика. Предельная величина коэффициента
вытяжки за один переход ограничена величиной
максимальных напряжения во фланце заготовки.
Разрушение заготовки произойдет тогда,
когда напряжение достигнет предела прочности
материала GВ. При этом значение коэффициента вытяжки
является максимальным. На величину предельного
коэффициента вытяжки, помимо других факторов,
влияет радиус скругления кромки матрицы
(rм) и скорость деформирования
(V).
Идея экстремальных экспериментов заключается
в линейной аппроксимации гиперповерхности
отклика, оценке составляющих градиента
и проведении серии «мысленных» опытов
(т.е. без выполнения реального эксперимента)
в направлении оптимума.
Метод планирования эксперимента Бокса-Уилсона
включает в себя построение линейной модели
исследуемого объекта в виде y=b0+b1x1+b2x2+G+bnxn,
где n — количество факторов. В этом случае
оценками составляющих вектора градиента
являются коэффициенты полинома. Для движения
по градиенту необходимо менять факторы
пропорционально величинам коэффициентов.
Такая процедура называется крутым восхождением.
При движении по градиенту факторы изменяют
с определенным шагом. Шаги изменения
рассчитывают в натуральном масштабе.
Таким образом процедура решения задачи
сводится к следующей последовательности
шагов:
- проведение натурного эксперимента, для получения линейной модели y=b0+b1x1+b2x2+b3x3 (1), где y= GBmax; x1, x2, x3 — факторы k, rм, V в кодовом масштабе (результаты натурного эксперимента заданы в качестве исходных данных);
- определению коэффициентов bi линейной модели;
- определению составляющих градиента в натуральном масштабе;
- осуществлении крутого восхождения — т.е. подбора такого шага в направлении градиента из центра плана, при котором в формуле (1) y = GВ. Предел прочности материала, используемого в опытах 310 МПа
Методы решения с использованием Excel:
Для определения коэффициентов линейной
модели (1) достаточно провести 4 опыта.
Интервалы варьирования факторов Xi относительно
центра плана Xi0 в проведенном
натурном эксперименте приведены в таблице
1. Матрица плана исходного натурного эксперимента
в кодированном масштабе приведена в таблице
2. Кодированные значения факторов связаны
с натуральными соотношениями вида:
(2)
Таблица 1. Уровни варьирования факторов
|
Факторы |
1 |
2 |
3 |
|
k |
rм, |
V, |
|
|
Xi0 |
1,3 |
3 |
0,5 |
|
DXi |
0,1 |
1 |
0,2 |
Таблица 2. Матрица плана исходного эксперимента
|
№ |
x1 |
x2 |
x3 |
y (Gs max, МПа) |
|
1 |
-1 |
-1 |
-1 |
189 |
|
2 |
1 |
-1 |
1 |
236 |
|
3 |
-1 |
1 |
1 |
167 |
|
4 |
1 |
1 |
-1 |
223 |
Коэффициенты регрессионной модели (1)
определяют с помощью уже известной вам
функции ЛИНЕЙН. Если вы забыли синтаксис
функции ЛИНЕЙН, воспользуйтесь встроенной
справкой Excel.
Исходная точка для крутого восхождения
— центр плана с координатами в натуральном
масштабе:
X1о=1.3, X2о=3, X3о=0.5 (3)
Составляющие градиента вычисляются
по формуле
gi=biGXi (4)
Шаг крутого восхождения в натуральном
масштабе по каждой из координат
Xi=Xi0+gi*S (5)
Подбор такой кратности шагов S, одинаковой
для всех координат, при котором y = GВ осуществляют
с помощью команды меню Excel «Сервис-Подбор
параметра».
Последовательность выполнения
- Запустить EXCEL
- Переименуйте Лист1 книги в «Крутое восхождение». Остальные листы книги удалите. Для этого необходимо щелкнуть правой клавишей мыши по ярлычку листа и в открывшемся контекстном меню выбрать пункт Удалить.
- На листе Крутое восхождение создать таблицу с исходными данными эксперимента и поясняющими надписями по следующему образцу (при заполнении таблиц пользуйтесь способами копирования и автозаполнения):
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
1 |
Определение |
|||||||
|
2 |
Уровни |
|||||||
|
3 |
1 |
2 |
3 |
|||||
|
4 |
Xi0 |
1,3 |
3 |
0,5 |
||||
|
5 |
DXi |
0,1 |
1 |
0,2 |
||||
|
6 |
Матрица |
|||||||
|
7 |
№ |
x1 |
x2 |
x3 |
Gs |
|||
|
8 |
1 |
-1 |
-1 |
-1 |
189 |
|||
|
9 |
2 |
1 |
-1 |
1 |
236 |
|||
|
10 |
3 |
-1 |
1 |
1 |
167 |
|||
|
11 |
4 |
1 |
1 |
-1 |
223 |
|||
|
12 |
Коэффициенты |
|||||||
|
13 |
b3 |
b2 |
b1 |
b0 |
||||
|
14 |
||||||||
|
15 |
Составляющие |
|||||||
|
16 |
g1 |
g2 |
g3 |
|||||
|
17 |
||||||||
|
18 |
С |
|||||||
|
19 |
g1 |
g2 |
g3 |
|||||
|
20 |
||||||||
|
21 |
Крутое |
|||||||
|
22 |
Xi=Xi0+S*gi |
xi= |
||||||
|
23 |
S |
X1 |
X2 |
X3 |
x1 |
x2 |
x3 |
xmax |
|
24 |
- В диапазон A14: D14 введите формулу для определения коэффициентов регрессии для модели напряжений G s
max, используя функцию ЛИНЕЙН и мастер функций. Последовательность действий приведена ниже:
- Выделить A14: D14
- Меню Вставка-Функция (или кнопка Вставка функции)
- Категория — Статистические, Функция — ЛИНЕЙН, Кнопка OK
- Окно Изв_знач_y — диапазон известных значений Gs
max - Окно Изв_знач_x — диапазон значений xi в опытах
- Окно Константа — 1
- Окно Стат — 0
- Нажать клавиатурную комбинацию Ctrl-Shift-Enter
- Формула массива вставится в выделенный диапазон и в нем появятся значения коэффициентов
- Введите в диапазон A17: C17 формулы (4) для определения составляющих градиента. Обратите внимание, что порядок следования составляющих градиента gi в диапазоне A17: C17 и порядок следования коэффициентов bi в диапазоне A14: С14 не совпадают.
- Обратите внимание, что полученные значения составляющих градиента для факторов 2 и 3 имеют отрицательные значения. Это означает, что шаги в этом направлении приведут к уменьшению Gs
max. Поэтому мы должны двигаться в направлении антиградиента по этим факторам (напомним, что направление градиента — это направление увеличения функции). Таким образом в ячейки A20: C20 следует внести следующие формулы:
- A20 à =A17
- B20 à = — C17
- C20 à = — C17
- Занесите в ячейку A24 значение 1, являющееся начальным значением кратности шагов S
- Занесите в диапазон B24: D24 формулы (5) для определения значений варьируемых факторов в натуральном масштабе. Составляющие градиента расположены в ячейках A20: C20. Значения центра плана Xi0 — в ячейках B4: D4. Для использования автозаполнения в формулах следует вводить абсолютный адрес ячейки $A$24
- В ячейки E24: G24 внесите формулы (2) для перехода от натурального масштаба к кодированному.
- В ячейку H24 введите формулу для определения Gs
max по значениям факторов xi в ячейках E24: G24 в соответствии с моделью (1). Коэффициенты модели bi были определены вами ранее в ячейках A14: D14. При вводе формулы обратите внимание на обратный порядок значений коэффициентов bi в диапазоне A14: D14. Обратите внимание, что величина напряжения получилась значительно большей, чем максимально возможное значение 310 МПа. - Меняя значение в ячейке A24 попытайтесь вручную подобрать такую кратность шагов S, при которой значение напряжения в ячейке H24 было бы равно 310 МПа.
- Верните в ячейку A24 значение 1 и подберите точное значение с помощью встроенных в Excel средств автоматического подбора значений. Для этого:
- Использование программы Office Binder в работе секретаря
- Использование программы SPSS при проведении маркетинговых исследований
- Использование программы Аccess в системе бронирования
- Использование программы «Специальные образовательные средства» в процессе автоматизации звуков т, л, м, н в школьном возрасте
- Использование проективных технологии в обучение студентов педагогического коллежджа при изучение педагогических дисциплин
- Использование проектной методики для обучения иноязычному общению на уроках иностранного языка в средней школе
- Использование проектной методики для обучения устному общению учащихся средней школы
- Использование проблемных ситуаций на уроках математики в развитии творческого мышления младших школьников
- Использование программного обеспечения в обработке статистических данных туристской отрасли
- Использование программного обеспечения при разработке организационных документов
- Использование программных средств Excel и Matcad Решение задач вычислительной математики
- Использование программных средств сегментации рынка на примере компании ГК «Виктория»
- Использование программы «Hot Potatoes» при обучении иноязычной лексике студентов неязыковых специальностей
- Использование программы Microsoft Excel для решения выбранной задачи