Построение графика функции с условием
в MS Excel.
Перед
выполнением задания изучите в п.24 логическую функцию Excel ЕСЛИ и
запись составных условий через И и ИЛИ.
Задание: Построить
график функции
на отрезке xÎ[-10;10] с шагом для x 0,78.
То есть наша функция F
ведет себя (рассчитывается) по-разному в зависимости от значения х.
Выполнение:
Все делается как и на прошлом уроке, но для
расчета значений функции используем функцию ЕСЛИ.
В общем виде она выглядит так :
=ЕСЛИ(условие; значение при выполнении
условия; значение при невыполнении условия)
Условие у нас составное, надо представить
через И или ИЛИ, в данном случае будет И(х>5;x<=8) –в нашей формуле x заменим на адрес соответствующей ячейки.
Чтобы построить график сначала создадим
таблицу точек этой функции на данном промежутке(как и на прошлом уроке, но
повторюсь):
|
A |
B |
|
|
1 |
X |
F |
|
2 |
-10 |
=ЕСЛИ(И(А2>5;А2<=8); |
|
3 |
=A2+0,78 |
|
Обратите внимание:
1) в ячейке А3 в
формуле к предыдущему значению добавляем наш шаг;
2) в ячейке В2
записываем формулу нашей функции по всем правилам Excel,
вместо х у нас ячейка слева, т.е. А2.
Обратите внимание
на синтаксис функции ЕСЛИ: в скобках 1 условие(составное в данном случае),
через ; 2-значение если условие
выполняется (2*А2*А2+3*А2-5), снова ; 3-
значение если условие не выполняется.
Затем для того
чтобы получить остальные точки используем автозаполнение:
Щелкаем по ячейке А3, наводим курсор на
маленький черный квадратик внизу справа этой ячейки –курсор превратится в
черный крестик, зажимаем левую кнопку и тянем мышь вниз. Можно потянуть наугад
до ячейки А30.
Но у нас отрезок от -10 до 10, значит, лишние
данные удаляем.
С помощью
автозаполнения так же получаем значения функции для этих аргументов из ячейки В2
(её тянем вниз до В27).
Точки готовы.
Теперь выделяем полученные данные, Вставка – Точечная (диаграмма), выбираем
гладкую непрерывную кривую…
В итоге у нас есть точки на данном отрезке и
график нашей функции. Видно, что функция от 5 до 8 ведет себя на графике иначе.
Если у Вас не получилось, пробуйте снова- тренируйтесь,
на следующем уроке работа на оценку.
Строим график функции, заданный системой уравнений, в EXCEL
history 8 января 2018 г.
-
Группы статей
- Контрольные работы и задания
- Диаграммы и графики
Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.
Пусть дана система уравнений
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12784 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение системы уравнений графическим методом средствами MS Excel
Цели и задачи.
- Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
- Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
- Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
- Закрепить навыки создания таблиц и диаграмм.
- Научить решать систему уравнений графическим методом, исследовать график функции.
Оборудование урока: компьютеры, мультимедиа проектор.
Программное обеспечение: Windows XP, пакет программ MS Office 2003.
Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.
Запишите в тетради тему урока и укажите дату.
Назовите мне кого из класса сегодня нет.
Давайте вспомним, что такое уравнение, и как его можно решить графически.
Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.
(Учащиеся приводят определения)
Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.
Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).
Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.
Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.
Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.
Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.
Но эту задачу может взять на себя ЭВМ.
Мы воспользуемся возможностями программы MS Excel.
Основная часть
Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.
Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.
С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.
И так. Мы запустили программу MS Excel.
Мы хотим разработать таблицу для решения системы уравнений:
Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.
Сформируем начальные данные.
В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.
В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.
Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.
Формулы, которые нам нужно ввести приведены на рисунке.
Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.
Заполните, пожалуйста, в каждой таблице 20-25 строчек.
Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.
Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.
Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.
Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.
Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.
Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.
У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.
Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.
Мы видим, что одно из решений нашей системы уравнений равно -1,5.
Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.
Сколько у вас получилось?
Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.
Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.
Для этого нужно внести изменения в таблицу и расчётные формулы.
Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.
Самостоятельно внесите все необходимые изменения.
Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.
Заключительный этап урока
Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?
А что легче для вас?
Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.
Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.
Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://urok.1sept.ru/articles/617119
#Руководства
- 24 июн 2022
-
0
Как из сотни автомобилей выбрать только те, что соответствуют запросу покупателя? Разбираемся на примере функции ЕСЛИ в Excel.
Иллюстрация: Meery Mary для Skillbox Media
Рассказывает просто о сложных вещах из мира бизнеса и управления. До редактуры — пять лет в банке и три — в оценке имущества. Разбирается в Excel, финансах и корпоративной жизни.
ЕСЛИ — логическая функция Excel. Она проверяет, выполняются ли заданные условия в выбранном диапазоне таблицы. Пользователь указывает критерий, который нужно проверить, — функция сравнивает этот критерий с данными в ячейках таблицы и выдаёт результат.
В статье разберёмся:
- как работает и для чего нужна функция ЕСЛИ в Excel;
- как запустить функцию ЕСЛИ с одним условием;
- как запустить функцию с несколькими условиями.
Функцию ЕСЛИ используют, когда нужно сравнить данные таблицы с критериями пользователя. У функции есть два результата: ИСТИНА и ЛОЖЬ. Первый результат функция выдаёт, когда данные ячейки полностью совпадают с заданным условием, второй — когда данные ячейки условию не соответствуют.
Например, если нужно определить в таблице значения меньше 500, то значение 265 будет отмечено функцией как истинное, а значение 3426 — как ложное.
Можно задавать несколько условий одновременно. Например, найти значения меньше 500, но больше 300. В этом случае функция определит значение 265 как ложное, а 402 — как истинное. Так можно проверять не только числовые значения, но и текст.
Часто функцию ЕСЛИ используют при работе с другими функциями Excel для расширения их возможностей. Например, в случае с ВПР функция ЕСЛИ позволяет настроить поиск сразу по двум критериям.
Рассмотрим, как работает функция ЕСЛИ в классическом виде на примере.
Представим, что в автосалон обратился покупатель с просьбой подобрать ему автомобиль. Его запрос — автомобили чёрного или красного цвета, с объёмом двигателя больше 1,5 л, стоимостью до 2,5 млн рублей. Есть каталог автомобилей, но все характеристики и цены расположены в нём вразброс.
Скриншот: Excel / Skillbox Media
Нужно выяснить, какие из представленных в салоне авто подходят покупателю. Разберёмся пошагово, как это можно сделать с помощью функции ЕСЛИ в Excel.
Готовимся к запуску функции ЕСЛИ
Для начала рассмотрим, как функция ЕСЛИ работает в классическом виде — для проверки одного условия пользователя. Определим автомобили стоимостью до 2,5 млн рублей.
Принцип действия функции ЕСЛИ следующий. Алгоритм просматривает выбранный диапазон таблицы и проверяет, соответствуют ли данные его ячеек запросу пользователя. Затем возвращается в отдельную ячейку и оставляет там результат: ИСТИНА или ЛОЖЬ. О том, как настроить алгоритм функции под наши потребности, поговорим ниже. А сейчас на примере покажем, как подготовить таблицу к запуску функции и как вызвать окно для её построения.
Функция ЕСЛИ приносит результаты в отдельную ячейку, поэтому создадим отдельный столбец для них. Лучше сразу назвать его так, чтобы было понятно, о чём речь. В нашем случае сделаем столбец «До 2,5 млн руб.».
Скриншот: Excel / Skillbox Media
Выделим первую ячейку нового столбца и откроем окно для поиска функций. Это можно сделать двумя способами:
1. Перейти во вкладку «Формулы» и нажать «Вставить функцию».
Скриншот: Excel / Skillbox Media
2. Нажать на «fx» в строке ссылок на любой вкладке Excel.
Скриншот: Excel / Skillbox Media
На экране справа появится окно «Построитель формул». В нём через поиск находим функцию ЕСЛИ и нажимаем «Вставить функцию».
Скриншот: Excel / Skillbox Media
Появляется окно для заполнения аргументов функции: «Лог_выражение», «Значение_если_истина», «Значение_если_ложь». Ниже разберёмся, как их заполнить.
Скриншот: Excel / Skillbox Media
Функция ЕСЛИ предполагает, что пользователь создаёт запрос и указывает два варианта ответа на него. Этот запрос и варианты ответа — и есть три аргумента функции.
«Лог_выражение» (логическое выражение) — запрос пользователя, который функция будет проверять. В нашем примере это стоимость автомобилей.
Нужно, чтобы функция определила автомобили стоимостью менее или равной 2 500 000 рублей. Порядок действий следующий:
1. Ставим курсор в окно «Лог_выражение» в построителе формул.
2. Выбираем первое значение столбца «Цена, руб.» — ячейку Е2. Обозначение ячейки переносится в окно «Лог_выражение» построителя формул и одновременно с этим появляется в строке ссылок.
Скриншот: Excel / Skillbox Media
3. Дополняем значение E2 запросом пользователя: <=2500000. Одновременно с этим формула в строке ссылок принимает вид:fx=ЕСЛИ(E2<=2500000).
Скриншот: Excel / Skillbox Media
«Значение_если_истина» — результат, который функция принесёт в ячейку, если значение совпадёт с запросом пользователя. В случае с примером — что напишет функция, если проверяемая стоимость авто будет меньше либо равна 2 500 000 рублей.
Наша задача — определить, подходят автомобили каталога под запрос клиента или нет. Поэтому в окне аргумента истины введём значение «Подходит» — можно вводить его без кавычек, Excel добавит их самостоятельно.
Скриншот: Excel / Skillbox Media
«Значение_если_ложь» — результат, который функция принесёт в ячейку, если значение не совпадёт с запросом пользователя. В нашем примере — что напишет функция, если проверяемая стоимость авто будет больше 2 500 000 рублей.
Введём в качестве аргумента ЛОЖЬ значение «Не подходит».
Итоговая формула в строке ссылок примет вид:
fx=ЕСЛИ(E2<=2500000;»Подходит»;»Не подходит»).
Скриншот: Excel / Skillbox Media
Чтобы получить результат функции, нажимаем кнопку «Готово» в построителе формул.
Скриншот: Excel / Skillbox Media
В выбранной ячейке появится результат работы функции: «Подходит». Это значит, что первый автомобиль каталога подходит под запрос пользователя, — его цена 1 910 000 рублей.
Скриншот: Excel / Skillbox Media
Дальше нужно протянуть результат первой ячейки вниз до конца таблицы, чтобы функция проверила стоимость всех остальных автомобилей и отметила, подходят они под запрос покупателя или нет.
Скриншот: Excel / Skillbox Media
Чтобы настроить функцию ЕСЛИ с несколькими условиями, нужно добавить к ней дополнительные операторы Excel — «И», «ИЛИ».
Они связывают несколько критериев и, в зависимости от того, совпадают они с данными таблицы или нет, выдают результат. Схематично это будет выглядеть так: «ЕСЛИ условие a = 1, И/ИЛИ условие b = 2, И/ИЛИ условие c = 3, то — ИСТИНА, иначе — ЛОЖЬ».
В нашем примере у покупателя было три условия: цвет автомобиля, цена и объём двигателя. Разберёмся, как настроить функцию ЕСЛИ в этом случае.
Создадим ещё один столбец для новых результатов работы функции. Назовём его в соответствии с запросом покупателя: «До 2,5 млн руб., чёрный или красный, больше 1,5 л».
Скриншот: Excel / Skillbox Media
Вызываем окно построителя формул, как делали выше, и заполняем аргументы функции.
Отличия от классического варианта использования функции ЕСЛИ будут при заполнении первого аргумента «Лог_выражение»:
- Ставим курсор в окно «Лог_выражение» в построителе формул, вводим дополнительный аргумент «И» и открываем скобку.
- Первым условием будем вводить два цвета автомобилей, которые выбрал покупатель, поэтому вводим второй дополнительный аргумент «ИЛИ» и открываем ещё одну скобку.
- Выбираем первое значение столбца «Цвет» — ячейку B2. Ставим знак равенства и находим в этом же столбце значение из запроса пользователя: «чёрный» — ячейку B5. Ставим знак точки с запятой.
- Снова выбираем первое значение столбца «Цвет», ставим знак равенства и находим второй цвет из запроса пользователя: «красный» — ячейку B8. Закрываем скобку и ставим знак точки с запятой.
- Закрепляем выбранные ячейки с цветами. На Windows для этого поочерёдно выбираем значения ячеек в строке ссылок и нажимаем клавишу F4, на macOS — выбираем значения ячеек в строке ссылок и нажимаем клавиши Cmd + T. Закрепить эти ячейки нужно, чтобы в дальнейшем можно было протянуть формулу вниз и она сработала корректно для всех остальных строк.
- Выбираем первое значение столбца «Объём двигателя, л» — ячейку D2. Дополняем его запросом пользователя: >1,5. Также ставим знак точки с запятой.
- Выбираем первое значение столбца «Цена, руб.» — ячейку Е2. Дополняем его запросом пользователя: <=2500000, как делали в первом примере. Закрываем скобку.
Формула в строке ссылок принимает вид:
fx=ЕСЛИ(И(ИЛИ(B2=$B$5;B2=$B$8);D2>1,5;E2<=2500000)). Она объединит три запроса покупателя оператором «И», а в первом запросе предоставит возможность выбора с помощью оператора «ИЛИ».
Скриншот: Excel / Skillbox Media
Аргументы «Значение_если_истина» и «Значение_если_ложь» оставляем такими же, как в первом случае: «Подходит» и «Не подходит».
Итоговая формула в строке ссылок принимает вид:
fx=ЕСЛИ(И(ИЛИ(B2=$B$5;B2=$B$8);D2>1,5;E2<=2500000);Подходит»;»Не подходит»). Нажимаем кнопку «Готово».
В выбранной ячейке появляется результат: «Не подходит». Это значит, что первый автомобиль каталога не подходит под запрос покупателя — у него жёлтый цвет, а объём двигателя равен 1,5 л.
Скриншот: Excel / Skillbox Media
Протягиваем результат первой ячейки вниз до конца таблицы — функция проверяет остальные автомобили в каталоге и отмечает, какие из них подходят под все запросы покупателя.
Скриншот: Excel / Skillbox Media
Как пользоваться функцией ЕСЛИ в «Google Таблицах»? В них тоже есть функция ЕСЛИ, но нет окна построителя формул. Поэтому нужно прописывать её вручную, добавляя все пробелы и кавычки самостоятельно. Готовая формула будет выглядеть так:
fx=ЕСЛИ(E2<=»2500000″;»Подходит»;»Не подходит»).
- Руководство: как сделать ВПР в Excel и перенести данные из одной таблицы в другую
- Инструкция: как закреплять строки и столбцы в Excel
- Руководство по созданию выпадающих списков в Excel — как упростить заполнение таблицы повторяющимися данными
- Гайд о теории ТРИЗ, которую изучают менеджеры по всему миру
- Статья с советами эксперта, как сохранить бизнес в условиях кризиса, — о рынке, рисках, зарплатах и возможностях
Научитесь: Excel + Google Таблицы с нуля до PRO
Узнать больше
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
Пример: y=x(√x – 2). Шаг – 0,3.
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Содержание
- Процедура создания графика
- Способ 1: создание графика зависимости на основе данных таблицы
- Способ 2: создание графика зависимости с несколькими линиями
- Способ 3: построение графика при использовании различных единиц измерения
- Способ 4: создание графика зависимости на основе алгебраической функции
- Вопросы и ответы
Одной из типичных математических задач является построение графика зависимости. В нем отображается зависимость функции от изменения аргумента. На бумаге выполнить данную процедуру не всегда просто. Но инструменты Excel, если в должной мере овладеть ими, позволяют выполнить данную задачу точно и относительно быстро. Давайте выясним, как это можно сделать, используя различные исходные данные.
Процедура создания графика
Зависимость функции от аргумента является типичной алгебраической зависимостью. Чаще всего аргумент и значение функции принято отображать символами: соответственно «x» и «y». Нередко нужно произвести графическое отображение зависимости аргумента и функции, которые записаны в таблицу, или представлены в составе формулы. Давайте разберем конкретные примеры построения подобного графика (диаграммы) при различных заданных условиях.
Способ 1: создание графика зависимости на основе данных таблицы
Прежде всего, разберем, как создать график зависимости на основе данных, предварительно внесенных в табличный массив. Используем таблицу зависимости пройденного пути (y) от времени (x).
- Выделяем таблицу и переходим во вкладку «Вставка». Кликаем по кнопке «График», которая имеет локализацию в группе «Диаграммы» на ленте. Открывается выбор различных типов графиков. Для наших целей выбираем самый простой. Он располагается первым в перечне. Клацаем по нему.
- Программа производит построение диаграммы. Но, как видим, на области построения отображается две линии, в то время, как нам нужна только одна: отображающая зависимость пути от времени. Поэтому выделяем кликом левой кнопки мыши синюю линию («Время»), так как она не соответствует поставленной задаче, и щелкаем по клавише Delete.
- Выделенная линия будет удалена.
Собственно на этом построение простейшего графика зависимости можно считать завершенным. При желании также можно отредактировать наименования диаграммы, её осей, удалить легенду и произвести некоторые другие изменения. Об этом подробнее рассказывается в отдельном уроке.
Урок: Как сделать график в Экселе
Способ 2: создание графика зависимости с несколькими линиями
Более сложный вариант построения графика зависимости представляет собой случай, когда одному аргументу соответствуют сразу две функции. В этом случае потребуется построить две линии. Для примера возьмем таблицу, в которой по годам расписана общая выручка предприятия и его чистая прибыль.
- Выделяем всю таблицу вместе с шапкой.
- Как и в предыдущем случае, жмем на кнопку «График» в разделе диаграмм. Опять выбираем самый первый вариант, представленный в открывшемся списке.
- Программа производит графическое построение согласно полученным данным. Но, как видим, в данном случае у нас имеется не только лишняя третья линия, но ещё и обозначения на горизонтальной оси координат не соответствуют тем, которые требуются, а именно порядку годов.
Сразу удалим лишнюю линию. Ею является единственная прямая на данной диаграмме — «Год». Как и в предыдущем способе, выделяем линию кликом по ней мышкой и жмем на кнопку Delete.
- Линия удалена и вместе с ней, как вы можете заметить, преобразовались значения на вертикальной панели координат. Они стали более точными. Но проблема с неправильным отображением горизонтальной оси координат все-таки остается. Для решения данной проблемы кликаем по области построения правой кнопкой мыши. В меню следует остановить выбор на позиции «Выбрать данные…».
- Открывается окошко выбора источника. В блоке «Подписи горизонтальной оси» кликаем по кнопке «Изменить».
- Открывается окошко ещё меньше предыдущего. В нём нужно указать координаты в таблице тех значений, которые должны отображаться на оси. С этой целью устанавливаем курсор в единственное поле данного окна. Затем зажимаем левую кнопку мыши и выделяем всё содержимое столбца «Год», кроме его наименования. Адрес тотчас отразится в поле, жмем «OK».
- Вернувшись в окно выбора источника данных, тоже щелкаем «OK».
- После этого оба графика, размещенные на листе, отображаются корректно.
Способ 3: построение графика при использовании различных единиц измерения
В предыдущем способе мы рассмотрели построение диаграммы с несколькими линиями на одной плоскости, но при этом все функции имели одинаковые единицы измерения (тыс. руб.). Что же делать, если нужно создать графики зависимости на основе одной таблицы, у которых единицы измерения функции отличаются? В Экселе существует выход и из этого положения.
Имеем таблицу, в которой представлены данные по объему продаж определенного товара в тоннах и по выручке от его реализации в тысячах рублей.
- Как и в предыдущих случаях выделяем все данные табличного массива вместе с шапкой.
- Клацаем по кнопке «График». Снова выбираем первый вариант построения из перечня.
- Набор графических элементов сформирован на области построения. Тем же способом, который был описан в предыдущих вариантах, убираем лишнюю линию «Год».
- Как и в предыдущем способе, нам следует на горизонтальной панели координат отобразить года. Кликаем по области построения и в списке действий выбираем вариант «Выбрать данные…».
- В новом окне совершаем щелчок по кнопке «Изменить» в блоке «Подписи» горизонтальной оси.
- В следующем окне, производя те же действия, которые были подробно описаны в предыдущем способе, вносим координаты столбца «Год» в область «Диапазон подписей оси». Щелкаем по «OK».
- При возврате в предыдущее окно также выполняем щелчок по кнопке «OK».
- Теперь нам следует решить проблему, с которой ещё не встречались в предыдущих случаях построения, а именно, проблему несоответствия единиц величин. Ведь, согласитесь, не могут располагаться на одной панели координат деления, которые одновременно обозначают и денежную сумму (тыс. рублей) и массу (тонны). Для решения данной проблемы нам потребуется произвести построение дополнительной вертикальной оси координат.
В нашем случае для обозначения выручки оставим ту вертикальную ось, которая уже имеется, а для линии «Объём продаж» создадим вспомогательную. Клацаем по данной линии правой кнопкой мышки и выбираем из перечня вариант «Формат ряда данных…».
- Запускается окно формата ряда данных. Нам нужно переместиться в раздел «Параметры ряда», если оно было открыто в другом разделе. В правой части окна расположен блок «Построить ряд». Требуется установить переключатель в позицию «По вспомогательной оси». Клацаем по наименованию «Закрыть».
- После этого вспомогательная вертикальная ось будет построена, а линия «Объём продаж» переориентируется на её координаты. Таким образом, работа над поставленной задачей успешно окончена.
Способ 4: создание графика зависимости на основе алгебраической функции
Теперь давайте рассмотрим вариант построения графика зависимости, который будет задан алгебраической функцией.
У нас имеется следующая функция: y=3x^2+2x-15. На её основе следует построить график зависимости значений y от x.
- Прежде, чем приступить к построению диаграммы, нам нужно будет составить таблицу на основе указанной функции. Значения аргумента (x) в нашей таблице будут указаны в диапазоне от -15 до +30 с шагом 3. Чтобы ускорить процедуру введения данных, прибегнем к использованию инструмента автозаполнения «Прогрессия».
Указываем в первой ячейке столбца «X» значение «-15» и выделяем её. Во вкладке «Главная» клацаем по кнопке «Заполнить», размещенной в блоке «Редактирование». В списке выбираем вариант «Прогрессия…».
- Выполняется активация окна «Прогрессия». В блоке «Расположение» отмечаем наименование «По столбцам», так как нам необходимо заполнить именно столбец. В группе «Тип» оставляем значение «Арифметическая», которое установлено по умолчанию. В области «Шаг» следует установить значение «3». В области «Предельное значение» ставим цифру «30». Выполняем щелчок по «OK».
- После выполнения данного алгоритма действий весь столбец «X» будет заполнен значениями в соответствии с заданной схемой.
- Теперь нам нужно задать значения Y, которые бы соответствовали определенным значениям X. Итак, напомним, что мы имеем формулу y=3x^2+2x-15. Нужно её преобразовать в формулу Excel, в которой значения X будут заменены ссылками на ячейки таблицы, содержащие соответствующие аргументы.
Выделяем первую ячейку в столбце «Y». Учитывая, что в нашем случае адрес первого аргумента X представлен координатами A2, то вместо представленной выше формулы получаем такое выражение:
=3*(A2^2)+2*A2-15Записываем это выражение в первую ячейку столбца «Y». Для получения результата расчета щелкаем по клавише Enter.
- Результат функции для первого аргумента формулы рассчитан. Но нам нужно рассчитать её значения и для других аргументов таблицы. Вводить формулу для каждого значения Y очень долгое и утомительное занятие. Намного быстрее и проще её скопировать. Эту задачу можно решить с помощью маркера заполнения и благодаря такому свойству ссылок в Excel, как их относительность. При копировании формулы на другие диапазоны Y значения X в формуле будут автоматически изменяться относительно своих первичных координат.
Наводим курсор на нижний правый край элемента, в который ранее была записана формула. При этом с курсором должно произойти преображение. Он станет черным крестиком, который носит наименование маркера заполнения. Зажимаем левую кнопку мыши и тащим этот маркер до нижних границ таблицы в столбце «Y».
- Вышеуказанное действие привело к тому, что столбец «Y» был полностью заполнен результатами расчета формулы y=3x^2+2x-15.
- Теперь настало время для построения непосредственно самой диаграммы. Выделяем все табличные данные. Снова во вкладке «Вставка» жмем на кнопку «График» группы «Диаграммы». В этом случае давайте из перечня вариантов выберем «График с маркерами».
- Диаграмма с маркерами отобразится на области построения. Но, как и в предшествующих случаях, нам потребуется произвести некоторые изменения для того, чтобы она приобрела корректный вид.
- Прежде всего, удалим линию «X», которая разместилась горизонтально на отметке 0 координат. Выделяем данный объект и жмем на кнопку Delete.
- Легенда нам тоже не нужна, так как мы имеем только одну линию («Y»). Поэтому выделяем легенду и снова жмем по клавише Delete.
- Теперь нам нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «X» в таблице.
Кликом правой кнопки мыши выделяем линию диаграммы. В меню перемещаемся по значению «Выбрать данные…».
- В активировавшемся окне выбора источника клацаем по уже хорошо знакомой нам кнопке «Изменить», располагающейся в блоке «Подписи горизонтальной оси».
- Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «X». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
- Вернувшись к окну выбора источника данных, клацаем по кнопке «OK» в нём, как до этого сделали в предыдущем окне.
- После этого программа произведет редактирование ранее построенной диаграммы согласно тем изменениям, которые были произведены в настройках. График зависимости на основе алгебраической функции можно считать окончательно готовым.
Урок: Как сделать автозаполнение в Майкрософт Эксель
Как видим, с помощью программы Excel процедура построения графика зависимости значительно упрощается в сравнении с созданием его на бумаге. Результат построения можно использовать как для обучающих работ, так и непосредственно в практических целей. Конкретный вариант построения зависит от того, на основе чего строится диаграмма: табличные значения или функция. Во втором случае перед построением диаграммы придется ещё создавать таблицу с аргументами и значениями функций. Кроме того, график может быть построен, как на основе одной функции, так и нескольких.
Еще статьи по данной теме:
Помогла ли Вам статья?
Аннотация:
Цель работы: научиться определять значения функций и строить графики, а также использовать логические функции в табличном процессоре Excel.
Содержание работы:
Построение графика функции с одной переменной.
Построение графика функции с двумя условиями.
Построение графика функции с тремя условиями.
Построение двух графиков в одной системе координат.
Построение поверхности.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Построение графика функции
Процесс построения графика функции состоит из двух этапов:
- создание таблицы значений функции
- непосредственного построения ее графика.
Для построения графика функции необходимо первоначально построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяют обычно с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала ее поведение на интервале табуляции.
Рассмотрим технологию построения графика на примере функции 
![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
Создание таблицы значений функции
В нашем случае возьмем в качестве шага изменения аргумента, например, 0.1. Нам надо найти у(0), у(0.1), у(0.2), …, у(1). С этой целью в ячейки диапазона A1:А11 последовательно введем 0, 0.1, …, 1, т. е. значения переменной х. Отметим, что эта последовательность значений представляет собой арифметическую прогрессию.
Ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию, можно двумя способами.
Первый способ заключается в следующем:
- В ячейки А1 и А2 введите первый и второй члены арифметической прогрессии, т.е. 0 и 0,1
- Выделите диапазон ячеек А1:А2.
- Расположите указатель мыши на маркере заполнения выделенного диапазона (рис. 4.1
рис.
4.1) и протяните его вниз (в данном случае на диапазон A3:А11) до тех пор, пока не получится числовой ряд нужной длины (рис. 4.2
рис.
4.2).
Второй способ позволяет пользоваться диалоговым окном Прогрессия. Для этого:
- В ячейку А1 введите первый член арифметической профессии.
- Выберите команду Главная > Редактирование > Заполнить > Прогрессия.
- В появившемся диалоговом окне Прогрессия (рис. 4.3
рис.
4.3) в группе Расположение выбираем переключатель по столбцам, а в группе Тип – переключатель арифметическая. В поле Шаг введите значение 0,1, а в поле Предельное значение – 1. - Нажмите кнопку ОК.
Рис.
4.1.
Вид указателя мыши на маркере заполнения
Рис.
4.2.
Арифметическая последовательность, построенная по первым ее двум членам с помощью маркера заполнения
Рис.
4.3.
Диалоговое окно Прогрессия
Диалоговое окно Прогрессия закроется, а на рабочем листе автоматически будет построена требуемая прогрессия.
Примечание. Диалоговое окно Прогрессия, отображаемое на экране выбором команды Главная > Редактировать > Заполнить > Прогрессия, также позволяет создавать геометрические прогрессии.
В ячейку В1 введите формулу: =СОS(ПИ( )*А1)^2.
Ввод формул в ячейку можно производить либо с клавиатуры, либо с помощью диалогового окна Мастер функций, которое отображается на экране либо выбором команды Формулы > Вставить Функцию, либо нажатием кнопки Вставка функции
Продемонстрируем работу с мастером функций на примере ввода упомянутой выше формулы.
- Выберите ячейку В1.
- Нажмите кнопку Вставка функции
панели инструментов Стандартная, либо выберите команду Формулы > Вставить Функцию. На экране отобразится диалоговое окно Мастер функций – шаг 1 из 2 (рис. 4.4
рис.
4.4). Оно состоит из двух частей: - Категория – со списком двенадцати категорий функций;
- Функция – со списком имен функций, входящих в выбранную категорию.
Категория Полный алфавитный перечень содержит все встроенные функции и их имена упорядочены в алфавитном порядке, категория 10 недавно использовавшихся содержит имена десяти последних примененных функций. Эта категория ускоряет вызов функций, постоянно используемых пользователем.
- Функция cos относится к категории Математические. Выберите эту функцию и нажмите кнопку ОК. На экране отобразится панель формул (рис. 4.5
рис.
4.5).
Рис.
4.4.
Диалоговое окно Мастер функций – шаг 1 из 2
Рис.
4.5.
Панель формул
В поле Число вводится аргумент функции – в рассматриваемом примере это ПИ ()*А1. С помощью клавиатуры в это поле введите только ПИ ( )*, а ссылку на ячейку А1 в формулу добавьте, щелкнув по ячейке А1 на рабочем листе. Конечно, ее можно было также ввести с клавиатуры, но предложенный способ дает дополнительную проверку правильности ввода. После нажатия кнопки ОК в ячейку В1 будет введена формула:
Примечание. При использовании мастера функции перед вводом формулы в ячейку не надо вводить знак =, он вставляется в формулу автоматически.
- С помощью клавиатуры добавьте в формуле =COS(ПИ ())*А1 операцию возведения в квадрат функции cos. После всех описанных действий в ячейке В1 должна появиться формула =COS(ПИ()*Al)^2
Таким образом, пока найдено значение функции cos2(x) для значения х из ячейки A1. Теперь нам осталось найти значения этой функции для диапазона ячеек А2:А11.
Для этого:
- Выберите ячейку В1.
- Расположите указатель мыши на маркере заполнения выделенной ячейки и протяните его вниз на диапазон В2:В11.
Процесс создания таблицы значений функции завершен (рис. 4.6
рис.
4.6).
На рис. 4.6
рис.
4.6 на правом рабочем листе приведены формулы, введенные в ячейки рабочего листа. Для того чтобы в ячейках рабочего листа отображались не значения, а формулы, надо выбрать команду Формулы > Зависимости формул и Показать формулы.
Рис.
4.6.
Результат табуляции функции до и после форматирования данных
На среднем рабочем листе (рис. 4.6
рис.
4.6) приведен результат табуляции функции. Выглядит он не очень презентабельно: после десятичной точки отображается различное количество десятичных знаков. Кроме того, происходит перемешивание числового и экспоненциального форматов.
А именно, в ячейке В6 вместо 0 отображается 3.75Е-33, что приблизительно и равно нулю. Поэтому форматы надо привести к какому-то общему виду, например, как показано на левом рабочем листе: значения аргумента выводятся в числовом формате с точностью до одного знака после десятичной точки, а значения функции – с точностью до трех знаков после десятичной точки. Отформатируем, например, значения аргумента.
Для этого надо выбрать диапазон A1:A11. Это можно сделать, например, следующим способом. Выберите ячейку А1, а затем при нажатой клавише <Shift> выделите ячейку А11. Диапазон А1:А11 выбран.
Переходим к форматированию данных. Выберите команду Главная > Число. В появившемся диалоговом окне Формат ячеек: Число в списке Числовые форматы выберите Числовой, а в поле Число десятичных знаков введите 1. Нажмите кнопку ОК. Данные в Al:A11 будут отформатированы, как показано на левом рабочем листе (рис. 4.6
рис.
4.6). Аналогичным образом разберитесь с диапазоном В1:В11.
Построение графика
Перейдем теперь к конструированию графика cos2(xх) функции по существующей таблице значений аргументов и соответствующих значений функции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм на выберите вариант График, а в списке Вид укажите стандартный график (рис. 4.7
рис.
4.7). Нажмите кнопку Далее. - Чтобы изменить (шаг 2 из 4): источник данных диаграммы (которое позднее переименовывается в окно Исходные данные) необходимо нажать на график, затем выбрать вкладку Конструктор, затем вкладку Данные, Выбрать данные. В поле Диапазон автоматически будет введена ссылка на необходимый диапазон в абсолютном формате. Проверьте его, удалите 1 ряд. В итоге у вас должно получится, что Диапазон, =Лист1!$В1$:$В$11.
Обратите внимание на полученный график функции, отображаемый на вкладке Диапазон данных. В нем по оси ординат откладываются значения функции, а вот по оси абсцисс порядковые номера точек, а не значения аргумента.
Для того чтобы по оси абсцисс откладывались значения аргумента, надо выделить диаграмму и воспользоваться командой Конструктор > Данные > Выбрать данные, далее Подписи горизонтальной оси (категории) > Изменить и указать диапазон ячеек в которых расположен аргумент х функции.
Рис.
4.7.
Вкладка Стандартные диалогового окна Мастер диаграмм (шаг 1 из 4): тип диаграммы
Рис.
4.8.
Вкладка Диапазон данных диалогового окна Исходные данные
Создав диаграмму, можно изменить любой из ее элементов. Например, можно изменить вид осей, добавить название диаграммы, переместить или скрыть легенду, а также добавить дополнительные элементы.
Чтобы изменить диаграмму, выполните одно или несколько из указанных ниже действий.
- Изменение вида осей диаграммы. Можно указать масштаб осей и изменить промежутки между значениями или категориями. Для удобства чтения диаграммы можно добавить на оси деления указать величину промежутков между ними.
- Добавление к диаграмме названий и меток данных. Для пояснения отображенных на диаграмме данных можно добавить название диаграммы, названия осей и метки данных.
- Добавление легенды и таблицы данных Можно отобразить или скрыть легенду, изменить ее расположение или элементы. Для некоторых диаграмм также можно отобразить таблицу данных, в которой содержатся ключи легенды и значения, представленные на диаграмме.
- Применение специальных параметров для диаграмм разных типов Для различных типов диаграмм можно применять различные специальные линии (например, коридор колебания и линии тренда), полосы (например, полосы повышения и понижения и планки погрешностей), маркеры данных и т.д.
Вместо того чтобы добавлять или изменять элементы диаграммы и форматировать их вручную, можно быстро применить к данным готовый макет или стиль диаграммы. В приложении Excel существует множество полезных готовых макетов и стилей, которые можно адаптировать, изменив вручную макет или формат отдельных элементов диаграммы, таких как область диаграммы, область построения, ряды данных и легенда.
При использовании готового макета диаграммы на ней в определенном порядке отображается заданный набор элементов (например, названия, легенда, таблица данных или метки данных). Можно подобрать подходящий макет из предоставленных для диаграмм конкретного типа.
При использовании готового стиля диаграммы ее форматирование основано на примененной теме документа, поэтому внешний вид диаграммы будет соответствовать цветам темы (набору цветов), шрифтам темы (набору шрифтов заголовков и основного текста) и эффектам темы (набору границ и заливок), принятым в организации или заданным пользователем.
Собственные стили или макеты диаграмм создавать нельзя, но можно создать шаблоны диаграмм, содержащие нужный макет и форматирование.
Помимо применения готового стиля диаграммы можно легко изменить форматирование ее отдельных элементов, например маркеров данных, области диаграммы, области построения, чисел и текста в названиях и подписях, что привлечет внимание и сделает диаграмму оригинальной. Можно также применять стили фигур и стили WordArt или форматировать фигуры и текст в элементах диаграммы вручную.
Чтобы изменить форматирование диаграммы, выполните одно или несколько из указанных ниже действий:
- Заливка элементов диаграммы. Для привлечения внимания к определенным элементам диаграммы можно залить их цветом, текстурой, рисунком или применить градиентную заливку.
- Изменение контуров элементов диаграммы. Для выделения элементов диаграммы можно изменить цвет, стиль или толщину линий.
- Добавление специальных эффектов к элементам диаграммы. Для придания диаграмме завершенности к ее элементам можно применить специальные эффекты, например тень, отражение, свечение, сглаживание краев, рельеф или объемное вращение.
- Форматирование текста и чисел Текст и числа в названиях, подписях и надписях на диаграмме можно форматировать так же, как текст и числа на листе. Чтобы выделить текст или число, можно даже применять стили WordArt.
Рис.
4.9.
Вкладка Конструктор: параметры диаграммы
Рис.
4.10.
Диалоговое окно Макет: параметры диаграммы
Рис.
4.11.
Результат построения графика функции
Математические функции рабочего листа
Наиболее часто употребляемые стандартные математические функции рабочего листа приведены в табл. 4.1
таблица
4.1.
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| ABS (число) | ABS (number) | Возвращает абсолютную величину аргумента |
| ACOS (число) | ACOS (number) | Возвращает арккосинус аргумента |
| ASIN (число) | ASIN (number) | Возвращает арксинус аргумента |
| ATAN (число) | ATAN (number) | Возвращает арктангенс аргумента |
| COS (число) | COS (number) | Возвращает косинус аргумента |
| EXP (число) | EXP (number) | Возвращает экспоненту аргумента, т.е результат возведения основания натурального логарифма в степень, равную значению аргумента |
| LN (число) | LN (number) | Возвращает натуральный логарифм аргумента |
| LOG (число) | LOG (number) | Возвращает логарифм аргумента по данному основанию, если основание опущено, то оно полагается равным 10 |
| LOG10 (число; основание) | LOG10 (number; base) | Возвращает десятичный логарифм аргумента |
| SIN (число) | SIN (number) | Возвращает синус аргумента |
| TAN (число) | TAN (number) | Возвращает тангенс аргумента |
| ЗНАК (число) | SGN (number) | Возвращает знак аргумента |
| ОСТАТ (число; делитель) | MOD (number1; number1) | Возвращает остаток от деления числа на делитель |
| ПИ ( ) | PI ( ) | Возвращает значение числа ? с точностью до 15 знаков (в данном случае 3.14159265358979). обратите внимание на то, что функция ПИ ( ) не имеет аргумента |
| СЛЧИС ( ) | RND ( ) | Возвращает случайное число между 0 и 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС ( )*(b-a)+a |
| ЦЕЛОЕ (число) | INT (number) | Округляет число до ближайшего меньшего целого |
График функции с двумя условиями
Рассмотрим пример построения графика функции при ![$хin[0;1]$$](https://intuit.ru/sites/default/files/tex_cache/5bbd057004769c8519124b98a54a24bf.png)
График строится по принципам, представленным в п. 4.1 «Построение графика функции»
«Построение графиков функций и использование логических формул»
, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.5;(1+ABS(0.2-А1))/(1+А1+А1^2);А1^ (1/3))
Примечание. Обратите внимание на то, что для возведения в степень в коде используется соответствующая операция, т.е. А1^(1/3), а не функция рабочего листа степень, т. е. степень (А1; 1/3). В обоих случаях получается один и тот же результат, но, применение операции возведения в степень здесь более разумно, т. к. делает код более очевидным.
В коде фигурирует функция логического ветвления Если (IF), которая имеет следующий синтаксис:
ЕСЛИ (лог выражение; значение_если_истина; значение_если_ложь)
Рассмотрим ее аргументы:
- лог выражение – это любое значение или выражение, принимающее значения истина или ложь. Например, А10=100 – это логическое выражение; если значение в ячейке А10 равно 100, то выражение принимает значение ИСТИНА. В противном случае – ЛОЖЬ. Данный аргумент может быть использован в любом операторе сравнения.
- значение_если_истина – это значение, которое возвращается, если лог выражение равно ИСТИНА. Например, если этот аргумент – строка «План реализации выполнен» и лог выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст План реализации выполнен. Если лог выражение равно, ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы отобразить слово ИСТИНА, необходимо использовать логическое значение ИСТИНА для этого аргумента. значение_если_истина может быть формулой.
- значение_если_ложь – это значение, которое возвращается, если лог выражение равно ЛОЖЬ. Например, если этот аргумент – строка «План реализации перевыполнен» и лог выражение равно ЛОЖЬ, то функция ЕСЛИ отобразит текст План реализации перевыполнен. Если лог выражение равно ЛОЖЬ, а значение_если_ложь опущено (т. е. после значение_если_истина нет точки с запятой), то возвращается логическое значение ЛОЖЬ. Если лог выражение равно ЛОЖЬ, а значение_если_ложь пусто (т. е. после значение_если_истина стоит точка с запятой с последующей закрывающей скобкой), то возвращается значение 0. значение_если_ложь может быть формулой.
Логические функции
В MS Excel имеются функции логических условий, перечисленные в табл. 4.2.
таблица
4.2
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| И (лог знач1; лог знач2; …) | AND (arg1, arg2, …) | Логическое умножение. |
| Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=5) возвращает значение ИСТИНА. | ||
| Если ячейка В4содержит число из интервала от 1 до 100, то функция И (1<В4; В4<100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| ИЛИ (лог знач1; лог знач2; …) | OR (arg1, arg2, …) | Логическое сложение. |
| Возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=6) возвращает значение ИСТИНА. | ||
| Если ячейка В4 содержит число меньше 1 или больше 100, то ИЛИ (В4<1; В4>100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| НЕ (лог знач) | NOT (arg) | Логическое отрицание. Изменяет на противоположное значение логическое значение своего аргумента. Например, НЕ (2+5=5) возвращает значение ИСТИНА. |
| Если ячейка В4 содержит число меньше 1 или больше 100, то НЕ (ИЛИ(В4<1;В4>100)) возвращает ЛОЖЬ, а в противном случае – ЛОЖЬ. |
Примечание. Кроме функции ЕСЛИ в MS Excel имеются еще две функции, использующие логические условия. Это функции:
СЧЁТЕСЛИ (COUNTIF) – подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию;
СУММЕСЛИ (SUMIF) – суммирует значения тех ячеек диапазона, удовлетворяющих заданному критерию.
График функции с тремя условиями
Рассмотрим пример построения графика функции у при ![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
График строится так, как описано в разд. «Построение графика функции» ранее в этой работе, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.2;1+ LN(1+A1); ЕСЛИ(И(А1>=0.2;А1<=0.8); (1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1)))
Тот же самый результат можно получить, введя в ячейку В1 более простую формулу:
=ЕСЛИ (A1<0.2; 1+LN (1+A1); ЕСЛИ (А1<=0.8; (1+А1^(1/2))/(1+А1); 2*ЕХР(-2*А1)))
Два графика в одной системе координат
Рассмотрим пример построения в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
- y = 2sin(x)
- z = 3 cos(2x) – sin(x)
Итак, начнем процесс построений.
- В ячейки А1, В1 и С1 введите соответственно х, у и z.
- Выделите диапазон А1:С1. Выберите команду Главная. На вкладке
Выравнивание появившегося диалогового окна Формат ячеек в группе Выравнивание в списке по горизонтали укажите значение по правому краю. Нажмите кнопку ОК. Заголовки столбцов окажутся выровненными по правому краю.
- В диапазон ячеек А2:А17 введите значения аргумента х от -3 до 0 с шагом 0.2.
- В ячейки В2 и С2 введите формулы: =2*SIN(A2), =3*COS(2*A2)-SIN(A2)
- Выделите диапазон В2:С2, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз так, чтобы заполнить диапазон В3:С17.
- Выделите диапазон В3:С17. Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы выберите значение График. Нажмите кнопку Далее.
- На вкладке Данные > выбрать данные диалогового окна Исходные данные в поле ввода Подписи оси X укажите ссылку на диапазон А2:А17, значения из которого откладываются по оси абсцисс (рис. 4.12
рис.
4.12). В списке Ряд приводятся ряды данных, откладываемых по оси ординат (в нашем случае имеется два ряда данных). Эти ряды автоматически определяются на основе ссылки, указанной в поле ввода Диапазон предыдущего шага алгоритма. В поле Значения автоматически выводится ссылка на диапазон, соответствующий выбранному ряду из списка Ряд. В поле ввода Имя отображается ссылка на ячейку, в которой содержится заголовок соответствующего ряда. Этот заголовок в дальнейшем используется мастером диаграмм для создания легенды.
Рис.
4.12.
Вкладка Ряд диалогового окна Исходные данные до задания имен рядов
- Выберите в списке Ряд элемент Ряд1. В поле ввода Имя укажите ссылку на ячейку В1, значение из которой будет использоваться в качестве идентификатора данного ряда. Вводить эту ссылку надо не с клавиатуры, а выбором с рабочего листа ячейки В1. Это приведет к тому, что в поле Имя автоматически будет введена ссылка на ячейку в абсолютном формате. В данном случае, =Лист1!$В$1. Теперь осталось только щелкнуть на элементе Ряд1 списка Ряд. Это приведет к тому, что элемент Ряд1 поменяется на у, т. е. на то значение, которое содержится в ячейке В1. Аналогично поступите с элементом Ряд2 списка Ряд. Сначала выберите его, затем в поле ввода Имя укажите ссылку на ячейку С1, а потом щелкните на элементе Ряд2. На рис. 4.13
рис.
4.13 показана вкладка Ряд диалогового окна Исходные данные после задания имен рядов. Теперь можно нажать кнопку Далее. - В появившемся диалоговом окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите График двух функций, в поле Ось X(категорий) введите х, в поле Ось Y(значений) введите у и z. На вкладке Легенда установите флажок Добавить легенду. Нажмите кнопку Далее.
- Нажмите кнопку Готово.
Результат проделанных шагов представлен на рисунке 4.14
рис.
4.14.
Рис.
4.13.
Вкладка Ряд диалогового окна Исходные данные после задания имен рядов
Для большей презентабельности построенной диаграммы в ней были произведены следующие изменения по сравнению с оригиналом:
- Изменена ориентация подписи оси ординат с вертикальной на горизонтальную. Для этого выберите подпись оси ординат. Нажмите правую кнопку мыши и в появившемся контекстном меню укажите команду Формат названия оси. На вкладке Выравнивание диалогового окна Формат названия оси в группе Ориентация установите горизонтальную ориентацию. Нажмите кнопку ОК.
- Для того чтобы пользователю было легче отличить, какая линия является графиком функции у, а какая – z, изменен вид графика функции z. С этой целью выделите график функции z. Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат рядов данных. На вкладке Вид диалогового окна Формат ряда данных, используя элементы управления групп Маркер и Линия, установите необходимый вид линии графика. Нажмите кнопку ОК.
- Изменен фон графика. С этой целью выделите диаграмму (но не область построения). Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат области диаграммы. На вкладке Вид диалогового окна Формат области диаграммы установите флажок скругленные углы, а используя элементы управления группы Заливка, установите цвет и вид заливки фона. Нажмите кнопку ОК.
Рис.
4.14.
Графики функций у(х) и z(x), построенные в одной системе координат
Построение поверхности
Продемонстрируем технологию построения поверхностей на примере следующей функции, зависящей от двух аргументов:
$z = x^{2}-y^{2}$ при ![$$хin [-2; 2], уin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/9ba0e461aae4f553cbb9279438619e6b.png)
Прежде чем воспользоваться мастером диаграмм, надо построить таблицу значений функции z по обоим ее аргументам, например, по аргументу х от -2 до 2 с шагом 0.2, а по у от -1 до 1 с шагом 0.2.
Для этого:
- Введите в ячейку А2 значение -2, а в ячейку А3 значение -1.8. Выберите диапазон ячеек А2:А3. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон А4:А22. Таким, образом, значения аргумента х протабулированы от -2 до 2 с шагом 0.2.
- Введите в ячейку В1 значение -1, а в ячейку С1 значение -0.8. Выберите диапазон ячеек В1:С1. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон D1:L1. Значения аргумента у протабулированы от -1 до 1 с шагом 0.2.
- В ячейку В2 введите формулу: =$А2^2 – В$1^2.
- Выберите ячейку В2, расположите указатель мыши на маркере ее заполнения и протяните его вниз на диапазон В2:L22.
На левом рабочем листе (рис. 4.15
рис.
4.15) показан результат табуляции функции, зависящей от двух аргументов, а на правом – часть формул, которые были введены в ячейке при копировании формулы, введенной в ячейку В2, перемещением маркера заполнения на диапазон В2:L22.
Рис.
4.15.
Таблица значений функции, зависящей от двух аргументов
Примечание. Использование в формуле абсолютной ссылки на строку и столбец существенно. Напомним, что знак $ в имени ячейки, стоящий перед номером строки, создает абсолютную ссылку на строку, а перед именем столбца – абсолютную ссылку на столбец. Поэтому при буксировке формулы из ячейки В2 на диапазоны B2:L22, в ячейках этого диапазона будут найдены значения функции z при соответствующих значениях аргументов х и у.
Перейдем к конструированию поверхности по результатам табуляции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы на вкладке Стандартные в списке Тип выберите значение Поверхность, а в списке Вид укажите стандартную поверхность. Нажмите кнопку Далее.
- В следующем диалоговом окне мастера диаграмм на вкладке Диапазон данных выберите переключатель Ряды в столбцах, т. к. данные располагаются в столбцах. В поле ввода Диапазон приведите ссылку на диапазон данных A1:L22, т. е. диапазон, который содержит в себе как значения аргументов, так и значения функции. Нажмите кнопку Далее.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): в параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите поверхность, в поле Ось X (категорий) укажите х, в поле Ось Y (рядов данных) задайте у, в поле Ось Z (значений) введите z. На вкладке Легенда сбросьте флажок Добавить легенду. Нажмите кнопку Готово.
- Поверхность построена, как показано на рисунке 4.16
рис.
4.16.
Рис.
4.16.
Построенная поверхность и диалоговое окно Формат трехмерной проекции
Примечание. MS Excel разрешает пользователю не только изменять размеры рабочей области диаграммы посредством маркеров изменения размеров, но и ориентацию поверхности в пространстве. Для этого достаточно выделить диаграмму, а затем выбрать команду Диаграмма > Объемный вид. На экране отобразится диалоговое окно Формат трехмерной проекции, элементы которого как раз и позволяют изменять ориентацию поверхности в пространстве.
ЗАДАНИЯ
Вариант 1.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 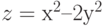
![$x,yin[-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/1dccee169ef8cd4747131b25d37db985.png)
Вариант 2.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 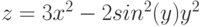
![$x, yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/53a8791dec1fce35a5f3ac0dd9605a3b.png)
Вариант 3.
1. Построить в разных системах координат при ![$xin[-2; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/075d390c8429b09a75c1effe8b21041a.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 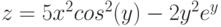
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 4.
1. Построить в разных системах координат при ![$хin [-1.5; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/f8ea986285591f482f6425385ca5802c.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность при мммх,yin [-1; 1]/ммм
Вариант 5.
1. Построить в разных системах координат при ![$хin [-1.8; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/78bc9ae987003e9c6801db7908c6bfbd.png)
2. Построить в одной системе координат при ![$хin [0; 3]$](https://intuit.ru/sites/default/files/tex_cache/153306b868b619790149dea95767b4f9.png)
3. Построить поверхность 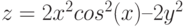
![$х,yin [-l; 1]$](https://intuit.ru/sites/default/files/tex_cache/f4f9de170788cb6bf2d9bec5dd801e0d.png)
Вариант 6.
1. Построить в разных системах координат при ![$хin [-2; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/0dbcf9e9bff0f78d00043ecdd4c74666.png)
2. Построить в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
3. Построить поверхность 
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 7.
1. Построить в разных системах координат при ![$хin [-1.7; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/68c9476760c3d9265176b82bcc296063.png)
2. Построить в одной системе координат при ![$хin [-3;0]$](https://intuit.ru/sites/default/files/tex_cache/625e1ce96d5bf506d83f626e5934b564.png)
3. Построить поверхность 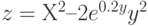
![$х,yin [-1;1]$](https://intuit.ru/sites/default/files/tex_cache/afd39bc8d16e67ea25b0fc35595fbb39.png)
Вариант 8.
1. Построить в разных системах координат при ![$хin [-1.5; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/2629a936172ba4ce71bd2c2e792ee4c2.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность при
Вариант 9.
1. Построить в разных системах координат при ![$хin [-1.4; 1.9]$](https://intuit.ru/sites/default/files/tex_cache/6c9405fb2d3d680c40a2b90ec8452bf2.png)
2. Построить в одной системе координат при ![$хin [0;2]$](https://intuit.ru/sites/default/files/tex_cache/adbba029f8747f8b59bce37c40dcc3a5.png)
3. Построить поверхность при
Вариант 10.
1. Построить в разных системах координат при ![$хin [-1.4; 1.4]$](https://intuit.ru/sites/default/files/tex_cache/077a3284889a9378e887806bcf4ea6f6.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность z = 3x2sin2(x) – 5e2yу при ![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Из каких этапов состоит процесс построения графика функции?
- Какими способами можно ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию?
- Как подписать ось X значениями аргумента?
Простой график для одной переменной
Проще всего разобраться, как построить график в Эксель по данным таблицы, состоящей всего из двух колонок. Для наглядного примера можно взять названия месяцев и объем полученной за это время прибыли. Ряд будет только один, а осей на графике — две. Строить диаграмму можно по следующей пошаговой инструкции:
- Выделить таблицу с данными.
- Перейти на вкладку «Вставка», где можно выбирать вариант диаграммы: например, простой график функции, круговой или точечный.
- Убедиться в том, что данные в таблице были автоматически распределены так, как это было запланировано. В данном случае ошибки нет: значения указаны по оси X, даты — по OY.
Если пользователь случайно ошибся при построении графика или хочет изменить информацию, он может поменять настройки, выделив область построения диаграммы и использовав контекстное меню. Попасть в него легко с помощью клика правой кнопкой мыши. Изменению подлежат тип графика, данные для его построения, форматы сетки и каждой оси.
Перейдя в контекстном меню к пункту «Выбрать данные», можно настроить, какая информация будет отображаться. Например, для указанного примера у пользователя есть возможность выделять данные только для конкретных месяцев. Для этого достаточно убирать галочки с ненужных дат или изменить формулу в графе «Диапазон данных для диаграммы».
Стоит отметить, что построение графика по представленным в табличной форме данным обеспечит автоматическую перестройку линии при изменении информации. Например, если в показатели прибыли были внесены корректировки на основании более точных сведений, диаграмма станет другой без дополнительных действий со стороны пользователя. Точно так же изменятся и все названия, если откорректировать их на графике.
Легенду с названием графика при использовании только одного изменяющегося показателя оставлять необязательно. В современных версиях Excel имя ряда данных не будет показано на диаграмме автоматически. В более старых пакетах MS Office легенду можно удалить вручную.
Чтобы оценивать информацию на графике было проще, стоит выделить линию, в виде которой представлен ряд, и в контекстном меню указать необходимость добавления подписей. Результатом станет появление значений прямо на диаграмме — с той же точностью, с которой они указаны в таблице.
На вкладке «Конструктор» можно поменять еще больше настроек — выбрать экспресс-макет и готовый шаблон, изменить цвета и добавить дополнительные элементы графика. В том числе — подписи к осям данных, названия которых в последних версиях MS Excel вводятся вручную.
Также читайте, как сделать кнопку в Excel, чтобы быстрее перейти у нужной таблице или графику.
График с несколькими переменными
Узнав, как в Эксель нарисовать график при наличии только одного столбца со значениями, стоит перейти к решению более сложной задачи — составлению диаграмм, на которых будет несколько рядов.
Если рассматривать тот же пример, вместе с прибылью могут быть представлены еще накладные расходы. Принцип создания будет включать такие шаги:
- Выделить таблицу с данными, захватив все колонки.
- На вкладке «Вставка» выбрать тип диаграммы.
- Проверить, соответствует ли автоматически построенный программой график нужным требованиям. Если нет — изменить настройки вручную.
Для графика с двумя и большим количеством рядов данных стоит оставить «легенду» с подписями. Она позволит разобраться, каким цветом, оттенком или типом линии отмечен нужный показатель. Однако название диаграммы в этом случае придется вносить вручную — или указать в настройках, в какой ячейке таблицы расположен нужный текст.
С помощью контекстного меню на состоящем из нескольких рядов графике можно менять различные настройки, характеристики осей и линий, добавлять подписи и менять шрифты. А при изменении информации в таблице это автоматически отразится и на диаграмме. Данные, которые вводились вручную, (например, название оси или графика) придется менять тем же способом.
Добавление второй оси
Иногда информация может быть представлена в таблице так, что поместить ее на одной общей диаграмме, на первый взгляд, невозможно. Если представить, что накладные расходы указаны не в рублях, а в долларах, график получится некорректным.
Можно построить две разных диаграммы для каждого ряда данных. Или перед тем, как сделать график в Экселе, пересчитать сумму по действующем курсу — но это будет не слишком правильно, если затраты определялись именно в валюте. Решение проблемы — добавить вторую ось со своими единицами измерения.
Для этого можно выполнить такие действия:
- Построить основу — график, единицы измерения у которого одинаковые для каждого ряда.
- Выделить диаграмму и на вкладке «Конструктор» перейти к изменению ее типа.
- Выбрать вариант «Комбинированная» и второй вариант в списке — гистограмму с группировкой и график на вспомогательной оси.
- Настроить отображение — указать, для какого ряда будет построена вспомогательная ось, изменить виды диаграмм.
- Нажать «ОК» для перехода к дальнейшим настройкам.
Теперь на графике будет две отличающихся друг от друга диаграммы, каждая из которых имеет свою шкалу с отдельными единицами измерения. Можно сделать так, чтобы на экране были, например, две похожих линии, выбрав соответствующие варианты на этапе изменения типа. Хотя это будет не так удобно даже при наличии легенды.
Двойная диаграмма с разными шкалами — отличный способ, как в Экселе сделать график по таблице для двух показателей, которые нельзя сравнить друг с другом. Зато оценку их значений и изменений можно провести на одном листе. Например, чтобы выполнить работу по поиску зависимости между разными видами расходов.
Читайте также:
- 5 способов как вставить презентацию в презентацию Powerpoint
- Как очистить оперативную память смартфона на Android



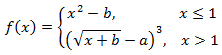
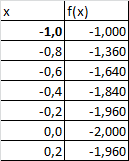
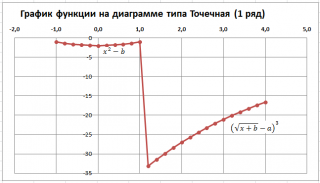
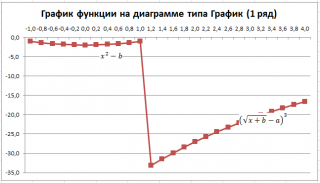
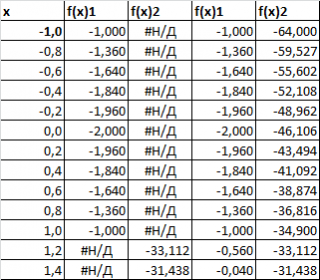
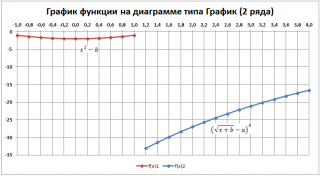













































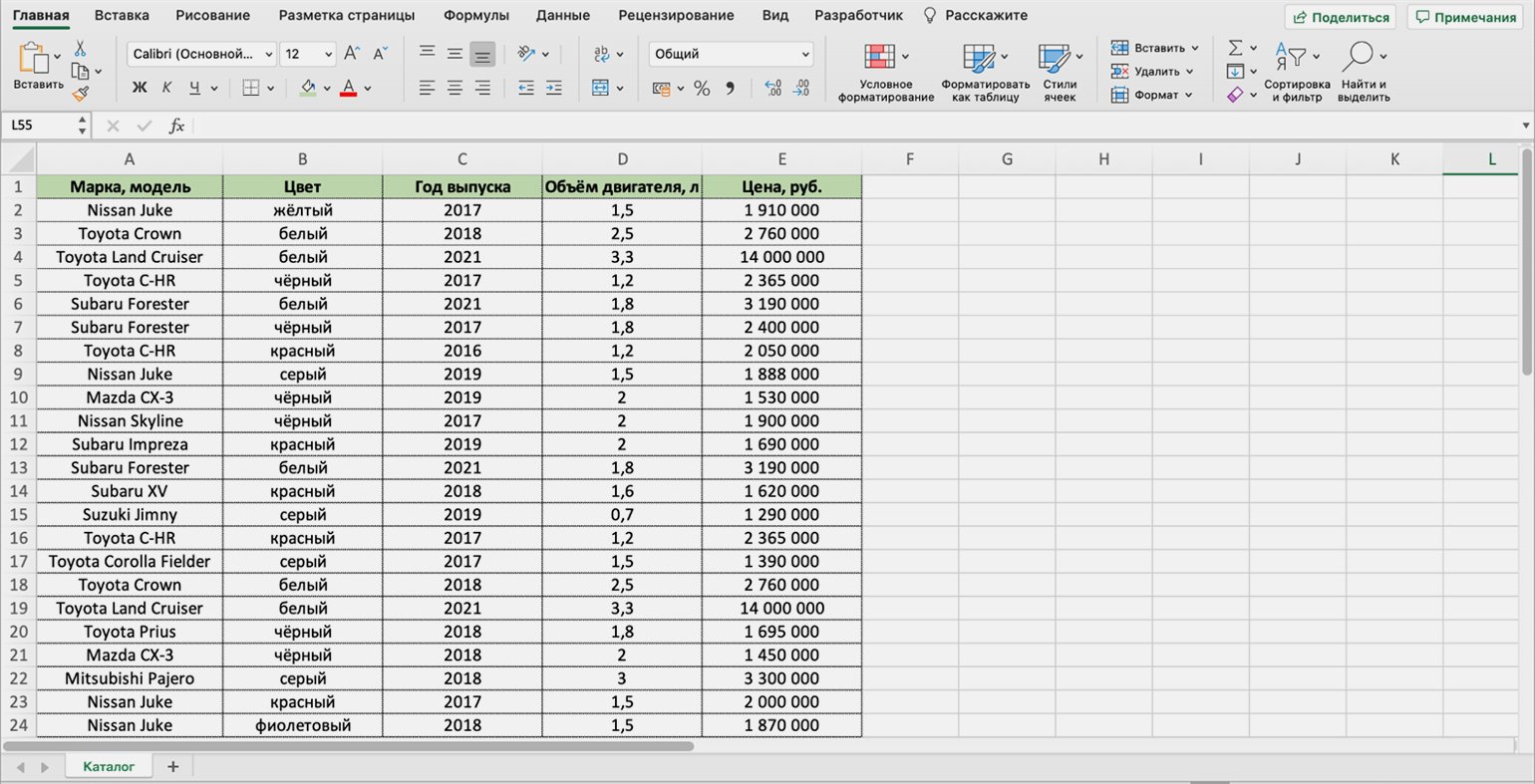
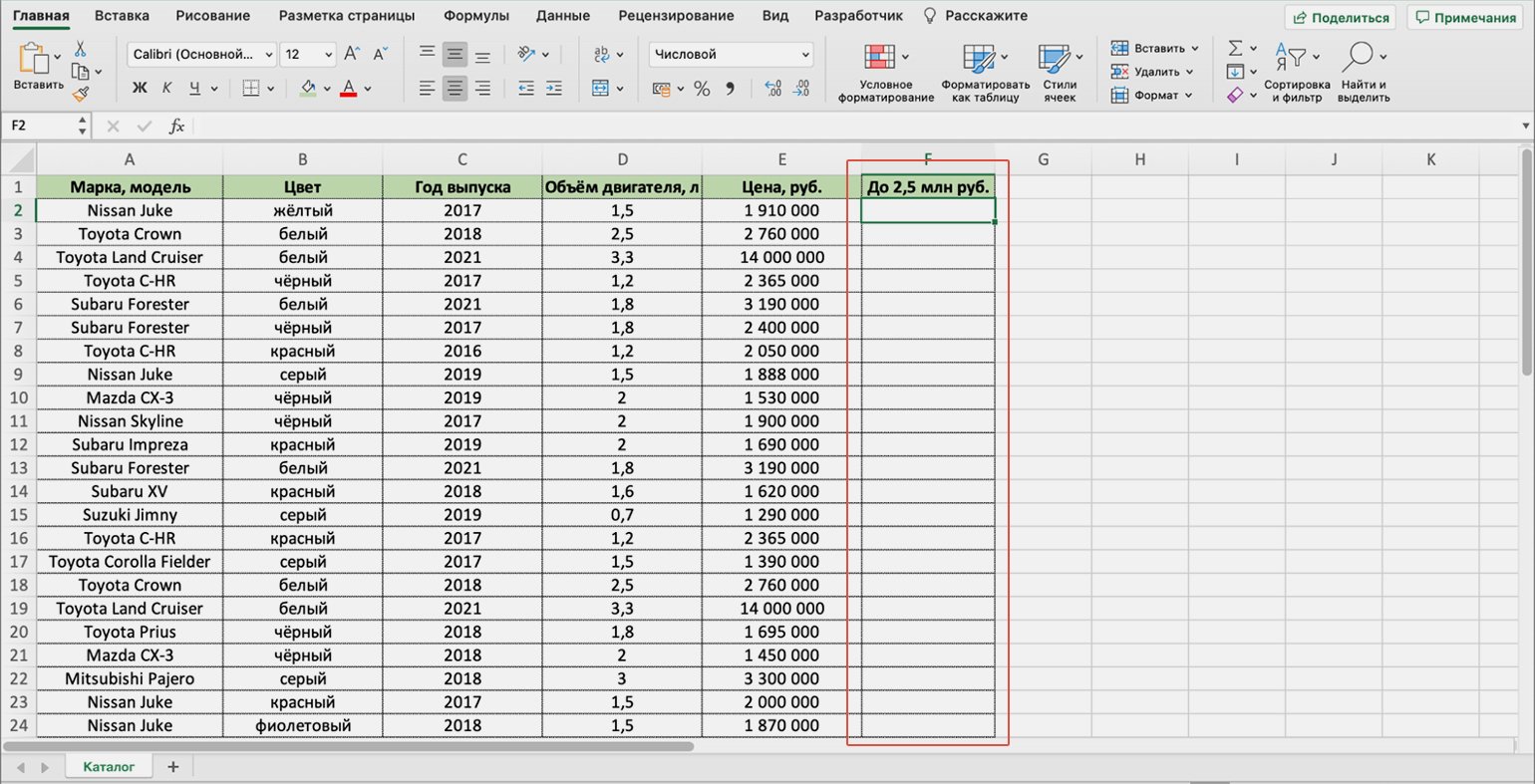
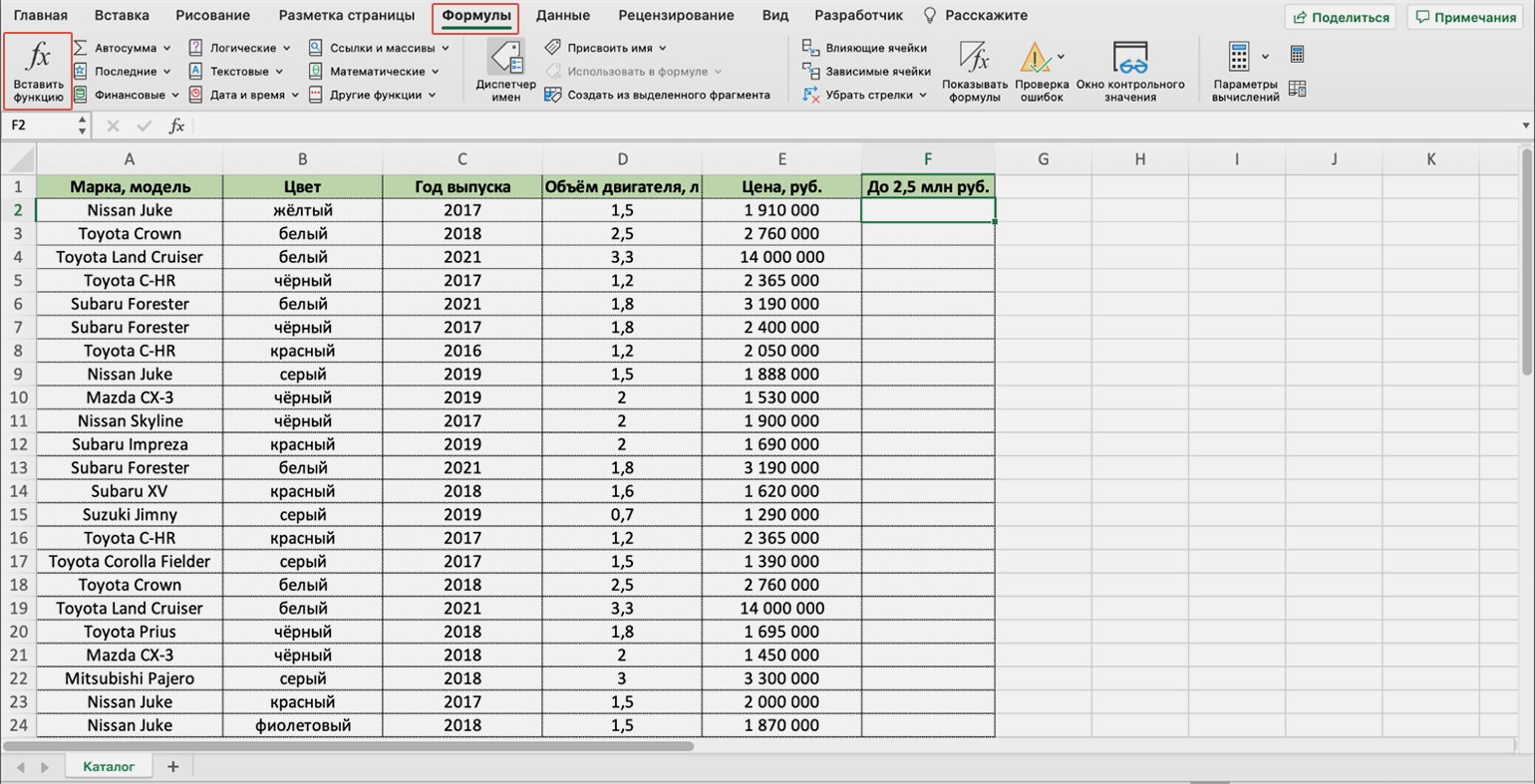
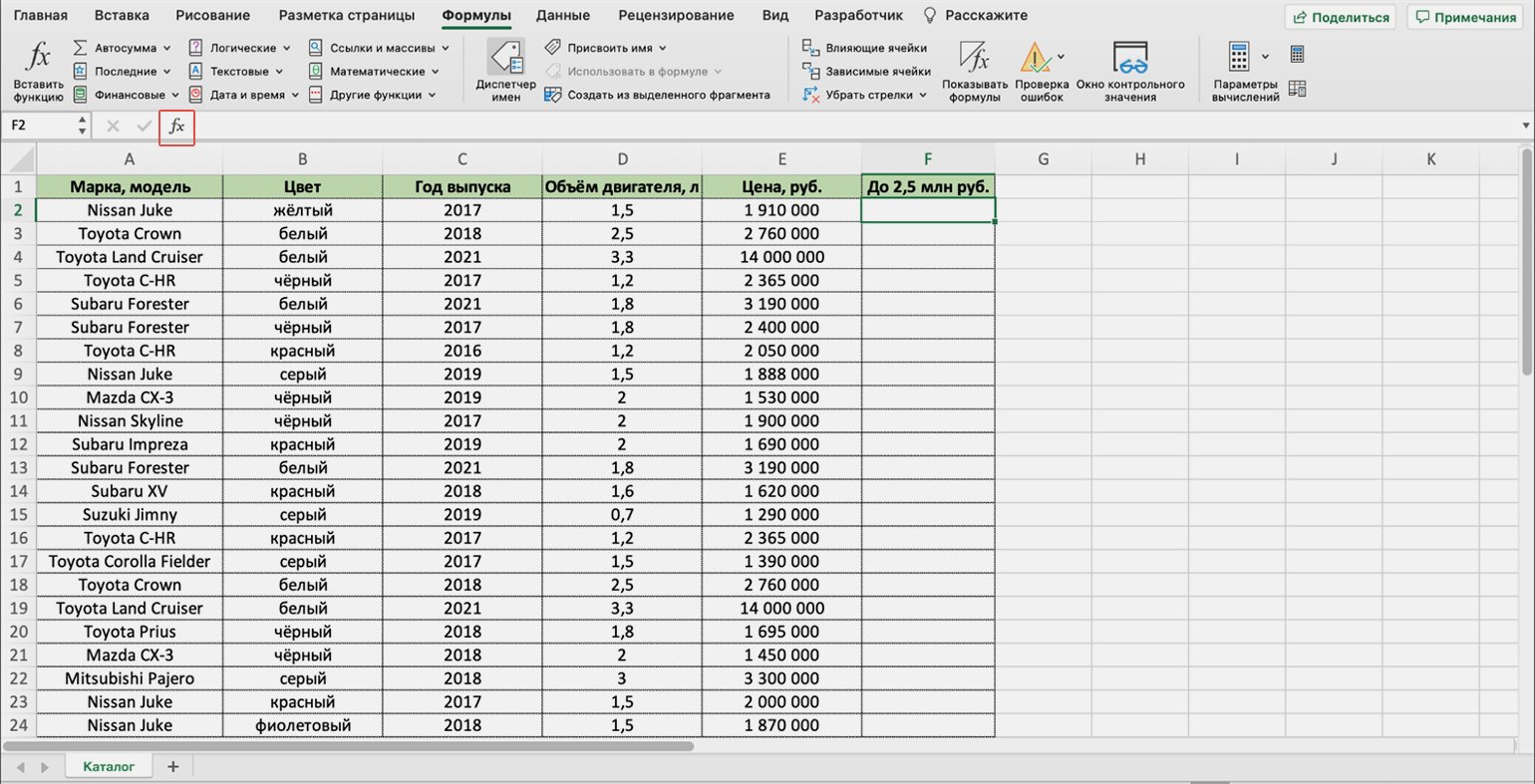
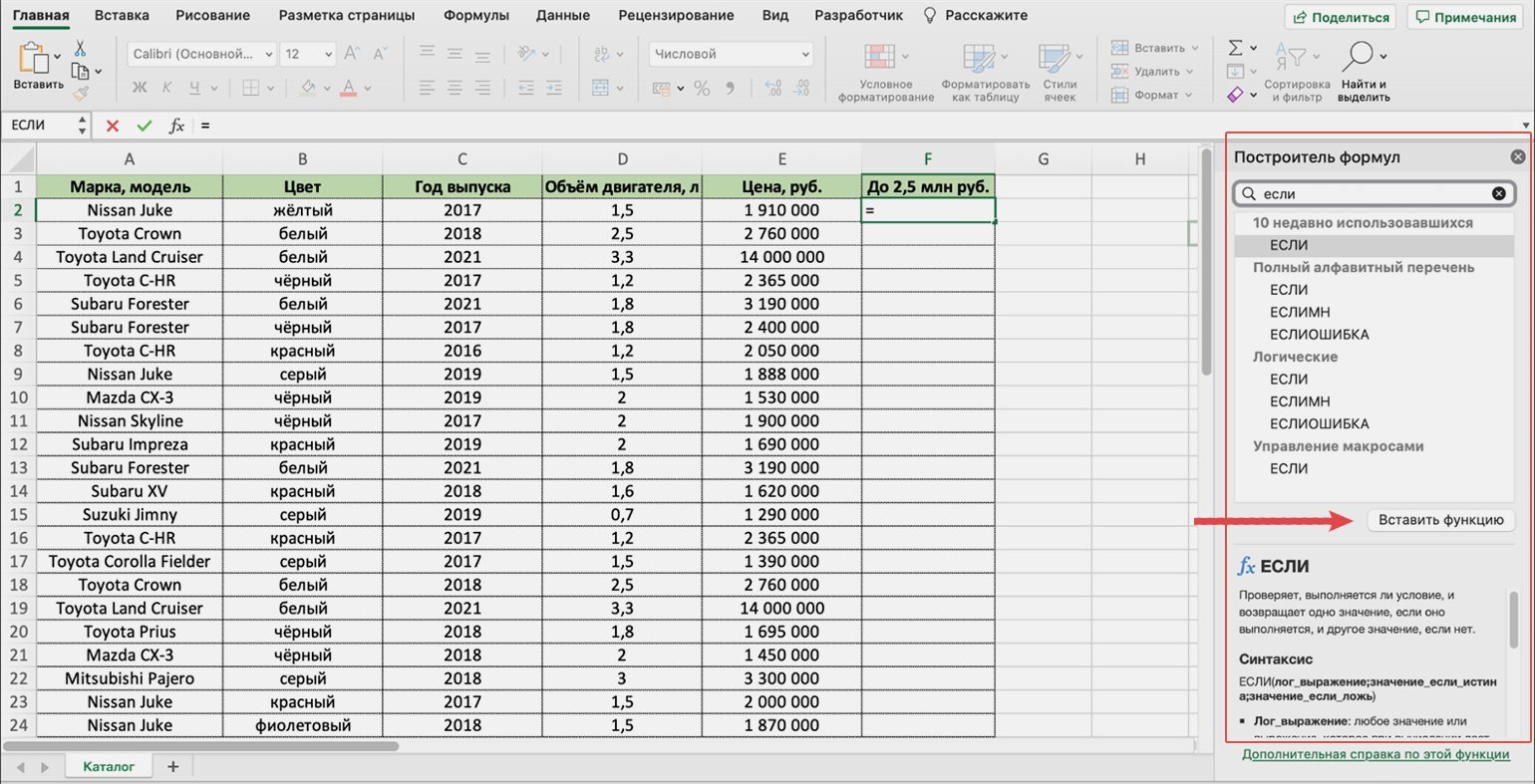
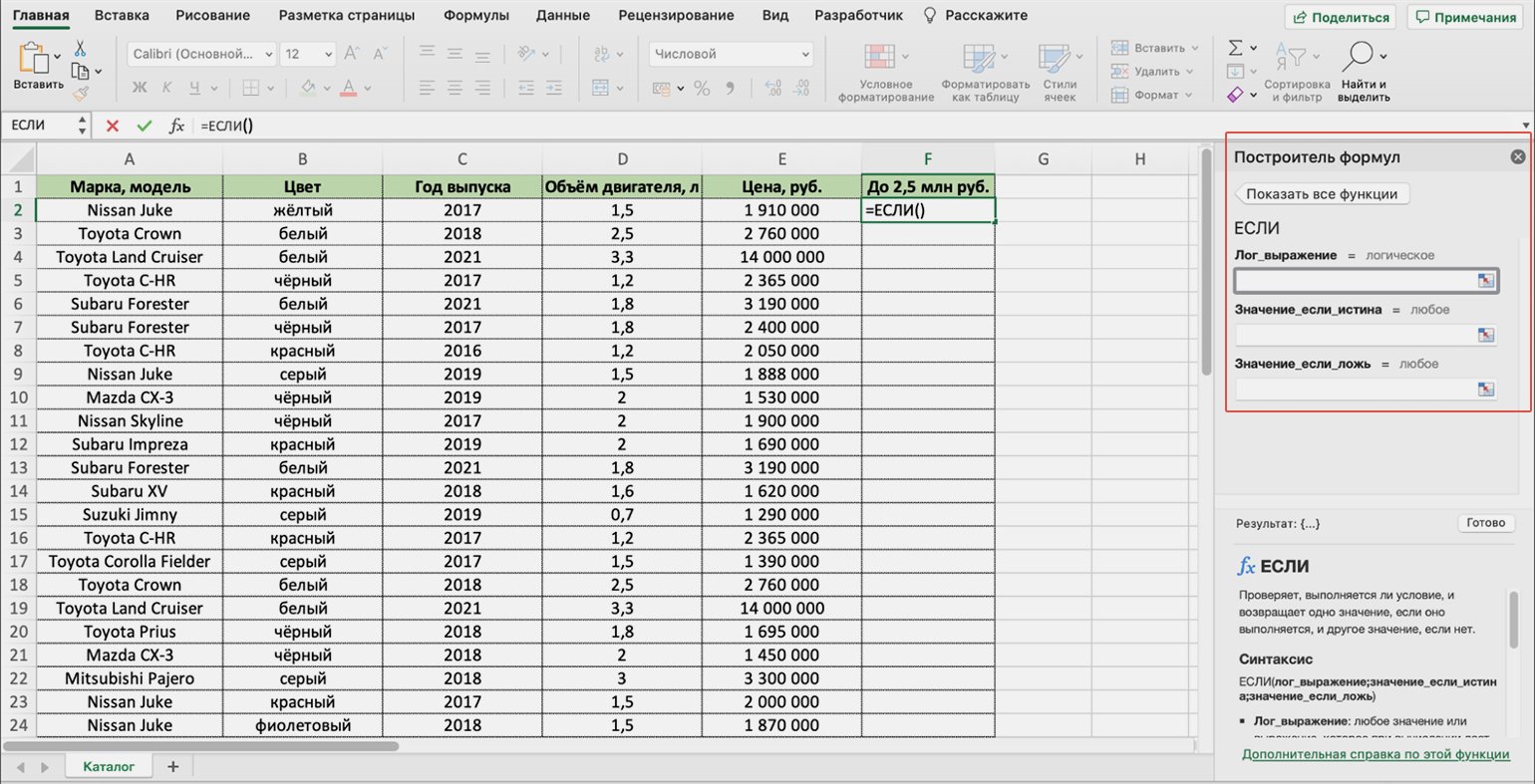
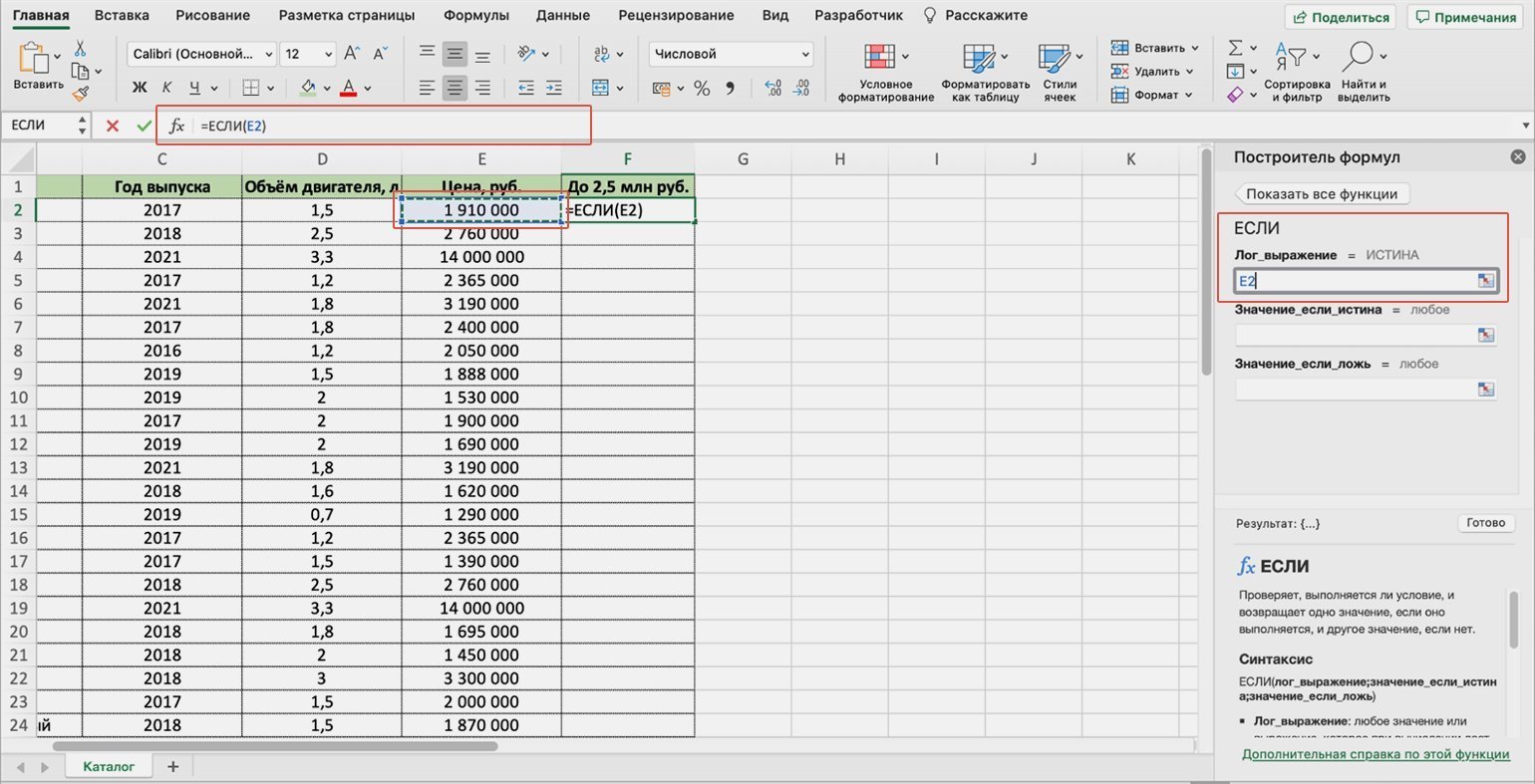
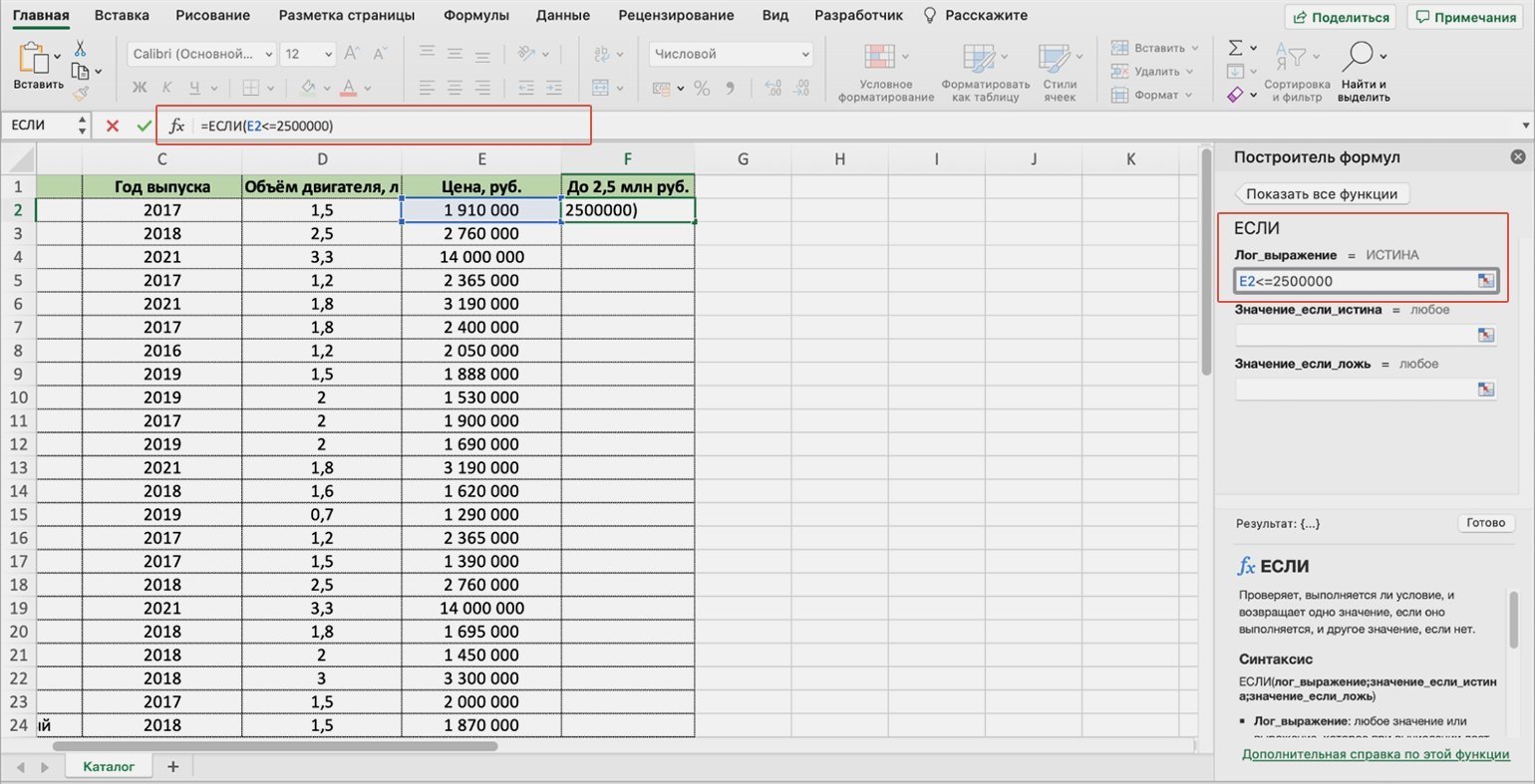
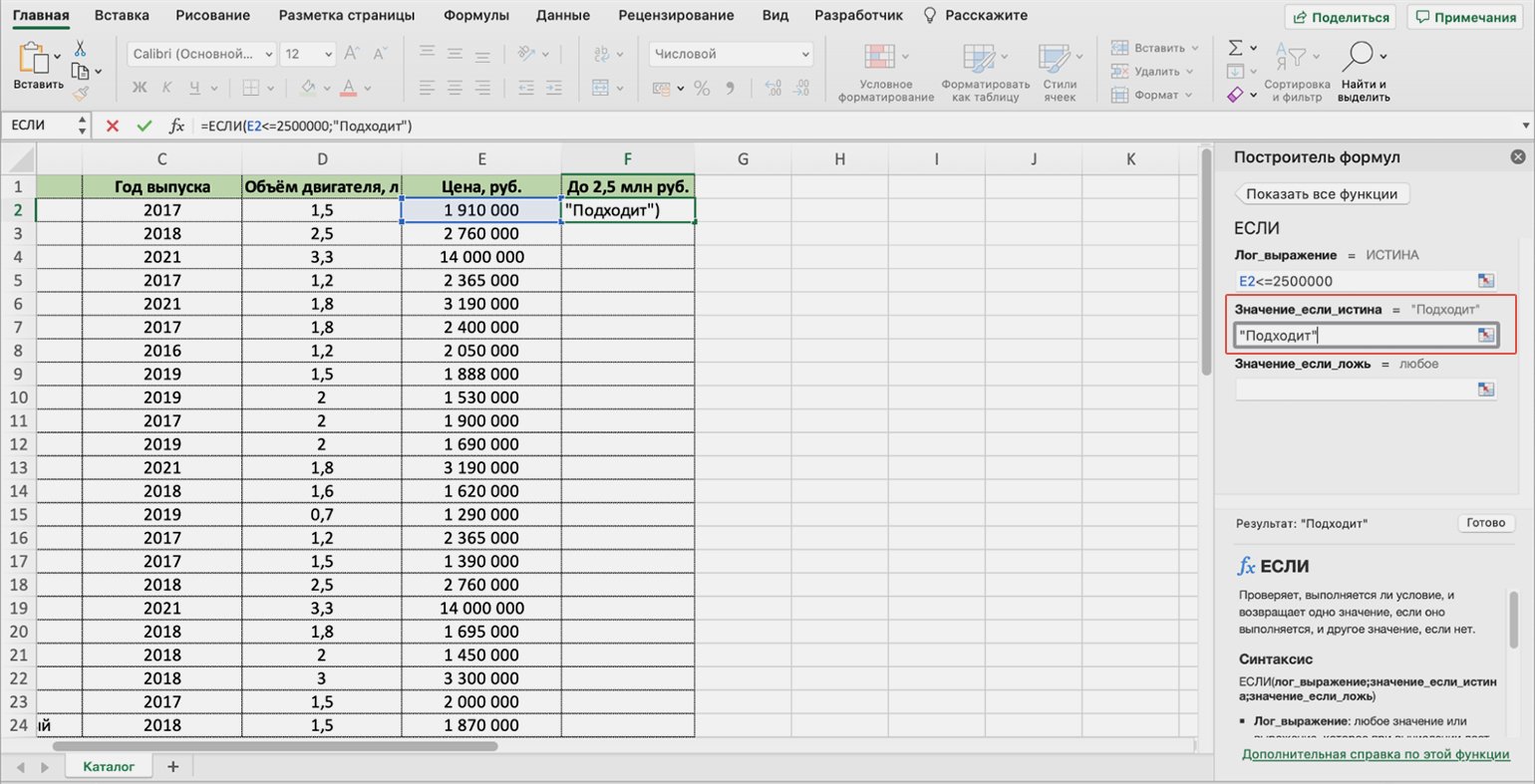
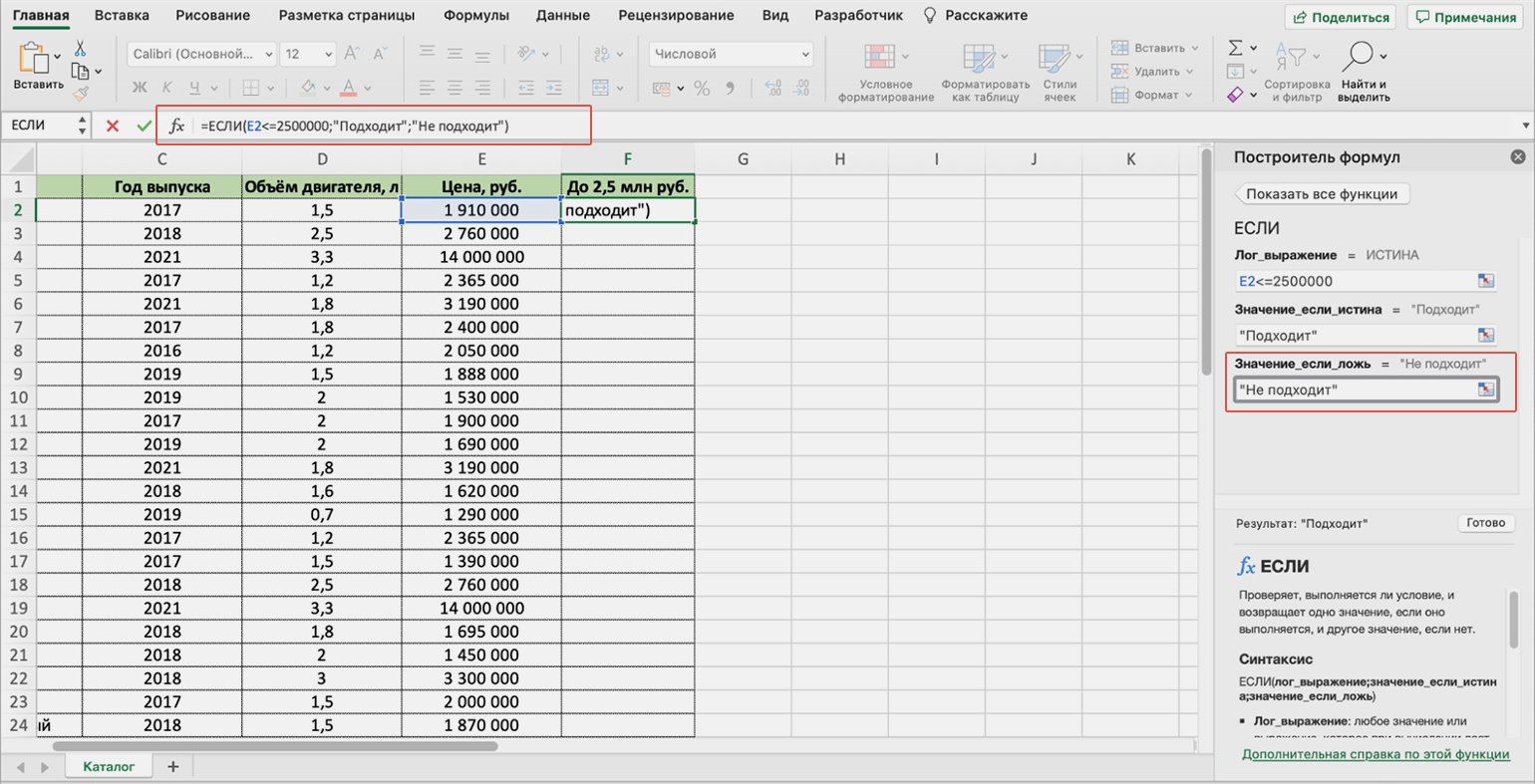
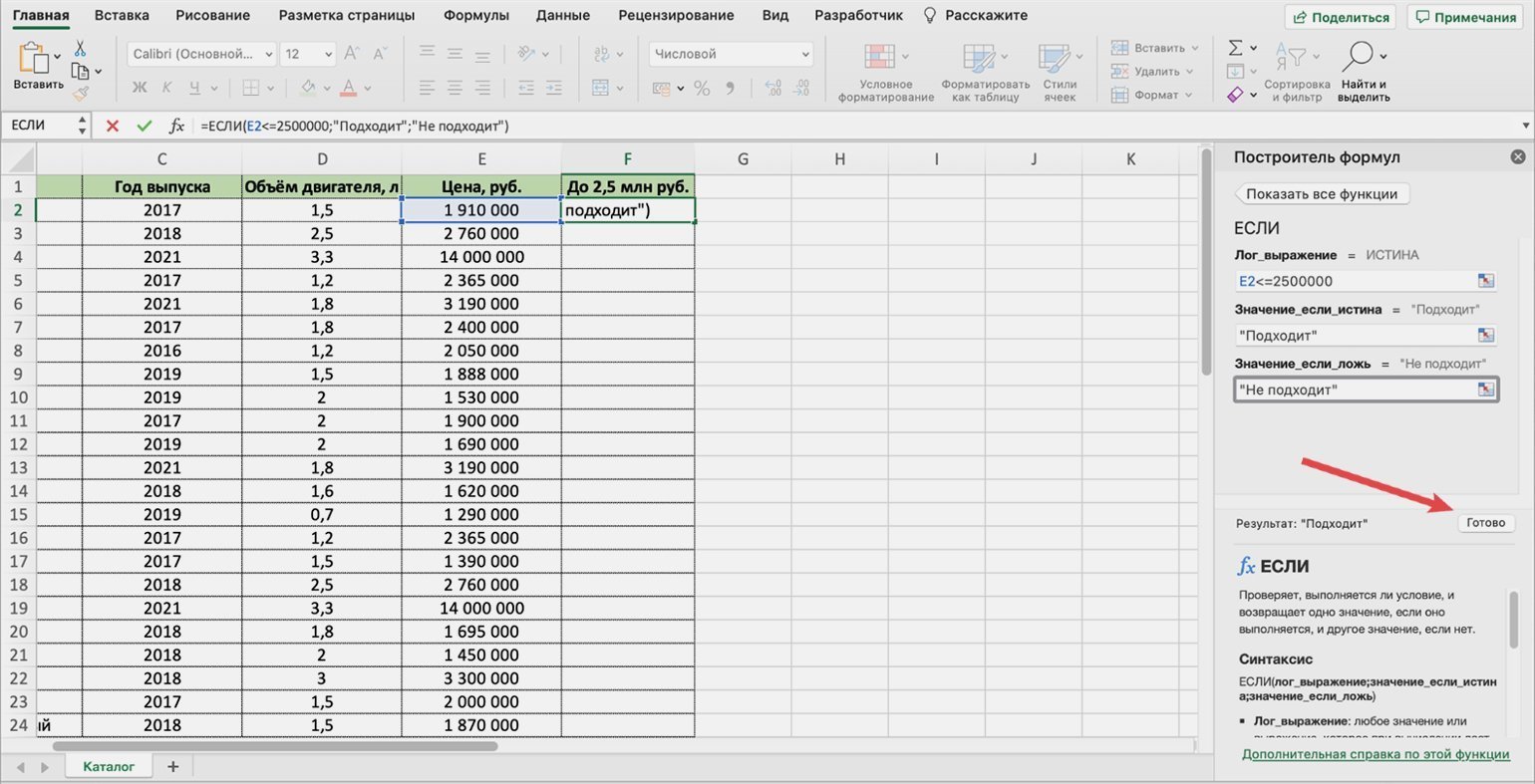
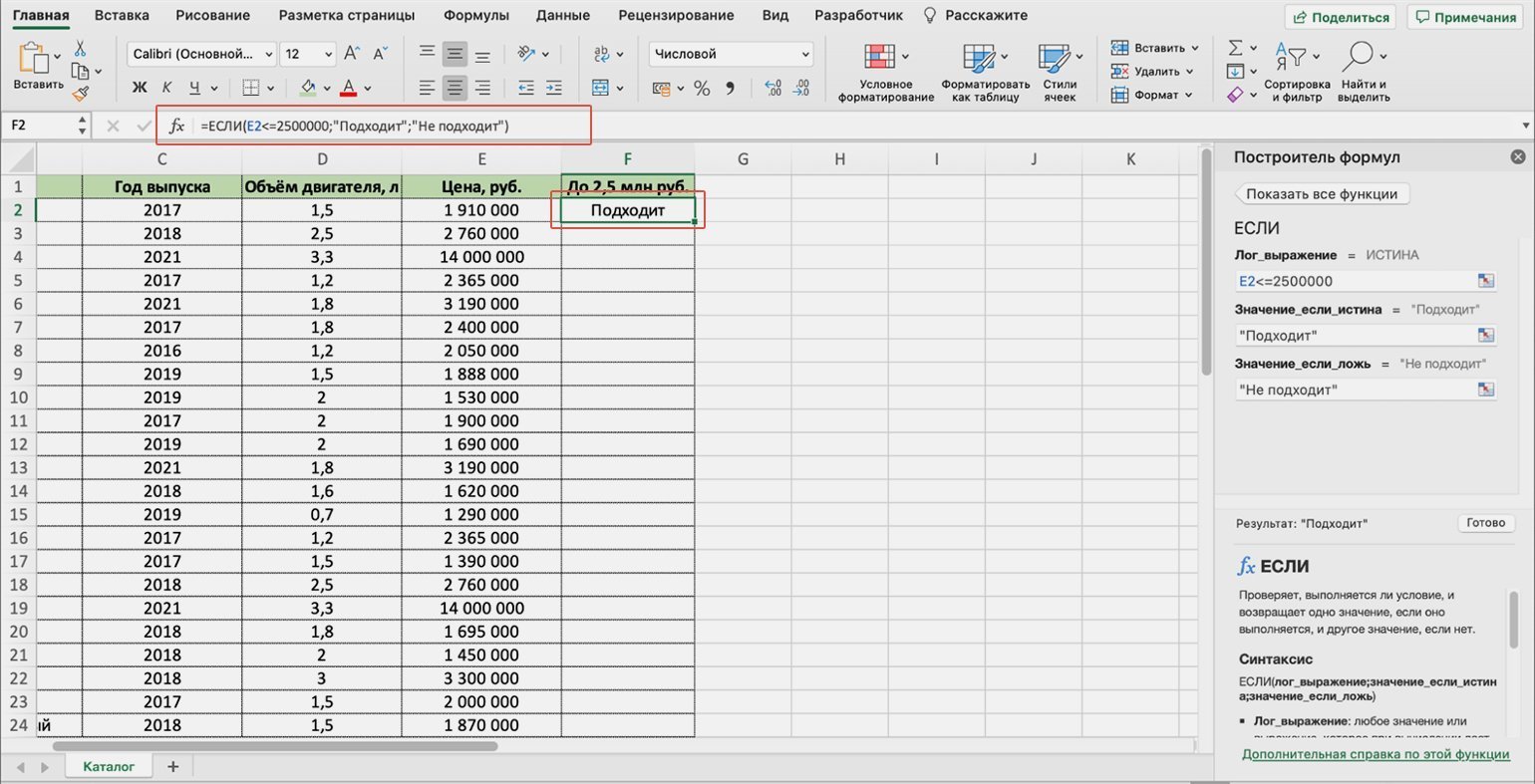
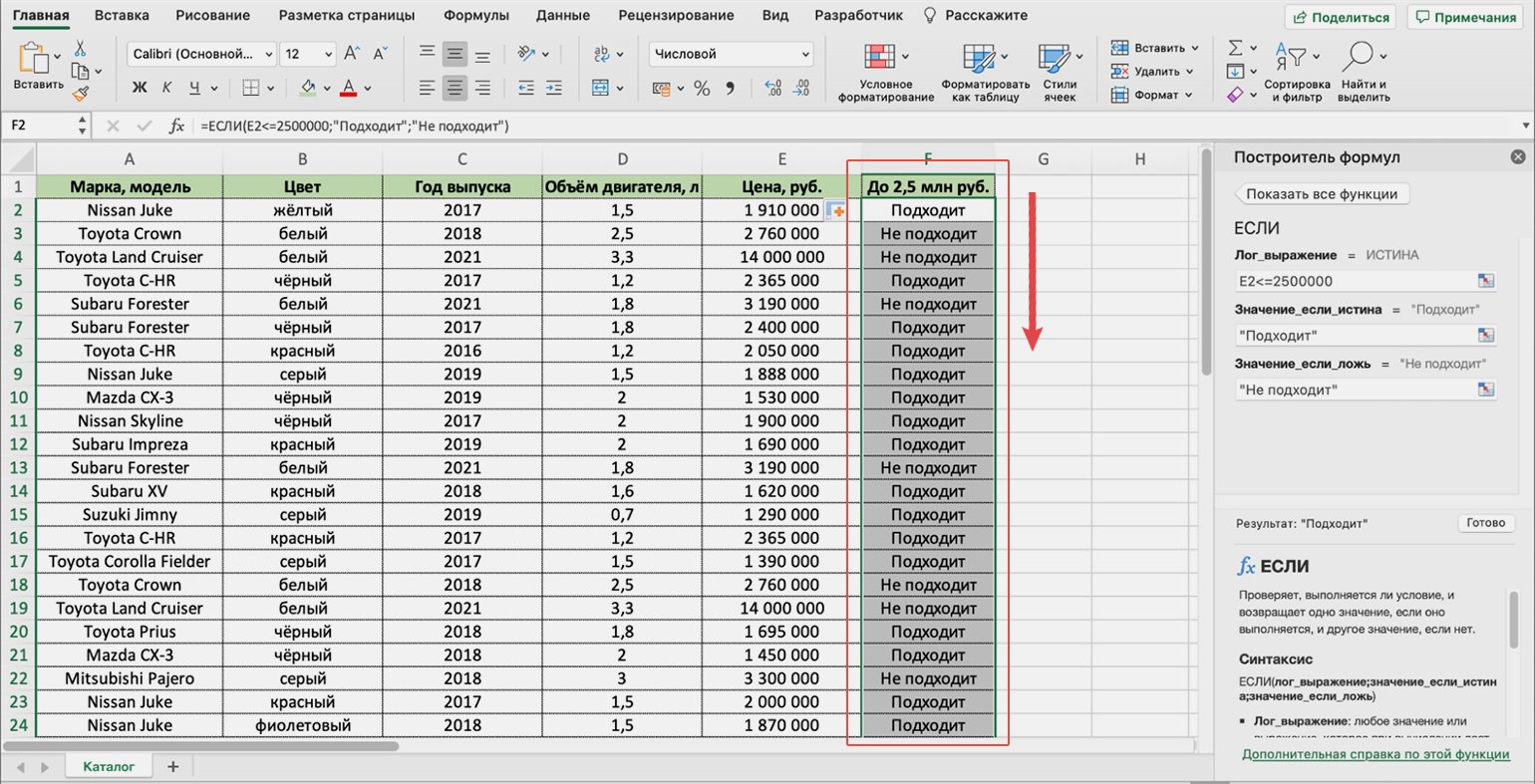
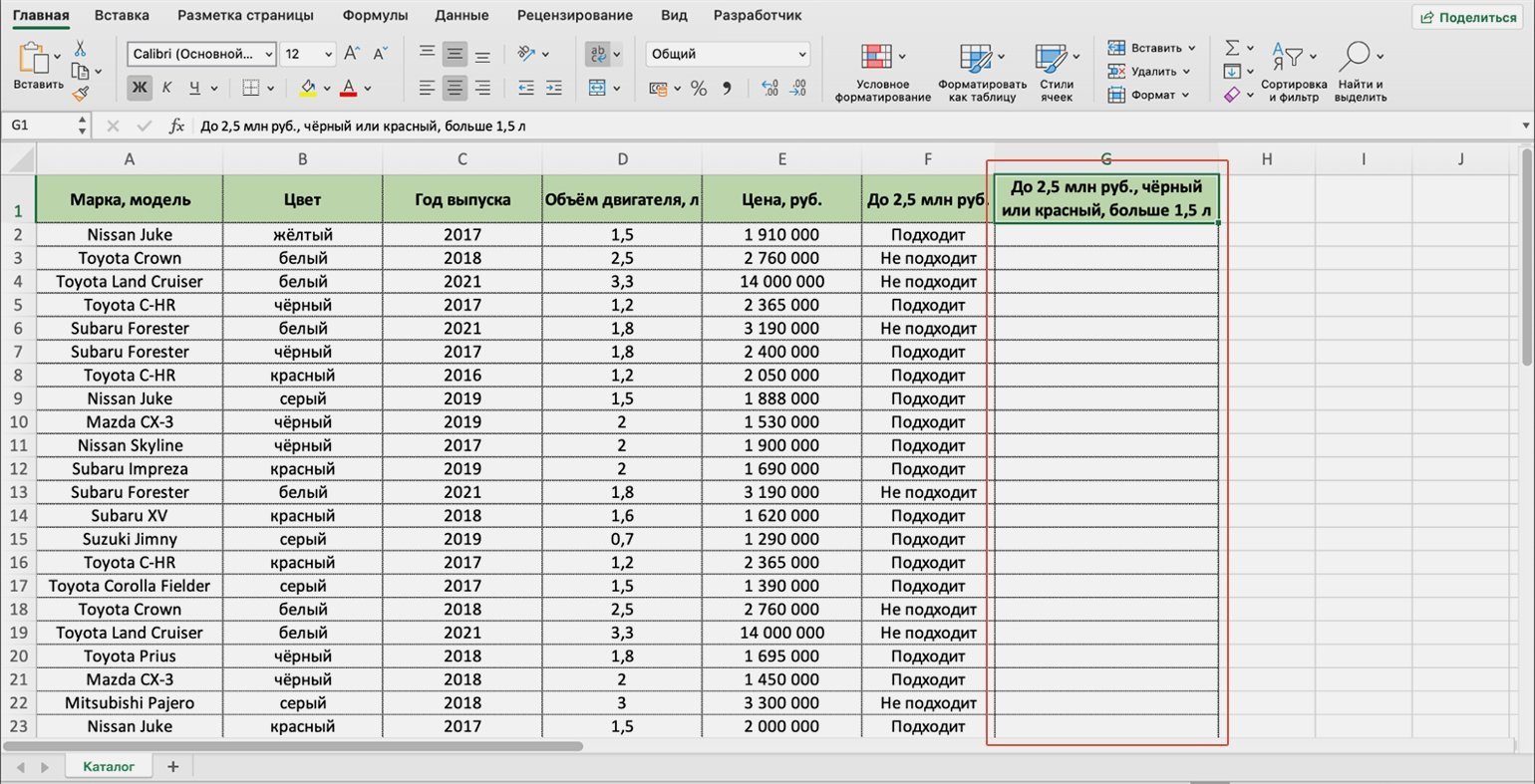
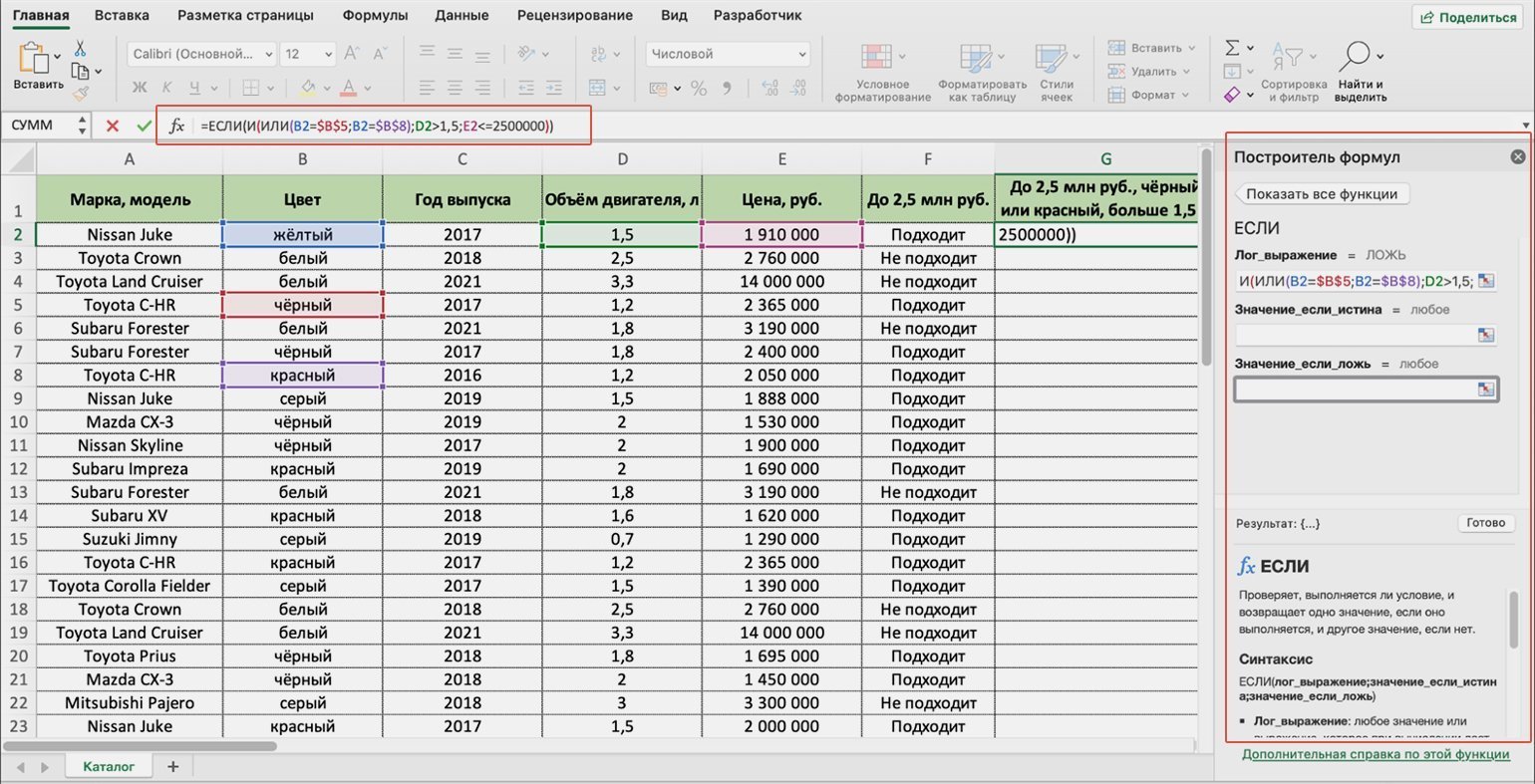
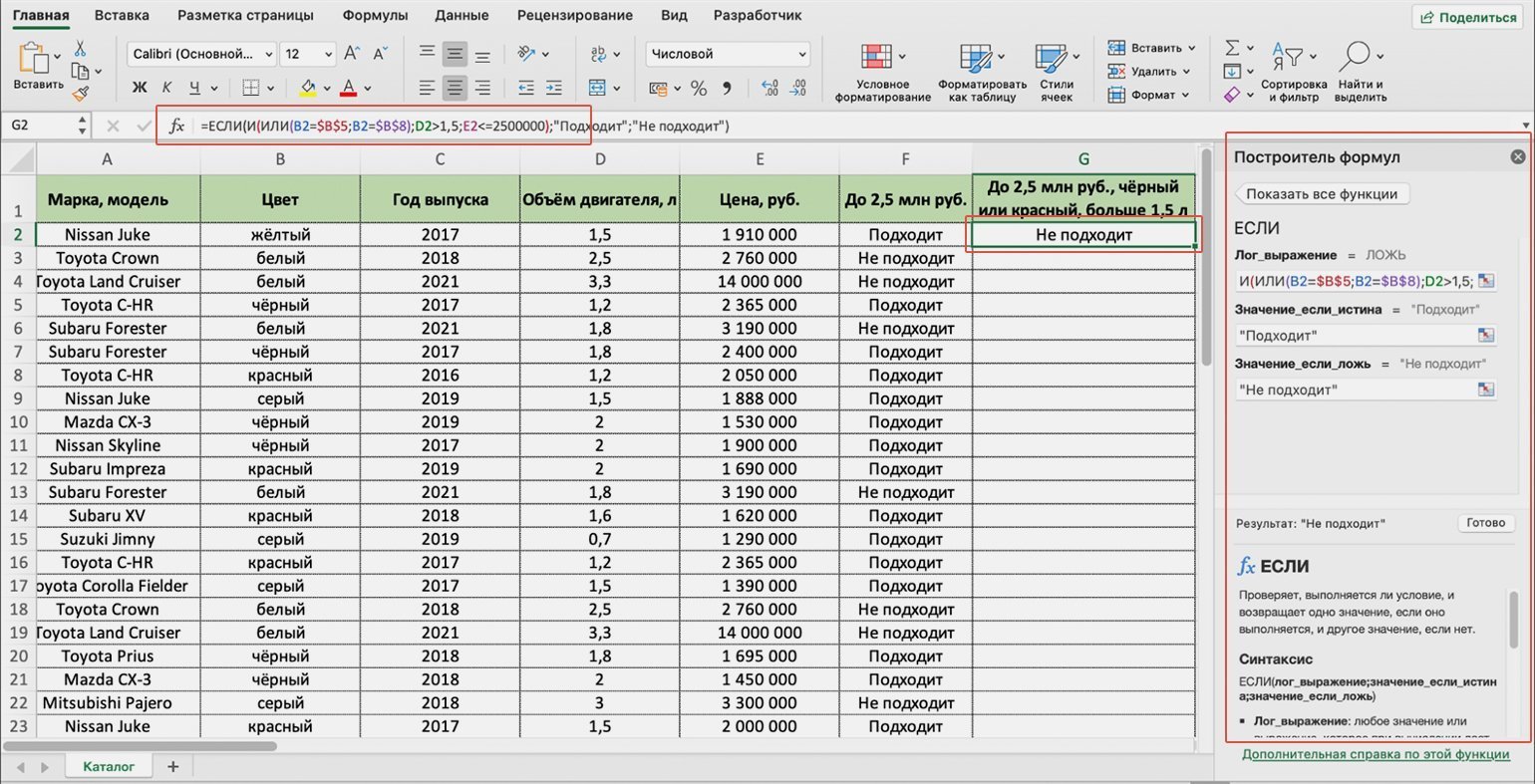
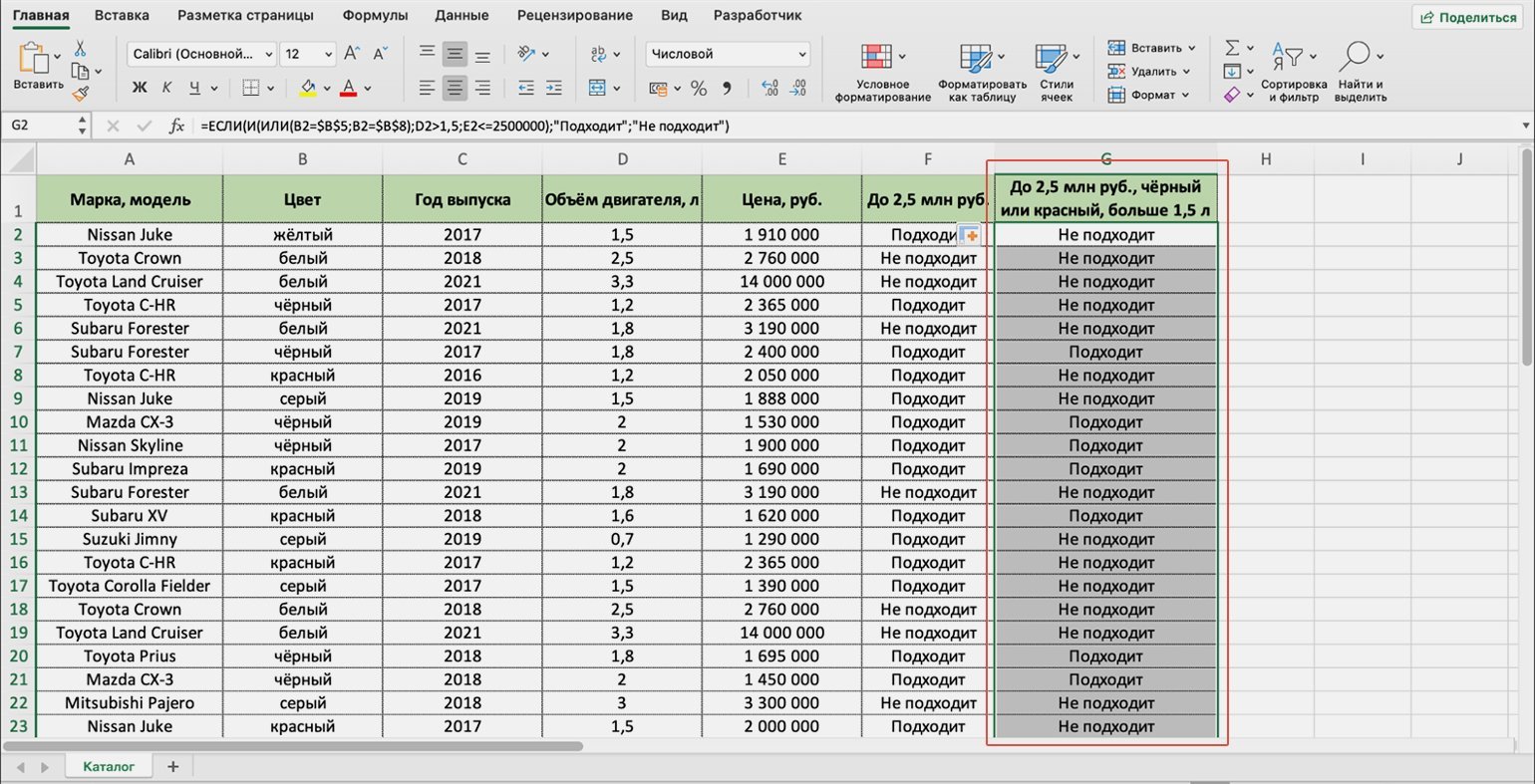

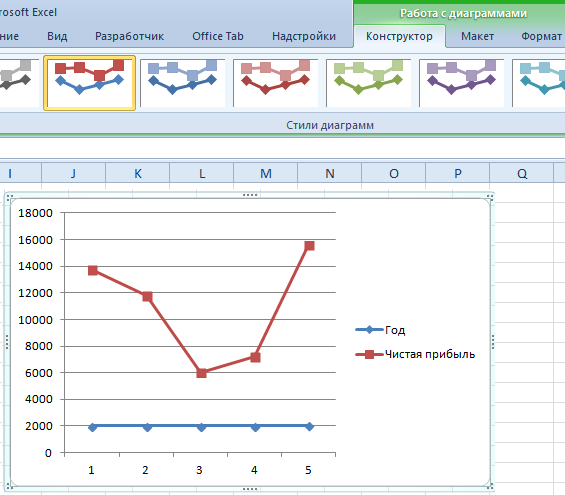
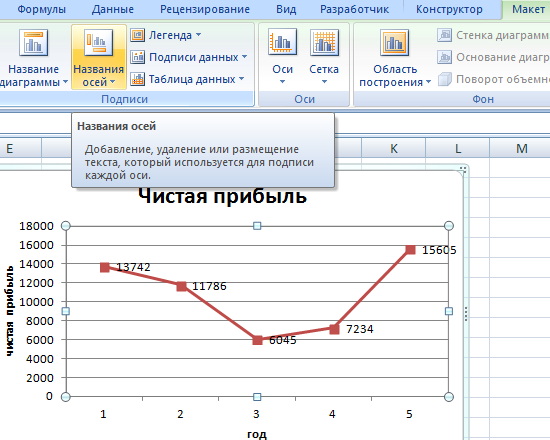
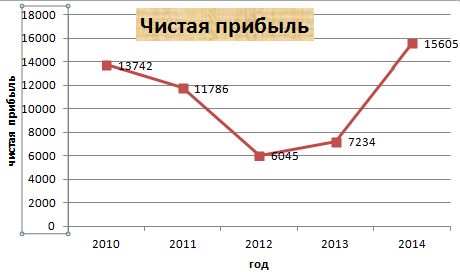
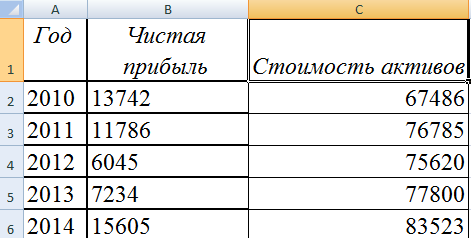
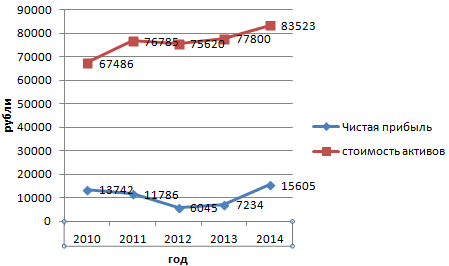
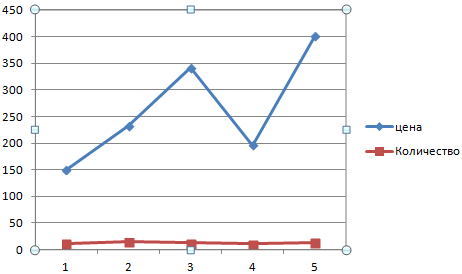
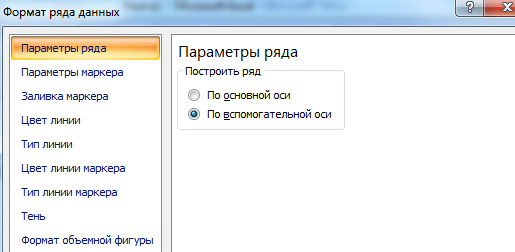
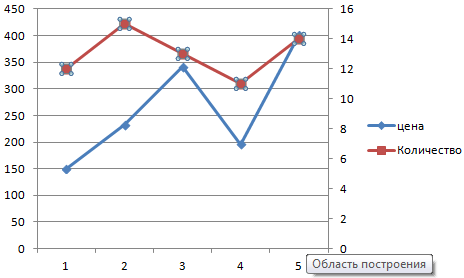
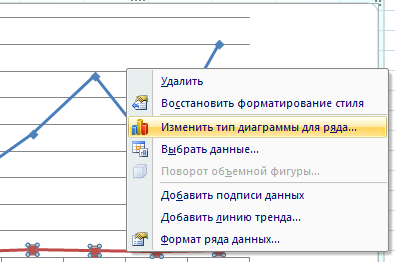
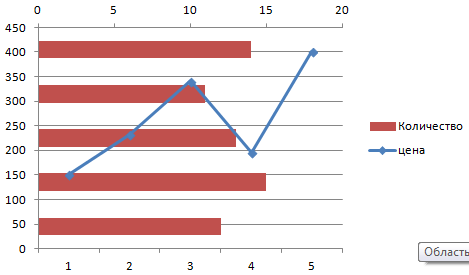
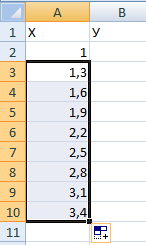
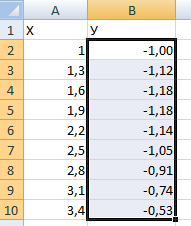
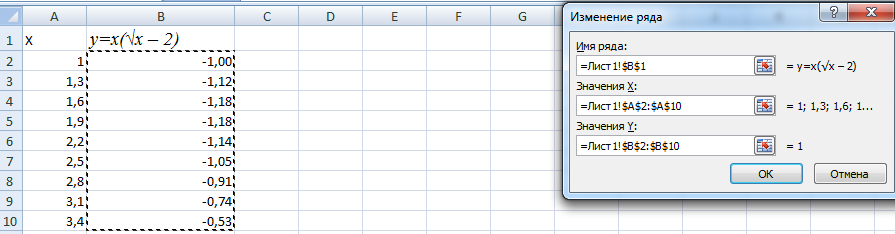
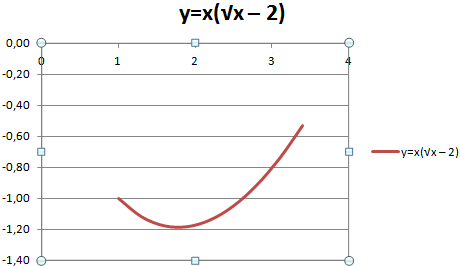
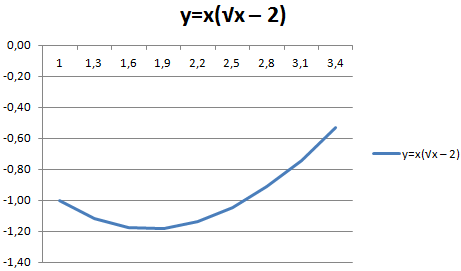
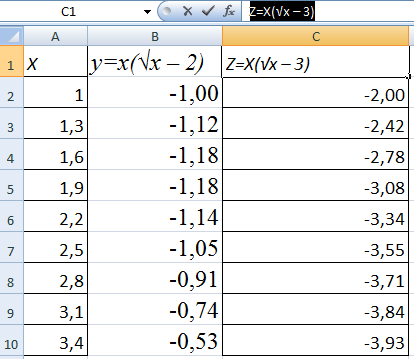
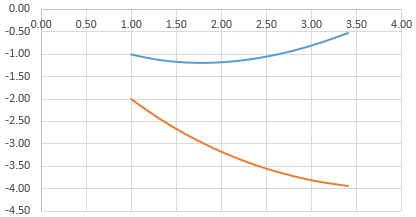
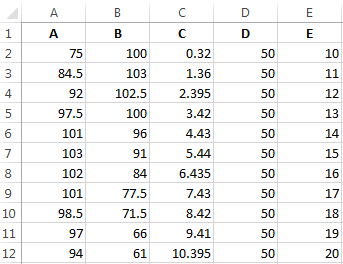
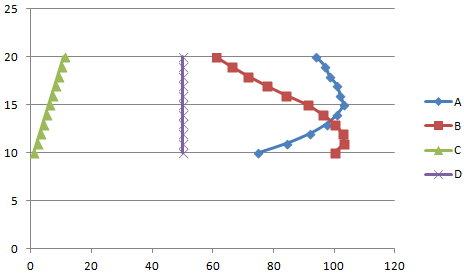


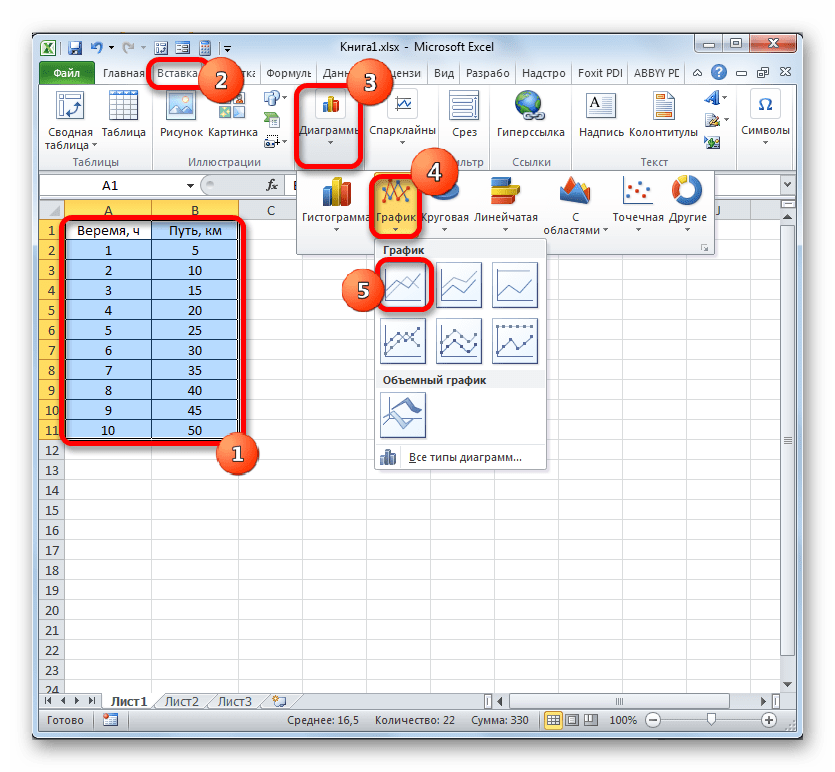

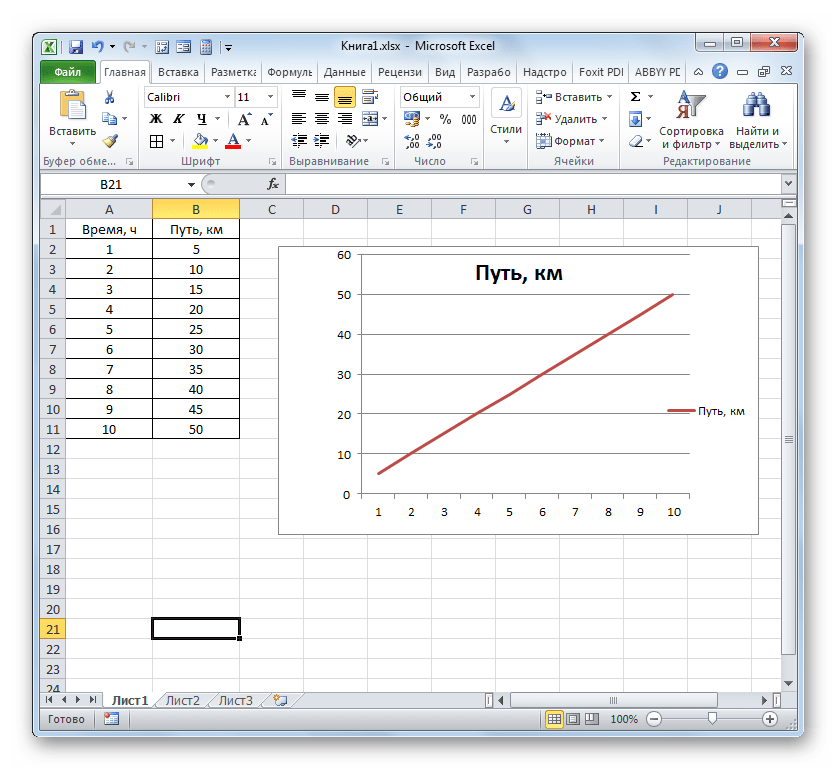
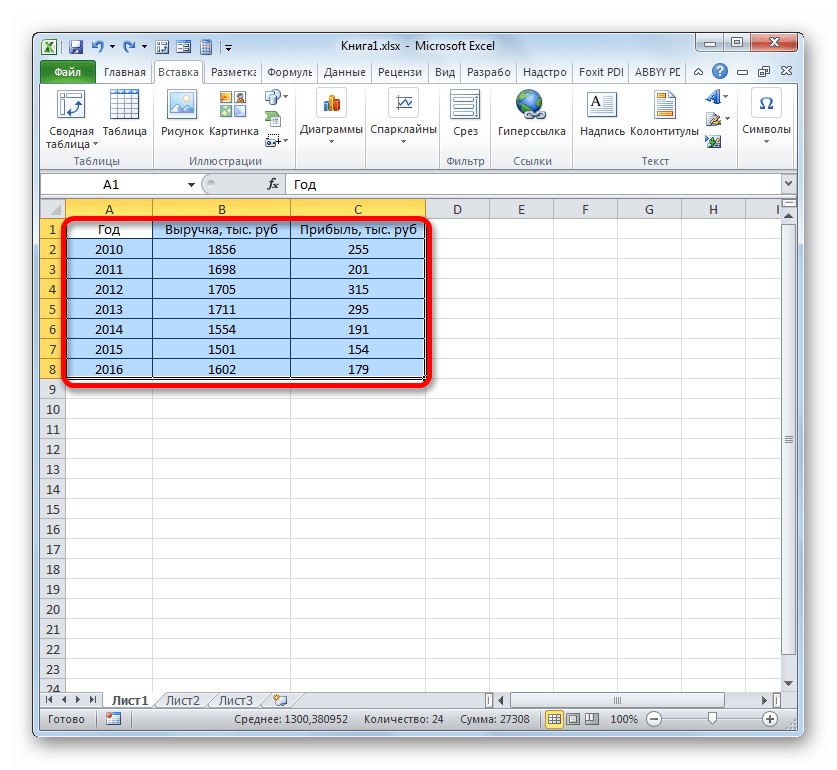
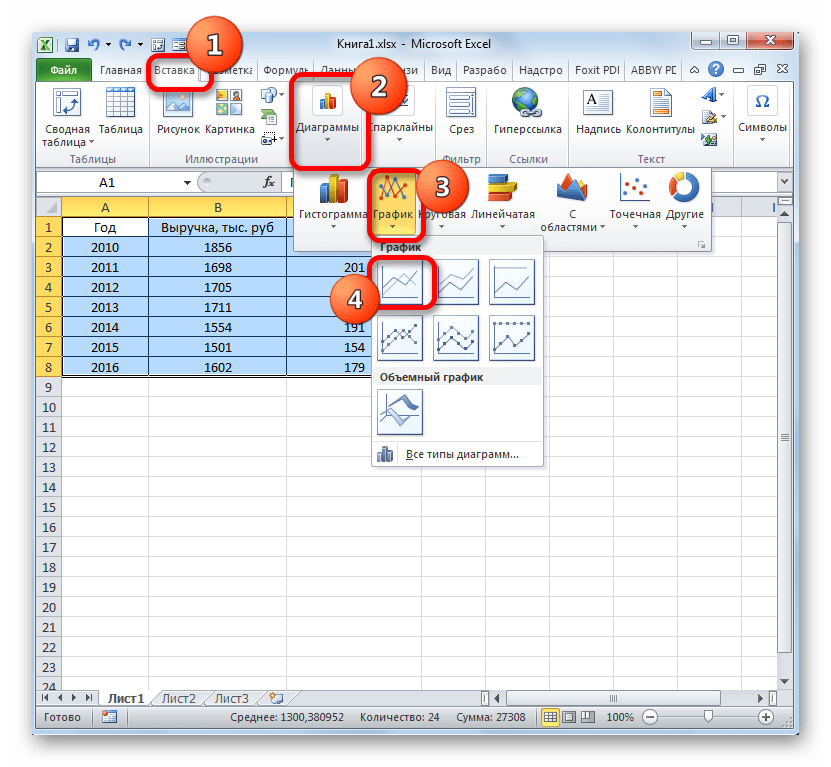
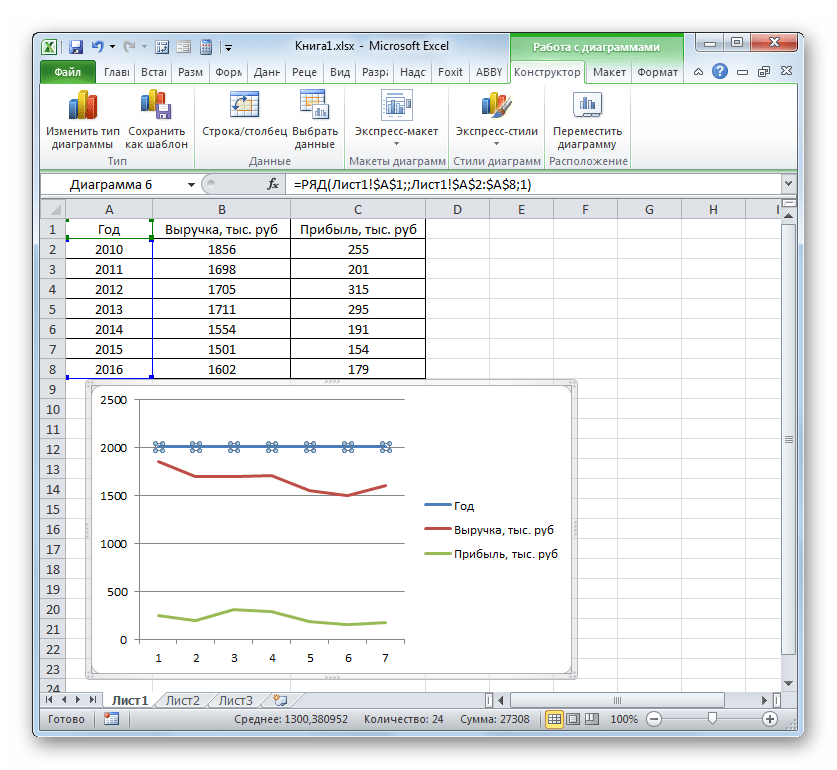
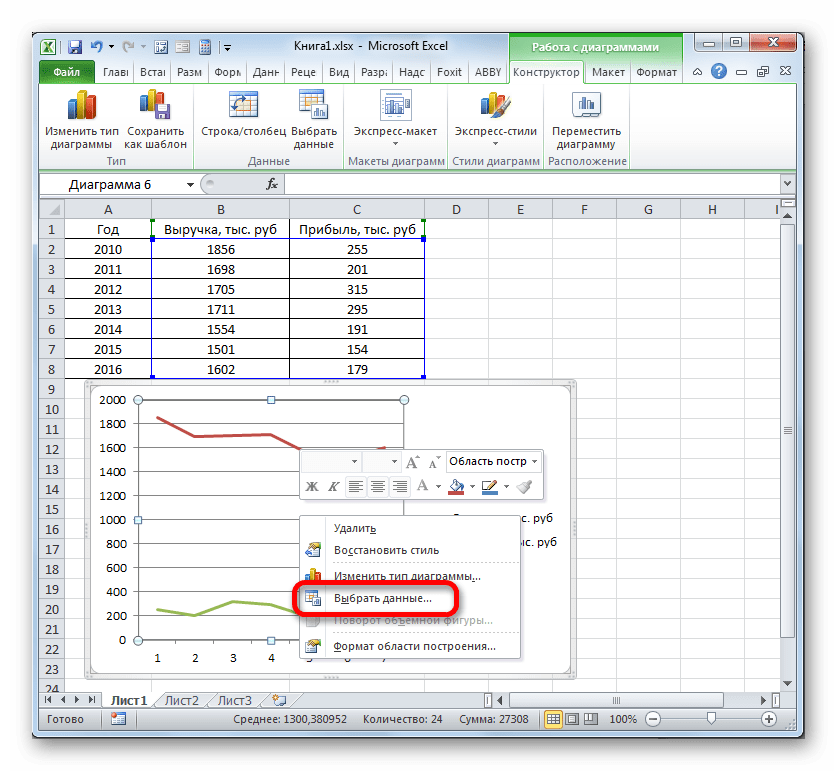
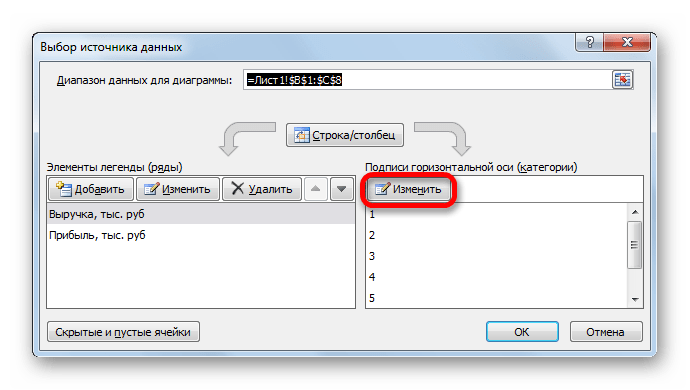
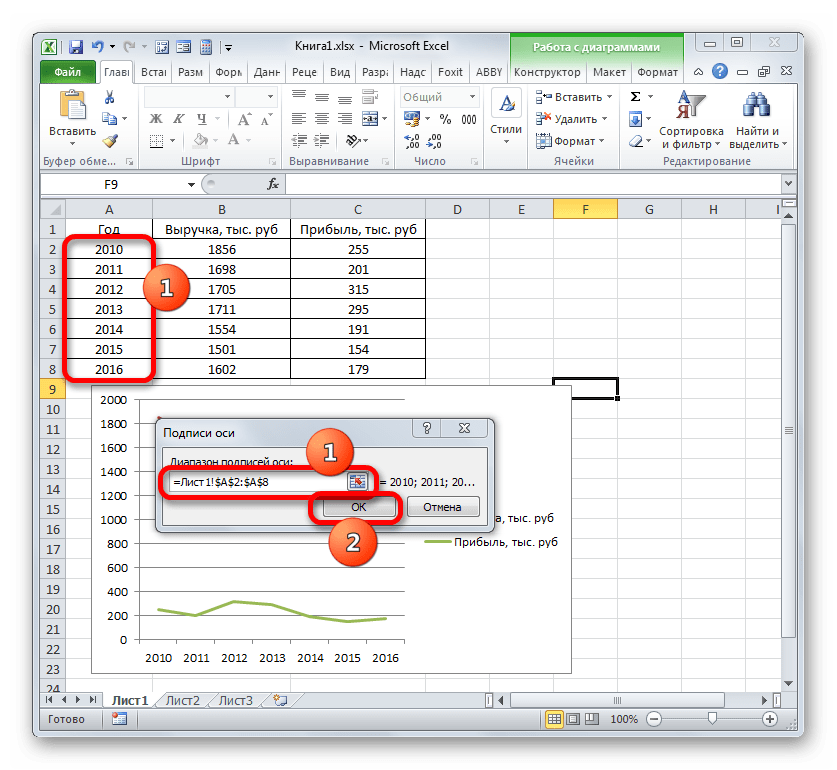
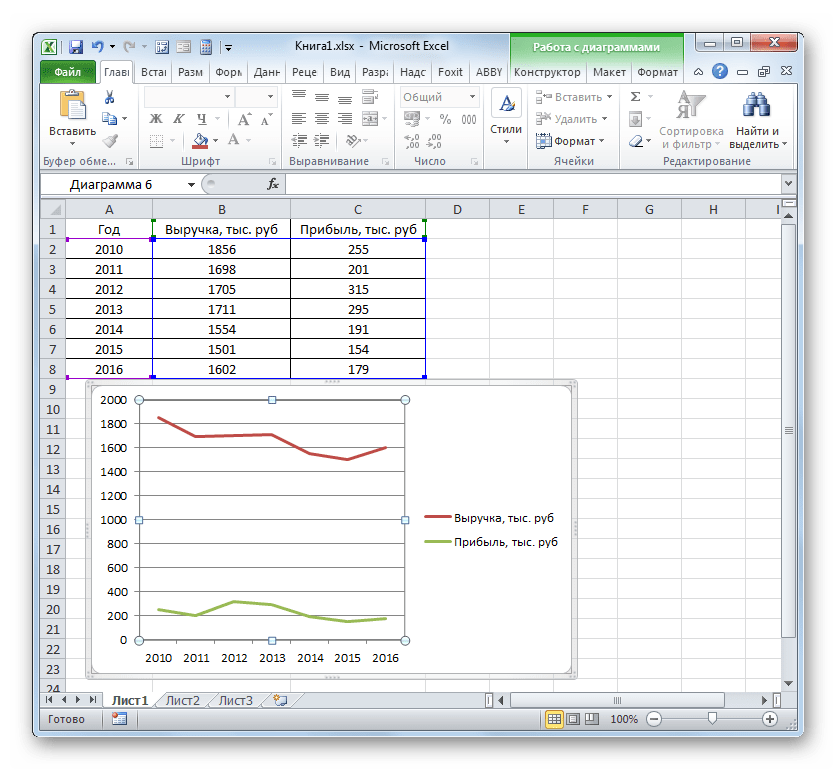
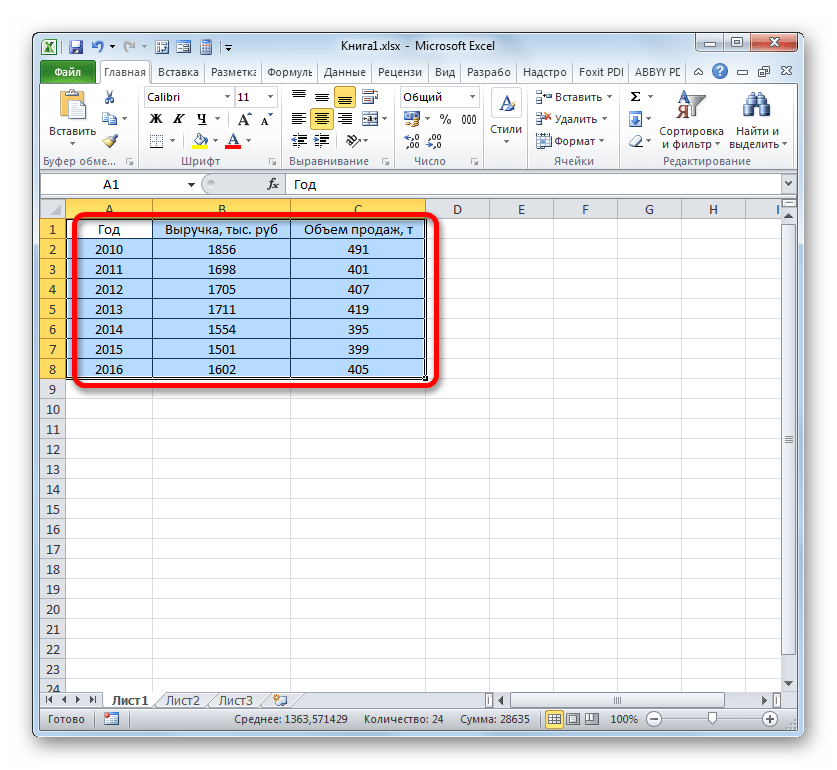
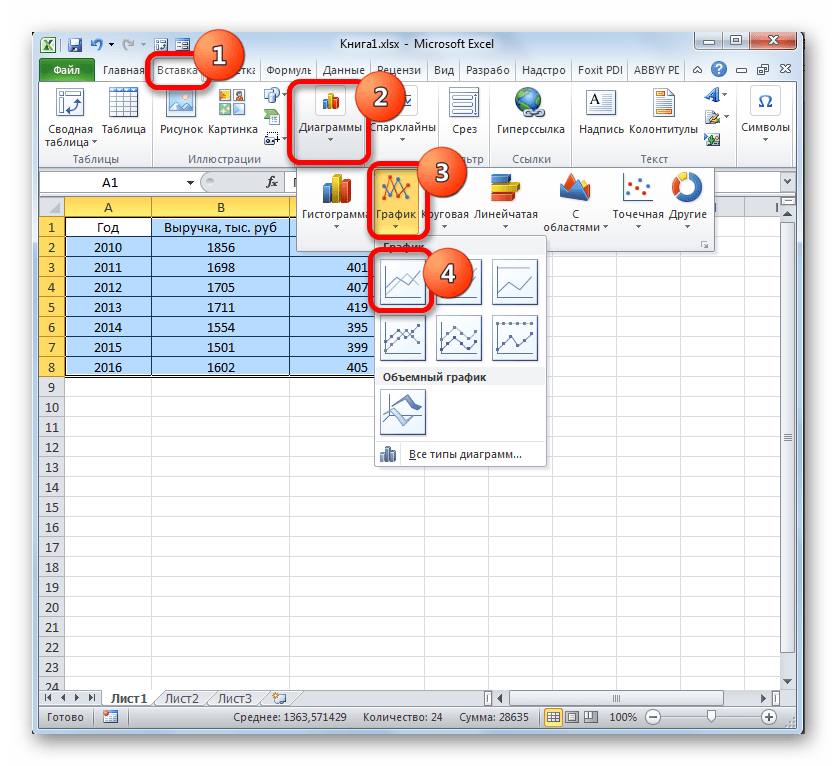

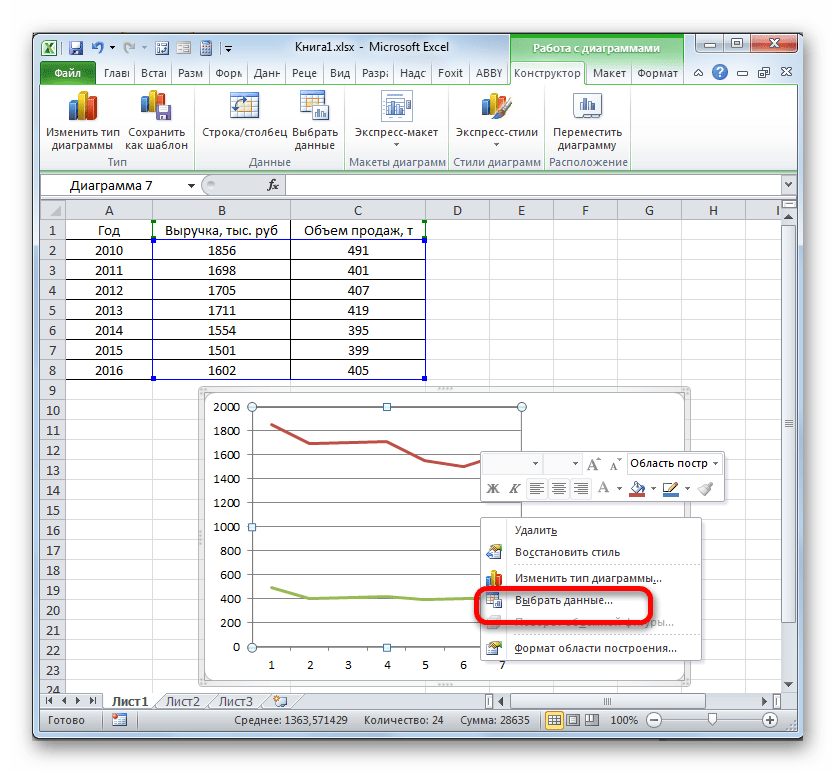


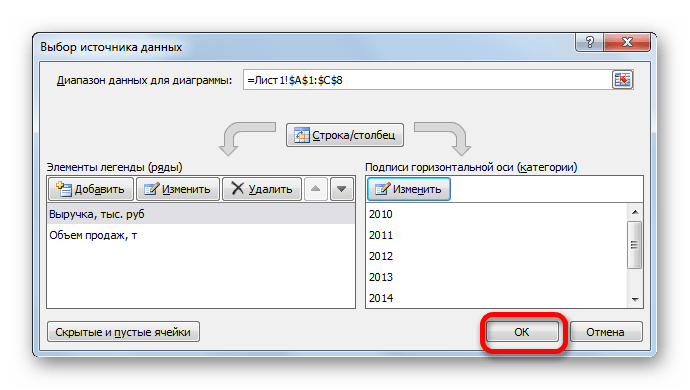
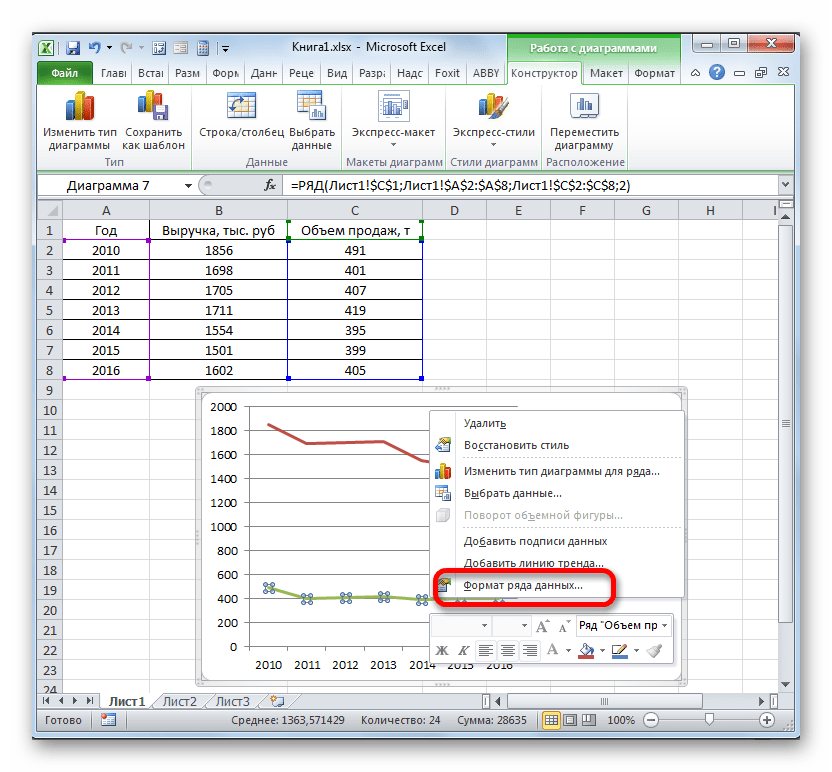
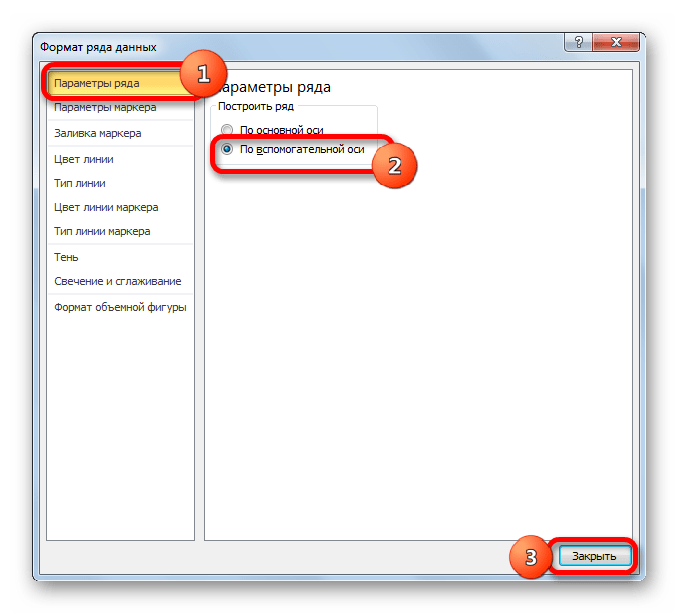
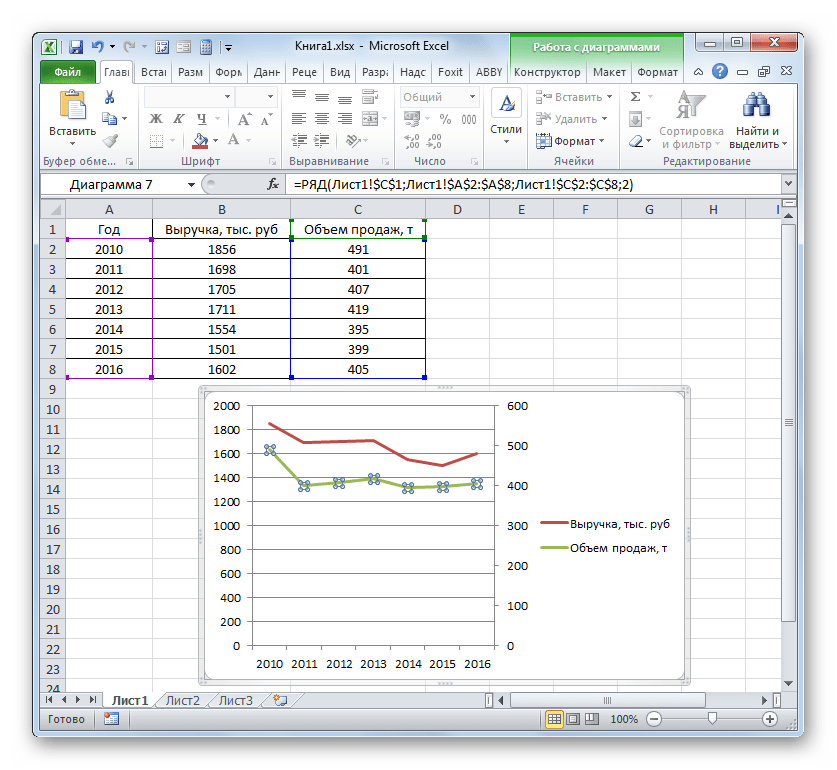
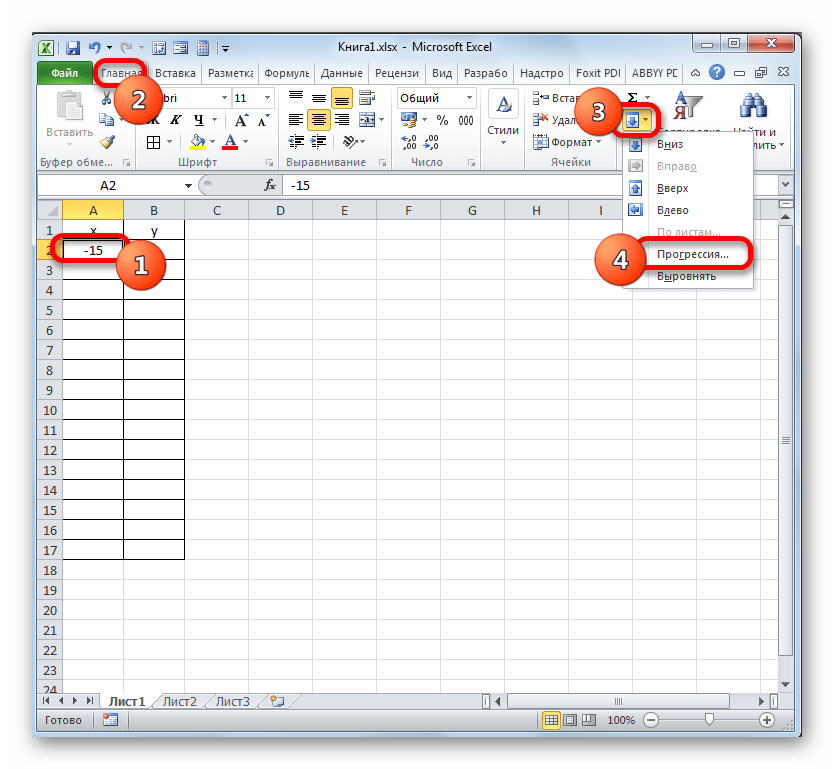
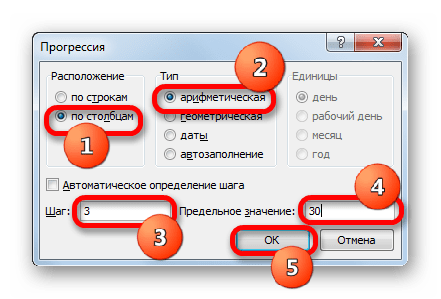
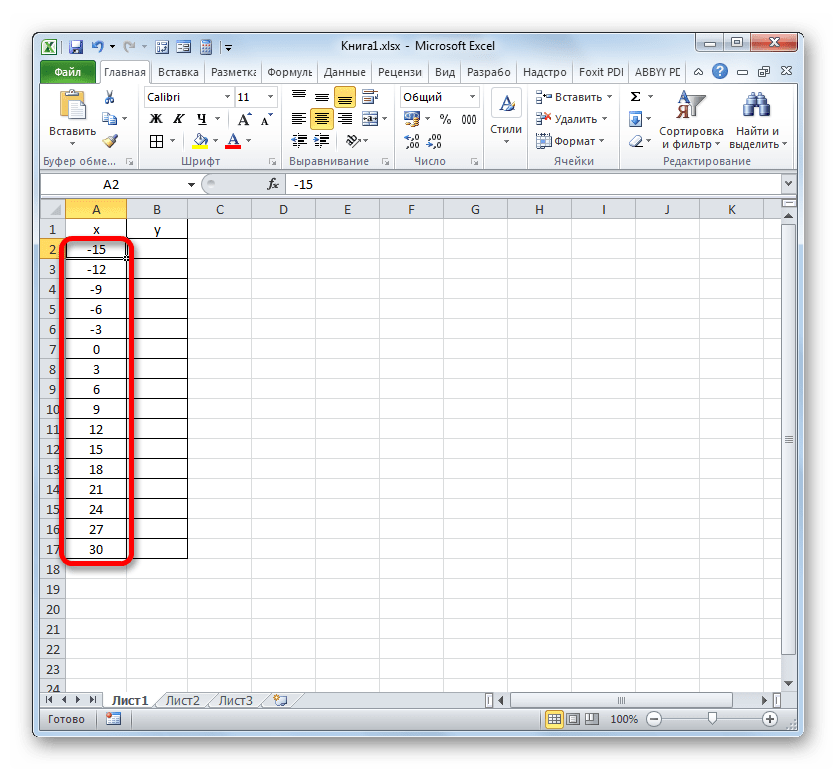
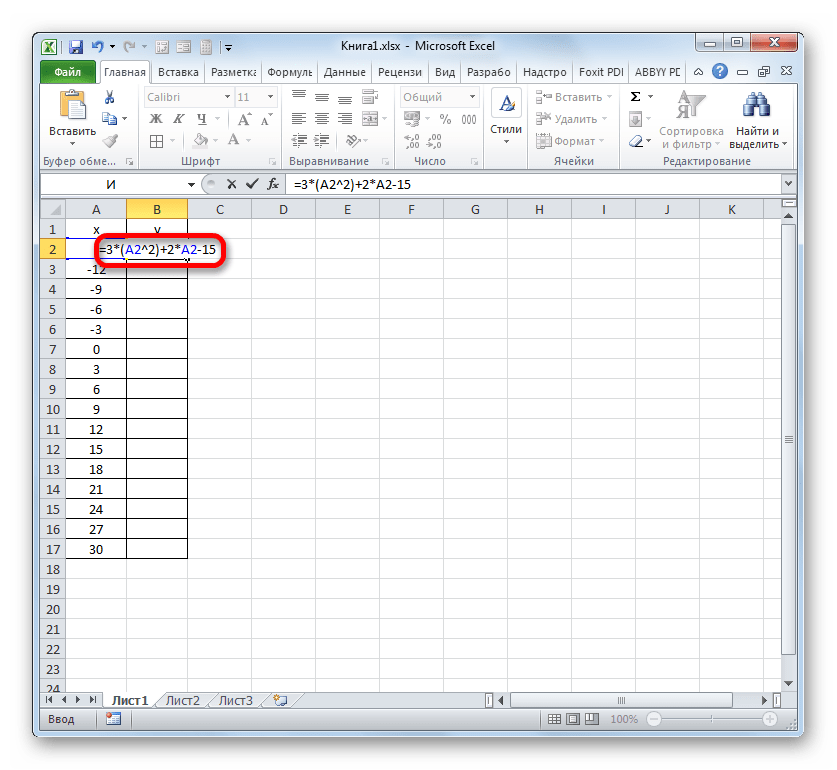
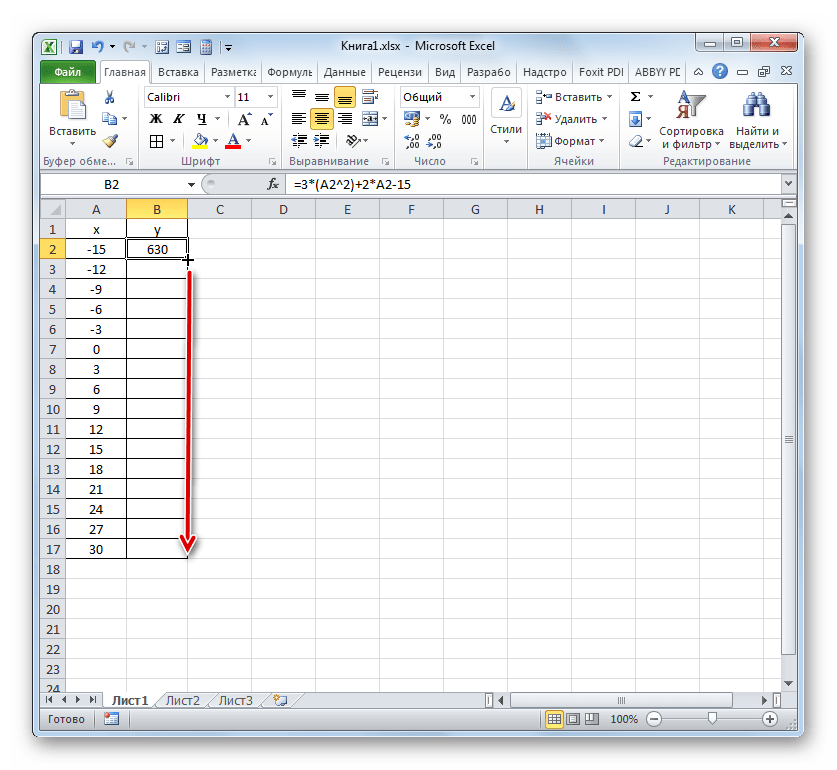
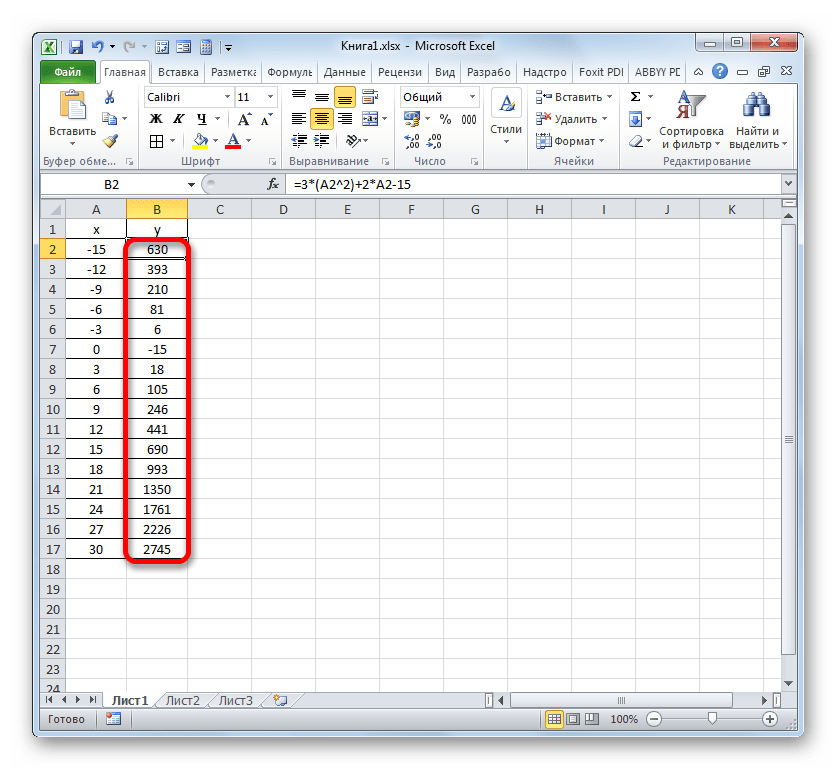
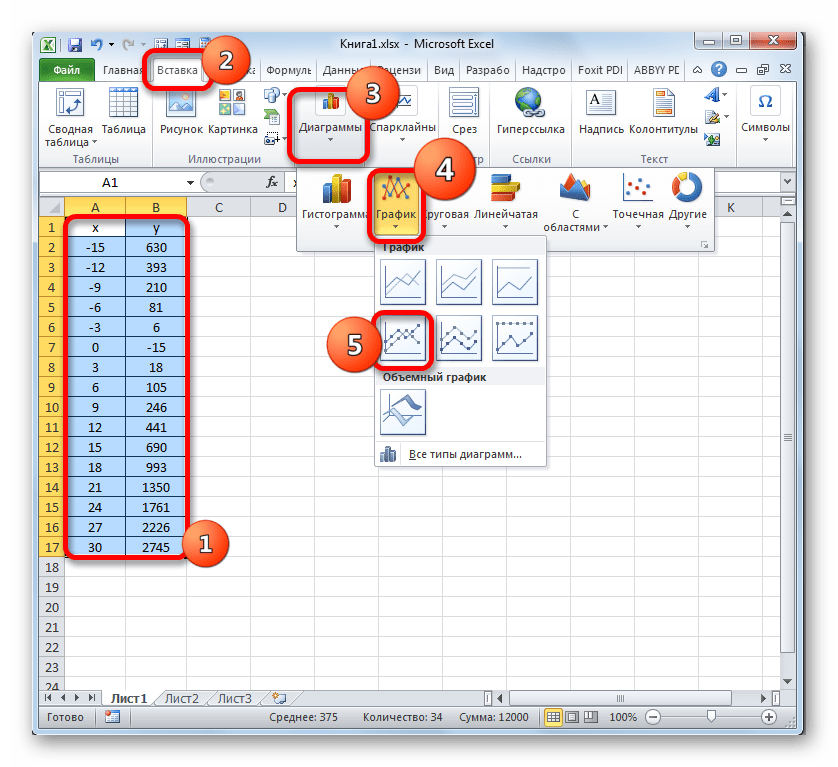
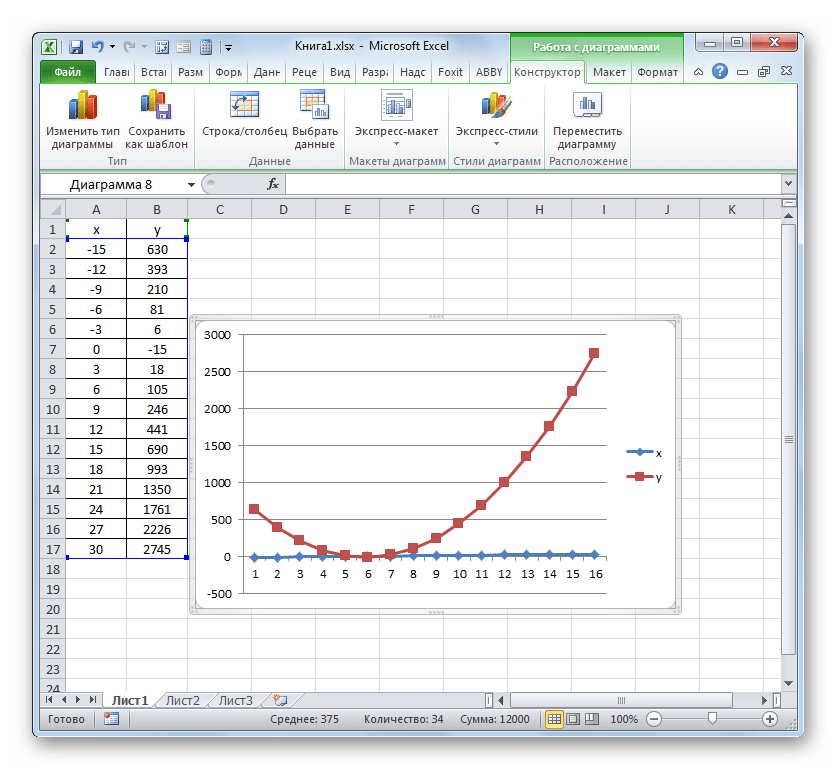
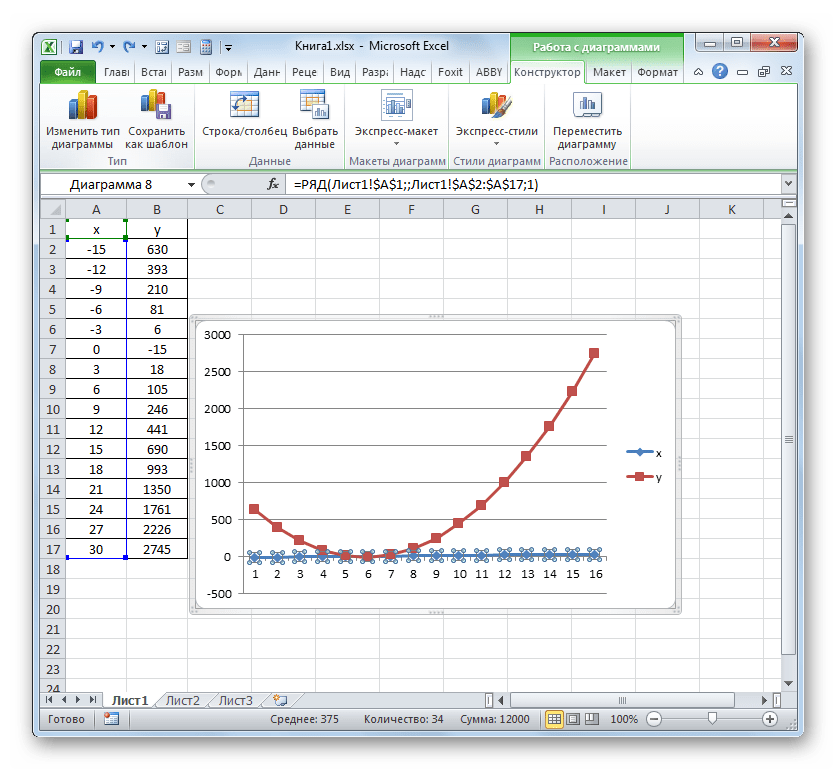
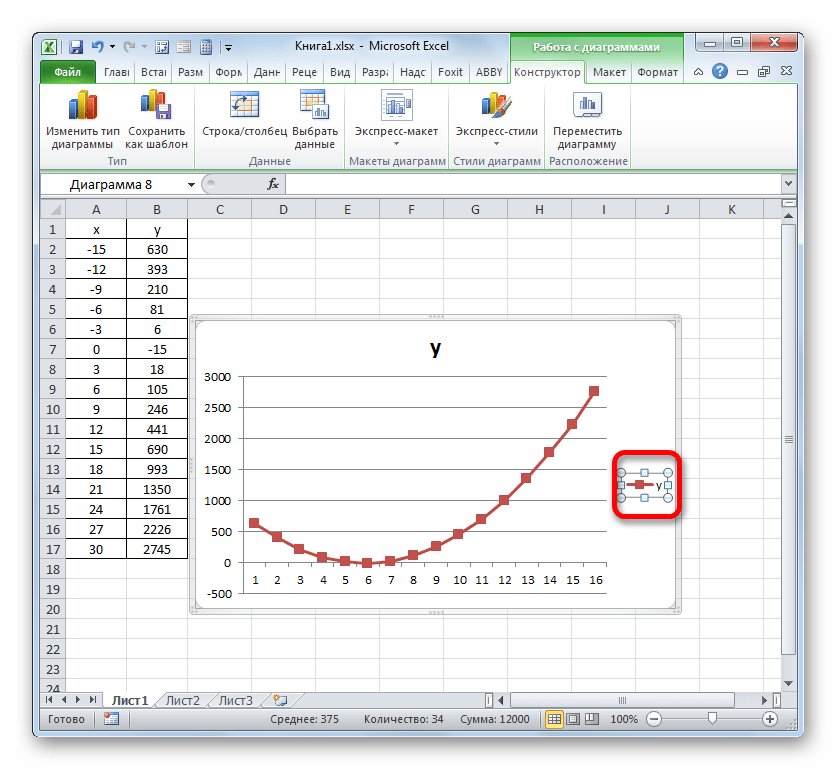
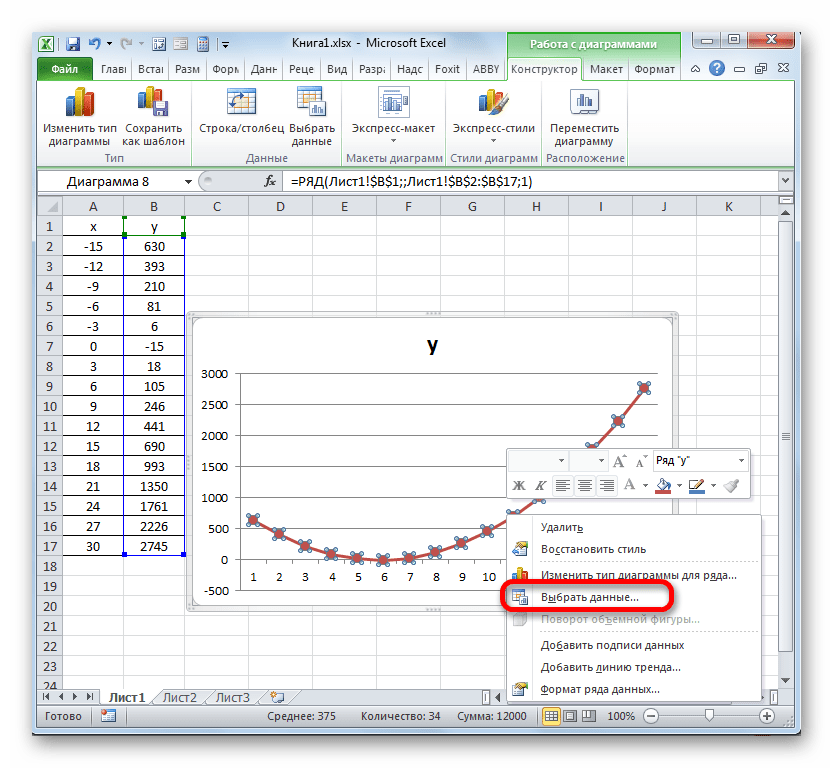
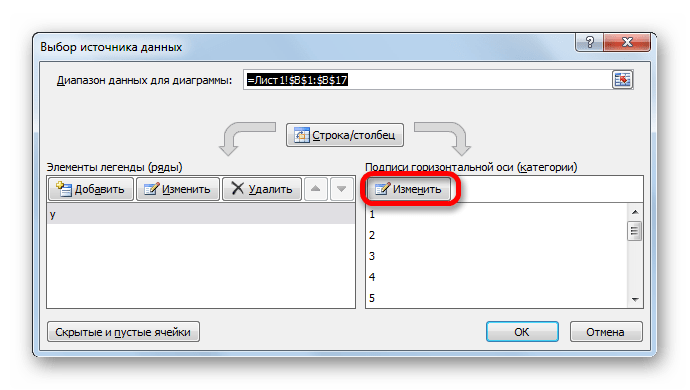
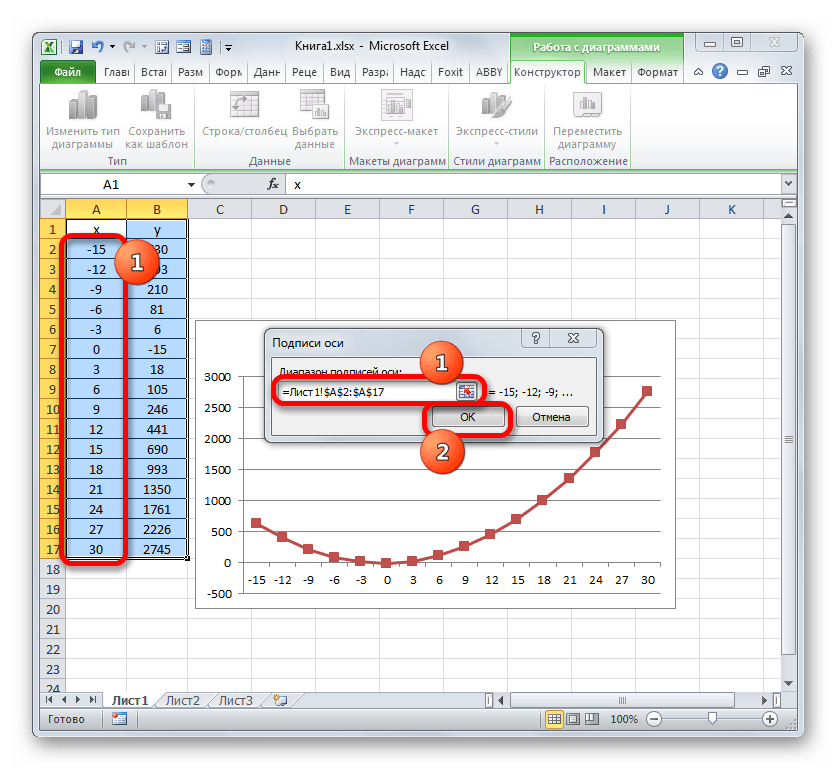
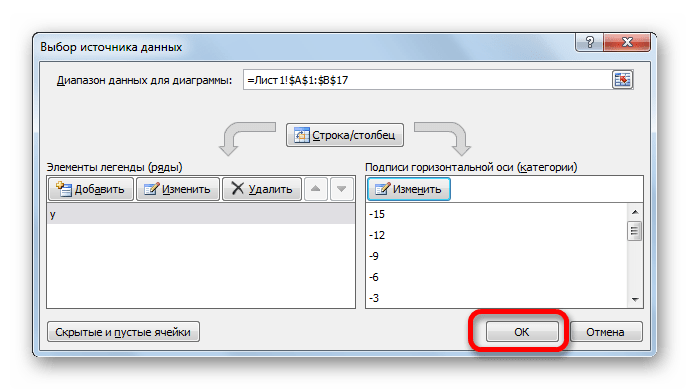
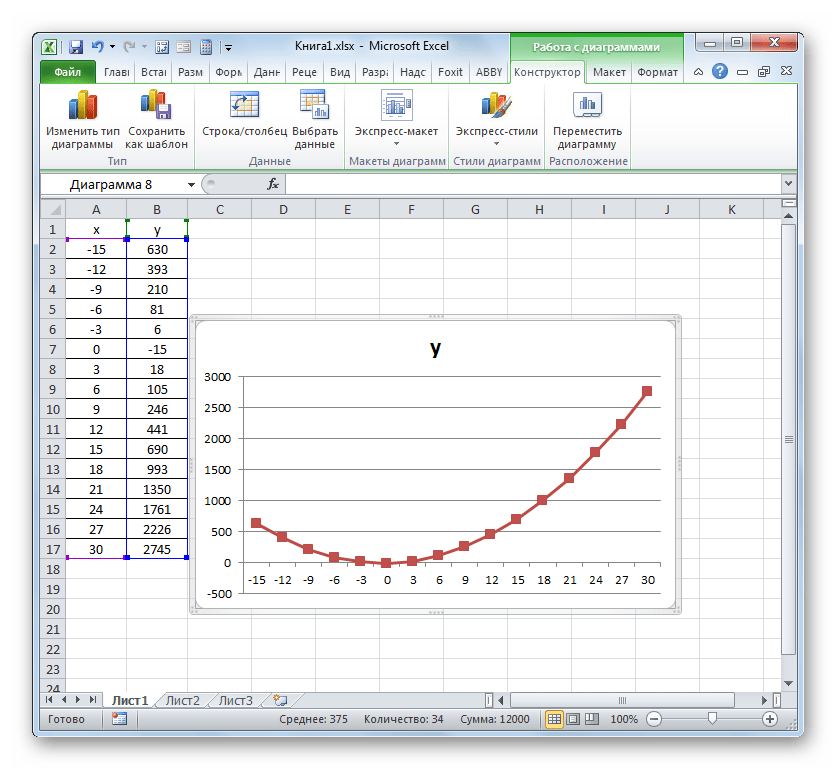











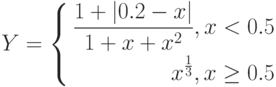
![$$
Y=left{
begin{aligned}
% nonumber to remove numbering (before each equation)
1+ln(1+x), x<0.2\
frac{1+x^{frac{1}{2}}}{1+x}, xin[0.2;0.8]\
2e^{-2x}, x>0.8
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/4205ce0704c58087ee2090c98d69defd.png)






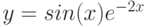
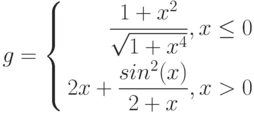
![$$
z=left{
begin{aligned}
frac{1+|x|}{sqrt[3]{1+x+x^{2}}},xleq-1\
2ln(1+x^{2}+frac{1+cos^{4}(x)}{2+x},xin [-1;0]\
(1+x)^{frac{3}{5}}, xgeq0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c4fbe6f0e5d1dfcbce7a704e471a929.png)
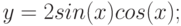
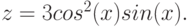
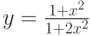
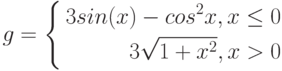
![$$
z=left{
begin{aligned}
frac{1+x}{sqrt[3]{1+x^{2}}},xleq0\
-x+2e^{-2x},xin(0,1)\
|2-x|^{frac{1}{3}},xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/b018b9edd908f216df636f345c6a0e0e.png)
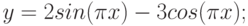
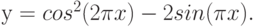
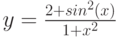
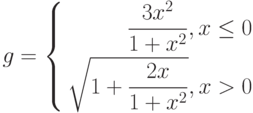
![$$
z=left{
begin{aligned}
3x+sqrt{1+x^{2}},x<0\
2cos(x)e^{-2x},xin[0,1]\
2sin(3x),x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/96eae18012c8cec7fa3195cb7cb16718.png)


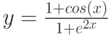
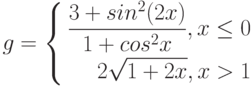
![$$
z=left{
begin{aligned}
sqrt{1+frac{x^{2}}{1+x^{2}}},x<0\
2cos^{2}(x),xin[0,1]\
sqrt{1+|2sin(3x)|^{frac{1}{3}}},x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0e0bd3f1b2b59b98e1d0aac6b9e4e060.png)

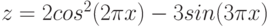
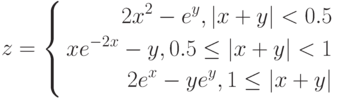
![$$y=sqrt[4]{1+e^{3x}}$$](https://intuit.ru/sites/default/files/tex_cache/38d26ef341d2e8b1539e5db30dd8d0fb.png)
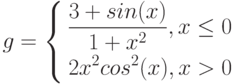
![$$
z=left{
begin{aligned}
|x|^{frac{1}{3}}, x<0\
-2x+frac{x}{1+x}, xin[0,1]\
frac{|3-x|}{1+x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/a336bbbfe739b8a27a42bc552dbba85d.png)
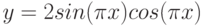

![$$
g=left{
begin{aligned}
sqrt{1+2x^{2}-sin(x)}, xleq0\
frac{2+x}{sqrt[3]{2+e^{-0.1x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/bf750a63e0bf1e99dcdc62a82b5ae8a1.png)
![$$
z=left{
begin{aligned}
frac{1+x}{1+x^{2}}, x<0\
sqrt{1+frac{x}{1+x}}, xin[0,1]\
2|sin(3x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0ba53b8c4d394ba14c7bea0640198a67.png)
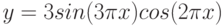
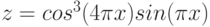
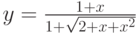
![$$
g=left{
begin{aligned}
sqrt{1+x^{2}}, x<0\
frac{1+x}{1+sqrt[3]{1+e^{-0.2x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c5f92dffe784f474d4780a60de478e2.png)
![$$
z=left{
begin{aligned}
frac{1+x+x^{2}}{1+x^{2}}, x<0\
sqrt{1+frac{2x}{1+x^{2}}}, xin[0,1]\
2|0.5+sin(x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/ea55ab481bac3e0b5e9e38e088173fa3.png)

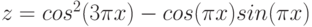
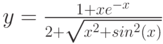
![$$
g=left{
begin{aligned}
sqrt{1+|x|}, xleq0\
frac{1+3x}{2+sqrt[3]{1+x}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5b2dfdc96ef1d57aec714b337234e6ad.png)
![$$
z=left{
begin{aligned}
1+frac{3+x}{1+x^{2}}, x<0\
sqrt{1+(1-x)^{2}},xin[0,1]\
frac{1+x}{1+cos^{2}(x)}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/d7447bf6d7e359d4eca3921d80e719a8.png)
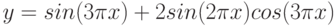

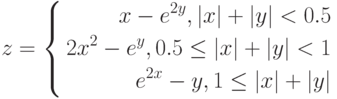
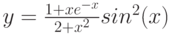
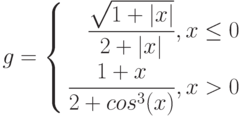
![$$
z=left{
begin{aligned}
frac{1+2x}{1+x^{2}}, x<0\
sin^{2}(x)sqrt{1+x},xin[0,1]\
sin^{2}(x)e^{0.2x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/12bdc437bdea736bdda75cef4a7e722c.png)
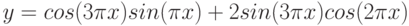
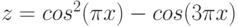
![$х,yin [-1; 1]$$](https://intuit.ru/sites/default/files/tex_cache/1398b5df6d8c02912de8ea030fafac71.png)
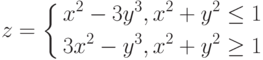
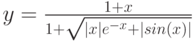
![$$
g=left{
begin{aligned}
sqrt[3]{1+x^{2}}, xleq0\
sin^{2}(x)+frac{1+x}{1+cos^{2}(x)}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5144de1617b0997002fd47d479761ecb.png)
![$$
z=left{
begin{aligned}
frac{|x|}{1+x^{2}}e^{-2x}, x<0\
sqrt{1+x^{2}},xin[0,1]\
frac{1+sin(x)}{1+x}+3x, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/fc2d46b4be846a82407b051315db3f0a.png)