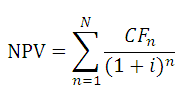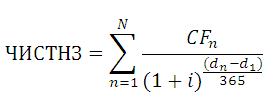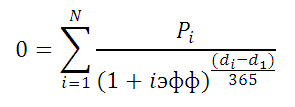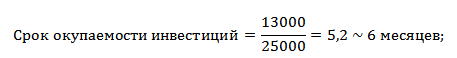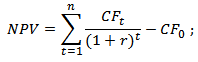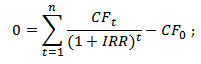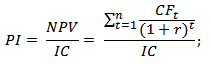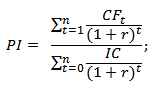Have you been losing sleep figuring out the best way to maximize profitability and minimize risk on your business investments? Stop tossing and turning. Relax and go with the flow.
Cash, that is. Take a look at your cash flow, or what goes into and what goes out of your business. Positive cash flow is the measure of cash coming in (sales, earned interest, stock issues, and so on), whereas negative cash flow is the measure of cash going out (purchases, wages, taxes, and so on). Net cash flow is the difference between your positive cash flow and your negative cash flow, and answers that most fundamental of business questions: How much money is left in the till?
To grow your business, you need to make key decisions about where to invest your money over the long term. Microsoft Excel can help you compare options and make the right choices, so that you can rest easy both day and night.
Asking questions about capital investment projects
If you want to take your money out of the till, make it working capital, and invest it in the projects that make up your business, you need to ask some questions about those projects:
-
Is a new long-term project going to be profitable? When?
-
Is the money better invested in another project?
-
Should I invest even more in an ongoing project, or is it time to cut my losses?
Now take a closer look at each of those projects, and ask:
-
What are the negative and positive cash flows for this project?
-
What impact will a large initial investment have, and how much is too much?
In the end, what you really need are bottom-line numbers that you can use to compare project choices. But to get there, you must incorporate the time value of money into your analysis.
My papa once told me, «Son, it’s better to get your money as soon as possible and hold on to it as long as possible.» Later in life, I learned why. You can invest this money at a compounded interest rate, which means that your money can make you more money — and then some. In other words, when cash goes out or comes in is just as important as how much cash goes out or comes in.
Answering questions by using NPV and IRR
There are two financial methods that you can use to help you answer all of these questions: net present value (NPV) and internal rate of return (IRR). Both NPV and IRR are referred to as discounted cash flow methods because they factor the time value of money into your capital investment project evaluation. Both NPV and IRR are based on a series of future payments (negative cash flow), income (positive cash flow), losses (negative cash flow), or «no-gainers» (zero cash flow).
NPV
NPV returns the net value of the cash flows — represented in today’s dollars. Because of the time value of money, receiving a dollar today is worth more than receiving a dollar tomorrow. NPV calculates that present value for each of the series of cash flows and adds them together to get the net present value.
The formula for NPV is:
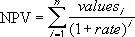
Where n is the number of cash flows, and i is the interest or discount rate.
IRR
IRR is based on NPV. You can think of it as a special case of NPV, where the rate of return that is calculated is the interest rate corresponding to a 0 (zero) net present value.
NPV(IRR(values),values) = 0
When all negative cash flows occur earlier in the sequence than all positive cash flows, or when a project’s sequence of cash flows contains only one negative cash flow, IRR returns a unique value. Most capital investment projects begin with a large negative cash flow (the up-front investment) followed by a sequence of positive cash flows, and, therefore, have a unique IRR. However, sometimes there can be more than one acceptable IRR, or sometimes none at all.
Comparing projects
NPV determines whether a project earns more or less than a desired rate of return (also called the hurdle rate) and is good at finding out whether a project is going to be profitable. IRR goes one step further than NPV to determine a specific rate of return for a project. Both NPV and IRR give you numbers that you can use to compare competing projects and make the best choice for your business.
Choosing the appropriate Excel function
hich Office Excel functions can you use to calculate NPV and IRR? There are five: NPV function, XNPV function, IRR function, XIRR function, and MIRR function. Which one you choose depends on the financial method that you prefer, whether cash flows occur at regular intervals, and whether the cash flows are periodic.
Note: Cash flows are specified as negative, positive, or zero values. When you use these functions, pay particular attention to how you handle immediate cash flows that occur at the beginning of the first period and all of the other cash flows that occur at the ends of periods.
|
Function syntax |
Use when you want to |
Comments |
|
|
Determine the net present value using cash flows that occur at regular intervals, such as monthly or annually. |
Each cash flow, specified as a value, occurs at the end of a period. If there is an additional cash flow at the start of the first period, it should be added to the value returned by the NPV function. See Example 2 in the NPV function Help topic. |
|
|
Determine the net present value using cash flows that occur at irregular intervals. |
Each cash flow, specified as a value, occurs at a scheduled payment date. |
|
|
Determine the internal rate of return using cash flows that occur at regular intervals, such as monthly or annually. |
Each cash flow, specified as a value, occurs at the end of a period. IRR is calculated through an iterative search procedure that starts with an estimate for IRR — specified as a guess — and then repeatedly varies that value until a correct IRR is reached. Specifying a guess argument is optional; Excel uses 10% as the default value. If there is more than one acceptable answer, the IRR function only returns the first one it finds. If the IRR doesn’t find any answer, it returns a #NUM! error value. Use a different value for the guess if you get an error or if the result is not what you expected. Note A different guess might return a different result if there is more than one possible internal rate of return. |
|
|
Determine the internal rate of return using cash flows that occur at irregular intervals. |
Each cash flow, specified as a value, occurs at a scheduled payment date. XIRR is calculated through an iterative search procedure that starts with an estimate for IRR — specified as a guess — and then repeatedly varies that value until a correct XIRR is reached. Specifying a guess argument is optional; Excel uses 10% as the default value. If there is more than one acceptable answer, the XIRR function only returns the first one it finds. If the XIRR doesn’t find any answer, it returns a #NUM! error value. Use a different value for the guess if you get an error or if the result is not what you expected. Note A different guess might return a different result if there is more than one possible internal rate of return. |
|
|
Determine the modified internal rate of return using cash flows that occur at regular intervals, such as monthly or annually, and consider both the cost of investment and the interest that is received on the reinvestment of cash. |
Each cash flow, specified as a value, occurs at the end of a period, except the first cash flow, which specifies a value at the beginning of the period. The interest rate that you pay on the money that is used in the cash flows is specified in finance_rate. The interest rate that you receive on the cash flows as you reinvest them is specified in reinvest_rate. |
More information
To learn more about using NPV and IRR, see Chapter 8, «Evaluating Investments with Net Present Value Criteria,» and Chapter 9, «Internal Rate of Return,» in Microsoft Excel Data Analysis and Business Modeling by Wayne L. Winston. to learn more about this book.
Top of Page
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
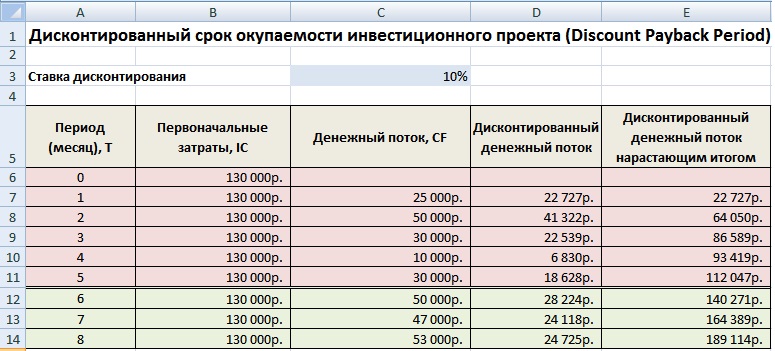
В статье будет приведен расчет показателей эффективности проекта, с учетом дисконтирования.
- ЧДД или чистый дисконтированный доход от инвестиционного проекта;
- Внутренняя норма доходности.
Рассмотрим эти два показателя подробнее и рассчитаем пример работы с ними в Excel. Еще больше о возможностях Excel можно узнать на нашем открытом курсе «Аналитика в Excel».
Net Present Value (NPV, чистый дисконтированный доход) — один из самых распространенных показателей эффективности инвестиционного проекта.
Это разность между дисконтированными по времени поступлениями от проекта и инвестиционными затратами на него.
Метод расчета NPV:
- Определяем текущую стоимость затрат (инвестиции в проект)
- Производим расчет текущей стоимости денежных поступлений от проекта, для этого доходы за каждый отчетный период приводятся к текущей дате

CF – денежный поток;
r – ставка дисконта.
3. Сравниваем текущую стоимость инвестиций (наши затраты) в проект (Io) с текущей стоимостью доходов (PV). Разница между ними будет чистый дисконтированный доход — NPV.

NPV показывает инвестору доход или убыток от вложений средств в проект по сравнению с доходом от хранения денег в банке.
Если NPV больше 0, то инвестиции принесут больше дохода, нежели чем аналогичный вклад в банке.
Формула 1 модифицируется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов).

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
r – ставка дисконтирования;
n – количество периодов.
Internal Rate of Return (Внутренняя норма доходности, IRR) определяет ставку дисконтирования при которой инвестиции равны 0 (NPV=0), или другими словами затраты на проект равны его доходам.
IRR = r, при которой NPV = f(r) = 0, находим из формулы:

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
n – количество периодов.
Этот показатель показывает норму доходности или возможные затраты при вложении денежных средств в проект (в процентах).
Пример расчета NPV в Excel
В MS Excel 2010 для расчета NPV используется функция =ЧПС().
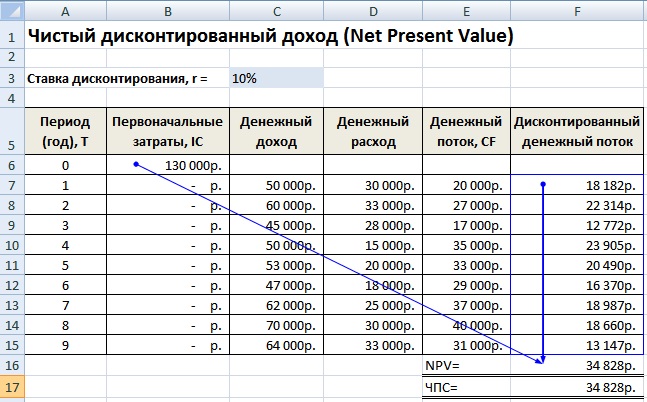
Найдем чистый дисконтированный доход (NPV) проекта, требующего вложений инвестиций на 90 тыс. руб., и денежный поток которого распределен по времени рис 1. , и ставка дисконта равна 10%.

Рассчитаем показатель NPV по формуле Excel:
=ЧПС(D3;C3;C4:C11)
D3 – ставка дисконта;
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект);
C4:C11 – денежный поток проекта за 8 периодов.

В итоге показатель чистого дисконтированного дохода равен 51,07 >0, это говорит о том, что в проект стоит инвестировать.

Расчет IRR в Excel
Для определения IRR в Excel используется встроенная функция
=ЧИСТВНДОХ()
Но так как у нас в примере данные поступали в равные интервалы времени можно использовать функцию
=ВСД(C3:C11)

Доходность вложения в проект равна 38%.
В завершение картинка финансового анализа проекта целиком.

КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.
Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.
Скачать пример
Оценка целесообразности проекта с помощью NPV
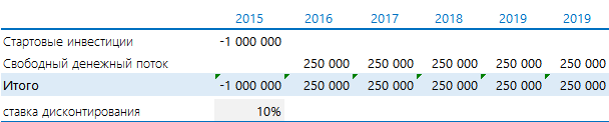
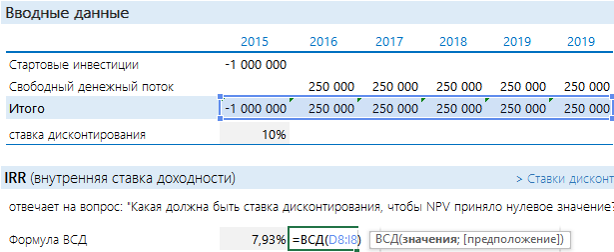
Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.
Оцениваем NPV проекта. Напомню формулу этого показателя:
Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:
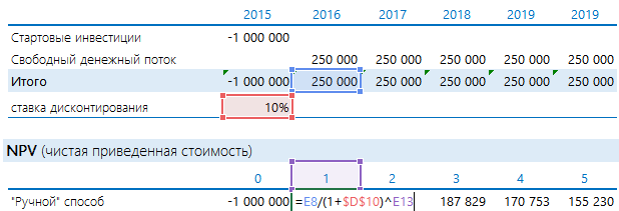
Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.
Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.
Получается «-52 303». Проект невыгоден.
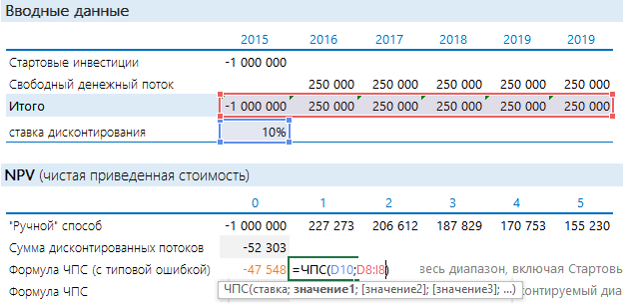
Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):
ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)
То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:
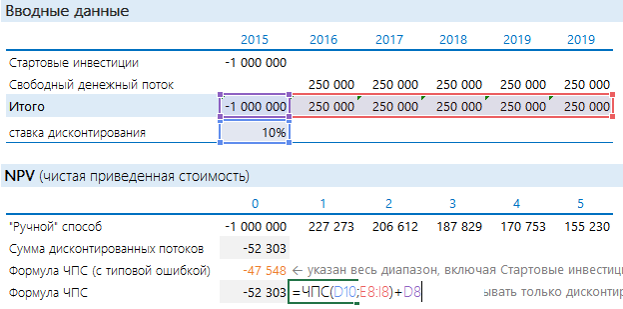
Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:
Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.
Оценка целесообразности проекта с помощью IRR
Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования < IRR, то проект стоит принять, если нет – отказаться. Рассчитать IRR с помощью Excel очень просто: подставляем в функцию ВСД итоговый денежный поток.
IRR оказался меньше ставки доходности. Проект невыгодный (тот же вывод, что и при NPV).
NPV и IRR по праву считаются главными экономическими критериями. Их используют и для инвестиционной оценки проектов, и для оценки стоимости существующего бизнеса. В том числе, показатель EVA (Economic Value Added) считается хорошим критерием в том числе потому, что при правильном расчете он равен NPV.
Но кроме всего прочего, NPV и IRR могут быть использованы финансистами в более прикладных вопросах, например, при общении с банками на тему реальной кредитной ставки. Как – давайте посмотрим.
Аннуитеты – любимая банковская цифра
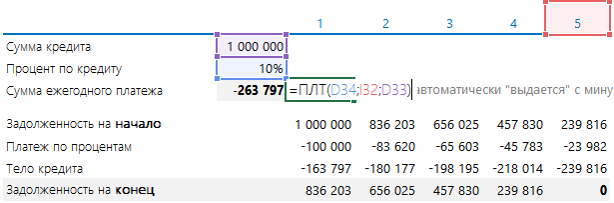
Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:
ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)
В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:
Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.
В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.
Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.
Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:
Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.
Нюансы и тонкости
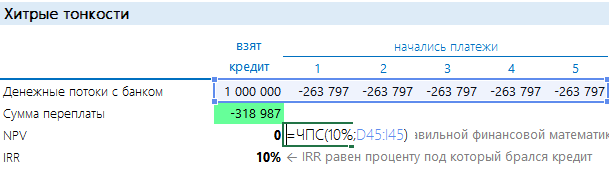
А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.
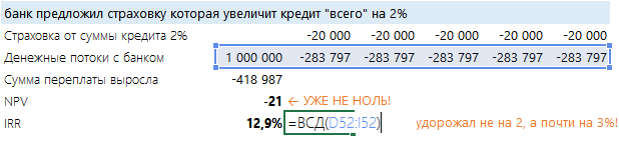
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:
В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…
Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.
Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул
MS
EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют
сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню
(взято из Википедии). Или так:
Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт
cfin.
ru)
Или так:
Текущая
стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика
.
Толковыйсловарь
. —
М
.
:
»
ИНФРА
—
М
«,
Издательство
»
ВесьМир
«.
Дж
.
Блэк
.)
Примечание1
. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется
ЧПС()
, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с
Приведенной стоимостью
.
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма
Приведенных стоимостей
денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет
: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи
Приведенная стоимость
.
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу
сложных процентов
.
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция
ЧПС()
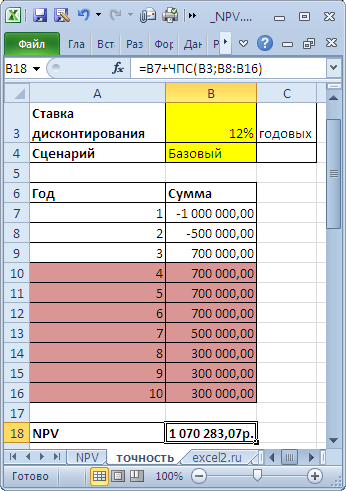
(английский вариант — NPV()). В ее основе используется формула:
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2
. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:
Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)
. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.
Выбор периода дисконтирования для функции ЧПС()
При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.
Примечание3
. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.
Определившись со сроками денежных потоков, для функции
ЧПС()
нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.
файл примера, лист NPV
).
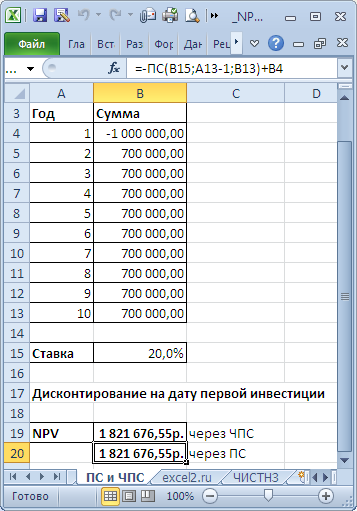
В таблице NPV подсчитан двумя способами: через функцию
ЧПС()
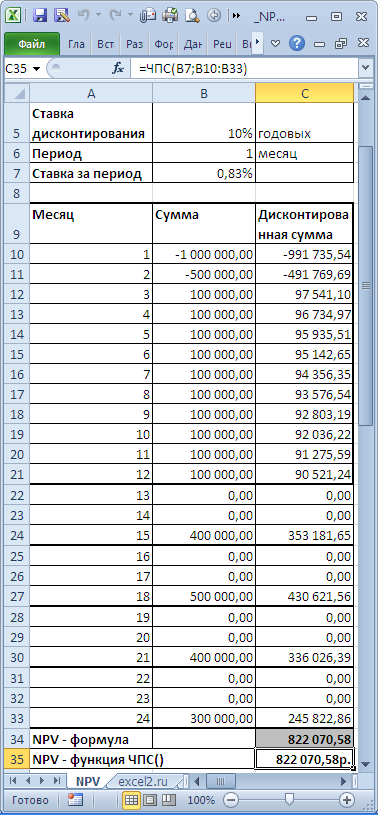
и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции
ЧПС()
, а нужно просто прибавить к получившемуся результату (см.
файл примера
). Сравнение 2-х вариантов дисконтирования приведено в
файле примера
, лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.
файл примера, лист Точность
).
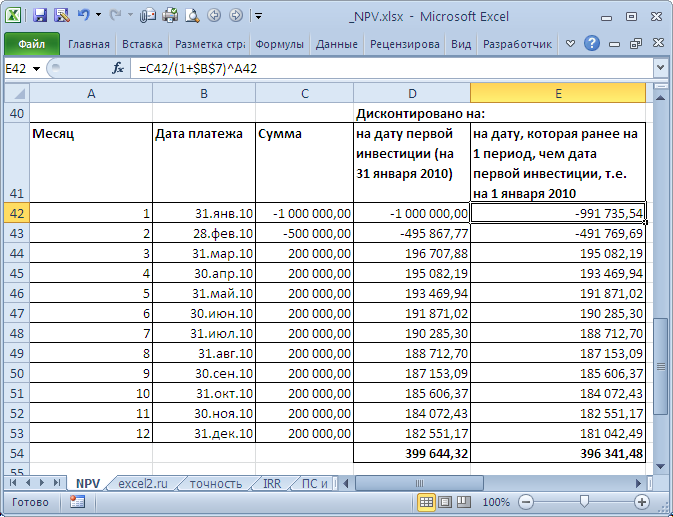
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
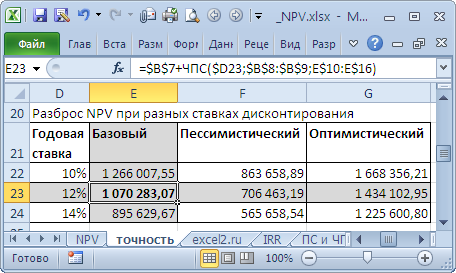
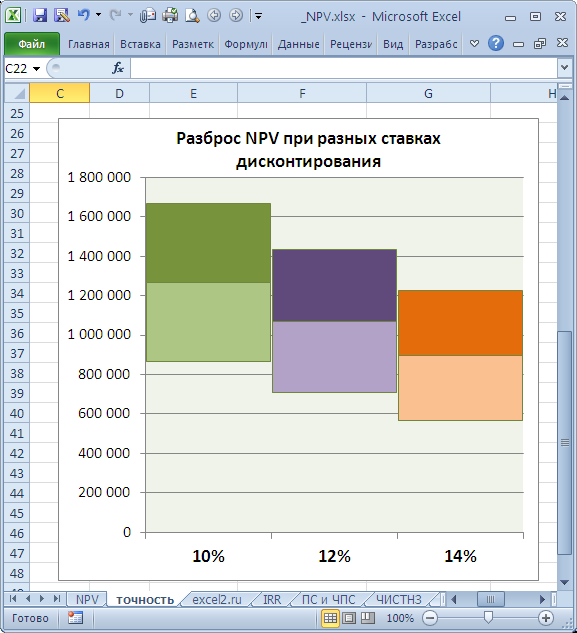
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
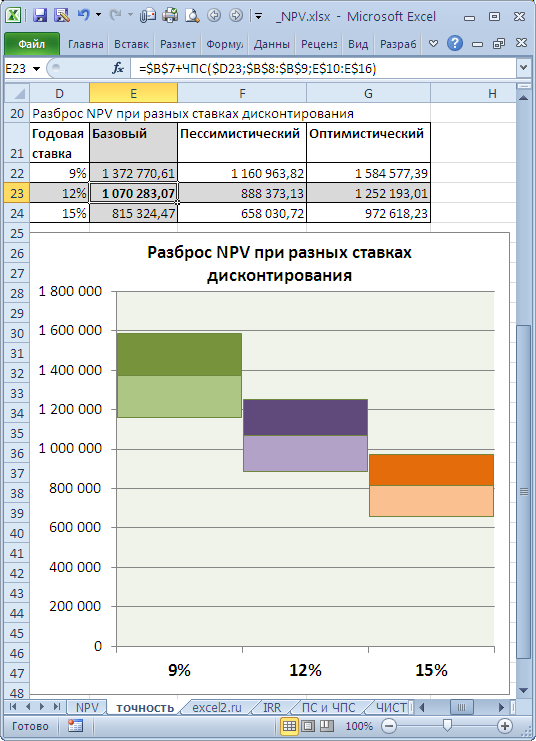
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности
IRR
(ВСД)
Внутренняя ставка доходности (англ.
internal rate of return
, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.
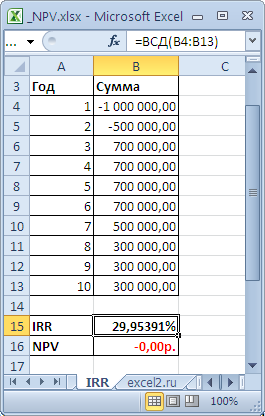
файл примера, лист IRR
).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
Для расчета IRR используется функция
ВСД()
(английский вариант – IRR()). Эта функция тесно связана с функцией
ЧПС()
. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией
ВСД()
, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:
=ЧПС(ВСД(B5:B14);B5:B14)
Примечание4
. IRR можно рассчитать и без функции
ВСД()
: достаточно иметь функцию
ЧПС()
. Для этого нужно использовать инструмент
Подбор параметра
(поле «Установить в ячейке» должно ссылаться на формулу с
ЧПС()
, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что
аннуитет
представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию
ПС()
(см.
файл примера, лист ПС и ЧПС
).
В этом случае все денежные потоки (диапазон
В5:В13
, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке
В4
. Ставка дисконтирования расположена в ячейке
В15
со знаком минус. В этом случае формула
=B4+ЧПС(B15;B5:B13)
дает тот же результат, что и
= B4-ПС(B15;9;B13)
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за
любые
промежутки времени, то используется функция
ЧИСТНЗ()
(английский вариант – XNPV()).
Функция
ЧИСТНЗ()
возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Принципиальным отличием от
ЧПС()
является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у
ЧИСТНЗ()
всегда годовая, т.к. указана база 365 дней, а не за период, как у
ЧПС()
. Еще отличие от
ЧПС()
: все денежные потоки всегда дисконтируются на дату первого платежа.
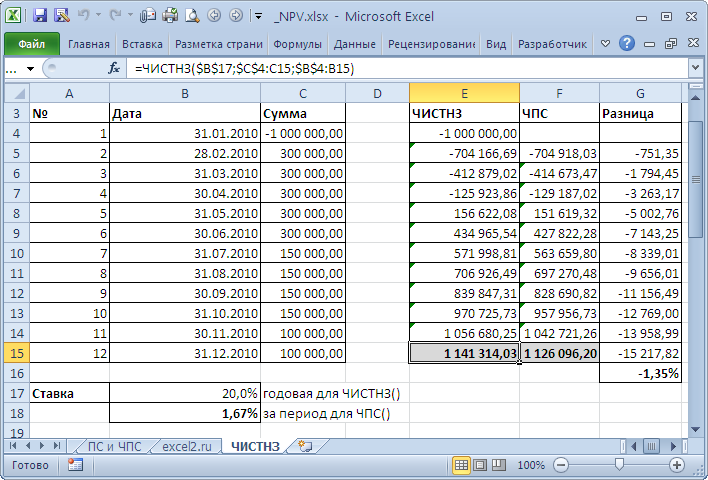
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций
ЧИСТНЗ()
и
ЧПС()
. Эти функции возвращают несколько отличающиеся результаты. Для задачи из
файла примера, Лист ЧИСТНЗ
разница составила порядка 1% (период = 1 месяцу).
Это связано с тем, что у
ЧИСТНЗ()
длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у
ЧПС()
указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет
високосного
года).
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с
ЧПС()
, у которой имеется родственная ей функция
ВСД()
, у
ЧИСТНЗ()
есть функция
ЧИСТВНДОХ()
, которая вычисляет годовую ставку дисконтирования, при которой
ЧИСТНЗ()
возвращает 0.
Расчеты в функции
ЧИСТВНДОХ()
производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Примечание5
. Функция
ЧИСТВНДОХ()
используется для
расчета эффективной ставки по потребительским кредитам
.
Excel allows a user to get an internal rate of return and a net present value of an investment using the NPV and IRR functions. This step by step tutorial will assist all levels of Excel users in calculating NPV and IRR Excel.
Syntax of the NPV Formula
The generic formula for the NPV function is:
=NPV(rate, values)
The parameter of the NPV function is:
- rate – a discount rate for the investment period
- values – values representing an investment (with a negative sign) and returns over periods.
Syntax of the IRR Formula
The generic formula for the IRR function is:
=IRR(values, [guess])
The parameter of the IRR function is:
- values – a range of cells containing values, including initial investment and incomes. The investment must have a negative sign, as it is a cost
- [guess] – an estimated value for the expected IRR. This parameter is non-mandatory. If it’s omitted, the function will take a default value of 0.1 (=10%).
Setting up Our Data for the NPV and IRR Functions
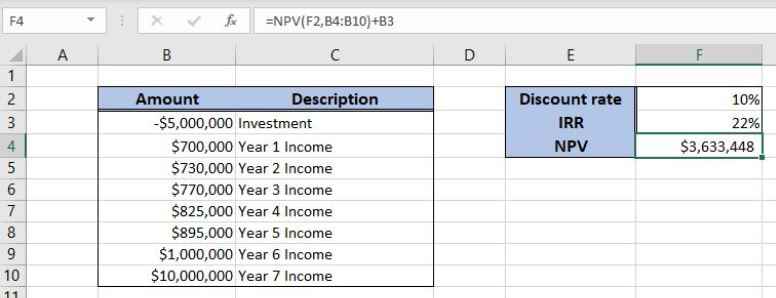
Let’s look at the structure of the data we will use. In column B (“Amount”), we have values including initial investment and yearly incomes. In column C (“Description”) we have a description of every amount. The discount rate is in F2. In the cell F3, we want to get the IRR, while in F4 NPV.

Get an NPV of Values Using the NPV Function
In our example, we want to get the NPV of the values in the range B3:B10. The result will be in the cell F4.
The formula looks like:
=NPV(F2, B4:B10) + B3
The parameter rate is the cell F2, while the values are in the range B4:B10. We omit the first value from B3, as it is negative and add it to the function result.
To apply the NPV function, we need to follow these steps:
- Select cell E3 and click on it
- Insert the formula:
=NPV(F2, B4:B10) + B3 - Press enter.

Finally, the result in the cell F4 is $3,633,448, which is the net present value of the investment and returns with the discount rate of 10%.
Get an IRR of Values Using the IRR Function
In this example, we want to get the IRR of the values in the range B3:B10. The result will be in the cell F3.
The formula looks like:
=IRR(B3:B10)
The parameter values is the range B3:B10
To apply the IRR function, we need to follow these steps:
- Select cell F3 and click on it
- Insert the formula:
=IRR(B3:B10) - Press enter.

Finally, the result in the cell E3 is 22%, which is the internal rate of the investment.
Most of the time, the problem you will need to solve will be more complex than a simple application of a formula or function. If you want to save hours of research and frustration, try our live Excelchat service! Our Excel Experts are available 24/7 to answer any Excel question you may have. We guarantee a connection within 30 seconds and a customized solution within 20 minutes.
Excel makes it possible for simple buy / not-buy or do / not-do financial decisions very easy to arrive at. The underpinning concept behind making such decisions is that a dollar tomorrow is worth lesser than a dollar today. That’s right, it’s because of the additional return you can get by “investing” a dollar today.
There are two notable functions in Excel which are particularly helpful in evaluating financial decisions: NPV and IRR. Yes, for the uninitiated in Finance, they might appear a bit off-putting. But don’t you worry, Rick Grantham is here to teach us the A, B, C through to Z of all this.
What are you waiting for? Let’s get started.
1 – The Setup
The setup is easy. Given the situation you are evaluating, all you need to know are two things:
- What amount of cash would be coming in / going out and in which year,
- What rate of return would you expected if you invested your money somewhere else.
As an illustration of the first part, look at the data in the picture.
LawnMower & Co. is considering buying a new type of lawnmower and these are the costs and benefits that will result. Note that time here represents the year. The second part seems a bit tricky, but we’ll explain a workaround to tackle this. For now, we will assume a rate of 15%.
2 – The Calculation
The first step in evaluating this financial situation would be to calculate the net cashflow or the net benefit for each year. Since we are already taking cost as negative numbers, we can just sum the cost and benefit to arrive at the figures required.
Net Present Value (NPV) is the widest used metric when it comes to making financial decisions. All it does is that it sums up the entire net benefit to be realized over many years but in today’s dollars. We use the following formula to calculate NPV in Excel:
=NPV(rate,values) + A
NPV is a built-in formula in Excel. For ‘rate’, we will refer to the cell containing the rate of return, i.e. 15% in our case. For ‘values’, we will select the array of net cashflows or net benefits from Year 1 till the end. ‘A’ is just the net benefit at Year 0, or today.
Internal Rate of Return (IRR) is another metric widely used in evaluating financial decisions. It simply calculates the rate at which NPV would become zero. Practically, it gives the rate of return at which you should be indifferent in your buy / not-buy or do / not-do decision. The formula is very simple. =IRR(values), where ‘values’ is the array of net benefits from Year 0 till the end.
3 – Evaluation
When we evaluated our example, the picture shows what we got. The NPV is negative. It means that if we can fetch 15% return on our investment somewhere else, than you should not buy this lawnmower.
4 – The Tricky Case
In big corporations, their Finance or Treasury departments are responsible for providing this figure. But for most small business owners, that’s not an option. In this case, IRR comes in handy. IRR gives the rate at which you will be indifferent between buying or not-buying. So, if you know you will always get less than 13.1% return on your money somewhere else (let’s say a bank deposit or some other investment), than surely go for this lawnmower.
What’s next?
Get your hands dirty and learn this awesome technique. Try out the example Rick explains in the video. And when you get comfortable with this, start employing it in your major financial decisions.
And do not forget to share this technique with your friends or colleagues, and write to us with your experiences in the comments section below.
This Article briefly covers methods of calculating the NPV and IRR variants in Excel as well as the limitations in calculating and interpreting IRR results.
Introduction
This Article briefly covers methods of calculating the NPV and IRR variants in Excel as well as the limitations in calculating and interpreting IRR results.
Paraphrasing Richard Shockley, author of my favourite finance reference text
«A fundamental principle of corporate finance is that management should maximise Net Present Value (NPV), NPV being the difference between the financial market price of an opportunities cashflows, and the manager’s cost of undertaking that opportunity. Investors and owners want management to maximise NPV as this maximises their own wealth.»
Copeland and Antikarov have noted that NPV is the single most widely used tool for major investments by corporations, the usage in the US having risen from 19% in 1958 (100 corporations) to 86% by 1978 (424 corporations). Whilst the most common application of NPV (and usage in Excel) is discounted cashflow analysis for now or never no flexibility (NONNF) opportunities, NPV can also be calculated using real option analysis in situations where management has deferral/expansion decision making ability.
Another common reported financial metric for an opportunity is Internal Rate of Return (IRR).
Excels NPV and IRR functions
A quickly summary in descending chronological order of the NPV and IRR functions available in Excel.
Excel 2010
Excel 2010 offers the following formulae as built-in functions.
NPV – Returns the net present value for evenly staged cashflows (measured as at the end of the period).
XNPV — Returns the net present value for a schedule of cash flows that is not necessarily periodic.
IRR — Returns the internal rate of return for evenly staged cashflows.
XIRR — Returns the internal rate of return for a schedule of cash flows that is not necessarily periodic.
MIRR – The modified rate of return includes an assumption for a separate re-investment amount for liberated cashflows.
NB: Microsoft has implemented a
new algorithm for IRR in xl2010. This update can produce different IRR results than earlier Excel versions.
Different IRR result, same data, Excel 2007 vs 2010 .
Excel 2007
These five functions are implemented in the same manner as xl 2010.
Excel 2003
XIRR and XNPV are not built-in functions, they need to be enabled via checking the Analysis Toolpak addin (Tools – Addins – check Analysis Toolpak).
The other three functions are included as native functions inside Excel.
Calculating NPV in Excel
There are three commonly used methods for calculating NPV in Excel:
NPV function
XNPV function
Calculation of manual PV by period
My advice is to always use the manual method and then double check this calculation with XNPV as:
— These two methods handle irregular timing periods for cashflows more straightforwardly than the NPV function.
— The manual approach forces modellers to think about when projects cashflows should be modelled as occurring (beginning or end of period, averaged at mid-period etc) and how far each period is away from the valuation date.
— I find this method also provides clarity as to how to deal with an initial part period — for example should a portion of the first period cashflow be excluded if this portion precedes the valuation date.
— A period by period approach provides insight as to how NPV is derived over time, highlighting possible inconsistencies, or perhaps opportunities in a deal sense (i.e. does all the valuable component happen in the short term).
— The NPV formula
ignores
blank cells and text. I have seen this impact reported values before, in one case the modeller had taken a NPV over a range that began with three empty cells (representing a project delay), and the NPV formula simply ignored these 3 blanks cells and took the 4th year as being period 1. Whereas XNPV spits out an error if any cashflow that should match a date is left blank.
The example below shows the NPV function applied to end-period cashflows.
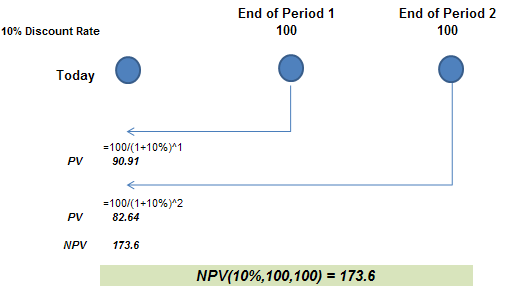
The distance of the periods from the valuation date follows an integer pattern expected for end period discounting, 1.0, 2.0, 3.0 …. X, X+1 etc.
Cashflows normally occur continuously over time, so for these cases mid-point discounting is applied to better approximate average cashflow timing over each period. Multiplying the NPV by the square root of (1+Discount Rate) converts the end-period NPV to mid-period NPV.
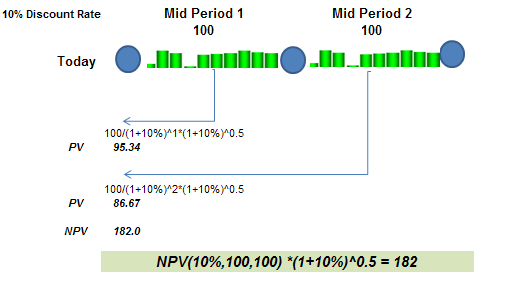
A common issue when calculating NPV is the need to cater for a partial first period. For example a company may forecast cashflows in financial years from 1 July to 30 June but then look to calculate value mid-way through the financial year (1 Jan).
Initial part periods raise two issues:
1) Excluding cashflows that occurred prior to the valuation date if these cashflows are either accounted for elsewhere (for example as cash on the balance sheet), or if these cashflows would not accrue to the entity undertaking the valuation (for example an acquirer may only have access to the cashflows after the valuation date).
2) The mid-point timing of both the first and second periods will change from the “normal” 1 year gap sequence in full period forecast models . In the example below the time to the mid-point of the partial first period is 3 months (0.25 years) and the time to the mid-point of the second period is 1 year. From this point on the 1 year gap repeats.
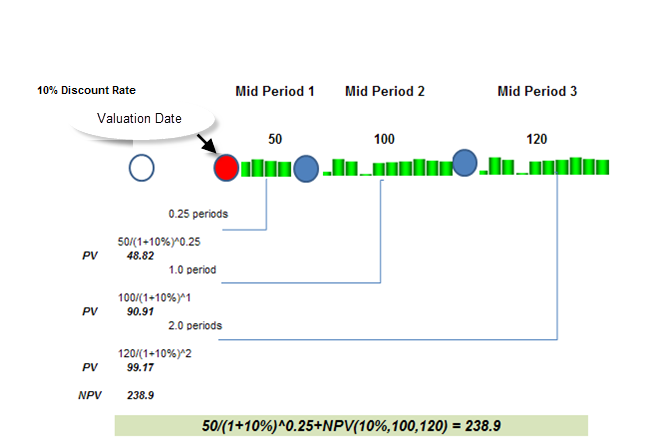
As per my initial comments in this section I prefer to:
— Use an actual date as the mid-period timing which also sets up the model to calculate XNPV in addition to the manual method. I use the DATE function to derive the midpoints of the full periods given that the model will be built either in calendar years (making 1-July a suitable midpoint) or financial years (1-Jan).
— Use YEARFRAC to calculate the distance of each midpoint date from the valuation date. Please note that YEARFRAC provides 5 calculation variants (see Excel help for the details), I prefer 3 which works on actual days in the year/365.
— Ensure that a partial first period is addressed properly (for example excluding cashflow prior to the valuation date).
— Check that the manual method (which uses actual days in the year/365 days) and XNPV (which somewhat confusingly both includes the impact of leap years by using total day count, but then normalises to a 365 day year — see figure below) are within .1% or so (there may be very minor differences depending on how any partial first portion cashflow is backed out of both methods)
Some people prefer to use “month end” measurement for valuation (30-Jun and 31-Dec etc) rather than the “month beginning factors” that I have used above. This has no significant impact on the valuation (Note that as there are more days in July-Dec than Jan-Feb, 31-Dec is slightly more accurate than 1-Jan as a true half year measurement)
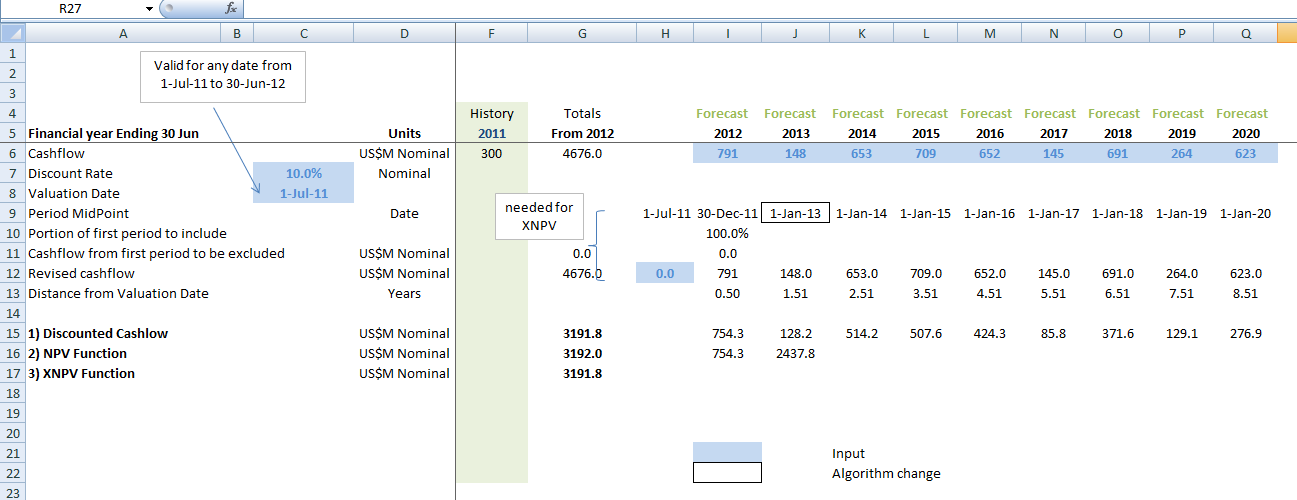
Calculating IRR Excel
If you asked any analyst what IRR is, then an automatic response would be along the lines of “it is discount rate at which NPV = 0”. If you followed up with “Great. So then how should I use IRR to inform decision making ” then more than likely you will get some blank looks or blustering, perhaps some commentary that the projects should be progressed if they exceed a hurdle rate, hopefully a response that you should rely on NPV. But if it is unclear as to how IRR should be used for a decision then the next question is “So why calculate it in the first place?” More on IRR’s limitation shortly.
Excel offers three native IRR functions
IRR function
XIRR function
MIRR function
The application of Excel’s IRR function’s usefulness is limited; it is suitable only for evenly spaced end-period cashflows (more on IRR as an overall technique later). This is because IRR is solved by an iterative process which means that unlike NPV, IRR cannot be adjusted algebraically to cater for mid-period discounting and/ or an initial partial period cashflow.
XIRR provides the means to apply an internal rate or return calculation for cashflows occurring at specific dates. A model that has been configured with date ranges for the XNPV function is immediately ready to apply XIRR.
Excel also offers a MIRR function which allows users to vary the re-investment assumption, although like IRR it is designed for evenly spaced end-period cashflows. MIRR is interesting as improves on the standard IRR function by separating project returns from the re-investment, but I have never seen it quoted for an actual investment decision.
David Hager overcomes the end period limitation of MIRR with this
VBA User Defined Function that produces a XMIRR.
Please note that IRR and XIRR samples are included in the attached worbook available at the end of this Article.
IRR – Irrationally Reported Return?
[]1] IRR measures return, not return against specific project risk (or stated another way, with no reference point to purchasing the projects cashflows in the market). This is inherently accounted for when calculating NPV.
[]2] IRR is solved by an iterative process, it cannot be calculated algebraically.
[]3] Actual returns do not match the internal rate of return unless the liberated cashflows can be re-invested elsewhere at the IRR rate.
[]4] Can easily be distorted by making non-value changing quasi financing decisions such replacing up front capital spending with ongoing leasing payments.
[]5] Assorted Issues
IRR
— requires at least one cashflow change before a calculation is possible.
— has no scale for positive returns, and beyond a certain point (which seems to have increased in Excel 2010) can’t differentiate between the size of negative returns
— can provide as many answers as there are cash flow changes.
— can return very positive results even if total cashlow …. let alone NPV …. is negative.
Expanding on the first four of these points in more detail:
[]1] IRR does not inherently adjust for specific project risk . This is inherently accounted for when calculating NPV
Consider a word where management have two mutually exclusive opportunities to invest their shareholders last $100.
The first opportunity returns identical cashflows in every conceivable macro-economic state. It offers an 8% nominal IRR.
The second opportunity is a communications company looking to build a fibreoptic broadband network in central Africa. This project is unlikely to make a profit for at least 10 years, faces possible expropriation, and is reliant on massive spending elsewhere on new infrastructure and significant improvement in local health conditions. It offers a 10% nominal IRR on a weighted scenario basis.
Which opportunity would you pick?
IRR does not distinguish between the fundamentally different risk profiles of these two opportunities. The first project is akin to investing in treasury bonds, it is a risk free investment which would be recognised in a NPV analysis by use of an appropriate risk free discount rate (perhaps 5% nominal). The second project is clearly high risk and speculative and would command a far higher discount rate (perhaps 12% nominal in which case this project would actually be NPV negative. NPV compares the returns from each project to the cost of buying these cashflows in the market – IRR makes no allowance for the market costs.
[]2]IRR is solved by an iterative process, it cannot be calculated algebraically
This makes the IRR calculation inflexible whereas the NPV function can be readily adapted for part periods and mid-point discounting. It also means that IRR answers may vary – as they can do in xl2010 compared to earlier versions.
[]3] Actual returns do not match the internal rate of return unless the liberated cashflows can be re-invested elsewhere at the same rate as the original project IRR
The example below shows the re-investment assumption necessary for IRR to match annual returns.
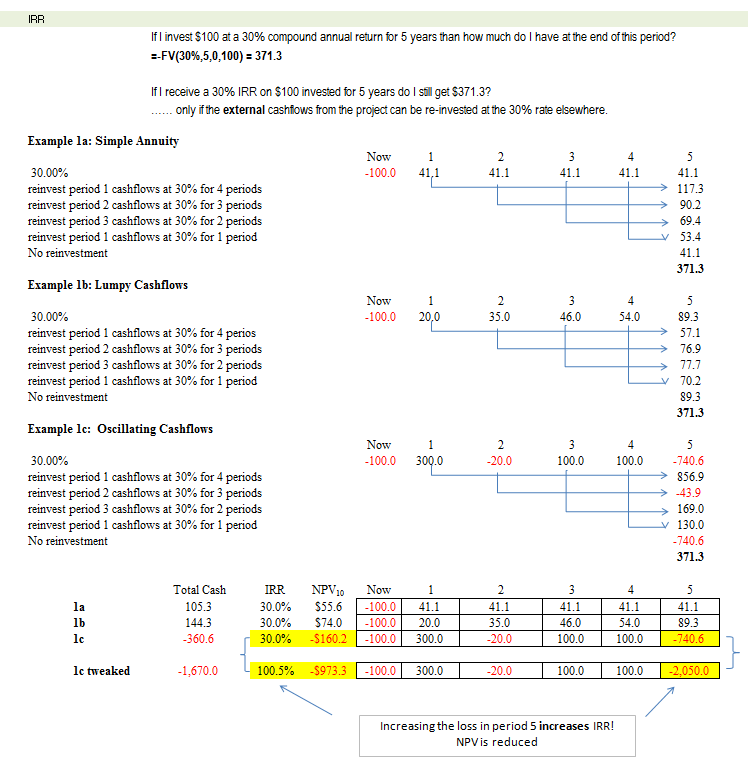
This example also picks up on two of the comments from point 5 namely IRR:
— can return very positive results even if total cashflow …. let alone NPV …. is negative
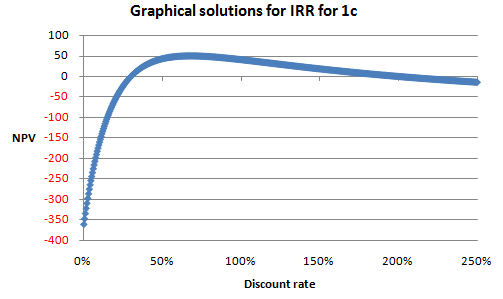
— can provide as many answers as there are cashflow changes. The figure below was generated using Excel’s Table function to solve IRR’s “roots” for 1c graphically, it is apparent that a second discount rate of 190% also produces NPV equal to 0 (NB if users enter a “guess” in the IRR formula then other results may be shown in preference to the default result depending on how close the guess is to the other solution roots).
[]4] Can easily be distorted by making non-value changing quasi financing decisions such replacing up front capital spending with ongoing leasing payments
Whew – that was a little wordy, please explain!
Projects often contain sub project decisions. A common example is the initial capital spend on a new coal mine where the project team may either choose to purchase and then operate the mobile mine equipment (shovels and trucks), or pay a mining contractor a leasing charge and operating cost to run the mobile equipment instead.
Three quick points on the leasing decision:
— It should be NPV neutral or close to it unless the contracting company can bring operator expertise that the company cannot deploy internally.
— If the project is short life and/or marginal the company may wish to out source risk to the contractor who receives a commensurate profit margin in return (else the company bears the risk of re-deploying labour and equipment).
— It is quasi financing as the leasing charges will reflect the contractors cost of debt finance on the equipment. Please note that it is an investment decision should always be considered prior to any financing decision.
The snapshot below shows the pure owner/operate investment case for a simplified coal mine example (ignoring tax, depreciation, royalties etc). Initial capital of US$1000M halfway through FY12 delivers flat nominal profits of US$220M nominal for the next 8 years. This produces a project NPV of US164.6M at a 10% discount rate (mid-point basis) and a XIRR of 14.6%.
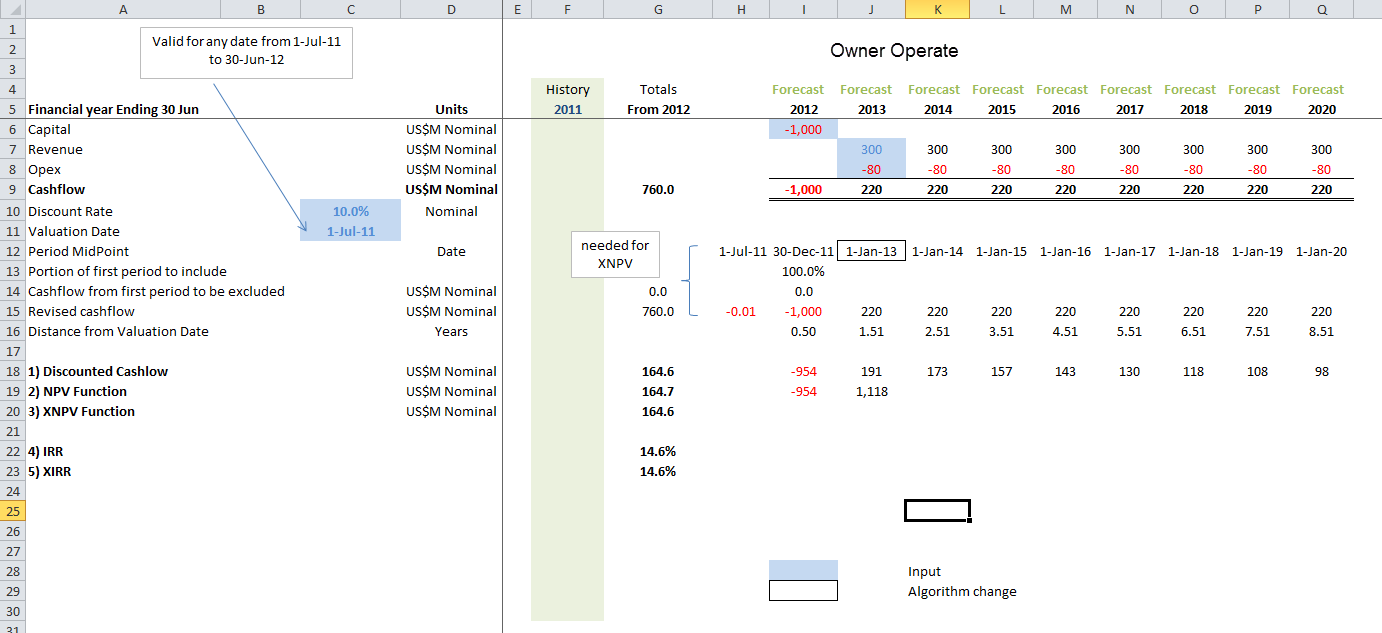
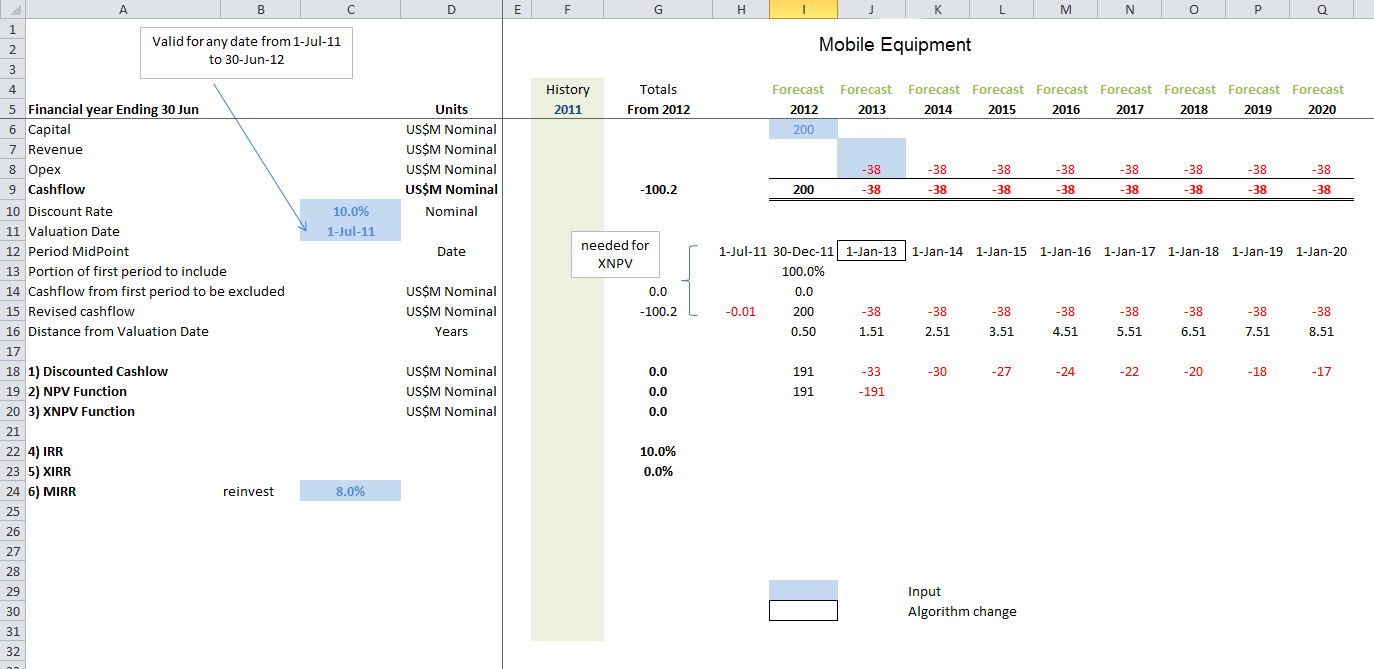
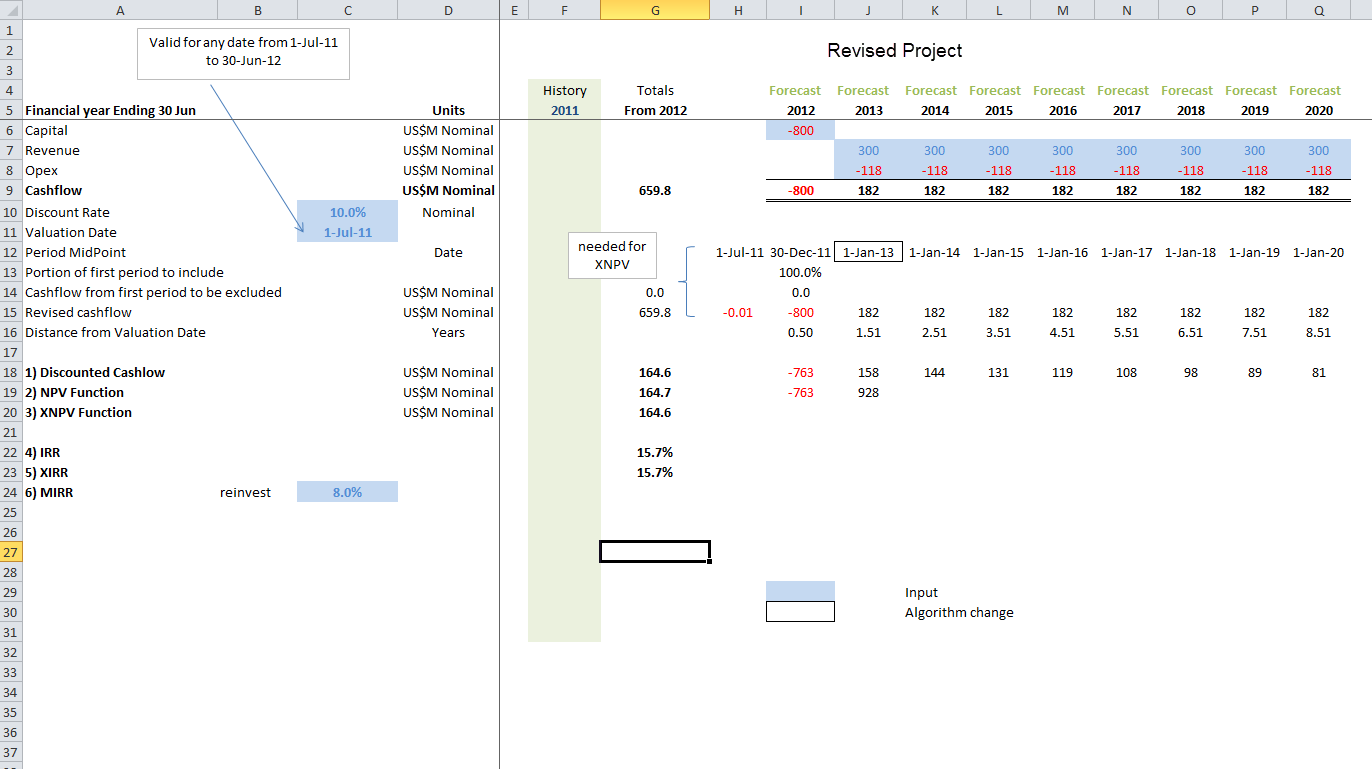
A good question is what would have happened had the mobile equipment contractor received a 14.6% IRR on the lease (the same return as the project) rather than 10.0%. Under this scenario the final IRR for the revised investment for a $800M capital spend would still be 14.6% — but the overall NPV would have been reduced from US$164.6M to US$132.1M. The project has been reduced in value even though IRR has remained constant.
This example provides an example of how to negotiate with a counterparty that is IRR — but not NPV — focused. A credible case can be fashioned without resorting to multiple IRR solutions by:
— minimising the counterpary’s initial investment by structuring the investment to return cashflow from the counterparty to you later in time (like the mobile equipment example)
— looking to return a large positive cashflow to the counterparty early in the investment lifecycle
Proponents of IRR
IRR has a significant supporter base. I have often heard comments along the lines of “I know IRR is flawed and we should use NPV for investment decisions but the Board/CFO/CEO/boss likes it”.
The other main defence of IRR is that it does have value in being used in conjunction with NPV. A Google search of “IRR criticism” produces this spirited
defence of IRR.
My brief responses to the author’s main points:
Criticism 1 This suggests we can turn around an unfavourable project by increasing our opportunity cost of capital. This is nonsensical, but incorporated then ignored in the negative-positive criticism.
Each project has an appropriate discount rate (cost of capital) that reflects the costs of buying that projects cashflows in the market. It is nonsensical to artificially increase those costs to make the project look better.
Criticism 2 A focus on NPV to the exclusion of IRR would build in a bias for large projects over smaller, perhaps more cost-effective ones.
A managers job is maximise NPV. If ten smaller projects contribute more NPV than a mutually exclusive larger one then the collection of smaller projects will be progressed – IRR offers no insights into this straightforward maximisation of NPV. Also as per an earlier example (the risk free project and the African IT venture) IRR does not take into account the cost of buying the project cashflows in the market.
Criticism 3 If we accept that both IRRs are mathematically correct, one solution is simply to take the smaller, more conservative 25 percent.
Would you have confidence in making a decision between two or more “correct” answers? Furthermore on what basis would you pick a conservative rather than aggressive IRR?
Criticism 4 Under some circumstances IRR is incalculable.
Yes it is.
Criticism 5Commonly, reinvestment at the IRR is an appropriate assumption.
So the better an project becomes then automatically the options for reinvesting the project cashflows also increase accordingly. Does this sound realistic?
Other Criticism “We cannot add IRRs for a meaningful number, but we can average them”
You can’t. The cashflows for these projects should be added together then a single IRR calculated.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
If you found the article helpful please click on the
«YES» button after the question below.
If you didn’t or otherwise want to vote No, please leave a comment and give me an opportunity to respond. It will give me a chance to improve this article and others I would like to write.
If you liked this article and want to see more from this author,
please click here.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Copeland and Antikarov, 2003,
«Real Options a practioners guide»
Shockley, 2007,
«An Applied Course in Real Options Valuation»
For calculating the internal rate of return (of the internal rate of return, IRR) in Excel the IRR function is used. Its features, syntax, examples we are discussed in this article.
The features and syntax of the IRR functions
One of the methods for evaluating of investment projects – is the internal rate of return. The calculation in automatic mode can be performed with using the =IRR() function in Excel. It finds the internal rate of return for a number of cash flows. The financial indicators should be represented by numerical values.
The amounts inside the flows can fluctuate, but the receipts are regular (every month, quarter or year). This is the required condition for a correct calculation.
The internal rate of return (IRR, internal rate of return) – this is the interest rate of the investment project, in what the present value of cash flows is zero. At this rate, the investor will return the funds originally invested. The investments consist of payments (amounts with the «-» sign) and income (with the «+» sign), which occur in the same length of time intervals.
The arguments of the IRR function in Excel:
The arguments of the IRR function in Excel:
- Values: The values. The range of cells containing the numerical expressions of money. For these amounts, you should to calculate the internal rate of return.
- Guess: The assumption. There is a figure that is supposedly close to the result. The argument is optional.
There are secrets of the function IRR work:
- In the range with money amounts must be contained at least one positive and one negative signification.
- For the IRR function so important the order of payments or receipts. That is, the cash flows should be entered into the table in conformity with the time of their occurrence.
- The texts or logical meaning, empty cells are ignored in the calculation.
- In the Excel program, the iteration (selection) method is used for calculating to the internal rate of return. The formula performs a cyclical calculations from the value that specified in the «Assumption» argument. If the argument is missed, it happens from the value 0. 1 (10%).
When calculating the IRR in Excel, the #NUMBER error may occur. Why? Using the iteration method in the calculation, the function finds the result with the accuracy of 0. 00001%. If after 20 attempts you can not get the result, the IRR will return to the error value.
When the function shows the error #NUMBER!, you need to reiterate the calculation with other meaning of the «Assumption» argument.
The examples of the IRR function in Excel
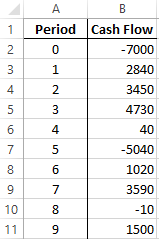
The calculation of the internal rate of return we consider in the elementary example. There are following input data:
The amount of the initial investment is 7000. During the analyzed period there were two more investments – there are 5040 and 10.
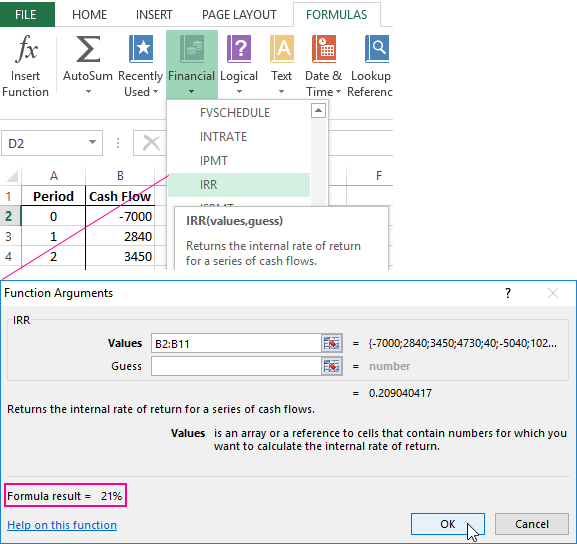
Let`s go in the «Formula» tab. In the category «Financial» we find the IRR function. We fill in these arguments.
The values – is the range with the sums of cash flows, for which it is necessary to calculate the internal rate of return. We are omitting the assumption now.
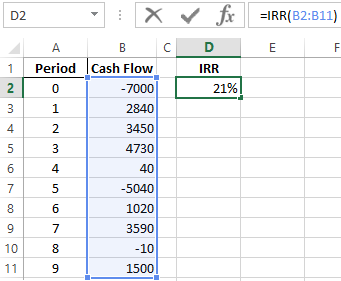
The required IRR (internal rate of return) of the analyzed project – is 0.209040416569432. If we transfer the decimal expression of the value in percentage, then we get the rate of 21%.
In our example, the calculation of the IRR is carried out for annual flows. If you need to find the IRR for monthly flows in just a few years, it’s better to enter the «Assumption» argument. The program can not cope with the calculation for 20 attempts – the error #NUMBER! will appear.
One more indicator of the efficiency of the investment project is NPV (the net discounted income). NPV and IRR are linked: the IRR defines the discount rate at which NPV = 0 (that is, the project costs are equal to the revenues).
For calculation NPV in Excel, the =NPV() function is applied. To find the internal rate of return using the graphical method, you need to build the change schedule in NPV. To do this, in the formula for calculating NPV we will substitute to the different values for discount rates.
On the grounds of the obtained data, we plot the schedule change in NPV.
The intersection of the graph with the X axis (when the project’s net present value of income is zero) will give us the IRR index for this project. The graphical method showed the result, that is similar to found in Excel.
How to use the IRR indicator:
If the IRR value of the project is higher than the cost of capital for the enterprise, you must accept this investment project.
That is, if the loan rate is less than the internal rate of profitability, then borrowed funds will bring profit. Since in the implementation of the project we will get a higher percentage of income, than the amount of capital will be higher.
Download example IRR and NPV functions count in Excel.
We return to our example now and suppose, that for the launch of the project a loan was taken in the bank at 15% per annum. The calculation showed that the internal rate of return was 20. 9%. You can earn on this project.
Главная » ⚡ Инвестиционный анализ » 6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI
На чтение 14 мин Просмотров 275к.
Рассмотрим 6 методов оценки эффективности инвестиций, дам различные формулы расчета инвестиционных коэффициентов, методику (алгоритм) расчета их в Excel. Данные методы будут полезны инвесторам, финансовым аналитикам, бизнес-аналитикам и экономистам. Сразу следует отметить, что под инвестициями будем понимать различные инвестиционные проекты, объекты вложения и активы. То есть данные методы могут быть широко использованы в оценочной деятельности любого предприятия/компании.
Все методы оценки эффективности инвестиционных проектов можно разделить на две большие группы:
- Статистические методы оценки инвестиционных проектов
- Срок окупаемости инвестиционного проекта (PP, Payback Period)
- Рентабельность инвестиционного проекта (ARR, Accounting Rate of Return)
- Динамические методы оценки инвестиционных проектов
- Чистый дисконтированный доход (NPV, Net Present Value)
- Внутренняя норма прибыл (IRR, Internal Rate of Return)
- Индекс прибыльности (PI, Profitability index)
- Дисконтированный срок окупаемости (DPP, Discounted Payback Period)
Содержание
- Статистические методы оценки эффективности инвестиций/инвестиционных проектов
- Срок окупаемости инвестиций (Payback Period)
- Формула расчета срока окупаемости инвестиций (инвестиционного проекта)
- Пример расчета срока окупаемости инвестиционного проекта в Excel
- Направления использования срока окупаемости инвестиций (инвестиционных проектов)
- Достоинства и недостатки показателя срока окупаемости инвестиций
- Коэффициент рентабельности инвестиций (Accounting Rate of Return)
- Формула расчета коэффициента рентабельности инвестиций
- Пример расчета коэффициента рентабельности инвестиций (инвестиционного проекта) в Excel
- Цели использования коэффициента рентабельности инвестиционного проекта
- Достоинства и недостатки коэффициента рентабельности инвестиций
- Динамические методы оценки эффективности инвестиций/инвестиционных проектов. Как рассчитать эффективность проекта
- Чистый дисконтированный доход (Net Present Value)
- Формула чистого дисконтированного дохода
- Оценка проекта на основе критерия NPV
- Пример расчета чистого дисконтированного дохода в Excel
- Мастер-класс: «Как рассчитать чистый дисконтированный доход для бизнес плана»
- Внутренняя норма прибыли инвестиционного проекта
- Формула расчета внутренней нормы прибыли инвестиционного проекта
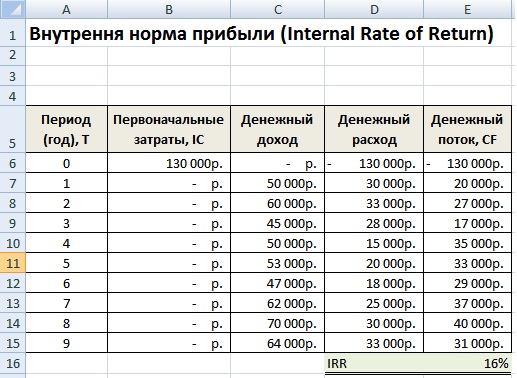
- Пример расчета IRR инвестиционного проекта в Excel
- Достоинства и недостатки внутренней нормы доходности IRR
- Мастер-класс: «Как рассчитать внутреннюю норму доходности для бизнес плана»
- Индекс прибыльности инвестиций (Profitability index)
- Формула расчета индекса прибыльности инвестиций
- Разновидность формулы индекса прибыльности инвестиций
- Оценка проекта на основе критерия PI
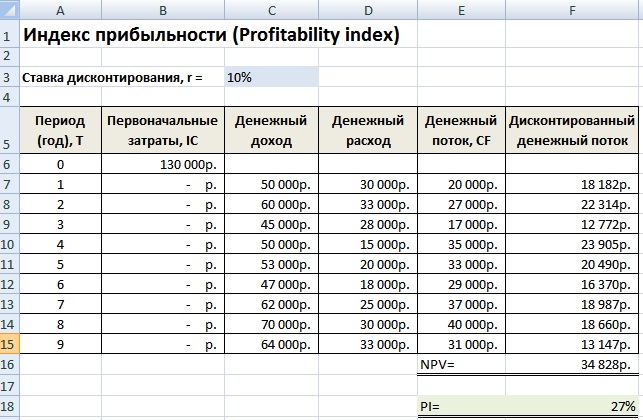
- Пример расчета индекса прибыльности проекта в Excel
- Дисконтированный срок окупаемости инвестиций
- Формула расчета дисконтированного срока окупаемости инвестиций
- Пример расчета дисконтированного срока окупаемости инвестиций в Excel
- Достоинства и недостатки дисконтированного срока окупаемости
- Мастер-класс: «Как рассчитать срок окупаемости для бизнес плана: инструкция»
- Выбор инвестиции на основе коэффициентов оценки эффективности
Статистические методы оценки эффективности инвестиций/инвестиционных проектов
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Статистические методы оценки являются самым простым классом подходов к анализу инвестиций и инвестиционных проектов. Несмотря на свою кажущуюся простоту расчета и использования, они позволяют сделать выводы по качеству объектов инвестиций, сравнить их между собой и отсеять неэффективные.
Срок окупаемости инвестиций (Payback Period)
Срок окупаемости инвестиций или инвестиционного проекта (англ. Payback Period, PP, период окупаемости) – данный коэффициент показывает период, за который окупятся первоначальные инвестиции (затраты) в инвестиционный проект. Экономический смысл данного показателя заключается в том, что бы показать срок, за который инвестор вернет обратно свои вложенные деньги (капитал).
Формула расчета срока окупаемости инвестиций (инвестиционного проекта)
где:
IC (Invest Capital) – инвестиционный капитал, первоначальные затраты инвестора в объект вложения. В формуле в иностранной практике иногда используют понятие не инвестиционный капитал, а затраты на капитал (Cost of Capital, CC), что по сути несет аналогичный смысл;
CF (Cash Flow) – денежный поток, который создается объектом инвестиций. Под денежным потоком иногда в формулах подразумевают чистую прибыль (NP, Net Profit).
Формулу расчета срока/период окупаемости можно расписать по-другому, такой вариант тоже часто встречается в отечественной литературе по финансам:
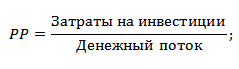
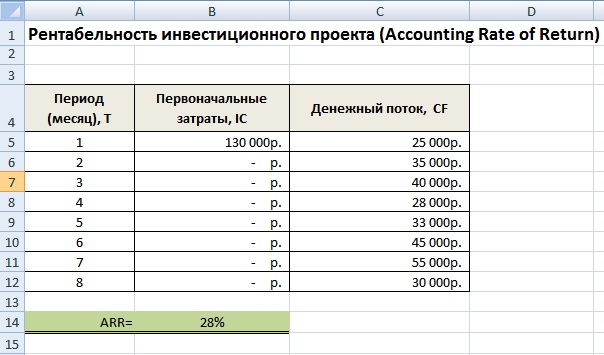
Пример расчета срока окупаемости инвестиционного проекта в Excel
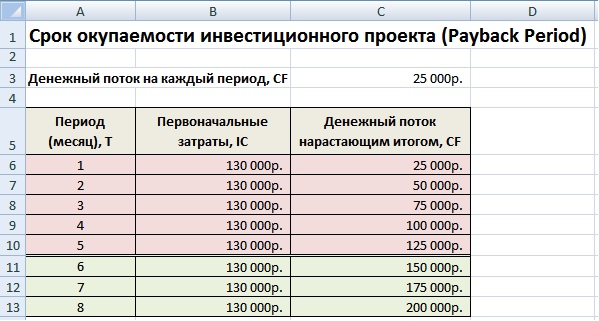
На рисунке ниже показан пример расчета срока окупаемости инвестиционного проекта. У нас имеются исходные данные, что стоимость первоначальных затрат составили 130000 руб., ежемесячно денежный поток от инвестиций составлял 25000 руб. В начале необходимо рассчитать денежный поток нарастающим итогом, для этого использовалась следующая простая формула:
Денежный поток нарастающим итогом рассчитывается в колонке С, C7=C6+$C$3
Если рассчитать срок окупаемости по формуле, то получится следующее:
Так как мы у нас период дискретный, то необходимо округлить этот период до 6 месяцев.
Направления использования срока окупаемости инвестиций (инвестиционных проектов)
Показатель периода окупаемости инвестиций использует как сравнительный показатель для оценки эффективности альтернативных инвестиционных проектов. Тот проект, у которого быстрее период окупаемости тот эффективнее. Данный коэффициент используют, как правило, всегда в совокупности с другими показателям, которые мы разберем ниже.
Достоинства и недостатки показателя срока окупаемости инвестиций
Достоинства показателя его скорость и простота расчета. Недостаток данного коэффициента очевиден – в его расчете используется постоянный денежный поток. В реальных условиях достаточно сложно спрогнозировать устойчивые будущие денежные поступления, поэтому период окупаемости может существенно измениться. Для того чтобы снизить возможные отклонения от плана окупаемости следует обеспечить надежность источников поступления денежного потока инвестиционного проекта. К тому же показатель не учитывает влияние инфляции на изменение стоимости денег во времени. Срок окупаемости инвестиций как может быть использован как критерий отсева на первом этапе оценки и отбора «тяжелых» инвестиционных проектов.
Коэффициент рентабельности инвестиций (Accounting Rate of Return)
Коэффициент рентабельности инвестиций или инвестиционного проекта (англ. Accounting Rate of Return, ARR, ROI, учетная норма прибыли, рентабельность инвестиций) – показатель отражающий прибыльность объекта инвестиций без учета дисконтирования.
Формула расчета коэффициента рентабельности инвестиций
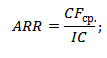
CFср – средний денежный поток (чистая прибыль) объекта инвестиций за рассматриваемый период (месяц, год);
IC (Invest Capital) – инвестиционный капитал, первоначальные затраты инвестора в объект вложения.
Существует также следующая разновидность формулы рентабельности инвестиций отражающая случай, когда в объект/проект в течение рассматриваемого периода вносят дополнительные инвестиционные вложения. Поэтому берется средняя стоимость капитала за период. Формула при этом имеет вид:
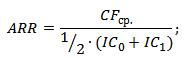
IC0, IC1 – стоимость инвестиций (затраченного капитала) на начало и конец отчетного периода.
Пример расчета коэффициента рентабельности инвестиций (инвестиционного проекта) в Excel
Для того чтобы лучше понять экономический смысл и алгоритм расчета воспользуемся программой Excel. Затраты, которые понес инвестор были только в первом периоде и составили 130000 руб., денежные поступления от инвестиций изменялись ежемесячно, поэтому мы рассчитываем средние поступления по месяцам. За расчетный период может браться любой временной отрезок, квартал, год. В нашем случае мы получаем месячную рентабельность инвестиционного проекта. Формула расчета в Excel следующая:
В14=СРЗНАЧ(C5:C12)/B5
Цели использования коэффициента рентабельности инвестиционного проекта
Данный показатель используется для сравнения различных альтернативных инвестиционных проектов. Чем выше ARR, тем выше привлекательность данного проекта для инвестора. Как правило, данный показатель используется для оценки уже существующих проектов, где можно проследить и статистически оценить эффективность создания денежного потока данной инвестиций.
Достоинства и недостатки коэффициента рентабельности инвестиций
Достоинства коэффициента в его простоте расчета и получения и на этом его достоинства заканчиваются. К недостаткам данного коэффициента можно отнести сложность прогнозирования будущих денежных поступлений/доходов от проекта. К тому же если проект венчурный, то данный показатель может сильно исказить картину восприятия проекта. ARR как правило используется для внешней демонстрации успешного того или иного проекта. Показатель в своей формуле не учитывает изменения стоимости денег во времени. Данный показатель может быть использован на первом этапе оценки и отбора инвестиционных проектов.
Динамические методы оценки эффективности инвестиций/инвестиционных проектов. Как рассчитать эффективность проекта
Рассмотрим ряд динамических методов оценки инвестиционных проектов, данные показатели используют дисконтирование, что является несомненным преимуществом по отношению к статистическим методам.
Чистый дисконтированный доход (Net Present Value)
Чистый дисконтированный доход (англ. Net Present Value, NPV, чистая текущая стоимость, чистый приведенный доход, текущая стоимость) – показатель, отражающий изменение денежных потоков и показывает разность между дисконтированными денежными доходами и расходами.
Чистый дисконтированный доход используют для того чтобы отобрать наиболее инвестиционно привлекательный проект.
Формула чистого дисконтированного дохода
где:
NPV – чистый дисконтированный доход проекта;
CFt – денежный поток в период времени t;
CF0 – денежный поток в первоначальный момент. Первоначальный денежный поток равняется инвестиционному капиталу (CF0 = IC);
r – ставка дисконтирования (барьерная ставка).
Оценка проекта на основе критерия NPV
| Критерий оценки NPV | Заключение по проекту |
| NPV<0 | Инвестиционный проект, имеющий отрицательное значение NPV следует исключить из рассмотрения |
| NPV=0 | Инвестиционный проект обеспечит уровень безубыточности, когда все доходы равны расходам |
| NPV>0 | Инвестиционный проект привлекателен для вложения |
| NPV1>NPV2* | Сравнение NPV одного проекта с NPV* другого, показывает большую инвестиционную привлекательность первого |
Пример расчета чистого дисконтированного дохода в Excel
Рассмотрим пример расчета чистого дисконтированного дохода в программе Excel. В программе есть удобная функция ЧПС (чистая приведенная стоимость), которая позволяет использовать ставку дисконтирования в расчетах. Рассчитаем ниже в двух вариантах NPV.
Вариант №1
Итак, разберем алгоритм последовательного расчета всех показателей NPV.
- Расчет денежного потока по годам: E7=C7-D7
- Дисконтирование денежного потока по времени: F7=E7/(1+$C$3)^A7
- Суммирование всех дисконтированных денежных поступлений по инвестиционному проекту и вычитание первоначальных капитальных затрат: F16 =СУММ(F7:F15)-B6
Вариант №2
Расчет с использованием встроенной формулы ЧПС. Следует заметить, что необходимо вычесть первоначальные капитальные затраты (В6).
=ЧПС($C$3;E7;E8;E9;E10;E11;E12;E13;E14;E15)-B6
Результаты в обоих методах подсчета NPV, как мы видим, совпадают.
Мастер-класс: «Как рассчитать чистый дисконтированный доход для бизнес плана»
Внутренняя норма прибыли инвестиционного проекта
Внутренняя норма прибыли (англ. Internal Rate of Return, IRR, внутренняя норма дисконта, внутренняя норма прибыли, внутренний коэффициент эффективности) – показывает такую ставку дисконтирования, при которой чистый дисконтированный доход равняется нулю.
Формула расчета внутренней нормы прибыли инвестиционного проекта
где:
CF (Cash Flow) – денежный поток, который создается объектом инвестиций;
IRR – внутренняя норма прибыли;
CF0 – денежный поток в первоначальный момент. В первом периоде, как правило, денежный поток равняется инвестиционному капиталу (CF0 = IC).
Пример расчета IRR инвестиционного проекта в Excel
Рассмотрим пример расчета внутренней нормы прибыли в Excel, в программе есть хорошая функция ВСД (внутренняя ставка доходности), которая позволяет быстро рассчитать IRR. Данную функцию корректно использовать в том случае если есть хотя бы один положительный и отрицательный денежный поток.
E16 =ВСД(E6:E15)
Достоинства и недостатки внутренней нормы доходности IRR
+ ) возможность сравнения инвестиционных проектов между собой, имеющих разный горизонт инвестирования;
+ )возможность сравнения не только проектов, но и альтернативных инвестиций, например банковский вклад. Если IRR проекта составляет 25%, а банковский вклад равен 15%, то проект более инвестиционно привлекателен.
+ ) экспресс-оценка проекта на его целесообразность дальнейшего развития.
Внутреннюю норму прибыли оценивают со средневзвешенной стоимостью привлеченного капитала, что позволяет сделать оценку целесообразности дальнейшего развития проекта.
| Оценка значений коэффициента IRR | Заключение по проекту |
| IRR > WACC | Вложенный в инвестиционный проект капитал будет создавать доходность выше, чем стоимость вложенного капитала. Такой проект инвестиционно привлекателен |
| IRR = WACC | Проект не принесет ни убытков, ни дохода в будущем периоде и такой проект не является привлекательным |
| IRR < WACC | Такой проект будет создавать отрицательный дисконтированный денежный поток в будущем |
— ) не отражен абсолютный рост стоимости инвестиционного проекта;
— ) денежные потоки часто имеют не систематическую структуру, что затрудняет правильный расчет данного показателя.
Мастер-класс: «Как рассчитать внутреннюю норму доходности для бизнес плана»
Индекс прибыльности инвестиций (Profitability index)
Индекс прибыльность инвестиций (англ. Profitability index, PI, индекс доходности, индекс рентабельности) – показатель эффективности инвестиций, показывающий отдачу (доходность) вложенного капитала. Индекс прибыли представляет собой отношение дисконтированной стоимости будущих денежных потоков к стоимости первоначальных инвестиций. Экономический смысл данного коэффициента – это оценка дополнительной ценности на каждый вложенный рубль.
Формула расчета индекса прибыльности инвестиций
где:
NPV – чистый дисконтированный доход;
n – срок реализации проекта;
r – ставка дисконтирования (%);
IC – вложенный (затраченный) инвестиционный капитал.
Разновидность формулы индекса прибыльности инвестиций
Если вложения в проект осуществляются не единовременно, а на протяжении всего времени реализации, то необходимо инвестиционный капитал (IC) привести к единой стоимости, т.е. дисконтировать его. Формула в этом случае станет иметь следующий вид:
Чем выше коэффициент прибыльности инвестиций, тем большую отдачу на вложенный капитал приносит данная инвестиция. Данный критерий используется для сравнения между собой нескольких инвестиционных проектов. На практике большой индекс прибыли не всегда показывает эффективность проекта, ведь в таком случае оценка будущих доходов могла быть завышена или периодичность их получения не правильно оценена.
Оценка проекта на основе критерия PI
| Критерий оценки PI | Заключение по выбору проекта |
| PI<1 | Инвестиционный проект не сможет возместить в полном размере вложенные в него капитальные затраты |
| PI=1 | Инвестиционный проект имеет доходность равную выбранной ставки дисконтирования |
| PI>1 | Проект инвестиционно привлекателен для вложения, так как сможет обеспечить дополнительную отдачу капитала. |
| PI1>PI2* | Сравнение между собой инвестиционной привлекательности нескольких проектов. Первый проект имеет большую рентабельность, поэтому второй будет отброшен |
Пример расчета индекса прибыльности проекта в Excel
Рассмотрим на примере вычисление индекса прибыльности. На рисунке ниже показан расчет PI в ячейке F18.
- Расчет столбца F – Дисконтированного денежного потока =E7/(1+$C$3)^A7
- Расчет чистого дисконтированного дохода NPV в ячейке F16 =СУММ(F7:F15)-B6
- Оценка прибыльности инвестиций в ячейке F18 =F16/B6
Если бы инвестиционные затраты были каждый год, то необходимо было индекс прибыльности рассчитывать по второй формуле и приводить их к настоящему времени (дисконтировать).
Дисконтированный срок окупаемости инвестиций
Дисконтированный срок окупаемости (англ. Discounted Payback Period, DPP) – показатель отражающий период, через который окупятся первоначальные инвестиционные затраты. Формула расчета коэффициента аналогична формуле оценки периода окупаемости инвестиций, только используется дисконтирование
Формула расчета дисконтированного срока окупаемости инвестиций

IC (Invest Capital)– инвестиционный капитал, первоначальные затраты инвестора в объект вложения;
CF (Cash Flow) – денежный поток, который создается объектом инвестиций;
r – ставка дисконтирования;
t –период оценки получаемого денежного потока.
Пример расчета дисконтированного срока окупаемости инвестиций в Excel
Рассчитаем коэффициент дисконтированного срока окупаемости инвестиций в Excel. На рисунке ниже показан пример расчета. Для этого необходимо выполнить следующие операции:
- Рассчитать дисконтированный денежный поток в колонке D =C7/(1+$C$3)^A7
- Посчитать нарастающим итогом прирост капитала в колоне E =E7+D8
- Оценить в какой период вложенные инвестиции (IC) окупились полностью.
Как мы видим окупаемость всех затрат дисконтированным денежным потоком произошла на 6 месяц. Чем меньше период окупаемости инвестиционного проекта, тем более привлекательны данные проекты.
Достоинства и недостатки дисконтированного срока окупаемости
Достоинством коэффициента является возможность использовать в формуле свойство денег изменять свою стоимость со временем за счет инфляционных процессов. Это повышает точность оценки периода возврата вложенного капитала. Сложность использования данного коэффициента заключаются в точном определении будущих денежных поступлений от инвестиции и оценке ставки дисконтирования. Ставка может изменяться на всем жизненном цикле инвестиции из-за действия различных экономических, политических, производственных факторов.
Мастер-класс: «Как рассчитать срок окупаемости для бизнес плана: инструкция»
Выбор инвестиции на основе коэффициентов оценки эффективности
На рисунке ниже показана таблица критериев выбора инвестиционного проекта/инвестиции на основе рассмотренных коэффициентов. Данные показатели позволяют дать экспресс-оценку привлекательности проекта. Следует заметить, что данные показатели плохо применяются для оценки венчурных проектов, потому что сложно спрогнозировать какие будут продажи, доходы и спрос в этом проекте. Показатели хорошо себя зарекомендовали в оценке уже реализованных проектов с четко выстроенными бизнес процессами.
| Показатель | Критерий выбора инвестиции |
| Статистические методы оценки эффективности инвестиций | |
| Период окупаемости | PP -> min |
| Рентабельность инвестиционного капитала | ARR>0 |
| Динамические методы оценки эффективности инвестиций | |
| Чистый дисконтированный доход | NPV>0 |
| Внутренняя норма прибыли | IRR>WACC |
| Индекс прибыльности | PI>1 |
| Дисконтированный период окупаемости | DPP -> min |
Резюме
Использование коэффициентов оценки инвестиционных проектов позволяет сделать выбрать наиболее привлекательные объекты для вложения. Мы рассмотрели как статистические, так и динамические методы оценки, на практике, первые подходят для отражения общей характеристики объекта, тогда как динамические позволяют более точно оценить параметры инвестиции. В современной экономике, во времена кризисов, использование данных показателей эффективно на сравнительно не большой горизонт инвестирования. Помимо внешних факторов, на оценку влияют внутренние – сложность точного определения будущих денежных поступлений от проекта. Показатели дают в большей степени финансовое описание жизни инвестиции и не раскрывают причинно-следственных связей с получаемыми доходами (сложно оценить венчурные проекты и стартапы ). В тоже время, простота расчетов коэффициентов позволяет уже на первом этапе анализа исключить не рентабельные проекты. На этом описание коэффициентов оценки эффективности инвестиций завершено. Изучайте инвестиционный анализ, в следующих статьях я расскажу про более сложные методы оценки проектов, спасибо за внимание, с вами были Иван Жданов.
Автор: к.э.н. Жданов Иван Юрьевич