
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
БРЯНСКИЙ ФИЛИАЛ
ПРАКТИКА ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ РАСЧЕТОВ В СРЕДЕ MS EXCEL
Брянск 2012
ББК 32.973.26-018.2 Н26
Новиков С.П. Практика инженерно-технических расчетов в среде MS Excel. – Брянск: БФ МИИТ, 2012, — 20 с.
Методические указания и задания для лабораторных работ по теме «Практика инженерно-технических расчетов в среде MS Excel» для студентов I курса заочной формы обучения инженерно-технических специальностей.
Разработал: к.т.н., доц. С.П. Новиков
© Новиков С.П., 2012 © БФ МИИТ, 2012
Общие указания
Рекомендуется для изучения дисциплины «Информатика» в рамках освоения табличного процессора MS Excel студентами-заочниками инже- нерно-технических специальностей 1 курса и сопровождается выполнением лабораторных работ 1-5 с подробными методическими указаниями.
Перечень тем лабораторных занятий
1.Изучение основ обработки инженерно-технической информации.
2.Табулирование и построение графиков функций.
3.Обработка результатов экспериментов.
4.Методика построение графиков объемных функций.
5.Изучение матричных операций в среде MS Excel.
3
Лабораторная работа № 1.
Изучение основ обработки инженерно-технической информации
Цель работы: Изучить основные приемы работы в MS Excel.
Настройка основных параметров системы MS Excel.
1.Запустите приложение MS Excel (Пуск Программы Microsoft Excel).
2.На вкладке Параметры Общие установите (или проверьте наличие установленного): шрифт — Arial Cyr, размер — 10 пт, проконтролируйте ОТСУТСТВИЕ флажка Стиль ссылок R1C1, на вкладке Вид проконтролируйте наличие установленного флажка: строка формул.
3.Создайте рабочую папку в своей личной папке с помощью любого файлового менеджера (например, программы «Проводник») и дайте ей название Работа в
Excel.
4.Сохраните текущую рабочую книгу под именем Расчеты в Excel в своей личной папке. Для этого воспользуйтесь пунктом меню Файл Сохранить как…
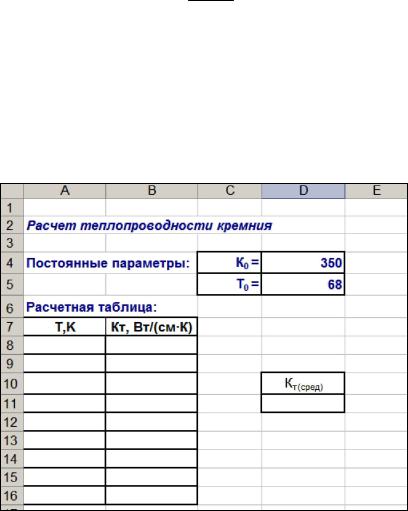
Задание 1. Рассчитать теплопроводность кремния ( KT ) с точность до 4 десятичных знаков после запятой для следующего диапазона значений температур T: от 200 до 600 К с шагом 50 К согласно следующей формуле:
KT K0
T T0
где K0 350,T0 68 заданные постоянные величины.
Найти среднее значение теплопроводности на заданном интервале температур.
Методические указания
1.Сформируйте электронную расчетную форму на листе №1, согласно предложенному ниже образцу.
4
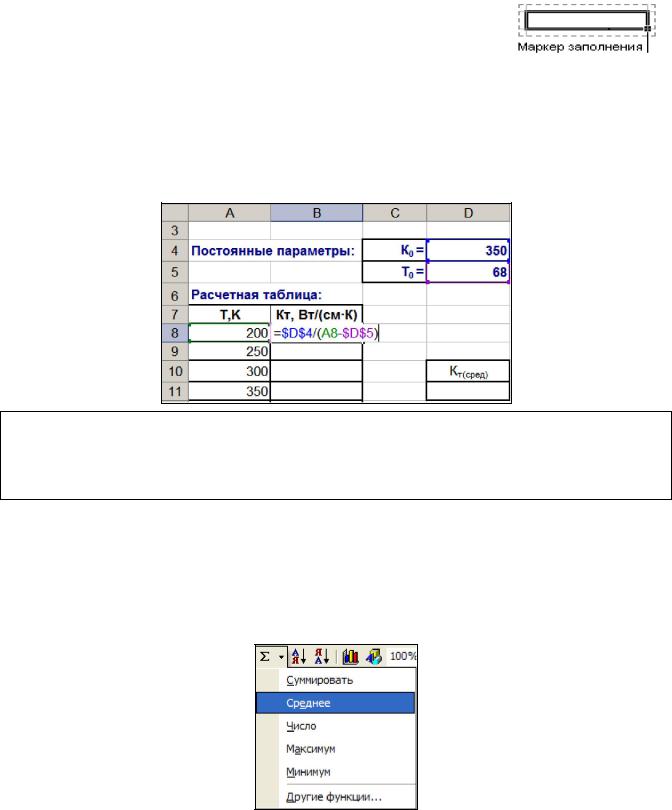
В процессе разработки формы используйте следующие указания:
1)Введите поясняющие надписи и отформатируйте их с помощью панели инструментов Форматирование. Для ввода нижнего индекса в постоянных коэффициентах воспользуйтесь пунктом меню Формат/Ячейки/Шрифт и выберите видоизменение: Подстрочный.
2)Сформируйте границы таблиц (выделите нужные ячейки и используйте кнопку
Границы), подкорректируйте размер строк и столбцов, согласно образцу.
2.Заполните первый столбец введенной таблицы. Для этого введите в ячейку А8 значение 200, а в ячейку А9 – значение 250. Далее выделите ОБЕ ЯЧЕЙКИ и протяните их вниз.
(необходимо подвести указатель мыши в правый нижний угол выделения и потянуть вниз за маркер, удерживая левую кнопку мыши).
3.Для расчета значений теплопроводности введите в ячейку B8 следующую формулу:
=$D$4/(A8-$D$5)
Вначале вводится знак, затем мышкой выбирается соответствующая ячейка. Для того, чтобы знаки доллара перед соответствующими координатами появились автоматически необходимо сразу же после ввода ячейки D4 нажать клавишу <F4>, аналогично следует поступить и при вводе координаты ячейки D5.
Обратите внимание, что знак доллара перед наименованием координаты строки и столбца указывает, что при копировании или протягивании введенной формулы адрес ячейки, содержащей исходное данное, не будет меняться. Такая конструкция называется абсолютной ссылкой на ячейку.
4.После ввода формулы выделите ее и протяните вниз. Проверьте появившиеся ниже формулы, осуществив двойной щелчок мышью на каждую из ячеек.
5.Рассчитайте среднее значение теплопроводности. Для этого:
1)Выделите ячейку D11 и раскройте содержимое кнопки Автосумма (на панели инструментов Редактирование). Для этого наведите указатель мыши на маркер справа от кнопки, раскройте список и выберите пункт Среднее.
5
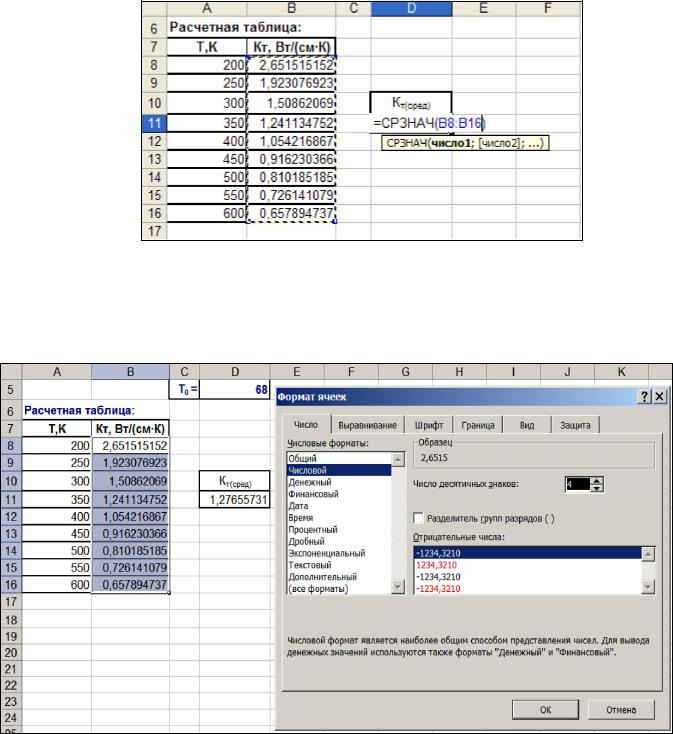
2)Далее, выделите диапазон значений, на основании которого будет производиться расчет среднего значения:
3)Нажмите клавишу <Enter>
6.Для задания нужной точности вычислений выделите второй столбец, содержащий рассчитанные значения, воспользуйтесь пунктом меню Формат/Ячейки и в появившемся диалоговом окне перейдите на закладку: Число. Далее выберите Числовой формат и укажите число десятичных знаков равное 4 и нажмите кнопку ОК.
Задание 2. Составить электронную таблицу для расчета влияния содержания углерода на механические свойства сталей:
|
Размеры |
Размеры |
Относительное |
Относительное |
||||||
|
№ |
образца |
образца |
|||||||
|
С, % |
сужение |
удлинение |
|||||||
|
образца |
до испытания |
после испытания |
|||||||
|
, % |
, % |
||||||||
|
L0 , мм |
F0 , мм |
L1 , мм |
F1 , мм |
||||||
|
1 |
0,1 |
25 |
20 |
36 |
8 |
||||
|
2 |
0,2 |
27 |
22 |
35 |
10 |
||||
|
3 |
0,3 |
28 |
24 |
34 |
12 |
||||
|
4 |
0,4 |
30 |
26 |
33 |
14 |
||||
|
6 |

Методические указания
1.Сформируйте электронную расчетную форму в виде таблицы по аналогии с предыдущим заданием. Греческие символы найдите и введите, воспользовавшись пунктом ме-
ню Вставка/Символ.
2.Рассчитайте относительное сужение и относительное удлинение по соответствующим
формулам: F0 F1 и L1 L0 . Для этого введите указанные формулы только в
F0 L1
верхние ячейки столбцов и ОБЯЗАТЕЛЬНО ВОСПОЛЬЗУЙТЕСЬ ПРОТЯГИВАНИЕМ для заполнения остальных ячеек.
3.Для задания процентного формата рассчитанным ячейкам выделите значения обоих столбцов и воспользуйтесь пунктом меню Формат/Ячейки. В появившемся диалоговом окне перейдите на закладку: Число. Далее выберите Процентный формат и укажите число десятичных знаков, равное 2 и нажмите кнопку ОК.
Задание 3. Известны данные о выбросах автомобильных газов в различных странах:
|
Кол-во |
Кол-во машин, соот- |
Допустимое |
Среднее значе- |
||
|
ветствующих санитар- |
кол-во выбросов |
ние выбросов с |
|||
|
Страна |
машин, |
||||
|
ным нормам (в % от |
одной машины |
одной машины |
|||
|
млн. шт. |
|||||
|
общего количества) |
за год, т |
за год, т |
|||
|
Россия |
86 |
54% |
59 |
63 |
|
|
Украина |
54 |
46% |
61 |
71 |
|
|
Германия |
71 |
87% |
43 |
58 |
|
|
Голландия |
45 |
89% |
35 |
45 |
|
|
США |
127 |
74% |
48 |
60 |
Рассчитать:
1. Допустимое количество выбросов на территории страны по формуле:
(Количество машин, соответствующих санитарным нормам [в шт.]* Допустимое количество выбросов одной машины за год);
2. Реальное количество выбросов в стране согласно формуле:
(Количество машин, соответствующих санитарным нормам [в шт.]* Допустимое количество выбросов одной машины за год + Количество машин, не соответствующих санитарным нормам [в шт.] * Среднее количество выбросов одной машины за год).
3. Самую загрязненную территорию по формуле:
(Наибольшая разность между реальным и допустимым количеством выбросов).
Методические указания
Выполнить и оформить расчет самостоятельно по аналогии с предыдущими заданиями.
Примерный образец решения задачи представлен ниже:
7
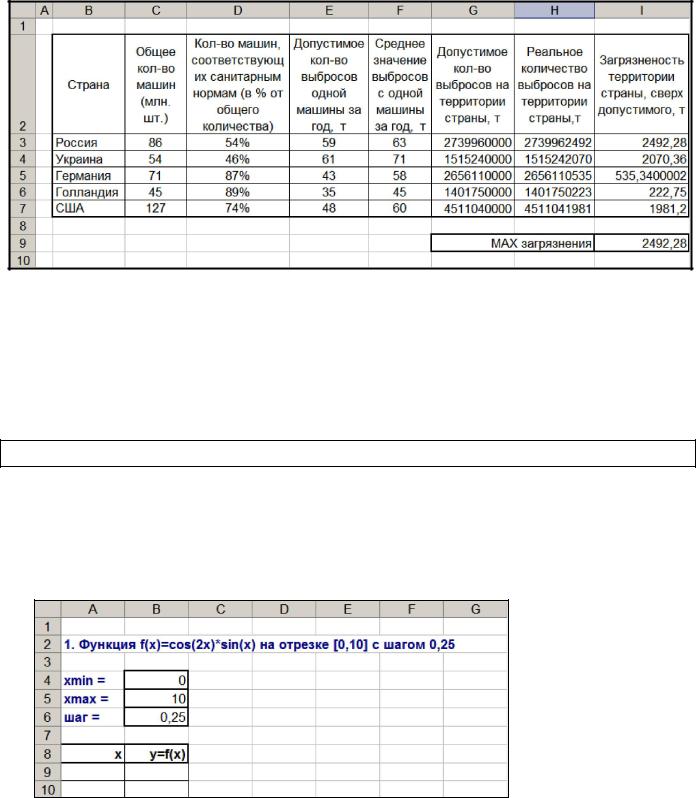
Лабораторная работа № 2. Табулирование и построение графиков функций
Задание 1. С использованием средств Excel вычислить значение заданной функции в диапазоне изменения переменной x от 0 до 10 с шагом 0,25 и построить ее график.
y cos( 2x )sin( x )
Методические указания
1.Зарезервируйте ячейки для ввода исходных данных и сформируйте границы (вы-
делите нужные ячейки и используйте кнопку Границы).
2.Введите начальные параметры и оформите в соответствии с образцом ниже:
3.Введите в ячейку A9 формулу: =B4, представляющую собой ссылку на ячейку, содержащую начальное значения аргумента x. В результате в данной ячейке появится значение: 0.
4.Далее, введите в ячейку A10 формулу, равную предыдущему значению аргумента x, увеличенному на величину шага: =A9+$B$6.
5.Выделите ячейку A10 и протяните вниз. Протягивание осуществляйте до 49-ой строки листа включительно.
6.С помощью формул заполните столбец значений функции f(x). Для этого:
8
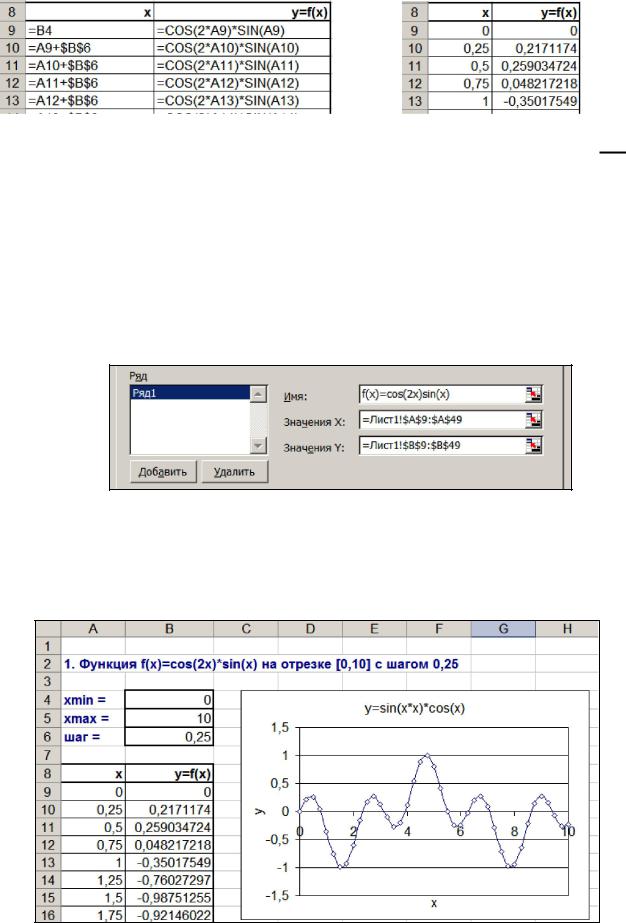
1)В ячейку B9 введите следующую формулу: =COS(2*A9)*SIN(A9).
2)Протяните формулу вниз до 49-ой строки листа включительно.
3)Фрагмент первых 5-ти формул каждого столбца представлен ниже (слева показаны сами формулы, а справа вычисленные значения):
7.Для построения графика заданной функции выполните следующие действия:
1)Вызовите Мастер диаграмм, воспользовавшись одноименной кнопкой (
2)В открывшемся диалоговом окне на вкладке Стандартные выберите тип диа-
граммы: Точечная и вид Со значениями, соединенными сглаживающими лини-
ями и нажмите на кнопку Далее.
3)Перейдите на вкладку Ряд и нажмите кнопку Добавить. Введите имя диаграммы: f(x)=cos(2x)sin(x). Перейдите в поле Значения X и выделите все значения в 1-ом столбце x, затем перейдите в поле Значения Y и выделите все значения во 2-ом столбце y=f(x).
После заполнения всех полей нажмите кнопку Далее.
4)В новом окне введите название осей: x и y, перейдите на вкладку Легенда и отмените ее добавление к графику, сняв галочку, затем нажмите кнопку Далее.
5)В последнем окне выберите размещение диаграммы: на имеющемся листе и нажмите кнопку Готово. Примерный образец диаграммы показан ниже:
9

Задание 2. С использованием средств Excel вычислить значение заданной сложной функции в диапазоне изменения переменной x от -1 до 1 с шагом 0,1 и построить ее график.
y x2 , если x 0;
y sin( x ), если x 0.
Методические указания
1.Откройте новый лист Excel.
2.По аналогии с предыдущим заданием сформируйте электронную форму для построения графика и введите исходные данные:
3.По аналогии с предыдущим заданием заполните 1-й столбец значениями от -1 до 1 с шагом 0,1.
4.В ячейку B11 введите логическую формулу: =ЕСЛИ(A11<=0;A11*A11;SIN(A11)). Для этого вызовите мастер функций, нажав на кнопку fx в строке формул. Далее выполните следующие действия:
1) В появившемся окне выберите категорию Логические и функцию ЕСЛИ.
2) В появившемся диалоговом окне функции ЕСЛИ в верхнем поле необходимо ввести условие, согласно которому функция будет выбирать вид функции для вычисления: A11<=0.
3) Далее во втором поле вводится команда вычисления функции y=x2: A11*A11 – (эта команда будет выполнена, если предыдущее условие верно), в нижнем поле – команда вычисления функции y=sin(x): SIN(A11) – (эта команда будет выполнена, если предыдущее условие не верно).
4) Нажмите ОК.
5.Протяните полученную формулу вниз для заполнения всех оставшихся значений функции.
6.По аналогии с предыдущим заданием постройте график полученной функции и оформите в соответствии с образцом:
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В настоящей статье на простых примерах показывается, как выполнить собственные расчеты с помощью табличного процессора Microsoft Excel, входящего в комплекс программ Microsoft Office и предназначенного для решения экономических и инженерных задач. Расчеты в Excel просты и удобны, позволяют быстро ответить на вопрос: «А что, если…?».
Вначале попробуем составить собственную таблицу «с ходу», затем договоримся о правилах оформления листов рабочей книги Excel, и в заключение рассмотрим пример расчета УМЗЧ на микросхеме LM4780.
Содержание статьи / Table Of Contents
Персональный компьютер изменил отношение к вычислениям. Создана масса компьютерных программ, быстро и безошибочно выполняющих нужные расчеты по известным формулам.
Наличие готовых компьютерных программ для расчетов практически всего, что только можно вычислить, на первый взгляд приводит к мысли, что можно особенно и не разбираться в сути проблемы. Многие так и живут. Зачем, например, помнить таблицу умножения, если есть калькулятор? Для чего изучать грамматику, если Word сам проверит правописание?
Очень важно в самом начале развеять это распространенное заблуждение. Привыкнув пользоваться готовыми программами, радиолюбитель теряет главное – возможность творить. Поэтому, разрабатывая любой узел или устройство, старайтесь сначала оценить его возможности на основе фундаментальных дисциплин и знаний и лишь в конечной стадии проектирования прибегайте к помощи компьютерных программ.
Чтобы знакомство с построением таблиц в Excel прошло с пользой, рассмотрим в качестве примера соотношения между диаметром проводов D в метрической системе и калибром в стандарте AWG.
Американская калибромерка
Аббревиатура AWG расшифровывается как American Wire Gauge – стандарт США на одножильные провода. Информация к месту, поскольку практически вся импортная кабельная продукция маркируется не в метрической системе, а в системах AWG или SWG (Standard Wire Gauge). Соотношение между диаметром провода в миллиметрах и его калибром AWG следующее:
где 1 mils = 0,0254 мм.
Внесем ясность в эту не совсем понятную на первый взгляд формулу. При разработке калибров AWG в качестве границ были приняты самый тонкий в то время провод 0,005 дюйма (AWG 36) и самый популярный толстый провод 0,46 дюймов (AWG 0000). Соотношение между диаметрами этих проводов оказалось 92 раза, и в этом диапазоне уместилось еще 38 калибров. Отношение между соседними калибрами выбрано постоянным и составляет корень 39 степени из 92 (примерно 1,123).
Проблема с обозначением толстых проводов решена введением отрицательных величин калибров. Чтобы не путать потребителей, в обозначение проводников толще калибра AWG 0 ввели дополнительные нули, а для удобства восприятия пишут m/0, где m – количество дополнительных нулей в обозначении.
Весь мир пользуется метрической системой СИ, но только не американцы, чем отчасти создают себе и другим проблемы. Как сказал бы Михаил Николаевич Задорнов: «Ну, тупые!»
Значение AWG берется равным – (m -1). Например, для калибра AWG 0000 (AWG 4/0) значение, подставляемое в формулу, составит – 3.
Для практического выбора проводов полезно уяснить, что чем меньше калибр провода, тем он толще, а также, что увеличение толщины проводника на 6 калибров соответствует увеличению толщины вдвое (1,123^6?2,005).
Вычислим также поперечное сечение провода:
S=?D^2/4,
здесь S – площадь сечения провода, кв. мм,
D – диаметр провода, мм.
И, наконец, подсчитаем активное сопротивление провода:
R=l/?S,
где l – длина провода, м; ?=53 м/(Ом мм^2) – среднее значение удельной проводимости медного провода при температуре 20°С.
Перейдем собственно к созданию таблицы в Excel (рис. 1). В ячейке А1 пишем заголовок таблицы, выделяем его и сохраняем в буфере обмена (Ctrl – C). После нажатия клавиши ввода вновь переходим в ячейку А1 и делаем шрифт заголовка полужирным, нажав кнопку с изображением буквы «Ж» на панели инструментов быстрого доступа.
Рис. 1. Соотношение между диаметром проводов в системе СИ и калибром в стандарте AWG
Сохраняем документ, для чего выбираем Файл ? Сохранить как и в появившемся окне Сохранение документа, в поле Имя файла копируем ранее сохраненный в буфере обмена заголовок таблицы (Ctrl – V).
Таким образом, уже на начальных этапах создания таблицы даем ей имя, что в дальнейшем избавит от многих бед, связанных с возможной потерей данных.
Следующим этапом создания таблиц является ввод заголовков ее строк и столбцов. В таблице потребуется ввести лишь заголовки столбцов. В ячейки A3:D3 последовательно вписываем необходимые заголовки. Исходными данными таблицы являются величины калибров проводов AWG, их заносим в ячейки A4:A32.
Теперь создадим формулы для одной из строк таблицы, для определенности, строки 4.
В ячейке B4 пишем: =5*0,0254*СТЕПЕНЬ(0,46/0,005;(36-A4)/39); в ячейке С4: =ПИ()*СТЕПЕНЬ(В4;2)/4, а в ячейке D4: =1000/(C4*53).
Напомним, что формулы удобно вносить, не вписывая адреса ячеек, а щелкая по нужным ячейкам мышью – так быстрее и надежнее (меньше ошибок при вводе). Также желательно пользоваться стандартными функциями Excel, расположенными в левой части строки ввода, а не вводить их вручную (в нашем случае это функции СТЕПЕНЬ и ПИ).
При отсутствии ошибок при вводе данных после нажатия клавиши Enter в соответствующей ячейке сразу появится результат, а введенная формула отобразится в строке ввода.
Поскольку по умолчанию связь в формулах между строками таблицы относительная, легко выполнить все оставшиеся вычисления. Для этого выделим мышью ячейки B4:D4, встанем в правый нижний угол выделенного диапазона ячеек, и в момент, когда курсор мыши изменит свое начертание на перекрестье, нажмем левую кнопку мыши, после чего протянем выделенный диапазон ячеек с формулами вниз до строки 32.
Для основной части таблицы, кроме первых шести строк мы получим положительный результат. В области формул шести строк отобразится надпись #ЗНАЧ!
Ошибка вызвана тем, что тип исходных данных в ячейках А4:А9 не числовой, а текстовый. Чтобы не усложнять вычисления, отредактируем формулы в ячейках B4:B9 и вручную занесем в них требуемый калибр. Например, в ячейке B4 формула выглядит следующим образом: =5*0,0254*СТЕПЕНЬ(0,46/0,005;(36+5)/39).
Таблица почти готова, осталось произвести ее оформление. Выделим диапазон формул B4:D32 и нажатием кнопки Уменьшить разрядность установим три знака после запятой (по желанию можно выбрать любое требуемое значение).
Далее, выделим весь диапазон таблицы А3:D32, установим с помощью кнопки Границы выделенных ячеек сначала Все границы, а затем, не снимая выделения – Толстая внешняя граница.
Теперь «подсветим» заголовки и исходные данные в таблице. Выделим ячейки A3:D3 и выберем цвет заливки Белый, Фон 1, более темный оттенок 15%. Затем выделим диапазон исходных данных (А4:А32) и установим для него цвет заливки Темно-синий, Текст 2, более светлый оттенок 80%. Сохраним созданную таблицу.
Подобным образом можно строить практически любые таблицы вычислений, применяемые в радиолюбительской практике [1, 2].
Далее сформулируем другие требования к созданию таблиц, позволяющие улучшить их наглядность и удобство работы.
При оформлении и документировании расчетов на рабочих листах файлов книг Microsoft Excel следует выработать некоторые стандарты, позволяющие сделать результаты наглядными, удобными для просмотра, редактирования и отладки. Примем подход, установленный авторами [3].
На рис. 2 показан простой пример расчета разветвителя телевизионного сигнала.
Рис. 2. Оформление расчетов на рабочем листе книги Microsoft Excel
Сформулируем правила оформления рабочих листов.
1. Все элементы рабочего листа должны находиться в поле зрения пользователя при условии, что активной является ячейка А1 и рабочем разрешении экрана монитора (у меня 1280х1024). В этом случае отпадает необходимость прибегать к прокрутке рабочего листа по горизонтали и по вертикали.
2. Каждый расчет или фрагмент расчета начинается с заголовка. Кроме наименования расчета здесь можно указать методику, по которой производились вычисления, библиографические данные и другие дополнительные сведения.
3. Далее следуют пояснения соотношений, по которым производится расчет. Для этого пользуются теоретическими формулами, которые вводят прямо в ячейки рабочего листа, либо создают с помощью редактора формул Microsoft Equation, входящего в стандартный комплект Excel.
При необходимости можно обновить редактор формул на MathType, разработанный фирмой Design Science. Это — более полная и мощная версия редактора формул. Пользователи, которым часто приходится включать формулы в документы, предпочитают работать с MathType. Данный редактор так же прост в использовании, однако имеет ряд дополнительных возможностей, ускоряющих работу и повышающих качество документов (набор шрифтов с огромным числом математических символов, профессиональные наборы для многих областей науки, работа с WEB документами и цветом, а также многое другое).
Теоретические формулы не имеют прямого отношения к расчету, а служат для пояснения правил вычислений.
4. Собственно расчет выполняется, как правило, в виде таблицы, содержащей заголовки строк и (или) столбцов, исходные данные и расчетные формулы. Ячейки, предназначенные для ввода пользователем исходных или промежуточных данных, выделяют соответственно, бледно-голубым или бледно-желтым цветом. Конечно, цвет ячеек может быть изменен в соответствии с желаниями пользователя.
Расчетная формула может содержать одну или несколько встроенных функций Excel.
5. Рядом с расчетными формулами могут располагаться подстановочные формулы, предназначенные, прежде всего для иллюстрации конкретных значений в расчетах, облегчающих поиск ошибок в исходных данных, введенных пользователем.
Подстановочная формула не выполняет расчет, а «собирает» вместе значения, указанные в формуле и отображает их. Для реализации подстановочных формул используется встроенная функция Excel =СЦЕПИТЬ() (=CONCATENATE()). В нашем случае используется простая (однострочная) подстановочная формула, помещенная в одной ячейке рабочего листа.
Для иллюстрации значений в сложных формулах (наличие натуральных дробей, корней, сложных математических символов) при изображении подстановочных формул следует проявить изобретательность: формулы на основе функции =СЦЕПИТЬ() размещаются в нескольких соседних ячейках, с помощью линий воспроизводятся сложные математические символы.
Подстановочные формулы целесообразно использовать в многоступенчатых вычислениях, которые могут потребовать последующей отладки. При простых вычислениях подстановочные формулы оказываются излишними.
6. На рабочем листе книги могут располагаться принципиальные схемы (фрагменты схем) рассчитываемых устройств, чертежи, рисунки и необходимые справочные таблицы значений. Если вся требуемая информация не помещается на рабочем листе книги, расчет выполняют на двух и более листах, следуя вышеприведенным соглашениям.
Несмотря на очевидность приведенных правил оформления рабочих листов, следовать им на практике не так просто, как кажется.
Возникает искушение пропустить отдельные фрагменты оформления, что спустя некоторое время приводит к бесполезности выполненной работы.
Здесь хочется в очередной раз вспомнить любимую поговорку одного из наших институтских преподавателей, бессменного руководителя стройотрядовского движения «Делай хорошо – плохо само получится!».
Рассмотрим процедуру расчета усилителя на интегральных микросхемах LM4780/81/82 фирмы National Semiconductor, выполненных в удобном для монтажа 27 выводном корпусе ТО-220. Эти УМЗЧ пришли на смену хорошо зарекомендовавшей себя у любителей высококачественного звуковоспроизведения микросхемы монофонического усилителя LM3886.
Все указанные микросхемы входят в линейку продукции Overture®, предназначенной для применения в малогабаритных стереосистемах домашних аудиокомплексов, телевизионных приемниках, акустических системах формата 5.1 Surround Sound и т. п. Основные характеристики микросхем сведены в табл. 1.
Для определенности выберем микросхему LM4780, которая является стереоусилителем с выходной мощностью до 60 Вт на нагрузке 8 Ом (в мостовом включении – 120 Вт) на канал при типовом коэффициенте гармоник 0,03% и коэффициенте интермодуляционных искажений 0,004% (метод SMPTE, 60 Гц, 7 кГц, 4:1). Отношение сигнал/шум (относительно выходной мощности Pвых=50 Вт) – 114 дБА. Частота единичного усиления 8 МГц, скорость изменения выходного напряжения 19 В/мкс, а коэффициент подавления пульсаций напряжения питания до 120 дБ, что позволяет подключить усилитель к нестабилизированному двухполярному источнику питания с конденсатором фильтра порядка 10000 мкФ. Принципиальная схема одного канала стереофонического УМЗЧ представлена на рис. 3. В скобках указаны номера выводов микросхемы DA1, относящиеся ко второму каналу.
Рис. 3. Стереофонический УМЗЧ на микросхеме LM4780
Диапазон напряжений питания достаточно широк – от ±10 до ±42В; ток потребления в режиме покоя 110 мА.
Фирма National Semiconductor снабдила новую линейку микросхем уникальной системой защиты от бросков температуры, вызванных внутренним разогревом (зарегистрированное торговое обозначение SPiKe™ — Self-Peak instantaneous temperature Ke). Система SPiKe обеспечивает динамически оптимизированную область безопасной работы и надежно предохраняет выводы от перегрузок, выбросов, просадок напряжения, коротких замыканий на шину питания или на «землю», температурного дрейфа параметров и тепловых бросков.
Для увеличения выходной мощности микросхема может быть включена не только по мостовой схеме (рис. 4), позволяющей получить удвоенное выходное напряжение (на нагрузке 8 или 16 Ом), но и по параллельной схеме (рис. 5), обеспечивающей удвоение максимального тока до 14-23 А на низкоомной нагрузке 2 или 4 Ома.
Рис. 4. Включение LM4780 по мостовой схеме
Рис. 5. Включение LM4780 по параллельной схеме
Все микросхемы линейки LM4780/81/82 оснащены входом приглушения звука Mute, обеспечивающим плавное нарастание и спад громкости.
Специалистами National Semiconductor подготовлен и выложен на сайте для свободного использования в табличном процессоре Excel файл Overture_Design_Guide15.xls, с помощью которого рассчитываются параметры усилителей на ИС группы Overture для фиксированных сопротивлений акустических систем 4, 6 или 8 Ом.
Причем наличие ошибок при проектировании усилителя отображается заполнением соответствующих ячеек таблицы красным цветом, условия работы, близкие к критичным – оранжевым. Скриншот работы с файлом Overture_Design_Guide15.xls показан на рис. 6, а результаты расчета усилителя для различных сопротивлений нагрузки сведены в табл. 2.
Рис. 6. Расчет с помощью файла электронной таблицы Overture_Design_Guide15.xls
Параметры внешних элементов УМЗЧ можно уточнить самостоятельно. Коэффициент усиления по напряжению
Для уменьшения шумов предпочтительны низкие значения сопротивлений резисторов Rf и Ri. Обычно принимают Ri=1 кОм, а величину Rf вычисляют исходя из требуемого коэффициента усиления, который для LM4780 должен находиться в диапазоне от 10 до 50.
Входной блокировочный конденсатор CIN совместно с резистором RIN образуют фильтр верхних частот, частота среза которого по уровню – 3 дБ:
Рекомендуемое значение RIN от 10 до 47 кОм.
Элементы RiCi в цепи отрицательной обратной связи образуют фильтр верхних частот с частотой среза по уровню – 3 дБ:
За нижнюю полосу пропускания усилителя в файле Overture_Design_Guide15.xls выбрана бОльшая из частот среза цепей Rin, Cin и Ri, Ci.
В нашем расчете принимается во внимание тот факт, что получившаяся АЧХ двухзвенного фильтра верхних частот будет произведением АЧХ его звеньев, а частота среза увеличивается в K=1/Sqrt(2^(1/n)-1)=1,554 раза, где n=2 – число звеньев первого порядка.
Небольшое отступление в связи с вышесказанным. На одном из форумов прозвучал вопрос, оставшийся без ответа: «В системе многоканального воспроизведения (это может быть любая другая система) на входах последовательно включенных модулей стоит в общей сложности десяток RC – цепей фильтров верхних частот. Как выбрать их параметры, чтобы нижняя частота была 20 Гц?».
Ответ: коэффициент К для числа RC – цепей n=10 равен K=Sqrt(2^(1/n)-1)=3,733. Частота среза каждой RC – цепи равна fc=20/K=5,36 Гц.
Последовательная цепочка в цепи отрицательной обратной связи, состоящая из резистора Rf2 и конденсатора Cf вместе с резисторами Rf и Ri образуют фильтр нижних частот, понижающий усиление на высоких частотах. Частота среза по уровню – 3 дБ рассчитывается по формуле:
Цепочка RSNCSN стабилизирует работу УМЗЧ на высоких частотах, создавая полюс на частоте
Элементы LR обеспечивают устойчивость усилителя при работе на емкостную нагрузку (более 0,2 мкФ). Значение элементов (L=0,7 мкГн, R=10 Ом) выбраны таким образом, чтобы минимизировать резонансные явления в звуковом диапазоне частот.
Элементы цепи Mute выбираются из условий:
Вид экрана компьютера с расчетом параметров внешних цепей УМЗЧ в Excel приведен на рис. 7.
Рис. 7. Расчет внешних цепей УМЗЧ на микросхеме LM4780
Проведем уточнение номиналов элементов, заведем значения в поля исходных данных и тут же получим результат. Для снижения уровня шумов и искажений, вызванных падением напряжения на конденсаторе Ci, увеличим его емкость по сравнению с типовой примерно в пять раз согласно рекомендации из
Полный усилитель на микросхемах. Часть 5-4. Токовая помпа Хоуленда в выходном каскаде УМЗЧ
.
На рис. 8 показан еще один скриншот расчета.
Рис. 8. Уточнение параметров внешних цепей УМЗЧ
Схема стереофонического УМЗЧ с учетом проведенных корректировок показана на рис. 9.
Рис. 9. Стереофонический УМЗЧ на микросхеме LM4780 для сборки
В конструкции применены резисторы МЛТ, С2-33, С1-4 или импортные мощностью 1 Вт (R15…R18), остальные мощностью 0,25 Вт. Пленочные конденсаторы МКТ или МKР (С2, С3, С5, С6, С10, С11, С16 и С17), импортные оксидные конденсаторы на рабочее напряжение не менее 50 В, с низким импедансом, большим сроком службы и возможностью работы при температуре до +105°С. Конденсаторы С1, С4 – неполярные (еще лучше — биполярные); С7, С8 – керамические с диэлектриком NPO (COG).
Катушка L1 (L2) намотана на оправке диаметром 10 мм проводом ПЭЛ, ПЭВ диаметром 1 мм и содержит 10 витков. Резистор R17 (R18) находится внутри катушки.
Основные характеристики усилителя:
Напряжение питания при Rн=8 Ом: ±35 В (±10…±35 В);
Частотный диапазон: 20 Гц-20 кГц (–0,8 дБ);
Коэффициент усиления: 26 дБ;
Соотношение сигнал/шум: 115 дБА;
Скорость нарастания сигнала: не менее 19 В/мкс;
Ток покоя: 110 мА;
Коэффициент гармоник при выходной мощности 2х30 Вт: 0,03%;
Выходная мощность при Kг=0,5%: 2х60 Вт.
Следующая микросхема линейки, LM4781 – это трехканальный УМЗЧ с выходной мощностью 35 Вт на канал на нагрузке 8 Ом, а LM4782 – трехканальный усилитель, развивающий выходную мощность 25 Вт на канал. Последняя из указанных микросхем имеет энергосберегающий режим ожидания Stand-by.
Представленные выше примеры расчетов в Excel показывают удобство и оперативность создания электронных таблиц. Подобным образом можно выполнить большинство расчетов, которые применяются в радиолюбительской практике.
Любителям ламповых схем будут полезны публикации [4, 5]. Автор Ради Годмэйр предложил интересную методику, использующую традиционный графоаналитический метод вычерчивания нагрузочных прямых на семействе вольтамперных характеристик лампы и табличный процессор Microsoft Excel. На всю процедуру ввода данных и исследование влияния нелинейности выбранного элемента схемы уходит порядка десяти минут. Файл ecc99designer.xls находится в прилагаемом архиве.
🎁Amateur_radio_calculations.zip
897.41 Kb ⇣ 89
1. Кочнев А. Радиотехнические расчеты в Excel // Радио, 2007, №12, с. 35.
2. Помощник при расчетах // Радио, 2008, №11, с. 41 (ftp://ftp.radio.ru/pub/2008/11/helpdsgn.zip).
3. Дубина А.Г., Орлова С.С., Шубина И.Ю. MS Excel в электротехнике и электронике. – СПб.: БХВ-Петербург, 2001. – 304 с.
4. Godmaire R. Designing Amps for Maximum Linearity with the ECC99 // AudioXpress, 2011, august, p. 6 – 12.
5. Дайджест. Проектирование максимально линейных аудиоусилителей (Ради Годмэйр) // Радиохобби, 2011, №5.
Арзамасцев С.В. Инженерные расчеты в Microsoft Excel — файл n1.doc
приобрести
Арзамасцев С.В. Инженерные расчеты в Microsoft Excel
скачать (1682 kb.)
Доступные файлы (1):
- Смотрите также:
- Тарасова Н.В., Гордеева Е.С. Лабораторный практикум по информатике. Основы работы в редакторах Microsoft Word и Microsoft Excel (Документ)
- Гершкович В. Расчеты систем отопления на Excel (Документ)
- «Логистикадағы деректерді басқару» пәні 2-дәріс: Microsoft Excel бағдарламасындағы функциялар (Документ)
- «Логистикадағы деректерді басқару» пәні 2-дәріс: Microsoft Excel бағдарламасындағы функциялар (Документ)
- Augen J. Microsoft Excel for stock and option traders: build your own analytical tools for higher returns (Документ)
- Борисов А.Ф. Инженерные расчеты систем безопасности труда и промышленной экологии (Документ)
- Мур, Джеффри, Уэдерфорд, Ларри Р.Экономическое моделирование в Microsoft Excel (Документ)
- Завадський І.О., Забарна А.П. Microsoft Excel у профільному навчанні (Документ)
- Ищенко В.А., Нагина Е.К., Орлова М.В. Информатика: Компьютерный практикум (Документ)
- Лабораторная работа — Решение транспортных задач в информационной среде Microsoft Office Excel 2003 (Лабораторная работа)
- Ганджумян Р.А., Калинин А.Г., Никитин Б.А. Инженерные расчеты при бурении глубоких скважин (Документ)
- Численные методы и инженерные расчеты в Excel (Документ)
n1.doc
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
ИНЖЕНЕРНЫЕ РАСЧЕТЫ В MICROSOFT EXCEL
Методические указания к выполнению лабораторных работ
по дисциплине «Моделирование и оптимизация
технологии полимерных материалов»
для студентов очной и заочной форм обучения специальности 240502.65
| Одобрено
редакционно-издательским советом Саратовского государственного технического университета |
Саратов 2009
Дисциплина «Моделирование и оптимизация технологии полимерных материалов» является завершающим этапом в технологической подготовке инженеров химиков-технологов.
Лабораторные работы по дисциплине «Моделирование и оптимизация технологии полимерных материалов» имеют следующие цели:
- ознакомление студентов с возможностями использования средств вычислительной техники для решения задач моделирования, оптимизации и управления производственными процессами в технологии полимерных материалов;
- привитие студентам навыков корректной постановки задач технологии полимерных материалов для решения на ЭВМ, реализация на них вычислительных алгоритмов и получение физически обоснованных результатов расчета;
- обучение студентов методологии решения расчетных задач моделирования и оптимизации технологии полимерных материалов на ЭВМ и использованию полученных знаний для решения задач проектирования и оптимизации химических процессов.
В настоящих методических указаниях к выполнению лабораторных работ по дисциплине «Моделирование и оптимизация технологии полимерных материалов» рассматриваются вопросы практического применения студентами приемов инженерных расчетов и статистической обработки результатов экспериментов, позволяющих перейти к реализации полного факторного эксперимента и оптимизации состава композиционного материала и технологических параметров.
Пример задания:
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2. По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Разрушающее напряжение при изгибе i=(3·Pi·L)/(2·Bi·Hi2).
- Среднеарифметическое значение ?ср.= ?i/N.
- Абсолютное отклонение от среднего ?i=?i-?ср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/?ср.
Задача: оценить зависимость разрушающего напряжения при изгибе (МПа) ПКМ на основе смолы СФ-342-А и отходов вискозных волокон от температуры прессования.
Примечание: 1 МПа10 кгс/см2 ; L=10 см.
Экспериментальные данные:
-
Температура, 0С Bi, cм Hi, см Pi, кгс 60 1,54 1,55
1,57
1,54
1,56
1,02 1,01
1,04
1,01
1,01
9,9 9,5
9,8
9,1
9,4
80 1,56 1,55
1,51
1,51
1,58
1,01 1,02
1,02
1,03
1,04
10,9 10,5
10,7
11,2
11,1
100 1,53 1,51
1,59
1,54
1,51
1,04 1,03
1,02
1,03
1,02
12,6 12,9
12,3
12,0
12,8
120 1,55 1,59
1,56
1,58
1,50
1,02 1,01
1,01
1,02
1,01
10,4 10,8
10,2
10,4
10,3
140 1,55 1,56
1,53
1,59
1,53
1,03 1,02
1,02
1,02
1,05
8,9 8,4
8,8
8,8
8,6
Пример расчета: Переносим данные таблицы задания на лист созданной книги Microsoft Excel и дополняем таблицу необходимыми столбцами для расчета заданных величин. Расчет ?i производим путем программирования соответствующих ячеек книги Microsoft Excel. Ввод формулы в ячейку всегда начинается со знака равенства. Для расчета ?i активизируем (выделяем мышью) ячейку E2 книги (рис. 1).
После этого при помощи клавиатуры вводим знак равенства, а затем вводим математическую формулу, соблюдая правила, и нажимаем «Enter». Затем, схватив мышкой правый нижний угол ячейки E2, перетягиваем формулу для расчета вниз до ячейки E26 (рис. 2), проводим форматирование ячеек выделенного диапазона: Формат ? Ячейка ? вкладка «Число» ? Числовые форматы: числовой и выбираем необходимое количество десятичных знаков (рис. 3).
Рис.1. Ввод формулы
Рис. 2. Результат расчета


. Выбираем в категории «Статистические» функцию «среднее значение» — СРЗНАЧ (рис. 4), нажимаем «ОК» и в открывшемся окне «Аргументы значения» вводим в поле «Число 1» диапазон ячеек, для которых требуется провести вычисление (рис. 5). Нажимаем «ОК».
Рис 4. Окно мастера функций.

Расчет отклонения ? ?i начинается с программирования ячейки G2, в которую вводится формула «=E2-F2». Поскольку в производимых расчетах необходимо всегда использовать одно и то же среднее значение, то ссылку на ячейку F2 делают абсолютной, выделив её в формуле и нажав на клавишу F4, в результате чего формула принимает вид «=E2-$F$2».
Аналогично производим расчет остальных данных таблицы.
Программирование ячейки H2 для расчета среднеквадратичного отклонения по формуле S= нужно проводить в два этапа, поскольку расчет будет вестись с использованием двух функций – КОРЕНЬ (квадратный корень) и СУММКВ (сумма квадратов). Программирование начинаем с организации вычислений по внутренней функции, которой является СУММКВ.
После знака равенства воспользуемся мастером функций, найдя в категории «Математические» функцию «СУММКВ» (рис 6).
Нажав на ОК и перейдя ко второму шагу, необходимо указать диапазон аргументов, для которых необходимо вычислить сумму квадратов (рис. 7). После нажатия на «ОК», в строке формул имеем запись: «=СУММКВ(G2:G6)». Устанавливаем курсор в строке формул после правой скобки и делим все выражение на N-1, т.е. на 4. Запись принимает вид: «=СУММКВ(G2:G6)/4».
Для программирования внешней функции заключаем в скобки все выражение кроме знака равенства и, установив курсор перед первой скобкой, вызываем мастер функций, отыскиваем в категории «математические» функцию КОРЕНЬ и нажимаем ОК. Надпись в строке формул имеет вид: «=КОРЕНЬ()СУММКВ(G2:G6)/4». После этого переносим правую скобку функции КОРЕНЬ в конец выражения, заключая тем самым в скобки выражение «СУММКВ(G2:G6)/4».


Таким образом, вычисление квадратного корня будет производиться из выражения, являющего результатом вычисления функции «сумма квадратов».
Аналогично производим вычисления в ячейках H7, H12, H17 и H22.
Для расчета коэффициента вариации K делим содержимое ячейки H2 на содержимое ячейки F2 и таким же образом вычисляем коэффициент вариации для других данных. Теперь таблица имеет вид, представленный на рис. 8.
Рис. 8. Окно книги Microsoft Excel
Далее по заданию требуется построить график зависимости разрушающего напряжения при изгибе (столбец F) от температуры прессования (столбец А). Поскольку построение графиков и диаграмм для несмежных диапазонов невозможно, переносим данные, находящиеся в указанных выше столбцах, в свободные ячейки на этом листе, например, содержимое столбца А заносим в ячейки А31-А35, а соответствующие им значения прочностных характеристик – в ячейки В31-В35. Выделяем мышкой диапазон ячеек А31:В35 и запускаем мастер диаграмм. Выбираем в качестве типа диаграммы точечную, со значениями, соединенными сглаживающими линиями, и нажимаем ОК (рис. 9). Второй шаг построения диаграммы пропускаем, нажимая «Далее». В открывшемся окне вводим в соответствующие поля название диаграммы, оси категорий и оси значений (рис. 10) и нажимаем «Готово».
Рис. 9. Окно мастера диаграмм.
Рис. 10. Окно мастера диаграмм.
Созданную диаграмму форматируем. Выделив область построения диаграммы и нажав на правую кнопку мыши, выбираем в контекстном меню «Форматирование области построения» (рис. 11). Устанавливаем, например, невидимую рамку и прозрачную заливку (рис. 12).
Рис 11. Контекстное меню работы с областью построения.

Выделив мышью ось Х и нажав на левую кнопку, в контекстном меню выбираем «Формат оси». В открывшемся окне выбираем вкладку «Шкала», устанавливаем требуемые минимальные и максимальные значения шкалы Х (рис. 13) и нажимаем ОК.


Выделив построенную кривую и нажав правую кнопку мыши, в контекстном меню выбираем «Добавить линию тренда». В открывшемся окне на вкладке «Параметры» устанавливаем галочку на «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)». Перейдя на вкладку «Тип» (рис. 14), эмпирическим путем выбираем наиболее подходящий алгоритм построения линии тренда и нажимаем ОК. Результат представлен на рис 15.

Результаты расчета записываются в виде файла, а выполненная лабораторная работа соответствующим образом оформляется и сдается на проверку преподавателю.
ЗАДАНИЯ
Вариант №1
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2 . По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Ударная вязкость Аудi.=Аi/(Bi·Hi), кДж/м2.
- Среднеарифметическое значение Аср.= Аудi/N
- Абсолютное отклонение от среднего Аi=Аудi-Аср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/Аср.
Задача: оценить зависимость ударной вязкости ПКМ на основе смолы СФ-342-А и ПАН волокон от температуры термообработки образцов.
Экспериментальные данные:
| Температура, 0С | Bi, мм | Hi, мм | Аi, кДж |
| 60 | 12,4
13,5 12,7 13,4 12,6 |
4,1
4,1 4,3 4,2 4,1 |
4,9
4,7 4,2 4,3 3,7 |
| 80 | 12,6
12,5 12,1 13,1 12,8 |
4,2
4,1 4,3 4,3 4,2 |
5,6
5,4 5,8 5,9 5,2 |
| 100 | 13,3
13,1 12,9 12,4 12,1 |
4,4
4,3 4,2 4,3 4,2 |
4,6
4,5 5,6 5,0 4,2 |
| 120 | 12,5
12,9 12,6 12,8 13,0 |
4,3
4,2 4,1 4,3 4,2 |
4,3
4,0 3,8 3,7 3,7 |
| 140 | 12,5
12,6 12,3 12,9 13,3 |
4,3
4,3 4,2 4,2 4,5 |
2,2
2,1 2,8 2,9 2,4 |
Вариант 2
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2 . По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Потери массы при горении ПMi=((g1i-g0i)/g1i) ·100%.
- Среднеарифметическое значение ПМср.= ПМi/N.
- Абсолютное отклонение от среднего ПМi=ПМi-ПМср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/Xср.
Задача: оценить зависимость потери массы ПКМ на основе смолы ЭД-20 и отходов триацетатных волокон от содержания модификатора.
Экспериментальные данные:
| Содержание модификатора, % | g0, г | g1, г |
|
0 |
12,4235
13,5235 12,7745 13,4541 12,6478 |
4,3510
4,9512 4,0549 4,9915 4,1651 |
|
0,5 |
12,6123
12,5654 12,1321 13,1851 12,8651 |
6,3061
6,3659 6,5684 6,2954 6,5987 |
|
1,0 |
13,3541
13,1654 12,9445 12,4533 12,1445 |
7,9956
8,0125 8,1125 8,0125 7,9996 |
|
2,0 |
12,5444
12,9545 12,6233 12,8015 13,0132 |
8,7598
8,6845 8,6532 8,3265 8,2354 |
|
3,0 |
12,5322
12,6322 12,3221 12,9133 13,3125 |
7,5684
7,5621 7,3568 7,3254 7,8421 |
Вариант 3
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2 . По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Водопоглощение материала Wi=((M1i-M0i)/M0i) ·100%.
- Среднеарифметическое значение Wср.= Хi/N.
- Абсолютное отклонение от среднего Wi=Wi-Wср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/Wср.
Задача: оценить зависимость водопоглощения ПКМ на основе смолы СФ-342-А и отходов полипропиленовых волокон от давления прессования
Экспериментальные данные:
| Давление прессования, МПа | № | М0, г | М1, г |
| 10 | 1
2 3 4 5 |
12,4654
13,5351 12,7685 13,4844 12,6241 |
13,7545
14,2356 13,6552 14,2569 13,2658 |
| 15 | 1
2 3 4 5 |
12,6654
12,5112 12,1222 13,1456 12,8655 |
13,6754
13,5487 13,2254 14,0012 13,7589 |
| 20 | 1
2 3 4 5 |
13,3651
13,1352 12,9321 12,4211 12,1211 |
14,0632
13,8654 13,6598 13,1125 13,0001 |
| 25 | 1
2 3 4 5 |
12,5011
12,9211 12,6212 12,8622 13,0685 |
13,0021
13,4251 13,1254 13,3254 13,6599 |
| 30 | 1
2 3 4 5 |
12,5541
12,6112 12,3654 12,9511 13,3456 |
12,8058
12,9356 12,6427 13,2458 13,7538 |
Вариант 4
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2 . По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Разрушающее напряжение при изгибе i=(3·Pi·L)/(2·Bi·Hi2).
- Среднеарифметическое значение ср.= i/N.
- Абсолютное отклонение от среднего i=i-ср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/ср.
Задача: оценить зависимость разрушающего напряжения при изгибе ПКМ на основе смолы МЛ-РС-100 и отходов ПАН волокон от количества пластификатора дибутилфталата. Примечание: 1 МПа10 кгс/см2; L=10 см.
Экспериментальные данные:
| Содержание пластификатора,% | Bi, мм | Hi, мм | Pi, кгс |
|
0 |
15,4
15,5 15,7 15,4 15,6 |
10,1
10,2 10,3 10,1 10,2 |
10,0
9,8 10,2 10,6 10,1 |
|
0,5 |
15,6
15,5 15,1 15,1 15,8 |
10,2
10,1 10,2 10,2 10,1 |
11,2
11,5 11,0 11,2 11,9 |
|
1,0 |
15,3
15,1 15,9 15,4 15,1 |
10,4
10,3 10,2 10,3 10,2 |
12,6
12,9 13,0 12,5 12,8 |
|
1,5 |
15,5
15,9 15,6 15,8 15,0 |
10,2
10,1 10,1 10,2 10,3 |
16,4
16,5 16,0 15,9 16,1 |
|
2,0 |
15,5
15,6 15,3 15,9 15,3 |
10,3
10,2 10,2 10,2 10,5 |
14,3
13,8 13,4 12,9 12,9 |
Вариант 5
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2 . По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Разрушающее напряжение при растяжении i=Pi/(Bi·Hi).
- Среднеарифметическое значение ср.= i/N.
- Абсолютное отклонение от среднего i=i-ср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/ср.
Задача: оценить зависимость разрушающего напряжения при растяжении (в МПа) ПКМ на основе смолы СФ-342-А и отходов вискозных волокон от температуры прессования. Примечание: 1 МПа 10 кгс/см2
Экспериментальные данные:
| Температура, 0С | Bi, мм | Hi, мм | Pi, кгс |
| 60 | 12,4
13,5 12,7 13,4 12,6 |
4,1
4,2 4,4 4,2 4,1 |
44,9
54,7 49,2 48,3 47,7 |
| 80 | 12,6
12,5 12,1 13,1 12,8 |
4,2
4,3 4,2 4,2 4,1 |
55,6
59,4 56,8 54,9 59,2 |
| 100 | 13,3
13,1 12,9 12,4 12,1 |
4,4
4,3 4,2 4,2 4,4 |
69,3
68,9 64,6 61,7 70,1 |
| 120 | 12,5
12,9 12,6 12,8 13,0 |
4,2
4,1 4,1 4,2 4,3 |
59,2
55,1 56,6 51,4 55,0 |
| 140 | 12,5
12,6 12,3 12,9 13,3 |
4,3
4,2 4,2 4,4 4,5 |
42,8
41,3 45,5 44,9 39,8 |
Вариант 6
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2. По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Водопоглощение материала Wi=((M1i-M0i)/M0i) ·100%.
- Среднеарифметическое значение Wср.= Wi/N.
- Абсолютное отклонение от среднего Wi=Wi-Wср.
- Среднеквадратичное отклонение S=
.
- Коэффициент вариации К=S/Wср.
Задача: оценить зависимость водопоглощения ПКМ на основе смолы ЭД-20 и отходов ПКА волокон от содержания модифицирующих добавок.
Экспериментальные данные:
| Содержание модификатора, % | M0, г | M1, г |
|
0 |
12,4251
13,5256 12,7325 13,4145 12,6256 |
13,0464
14,3372 13,4073 14,0718 13,3211 |
|
0,5 |
12,6562
12,5245 12,1658 13,1545 12,8457 |
13,1625
13,0130 12,5916 13,5754 13,3595 |
|
1,0 |
13,3554
13,1456 12,9951 12,4954 12,1235 |
14,0232
13,8292 13,7098 13,1452 12,8145 |
|
3,0 |
12,5128
12,9548 12,6632 12,8363 13,0693 |
13,3762
13,9005 13,5496 13,8632 14,1246 |
|
5,0 |
12,5235
12,6214 12,3548 12,9256 13,3658 |
13,9011
14,1360 13,8992 14,5930 14,8229 |
Вариант 7
На основании экспериментальных данных сделать в Microsoft Excel необходимые расчеты текущих физико-механических характеристик, среднеарифметического значения, среднеквадратичного отклонения и коэффициента вариации. По полученным данным построить график зависимости, описать его математическим уравнением (например, при помощи полиномиальной модели), рассчитать значение величины достоверности аппроксимации R2. По полученному графику сделать вывод о характере полученной зависимости.
Формулы для расчетов:
- Разрушающее напряжение при растяжении i=Pi/(Bi·Hi).
- Среднеарифметическое значение ср.= i/N.
- Абсолютное отклонение от среднего i=i-ср.
- Среднеквадратичное отклонение S=
- Коэффициент вариации K=S/ср.
Задача: оценить зависимость разрушающего напряжения при растяжении (в МПа) ПКМ на основе смолы МЛ-РС-100 и отходов ПКА волокон от количества смолы в композиции. Примечание: 1 МПа 10 кгс/см2
Экспериментальные данные:
| Количество смолы в композиции, % | Bi, мм | Hi, мм | Pi, кгс |
|
10 |
13,4
14,5 13,7 14,4 13,6 |
4,10
4,12 4,09 4,15 4,11 |
34,9
41,7 42,2 40,3 39,7 |
|
20 |
13,6
13,5 13,1 14,1 13,8 |
4,15
4,12 4,23 4,22 4,14 |
59,6
64,4 59,8 57,9 65,2 |
|
30 |
14,3
14,1 13,9 13,4 13,1 |
4,45
4,37 4,26 4,33 4,28 |
86,3
89,9 96,6 86,7 87,1 |
|
40 |
13,5
13,9 13,6 13,8 14,0 |
4,21
4,15 4,11 4,22 4,13 |
45,2
50,1 47,6 43,4 50,0 |
|
50 |
13,5
13,6 13,3 13,9 14,3 |
4,33
4,23 4,25 4,26 4,55 |
39,0
35,6 36,8 39,9 32,7 |
ЛИТЕРАТУРА
- Джинджер Саймон. Расчеты и анализ данных в Excel./ Саймон Джинджер. – М.: НТ Пресс, 2009. – 512 с.
- Серогодский В.В. Графики, вычисления и анализ данных в Excel 2007. Самоучитель./ В.В Серогодский., Д.А. Козлов, Р.Г. Прокди , А.Ю. Дружинин. – М.: Наука и техника, 2009. – 336 с.
- Кашаев С.М. Программирование в Microsoft Excel на примерах./ С.М. Кашаев. – М.: BHV, 2007. – 320 с.
- Юдин М. В., Куприянова А. В. Microsoft Excel 2007. Работаем с таблицами./ М. В. Юдин, А. В. Куприянова. – М.: Наука и техника, 2009 – 80 с.
- Далглеиш Дебра. Сводные таблицы в Excel. Технологии PivotTables./ Дебра Далглеиш. – М.: Питер, 2009. – 288 с.
- Ларсен Рональд У. Инженерные расчеты в Excel./ Рональд У. Ларсен. – М.: Вильямс, 2004. – 544 с.
- Леонтьев В.П. Новейшая энциклопедия персонального компьютера 2009./В.П. Леонтьев. – М.: ОЛМА Медиа Групп, 2009. – 928 с.
- Вадзинский Ратмир. Статистические вычисления в среде Excel./ Ратмир Вадзинский. – М.: Питер, 2008. – 602 с.
ИНЖЕНЕРНЫЕ РАСЧЕТЫ В MICROSOFT EXCEL
Методические указания к выполнению лабораторных работ
по дисциплине «Моделирование и оптимизация
технологии полимерных материалов»
Составил: Арзамасцев Сергей Владимирович.
Рецензент Н.Л. Левкина
Редактор О.А. Панина.
Подписано в печать Формат 60х84 1/16
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054, Саратов, Политехническая ул., 77
Отпечатано в РИЦ СГТУ. 410054, Саратов, Политехническая ул., 77
Пособие содержит четыре взаимосвязанных раздела: простейшие вычисления в таблицах, использование стандартных формул, построение графиков; работа с массивами данных, построение сводных таблиц данных, поиск решений, анализ «Что — если», решение оптимизационных задач; использование макрокоманд и основы программирования в VBA; разработка приложений с использованием визуальных компонентов, создание собственных интерфейсов. Рассмотрены основные режимы работы в MS Excel для решения специальных задач, возникающих в практической деятельности инженеров и научных работников. Теоретический материал иллюстрирован примерами решения задач различной сложности с подробными комментариями. Подробно изложены основы разработки приложений в среде VBA, программирование элементов интерфейса. Предназначено для студентов, обучающихся по техническим направлениям подготовки высшего образования.
Название: Методы MS Excel для решения инженерных задач
Автор: Бильфельд Н. В., Фелькер М. Н.
Издательство: Лань
Год: 2020
Страниц: 164
Формат: pdf, rtf
Язык: русский
Размер: 16,65 Мб
Скачать Бильфельд Н.В., Фелькер М.Н. Методы MS Excel для решения инженерных задач
Практическая работа позволит изучить возможности электронных таблиц для выполнения инженерных расчетов, научит выполнять расчет уравнений зависимостей и достоверность аппроксимации.
Описание разработки
Цель работы:
изучить возможности электронных таблиц для выполнения инженерных расчетов. Научиться выполнять расчет уравнений зависимостей и достоверность аппроксимации.
Оборудование:
Персональный компьютер
Программное обеспечение MS EXCEL
Контрольные вопросы:
Назначение электронной таблицы
Возможности электронной таблицы при выполнении научно-инженерных расчетов
Приближенные расчеты с помощью линий тренда и аппроксимации
Краткая теория:
Excel является отличным средством автоматизации решения самых различных расчетных задач. В первую очередь (вполне оправданно) Excel используется в финансовой сфере и как средство обработки больших массивов числовой информации. Однако в настоящее время все большее количество технических специалистов, инженеров и ученных начинают применять Excel для сложных технических расчетов.
В этой связи можно выделить две большие категории принципиально разных задач, для решения которых целесообразно использовать Excel:
Цепочные расчеты по сложным формулам, при этом объем исходных данных невелик, и они вводятся преимущественно вручную (мало данных, сложные расчеты).
Аналитическая обработка данных, которая во многих случаях сводится к простым операциям с большим объемом данных. Несмотря на простоту этих операций вычисления с большими массивами информации целесообразно проводить с помощью Excel.
Аппроксимация — приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В инженерных расчетах целью аппроксимации часто является укрупнение характеристик моделируемых технических объектов.
В расчетах часто используют достоверность аппроксимации, чем ближе эта достоверность к 1 (единице), тем точнее выполнен расчет.
Практическая часть.
Задание 1.
Построить график зависимости теплоемкости компоненты от температуры. Значения теплоемкостей и соответствующие температуры приведены в табл. 1.
Последовательность выполнения операций:
1. Запустите программу Excel.
2. Поставьте курсор в ячейку А1 и, пользуясь клавиатурой, приступите к набору табличных данных (вещественная часть отделяется запятой). В верхнюю строку помещается шапка таблицы, в левый столбец – значения аргумента.
3. Выделите данные по которым строится график следующим образом: переместите курсор с помощью мыши в ячейку А1, нажав на левую клавишу мыши обведите область, содержащую данные для построения графика, при этом область будет выделена контрастным цветом (кроме ячейки А1).
4. На верхней панели инструментов выберите раздел Мастер диаграмм (в виде диаграммы с цветными столбцами) и откройте его.
5. Выберите тип диаграммы: точечная, т. к. исходные данные содержат координаты точек и нужный вид диаграмм.
6. Мышью нажмите клавишу далее, войдите в источник данных диаграммы.
7. Выберите строку: ряды: в столбцах.
8. Нажмите клавишу далее, войдите в параметры диаграммы.
9. В разделе заголовки подпишите название диаграммы и обозначения осей, нажмите клавишу далее и войдите в раздел – размещение диаграммы.
10. Выберите место расположения диаграммы (на имеющемся листе). Нажмите клавишу готово.
11. Сохраните рабочую книгу в файл под именем, например, инженерные расчеты. xls
Задание 2.
Выполнить аппроксимацию зависимости теплоемкости от температуры (табл. 1).
Последовательность выполнения операций:
1. Запустите программу Excel и откройте рабочую книгу инженерные расчеты. xls, созданную ранее.
2. На графике выделите ряд данных щелчком мыши на экспериментальной точке.
На верхней панели откройте раздел Диаграмма и подраздел – Добавить линию тренда. Добавить линию тренда можно также следующим образом: подвести курсор к графику, щелкнуть правой кнопкой мыши и в появившемся меню выбрать: Добавить линию тренда. В открывшемся окне выберите один из типов функции (линейная, логарифмическая, полиномиальная, степенная, экспоненциальная).
Весь материал — в документе.
Содержимое разработки
МДК 03.02 Применение пакета прикладных программ
Практическая работа
Тема: Научно-инженерные расчеты в электронных таблицах.
Цель работы: изучить возможности электронных таблиц для выполнения инженерных расчетов. Научиться выполнять расчет уравнений зависимостей и достоверность аппроксимации.
Оборудование:
-
Персональный компьютер
-
Программное обеспечение MS EXCEL
Контрольные вопросы:
-
Назначение электронной таблицы
-
Возможности электронной таблицы при выполнении научно-инженерных расчетов
-
Приближенные расчеты с помощью линий тренда и аппроксимации
Литература:
-
Фуфаев Э.В., Л.И. Фуфаева Пакеты прикладных программ: учеб. пособ. для студентов учреждений среднего проф. образования – 7-е изд
-
books.google.ru/books?isbn=5458269098 Справочник технолога-машиностроителя (Электронная книга Google)
-
http://window.edu.ru/resource/308/63308/files/excel99.pdf Инженерные расчеты в EXCEL
Краткая теория:
Excel является отличным средством автоматизации решения самых различных расчетных задач. В первую очередь (вполне оправданно) Excel используется в финансовой сфере и как средство обработки больших массивов числовой информации. Однако в настоящее время все большее количество технических специалистов, инженеров и ученных начинают применять Excel для сложных технических расчетов.
В этой связи можно выделить две большие категории принципиально разных задач, для решения которых целесообразно использовать Excel:
• Цепочные расчеты по сложным формулам, при этом объем исходных данных невелик, и они вводятся преимущественно вручную (мало данных,сложные расчеты).
• Аналитическая обработка данных, которая во многих случаях сводится к простым операциям с большим объемом данных. Несмотря на простоту этих операций вычисления с большими массивами информации целесообразно проводить с помощью Excel.
Аппроксимация — приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В инженерных расчетах целью аппроксимации часто является укрупнение характеристик моделируемых технических объектов.
В расчетах часто используют достоверность аппроксимации, чем ближе эта достоверность к 1 (единице), тем точнее выполнен расчет.
Практическая часть
Задание 1. Построить график зависимости теплоемкости компоненты от температуры. Значения теплоемкостей и соответствующие температуры приведены в табл. 1.
Таблица 1
|
Температура, К |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Теплоемкость, кал/(моль *К) |
97,71 |
132,32 |
146,42 |
166,00 |
182,65 |
196,80 |
209,01 |
219,50 |
Последовательность выполнения операций:
-
Запустите программу Excel.
-
Поставьте курсор в ячейку А1 и, пользуясь клавиатурой, приступите к набору табличных данных (вещественная часть отделяется запятой). В верхнюю строку помещается шапка таблицы, в левый столбец – значения аргумента.
-
Выделите данные по которым строится график следующим образом: переместите курсор с помощью мыши в ячейку А1, нажав на левую клавишу мыши обведите область, содержащую данные для построения графика, при этом область будет выделена контрастным цветом (кроме ячейки А1).
-
На верхней панели инструментов выберите раздел Мастер диаграмм (в виде диаграммы с цветными столбцами) и откройте его.
-
Выберите тип диаграммы: точечная, т.к. исходные данные содержат координаты точек и нужный вид диаграмм.
-
Мышью нажмите клавишу далее, войдите в источник данных диаграммы.
-
Выберите строку: ряды: в столбцах.
-
Нажмите клавишу далее, войдите в параметры диаграммы.
-
В разделе заголовки подпишите название диаграммы и обозначения осей, нажмите клавишу далее и войдите в раздел – размещение диаграммы.
-
Выберите место расположения диаграммы (на имеющемся листе). Нажмите клавишу готово.
-
Сохраните рабочую книгу в файл под именем, например, инженерные расчеты.xls
Задание 2. Выполнить аппроксимацию зависимости теплоемкости от температуры (табл. 1).
Последовательность выполнения операций:
-
Запустите программу Excel и откройте рабочую книгу инженерные расчеты.xls, созданную ранее.
-
На графике выделите ряд данных щелчком мыши на экспериментальной точке.
-
На верхней панели откройте раздел Диаграмма и подраздел – Добавить линию тренда. Добавить линию тренда можно также следующим образом: подвести курсор к графику, щелкнуть правой кнопкой мыши и в появившемся меню выбрать: Добавить линию тренда. В открывшемся окне выберите один из типов функции (линейная, логарифмическая, полиномиальная, степенная, экспоненциальная). Пометьте его щелчком мыши. В этом же окне выберите раздел Параметры и отметьте строки:
|
|
– показывать уравнение на диаграмме; |
|
|
– поместить на диаграмму величину достоверности аппроксимации (R2). |
Нажмите клавишу ОК.
Запишите уравнение процесса и величину аппроксимации в отчет.
Повторите операции для всех типов линий тренда: линейная, логарифмическая, полиномиальная, степенная и экспоненциальная.
-
По величине достоверности аппроксимации (R2) определите, какой тип линии тренда дает наибольшую точность при обработке экспериментальных данных.
В результате обработки экспериментальных данных постройте таблицу следующих зависимостей:
|
Тип зависимости |
Уравнение Y(X) |
Аппроксимация R2 |
|
линейная |
||
|
логарифмическая |
||
|
полиномиальная 2-ого порядка |
||
|
степенная |
||
|
экспоненциальная |
Определите, в каком случае аппроксимация наибольшая. Эти уравнения можно эффективно использовать для описания экспериментальных данных.
-
Используя наилучшее уравнение зависимости теплоемкости от температуры определите величину теплоемкости для следующих значений температуры, данные оформите в виде таблицы
|
Температура, К |
10 |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
250 |
|
Теплоемкость, кал/(моль *К) |
-
Сделайте вывод по работе.
-80%
Скачать разработку
Сохранить у себя:































