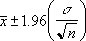Интервальная оценка в excel

Одним из методов решения статистических задач является вычисление доверительного интервала. Он используется, как более предпочтительная альтернатива точечной оценке при небольшом объеме выборки. Нужно отметить, что сам процесс вычисления доверительного интервала довольно сложный. Но инструменты программы Эксель позволяют несколько упростить его. Давайте узнаем, как это выполняется на практике.

Читайте также: Статистические функции в Экселе

Процедура вычисления

Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.

В Экселе существуют два основных варианта произвести вычисления с помощью данного метода: когда дисперсия известна, и когда она неизвестна. В первом случае для вычислений применяется функция ДОВЕРИТ.НОРМ, а во втором — ДОВЕРИТ.СТЮДЕНТ.

Способ 1: функция ДОВЕРИТ.НОРМ

Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.

Его синтаксис выглядит следующим образом:

=ДОВЕРИТ.НОРМ(альфа;стандартное_откл;размер)

«Альфа» — аргумент, указывающий на уровень значимости, который применяется для расчета доверительного уровня. Доверительный уровень равняется следующему выражению:

(1-«Альфа»)*100

«Стандартное отклонение» — это аргумент, суть которого понятна из наименования. Это стандартное отклонение предлагаемой выборки.

«Размер» — аргумент, определяющий величину выборки.

Все аргументы данного оператора являются обязательными.

Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:

=ДОВЕРИТ(альфа;стандартное_откл;размер)

Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.

Граница доверительного интервала определяется при помощи формулы следующего вида:

X+(-)ДОВЕРИТ.НОРМ

Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.

Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.

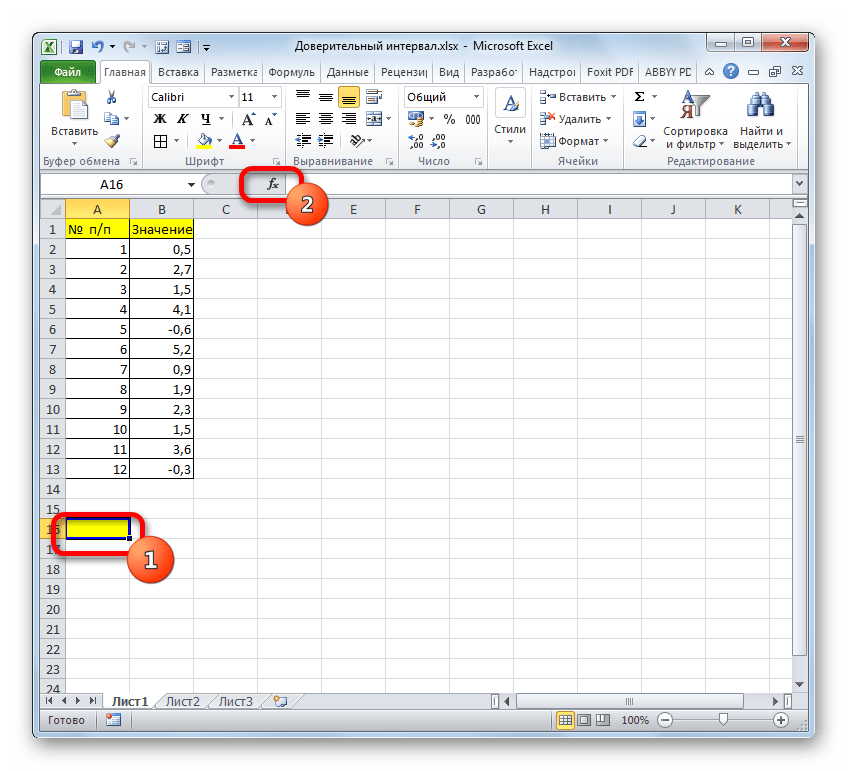
1. Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».



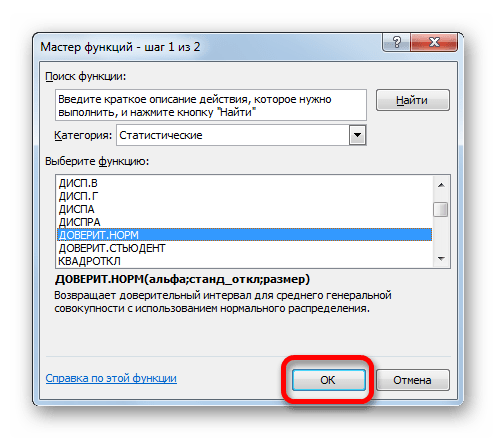
2. Появляется Мастер функций. Переходим в категорию «Статистические» и выделяем наименование «ДОВЕРИТ.НОРМ». После этого клацаем по кнопке «OK».



3. Открывается окошко аргументов. Его поля закономерно соответствуют наименованиям аргументов.
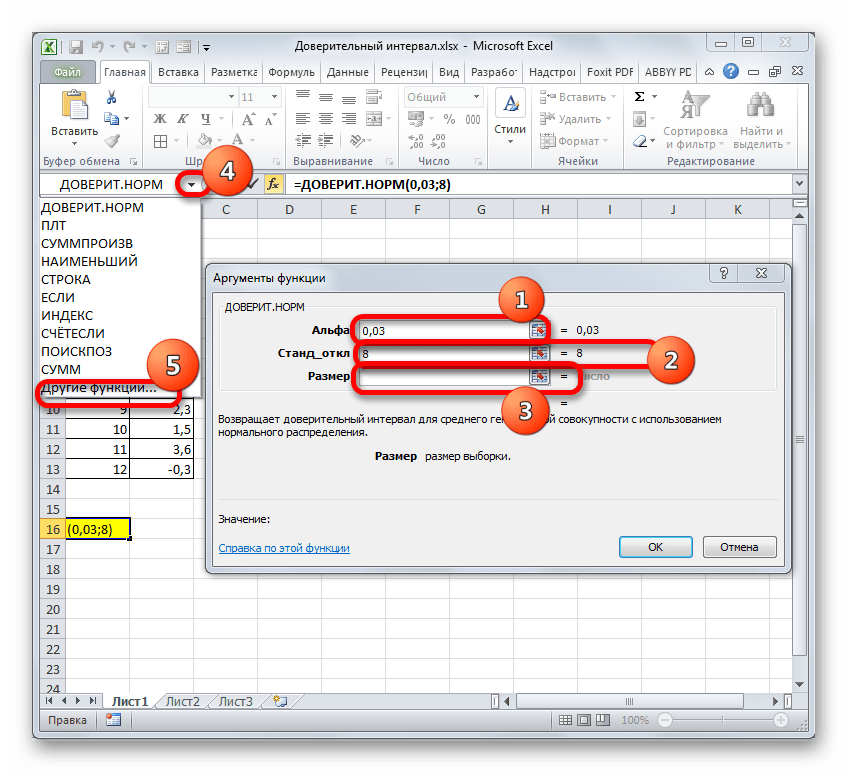
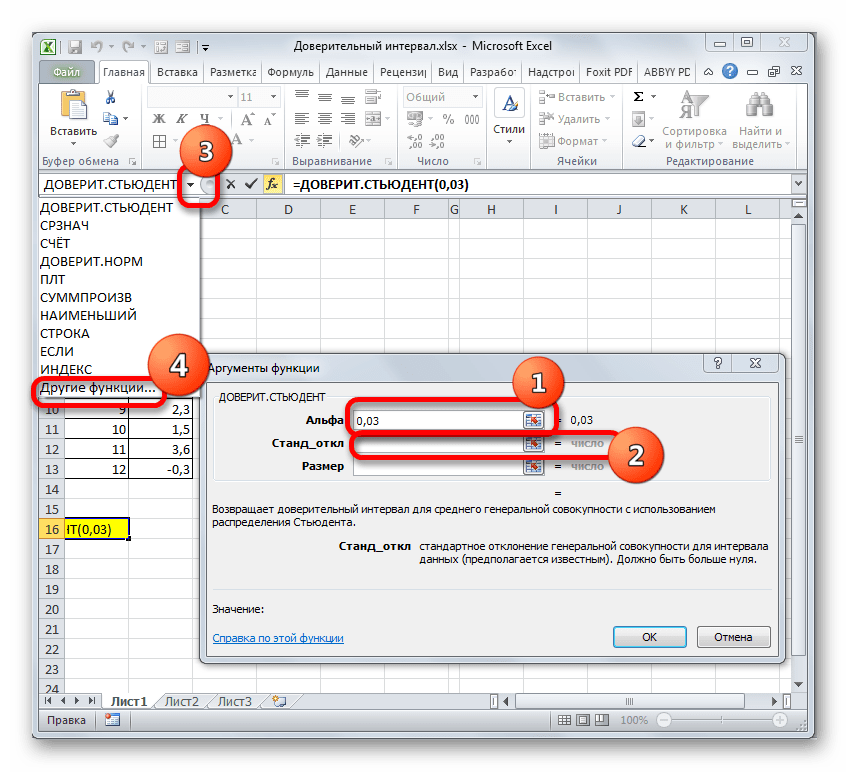
   Устанавливаем курсор в первое поле – «Альфа». Тут нам следует указать уровень значимости. Как мы помним, уровень доверия у нас равен 97%. В то же время мы говорили, что он рассчитывается таким путем:

   (1-«Альфа»)*100

   Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:

   (1-уровень доверия)/100

   То есть, подставив значение, получаем:

   (1-97)/100

   Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.

   Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.

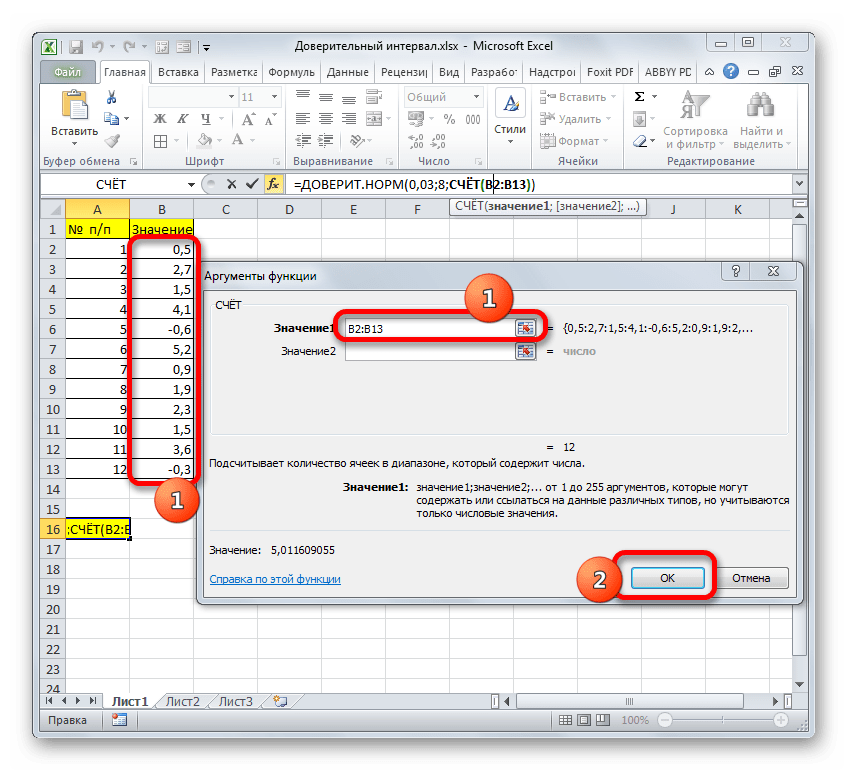
   В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.

   Появляется список недавно применяемых функций. Если оператор СЧЁТ применялся вами недавно, то он должен быть в этом списке. В таком случае, нужно просто кликнуть по его наименованию. В обратном же случае, если вы его не обнаружите, то переходите по пункту «Другие функции…».



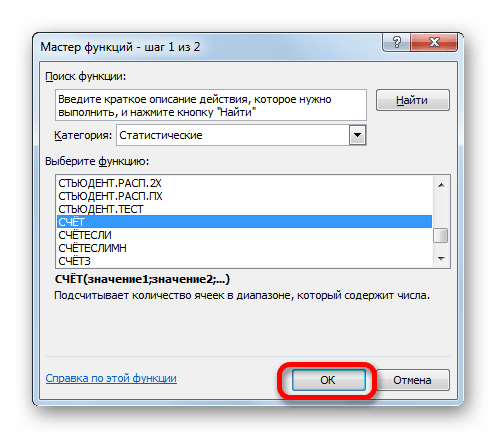
4. Появляется уже знакомый нам Мастер функций. Опять перемещаемся в группу «Статистические». Выделяем там наименование «СЧЁТ». Клацаем по кнопке «OK».



5. Появляется окно аргументов вышеуказанного оператора. Данная функция предназначена для того, чтобы вычислять количество ячеек в указанном диапазоне, которые содержат числовые значения. Синтаксис её следующий:

   =СЧЁТ(значение1;значение2;…)

   Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.

   Устанавливаем курсор в поле «Значение1» и, зажав левую кнопку мыши, выделяем на листе диапазон, который содержит нашу совокупность. Затем его адрес будет отображен в поле. Клацаем по кнопке «OK».



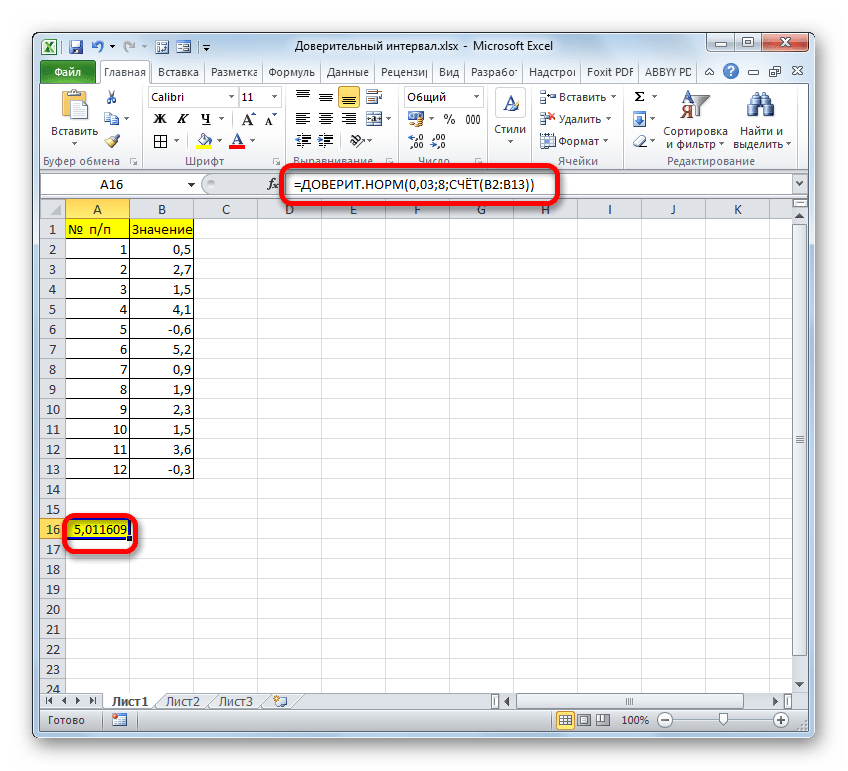
6. После этого приложение произведет вычисление и выведет результат в ту ячейку, где она находится сама. В нашем конкретном случае формула получилась такого вида:

   =ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

   Общий результат вычислений составил 5,011609.



7. Но это ещё не все. Как мы помним, граница доверительного интервала вычисляется путем сложения и вычитания от среднего выборочного значения результата вычисления ДОВЕРИТ.НОРМ. Таким способом рассчитывается соответственно правая и левая граница доверительного интервала. Само среднее выборочное значение можно рассчитать при помощи оператора СРЗНАЧ.

   Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:

   =СРЗНАЧ(число1;число2;…)

   Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.

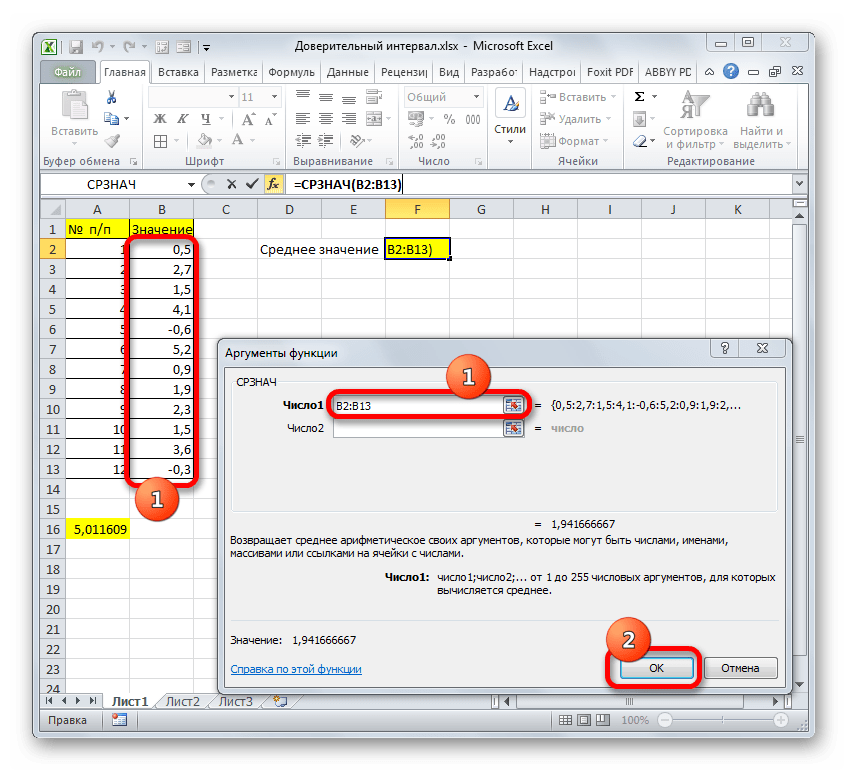
   Итак, выделяем ячейку, в которую будет выводиться расчет среднего значения, и щелкаем по кнопке «Вставить функцию».



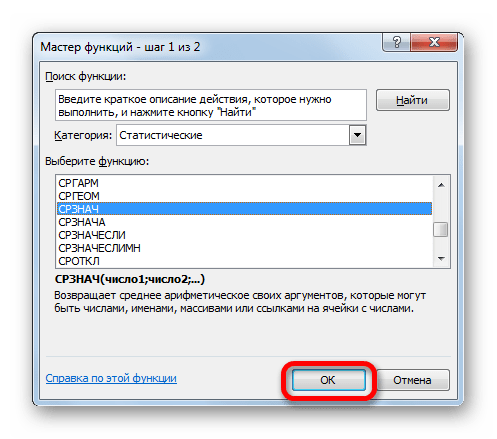
8. Открывается Мастер функций. Снова переходим в категорию «Статистические» и выбираем из списка наименование «СРЗНАЧ». Как всегда, клацаем по кнопке «OK».



9. Запускается окно аргументов. Устанавливаем курсор в поле «Число1» и с зажатой левой кнопкой мыши выделяем весь диапазон значений. После того, как координаты отобразились в поле, клацаем по кнопке «OK».



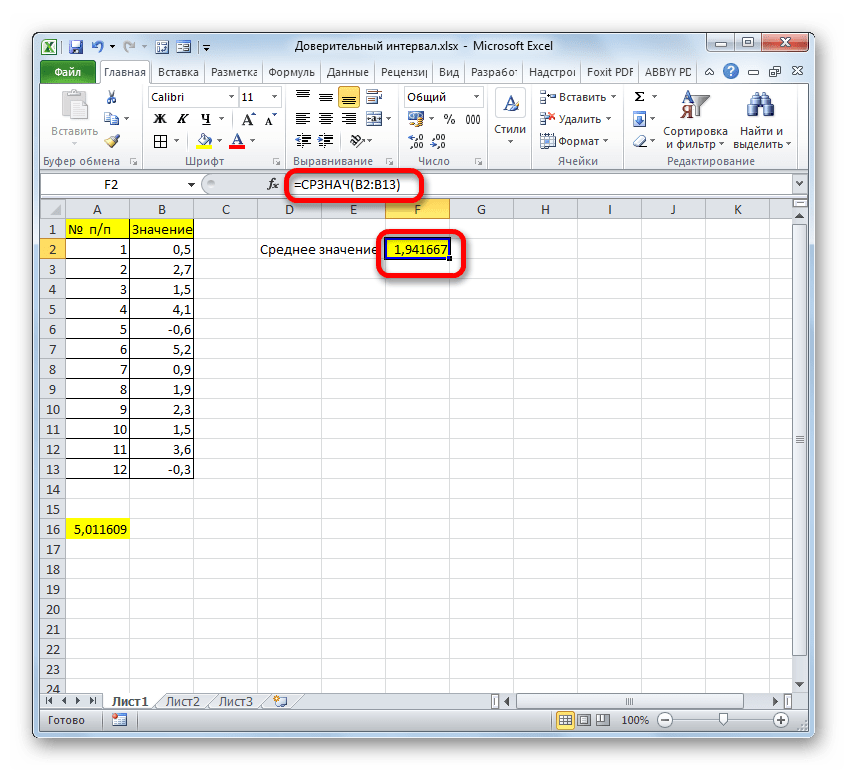
10. После этого СРЗНАЧ выводит результат расчета в элемент листа.



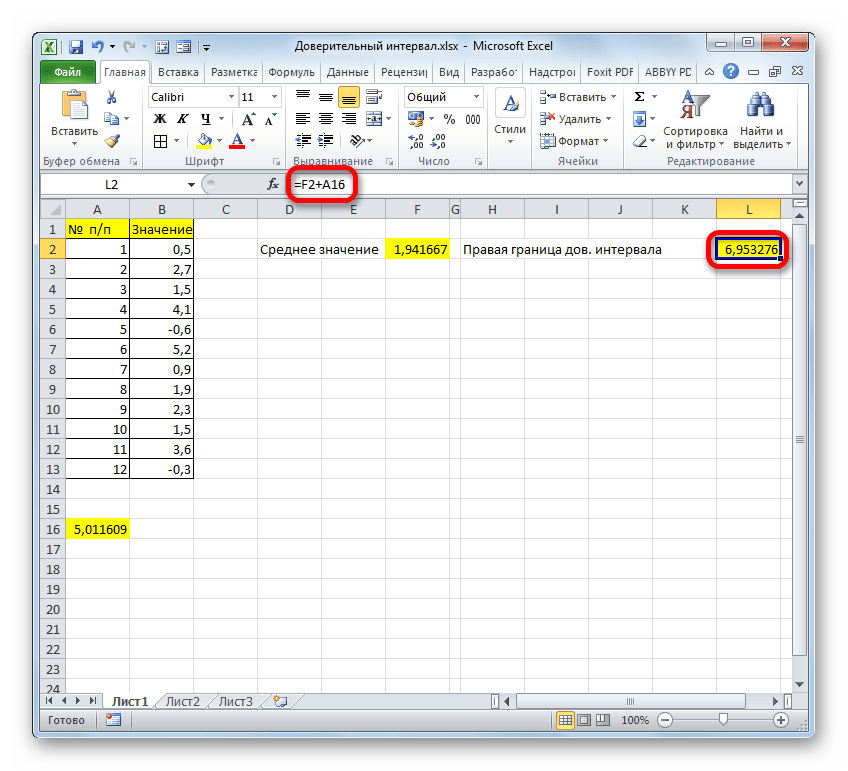
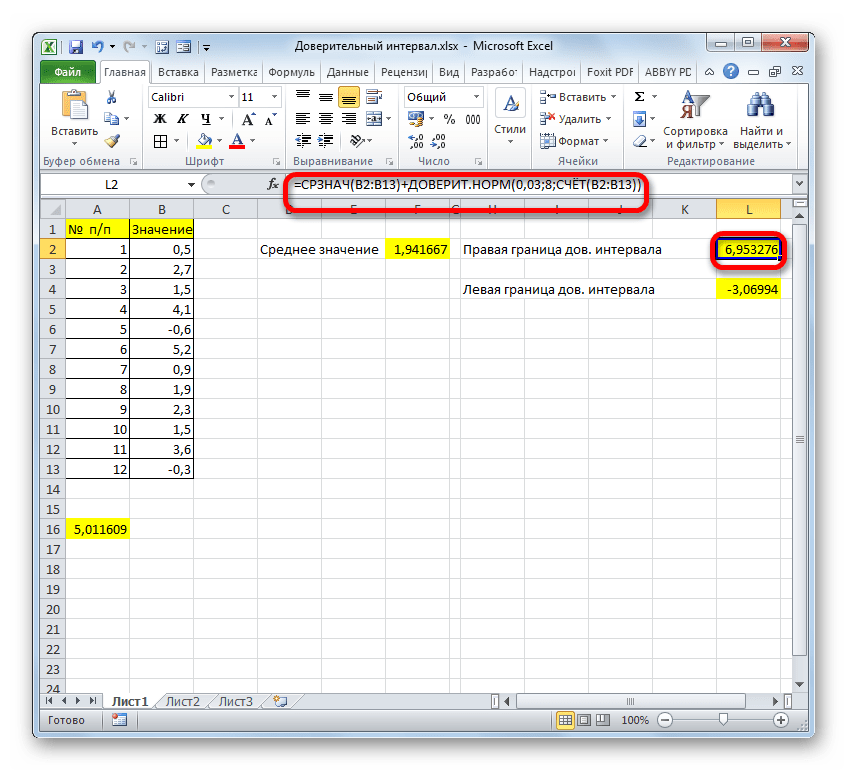
11. Производим расчет правой границы доверительного интервала. Для этого выделяем отдельную ячейку, ставим знак «=» и складываем содержимое элементов листа, в которых расположены результаты вычислений функций СРЗНАЧ и ДОВЕРИТ.НОРМ. Для того, чтобы выполнить расчет, жмем на клавишу Enter. В нашем случае получилась следующая формула:

    =F2+A16

    Результат вычисления: 6,953276



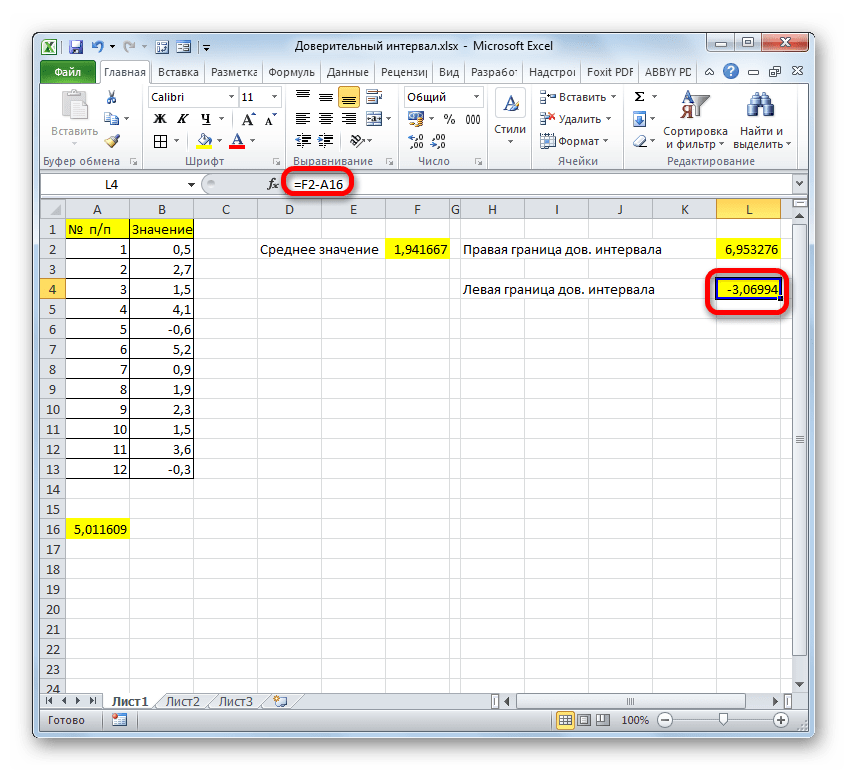
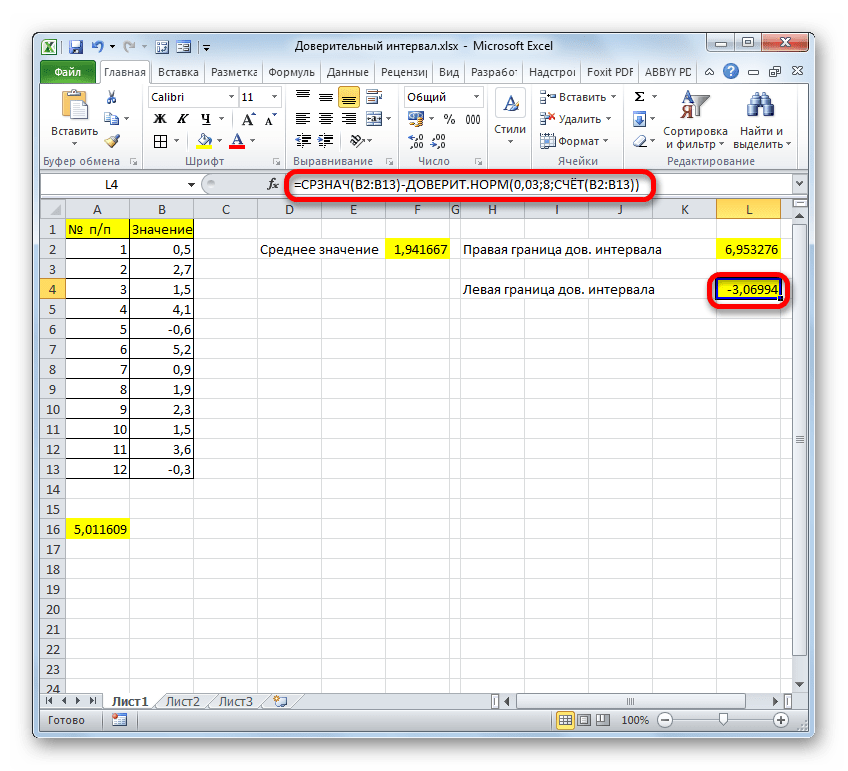
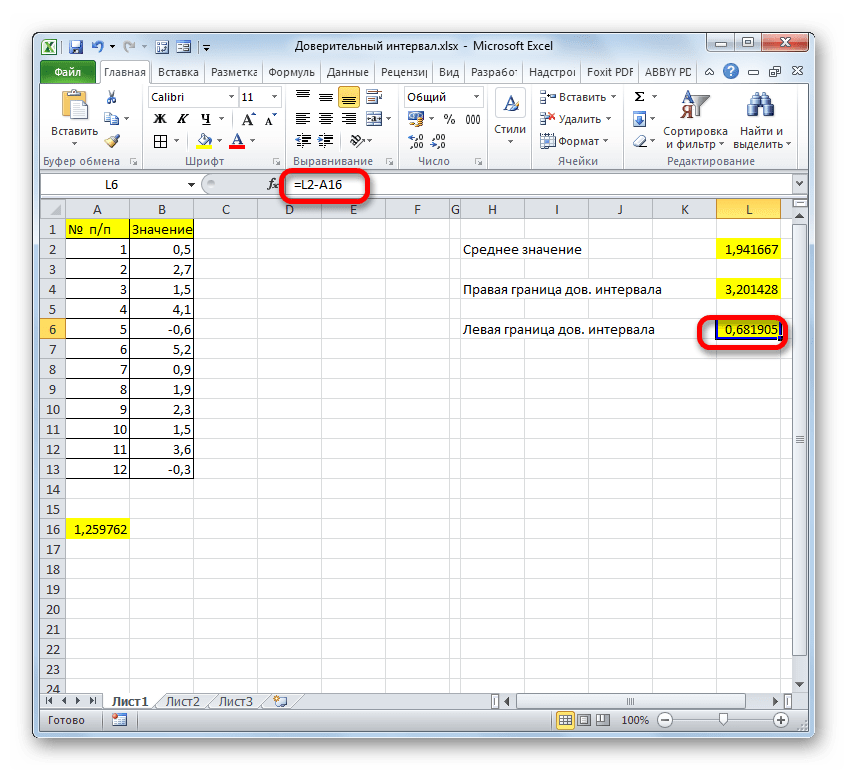
12. Таким же образом производим вычисление левой границы доверительного интервала, только на этот раз от результата вычисления СРЗНАЧ отнимаем результат вычисления оператора ДОВЕРИТ.НОРМ. Получается формула для нашего примера следующего типа:

    =F2-A16

    Результат вычисления: -3,06994



13. Мы попытались подробно описать все действия по вычислению доверительного интервала, поэтому детально расписали каждую формулу. Но можно все действия соединить в одной формуле. Вычисление правой границы доверительного интервала можно записать так:

    =СРЗНАЧ(B2:B13)+ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))



14. Аналогичное вычисление левой границы будет выглядеть так:

    =СРЗНАЧ(B2:B13)-ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

Способ 2: функция ДОВЕРИТ.СТЮДЕНТ

Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:

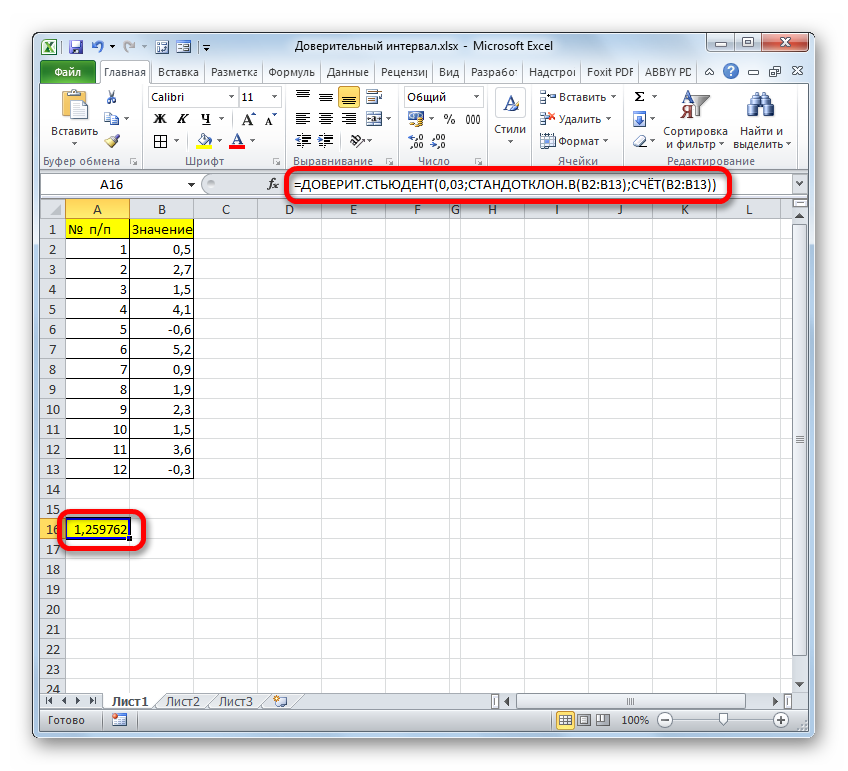
=ДОВЕРИТ.СТЬЮДЕНТ(альфа;стандартное_откл;размер)

Как видим, наименования операторов и в этом случае остались неизменными.

Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.

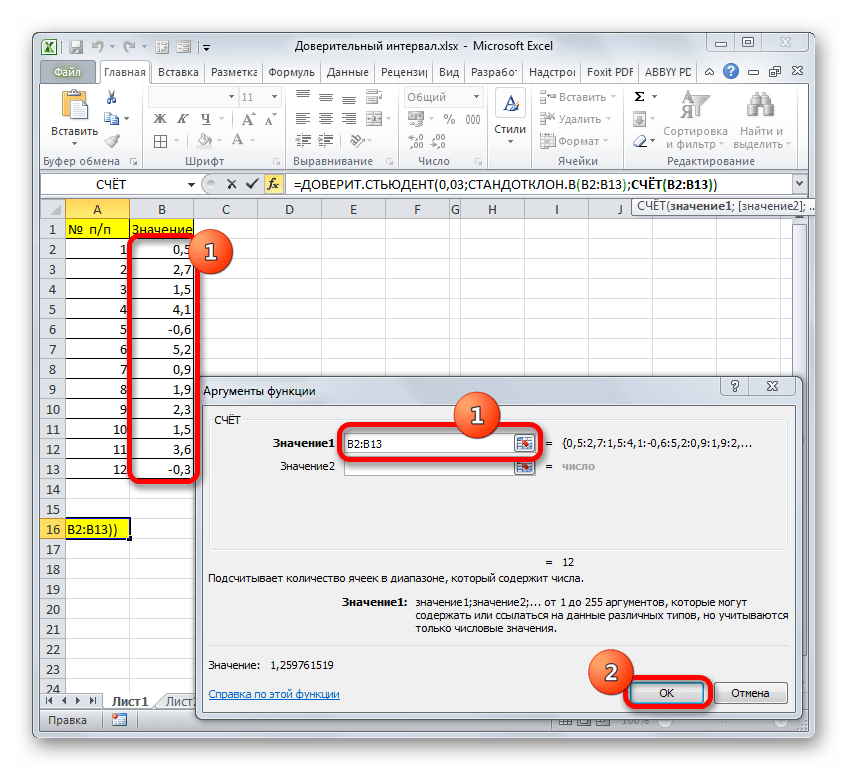
1. Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».



2. В открывшемся Мастере функций переходим в категорию «Статистические». Выбираем наименование «ДОВЕРИТ.СТЮДЕНТ». Клацаем по кнопке «OK».



3. Производится запуск окна аргументов указанного оператора.

   В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.

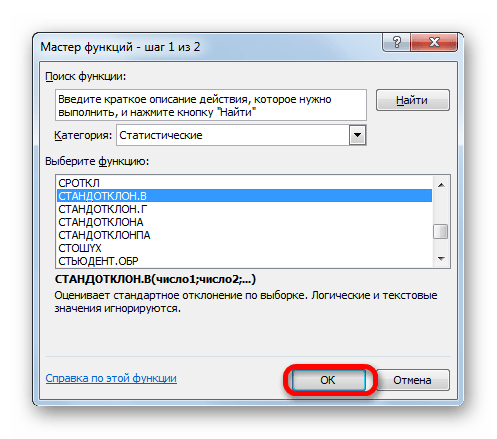
   После этого устанавливаем курсор в поле «Стандартное отклонение». На этот раз данный показатель нам неизвестен и его требуется рассчитать. Делается это при помощи специальной функции – СТАНДОТКЛОН.В. Чтобы вызвать окно данного оператора, кликаем по треугольнику слева от строки формул. Если в открывшемся списке не находим нужного наименования, то переходим по пункту «Другие функции…».



4. Запускается Мастер функций. Перемещаемся в категорию «Статистические» и отмечаем в ней наименование «СТАНДОТКЛОН.В». Затем клацаем по кнопке «OK».



5. Открывается окно аргументов. Задачей оператора СТАНДОТКЛОН.В является определение стандартного отклонения при выборке. Его синтаксис выглядит так:

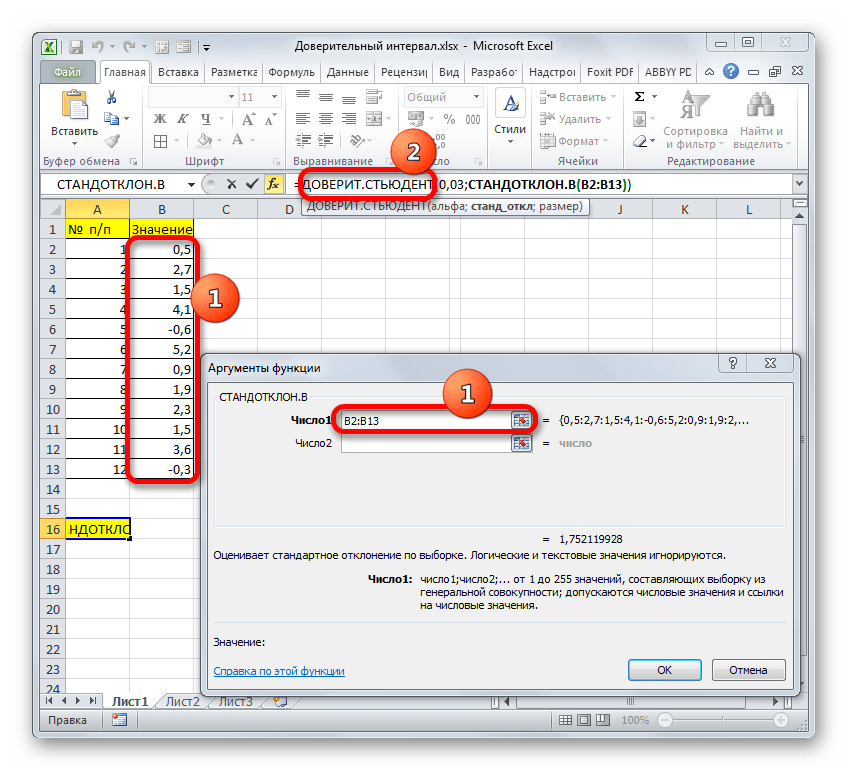
   =СТАНДОТКЛОН.В(число1;число2;…)

   Нетрудно догадаться, что аргумент «Число» — это адрес элемента выборки. Если выборка размещена единым массивом, то можно, использовав только один аргумент, дать ссылку на данный диапазон.

   Устанавливаем курсор в поле «Число1» и, как всегда, зажав левую кнопку мыши, выделяем совокупность. После того, как координаты попали в поле, не спешим жать на кнопку «OK», так как результат получится некорректным. Прежде нам нужно вернуться к окну аргументов оператора ДОВЕРИТ.СТЮДЕНТ, чтобы внести последний аргумент. Для этого кликаем по соответствующему наименованию в строке формул.



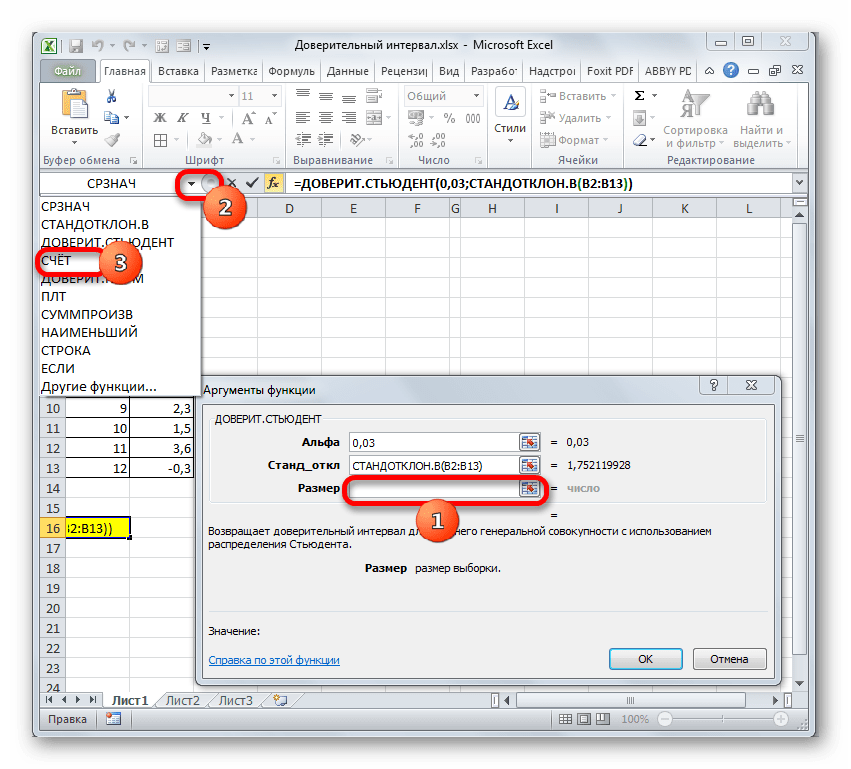
6. Снова открывается окно аргументов уже знакомой функции. Устанавливаем курсор в поле «Размер». Опять жмем на уже знакомый нам треугольник для перехода к выбору операторов. Как вы поняли, нам нужно наименование «СЧЁТ». Так как мы использовали данную функцию при вычислениях в предыдущем способе, в данном списке она присутствует, так что просто щелкаем по ней. Если же вы её не обнаружите, то действуйте по алгоритму, описанному в первом способе.



7. Попав в окно аргументов СЧЁТ, ставим курсор в поле «Число1» и с зажатой кнопкой мыши выделяем совокупность. Затем клацаем по кнопке «OK».



8. После этого программа производит расчет и выводит значение доверительного интервала.



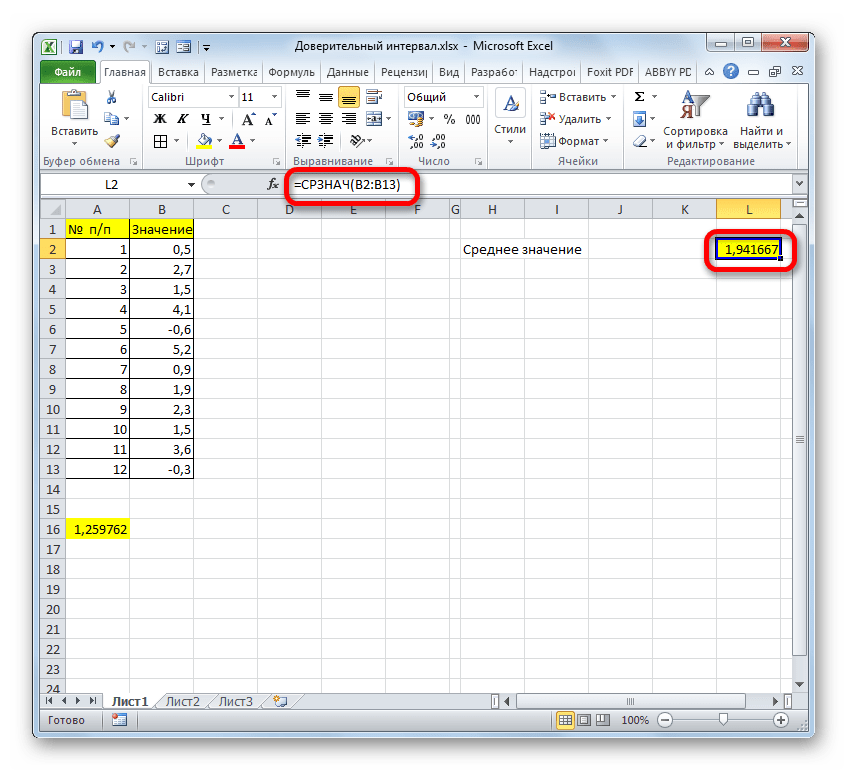
9. Для определения границ нам опять нужно будет рассчитать среднее значение выборки. Но, учитывая то, что алгоритм расчета при помощи формулы СРЗНАЧ тот же, что и в предыдущем способе, и даже результат не изменился, не будем на этом подробно останавливаться второй раз.



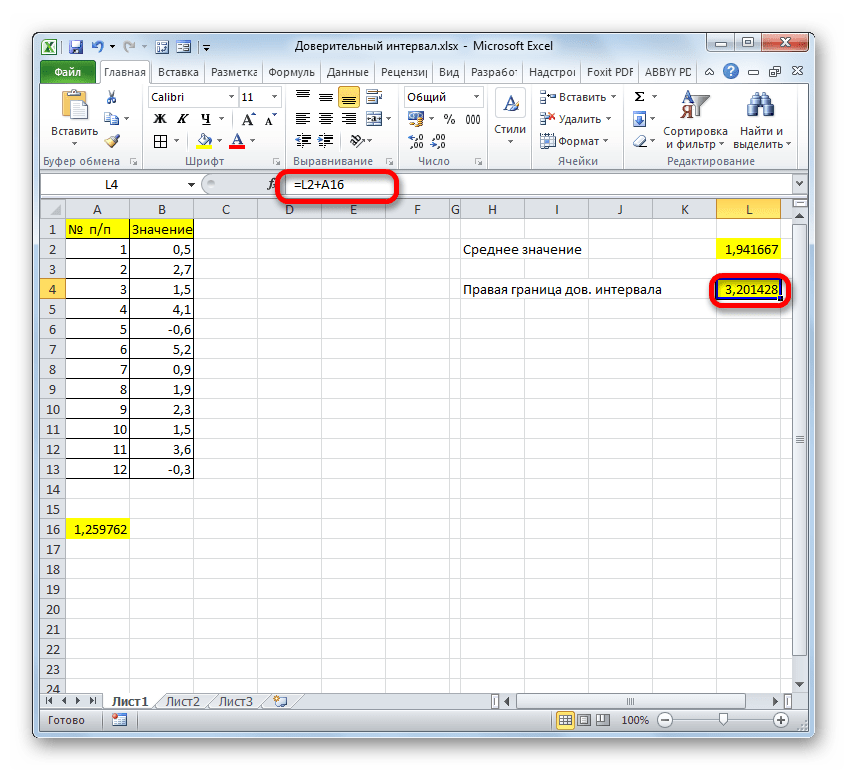
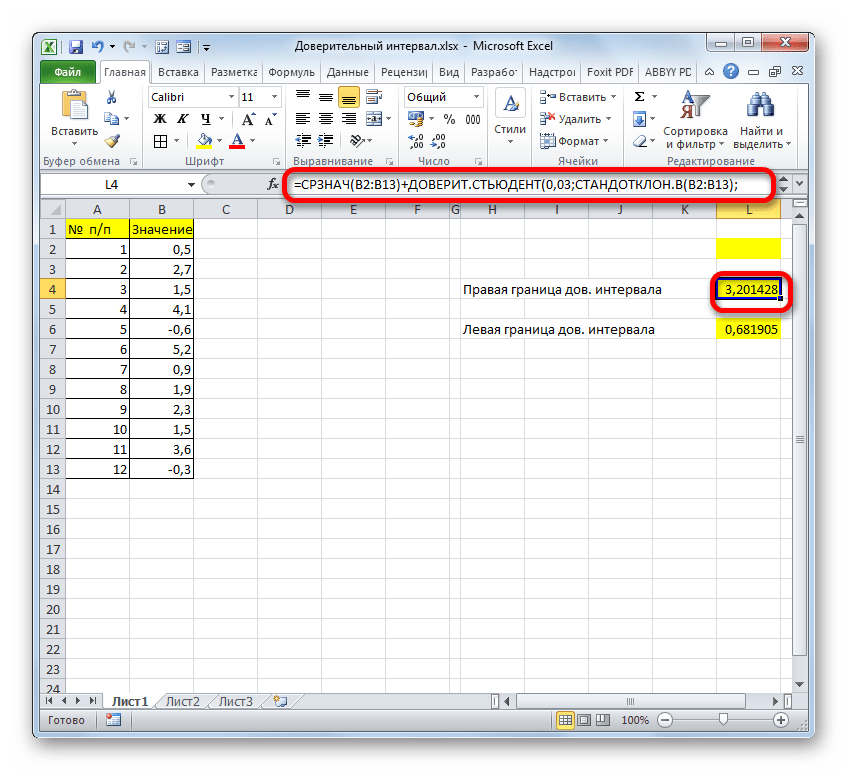
10. Сложив результаты вычисления СРЗНАЧ и ДОВЕРИТ.СТЮДЕНТ, получаем правую границу доверительного интервала.



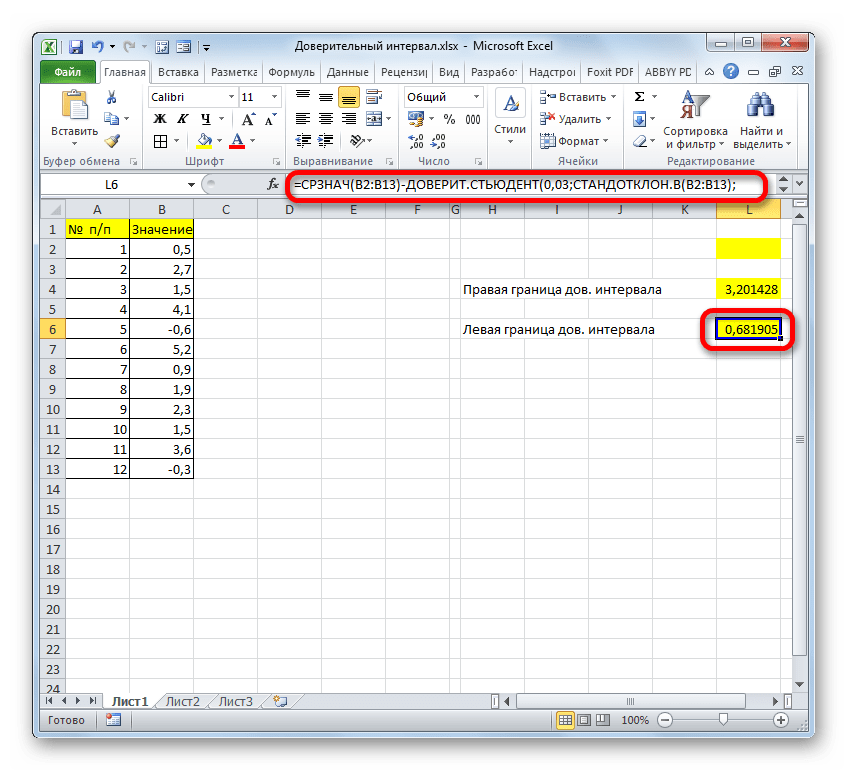
11. Отняв от результатов расчета оператора СРЗНАЧ результат расчета ДОВЕРИТ.СТЮДЕНТ, имеем левую границу доверительного интервала.



12. Если расчет записать одной формулой, то вычисление правой границы в нашем случае будет выглядеть так:

    =СРЗНАЧ(B2:B13)+ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))



13. Соответственно, формула расчета левой границы будет выглядеть так:

    =СРЗНАЧ(B2:B13)-ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))

Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.

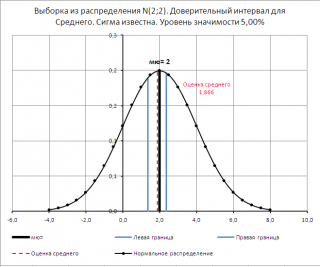
Построим в MS EXCEL доверительный интервал для оценки среднего значения распределения в случае известного значения дисперсии.

В статье

Статистики, выборочное распределение и точечные оценки в MS EXCEL

дано определение

точечной оценки

параметра распределения (point estimator). Однако, в силу случайности выборки,

точечная оценка

не совпадает с оцениваемым параметром и более разумно было бы указывать интервал, в котором может находиться неизвестный параметр при наблюденной выборке х

₁

, x

₂

, …, х

_n

. Поэтому цель использования

доверительных интервалов

состоит в том, чтобы по возможности избавиться от неопределенности и сделать как можно более полезный

статистический вывод

.

Примечание

: Процесс обобщения данных

выборки

, который приводит к

вероятностным

утверждениям обо всей

генеральной совокупности

, называют

статистическим выводом

(statistical inference).

СОВЕТ

: Для построения

Доверительного интервала

нам потребуется знание следующих понятий:

• дисперсия и стандартное отклонение

  ,

• выборочное распределение статистики

  ,

• уровень доверия/ уровень значимости

  ,

• стандартное нормальное распределение

  и

  его квантили

  .

К сожалению, интервал, в котором

может

находиться неизвестный параметр, совпадает со всей возможной областью изменения этого параметра, поскольку соответствующую

выборку

, а значит и

оценку параметра

, можно получить с ненулевой вероятностью. Поэтому приходится ограничиваться нахождением границ изменения неизвестного параметра с некоторой заданной наперед вероятностью.

Определение

:

Доверительным интервалом

называют такой интервал изменения случайной величины

,

которыйс заданной вероятностью

,

накроет истинное значение оцениваемого параметра распределения.

Эту заданную вероятность называют

уровнем доверия

(или

доверительной вероятностью

).

Обычно используют значения

уровня доверия

90%; 95%; 99%, реже 99,9% и т.д. Например,

уровень

доверия

95% означает, что дополнительное событие, вероятность которого 1-0,95=5%, исследователь считает маловероятным или невозможным.

Примечание

:

Вероятность этого дополнительного события называется

уровень значимости

или

ошибка первого рода

. Подробнее см. статью

Уровень значимости и уровень надежности в MS EXCEL

.

Разумеется, выбор

уровня доверия

полностью зависит от решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.

Примечание

:

Построение

доверительного интервала

в случае, когда

стандартное отклонение

неизвестно, приведено в статье

Доверительный интервал для оценки среднего (дисперсия неизвестна) в MS EXCEL

. О построении других

доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

.

Формулировка задачи

Предположим, что из

генеральной совокупности

имеющей

нормальное распределение

взята

выборка

размера n. Предполагается, что

стандартное отклонение

этого распределения известно. Необходимо на основании этой

выборки

оценить неизвестное

среднее значение распределения

(μ,

математическое ожидание

) и построить соответствующий

двухсторонний

доверительный интервал

.

Точечная оценка

Как известно из

Центральной предельной теоремы

,

статистика

(обозначим ее

Х

_ср

) является

несмещенной оценкой среднего

этой

генеральной совокупности

и имеет распределение N(μ;σ

²

/n).

Примечание

:

Что делать, если требуется построить

доверительный интервал

в случае распределения, которое

не является

нормальным?

В этом случае на помощь приходит

Центральная предельная теорема

, которая гласит, что при достаточно большом размере

выборки

n из распределения

не являющемся

нормальным

,

выборочное распределение статистики Х

_ср

будет

приблизительно

соответствовать

нормальному распределению

с параметрами N(μ;σ

²

/n).

Итак,

точечная оценка

среднего

значения распределения

у нас есть – это

среднее значение выборки

, т.е.

Х

_ср

. Теперь займемся

доверительным интервалом.

Построение доверительного интервала

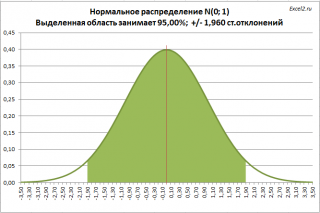
Обычно, зная распределение и его параметры, мы можем вычислить вероятность того, что случайная величина примет значение из заданного нами интервала. Сейчас поступим наоборот: найдем интервал, в который случайная величина попадет с заданной вероятностью. Например, из свойств

нормального распределения

известно, что с вероятностью 95%, случайная величина, распределенная по

нормальному закону

, попадет в интервал примерно +/- 2

стандартных отклонения

от

среднего значения

(см. статью про

нормальное распределение

). Этот интервал, послужит нам прототипом для

доверительного интервала

.

Теперь разберемся,знаем ли мы распределение

,

чтобы вычислить этот интервал? Для ответа на вопрос мы должны указать форму распределения и его параметры.

Форму распределения мы знаем – это

нормальное распределение

(напомним, что речь идет о

выборочном распределении

статистики

Х

_ср

).

Параметр μ нам неизвестен (его как раз нужно оценить с помощью

доверительного интервала

), но у нас есть его оценка

Х

_ср

,

вычисленная на основе

выборки,

которую можно использовать.

Второй параметр –

стандартное отклонение выборочного среднего

будем считать известным

, он равен σ/√n.

Т.к. мы не знаем μ, то будем строить интервал +/- 2

стандартных отклонения

не от

среднего значения

, а от известной его оценки

Х

_ср

. Т.е. при расчете

доверительного интервала

мы НЕ будем считать, что

Х

_ср

попадет в интервал +/- 2

стандартных отклонения

от μ с вероятностью 95%, а будем считать, что интервал +/- 2

стандартных отклонения

от

Х

_ср

с вероятностью 95% накроет μ

– среднее генеральной совокупности,

из которого взята

выборка

. Эти два утверждения эквивалентны, но второе утверждение нам позволяет построить

доверительный интервал

.

Кроме того, уточним интервал: случайная величина, распределенная по

нормальному закону

, с вероятностью 95% попадает в интервал +/- 1,960

стандартных отклонений,

а не+/- 2

стандартных отклонения

. Это можно рассчитать с помощью формулы

=НОРМ.СТ.ОБР((1+0,95)/2)

, см.

файл примера Лист Интервал

.

Теперь мы можем сформулировать вероятностное утверждение, которое послужит нам для формирования

доверительного интервала

: «Вероятность того, что

среднее генеральной совокупности

находится от

среднего выборки

в пределах 1,960 «

стандартных отклонений выборочного среднего»

, равна 95%».

Значение вероятности, упомянутое в утверждении, имеет специальное название

уровень доверия

, который связан с

уровнем значимости α (альфа) простым выражением

уровень доверия

=

1

-α

.

В нашем случае

уровень значимости

α

=1-0,95=0,05

.

Теперь на основе этого вероятностного утверждения запишем выражение для вычисления

доверительного интервала

:

где Z

_α/2

–

верхний α/2-квантиль

стандартного

нормального распределения

(такое значение случайной величины

z

,

что

P

(

z

>=

Z

_α/2

)=α/2

).

Примечание

:

Верхний α/2-квантиль

определяет ширину

доверительного интервала

в

стандартных отклонениях

выборочного среднего.

Верхний α/2-квантиль

стандартного

нормального распределения

всегда больше 0, что очень удобно.

В нашем случае при α=0,05,

верхний α/2-квантиль

равен 1,960. Для других уровней значимости α (10%; 1%)

верхний α/2-квантиль

Z

_α/2

можно вычислить с помощью формулы

=НОРМ.СТ.ОБР(1-α/2)

или, если известен

уровень доверия

,

=НОРМ.СТ.ОБР((1+ур.доверия)/2)

.

Обычно при построении

доверительных интервалов для оценки среднего

используют только

верхний α

/2-

квантиль

и не используют

нижний α

/2-

квантиль

. Это возможно потому, что

стандартное

нормальное распределение

симметрично относительно оси х (

плотность его распределения

симметрична относительно

среднего, т.е. 0

)

.

Поэтому, нет нужды вычислять

нижний α/2-квантиль

(его называют просто α

/2-квантиль

), т.к. он равен

верхнему α

/2-

квантилю

со знаком минус.

Напомним, что, не смотря на форму распределения величины х, соответствующая случайная величина

Х

_ср

распределена

приблизительно

нормально

N(μ;σ

²

/n) (см. статью про

ЦПТ

). Следовательно, в общем случае, вышеуказанное выражение для

доверительного интервала

является лишь приближенным. Если величина х распределена по

нормальному закону

N(μ;σ

²

/n), то выражение для

доверительного интервала

является точным.

Расчет доверительного интервала в MS EXCEL

Решим задачу.

Время отклика электронного компонента на входной сигнал является важной характеристикой устройства. Инженер хочет построить доверительный интервал для среднего времени отклика при уровне доверия 95%. Из предыдущего опыта инженер знает, что стандартное отклонение время отклика составляет 8 мсек. Известно, что для оценки времени отклика инженер сделал 25 измерений, среднее значение составило 78 мсек.

Решение

: Инженер хочет знать время отклика электронного устройства, но он понимает, что время отклика является не фиксированной, а случайной величиной, которая имеет свое распределение. Так что, лучшее, на что он может рассчитывать, это определить параметры и форму этого распределения.

К сожалению, из условия задачи форма распределения времени отклика нам не известна (оно не обязательно должно быть

нормальным

).

Среднее, т.е. математическое ожидание

, этого распределения также неизвестно. Известно только его

стандартное отклонение

σ=8. Поэтому, пока мы не можем посчитать вероятности и построить

доверительный интервал

.

Однако, не смотря на то, что мы не знаем распределение

времени

отдельного отклика

, мы знаем, что согласно

ЦПТ

,

выборочное распределение

среднего времени отклика

является приблизительно

нормальным

(будем считать, что условия

ЦПТ

выполняются, т.к. размер

выборки

достаточно велик (n=25))

.

Более того,

среднее

этого распределения равно

среднему значению

распределения единичного отклика, т.е. μ. А

стандартное отклонение

этого распределения (σ/√n) можно вычислить по формуле

=8/КОРЕНЬ(25)

.

Также известно, что инженером была получена

точечная оценка

параметра μ равная 78 мсек (Х

_ср

). Поэтому, теперь мы можем вычислять вероятности, т.к. нам известна форма распределения (

нормальное

) и его параметры (Х

_ср

и σ/√n).

Инженер хочет знать

математическое ожидание

μ распределения времени отклика. Как было сказано выше, это μ равно

математическому ожиданию выборочного распределения среднего времени отклика

. Если мы воспользуемся

нормальным распределением

N(Х

_ср

; σ/√n), то искомое μ будет находиться в интервале +/-2*σ/√n с вероятностью примерно 95%.

Уровень значимости

равен 1-0,95=0,05.

Наконец, найдем левую и правую границу

доверительного интервала

. Левая граница:

=78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)

=

74,864

Правая граница:

=78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136

или так

Левая граница:

=НОРМ.ОБР(0,05/2; 78; 8/КОРЕНЬ(25))

Правая граница:

=НОРМ.ОБР(1-0,05/2; 78; 8/КОРЕНЬ(25))

Ответ

:

доверительный интервал

при

уровне доверия 95% и σ

=8

мсек

равен

78+/-3,136 мсек.

В

файле примера на листе Сигма

известна создана форма для расчета и построения

двухстороннего

доверительного интервала

для произвольных

выборок

с заданным σ и

уровнем значимости

.

Функция

ДОВЕРИТ.НОРМ()

Если значения

выборки

находятся в диапазоне

B20:B79

, а

уровень значимости

равен 0,05; то формула MS EXCEL:

=СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))

вернет левую границу

доверительного интервала

.

Эту же границу можно вычислить с помощью формулы:

=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))

Примечание

: Функция

ДОВЕРИТ.НОРМ()

появилась в MS EXCEL 2010. В более ранних версиях MS EXCEL использовалась функция

ДОВЕРИТ()

.

Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.

Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.

Вычисление доверительного интервала

Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.

В Microsoft Excel существует два метода выполнения данной задачи:

• Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
• Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.

Ниже мы пошагово разберем оба метода на практике.

Метод 1: оператора ДОВЕРИТ.НОРМ

Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.

Формула функции ДОВЕРИТ.НОРМ выглядит так:

=ДОВЕРИТ.НОРМ(Альфа;Станд_откл;Размер)

Как мы видим, у функции есть три аргумента:

• “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
  • 1-"Альфа". Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.
  • (100-"Альфа")/100. Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
• “Стандартное отклонение” — соответственно, стандартное отклонение анализируемой выборки данных.
• “Размер” – объем выборки данных.

Примечание: У данной функции наличие всех трех аргументов является обязательным условием.

Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.

Формула функции ДОВЕРИТ выглядит следующим образом:

=ДОВЕРИТ(Альфа;Станд_откл;Размер)

Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.

Граница доверительного интервала определяется следующей формулой:

X+(-)ДОВЕРИТ.НОРМ

где Х – это среднее значение по заданному диапазону.

Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.

Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.

1. Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
2. Откроется окно Мастера функций. Кликнув по текущей категории функций, раскрываем список и щелкаем в нем по строке “Статистические”.
3. В предложенном перечне кликаем по оператору “ДОВЕРИТ.НОРМ”, затем жмем OK.
4. Перед нами появится окно с настройками аргументов функции, заполнив которые нажимаем кнопку OK.
   • в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение: (100-95)/100. Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05).
   • в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
   • в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
5. Чтобы при изменении данных не пришлось заново настраивать функцию, можно автоматизировать ее. Для это применим функцию “СЧЁТ”. Ставим указатель в область ввода информации аргумента “Размер”, затем щелкаем по значку треугольника с левой стороны от строки формул и кликаем по пункту “Другие функции…”.
6. В результате откроется еще одно окно Мастера функций. Выбрав категорию “Статистические”, кликаем по функции “СЧЕТ”, затем – OK.
7. На экране отобразится еще одно окно с настройками аргументов функции, которая применяется для определения числа ячеек в заданном диапазоне, в которых находятся числовые данные.
   Формула функции СЧЕТ пишется так: =СЧЁТ(Значение1;Значение2;...).
   Количество доступных аргументов этой функции может достигать 255 штук. Здесь можно прописать, либо конкретные числа, либо адреса ячеек, либо диапазоны ячеек. Мы воспользуемся последним вариантом. Для этого кликаем по области ввода информации для первого аргумента, затем зажав левую кнопку мыши выделяем все ячейки одного из столбцов нашей таблицы (не считая шапки), после чего жмем кнопку OK.
8. В результате проделанных действий в выбранной ячейке будет выведено результат расчетов по оператору ДОВЕРИТ.НОРМ. В нашей задаче его значение оказалось равным 4,9583603.
9. Но это еще не конечный результат в нашей задаче. Далее требуется рассчитать среднее значение по заданному интервалу. Для этого потребуется применить функцию “СРЗНАЧ”, которая выполняет задачу по вычислению среднего значения в пределах указанного диапазона данных.
   Формула оператора пишется так: =СРЗНАЧ(число1;число2;...).
   Выделяем ячейку, куда планируем вставить функцию и жмем кнопку “Вставить функцию”.
10. В категории “Статистические” выбираем нудный оператор “СРЗНАЧ” и кликаем OK.
11. В аргументах функции в значении аргумента “Число” указываем диапазон, в который входят все ячейки со значениями всех замеров. Затем кликаем OK.
12. В результате проделанных действий среднее значение будет автоматически подсчитано и выведено в ячейку с только что вставленной функцией.
13. Теперь нам нужно рассчитать границы ДИ (доверительного интервала). Начнем с расчета значения правой границы. Выбираем ячейку, куда хотим вывести результат, и выполняем в ней сложение результатов, полученных с помощью операторов “СРЗНАЧ” и “ДОВЕРИТ.НОРМ”. В нашем случае формула выглядит так: A14+A16. После ее набора жмем Enter.
14. В результате будет произведен расчет и результат немедленно отобразится в ячейке с формулой.
15. Затем аналогичным способом выполняем расчет для получения значения левой границы ДИ. Только в этом случае значение результата “ДОВЕРИТ.НОРМ” нужно не прибавлять, а вычитать из результата, полученного при помощи оператора “СРЗНАЧ”. В нашем случае формула выглядит так: =A16-A14.
16. После нажатия Enter мы получим результат в заданной ячейке с формулой.

Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:

• Для определения правой границы ДИ общая формула будет выглядеть так:
  =СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).
• Точно также и для левой границы, только вместо плюса нужно поставить минус:
  =СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).

Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ

Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.

Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:

=ДОВЕРИТ.СТЬЮДЕНТ(Альфа;Cтанд_откл;Размер)

Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.

1. Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
2. Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
3. В следующем окне нам нужно настроить аргументы функции:.
4. В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
5. Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
6. Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
   • Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
   • Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ

Заключение

Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.

В этой статье описаны синтаксис формулы и использование
 в Microsoft Excel.

Описание

Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.

Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.

Синтаксис

ДОВЕРИТ(альфа;стандартное_откл;размер)

Аргументы функции ДОВЕРИТ описаны ниже.

• Альфа     — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.

• Стандартное_откл     — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.

• Размер     — обязательный аргумент. Размер выборки.

Замечания

• Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.

• Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.

• Если значение аргумента «размер» не является целым числом, оно усекается.

• Если размер < 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,05	Уровень значимости
2,5	Стандартное отклонение для генеральной совокупности
50	Размер выборки
Формула	Описание	Результат
=ДОВЕРИТ(A2;A3;A4)	Доверительный интервал для математического ожидания генеральной совокупности. Иными словами, доверительный интервал средней продолжительности поездки на работу для генеральной совокупности составляет 30 ± 0,692952 минуты или от 29,3 до 30,7 минут.	0,692951912

В этой статье описаны синтаксис формулы и использование в Microsoft Excel.

Описание

Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.

Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.

Синтаксис

Аргументы функции ДОВЕРИТ описаны ниже.

Альфа — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.

Стандартное_откл — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.

Размер — обязательный аргумент. Размер выборки.

Замечания

Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.

Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.

Если значение аргумента «размер» не является целым числом, оно усекается.

Если размер < 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Подсчет ЧИСЕЛ попадающих в интервал в EXCEL

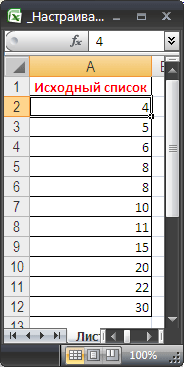
В качестве примера подсчета чисел возьмем список с числовыми значениями от 4 до 30 (См. файл примера ).

Будем подсчитывать значения, попадающие в интервал, например, (4;15]. Причем, границы интервала «включает [ ]» и «не включает ( )» будем выбирать из Выпадающего (раскрывающегося) списка .

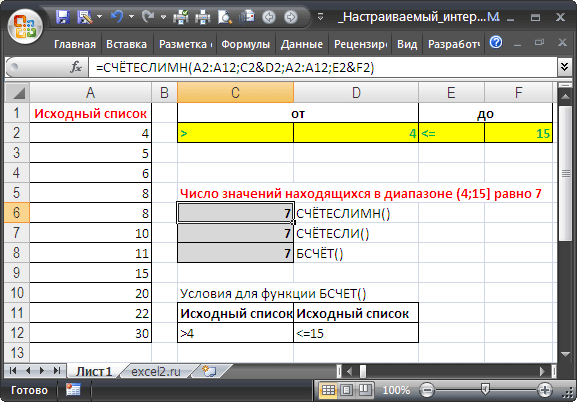
Для настройки границ интервала используем Проверку данных с типом данных Список . В качестве источника укажем для левой границы >;>= и для правой <;<=. Границы интервала будем вводить в диапазон H2 : I3 .

Подсчет можно реализовать множеством формул, приведем несколько:

• = СЧЁТЕСЛИМН(A2:A12;C2&D2;A2:A12;E2&F2)
• = СЧЁТЕСЛИ($A$2:$A$12;C2&D2)-(СЧЁТЗ($A$2:$A$12)-СЧЁТЕСЛИ($A$2:$A$12;E2&F2))
• Формула = БСЧЁТ(A1:A12;A1;H2:I3) требует предварительного создания таблицы с условиями. Заголовки этой таблицы должны в точности совпадать с заголовками исходной таблицы.

СОВЕТ: Более сложные условия подсчета рассмотрены в статье Подсчет значений с множественными критериями (Часть 1. Условие И) .

Функция ДОВЕРИТ и нормальный доверительный интервал в Excel

Функция ДОВЕРИТ в Excel предназначена для определения доверительного интервала для среднего значения, найденного для генеральной совокупности, которая имеет нормальное распределение.

Другими словами, рассматриваемая функция позволяет определить допустимые отклонения для найденного среднего значения с учетом известных уровня значимости (заданная вероятность того, что некоторое значение находится в доверительном интервале) и стандартного отклонения (меры степени разброса значений относительно среднего значения для генеральной совокупности).

Как построить доверительный интервал нормального распределения в Excel

Поскольку интервал значений, в котором находится некоторая неизвестная величина, совпадает с областью, в которой могут изменяться значения этой величины, то вероятность правильности оценки данной величины стремится к нулю. Поэтому, принято устанавливать определенное значение вероятности для нахождения границ изменения некоторой величины. Значения, находящиеся между этими границами, называют доверительным интервалом.

Рассматриваемая функция была заменена функцией ДОВЕРИТ.НОРМ с версии Excel 2010. Функция ДОВЕРИТ была оставлена для обеспечения совместимости с документами, созданными в более ранних версиях табличного редактора.

Пример расчета доверительного интервала в Excel

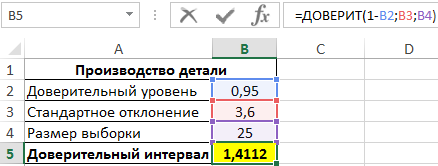
Пример 1. В заводском цехе производят деталь, длина которой должна составлять 200 мм. Стандартное отклонение от длины – 3,6 мм. Для контроля качества деталей из партии (генеральная совокупность) делают выборку из 25 деталей. Определить интервал с доверительный уровнем 95%.

Вид таблицы данных:

Для определения доверительного интервала используем функцию:

• 1-B2 – уровень значимости (рассчитан с учетом зависимости от доверительного уровня);
• B3 – значение стандартного отклонения;
• B4 – количество деталей в выборке.

То есть, границы доверительного интервала соответствуют: (Xср-1,4112;Xср+1,4112). Допустим, было определено среднее значение выборки – 199,5 мм. Тогда доверительный интервал примерно определяется как (198,1;200,9), при этом номинальная длина детали (200 мм) находится в доверительном диапазоне, то есть производственный процесс не нарушен.

Как найти границы доверительного интервала в Excel

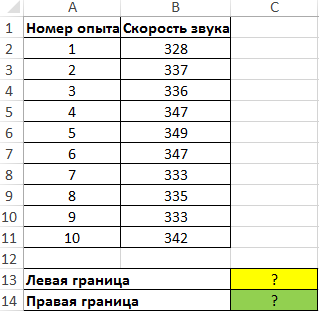
Пример 2. Были проведены опыты по определению скорости распространения звуковой волны в воздухе. Результаты 10 опытов записаны в таблицу. Определить левую и правую границы доверительного интервала для среднего значения.

Вид таблицы данных:

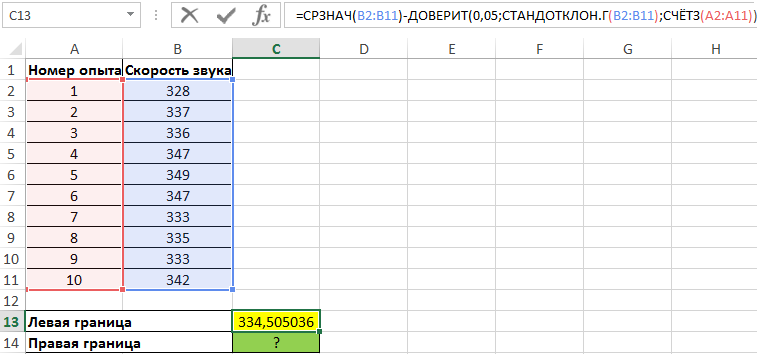
Для нахождения левой границы используем формулу:

В данном случае выборка и генеральная совокупность приняты как имеющиеся данные для 10 проведенных опытов. Среднее выборочное значение рассчитано с помощью функции СРЗНАЧ. Для получения левой границы доверительного интервала из данного значения вычитаем число, полученное в результате выполнения функции ДОВЕРИТ, в которой значение второго аргумента определено с помощью функции СТАНДОТКЛОН.Г, а число опытов – подсчетом количества ячеек функцией СЧЁТЗ.

Поскольку уровень значимости не задан, используем стандартное значение – 0,05.

Правая граница определяется аналогично с разницей в том, что к среднему значению выборки прибавляется результат расчета функции ДОВЕРИТ: