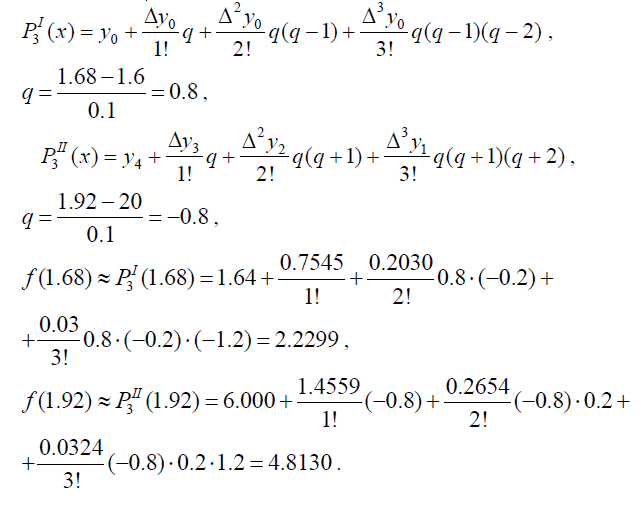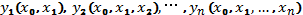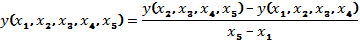Интерполяционный многочлен Ньютона
Задача:
построить интерполяционный многочлен
Ньютона вручную использую Excel.
Таблица
зависимости значений функции от аргумента
|
X |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
Y |
0,9 |
1,9 |
3,2 |
3,8 |
5,1 |
6,1 |
Ручной
счет:
Многочлен
Ньютона находится по формуле:
В
Excel вычислим коэффициенты
В
столбце А
находятся Xi,
в столбце B
находятся Yi.
Вычисленные коэффициенты располагаются
так:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
X0 |
Y0 |
|||||
|
2 |
Y(X0,X1) |
||||||
|
3 |
X1 |
Y1 |
Y(X0,X1,X2) |
||||
|
4 |
Y(X1,X2) |
Y(X0,X1,X2,X3) |
|||||
|
5 |
X2 |
Y2 |
Y(X1,X2,X3) |
Y(X0,X1,X2,X3,X4) |
|||
|
6 |
Y(X2,X3) |
Y(X1,X2,X3,X4) |
Y(X0,X1,X2,X3,X4,X5,X6) |
||||
|
7 |
X3 |
Y3 |
Y(X2,X3,X4) |
Y(X1,X2,X3,X4,X5) |
|||
|
8 |
Y(X3,X4) |
Y(X2,X3,X4,X5) |
|||||
|
9 |
X4 |
Y4 |
Y(X3,X4,X5) |
||||
|
10 |
Y(X4,X5) |
||||||
|
11 |
X5 |
Y5 |
Коэффициенты
вычисляются так:
,
,
и т.д.
,
и т.д.
,
и т.д.
,
Формулы
в Excel:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
1 |
0,9 |
|||||
|
2 |
=(B3-B1)/(A3-A1) |
||||||
|
3 |
1,2 |
1,9 |
=(C4-C2)/(A5-A1) |
||||
|
4 |
=(B5-B3)/(A5-A3) |
=(D5-D3)/(A7-A1) |
|||||
|
5 |
1,4 |
3,2 |
=(C6-C4)/(A7-A3) |
=(E6-E4)/(A9-A1) |
|||
|
6 |
=(B7-B5)/(A7-A5) |
=(D7-D5)/(A9-A3) |
=(F7-F5)/(A11-A1) |
||||
|
7 |
1,6 |
3,8 |
=(C8-C6)/(A9-A5) |
=(E8-E6)/(A11-A3) |
|||
|
8 |
=(B9-B7)/(A9-A7) |
=(D9-D7)/(A11-A5) |
|||||
|
9 |
1,8 |
5,1 |
=(C10-C8)/(A11-A7) |
||||
|
10 |
=(B11-B9)/(A11-A9) |
||||||
|
11 |
2 |
6,1 |
В
итоге получаем такую таблицу значений:
|
A |
B |
C |
D |
F |
E |
G |
|
|
1 |
1 |
0,9 |
|||||
|
2 |
5 |
||||||
|
3 |
1,2 |
1,9 |
3,75 |
||||
|
4 |
6,5 |
-20,8333 |
|||||
|
5 |
1,4 |
3,2 |
-8,75 |
62,5 |
|||
|
6 |
3 |
29,16667 |
-125 |
||||
|
7 |
1,6 |
3,8 |
8,75 |
-62,5 |
|||
|
8 |
6,5 |
-20,8333 |
|||||
|
9 |
1,8 |
5,1 |
-3,75 |
||||
|
10 |
5 |
||||||
|
11 |
2 |
6,1 |
Нужные
коэффициенты выделены жирным. Подставим
их в многочлен Ньютона:
N(x)=0,9+5(х-1)+3,75(х-1)(х-1,2)-20,8333(х-1)(х-1,2)(х-1,4)+62,5(х-1)(х-1,2)(х-1,4)(х-1,6)-125(х-1)(х-1,2)(х-1,4)(х-1,6)(х-1,8)=0,9+5х-5+3,75
X2
-8,25х+4,5-20,8333 X3
+74,99988 X2
-89,166524х+34,999944+62,5 X4
-325 X3
+627,5 X2
-533х+168-125 X5
+875 X4
-2425 X3
+3325 X2
-2254,8х+604,8
В
результате получим многочлен:
N(х)=-125
X5
+937,5 X4
-2770,8333 X3
+4031,2498 X2
-2880,21624+808,199944
Проверим
значения полученной функции в первых
шести точках:
N(1)=-125
*15
+937,5 *14
-2770,8333 *13
+4031,2498 *12
-2880,21624*1+808,199944≈0,9
N(1,2)=-125
*(1,2)5
+937,5 *(1,2)4
-2770,8333 *(1,2)3
+4031,2498 *(1,2)2
-2880,21624*1,2+808,199944≈1,9
N(1,4)=-125
*(1,4)5
+937,5 *(1,4)4
-2770,8333 *(1,4)3
+4031,2498 *(1,4)2
-2880,21624*1,4+808,199944≈3,2
N(1,6)=-125
*(1,6)5
+937,5 *(1,6)4
-2770,8333 *(1,6)3
+4031,2498 *(1,6)2
-2880,21624*1,6+808,199944≈3,8
N(1,8)=-125
*(1,8)5
+937,5 *(1,8)4
-2770,8333 *(1,8)3
+4031,2498 *(1,8)2
-2880,21624*1,8+808,199944≈5,1
N(2)=-125
*(2)5
+937,5 *(2)4
-2770,8333 *(2)3
+4031,2498 *(2)2
-2880,21624*2+808,199944≈6,1
Полученные
значения функции совпадают с табличными
значениями. Многочлен Ньютона вычислен
верно.
Формула
в Excel для проверки найденного многочлена
Ньютона:
=B1+C2*(A111-A1)+D3*(A11-A1)*(A11-A3)+E4*(A11-A1)*(A11-A3)*(A11-A5)+F5*(A11-A1)*(A11-A3)*(A11-A5)*(A11-A7)+G6*(A11-A1)*(A11-A3)*(A11-A5)*(A11-A7)*(A11-A9)
В
ячейку А11
подставляем
значение Х,
для которого надо узнать значение
многочлена.
Таблица
результатов в Excel для табличных значения
Х:
|
1 |
0,9 |
|
1,2 |
1,9 |
|
1,4 |
3,2 |
|
1,6 |
3,8 |
|
1,8 |
5,1 |
|
2 |
6,1 |
Всё
вычислено верно.
Получение
аппроксимирующей функции методом
наименьших квадратов.
Задача:
методом наименьших квадратов получить
аппроксимирующую функцию и построить
график.
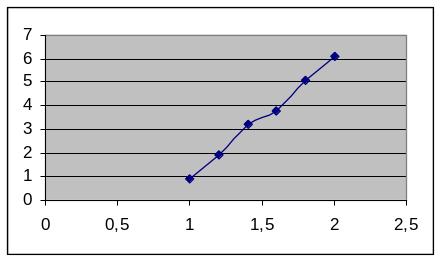
Таблица
зависимости значений функции от аргумента
|
X |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
Y |
0,9 |
1,9 |
3,2 |
3,8 |
5,1 |
6,1 |
Ручной
счет:
Будем
получать функцию вида
Находя
частные производные, получим систему
уравнений:
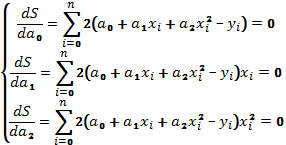
Найдем
коэффициенты:
(n+1)=6
|
x |
x^2 |
x^3 |
x^4 |
y |
y*x |
y*x^ |
|||
|
1 |
1 |
1 |
1 |
0,9 |
0,9 |
0,9 |
|
|
1,2 |
1,44 |
1,728 |
2,0736 |
1,9 |
2,28 |
2,736 |
|
|
1,4 |
1,96 |
2,744 |
3,8416 |
3,2 |
4,48 |
6,272 |
|
|
1,6 |
2,56 |
4,096 |
6,5536 |
3,8 |
6,08 |
9,728 |
|
|
1,8 |
3,24 |
5,832 |
10,4976 |
5,1 |
9,18 |
16,524 |
|
|
2 |
4 |
8 |
16 |
6,1 |
12,2 |
24,4 |
|
|
9 |
14,2 |
23,4 |
39,9664 |
21 |
35,12 |
60,56 |
Сумма:
6a
0 +9
a
1+14,2
a
2 =21
9
a
0+14,2
a
1 +23,4
a
2 =35,12
14,2
a
0 +23,4
a
1 +39,9664
a
2 =60,56
6a
0 +9
a
1+14,2
a
2 =21
(*9)
9
a
0+14,2
a
1 +23,4
a
2 =35,12
(*6)
14,2
a
0 +23,4
a
1 +39,9664
a
2 =60,56
6
a
0 +9
a
1+14,2
a
2 =21
( *14,2)
-4,2 a
1 +12,6
a
2 =-21,72
14,2
a
0 +23,4
a
1 +39,9664
a
2 =60,56
(*6)
6
a
0 +9
a
1+14,2
a
2 =21
-4,2 a
1 -12,6
a
2 =-21,72
-12,6
a
1 -38,1584
a
2 =-65,
16
В
результате
получаем
:
6
a
0 +9
a
1+14,2
a
2 =21
-4,2 a
1 -12,6
a
2 =-21,72
0б3584
a
2 =0
a
2 =0
a
1 =5,17
a
0 =-4,257
Коэффициенты
вычислены, подставим их в уравнение:
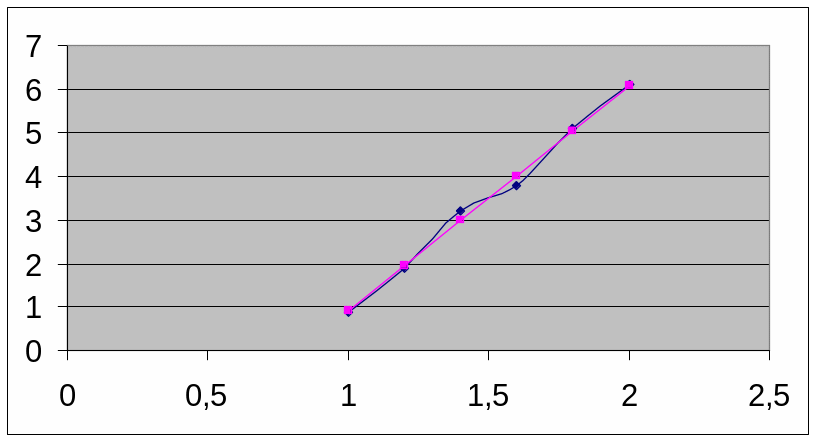
Построим
график полученной функции в Excel:
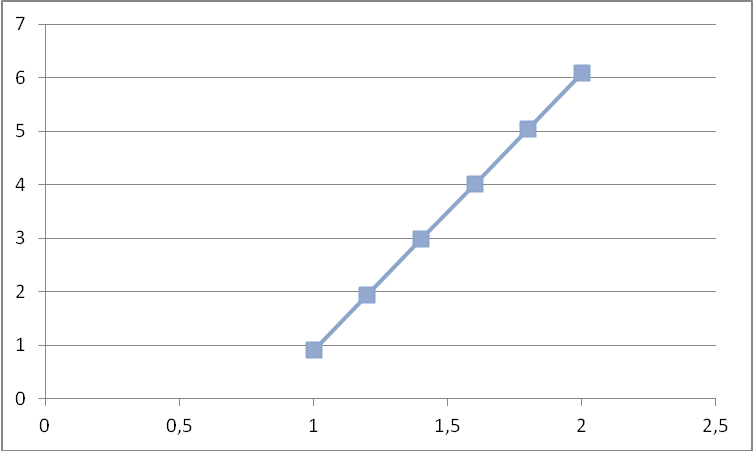
Подставляя
в полученную функцию табличные значение
x, посмотрим на отклонения значений
функции от табличных:
|
X |
Y |
Yвыч |
|Yвыч-Yтабл| |
|
1 |
0,9 |
0,9133 |
0,013 |
|
1,2 |
1,9 |
1,947 |
0,047 |
|
1,4 |
3,2 |
2,981 |
0,219 |
|
1,6 |
3,8 |
4,015 |
0,215 |
|
1,8 |
5,1 |
5,049 |
0,051 |
|
2 |
6,1 |
6,083 |
0,017 |
ϐ=√(0,013
2/5)+
(0,047)
2/5+(0,219)
2/5++(0,215)2/5+(0,051)
2/5+(0,017)
2/5
=0,141035
Угол
отклонение :
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Использование интерполяции
- Способ 1: интерполяция для табличных данных
- Способ 2: интерполяция графика с помощью его настроек
- Способ 3: интерполяция графика с помощью функции
- Вопросы и ответы
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Использование интерполяции
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
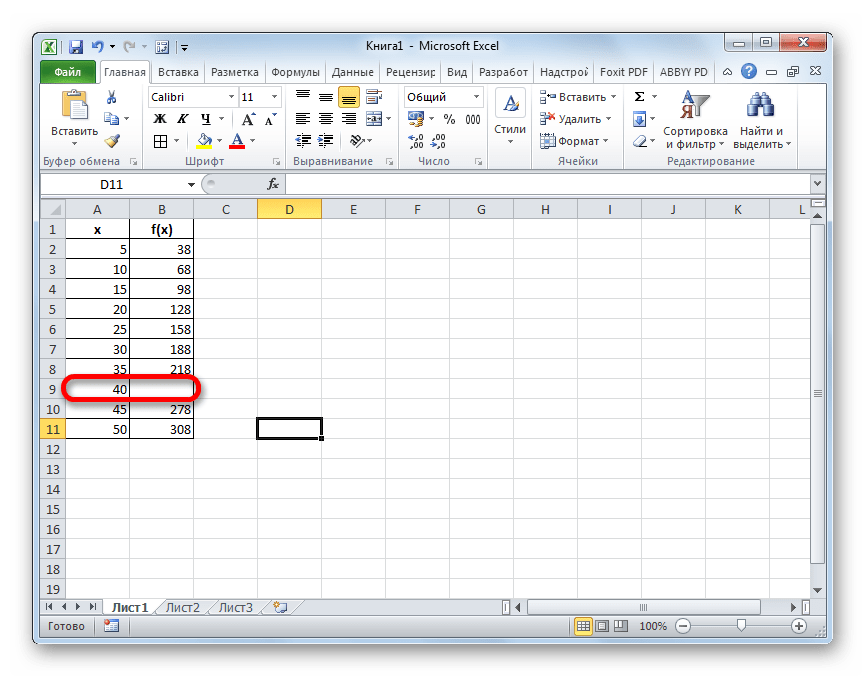
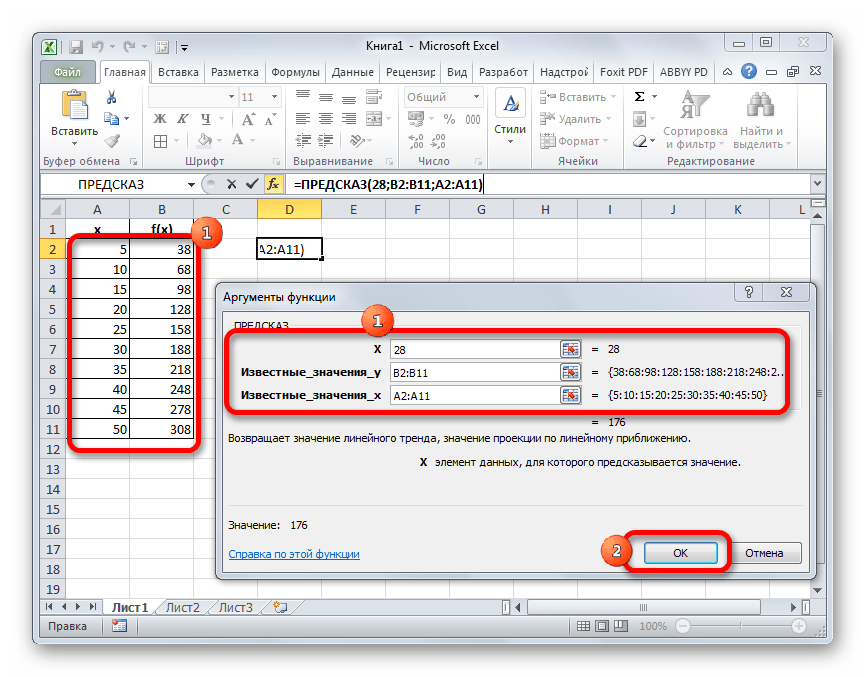
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.
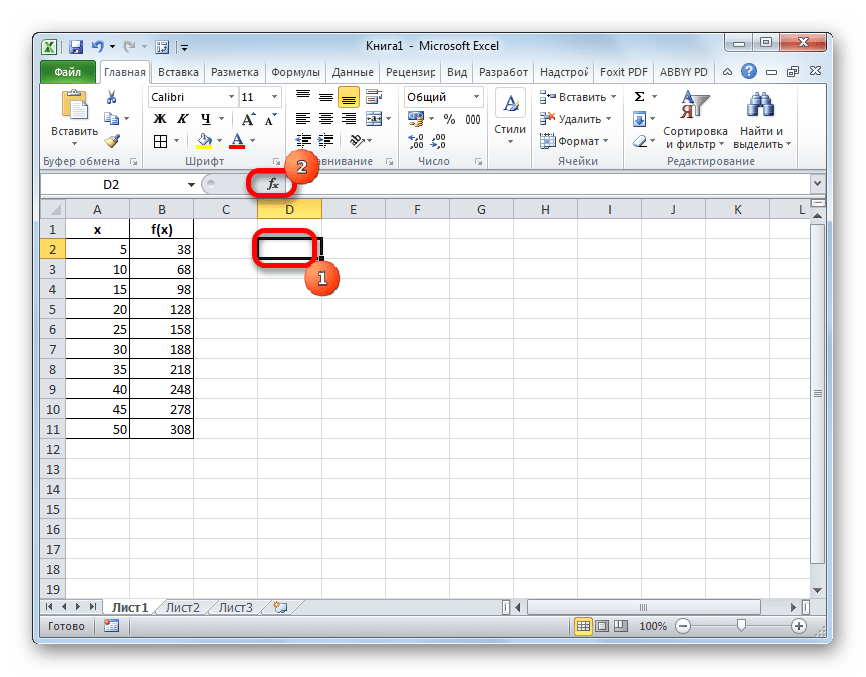
- Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.
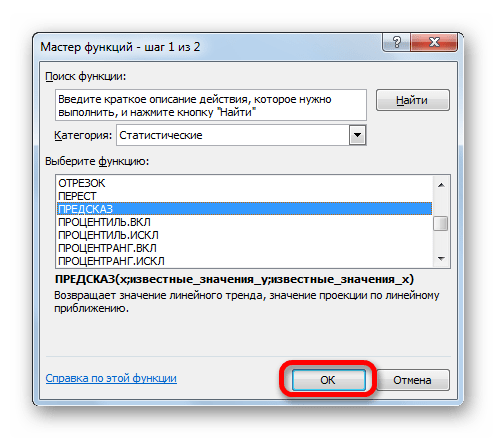
- Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».
- Запускается окно аргументов функции ПРЕДСКАЗ. В нем имеется три поля:
- X;
- Известные значения y;
- Известные значения x.
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.
После того, как все нужные данные введены, жмем на кнопку «OK».
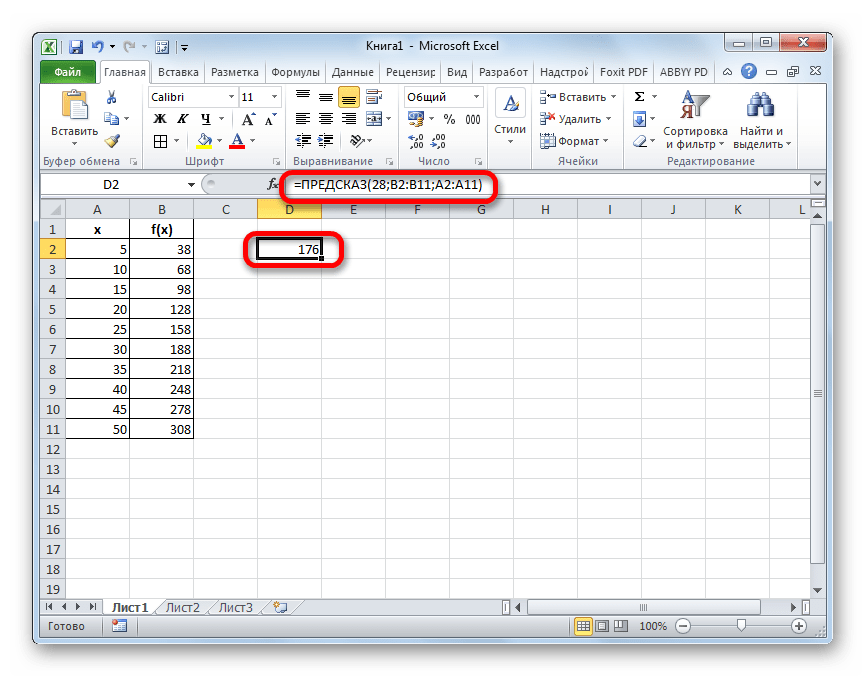
- Искомое значение функции будет отображено в той ячейке, которую мы выделили ещё в первом шаге данного способа. В результате получилось число 176. Именно оно и будет итогом проведения процедуры интерполяции.
Урок: Мастер функций в Экселе
Способ 2: интерполяция графика с помощью его настроек
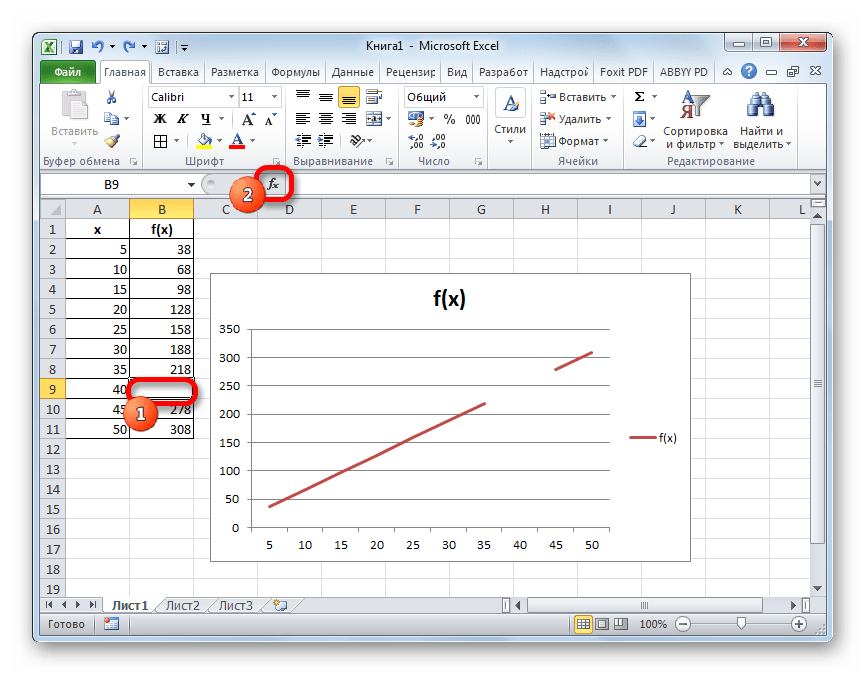
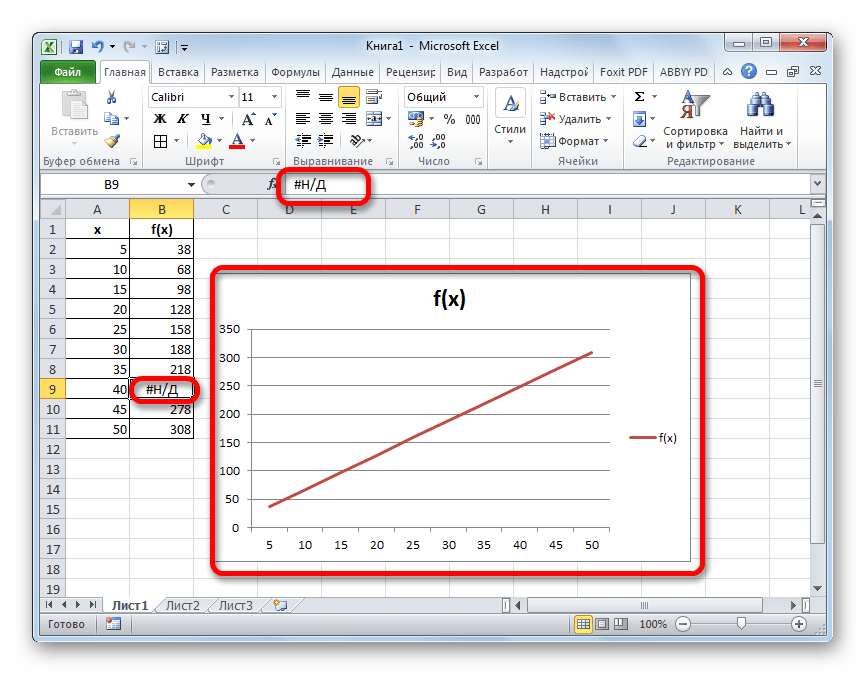
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
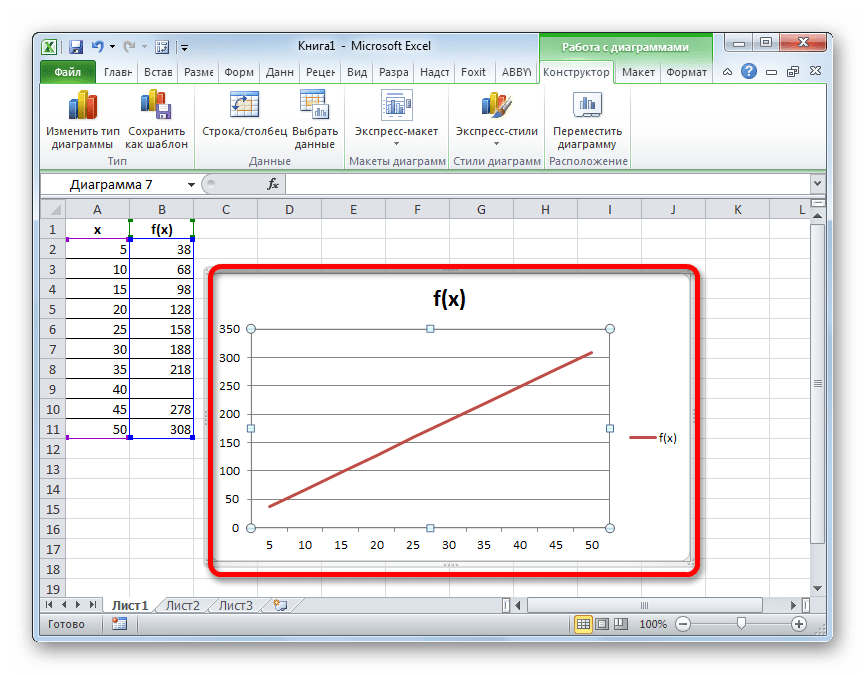
- Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
- Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.
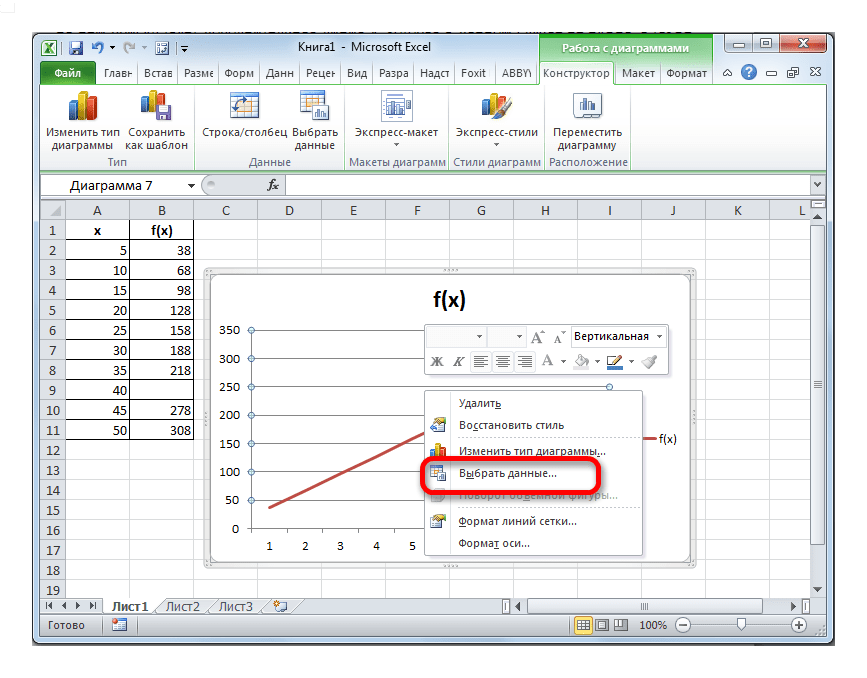
- Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».
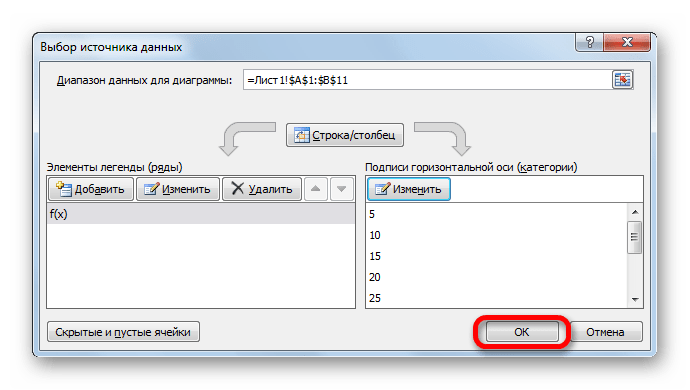
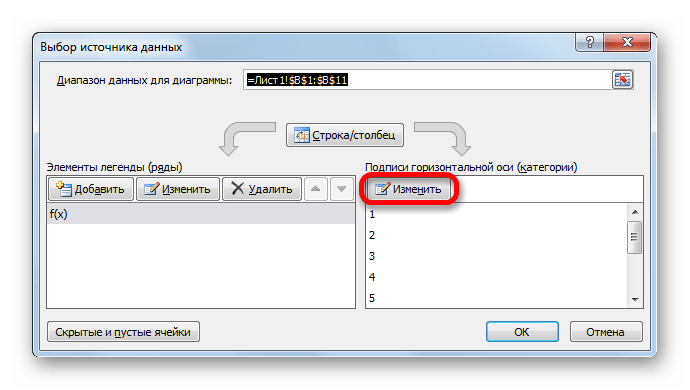
- Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».
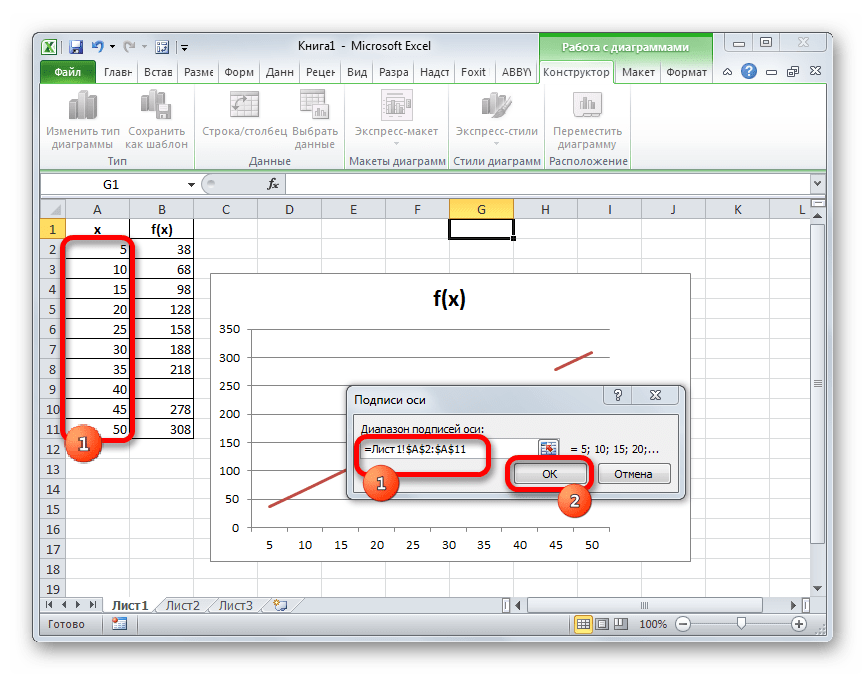
- Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле «Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK».
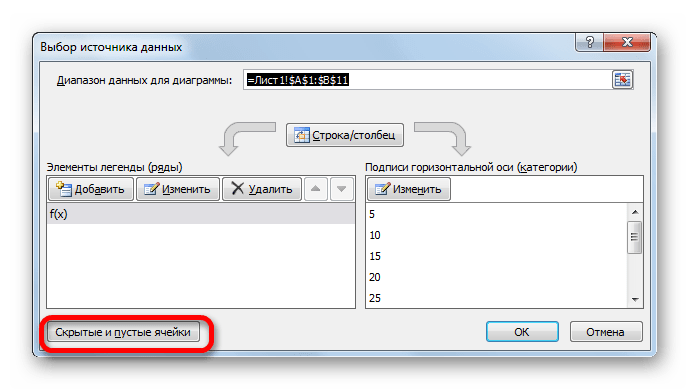
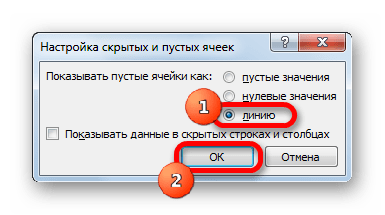
- Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.
- Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».
- После возвращения в окно выбора источника подтверждаем все сделанные изменения, щелкнув по кнопке «OK».
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Урок: Как построить график в Excel
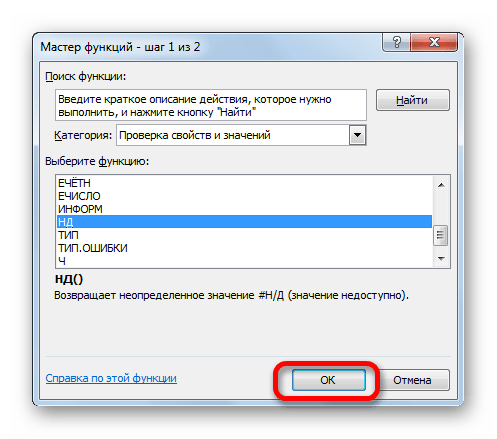
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
- После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».
- Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
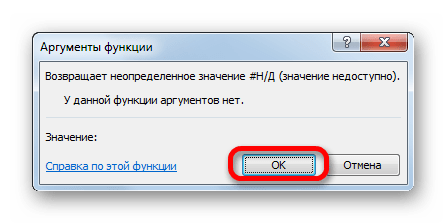
- У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
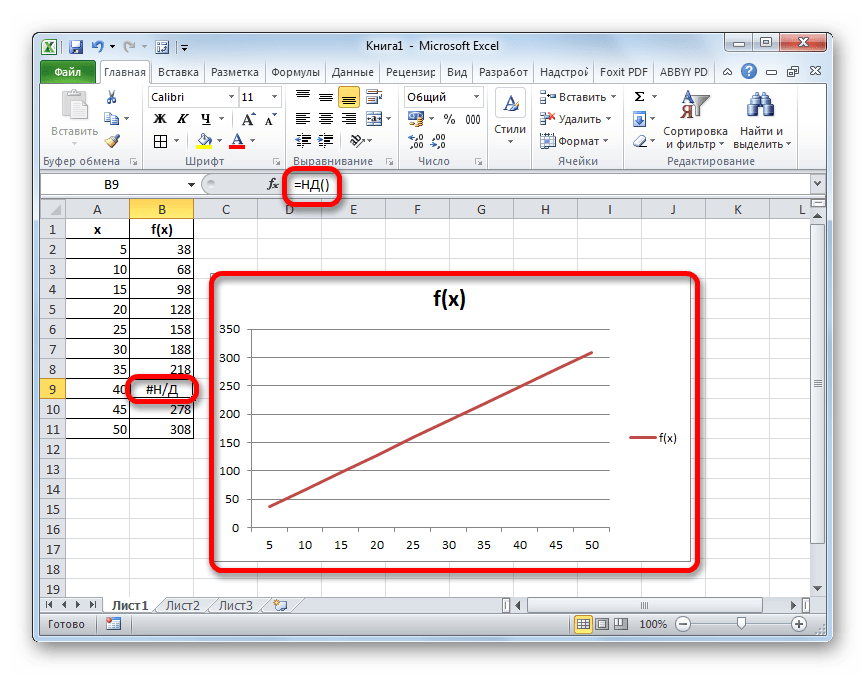
- После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Еще статьи по данной теме:
Помогла ли Вам статья?
Дана таблица значений функции y = f(x)
|
x |
x0 |
x1 |
… |
xn |
|
y |
y0 |
y1 |
… |
yn |
и два значения аргумента x= a и x = b, отличные от данных в таблице. Требуется с
помощью полиномов Ньютона третьей степени вычислить приближенные значения функции
y = f(x) в точках x = a и x = b,
т.е. f(a) и f(b).
Пример решения
|
x |
1.6 |
1.7 |
1.8 |
1.9 |
2.0 |
a = 1.92 |
|
y |
1.6416 |
2.3961 |
3.3536 |
4.5441 |
6.0000 |
b = 1.68 |
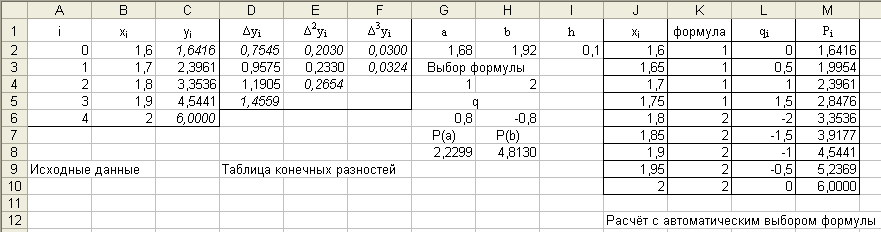
Построим таблицу конечных разностей:
|
i |
xi |
yi |
Δyi |
Δ2yi |
Δ3yi |
|
0 |
1.6 |
1.6416 |
0.7545 |
0.2030 |
0.0300 |
|
1 |
1.7 |
2.3961 |
0.9575 |
0.2330 |
0.0324 |
|
2 |
1.8 |
3.3536 |
1.1905 |
0.2654 |
|
|
3 |
1.9 |
4.5441 |
1.4559 |
||
|
4 |
2.0 |
6.0000 |
Поскольку точка b =
1.68 находится ближе к началу таблицы, а точка a = 1.92 – ближе к концу таблицы,
то для нахождения значения f(b) будем использовать первый полином
Ньютона, а для нахождения f(a) – второй. Ближайшее меньшее к точке
b значение узла таблицы = 1.6, а ближайшее большее к точке a = 2.
Выпишем первый и второй полиномы
третьей степени:
Скриншот реализации задачи в Excel показан ниже. Значения полинома вычисляются в точках a и b,
а также строятся значения полинома в пределах изменения x с шагом, равным 0.05 и автоматическим выбором первой или второй формулы.
Интерполяционный полином Ньютона — скачать пример в Excel XP/2003 (28 Кб)
Следует учесть, что в документе расчёт делается всегда по первым конечным разностям (от точек y0, y1), если точка a или b лежит ближе к началу интервала, и по последним (от точек y3, y4), если она ближе к концу. Есть и другие способы расчёта, берущие ближайший слева или справа узел.
Численные методы расчетов в Exel
Федеральное
агентство по образованию
Государственное
образовательное учреждение высшего профессионального образования
Северо-Западный
государственный заочный
технический
университет
Институт
управления производственными и
инновационными
программами
Кафедра
информатики
Контрольная
работа по дисциплине
«Математика.
Часть 2.»
Тема: “
Численные методы и расчеты в EXCEL.”
Задача 1. Интерполяция функции с равноотстоящими узлами.
Анализ и
прогнозирование в EXCEL.
Задача 2. Решение систем уравнений в EXCEL.
Задача 3. Комплексные числа.
Выполнила студентка: Шестакова Мария
Дмитриевна
ИУПиИП
Курс: II
Специальность: 80502.65
Шифр: 578030493
Преподаватель: Ходоровская Валентина
Сергеевна
Подпись преподавателя:
Санкт-Петербург
2007
Тема .
Численные методы и расчеты в EXCEL.
Задача 1.
Интерполяция функции с равноотстоящими узлами.
Анализ и прогнозирование в EXCEL.
I. Написать выражение для интерполяционного полинома Ньютона.
II. Составить программу для вычисления значения функции в заданных точках
x1 ; x2 ; x3 ; x4
:
1) при помощи полинома Ньютона для реализации
ее в EXCEL ;
2) при помощи функций, осуществляющих прогноз вычислений
(ТЕНДЕНЦИЯ и ПРЕДСКАЗАНИЕ).
Функция задана таблицей с равноотстоящими узлами:
x
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
y
0.860
0.819
0.779
0.741
0.705
0.670
0.638
0.606
0.577
0.549
Значения
x1 = 0.149
x2 = 0.240
x3
= 0.430
x4 = 0.560
Основные понятия.
Цель работы: научиться пользоваться программой EXCEL
для получения аналитической зависимости по экспериментальным данным и изучение
режимов экстраполяции данных в EXCEL.
Задача интерполяции сводится к требованию точного совпадения в узловых
точках функции и ее приближения, где число определяемых параметров
аппроксимирующей зависимости равно числу точек. При выборе данного критерия
задача сводится к построению интерполяционных многочленов (полиномов).
По определению интерполяция — это отыскание промежуточных значений
величины по некоторым известным ее значениям. Само слово интерполяция
происходит от латинского “interpolation”, что в переводе
значит “изменение, переделка”.
Экстраполяция — это процедура аналогичная интерполяции, но
при условии, что x лежит вне интервала (x0 , xn) . Происходит от “экстра…” и
латинского “polio”, что значит “приглаживаю, изменяю”.
Аппроксимация — это замена одних математических объектов
(например, чисел или
функций) другими, более простыми и в том или ином смысле
близкими к исходным(например, кривых линий близкими к ним ломаными). Слово происходит от
латинского “approximo”, что значит “приближаюсь”.
Графически задача интерполяции заключается в том, чтобы
построить такую интерполирующую функцию, которая бы проходила
через все узлы интерполяции. Чаще всего в качестве интерполирующей
функции F (x) используются многочлены Pn
(x). Задача состоит в том, чтобы подобрать многочлен Pn (x),
обеспечивающий требуемую интерполяцию е.
Наиболее успешно для интерполяции используется полином
Ньютона, для записи которого в случае интерполяции
функции с равноотстоящими узлами используются конечные
разности.
Термин “полином” имеет то же значение, что и слово “многочлен”
и происходит от “поли…” — часть сложных слов,
указывающая на множество, всесторонний охват или разнообразный состав чего-либо
(от греческого “polys” – многий, многочисленный, обширный) и
латинского “nomen”, т.е. имя.
Конечной разностью первого порядка называется
разность:
Дyi = yi + 1 — yi
, i = 0,1, …. , n – 1
Аналогично определяются конечные разности второго
и более высоких порядков.
Интерполяционный полином Ньютона.
Интерполяционный многочлен Ньютона для
равноотстоящих узлов записывается в виде:
Pn (x) = y0 + (x-x0) · Дy0
/1!h + (x-x0)(x-x1) · ДІy0 /2!hІ+….+ (x—x0)(x—x1)…..(x—xn-1) · Дny0 / n!hn
Решение.
Выполнение задания I.
Напишем выражение для интерполяционного полинома
Ньютона для экспериментальных данных, приведенных в вышеуказанной
таблице. Конечные разности указаны в “Приложение 2”.
Из таблицы видно, что значения x являются равноотстоящими
узлами, так как возрастают равномерно с шагом h = 0,05.
Степень полинома определяется числом (порядком) конечных
разностей ( в данном случае их девять ).
Pn(x) = P9(x)= y0 + (x-x0)
Дy0 / 1!h + (x-x0) (x-x1) ДІy0
/2!h2+..
..+
(x-x0)(x-x1)
(x-x2) (x-x3) (x-x4) (x-x5) (x-x6)
(x-x7) (x-x8) (x-x9) Д9y0 / 9!h9 =
0,860
+ (x- 0,15) (-0,041) / 1! · 0,05 + (x- 0,15) (x- 0,20) · 0,001 /
2! · 0,05
2 +
(x-
0,15) (x- 0,20) (x- 0,25) · 0,001 / 3! · 0,05 3 +(x-
0,15) (x- 0,20) (x- 0,25) (x- 0,30) · (-0,001) / 4! · 0,05
4 +
(x-
0,15) (x- 0,20) (x- 0,25) (x- 0,30)(x- 0,35) · 0 / 5! ·
0,05 5 +
(x-
0,15) (x- 0,20) (x- 0,25) (x- 0,30)(x- 0.35)(x- 0,40) · 0,004 / 6! ·
0,05 6
+
(x-
0,15) (x- 0,20) (x- 0,25) (x- 0,30) (x- 0,35) (x- 0,40) (x- 0,45) ·(-0,016) /
7! 0,05 +
(x-
0,15) (x- 0,20) (x- 0,25) (x- 0,30) (x- 0,35) (x- 0,40) (x- 0,45) ( x-
0,50) · 0,047 / 8! · 0,05 8
+
(x— 0,15) (x— 0,20) (x— 0,25) (x— 0,30) (x— 0,35) (x— 0,40) (x— 0,45) (x— 0,50) (x— 0,55) · (-0,119) / 9! · 0,05 9.
Выполнение задания II.
1)Составление программы для вычисления значений
функции в заданных точках при помощи полинома Ньютона.
Шаг первый:
Подготовка исходных данных электронной таблицы в EXCEL:
а) Введем текстовые и числовые константы (ячейки A1 : N4).
б) Введем номера по порядку в ячейки A5 : A14.
в) Введем исходные данные в ячейки B5 : C14.
Таким образом подготовлена таблица для выполнения работы.
Шаг второй:
Ввод формул:
а) Ввод формул для вычисления конечных разностей первого порядка:
а.1) в ячейку D5 введем формулу для вычисления Дy0
= y1 – y0, которая примет вид: =C6–C5;
a.2) копируем эту формулу в ячейки D6 : D13. В результате
в ячейке D6
получаем формулу =C7-C6 (т.е.Дy1 =y2
— y1 = 0,779 – 0,819 = -0,040),в ячейке D7
получаем формулу =C8-C7 (т.е. Дy2 = y3
– y2 = 0,741 – 0,779= -0,038) и т.д. до ячейки D13, где
получаем формулу
=C14-C13 (т.е. Дy8 = y9 – y8 =
0,549 – 0,577= -0,028)
б) Ввод формул для вычисления конечных
разностей второго порядка:
б.1) в ячейку E5 копируем формулу из
ячейки D5. В ячейке E5 появится формула
=D6-D5 (т.е. ДІy0 = Дy1 — Дy0
= -0,040 — ( -0,041) = 0,001). Копируем эту формулу в ячейки E6 :
E12.
В ячейке E12 получаем формулу =D13 — D1 (т.е. ДІy7
= Дy8 — Дy7= — 0,028 — ( -0,029) = 0,001).
в) Ввод формул для вычисления конечных разностей вплоть до
девятого порядка:
для вычисления всех конечных разностей необходимо ввести только
одну формулу(в ячейке D5), все
остальные будут получены копированием, т.е. из ячейки E5 копируем
формулу в ячейку F5, из F5 в G5 и т.д.
Отображение в режиме формул см. в “Приложении 1”.
Отображение в режиме значений см. в “Приложении 2”.
Шаг третий:
Ввод формул:
а) Ввод формул для вычисления промежуточных коэффициентов:
а.1) для вычисления первого промежуточного коэффициента (x-x0/1!h)
в ячейку M5 введем формулу
=($N$2 — B5) / (A5 + 1) / $F$2. В ячейке N2 находится текущее
значение x. При копировании адрес этой ячейки изменять
нельзя, поэтому мы используем абсолютный адрес (значок $). В ячейке F2
находится шаг интерполяции, адрес этой ячейки тоже абсолютный
(значок $).
а.2) для вычисления второго промежуточного коэффициента
(x-x0) (x- x1)/2!hІ = (x-x0)/1·h · (x-x1)/
2·h = a · b,
где a коэффициент в ячейке M5, a = (x-x0)/1h,
b коэффициент, на который нужно умножить M5, b = (x-x1)
/ 2h,
вводим в M6 формулу: =M5*($N$2 – B6) / (A6 + 1) / $F$2.
а.3) после ввода данных в M5 и M6, для вычисления остальных промежуточных
коэффициентов
копируем формулу из M6 в остальные 7 нижестоящие ячейки. Вячейке M7 мы
увидим формулу:
=M6*($N$2 – B7) / (A7 + 1) / $F$2 , в ячейке M8 мы увидим
формулу: =M7*($N$2 – B8) / (A8 + 1) / $F$2 и
т.д.
Шаг четвертый:
Ввод формул:
а) Ввод формул для вычисления полинома Ньютона:
а.1) для вычисления первого полинома Ньютона,
который равен (x-x0) · Дy0 / 1!h = (x-x0)
/ 1h ·Дy0, содержимое ячейки M5 надо умножить на содержимое
ячейки D5, где хранятся конечные разности первого порядка. Вводим
в ячейку N5 формулу =M5*D$5. Знак $ перед номером строки
необходим, т.к. в полиноме Ньютона находятся только конечные
разности с индексом ноль, т.е. все конечные разности берутся
только из строки с номером 5;
а.2) для ввода остальных членов полинома Ньютона копируем
формулу из N5 в остальные 8 нижестоящих ячеек (включительно по N13). Получаем
в N6 формулу =M6*E$5, в N7 формулу =M7*F$5, в N8
формулу =M8*G$5 и т.д. до ячейки N13.
Шаг пятый:
Ввод формул:
а) Ввод формул для вычисления суммы коэффициентов полинома
Ньютона:
а.1) объединим ячейки A16 : M16, затем в объединенные ячейки
введем комментарий
«Сумма коэффициентов полинома”;
а.2) в ячейку N16 вводим формулу =СУММ(N5:N13).
Теперь в N16 будет сумма всех членов полинома Ньютона, кроме y0.
При x = 0,149 в ячейке N16 получается
число 0,001.
Шаг шестой:
Ввод формул:
а) Ввод формул для вычисления значения полинома:
а.1) объединим ячейки A18 : M18, затем в объединенные ячейки
введем комментарий «Значение полинома»;
а.2) в ячейку N18 вводим формулу =N16+C5. В ячейке
N18 появится число 0,861 , которое и есть значение полинома,
вычисленное в точке x = 0,149
Шаг седьмой:
Вычисление сумм коэффициентов полинома и значений полинома
при x = 0,240; x = 0,430;
x = 0,560.
а) в ячейку N2 вводим 0,240. Результат:
в ячейке N16 — (-0,073); в ячейке N18 — (0.787);
б) в ячейку N2 вводим 0,430. Результат:
в ячейке N16 — (-0,209); в ячейке N18 —
(0,651);
в) в ячейку N2 вводим 0.560. Результат:
в ячейке N16 — (-0,287); в ячейке N18 — (0,573).
Шаг восьмой:
Для удобства полученные данные занесем в нашу таблицу.
Таблицы прилагаются. Режим формул — “Приложение 1”. Режим
значений — “Приложение 2.
2)Составление программы для вычисления значений функции в
заданных точках при помощи функций, осуществляющих прогноз вычислений
(ТЕНДЕНЦИЯ и ПРЕДСКАЗАНИЕ).
Экстраполяция (прогнозирование) с помощью функции
аппроксимации кривой.
Табличный процессор EXCEL предоставляет возможность аппроксимации
с использованием “функций аппроксимации кривой”
Пусть в узлах x0 , x1, …, x n
известны значения f(x0), f(x1), … ,f(x n).
Необходимо осуществить экстраполяцию (прогнозирование), т.е.
вычислить значения f(x n+1), f(x n+2),
… .
В категории Статистические функции EXCEL для этого
используются две функции: ТЕНДЕНЦИЯ и ПРЕДСКАЗАНИЕ,
осуществляющие линейную аппроксимацию кривой для данных массивов
x (x0 , x1 , … , x n) и y (y0
,y1 , … , y n) методом наименьших квадратов.
Функция ТЕНДЕНЦИЯ имеет структуру:
ТЕНДЕНЦИЯ (y массив, x массив, x
список)
y массив , x массив — даны из условия.
x список — это те значения x, для которых
требуется сосчитать значения функции f(x).
Функция ПРЕДСКАЗАНИЕ имеет структуру:
ПРЕДСКАЗАНИЕ ( x; y массив; x массив)
После аппроксимации эта функция возвращает только одно
прогнозируемое значение y (для одного из заданных значений
аргументов.
Работа с функцией ТЕНДЕНЦИЯ.
Шаг первый:
Создадим электронную таблицу в EXCEL , используя исходные данные.
Шаг второй:
Для того, чтобы поместить результат в список итоговых ячеек C6:F6,
выделим эти ячейки.
Шаг третий:
Далее необходимо щелкнуть по пиктограмме Мастер функций.
Шаг четвертый:
а) В первом окне выберем категорию Статистические,
функцию ТЕНДЕНЦИЯ,
затем щелкнем по OK.
б) В окне “Известные значения y” введем
адрес блока ячеек C3:L3.
в) В окне “Известные значения x”
введем адрес блока ячеек C2:L2.
г) В окне “Новые значения x” укажем
адрес блока ячеек C5:F5.
Шаг пятый:
Для подтверждения этой функции одновременно нажмем клавиши SHIFT /
CTRL и ENTER. В ячейках C6:F6 мы увидим прогноз.
В режиме формул:в ячейке C6 — =ТЕНДЕНЦИЯ(C3:L3;C2:L2;C5)
в ячейке D6 — =ТЕНДЕНЦИЯ(C3:L3;C2:L2;D5)
в ячейке E6 — =ТЕНДЕНЦИЯ(C3:L3;C2:L2;E5)
в ячейке F6 — =ТЕНДЕНЦИЯ(C3:L3;C2:L2;F5)
В режиме значений: в ячейке C6 — 0,8610
в ячейке D6 — 0,7951
в ячейке E6 — 0,6576
в ячейке F6 — 0,5635
Таблицы прилагаются.
Режим формул — “Приложение
3”. Режим значений “Приложение 4”.
Работа
с функцией ПРЕДСКАЗАНИЕ.
Шаг первый:
Создадим электронную таблицу в EXCEL, используя исходные
данные.
Шаг второй:
Для размещения результата активизируем ячейку С6.
Шаг третий:
а) При помощи Мастера функций вызовем функцию ПРЕДСКАЗАНИЕ,
категория Статистические.
б) В окне “x” укажем адрес ячейки C6.
в) В окне “Известные значения y” укажем
адрес блока ячеек C3:L3.
г) В окне “Известные значения x” укажем
адрес блока ячеек C2:L2.
Шаг четвертый:
Для подтверждения этой функции щелкнем по OK. В ячейке C6
появится результат. Для появления результата в остальных ячейках, проделаем
все то же самое, поочередно активизируя ячейки D6, E6, F6.
В результате мы увидим:
В режиме формул:
в ячейке C6 — =ПРЕДСКАЗ(C5;C3:L3;C2:L2)
в ячейке D6 — =ПРЕДСКАЗ(D5;C3:L3;C2:L2)
в ячейке E6 — =ПРЕДСКАЗ(E5;C3:L3;C2:L2)
в ячейке F6 — =ПРЕДСКАЗ(F5;C3:L3;C2:L2)
В режиме значений: в ячейке C6 — 0,8506
в ячейке D6 — 0,7877
в ячейке E6 — 0,6564
в ячейке F6 — 0,5665
Таблицы прилагаются. Режим формул — “Приложение 5”. Режим
значений — “Приложение 6”.
Итоговая сравнительная таблица.
Для сравнения значений функции в точках:
x 1 = 0,149;
x 2 = 0,240;
x 3 = 0,430;
x 4 = 0,560;
полученных при помощи трех разных способов:
1
полинома Ньютона,
2
функции ТЕНДЕНЦИЯ,
3
функции ПРЕДСКАЗАНИЕ;
создадим сравнительную таблицу,
x
Значение полинома
Ньютона
Прогнозирование значения функции при помощи функций:
ТЕНДЕНЦИЯ
ПРЕДСКАЗАНИЕ
0,149
0,861
0,86*
0,861
0,86*
0,8506
0,85*
0,240
0,787
0,79*
0,795
0,80*
0,7877
0,79*
0,430
0,651
0,65*
0,658
0,66*
0,6564
0,66*
0,560
0,573
0,57*
0,564
0,56*
0,5665
0,57*
*Результаты
вычислений округлены до двух знаков после запятой.
Вывод: значение функции в заданных четырех точках мы получили тремя
разными способами. Для наглядности все полученные данные мы свели в итоговую
сравнительную таблицу. Видно, что результаты получились не совсем одинаковые.
Но однако в целом, отклонения в значениях в пределах 0,01 , что вполне
допустимо для наших данных. Для того, чтобы получить более точные значения
функции в определенной точке, необходимо, чтобы исходные данные были
представлены более широким спектром узлов.
Задача 2.
Решение систем уравнений в EXCEL.
Решить заданную систему уравнений:
1) методом обратной матрицы;
2) методом простых итераций.
0,1 x1 + 4,6 x2 + 7,8 x3
= 9,8
2,8 x1 + 6,1 x2 + 2,8 x3
= 6,7
4,5 x1 + 5,7 x2 + 1,2 x3
= 5,8
Цель работы: научиться решать в EXCEL системы
конечных уравнений методом обратной матрицы и простых итераций.
Основные понятия.
Уравнение — это математическая
запись задачи о разыскании значений аргументов, при которых значения данных
функций равны. Аргументы, от которых зависят функции, называются неизвестными,
а значения неизвестных, при которых значения функций равны, называются
решениями (корнями).
Матрица — это прямоугольная таблица
каких-либо элементов aik (чисел, математических выражений),
состоящая из m строк и n столбцов. Если m = n , то матрица называется
квадратной.
Детерминант (определитель) — это число detA, которое можно
сопоставить квадратной матрице А.
Минором некоторого элемента аij определителя n-го
порядка называется определитель n первого порядка, полученный из исходного
путем вычеркивания строки и столбца, на пересечении которых находится выбранный
элемент.
Алгебраическим дополнением элемента аij определителя
называется его минор, взятый со знаком “+”, если сумма “ i+j” четное число, и
со знаком “-“ , если эта сумма нечетная.
Итерация — это повторное применение
каких-либо математических операций. Происходит от латинского “iteratio”
,что в переводе значит “повторение”.
Решение.
1). Математический расчет решения системы уравнений методом обратной
матрицы.
Дана система трех линейных уравнений с тремя неизвестными.
а). Рассмотрим матрицы:
— матрица системы (составлена из коэффициентов при неизвестных):
0,1 4,6 7,8
А = 2,8 6,1 2,8
4,5 5,7 1,2
— матрица неизвестных:
x1
X = x2
x3
— матрица свободных членов:
9,8
B = 6,7
5,8
б). Найдем детерминант (определитель) матрицы
А.
По определению: det A = a11
· A11 + a12 · A12 + a13 · A13
,
где a11 , a12 , a13
— элементы первой строки матрицы A,
A11 , A12 , A13
— их алгебраические дополнения.
— если detA = 0, то обратной матрицы не
существует;
— если detA ≠ 0, то обратная матрица существует.
Для того, чтобы найти детерминант необходимо сосчитать алгебраические
дополнения.
По определению: Aik = (-1)i+k · Mik
,
где i — номер строки матрицы,
k — номер столбца матрицы,
M — минор.
— если сумма i+k четная, то Aik = 1 · Mik
A11 = 6,1 · 1,2 — 5,7 · 2,8 = 7,32
— 15,96 = — 8,64
A12 = 2,8 · 1,2 — 4,5 · 2,8 = 3,36
— 12,6 = 9,24
A13 = 2,8 · 5,7 — 4,5 · 6,1 = 15,96
— 27,45 = -11,49
Теперь мы можем сосчитать детерминант.
detA = 0,1 · (-8,64) + 4,6 · 9,24 + 7,8 · (-11,49) = -0,864 +
42,504 — 89,622 = — 47,982
detA ≠ 0 => обратная матрица существует
и можно продолжать вычисления.
в). Найдем обратную матрицу А-1.
По определению:
A11 A21 A31
A-1
= A12 A22 A32 · 1/ detA ,
A13
A23 A33
где А11 , …, А33 —
алгебраические дополнения матрицы А.
Для нахождения обратной матрицы А-1, сначала
сосчитаем все алгебраические дополнения матрицы А:
A21 = 4,6 7,8 = 4,6 · 1,2 — 7,8 · 5,7 =
5,52 — 44,46 = + 38,94
5,7 1,2
A22 = 0,1 7,8 = 0,1 · 1,2 — 7,8 · 4,5 = 0,12
— 35,1 = — 34,98
4,5 1,2
A23 = 0,1 4,6 = 0,1 · 5,7 — 4,6 · 4,5 = 0,57
— 20,7 = + 20,13
4,5 5,7
A31 = 4,6 7,8 = 4,6 · 2,8 — 7,8 · 6,1 =
12,88 — 47,58 = — 34,7
6,1 2,8
A32 = 0,1 7,8 = 0,1 · 2,8 — 2,8 · 7,8 =
0,28 — 21,84 = + 21,56
2,8 2,8
A33 = 0,1 4,6 = 0,1 · 6.1 — 4,6 · 2,8 =
0,61 — 12,88 = — 12,24
2,8 6,1
1/detA = 1 / — 47,982 = — 0,0208411
— 8,64 38,94 — 34,7 0,1800675 — 0,8115543
0,72318786 A-1 = —
0,0208411 · 9,24 — 34,98 21,56 = — 0,1925722 0,7290234
0,44933516
— 11,49 20,13 — 12,27 0,2394647 — 0,4195323
0,25572089
Чтобы узнать правильно ли мы нашли обратную матрицу, необходимо
сделать проверку. Если выполняется равенство:
A-1 · A = E, где E —
единичная матрица, то обратная матрица найдена верно.
0,1800675 — 0,8115543 0,7231879
0,1 4,6 7,8
A-1 · A = — 0,1925722 0,7290234
— 0,4493352 · 2,8 6,1 2,8
0,2394647 — 0,4195323 0,2557209
4,5 5,7 1,2
Произведем промежуточные вычисления:
С11 = 0,1800675 · 0,1 + (-0,8115543) · 2,8 + 0,7231879 ·
4,5 = 1
C12 = 0,1800675 · 4,6 + (-0,8115543) · 6,1 + 0,7231879 ·
5,7 = 0
C13 = 0,1800675 · 7,8 + (-0,8115543) · 2,8 + 0,7231879 ·
1,2 = 0
C21 = (-0,1925722) · 0,1 + 0,7290234 · 2,8 + (-0,4493352) ·
4,5 = 0
C22 = (-0,1925722) · 4,6 + 0,7290234 · 6,1 + (-0,4493352) ·
5,7 = 1
C23 = (-0,1925722) · 7,8 + 0,7290234 · 2,8 + (-0,4493352) ·
1,2 = 0
C31 = 0,2394647 · 0,1 + (-0,4195323) · 2,8 + 0,2557209 · 4,5
= 0
C32 = 0,2394647 · 4,6 + (-0,4195323) · 6,1 + 0,2557209 ·
5,7 = 0
С33 = 0,2394647 · 7,8 + (-0,4195323) · 2,8 + 0,2557209 ·
1,2 = 1
1 0 0
A-1 · A = 0 1
0 = E
0 0 1
Обратную матрицу нашли верно.
г). Найдем матрицу X (матрицу неизвестных).
По определению: X = A-1 · B ,
где B — исходная матрица B (матрица свободных членов).
0,1800675 — 0,8115543 0,7231879 9,8
0,521737
X = — 0,1925722 0,7290234 — 0,4493352 · 6,7
= 0,391105
0,2394647 — 0,4195323 0,2557209 5,8
1,019069
Матрицу X нашли, соответственно корни уравнений:
x1 = 0,521737
x2 = 0,391105
x3 = 1,019069
д). Проверка. Подставим в исходную систему уравнений
полученные значения:
0,1 · 0,521737 + 4,6 · 0,391105 + 7,8 · 1,019069 = 0,0521737 +
1,799083 + 7,9487382 = 9,7999949 = 9,8
2,8 · 0,521737 + 6,1 · 0,391105 + 2,8 · 1,019069 = 1,4608636 +
2,385745 + 2,8533932 = 6,6999742 = 6,7
4,5 · 0,521737 + 5,7 · 0,391105 + 1,2 · 1,019069 = 2,3478165 +
2,229298 + 1,2229152 = 5,8000252 = 5,8
Система уравнений методом обратной матрицы решена верно.
1.1). Составление программы для решения системы уравнений методом
обратной матрицы в EXCEL.
Шаг первый:
Для решения системы уравнений в EXCEL необходимо подготовить
таблицу с исходными данными:
а). Введем текстовые и числовые константы (ячейки A1:E10).
Шаг второй:
Необходимо обратить матрицу А. Применяемая для
обращения матрицы функция МОБР возвращает массив значений, который
вставляется сразу в целый столбец ячеек.
а). Выделим ячейки А11:С13, куда будет помещена обратная матрица.
б). При помощи Мастера функций вызовем функцию МОБР,
категория Математические.
в). В окне “Массив” укажем адрес массива исходной
матрицы A6:C8.
г). Для того, чтобы вставить формулу во все выделенные ячейки
(A11:C13), нажмем одновременно клавиши Ctrl+Shift+Enter.
В ячейках A11:C13 появится:
— в режиме формул — =МОБР(А6:C8) ;
— в режиме значений — массив обратной матрицы.
Шаг третий:
Для умножения обратной матрицы на столбец свободных членов:
а). Выделим ячейки E11:E13.
б). При помощи Мастера функций выберем функцию МУМНОЖ,
категория Математические.
в). В окно “Массив 1” введем адрес массива обратной
матрицы A11:C13.
г). В окно “Массив 2” введем адрес массива матрицы
свободных членов E6:E8.
д). Для вставки Формулы во все выделенные ячейки (E11:E13),
нажмем одновременно клавиши Ctrl+Shift+Enter.
В ячейках E11:E13 появится:
— в режиме формул — =МУМНОЖ(А11:C13;E6:E8) ;
— в режиме значений — компоненты векторов решения x1 ,
x2 , x3 .
Таблицы прилагаются. Режим формул — “Приложение 7”. Режим
значений — “Приложение 8”.
1.2). Проверка — сравнение результатов, полученных разными
способами.
Для наглядности создадим сравнительную таблицу:
Математический расчет методом
обратной матрицы
Обращение матрицы в EXCEL
x1
0,521737
0,521737318
x2
0,391105
0,391104998
x3
1,019069
1,019069651
1.3). Вывод.
Сначала предложенную нам систему уравнений мы решили методом
обратной матрицы. Затем в EXCEL составили специальную
программу, позволяющую решить систему уравнений путем обращения
матрицы.
Для наглядности полученные результаты занесли в сравнительную таблицу.
Из таблицы видно, что результаты получились практически одинаковыми.
Отклонения в значениях расходятся в столь малых пределах, что являются
допустимыми для нашего случая. Однако это произошло из-за того, что при
выполнении математических расчетов значения округлялись.
Таким образом, мы выявили, что в EXCEL результаты
получаются более точные.
2) Решение заданной системы уравнений методом простых
итераций.
Для того, чтобы решить систему трех линейных уравнений методом
простых итераций, необходимо ее преобразовать так, чтобы диагональные
коэффициенты матрицы x1 , x2 , x3
были максимальными по модулю. Этим выполняется 1-е условие
сходимости итерационного процесса.
Заданная нам система имеет вид:
0,1x1
+ 4,6x2 + 7,8x3
= 9,8
2,8x1 + 6,1x2
+ 2,8x3 = 6,7
4,5x1 + 5,7x2 + 1,2x3
= 5,8
a) Достаточно хорошо видно, что для преобразования нам
достаточно только поменять местами первое и третье уравнения. Получится
система вида:
4,5x1 + 5,7x2 + 1,2x3
= 5,8
2,8x1 + 6,1x2
+ 2,8x3 = 6,7
0,1x1 + 4,6x2 + 7,8x3
= 9,8
б) Для решения системы уравнений методом простых итераций
необходимо представить полученную систему уравнений в итерационной
форме, записав каждое из трех уравнений в виде решения относительно
той неизвестной переменной, которая имеет наибольший по модулю коэффициент.
4,5x1 + 5,7x2 + 1,2x3
= 5,8
x1 = — 5,7x2 /
4,5 — 1,2x3 / 4,5 + 5,8 / 4,5
2,8x1 + 6,1x2 + 2,8x3
= 6,7
x2 = — 2,8x1 /
6,1 — 2,8x3 / 6,1 + 6,7 / 6,1
0,1x1 + 4,6x2 + 7,8x3
= 9,8
x3 = — 0,1x1 /
7,8 — 4,6x2 / 7,8 + 9,8 / 9,7
В итерационной форме получили систему:
x1 = — 5,7x2 / 4,5 — 1,2x3
/ 4,5 + 5,8 / 4,5
x2 = — 2,8x1 / 6,1
— 2,8x3 / 6,1 + 6,7 / 6,1
x3 = — 0,1x1 / 7,8 — 4,6x2 /
7,8 + 9,8 / 9,7
в) Проверка выполнения первого условия сходимости метода для
данной системы.
При использовании итерационного метода решения необходимо
обязательно проверить два условия сходимости метода для данной системы. Первое
условие у нас выполнено (диагональные коэффициенты матрицы x1
, x2 , x3 в полученной системе являются максимальными
по модулю).
г) Проверка выполнения второго условия сходимости метода для
данной системы (условие “НОРМА”).
Теперь необходимо проверить условие “НОРМА” (обозначается ║C║),
т.е. необходимо оценить сходимость метода для данной системы,
которая зависит только от матрицы коэффициентов [ C ]. Процесс
сходится только в том случае,если норма матрицы [ С ] меньше
единицы, т.е.
║C║=√Σaaj2
<1
В итерационной форме имеем систему:
x1 = — 5,7x2 / 4,5 — 1,2x3 / 4,5
+ 5,8 / 4,5
x2 = — 2,8x1 / 6,1 — 2,8x3 / 6,1
+ 6,7 / 6,1
x3 = — 0,1x1 / 7,8 — 4,6x2 /
7,8 + 9,8 / 7,8
или
x1 = 0 — 5,7x2 / 4,5 — 1,2x3
/ 4,5 + 1,288889
x2 = 2,8x1 / 7,8 — 0 — 2,8x3
/ 6,1 + 1,0983607
x3 = 0,1x1 / 7,8 — 4,6x2
/ 7,8 — 0 + 1,2564103
Проверка выполнения второго условия “НОРМА” :
0 — 5,7 / 4,5 — 1,2 / 4,5
[C] = — 2,8 / 6,1 0 — 2,8 / 6,1
— 0,1 / 7,8 — 4,6 / 7,8 0
║C║ = √ У aij2 < 1
║C║ = √ (-5,7 / 4,5)2 + (-1,2 / 4,5)2
+ (-2,8 / 6,1 )2 + (-2,8 / 6,1)2 + (-0,1 / 7,8)2
+ (-4,6 / 7,8)2
║C║= √ (-1,2666667)2 +(-0,2666667)2
+(-0,4590164)2 +(-0,4590164)2 +(-0,0128205)2
+(-0,5897436)2
║C║= √ (1,6044445) + (0,0711111) + (0,2106961) +
(0,2136961) + (0,0001691) + (0,3477975)
║C║ =√ 2,4449144
║C║ = 1,5636222 > 1
Таким образом, условие “НОРМА” не выполнено.
Вывод: так как второе условие сходимости итерационного
процесса не выполнено, то решение данной системы уравнений не
может быть получено методом простых итераций.
Задача 3.
Комплексные числа.
Даны два комплексных числа, записанные в показательной форме.
z1 = 3e -(р/4) i
z2 = е (р/4) i
1). Записать эти числа в тригонометрической форме;
2). Найти сумму z1 + z2
и произведение z1 · z2 ,
переведя их в алгебраическую форму записи;
3). Изобразить на комплексной плоскости операнды и результаты.
Основные понятия.
Комплексным числом называется выражение вида
z = x + iy , где
“x” и “y” — действительные числа,
“i” — символ, называемый мнимой единицей и
удовлетворяющий условию i2 = -1.
Операнд — величина, представляющая собой объект операции,
реализуемой ЭВМ в ходе выполнения программы вычислений.
Решение.
1). Тригонометрическая форма записи.
Положение точки z на комплексной плоскости однозначно
определяется не только декартовыми координатами x , y ,
но и полярными координатами r , ц. Воспользовавшись
связью декартовых и полярных координат, получим тригонометрическую форму записи
комплексного числа
z
= r cos ц + i r sin ц = r ( cos ц + i sin ц ),
где cos ц + sin ц = eiц => ц = р/4
При этом r называют модулем, а ц —
аргументом комплексного числа.
1.1)
z1
= 3 · (cos р/4 i sin р/4) = 3√2/2 i 3√2/2
1.2)
z2
= r · eiц = r (cos р/4 + i sin р/4) = √2/2 + i √2/2
2). Алгебраическая форма записи:
2.1) Сумма.
Если z1 = x1 + iy1 , а z2
= x2 + iy2 , то
z1
+ z2 = (x1 + iy1) + (x2 + iy2)
= (x1 + x2) + i (y1 + y2)
z1 + z2 = (3√2/2 +
√2/2) + i (3√2/2 + √2/2) = 4√2/2 i
2√2/2= = 2√2 — i√2
2.2) Произведение.
Если z1 = x1 + iy1 , а z2
= x2 + iy2 , то
z1
· z2 = (x1 + iy1) · (x2 + iy2)
= (x1x2 y1y2) + i (x1y2 + x2y1)
z1·z2 =(3√2/2 ·√2/2
+ 3√2/2 · √2/2)+ i(3√2/2 · √2/2
— √2/2 · 3√2/2 )=
= 3· 2/4 + 3 · 2/4 + i · 0 = 3
3).Изображение на комплексной плоскости операнд и
результатов.
Для упрощения преобразуем значения x и y из
простых дробей в десятичные.
x1
= 3√2/2 = 2,1 y1 = — 3√2/2 = -2,1
x2
= √2/2 = 0,7 y2 = √2/2 = 0,7
x3
= 2√2 = 2,8 y3 = -√2 = -1,4
x4 =
3 y4 = 0
y
0,7 Z2
0,7 2,1 2,8
0 Z4
3 x
— 1,4 Z3
— 2,1 Z1
Операнды — Z1 и Z2
Результаты — Z1 + Z2 =
Z3
Z1
· Z2 =
Z4
Страницы работы
Фрагмент текста работы
Проведя аналогичные преобразования
для Х=Х3 и Х=Х4, получим
 |
Подставив (24) в (21), получим
 |
На примере
исходных данных, приведенной в таблице 2, рассмотрим методику вычислений
значений интерполируемой функции для значений аргумента х, не совпадающих с
узловыми точками таблицы. Вычислим значение функции Y
для Х=1.
P4(1)=0,696+1,579/0,4*(1-0,0)+(-2,685)*(1-0,0)*(1-0,4)/(2*0,42)
+ 8,246*(1‑0,0)*(1-0,4)*(1-0,8)/(6*0,43)+ (‑25,06)*(1‑0,0)*(1‑0,4)*(1‑0,8)*(1‑1,2)/(24*0,44)
= 3,1649
1.5.3.
Организация ручных вычислений по первой формуле Ньютона
Рассмотрим пример выполнения
ручных вычислений по первой формуле Ньютона.
Задана
таблица значений функции, содержащая 4 узла:
Для данных
этой таблицы вычислим таблицу конечных разностей
|
i |
Xi |
Yi |
ΔYi |
Δ2Yi |
Δ3Yi |
|
0 |
1 |
2 |
2 |
1 |
-5 |
|
1 |
2 |
4 |
3 |
-4 |
|
|
2 |
3 |
7 |
-1 |
||
|
3 |
4 |
6 |
Вычислим значения коэффициентов полинома Ньютона
a0=Y0=2;
a1= Δy0/h=
2/1!/1=2;
a2= Δ2Y0/(2!h2)=1/(2!*12) =0,5;
a3= Δ3Y0/(3!h3)=-5/6.
Используя вычисленные значения коэффициентов a0 ,a1
, a2 , a3 запишем формулу для полинома Ньютона:
P3(x)=2+2(x-1)+0,5(x-1)(x-2)-5/6(x-1)(x-2)(x-3)=
=-5/6x3+5,5x2-26/3x+6
Эту формулу мы можем использовать для вычисления значений
функции Y(x) в любой точке интервала
от х=1 до х=4.
1.5.4.
Реализация алгоритма интерполяции по первой формуле Ньютона в среде программы Microsoft Excel
1. Введем в таблицу
на листе Excel исходные данные, записанные в столбцах Х
и Y(X) таблицы 2.
2. По формулам
(19), (20) и формулам, приведённым в таблице 1, сформируем таблицу 2 — таблицу
конечных разностей до четвёртого уровня. Эти формулы, введенные в ячейки
таблицы Excel, приведены на рис. 13.
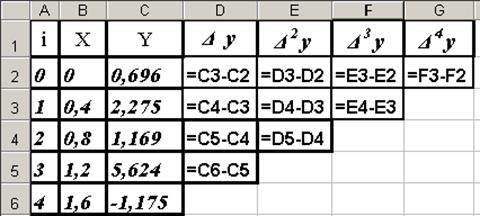 |
Рис. 13. Формулы, использованные для вычисления
значений конечных разностей функции Y(Х)
в таблице 2
3. В ячейку G6 для вычисления значения шагового
приращения аргумента h введем формулу «=$В$3-$В$2».
4. В ячейки строки
7 введём значения индекса i, определяющего
индекс строки таблицы.
5. В ячейках строки
8 вычислим степени hi, а
в ячейках строки девять запишем формулы для определения факториалов i!.
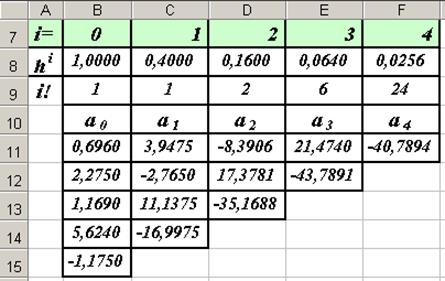
6. На рис. 14
показаны формулы, используемые в таблице для вычисления значений коэффициентов ai (i=0,1,2,3,4) для вычислительной формулы полинома Ньютона.
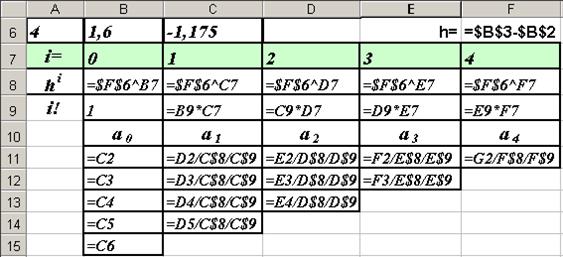 |
Рис.
14. Формулы, введенные в ячейки листа Excel, для вычисления
коэффициентов интерполирующего многочлена Ньютона
Для
формирования этой таблицы достаточно ввести в ячейку В11 формулу «=С2»
и протянуть её до ячейки В15 (формируется столбец ссылок на
ячейки со значениями Yi)
7. На рис. 15
приведена таблица рис.14. в режиме отображения числовых значений, вычисленных
по формулам рис. 14.
8. Для выполнения
вычислений значений интерполирующего полинома Ньютона в столбцах H, I и J
сформируем разреженную таблицу. В столбец Н
запишем номера строк таблицы от 0 до 8. В столбец I записываем
значения аргумента Х от Х0 = 0
до Хk = 1,6.
9. В ячейку J2 и введём формулу для вычисления
значения интерполирующего полинома Ньютона:
=$B$11+(I2-$B$2)*$C$11+
(I2-$B$2)*(I2-$B$3)*$D$11+
(I2-$B$2)*(I2-$B$3)*(I2-$B$4)*$E$11+
(I2-$B$2)*(I2-$B$3)*(I2-$B$4)*(I2-$B$5)*$F$11
Здесь $B$11,
$C$11, $D$11, $E$11, $F$11 — ссылки на коэффициенты ai (i=0,1,2,3,4); I2
— ссылка на ячейку со значением аргумента x
для точки, в которой вычисляется значение
интерполирующего полинома Ньютона, $B$2, $B$3, $B$4, $B$5 — ссылки на
ячейки, в которых записаны значения аргументов Xi (i=0,1,2,3,4).
|
Рис. |
10.Протянув
формулу, записанную в ячейку J2, по
столбцу до ячейки J10, получим
значения интерполирующего полинома для всех точек вектора Х.
Результаты вычислений и график, построенный по таблице значений, показан на
рис. 16.
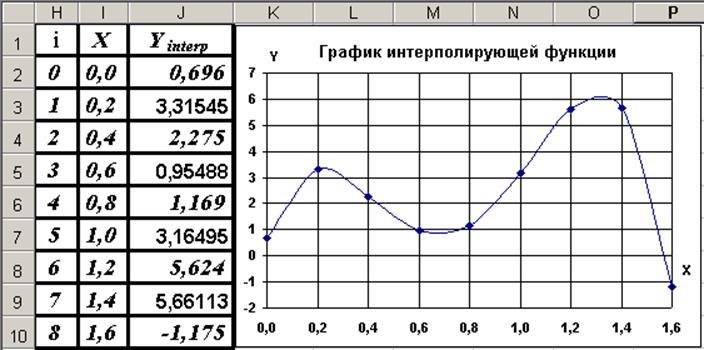 |
Рис. 16. Таблица и график с результатами интерполяции
График, построенный по результатам
интерполяции, сглажен. Для этого после выделения графика в окне «Формат ряда данных» на вкладке
«Вид» включаем флажок «Сглаженная линия».Литература
1. Мудров А.Е.
Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП
“РАСКО”, 1991. – 272 с.: ил.
2. Калиткин Н. Н.
Численные методы. – М.: Наука, 1978. – 512 с.
3. Любимов Е.Б. и
др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel.
Методические указания. СПбГАСУ, — СПб., 2005. — 16 с.
4. Заварыкин В.М. и
др. Численные методы. — М.: Просвещение, 1990. -176 с.
Оглавление
Интерполяция. Введение. Общая постановка задачи………………………. 1
1. Методы интерполяции …………………………………………………………. 1
1.1
Постановка задачи интерполяции……………………………………… 1
1.2
Линейная интерполяция…………………………………………………… 2
1.3 Интерполяция
каноническим полиномом………………………….. 3
Определителем Вандермонда называется
определитель………….. 3
1.4.
Интерполяционная формула Лагранжа…………………………….. 5
1.4.1.
Организация ручных вычислений по формуле Лагранжа ……………………………………………………………………………….. 6
1.4.2.
Реализация алгоритма интерполяции по формулам Лагранжа
Похожие материалы
- Visual Basic for Application. Свойства, методы и события объектов VBA. Переменная
- Базовые сведения по работе в табличном процессоре MicroSoft Excel
- Установление первоначальных настроек текстового процессора Word
Информация о работе
Содержание
- Применение интерполяции в Microsoft Excel
- Использование интерполяции
- Способ 1: интерполяция для табличных данных
- Способ 2: интерполяция графика с помощью его настроек
- Способ 3: интерполяция графика с помощью функции
- Интерполяционная формула ньютона эксель
- Интерполяционный многочлен Ньютона
- Интерполяция. Введение. Общая постановка задачи (Решение задач в среде программ Microsoft Excel или OpenOffice.org Calc)
- Страницы работы
- Фрагмент текста работы
- 1.5.3. Организация ручных вычислений по первой формуле Ньютона
- 1.5.4. Реализация алгоритма интерполяции по первой формуле Ньютона в среде программы Microsoft Excel
- График, построенный по результатам интерполяции, сглажен. Для этого после выделения графика в окне «Формат ряда данных» на вкладке «Вид» включаем флажок «Сглаженная линия».Литература
Применение интерполяции в Microsoft Excel
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Использование интерполяции
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.
- Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.
- Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.
После того, как все нужные данные введены, жмем на кнопку «OK».
Способ 2: интерполяция графика с помощью его настроек
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
- Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре. 
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Способ 3: интерполяция графика с помощью функции
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
- После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».
- Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
- У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
- После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Источник
Интерполяционная формула ньютона эксель
Pers.narod.ru. Обучение. Интерполяционный полином Ньютона
Дана таблица значений функции y = f(x)
и два значения аргумента x= a и x = b, отличные от данных в таблице. Требуется с помощью полиномов Ньютона третьей степени вычислить приближенные значения функции y = f(x) в точках x = a и x = b, т.е. f(a) и f(b).
Построим таблицу конечных разностей:
Поскольку точка b = 1.68 находится ближе к началу таблицы, а точка a = 1.92 – ближе к концу таблицы, то для нахождения значения f(b) будем использовать первый полином Ньютона, а для нахождения f(a) – второй. Ближайшее меньшее к точке b значение узла таблицы = 1.6, а ближайшее большее к точке a = 2.
Выпишем первый и второй полиномы третьей степени:
Скриншот реализации задачи в Excel показан ниже. Значения полинома вычисляются в точках a и b , а также строятся значения полинома в пределах изменения x с шагом, равным 0.05 и автоматическим выбором первой или второй формулы.

Следует учесть, что в документе расчёт делается всегда по первым конечным разностям (от точек y0 , y1 ), если точка a или b лежит ближе к началу интервала, и по последним (от точек y3 , y4 ), если она ближе к концу. Есть и другие способы расчёта, берущие ближайший слева или справа узел.
Источник
Интерполяционный многочлен Ньютона
Задача: построить интерполяционный многочлен Ньютона вручную использую Excel.
Таблица зависимости значений функции от аргумента
Многочлен Ньютона находится по формуле:
В Excel вычислим коэффициенты
Коэффициенты вычисляются так:
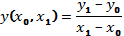

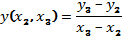
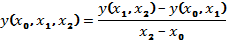
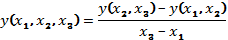
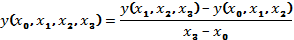
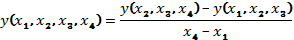
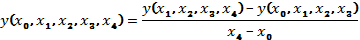
Формулы в Excel:
В итоге получаем такую таблицу значений:
Нужные коэффициенты выделены жирным. Подставим их в многочлен Ньютона:
N(x)=0,9+5(х-1)+3,75(х-1)(х-1,2)-20,8333(х-1)(х-1,2)(х-1,4)+62,5(х-1)(х-1,2)(х-1,4)(х-1,6)-125(х-1)(х-1,2)(х-1,4)(х-1,6)(х-1,8)=0,9+5х-5+3,75 X 2 -8,25х+4,5-20,8333 X 3 +74,99988 X 2 -89,166524х+34,999944+62,5 X 4 -325 X 3 +627,5 X 2 -533х+168-125 X 5 +875 X 4 -2425 X 3 +3325 X 2 -2254,8х+604,8
В результате получим многочлен:
N(х)=-125 X 5 +937,5 X 4 -2770,8333 X 3 +4031,2498 X 2 -2880,21624+808,199944
Проверим значения полученной функции в первых шести точках:
N(1)=-125 *1 5 +937,5 *1 4 -2770,8333 *1 3 +4031,2498 *1 2 -2880,21624*1+808,199944≈0,9
N(1,2)=-125 *(1,2) 5 +937,5 *(1,2) 4 -2770,8333 *(1,2) 3 +4031,2498 *(1,2) 2 -2880,21624*1,2+808,199944≈1,9
N(1,4)=-125 *(1,4) 5 +937,5 *(1,4) 4 -2770,8333 *(1,4) 3 +4031,2498 *(1,4) 2 -2880,21624*1,4+808,199944≈3,2
N(1,6)=-125 *(1,6) 5 +937,5 *(1,6) 4 -2770,8333 *(1,6) 3 +4031,2498 *(1,6) 2 -2880,21624*1,6+808,199944≈3,8
N(1,8)=-125 *(1,8) 5 +937,5 *(1,8) 4 -2770,8333 *(1,8) 3 +4031,2498 *(1,8) 2 -2880,21624*1,8+808,199944≈5,1
N(2)=-125 *(2) 5 +937,5 *(2) 4 -2770,8333 *(2) 3 +4031,2498 *(2) 2 -2880,21624*2+808,199944≈6,1
Полученные значения функции совпадают с табличными значениями. Многочлен Ньютона вычислен верно.
Формула в Excel для проверки найденного многочлена Ньютона:
В ячейку А11 подставляем значение Х, для которого надо узнать значение многочлена.
Таблица результатов в Excel для табличных значения Х:
Источник
Интерполяция. Введение. Общая постановка задачи (Решение задач в среде программ Microsoft Excel или OpenOffice.org Calc)
Страницы работы
Фрагмент текста работы
Проведя аналогичные преобразования для Х=Х3 и Х=Х4, получим
Подставив (24) в (21), получим
На примере исходных данных, приведенной в таблице 2, рассмотрим методику вычислений значений интерполируемой функции для значений аргумента х, не совпадающих с узловыми точками таблицы. Вычислим значение функции Y для Х=1.
1.5.3. Организация ручных вычислений по первой формуле Ньютона
Рассмотрим пример выполнения ручных вычислений по первой формуле Ньютона.
Задана таблица значений функции, содержащая 4 узла:
Для данных этой таблицы вычислим таблицу конечных разностей
Вычислим значения коэффициентов полинома Ньютона
Эту формулу мы можем использовать для вычисления значений функции Y(x) в любой точке интервала от х=1 до х=4.
1.5.4. Реализация алгоритма интерполяции по первой формуле Ньютона в среде программы Microsoft Excel
1. Введем в таблицу на листе Excel исходные данные, записанные в столбцах Х и Y(X) таблицы 2.
2. По формулам (19), (20) и формулам, приведённым в таблице 1, сформируем таблицу 2 — таблицу конечных разностей до четвёртого уровня. Эти формулы, введенные в ячейки таблицы Excel, приведены на рис. 13.
Рис. 13. Формулы, использованные для вычисления значений конечных разностей функции Y(Х) в таблице 2
3. В ячейку G6 для вычисления значения шагового приращения аргумента h введем формулу «=$В$3-$В$2».
4. В ячейки строки 7 введём значения индекса i, определяющего индекс строки таблицы.
5. В ячейках строки 8 вычислим степени h i , а в ячейках строки девять запишем формулы для определения факториалов i!.
6. На рис. 14 показаны формулы, используемые в таблице для вычисления значений коэффициентов ai (i=0,1,2,3,4) для вычислительной формулы полинома Ньютона.
Рис. 14. Формулы, введенные в ячейки листа Excel, для вычисления коэффициентов интерполирующего многочлена Ньютона
Для формирования этой таблицы достаточно ввести в ячейку В11 формулу «=С2» и протянуть её до ячейки В15 (формируется столбец ссылок на ячейки со значениями Yi)
7. На рис. 15 приведена таблица рис.14. в режиме отображения числовых значений, вычисленных по формулам рис. 14.
8. Для выполнения вычислений значений интерполирующего полинома Ньютона в столбцах H, I и J сформируем разреженную таблицу. В столбец Н запишем номера строк таблицы от 0 до 8. В столбец I записываем значения аргумента Х от Х0 = 0 до Хk = 1,6.
9. В ячейку J2 и введём формулу для вычисления значения интерполирующего полинома Ньютона:
Здесь $B$11, $C$11, $D$11, $E$11, $F$11 — ссылки на коэффициенты ai (i=0,1,2,3,4); I2 — ссылка на ячейку со значением аргумента x для точки, в которой вычисляется значение интерполирующего полинома Ньютона, $B$2, $B$3, $B$4, $B$5 — ссылки на ячейки, в которых записаны значения аргументов Xi (i=0,1,2,3,4).
Рис. 15. Результаты вычислений коэффициентов ai (i=0,1,2,3,4) по формулам рис. 14
10.Протянув формулу, записанную в ячейку J2, по столбцу до ячейки J10, получим значения интерполирующего полинома для всех точек вектора Х. Результаты вычислений и график, построенный по таблице значений, показан на рис. 16.
Рис. 16. Таблица и график с результатами интерполяции
График, построенный по результатам интерполяции, сглажен. Для этого после выделения графика в окне «Формат ряда данных» на вкладке «Вид» включаем флажок «Сглаженная линия».Литература
1. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП “РАСКО”, 1991. – 272 с.: ил.
2. Калиткин Н. Н. Численные методы. – М.: Наука, 1978. – 512 с.
3. Любимов Е.Б. и др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel. Методические указания. СПбГАСУ, — СПб., 2005. — 16 с.
4. Заварыкин В.М. и др. Численные методы. — М.: Просвещение, 1990. -176 с.
Интерполяция. Введение. Общая постановка задачи. 1
1. Методы интерполяции . 1
1.1 Постановка задачи интерполяции. 1
1.2 Линейная интерполяция. 2
1.3 Интерполяция каноническим полиномом. 3
Определителем Вандермонда называется определитель. 3
1.4. Интерполяционная формула Лагранжа. 5
1.4.1. Организация ручных вычислений по формуле Лагранжа . 6
1.4.2. Реализация алгоритма интерполяции по формулам Лагранжа
Источник