Интегральный процент в excel это

Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции

ЧАСТОТА()

и диаграммы.

Гистограмма (frequency histogram) – это

столбиковая диаграмма MS EXCEL

, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).

Гистограмма поможет визуально оценить распределение набора данных, если:

• в наборе данных как минимум 50 значений;
• ширина интервалов одинакова.

Построим гистограмму для набора данных, в котором содержатся значения

непрерывной случайной величины

. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе

Гистограмма AT

в

файле примера.

Данные содержатся в диапазоне

А8:А57

.

Примечание

: Для удобства написания формул для диапазона

А8:А57

создан

Именованный диапазон

Исходные_данные.

Построение гистограммы с помощью надстройки

Пакет анализа

Вызвав диалоговое окно

надстройки Пакет анализа

, выберите пункт

Гистограмма

и нажмите ОК.

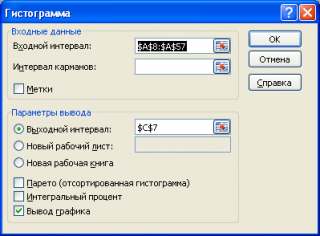
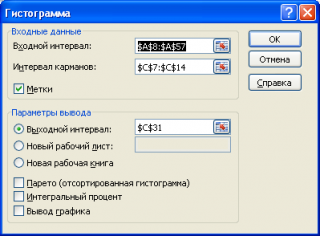
В появившемся окне необходимо как минимум указать:

входной интервал

и левую верхнюю ячейку

выходного интервала

. После нажатия кнопки

ОК

будут:

• автоматически рассчитаны интервалы значений (карманы);
• подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
• если поставлена галочка напротив пункта
  
  Вывод графика
  
  , то вместе с таблицей частот будет выведена гистограмма.

Перед тем как анализировать полученный результат —

отсортируйте исходный массив данных

.

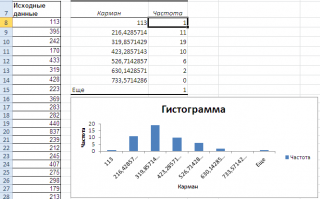
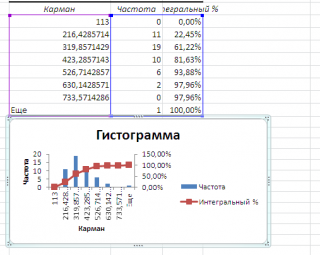
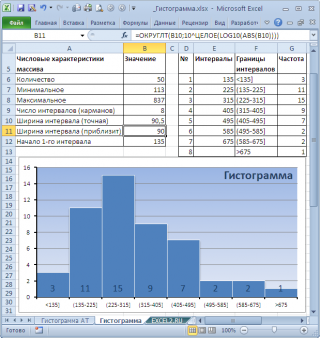
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).

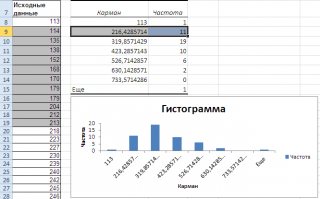
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием

Еще

) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).

Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:

=(МАКС(

Исходные_данные

)-МИН(

Исходные_данные

))/7

где

Исходные_данные –

именованный диапазон

, содержащий наши данные.

Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).

Примечание

:

Похоже, что инструмент

Гистограмма

для подсчета общего количества интервалов (с учетом первого) использует формулу

=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(

Исходные_данные

)))+1

Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция

ЦЕЛОЕ()

округляет до ближайшего меньшего целого

(ЦЕЛОЕ(КОРЕНЬ(35))=5

, а

ЦЕЛОЕ(КОРЕНЬ(36))=6)

.

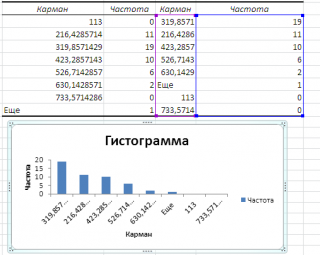
Если установить галочку напротив поля

Парето (отсортированная гистограмма)

, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.

Если установить галочку напротив поля

Интегральный процент

, то к таблице с частотами будет добавлен столбец с

нарастающим итогом

в % от общего количества значений в массиве.

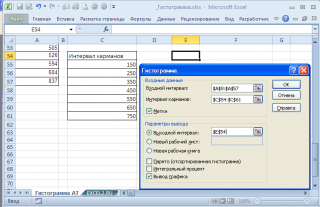
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля

Метка

).

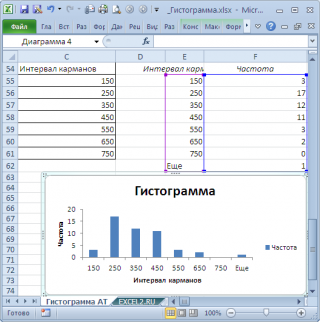
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.

В результате получим практически такую же по форме

гистограмму

, что и раньше, но с более красивыми границами интервалов.

Как видно из рисунков выше, надстройка

Пакет анализа

не осуществляет никакого

дополнительного форматирования диаграммы

. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении

гистограммы

с помощью функции

ЧАСТОТА()

без использовании надстройки

Пакет анализа

.

Построение гистограммы распределения без использования надстройки Пакет анализа

Порядок действий при построении гистограммы в этом случае следующий:

• определить количество интервалов у гистограммы;
• определить ширину интервала (с учетом округления);
• определить границу первого интервала;
• сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
• построить гистограмму.

СОВЕТ

: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент

описательной статистики

, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.

В наших расчетах для определения количества интервалов мы будем пользоваться формулой

=ЦЕЛОЕ(КОРЕНЬ(n))+1

.

Примечание

: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.

Расчет ширины интервала и таблица интервалов приведены в

файле примера на листе Гистограмма

. Для вычисления количества значений, попадающих в каждый интервал, использована

формула массива

на основе функции

ЧАСТОТА()

. О вводе этой функции см. статью

Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL

.

В MS EXCEL имеется диаграмма типа

Гистограмма с группировкой

, которая обычно используется для построения

Гистограмм распределения

.

В итоге можно добиться вот такого результата.

Примечание

: О построении и настройке макета диаграмм см. статью

Основы построения диаграмм в MS EXCEL

.

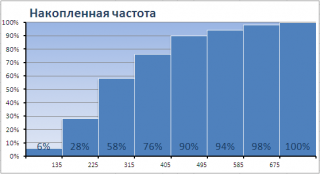
Одной из разновидностей гистограмм является

график накопленной частоты

(cumulative frequency plot).

На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.

СОВЕТ

: О построении

двумерной гистограммы

см. статью

Двумерная гистограмма в MS EXCEL

.

Примечание

: Альтернативой

графику накопленной частоты

может служить

Кривая процентилей

, которая рассмотрена в

статье про Процентили

.

Примечание

: Когда количество значений в выборке недостаточно для построения полноценной

гистограммы

может быть полезна

Блочная диаграмма

(иногда она называется

Диаграмма размаха

или

Ящик с усами

).

Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неиз­вестных параметров. В частности, невозможно
рассчитать точное значение соот­ветствующих вероятностей, так как нельзя
определить количество общих и благо­приятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в ко­торых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.

Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой со­бытия
и его вероятностью.

Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов). 

Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
чис­ла на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.

По
найденным относительным час­тотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.

Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того  интервала
включительно, для которого определяется накопленная частота.

В Excel для построения выборочных функций распределения
используются спе­циальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интер­валах
значений и выводит их как массив цифр, где

•     
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;

•     
двоичный_массив
— это массив интервалов, по
ко­торым группируются значения выборки.

Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:

•     
Входной диапазон — диапазон исследуемых данных
(выборка);

•     
Интервал карманов — диа­пазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в воз­растающем порядке. Если
диапазон карманов не был введен, то набор интерва­лов, равномерно распределенных между минимальным и
максимальным зна­чениями данных, будет создан
автоматически.

•     
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.

•     
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму гра­фика интегральных
процентов.

•     
переключатель
Вывод графика позволяет установить режим автоматическо­го создания встроенной диаграммы на листе, содержащем
выходной диапа­зон.

Пример 1. Построить эмпирическое распределение веса
студентов в килограм­мах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.

Решение

1.  В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).

2.        
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения ин­тервалов (40, 45,
50, 55, 60, 65, 70).

3.        
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные час­тоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накоплен­ные частоты.(см. рис. 1).

4.        
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
па­нели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появив­шемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться мас­сив абсолютных частот (см. рис.1).

5.        
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Ав­тосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.

6.        
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.

7.        
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение от­носительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.

                     Рис. 1. Результат вычислений из
примера 1

8.   
Постройте диаграмму относительных и накопленных частот. Щелчком ука­зателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаг­раммы График/гистограмма. После 
редактирования диаграмма будет иметь такой вид, как на рис. 2.

Рис. 2
Диаграмма относительных и накопленных частот из примера 1

Задания для самостоятельной работы

1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.

2.  Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.

3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).

4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.

Обозначим 
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).

Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания

При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.

Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).

Таблица 2.
Результаты опроса ста учителей

Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=

где

W(x) – относительная частота наступления события;

          — стандартное
отклонение;

          =3,14.

Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.

Построение гистограмм в Microsoft Excel

Перед построением гистограммы выполняется группировка данных по близким признакам. При группировании по количественному признаку все множество значений признака делится на

интервалы.

Для определения оптимального количества интервалов может быть использована формула Стерджесса:

n = 1 + (3,322× lgN)

где N — количество наблюдений. В этом случае величина интервала:

h = (Vmax — Vmin)/n

Поскольку количество групп не может быть дробным числом, то полученную по этой формуле величину округляют до целого большего числа.

Нижнюю границу первого интервала принимают равной минимальному значению xmin. Верхняя граница первого интервала соответствует значению (xmin + h). Для последующих групп

границы определяются аналогично, то есть последовательно прибавляется величина интервала h.

В Excel для построения гистограмм используются статистическая функция ЧАСТОТА в сочетании с мастером построения обычных диаграмм и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных, двоичный_массив) вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр, где

•Массив_данных —массив исходных данных, для которых вычисляются частоты;

•Массив_интервалов — это массив интервалов, по которым группируются значения выборки.

Перед вызовом функции ЧАСТОТА необходимо выделить столбец c числом ячеек, равным числу интервалов n, в который будут выведены результаты выполнения функции.

Вызвать Мастер функций (кнопка fx):

и функцию ЧАСТОТА.

В появившемся списке выбрать инструмент Гистограмма и щелкнуть на кнопке ОК. Появится окно гистограммы, где задаются следующие параметры:

Входной интервал:– адреса ячеек, содержащие выборочные данные.

Интервал карманов: (необязательный параметр) – адреса ячеек, содержащие границы интервалов. Это поле предлагается оставить пустым, предоставив Excel самому вычислить границы интервалов (карманов – в терминах Excel).

Метки – флажок, включаемый, если первая строка во входных данных содержит заголовки. Если заголовки отсутствуют, то флажок следует выключить.

Выходной интервал: / Новый рабочий лист: / Новая рабочая книга.

Включенный переключатель Выходной интервал требует ввода адреса верхней ячейки, начиная с которой будут размещаться вычисленные относительные частоты j .

Вположении переключателя Новый рабочий лист: открывается новый лист, в котором начиная с ячейки А1 размещаются частности j .

Вположении переключателя Новая рабочая книга открывается новая книга, на первом листе которой начиная с ячейки А1 размещаются частности j .

Парето (отсортированная гистограмма) – устанавливается, чтобы представить j в порядке их убывания. Если параметр выключен, то j приводятся в порядке следования интервалов.

Интегральный процент – устанавливается в активное состояние для расчета выраженных в процентах накопленных относительных частот (аналог значений столбца Накопленные частоты).

Вывод графика – устанавливается в активное состояние для автоматического создания встроенной диаграммы на листе, содержащем частоты.

Замечание.

Как правило, гистограммы изображаются в виде смежных прямоугольных областей. Поэтому столбики гистограммы следует расширить до соприкосновения друг с другом. Для этого необходимо щелкнуть мышью на диаграмме, далее на панель инструментов Диаграмма, раскрыть список инструментов и выбрать элемент Ряд ‘Частота’, после чего щелкнуть на кнопке Формат ряда. В появившемся одноименном диалоговом окне необходимо активизировать закладку Параметры и в поле Ширина зазора установить значение 0 ((Excel 2003):

В Excel 2007…2010 встать на любой столбик гистограммы и правой кнопкой мыши выбрать

Формат ряда данных:

Для построения теоретической кривой нормального распределения по эмпирическим данным необходимо найти теоретические частоты.

В Excel для вычисления значений нормального распределения используются функция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения.

Функция имеет параметры:

НОРМРАСП (х; среднее; стандартное_откл; интегральная), где:

х — значения выборки, для которых строится распределение; среднее — среднее арифметическое выборки; стандартное_откл — стандартное отклонение распределения;

интегральный — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения.

Для получения абсолютных значений плотностей распределения (теоретических частот) достаточно найденные значения вероятности умножить на величину интервала h и количество наблюдений N = 100 по каждой строке.

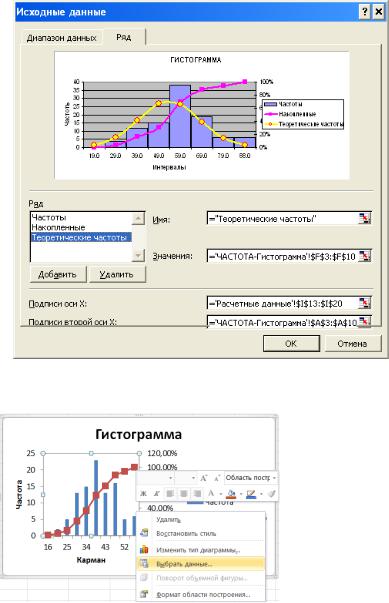
Для завершения выполнения задания необходимо внести полученные значения теоретических частот на рисунок с гистограммой, добавив ряд в закладке Исходные данные и выбрав тип диаграммы

– график ((Excel 2003):

В Excel 2007…2010 находясь в обласи гистограммы по правой кнопке мыши выбрать Выбрать данные (или по одноименной кнопке на вкладке Конструктор):

и в появившемся окне провести манипуляции с вводом нового ряда «Теоретические частоты»:

Распределение частот [1]

При увеличении объема выборки ни упорядоченный массив, ни диаграмма «ствол и листья» уже не позволяют легко представлять, анализировать и интерпретировать результаты. Для больших наборов данных следует создавать сводные таблицы, распределяя данные по группам (или категориям). Такой способ представления данных называется распределением частот. Распределение частот представляет собой сводную таблицу, в которой данные распределены по группам или категориям. Если данные сгруппированы в виде распределения частот, процесс их анализа и интерпретации становится более управляемым и осмысленным. При распределении частот следует внимательно выбирать интервал группирования, или размах групп, а также вычислять границы каждой группы, не допуская их перекрытия.

Выбор количества групп

Количество групп, выбранных для группировки данных, непосредственно зависит от объема исходной выборки. Чем больше элементов содержит выборка, тем больше групп можно создать. Как правило, распределение частот должно содержать не менее 5 и не более 15 групп. Если групп слишком мало или слишком много, новую информацию получить сложно. Выделение групп процесс творческий, и я бы рекомендовал в качестве первого подхода использовать формулу Стерджесcа:

(1) k = 1 + log₂n

где k – число групп, n – объем выборки; далее визуально определить по графику, насколько удачным получилось разбиение и, если требуется, скорректировать число групп на величину ± 1.

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Вычисление интервала группирования

Каждая группа, образующая распределение частот, должна иметь одинаковый размах. Чтобы определить ширину интервала группирования, диапазон изменения данных делят на заданное количество групп.

(2) Ширина интервала группирования = Диапазон / Количество групп

В нашем примере (см. первое упоминание в заметке Как упорядочить массив данных) имеются данные о 158 фондах (рис. 1).

Рис. 1. Упорядоченный массив, содержащий данные о пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, за период с 1 января 1997 до 31 декабря 2001

Для такого массива достаточно создать восемь групп (k = 1 + log₂158 = 8,3). Диапазон значений массива вычисляется по формуле 26,3 – (–6,1) = 32,4. С учетом формулы (2) ширина интервала группирования = 32,4 / 8 = 4,05. Для удобства округляем до 5 (в меньшую сторону округлять нельзя, так как какие-то значения выпадут из рассмотрения).

Вычисление границ групп

Для вычисления распределения частот необходимо так определить границы групп, чтобы они не пересекались. Перекрытие групп не допускается. Поскольку размах каждой группы, построенной на основе данных о пятилетней среднегодовой доходности фондов, равен 5%, границы групп должны быть установлены так, чтобы учесть все данные. По возможности эти границы должны быть достаточно наглядными. Например, величины из первой группы должны изменяться в диапазоне от –10% до –5% и так далее, пока не будут сформированы 8 неперекрывающихся групп, ширина каждой из которых равна 5% (рис. 2).

Рис. 2. Распределение частот для пятилетней среднегодовой доходности 158 фондов

Главным преимуществом этой таблицы является возможность легко вычислять основные характеристики данных. Например, таблица демонстрирует, что диапазон среднегодовой доходности 158 фондов ограничен числами –10% и 30%, причем показатели в основном группируются в диапазоне 5…15%.

С другой стороны, эта сводная таблица имеет недостаток: по ней невозможно определить, как распределены индивидуальные данные внутри групп. Например, доходность трех фондов из представленных в таблице, изменяется в диапазоне 20–25%, но определить, вокруг какого значения они сконцентрированы (20 или 25%), невозможно. Для представления средней доходности этих трех фондов выбирается срединная точка (22,5%). Срединной точкой интервала –10…–5%, является значение –7,5% и т.д.

Субъективность при выборе границ групп

Выбор границ групп при вычислении распределения частот является субъективным. Если наборы данных невелики, одинаковый выбор границ групп для разных выборок может привести к разным результатам. Например, если при вычислении распределения частот для показателей пятилетней среднегодовой доходности ширину интервалов группирования установить равной 4%, а не 5%, возникнет смещение распределения. Особенно сильно этот эффект проявляется при работе с малыми выборками.

Смещение распределения возникает не только в результате изменения границ групп. Например, ширину интервала группирования можно оставить равной 5%, изменив границы первой и последней групп. Эта манипуляция также приводит к смещению распределения, особенно, если объем выборки невелик. К счастью, по мере увеличения объема выборки этот эффект становится менее выраженным.

Распределение относительных частот и процентное распределение

Для более углубленного анализа распределения частот можно построить либо распределение относительных частот (долей) либо процентное распределение. Выбор распределения зависит от того, с какими данными желает работать пользователь: с долями или процентами (рис. 3).

Рис. 3. Распределение относительных частот и процентное распределение для пятилетней среднегодовой доходности 158 фондов

Таким образом, доля фондов, ориентированных на быстрый рост капитала, среднегодовая доходность которых изменяется от 10 до 15%, равна 0,386, а процент — 38,6%. Работать с долями или процентами удобнее, чем с количеством элементов в группе. Распределение относительных частот, как и процентное распределение, позволяет сравнивать даже наборы данных, имеющие разные объемы.

Функция распределения

Часто оказывается полезной таблица интегральных процентов, которую также называют распределением интегральных процентов. Функция распределения позволяет обнаружить информацию, которая ускользает от распределения частот (рис. 4). (Для построения распределение интегральных процентов были использованы данные, приведенные на рис. 3.)

Рис. 4. Распределение интегральных процентов

Для вычисления распределения частот можно воспользоваться командой Данные → Анализ данных (рис. 5).

Рис. 5. Анализ данных

Если надстройка Анализ данных не отражается, ее нужно предварительно установить. Выберите меню Файл → Параметры (рис. 6). В открывшемся окне Параметры Excel, выберите меню Надстройки → Пакет анализа и кликните на кнопке Перейти.

Рис. 6. Параметры Excel

В открывшемся окне Надстройки поставьте галочку на опции Пакет анализа и кликните Ok (рис. 7).

Рис. 7. Надстройки

Теперь нужно подготовить исходные данные. Расположим числа доходности 158 фондов (как на рис. 1) в столбце А (рис. 8). Вообще говоря, это не обязательно. Можно расположить данные и в виде двумерного массива, как на рис. 1.  В столбце С размещаем упорядоченный массив верхних границ диапазонов. Именно этот массив и будет чуть позже введен в поле Интервал карманов. Здесь есть маленькая тонкость. Excel включит верхнюю границу в диапазон. Например, интервал, для которого указана верхняя граница 10, фактически является интервалом 5,00001…10. Именно к этому интервалу будет относиться число 10, а не к следующему интервалу 10…15. Можно сказать и иначе: нижняя граница не входит в интервал, а верхняя – входит. Запускаем надстройку Анализ данных, из списка Инструменты анализа выбираем пункт Гистограмма, жмем ОК.

Рис. 8. Подготовка исходных данных и запуск надстройки

В диалоговом окне Гистограмма (рис. 9) в поле Входной интервал выбираем наш массив А1:А158, в поле Интервал карманов интервал С1:С8, переключатель Параметры вывода ставим в положение Новый рабочий лист, включаем Интегральный процент и Вывод графика, жмем ОК.

Рис. 9. Настройка гистограммы

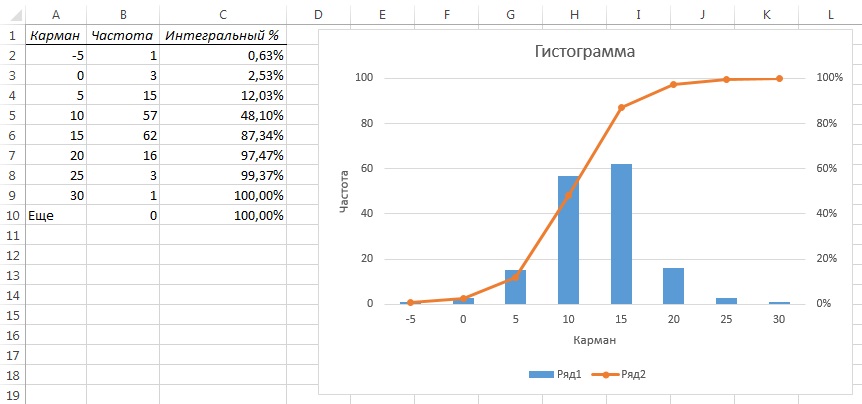
На отдельном листе выводится таблица, аналогичная рис. 3, а также график (гистограмма) с функцией распределения по диапазонам и интегральным процентом (рис. 10). В столбце Карман таблицы и на оси абсцисс гистограммы указаны верхние границы диапазонов. При этом в первый диапазон попадают все значения меньше первой указанной границы, то есть все значения меньше «минус 5» (включая -5), а в диапазон под названием Еще – все значения превышающие самую большую границу, то есть больше 30. Вы можете «поиграть» значениями Карманов, чтобы почувствовать, как они работают.

Рис. 10. Гистограмма с функцией распределения по диапазонам и интегральным процентом

Гистограмма

Следуя принципу «лучше один раз увидеть, чем сто раз услышать», для анализа статистических данных часто используют графические изображения, а не таблицы. Например, с помощью гистограммы описывают числовые данные, сгруппированные по частоте, относительной частоте или процентной доле. Гистограмма — это диаграмма, на которой изображены столбики, границы которых совпадают с границами групп. При построении гистограмм исследуемая случайная величина откладывается по оси Х, а количество элементов в соответствующих группах, их относительная частота или процентная доля — по оси Y. На рис. 10 изображена гистограмма, построенная на основе данных о пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала. По оси Y отложено количество элементов в группах.

При сравнении нескольких наборов данных бывает довольно сложно создавать диаграммы «ствол и листья» и гистограммы. Например, иногда трудно правильно интерпретировать разницу между высотами соответствующих столбцов разных гистограмм. Для нескольких наборов данных предпочтительными оказываются полигоны, построенные по относительным частотам или процентным долям.

Полигон

Как и при построении гистограмм, величина исследуемой переменной откладывается вдоль горизонтальной оси. По вертикальной оси откладывается количество элементов в каждой группе, их относительная доля или процент. Процентный полигон представляет собой график, построенный путем соединения средних точек, соответствующих процентной доле каждой группы (рис. 11). Надстройка Анализ данных не умеет строить полигоны; с методом, использованным при построении графика на рис. 11 можно ознакомиться на соответствующем листе Excel-файла.

Рис. 11. Процентный полигон для пятилетней доходности

Полигон интегральных процентов, или кривая распределения, является графическим изображением распределения суммарных процентов (накопительным итогом).

Рис. 12. Полигон интегральных процентов

На рис. 12 изображены полигоны интегральных процентов (метод построения см. Excel-файл) на основе пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, и 101 фонда, ориентированного на медленный рост капитала. На оси X отложены средние значения диапазонов. Видно, что среднегодовая доходность 48,1% фондов, ориентированных на быстрый рост капитала, не превышает 10%, в то время как доля фондов, ориентированных на медленный рост капитала, в этом интервале равна 36,7%. Обратите внимание на то, что в интервале до 20% кривая распределения среднегодовой доходности фондов, ориентированных на быстрый рост капитала, расположена слева от кривой распределения доходности фондов, ориентированных на медленный рост капитала. В то же время количество фондов, ориентированных на быстрый и медленный рост капитала, доходность которых не превышает 20,0%, приблизительно одинаково.

Изображение двумерных числовых данных

Выше мы рассмотрели гистограммы, полигоны, кривые распределений и полигоны накопленных частот, представляющие собой удобные графические инструменты для анализа числовых одномерных данных. Для анализа двумерных числовых величин используется иной вид графического представления – диаграмма разброса. В программе Excel эта диаграмма называется точечной, а в научной литературе — корреляционной. Такие диаграммы оказываются полезными в разных областях деловой активности. Например, специалисты по маркетингу с помощью таких диаграмм могут исследовать эффективность рекламной кампании, сравнивая объемы недельных продаж и расходы на рекламу, а менеджеры по кадрам — изучать систему оплаты труда в компании, сравнивая трудовой стаж сотрудников и их текущую зарплату.

Используя диаграмму разброса, менеджер по логистике может анализировать вклад таможенного сбора в суммарные логистические затраты (рис. 13). Диаграммы разброса играют важную роль при изучении коэффициента корреляции, а также в регрессионном анализе.

Рис. 13. Корреляция таможенного сбора (как процентной доли таможенной стоимости, ось Y) и таможенной стоимости, ось Х

Для построения диаграммы разброса выберите два столбца и кликните на типе диаграммы Точечная (рис. 14). Обратите внимание на то, что Мастер диаграмм по умолчанию считает, что переменная X находится в первом столбце диапазона. Если данные на вашем листе расположены иначе, поменяйте столбцы местами.

Рис. 14. Построение точечной диаграммы

Предыдущая заметка Как упорядочить массив данных

Следующая заметка Представление категорийных данных в виде таблиц и диаграмм

К оглавлению Статистика для менеджеров с использованием Microsoft Excel

---

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 105–124

Процедура «Гистограмма» пакета «Анализ данных. Вычисление частот и накопленных частот. Построение гистограмм.

В процедуре автоматически выполняются следующие вычисления:

находится промежуток [x_min, x_max];

выбирается число m интервалов группировки (7£ m £20);

вычисляются середины интервалов группировки , , ;

для каждого интервала  вычисляются частоты  n_j  — количество выборочных значений, которые попали в j-й интервал;

для каждого интервала  вычисляются накопленные частоты — количество выборочных значений, не превышающих верхней границы  j-го интервала;

Строится гистограмма – график ступенчатой функции , , , D_j = (a_j, b_j) , .

Для того чтобы вычислять накопленные частоты и отобразить гистограмму в листе  в листе Excel, в окне процедуры следует пометить соответствующие поля.

 

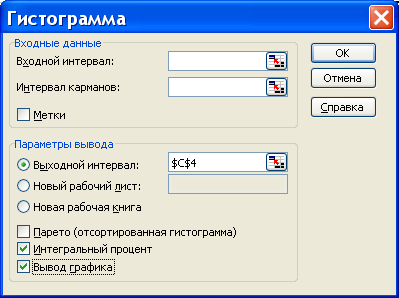
Результаты вычислений процедуры представлены в виде таблицы (ниже приведены две таблицы, первая – когда поле «Интегральный процент» не помечено, вторая – когда помечено)

Карман	Частота
114.46	1
115.581	1
116.702	6
117.823	6
118.944	12
120.065	21
121.186	23
122.307	18
123.428	5
124.549	4
Еще	2

Карман	Частота	Интегральный %
114.46	1	1.01%
115.581	1	2.02%
116.702	6	8.08%
117.823	6	14.14%
118.944	12	26.26%
120.065	21	47.47%
121.186	23	70.71%
122.307	18	88.89%
123.428	5	93.94%
124.549	4	97.98%
Еще	2	100.00%

Здесь Карман – середины интервалов группировки, Интегральный % – накопленные частоты в процентах. Для того чтобы получить числовое значение накопленных частот, следует изменить формат ячеек с «Процентного» на «Числовой».

Использование «Мастера диаграмм» для построения полигонов.

Для построения полигона накопленных частот  в поле «Диапазон» следует указать ячейки столбца «Интегральный процент» таблицы, полученной  в процедуре «Гистограммы» пакета «Анализ данных».

Для построения полигона частот можно указать ячейки столбца «Частота» таблицы, полученной  в процедуре «Гистограммы» пакета «Анализ данных». Можно –  вычислить относительные частоты  и указать в поле «Диапазон» соответствующие ячейки.