Содержание
- Интеграл вероятности
- Экспоненциальное распределение. Непрерывные распределения в EXCEL
- Экспоненциальное распределение в MS EXCEL
- Графики функций
- Генерация случайных чисел
- Задачи
Интеграл вероятности



| x | erf(x) | x | erf(x) | x | erf(x) | x | erf(x) |
| 0,000 | 0,0000 | 0,400 | 0,4283 | 1,250 | 0,9229 | 2,250 | 0,9985 |
| 0,020 | 0,0225 | 0,420 | 0,4474 | 1,300 | 0,9340 | 2,300 | 0,9988 |
| 0,040 | 0,0451 | 0,440 | 0,4662 | 1,350 | 0,9437 | 2,350 | 0,9991 |
| 0,060 | 0,0676 | 0,460 | 0,4846 | 1,400 | 0,9522 | 2,400 | 0,9993 |
| 0,080 | 0,0900 | 0,480 | 0,5027 | 1,450 | 0,9597 | 2,450 | 0,9994 |
| 0,100 | 0,1124 | 0,500 | 0,5205 | 1,500 | 0,9661 | 2,500 | 0,9995 |
| 0,120 | 0,1347 | 0,550 | 0,5633 | 1,550 | 0,9716 | 2,550 | 0,9996 |
| 0,140 | 0,1569 | 0,600 | 0,6038 | 1,600 | 0,9763 | 2,600 | 0,9997 |
| 0,160 | 0,1790 | 0,650 | 0,6420 | 1,650 | 0,9803 | 2,650 | 0,9998 |
| 0,180 | 0,2009 | 0,700 | 0,6778 | 1,700 | 0,9837 | 2,700 | 0,9998 |
| 0,200 | 0,2227 | 0,750 | 0,7111 | 1,750 | 0,9866 | 2,750 | 0,9999 |
| 0,220 | 0,2443 | 0,800 | 0,7421 | 1,800 | 0,9890 | 2,800 | 0,9999 |
| 0,240 | 0,2657 | 0,850 | 0,7706 | 1,850 | 0,9911 | 2,850 | 0,9999 |
| 0,260 | 0,2869 | 0,900 | 0,7969 | 1,900 | 0,9927 | 2,900 | 0,9999 |
| 0,280 | 0,3078 | 0,950 | 0,8208 | 1,950 | 0,9941 | 2,950 | 0,9999 |
| 0,300 | 0,3286 | 1,000 | 0,8427 | 2,000 | 0,9953 | 3,000 | 0,9999 |
| 0,320 | 0,3491 | 1,050 | 0,8624 | 2,050 | 0,9962 | ∞ | 1,0000 |
| 0,340 | 0,3693 | 1,100 | 0,8802 | 2,100 | 0,9970 | ||
| 0,360 | 0,3893 | 1,150 | 0,8961 | 2,150 | 0,9976 | ||
| 0,380 | 0,4090 | 1,200 | 0,9103 | 2,200 | 0,9981 |
7.2. Интегральная показательная функция E1(x) = -Ei(-x)
| x | E1(x) | x | E1(x) | x | E1(x) | x | E1(x) |
| 0,010 | 4,037 | 0,078 | 2,050 | 0,560 | 0,493 | 3,40 | 0,00789 |
| 0,012 | 3,857 | 0,080 | 2,026 | 0,580 | 0,473 | 3,60 | 0,00616 |
| 0,014 | 3,705 | 0,082 | 2,004 | 0,600 | 0,454 | 3,80 | 0,00482 |
| 0,016 | 3,573 | 0,084 | 1,982 | 0,620 | 0,436 | 4,00 | 0,00377 |
| 0,018 | 3,458 | 0,086 | 1,960 | 0,640 | 0,419 | 4,20 | 0,00296 |
| 0,020 | 3,354 | 0,088 | 1,939 | 0,660 | 0,403 | 4,40 | 0,00233 |
| 0,022 | 3,261 | 0,090 | 1,918 | 0,680 | 0,388 | 4,60 | 0,00184 |
| 0,024 | 3,176 | 0,092 | 1,898 | 0,700 | 0,373 | 4,80 | 0,00145 |
| 0,026 | 3,098 | 0,094 | 1,879 | 0,720 | 0,359 | 5,00 | 0,00114 |
| 0,028 | 3,026 | 0,096 | 1,859 | 0,740 | 0,346 | 5,20 | 0,00090 |
| 0,030 | 2,959 | 0,098 | 1,841 | 0,760 | 0,334 | 5,40 | 0,00071 |
| 0,032 | 2,896 | 0,100 | 1,822 | 0,780 | 0,322 | 5,60 | 0,00057 |
| 0,034 | 2,837 | 0,120 | 1,659 | 0,80 | 0,310 | 5,80 | 0,00045 |
| 0,036 | 2,782 | 0,140 | 1,524 | 0,82 | 0,299 | 6,00 | 0,00036 |
| 0,038 | 2,730 | 0,160 | 1,409 | 0,84 | 0,289 | 6,20 | 0,00028 |
| 0,040 | 2,681 | 0,180 | 1,309 | 0,86 | 0,279 | 6,40 | 0,00022 |
| 0,042 | 2,634 | 0,200 | 1,222 | 0,88 | 0,269 | 6,60 | 0,00018 |
| 0,044 | 2,589 | 0,220 | 1,145 | 0,90 | 0,260 | 6,80 | 0,00014 |
| 0,046 | 2,547 | 0,240 | 1,076 | 0,92 | 0,251 | 7,0 | 1,15 10 -4 |
| 0,048 | 2,506 | 0,260 | 1,013 | 0,94 | 0,242 | 7,2 | 9,21 10 -5 |
| 0,050 | 2,467 | 0,280 | 0,957 | 0,96 | 0,234 | 7,4 | 7,36 10 -5 |
| 0,052 | 2,430 | 0,300 | 0,905 | 0,98 | 0,226 | 7,6 | 5,88 10 -5 |
| 0,054 | 2,394 | 0,320 | 0,858 | 1,00 | 0,219 | 7,8 | 4,70 10 -5 |
| 0,056 | 2,360 | 0,340 | 0,814 | 1,20 | 0,158 | 8,0 | 3,76 10 -5 |
| 0,058 | 2,327 | 0,360 | 0,774 | 1,40 | 0,116 | 8,2 | 3,01 10 -5 |
| 0,060 | 2,295 | 0,380 | 0,737 | 1,60 | 0,0863 | 8,4 | 2,41 10 -5 |
| 0,062 | 2,264 | 0,400 | 0,702 | 1,80 | 0,0647 | 8,6 | 1,93 10 -5 |
| 0,064 | 2,234 | 0,420 | 0,669 | 2,00 | 0,0489 | 8,8 | 1,55 10 -5 |
| 0,066 | 2,205 | 0,440 | 0,639 | 2,20 | 0,0371 | 9,0 | 1,24 10 -5 |
| 0,068 | 2,177 | 0,460 | 0,611 | 2,40 | 0,0284 | 9,2 | 9,99 10 -6 |
| 0,070 | 2,150 | 0,480 | 0,584 | 2,60 | 0,0218 | 9,4 | 8,02 10 -6 |
| 0,072 | 2,124 | 0,500 | 0,559 | 2,80 | 0,0168 | 9,6 | 6,44 10 -6 |
| 0,074 | 2,099 | 0,520 | 0,536 | 3,00 | 0,0130 | 9,8 | 5,17 10 -6 |
| 0,076 | 2,074 | 0,540 | 0,514 | 3,20 | 0,0101 |
При значениях x
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Самое популярное на сайте:
Формы и системы оплаты труда В современном понимании формы и системы оплаты труда можно определить как организационно-экономические механизмы соотнесения затрат и.
Задания для закрепления. 1. Технологический процесс ремонта представляет собой ________________________ 1. Технологический процесс ремонта представляет собой.
ЧТО ДЕЛАТЬ МУЖЧИНАМ СО СЛАБОЙ ЭРЕКЦИЕЙ Современный последователь учения дао любви Чжан Чжунлань сравнивает импотенцию с простудой — неприятно и раздражает.
Эллинизм. Эллинизм (323-146 до н.э.) стал заключительным этапом древнегреческой культуры Эллинизм (323-146 до н.э.) стал заключительным этапом древнегреческой культуры. Этап эллинизма — начинается с походов Александра.
Условия развития творческих способностей Для развития творчества детям необходимы определенные знания, навыки и умения, способы деятельности, которыми они сами, без помощи.
Источник
Экспоненциальное распределение. Непрерывные распределения в EXCEL
history 8 ноября 2016 г.
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:
Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
history 27 ноября 2022 г.
- Группы статей
Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson’s rule). Покажем как оценить ошибку интегрирования, построим график функции.
Примечание: Основная статья про численное интегрирование — Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.
В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0.
Построение модели
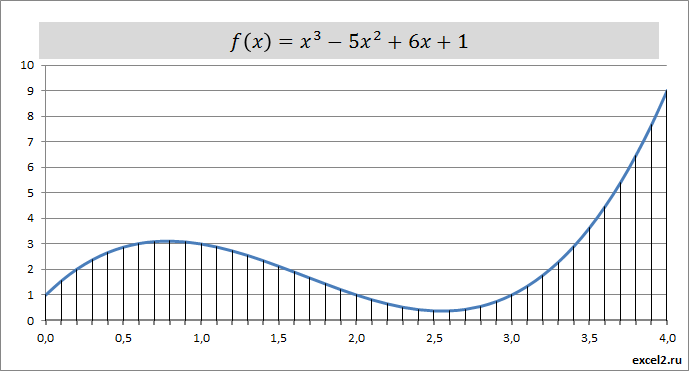
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).
Формула для вычисления интеграла Методом Симпсона следующая:
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.
Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:
- Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
- Значения в узлах с нечетным индексом берутся с весом 4;
- Значения в узлах с четным индексом берутся с весом 2.
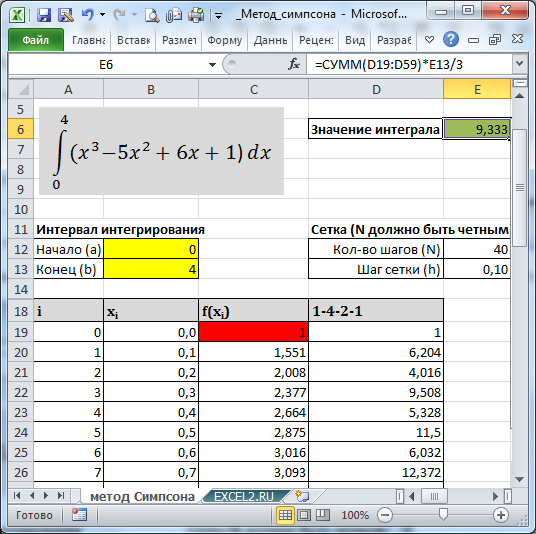
В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы =ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)). В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).
В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3
Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).
Ошибка интегрирования
Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL.
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.
Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/
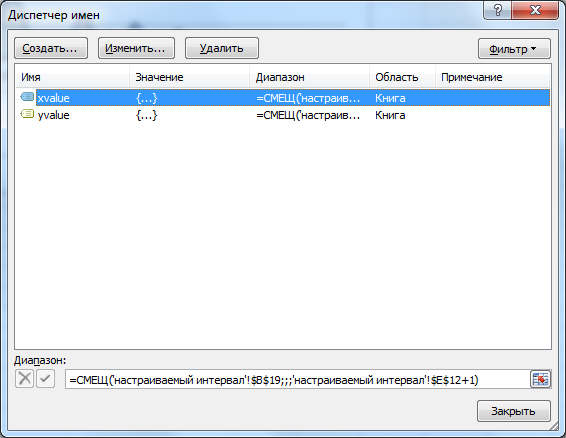
Настраиваемый интервал
На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ().
Данная форма удобна когда необходимо ответить на вопрос «Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?». Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.
Лирическое отступление
Зачем оценивать ошибку интегрирования? Можно ведь взять «маленький» шаг сетки и заведомо получить «точный» результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы!
На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).
ТРЕНИНГИ
Быстрый старт
Расширенный Excel
Мастер Формул
Прогнозирование
Визуализация
Макросы на VBA
КНИГИ
Готовые решения
Мастер Формул
Скульптор данных
ВИДЕОУРОКИ
Бизнес-анализ
Выпадающие списки
Даты и время
Диаграммы
Диапазоны
Дубликаты
Защита данных
Интернет, email
Книги, листы
Макросы
Сводные таблицы
Текст
Форматирование
Функции
Всякое
Коротко
Подробно
Версии
Вопрос-Ответ
Скачать
Купить
ПРОЕКТЫ
ОНЛАЙН-КУРСЫ
ФОРУМ
Excel
Работа
PLEX
© Николай Павлов, Planetaexcel, 2006-2022
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
Техническая поддержка сайта
|
ООО «Планета Эксел» ИНН 7735603520 ОГРН 1147746834949 |
ИП Павлов Николай Владимирович ИНН 633015842586 ОГРНИП 310633031600071 |
Интегральная показательная функция
| Два значения n и z, функции E(n,z) |
В данной статье речь пойдет об интегральной показательной функции, из семейства специальных функций.
Область применения её достаточна специфична, но как говорят в народе, она тем не менее широко известна в узких кругах.
Используется в основном в теории вероятности, статистике, теории игр и для решение некоторых дифференциальных уравнений.
Есть обобщенная формула
Есть формула разложения функции в ряд при n=1
Есть реккурентная формула, при которой можно узнать результат при других значениях n
где n=2,3,4,5….
Есть формула по которой можно определить значения неполной гаммы функции через формулу
Непрерывные цепи
Наиболее интересной особенностью при вычислениях интегральной показательной функции является формула разложения в непрерывную дробь.
Эта формула однозначно и с высокой точностью определяет значение функции при всех n и z, в том числе и на комплексной плоскости, кроме одного случая, когда действительная часть комплексного числа z является отрицательным числом ИЛИ когда модуль z меньше 1. В этом случае, результат не будет верным, и хотя порядок цифр совпадет, все таки погрешность достаточно велика, что бы использовать результат в дальнейших вычислениях.
Можно конечно использовать в этих случаях разложение в ряд, как альтернативный способ, но я пока поищу другой способ.
Использовав разложение функции в непрервывную дробь, мы можем построить реккурентную формулу :
Первоначальное значение 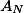
значение N для приемлемой точности можно брать больше 30, но никто не ограничивает Вас поставить и значение 700 или 1000, для высокой точности.
Бот вычисляет значение функции при всех действительных и комплексных значениях, без ограничений. Просьба самим учитывать что при отрицательной действительной части комплексного числа z получаем неверное значение.
Рассмотрим примеры:
| Полученный результат |
%20=%20-0.33740392290097+0.62471325642772i) |
| Полученный результат |
%20=%20-3.016741054E-6+1.91291945E-7i) |
Сравнивая со справочниками и профессиональными математическими программами, мы видим что точность практически 100%.
Теперь примеры где результат неправильный.
А теперь покажем как рассчитывается при вышеуказанных пограничных условиях.
| Полученный результат |
%20=%20-923.51515560353-543.38510375679i) |
На самом деле правильный ответ
-882.633010-536.16514i
Еще раз просьба учитывать этот нюанс. Возможно в дальнейшем автор бота, доработает его, что бы правильные вычисления были на всей комплексной плоскости.
Если есть какие то пожелания, пишите!
Удачных расчетов!
Здесь
мы опишем возможности Excel
при вычислении статистических функций
и дадим пояснения к способу их вызова.
-
Нормальное
распределение.
См. стр.
16-17 пособия [4].
Практически любой справочник по
математической статистике содержит
таблицы функции
и её квантилей. Так как стандартное
нормальное распределение симметрично,
то эти таблицы составляют для значений
и
.
Приведем фрагмент таблицы из сборника
[1].
Таблица 1.1. Функция
нормального распределения Ф(x)
|
x |
0 |
1 |
2 |
3 |
4 |
… |
8 |
9 |
|
… |
||||||||
|
2,05 |
0,97 9818 |
9867 |
9915 |
9964 |
0012 |
… |
0205 |
0253 |
|
06 |
0,98 0301 |
0349 |
0396 |
0444 |
0491 |
… |
0680 |
0727 |
|
07 |
0774 |
0821 |
0867 |
0914 |
0960 |
… |
1145 |
1191 |
|
… |
Слева
в таблице представлено входное значение
с точностью до второго знака после
запятой. Третий знак указан в самой
верхней строке таблицы. С целью
представления на одном листе по
возможности большей информации, таблица
разбита на блоки (выделенные чертой), в
которых числа имеют несколько одинаковых
первых цифр. Эти совпадающие части
приведены только для одного значения
(в столбце под верхней первой ячейкой
с цифрой 0). Так, например,
Ф(2,052)
= 0,97 9915, Ф(2,058)
= 0,98 0205, Ф(2,074)
= 0,98 0960.
Для нахождения квантилей можно
использовать таблицу исходной функции
распределения, отыскивая значение
вероятности внутри таблицы и находя
соответствующее входное значение.
Например, при
верхняя p-квантиль
(то есть решение уравнения
)
будет находиться где-то между 2,053 и
2,054, так как
.
Простая линейная аппроксимация дает
.
В этом же сборнике [1] имеется таблица
значений обратной функции нормального
распределения, иными словами – таблица
p-квантилей (не верхних).
Таблица 1.3.
Функция, обратная функции нормального
распределения
|
p |
0 |
1 |
2 |
3 |
4 |
… |
8 |
9 |
|
… |
||||||||
|
977 |
1,9 |
9723 |
9908 |
0093 |
0279 |
… |
1030 |
1219 |
|
978 |
2,0 1409 |
1600 |
1792 |
1984 |
2177 |
… |
2957 |
3154 |
|
979 |
3352 |
3551 |
3750 |
3950 |
4151 |
… |
4964 |
5169 |
|
0,980 |
5375 |
5582 |
5790 |
6000 |
6208 |
… |
7056 |
7270 |
|
… |
Таким образом,
,
что весьма близко к полученному выше
приближенному значению.
Пакет Excel
располагает четырьмя функциями,
связанными с нормальным распределением.
Для вызова этих функций необходимо
-
вызвать
«Мастера Функций»-
нажать
кнопку
панели инструментов или
-
перейти
в подраздел “Функция”
раздела “Вставка”
главного меню Excel;
-
-
-
в
категории “Статистические”
найти соответствующую функцию; -
заполнить таблицу
аргументов функции.
Альтернативный
способ вызова состоит в непосредственном
обращении к соответствующей функции
из ячейки листа Excel.
Общий вид такого обращения можно
представить следующим образом:
=ИМЯФУНКЦИИ(аргумент1;аргумент2;
…)
Аргументами функции могут быть либо
числа, либо ссылки на ячейки, их хранящие.
Рассмотрим каждую из этих функций по
отдельности.
-
НОРМСТРАСП
– функция стандартного нормального
распределения
.
Аргумент – значение(любое число).
-
НОРМСТОБР
– обратная функция стандартного
нормального распределения
.
Аргумент –(число от 0 до 1).
-
НОРМРАСП –
функция распределения
или функция плотности
нормального
закона. Имеет 4 аргумента:
|
x |
не |
||
|
Среднее |
среднее |
||
|
Стандартное_откл |
корень |
||
|
Интегральная |
0
1 |
||
-
НОРМОБР –
функция, обратная функции нормального
распределения
.
Имеет 3 аргумента, аналогичные первым
трем аргументам предыдущей функции.
Приведем несколько примеров применения
этих функций.
|
Функция |
Значение в |
Характеристика распределения |
|
=НОРМСТРАСП(2,058) |
0,98020500 |
Ф(2,058) |
|
=НОРМСТОБР(0,05) |
-1,64485348 |
t0,95 |
|
=НОРМРАСП(-1; |
0,15865526 |
Ф((2,058-0)/1) |
|
=НОРМРАСП(-1; |
0,24197073 |
φ((2,058-0)/1) |
|
=НОРМОБР(0,95; |
1,64485348 |
0+1* – |
Задание.
Объясните совпадение значений (с
точностью до знака) во второй и пятой
строках этой таблицы.
-
Хи-квадрат
распределение.
См. стр.
18-19 пособия [4].
Сборник таблиц [1] содержит значения так
называемого интеграла
вероятностей хи-квадрат
– в нашей терминологии это просто
функция надежности
.
Таблица имеет два входа – по числу
степеней свободы (верхняя строка) и по
аргументу функции (левый столбец).
Таблица 2.1а.
Интеграл вероятностей
|
x |
m=16 |
… |
m=20 |
||
|
P |
-Δ |
P |
-Δ |
||
|
… |
… |
… |
|||
|
15,0 |
0,52464 |
3627 |
… |
0,77641 |
2929 |
|
5 |
48837 |
3541 |
… |
74712 |
3050 |
|
… |
… |
… |
Здесь,
кроме значения функции распределения
(столбец P),
приведены также первые разности этой
функции (столбец -Δ),
точнее, только 5 значащих цифр после
запятой без первых нулей. Таким образом,
(после запятой поставлен один ноль,
чтобы получилось пять цифр). Если
и
– два рядом стоящие значения аргумента,
то для нахождения значения функции в
промежуточной точке
можно применить аппроксимацию
.
В приведенном нами фрагменте
.
Поэтому
.
Значения верхних p-квантилей
распределения хи-квадрат содержатся
в следующей таблице на стр.166 сборника
[1].
Таблица 2.2а.
Процентные точки распределения
|
Q m |
… |
97,5% |
95% |
… |
5% |
2,5% |
… |
|
… |
… |
||||||
|
19 |
… |
8,907 |
10,117 |
… |
30,144 |
32,852 |
… |
|
20 |
… |
9,591 |
10,851 |
… |
31,410 |
34,170 |
… |
|
… |
… |
Вход в
таблицу осуществляется по числу степеней
свободы (m в левом
столбце) и по вероятности, выраженной
в процентах (Q в верхней
строке). Таким образом,
.
Пакет Excel предоставляет
возможность вычисления как значений
функции надежности
,
так и значений p-квантилей
хи-квадрат распределения. Эти функции
называются ХИ2РАСП
и ХИ2ОБР. Рассмотрим
несколько примеров применения этих
функций.
|
Функция |
Значение в |
Характеристика |
|
=ХИ2РАСП(15,2; |
0,510041 |
|
|
=ХИ2РАСП(15; |
0,776408 |
|
|
=ХИ2ОБР(0,05; |
30,14351 |
|
|
=ХИ2ОБР(0,025; |
34,16958 |
|
-
Распределение
Стьюдента.
См. стр.
19-20 пособия [4].
Таблицы распределения Стьюдента также
имеются в любом справочнике по
математической статистике. Приведем
здесь фрагмент соответствующей
таблицы из сборника [1].
Таблица 3.1а.
Функция распределения Стьюдента
|
k t |
11 |
12 |
… |
19 |
20 |
|
… |
… |
||||
|
2,0 |
0,9646 |
0,9657 |
… |
0,9700 |
0,9704 |
|
1 |
9702 |
9712 |
… |
9753 |
9757 |
|
… |
… |
Эта
таблица имеет два входа – число степеней
свободы
(верхняя строка) и аргумент функции
(левый столбец). Из этой таблицы находим,
что
.
При степенях свободы больше 20 можно
воспользоваться нормальным приближением:
.
Следующая таблица указанного сборника
[1] содержит значения верхних
-квантилей
.
Эта таблица также имеет два входа –
число степеней свободы (левый столбец)
и вероятность в процентах
(верхняя строка). Для наглядности целые
части вместе с запятой приведены только
для верхних чисел в блоке из пяти чисел.
Таблица 3.2.
Процентные точки распределения
Стьюдента
|
Q k |
… |
10% |
5% |
2,5% |
… |
0,05% |
|
… |
… |
|||||
|
19 |
… |
1,3277 |
1,7291 |
2,0930 |
… |
3,8834 |
|
20 |
… |
3253 |
7247 |
0860 |
… |
8495 |
|
… |
… |
Таким
образом,
.
В пакете Excel
имеются встроенные функции
СТЬЮДРАСП,
вычисляющая функцию надежности, и
СТЬЮДРАСПОБР, вычисляющая
верхние квантили.
Функция
СТЬЮДРАСП имеет
три аргумента. Кроме двух естественных
(аргумента
и числа степеней свободы
),
при обращении к этой функции требуется
указать количество хвостов распределения,
которые нужно учитывать (1 или 2). Под
“хвостом” распределения понимается
любой интервал с одним конечным и одним
бесконечным концом. Например, при
вычислении функции надежности ищется
вероятность попадания в область
.
Поэтому
— это функция СТЬЮДРАСП
с одним “хвостом”. Очень часто в
статистической практике требуется
найти вероятность попадания в область
при
,
то есть в область с двумя “хвостами”.
Легко видеть, что функция, вычисляющая
вероятности таких симметричных
интервалов, представляет собой не что
иное, как функцию надежности распределения
модуля
.
Обращение к функции СТЬЮДРАСПОБР
вполне тривиально и полностью аналогично
обращению к функции ХИ2ОБР
(см. выше).
-
Показательное
(экспоненциальное) распределение.
См. стр.
21 пособия [4].
Как функция плотности, так и функция
распределения показательного закона
могут быть вычислены посредством
калькулятора. В Excel
обе эти функции можно вычислить,
воспользовавшись функцией EXP(…).
-
Биномиальное
распределение.
См. стр.
22 пособия [4].
В пакете Excel
имеется возможность вычисления функции
,
которая
при
есть не что иное, как функция распределения
(обратите внимание на различие в первом
аргументе этих функций). Четвертый
параметр функции БИНОМРАСП,
если он не равен нулю, указывает на
необходимость вычисления именно функции
распределения, то есть суммы всех
биномиальных вероятностей до
включительно (в отличие от функции
,
которая вычисляет вероятности до
).
При
функция БИНОМРАСП
вычисляет индивидуальную вероятность
.
Приведем несколько примеров.
|
Функция Excel |
n |
p |
Вероятность |
Результат |
|
БИНОМРАСП(3;10;0,5;1) |
10 |
0,5 |
|
0,171865 |
|
БИНОМРАСП(3;10;0,5;0) |
10 |
0,5 |
|
0,117188 |
|
1-БИНОМРАСП(29;100;0,5;1) |
100 |
0,5 |
|
0,999984 |
|
1-БИНОМРАСП(30;100;0,5;0) |
100 |
0,5 |
|
0,999977 |
80
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10.02.20152.79 Mб19k_5New.pdf



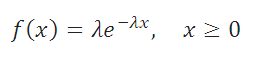

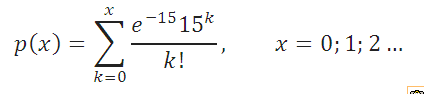
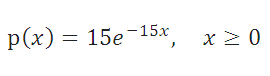
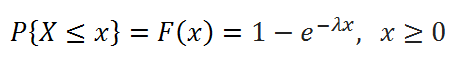
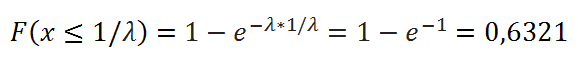
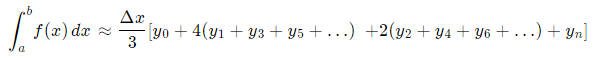
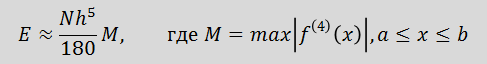
=%20intlimits_1^infty%20{frac{e^{%20-zt}}{t^n}%20dt})
%20=-gamma-operatorname{ln}z+sumlimits_{n=1}^{infty}frac{(-1)^nz^n}{n!cdot%20n},|arg(z)|%3Cpi)
=frac{1}{n-1}(e^{-z}-zE_{n-1}(z)))
=z^{n-1}Gamma(1-n,z))
={cfrac%20{e^{-z}}{z+{cfrac%20{n}{1+{cfrac%20{1}{z+{cfrac%20{n+1}{1+{cfrac%20{2}{z+ldots}%20}}}}}}}})
=frac{1}{e^{z}A_0})

+Nz=0)