Интегральная кривая гранулометрического состава excel

• Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.
• Регистрация

• Узнайте сколько стоит уникальная работа конкретно по Вашей теме:
• Сколько стоит заказать работу?

Это просто были мои попытки построить график, короче говоря, не обращайте внимание!

Шикарный график! Это гениально! Вы мастер экселя!
Огромное Вам спасибо за помощь! Долго не мог построить такой вид графика!

А можете, если не затруднит, дать ссылку на какой нибудь источник, где написано как строить такие графики (нестандартные, с определнными значениями абсцисс, как в моем случае: 0,14, 0,315, 0,63, 1,25, 2,5, 5), если таковые существуют конечно.

Ну или можно попросить Вас написать, как Вы сделали на горизонтальной оси только значения: 0,14, 0,315, 0,63, 1,25, 2,5, 5?

Буду благодарен за ответ!

Суммарная кривая гранулометрического состава

1. Для построения кривой в полулогарифмическом масштабе по оси абсцисс откладывают не диаметры частиц, а их логарифмы. В начале координат ставят обычно число 0,001, а затем, принимая lg 10 равным производному отрезку, откладывают этот отрезок в правую сторону три-четыре раза, делая отметки и ставя против них последовательно числа 0,01; 0,10; 1,00 и 10,00 (см. рис. 9).

2. Расстояния между каждыми двумя метками делят на девять частей пропорционально логарифмам чисел 2, 3, 4, 5, 6, 7, 8 и 9.

3. В первом от начала координат интервале выделенные отрезки будут отвечать диаметрам частиц от 0,002 до 0,009 мм, во втором – от 0,02 до 0,09 мм, в третьем – от 0,2 до 0,9 мм, в четвертом — от 2 до 9 мм.

4. Например, если принять, что lg 10 =1 соответствует отрезку длиной 4 см, то

lg 2 = 0,301 будет соответствовать отрезку 0,301×4 = 1,2 см

lg 3 = 0,477 » » » » 0,477×4 = 1,9 см

lg 4 = 0,602 » » » » 0,602×4 = 2,4 см и т. д.

Указанные отрезки откладывают по оси абсцисс от начала координат и от каждой метки, ограничивающей отрезок длиной 4 см.

5. По оси ординат откладывают суммарное содержание фракций в процентах. Для этого последовательно суммируют содержание фракций, начиная с наиболее мелкой, и по этим числам строят кривую. Каждое из полученных чисел указывает, таким образом, суммарное содержание фракций меньше определенного диаметра.

Рис. 9. Кривая гранулометрического состава в полулогарифмическом масштабе.

Пример расчета кривой, изображенной на рисунке, дан в таблице 5.

Источник

Исходные данные для построения кумулятивной кривой гранулометрического состава горных пород

Логарифм диаметра частиц,

от начала оси абсцисс, см

Для построения логарифмической шкалы по оси абсцисс от начальной точки в некотором масштабе откладываются отрезки, равные десятичным логарифмам ряда чисел. Если отложено число, равное lg d, то около соответствующей точки ставится d. Около начальной точки должна стоять пометка 1, т.к. lg 1 = 0. Таким образом, на логарифмической шкале расстояние от пометки 1 до пометки d равно в выбранном масштабе lg α. Так как lg (10d) = 1+ lg d, то пометки на логарифмической шкале на участке от 10 до 100 будут в точности соответствовать пометкам на участке от 1 до 10. Это же рассуждение может быть проведено и для других участков шкалы. Поэтому, для изображения чисел от 1 до 100 на логарифмической оси требуется увеличить длину оси всего в два раза по сравнению с осью, размеченной от 1 до 10.

При построении кумулятивных кривых гранулометрического состава горных пород, диапазон изменений диаметра частиц превышает их порядок (d_мин = 1 мк, d_мах = 2000 мк). Таким образом, на оси абсцисс необходимо отобразить числа от 1 до 2000. Целесообразно разделить ось на 4 декады, включающие диаметры 1–10 мк, 10–100 мк, 100–1000 мк и 1000–2000 мк. Примем длину оси равной 12 см, тогда на одну декаду будет приходиться 3 см. Соответственно, деление 5 должно стоять на расстоянии L = lg5 × 3 = 2,1 см от начала оси абсцисс, деление 50 – на расстоянии L = lg50 × 3 = 5,1 см, деление 500 – на расстоянии L = lg500 × 3 = 8,1 см.

Процентное содержание по оси ординат откладывают, начиная с самой мелкой фракции. Для каждой последующей фракции величину ординаты получают последовательным суммированием данных для предыдущих размеров, т.е. к процентному содержанию предыдущей фракции прибавляют процентное содержание следующей и т.д. (см. табл. 5.3).

Таким образом, каждая точка графика дает суммарное количество частиц данного размера и размеров, меньших, чем этот размер. По пересечению диаметров частиц строят кривую, которая называется кумулятивной кривой.

Для построения кумулятивной кривой, изображенной на рис. 5.4, использованы исходные данные, представленные в таблице 5.3.

Кумулятивные кривые позволяют определить действующий или эффективный и контролирующий диаметры частиц и вычислить на их основе коэффициент неоднородности, показывающий степень отсортированности пород.

Коэффициент неоднородности (К_н) представляет собой отношение величины контролирующего диаметра частиц (d₆₀) к величине действующего их диаметра (d₁₀):

(5.1)

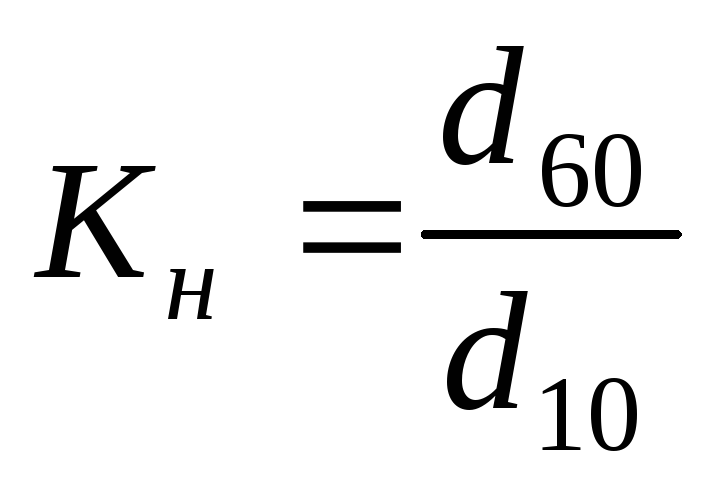
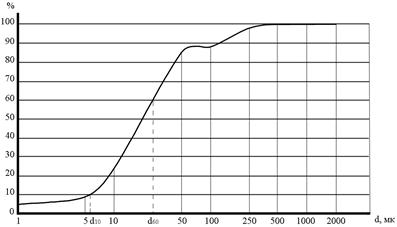
Рис. 5.4. Кумулятивная кривая гранулометрического состава горной породы

Действующим (эффективным) диаметром частиц является такой диаметр, меньше которого в породе содержится 10 % частиц.

Контролирующим диаметром называется диаметр, меньше которого в породе 60 % частиц.

Для определения действующего и контролирующего диаметров частиц, из точек на оси ординат, соответствующих 10 и 60 % их содержанию проводятся линии, параллельные оси абсцисс до пересечения с кумулятивной кривой. Из точек пересечения опускаются перпендикуляры на ось абсцисс (см. рис. 5.4) и определяются значения диаметров частиц. Значение коэффициента неоднородности определяется с точностью до запятой.

Для определения диаметров частиц необходимо определить расстояние от места пересечения соответствующих перпендикуляров до начала оси абсцисс (L). Диаметр частиц определится из выражения lg d = L/3.

Коэффициент неоднородности не может быть меньше единицы и практически не бывает больше 200. Чем меньше его величина − тем однороднее порода. Принято, что при К_н = 5 порода считается однородной и для нее характерно ламинарное движение подземных вод. Если К_н > 5, то порода считается неоднородной по гранулометрическому составу, и подземные воды в ней имеют турбулентный характер движения.

.

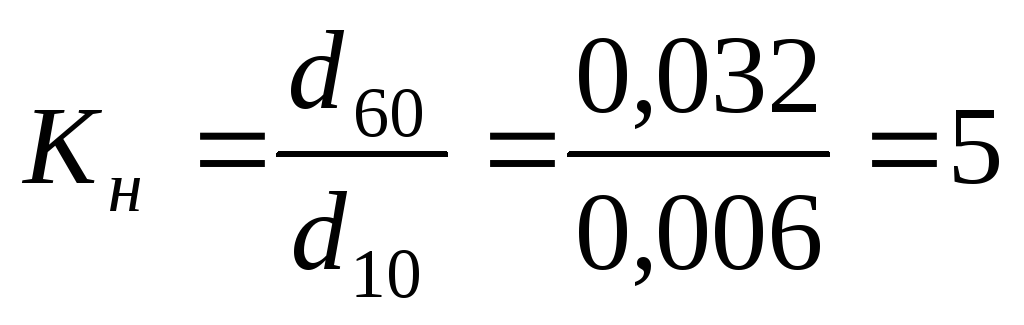
Так как К_н > 5, то горная порода по гранулометрическому составу считается неоднородной, и подземные воды в ней имеют турбулентный характер движения.

В соответствии с указанным вариантом (см. прил. 3, 4) представьте результаты анализа гранулометрического состава горных пород в виде гистограммы, циклограммы, графика – треугольника и интегральной (кумулятивной) кривой. Определите коэффициент неоднородности горной породы.

Источник

Графическая обработка данных гранулометрического анализа

Лабораторная работа 4

Цель и содержание. Ознакомить студентов с графическими методами обработки данных гранулометрического анализа и использованием этих данных в генетических целях. В методических указаниях дается краткая характеристика наиболее распространенных способов графической обработки данных гранулометрического анализа, оценивается степень их наглядности и применимости и приводится методика построения различных графиков. Знания, полученные при выполнении этой работы, используются студентами при выполнении курсовой работы по дисциплине «Литология».

Теоретическое обоснование. Графическое изображение результатов гранулометрического анализа позволяет более наглядно представить полученные данные (гистограммы и циклограммы), сопоставить их в целях обобщения (кумулятивные кривые и треугольные диаграммы) и использовать для решения вопросов генезиса песчано-алевритовых пород (кривые распределения, генетическая диаграмма Passega).

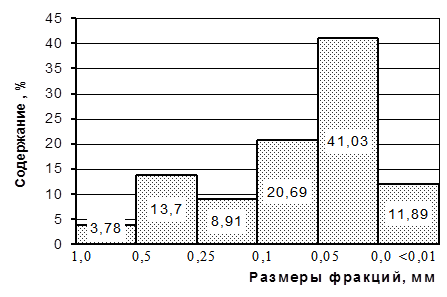
Самый наглядный график — гистограмма, на котором содержание каждой фракции изображается отдельно, чаще всего высотой столбика (рис.10).

Рисунок 10 — Гистограмма

Достоинство гистограмм — большая наглядность и возможность показа раздельно любой фракции. Недостаток — невозможность совмещения на одной диаграмме нескольких анализов. По гистограммам и кривым распределения, на которых отчетливо отображается как диапазон размерностей зерен, участвующих в строении породы, так и размер преобладающих фракций и ее содержание, может быть произведена оценка отсортированности породы.

По ее виду кривой распределения можно судить об отсортированности породы: высокая, узкая вершина будет у хорошо отсортированных пород; менее резкая — у плохо отсортированных.

Циклограмма представляет круг, разделенный на секторы, площади или дуги которых пропорциональны содержанию фракций (рис. 11). Данный график для сопоставления массовых анализов неудобен.

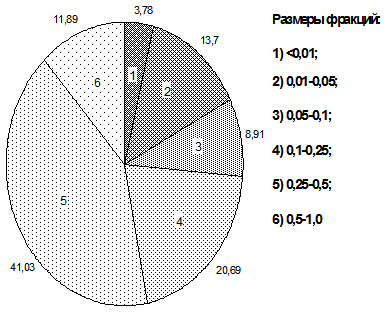
Рисунок 11 — Циклограмма

Кумулятивные или суммарные нарастающие кривые применяют как для изображения одного анализа и вычисления гранулометрических коэффициентов, так и для сопоставления небольшого числа анализов. Кумулятивные кривые по сравнению с гистограммами менее наглядны, т.к. содержания отдельных фракций на них непосредственно не выражаются. Однако по кумулятивной кривой можно определить содержание любой фракции, даже не определявшейся механическим анализом. Кроме того, более простой вид графика позволяет наносить на одну диаграмму несколько кривых и затем сравнивать их (рис.12).

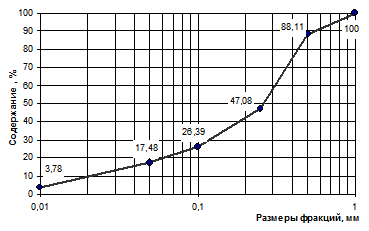
Рисунок 12 –Кумулятивная кривая

Простейшим математическим способом обработки кумулятивных кривых является вычисление трех гранулометрических коэффициентов: среднего размера зерен, коэффициента сортировки и коэффициента асимметрии. Средним или медианным диаметром (Мd) называется такой размер зерен, меньше и больше которого содержится по 50% частиц.

Величина коэффициента сортировки So характеризует степень однородности обломочного материала в породе. So всегда > 1 (обычно от 1,5 до 3), лишь для абсолютно однородного песка, состоящего из обломков, принадлежащих одной фракции, So = 1. Часто So (особенно в иностранной литературе) определяют по соотношению

Отсортированность песков определяется по таблице:

Степень отсортированности песков	So=Qз / Q1 —	So= √Q3/Q1
Хорошо отсортированы	1 — 2,5	1 — 1,58
Средне отсортированы	2,5 — 4, 5	1,58- 2,12
Плохо отсортированы	> 4,5	> 2,5

Коэффициент асимметрии Sк указывает, в какую сторону (больших или меньших размеров) сдвинута мода (диаметр наиболее распространенных частиц) относительно вычисленного медианного диаметра. По кумулятивной кривой можно определить коэффициент К, характеризующий крупнозернистую часть породы. Эта величина характеризует такую размерность зерен, относительно которой более крупные зерна, встречаемые в породе, составляют 1% от всей породы. Крупнозернистая часть важна в том отношении, что она соответствует максимальной силе потока.

Треугольные диаграммы применяют для сопоставления результатов многих анализов — в этом его преимущество перед всеми ранее рассмотренными. Анализы здесь изображаются одной точкой, но содержания фракций определены быть не могут, т.к. при нанесении на треугольную диаграмму, допускающую показ лишь трех компонентов, фракции объединяются.

Материалы. Таблицы данных гранулометрического анализа, полулогарифмическая сетка для построения кривых распределения и кумулятивных кривых, сетка с двойным логарифмическим масштабом для построения генетической диаграммы Пассега.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Построение кривых гранулометрического состава.

1.Используя данные графы 1 и 4 табл.1,строят гранулометрическую кривую в двух вариантах

Характер кривых показывает степень однородности частиц слагающих грунт.

Так, например, если кривая крутая, то грунт однороден, если кривая пологая, то грунт неоднороден.

2. По графику определяют диаметры частиц, соответствующие 10 – и 60 % — ному содержанию суммы всех частиц.

3. По кривым гранулометрического состава определяют коэффициент неоднородности.

Коэффициент неоднородности представляет собой величину отношения :

Действующим диаметром пользуются при определении коэффициента фильтрации песчаных грунтов по эмпирическим формулам.

4. Гранулометрическая кривая дает возможность определить наименование исследуемой породы по таблицам А.В.Приклонского (табл.2 и табл.3)

Общая классификация пород по гранулометрическому составу

Размер частиц, мм

При преобладании песчаных частиц, наименование породы определяется в зависимости от процентного содержания частиц с диаметром d

Порядок выполнения работы:

По результатам разделения горной породы на фракции построить гранулометрическую кривую в нормальном и полулогарифмическом масштабе.

Источник

2.3. Способы графического изображения гранулометрического состава грунтов

Для графического изображения гранулометрического состава существует ряд способов, из которых наиболее распространены способы циклограммы, кривой гранулометрического состава и диа­граммы-треугольника.

2.3.1. Циклограмма гранулометрического состава

Площадь круга, очерченного произвольным диаметром, разбивается на секторы с длинами дуг, пропорционально содержанию каждой фракции. Площади секторов закрашивается или заштриховывается в соответствии с принятыми условными обозначениями фракций. Возле каждого отрезка дуги снаружи указывается процентное содержание соответству­ющей фракции

2.3.2. Суммарная кривая гранулометрического состава

Способ суммарной кривой гранулометрического состава имеет наибольшее распространение. К ривая гранулометрического состава может быть построена в обыкновенном или в полулогарифмическом масштабе. Обыкновенный масштаб неудобен тем, что вследствие широкого диапазона диаметров частиц графики получаются непомерно растянутыми по оси абсцисс.

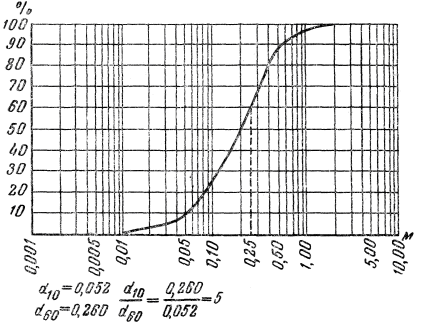
Рис.1. Интегральная кривая гранулометрического состава

Построение кривых в полулогарифмическом масштабе позволяет наносить содержание легких фракций с достаточной точ­ностью, не удлиняя кривую по оси абсцисс.

Для построения кривой в полулогарифмическом масштабе (рис. 1) по оси абсцисс откладывают не диаметры частиц, а их логарифмы или величины, пропорциональные логарифмам. В начале координат ставят обычно число 0,001, а затем, принимая lg 10 равным произвольному отрезку, откладывают этот отрезок в правую сторону три–четыре раза, делая отметки и ставя против них последовательно числа 0,01; 0,10; 1,00 и 10,00. Расстояния между каждыми двумя метками делят на девять частей пропорционально логарифмам чисел 2, 3, 4, 5, 6, 7, 8 и 9.

В первом интервале от начала координат, выделенные отрезки будут соответствовать диаметрам частиц размером от 0,002 до 0,009 мм, во втором – от 0,02 до 0,09 мм, в третьем – от 0,2 до 0,9 мм, в четвертом – от 2 до 10 мм.

Например, если принять, что lg 10 = 1 – соответствует отрезку дли­ной 4 см, то lg 2 = 0,301 будет соответствовать отрезку 0,301 4 = 1,2 см, а lg 9 = 0,954 будет соответствовать отрезку 0,954 4 = 3,82 см.

Указанные отрезки откладывают по оси абсцисс от начала коор­динат и от каждой метки, ограничивающей отрезок длиной 4 см.

Аналогичную шкалу можно разметить на графике, пользуясь шкалой делений логарифмической линейки. По оси ординат откладывают суммарное содержание фракций в процентах. Для этого последовательно суммируют содержание фракций, начиная с наиболее мелкой, и по этим числам строят кри­вую. Каждое из полученных чисел указывает, таким образом, сум­марное содержание фракций меньше определенного диаметра.

Данные, использованные для построения кривой, изображенной на рис.1, приведены в табл. 7.

Таблица 7 – Данные гранулометрического анализа

Источник

Adblock
detector

Обновлено: 14.04.2023

Наиболее распространёнными графическими представлением анализов гранулометрического состава горных пород (табл. 3.2) являются гистограммы, циклограммы, графики треугольники и интегральные (кумулятивные) кривые.

Результаты гранулометрического анализа горных пород

Гистограмма – столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Гистограмма представляет собой совокупность смежных прямоугольников, построенных на прямой линии.

Для изображения на гистограмме гранулометрического состава горных пород на вертикальной оси откладывают процентное содержание фракций, а на горизонтальной оси – произвольно выбранные равные отрезки.

На отрезках, соответствующих каждой фракции, строится как на основании прямоугольник высотой, равной процентному содержанию частиц во фракции.

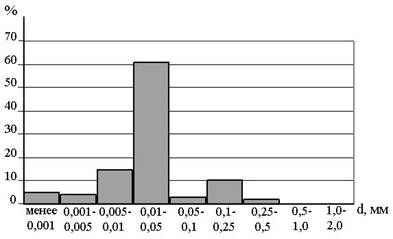
Гистограмма, изображающая гранулометрический состав горной породы анализа № 1 представлена на рис. 3.1.

Рис. 3.1. Гистограмма гранулометрического состава пород анализа №1

При построении циклограмм, характеризующих гранулометрический состав горных пород, вычерчивается окружность произвольного радиуса. Площадь окружности принимается за 100 %. Величина отдельной фракции показывается в виде сектора, площадь которого пропорциональна ее процентному содержанию. Сектора заштриховываются в соответствии с принятыми к фракциям условным обозначениям.

Циклограмма, изображающая гранулометрический состав горной породы анализа № 1 представлена на рис. 3.2.

Рис. 3.2. Циклограмма гранулометрического состава пород анализа №1

Графические изображения результатов гранулометрического анализа в виде гистограмм и циклограмм имеют существенный недостаток, который заключается в невозможности изображения результатов массовых определений гранулометрического состава на одной гистограмме или циклограмме.

График-треугольник (см. приложение 1) представляет собой равносторонний треугольник, каждая сторона которого разделена на 100 равных частей. Если принять, что каждая из вершин треугольника отражает нулевое содержание одной из основных фракций, тогда по углам треугольника будет отмечаться стопроцентное содержание этих фракций. Линии, параллельные сторонам, будут соответствовать процентному содержанию той или иной фракции, а это значит, что точка внутри треугольника будет соответствовать составу породы.

По положению точки внутри графика – треугольника можно судить о распределении фракции в горной породе и в зависимости от этого дать определение породы.

График-треугольник гранулометрического состава горной породы анализа № 1 представлен на рис. 3.3.

Рис. 3.3. График-треугольник гранулометрического состава горной породы анализа № 1

Анализируя расположение точки 1 внутри графика – треугольника, можно сделать вывод, что рассматриваемая порода относится к пылеватым суглинкам.

Интегральные (кумулятивные) кривые гранулометрического состава строятся в прямоугольной системе координат в полулогарифмическом масштабе (когда по одной оси задается логарифмический масштаб, а по другой – линейный).

Использование полулогарифмического масштаба вызвано тем, что при гранулометрическом анализе частицы подразделяются на фракции, размеры которых убывают в геометрической прогрессии. По оси абсцисс откладываются логарифмы диаметров фракций частиц, а по оси ординат – содержание данной фракции в породе в процентах.

Для удобства определения логарифмов диаметров частиц переводят эти размеры из миллиметров в микроны для того, чтобы не получать отрицательных логарифмов (табл. 3.3).

Исходные данные для построения кумулятивной кривой

гранулометрического состава горных пород

Фракция	Сумма фракций	Расчетные значения
Диаметр частиц, мм	Содержание частиц, %	Диаметр частиц, мм	Содержание частиц, %	Логарифм диаметра частиц, lg d	Расстояние от начала оси абсцисс, см
0,001
0,001–0,005	0,7	2,3
0,005–0,01	1,0	3,3
0,01–0,05	1,7	5,6
0,05–0,1	2,0	6,6
0,1–0,25	2,4	7,9
0,25–0,5	2,7	8,9
0,5–1,0	3,0	9,9
1,0–2,0	3,3	12,0

Так как lg (10d) = 1+ lg d, то пометки на логарифмической шкале на участке от 10 до 100 будут в точности соответствовать пометкам на участке от 1 до 10. Это же рассуждение может быть проведено и для других участков шкалы. Поэтому, для изображения чисел от 1 до 100 на логарифмической оси требуется увеличить длину оси всего в два раза по сравнению с осью, размеченной от 1 до 10.

При построении кумулятивных кривых гранулометрического состава горных пород, диапазон изменений диаметра частиц превышает их порядок (d_мин = 1 мк, d_мах = 2000 мк). Таким образом, на оси абсцисс необходимо отобразить числа от 1 до 2000. Целесообразно разделить ось на 4 декады, включающие диаметры 1–10 мк, 10–100 мк, 100–1000 мк и 1000–2000 мк. Примем длину оси равной 12 см, тогда на одну декаду будет приходиться 3 см. Соответственно, деление 5 должно стоять на расстоянии L = lg5 × 3 = 2,1 см от начала оси абсцисс, деление 50 – на расстоянии L = lg50 × 3 = 5,1 см, деление 500 – на расстоянии L = lg500 × 3 = 8,1 см.

Процентное содержание по оси ординат откладывают, начиная с самой мелкой фракции. Для каждой последующей фракции величину ординаты получают последовательным суммированием данных для предыдущих размеров, т.е. к процентному содержанию предыдущей фракции прибавляют процентное содержание следующей и т.д. (см. табл. 3.3).

Таким образом, каждая точка графика дает суммарное количество частиц данного размера и размеров, меньших, чем этот размер. По пересечению диаметров частиц строят кривую, которая называется кумулятивной кривой (рис. 3.4).

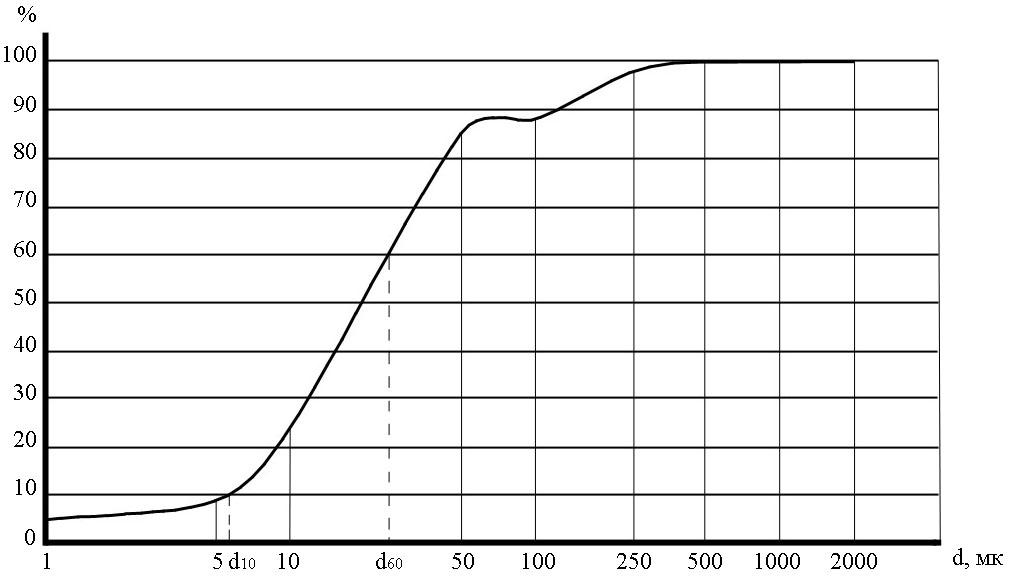
Кумулятивные кривые позволяют определить действующий или эффективный и контролирующий диаметры частиц и вычислить на их основе коэффициент неоднородности, показывающий степень отсортированности пород.

Рис. 3.4. Кумулятивная кривая гранулометрического состава горной породы

Коэффициент неоднородности (К_н) представляет собой отношение величины контролирующего диаметра частиц (d₆₀) к величине действующего их диаметра (d₁₀):

Действующим (эффективным) диаметром частиц является такой диаметр, меньше которого в породе содержится 10 % частиц.

Контролирующим диаметром называется диаметр, меньше которого в породе 60 % частиц.

Для определения действующего и контролирующего диаметров частиц, из точек на оси ординат, соответствующих 10 и 60 % их содержанию проводятся линии, параллельные оси абсцисс до пересечения с кумулятивной кривой. Из точек пересечения опускаются перпендикуляры на ось абсцисс (см. рис. 5.4) и определяются значения диаметров частиц. Значение коэффициента неоднородности определяется с точностью до запятой.

Для определения диаметров частиц необходимо определить расстояние от места пересечения соответствующих перпендикуляров до начала оси абсцисс (L). Диаметр частиц определится из выражения lg d = L/3.

lg d₁₀ = 2,5/3; d₁₀ = 10 0,8 = 6 мк = 0,006 мм;

lg d₆₀ = 4,4/3; d₁₀ = 10 1,5 = 32 мк = 0,032 мм.

Так как К_н > 5, то горная порода по гранулометрическому составу считается неоднородной, и подземные воды в ней имеют турбулентный характер движения.

По приведенным в табл.2 результатам зернового анализа сыпучего грунта постройте кривую зернового состава, определите степень неоднородности и дайте наименование грунта по этим показателям.

Для построения кривой зернового состава составим таблицу № 2:

Зерновой состав грунта по массе ,%, при размере частиц

По данным таблицы 2 результатам зернового анализа сыпучести грунта построим кривую зернового состава.

Гранулометрический (зерновой) состав грунта является одной из важнейших характеристик. Он выражается кривой гранулометрического состава — интегральной кривой распределения зерен грунта по размеру. Чем более неоднородным является грунт, тем более пологой будет кривая его состава.

По данным таблицы 1 приложения 2 (методические указания стр.28) определим наименование грунта: песок крупный (масса частиц с d< 0.5 мм 25%, а частиц с d< 10 мм составляет 80%).

Строим кривую гранулометрического состава в полулогарифмическом масштабе.

Рис.1. Кривая гранулометрического состава грунта (С_v = 15).

Степень неоднородности гранулометрического состава рассчитывается по формуле

Данный вид грунта: песок крупный является неоднородным, т.к. С_v>3.

Чем ближе степень неоднородности к единице, тем более однородным по гранулометрическому составу является грунт.

Задача 3. Письменный ответ

. Какие вопросы рассматриваются в курсе механики грунтов, его задачи?

Механика грунтов — научная дисциплина, в которой изучаются напряженно-деформированное состояние грунтов и грунтовых массивов, условия прочности грунтов, давление на ограждения, устойчивость грунтовых массивов против сползания и разрушения, взаимодействие грунтовых массивов с сооружениями и ряд других вопросов. Механика грунтов является составной частью геомеханики.

Задачи прогноза механического поведения грунтов и грунтовых массивов. Для этого производятся:

установление физических и механических свойств грунтов и возможности их использования в нужных целях, а, в случае необходимости, и улучшение строительных свойств грунтов;

определение напряженно-деформированного состояния грунтовых массивов, возможного его изменения в последующем;

определение общей устойчивости этих массивов, взаимодействующих с инженерными сооружениями или непосредственно устойчивости их самих, если они являются сооружениями. Таким образом, основная задача — это оценка состояния в настоящий момент и прогноз дальнейшего поведения грунтов и массивов из них, прогноз происходящих в них процессов.

. Какие основные характеристики грунта являются основными?

Основные физические характеристики грунта

Основными физическими характеристиками грунта (являются:

Остальные физические характеристики могут быть вычислены с их использованием.

. Что называется коэффициентом бокового давления грунта, от чего он зависит и как связан с коэффициентом Пуассона?

Боковое давление в этом случае является реактивным. Примером может служить грунт, обжимаемый в одометре (компрессионном приборе). Коэффициент бокового давления зависит от вида грунта, его плотности и влажности. С коэффициентом Пуассона он связан следующей зависимостью:

Он изменяется в пределах от 0 до 1.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

из интернета
Основой для построения градуировочного графика является приготовление стандартных растворов.
Стандартные растворы необходимо готовить из аттестованных государственных образцов (ГСО). Если таковых не имеется, необходимо четко придерживаться основных требований к точности приготовления стандартных растворов:
• следует применять соединения квалификации не ниже ч.д.а;
• использование реактивов с просроченным сроком годности недопустимо;
• для приготовления стандартных растворов использовать только гостированную мерную посуду.
Особое внимание обратить на условия и сроки хранения растворов с содержанием вещества 1 мг/см3 хранят 1 год, 0,1 мг/см3 – 3 месяца (если нет других указаний, а также если нет помутнения, хлопьев, осадка), растворы с меньшим содержанием применяются свежеприготовленными. Стандартные растворы фильтровать не допускается.
Для определения содержания вещества методом градуировочного графика готовят 3 серии шкал стандартов. Указания по приготовлению шкалы стандартов конкретно оговорены в каждой методике.
При приготовлении параллельных шкал рабочие растворы готовят соответствующим разбавлением основного стандартного раствора, который готовится из одной взятой навески или ГСО.
Градуировочный график строят на миллиметровой бумаге или в электронной форме при помощи Excel, откладывая на оси абсцисс, указанную в методике определения концентрацию, а по оси ординат – измеренные значения оптической плотности.
Количественное значение оптической плотности для каждой точки градуировочного графика определяется как среднее арифметическое результатов параллельных измерений 3-х шкал.
С целью уменьшения погрешности графического измерения, необходимо подобрать такой масштаб графика, чтобы угол его наклона приблизительно равнялся 45º.
Градуировочный график должен нести следующую информацию:
• название определения;
• НД на метод проведения исследования;
• метод определения;
• марка КФК, его заводской номер;
• длина волны;
• длина рабочей грани кюветы;
• раствор сравнения (растворитель, нулевой раствор и т.д.), т.е. относительно чего снимались показания испытуемого раствора;
• дата построения;
• даты поверки;
• на графике должны присутствовать данные 3-х параллельных измерений и среднее арифметическое значение (в виде таблицы).
Градуировочный график строится один раз в год и после ремонта прибора. Поверка графика должна проводиться 1 раз в квартал (если нет других указаний в методике определения), а также после приготовления реактивов из новой партии, поверки прибора. Поверка проводится по 3-м точкам графика наиболее часто встречающихся в работе концентраций. Данные поверки заносятся в журнал поверок градуировочных графиков или наносятся на обратную сторону графика в виде таблицы.

При построении градуировочного графика должна соблюдаться прямая зависимость между оптической плотностью и концентрацией. Прямолинейность графика сохраняется только в интервале концентраций, указанных в методике. Поэтому продлевать градуировочную прямую выше последней указанной в методике точки не допустимо. Находить значение концентраций испытуемого раствора по градуировочному графику ниже первой точки графика не рекомендуется, т.к. это определение несет большую погрешность. В таком случае результат исследования следует записывать в виде «менее . мг/дм3».
Применение регрессионного анализа для построения градуировочного графика при фотометрическом анализе
В практике фотометрического анализа для построения градуировочных графиков и расчета коэффициентов уравнения регрессии используется метод наименьших квадратов, который имеет погрешность 1–5% при доверительной вероятности 95%.

Точная зависимость между концентрацией определяемого ингредиента (Х) и оптической плотностью (Y) будет выражаться уравнением:
y=a+bх,
которое называется уравнением регрессии или уравнением градуировочного графика. На градуировочном графике это уравнение представляет уравнение прямой. Первая и последняя точка отрезка есть диапазон определения, регламентируемый данной методикой.
Метод расчётов коэффициентов а и b уравнения регрессии:
Коэффициенты а и bопределяются по следующим формулам:
а = 1/n (∑y — b∑x) ,
b = (∑xy – nx¯y¯) / (∑x2 – nx¯2),
где x¯ и y¯ — средние значения xи y.
Для расчётов используются упрощённые выражения для сумм квадратов:
∑U2 = ∑(x – x¯)2 = ∑x2 – nx¯2 = ∑x2 – (∑x)2/n
∑V2 = ∑(y – y¯)2 = ∑y2 – ny¯2 = ∑y2 – (∑y)2/n
∑UV = ∑(x – x¯)(y – y¯) = ∑xy – nx¯y¯ = ∑xy – (∑x∑y)/n
Используя упрощённые уравнения, получаем следующее выражение для расчёта коэффициента b:
b = ∑UV / ∑U2
После того как bнайдено, его подставляют в уравнение для вычисления коэффициента а.
Получив оба коэффициента, мы получаем уравнение уточнённой прямой градуировочного графика.
Пример расчёта:
Рассмотрим пример построения градуировочного графика на примере фотометрического определения железа (II). Сведём, полученные в результате измерения значения поглощений шести (n=6) стандартных растворов в таблицу:

НЕ ТРЕБУЕТ ПАРОЛЬ
требования >=Excel 2010
Рабочая версия, прежде чем мне писать посмотрите видео, программа не подвисает а необходимо подождать расчёта.
Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления.
Исправлено: Блокировка некоторых полей, скрытие ненужных листов.

texadmin писал(а): ↑ 15 Октябрь 2017 из интернета
Основой для построения градуировочного графика является приготовление стандартных растворов.
Стандартные растворы необходимо готовить из аттестованных государственных образцов (ГСО). Если таковых не имеется, необходимо четко придерживаться основных требований к точности приготовления стандартных растворов:
• следует применять соединения квалификации не ниже ч.д.а;
• использование реактивов с просроченным сроком годности недопустимо;
• для приготовления стандартных растворов использовать только гостированную мерную посуду.
Особое внимание обратить на условия и сроки хранения растворов с содержанием вещества 1 мг/см3 хранят 1 год, 0,1 мг/см3 – 3 месяца (если нет других указаний, а также если нет помутнения, хлопьев, осадка), растворы с меньшим содержанием применяются свежеприготовленными. Стандартные растворы фильтровать не допускается.
Для определения содержания вещества методом градуировочного графика готовят 3 серии шкал стандартов. Указания по приготовлению шкалы стандартов конкретно оговорены в каждой методике.
При приготовлении параллельных шкал рабочие растворы готовят соответствующим разбавлением основного стандартного раствора, который готовится из одной взятой навески или ГСО.
Градуировочный график строят на миллиметровой бумаге или в электронной форме при помощи Excel, откладывая на оси абсцисс, указанную в методике определения концентрацию, а по оси ординат – измеренные значения оптической плотности.
Количественное значение оптической плотности для каждой точки градуировочного графика определяется как среднее арифметическое результатов параллельных измерений 3-х шкал.
С целью уменьшения погрешности графического измерения, необходимо подобрать такой масштаб графика, чтобы угол его наклона приблизительно равнялся 45º.
Градуировочный график должен нести следующую информацию:
• название определения;
• НД на метод проведения исследования;
• метод определения;
• марка КФК, его заводской номер;
• длина волны;
• длина рабочей грани кюветы;
• раствор сравнения (растворитель, нулевой раствор и т.д.), т.е. относительно чего снимались показания испытуемого раствора;
• дата построения;
• даты поверки;
• на графике должны присутствовать данные 3-х параллельных измерений и среднее арифметическое значение (в виде таблицы).
Градуировочный график строится один раз в год и после ремонта прибора. Поверка графика должна проводиться 1 раз в квартал (если нет других указаний в методике определения), а также после приготовления реактивов из новой партии, поверки прибора. Поверка проводится по 3-м точкам графика наиболее часто встречающихся в работе концентраций. Данные поверки заносятся в журнал поверок градуировочных графиков или наносятся на обратную сторону графика в виде таблицы.

При построении градуировочного графика должна соблюдаться прямая зависимость между оптической плотностью и концентрацией. Прямолинейность графика сохраняется только в интервале концентраций, указанных в методике. Поэтому продлевать градуировочную прямую выше последней указанной в методике точки не допустимо. Находить значение концентраций испытуемого раствора по градуировочному графику ниже первой точки графика не рекомендуется, т.к. это определение несет большую погрешность. В таком случае результат исследования следует записывать в виде «менее . мг/дм3».
Применение регрессионного анализа для построения градуировочного графика при фотометрическом анализе
В практике фотометрического анализа для построения градуировочных графиков и расчета коэффициентов уравнения регрессии используется метод наименьших квадратов, который имеет погрешность 1–5% при доверительной вероятности 95%.

Точная зависимость между концентрацией определяемого ингредиента (Х) и оптической плотностью (Y) будет выражаться уравнением:
y=a+bх,
которое называется уравнением регрессии или уравнением градуировочного графика. На градуировочном графике это уравнение представляет уравнение прямой. Первая и последняя точка отрезка есть диапазон определения, регламентируемый данной методикой.
Метод расчётов коэффициентов а и b уравнения регрессии:
Коэффициенты а и bопределяются по следующим формулам:
а = 1/n (∑y — b∑x) ,
b = (∑xy – nx¯y¯) / (∑x2 – nx¯2),
где x¯ и y¯ — средние значения xи y.
Для расчётов используются упрощённые выражения для сумм квадратов:
∑U2 = ∑(x – x¯)2 = ∑x2 – nx¯2 = ∑x2 – (∑x)2/n
∑V2 = ∑(y – y¯)2 = ∑y2 – ny¯2 = ∑y2 – (∑y)2/n
∑UV = ∑(x – x¯)(y – y¯) = ∑xy – nx¯y¯ = ∑xy – (∑x∑y)/n
Используя упрощённые уравнения, получаем следующее выражение для расчёта коэффициента b:
b = ∑UV / ∑U2
После того как bнайдено, его подставляют в уравнение для вычисления коэффициента а.
Получив оба коэффициента, мы получаем уравнение уточнённой прямой градуировочного графика.
Пример расчёта:
Рассмотрим пример построения градуировочного графика на примере фотометрического определения железа (II). Сведём, полученные в результате измерения значения поглощений шести (n=6) стандартных растворов в таблицу:

По результатам лабораторных исследований свойств грунтов:

а). построить для образцов песчаного грунта интегрированную кривую гранулометрического состава, определить тип грунта по гранулометрическому составу и степени его неоднородности, произвести оценку плотности сложения и степени водонасыщения; для образцов глинистого грунта определить тип грунта по числу пластичности и разновидность по показателю текучести, произвести предварительную оценку способности грунта к просадочному и набухающему явлениям по исходным данным из таблицы 1

Таблица 1 — Исходные данные к задаче 1а

Плот-ность частиц грунта

границы раскатывания ωр, доли ед.

Влажность границы текучести ωL, доли ед.

Содержание частиц, при их размере

Суммарный состав частиц крупнее 2 мм. составляет 3,8% значит, песок не гравелистый; суммарный состав частиц крупнее 0,5 мм. составляет 33,6% значит, песок не крупный; суммарный состав частиц крупнее 0,25 мм. составляет 63% значит, грунт относится к песку средней крупности.

Для определения однородности грунта необходимо построить кривую однородности грунта, в которой по оси абсцисс откладывают диаметры частиц в миллиметрах, а по оси ординат – процентное содержание частиц нарастающим итогом.

По степени неоднородности гранулометрического состава определяем по формуле

где — диаметры частиц, определяемые по кривой однородности. Пересечения полученной кривой с линиями, которые соответствуют содержанию частиц , дают искомые значения диаметров (рисунок 1).

Так как то по гранулометрической степени грунт является неоднородным.

Важным показателем оценки свойств грунта является плотность их сложения. Плотности сложения песка зависят от коэффициента пористости в естественном состоянии. Значение коэффициента пористости можно определить по формуле:

где — плотность частиц грунта (2,66 т/м 3 ); — природная влажность грунта (0,15); — плотность грунта (1,89 т/м 3 ).

По коэффициенту пористости можем сказать, что наш грунт средней плотности.

Разновидность грунта по степени влажности определяем по коэффициенту водонасыщения:

где – плотность воды (1 т/м 3 ).

Коэффициент водонасыщения равен 0,646, следовательно, грунт средней степени водонасыщения.

Вывод: исследуемый грунт является песком средней крупности, неоднородным, средней плотности и средней степени водонасыщения.

Определение глинистого грунта.

Пластичность грунта определяют в % по формуле:

где — влажность на границе текучести грунтов (0,42=42%); — влажность на стыке раскатывания грунта (0,23=23%).

Также благодаря этим показателям можно определить характеристику текучести грунта

По полученным результатам можем сделать вывод, что исследуемый грунт по пластичности – глина (легкая пылеватая глина), по степени текучести – глина твердая.

В подгруппе пылевато — глинистых грунтов выделяются грунты, обладающие просадочными свойствами. Под действием внешних нагрузок или собственного веса при замачивание эти грунты дают просадку. Поэтому необходимо определить степень просадки грунта.

Для предварительной оценки к просадочным и набухающим свойствам необходимо определить :

где – коэффициент пористости при влажности на границе текучести равный

По результату , следовательно, грунт просадочный; — грунт не набухающий.

Вывод: по исследованиям мы определили, что этот грунт легкая пылеватая глина, твердая, просадочная, но не набухающая.

б). построить график компрессионной зависимости вида ; определить для заданного расчетного интервала давлений коэффициент относительной сжимаемости грунта и охарактеризовать степень его сжимаемости. Необходимые данные сведены в таблицу 2.

Читайте также:

  

• Сколько слотов памяти в ноутбуке gl 75

  

• Черный или серебристый ноутбук

  

• Чем открыть файл яма

  

• Как сделать торрент файл qbittorrent

  

• Как сделать пиксельные пои своими руками

Требуется построить диаграмму стандартного нормального интегрального распределения (стандартное нормальное распределение имеет М = 0 и = 1), используя функцию НОРМСТРАСП.

1. В ячейку A3 введем символ х, а в ячейку ВЗ — символ функции плотности вероятности f(x).

2. Вычислим нижнюю М — За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =0-3*1, а также верхнюю границу — в ячейку Е2 введем формулу =0+3*1.

3. Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.

4. Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.

5. В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение — число, равное верхней границе диапазона.

Функция НОРМРАСПР в EXCEL

6. Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.

7. Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций — НОРМРАСП.

8. Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее — введем число 0, для параметра Стандартное_откл — число 1, для параметра Интегральное — число 0 (весовая).

Диаграмма нормального интегрального распределения в EXCEL

9. Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В16.

10. Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В16) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид — вид графика, щелкнем на кнопке Далее.

11. В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А16). Щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности .

Нормальное распределение. Построение графика в Excel. Концепция шести сигм

Наверное, не все знают, что в Excel есть встроенная функция для построения нормального распределения. Графики нормального распределения часто используются для демонстрации идей статистической обработки данных.

Функция НОРМРАСП имеет следующий синтаксис:

НОРМРАСП (Х; среднее; стандартное_откл; интегральная)

Х — аргумент функции; фактически НОРМРАСП можно трактовать как y=f(x); при этом функция возвращает вероятность реализации события Х

Среднее (µ) — среднее арифметическое распределения; чем дальше Х от среднего, тем ниже вероятность реализации такого события

Стандартное_откл (σ) — стандартное отклонение распределения; мера кучности; чем меньше σ, тем выше вероятность у тех Х, которые расположены ближе к среднему

Интегральная — логическое значение, определяющее форму функции. Если «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения, тот есть суммарную вероятность всех событий для аргументов от -∞ до Х; если «интегральная» имеет значение ЛОЖЬ, возвращается вероятность реализации события Х, точнее говоря, вероятность событий находящихся в некотором диапазоне вокруг Х

Например, для µ=0 имеем:

Скачать заметку в формате Word, пример в формате Excel

Здесь по оси абсцисс единица измерения – σ, или (что то же самое), можно сказать, что график построен для σ = 1. То есть, «-2» на графике означает -2σ. По оси ординат шкала убрана умышленно, так как она лишена смысла. Точнее говоря, высота кривой зависит от плотности точек на оси абсцисс, по которым мы строим график. Например, если на интервал от 0 до 1σ приходится 10 точек, то высота в максимуме составит 4%, а если 20 точек – 2%. Здесь проценты означают вероятность попадания случайной величины в узкий диапазон окрестности точки на оси абсцисс. Зато имеет смысл площадь под кривой на определенном интервале. И эта площадь не зависит от плотности точек. Так, например, площадь под кривой на интервале от 0 до 1σ составляет 34,13%. Это значение можно интерпретировать следующим образом: с вероятностью 68,26% случайная величина Х попадет в диапазон µ ± σ.

Теперь, наверное, вам будет лучше понятен смысл выражения «качество шести сигм». Оно означает, что производство налажено таким образом, что случайная величина Х (например, диаметр вала) находясь в диапазон µ ± 6σ, всё еще удовлетворяет техническим условиям (допускам). Это достигается за счет значительного уменьшения сигмы, то есть случайная величина Х очень близка к нормативному значению µ. На графике ниже представлено три ситуации, когда границы допуска остаются неизменными, а благодаря повышению качества (уменьшению вариабельности, сужению сигма) доля брака сокращается:

На первом рисунке только 1,5σ попадают в границы допуска, то есть только 86,6% деталей являются годными. На втором рисунке уже 3σ попадают в границы допуска, то есть 99,75% являются годными. Но всё еще 25 деталей из каждых 10 000 произведенных являются браком. На третьем рисунке целых 6σ попадают в границы допуска, то есть в брак попадут только две детали на миллиард изготовленных!

Вообще-то говоря, измерение качества в терминах сигм использует не совсем нормальное распределение. 🙂 Вот что пишет на эту тему Википедия:

Опыт показывает, что показатели процессов имеют тенденцию изменяться с течением времени. В результате со временем в промежуток между границами поля допуска будет входить меньше, чем было установлено первоначально. Опытным путём было установлено, что изменение параметров во времени можно учесть с помощью смещения в 1,5 сигма. Другими словами, с течением времени длина промежутка между границами поля допуска под кривой нормального распределения уменьшается до 4,5 сигма вследствие того, что среднее процесса с течением времени смещается и/или среднеквадратическое отклонение увеличивается.

Широко распространённое представление о «процессе шесть сигма» заключается в том, что такой процесс позволяет получить уровень качества 3,4 дефектных единиц на миллион готовых изделий при условии, что длина под кривой слева или справа от среднего будет соответствовать 4,5 сигма (без учёта левого или правого конца кривой за границей поля допуска). Таким образом, уровень качества 3,4 дефектных единиц на миллион готовых изделий соответствует длине промежутка 4,5 сигма, получаемых разницей между 6 сигма и сдвигом в 1,5 сигма, которое было введено, чтобы учесть изменение показателей с течением времени. Такая поправка создана для того, чтобы предупредить неправильною оценку уровня дефектности, встречающееся в реальных условиях.

С моей точки зрения, не вполне внятное объяснение. Тем не менее, во всем мире принята следующая таблица соответствия числа дефектов и уровня качества в сигмах:

Число сигм	Число дефектов на миллион измерений	Процент дефектов (несоответствий)	Уровень качества
6σ	3,4	0,00034%	идеал
5σ	233	0,023%	мировой уровень
4σ	6210	0,62%	приемлемый уровень
3σ	66 807	6,68%	недостаточный уровень
2σ	308 537	30,9%	неприемлемый уровень
1σ	691 462	69,1%

Для сравнения приведу таблицу для нормального распределения: