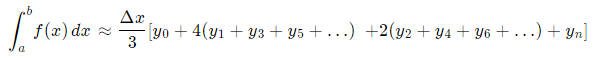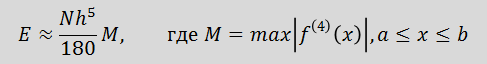history 27 ноября 2022 г.
- Группы статей
Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson’s rule). Покажем как оценить ошибку интегрирования, построим график функции.
Примечание: Основная статья про численное интегрирование — Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.
В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0.
Построение модели
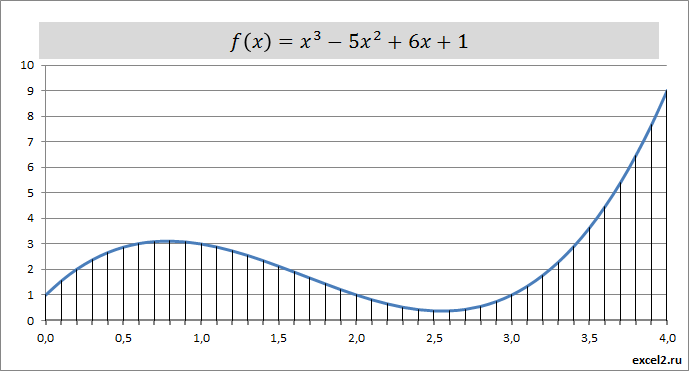
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).
Формула для вычисления интеграла Методом Симпсона следующая:
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.
Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:
- Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
- Значения в узлах с нечетным индексом берутся с весом 4;
- Значения в узлах с четным индексом берутся с весом 2.
В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы =ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)). В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).
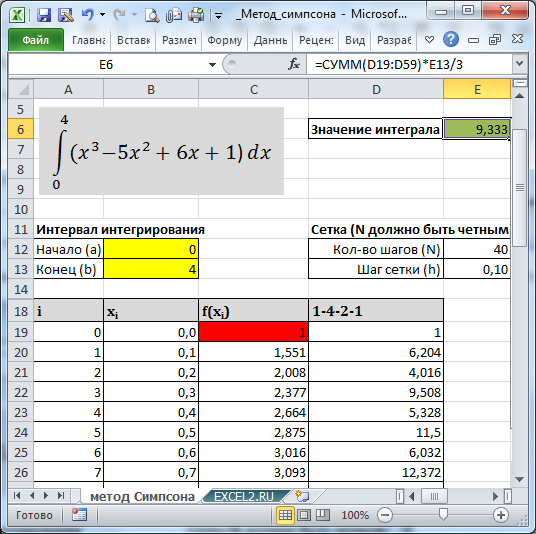
В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3
Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).
Ошибка интегрирования
Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL.
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.
Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/
Настраиваемый интервал
На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ().
Данная форма удобна когда необходимо ответить на вопрос «Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?». Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.
Лирическое отступление
Зачем оценивать ошибку интегрирования? Можно ведь взять «маленький» шаг сетки и заведомо получить «точный» результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы!
На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).
Опубликовано 10 Авг 2015
Рубрика: Справочник Excel | 13 комментариев

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Например:
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
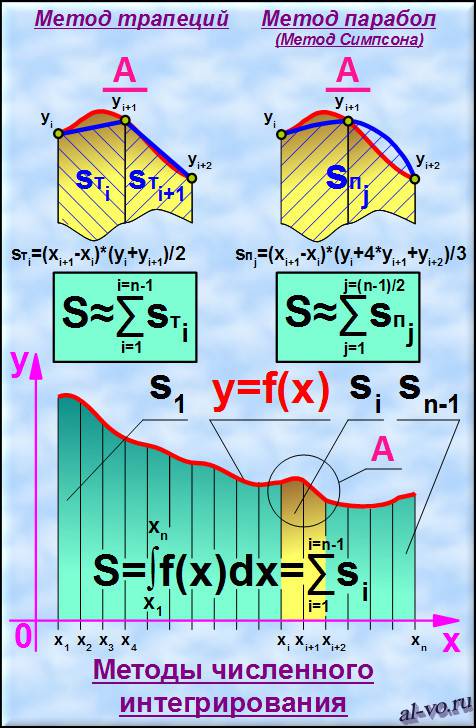
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f (x) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y=f (x). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
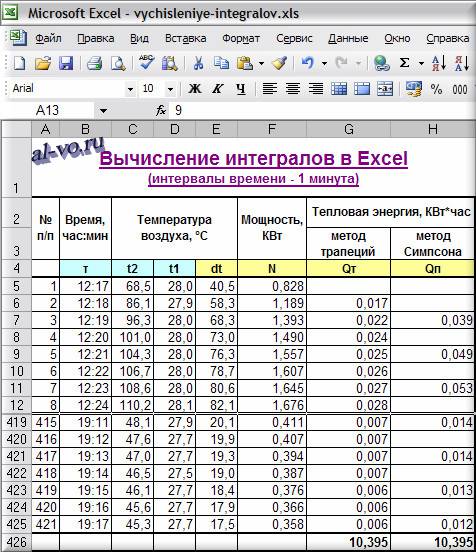
Заполним таблицу.
1. В столбец B вписываем время проведения измерения τi.
2. В столбец C заносим температуры нагретого воздуха t2i, измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i, поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
dti=t2i—t1i
5. Зная удельную теплоемкость воздуха c=1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G=0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
Ni=c*G*dti
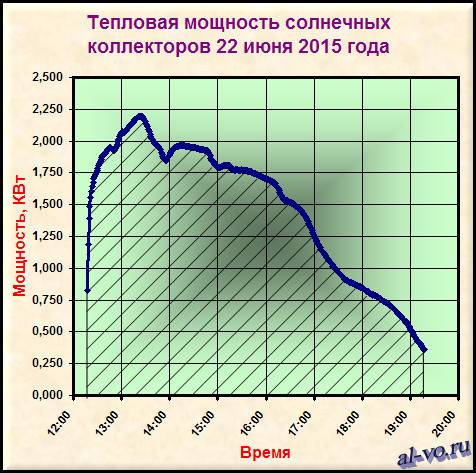
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Qi=(Ni+1+Ni)*(τi+1—τi)/2
Q=ΣQi=10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Qj=(Ni+4*Ni+1+Ni+2)*(τi+1—τi)/3
Q=ΣQj=10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
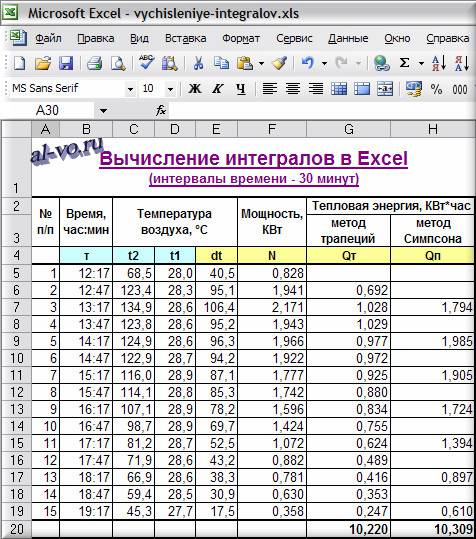
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q=10,220 КВт*час (-1,684%)
По методу Симпсона: Q=10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Численное интегрирование Постановка задачи
Требуется
найти значение определенного интеграла
для некоторой заданной на отрезке
функции
.
Для некоторых функций значение интеграла
можно найти точно. Однако в общем случае
значение интеграла можно найти только
приближенно, используя тот или иной
способ численного интегрирования.
Численное
интегрирование основано на замене
интеграла некой суммой
.
Такая замена следует из определения
интеграла как предела суммы
.
Зафиксировав
,
мы получим предыдущую сумму.
Приближенное
равенство
называется квадратурной
формулой,
– узлами,
а
— коэффициентами
квадратурной
формулы. Разность
называется погрешностью
квадратурной
формулы.
Разобьем
отрезок
на
равных частей точками
.
Получим равномерную сетку:
.
Тогда

Для
построения квадратурной формулы на
всем отрезке
достаточно построить квадратурную
формулу на частичном отрезке
.
Формулы прямоугольников
Пусть
,
т.е. мы аппроксимируем
левой кусочно-постоянной интерполяцией.
Тогда получим

Таким
образом,
.
Эта формула называется формулой левых
прямоугольников.
Рис.
4.1. Метод
левых прямоугольников
Геометрическая
интерпретация метода левых прямоугольников
представлена на рис. 4.1, который показывает,
что точное значение интеграла (площадь
криволинейной области под графиком
)
заменяется на сумму площадей
прямоугольников, построенных под
кусочно-постоянной интерполирующей
функцией.
Аналогично
может быть получена формула
правых прямоугольников.
Здесь
.
В результате получим:
.
Рис.
4.2. Метод
правых прямоугольников
Оценим
погрешность формулы левых прямоугольников:

Воспользуемся
формулой Тейлора:
.
Тогда

,
тогда
,
т.е. формула левых прямоугольников
имеет первый
по
порядок точности.
Аналогичную оценку можно получить для
формулы правых прямоугольников.
Если
на каждом отрезке
заменить значение функции f(x)
на ее значение в середине отрезка, т.е.
получим формулу
средних прямоугольников:

Если
функция
задана таблично, среднее значение на
локальном отрезке можно вычислить с
помощью линейной интерполяции
,
и тогда метод средних имеет вид:
Для
оценки погрешности метода

воспользуемся
формулой Тейлора:
.
Тогда

и
,
то
Пусть
,
тогда
,
т.е.
формула средних прямоугольников имеет
второй порядок
точности.
Формула трапеций
Во всех рассмотренных
формулах площадь криволинейной трапеции
заменялась на площадь прямоугольников.
В
методе трапеций криволинейная трапеция
заменяется на прямоугольную (рис. 4.3),
площадь которой вычисляется по известным
формулам:

Рис.
4.3. Метод
трапеций
Формула
трапеций может быть также получена
путем замены подынтегральной функции
интерполяционным полиномом первой
степени:
.
Действительно

Тогда
для всего отрезка
получим:

Можно
показать, что формула трапеций совпадает
с формулой средних для таблично заданной
функции и также имеет второй порядок
точности.
Формулу
трапеций можно также записать в виде:

Формула Симпсона
При
вычислении интеграла
с помощью метода Симпсона (парабол),
функцию
на локальном отрезке
заменяют параболой, проходящей через
точки
,
,
,
где
– середина локального отрезка. Построим
полином Лагранжа второй степени:

Здесь
,
,
.
Тогда
Таким
образом, мы получаем формулу
Симпсона

Можно
показать, что формула Симпсона имеет
четвертый
порядок точности.
ПРИМЕР
4.1. Вычислить
интеграл J=.
Найдем
значение определенного интеграла точно:
5,25.
Разобьем
отрезок
на 10 частей, т.е.
.
Вычислим значение интеграла по формулам
левых, правых, средних прямоугольников,
по формуле трапеций и формуле Симпсона.
Для этого составим таблицы:
|
|
|
|
|
|
|
|
0 |
-1 |
4 |
-0.85 |
4.213375 |
25.1205 |
|
1 |
-0.7 |
4.267 |
-0.55 |
4.181125 |
24.9675 |
|
2 |
-0.4 |
3.976 |
-0.25 |
3.671875 |
21.9525 |
|
3 |
-0.1 |
3.289 |
0.05 |
2.847625 |
17.0475 |
|
4 |
0.2 |
2.368 |
0.35 |
1.870375 |
11.2245 |
|
5 |
0.5 |
1.375 |
0.65 |
0.902125 |
5.4555 |
|
6 |
0.8 |
0.472 |
0.95 |
0.104875 |
0.7125 |
|
7 |
1.1 |
-0.179 |
1.25 |
-0.35938 |
-2.0325 |
|
8 |
1.4 |
-0.416 |
1.55 |
-0.32863 |
-1.8075 |
|
9 |
1.7 |
-0.077 |
1.85 |
0.359125 |
2.3595 |
|
10 |
2 |
1 |
Для
нахождения интеграла методом левых
прямоугольников, необходимо просуммировать
элементы третьего ряда в диапазоне
и умножить на шаг
.
Аналогично для формулы правых
прямоугольников, суммировать в диапазоне
.
Сумма элементов пятого столбца,
помноженная на шаг, даст результат по
формуле средних прямоугольников.
Согласно формуле трапеций, необходимо
к полусумме первого и последнего значения
элементов третьего столбца добавить
сумму всех остальных членов этого
столбца, и умножить результат на шаг
.
Суммируя значения последнего столбца
и умножая ее на
=0,05,
найдем интеграл по методу Симпсона,
результаты соберем в таблицу:
|
Формула |
5.7225 |
|
Формула |
4.8225 |
|
Формула |
5.23875 |
|
Формула |
5.2725 |
|
Формула |
5.25 |
Как
следует из таблицы, для данной
подынтегральной функции формула левых
прямоугольников дает приближенное
значение с избытком, а формула правых
прямоугольников – с недостатком. Хорошую
точность дали метод трапеций и метод
средних прямоугольников. Результаты
различаются, поскольку значения известной
подынтегральной функции в методе средних
были вычислены в средних точках, а не
получены путем интерполяции. Метод
Симпсона дал абсолютно точное значение
интеграла. Это связано с тем, что
первообразная функция в данном примере
является полиномом четвертого порядка,
для которых метод Симпсона дает точное
значение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
14.03.20161.32 Mб29МК3, большепролетное здание.pdf
- #
Simpson’s rule is a method for evaluating definite integrals. Simpson’s rule uses quadratic polynomials. It often provides more accurate estimates than the trapezoidal rule. If the function you are integrating can be evaluated in Excel, then you can implement Simpson’s rule in Excel.
Subtract the lower endpoint from the upper endpoint and divide by 2. For example, if you want to find the definite integral of cos(x) between 0 and pi/2 radians, subtract 0 from pi/2 and divide by 2 to get pi/4. (Radians are the usual method of measuring angles in calculus; Excel also assumes that angles are measured in radians).
Enter column headers in Excel. Enter «value» in cell A1 and «function» in cell B1, where «function» is the function you are evaluating. In the example, put cos(x) in cell B1.
Enter the lower endpoint, the midpoint and the upper endpoint of the integral in cells A2, A3 and A4 respectively. In the example, put 0 in cell A2, =PI/4 in cell A3 and =PI()/2 in cell A4.
Use Excel to evaluate the function at these three points. In cell B2, enter =function(A2). In the example, put =COS(A2) in cell B2 and copy this to cells B3 and B4.
Evaluate Simpson’s rule. In cell A5, enter =(A3-A2)_(B2+4_B3+B4)/3. The result is the approximation of the integral by Simpson’s rule.
Введение.
Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т.д.
Курс математического анализа содержит разнообразный материал, однако, одним из его центральных разделов является определенный интеграл. Интегрирование многих видов функций подчас представляет собой одну из труднейших проблем математического анализа.
Вычисление определенного интеграла имеет не только теоретический интерес. К его вычислению сводятся иногда задачи, связанные с практической деятельностью человека.
Также понятие определенного интеграла широко используется в физике.
Если же говорить о программе Excel, которая является одной из наиболее известных в обработке электронных таблиц, то без преувеличения можно утверждать, что ее возможности практически неисчерпаемы.
Обработка текста, управление базами данных — программа настолько мощна, что во многих случаях превосходит специализированные программы — редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, нежели заставить применять их на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей Excel тяжело достичь.
За всю историю табличных расчетов с применением персональных компьютеров требования пользователей к подобным программам существенно изменились. В начале основной акцент в такой программе, как, например, Visi Calc, ставился на счетные функции. Сегодня, положение другое. Наряду с инженерными и бухгалтерскими расчетами организация и графическое изображение данных приобретают все возрастающее значение. Кроме того, многообразие функций, предлагаемое такой расчетной и графической программой, не должно осложнять работу пользователя. Программы для Windows создают для этого идеальные предпосылки.
Ряд технологических задач требует увязки в математическое описание всей информации о процессе. Например, для математических моделей химико-технологических процессов одними из основных параметров, характеризующих процессы, являются концентрации реагирующих веществ, температура процесса и др. Как правило, большинство балансовых уравнений в химической технологии представлены системой интегральных и дифференциальных уравнений, в результате решения которых могут быть получены зависимости, характеризующие протекание процесса.
Часто на практике не удается вычислить интеграл аналитическим путем. В этих случаях применяют приближенные методы численного интегрирования.
Постановка задачи
Вычислить определенный интеграл
при условии, что а и b конечны и F(х) является непрерывной функцией х на всем интервале х[a,b]. Во многих случаях, когда подынтегральная функция задана в аналитическом виде, интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница:
Однако этой формулой часто нельзя воспользоваться по следующим причинам:
- первообразная функция f(x) слишком сложна и ее нельзя выразить в элементарных функциях;
- функция f(x) задана в виде таблицы, что особенно часто встречается в задачах химической технологии при обработке экспериментальных данных.
В этих случаях используются методы численного интегрирования.
Задача численного интегрирования состоит в нахождении приближенного значения интеграла по заданным или вычисленным значениям.
Общий подход к решению задачи будет следующим. Определенный интеграл I представляет собой площадь, ограниченную кривой f(x), осью х и переменными х=а и х=b. Необходимо вычислить интеграл, разбивая интервал [a,b] на множество меньших интервалов, находя приблизительно площадь каждой полоски и суммируя их.
В зависимости от способа вычисления подынтегральной суммы существуют различные методы численного интегрирования (методы прямоугольников, трапеций, парабол, сплайнов и др.).
Все методы будут рассматриваться на примере вычисления следующего интеграла:
Метод прямоугольников.
Существует несколько видов формул прямоугольников:
Формула левых прямоугольников.
В общем виде формула левых прямоугольников на отрезке [x0;xn] выглядит следующим образом:
Формула правых прямоугольников.
В общем виде формула правых прямоугольников на отрезке [x0;xn] выглядит следующим образом:
В данной формуле x0=a, xn=b.
Формула средних прямоугольников.
В общем виде формула средних прямоугольников на отрезке [x0;xn] выглядит следующим образом:
где xi=xi-1+h.
В данной формуле, как и в предыдущих, требуется h умножать сумму значений функции f(x), но уже не просто подставляя соответствующие значения x0,x1,…,xn-1 в функцию f(x), а прибавляя к каждому из этих значений h/2 (x0+h/2, x1+h/2,…, xn-1+h/2), а затем только подставляя их в заданную функцию.
На практике данные способы реализуются следующим образом:
Для того, чтобы вычислить интеграл по формуле левых прямоугольников в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст a=.
Ввести в ячейку B1 число 0.
Ввести в ячейку A2 текст b=.
Ввести в ячейку B2 число 3,2.
Ввести в ячейку A3 текст n=.
Ввести в ячейку B3 число 10.
Ввести в ячейку A4 текст h=.
Ввести в ячейку B4 формулу =(B2-B1)/B3.
Вести в ячейку A6 текст i, в B6 — x, в C6 — y0,…,y(n-1).
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число 0.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек C8:C16.
Ввести в ячейку B18 текст сумма:.
Ввести в ячейку B19 текст интеграл=.
Ввести в ячейку C18 формулу =СУММ(C7:C16).
Ввести в ячейку C19 формулу =B4*C18.
Ввести в ячейку C20 текст левых.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 12,500377.
Для того, чтобы вычислить интеграл по формуле правых прямоугольников в Excel, необходимо выполнить следующие действия:
Продолжить работу в том же документе, что и при вычислении интеграла по формуле левых прямоугольников.
В ячейку D6 ввести текст y1,…,yn.
Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D9:D17
Ввести в ячейку D18 формулу =СУММ(D7:D17).
Ввести в ячейку D19 формулу =B4*D18.
Ввести в ячейку D20 текст правых.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 14,45905.
Для того, чтобы вычислить интеграл по формуле средних прямоугольников в Excel, необходимо выполнить следующие действия:
Продолжить работу в том же документе, что и при вычислении интеграла по формулам левых и правых прямоугольников.
В ячейку E6 ввести текст xi+h/2, а в F6 — f(xi+h/2).
Ввести в ячейку E7 формулу =B7+$B$4/2, скопировать эту формулу методом протягивания в диапазон ячеек E8:E16
Ввести в ячейку F7 формулу =КОРЕНЬ(E7^4-E7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек F8:F16
Ввести в ячейку F18 формулу =СУММ(F7:F16).
Ввести в ячейку F19 формулу =B4*F18.
Ввести в ячейку F20 текст средних.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 13,40797.
Исходя из полученных результатов, можно сделать вывод, что формула средних прямоугольников является наиболее точной, чем формулы правых и левых прямоугольников.
Метод трапеций.
В общем виде формула трапеций на отрезке [x0;xn] выглядит следующим образом:
В данной формуле x0=a, xn=b, так как любой интеграл в общем виде выглядит:
h можно вычислить по следующей формуле: h=(b-a)/n (19).
y0, y1,…, yn — это значения соответствующей функции f(x) в точках x0, x1,…, xn (xi=xi-1+h)» [3].
На практике данный способ реализуется следующим образом:
Для того, чтобы вычислить интеграл по формуле трапеций в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст n=.
Ввести в ячейку B1 число 10.
Ввести в ячейку A2 текст a=.
Ввести в ячейку B2 число -1.
Ввести в ячейку A3 текст b=.
Ввести в ячейку B3 число 1.
Ввести в ячейку A4 текст h=(b-a)/n.
Ввести в ячейку B4 формулу =(B3-B2)/B1.
Заполнить диапазон ячеек A6:D6 следующим образом:
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число -1.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), а в ячейку C17 формулу =КОРЕНЬ(B17^4-B17^3+8).
Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D8:B16.
Ввести в ячейку B18 текст суммы:.
Ввести в ячейку C18 формулу =СУММ(C7;C17).
Ввести в ячейку D18 формулу =СУММ(D8:D16).
Ввести в ячейку A19 текст интеграл=.
Ввести в ячейку B19 формулу =B4*(C18/2+D18).
Метод парабол или Симпсона.
Этот метод более точный по сравнению с методами прямоугольников и трапеций, а поэтому наиболее широко известный и применяемый метод численного интегрирования.
Метод аналогичен рассмотренным ранее методам прямоугольников и трапеций: интервал интегрирования разбивается на множество более мелких отрезков; однако для вычисления площади под каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная парабола.
Формулу Симпсона получаем, проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.
Поскольку в методе Симпсона парабола проводится через три ординаты на концах двух соседних интервалов, то при реализации этого метода необходимо требовать, чтобы «n» было четным числом.
На практике данный способ реализуется следующим образом:
Для того, чтобы вычислить интеграл по формуле Симпсона в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст n=.
Ввести в ячейку B1 число 10.
Ввести в ячейку A2 текст a=.
Ввести в ячейку B2 число 0.
Ввести в ячейку A3 текст b=.
Ввести в ячейку B3 число 3,2.
Ввести в ячейку A4 текст h=.
Ввести в ячейку B4 формулу =(B3-B2)/B1.
Заполнить диапазон ячеек A6:D6 следующим образом:
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число 0.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), а в ячейку C17 формулу =КОРЕНЬ(B17^4-B17^3+8).
Заполнить нижеприведенные ячейки:
Ввести в ячейку C18 формулу =(C7-C17)/2.
Ввести в ячейку D18 формулу =2*D8+2*D10+2*D12+2*D14+2*D16.
Ввести в ячейку E18 формулу =E9+E11+E13+E15+E17.
Ввести в ячейку A19 текст интеграл=.
Ввести в ячейку B19 формулу =(2*B4/3)*(C18+D18+E18).
В итоге получаем следующее:
Заключение
Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.
Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения работы нами были рассмотрены примеры практических задач в области физики, геометрии, механики, биологии и экономики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.
Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл — это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.
Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.
Литература
- Волков Е.А. Численные методы. М., Наука, 1988.
- Пискунов Н.С. Дифференциальное и интегральное исчисление. М., Интеграл-Пресс, 2004. Т. 1.
- Шипачев В.С. Высшая математика. М., Высшая школа, 1990.
- Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике для инженеров и учащихся втузов. — М.: Наука , 1981 . — 718 с.
- Белецкий Я. Excel с графикой для персональных компьютеров перевод с польского Д.И.Юренкова. -М.: Машиностроение , 1991. — 320 с.
- Самарский А.А, Гулин А.В. Численные методы.М.:Наука,1989. – 430 с.
- http://tgspa.ru/info/education/faculties
- http://www.machinelearning.ru/wiki