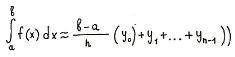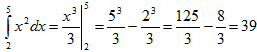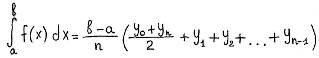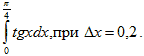Введение.
Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т.д.
Курс математического анализа содержит разнообразный материал, однако, одним из его центральных разделов является определенный интеграл. Интегрирование многих видов функций подчас представляет собой одну из труднейших проблем математического анализа.
Вычисление определенного интеграла имеет не только теоретический интерес. К его вычислению сводятся иногда задачи, связанные с практической деятельностью человека.
Также понятие определенного интеграла широко используется в физике.
Если же говорить о программе Excel, которая является одной из наиболее известных в обработке электронных таблиц, то без преувеличения можно утверждать, что ее возможности практически неисчерпаемы.
Обработка текста, управление базами данных — программа настолько мощна, что во многих случаях превосходит специализированные программы — редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, нежели заставить применять их на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей Excel тяжело достичь.
За всю историю табличных расчетов с применением персональных компьютеров требования пользователей к подобным программам существенно изменились. В начале основной акцент в такой программе, как, например, Visi Calc, ставился на счетные функции. Сегодня, положение другое. Наряду с инженерными и бухгалтерскими расчетами организация и графическое изображение данных приобретают все возрастающее значение. Кроме того, многообразие функций, предлагаемое такой расчетной и графической программой, не должно осложнять работу пользователя. Программы для Windows создают для этого идеальные предпосылки.
Ряд технологических задач требует увязки в математическое описание всей информации о процессе. Например, для математических моделей химико-технологических процессов одними из основных параметров, характеризующих процессы, являются концентрации реагирующих веществ, температура процесса и др. Как правило, большинство балансовых уравнений в химической технологии представлены системой интегральных и дифференциальных уравнений, в результате решения которых могут быть получены зависимости, характеризующие протекание процесса.
Часто на практике не удается вычислить интеграл аналитическим путем. В этих случаях применяют приближенные методы численного интегрирования.
Постановка задачи
Вычислить определенный интеграл
при условии, что а и b конечны и F(х) является непрерывной функцией х на всем интервале х[a,b]. Во многих случаях, когда подынтегральная функция задана в аналитическом виде, интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница:
Однако этой формулой часто нельзя воспользоваться по следующим причинам:
- первообразная функция f(x) слишком сложна и ее нельзя выразить в элементарных функциях;
- функция f(x) задана в виде таблицы, что особенно часто встречается в задачах химической технологии при обработке экспериментальных данных.
В этих случаях используются методы численного интегрирования.
Задача численного интегрирования состоит в нахождении приближенного значения интеграла по заданным или вычисленным значениям.
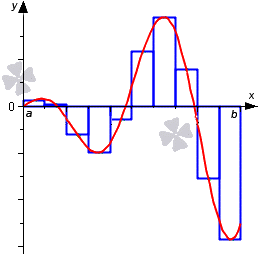
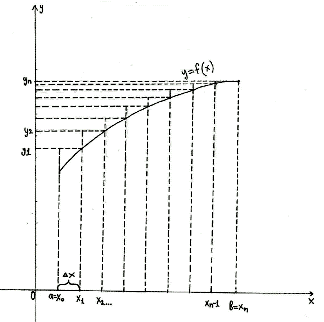
Общий подход к решению задачи будет следующим. Определенный интеграл I представляет собой площадь, ограниченную кривой f(x), осью х и переменными х=а и х=b. Необходимо вычислить интеграл, разбивая интервал [a,b] на множество меньших интервалов, находя приблизительно площадь каждой полоски и суммируя их.
В зависимости от способа вычисления подынтегральной суммы существуют различные методы численного интегрирования (методы прямоугольников, трапеций, парабол, сплайнов и др.).
Все методы будут рассматриваться на примере вычисления следующего интеграла:
Метод прямоугольников.
Существует несколько видов формул прямоугольников:
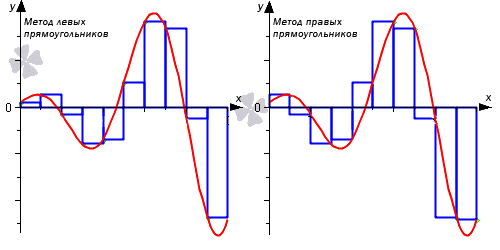
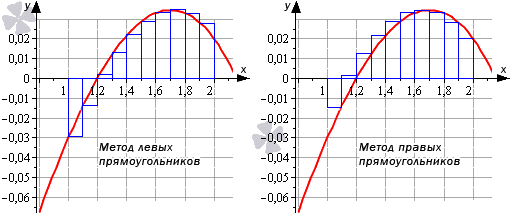
Формула левых прямоугольников.
В общем виде формула левых прямоугольников на отрезке [x0;xn] выглядит следующим образом:
Формула правых прямоугольников.
В общем виде формула правых прямоугольников на отрезке [x0;xn] выглядит следующим образом:
В данной формуле x0=a, xn=b.
Формула средних прямоугольников.
В общем виде формула средних прямоугольников на отрезке [x0;xn] выглядит следующим образом:
где xi=xi-1+h.
В данной формуле, как и в предыдущих, требуется h умножать сумму значений функции f(x), но уже не просто подставляя соответствующие значения x0,x1,…,xn-1 в функцию f(x), а прибавляя к каждому из этих значений h/2 (x0+h/2, x1+h/2,…, xn-1+h/2), а затем только подставляя их в заданную функцию.
На практике данные способы реализуются следующим образом:
Для того, чтобы вычислить интеграл по формуле левых прямоугольников в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст a=.
Ввести в ячейку B1 число 0.
Ввести в ячейку A2 текст b=.
Ввести в ячейку B2 число 3,2.
Ввести в ячейку A3 текст n=.
Ввести в ячейку B3 число 10.
Ввести в ячейку A4 текст h=.
Ввести в ячейку B4 формулу =(B2-B1)/B3.
Вести в ячейку A6 текст i, в B6 — x, в C6 — y0,…,y(n-1).
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число 0.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек C8:C16.
Ввести в ячейку B18 текст сумма:.
Ввести в ячейку B19 текст интеграл=.
Ввести в ячейку C18 формулу =СУММ(C7:C16).
Ввести в ячейку C19 формулу =B4*C18.
Ввести в ячейку C20 текст левых.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 12,500377.
Для того, чтобы вычислить интеграл по формуле правых прямоугольников в Excel, необходимо выполнить следующие действия:
Продолжить работу в том же документе, что и при вычислении интеграла по формуле левых прямоугольников.
В ячейку D6 ввести текст y1,…,yn.
Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D9:D17
Ввести в ячейку D18 формулу =СУММ(D7:D17).
Ввести в ячейку D19 формулу =B4*D18.
Ввести в ячейку D20 текст правых.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 14,45905.
Для того, чтобы вычислить интеграл по формуле средних прямоугольников в Excel, необходимо выполнить следующие действия:
Продолжить работу в том же документе, что и при вычислении интеграла по формулам левых и правых прямоугольников.
В ячейку E6 ввести текст xi+h/2, а в F6 — f(xi+h/2).
Ввести в ячейку E7 формулу =B7+$B$4/2, скопировать эту формулу методом протягивания в диапазон ячеек E8:E16
Ввести в ячейку F7 формулу =КОРЕНЬ(E7^4-E7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек F8:F16
Ввести в ячейку F18 формулу =СУММ(F7:F16).
Ввести в ячейку F19 формулу =B4*F18.
Ввести в ячейку F20 текст средних.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 13,40797.
Исходя из полученных результатов, можно сделать вывод, что формула средних прямоугольников является наиболее точной, чем формулы правых и левых прямоугольников.
Метод трапеций.
В общем виде формула трапеций на отрезке [x0;xn] выглядит следующим образом:
В данной формуле x0=a, xn=b, так как любой интеграл в общем виде выглядит:
h можно вычислить по следующей формуле: h=(b-a)/n (19).
y0, y1,…, yn — это значения соответствующей функции f(x) в точках x0, x1,…, xn (xi=xi-1+h)» [3].
На практике данный способ реализуется следующим образом:
Для того, чтобы вычислить интеграл по формуле трапеций в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст n=.
Ввести в ячейку B1 число 10.
Ввести в ячейку A2 текст a=.
Ввести в ячейку B2 число -1.
Ввести в ячейку A3 текст b=.
Ввести в ячейку B3 число 1.
Ввести в ячейку A4 текст h=(b-a)/n.
Ввести в ячейку B4 формулу =(B3-B2)/B1.
Заполнить диапазон ячеек A6:D6 следующим образом:
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число -1.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), а в ячейку C17 формулу =КОРЕНЬ(B17^4-B17^3+8).
Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D8:B16.
Ввести в ячейку B18 текст суммы:.
Ввести в ячейку C18 формулу =СУММ(C7;C17).
Ввести в ячейку D18 формулу =СУММ(D8:D16).
Ввести в ячейку A19 текст интеграл=.
Ввести в ячейку B19 формулу =B4*(C18/2+D18).
Метод парабол или Симпсона.
Этот метод более точный по сравнению с методами прямоугольников и трапеций, а поэтому наиболее широко известный и применяемый метод численного интегрирования.
Метод аналогичен рассмотренным ранее методам прямоугольников и трапеций: интервал интегрирования разбивается на множество более мелких отрезков; однако для вычисления площади под каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная парабола.
Формулу Симпсона получаем, проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.
Поскольку в методе Симпсона парабола проводится через три ординаты на концах двух соседних интервалов, то при реализации этого метода необходимо требовать, чтобы «n» было четным числом.
На практике данный способ реализуется следующим образом:
Для того, чтобы вычислить интеграл по формуле Симпсона в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст n=.
Ввести в ячейку B1 число 10.
Ввести в ячейку A2 текст a=.
Ввести в ячейку B2 число 0.
Ввести в ячейку A3 текст b=.
Ввести в ячейку B3 число 3,2.
Ввести в ячейку A4 текст h=.
Ввести в ячейку B4 формулу =(B3-B2)/B1.
Заполнить диапазон ячеек A6:D6 следующим образом:
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число 0.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), а в ячейку C17 формулу =КОРЕНЬ(B17^4-B17^3+8).
Заполнить нижеприведенные ячейки:
Ввести в ячейку C18 формулу =(C7-C17)/2.
Ввести в ячейку D18 формулу =2*D8+2*D10+2*D12+2*D14+2*D16.
Ввести в ячейку E18 формулу =E9+E11+E13+E15+E17.
Ввести в ячейку A19 текст интеграл=.
Ввести в ячейку B19 формулу =(2*B4/3)*(C18+D18+E18).
В итоге получаем следующее:
Заключение
Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.
Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения работы нами были рассмотрены примеры практических задач в области физики, геометрии, механики, биологии и экономики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.
Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл — это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.
Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.
Литература
- Волков Е.А. Численные методы. М., Наука, 1988.
- Пискунов Н.С. Дифференциальное и интегральное исчисление. М., Интеграл-Пресс, 2004. Т. 1.
- Шипачев В.С. Высшая математика. М., Высшая школа, 1990.
- Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике для инженеров и учащихся втузов. — М.: Наука , 1981 . — 718 с.
- Белецкий Я. Excel с графикой для персональных компьютеров перевод с польского Д.И.Юренкова. -М.: Машиностроение , 1991. — 320 с.
- Самарский А.А, Гулин А.В. Численные методы.М.:Наука,1989. – 430 с.
- http://tgspa.ru/info/education/faculties
- http://www.machinelearning.ru/wiki
Метод прямоугольников.
Вычисление определенных интегралов по формуле Ньютона-Лейбница не всегда возможно. Многие подынтегральные функции не имеют первообразных в виде элементарных функций, поэтому мы во многих случаях не можем найти точное значение определенного интеграла по формуле Ньютона-Лейбница. С другой стороны, точное значение не всегда и нужно. На практике нам часто достаточно знать приближенное значение определенного интеграла с некоторой заданной степенью точности (например, с точностью до одной тысячной). В этих случаях нам на помощь приходят методы численного интегрирования, такие как метод прямоугольников, метод трапеций, метод Симпсона (парабол) и т.п.
В этой статье подробно разберем метод прямоугольников для приближенного вычисления определенного интеграла.
Сначала остановимся на сути этого метода численного интегрирования, выведем формулу прямоугольников и получим формулу для оценки абсолютной погрешности метода. Далее по такой же схеме рассмотрим модификации метода прямоугольников, такие как метод правых прямоугольников и метод левых прямоугольников. В заключении рассмотрим подробное решение характерных примеров и задач с необходимыми пояснениями.
Навигация по странице.
Суть метода прямоугольников.
Пусть функция y = f(x) непрерывна на отрезке [a; b] . Нам требуется вычислить определенный интеграл 
Обратимся к понятию определенного интеграла. Разобьем отрезок [a;b] на n частей 





Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму (далее мы покажем, какую именно интегральную сумму берут в методе прямоугольников).
Метод средних прямоугольников.
Формула метода средних прямоугольников.
Если отрезок интегрирования [a;b] разбить на РАВНЫЕ части длины h точками 








Приведем графическую иллюстрацию метода средних прямоугольников.
Из чертежа видно, что подынтегральная функция y=f(x) приближается кусочной ступенчатой функцией 
С геометрической точки зрения для неотрицательной функции y=f(x) на отрезке [a;b] точное значение определенного интеграла представляет собой площадь криволинейной трапеции, а приближенное значение по методу прямоугольников – площадь ступенчатой фигуры.
Оценка абсолютной погрешности метода средних прямоугольников.
Перейдем к оценке абсолютной погрешности метода прямоугольников. Сначала оценим погрешность на элементарном интервале. Погрешность метода прямоугольников в целом будет равна сумме абсолютных погрешностей на каждом элементарном интервале.
На каждом отрезке 







Если считать, что функция y = f(x) имеет в точке 

По свойствам определенного интеграла равенства можно интегрировать почленно:

где 
Таким образом, 

Абсолютная погрешность формулы прямоугольников на отрезке [a; b] равна сумме погрешностей на каждом элементарном интервале, поэтому


Полученное неравенство представляет собой оценку абсолютной погрешности метода прямоугольников.
Метод левых прямоугольников и метод правых прямоугольников.
Перейдем к модификациям метода прямоугольников.


Отличие от метода средних прямоугольников заключается в выборе точек 
Абсолютная погрешность методов левых и правых прямоугольников оценивается как 
Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов.
Перейдем к решению примеров, в которых требуется вычислить приближенное значение определенного интеграла методом прямоугольников.
В основном, встречаются два типа задач. В первом случае задается количество интервалов, на которые разбивается отрезок интегрирования. Во втором случае задается допустимая абсолютная погрешность.
Формулировки задач примерно следующие:
- вычислить приближенно определенный интеграл методом прямоугольников, разбив отрезок интегрирования на n частей;
- Методом прямоугольников найти приближенное значение определенного интеграла с точностью до одной сотой (одной тысячной и т.п.).
Разберем каждый случай.
Сразу оговоримся, что в примерах подынтегральные функции будем брать такие, чтобы можно было найти их первообразные. В этом случае мы сможем вычислить точное значение определенного интеграла и сравнить его с приближенным значением, полученным по методу прямоугольников.
Вычислить определенный интеграл 
В нашем примере a = 4, b = 9, n = 10 , 
Внимательно посмотрим на формулу прямоугольников 
Чтобы ее применить, нам нужно вычислить шаг h и значения функции 

Вычислим шаг: 
Так как 

Для i = 1 имеем 

Для i = 2 имеем 

И так продолжаем вычисления до i = 10 .
Для удобства представим результаты в виде таблицы.
Подставляем полученные значения в формулу прямоугольников:
Значение исходного определенного интеграла можно вычислить по формуле Ньютона-Лейбница: 
Первообразная 

Как видите, точное значение определенного интеграла отличается от значения, полученного по методу прямоугольников для n = 10 , менее чем на шесть сотых долей единицы.
Вычислите приближенное значение определенного интеграла 
По условию имеем a = 1, b = 2 , 
Чтобы применить формулы правых и левых прямоугольников нам необходимо знать шаг h , а чтобы вычислить шаг h необходимо знать на какое число отрезков n разбивать отрезок интегрирования. Так как в условии задачи нам указана точность вычисления 0.01 , то число n мы можем найти из оценки абсолютной погрешности методов левых и правых прямоугольников.
Нам известно, что 

Найдем 

Графиком функции производной подынтегральной функции является парабола, ветви которой направлены вниз, на отрезке [1; 2] ее график монотонно убывает. Поэтому достаточно вычислить модули значения производной на концах отрезка и выбрать наибольшее:
В примерах со сложными подынтегральными функциями Вам может потребоваться теория раздела наибольшее и наименьшее значение функции.
Таким образом:
Число n не может быть дробным (так как n – натуральное число – количество отрезков разбиения интервала интегрирования). Поэтому, для достижения точности 0.01 по методу правых или левых прямоугольников, мы можем брать любое n = 9, 10, 11, … Для удобства расчетов возьмем n = 10 .
Формула левых прямоугольников имеет вид 


Итак,
Точки разбиения отрезка [a; b] определяются как 
Для i = 0 имеем 

Для i = 1 имеем 

И так далее до i = 10 .
Полученные результаты удобно представлять в виде таблицы:
Подставляем в формулу левых прямоугольников:
Подставляем в формулу правых прямоугольников:
Вычислим точное значение определенного интеграла по формуле Ньютона-Лейбница:
Очевидно, точность в одну сотую соблюдена.
Во многих случаях нахождение наибольшего значения модуля первой производной (или второй производной для метода средних прямоугольников) подынтегральной функции на отрезке интегрирования является очень трудоемкой процедурой.
Поэтому можно действовать без использования неравенства для оценки абсолютной погрешности методов численного интегрирования. Хотя оценки предпочтительнее.
Для методов правых и левых прямоугольников можно использовать следующую схему.
Берем произвольное n (например, n = 5 ) и вычисляем приближенное значение интеграла. Далее удваиваем количество отрезков разбиения интервала интегрирования, то есть, берем n = 10 , и вновь вычисляем приближенное значение определенного интеграла. Находим разность полученных приближенных значений для n = 5 и n = 10 . Если абсолютная величина этой разности не превышает требуемой точности, то в качестве приближенного значения определенного интеграла берем значение при n = 10 , предварительно округлив его до порядка точности. Если же абсолютная величина разности превышает требуемую точность, то вновь удваиваем n и сравниваем приближенные значения интегралов для n = 10 и n = 20 . И так продолжаем до достижения требуемой точности.
Для метода средних прямоугольников действуем аналогично, но на каждом шаге вычисляем треть модуля разности полученных приближенных значений интеграла для n и 2n . Этот способ называют правилом Рунге.
Вычислим определенный интеграл из предыдущего примера с точностью до одной тысячной по методу левых прямоугольников.
Не будем подробно останавливаться на вычислениях.
Для n = 5 имеем 

Так как 

Так как 

Так как 

В заключении остановимся на погрешности методов левых, правых и средних прямоугольников более детально.
Из оценок абсолютных погрешностей видно, что метод средних прямоугольников даст большую точность, чем методы левых и правых прямоугольников для заданного n . В то же время, объем вычислений одинаков, так что использование метода средних прямоугольников предпочтительнее.
Если говорить о непрерывных подынтегральных функциях, то при бесконечном увеличении числа точек разбиения отрезка интегрирования приближенное значение определенного интеграла теоретически стремиться к точному. Использование методов численного интегрирования подразумевает использование вычислительной техники. Поэтому следует иметь в виду, что при больших n начинает накапливаться вычислительная погрешность.
Еще заметим, если Вам требуется вычислить определенный интеграл с некоторой точностью, то промежуточные вычисления проводите с более высокой точностью. Например, Вам требуется вычислить определенный интеграл с точностью до одной сотой, тогда промежуточные вычисления проводите с точностью как минимум до 0.0001 .
При вычислении определенного интеграла методом прямоугольников (методом средних прямоугольников) пользуемся формулой 

Для метода левых и правых прямоугольников пользуемся формулами 


Вычисление интегралов по формулам прямоугольников и трапеций. Оценка погрешности
- Дидактическая цель. Познакомить учащихся с методами приближённого вычисления определённого интеграла.
- Воспитательная цель. Тема данного занятия имеет большое практическое и воспитательное значение. Наиболее просто к идее численного интегрирования можно подойти, опираясь на определение определённого интеграла как предела интегральных сумм. Например, если взять какое-либо достаточно мелкое разбиение отрезка [a; b] и построить для него интегральную сумму, то её значение можно приближённо принять за значение соответствующего интеграла. При этом важно быстро и правильно производить вычисления с привлечением вычислительной техники.
Основные знания и умения. Иметь понятие о приближённых методах вычисления определённого интеграла по формулам прямоугольников и трапеций.
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора).
- Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится вычислять определённые интегралы, для которых невозможно найти первообразную. В этом случае применяют приближённые методы вычисления определённых интегралов. Иногда приближённый метод применяют и для “берущихся” интегралов, если вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого вычисления интеграла заключается в том, что кривая 
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных методов интегрирования, геометрический смысл определённого интеграла.
Решение многих технических задач сводится к вычислению определённых интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближённого значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение которой неизвестно. В этом случае можно заменить данную линию более простой, уравнение которой известно. Площадь полученной таким образом криволинейной трапеции принимается за приближённое значение искомого интеграла.
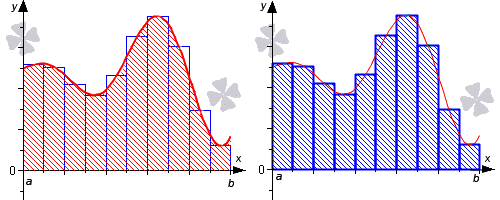
Простейшим приближённым методом является метод прямоугольников. Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой площадей прямоугольников, одна сторона которых равна 

Если суммировать площади прямоугольников, которые показывают площадь криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
то получим формулу:
Если с избытком
то
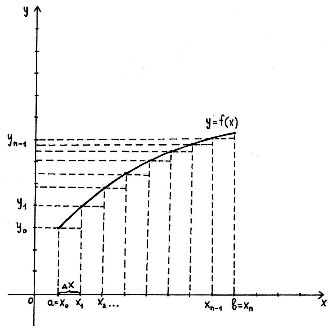
Значения у0, у1. уn находят из равенств 
Итак, чтобы найти приближённое значение интеграла 
- разделить отрезок интегрирования [a, b] на n равных частей точками х0= а, х1, х2. х n -1, х n = b ;
- вычислить значения подынтегральной функции
в точках деления, т.е. найти у 0 =f (x0), у 1 =f (x1), у 2 =f (x2), у n -1 =f (xn-1), у n =f (xn) ;
- воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:

Пример 1. Вычислить по формуле прямоугольников 
Разобьём отрезок [a, b] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3 ,
х k = a + k 

х0 = 2 + 0 

х1 = 2 + 1 

х2 = 2 + 2 

х3 = 2 + 3 

х4 = 2 + 4 

х5 = 2 + 5 

| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:


Вычисления проходили долго и мы получили довольно-таки грубое округление. Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в диапазоне х 

- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец будет значениями х, а второй соответствующими показателями f(x). Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 – слово Функция. В ячейку А2 вводится первое значение аргумента – левая граница диапазона (2). В ячейку А3 вводится второе значение аргумента – левая граница диапазона плюс шаг построения (2,1). Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А32, до значения х=5).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо записать её уравнение. Для этого табличный курсор необходимо установить в ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется 4. Теперь необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В33 может быть найдено приближённое значение интеграла. Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции (f(x)). В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция — функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В ячейке В33 появляется приближённое значение искомого интеграла с недостатком (37,955) .
Сравнивая полученное приближённое значение с истинным значением интеграла (39), можно видеть, что ошибка приближения метода прямоугольников в данном случае равна

Пример 2. Используя метод прямоугольников, вычислить 

- Для нахождения определённого интеграла значения подынтегральной функции f(x) должны быть введены в рабочую таблицу Excel в диапазоне
с заданным шагом
х = 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница интегрирования (0). В ячейку А3 вводится второе значение аргумента – левая граница диапазона плюс шаг построения (0,05). Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А33, до значения х=1,55).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо записать её уравнение. Для этого табличный курсор необходимо установить в ячейку В2. Здесь должно оказаться значение косинуса, соответствующее значению аргумента в ячейке А2. Для получения значения косинуса воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции ( fх ) . В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция — функцию COS. Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец данных (А). Указываем значение аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 1. Теперь необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В результате должна быть получена таблица данных для нахождения интеграла.
- Теперь в ячейке В34 может быть найдено приближённое значение интеграла. Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции ( ( fх )) . В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция — функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).
Сравнивая полученное приближённое значение с истинным значением интеграла 

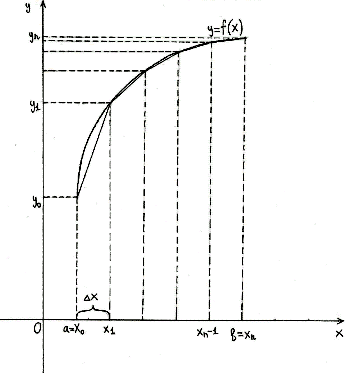
Метод трапеций обычно даёт более точное значение интеграла, чем метод прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций и приближённое значение определённого интеграла находится как сумма площадей трапеций
Пример 3. Методом трапеций найти 

- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец будет значениями х, а второй соответствующими показателями f(x). Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 – слово Функция. В ячейку А2 вводится первое значение аргумента – левая граница диапазона (0). В ячейку А3 вводится второе значение аргумента – левая граница диапазона плюс шаг построения (0,1). Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А33, до значения х=3,1).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо записать её уравнение (в примере синуса). Для этого табличный курсор необходимо установить в ячейку В2. Здесь должно оказаться значение синуса, соответствующее значению аргумента в ячейке А2. Для получения значения синуса воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции f(x). В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция — функцию SIN. Нажимаем кнопку ОК. Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец данных (А). Указываем значение аргумента синуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В результате должна быть получена таблица данных для нахождения интеграла.
- Теперь в ячейке В34 может быть найдено приближённое значение интеграла по методу трапеций. Для этого в ячейку В34 вводим формулу = 0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции (f(x)). В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция — функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке В34 появляется приближённое значение искомого интеграла с недостатком (1,997) .
Сравнивая полученное приближённое значение с истинным значением интеграла 

- Решение упражнений.
- Вычислить
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить
разделив отрезок [0;4] на 40 равных частей.
- Вычислить
разделив отрезок [0;8] на 40 равных частей.
- Вычислить
Метод прямоугольников
Не всегда имеется возможность вычисления интегралов по формуле Ньютона-Лейбница. Не все подынтегральные функции имеют первообразные элементарных функций, поэтому нахождение точного числа становится нереальным. При решении таких задач не всегда необходимо получать на выходе точные ответы. Существует понятие приближенного значения интеграла, которое задается методом числового интегрирования типа метода прямоугольников, трапеций, Симпсона и другие.
Данная статья посвящена именно этому разделу с получением приближенных значений.
Будет определена суть метода Симпсона, получим формулу прямоугольников и оценки абсолютной погрешности, метод правых и левых треугольников. На заключительном этапе закрепим знания при помощи решения задач с подробным объяснением.
Суть метода прямоугольников
Если функция y = f ( x ) имеет непрерывность на отрезке [ a ; b ] и необходимо вычислить значение интеграла ∫ a b f ( x ) d x .
Необходимо воспользоваться понятием неопределенного интеграла. Тогда следует разбить отрезок [ a ; b ] на количество n частей x i — 1 ; x i , i = 1 , 2 , . . . . , n , где a = x 0 x 1 x 2 . . . x n — 1 x n = b . В промежутке отрезка x i — 1 ; x i , i = 1 , 2 , . . . , n выберем точку со значением ζ i . Из определения имеем, что существует определенный тип интегральных сумм при бесконечном уменьшении длины элементарного отрезка, который уже разбили. Это выражается формулой λ = m a x i = 1 , 2 , . . . , n ( x i — x i — 1 ) → 0 , тогда получаем, что любая из таких интегральных сумм – приближенное значение интеграла ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 ) .
Суть метода прямоугольников выражается в том, что приближенное значение считается интегральной суммой.
Метод средних прямоугольников
Если разбить интегрируемый отрезок [ a ; b ] на одинаковые части точкой h , то получим a = x 0 , x 1 = x 0 + h , x 2 = x 0 + 2 h , . . . , x — 1 = x 0 + ( n — 1 ) h , x n = x 0 + n h = b , то есть h = x i — x i — 1 = b — a n , i = 1 , 2 , . . . , n . Серединами точек ζ i выбираются элементарные отрезки x i — 1 ; x i , i = 1 , 2 , . . . , n , значит ζ i = x i — 1 + h 2 , i = 1 , 2 , . . . , n .
Тогда приближенное значение ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 ) записывается таким образом ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i — 1 + h 2 . Данная формула называется формулой метода прямоугольников.
Такое название метод получает из-за характера выбора точек ζ i , где шаг разбиения отрезка берется за h = b — a n .
Рассмотрим на приведенном ниже рисунке данный метод.
Чертеж явно показывает, что приближение к кусочной ступенчатой функции
y = f x 0 + h 2 , x ∈ [ x 0 ; x 1 ) f x 1 + h 2 , x ∈ [ x 1 ; x 2 ) . . . f x n — 1 + h 2 , x ∈ [ x n — 1 ; x n ] происходит на всем пределе интегрирования.
С геометрической стороны мы имеем, что неотрицательная функция y = f ( x ) на имеющемся отрезке [ a ; b ] имеет точное значение определенного интеграла и выглядит как криволинейная трапеция, площадь которой необходимо найти. Рассмотрим на рисунке, приведенном ниже.
Оценка абсолютной погрешности метода средних прямоугольников
Для оценки абсолютной погрешности необходимо выполнить ее оценку на заданном интервале. То есть следует найти сумму абсолютных погрешностей каждого интервала. Каждый отрезок x i — 1 ; x i , i = 1 , 2 , . . . , n имеет приближенное равенство ∫ x i — 1 x i f ( x ) d x ≈ f x i — 1 + h 2 · h = f x i — 1 + h 2 · ( x i — x i — 1 ) . Абсолютная погрешность данного метода треугольников δ i , принадлежащей отрезку i , вычисляется как разность точного и приближенного определения интеграла . Имеем, что δ i = ∫ x i — 1 x i f ( x ) d x — f x i — 1 + h 2 · x i — x i — 1 . Получаем, что f x i — 1 + h 2 является некоторым числом, а x i — x i — 1 = ∫ x i — 1 x i d x , тогда выражение f x i — 1 + h 2 · x i — x i — 1 по 4 свойству определения интегралов записывается в форме f x i — 1 + h 2 · x i — x i — 1 = ∫ x — 1 x f x i — 1 + h 2 d x . Отсюда получаем, что отрезок i имеет абсолютную погрешность вида
δ i = ∫ x i — 1 x i f ( x ) d x — f x i — 1 + h 2 · x i — x i — 1 = = ∫ x i — 1 x i f ( x ) d x — ∫ x i — 1 x i x i — 1 + h 2 d x = ∫ x i — 1 x i f ( x ) = — f x i — 1 + h 2 d x
Если взять, что функция y = f ( x ) имеет производные второго порядка в точке x i — 1 + h 2 и ее окрестностях, тогда y = f ( x ) раскладывается в ряд Тейлора по степеням x — x i — 1 + h 2 с остаточным членом в форме разложения по Лагранжу. Получаем, что
f ( x ) = f x i — 1 + h 2 + f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 + + f » ( ε i ) x — x i — 1 + h 2 2 2 ⇔ ⇔ f ( x ) = f ( x i — 1 + h 2 ) = f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 + + f » ( ε i ) x — x i — 1 + h 2 2 2
Исходя из свойства определенного интеграла, равенство может интегрироваться почленно. Тогда получим, что
∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x = ∫ x i — 1 x i f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 d x + + ∫ x i — 1 x i f » ε i · x — x i — 1 + h 2 2 2 d x = = f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 2 2 x i — 1 x i + f » ε i · x — x i — 1 + h 2 3 6 x i — 1 x i = = f ‘ x i — 1 + h 2 · x i — h 2 2 2 — x i — 1 — x i — 1 + h 2 2 2 + + f » ε i · x i — h 2 3 6 — x i — 1 — x i — 1 + h 2 3 6 = = f ‘ x i — 1 + h 2 · h 2 8 — h 2 8 + f » ( ε i ) · h 3 48 + h 3 48 = f » ε i · h 3 24
где имеем ε i ∈ x i — 1 ; x i .
Отсюда получаем, что δ i = ∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x = f » ε i · h 3 24 .
Абсолютная погрешность формулы прямоугольников отрезка [ a ; b ] равняется сумме погрешностей каждого элементарного интервала. Имеем, что
δ n = ∑ i = 1 n ∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x и δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f » ( x ) = b — a 3 24 n 2 .
Неравенство является оценкой абсолютной погрешности метода прямоугольников.
Метод левых прямоугольников и метод правых прямоугольников
Для модификации метода рассмотрим формулы.
∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) является формулой левых треугольников.
∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) является формулой правых треугольников.
Рассмотрим на примере рисунка, приведенного ниже.
Отличием метода средних прямоугольников считается выбор точек не по центру, а на левой и правой границах данных элементарных отрезков.
Такая абсолютная погрешность методов левых и правых треугольников можно записать в виде
δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n
Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов
Необходимо рассмотреть решение примеров, где нужно вычислять примерное значение имеющегося определенного интеграла при помощи метода прямоугольников. Рассматривают два типа решения заданий. Суть первого случая – задание количества интервалов для разбивания отрезка интегрирования. Суть второго заключается в наличии допустимой абсолютной погрешности.
Формулировки задач выглядят следующим образом:
- произвести приближенное вычисление определенного интеграла при помощи метода прямоугольников, разбивая на nколичество отрезков интегрирования;
- найти приближенное значение определенного интеграла методом прямоугольников с точностью до одной сотой.
Рассмотрим решения в обоих случаях.
В качестве примера выбрали задания, которые поддаются преобразованию для нахождения их первообразных. Тогда появляется возможность вычисления точного значения определенного интеграла и сравнения с приближенным значением при помощи метода прямоугольников.
Произвести вычисление определенного интеграла ∫ 4 9 x 2 sin x 10 d x при помощи метода прямоугольников, разбивая отрезок интегрирования на 10 частей.
Из условия имеем, что a = 4 , b = 9 , n = 10 , f ( x ) = x 2 sin x 10 . Для применения ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f x i — 1 + h 2 необходимо вычислить размерность шага h и значение функции f ( x ) = x 2 sin x 10 в точках x i — 1 + h 2 , i = 1 , 2 , . . . , 10 .
Вычисляем значение шага и получаем, что
h = b — a n = 9 — 4 10 = 0 . 5 .
Потому как x i — 1 = a + ( i — 1 ) · h , i = 1 , . . . , 10 , тогда x i — 1 + h 2 = a + ( i — 1 ) · h + h 2 = a + i — 0 . 5 · h , i = 1 , . . . , 10 .
Так как i = 1 , то получаем x i — 1 + h 2 = x 0 + h 2 = a + ( i — 0 . 5 ) · h = 4 + ( 1 — 0 . 5 ) · 0 . 5 = 4 . 25 .
После чего необходимо найти значение функции
f x i — 1 + h 2 = f x 0 + h 2 = f ( 4 . 25 ) = 4 . 25 2 sin ( 4 . 25 ) 10 ≈ — 1 . 616574
При i = 2 получаем x i — 1 + h 2 = x 1 + h 2 = a + i — 0 . 5 · h = 4 + ( 2 — 0 . 5 ) · 0 . 5 = 4 . 75 .
Нахождение соответствующего значения функции получает вид
f x i — 1 + h 2 = f x 1 + h 2 = f ( 4 . 75 ) = 4 . 75 2 sin ( 4 . 75 ) 10 ≈ — 2 . 254654
Вычисления производятся до i = 10 .
Представим эти данные в таблице, приведенной ниже.
| i | 1 | 2 | 3 | 4 | 5 |
| x i — 1 + h 2 | 4 . 25 | 4 . 75 | 5 . 25 | 5 . 75 | 6 . 25 |
| f x i — 1 + h 2 | — 1 . 616574 | — 2 . 254654 | — 2 . 367438 | — 1 . 680497 | — 0 . 129606 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i — 1 + h 2 | 6 . 75 | 7 . 25 | 7 . 75 | 8 . 25 | 8 . 75 |
| f x i — 1 + h 2 | 2 . 050513 | 4 . 326318 | 5 . 973808 | 6 . 279474 | 4 . 783042 |
Значения функции необходимо подставить в формулу прямоугольников. Тогда получаем, что
∫ 4 9 x 2 sin x 10 d x ≈ h · ∑ i = 1 n f x i — 1 + h 2 = = 0 . 5 · — 1 . 616574 — 2 . 25654 — 2 . 367438 — 1 . 680497 — 0 . 129606 + + 2 . 050513 + 4 . 326318 + 5 . 973808 + 6 . 279474 + 4 . 783042 = = 7 . 682193
Исходный интеграл можно вычислить при помощи формулы Ньютона-Лейбница. Получаем, что
∫ 4 9 x 2 · sin x 10 d x = — 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x 4 9 = = 7 5 cos 4 — 4 5 sin 4 — 79 10 cos 9 + 9 5 sin 9 ≈ 7 . 630083
Находим первообразную выражения — 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x соответствующую функции f ( x ) = x 2 sin x 10 . Нахождение производится методом интегрирования по частям.
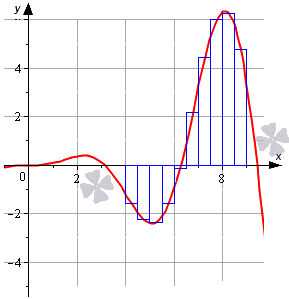
Отсюда видно, что определенный интеграл отличается от значения, полученном при решении методом прямоугольников, где n = 10 , на 6 долей единицы. Рассмотрим на рисунке, приведенном ниже.
Вычислить приближенного значение определенного интеграла ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x при помощи метода левых и правых прямоугольников с точностью до одной сотой.
Из условия мы имеем, что a = 1 , b = 2 и f ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 .
Для применения формулы правых и левых прямоугольников нужно знать размерность шага h , а для его вычисления разбиваем отрезок интегрирования на n отрезков. По условию имеем, что точность должна быть до 0 , 01 , тогда нахождение n возможно при помощи оценки абсолютной погрешности методов левых и правых прямоугольников.
Известно, что δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n . Для достижения необходимой степени точности необходимо найти такое значение n , для которого неравенство m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n ≤ 0 . 01 будет выполнено.
Найдем наибольшее значение модуля первой производной, то есть значение m a x x ∈ [ a ; b ] f ‘ ( x ) подынтегральной функции f ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 , определенной на отрезке [ 1 ; 2 ] . В нашем случае необходимо выполнить вычисления:
f ‘ ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ‘ = — 0 . 09 x 2 + 0 . 26
Парабола является графиком подынтегральной функции с ветвями, направленными вниз, определенная на отрезке [ 1 ; 2 ] , причем с монотонно убывающим графиком. Необходимо произвести вычисление модулей значений производных на концах отрезков, а из них выбрать наибольшее значение. Получаем, что
f ‘ ( 1 ) = — 0 . 09 · 1 2 + 0 . 26 = 0 . 17 f ‘ ( 2 ) = — 0 . 09 · 2 2 + 0 . 26 = 0 . 1 → m a x x ∈ [ 1 ; 2 ] f ‘ ( x ) = 0 . 17
Решение сложных подынтегральных функций подразумевает обращение к разделу наибольше и наименьшее значение функции.
Тогда получаем, что наибольшее значение функции имеет вид:
m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n ≤ 0 . 01 ⇔ ⇔ 0 . 17 · ( 2 — 1 ) 2 2 n ≤ 0 . 01 ⇔ 0 . 085 n ≤ 0 . 01 ⇔ n ≥ 8 . 5
Дробность числа n исключается, так как n является натуральным числом. Чтобы прийти к точности 0 . 01 , используя метод правых и левых прямоугольников, не обходимо выбирать любое значение n . Для четкости расчетов возьмем n = 10 .
Тогда формула левых прямоугольников примет вид ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) , а правых — ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Для применения их на практике необходимо найти значение размерности шага h и f ( x i ) , i = 0 , 1 , . . . , n , где n = 10 .
h = b — a n = 2 — 1 10 = 0 . 1
Определение точек отрезка [ a ; b ] производится с помощью x i = a + i · h , i = 0 , 1 , . . . , n .
При i = 0 , получаем x i = x 0 = a + i · h = 1 + 0 · 0 . 1 = 1 и f ( x i ) = f ( x 0 ) = f ( 1 ) = — 0 . 03 · 1 3 + 0 . 26 · 1 — 0 . 26 = — 0 . 03 .
При i = 1 , получаем x i = x 1 = a + i · h = 1 + 1 · 0 . 1 = 1 . 1 и f ( x i ) = f ( x 1 ) = f ( 1 . 1 ) = — 0 . 03 · ( 1 . 1 ) 3 + 0 . 26 · ( 1 . 1 ) — 0 . 26 = — 0 . 01393 .
Вычисления производятся до i = 10 .
Вычисления необходимо представить в таблице, приведенной ниже.
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| x i | 1 | 1 . 1 | 1 . 2 | 1 . 3 | 1 . 4 | 1 . 5 |
| f ( x i ) | — 0 . 03 | — 0 . 01393 | 0 . 00016 | 0 . 01209 | 0 . 02168 | 0 . 02875 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i | 1 . 6 | 1 . 7 | 1 . 8 | 1 . 9 | 2 |
| f ( x i ) | 0 . 03312 | 0 . 03461 | 0 . 03304 | 0 . 02823 | 0 . 02 |
Подставим формулу левых треугольников
∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) = = 0 . 1 · — 0 . 03 — 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + + 0 . 02875 + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 = = 0 . 014775
Подставляем в формулу правых треугольников
∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ h · ∑ i = 1 n f ( x i ) = = 0 . 1 · — 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + 0 . 02875 + + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 + 0 . 02 = 0 . 019775
Произведем вычисление по формуле Ньютона-Лейбница:
∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x = = — 0 . 03 x 4 4 + 0 . 13 x 2 — 0 . 26 x 1 2 = 0 . 0175
Рассмотрим рисунок, приведенный ниже.
Замечание
Нахождение наибольшего значения модуля первой производной является трудоемкой работой, поэтому можно исключить использование неравенства для оценивания абсолютной погрешности и методов численного интегрирования. Разрешено применять схему.
Берем значение n = 5 для вычисления приближенного значения интеграла. Необходимо удвоить количество отрезков интегрирования, тогда n = 10 , после чего производится вычисление примерного значения. необходимо найти разность этих значений при n = 5 и n = 10 . Когда разность не соответствует требуемой точности, то приближенным значением считается n = 10 с округлением до десятка.
Когда погрешность превышает необходимую точность, то производится удваивание n и сравнивание приближенных значений. Вычисления производятся до тех пор, пока необходимая точность не будет достигнута.
Для средних прямоугольников выполняются аналогичные действия, но вычисления на каждом шаге требуют разности полученных приближенных значений интеграла для n и 2 n . Такой способ вычисления называется правилом Рунге.
Произведем вычисление интегралов с точностью до одной тысячной при помощи метода левых прямоугольников.
При n = 5 получаем, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 0116 , а при n = 10 — ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 014775 . Так как имеем, что 0 . 0116 — 0 . 014775 = 0 . 003175 > 0 . 001 , возьмем n = 20 . Получаем, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 01619375 . Имеем 0 . 014775 — 0 . 01619375 = 0 . 00141875 > 0 . 001 , возьмем значение n = 40 , тогда получим ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 01686093 . Имеем, что 0 . 1619375 — 0 . 01686093 = 0 . 00066718 0 . 001 , тогда после округления значения проверим, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x равняется значению 0 , 017 с погрешностью 0 , 001 . Из оценок абсолютных погрешностей видно, что данный метод дает максимальную точность в отличие от метода левых и правых координат для заданного n . Отдается предпочтение методу средних прямоугольников.
Непрерывные подынтегральные функции при бесконечном разделении на отрезки данное приближенно число стремится к точному. Чаще всего такой метод выполняется при помощи специальных программ на компьютере. Поэтому чем больше значение n , тем больше вычислительная погрешность.
Для наиболее точного вычисления необходимо выполнять точные промежуточные действия, желательно с точностью до 0 , 0001 .
Итоги
Для вычисления неопределенного интеграла методом прямоугольников следует применять формулу такого вида ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i — 1 + h 2 и оценивается абсолютная погрешность с помощью δ n ≤ m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · b — a 3 24 n 2 .
Для решения с помощью методов правых и левых прямоугольников применяют формулы, имеющие вид, ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) и ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Абсолютная погрешность оценивается при помощи формулы вида δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · b — a 2 2 n .
источники:
http://urok.1sept.ru/articles/549599
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/metod-prjamougolnikov/
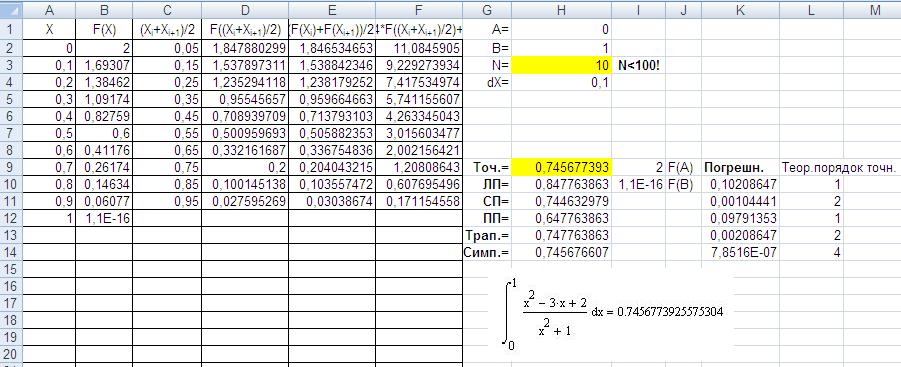
Документ представляет собой «заготовку» для численного вычисления определённых интегралов в Excel. Интеграл считается методами левых прямоугольников (ЛП), средних прямоугольников (СП), правых прямоугольников (ПП), трапеций (Трап.) и Симпсона (Симп.). При введённом точном значениии интеграла в учебных целях оцениваются погрешности методов.
Теория по методам есть, например, здесь.
С помощью функции ЕСЛИ здесь обеспечивается автозаполнение таблиц численного интегрирования, так что для пересчёта интегралов с более мелким шагом достаточно изменить значение в ячейке H3, отведённой для хранения числа интервалов, на которые разбивается отрезок [A,B].
Ограничение N<100 связано лишь с тем, что формулы растянуты вниз до 100-й строки, если растянуть дальше, его можно изменить.
К сожалению, без применения макросов на VBA в Excel проблематично запрограммировать функцию, которую можно было бы вызывать без включения её непосредственно в текст формулы, так что при интегрировании другой функции её нужно «вбить» в ячейки B2 (от аргумента A2) и D2 (от аргумента C2), после чего растянуть изменённые формулы. Разумеется, точное значение интеграла в ячейке H9 и картинку из Mathcad, в котором оно вычислено, также можно и нужно менять.
Скачать пример в Excel XP/2003 (56 Кб)
Учебно-воспитательные задачи:
- Дидактическая цель. Познакомить учащихся с методами
приближённого вычисления определённого интеграла. - Воспитательная цель. Тема данного занятия имеет большое
практическое и воспитательное значение. Наиболее просто к идее численного
интегрирования можно подойти, опираясь на определение определённого
интеграла как предела интегральных сумм. Например, если взять какое-либо
достаточно мелкое разбиение отрезка [a; b] и построить для
него интегральную сумму, то её значение можно приближённо принять за
значение соответствующего интеграла. При этом важно быстро и правильно
производить вычисления с привлечением вычислительной техники.
Основные знания и умения. Иметь понятие о приближённых методах
вычисления определённого интеграла по формулам прямоугольников и трапеций.
Обеспечение занятия
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод
прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора). - Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится
вычислять определённые интегралы, для которых невозможно найти первообразную. В
этом случае применяют приближённые методы вычисления определённых интегралов.
Иногда приближённый метод применяют и для “берущихся” интегралов, если
вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого
вычисления интеграла заключается в том, что кривая
заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.
Последовательность занятия.
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
План занятия
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных
методов интегрирования, геометрический смысл определённого интеграла.
- Выполнение практической работы.
Решение многих технических задач сводится к вычислению определённых
интегралов, точное выражение которых сложно, требует длительных вычислений и не
всегда оправдано практически. Здесь бывает вполне достаточно их приближённого
значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение
которой неизвестно. В этом случае можно заменить данную линию более простой,
уравнение которой известно. Площадь полученной таким образом криволинейной
трапеции принимается за приближённое значение искомого интеграла.
Простейшим приближённым методом является метод прямоугольников. Геометрически
идея способа вычисления определённого интеграла по формуле прямоугольников
состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой
площадей прямоугольников, одна сторона которых равна
, а друга —
.
Если суммировать площади прямоугольников, которые показывают площадь
криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
[Рисунок1]
то получим формулу:
Если с избытком
[Рисунок2],
то
Значения у0, у1,…, уn находят из
равенств ,
к
=
0, 1…,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла
, нужно:
- разделить отрезок интегрирования [a, b] на n равных частей
точками х0=а,
х1, х2,…, х
n
-1,
х
n
=
b
; - вычислить значения подынтегральной функции
в
точках деления, т.е. найтиу
0
=
f (x0),
у
1
=
f (x1),
у
2
=
f (x2),
у
n
-1
=
f (xn-1),
у
n
=
f (xn)
; - воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Пример 1. Вычислить по формуле прямоугольников
. Найти
абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных
частей. Тогда а
=
0,
b =
3
,
х
k = a + k
х
х0 = 2 + 0
= 2
х1 = 2 + 1
= 2,5
х2 = 2 + 2
=3
х3 = 2 + 3
= 3
х4 = 2 + 4
= 4
х5 = 2 + 5
= 4,5
f (x0) = 22 = 4
f
(x
1
)
= 2
,5
2
=
6,25
f
(x
2
)
=
32
=
9
f
(x
3
)
=
3,52
=
12,25
f
(x
4
)
=
42
=
16
f
(x
5
)
=
4,52
=
20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти
точное значение интеграла:
Вычисления проходили долго и мы получили довольно-таки грубое округление.
Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться
техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х
[2
;5
]
с заданным шагом
х = 0,1.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (2). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (2,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А32, до значения х=5). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской
раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется
4. Теперь необходимо скопировать функцию из ячейки В2.
Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В33 может быть найдено приближённое значение интеграла.
Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции (f(x)).
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция — функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В
ячейке В33 появляется приближённое значение искомого интеграла с недостатком
(37,955) .
Сравнивая полученное приближённое значение с истинным значением интеграла (39),
можно видеть, что ошибка приближения метода прямоугольников в данном случае
равна
=
|39 — 37
,
955| = 1
,045
Пример 2. Используя метод прямоугольников, вычислить
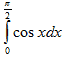
заданным шагом х =
0,05.
Решение:
- Для нахождения определённого интеграла значения подынтегральной функции
f(x) должны быть введены в рабочую таблицу Excel в диапазоне
с
заданным шагомх
= 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
интегрирования (0). В ячейку А3 вводится второе значение аргумента –
левая граница диапазона плюс шаг построения (0,05). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=1,55). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2. Здесь должно оказаться значение косинуса, соответствующее
значению аргумента в ячейке А2. Для получения значения косинуса
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку
Вставка функции (
f
х
)
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция — функцию COS.
Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя
указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле
вправо, чтобы открыть столбец данных (А). Указываем значение
аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В
ячейке В2 появляется 1. Теперь необходимо скопировать функцию из
ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В
результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла.
Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер
функций (нажатием на панели инструментов кнопки Вставка функции(
(
f
х
))
.
В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле
Категория выбираем Математические. Справа в поле Функция — функцию Сумм.
Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле
мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В
ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).
Сравнивая полученное приближённое значение с истинным значением интеграла
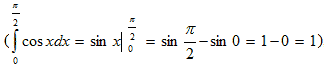
видеть, что ошибка приближения метода прямоугольников в данном случае равна
Метод трапеций обычно даёт более точное значение интеграла, чем метод
прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций
и приближённое значение определённого интеграла находится как сумма площадей
трапеций
[Рисунок3]
Пример 3. Методом трапеций найти
с шагом
х = 0,1.
Решение.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х, а второй соответствующими показателями f(x).
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 –
слово Функция. В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (0). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (0,1). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=3,1). - Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение (в примере синуса). Для этого табличный курсор
необходимо установить в ячейку В2. Здесь должно оказаться значение синуса,
соответствующее значению аргумента в ячейке А2. Для получения значения
синуса воспользуемся специальной функцией: нажимаем на панели инструментов
кнопку Вставка функции f(x). В появившемся диалоговом окне
Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические.
Справа в поле Функция — функцию SIN. Нажимаем кнопку ОК.
Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле
окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец
данных (А). Указываем значение аргумента синуса щелчком мыши на
ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
формулу в диапазон В2:В33. В результате должна быть получена таблица данных
для нахождения интеграла. - Теперь в ячейке В34 может быть найдено приближённое значение интеграла
по методу трапеций. Для этого в ячейку В34 вводим формулу =
0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели
инструментов кнопки Вставка функции (f(x)). В появившемся
диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем
Математические. Справа в поле Функция — функцию Сумм. Нажимаем кнопку ОК.
Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон
суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке
В34 появляется приближённое значение искомого интеграла с недостатком (1,997)
.
Сравнивая полученное приближённое значение с истинным значением интеграла
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
- Решение упражнений.
- Вычислить
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить методом трапеций
- Вычислить
разделив отрезок [0;4] на 40 равных частей. - Вычислить
разделив отрезок [0;8] на 40 равных частей. - Вычислить
Цель
работы:
Освоение приемов работы в Ms Excel при
вычислении сумм и интегралов.
Содержание
работы
1. Приближенное
вычисление определенных интегралов
методом прямоугольников и методом
трапеций.
2. Приближенное
вычисление длины кривой.
3. Проведение
экспериментов и решение задач.
Пояснения к выполнению работы
1.
С геометрической точки зрения определенный
интеграл
– есть площадь фигуры, ограниченной
графиком функциии прямыми
,
,
.
Функцияназывается
подынтегральной функцией.
Чтобы
приближенно вычислить эту площадь,
разделим интервал интегрирования
на
равных отрезков длиной
каждый.
Тогда координата левого концаi-го
отрезка определяется по формуле
,
где,
.
Простейший приближенный расчет площади
под кривойсостоит в нахождении суммы площадей
прямоугольников, у каждого из которых
основание совпадает с отрезком,
а высота равна значению функции в точке(метод левых прямоугольников). Можно
высоту брать равной значению функции
в точке(метод правых прямоугольников) или в
точке(метод центральных прямоугольников).
При использовании метода левых
прямоугольников формула для вычисления
площади выглядит следующим образом:
.
Можно
повысить точность вычисления определенного
интеграла, если заменить на каждом
интервале
,
дугу графика
отрезком (хордой), соединяющем точки с
координатамии
.
В этом случае фигура, ограниченная
графиком функции и прямыми,
,
приближенно заменяется не прямоугольником,
а трапецией, и искомый определенный
интеграл рассчитывается как сумма
площадей всех таких трапеций:
.
Формула
может быть существенно упрощена, но мы
оставим это для курса вычислительной
математики (сейчас можете попытаться
упростить ее самостоятельно).
2.
Замена графика функции
хордами, описанная в методе трапеций,
позволяет при помощи электронных таблиц
довольно легко определять приближенное
значение длины дуги графикана интервале
.
В этой задаче рассматриваемая кривая
представляется в виде
ломанной,
длина s
которой равна сумме длин
её звеньев. Длину
звена, построенного на отрезке
,
можно найти как длину гипотенузы
прямоугольного треугольника с катетами,
равнымии
,
используя известную теорему Пифагора.
В результате суммирования длин всех
звеньев, получаем:
.
Следует
отметить, что точность приближенного
вычисления интегралов зависит от
величины
,
то есть от количества отрезков, на
которые разбивается интервал интегрирования.
При отсутствии погрешностей округления,
чем больше,
тем выше точность (с ростомN
погрешность вычислений сходится к
нулю).
3.
В качестве примера вычислим интеграл
с точностью представления результатов
вычислений до 4 знаков после запятой.
В
ячейку А6
вводим нижнюю границу интервала
интегрирования
,
равную 0,5. В следующую ячейкуА7
вводим значение 0,51, отстоящее от нижней
границы на шаг
.
Рекомендуется выбирать шаг в зависимости
от требуемой точности вычисления
интеграла. Затем выделяем обе ячейкиА6
и А7.
В правой нижней части выделенной области
есть жирная черная точка – маркер
заполнения, – тянем её мышкой вниз, пока
не получим число, соответствующее
верхней границе интеграла, т. е. значению
.
Это достигается в ячейкеА206.
Выделим
мышкой столбцы
С,
Е
и G,
указывая мышкой их заголовки. Вызовем
с помощью правой кнопки мыши контекстное
меню выделенных столбцов и выберем в
нем опцию Формат
ячеек.
Далее, на закладке Число,
выберем в качестве числового формата
– Числовой
и укажем отображаемое число десятичных
знаков 4. Нажмем клавишу OК.
3.1.
Теперь вычислим определенный интеграл
с помощью метода левых прямоугольников.
Для этого введем в ячейку С6
формулу =(А7-А6)*(Ln(А6))
(величина логарифма и есть высота
соответствующего прямоугольника).
Выделим ячейку С6
и протянем маркер заполнения вниз, до
ячейки С205.
Таким образом, в столбце C
мы получили площади всех прямоугольников.
Выделим
ячейку С206
и нажмем на кнопку Автосумма
на панели Стандартные.
Нажмем Enter,
подтверждая этим предложенную формулу.
В результате получим сумму всех выше
расположенных чисел в столбце, т. е.
значение интеграла, вычисленное методом
прямоугольников.
3.2.
Вычислим определенный интеграл с помощью
метода трапеций. Для этого введем в
ячейку Е6
следующую формулу =(А7-А6)*(Ln(А7)+Ln(А6))/2.
Выделите ячейку Е6
и протяните маркер заполнения вниз до
ячейки Е205.
Так мы вычислили площади всех трапеций.
Выделив ячейку Е206,
вычислите их сумму с помощью кнопки
Автосумма
на панели Стандартные.
Мы
получили
значение интеграла, найденное методом
трапеций.
3.3.
Вычислим длину графика функции
на интервале [0,5; 2,5].
Для
вычисления длин хорд введите в ячейку
G6
формулу
=((A7-A6)^2+(Ln(A7)-Ln(A6))^2)^(0,5).
Выделите ячейку G6
и протяните маркер заполнения вниз до
ячейки G205.
В ячейке G206,
используя Автосумму,
найдите приближенное значение искомой
длины графика.
3.4.
Повторите в соседних столбцах все
расчеты при меньшем шаге интегрирования,
например, при шаге 0,001. Сравните результаты
с полученными ранее. Проанализируйте
их и сделайте выводы.
3.5. Вычисления
провести по варианту и записать в отчет.
Соседние файлы в папке Рабочая профессия
- #
- #
13.03.201652.81 Кб36Графики.xlsm
- #
13.03.2016656.9 Кб132Лабораторная 2.xls
- #
13.03.201640.96 Кб79Лабораторная 3.xls
- #
- #





























 с заданным шагом
с заданным шагом 




 методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей. 



 разделив отрезок [0;4] на 40 равных частей.
разделив отрезок [0;4] на 40 равных частей. разделив отрезок [0;8] на 40 равных частей.
разделив отрезок [0;8] на 40 равных частей.