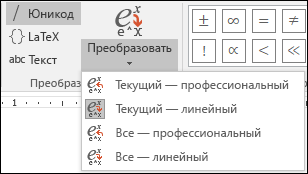
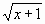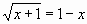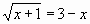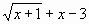Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
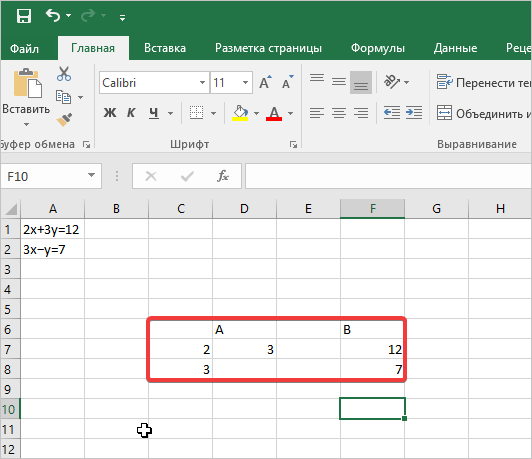
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
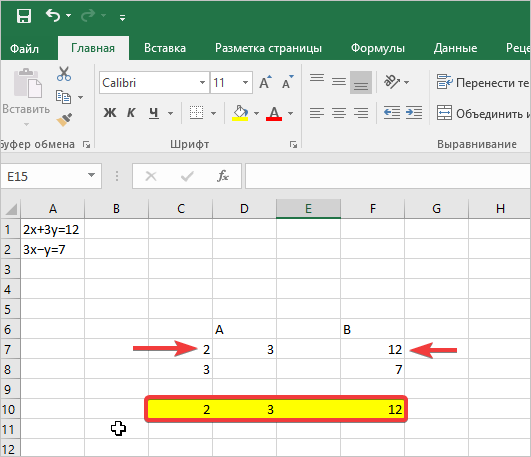
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
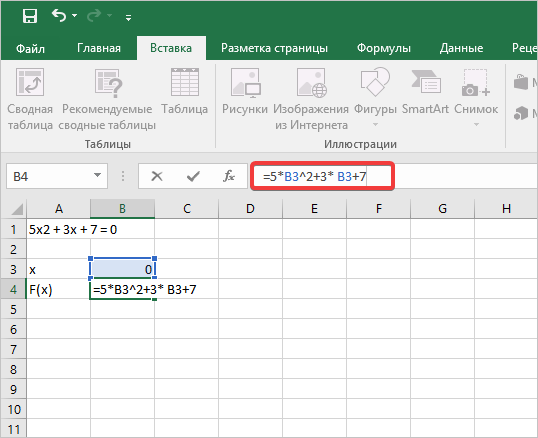
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
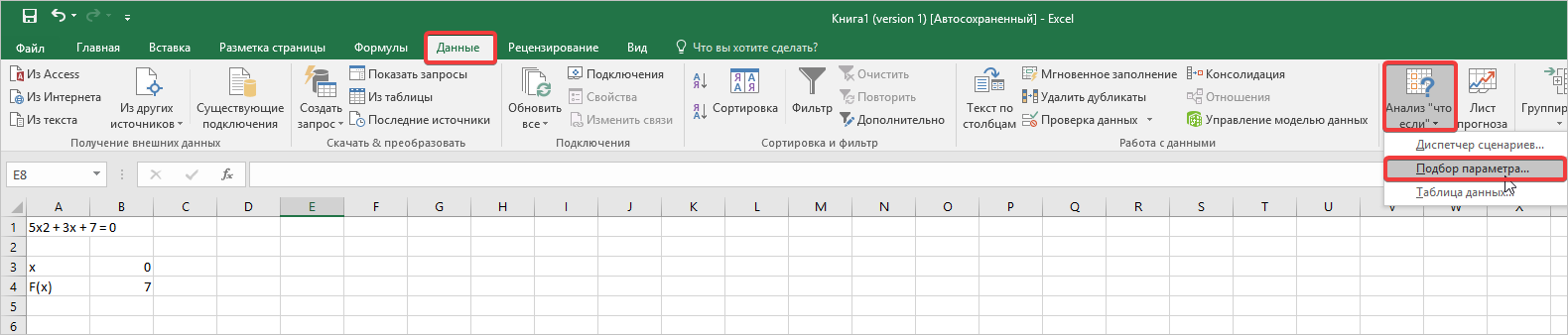
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
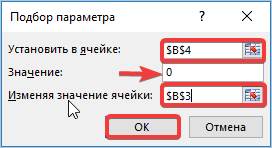
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
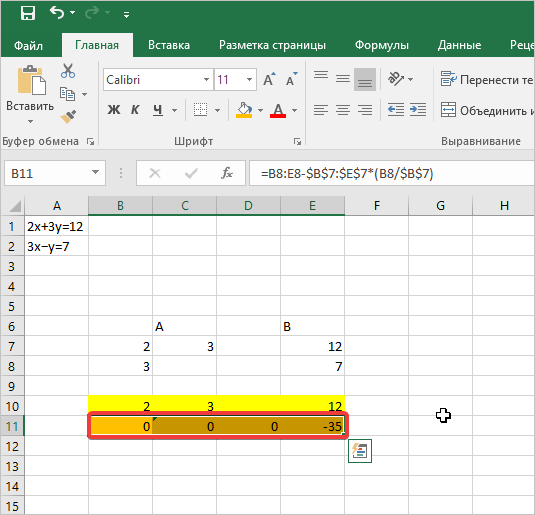
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
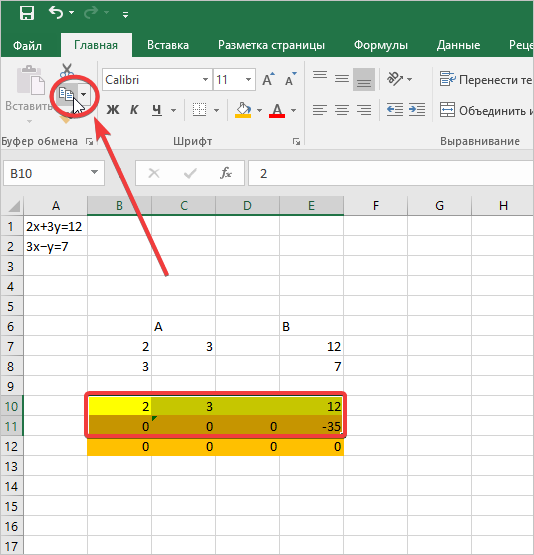
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12689 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
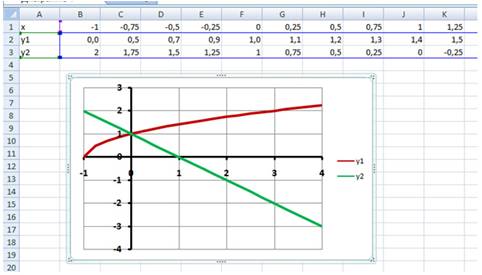
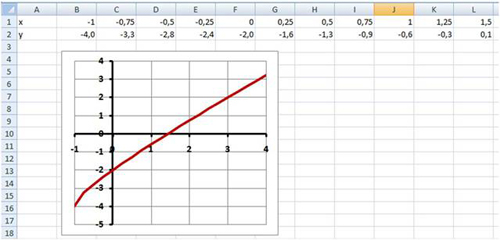
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.

Данную систему уравнений можно представить в матричной форме:




Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
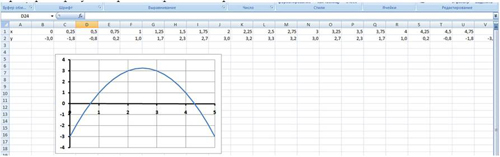
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
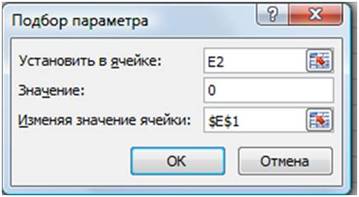
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
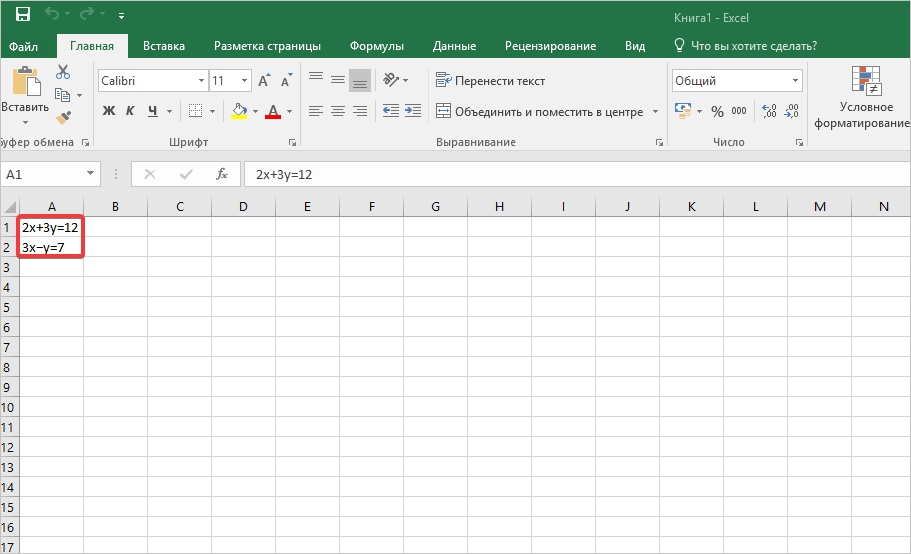
Решить систему уравнений:

1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://zf.bsut.by/it/fbo/zb1/lab2.htm
17 авг. 2022 г.
читать 3 мин
Часто вас может заинтересовать построение уравнения или функции в Excel. К счастью, это легко сделать с помощью встроенных формул Excel.
В этом руководстве представлено несколько примеров того, как строить уравнения/функции в Excel.
Пример 1: построение линейного уравнения
Предположим, вы хотите построить следующее уравнение:
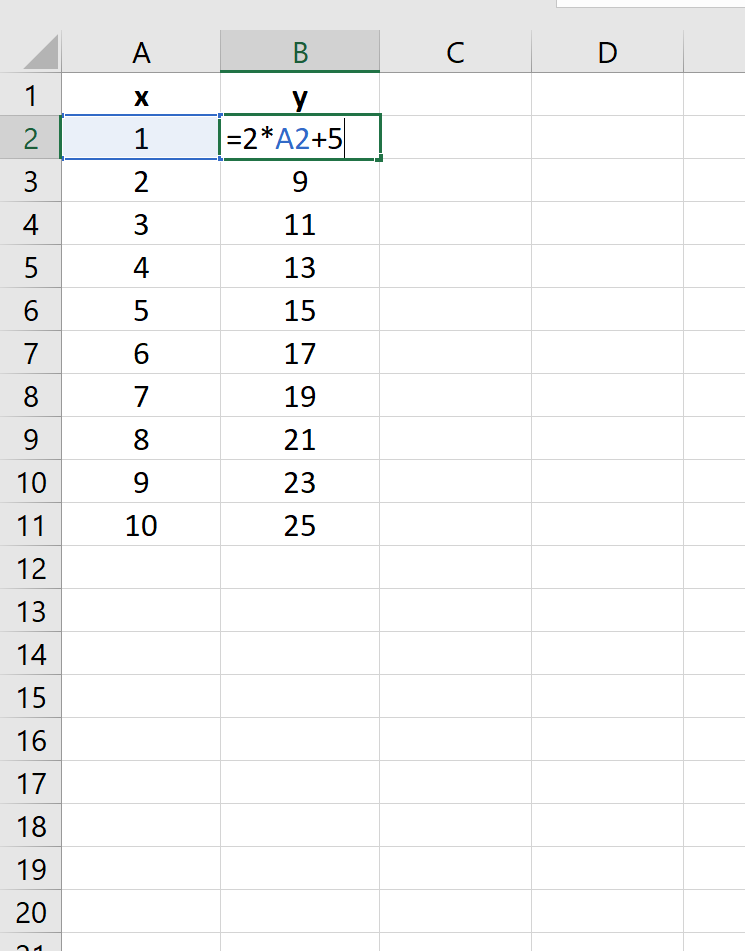
у = 2х + 5
На следующем изображении показано, как создать значения y для этого линейного уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
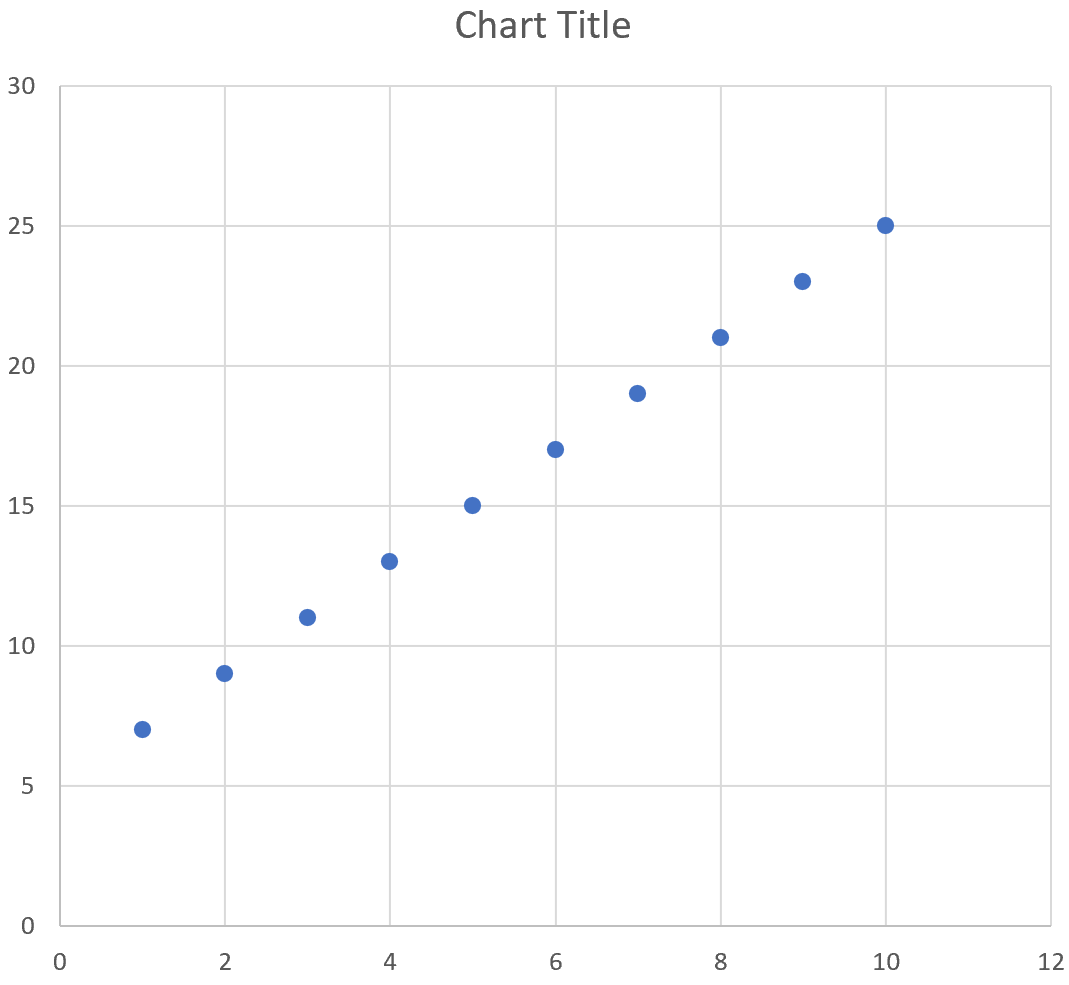
Автоматически появится следующий график:
Мы видим, что график следует прямой линии, поскольку уравнение, которое мы использовали, было линейным по своей природе.
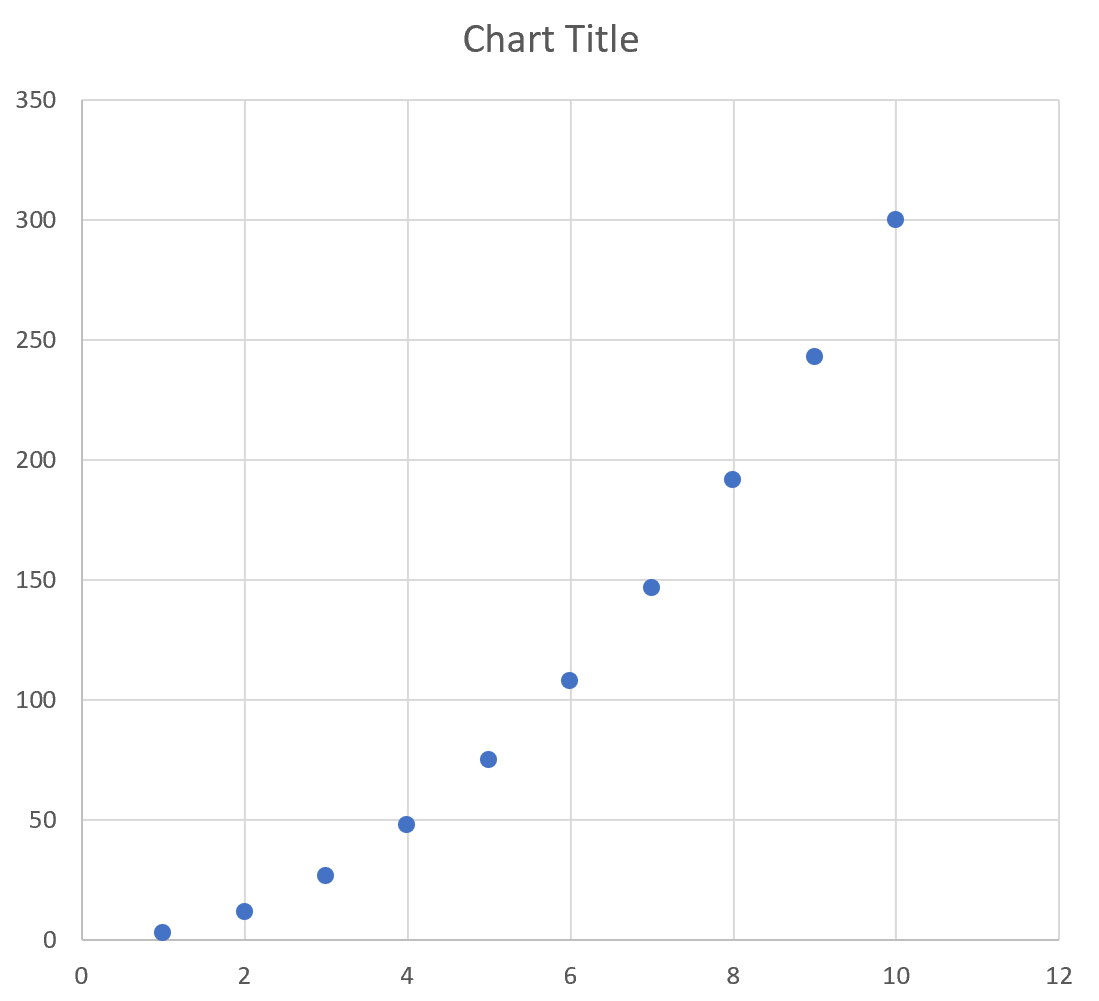
Пример 2. Построение квадратного уравнения
Предположим, вы хотите построить следующее уравнение:
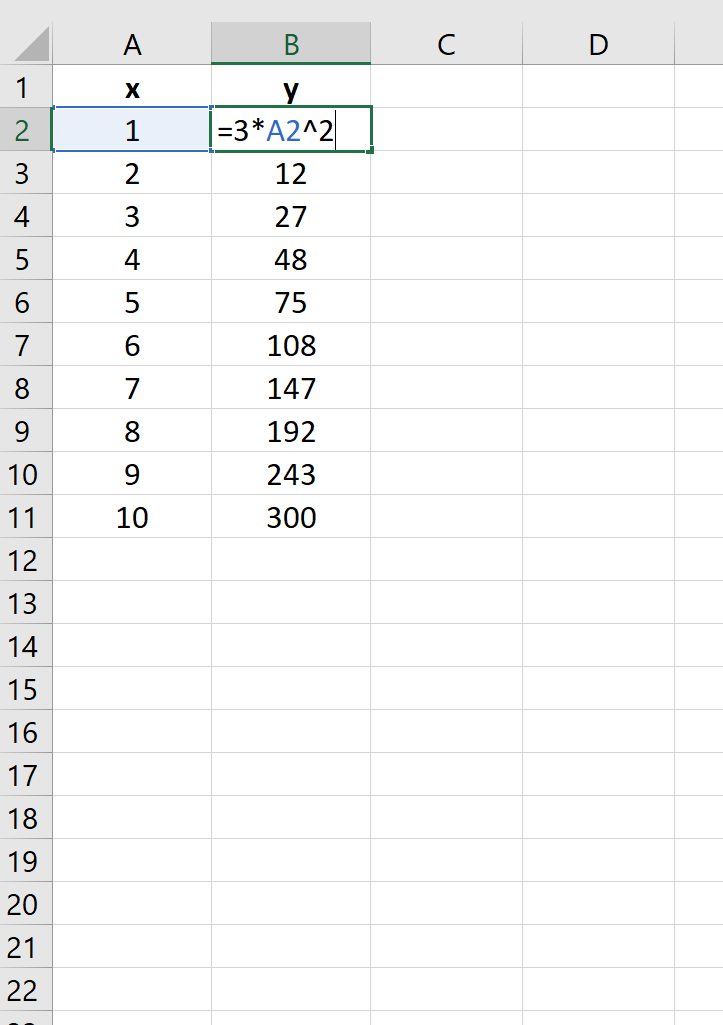
у = 3x 2
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует изогнутой линии, поскольку уравнение, которое мы использовали, было квадратным.
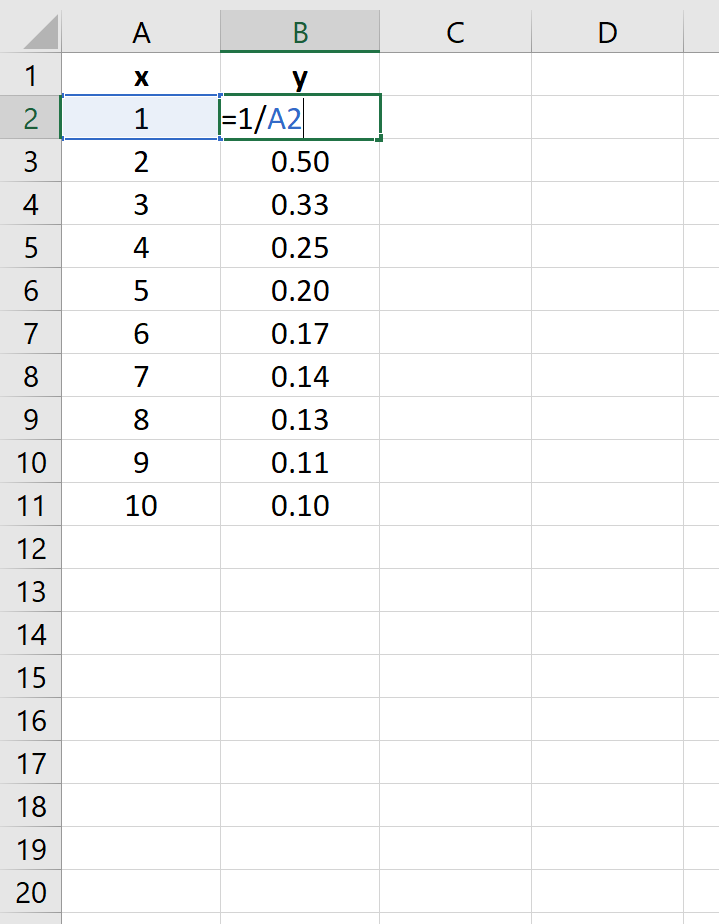
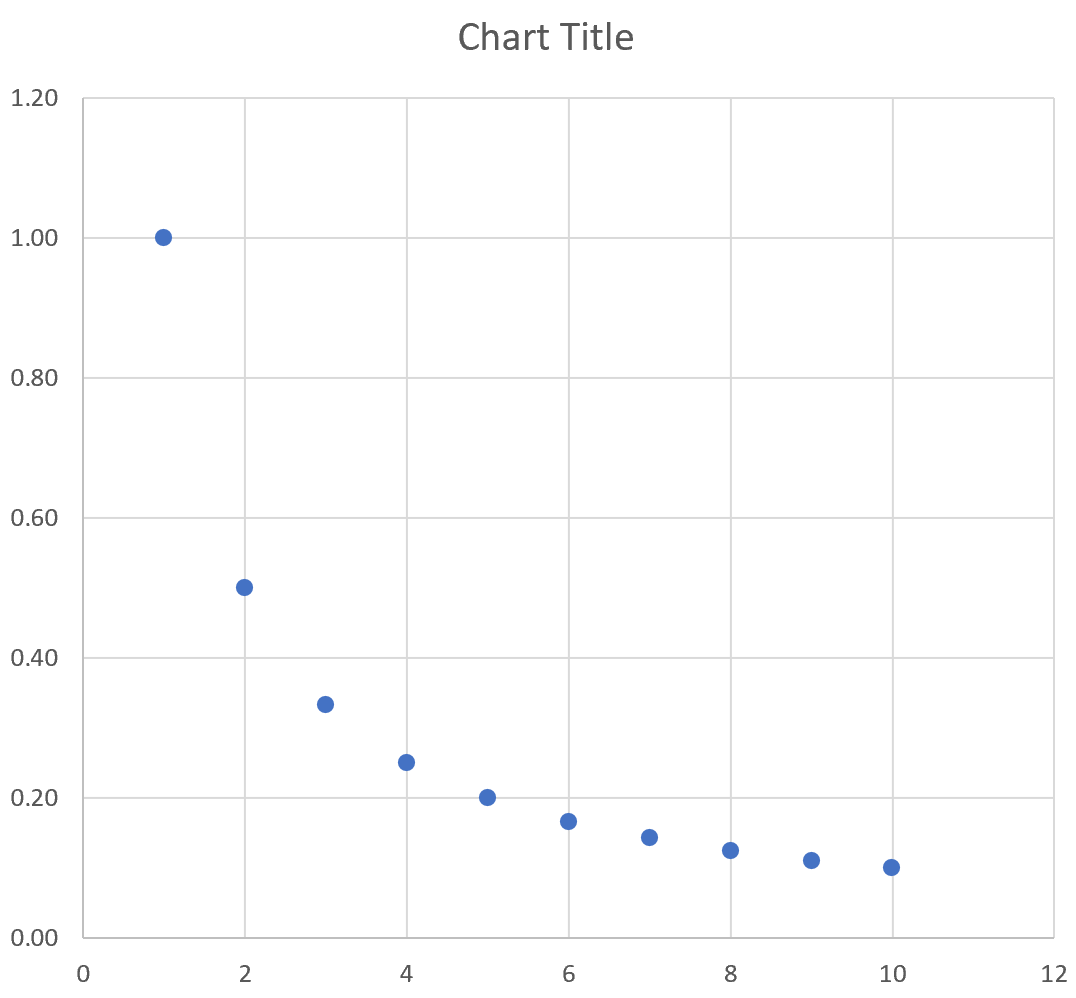
Пример 3: построение уравнения обратной связи
Предположим, вы хотите построить следующее уравнение:
у = 1/х
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует по изогнутой линии вниз, поскольку это представляет уравнение y = 1/x.
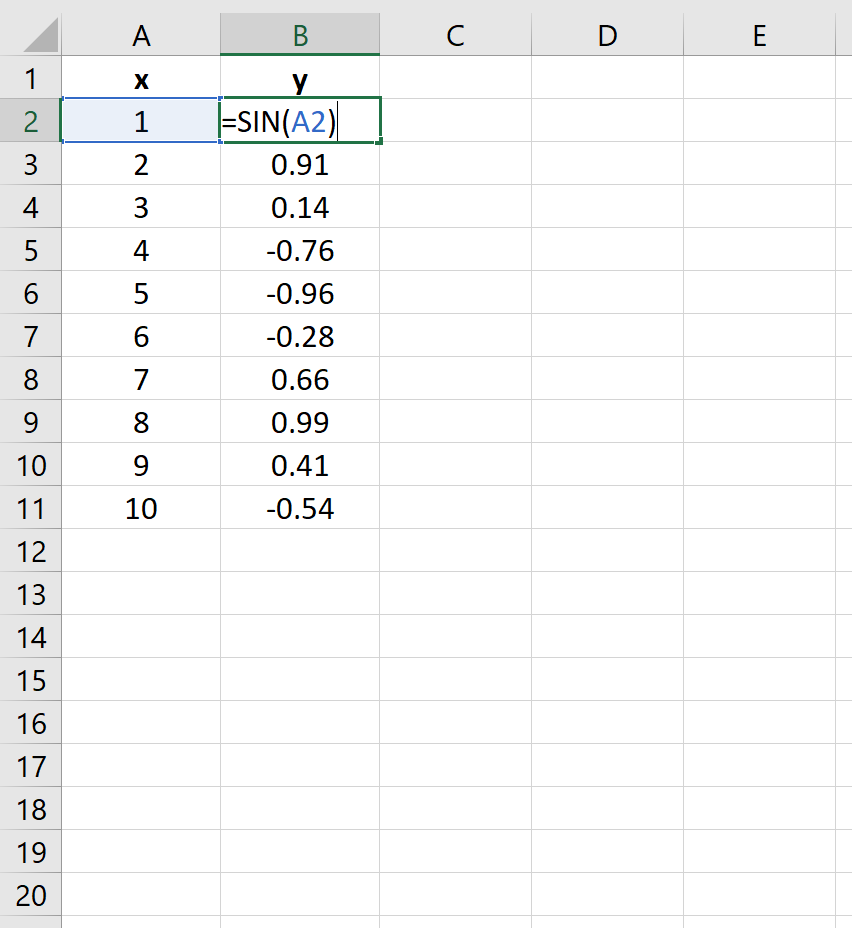
Пример 4. Построение уравнения синуса
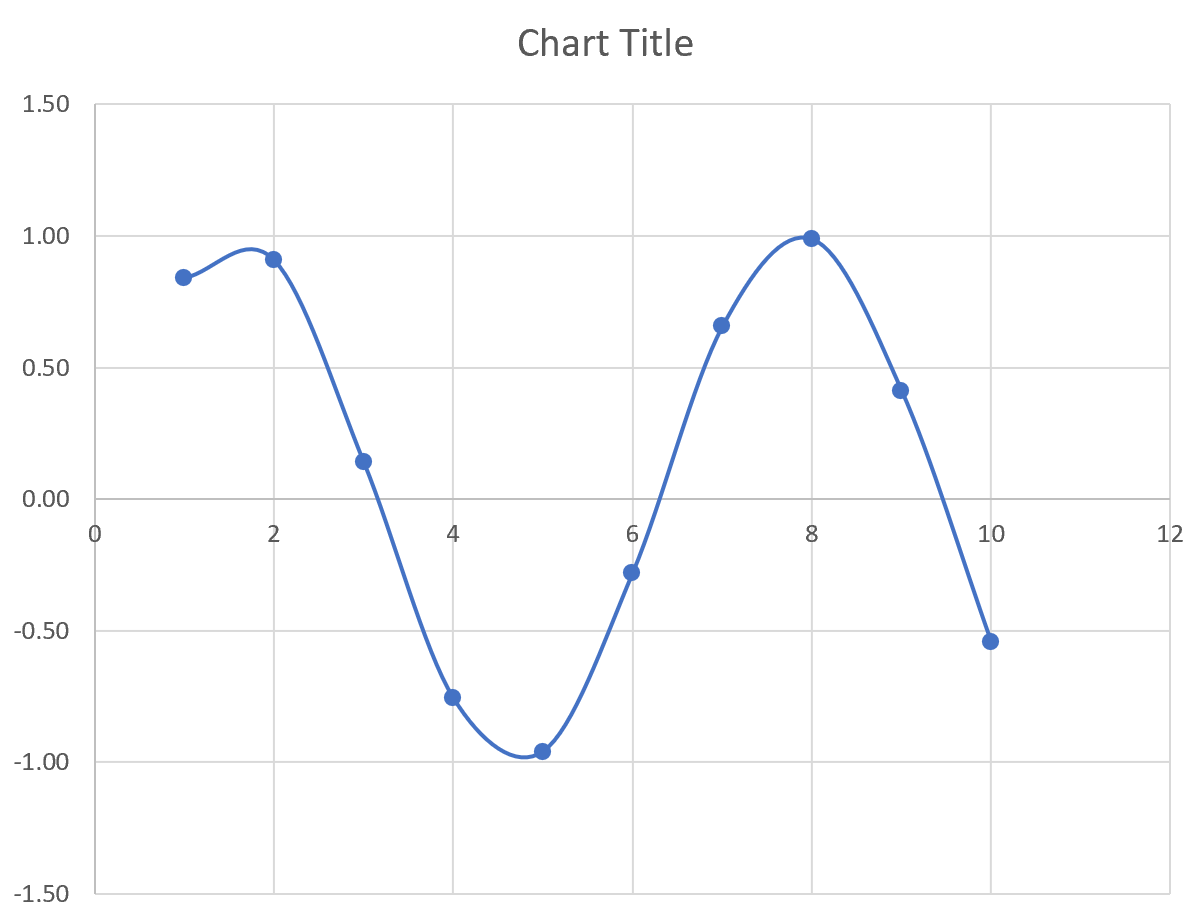
Предположим, вы хотите построить следующее уравнение:
у = грех (х)
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика « Разброс с плавными линиями и маркерами» .
Автоматически появится следующий график:
Вывод
Вы можете использовать аналогичную технику для построения графика любой функции или уравнения в Excel. Просто выберите диапазон значений x для использования в одном столбце, затем используйте уравнение в отдельном столбце, чтобы определить значения y на основе значений x.
Практическое занятие
Математические задачи. Решение уравнений и систем уравнений.
Пояснения к работе
Excel включает
большое число надстроек – откомпилированных программ, добавляющих табличному
процессору новые функциональные возможности. К таким надстройкам относятся
«Подбор параметра», «Поиск решения».
«Подбор параметра» помогает
находить в общем случае приближенные решения уравнений вида f(x)
= 0. Решим простое уравнение:
f(x) = x2 — 5x + 6 = 0
Для решения этого уравнения
подготовим рабочий лист. Ячейка B4 будет содержать значение неизвестной x, а
ячейка B5 – значение функции f(x).
Для этого в B5
поместим формулу = B4* B4 — 5* B4+6, как показано на рис. 1
Рис. 1. Подготовка к решению уравнения
Выберем команду. Сервис/Подбор
параметра. Excel отобразит диалоговое окно Подбор
параметра, приведенное на рисунке 2.В этом окне заполним все три окна в
соответствии с результатом, который мы хотим получить. В поле Установить в
ячейке введем адрес формулы (B5),
результаты которой будут подобраны. В поле Значение введем желаемый
результат вычисления формулы (0). Наконец, используя поле Изменяя значения
ячейки, определим адрес ячейки, которая содержит значение, которое нужно
изменить.
Рис. 2. Заполнение окна Подбор
параметра
После щелчка кнопкой Ok Excel выполнит необходимые вычисления и
выведет диалоговое окно Результат подбора параметра.
Рис. 3. Результат Подбора параметра
Ячейка B4 будет содержать найденный корень
уравнения.
Примечание. В нашем случае уравнение имеет
два корня x1 =2 и x2 = 3. Excel всегда дает только один корень в
зависимости от начального значения изменяемой ячейки.
Примечание. Решение уравнений можно выполнить,
представив функцию в табличном виде. Построив график функции на некотором
отрезке с заданным шагом изменения аргумента, грубо приближенно можно
определить корень уравнения. Затем, используя метод Подбора параметра,
уточнить корень уравнения.
Решение систем уравнений.
Для решения систем уравнений с несколькими
неизвестными используется надстройка «Поиск решения». Пусть требуется решить
систему уравнений
x2 + 5y = 29
5x + y2 = 31
Подготовим рабочий лист так, как показано
на рис. 4. Ячейки D4 и D5
содержат формулы, выражающие левые части уравнений, ячейки E1 и E2 – значения неизвестных x и y
(изменяемые ячейки).
Рис. 4. Подготовка к решению системы
уравнений
Выполним команду Сервис/Поиск решения, на
экране откроется диалоговое окно Поиск решения (рис.5).
Рис. 5. Поиск решения. Надстройки
Установим в поле Установить целевую ячейку
адрес первой формулы D4, в поле Равной значению – число 29 (правая
часть первого уравнения), а в поле Изменяя ячейки диапазон E1:E2 (рис.
6)
Рис. 6. Поиск решения
Второе уравнение мы запишем как ограниченное в поле Ограничения.
Для этого нажмите кнопку Добавить в открывшемся диалоговом окне Добавить
ограничения. Заполним соответствующие поля как показано на рис. 7
Рис. 7. Результат поиска решения
После нажатия кнопки ОК произойдет возврат в окно Поиск
решения. Нам остается только щелкнуть по кнопке Выполнить.
Результат поиска решения показан на рис. 7. Полученные
результаты можно сохранить, нажав кнопку ОК.
Чтобы решить систему из более, чем двух уравнений,
надо одно из них, например первое, выбрать как целевое, т.е. адрес
соответствующей формулы внести в поле Установить целевую ячейку, а
остальные как ограничения.
Надстройка «Поиск решения» как и «Выбор параметра»
позволяет находить только одно решение системы.
Надстройка «Поиск решения» помогает решать довольно
сложные задачи на экстремумы функций нескольких переменных при наличии
ограничений на эти переменные.
Варианты заданий
Задание 1

Определить, сколько точек попадает в заданную фигуру, рис. 1а.
Результат определения принадлежности точек и подсчет
количества точек, принадлежащих заданной фигуре, представлен на рис. 2. В
ячейку C4 помещена формула для определения принадлежности
точек фигуре.
Рис. 2. Подсчет количества точек
Количество точек
находим с помощью автосуммы.
Задание 2. Решить
уравнения и системы уравнений
1.
x3 – x2 + 4 cos πx/2 = 0
2.
x = log x + 5
3.
x2 + xy = 7 –y2
x + 5y2 = 9 –x/3
4.
2x2 + 3y
= 10
—x
+ 6y2 =4
5.
3x
-4y = 3
6.
x3 – sinx – 0,5 = 0
7.
x2 –sinx + 0,1 = 0
8.
x3 + x2
-12x = 0
9.
x3 -19 x – 30 = 0
10.
x3 – x2 +
3x – 10 = 0
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
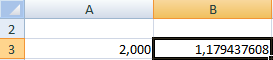
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Содержание
- Варианты решений
- Способ 1: матричный метод
- Способ 2: подбор параметров
- Способ 3: метод Крамера
- Способ 4: метод Гаусса
- Вопросы и ответы
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
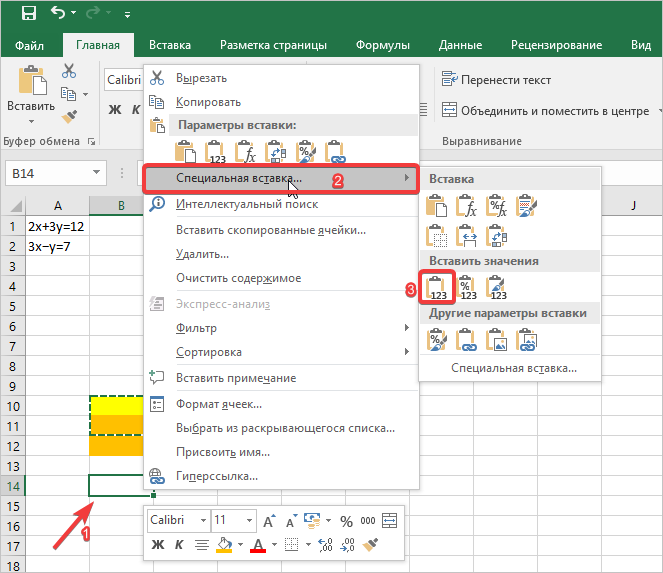
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
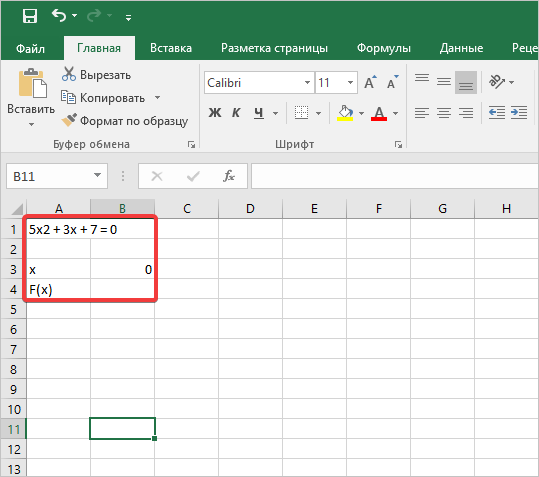
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
3x^2+4x-132=0
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
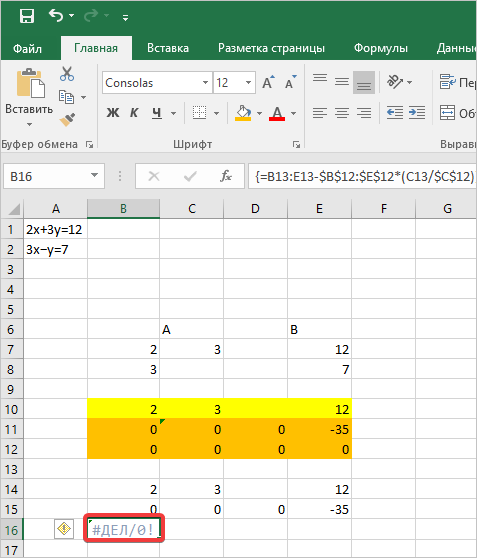
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
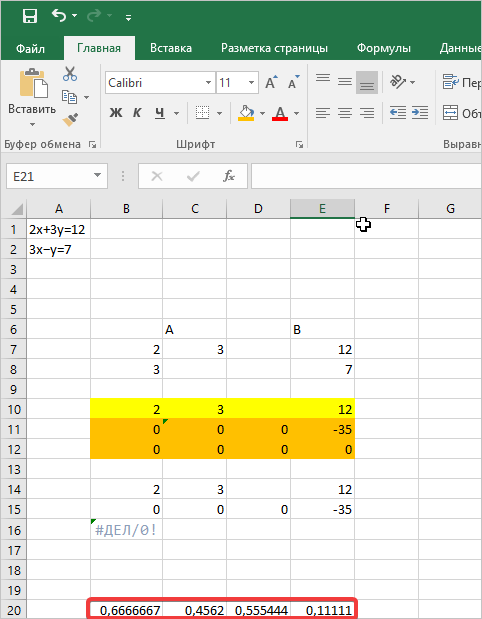
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Еще статьи по данной теме:
Помогла ли Вам статья?
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
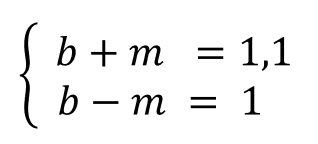
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
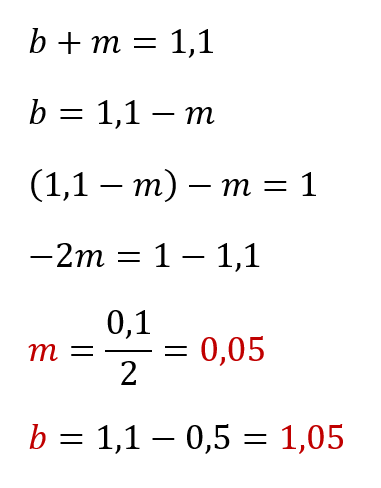
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
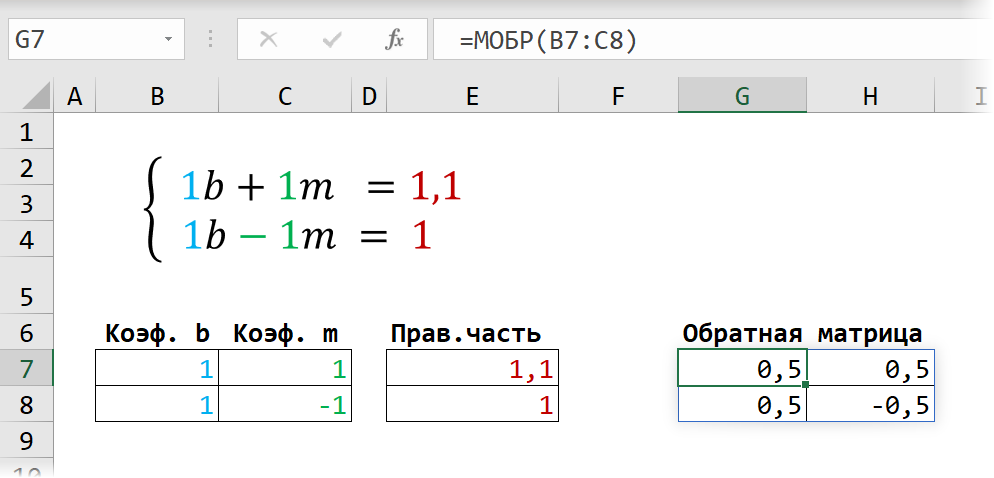
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
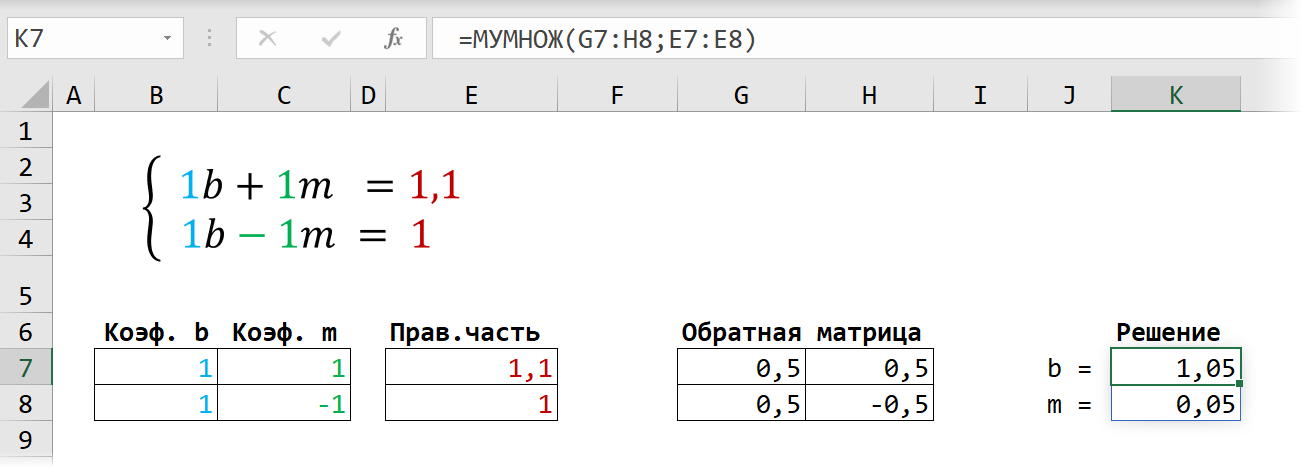
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
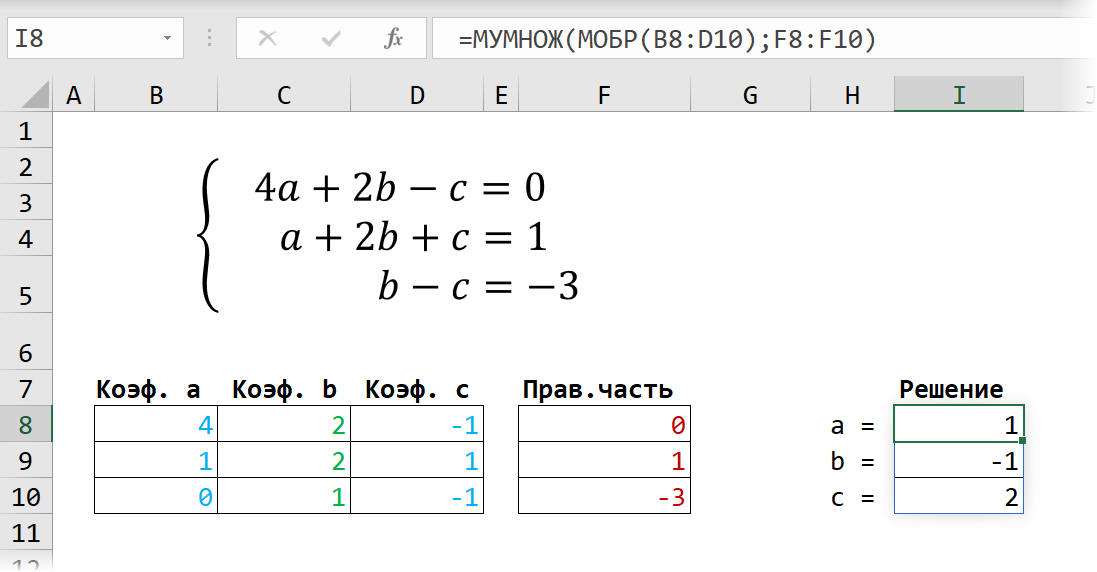
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
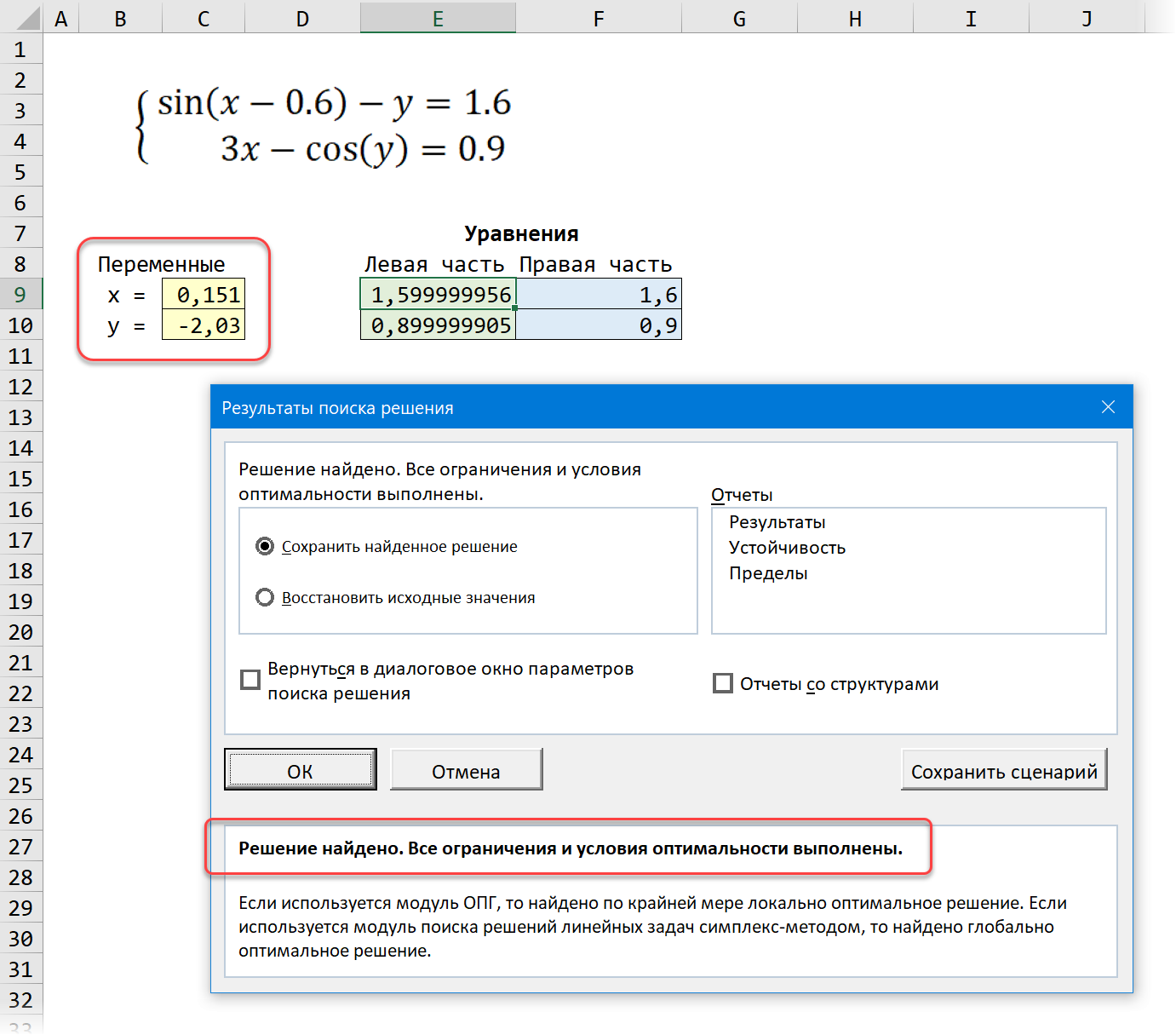
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
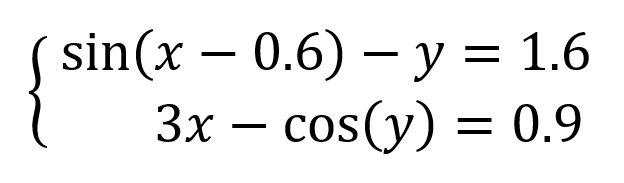
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
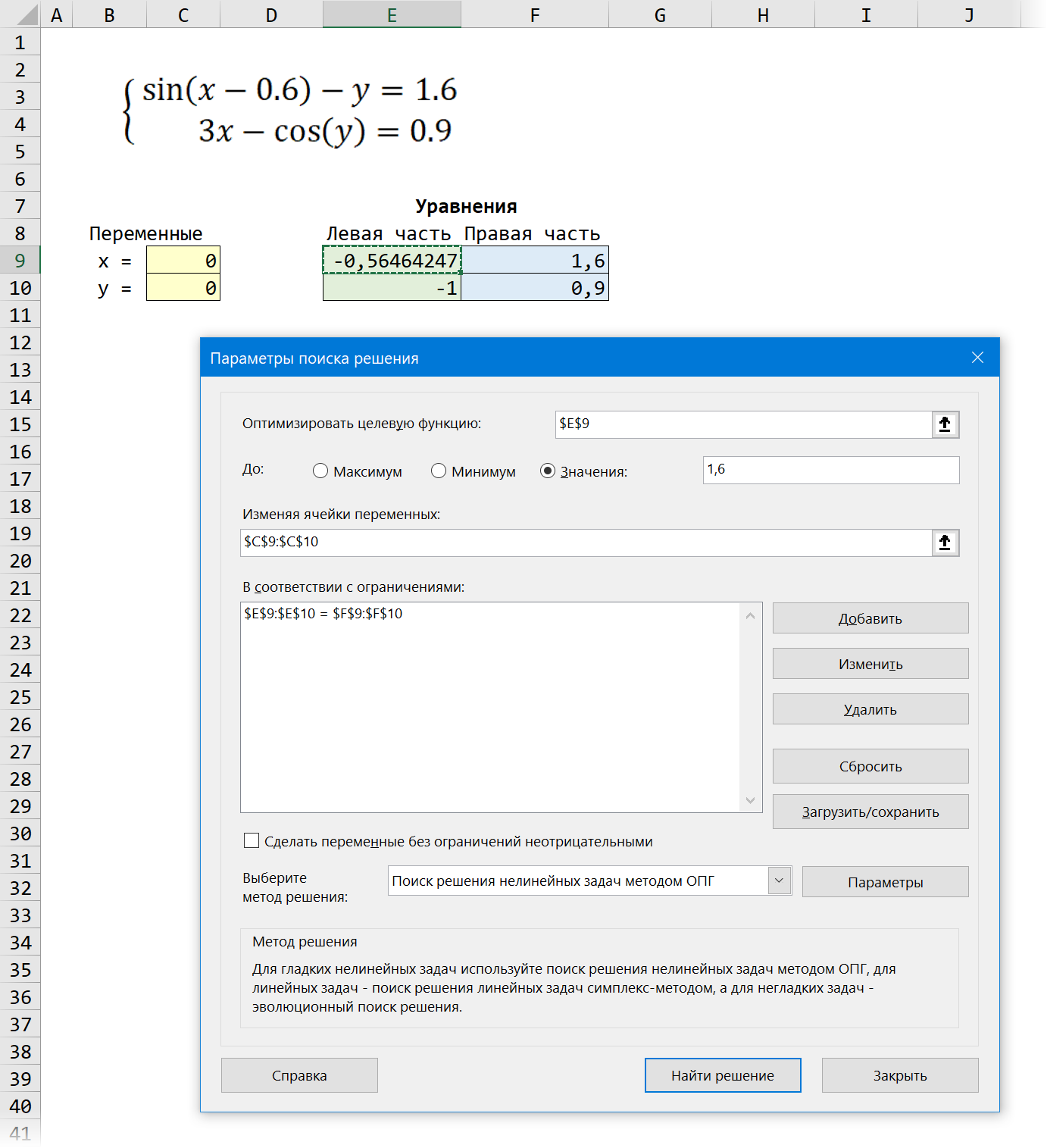
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
- Решение уравнений в среде MS EXCEL
Одна из наиболее актуальных проблем компьютерного обучения – проблема отбора и использования педагогически целесообразных обучающих программ.
При изучении отдельных тем и решении некоторых задач на уроках математики в старших классах громоздкие вычисления как, например, при решении уравнений методом деления отрезка пополам или методом последовательных приближений, затмевают существо математической задачи, не дают увидеть красоту, рациональность применяемого метода решения.
В данной статье я представила те задачи, решение которых с помощью MS EXCEL позволяет получить наглядное, доступное для понимания учащимися решение, показать его логику, рациональность. Попутно учащиеся получают устойчивые навыки работы с программой.
- Нахождение корней уравнения с помощью подбора параметра
Пример 1.
Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 1000 000 условных единиц. Необходимо определить, какими должны быть оклады сотрудников больницы.
Решение такой задачи можно искать методом перебора. Однако в лучшем случае на это уходит много времени. Можно предложить другой способ решения. В EXCEL он реализован как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.
Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: Ai*С+Вi, где С — оклад санитарки; Аi и Вi — коэффициенты, которые для каждой должности определяют следующим образом:
- медсестра получает в 1,5 раза больше санитарки (А2=1,5; В2=0);
- врач — в 3 раза больше санитарки (А3=3; В3=0);
- заведующий отделением — на 30 y.e. больше, чем врач (А4=3; B4=30);
- заведующий аптекой — в 2 раза больше санитарки (А5=2; В5=0);
- заведующий хозяйством — на 40 y.e. больше медсестры (А6=1,5; В6=40);
- заведующий больницей — на 20 y.e. больше главного врача (А8=4; В8=20);
- главный врач — в 4 раза больше санитарки (А7=4; В7=0);
Зная количество человек на каждой должности, нашу модель можно
записать как уравнение: N1*(A1*C+B1)+N2*(A2*C+B2)+…+N8*(A8*C+B8) = 1000000,
где N1 — число санитарок, N2 — число медсестер и т.д.
В этом уравнении нам известны A1…A8, B1…B8 и N1…N8, а С неизвестно. Анализ уравнения показывает, что задача вычисления заработной платы свелась к решению линейного уравнения относительно С. Предположим, что зарплата у санитарки 150,00 y.e.
Введите исходные данные в рабочий лист электронной таблицы, как показано ниже.
|
A |
B |
C |
D |
E |
F |
|
Оклад мед. Работников |
|||||
|
Должность |
Коэф. A |
Коэф. B |
|
Количество сотрудников |
Суммарная зарплата |
|
Санитарка |
1 |
0,00 |
150,00 |
6 |
|
|
Медсестра |
1,5 |
0,00 |
8 |
||
|
Врач |
3 |
0,00 |
10 |
||
|
Зав. отделением |
3 |
30,00 |
3 |
||
|
Зав. аптекой |
2 |
0,00 |
1 |
||
|
Завхоз |
1,5 |
40,00 |
1 |
||
|
Главврач |
4 |
0,00 |
1 |
||
|
Зав. больницей |
4 |
20,00 |
1 |
||
|
Общий фонд равен |
В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D4 формула расчета имеет вид =B4*$D$3+C4.
В столбце F вычислите заработную плату всех работников данной должности. Например, для ячейки F3 формула расчета имеет вид =D3*E3.
В ячейке F11вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже.
|
A |
B |
C |
D |
E |
F |
|
Оклад мед. Работников |
|||||
|
Должность |
Коэф. A |
Коэф. B |
Зарплата |
Количество сотрудников |
Суммарная зарплата |
|
Санитарка |
1 |
0,00 |
150,00 |
6 |
900,00 |
|
Медсестра |
1,5 |
0,00 |
225,00 |
8 |
1800,00 |
|
Врач |
3 |
0,00 |
450,00 |
10 |
4500,00 |
|
Зав. отделением |
3 |
30,00 |
480,00 |
3 |
1440,00 |
|
Зав. аптекой |
2 |
0,00 |
300,00 |
1 |
300,00 |
|
Завхоз |
1,5 |
40,00 |
265,00 |
1 |
265,00 |
|
Главврач |
4 |
0,00 |
600,00 |
1 |
600,00 |
|
Зав. больницей |
4 |
20,00 |
620,00 |
1 |
620,00 |
|
Общий фонд равен |
10425,00 |
Чтобы определите оклад санитарки так, чтобы расчетный фонд был равен заданному надо:
- Активизировать команду Подбор параметра во вкладке Данные / Работа с данными /Анализ «Что, если»;
- В поле «Установить в ячейке» появившегося окна ввести ссылку на ячейку F11, содержащую формулу;
- В поле «Значение» набрать искомый результат 1000000;
- В поле «Изменяя значение ячейки» ввести ссылку на изменяемую ячейку D3 и щелкните на кнопке ОК.
Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако, благодаря этому простому примеру стало, очевидным, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, – это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решать любые уравнения с одной переменной.
Приложение 1
Задание для учащихся:
Составить несколько вариантов штатного расписания с использованием функции Подбор параметра и оформить их в виде таблицы:
- Изменить количество сотрудников на различных должностях;
- Подобрать зарплату санитарки в новых условиях;
- Составить таблицу нескольких вариантов штатного расписания.
Рассмотрим еще один пример нахождения корней уравнения с помощью подбора параметра. При решении этого уравнения используется также метод последовательных приближений. Учащиеся в классах с углубленным изучением математики знакомы с этим методом. Поэтому, чтобы этот пример был доступен для других учащихся, предлагаю краткую теорию этого метода.
Пусть дано уравнение, записанное в виде x=F(x). Выбирают некоторое начальное приближение x1 и подставляют его вместо x в F(x). Полученное значение x2=F(x1) этой функции считают вторым приближением. Далее находят третье приближение по формуле x3=F(x2) и так далее. Таким образом, получаем последовательность x1, x2, x3,…, xn,… чисел, имеющая предел α. Тогда если функция F(x) непрерывна, из равенства x n+1=F(xn) получаем α=F(α). Это означает, что α является решением уравнения x=F(x).
Пример 2.
Пусть нам дан многочлен третьей степени:
x³-0,01x²-0,7044x+0,139104=0.
Так как мы ищем корни полинома третьей степени, то имеются не более трех вещественных корней. Для нахождения корней их первоначально надо локализовать, то есть найти интервалы, на которых они существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположный знак. С целью нахождения интервалов, на концах которых функция изменяет знак, необходимо построить ее график или протабулировать ее. Составим таблицу значений функции на интервале [-1;1] с шагом 0,2. Для этого необходимо:
- Ввести в ячейку A2 значение -1, а в ячейку A3 значение -0,8.
- Выбрать диапазон A2:A3, расположить указатель мыши на маркере заполнения этого диапазона и протянуть его на диапазон A4:A12, аргумент протабулирован.
- В ячейку B2 ввести формулу:
=A2^3-0,01*A2^2-0,7044*A2+0,139104
- Выбрать ячейку B2. Расположить указатель мыши на маркере заполнения этой ячейки и протянуть его на диапазон B3:B12. Функция также протабулирована.
|
Значение аргумента х |
Значение функции у |
|
-1,00 |
-0,1665 |
|
-0,8 |
0,1842 |
|
-0,60 |
0,3421 |
|
-0,4 |
0,3553 |
|
-0,20 |
0,2716 |
|
0 |
0,1391 |
|
0,20 |
0,0058 |
|
0,4 |
-0,0803 |
|
0,60 |
-0,0711 |
|
0,8 |
0,0812 |
|
1,00 |
0,4247 |
Из таблицы видно, что полином меняет знак на интервалах [-1; -0,8], [0,2; 0,4] и [0,6; 0,8], и поэтому на каждом из этих интервалов имеется свой корень. Так как полином третьей степени имеет не более трех корней, то они все локализованы.
Прежде чем приступить к нахождению корней при помощи подбора параметра, необходимо выполнить некоторую подготовительную работу:
- Установить точность, с которой находится корень. Корень при помощи подбора параметра находится методом последовательных приближений. Для этого в Настройке панели быстрого доступа / Другие команды, и на вкладке Формулы диалогового окна Параметры Exel задайте в Параметрах вычислений относительную погрешность и предельное число итераций равными 0,00001 и 1000, соответственно.
- Отвести на рабочем листе ячейку, например С2, под искомый корень. Эта ячейка будет играть двойную роль. До применения подбора параметра в ней находится начальное приближение к корню уравнения, а после применения – найденное приближенное значение корня.
- Корень при помощи подбора параметра находим методом последовательных приближений. Поэтому в ячейку C2 надо ввести значение, являющееся приближением к искомому корню. В нашем случае, первым отрезком локализации корня является [-1;-0,8]. Следовательно, за начальное приближение к корню разумно взять среднюю точку этого отрезка -0,9.
- Отвести ячейку, например D2, под функцию, для которой ведется поиск корня, причем вместо неизвестной у этой функции должна указываться ссылку на ячейку, отведенную под искомый корень. Таким образом, в ячейку D2 введите формулу:
=C2^3-0,01*C2^2-0,7044*C2+0,139104
Аналогично надо поступить с двумя другими искомыми корнями:
- Отвести ячейку C8 под второй корень, ввести в нее начальное приближение 0,3, а в ячейку D8 ввести следующую формулу:
=C8^3-0,01*C8^2-0,7044*C8+0,139104
- Отвести ячейку C10 под второй корень, ввести в нее начальное приближение 0,7, а в ячейку D10 ввести следующую формулу:
=C10^3-0,01*C10^2-0,7044*C10+0,139104
Результаты выполненных действий приведены в таблице.
|
Значение х |
Значение у |
Начальное приближение до применения метода |
Значение функции |
|
-1,00 |
-0,1665 |
-0,9 |
0,0360 |
|
-0,8 |
0,1842 |
||
|
-0,60 |
0,3421 |
||
|
-0,4 |
0,3553 |
||
|
-0,20 |
0,2716 |
||
|
0 |
0,1391 |
||
|
0,20 |
0,0058 |
0,3 |
-0,0461 |
|
0,4 |
-0,0803 |
||
|
0,60 |
-0,0711 |
0,7 |
-0,0159 |
|
0,8 |
0,0812 |
||
|
1,00 |
0,4247 |
Теперь можно переходить к нахождению первого корня уравнения:
Выберете команду Подбор параметра. На экране отобразится диалоговое окно Подбор параметра.
- В поле Установить в ячейке введите ссылку на ячейку D2. В этом поле дается ссылка на ячейку, в которой введена формула, вычисляющая значение левой части уравнения. Для нахождения корня с помощью подбора параметра уравнение надо представить в таком виде, чтобы его правая часть не содержала переменную.
- В поле Значение введите 0. Здесь указывается значение из правой части уравнения.
- В поле Изменяя значение ячейки введите C2. В данном поле приводится ссылка на ячейку, отведенную под переменную.
- Нажмите кнопку OK.
На экране отображается окно Результат подбора параметра с результатами работы команды Подбор параметра. Кроме того, рассматриваемое средство помещает найденное приближенное значение корня в ячейку C2. В данном случае оно равно -0,920. Аналогично в ячейках C8 и C10 находятся два оставшихся корня. Они равны 0,210 и 0,721.
|
Значение х |
Значение у |
Корень уравнения |
Значение функции |
|
-1,00 |
-0,1665 |
-0,920 |
0,00 |
|
-0,8 |
0,1842 |
||
|
-0,60 |
0,3421 |
||
|
-0,4 |
0,3553 |
||
|
-0,20 |
0,2716 |
||
|
0 |
0,1391 |
||
|
0,20 |
0,0058 |
0,210 |
0,00 |
|
0,4 |
-0,0803 |
||
|
0,60 |
-0,0711 |
0,721 |
0,00 |
|
0,8 |
0,0812 |
||
|
1,00 |
0,4247 |
Приложение 2
Задание для учащихся:
Найти все корни уравнений
1. Х3-2,92Х2+1,4355Х+0,791136=0
2. Х3-2,56Х2-1,3251Х+4,395006=0
3. Х3+2,84Х2-5,6064Х-14,766336=0
- Нахождение корней уравнения методом деления отрезка пополам
Краткая теория метода. Пусть непрерывная функция F(x) имеет значения разных знаков на концах отрезка [a;b], то есть F(a)F(b)<0.Тогда уравнение F(x)=0 имеет корень внутри этого отрезка. Отрезок [a;b] отрезком локализации корня. Пусть c=(a+b)/2 — середина отрезка [a;b]. Если F(a)F(c)<=0, то корень находится на отрезке [a;c], который берем за новый отрезок локализации корня. Если F(a)F(c)>0, то за новый отрезок локализации корня берем [c;b].Отметим, что новый отрезок локализации корня в два раза меньше первоначального. Процесс деления отрезка для локализации корня продолжаем до тех пор, пока его длина не станет меньше ε, точности нахождения корня. В этом случае любая точка отрезка локализации отличается от корня не более чем на ε/2.
Найдем корни уравнения x²–2=0 с точностью до 0,001 методом деления отрезка пополам. За первоначальный отрезок локализации корня выбран [0;2]. Для реализации этого метода введите в ячейки рабочего листа формулы либо значения, приведенные ниже в таблице:
|
Ячейка |
Формула или значение |
|
B1 |
0,001 |
|
A3 |
0 |
|
B3 |
2 |
|
C3 |
=(A3+B3)/2 |
|
D3 |
=(A3^2-2)*(C3^2-2) |
|
E3 |
=C3^2-2 |
|
F3 |
=ЕСЛИ(B3–A3<$B$1;»Корень найден и равен » & текст (C3;»0,000»); » ») |
|
A4 |
=ЕСЛИ (D3<=0; A3;C3) |
|
B4 |
= ЕСЛИ(D3<=0; C3; B3) |
|
C4 |
=(A4+B4)/2 |
|
D4 |
=(A4^2-2)*(C4^2-2) |
|
E4 |
C4^2-2 |
|
F4 |
=ЕСЛИ(B4-A4<$B$1; »Корень найден и равен » & текст(C4; »0,000»); » ») |
Теперь осталось только выбрать диапазон A4:F4, расположить указатель мыши на маркере его заполнения и пробуксировать его вниз до тех пор, пока в столбце F не появится сообщение о том, что корень найден. В данном случае сообщение появится в ячейке F14, а значение корня с точностью до 0,001 равно 1,415.
Число шагов можно определить заранее и скопировать формулы в диапазон из необходимого числа строк. Число шагов до нахождения корня определяется по формуле: [log2((b-a)/(2*t))]+1 (1), где [x] есть целая часть числа х, t — заданная точность.
В заключение отмечу, что в рассмотренном примере использовались:
- Операция конкатенации строк, которая объединяет несколько строк в одну (обозначается символом амперсанта &). При объединении двух строк вторая строка добавляется непосредственно в конец первой строки.
- Функция рабочего листа из категории функций по работе с текстом ТЕКСТ (TEXT). Данная функция преобразует значение в текст в заданном числовом формате.
Приложение 3
Задание для учащихся:
Вычислить корень уравнения Cosx=x на отрезке [0;2] с точностью до 0,001. Число шагов для определения корня вычислить при помощи формулы (1).
Использование MS EXEL значительно расширяет круг задач, которые можно использовать в обучении. Это обусловлено возможностью передачи трудоемких операций компьютеру, например, при решении уравнений методами итераций и деления отрезка пополам.
Литература
- Информатика в школе / Под ред. Макаровой Н. В. – СПб: Питер Ком, 1999.
- Символоков Л. В. Решение бизнес задач в Microsoft Office – М.: ЗАО «Издательство БИНОМ», 2001.
- Шохолович В. Ф. Информационные технологии обучения. Информатика и образование. 1998. – №2.
- Игнекова Г. С. Методические аспекты подготовки учителя информатики. Информатика и образование. 1998. – №3.
Тип урока: Обобщение, закрепление
пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического
способа решения уравнений; - закрепление навыков записи и
копирования формул, построения графиков
функций в электронных таблицах Excel 2007; - формирование и первичное закрепление
знаний о решении уравнений с
использованием возможностей электронных
таблиц Excel 2007; - формирование мышления, направленного на
выбор оптимального решения; - формирование информационной культуры
школьников.
Оборудование: персональные
компьютеры, мультимедиапроектор,
проекционный экран.
Материалы к уроку: презентация Power Point
на компьютере учителя (Приложение 1).
Ход урока
Организационный момент.
Слайд 1 из Приложения1 ( далее
ссылки на слайды идут без указания
Приложения1).
Объявление темы урока.
1. Устная работа (актуализация
знаний).
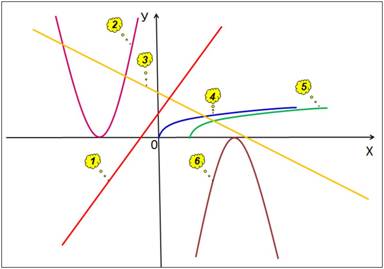
Слайд 2 — Соотнесите перечисленные
ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3)2; у = -(х — 4)2;
Рис. 1.
Слайд 3 Графический способ решения
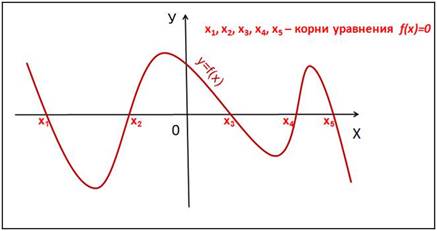
уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются
значения х1, х2, … точек
пересечения графика функции y=f(x) с осью
абсцисс (Рис. 2).
Рис. 2.
Слайд 4
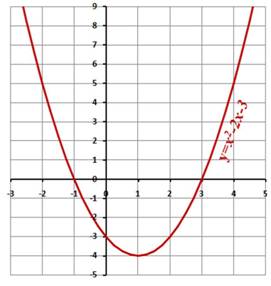
Найдите корни уравнения х2-2х-3=0,
используя графический способ решения
уравнений (Рис.3).
Ответ: -1; 3.
Рис. 3.
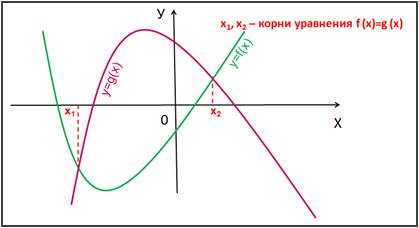
Слайд 5 Графический способ решения
уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются
значения х1, х2, … точек
пересечения графиков функций y=f(x) и у=g(x).
(Рис. 4):
Рис. 4.
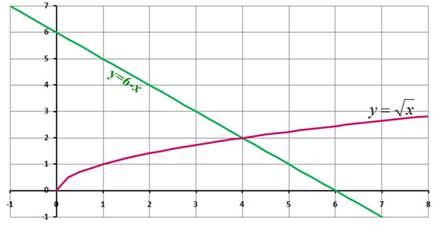
Слайд 6 Найдите корни уравнения 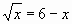
используя графический способ решения
уравнений (Рис. 5).
Ответ: 4.
Рис. 5.
2. Объяснение нового материала.
Практическая работа.
Решение уравнений графическим способом
требует больших временных затрат на
построение графиков функций и в
большинстве случаев дает грубо
приближенные решения. При использовании
электронных таблиц, в данном случае – Microsoft
Excel 2007, существенно экономится время на
построение графиков функций, и появляются
дополнительные возможности нахождения
корней уравнения с заданной точностью (метод
Подбор параметра).
I. Графический способ решения
уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в
Excel одновременно с учениками с подробными (при
необходимости) инструкциями и выводом
результатов на проекционный экран. Слайды
Приложения 1 используются для формулировки
задач и подведения промежуточных итогов.
Слайд 7
Пример1: Используя средства построения
диаграмм в Excel, решить графическим способом
уравнение —х2+5х-4=0.
Для этого: построить график функции у=-х2+5х-4
на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения
графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в
табличной форме (рис. 6):
Рис. 6.
Для этого:
- в ячейку А1 ввести текст Х, в
ячейку A2 — Y; - в ячейку В1 ввести число 0, в ячейку С1
– число 0,25; - выделить ячейки В1:С1, подвести
указатель мыши к маркеру выделения, и в
тот момент, когда указатель мыши примет
форму черного крестика, протянуть маркер
выделения вправо до ячейки V1 (Рис. 7).
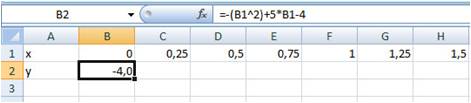
Рис. 7.
- в ячейку B2 ввести формулу =-(B1^2)+5*B1-4;
При вводе формулы можно
вводить адрес ячейки с клавиатуры (не
забыть переключиться на латиницу), а
можно просто щелкнуть мышью на ячейке с
нужным адресом.
После ввода формулы в ячейке
окажется результат вычисления по
формуле, а в поле ввода строки формул —
сама формула (Рис. 8):
Рис. 8.
- скопировать содержимое ячейки B2 в
ячейки C2:V2 за маркер выделения. Весь
ряд выделенных ячеек заполнится
содержимым первой ячейки. При этом ссылки
на ячейки в формулах изменятся
относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
Для этого:
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График
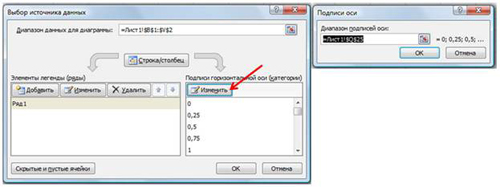
выбрать вид График; - на вкладке Конструктор|Выбрать данные
(Рис. 9) в открывшемся окне «Выбор
источника данных» щелкнуть по кнопке Изменить
в поле Подписи горизонтальной оси —
откроется окно «Подписи оси». Выделить в
таблице диапазон ячеек B1:V1 (значения
переменной х). В обоих окнах щелкнуть
по кнопкам ОК;
Рис. 9.
- на вкладке Макет|Оси|Основная
горизонтальная ось|Дополнительные
параметры основной горизонтальной оси
выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица
измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки
Тип
линии и Цвет линии);
- самостоятельно изменить ширину и цвет
линии для вертикальной оси; - на вкладке Макет|Сетка|Вертикальные
линии сетки по основной оси выбрать Основные
линии сетки.
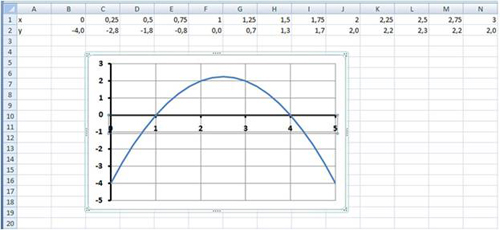
Примерный результат работы приведен на
рис. 10:
Рис. 10.
3 этап: Определение корней уравнения.
График функции у=-х2+5х-4
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня: х1=1; х2=4.
II. Графический способ решения уравнений
вида f(x)=g(x) в Excel.
Слайд 8
Пример 2: Решить графическим способом
уравнение 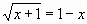
Для этого: в одной системе координат
построить графики функций у1=
и у2=1-х
на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки
пересечения графиков функций.
1 этап: Представление функций в
табличной форме (рис. 1):
- Перейти на Лист2.
- Аналогично Примеру 1, применив
приемы копирования, заполнить таблицу.
При табулировании функции у1=
воспользоваться встроенной функцией Корень
(Рис. 11).
Рис. 11.
2 этап: Построение диаграммы типа График.
- Выделить диапазон ячеек (А2:V3);
- Аналогично Примеру 1 вставить и
отформатировать диаграмму типа График,
выбрав дополнительно в настройках
горизонтальной оси: вертикальная ось
пересекает в категории с номером 5.
Примерный результат работы приведен на
Рис. 12:
Рис. 12.
3 этап: Определение корней уравнения.
Графики функций у1=
и у2=1-х пересекаются в одной
точке (0;1) и, следовательно, уравнение
имеет один корень – абсцисса этой точки: х=0.
III. Метод Подбор параметра.
Слайд 9
Графический способ решения уравнений
красив, но далеко не всегда точки
пересечения могут быть такими «хорошими»,
как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц
позволяют находить приближенные значения
коней уравнения с заданной точностью. Для
этого используется метод Подбор
параметра.
Слайд 10
Пример 3: Разберем метод Подбор
параметра на примере решения уравнения —х2+5х-3=0.
1 этап: Построение диаграммы типа График
для приближенного определения корней
уравнения.
Построить график функции у=—х2+5х-3,
отредактировав полученные в Примере 1
формулы.
Для этого:
- выполнить двойной щелчок по ячейке B2,
внести необходимые изменения; - с помощью маркера выделения
скопировать формулу во все ячейки
диапазона C2:V2.
Все изменения сразу отобразятся на
графике.
Примерный результат работы приведен на
Рис. 13:
Рис. 13.
2 этап: Определение приближенных
значений корней уравнения.
График функции у=-х2+5х-3
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня.
По графику приближенно можно
определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения
уравнения с заданной точностью методом Подбор
параметра.
1) Начать с поиска более точного
значения меньшего корня.
По графику видно, что ближайший
аргумент к точке пересечения графика с
осью абсцисс равен 0,75. В таблице
значений функции этот аргумент
размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор
параметра…;
В открывшемся диалоговом окне Подбор
параметра (Рис. 14) в поле Значение
ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки:
ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
Рис. 14.
Рис. 15.
- В окне Результат подбора (Рис. 15)
выводится информация о величине
подбираемого и подобранного значения
функции: - В ячейке E1 выводится подобранное
значение аргумента 0,6972 с требуемой
точностью (0,0001).
Установить точность можно путем
установки в ячейках таблицы точности
представления чисел – числа знаков
после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения
определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение
большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для
решения уравнений вида f(x)=g(x).
При использовании метода Подбор
параметров для решения уравнений вида f(x)=g(x)
вводят вспомогательную функцию y(x)=f(x)-g(x)
и находят с требуемой точностью значения х
точек пересечения графика функции y(x) с
осью абсцисс.
3. Закрепление изученного материала. Самостоятельная
работа.
Слайд 11
Задание: Используя метода Подбор
параметров, найти корни уравнения
с точностью до 0,001.
Для этого:
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с
шагом 0,25 (Рис. 16):
Рис. 16.
- найти приближенное значение х
точки пересечения графика функции с
осью абсцисс (х≈1,4); - найти приближенное решение уравнения с
точностью до 0,001 методом Подбор
параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной
работы.
Слайд 13 Повторение графического
способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического
способа решения уравнения вида f(x)=g(x).
Выставление оценок.
5. Домашнее задание.
Слайд 15 .
Используя средства построения диаграмм
в Excel и метод Подбор параметра, определите
корни уравнения х2-5х+2=0 с
точностью до 0,01.
Создание уравнений и формул
В этом курсе:
Office содержит формулы, которые вы можете легко вставлять в документы. Если встроенные формулы Office вас не устраивают, можно править и изменять существующие уравнения или написать собственную формулу с нуля.
Новые возможности для работы с формулами в Word
Учащиеся и преподаватели, участвующие в программе предварительной оценки Ваши пожелания услышаны! Вот верхний требуемый синтаксис математического уравнения LaTeX.
Доступно для подписчиков версии 1707 (сборка 8326,2058) и более новой.
На вкладке Вставка нажмите кнопку Уравнение и выберите нужную формулу в коллекции.
После вставки формулы откроется вкладка Работа с формулами > Конструктор, содержащая символы и структуры, которые можно добавить к вашей формуле.
Для набора новой формулы с нуля нажмите Alt += на клавиатуре.
Выберите Вставка > Формула и выберите Вставить новую формулу в нижней части встроенной коллекции формул. Вставится заполнитель, в котором можно ввести формулу.
Добавление формулы в коллекцию
Выделите формулу, которую нужно добавить.
Щелкните стрелку вниз и выберите Сохранить как новую формулу. .
В диалоговом окне Создание нового стандартного блока введите имя формулы.
В списке коллекции выберите пункт Формулы.
Нажмите кнопку ОК.
Для изменения или правки созданных ранее формул:
Выберите формулу для открытия вкладки Работа с формулами в ленте.
Примечание: Если вы не видите вкладку Работа с формулами, то, вероятно, формула была создана в более поздней версии Word. Если это так, то см. раздел Изменение формулы, созданной в предыдущей версии Word.
Выберите Конструктор, чтобы увидеть инструменты для добавления в формулу различных элементов. Можно добавить или изменить следующие элементы формулы.
В группе Символы находятся математические символы. Чтобы увидеть все символы, нажмите кнопку Еще. 
В группе Структуры представлены структуры, которые можно вставить. Просто выберите элемент, а затем замените заполнители в структуре (штрихпунктирные прямоугольники) нужными значениями.
Параметр Профессиональный отображает формулу в профессиональном формате, оптимизированном для отображения. Параметр Линейный отображает формулу как исходный текст, который при необходимости можно использовать для внесения изменений в формулу. Параметр «Линейный» отображает формулу в формате UnicodeMath или в формате LaTeX, который можно выбрать в блоке «Преобразования».
Преобразовать в формат «Профессиональный» или «Линейный» можно все формулы в документе или только одну, если выбрать математическую зону или навести курсор на формулу.
На устройствах с поддержкой сенсорного ввода и пера можно писать формулы пером или пальцем. Для рукописного ввода формулы
Выберите Рисование > Преобразовать рукописный фрагмент в математические символы, а затем выберите Рукописное уравнение в нижней части встроенной галереи.
С помощью пера или пальца введите математическую формулу от руки. Если у устройства нет сенсорного экрана, напишите уравнение с помощью мыши. Вы можете выделять части формулы и редактировать их по мере ввода, а затем с помощью окна предварительного просмотра проверять, правильно ли Word распознает то, что вы написали.
Завершив ввод, щелкните Вставить, чтобы преобразовать текст, который вы только что написали, в формулу.
См. также
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Решение систем линейных уравнений в Excel
В дополнение темы по построению балансовых моделей в Microsoft Excel я решил выпустить отдельную статью на тему решения систем линейных алгебраических уравнений (СЛАУ) в Excel, которая имеет более широкое применение.
В математике есть несколько методов решения СЛАУ. Применительно к Excel самым эффективным и простым является так называемый матричный метод. Приведенная методика решения уравнений проста в освоении и очень производительна. Данная информация будет полезна для учащихся, тем, кто связан в работе с математическими расчетами, а также всем, кто интересуется продвинутыми возможностями Excel.
Рассмотрим систему из трех линейных уравнений:
Данную систему уравнений можно записать в так называемом матричном виде, то есть обобщить все элементы системы:
Преобразования над уравнением в матричной записи аналогичны обычному уравнению, таким образом, получим:
Таким образом, для решения системы уравнений необходимо решить полученное уравнение в матричном виде относительно X. Произведем несложные расчеты в Excel с применением функций по работе с матрицами.
Сформируем на листе Excel матрицы коэффициентов и свободных членов, как показано на рисунке.
Рис. 1 — Исходные данные
Вычислим обратную матрицу коэффициентов, т.е. A^-1, воспользовавшись специальной функцией МОБР() (вводится через формулы массива, т.е. при помощи нажатия Ctrl+Shift+Enter):
Рис.2 — Вычисление обратной матрицы коэффициентов
Результат работы команды:
Рис.3 — Обратная матрица коэффициентов
Далее перемножим полученную матрицу с матрицей линейных коэффициентов, т.е. вычислим Y*A^-1 через функцию по перемножению матриц МУМНОЖ() (также формулы массивов!), что и будет решением уравнения:
Рис.4 — Вычисление корней уравнения
Рис.5 — Корни уравнения
Данные вычисления можно сделать вручную, как показано в приведенном примере, но можно и автоматизировать! В нашей надстройке SubEx для Excel есть мастер решения систем уравнений. Задайте матрицы коэффициентов и свободных членов — все вычисления программа сделает автоматически:
Как было сказано выше, приведенный метод очень производительный и может с легкостью решать системы из сотен и более уравнений.
Пример использования данного метода на практике приведен в статье на сайте по составлению балансовой модели по расчету себестоимости продукции предприятия.
Многие задачи математики и статистики приходится решать электронно. В этом уроке мы подробно разберем, как без сложностей решить систему уравнений в Excel. Используя предложенные методики, вы сможете быстро и правильно справится даже с самыми сложными уравнениями.
Метод Гаусса для простых уравнений
Для простых уравнений, где три или меньше неизвестных, можно воспользоваться методом Гаусса. Вы можете решить одно уравнение или несколько одновременно. Будем решать по следующим данным:
2x+3y=12
3x−y=7.
- Вставим наши уравнения в ячейки (желательно их оформить у самого края электронной книги).
- Чуть ниже на этой странице делаем две небольшие таблицы, куда будут вноситься коэффициенты и свободные члены. Для этого оформим несколько ячеек со значением А (для коэффициентов) и несколько с шапкой В (для свободных членов)
Будьте внимательны при внесении записей, все значения, которые расположены после знака равно, записываются в табличку В.
- Теперь занимаемся первым уравнением. Для этого скопируем первую матрицу вместе со значением после знака равно. Размещаем ее ниже наших табличек на одну строчку.
- Далее в ячейку ниже вводим подготовленную формулу: =B8:E8-$B7:7:E7∗(B8/7*(B8/B$7). Затем нажимаете комбинацию клавиш CTRL+SHIFT+ENTER. Во всей строке проставятся точные значения.
- Далее вам нужно скопировать эту строку и продублировать ее на ячейку ниже. Теперь скопируем две первые строчки после пустующей строки. Для этого выделим их и нажмем комбинацию CTRL+C или при помощи встроенного инструмента «Копировать» на панели управления.
- Отступаем одну строчку и на следующей делаем выделение пустой ячейки курсором мыши. Затем вызываем выпадающий список путем нажатия на правую кнопку мыши. Теперь выбираем пункт «Специальная вставка», появится дополнительный список, в котором необходимо отметить «Вставить значения».
- Как видим, в нашем случае высвечивается ошибка о запрете деления на «0». В вашем случае, это будут другие значения.
- В дальнейшем вам необходимо сделать обратную прогонку. Для этого отступим три пустые строки на странице, а в четвертую вставим формулу: =B17:E17/D17. Затем выделяем строчку и жмем все ту же комбинацию клавиш CTRL+SHIFT+ENTER.
В результате, при проведении правильных расчетов вы должны получить ответы на буквенные символы. Однако, этот метод требует внимательности и точного ввода формул, с чем не каждый пользователь справляется, поэтому рассмотрим другой вариант для решения.
Аналогичным способом проводим вычисление неизвестных аргументов для второго и третьего уравнений, если они присутствуют, и представляют собой целую систему.
Решение квадратного уравнения с подбором параметров
Предположим, есть буквенное выражение 5×2 + 3x + 7 = 0. Чтобы его решить вручную, придется тратить время на каждое действие. При помощи Excel, а именно подбора параметров, сделать это можно в считанные минуты.
- Открываем новый лист Excel и вносим уравнение в первую ячейку. Отступим одну строку вниз и пропишем значение для Х=0. Далее будем высчитывать его через строку формул F(х), обязательно прописываем выражение в отдельной ячейке.
- После этого заносим следующую формулу после знака равно в строке формул. Обязательно учитывайте, что ваши значения будут другими. Делайте на примере нашего выражения. Итак, вставляем =5x^2+3 x+7, при этом вместо значения X вы должны вставить адрес ячейки, в которой обозначено, за какое число принято неизвестное, то есть «0». Затем нажимаем кнопку ENTER.
- В ячейке, отвечающей за значение в строке формулы, вы получаете конкретное число. Теперь заходим во вкладку «Данные», переходим к пункту «Анализ «что, если»». Нажимаем на него и открываем дополнительный список, в котором кликаем по записи «Подбор параметра».
- Перед вами открывается окно с ячейками для заполнения. Нам необходимо прописать значения во всех трех ячейках. Давайте сделаем все по порядку. В поле «Установить в ячейке» прописываем адрес ячейки с найденным числом. Следующее поле «Значение» ставим «0», а в ячейке «Изменяя значение», указываем адрес значения X, то есть ту графу, где прописан «0». После проделанных манипуляций нажимаем кнопку «Ок».
Обратите внимание, при правильном вводе всех данных начнется автоматический расчет с посекундным изменением чисел в ячейках. Поэтому дождитесь остановки и внесите подтверждение для всплывшего окна.
Теперь в появившемся окне нажимаем кнопку «ОК» для сохранения. Мы видим, что программа нашла ответ на наше уравнение, это будет «-1». Таким образом мы разобрали самые простые способы решения уравнений, с которыми разберётся даже начинающий пользователь офисной программы Microsoft Excel.