Работа добавлена на сайт samzan.net: 2015-07-10
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
Задание 11
В Microsoft Excel создать электронную таблицу, имитирующую работу банка и сохранить её под именем таблица.xls. Даны фамилии вкладчиков, суммы их вкладов и даты вкладов. В качестве даты закрытия счетов использовать сегодняшнюю дату (с помощью функции) или заполнить произвольными датами превышающими дату вклада.
Налоговая ставка: если клиент продержал деньги более года, то он должен заплатить 10% налогов, если менее года, то 20%. Процентные ставки: если клиент продержал деньги боле 2-х лет, то он получит 25% годовых, если более года, но менее двух лет, то 20% годовых, если менее года, то 15%.
Рассчитать прибыль, которую получит клиент и перевести её в у.е. (у.е. = 8,25)
|
№ |
Вкладчик |
Сумма вклада |
Дата вклада |
Дата закрытия счета |
Процентные ставки |
Налоговая ставка |
Прибыль, грн. |
Прибыль, у.е. |
|
|
Буданов |
100 |
20.01.2003 |
|||||
|
|
Гартвик |
20000 |
05.10.2002 |
|||||
|
|
Евтушенко |
5000 |
06.01.2000 |
|||||
|
|
Ермоленко |
3590 |
01.12.1989 |
|||||
|
|
Закирова |
10000 |
03.04.1998 |
|||||
|
|
Комиров |
20000 |
01.08.1996 |
|||||
|
|
Крахмалов |
5000 |
02.10.2002 |
|||||
|
|
Ляшков |
3590 |
21.01.2001 |
|||||
|
|
Пезиков |
10000 |
12.02.2003 |
|||||
|
|
Пейзак |
300 |
12.06.2000 |
Подборка по базе: Конспект урока Файл и файловая система.docx, Презентация к уроку Файл и файловая система.ppt, овершенствование нормативно-м етодического и правового обеспечени, Электронные платежные системы2.docx, Практическое задание по дисциплине — организация ЭВМ и систем. Ч, ОСОБЕННОСТИ РАЗВИТИЯ СИСТЕМЫ ФИНАНСИРОВАНИЯ НЕДВИЖЕМОСТИ В КИТАЕ, План занятия по ОГП Кодекс чести сотрудника системы МЧС России.D, НАЛОГОВАЯ СИСТЕМА ИСПАНИИ.pptx, Пенсионные системы в РФ.doc, Методическая систему учителя иностранного языка при подготовки у
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ОТЧЁТ
по лабораторной работе №2 на тему:
«ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ»
по дисциплине «Моделирование процессов и систем»
Выполнил: студент группы ИСТ-032, Вахитов А.А.
«___» ________ 2022г. __________/А.А. Вахитов
Принял: к. т. н. доцент ИУС, Козлова Л.П.
«___» ________ 2022 г. ________/Л. П. Козлова/
Санкт-Петербург
2021
Цель работы
Разработать модель системы массового обслуживания на примере банка.
Задание 1
Выполните имитацию работы банка, осуществляющего прием вкладов. Размер депозита является случайной величиной с нормальным законом распределения (среднее значение -MD ; среднее квадратическое отклонение — SD ). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение — tz ), а время обслуживания равномерно распределено на интервале [ a ; b ].
Пусть исходные значения равны величинам: MD =30000 руб.; SD =10000 руб.; tz =1 час; a =20 мин.; b =30 мин.; tn =9 ч., число заявок равно 5.
Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлена) после прихода пяти клиентов; б) к моменту времени 12:00 ч.?
Задание 2
Проведите 10 экспериментов и рассчитайте величины:
— среднее время ожидания;
— среднее число обслуженных заявок за период с 9:00 до 15:00 ч.
Задание 3
Предположите, что tn = 0 и выполните имитацию описанным на рис. 1.3 способом.
Задание 4
Пусть банковская автоматизированная система может выходить из строя, что приводит к необходимости вызова специалистов, устраняющих неполадку. Выполните имитацию периодов нормальной работы системы и ее ремонта, если данные величины являются случайными с показательным законом распределения, а tz =30 дней, to =3 ч. Рассмотрите процесс поступления 5 заявок (отказов).
Ход работы
Задание 1
- Формируем таблицу исходя из начальных значений в задании. Начальные значения выделены синим цветом и находяться в ячейках: F2, F3, I2, I3, D7.
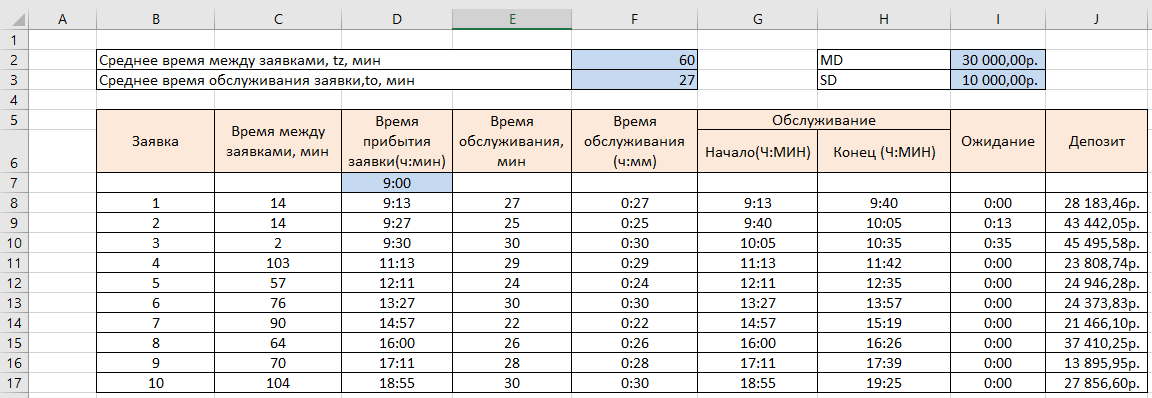
- Размер депозита сформирован с помощью формулы:
- Время между приходом двух вкладчиков сформировано с помощью формулы:
- Основываясь на полученных значениях в столбце «Время между заявками», рассчитывается для каждой заявки время ее прибытия
- С помощью функций Excel формируются случайные значения для столбца «Время обслуживания»
- Столбец «Время обслуживания (ч:мм)»
- Для каждой заявки рассчитывается время начала ее обслуживания
- И время окончания обслуживания заявки
- Находится время ожидания для каждой заявки
Теперь определяем время прихода последнего клиента, среднее время пребывания клиента в системе, общий размер вкладов после прихода пяти клиентов, общий размер вкладов к моменту времени 12:00 ч.
Получаем такую таблицу:
в котором:
- Время прихода последнего клиента:
- Среднее пребывание клиента в системе, мин:
- Общий размер вкладов после прихода 5 клиентов:
- Общий размер вкладов к моменту времени 12ч:
Можно сформировать такого рода диаграмму «Ожидание — Время обслуживания»:
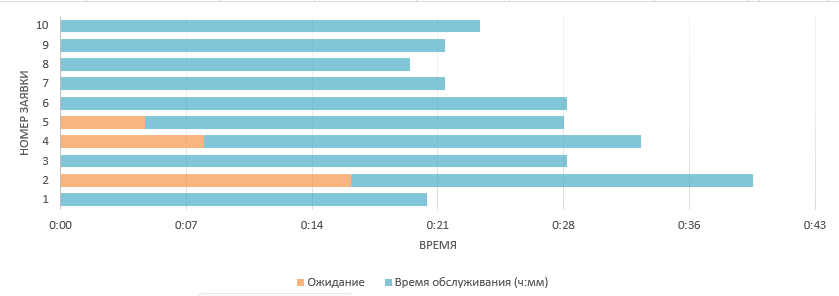
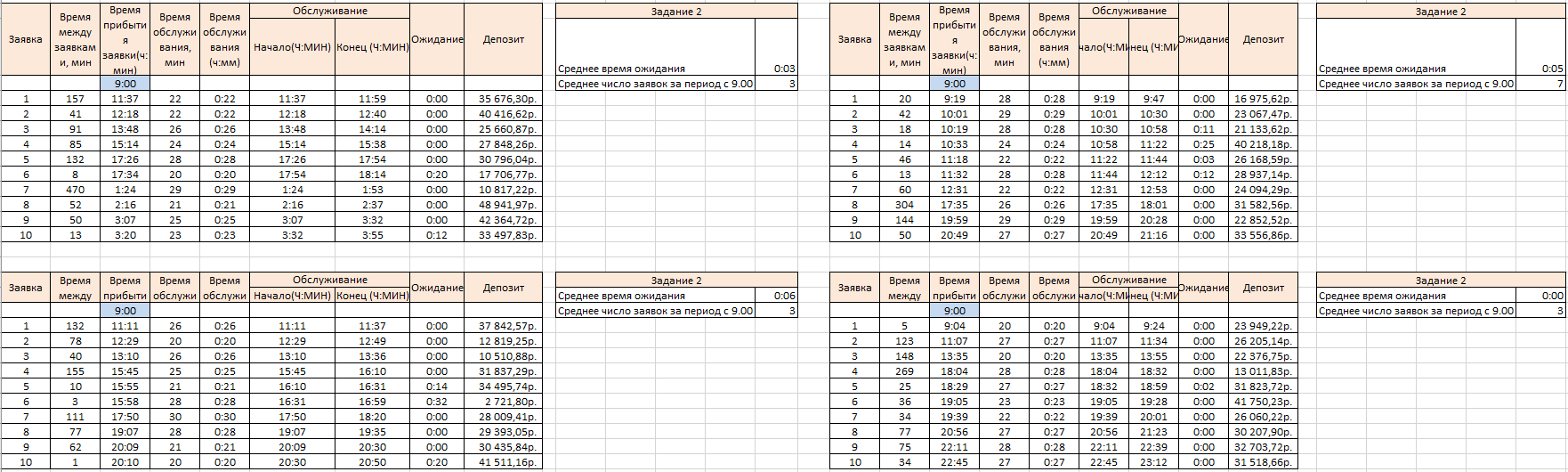
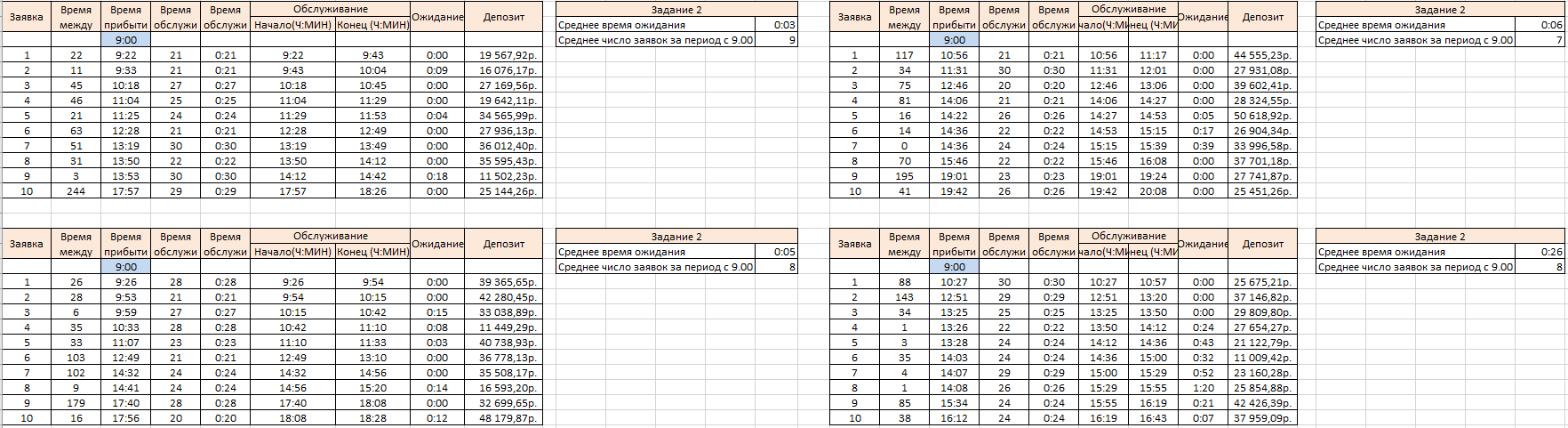
Задание 2
Проводим 10 экспериментов:
На основании этих экспериментов проводим расчет
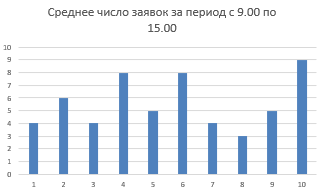
- Среднее время ожидания
- Среднее число заявок за период с 9:00 до 15:00 ч.
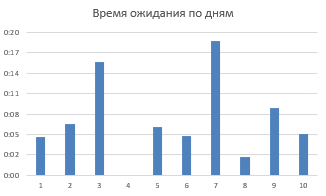
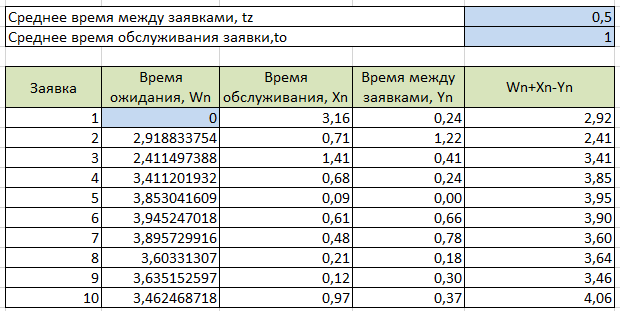
Задание 3
Основываясь на начальных данных, создаем таблицу
Формулы для расчета таблицы:
- Время ожидания
- Время обслуживания
- Время между заявками
- Wn+Xn-Yn
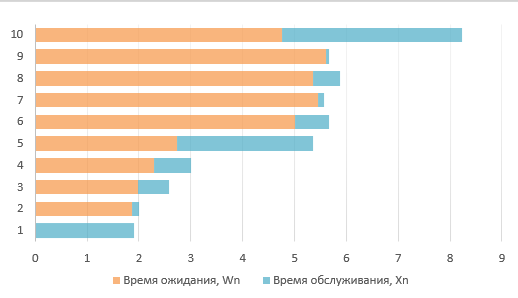
Диаграмма «Время ожидания – Время обслуживания»:
Задание 4
Для выполнения имитации периодов нормальной работы системы и ее ремонта, к таблице представленной в Задании 1 добавляются еще и столбцы «Нормальная работа» и «Ремонт»
Формулы для вычисления полей:
- Нормальная работа, дн.
- Ремонт, дн.
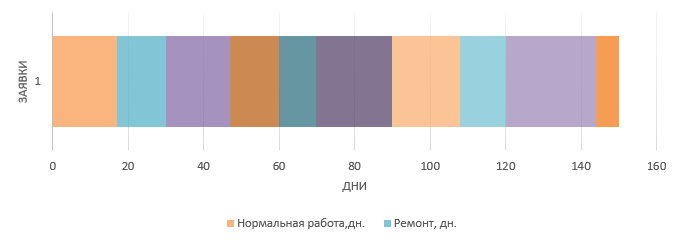
Диаграмма «Нормальная работа — Ремонт»:
Вывод: была разработана простейшая модель системы массового обслуживания для банка.
0
Компания Microsoft запустила новый программный инструмент под названием «Money in Excel», который предназначен для обработки финансовых данных пользователей. Это вторая в истории официальная попытка получить доступ к такого рода данным и стать посредников в финоперациях физических лиц. Первой была программа «Microsoft Money», от которой отказались более десяти лет назад.
По своей сути Money in Excel – шаблон для Office 365, который подкупает возможностью автоматического переноса всей финансовой информации клиента из банка в электронные таблицы. Причем импорт данных «умный», с автоматической сортировкой, распределением по разным таблицам, анализом и фильтрацией. В Microsoft обращаются к тем, кто любит использовать Excel для обработки финансовой информации, но устал от ручного переноса данных.
Заявлена работа с банковскими, кредитными картами, инвестиционными или ссудными счетами, возможность импортировать данные обо всех транзакциях и анализировать их, распределяя по разным категориям. Например, программа проконтролирует сроки наступления овердрафта, изменения в тарифах, даст советы по оптимизации расходов и т.д. Предусмотрена визуализация операций через составление графиков, выписок и рабочих книг.
Стоимость подписки для использования Money in Excel составляет $6,99 для одиночных аккаунтов и $9,99 для семейных групп. Программа работает со всеми финансовыми структурами США, но пока только с ними, для иностранцев услуга сейчас недоступна.
Источник — Microsoft
Понравился пост? Есть что сказать? Присоединяйтесь:
ЧИТАЙТЕ ТАКЖЕ
В разных областях техники, в организации производства, в экономике и медицине, в социальной сфере, в военном деле и во многих других сферах человеческой деятельности постоянно возникает необходимость решения вероятностных задач, связанных с работой систем массового обслуживания (СМО). Многообразие приложений теории массового обслуживания определяет постоянно растущий интерес к ней, а сложность возникающих задач не позволяет получить исчерпывающие решения на базе аналитических методов. В таких ситуациях часто прибегают к имитационному моделированию. Для имитации подобных систем предназначен язык моделирования GPSS, а также создаются сложные программные системы (ObjectSim, Pigrim [10]), позволяющие реализовать модели систем массового обслуживания с помощью развитой CASEоболочки путем выбора и связи различных строительных блоков. Среди работ, описывающих моделирование СМО с помощью электронных таблиц можно привести следующие — [3-7]. Авторы рассматривают моделирование систем с неограниченным, ограниченным по времени и/или длине очереди ожиданием, которые располагают от 1 до 12 обслуживающими устройствами [7]. При этом различают два основных подхода к моделированию СМО: ориентированный на события и ориентированный на процессы. Событийный подход имеет преимущества в отношении гибкости и эффективности вычислений, однако менее подходит для обучения, поскольку скрывает «жизненный цикл» заявок и является менее понятным на интуитивном уровне. Кроме того, для его реализации требуется управляющая событиями подпрограмма, что приводит к необходимости использования внутреннего языка VBA [11]. Рассмотренные ниже модели будут реализованы с использованием процессно-ориентированного подхода.
Рассмотрим структуру СМО. Каждая СМО состоит из определенного числа обслуживающих единиц, которые называются каналами обслуживания. На вход СМО поступает поток требований (заявок). Таким образом, различают следующие элементы СМО:
1.входной поток заявок;
2.очередь;
3.узел обслуживания;
4.выходной поток.
На рис. 2.1 указаны эти элементы для следующей СМО: бензоколонка занимается заправкой автомобилей.
Рис. 2.1 – Пример системы массового обслуживания
Входной поток заявок может быть случайным или детерминированным. В первом случае время между поступлением двух заявок является случайной величиной, а во втором – величиной детерминированной (поступление происходит в соответствие с определенным графиком). Интенсивность потока –
частота появления событий, поступающих в СМО в единицу времени. В СМО может поступать несколько входных потоков, имеющих различные характеристики (интервал поступления, приоритет и т.д.).
Очередь – место, где поступившие заявки ждут начала обслуживания. В том случае, если элемент очередь в системе отсутствует, то данная система без ожидания. Это означает, что в том случае, если в момент поступления заявки все каналы обслуживания заняты, то эта заявка покидает систему необслуженной. Очередь может иметь ограниченную или неограниченную длину. Кроме того, время ожидания в очереди может быть ограничено (говорят, что рассматриваются нетерпеливые заявки). Следующая характеристика очереди – дисциплина очереди. Она связана с правилом, в соответствии с которым обслуживаются клиенты. Различают следующие дисциплины: первый пришел – первый ушел, первый пришел – последний ушел, а также существуют дисциплины с приоритетами.
Рассмотрим теперь характеристики средств обслуживания. Системы обслуживания характеризуются по числу каналов обслуживания (например, если на рис. 2.1 машины могут быть обслужены несколькими устройствами, то система
будет многоканальной), числу фаз обслуживания. Время обслуживание может быть случайной величиной или детерминированным.
Также существую системы, в которых обслуженные требования после некоторой задержки опять поступают на вход. Такие системы называются замкнутыми.
В качестве показателей эффективности СМО рассматриваются: среднее
|
время, |
которое клиент проводит в очереди, средняя длина очереди, среднее |
|||||
|
время, |
которое |
клиент |
проводит |
в |
системе |
обслуживания |
(
|
TimeSystem |
TotalTimeSystem |
|
|
N |
||
, где
TotalTimeSystem
— общее время пребывания в
системе для всех заявок, а N -число заявок), среднее число клиентов в системе обслуживания, вероятность того, что система окажется свободной и т.д.
2.1 Одноканальная система массового обслуживания
Рассмотрим простую систему массового обслуживания: число каналов равно единице, время ожидания неограниченно, время между заявками и время обслуживания заявок являются случайными величинами с показательным законом распределения (среднее значение времени обслуживания равно to ,
среднее время между заявками — tz ) (рис.2.2).
Рис. 2.2 – Одноканальная система массового обслуживания
Рассмотрим процесс поступления десяти заявок, если tz =0,5 ч., to =1 ч.
В [6] использован следующий способ моделирования такой системы (рис.2.3). Величины времени обслуживания и между заявками рассчитываются согласно способу моделирования случайной величины с показательным законом распределения
D7=-$F$3*LN(СЛЧИС())
E7=-$F$2*LN(СЛЧИС()).
Wn Xn Yn
В последнем столбце рассчитывается величина
F7=C7+D7-E7.
Если ее значение является отрицательным, то это означает, что следующая заявка поступит после того, как будет обслужена текущая и потому время ее ожидания будет равно нулю, а в противном случае, время ожидания составит Wn Xn Yn С8=ЕСЛИ(F7>0;F7;0).
.
Изменим исходные данные ( tz =1 ч., to =0,5 ч.). Из рис. 2.4 можно увидеть, что в этом случае уменьшится время ожидания обслуживания.
Рис.2.3 – Результаты моделирования одноканальной СМО при
tz
=0,5 ч.,
to
=1 ч.
Рис. 2.4 – Результаты моделирования одноканальной СМО при
tz
=1 ч.,
to
=0,5 ч.
Теперь выполним моделирование, учитывая начальное время tn . Пусть tz =8
мин., to =7 мин.; tn =9 ч. Рассмотрим процесс поступления семи заявок (рис.2.5).
Определение времени между заявками и времени обслуживания (мин.) остается без изменения.
Для того чтобы перевести эти значения в используемый формат времени необходимо осуществить следующие операции
F8=E8/1440
D8=D7+C8/1440.
Т.е. время поступления очередной заявки равно сумме времени прибытия предыдущей и случайной величины, распределенной по показательному закону.
Время начала обслуживания первой поступившей заявки равно времени ее поступлению
G8=D8.
Начиная со второй заявки, эта величина будет определяться как максимальное значение из момента окончания обслуживания предыдущей заявки и времени поступления текущей
G9=ЕСЛИ(D9>=H8;D9;H8).
Время окончания обслуживания рассчитывается по формуле
H8=G8+F8.
Период ожидания равен разности времени начала обслуживания и времени поступления
I8=G8-D8.
Также встречаются системы, в которых новая заявка может поступить только после того, как была обслужена предыдущая. В качестве примера, можно назвать систему, которая периодически может выходить из строя и требовать ремонта (ее отказы в данном случае рассматриваются как заявки): время между ее отказами и время обслуживания распределено по показательному закону. Очевидно, что не может произойти выход из строя системы прежде, чем будет выполнен ремонт предыдущего отказа. Такие заявки будем называть не перекрывающимися.
Для того чтобы выполнить моделирование данной СМО необходимо изменить только расчет времени прибытия заявки, которое будет равно сумме момента окончания обслуживания предыдущей заявки и случайной величины, распределенной по показательному закону
D9=H8+C9/1440.
Результаты моделирования представлены на рис.2.6 ( tz =5 мин., to =6 мин.).
Можно заметить, что в Диаграмме заявок теперь отсутствуют периоды ожидания обслуживания.
Рис. 2.5 – Моделирование одноканальной СМО с учетом начального времени
Рис. 2.6 – Моделирование одноканальной СМО с не перекрывающимися заявками
Задание
1.Выполните имитацию работы банка, осуществляющего прием вкладов. Размер депозита является случайной величиной с нормальным законом распределения (среднее значение — MD ; среднее квадратическое отклонение — SD ). Время между приходом двух вкладчиков – случайная
|
величина с показательным законом распределения (среднее значение — |
tz ), |
|||
|
а время обслуживания равномерно распределено на интервале [ a |
; b ]. |
|||
|
Пусть исходные значения равны величинам: |
MD =30000 |
руб.; |
SD =10000 |
|
|
руб.; tz =1 час; a =20 мин.; b =30 мин.; tn =9 |
ч., число |
заявок |
равно 5. |
Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлен а) после прихода пяти клиентов; б) к моменту времени 12:00 ч.?
Рис.2.7 – Система массового обслуживания «Банк»
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Демонстрация прибыли и убытков компании за нужный месяц
Автоматическое присвоение статей ДДС отчетам из банка
Поддержка: Альфа-Банк, ФК ОТКРЫТИЕ, СберБанк, Тинькофф и других.
Чтение любых форм финансового отчета в формате Excel или Google.Таблиц
Движение денежных средств по месяцам в отчете CashFlow
Что представляет собой шаблон?
Для автоматического присвоения ваших статей ДДС операциям из выписок необходимо указать саму статью и имя банка. Укажите имя контрагента, ИНН или часть комментария. Когда таблица найдет совпадение, статья ДДС будет присвоена.
Лист Cash Flow покажет движение денежных средств по разделам, а лист P&L — прибыль и убытки компании за выбранный период.
Таблица читает файлы выписок в формате Excel или Google.Таблиц из папки с выписками, оригиналы переносит в папку корзины, а прочитанные файлы — в папку архива.
