Имитационное моделирование практикум excel - Word и Excel

Содержание

Создать симуляцию Монте-Карло с помощью Excel
RuleOfThumb — Метод Монте-Карло (Марш 2023)
Оглавление:
Моделирование Монте-Карло
Игра в кости
Шаг 1: События прокатки в кости
Шаг 2: Диапазон результатов
Шаг 3: Выводы
Шаг 4: Количество рулонов кости
Шаг 5: Моделирование
Шаг 6: Вероятность
Как создать капиталозащищенные инвестиции с помощью опций? (MSFT)
Как мне создать торговую стратегию с помощью Bollinger Bands® и скользящих средних?
Как мне создать торговую стратегию с помощью групп Боллинджера® и индикатора относительной силы (RSI)?
Практикум в MS Excel «Оценка риска инвестиционного проекта с помощью метода имитационного моделирования Монте-Карло»
Таблица 1 – Расчет доходов от реализации проекта
Создание моделирования Монте-Карло с помощью Excel
Ключевые выводы
Моделирование Монте-Карло
Когда использовать моделирование Монте-Карло
Игра в кости
Краткий обзор
Шаг 1. События с броском игральных костей
Шаг 2: Диапазон результатов
Шаг 3: выводы
Шаг 4: Количество бросков костей
Шаг 5: Моделирование
Шаг 6: вероятность

Создать симуляцию Монте-Карло с помощью Excel

RuleOfThumb — Метод Монте-Карло (Марш 2023)

Мы разработаем симуляцию Монте-Карло с использованием Microsoft Excel и игра в кости. Моделирование Монте-Карло — математический численный метод, который использует случайные ничьи для выполнения вычислений и сложных проблем. Сегодня он широко используется и играет ключевую роль в различных областях, таких как финансы, физика, химия, экономика и многие другие.

Моделирование Монте-Карло

Метод Монте-Карло был изобретен Николаем Метрополисом в 1947 году и направлен на решение сложных проблем с использованием случайных и вероятностных методов. Термин «Монте-Карло» происходит от административного района Монако, широко известного как место, где европейские элиты играют в азартные игры. Мы используем метод Монте-Карло, когда проблема слишком сложна и сложна при непосредственном вычислении. Большое количество итераций позволяет моделировать нормальное распределение.

Метод моделирования методом Монте-Карло вычисляет вероятности для интегралов и решает уравнения в частных производных, тем самым вводя статистический подход к риску в вероятностном решении. Несмотря на то, что существует множество современных статистических инструментов для создания симуляций Монте-Карло, проще моделировать нормальный закон и единообразный закон с использованием Microsoft Excel и обходить математические основы.

Для моделирования Монте-Карло мы выделяем ряд ключевых переменных, которые контролируют и описывают результат эксперимента и назначают распределение вероятности после выполнения большого количества случайных выборок. Давайте возьмем игру в кости как модель.

Игра в кости

Вот как игра в кости играется:

• Игрок бросает три кости, которые имеют 6 сторон 3 раза.

• Если общее количество 3 бросков составляет 7 или 11, игрок выигрывает.

• Если общее количество 3 бросков: 3, 4, 5, 16, 17 или 18, проигрыватель проигрывает.

• Если общий результат — любой другой результат, игрок снова играет и повторно свертывает штамп.

• Когда игрок снова бросает кубик, игра продолжается таким же образом, за исключением того, что игрок выигрывает, когда сумма равна сумме, определенной в первом раунде.

Рекомендуется также использовать таблицу данных для генерации результатов. Более того, для подготовки моделирования методом Монте-Карло требуется 5 000 результатов.

Шаг 1: События прокатки в кости

Сначала мы разрабатываем ряд данных с результатами каждого из 3 кубиков для 50 рулонов. Для этого предлагается использовать функцию «RANDBETWEEN (1. 6)». Таким образом, каждый раз, когда мы нажимаем F9, мы генерируем новый набор результатов каротажа. Ячейка «Результат» — это сумма итогов трех рулонов.

Шаг 2: Диапазон результатов

Затем нам нужно разработать ряд данных для определения возможных результатов для первого раунда и последующих раундов. Ниже приведен диапазон данных с тремя столбцами.В первом столбце у нас есть числа от 1 до 18. Эти цифры представляют собой возможные результаты после того, как катятся кости 3 раза: максимум составляет 3 * 6 = 18. Вы заметите, что для ячеек 1 и 2 результаты N / A, так как невозможно получить 1 или 2, используя 3 кости. Минимальное значение равно 3.

Во втором столбце включены возможные выводы после первого раунда. Как указано в первоначальном заявлении, либо игрок выигрывает (выигрывает), либо проигрывает (проигрывает), либо повторяет его (Re-roll), в зависимости от результата (всего 3 кубика).

В третьей колонке регистрируются возможные выводы для последующих раундов. Мы можем достичь этих результатов, используя функцию «If. «Это гарантирует, что если полученный результат будет эквивалентен результату, полученному в первом раунде, мы выиграем, иначе мы будем следовать первоначальным правилам первоначальной игры, чтобы определить, будем ли мы повторно бросать кости.

Шаг 3: Выводы

На этом этапе мы определяем результат 50 кубиков. Первый вывод можно получить с помощью индексной функции. Эта функция выполняет поиск возможных результатов первого раунда, вывод, соответствующий полученному результату. Например, при получении 6, как это имеет место на рисунке ниже, мы снова играем.

Можно получить результаты других рулонов кости, используя функцию «Or» и функцию индекса, вложенную в функцию «If». Эта функция сообщает Excel: «Если предыдущий результат -« Выиграть или проиграть », перестаньте бросать кости, потому что как только мы выиграли или проиграли, мы закончили. В противном случае мы переходим к столбцу следующих возможных выводов, и мы определяем вывод результата.

Шаг 4: Количество рулонов кости

Теперь мы определяем количество бросков кубиков, необходимых до проигрыша или выигрыша. Для этого мы можем использовать функцию «Countif», которая требует, чтобы Excel подсчитывал результаты «Re-Roll» и добавлял номер 1 к ней. Он добавляет один, потому что у нас есть один дополнительный раунд, и мы получаем окончательный результат (выигрываем или проигрываем).

Шаг 5: Моделирование

Мы разрабатываем диапазон для отслеживания результатов различных симуляций. Для этого мы создадим три столбца. В первом столбце одна из приведенных цифр — 5 000. Во второй колонке мы будем искать результат после 50 кубиков. В третьем столбце, в заголовке столбца, мы будем искать количество бросков кубиков, прежде чем получить окончательный статус (выиграть или проиграть).

Затем мы создадим таблицу анализа чувствительности с использованием данных характеристик или таблицы данных таблицы (эта чувствительность будет вставлена во вторую таблицу и в третьи столбцы). В этом анализе чувствительности номера событий 1 — 5, 000 должны быть вставлены в ячейку A1 файла. Фактически, можно было выбрать любую пустую ячейку. Идея состоит в том, чтобы просто произвести перерасчет каждый раз и таким образом получить новые броски кубиков (результаты новых симуляций), не повредив формулы на месте.

Шаг 6: Вероятность

Мы можем, наконец, вычислить вероятности выигрыша и проигрыша. Мы делаем это с помощью функции «Countif».Формула подсчитывает количество «выигрышей» и «проиграет», а затем делит на общее количество событий, 5, 000, чтобы получить соответствующую долю одного и другого. Наконец, мы видим, что вероятность получить выигрыш составляет 73. 2%, а результат Lose — 26,8%.

Как создать капиталозащищенные инвестиции с помощью опций? (MSFT)

Гарантирует ли «Капитал-защита» в инвестиционном продукте звук привлекательный? Подождите! Вот как вы можете создать лучший для себя, по низким ценам!

Как мне создать торговую стратегию с помощью Bollinger Bands® и скользящих средних?

Узнайте больше о том, как идентифицировать торговые сигналы покупки и продажи при реализации стратегии кроссингового скользящего среднего с полосами Боллинджера.

Как мне создать торговую стратегию с помощью групп Боллинджера® и индикатора относительной силы (RSI)?

Узнайте, как технические аналитики создают торговую стратегию с использованием полос Боллинджера и индекса относительной силы в сочетании с другими.

Источник

Практикум в MS Excel «Оценка риска инвестиционного проекта с помощью метода имитационного моделирования Монте-Карло»

Практикум в MS Excel

«Оценка риска инвестиционного проекта с помощью метода имитационного моделирования Монте-Карло»

По заданию руководства компании необходимо оценить риск инвестиционного проекта организации сети связи. Прогнозируемое количество пользователей и ожидаемая доходность представлены в таблице 1.

Таблица 1 – Расчет доходов от реализации проекта

1 Общее количество пользователей сети, чел.

3 Доходы, тыс. руб.

§ Строительство сети начинается в январе 2011 года и должно завершиться в марте 2011 года. Горизонт расчета охватывает временной период с 2011по 2013 год.

§ Капитальные затраты проектируемой сети складываются из затрат на покупку оборудования, его транспортировку, инсталляцию и пусконаладочные работы. Сумма капитальных затрат, переходящих в основные производственные фонды составляет 2 970 тыс. руб.

§ Прирост оборотных средств составляет 2% от прироста основных производственных фондов.

§ Амортизация начисляется линейным способом.

§ Численность персонала, необходимая для реализации инвестиционного проекта составляет 6 человек, средняя заработная плата – 15 тыс. руб.

§ При расчете фонда оплаты труда предусмотреть ежегодное повышение оплаты труда на 15%.

§ Ставку дисконтирования принять равной 25%

§ Затраты на электроэнергию в 2011 году составят 175.2 тыс. руб. Прогнозируемый темп роста тарифов на электроэнергию составляет 10%.

§ В 2011 году планируется провести активную рекламную кампанию, для чего потребуется 110 тыс. руб. (затраты на рекламу, сувенирную и полиграфическую продукцию), в последующие годы для привлечения пользователей и поддержания имиджа компании потребуется 50 и 30 тыс. руб. соответственно.

Алгоритм выполнения лабораторной работы

1 Ознакомиться с расчетом показателей эффективности проекта (см. динамическую модель в MS Excel)

2 Ознакомиться со структурой имитационной модели MS Excel (для расчета чистого потока денежных средств для каждого года)

Рисунок 7 – Имитационная модель чистого потока денежных средств (NCF1)

3 Для выполнения имитационного моделирования необходимо зайти в пункт СЕРВИС/ АНАЛИЗ ДАННЫХ / ГЕНЕРАЦИЯ СЛУЧАЙНЫХ ЧИСЕЛ

В появившемся диалоговом окне необходимо выбрать тип вероятностного распределения и задать соответствующие входные параметры:

Провести имитационное моделирование на основе распределений различного типа (не менее двух).

Рисунок 8 – Имитационная модель (фрагмент)

Аналогичным образом выполняется имитационное моделирование для всех стохастических переменных. Результаты имитации представлены на рисунке:

Рисунок 9 — Результаты имитационного моделирования

Копируя значения и формулы ячеек D7:U7 на диапазон соответствующий результатам имитационного моделирования, получим эмпирическое распределения чистого потока денежных средств (NCF1)

Рисунок 10 – Имитационная модель NCF1 (итог)

Аналогичным образом разрабатывается имитационная модель чистого потока денежных средств для последующих периодов (2 и 3-го годов).

Рисунок 12 – Имитационная модель NCF2 (итог)

В процессе разработки имитационной модели NCF2 необходимо установить динамические связи с имитационной моделью NCF1.

Например, при расчете фонда оплаты труда предусматривается ежегодный темп роста на уровне 15%. Таким образом, необходимо сделать ссылку:

Рисунок – Динамические связи между имитационными моделями NCF1 и NCF2

Рисунок – Имитационная модель NCF3(итог)

Далее на основе данных имитационного моделирования необходимо рассчитать NPV инвестиционного проекта.

Для оценки риска ИП необходимо выполнить экономико-статистический анализ результатов имитации.

Для этого необходимо зайти в пункт СЕРВИС / АНАЛИЗ ДАННЫХ / ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Сделать выводы по результатам статистического анализа (см. табл.)

Источник

Создание моделирования Монте-Карло с помощью Excel

Опубликовано 12.07.2021 · Обновлено 12.07.2021

Моделирование методом Монте – Карло может быть разработан с использованием Microsoft Excel и игрой в кости. Моделирование Монте-Карло – это математический численный метод, который использует случайные розыгрыши для выполнения вычислений и сложных задач. Сегодня он широко используется и играет ключевую роль в различных областях, таких как финансы, физика, химия и экономика.

Ключевые выводы

Метод Монте-Карло направлен на решение сложных задач с использованием случайных и вероятностных методов.
Моделирование Монте-Карло можно разработать с помощью Microsoft Excel и игры в кости.
Таблицу данных можно использовать для получения результатов – в общей сложности для подготовки моделирования Монте-Карло необходимо 5000 результатов.

Моделирование Монте-Карло

Метод Монте-Карло был изобретен Джоном фон Нейманом и Станиславом Уламом в 1940-х годах и направлен на решение сложных задач с использованием случайных и вероятностных методов.Термин Монте-Карло относится к административному району Монако, широко известному как место, где европейская элита играет в азартные игры.

Метод моделирования Монте-Карло вычисляет вероятности для интегралов и решает уравнения в частных производных, тем самым вводя статистический подход к риску в вероятностном решении. Несмотря на то, что существует множество передовых статистических инструментов для моделирования Монте-Карло, проще смоделировать нормальный закон и единый закон с помощью Microsoft Excel и обойти математические основы.

Когда использовать моделирование Монте-Карло

Мы используем метод Монте-Карло, когда задача слишком сложна и ее трудно решить прямым расчетом. Использование моделирования может помочь найти решения для ситуаций, которые оказываются неопределенными. Большое количество итераций позволяет моделировать нормальное распределение. Его также можно использовать для понимания того, как работает риск, и для понимания неопределенности в моделях прогнозирования.

Как отмечалось выше, моделирование часто используется во многих различных дисциплинах, включая финансы, науку, технику и управление цепочками поставок, особенно в случаях, когда в игре слишком много случайных величин. Например, аналитики могут использовать моделирование методом Монте-Карло для оценки деривативов, включая опционы, или для определения рисков, включая вероятность того, что компания может объявить дефолт по своим долгам.

Игра в кости

Для моделирования методом Монте-Карло мы выделяем ряд ключевых переменных, которые контролируют и описывают результат эксперимента, а затем назначаем распределение вероятностей после выполнения большого количества случайных выборок. Для демонстрации возьмем за модель игру в кости. Вот как катится игра в кости:

• Игрок трижды бросает три шестиугольных кубика.

• Если сумма трех бросков равна семи или 11, игрок выигрывает.

• Если сумма трех бросков равна: три, четыре, пять, 16, 17 или 18, игрок проигрывает.

• Если результат – любой другой, игрок снова играет и перебрасывает кости.

• Когда игрок снова бросает кости, игра продолжается таким же образом, за исключением того, что игрок выигрывает, когда общая сумма равна сумме, определенной в первом раунде.

Также рекомендуется использовать таблицу данных для получения результатов. Кроме того, для подготовки моделирования Монте-Карло необходимо 5 000 результатов.

Краткий обзор

Чтобы подготовить симуляцию Монте-Карло, вам нужно 5000 результатов.

Шаг 1. События с броском игральных костей

Сначала мы разрабатываем ряд данных с результатами каждого из трех кубиков для 50 бросков. Для этого предлагается использовать функцию «СЛУЧМЕЖДУ (1,6)». Таким образом, каждый раз, когда мы нажимаем F9, мы генерируем новый набор результатов броска. Ячейка «Результат» – это сумма результатов трех бросков.

Шаг 2: Диапазон результатов

Затем нам необходимо получить ряд данных для определения возможных результатов первого и последующих раундов. Имеется диапазон данных из трех столбцов. В первом столбце у нас есть числа от 1 до 18. Эти цифры представляют возможные результаты после трехкратного броска кубиков: Максимальное значение 3 x 6 = 18. Вы заметите, что для ячеек 1 и 2 результаты равны N / A, поскольку невозможно получить один или два, используя три кубика. Минимум три.

Во втором столбце приведены возможные выводы после первого раунда. Как указано в начальном утверждении, игрок либо выигрывает (Победа), либо проигрывает (Проигрыш), либо он переигрывает (Перебрасывает), в зависимости от результата (всего три броска кубиков).

В третьем столбце заносятся возможные выводы для последующих раундов. Мы можем добиться этих результатов с помощью функции «ЕСЛИ». Это гарантирует, что если полученный результат эквивалентен результату, полученному в первом раунде, мы выиграем, в противном случае мы будем следовать исходным правилам исходной игры, чтобы определить, перебрасываем ли мы кости.

Шаг 3: выводы

На этом этапе мы определяем результат бросков 50 кубиков. Первый вывод можно получить с помощью индексной функции. Эта функция ищет возможные результаты первого раунда, вывод, соответствующий полученному результату. Например, когда мы выбрасываем шестерку, мы снова играем.

Можно получить результаты других бросков костей, используя функцию «ИЛИ» и функцию индекса, вложенную в функцию «ЕСЛИ». Эта функция сообщает Excel: «Если предыдущий результат – победа или поражение», прекратить бросать кости, потому что, как только мы выиграли или проиграли, мы закончили. В противном случае мы переходим к столбцу следующих возможных выводов и идентифицируем вывод результата.

Шаг 4: Количество бросков костей

Теперь мы определяем количество бросков кубиков, необходимое для проигрыша или выигрыша. Для этого мы можем использовать функцию «СЧЁТЕСЛИ», которая требует, чтобы Excel подсчитал результаты «Повторного прокрутки» и прибавил к нему число один. Он добавляет один, потому что у нас есть один дополнительный раунд, и мы получаем окончательный результат (победа или поражение).

Шаг 5: Моделирование

Мы разрабатываем серию для отслеживания результатов различных симуляций. Для этого мы создадим три столбца. В первом столбце одна из цифр – 5000. Во втором столбце мы будем искать результат после 50 бросков кубиков. В третьем столбце, заголовке столбца, мы будем искать количество бросков кубиков до получения окончательного статуса (выигрыш или проигрыш).

Затем мы создадим таблицу анализа чувствительности, используя данные функций или таблицу данных таблицы (эта чувствительность будет вставлена во вторую таблицу и третий столбцы). В этом анализе чувствительности номера событий от одного до 5000 должны быть вставлены в ячейку A1 файла. Фактически, можно было выбрать любую пустую ячейку. Идея состоит в том, чтобы каждый раз принудительно производить пересчет и таким образом получать новые броски кубиков (результаты новых симуляций), не повреждая существующие формулы.

Шаг 6: вероятность

Наконец-то мы можем рассчитать вероятность выигрыша и проигрыша. Мы делаем это с помощью функции «СЧЁТЕСЛИ». Формула подсчитывает количество «выигрышей» и «проигрышей», а затем делит их на общее количество событий, 5000, чтобы получить соответствующую пропорцию одного и другого. Наконец, мы видим, что вероятность получения результата «Победа» составляет 73,2%, а вероятность получения результата «Проигрыш» составляет 26,8%.

Источник

Пример имитационной модели

NOTE:

To change the image on this slide, select the picture and delete it. Then click the Pictures icon in the placeholder to insert your own image.

§26

Информатика, 8 класс

Учитель информатики

Дворецкая Ю.Ю,

Основные темы параграфа

Что такое имитационная модель
Пример имитационного моделирования в электронной таблице

ОПРЕДЕЛЕНИЕ

ИМИТАЦИОННАЯ МОДЕЛЬ – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

Имитационная модель имеет определенную минимальную опорную структуру, которую пользователь может дополнить и расширить с учетом специфики решаемых задач и базовых методов обработки.

ОПРЕДЕЛЕНИЕ

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе.

Отличие от математического моделирования

имитационное моделирование исследует математические модели в виде алгоритмов , воспроизводящих функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций .
в имитационных моделях для получения необходимой информации или результатов необходимо осуществлять их «прогон» в отличие от аналитических моделей, которые необходимо «решать».
имитационные модели неспособны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.

Имитационные модели

В общем виде структуру имитационной модели в математической форме можно представляет следующим образом: ,

где E – результат действия системы;

x i – переменные и параметры, которыми мы можем управлять;

y i – переменные и параметры, которыми мы управлять не можем;

f – функциональная зависимость между x i и y i , которая определяет величину E .

Имитационные модели

Имитационная модель представляет собой комбинацию таких составляющих, как:

компоненты;
переменные;
параметры;
функциональные зависимости;
ограничения;
целевые функции.

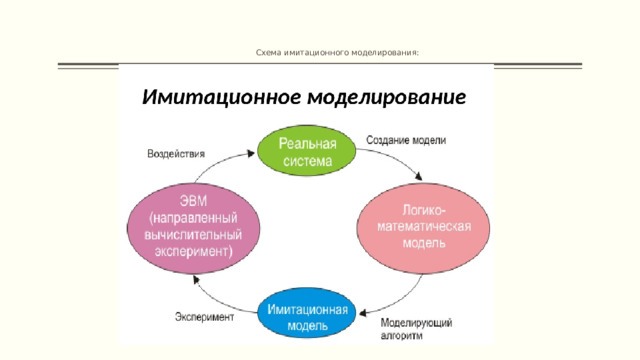
Схема имитационного моделирования:

НЕДОСТАТКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ:

разработка имитационных моделей требует больших затрат, времени и сил;
любая имитационная модель сложной системы менее объективна, чем аналитическая модель;
результаты имитационного моделирования носят как правило частный характер, поэтому для предоставления обоснованных выводов необходимо провести серии модельных экспериментов.

Пример имитационного моделирования на компьютере

Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.

Модель – эволюция популяций

Пусть на определенном пространстве случайным образом расселяются живые организмы.
В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает.
Эти процессы протекают в соответствии с законами эволюции (формальными правилами).

Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.

Имитационные модели

Законы эволюции:

В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет.
В живой ячейке жизнь может либо сохраниться, либо исчезнуть
На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа.
Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения).
Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.

Модельное описание процесса эволюции популяции

Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других.
У ячейки номер 2 соседи: 1, 3 и 4.
Но ячейка 1 всегда пустая.
У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5).
Аналогичная ситуация у крайних правых ячеек.

Кодирование

Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц.
Ноль обозначает пустую ячейку , единица — живую .
Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:

00001001000100000000

Имитационные модели

Введем обозначения:

n — номер ячейки,

R (n) — значение двоичного числа, соответствующего этой ячейке в текущем поколении.

В рассматриваемом примере R (5) = R (8) = R (12) = 1 .

Все остальные значения ячеек равны нулю.

Значения кода в n -й ячейке для следующего поколения будем обозначать S ( n ) .

Проанализировав правила эволюции, приходим к следующей формуле:

Если 1 R ( n — 2) + R ( n — 1) + R ( n ) + R ( n + 1) + R ( n + 2) 3, то S ( n ) = 1, иначе S ( n ) = 0.

Имитационные модели

Эта формула работает для значений n от 3 до 18 .

Всегда: S (1) = S (20) = 0 .

Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе: для этого к отрезку добавим по одной фиктивной ячейке справа и слева.

Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.

Итак, модель построена и формализована.

Имитационные модели

Для реализации применим табличный процессо р.

Моделью жизненного пространства будет строка электронной таблицы.

Первая строка — первое поколение,

вторая строка — второе поколение и т. д.

Тогда номера ячеек будут идентифицироваться именами столбцов таблицы.

Ячейка номер 0 — столбец А,

ячейка 1 — столбец В и т. д.,

ячейка 21 — столбец F.

=1; А1 + В1 + С1 + D1 + Е1 Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении. Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно. » width=»640″

В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1 . Незаполненные ячейки по умолчанию приравниваются к нулю.
Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:

ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 =1; А1 + В1 + С1 + D1 + Е1

Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.

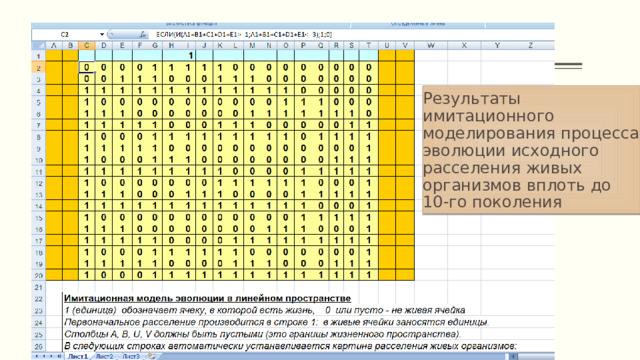
Результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения

Модель Дж. Конуэя «Жизнь»

В этой модели эволюция популяции живых организмов происходит в двумерном пространстве.

Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток.

Но теперь правила эволюции такие:

если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения;

если же живых соседей меньше двух, то она погибает от одиночества.

в пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.

Домашнее задание

§26 конспект

Источник

_{––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––}

Министерство образования Российской
Федерации

Петрозаводский государственный
университет

А. В. Коросов

Имитационное
моделирование

в
среде MS
Excel

(на
примерах из экологии)

Петрозаводск

2002

УДК 28.08:22.172

К686

Рецензенты:

член.-корр. РАН, профессор, доктор
биологических наук Э. В. Ивантер;

доцент, кандидат физико-математических
наук В. Б. Ефлов;

доцент, кандидат физико-математических
наук С. Р. Богданов

Печатается по решению редакционно-издательского
совета

Петрозаводского государственного
университета

Коросов
А. В.

К686 Имитационное моделирование в среде
MS Excel (на примерах из
экологии): Монография / ПетрГУ.
Петрозаводск, 2002. 212 с. ISBN
5-8021-0168-7

В книге изложены
основы общедоступного метода построения
арифметических
имитационных моделей в среде Excel. Метод
позволяет конструировать описательные
и динамические модели любой сложности
и оценивать их параметры.

Рассмотрены
идеология имитационного моделирования
(основы системного подхода), процедура
построения моделей (табличное
программирование), приемы и примеры
моделирования реальных биоэкологических
объектов, в том числе аппроксимация
функций, декомпозиция сложных криволинейных
зависимостей на более простые, декомпозиция
сложных распределений на серию нормальных,
интеграция серии простых моделей в
общую более сложную модель, описание
динамики многокомпонентных систем с
помощью латентных переменных и мн. др.

Книга адресована
широкому кругу читателей, использующих
компьютер для расчетов, но в первую
очередь научным сотрудникам (не только
биологических специальностей) и
студентам.

УДК 28.08:22.172

университет, 2002

Издание осуществлено при финансовой
поддержке Института “Открытое общество.
Фонд содействия” (Фонд Сороса – Россия)

Краткое
содержание

	Предисловие	4
	Введение Освоение методики моделирования за 10 мин.	5
	Постановка проблемы Концепция имитационного моделирования в приложении к экологическим исследовательским задачам: ретроспективная оценка параметров.	13
1	Идеология моделирования Основы системного подхода к моделированию биоэкологических явлений: 7 принципов системного мышления, 4 рекурсивных этапа движения системной мысли, 5 этапов моделирования.	19
2	Процедура моделирования Практикум построения имитационной системы на листе Excel: техника табличного программирования, настройка имитационной модели, оптимизация функции различий, оценка параметров, расчет статистических ошибок и адекватности модели.	37
3	Приемы моделирования Типология задач имитационного моделирования; опыт решения разнообразных задач: аппроксимация, декомпозиция, …; структурированное описание модельных понятий.	105
4	Теория оптимизации Математические основы оптимизации: методы Ньютона, градиентов.	183
	Литература Список источников по моделированию.	199
	Основное содержание Дробная рубрикация книги.	208

«…Невозможно
написать учебник по построению моделей».

Р. Л. Акоф,
М. Сасиени¹

Предисловие

Лет 15 тому назад автор сформулировал
для себя направление поиска приемов
моделирования в виде небольшого эссе
«Модели —
биологу». Уже тогда было понятно —
чтобы войти в широкую биологическую
практику, моделирование должно быть
максимально простым по использованию
(в программировании свои бесконечные
проблемы), но абсолютно жестким по
логическому оформлению (биологические
высказывания должны выверяться числом).
Работа в этом направлении (Ивантер,
Коросов, 1992; Коросов, 1995; Коросов, 1996)
позволила в конце концов наметить
контуры простой процедуры построения
сложных количественных описаний
природных объектов. Когда идеи оформились
в метод (Коросов, 1999), он был успешно
апробирован при подготовке докторской
диссертации по зоолого-экологической
тематике (Коросов, 2000). Его следует
назвать табличное программирование
арифметических имитационных моделей
в среде Excel. Об этом методе и пойдет речь
дальше.

Трудно точно определить жанр предлагаемой
книги. Это и монография, поскольку
содержит главы, посвященные методологии
общедоступного моделирования, описание
новых моделей, оригинальные результаты
исследований. Это и учебное пособие,
предназначенное для пользователей ЭВМ,
желающих освоить новый количественный
метод (автор читает учебный курс
«Компьютерные методы в экологии»).
Это и вариант научно-популярной
литературы, вводящей читателя в круг
проблем количественной биологии. Книга
может быть интересна как научным
сотрудникам (биоэкологам), так и студентам
(разных специальностей), а также
школьникам.

Автор будет признателен всем читателям,
которые пришлют свои комментарии и
положительные отзывы по адресу: 185640,
Республика Карелия, г. Петрозаводск,
пр. Ленина, 33. Петрозаводский
госуниверситет. Кафедра зоологии и
экологии.

E-mail:
korosov@karelia.ru

____________________________________________________________

¹Акоф
Р. Л., Сасиени М. Основы исследования
операций. М.: Мир, 1971, С. 84.

«Честная неудача
не позорна; позорен страх перед неудачей».

Г. Форд¹

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Рассматривается реализация табличных имитационных моделей объектов экономики в среде Excel. Приводятся модели систем управления запасами с комбинированными стратегиями, массового обслуживания (с групповым поступлением и обслуживанием заявок, замкнутые, многофазные, с неограниченным числом обслуживаемых заявок, с взаимопомощью и т.д.), социальных и экономических сетей, финансовых механизмов, а также различных игр. Также рассматривается решение задач оптимизации с помощью случайных чисел. Приводится описание разработанной авторами программы для реализации типовых сценариев работы с табличными моделями. Пособие включает следующие разделы: моделирование случайных событий, моделирование случайных величин, моделирование систем массового обслуживания, моделирование систем управления запасами, моделирование торгов, моделирование игр, моделирование социальных и экономических сетей, решение задач оптимизации, система табличного моделирования экономических процессов. В приложениях содержится справочная информация: описание основных функций, обработка статистических данных с помощью циклических ячеек, проведение в Excel экспериментов «что будет если», построение графиков, макросы типовых сценариев.
Соответствует ФГОС ВО последнего поколения.
Для студентов бакалавриата, обучающихся по направлениям подготовки «Прикладная информатика», «Бизнес-информатика», «Информационная безопасность» и «Экономика».

Год выпуска: 2020
Авторы: Екатерина Борисовна Грибанова, Игорь Николаевич Логвин
ISBN: 978-5-406-01581-0

Скачать книгу

Источник

код 631678

Год издания: 2022 г.

ISBN:
978-5-406-08812-8

Гриф:
Рекомендовано Экспертным советом УМО в системе ВО и СПО в качестве учебного пособия для направлений бакалавриата «Прикладная информатика», «Бизнес-информатика», «Информационная безопасность» и «Экономика»

Страниц:
228

Вид издания:
Учебное пособие

Оптовая цена:

899 руб.

Купить в интернет-магазине:

Грибанова, Е. Б., Имитационное моделирование экономических процессов. Практикум в Excel : учебное пособие / Е. Б. Грибанова, И. Н. Логвин.

Компьютеры. Интернет. Информатика

Источник

Создать симуляцию Монте-Карло с помощью Excel

RuleOfThumb — Метод Монте-Карло (Марш 2023)

Оглавление:

Моделирование Монте-Карло

Игра в кости

Шаг 1: События прокатки в кости

Шаг 2: Диапазон результатов

Шаг 3: Выводы

Шаг 4: Количество рулонов кости

Шаг 5: Моделирование

Шаг 6: Вероятность

Как создать капиталозащищенные инвестиции с помощью опций? (MSFT)

Как мне создать торговую стратегию с помощью Bollinger Bands® и скользящих средних?

Как мне создать торговую стратегию с помощью групп Боллинджера® и индикатора относительной силы (RSI)?

Практикум в MS Excel «Оценка риска инвестиционного проекта с помощью метода имитационного моделирования Монте-Карло»

Практикум в MS Excel

Таблица 1 – Расчет доходов от реализации проекта

Алгоритм выполнения лабораторной работы

Создание моделирования Монте-Карло с помощью Excel

Ключевые выводы

Моделирование Монте-Карло

Когда использовать моделирование Монте-Карло

Игра в кости

Краткий обзор

Шаг 1. События с броском игральных костей

Шаг 2: Диапазон результатов

Шаг 3: выводы

Шаг 4: Количество бросков костей

Шаг 5: Моделирование

Шаг 6: вероятность

А. В. Коросов

Компьютеры. Интернет. Информатика