Имитационное моделирование excel скачать

Пример имитационной модели

NOTE:

To change the image on this slide, select the picture and delete it. Then click the Pictures icon in the placeholder to insert your own image.

§26

Информатика, 8 класс

Учитель информатики

Дворецкая Ю.Ю,

1

Основные темы параграфа

• Что такое имитационная модель
• Пример имитационного моделирования в электронной таблице

ОПРЕДЕЛЕНИЕ

ИМИТАЦИОННАЯ МОДЕЛЬ – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

Имитационная модель имеет определенную минимальную опорную структуру, которую пользователь может дополнить и расширить с учетом специфики решаемых задач и базовых методов обработки.

ОПРЕДЕЛЕНИЕ

• ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе.

Отличие от математического моделирования

• имитационное моделирование исследует математические модели в виде алгоритмов , воспроизводящих функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций .
• в имитационных моделях для получения необходимой информации или результатов необходимо осуществлять их «прогон» в отличие от аналитических моделей, которые необходимо «решать».
• имитационные модели неспособны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.

Имитационные модели

В общем виде структуру имитационной модели в математической форме можно представляет следующим образом: ,

где E – результат действия системы;

x i – переменные и параметры, которыми мы можем управлять;

y i – переменные и параметры, которыми мы управлять не можем;

f – функциональная зависимость между x i и y i , которая определяет величину E .

Имитационные модели

Имитационная модель представляет собой комбинацию таких составляющих, как:

• компоненты;
• переменные;
• параметры;
• функциональные зависимости;
• ограничения;
• целевые функции.

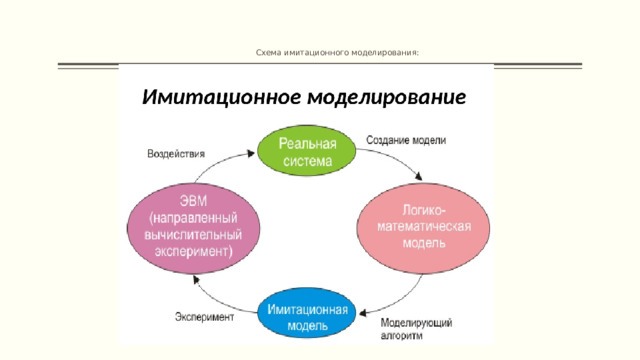
Схема имитационного моделирования:

НЕДОСТАТКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ:

• разработка имитационных моделей требует больших затрат, времени и сил;
• любая имитационная модель сложной системы менее объективна, чем аналитическая модель;
• результаты имитационного моделирования носят как правило частный характер, поэтому для предоставления обоснованных выводов необходимо провести серии модельных экспериментов.

Пример имитационного моделирования на компьютере

Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.

Модель – эволюция популяций

• Пусть на определенном пространстве случайным образом расселяются живые организмы.
• В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает.
• Эти процессы протекают в соответствии с законами эволюции (формальными правилами).

Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.

Имитационные модели

Законы эволюции:

• В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет.
• В живой ячейке жизнь может либо сохраниться, либо исчезнуть
• На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа.
• Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения).
• Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.

Модельное описание процесса эволюции популяции

• Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других.
• У ячейки номер 2 соседи: 1, 3 и 4.
• Но ячейка 1 всегда пустая.
• У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5).
• Аналогичная ситуация у крайних правых ячеек.

Кодирование

• Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц.
• Ноль обозначает пустую ячейку , единица — живую .
• Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:

00001001000100000000

Имитационные модели

Введем обозначения:

n — номер ячейки,

R (n) — значение двоичного числа, соответствующего этой ячейке в текущем поколении.

В рассматриваемом примере R (5) = R (8) =  R (12) = 1 .

Все остальные значения ячеек равны нулю.

Значения кода в n -й ячейке для следующего поколения будем обозначать S ( n ) .

Проанализировав правила эволюции, приходим к следующей формуле:

Если 1 R ( n — 2) + R ( n — 1) + R ( n ) + R ( n + 1) + R ( n + 2) 3, то S ( n ) = 1, иначе S ( n ) = 0.

Имитационные модели

Эта формула работает для значений n от 3 до 18 .

Всегда: S (1) = S (20) = 0 .

Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе: для этого к отрезку добавим по одной фиктивной ячейке справа и слева.

Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.

Итак, модель построена и формализована.

Имитационные модели

Для реализации применим табличный процессо р.

Моделью жизненного пространства будет строка электронной таблицы.

Первая строка — первое поколение,

вторая строка — второе поколение и т. д.

Тогда номера ячеек будут идентифицироваться именами столбцов таблицы.

Ячейка номер 0 — столбец А,

ячейка 1 — столбец В и т. д.,

ячейка 21 — столбец F.

=1; А1 + В1 + С1 + D1 + Е1 Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении. Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно. » width=»640″

• В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1 . Незаполненные ячейки по умолчанию приравниваются к нулю.
• Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:

ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 =1; А1 + В1 + С1 + D1 + Е1

• Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
• Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.

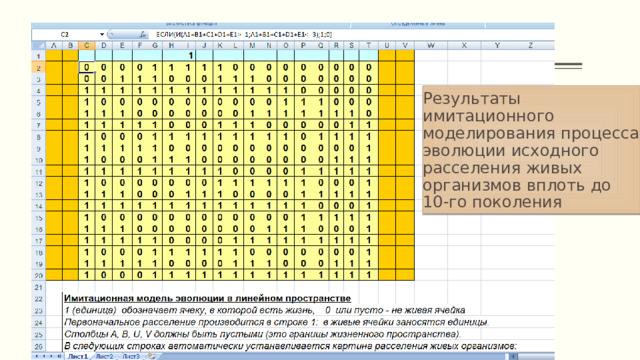
Результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения

Модель Дж. Конуэя «Жизнь»

В этой модели эволюция популяции живых организмов происходит в двумерном пространстве.

Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток.

Но теперь правила эволюции такие:

• если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения;
• если же живых соседей меньше двух, то она погибает от одиночества.
• в пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.

Домашнее задание

§26 конспект

Имитационное моделирование методом Монте-Карло.

31.01.2014 Бизнес-планирование, Калькуляторы, шаблоны, форматы, Малый бизнес

Предлагаю вашему вниманию шаблон для анализа инвестиционного проекта методом Монте-Карло.

Предлагаемый шаблон на основе анализа инвестиционного проекта служит иллюстрацией реализации метода моделирования получившим название «Монте-Карло». Название метода говорит само за себя: в основе моделирования будущих событий лежит использование большого количества случайных величин.

Подобный метод моделирования событий приемлем в тех случаях, когда существует неопределенность относительно значений тех или иных величин.

Считается, что данный метод был использован в работах над атомной бомбой, когда пытались рассчитать количество обогащённого урана необходимое для производства заряда. Слишком маленькое количество могло не дать развиться цепной реакции, а слишком большое было чревато дополнительными месяцами работы над получением необходимого количества урана.

Итак, мы имеем инвестиционный проект, который будет реализован в течение, предположим, 5 лет.

Нам точно не известна цена за которую мы будем реализовывать нашу продукцию, неизвестно точное количество продукции и неизвестно точное значение переменных затрат на ее производство. Это будут случайные величины.

Однако экспертным путем мы определили некий диапазон, в котором будут лежать эти значения.

Например, цена будет не ниже 30 руб. и не выше 40 руб., количество не меньше 150 и не больше 300 единиц, переменные затраты в диапазоне 15 до 20 руб. Цифры могут быть совершенно различными. Важно то, что мы имеем представление о диапазоне их вероятных значений.

 Именно значения в этих диапазонах мы и будем моделировать для оценки общей привлекательности проекта.

Для генерации случайных величин мы будем использовать функцию СЛУЧМЕЖДУ, с указанием в качестве аргументов нижней и верхней границы диапазона.

Полученные величины будут использоваться для расчета денежных потоков и чистой приведенной стоимости проекта (NPV).

Генерируется достаточно большое количество вариантов (опытов) и все они обрабатываются методами статистического анализа. В нашем шаблоне мы используем 5 000 опытов, но их может быть и 1 000 000, правда кардинально на результаты это не повлияет.

Это основная философия данного метода. Далее лишь техника реализации.

На листе «Имитация» указываем диапазоны изменения величин, указываем постоянные параметры проекта, а также формируем таблицу в 5 000 строк.

В каждой строке у нас есть случайное значение объема производства, переменных затрат и цены реализации. Также по каждой строке на основе этих данных рассчитываются такие показатели как выручка, прибыль (за минусом постоянных расходов и налога), денежный поток и чистая приведенная стоимость проекта за 5 лет с учетом заданной ставки дисконтирования.

Далее переходим к анализу полученных результатов.

На листе «Результаты анализа» выводим значение минимума, максимума, среднего значения, стандартного отклонения и коэффициента вариации интересующих нас показателей.

По большому счету, нас интересует показатель NPV.

Для него мы рассчитываем также количество случаев, когда NPV<0, и когда NPV>0 для всей совокупности в 5000 опытов.

Вместе с сумой убытков и суммой доходов, эти значения могут дать представление о мере рискованности проекта и масштабе возможных потерь.

Далее, используя стандартное распределение оцениваем вероятность получения того или иного значения NPV. Например, безубыточный проект имеет NPV > 0.

Установив в качестве значения Х (это наше NPV) ноль, мы получим вероятность получения убытка в 3%.

Для определения вероятности используем функцию НОРМ.СТ.РАСП, имеющую следующий синтаксис:

=НОРМ.СТ.РАСП(z,интегральная)

Z   Обязательный. Значение, для которого строится распределение.

Интегральная   Обязательный. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМ.СТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.

Для определения значения Z используем функцию НОРМАЛИЗАЦИЯ, имеющую следующий синтаксис:

=НОРМАЛИЗАЦИЯ(x, среднее, стандартное_откл)

x  Обязательный. Нормализуемое значение. В нашем случае это NPV.

Среднее  Обязательный. Среднее арифметическое распределения.

Стандартное_откл  Обязательный. Стандартное отклонение распределения.

Среднее значение и стандартное отклонение для NPV мы рассчитали в таблице «Результаты анализа».

---

Подборка по базе: _Методическая разработка урока истории России по теме «Курс В.В., 14.04 Технология К.р..docx, Синий и Серый Системы Аналитик Технология Резюме.pdf, К выходным параметрам моделирования в системе.docx, С.К. Хамзин, А.К. Карасев Технология строительного производства., Лекции по безопасной среде (хирургия) (2).doc, Практическая работа. ( технология сооружения объектов нефтегазод, Проблемные ситуации в объектах и городской среде с точки зрения , 2. Конспект лекций Технология приборостроения.doc, Практические задания по информационным технологиям в психологии

---

«Технология имитационного моделирования в среде MS Excel»

Введение

Имитационное моделирование (simulation) является одним из мощнейших методов анализа экономических систем.

В общем случае, под имитацией понимают процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира.

Цели проведения подобных экспериментов могут быть самыми различными – от выявления свойств и закономерностей исследуемой системы, до решения конкретных практических задач. С развитием средств вычислительной техники и программного обеспечения, спектр применения имитации в сфере экономики существенно расширился. В настоящее время ее используют как для решения задач внутрифирменного управления, так и для моделирования управления на макроэкономическом уровне. Рассмотрим основные преимущества применения имитационного моделирования в процессе решения задач финансового анализа.

Как следует из определения, имитация – это компьютерный эксперимент. Единственное отличие подобного эксперимента от реального состоит в том, что он проводится с моделью системы, а не с самой системой. Однако проведение реальных экспериментов с экономическими системами, по крайней мере, неразумно, требует значительных затрат и вряд ли осуществимо на практике. Таким образом, имитация является единственным способом исследования систем без осуществления реальных экспериментов.

Часто практически невыполним или требует значительных затрат сбор необходимой информации для принятия решений. Например, при оценке риска инвестиционных проектов, как правило, используют прогнозные данные об объемах продаж, затратах, ценах и т.д.

Однако чтобы адекватно оценить риск необходимо иметь достаточное количество информации для формулировки правдоподобных гипотез о вероятностных распределениях ключевых параметров проекта. В подобных случаях отсутствующие фактические данные заменяются величинами, полученными в процессе имитационного эксперимента (т.е. сгенерированными компьютером).

При решении многих задач финансового анализа используются модели, содержащие случайные величины, поведение которых не поддается управлению со стороны лиц, принимающих решения. Такие модели называют стохастическими. Применение имитации позволяет сделать выводы о возможных результатах, основанные на вероятностных распределениях случайных факторов (величин). Стохастическую имитацию часто называют методом Монте-Карло. Существуют и другие преимущества имитации.

Мы же рассмотрим технологию применения имитационного моделирования для анализа рисков инвестиционных проектов в среде MS Excel.

1. Имитационное моделирование

Имитационное моделирование (ситуационное моделирование) – метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.

Имитационное моделирование – это метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему, с которой проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация – это постижение сути явления, не прибегая к экспериментам на реальном объекте).

Имитационное моделирование – это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае аналитическая модель заменяется имитатором или имитационной моделью.

Имитационным моделированием иногда называют получение частных численных решений сформулированной задачи на основе аналитических решений или с помощью численных методов.

Имитационная модель – логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

К имитационному моделированию прибегают, когда:

• дорого или невозможно экспериментировать на реальном объекте;

• невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;

• необходимо сымитировать поведение системы во времени.

Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами или другими словами – разработке симулятора (англ. simulation modeling) исследуемой предметной области для проведения различных экспериментов.

Имитационное моделирование позволяет имитировать поведение системы во времени. Причём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны или опасны. С наступлением эпохи персональных компьютеров производство сложных и уникальных изделий, как правило, сопровождается компьютерным трёхмерным имитационным моделированием. Эта точная и относительно быстрая технология позволяет накопить все необходимые знания, оборудование и полуфабрикаты для будущего изделия до начала производства. Компьютерное 3D моделирование теперь не редкость даже для небольших компаний.

Имитация, как метод решения нетривиальных задач, получила начальное развитие в связи с созданием ЭВМ в 1950-х – 1960-х годах.

Можно выделить две разновидности имитации:

• Метод Монте-Карло (метод статистических испытаний);

• Метод имитационного моделирования (статистическое моделирование).

Виды имитационного моделирования:

• Агентное моделирование – относительно новое (1990-е-2000-е гг.) направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот, когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей – получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении её отдельных активных объектов и взаимодействии этих объектов в системе. Агент – некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться.

• Дискретно-событийное моделирование – подход к моделированию, предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы, такие как: «ожидание», «обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений – от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов. Основан Джеффри Гордоном в 1960-х годах.

• Системная динамика – парадигма моделирования, где для исследуемой системы строятся графические диаграммы причинных связей и глобальных влияний одних параметров на другие во времени, а затем созданная на основе этих диаграмм модель имитируется на компьютере. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики строят модели бизнес-процессов, развития города, модели производства, динамики популяции, экологии и развития эпидемии. Метод основан Джеем Форрестером в 1950 годах.

2. Моделирование рисков инвестиционных проектов
Имитационное моделирование представляет собой серию численных экспериментов призванных получить эмпирические оценки степени влияния различных факторов (исходных величин) на некоторые зависящие от них результаты (показатели).

В общем случае, проведение имитационного эксперимента можно разбить на следующие этапы:

• Установка взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства.

• Задание законов распределения вероятностей для ключевых параметров модели.

• Проведение компьютерной имитации значений ключевых параметров модели.

• Расчет основных характеристик распределения исходных и выходных показателей.

• Анализ полученных результатов и принятие решения.

Результаты имитационного эксперимента могут быть дополнены статистическим анализом, а также использоваться для построения прогнозных моделей и сценариев.

Осуществим имитационное моделирование анализа рисков инвестиционного проекта на основании данных примера.

Пример 1.

Фирма рассматривает инвестиционный проект по производству продукта «А». В процессе предварительного анализа экспертами были выявлены три ключевых параметра проекта и определены возможные границы их изменений (табл. 1.). Прочие параметры проекта считаются постоянными величинами (табл. 2.).
Таблица 1. Ключевые параметры проекта по производству продукта «А»

	Показатели__Наихудший__Наилучший__Вероятный’>Показатели
Наихудший	Наилучший	Вероятный
Объем выпуска – Q	150	300	200
Цена за штуку – P	40	55	50
Переменные затраты – V	35	25	30

Таблица 2. Неизменяемые параметры проекта по производству продукта «А»

Показатели	Наиболее вероятное значение
Постоянные затраты – F	500
Амортизация – A	100
Налог на прибыль – T	60%
Норма дисконта – r	10%
Срок проекта – n	5
Начальные инвестиции – I0	2000

Первым этапом анализа согласно сформулированному выше алгоритму является определение зависимости результирующего показателя от исходных. При этом в качестве результирующего показателя обычно выступает один из критериев эффективности: NPV, IRR, PI.

Предположим, что используемым критерием является чистая современная стоимость проекта NPV: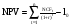
(1)

где NCF_t – величина чистого потока платежей в периоде t.

По условиям примера, значения нормы дисконта r и первоначального объема инвестиций I₀ известны и считаются постоянными в течении срока реализации проекта (табл. 2.).

По условиям примера ключевыми варьируемыми параметрами являются: переменные расходы V, объем выпуска Q и цена P. Диапазоны возможных изменений варьируемых показателей приведены в табл. 1. При этом будем исходить из предположения, что все ключевые переменные имеют равномерное распределение вероятностей.

Реализация третьего этапа может быть осуществлена только с применением ЭВМ, оснащенной специальными программными средствами. Поэтому прежде чем приступить к третьему этапу – имитационному эксперименту, познакомимся с соответствующими средствами MS Excel, автоматизирующими его проведение.

3. Технология имитационного моделирования в среде MS Excel
Проведение имитационных экспериментов в среде MS Excel можно осуществить двумя способами – с помощью встроенных функций и путем использования инструмента «Генератор случайных чисел» дополнения «Анализ данных» (Analysis ToolPack). В работе будет использован первый способ проведения имитационных экспериментов – с помощью встроенных функций MS Excel.

Следует отметить, что применение встроенных функций целесообразно лишь в том случае, когда вероятности реализации всех значений случайной величины считаются одинаковыми. Тогда для имитации значений требуемой переменной можно воспользоваться математическими функциями СЛЧИС или СЛУЧМЕЖДУ. Форматы функций приведены в табл. 3.
Таблица 3. Математические функции для генерации случайных чисел

Наименование функции	Формат функции
Оригинальная версия	Локализованная версия
RAND	СЛЧИС	СЛЧИС () – не имеет аргументов
RANDBETWEEN	СЛУЧМЕЖДУ	СЛУЧМЕЖДУ (нижн_граница; верхн_граница)

Функция «СЛЧИС»

Функция СЛЧИС () возвращает равномерно распределенное случайное число E, большее, либо равное 0 и меньшее 1, т.е.: 0 ≤ E < 1. Вместе с тем, путем несложных преобразований, с ее помощью можно получить любое случайное вещественное число. Например, чтобы получить случайное число между a и b, достаточно задать в любой ячейке ЭТ следующую формулу:

=СЛЧИС () * (b-a) +a

Эта функция не имеет аргументов. Если в ЭТ установлен режим автоматических вычислений, принятый по умолчанию, то возвращаемый функцией результат будет изменяться всякий раз, когда происходит ввод или корректировка данных. В режиме ручных вычислений пересчет всей ЭТ осуществляется только после нажатия клавиши [F9].

Настройка режима управления вычислениями производится установкой соответствующего флажка в подпункте «Вычисления» пункта «Параметры» темы «Сервис» главного меню.

В целом применение данной функции при решении задач финансового анализа ограничено рядом специфических приложений. Однако ее удобно использовать в некоторых случаях для генерации значений вероятности событий, а также вещественных чисел.

Функция «СЛУЧМЕЖДУ»

Как следует из названия этой функции, она позволяет получить случайное число из заданного интервала. При этом тип возвращаемого числа (т.е. вещественное или целое) зависит от типа заданных аргументов.

В качестве примера, сгенерируем случайное значение для переменной Q (объем выпуска продукта). Согласно табл. 1., эта переменная принимает значения из диапазона 150 – 300.

Введем в любую ячейку ЭТ формулу:

=СЛУЧМЕЖДУ (150; 300) (Результат: 210).

Если задать аналогичные формулы для переменных P и V, а также формулу для вычисления NPV и скопировать их требуемое число раз, можно получить генеральную совокупность, содержащую различные значения исходных показателей и полученных результатов. После чего, используя статистические функции, нетрудно рассчитать соответствующие параметры распределения и провести вероятностный анализ. Продемонстрируем изложенный подход на решении примера 1. Перед тем, как приступить к разработке шаблона, целесообразно установить в ЭТ режим ручных вычислений.

Приступаем к разработке шаблона. С целью упрощения и повышения наглядности анализа выделим для его проведения в рабочей книге MS Excel два листа.

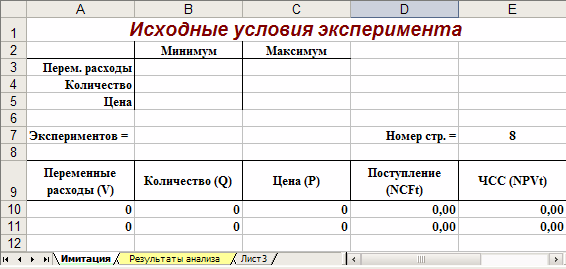
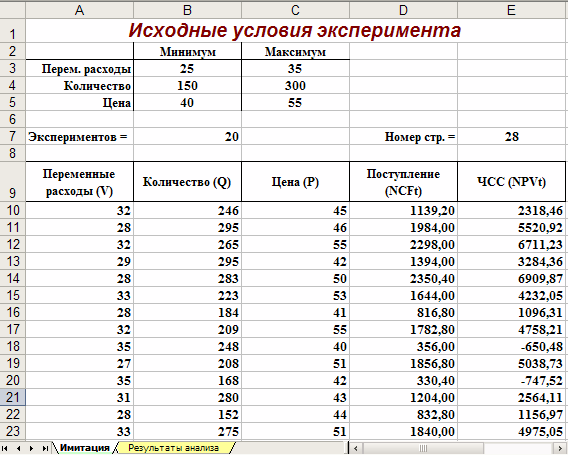
Первый лист – «Имитация», предназначен для построения генеральной совокупности (рис. 1.). Определенные в данном листе формулы и собственные имена ячеек приведены в табл. 4. и 5.

Рис. 1. Лист «Имитация»
Таблица 4. Формулы листа «Имитация»

Ячейка	Формула
Е7	=B7+10–2
A10	=СЛУЧМЕЖДУ ($B$3; $C$3)
A11	=СЛУЧМЕЖДУ ($B$3; $C$3)
B10	=СЛУЧМЕЖДУ ($B$4; $C$4)
B11	=СЛУЧМЕЖДУ ($B$4; $C$4)
C10	=СЛУЧМЕЖДУ ($B$5; $C$5)
C11	=СЛУЧМЕЖДУ ($B$5; $C$5)
D10	= (B10* (C10-A10) – Пост_расх-Аморт) * (1-Налог) +Аморт
D11	= (B11* (C11-A11) – Пост_расх-Аморт) * (1-Налог) +Аморт
E10	=ПС (Норма; Срок; – D10) – Нач_инвест
E11	=ПС (Норма; Срок; – D11) – Нач_инвест

Таблица 5. Имена ячеек листа «Имитация»

Адрес ячейки	Имя	Комментарии
Блок A10: A11	Перем_расх	Переменные расходы
Блок B10: B11	Количество	Объем выпуска
Блок C10: C11	Цена	Цена изделия
Блок D10: D11	Поступления	Поступления от проекта NCFt
Блок E10: E11	ЧСС	Чистая современная стоимость NPV

Первая часть листа (блок ячеек А1. Е7) предназначена для ввода диапазонов изменений ключевых переменных, значения которых будут генерироваться в процессе проведения эксперимента. В ячейке В7 задается общее число имитаций (экспериментов). Формула, заданная в ячейке Е7, вычисляет номер последней строки выходного блока, в который будут помещены полученные значения. Смысл этой формулы будет раскрыт позже.

Вторая часть листа (блок ячеек А9. Е11) предназначена для проведения имитации. Формулы в ячейках А10. С11 генерируют значения для соответствующих переменных с учетом заданных в ячейках В3. С5 диапазонов их изменений. Обратим внимание на то, что при указании нижней и верхней границы изменений используется абсолютная адресация ячеек.

Формулы в ячейках D10. E11 вычисляют величину потока платежей и его чистую современную стоимость соответственно. При этом значения постоянных переменных берутся из следующего листа шаблона – «Результаты анализа».

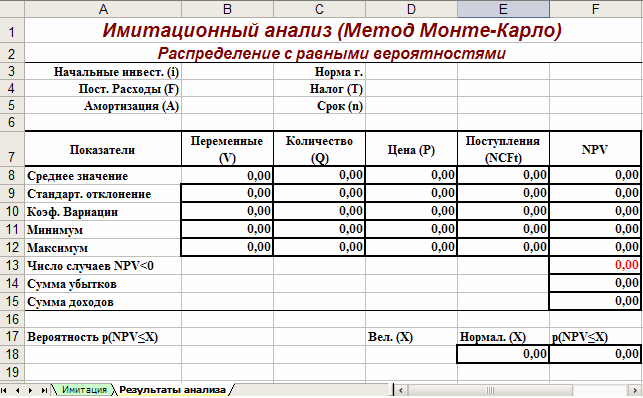
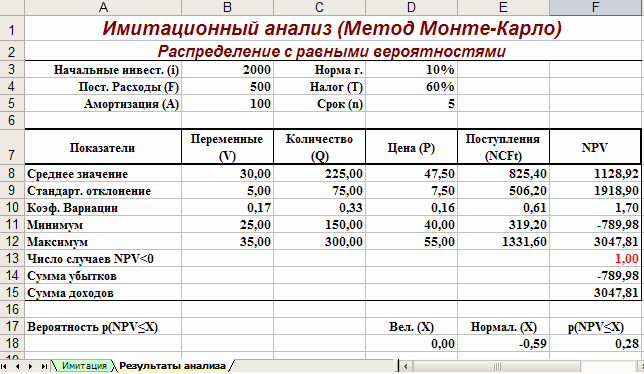
Лист «Результаты анализа» кроме значений постоянных переменных содержит также функции, вычисляющие параметры распределения изменяемых (Q, V, P) и результатных (NCF, NPV) переменных и вероятности различных событий. Определенные для данного листа формулы и собственные имена ячеек приведены в табл. 6. и 7. Общий вид листа показан на рис. 2.
Таблица 6. Формулы листа «Результаты анализа»

Ячейка	Формула
B8	=СРЗНАЧ (Перем_расх)
B9	=СТАНДОТКЛОНП (Перем_расх)
B10	=B9/B8
B11	=МИН (Перем_расх)
B12	=МАКС (Перем_расх)
C8	=СРЗНАЧ (Количество)
C9	=СТАНДОТКЛОНП (Количество)
C10	=C9/C8
C11	=МИН (Количество)
C12	=МАКС (Количество)
D8	=СРЗНАЧ (Цена)
D9	=СТАНДОТКЛОНП (Цена)
D10	=D9/D8
D11	=МИН (Цена)
D12	=МАКС (Цена)
E8	=СРЗНАЧ (Поступления)
E9	=СТАНДОТКЛОНП (Поступления)
E10	=E9/E8
E11	=МИН (Поступления)
E12	=МАКС (Поступления)
F8	=СРЗНАЧ (ЧСС)
F9	=СТАНДОТКЛОНП (ЧСС)
F10	=F9/F8
F11	=МИН (ЧСС)
F12	=МАКС (ЧСС)
F13	=СЧЁТЕСЛИ (ЧСС; «<0»)
F14	=СУММЕСЛИ (ЧСС; «<0»)
F15	=СУММЕСЛИ (ЧСС; «>0»)
Е18	=НОРМАЛИЗАЦИЯ (D18; $F$8; $F$9)
F18	=НОРМСТРАСП (E18)

Таблица 7. Имена ячеек листа «Результаты анализа»

Адрес ячейки	Имя	Комментарии
B2	Нач_инвест	Начальные инвестиции
B3	Пост_расх	Постоянные расходы
B4	Аморт	Амортизация
D2	Норма	Норма дисконта
D3	Налог	Ставка налога на прибыль
D4	Срок	Срок реализации прока

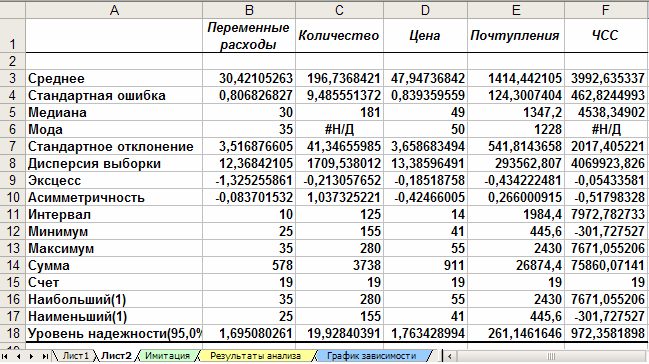
Рис. 2. Лист «Результаты анализа»
Поскольку формулы листа содержат ряд новых функций, приведем необходимые пояснения.

Функции МИН () и МАКС () вычисляют минимальное и максимальное значение для массива данных из блока ячеек, указанного в качестве их аргумента. Имена и диапазоны этих блоков приведены в табл. 7.

Функция СЧЕТЕСЛИ () осуществляет подсчет количества ячеек в указанном блоке, значения которых удовлетворяют заданному условию. Функция имеет следующий формат:

=СЧЕТЕСЛИ (блок; «условие»).

В данном случае, заданная в ячейке F13, эта функция осуществляет подсчет количества отрицательных значений NPV, содержащихся в блоке ячеек ЧСС (см. табл. 7).

Механизм действия функции СУММЕСЛИ () аналогичен функции СЧЕТЕСЛИ (). Отличие заключается лишь в том, что эта функция суммирует значения ячеек в указанном блоке, если они удовлетворяют заданному условию. Функция имеет следующий формат:

=СУММЕСЛИ (блок; «условие»).

В данном случае, заданные в ячейках F14, F15, функции осуществляет подсчет суммы отрицательных (ячейка F14) и положительных (ячейка F14) значений NPV, содержащихся в блоке ЧСС. Смысл этих расчетов будет объяснен позже.

Две последние формулы (ячейки Е18 и F18) предназначены для проведения вероятностного анализа распределения NPV и требуют небольшого теоретического отступления.

В рассматриваемом примере мы исходим из предположения о независимости и равномерном распределении ключевых переменных Q, V, P. Однако какое распределение при этом будет иметь результатная величина – показатель NPV, заранее определить нельзя.

Одно из возможных решений этой проблемы – попытаться аппроксимировать неизвестное распределение каким-либо известным. При этом в качестве приближения удобнее всего использовать нормальное распределение. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет распределение, приблизительно соответствующее нормальному.

В прикладном анализе для целей аппроксимации широко применяется частный случай нормального распределения – т. н. стандартное нормальное распределение. Математическое ожидание стандартно распределенной случайной величины Е равно 0: M (E) = 0. График этого распределения симметричен относительно оси ординат и оно характеризуется всего одним параметром – стандартным отклонением s, равным 1.

Приведение случайной переменной E к стандартно распределенной величине Z осуществляется с помощью т. н. нормализации – вычитания средней и последующего деления на стандартное отклонение: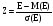
(2)
Как следует из (2), величина Z выражается в количестве стандартных отклонений. Для вычисления вероятностей по значению нормализованной величины Z используются специальные статистические таблицы.

В MS Excel подобные вычисления осуществляются с помощью статистических функций НОРМАЛИЗАЦИЯ () и НОРМСТРАСП ().

Функция «НОРМАЛИЗАЦИЯ»

НОРМАЛИЗАЦИЯ (X; СРЕДНЕЕ; СТАНД_ОТКЛ)

Эта функция возвращает нормализованное значение Z величины x, на основании которого затем вычисляется искомая вероятность p (E ≤ x). Она реализует соотношение (2). Функция требует задания трех аргументов:

х – нормализуемое значение;

среднее – математическое ожидание случайной величины Е;

станд_откл – стандартное отклонение.

Полученное значение Z является аргументом для следующей функции – НОРМСТРАСП ().

Функция «НОРМСТРАСП»

НОРМСТРАСП (Z)

Эта функция возвращает стандартное нормальное распределение, т.е. вероятность того, что случайная нормализованная величина Е будет меньше или равна х. Она имеет всего один аргумент – Z, вычисляемый функцией НОРМАЛИЗАЦИЯ ().

Нетрудно заметить, что эти функции следует использовать в тандеме. При этом наиболее эффективным и компактным способом их задания является указание функции НОРМАЛИЗАЦИЯ () в качестве аргумента функции – НОРМСТРАСП (), т.е.:

=НОРМСТРАСП (НОРМАЛИЗАЦИЯ (x; среднее; станд_откл)).

С целью повышения наглядности, в проектируемом шаблоне функции заданы раздельно (ячейки Е18 и F18).

Приступаем к имитационному эксперименту. Для его проведения необходимо выполнить следующие шаги:

• Ввести значения постоянных переменных (табл. 2.) в ячейки В2, В4 и D2, D4 листа «Результаты анализа».
• Ввести значения диапазонов изменений ключевых переменных (табл. 1.) в ячейки В3, С5 листа «Имитация».
• Задать в ячейке В7 требуемое число экспериментов.
• Установить курсор в ячейку А11 и вставить необходимое число строк в шаблон (номер последней строки будет вычислен в Е7).
• Скопировать формулы блока А10, Е10 требуемое количество раз.
• Перейти к листу «Результаты анализа» и проанализировать полученные результаты.

Рассмотрим реализацию выделенных шагов более подробно. Введем значения постоянных переменных в ячейки В2, В4 листа «Результаты анализа». Введем значения диапазонов изменений ключевых переменных в ячейки В3, С5 листа «Имитация». Укажем в ячейке В7 число проводимых экспериментов, например – 20. Установим табличный курсор в ячейку А11.

На следующем шаге необходимо вставить в шаблон нужное количество строк (18).

Теперь необходимо заполнить вставленные строки формулами блока ячеек А10. Е10.

Рис. 4. Результаты имитации

Рис. 5. Результаты анализа
Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

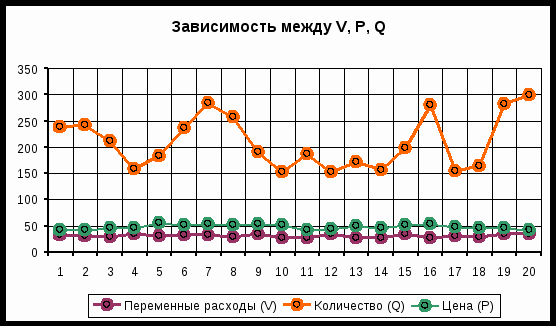
На практике одним из важнейших этапов анализа результатов имитационного эксперимента является исследование зависимостей между ключевыми параметрами. Количественная оценка вариации напрямую зависит от степени корреляции между случайными величинами. На рис. 6. приведен график распределения значений ключевых параметров V, P и Q, построенный на основании 20 имитаций.

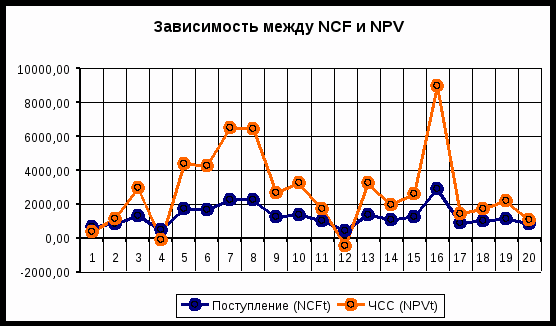
Нетрудно заметить, что в целом, вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу о их независимости. Для сравнения ниже приведен график распределений потока платежей NCF и величины NPV (рис. 7).

Рис. 6. Распределение значений параметров V, P и Q

Рис. 7. Зависимость между NCF и NPV
Как и следовало ожидать, направления колебаний здесь в точности совпадают и между этими величинами существует сильная корреляционная связь, близкая к функциональной.

4. Статистический анализ результатов имитации

Как уже отмечалось, в анализе стохастических процессов важное значение имеют статистические взаимосвязи между случайными величинами. В предыдущем примере для установления степени взаимосвязи ключевых и расчетных показателей мы использовали графический анализ. В качестве количественных характеристик подобных взаимосвязей в статистике используют два показателя: ковариацию и корреляцию.

имитационный моделирование excel корреляция

4.1 Ковариация и корреляция

Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения: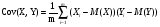
(3)
где X, Y – множества значений случайных величин размерности m; M (X) – математическое ожидание случайной величины Х; M (Y) – математическое ожидание случайной величины Y.

Как следует из (3), положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0.

Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель – коэффициент корреляции R, вычисляемый по формуле: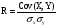
(4)
Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.

Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в MS Excel может быть осуществлено двумя способами:

• с помощью статистических функций КОВАР () и КОРРЕЛ ();
• с помощью специальных инструментов статистического анализа.

Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа.

4.2 Инструмент анализа данных «Корреляция»

Определим степень тесноты взаимосвязей между переменными V, Q, P, NCF и NPV. При этом в качестве меры будем использовать показатель корреляции R.

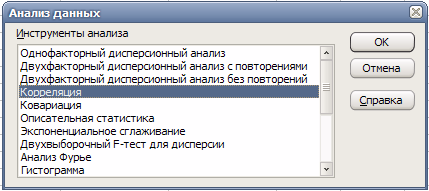
Выберем в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.

Выберем из списка «Инструменты анализа» пункт «Корреляция» и нажмем кнопку «ОК» (рис. 8). Результатом будет появление окна диалога инструмента «Корреляция».

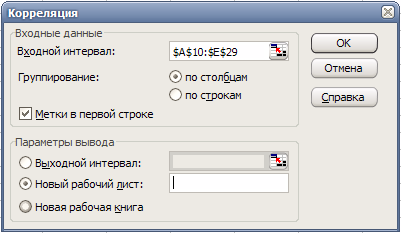
Заполним поля диалогового окна, как показано на рис. 9 и нажмем кнопку «ОК».

Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рис. 10.

Рис. 8. Список инструментов анализа (выбор пункта «Корреляция»)

Рис. 9. Заполнение окна диалога инструмента «Корреляция»

Рис. 10

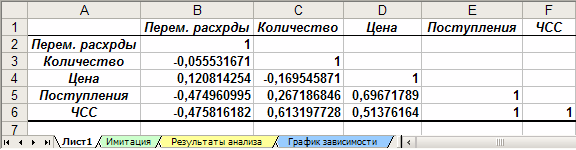
4.3 Результаты корреляционного анализа
Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.

Как следует из результатов корреляционного анализа, гипотеза о независимости распределений ключевых переменных V, Q, P в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q и ценой Р (ячейки В3. В4, С4) достаточно близки к 0.

В свою очередь величина показателя NPV напрямую зависит от величины потока платежей (R = 1). Кроме того, существует корреляционная зависимость средней степени между Q и NPV (R = 0,613), P и NPV (R = 0,513). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (R = -0,475).

Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. В частности в рассматриваемом примере, отсутствие взаимосвязи между переменными затратами V и объемами выпуска продукта Q требует дополнительных объяснений, так как с увеличением последнего, величина V также должна расти. Таким образом, установленный диапазон изменений переменных затрат V нуждается в дополнительной проверке и, возможно, корректировке.

Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей.

При проведении имитационного эксперимента и последующего вероятностного анализа полученных результатов мы исходили из предположения о нормальном распределении исходных и выходных показателей. Вместе с тем, справедливость сделанных допущений, по крайней мере для выходного показателя NPV, нуждается в проверке.

Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова. В целом MS Excel позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.

Однако в простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия (скос) и эксцесс. Напомним, что для нормального распределения эти характеристики должны быть равны 0. На практике близкими к нулевым значениями можно пренебречь. Для вычисления коэффициента асимметрии и эксцесса в MS Excel реализованы специальные статистические функции – СКОС () и ЭКСЦЕСС ().

4.4 Инструмент анализа данных «Описательная статистика»

Чем больше характеристик распределения случайной величины нам известно, тем точнее мы можем судить об описываемых ею процессов. Инструмент «Описательная статистика» автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных.

Определим параметры описательной статистики для переменных V, Q, P, NCF, NPV. Для этого необходимо выполнить следующие шаги.

Выберем в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.

Выберем из списка «Инструменты анализа» пункт «Описательная статистика» и нажмем кнопку «ОК». Результатом будет появление окна диалога инструмента «Описательная статистика».

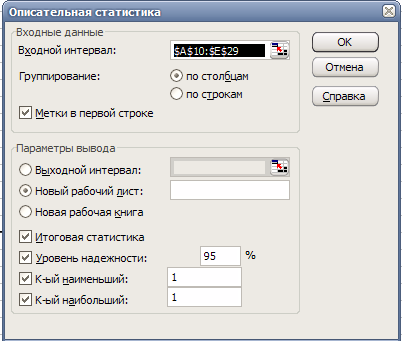
Заполним поля диалогового окна, как показано на рис. 11 и нажмем кнопку «ОК».

Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. Выполнив операции форматирования, можно привести полученную ЭТ к более наглядному виду (рис. 12).

Рис. 11. Заполнение полей диалогового окна «Описательная статистика»

Рис. 12. Описательная статистика для исследуемых переменных
Многие из приведенных в данной ЭТ характеристик нам уже хорошо знакомы, а их значения уже определены с помощью соответствующих функций на листе «Результаты анализа». Поэтому рассмотрим лишь те из них, которые не упоминались ранее.

Вторая строка ЭТ содержит значения стандартных ошибок e для средних величин распределений. Другими словами среднее или ожидаемое значение случайной величины М(Е) определено с погрешностью ± e.

Медиана – это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию.

Как следует из полученных результатов, данное условие соблюдается для исходных переменных V, Q, P (значения медиан лежат в диапазоне М (Е) ± e, т.е. – практически совпадают со средними). Однако для результатных переменных NCF, NPV значения медиан лежат ниже средних, что наводит на мысль о правосторонней асимметричности их распределений.

Мода – наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать. В данном случае, в некоторых ячейках таблицы MS Excel вернул сообщение об ошибке. Таким образом, вычисление моды не представляется возможным.

Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.

В рассматриваемом примере положительный эксцесс у функций различен. Таким образом, графики этих распределений будут более пологими, по отношению к нормальному (если бы значения функций были примерно одинаковы).

Асимметричность (коэффициент асимметрии или скоса – s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь.

В частности асимметрию распределения переменной V в данном случае можно считать несущественной, чего нельзя сказать о распределениях других величин.

Осуществим оценку значимости коэффициента асимметрии для распределения Q. Наиболее простым способом получения такой оценки является определение стандартной (среднеквадратической) ошибки асимметрии, рассчитываемой по формуле:

(5)
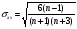
где n – число значений случайной величины (в данном случае – 20).

Если отношение коэффициента асимметрии s к величине ошибки s as меньше трех (т.е.: s /s as < 3), то асимметрия считается несущественной, а ее наличие объясняется воздействием случайных факторов. В противном случае асимметрия статистически значима и факт ее наличия требует дополнительной интерпретации. Осуществим оценку значимости коэффициента асимметрии для рассматриваемого примера.

Введем в любую ячейку ЭТ формулу:

=1,037325221/КОРЕНЬ (6*19/21*23) (Результат: 0,092834252).

Поскольку отношение s /s as < 3, асимметрию следует считать несущественной. Таким образом наше первоначальное предположение о правосторонней скошенности распределения Q не подтвердилась.

Для рассматриваемого примера наличие левосторонней асимметрии может считаться отрицательным моментом, так как это означает, что большая часть распределения лежит ниже математического ожидания, т.е. большие значения Q являются менее вероятными.

Аналогичным способом можно осуществить проверку значимости величины эксцесса – е. Формула для расчета стандартной ошибки эксцесса имеет следующий вид: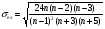
(6)
где n – число значений случайной величины.

Если отношение e /s ex < 3, эксцесс считается незначительным и его величиной можно пренебречь.

Для вычисления коэффициента асимметрии в этой формуле использована статистическая функция СКОС(). Формула для проверки значимости показателя эксцесса задается аналогичным образом. Числителем этой формулы будет функция ЭКСЦЕСС (), а знаменателем соотношение (6), реализованное средствами MS Excel.

Оставшиеся показатели описательной статистики (рис. 12) представляют меньший интерес. Величина «Интервал» определяется как разность между максимальным и минимальным значением случайной величины (численного ряда). Параметры «Счет» и «Сумма» представляют собой число значений в заданном интервале и их сумму соответственно.

Последняя характеристика «Уровень надежности» показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.

Для рассматриваемого примера это означает, что с вероятностью 0, 95 (95%) величина математического ожидания NPV попадет в интервал 3992,63 ± 972,35.

Расчет доверительного интервала для среднего значения можно также осуществить с помощью специальной статистической функции ДОВЕРИТ ().

Дополнение «Анализ данных» содержит целый ряд других полезных инструментов, позволяющих быстро и эффективно осуществить требуемый вид обработки данных. Вместе с тем, большинство из них требует осмысленного применения и соответствующей подготовки пользователя в области математической статистики.

Заключение

Имитационное моделирование позволяет учесть максимально возможное число факторов внешней среды для поддержки принятия управленческих решений и является наиболее мощным средством анализа инвестиционных рисков. Необходимость его применения в отечественной финансовой практике обусловлена особенностями российского рынка, характеризующегося зависимостью от внеэкономических факторов и высокой степенью неопределенности.

Результаты имитации могут быть дополнены вероятностным и статистическим анализом и в целом обеспечивают менеджера наиболее полной информацией о степени влияния ключевых факторов на ожидаемые результаты и возможных сценариях развития событий.

К недостаткам рассмотренного подхода следует отнести:

• трудность понимания и восприятия имитационных моделей, учитывающих большое число внешних и внутренних факторов, вследствие их математической сложности и объемности;

• при разработке реальных моделей может возникнуть необходимость привлечения специалистов или научных консультантов со стороны;

• относительную неточность полученных результатов, по сравнению с другими методами численного анализа и др.

Несмотря на отмеченные недостатки, в настоящее время имитационное моделирование является основой для создания новых перспективных технологий управления и принятия решений в сфере бизнеса, а развитие вычислительной техники и программного обеспечения делает этот метод все более доступным для широкого круга специалистов-практиков.

Библиография

1. А.А. Емельянов. Структурный анализ и динамические имитационные модели в экономике. – М.: Финансы и статистика, 2005.
2. Н.Б. Кобелев Основы имитационного моделирования сложных экономических задач. – М.: Дело. 2006.
3. Д. Круглински, С. Уингоу, Дж. Шеферд. Microsoft Excel – справочник пользователя. Спб.:Питер., 2010.
4. А.А. Емельянов, Е.А. Власова, Р.В. Дума. Имитационное моделирование экономических процессов. М. Финансы и статистика, 2005
5. Е.В. Бережная, В.И. Бережной. Математические методы моделирования экономических систем. М.: 2006.
6. А.А. Емельянов. Имитационное моделирование экономических процессов. М.: 2005.

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Учебное пособие. Теория + Практика. — Юрга: Изд-во ЮТИ (филиал) ТПУ, 2016. — 115 с.

Приводятся существующие работы по моделированию экономических объектов с помощью данного пакета (одноканальной системы массового обслуживания с неограниченным ограниченным ожиданием; системы управления запасами с пороговой и периодическими стратегиями подачи заявок, с учетом и без учета отложенного спроса и т.д.), а также имитационные модели и шаблоны, разработанные авторами для имитации финансовых механизмов (аукционов, конкурсов), управления производственными запасами, массового обслуживания (с групповым поступлением и обслуживанием заявок), а также различных игр и др. Рассмотрена реализация более 30 моделей.
Пособие включает следующие разделы: имитационное моделирование систем массового обслуживания, имитационное моделирование инвестиционных рисков, имитационное моделирование систем управления запасами, имитационное моделирование аукционов и конкурсных механизмов, имитационное моделирование игр. К каждому разделу дана краткая теория, включающая основные понятия и описание существующих в данной области решений, а также задачи для самостоятельного выполнения, связанные с моделированием какого-либо экономического объекта.
В приложениях содержится справочная информация, которая может быть полезна при проведении моделирования в среде Excel: основные приемы работы с данным пакетом, способы генерирования с его помощью случайных чисел и событий, а также описание основных функций, этапов построение диаграмм, проведения экспериментов «что будет, если…».
Учебное пособие предназначено для студентов направления 09.03.03 – прикладная информатика (профиль «экономика»). Кроме того, это пособие может быть использовано студентами других смежных экономических специальностей.

Введение.
Электронные таблицы Excel как средство реализации имитационных моделей.
Имитационное моделирование систем массового обслуживания.
Одноканальная система массового обслуживания.
Двухканальная система массового обслуживания.
Система массового обслуживания с ограниченным по времени ожиданием.
Система массового обслуживания с очередью.
Система с групповым обслуживанием заявок.
Система массового обслуживания с групповым поступлением заявок.
Имитационное моделирование инвестиционных рисков.
Общая модель оценки рисков.
Модель инвестиционного проекта по производству продукта.
Имитационное моделирование систем управления запасами.
Однопериодная модель со случайным спросом.
Производственная модель управления запасами.
Модель с периодической стратегией подачи заявок.
Модель с пороговой стратегией подачи заявок.
Имитационное моделирование торгов и конкурсных механизмов.
Обратный аукцион.
Голландский аукцион.
Английский аукцион.
Аукционы Vickery и FPSB.
Японский аукцион.
Аукцион с резервированной ценой.
Аукцион с фиксированной ценой.
Китайский аукцион.
Конкурсное распределение средств.
Имитационное моделирование игр.
Игра «Найдите слово».
Игра «Эксперты».
Игра «Выиграй миллион».
Игра «Акция».
Литература.
Приложение 1. Основные приемы работы с пакетом Excel.
Приложение 2. Моделирование случайных чисел и событий в Excel.
Приложение 3. Основные используемые функции Excel.
Приложение 4. Построение диаграмм в Excel.
Приложение 5. Проведение экспериментов «что будет, если…» в Excel.