From Wikipedia, the free encyclopedia
«⟺» and «⇔» redirect here. For other uses, see Arrow (symbol).
↔⇔≡⟺
Logical symbols representing iff
In logic and related fields such as mathematics and philosophy, «if and only if» (shortened as «iff«) is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is biconditional (a statement of material equivalence),[1] and can be likened to the standard material conditional («only if», equal to «if … then») combined with its reverse («if»); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English «if and only if»—with its pre-existing meaning. For example, P if and only if Q means that P is true whenever Q is true, and the only case in which P is true is if Q is also true, whereas in the case of P if Q, there could be other scenarios where P is true and Q is false.
In writing, phrases commonly used as alternatives to P «if and only if» Q include: Q is necessary and sufficient for P, for P it is necessary and sufficient that Q, P is equivalent (or materially equivalent) to Q (compare with material implication), P precisely if Q, P precisely (or exactly) when Q, P exactly in case Q, and P just in case Q.[2] Some authors regard «iff» as unsuitable in formal writing;[3] others consider it a «borderline case» and tolerate its use.[4]
In logical formulae, logical symbols, such as 

Definition[edit]
The truth table of P 
| P | Q | P  Q Q
|
P  Q Q
|
P  Q Q
|
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |
It is equivalent to that produced by the XNOR gate, and opposite to that produced by the XOR gate.[8]
Usage[edit]
Notation[edit]
The corresponding logical symbols are «↔», «
Another term for the logical connective, i.e., the symbol in logic formulas, is exclusive nor.
In TeX, «if and only if» is shown as a long double arrow: 
Proofs[edit]
In most logical systems, one proves a statement of the form «P iff Q» by proving either «if P, then Q» and «if Q, then P», or «if P, then Q» and «if not-P, then not-Q». Proving these pair of statements sometimes leads to a more natural proof, since there are not obvious conditions in which one would infer a biconditional directly. An alternative is to prove the disjunction «(P and Q) or (not-P and not-Q)», which itself can be inferred directly from either of its disjuncts—that is, because «iff» is truth-functional, «P iff Q» follows if P and Q have been shown to be both true, or both false.
Origin of iff and pronunciation[edit]
Usage of the abbreviation «iff» first appeared in print in John L. Kelley’s 1955 book General Topology.[12]
Its invention is often credited to Paul Halmos, who wrote «I invented ‘iff,’ for ‘if and only if’—but I could never believe I was really its first inventor.»[13]
It is somewhat unclear how «iff» was meant to be pronounced. In current practice, the single ‘word’ «iff» is almost always read as the four words «if and only if». However, in the preface of General Topology, Kelley suggests that it should be read differently: «In some cases where mathematical content requires ‘if and only if’ and euphony demands something less I use Halmos’ ‘iff'». The authors of one discrete mathematics textbook suggest:[14] «Should you need to pronounce iff, really hang on to the ‘ff’ so that people hear the difference from ‘if'», implying that «iff» could be pronounced as [ɪfː].
Usage in definitions[edit]
Technically, definitions are «if and only if» statements; some texts — such as Kelley’s General Topology — follow the strict demands of logic, and use «if and only if» or iff in definitions of new terms.[15]
However, this logically correct usage of «if and only if» relatively uncommon and overlooks the linguistic fact that the «if» of a definition is interpreted as meaning «if and only if». The majority of textbooks, research papers and articles (including English Wikipedia articles) follow the linguistic convention to interpret «if» as «if and only if» whenever a mathematical definition is involved (as in «a topological space is compact if every open cover has a finite subcover»).[16]
Distinction from «if» and «only if»[edit]
- «Madison will eat the fruit if it is an apple.» (equivalent to «Only if Madison will eat the fruit, can it be an apple» or «Madison will eat the fruit ← the fruit is an apple»)
- This states that Madison will eat fruits that are apples. It does not, however, exclude the possibility that Madison might also eat bananas or other types of fruit. All that is known for certain is that she will eat any and all apples that she happens upon. That the fruit is an apple is a sufficient condition for Madison to eat the fruit.
- «Madison will eat the fruit only if it is an apple.» (equivalent to «If Madison will eat the fruit, then it is an apple» or «Madison will eat the fruit → the fruit is an apple»)
- This states that the only fruit Madison will eat is an apple. It does not, however, exclude the possibility that Madison will refuse an apple if it is made available, in contrast with (1), which requires Madison to eat any available apple. In this case, that a given fruit is an apple is a necessary condition for Madison to be eating it. It is not a sufficient condition since Madison might not eat all the apples she is given.
- «Madison will eat the fruit if and only if it is an apple.» (equivalent to «Madison will eat the fruit ↔ the fruit is an apple»)
- This statement makes it clear that Madison will eat all and only those fruits that are apples. She will not leave any apple uneaten, and she will not eat any other type of fruit. That a given fruit is an apple is both a necessary and a sufficient condition for Madison to eat the fruit.
Sufficiency is the converse of necessity. That is to say, given P→Q (i.e. if P then Q), P would be a sufficient condition for Q, and Q would be a necessary condition for P. Also, given P→Q, it is true that ¬Q→¬P (where ¬ is the negation operator, i.e. «not»). This means that the relationship between P and Q, established by P→Q, can be expressed in the following, all equivalent, ways:
- P is sufficient for Q
- Q is necessary for P
- ¬Q is sufficient for ¬P
- ¬P is necessary for ¬Q
As an example, take the first example above, which states P→Q, where P is «the fruit in question is an apple» and Q is «Madison will eat the fruit in question». The following are four equivalent ways of expressing this very relationship:
- If the fruit in question is an apple, then Madison will eat it.
- Only if Madison will eat the fruit in question, is it an apple.
- If Madison will not eat the fruit in question, then it is not an apple.
- Only if the fruit in question is not an apple, will Madison not eat it.
Here, the second example can be restated in the form of if…then as «If Madison will eat the fruit in question, then it is an apple»; taking this in conjunction with the first example, we find that the third example can be stated as «If the fruit in question is an apple, then Madison will eat it; and if Madison will eat the fruit, then it is an apple».
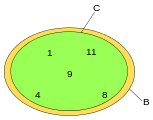
In terms of Euler diagrams[edit]
-
A is a proper subset of B. A number is in A only if it is in B; a number is in B if it is in A.
-
C is a subset but not a proper subset of B. A number is in B if and only if it is in C, and a number is in C if and only if it is in B.
Euler diagrams show logical relationships among events, properties, and so forth. «P only if Q», «if P then Q», and «P→Q» all mean that P is a subset, either proper or improper, of Q. «P if Q», «if Q then P», and Q→P all mean that Q is a proper or improper subset of P. «P if and only if Q» and «Q if and only if P» both mean that the sets P and Q are identical to each other.
More general usage[edit]
Iff is used outside the field of logic as well. Wherever logic is applied, especially in mathematical discussions, it has the same meaning as above: it is an abbreviation for if and only if, indicating that one statement is both necessary and sufficient for the other. This is an example of mathematical jargon (although, as noted above, if is more often used than iff in statements of definition).
The elements of X are all and only the elements of Y means: «For any z in the domain of discourse, z is in X if and only if z is in Y.»
See also[edit]
- Equivalence relation
- Logical biconditional
- Logical equality
- Logical equivalence
- Polysyllogism
References[edit]
- ^ Copi, I. M.; Cohen, C.; Flage, D. E. (2006). Essentials of Logic (Second ed.). Upper Saddle River, NJ: Pearson Education. p. 197. ISBN 978-0-13-238034-8.
- ^ Weisstein, Eric W. «Iff.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/Iff.html
- ^ E.g. Daepp, Ulrich; Gorkin, Pamela (2011), Reading, Writing, and Proving: A Closer Look at Mathematics, Undergraduate Texts in Mathematics, Springer, p. 52, ISBN 9781441994790,
While it can be a real time-saver, we don’t recommend it in formal writing.
- ^ Rothwell, Edward J.; Cloud, Michael J. (2014), Engineering Writing by Design: Creating Formal Documents of Lasting Value, CRC Press, p. 98, ISBN 9781482234312,
It is common in mathematical writing
- ^ a b Peil, Timothy. «Conditionals and Biconditionals». web.mnstate.edu. Archived from the original on 24 October 2020. Retrieved 4 September 2020.
- ^ p <=> q. Wolfram|Alpha
- ^ If and only if, UHM Department of Mathematics,
Theorems which have the form «P if and only Q» are much prized in mathematics. They give what are called «necessary and sufficient» conditions, and give completely equivalent and hopefully interesting new ways to say exactly the same thing.
- ^ «XOR/XNOR/Odd Parity/Even Parity Gate». www.cburch.com. Retrieved 22 October 2019.
- ^ Weisstein, Eric W. «Equivalent». mathworld.wolfram.com. Retrieved 4 September 2020.
- ^ «Jan Łukasiewicz > Łukasiewicz’s Parenthesis-Free or Polish Notation (Stanford Encyclopedia of Philosophy)». plato.stanford.edu. Retrieved 22 October 2019.
- ^ «LaTeX:Symbol». Art of Problem Solving. Retrieved 22 October 2019.
- ^ General Topology, reissue ISBN 978-0-387-90125-1
- ^ Nicholas J. Higham (1998). Handbook of writing for the mathematical sciences (2nd ed.). SIAM. p. 24. ISBN 978-0-89871-420-3.
- ^ Maurer, Stephen B.; Ralston, Anthony (2005). Discrete Algorithmic Mathematics (3rd ed.). Boca Raton, Fla.: CRC Press. p. 60. ISBN 1568811667.
- ^ For instance, from General Topology, p. 25: «A set is countable iff it is finite or countably infinite.» [boldface in original]
- ^ Krantz, Steven G. (1996), A Primer of Mathematical Writing, American Mathematical Society, p. 71, ISBN 978-0-8218-0635-7
External links[edit]
- «Tables of truth for if and only if». Archived from the original on 5 May 2000.
- Language Log: «Just in Case»
- Southern California Philosophy for philosophy graduate students: «Just in Case»
$begingroup$
In some books the word «if» is used in definitions and it is not clear if they actually mean «iff» (i.e «if and only if»).
I’d like to know if in mathematical literature in general «if» in definitions means «iff».
For example I am reading «Essential topology» and the following definition is written:
In a topological space $T$, a collection $B$ of open subsets of $T$ is said
to form a basis for the topology on $T$ if every open subset of $T$ can be written as a union of sets in $B$.
Should I assume the converse in such a case?
Should I assume that given a basis $B$ for a topological space, every open set can be written as a union of sets in $B$?
This is just an example, I am not asking specifically about this sentence.
asked Nov 14, 2013 at 9:12
$endgroup$
10
$begingroup$
As it is a definition, the validity of the property (here «being a basis for the topology») must be defined by it in all cases. So implicitly all cases not mentioned do not have the property.
This convention is even stronger than the «if» meaning «iff» in definitions. Take as example the definition «an integer $p>1$ is called a prime number if it cannot be written as a product $p=ab$ of integers $a,b>1$». This says that $6$ is not a prime number, since $6=2times 3$; this is an instance of the «iff» meaning in definitions. But it also says implicitly that $1$ is not a prime number, nor $-5$ nor $pi$ nor $exp(pimathbf i/3)$ nor $mathbf{GL}(3,Bbb R)$, as none of these can be described as integers $p>1$; even a statement with «iff» would in itself not seem to state non-primality of those objects. But since it is a definition, anything that does not match its description is implicitly excluded from the property.
Without this implicit exclusion of cases not mentioned, it would be very hard indeed to give a complete definition of any property. Imagine (assuming the «everything is a set» philosophy) the ugliness of «a set $x$ is called a prime number if $xinBbb Z$ and $x>1$ and …».
answered Nov 14, 2013 at 10:00
Marc van LeeuwenMarc van Leeuwen
111k8 gold badges159 silver badges325 bronze badges
$endgroup$
20
$begingroup$
As other pointed out, the «only if» part wouldn’t make any sense as the process of defining the object is not over yet at the time you read the «only if».
But if it bothers you, you can always reformulate
An object $A$ is said to be new term if $P(A)$.
by
A new term is an object $A$ such that $P(A)$.
In your example, the reformulation would be :
A basis $mathcal B$ of a topological space $T$ is a collection of open sets of $T$ such that every open set of $T$ is a union of elements of $mathcal B$.
answered Nov 14, 2013 at 10:11
PecePece
11.3k1 gold badge18 silver badges49 bronze badges
$endgroup$
5
$begingroup$
The deeper point here is that regardless whether we write «if» or «if and only if» in a definition, this is not the same as the usual meaning of «if and only if» as a material equivalence. The material equivalence of two propositions is the assertion that each one independently has a truth value, and the truth values are the same.
In a definition such as
a natural number $n$ is even if and only if $n$ is a multiple of $2$
we cannot read the «if and only if» as a material equivalence, because the left hand side does not have any truth value until after the definition is made. To view this definition as expressing an equivalence of two statements, we would need to already know that each side of the equivalence statement already has a truth value, but «$n$ is even» is (trivially) undefined before the definition is made.
Instead of expressing an equivalence, a definition tells us that the defined term is to be viewed as a synonym for the definition: a definition expresses an «is» relationship, not an «is equivalent to» relationship. For example, if I prove that $8$ is even, I do not need to apply modus ponens and the definition of an even number to conclude that $8$ is a multiple of $2$. Instead, I can directly «apply the definition»: proving that «$8$ is even» already proves that «$8$ is a multiple of $2$», because the quoted phrases are synonyms for each other. One could also say that «$8$ is even» is an abbreviation of «$8$ is a multiple of $2$». In turn, that latter phrase is an abbreviation for «there is a natural number $m$ with $8=2m$».
In principle, one can remove all later definitions from an axiomatic theory, so that in the end one is left with synonymous statements that involve only the «undefined terms» of the theory.
For example, in Hilbert’s axiomatic Euclidean plane geometry, there are only three undefined types of objects: point, lines, and planes. Every other statement, such as «the three angles in an equilateral triangle are all congruent», is in fact an abbreviation for a much longer statement about lines and points. This is not to say that the statement is equivalent to the longer statement about lines and points. The statement about angles has no truth value at all in this axiomatic framework except by virtue of its definition.
answered Nov 15, 2013 at 13:17
Carl MummertCarl Mummert
79.7k10 gold badges162 silver badges301 bronze badges
$endgroup$
6
$begingroup$
Yes. This is an unfortunate convention but is firmly established.
answered Nov 14, 2013 at 9:49
hunterhunter
27.5k3 gold badges39 silver badges65 bronze badges
$endgroup$
9
$begingroup$
My usual interpretation of this is that the «only if» is implicit. As an example, take the sentence «We call a gadget $A$ a widget if property $P$ holds for $A$», where the sentence is defining the word «widget». Because you just «invented» the word widget, it can only possibly apply to gadgets satisfying property $P$; any gadget that doesn’t satisfy this property (or anything that isn’t a gadget) cannot be a widget, because you didn’t say it was.
So while the statement only gave the «if» statement, the fact that this statement is a definition implies the «only if» statement. (I’m not really claiming to have given a proof of anything, but merely some justification of why the convention is not as crazy or unfortunate as it might appear).
answered Nov 14, 2013 at 9:54
mdpmdp
14.2k1 gold badge35 silver badges61 bronze badges
$endgroup$
9
$begingroup$
Usually, in definitions you will not read iff, since the inverse inclusion makes no sense, for a definition establishes no relationship between two mathematical objects, but instead provides a name to one of both.
answered Nov 14, 2013 at 16:02
NicoNico
2151 silver badge6 bronze badges
$endgroup$
$begingroup$
I would say that the use of ‘if’ in such a sentence should be considered a non-mathematical use of ‘if’ as opposed to a mathematical if. This is because statements of the form ‘x is called y’ are meta-mathematical rather than mathematical.
A strict reading of ‘if’ in its logical meaning often does not make sense.
A function is called ‘continuous’ if it satisfies …
Many functions which satisfy the property in question are never and have never been called ‘continuous’ (because no-one has ever had cause to study, name or classify them). ‘Only if’ would actually be more appropriate here.
answered Nov 14, 2013 at 15:02
jwgjwg
2,73620 silver badges28 bronze badges
$endgroup$
$begingroup$
See Tarski’s contribution in his Introduction to Logic and to the Methodology of Deductive Sciences, pt 1 «Elements of Logic. Deductive Method.», §II. «On the Sentential Calculus»:
10. Equivalence of sentences
We shall consider one more expression from the field of sentential
calculus. It is one which is comparatively rarely met in everyday
language, namely, the phrase “if, and only if”. If any two
sentences are joined up by this phrase, the result is a compound
sentence called an EQUIVALENCE. The two sentences connected in this
way are referred to as the LEFT and RIGHT SIDE OF THE EQUIVALENCE. By
asserting the equivalence of two sentences, it is intended to exclude
the possibility that one is true and the other false; an equivalence,
therefore, is true if its left and right sides are either both true or
both false, and otherwise the equivalence is false.The sense of an equivalence can also be characterized in still another
way. If, in a conditional sentence, we interchange antecedent and
consequent, we obtain a new sentence which, in its relation to the
original sentence, is called the CONVERSE SENTENCE (or the CONVERSE OF
THE GIVEN SENTENCE). Let us take, for instance, as the original
sentence the implication:(I) if $x$ is a positive number, then $2x$ is a positive number;
the converse of this sentence will then be:
(II) if $2x$ is a positive number, then $x$ is a positive number.
As is shown by this example, it occurs that the converse of a true
sentence is true. In order to see, on the other hand, that this is not
a general rule, it is sufficient to replace “$2x$” by “$x^2$” in
(I) and (II); the sentence (I)
will remain true, while the sentence (II) becomes false.
If, now, it happens that two conditional sentences, of which one is
the converse of the other, are both true, then the fact of their
simultaneous truth can also be expressed by joining the antecedent and
consequent of any one of the two sentences by the words “if, and
only if”. Thus, the above two implications—the original sentence
(I) and the converse sentence (II)—may be
replaced by a single sentence:$x$ is a positive number if, and only if, $2x$ is a positive number
(in which the two sides of the equivalence may yet be interchanged).
There are, incidentally, still a few more possible formulations which
may serve to express the same idea, e.g.:from: $x$ is a positive number, it follows: $2x$ is a positive number, and conversely;
the conditions that $x$ is a positive number and that $2x$ is a positive number are equivalent with each other;
the condition that $x$ is a positive number is both necessary and sufficient for $2x$ to be a positive number;
for $x$ to be a positive number it is necessary and sufficient that $2x$ be a positive number.
Instead of joining two sentences by the phrase “if, and only if”,
it is therefore, in general, also possible to say that the RELATION OF
CONSEQUENCE holds between these two sentences IN BOTH DIRECTIONS, or
that the two sentences are EQUIVALENT, or, finally, that each of the
two sentences represents a NECESSARY AND SUFFICIENT CONDITION for the
other.
For me Tarski’s authority is beyond discussion.
answered Nov 15, 2013 at 11:57
Tony PiccoloTony Piccolo
4,3462 gold badges13 silver badges24 bronze badges
$endgroup$
5
$begingroup$
I want to add some comments on this topic and in particular regarding Tarski’s reference [see Tony Piccolo’s answer and Carl Mummert’s comments].
Ref to George Tourlakis, Lectures in Logic and Set Theory : Volume 1, Mathematical Logic (2003), I.7. Defined Symbols [page 112-on] :
There are three possible kinds of formal abbreviations, namely, abbreviations of formulas, abbreviations of variable terms (i.e., “objects” that depend on free variables), and abbreviations of constant terms (i.e., “objects” that do not depend on free variables). Correspondingly, we introduce a new nonlogical symbol for a predicate, a function, or a constant in order to accomplish such abbreviations.
I will consider only the predicate case, in order to cope with Tarski’s example, i.e. :
$x le y =_{def} lnot (x > y)$.
We have that :
if $Q(overrightarrow{x}_n)$ is some formula, we then can introduce a new predicate symbol “$P$” that stands for $Q$.
Note. In the present description, $Q$ is a syntactic (meta-)variable, while $P$ is a new
formal predicate symbol.This entails adding $P$ to [the language] $mathcal L$ (i.e., to its alphabet $mathcal V_k$) as a new $n$-ary predicate symbol [obtaining a new language $mathcal L_1$], and adding
$Poverrightarrow{x}_n leftrightarrow Q(overrightarrow{x}_n) quad quad$ (i)
to [the theory] $Gamma$ as the defining axiom for $P$ [obtaining a new theory $Gamma_1$].
Suppose that $mathcal F$ is a formula over $mathcal L_1$, and that the predicate $P$ whose definition took us from $mathcal L$ to $mathcal L_1$, and hence is a symbol of $mathcal L_1$ but not of $mathcal L$) occurs in $mathcal F$ zero or more times. Assume that $P$ has been defined by the axiom (i) above (included in $Gamma_1$), where $Q$ is a formula over $mathcal L$.
We eliminate $P$ from $mathcal F$ by replacing all its occurrences by $Q$. […] This results to a formula $mathcal F^*$ over $mathcal L$.
Now we have two basic (meta)-theorems :
I.7.1 Metatheorem (Elimination of Defined Symbols: I). Let $Gamma$ be any theory
over some formal language $mathcal L$ [page 116] .(a) Let the formula $Q$ be over $mathcal L$, and $P$ be a new predicate symbol that extends $mathcal L$ into $mathcal L’$ and $Gamma$ into $Gamma’$ via the axiom $Poverrightarrow{x}_n leftrightarrow Q(overrightarrow{x}_n)$. Then, for any formula $mathcal F$ over $mathcal L$, the elimination [of $P$] as above yields a $mathcal F^*$ over $mathcal L$ such that :
$Gamma vdash mathcal F leftrightarrow mathcal F^*$.
(b) [consider the case of a $n$-ary ($n ge 0$) function symbol “$f$”, where the case $n=0$ applies to constants].
And :
I.7.3 Metatheorem (Elimination of Defined Symbols: II). Let $Gamma$ be a theory
over a language $mathcal L$ [page 118] .(a) If $mathcal L’$ denotes the extension of $mathcal L$ by the new predicate symbol $P$, and $Gamma’$ denotes the extension of $Gamma$ by the addition of the axiom $Poverrightarrow{x}_n leftrightarrow Q(overrightarrow{x}_n)$, where $Q$ is a formula over $mathcal L$, then $Gamma vdash mathcal F$ for any formula $mathcal F$ over $mathcal L$ such that $Gamma ‘ vdash mathcal F$.
(b) [consider the case of a $n$-ary ($n ge 0$) function symbol “$f$”, where the case $n=0$ applies to constants].
According to this formal treatment of definition, it is the «defining axiom» :
$x le y leftrightarrow lnot (x > y)$
that licenses the use of $le$ in the «extended» theory.
answered Apr 9, 2014 at 16:35
Mauro ALLEGRANZAMauro ALLEGRANZA
91.3k7 gold badges63 silver badges140 bronze badges
$endgroup$
1
$begingroup$
In a definition, when we say that X is called by the name Y, if it satisfies certain properties, we usually mean that entities in the same universe of discourse and of the same kind as X are not called by the name Y if they do not satisfy those properties.
The predicate is_called(X, "Y") is not a proposition in the domain of discourse; it is in the layer of symbols that are being used to discuss the domain, the «meta-domain», if you will.
Something in the actual domain cannot be put in a logical relationship with
something in the meta-domain; that is a level violation.
It is never sensible to say:
If a number is divisible by four, it is called «even».
because a definition is expected to be complete, and some numbers that are not divisible by four are also even. If we drop the «called», it’s something completely different:
If a number is divisible by four, it is even.
Now the symbol «even» is not being quoted for the purposes of being defined; it is evaluated and replaced by the properties that it denotes, and so we have a logical relationship being expressed purely in the domain of discourse.
So, in a way, the «if» in a definition is related to «if and only if»: clearly, a number is not called even if it is not divisible by two, therefore a number is called even if, and only if it is divisible by two. However, it is redundant and verbose. Moreover, definitions which use «if» can always be rewritten into ones which do not use if at all:
Integers divisible by two are called «even».
We can, and should, use «if and only if», whenever we give a definition in such a way that we are not quoting the name. Suppose I have never defined what it means to be «even». It is appropriate to say:
-
Integers can have certain property: they can be called even under certain conditions.
-
An integer is even if and only if it is divisible by two.
Here, the iff is necessary, because the second statement isn’t asserting itself as a definition of the term. I didn’t use the word «called» or similar.
One or more such statements can constitute an implicit definition of the term, when they specify enough rules that every integer can be classified as even or not even.
The use of iff in the second statement above informs the reader, «I am the only rule you need to deduce what set of properties are denoted by the term ‘even'».
answered Nov 15, 2013 at 20:11
KazKaz
6,7911 gold badge18 silver badges31 bronze badges
$endgroup$
$begingroup$
In a definition, the meaning of a new phrase or word is described with the help of known terms. After the definition, «if» becomes «if and only if».
answered Nov 20, 2013 at 5:50
R K SinhaR K Sinha
7738 silver badges6 bronze badges
$endgroup$
$begingroup$
- Think about the definition: «All x are A if they are B».
This actually says that all B’s are A.
- Now, think about this: «All x are A if and only if they are B».
This says that all B’s are A and all A’s are B.
- Now, if you say «All x are A if they are B and they are C».
What is told here is if something is both B and C, then it is A.
- Last one, «All x are A if and only if they are B and they are C».
This means, if something is both B and C, they it is A, besides, if something is A, then it is both B and C.
Now what does it actually mean?
- $forall x, xin B implies xin A$
This is equivalent to: $B subset A$
- $forall x, xin B iff xin A$
This is equivalet to: $B = A$
- $forall x, (xin B land xin C) implies xin A$
This is equivalent to: $xin (Bcap C) implies xin A$
And thus, $(Bcap C) subset A$
- $forall x(ain B land xin C) iff xin A$
And finally what this says is : $(Bcap C) =A$
answered Nov 15, 2013 at 7:38
$endgroup$
$begingroup$
My answer to your question, in short, is: Strictly speaking, no, ‘if’ and ‘iff’ are not interchangeable, but nevertheless there is a very general tacit convention for using ‘if’ in definitions where ‘iff’ is meant.
The Tarski quote referred to by Tony Piccolo establishes (by authority) that using ‘if’ where ‘if, and only if’ is (or should be) meant, is a tacit convention.
The answer by hunter mentions that it is an ‘unfortunate convention’, but gives no justification for judging it unfortunate. I concur with hunter and in this answer give arguments that I feel justify his claim.
- A first argument is the fact that you asked this question (and others did as well: there are several duplicates). When the convention would be to use ‘iff’, you would not have asked the question.
- A second argument is the fact that, in case you stumble upon a text in which the convention is not followed, misinterpretation of that text is possible.
-
A third argument is that it limits expressiveness, or at least forces one to find alternate formulations to one that would seem the first to present itself.
This argument requires a bit more explanation: In other answers, it was stressed that the ‘if’ (or ‘iff’) linking definiendum and definiens should not be confused with material implication $Rightarrow$ (or equivalence $Leftrightarrow$), but give meaning on a higher level. We also have this distinction with other mathematical terms, ‘equality’ $=$, for example. When equality is used to define an object, many authors use some distinctive variant of $=$ to make this clear, e.g., $:=$ or $triangleq$; let me use the former. Once $a:=3$, i.e., I have defined $a$ to be $3$, I can state $a=3$, i.e., $a$ is equal to $3$.
Now, of course it is possible to introduce similar notation for $Rightarrow$ and $Leftrightarrow$ (and I have come across texts where this was done, but don’t ask me for a reference):
- Stating $xin X mathbin{:Rightarrow} x/2inmathbb{Z}$ means that you’ve defined (specified) that $X$ only contains even numbers (but not necessarily all of them).
- Stating $xin X mathbin{:Leftrightarrow} x/2inmathbb{Z}$ defines $X$ to be the set of even numbers.
- Stating $xin X mathbin{:Leftarrow} x/2inmathbb{Z}$ means that you’ve defined (specified) that $X$ contains at least all even numbers (and possibly other objects).
As in general, using much mathematical notation reduces the readability, so one would like to be able to express the above definition variants using natural language. Two natural pairs of correspondences that present themselves are ($:Leftrightarrow$, ‘iff’) and ($:Leftarrow$, ‘if’). As the convention conflates ‘if’ with ‘iff’, the latter pair cannot be used, and alternative, less natural formulations for it have to be found. This is what I meant when stating that the convention limits expressiveness.
One can argue that natural language involving ‘if’ in day-to-day usage is not strict enough for it to be safely used in a more formal mathematical context. This is a valid criticism, but it would also proscribe the usage of ‘if’ in definitions where ‘iff’ is meant (as per Tarski’s quote referred to above). The usage of ‘iff’ (or ‘if, and only if’), however, is not affected by this criticism: its verbosity makes it robust against misinterpretation.
answered Mar 4, 2014 at 21:44
$endgroup$
$begingroup$
There is a logical difference between saying:
- The sidewalk is wet if it rained.
- «it rained» ⇒ «the sidewalk is wet»
and
- The sidewalk is wet iff it rained.
- «the sidewalk is wet» ⇒ «it rained»
& - «it rained» ⇒ «the sidewalk is wet» (← converse)
- «the sidewalk is wet» ⇒ «it rained»
(«• ⇒ •» meaning «If •, then •.»)
(1) means that «it rained» being true is a sufficient but not necessarily the sole condition for «The sidewalk is wet» to be true; other conditions might make it true.
(2) means that «it rained» is the only way «The sidewalk is wet» can be true (necessary & sufficient condition).
So, are «iff» and «if» interchangeable? Not necessarily:
-
Given a true iff statement, replacing «iff» with «if» always results in another true statement.
(«iff» is stronger; it says more; it’s a shorthand for two conditional propositions; cf. (1) vs. (2) above.) -
Given a true if statement, replacing «if» with «iff» doesn’t necessarily result in another true statement.
The OED‘s definition of «iff» corroborates what I wrote above:
to introduce a condition that is necessary as well as sufficient, or a statement that is implied by and implies the preceding one.
answered Feb 6, 2018 at 3:14
GeremiaGeremia
2,38312 silver badges25 bronze badges
$endgroup$
$begingroup$
«if» and «iff (if and only if)» have the difference. This difference is about their imperativeness. The «iff» is more imperative than just «if».
The analogous can be found in «needed and sufficient condition». «if» is analogue to «sufficient condition», whereas «iff» is analogue to «needed and sufficient condition».
answered Nov 14, 2013 at 12:11
$endgroup$
4
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Assessment |
Biopsychology |
Comparative |
Cognitive |
Developmental |
Language |
Individual differences |
Personality |
Philosophy |
Social |
Methods |
Statistics |
Clinical |
Educational |
Industrial |
Professional items |
World psychology |
Philosophy Index:
Aesthetics ·
Epistemology ·
Ethics ·
Logic ·
Metaphysics ·
Consciousness ·
Philosophy of Language ·
Philosophy of Mind ·
Philosophy of Science ·
Social and Political philosophy ·
Philosophies ·
Philosophers ·
List of lists
↔
⇔
≡
Logical symbols
representing iff
In logic and related fields such as mathematics and philosophy, if and only if (shortened iff) is a biconditional logical connective between statements.
In that it is biconditional, the connective can be likened to the standard material conditional («only if», equal to «if … then») combined with its reverse («if»); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other, i.e., either both statements are true, or both are false. It is controversial whether the connective thus defined is properly rendered by the English «if and only if», with its pre-existing meaning. Of course, there is nothing to stop us stipulating that we may read this connective as «only if and if», although this may lead to confusion.
In writing, phrases commonly used, with debatable propriety, as alternatives to P «if and only if» Q include Q is necessary and sufficient for P, P is equivalent (or materially equivalent) to Q (compare material implication), P precisely if Q, P precisely (or exactly) when Q, P exactly in case Q, and P just in case Q. Many authors regard «iff» as unsuitable in formal writing; others use it freely.[citation needed]
In logic formulae, logical symbols are used instead of these phrases; see the discussion of notation.
Definition
The truth table of p ↔ q is as follows:[1]
| p | q |
p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Note that it is equivalent to that produced by the XNOR gate, and opposite to that produced by the XOR gate.
Usage
Notation
The corresponding logical symbols are «↔», «⇔» and «≡», and sometimes «iff». These are usually treated as equivalent. However, some texts of mathematical logic (particularly those on first-order logic, rather than propositional logic) make a distinction between these, in which the first, ↔, is used as a symbol in logic formulas, while ⇔ is used in reasoning about those logic formulas (e.g., in metalogic). In Łukasiewicz‘s notation, it is the prefix symbol ‘E’.
Another term for this logical connective is exclusive nor.
Proofs
In most logical systems, one proves a statement of the form «P iff Q» by proving «if P, then Q» and «if Q, then P». Proving this pair of statements sometimes leads to a more natural proof, since there are not obvious conditions in which one would infer a biconditional directly. An alternative is to prove the disjunction «(P and Q) or (not-P and not-Q)», which itself can be inferred directly from either of its disjuncts—that is, because «iff» is truth-functional, «P iff Q» follows if P and Q have both been shown true, or both false.
Origin of iff
Usage of the abbreviation «iff» first appeared in print in John L. Kelley‘s 1955 book General Topology.[2]
Its invention is often credited to Paul Halmos, who wrote «I invented ‘iff,’ for ‘if and only if’—but I could never believe I was really its first inventor.»[3]
Distinction from «if» and «only if»
- «If the fruit is an apple, then Madison will eat it.» or «Madison will eat the fruit if it is an apple.» (equivalent to «Only if Madison will eat the fruit, is it an apple;» or «Madison will eat the fruit ← fruit is an apple»)
- This states only that Madison will eat fruits that are apples. It does not, however, preclude the possibility that Madison might also have occasion to eat bananas. Maybe she will, maybe she will not—the sentence does not tell us. All we know for certain is that she will eat any and all apples that she happens upon. That the fruit is an apple is a sufficient condition for Madison to eat the fruit.
- «Only if the fruit is an apple, will Madison eat it.» or «Madison will eat the fruit only if it is an apple.» (equivalent to «If Madison will eat the fruit, then it is an apple» or «Madison will eat the fruit → fruit is an apple»)
- This states that the only fruit Madison will eat is an apple. It does not, however, preclude the possibility that Madison will refuse an apple if it is made available, in contrast with (1), which requires Madison to eat any available apple. In this case, that a given fruit is an apple is a necessary condition for Madison to be eating it. It is not a sufficient condition since Madison might not eat any and all apples she is given.
- «If and only if the fruit is an apple will Madison eat it» or «Madison will eat the fruit if and only if it is an apple» or «Madison will eat the fruit ↔ fruit is an apple.»
- This, however, makes it quite clear that Madison will eat all and only those fruits that are apples. She will not leave any such fruit uneaten, and she will not eat any other type of fruit. That a given fruit is an apple is both a necessary and a sufficient condition for Madison to eat the fruit.
Sufficiency is the inverse of necessity. That is to say, given P→Q (i.e. if P then Q), P would be a sufficient condition for Q, and Q would be a necessary condition for P. Also, given P→Q, it is true that ¬Q→¬P (where ¬ is the negation operator, i.e. «not»). This means that the relationship between P and Q, established by P→Q, can be expressed in the following, all equivalent, ways:
- P is sufficient for Q
- Q is necessary for P
- ¬Q is sufficient for ¬P
- ¬P is necessary for ¬Q
As an example, take (1), above, which states P→Q, where P is «the fruit in question is an apple» and Q is «Madison will eat the fruit in question». The following are four equivalent ways of expressing this very relationship:
- If the fruit in question is an apple, then Madison will eat it.
- Only if Madison will eat the fruit in question, is it an apple.
- If Madison will not eat the fruit in question, then it is not an apple.
- Only if the fruit in question is not an apple, will Madison not eat it.
So we see that (2), above, can be restated in the form of if…then as «If Madison will eat the fruit in question, then it is an apple»; taking this in conjunction with (1), we find that (3) can be stated as «If the fruit in question is an apple, then Madison will eat it; AND if Madison will eat the fruit, then it is an apple».
Advanced considerations
Philosophical interpretation
A sentence that is composed of two other sentences joined by «iff» is called a biconditional. «Iff» joins two sentences to form a new sentence. It should not be confused with logical equivalence which is a description of a relation between two sentences. The biconditional «A iff B» uses the sentences A and B, describing a relation between the states of affairs which A and B describe. By contrast «A is logically equivalent to B» mentions both sentences: it describes a logical relation between those two sentences, and not a factual relation between whatever matters they describe. See use–mention distinction for more on the difference between using a sentence and mentioning it.
The distinction is a very confusing one, and has led many a philosopher astray. Certainly it is the case that when A is logically equivalent to B, «A iff B» is true. But the converse does not hold. Reconsidering the sentence:
- If and only if the fruit is an apple will Madison eat it.
There is clearly no logical equivalence between the two halves of this particular biconditional. For more on the distinction, see W. V. Quine’s Mathematical Logic, Section 5.
One way of looking at «A if and only if B» is that it means «A if B» (B implies A) and «A only when B» (not B implies not A). «Not B implies not A» means A implies B, so then we get two way implication.
Definitions
In philosophy and logic, «iff» is used to indicate definitions, since definitions are supposed to be universally quantified biconditionals. In mathematics and elsewhere, however, the word «if» is normally used in definitions, rather than «iff». This is due to the observation that «if» in the English language has a definitional meaning, separate from its meaning as a propositional connective. This separate meaning can be explained by noting that a definition (for instance: A group is «abelian» if it satisfies the commutative law; or: A grape is a «raisin» if it is well dried) is not an equivalence to be proved, but a rule for interpreting the term defined.
Examples
Here are some examples of true statements that use «iff» — true biconditionals (the first is an example of a definition, so it should normally have been written with «if»):
- A person is a bachelor iff that person is a marriageable man who has never married.
- «Snow is white» in English is true iff «Schnee ist weiß» in German is true.
- For any p, q, and r: (p & q) & r iff p & (q & r). (Since this is written using variables and «&«, the statement would usually be written using «↔», or one of the other symbols used to write biconditionals, in place of «iff»).
- For any real numbers x and y, x=y+1 iff y=x−1.
- A subset containing n elements of an n-dimensional vector space is linearly independent iff it spans the vector space.
- The triangular number n(n+1)/2 is an even perfect number iff n = 2p-1 is a Mersenne prime, with p being a prime number. As of Feb 2013, only 48 such even perfect numbers and Mersenne primes have been discovered.
- y(x) is a solution to the differential equation y=f(x,y) if and only if, the curve associated with y(x) is an integral curve of the direction field associated with y=f(x,y).
Analogs
Other words are also sometimes emphasized in the same way by repeating the last letter; for example orr for «Or and only Or» (the exclusive disjunction).
The statement «(A iff B)» is equivalent to the statement «(not A or B) and (not B or A),» and is also equivalent to the statement «(not A and not B) or (A and B)».
It is also equivalent to: not[(A or B) and (not A or not B)],
or more simply:
- ¬ [ ( ¬A ∨ ¬B ) ∧ ( A ∨ B ) ]
which converts into
- [ ( ¬A ∧ ¬B) ∨ (A ∧ B) ]
and
- [ ( ¬A ∨ B) ∧ (A ∨ ¬B) ]
which were given in verbal interpretations above.
More general usage
Iff is used outside the field of logic, wherever logic is applied, especially in mathematical discussions. It has the same meaning as above: it is an abbreviation for if and only if, indicating that one statement is both necessary and sufficient for the other. This is an example of mathematical jargon. (However, as noted above, if, rather than iff, is more often used in statements of definition.)
The elements of X are all and only the elements of Y is used to mean: «for any z in the domain of discourse, z is in X if and only if z is in Y.»
See also
- Covariance
- Logical biconditional
- Logical equality
- Necessary and sufficient condition
- Polysyllogism
Notes
- ↑ p <=> q. Wolfram|Alpha
- ↑ General Topology, reissue ISBN 978-0-387-90125-1
- ↑ Nicholas J. Higham (1998). Handbook of writing for the mathematical sciences, 2nd, SIAM.
Part I: Propositional Logic
9.1 A historical example
The philosopher David Hume (1711-1776) is remembered for being a brilliant skeptical empiricist. A person is a skeptic about a topic if that person both has very strict standards for what constitutes knowledge about that topic and also believes we cannot meet those strict standards. Empiricism is the view that we primarily gain knowledge through experience, particular experiences of our senses. In his book, An Inquiry Concerning Human Understanding, Hume lays out his principles for knowledge, and then advises us to clean up our libraries:
When we run over libraries, persuaded of these principles, what havoc must we make? If we take in our hand any volume of divinity or school metaphysics, for instance, let us ask, Does it contain any abstract reasoning concerning quantity or number? No. Does it contain any experimental reasoning concerning matter of fact and existence? No. Commit it then to the flames, for it can contain nothing but sophistry and illusion.[11]
Hume felt that the only sources of knowledge were logical or mathematical reasoning (which he calls above “abstract reasoning concerning quantity or number”) or sense experience (“experimental reasoning concerning matter of fact and existence”). Hume is led to argue that any claims not based upon one or the other method is worthless.
We can reconstruct Hume’s argument in the following way. Suppose t is some topic about which we claim to have knowledge. Suppose that we did not get this knowledge from experience or logic. Written in English, we can reconstruct his argument in the following way:
We have knowledge about t if and only if our claims about t are learned from experimental reasoning or from logic or mathematics.
Our claims about t are not learned from experimental reasoning.
Our claims about t are not learned from logic or mathematics.
_____
We do not have knowledge about t.
What does that phrase “if and only if” mean? Philosophers think that it, and several synonymous phrases, are used often in reasoning. Leaving “if and only” unexplained for now, we can use the following translation key to write up the argument in a mix of our propositional logic and English.
P: We have knowledge about t.
Q: Our claims about t are learned from experimental reasoning.
R: Our claims about t are learned from logic or mathematics.
And so we have:
P if and only if (QvR)
¬Q
¬R
_____
¬P
Our task is to add to our logical language an equivalent to “if and only if”. Then we can evaluate this reformulation of Hume’s argument.
9.2 The biconditional
Before we introduce a symbol synonymous with “if and only if”, and then lay out its syntax and semantics, we should start with an observation. A phrase like “P if and only if Q” appears to be an abbreviated way of saying “P if Q and P only if Q”. Once we notice this, we do not have to try to discern the meaning of “if and only if” using our expert understanding of English. Instead, we can discern the meaning of “if and only if” using our already rigorous definitions of “if”, “and”, and “only if”. Specifically, “P if Q and P only if Q” will be translated “((Q→P)^(P→Q))”. (If this is unclear to you, go back and review section 2.2.) Now, let us make a truth table for this formula.
| P | Q | (Q → P) | (P → Q) | ((Q→P)^(P→Q)) |
| T | T | T | T | T |
| T | F | T | F | F |
| F | T | F | T | F |
| F | F | T | T | T |
We have settled the semantics for “if and only if”. We can now introduce a new symbol for this expression. It is traditional to use the double arrow, “↔”. We can now express the syntax and semantics of “↔”.
If Φ and Ψ are sentences, then
(Φ↔Ψ)
is a sentence. This kind of sentence is typically called a “biconditional”.
The semantics is given by the following truth table.
| Φ | Ψ | (Φ↔Ψ) |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
One pleasing result of our account of the biconditional is that it allows us to succinctly explain the syntactic notion of logical equivalence. We say that two sentences Φ and Ψ are “equivalent” or “logically equivalent” if (Φ↔Ψ) is a theorem.
9.3 Alternative phrases
In English, it appears that there are several phrases that usually have the same meaning as the biconditional. Each of the following sentences would be translated as (P↔Q).
P if and only if Q.
P just in case Q.
P is necessary and sufficient for Q.
P is equivalent to Q.
9.4 Reasoning with the biconditional
How can we reason using a biconditional? At first, it would seem to offer little guidance. If I know that (P↔Q), I know that P and Q have the same truth value, but from that sentence alone I do not know if they are both true or both false. Nonetheless, we can take advantage of the semantics for the biconditional to observe that if we also know the truth value of one of the sentences constituting the biconditional, then we can derive the truth value of the other sentence. This suggests a straightforward set of rules. These will actually be four rules, but we will group them together under a single name, “equivalence”:
and
and
and
What if we instead are trying to show a biconditional? Here we can return to the insight that the biconditional (Φ↔Ψ) is equivalent to ((Φ→Ψ)^(Ψ→Φ)). If we could prove both (Φ→Ψ) and (Ψ→Φ), we will know that (Φ↔Ψ) must be true.
We can call this rule “bicondition”. It has the following form:
(Φ→Ψ)
(Ψ→Φ)
_____
(Φ↔Ψ)
This means that often when we aim to prove a biconditional, we will undertake two conditional derivations to derive two conditionals, and then use the bicondition rule. That is, many proofs of biconditionals have the following form:
9.5 Returning to Hume
We can now see if we are able to prove Hume’s argument. Given now the new biconditional symbol, we can begin a direct proof with our three premises.
We have already observed that we think (QvR) is false because ¬Q and ¬R. So let’s prove ¬(QvR). This sentence cannot be proved directly, given the premises we have; and it cannot be proven with a conditional proof, since it is not a conditional. So let’s try an indirect proof. We believe that ¬(QvR) is true, so we’ll assume the denial of this and show a contradiction.
Hume’s argument, at least as we reconstructed it, is valid.
Is Hume’s argument sound? Whether it is sound depends upon the first premise above (since the second and third premises are abstractions about some topic t). Most specifically, it depends upon the claim that we have knowledge about something just in case we can show it with experiment or logic. Hume argues we should distrust—indeed, we should burn texts containing—claims that are not from experiment and observation, or from logic and math. But consider this claim: we have knowledge about a topic t if and only if our claims about t are learned from experiment or our claims about t are learned from logic or mathematics.
Did Hume discover this claim through experiments? Or did he discover it through logic? What fate would Hume’s book suffer, if we took his advice?
9.6 Some examples
It can be helpful to prove some theorems that make use of the biconditional, in order to illustrate how we can reason with the biconditional.
Here is a useful principle. If two sentences have the same truth value as a third sentence, then they have the same truth value as each other. We state this as (((P↔Q)^(R↔Q))→(P↔R)). To illustrate reasoning with the biconditional, let us prove this theorem.
This theorem is a conditional, so it will require a conditional derivation. The consequent of the conditional is a biconditional, so we will expect to need two conditional derivations, one to prove (P→R) and one to prove (R→P). The proof will look like this. Study it closely.
We have mentioned before the principles that we associate with the mathematician Augustus De Morgan (1806-1871), and which today are called “De Morgan’s Laws” or the “De Morgan Equivalences”. These are the recognition that ¬(PvQ) and (¬P^¬Q) are equivalent, and also that ¬(P^Q) and (¬Pv¬Q) are equivalent. We can now express these with the biconditional. The following are theorems of our logic:
(¬(PvQ)↔(¬P^¬Q))
(¬(P^Q)↔(¬Pv¬Q))
We will prove the second of these theorems. This is perhaps the most difficult proof we have seen; it requires nested indirect proofs, and a fair amount of cleverness in finding what the relevant contradiction will be.
9.7 Using theorems
Every sentence of our logic is, in semantic terms, one of three kinds. It is either a tautology, a contradictory sentence, or a contingent sentence. We have already defined “tautology” (a sentence that must be true) and “contradictory sentence” (a sentence that must be false). A contingent sentence is a sentence that is neither a tautology nor a contradictory sentence. Thus, a contingent sentence is a sentence that might be true, or might be false.
Here is an example of each kind of sentence:
(Pv¬P)
(P↔¬P)
P
The first is a tautology, the second is a contradictory sentence, and the third is contingent. We can see this with a truth table.
| P | ¬P | (Pv¬P) | (P↔¬P) | P |
| T | F | T | F | T |
| F | T | T | F | F |
Notice that the negation of a tautology is a contradiction, the negation of a contradiction is a tautology, and the negation of a contingent sentence is a contingent sentence.
¬(Pv¬P)
¬(P↔¬P)
¬P
| P | ¬P | (Pv¬P) | ¬(Pv¬P) | (P↔¬P) | ¬(P↔¬P) |
| T | F | T | F | F | T |
| F | T | T | F | F | T |
A moment’s reflection will reveal that it would be quite a disaster if either a contradictory sentence or a contingent sentence were a theorem of our propositional logic. Our logic was designed to produce only valid arguments. Arguments that have no premises, we observed, should have conclusions that must be true (again, this follows because a sentence that can be proved with no premises could be proved with any premises, and so it had better be true no matter what premises we use). If a theorem were contradictory, we would know that we could prove a falsehood. If a theorem were contingent, then sometimes we could prove a falsehood (that is, we could prove a sentence that is under some conditions false). And, given that we have adopted indirect derivation as a proof method, it follows that once we have a contradiction or a contradictory sentence in an argument, we can prove anything.
Theorems can be very useful to us in arguments. Suppose we know that neither Smith nor Jones will go to London, and we want to prove, therefore, that Jones will not go to London. If we allowed ourselves to use one of De Morgan’s theorems, we could make quick work of the argument. Assume the following key.
P: Smith will go to London.
Q: Jones will go to London.
And we have the following argument:
This proof was made very easy by our use of the theorem at line 2.
There are two things to note about this. First, we should allow ourselves to do this, because if we know that a sentence is a theorem, then we know that we could prove that theorem in a subproof. That is, we could replace line 2 above with a long subproof that proves (¬(P v Q)↔(¬P ^ ¬Q)), which we could then use. But if we are certain that (¬(P v Q)↔(¬P ^ ¬Q)) is a theorem, we should not need to do this proof again and again, each time that we want to make use of the theorem.
The second issue that we should recognize is more subtle. There are infinitely many sentences of the form of our theorem, and we should be able to use those also. For example, the following sentences would each have a proof identical to our proof of the theorem (¬(P v Q)↔(¬P ^ ¬Q)), except that the letters would be different:
(¬(R v S) ↔ (¬R ^ ¬S))
(¬(T v U) ↔ (¬T ^ ¬U))
(¬(V v W) ↔ (¬V ^ ¬W))
This is hopefully obvious. Take the proof of (¬(P v Q)↔(¬P ^ ¬Q)), and in that proof replace each instance of P with R and each instance of Q with S, and you would have a proof of (¬(R v S)↔(¬R ^ ¬S)).
But here is something that perhaps is less obvious. Each of the following can be thought of as similar to the theorem (¬(P v Q)↔(¬P ^ ¬Q)).
(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))
(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))
(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))
For example, if one took a proof of (¬(P v Q)↔(¬P ^ ¬Q)) and replaced each initial instance of P with (Q↔P) and each initial instance of Q with (¬R→¬Q), then one would have a proof of the theorem (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q))).
We could capture this insight in two ways. We could state theorems of our metalanguage and allow that these have instances. Thus, we could take (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) as a metalanguage theorem, in which we could replace each Φ with a sentence and each Ψ with a sentence and get a particular instance of a theorem. An alternative is to allow that from a theorem we can produce other theorems through substitution. For ease, we will take this second strategy.
Our rule will be this. Once we prove a theorem, we can cite it in a proof at any time. Our justification is that the claim is a theorem. We allow substitution of any atomic sentence in the theorem with any other sentence if and only if we replace each initial instance of that atomic sentence in the theorem with the same sentence.
Before we consider an example, it is beneficial to list some useful theorems. There are infinitely many theorems of our language, but these ten are often very helpful. A few we have proved. The others can be proved as an exercise.
T1 (P v ¬P)
T2 (¬(P→Q) ↔ (P^¬Q))
T3 (¬(P v Q) ↔ (¬P ^ ¬Q))
T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))
T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))
T6 (¬P → (P → Q))
T7 (P → (Q → P))
T8 ((P→(Q→R)) → ((P→Q) → (P→R)))
T9 ((¬P→¬Q) → ((¬P→Q) →P))
T10 ((P→Q) → (¬Q→¬P))
Some examples will make the advantage of using theorems clear. Consider a different argument, building on the one above. We know that neither is it the case that if Smith goes to London, he will go to Berlin, nor is it the case that if Jones goes to London he will go to Berlin. We want to prove that it is not the case that Jones will go to Berlin. We add the following to our key:
R: Smith will go to Berlin.
S: Jones will go to Berlin.
And we have the following argument:
Using theorems made this proof much shorter than it might otherwise be. Also, theorems often make a proof easier to follow, since we recognize the theorems as tautologies—as sentences that must be true.
9.8 Problems
- Prove each of the following arguments is valid.
- Premises: ((P^Q) ↔ R), (P ↔ S), (S ^ Q). Conclusion: R.
- Premises: (P ↔ Q). Conclusion: ((P → Q) ^ (Q → P)).
- Premises: P, ¬Q. Conclusion: ¬(P ↔ Q).
- Premises: (¬PvQ), (Pv¬Q). Conclusion: (P ↔ Q).
- Premises: (P ↔ Q), (R ↔ S). Conclusion: ((P^R) ↔ (Q^S)).
- Premises: ((PvQ) ↔ R), ¬(P ↔ Q). Conclusion: R.
- Conclusion: ((P ↔ Q) ↔ (¬P ↔ ¬Q)).
- Conclusion: ((P → Q) ↔ (¬P v Q)).
- Prove each of the following theorems.
- T2
- T3
- T5
- T6
- T7
- T8
- T9
- ((P^Q) ↔ ¬(¬Pv¬Q))
- ((P→ Q) ↔ ¬(P^¬Q))
- Here are some passages from literature, philosophical works, and important political texts. Hopefully you recognize some of them. Find the best translation into propositional logic. Because these are from diverse texts you will find it easiest to make a new key for each sentence.
- “Neither a borrower nor a lender be.” (Shakespeare, Hamlet.)
- “My copy-book was the board fence, brick wall, and pavement.” (Frederick Douglass, Narrative of the Life of Frederick Douglass.)
- “The bourgeoisie has torn away from the family its sentimental veil, and has reduced the family relation to a mere money relation.” (Marx and Engels, The Communist Manifesto.)
- “The Senate shall chuse their other Officers, and also a President pro tempore, in the Absence of the Vice President, or when he shall exercise the Office of President of the United States.” (The Constitution of the United States.)
- “Excessive bail shall not be required, nor excessive fines imposed, nor cruel and unusual punishments inflicted.” (The Constitution of the United States.)
- “Annual income twenty pounds, annual expenditure nineteen nineteen and six, result happiness. Annual income twenty pounds, annual expenditure twenty pounds ought and six, result misery.” (Charles Dickens, Great Expectations.)
- “Thou shalt get kings, though thou be none.” (Shakespeare, Macbeth.)
- “If a faction consists of less than a majority, relief is supplied by the republican principle, which enables the majority to defeat its sinister views by regular vote.” (Federalist Papers.)
- In normal colloquial English, write your own valid argument with at least two premises, at least one of which is a biconditional. Your argument should just be a paragraph (not an ordered list of sentences or anything else that looks like formal logic). Translate it into propositional logic and prove it is valid.
- In normal colloquial English, write your own valid argument with at least two premises, and with a conclusion that is a biconditional. Your argument should just be a paragraph (not an ordered list of sentences or anything else that looks formal like logic). Translate it into propositional logic and prove it is valid.
- Here is a passage from Aquinas’s reflections on the law, The Treatise on the Laws. Symbolize this argument and prove it is valid.
A law, properly speaking, regards first and foremost the order to the common good. Now if a law regards the order to the common good, then its making belongs either to the whole people, or to someone who is the viceregent of the whole people. And therefore the making of a law belongs either to the whole people or to the viceregent of the whole people.
[11] From Hume’s Enquiry Concerning Human Understanding, p.161 in Selby-Bigge and Nidditch (1995 [1777]).
Выражение может быть именем закладки, строкой текста, числом, вложенным полем, возвращающим значение, или математической формулой.
Как я понимаю, строка текста — это текст, который вводится в поле IF, а не текст из файла.
Коды полей: IF
{ IF Выражение1 Оператор Выражение2 Текст1 Текст2 }
В зависимости от результата сравнения двух выражений вставляет тот или иной текст. В основном документе слияния поле IF можно использовать для анализа записей данных, таких как почтовые индексы или номеров банковских счетов. Например, можно разослать письма только клиентам, проживающим в определенном городе.
Инструкции
Выражение1, Выражение2
Значения, которые требуется сравнить. Выражение может быть именем закладки, строкой текста, числом, вложенным полем, возвращающим значение, или математической формулой. Если выражение содержит пробелы, оно должно быть заключено в кавычки.Оператор
Оператор сравнения. Пробелы перед оператором и после него являются обязательными.
Оператор Описание
= Равно
<> Не равно
> Больше
< Меньше
>= Больше или равно
<= Меньше или равноТекст1, Текст2
Текст, который вставляется в случае истинности (Текст1) или ложности (Текст2) логического выражения. Если Текст2 не указан, а логическое выражение ложно, не будет вставлено никакого текста. Каждая строка, содержащая несколько слов, должна быть заключена в кавычки.Примечание. Если используется оператор = или <>, то Выражение2 может содержать вопросительный знак (?), заменяющий любой отдельный знак, или звездочку (*), заменяющую любую строку символов. Такое выражение должно быть заключено в кавычки. Если Выражение2 содержит звездочку, то сумма длин фрагмента Выражения1, соответствующего этой звездочке, и остальных знаков значения Выражения2 не должна превышать 128 знаков.
Примеры
В приведенном ниже примере указано, что если заказ клиента равен или больше 100 единиц продукции, то будет выведено слово «Спасибо», а если клиент заказывает менее 100 единиц продукции, то будет выведено уведомление «Минимальный заказ равен 100 единиц».
{IF заказ>=100 «Спасибо» «Минимальный заказ равен 100 единиц»}Примеры полей IF
Поле IF выполняет одну из двух операций в зависимости от указанных условий. Например, утверждение «Если погода будет хорошей, мы прогуляемся по парку, а если нет — пойдем в кино» определяет условие, (хорошая погода), при котором произойдет определенное событие (прогулка по парку). Если это условие не соблюдено, происходит альтернативное событие (поход в кино).
Приведенное ниже поле IF представляет собой утверждение того же типа. Если текущая запись данных содержит значение «Саратов» в поле «Город», в документ, полученный в результате слияния с этой записью данных, будет включен текст, содержащийся в первых кавычках. В противном случае будет добавлен второй текст. Следующий пример использует поля IF и MERGEFIELD.
{ IF { MERGEFIELD Город } = «Саратов» «Пожалуйста, позвоните в местное отделение нашей фирмы.» «Пожалуйста, отправьте заполненный формуляр в приложенном конверте.» }
Чтобы вставить поле IF в документ, на панели инструментов Слияние нажмите кнопку Добавить поле Word, а затем выберите поле IF…THEN…ELSE.
Ниже приведены некоторые примеры способов изменения кодов поля IF.Сравнение поля данных с другим полем или закладкой
В приведенном ниже примере выполняется сравнение значения поля данных «Ставка» со значением поля данных «Скидка». Если числа равны, печатается указанный текст.
{ IF { MERGEFIELD Ставка } = { MERGEFIELD Скидка } «Мы предложим вам еще большую скидку. » » » }
(Если число в поле данных «Ставка» не равно числу в поле данных «Скидка», текст не печатается.)Вставка других полей Word в поле IF
Пример 1
В случае выполнения условия, указанного в приведенном ниже поле IF, в документ вставляется содержимое файла, указанного в поле INCLUDETEXT. При задании местоположения и имени включаемого документа следует использовать двойные обратные косые черты (), как показано в примере. Если условие не будет выполнено, будет вставлен элемент списка автотекста «Авторское право».
{ IF { MERGEFIELD Штат } = » Нью-Йорк » «{ INCLUDETEXT c:\worddocs\contract.doc }» «{ AUTOTEXT Авторское право }» }Пример 2
Если поле «Компания» в записи данных содержит какую-либо информацию — т. е. не является пустым, — печатается текст из поля «АдресКомпании». В противном случае печатается текст из поля «ДомашнийАдрес».
{ IF { MERGEFIELD Компания } <> » » «{ MERGEFIELD АдресКомпании }» «{ MERGEFIELD ДомашнийАдрес }» }Выполнение вычислений в поле IF
В приведенном ниже примере первое поле = (Формула) вычисляет текущее сальдо для каждого счета. Если сальдо положительно, печатается значение второго поля = (Формула). Если вычисленное сальдо равно 0 (нулю) или отрицательно, печатается альтернативный текст «Ваш счет пуст. Спасибо.».
{ IF { = { MERGEFIELD Сальдо } — {MERGEFIELD Платеж } } > 0 «Текущее сальдо { = { MERGEFIELD Сальдо } — { MERGEFIELD Платеж } # «#,##0.00р.; » }.» «Ваш счет пуст. Спасибо» }Задание нескольких условий
Чтобы задать несколько условий в поле IF, в него следует включить поле COMPARE или другие поля IF.Пример 1
В приведенном ниже примере при слиянии каждой записи данных поле COMPARE сравнивает поля данных «НомерКлиента» и «РангКлиента». Функция AND в поле = (Формула) возвращает значение «1» (истина), если значения обоих полей указывают на удовлетворительное состояние счета. В этом случае печатается текст из первых кавычек.
{ IF { = AND ( { COMPARE { MERGEFIELD НомерКлиента } >= 4 }, { COMPARE { MERGEFIELD РангКлиента } <= 3 } ) } = 1 » Удовлетворительно » » Неудовлетворительно «}Пример 2
В приведенном ниже примере жителям Калифорнии и Вашингтона предоставляются особые скидки. Если в поле «Штат» указан другой штат, никакой текст не печатается, поскольку во втором поле IF не указан альтернативный текст.
{IF {MERGEFIELD Штат } = » Калифорния » » Для жителей Калифорнии предлагаются особые скидки на посещение Азии и Японии.» «{IF {MERGEFIELD Штат } = «Вашингтон» «Для жителей Вашингтона предлагаются особые скидки на посещение Азии и Японии.» » «} «}
Удобной и приятной работы в Word!
Перевести спасибо на Яндекс кошелёк — 41001162202962; на WebMoney — R581830807057.


![Rendered by QuickLaTeX.com [ fitchctx{ subproof{pline{phi}}{ ellipsesline\ pline{psi} } fpline{(phi lif psi)}\ subproof{pline{psi}}{ ellipsesline\ pline{phi} } fpline{(psi lif phi)}\ pline{(phi liff psi)} } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-2ff44b82fd1de4fdf6de7986bd62b690_l3.png)
![Rendered by QuickLaTeX.com [ fitchprf{pline[1.] {(P liff (Q lor R))} [premise]\ pline[2.]{lnot Q} [premise]\ pline[3.]{lnot R} [premise]\ } { } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-5de24737ff424b5cef0d9b4592f81177_l3.png)
![Rendered by QuickLaTeX.com [ fitchprf{pline[1.] {(P liff (Q lor R))} [premise]\ pline[2.]{lnot Q} [premise]\ pline[3.]{lnot R} [premise]\ } { subproof{pline[4.]{lnot lnot (Q lor R)}[assumption for indirect derivation]}{ pline[5.]{(Q lor R)}[double negation, 4]\ pline[6.]{R}[modus tollendo ponens, 5, 2]\ pline[7.]{lnot R}[repetition, 3] } pline[8.]{lnot (Q lor R)}[indirect proof, 4-7]\ pline[9.]{lnot P}[equivalence, 1, 8] } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-afa8e172e6e0a5b3e0e10ba480da456a_l3.png)
![Rendered by QuickLaTeX.com [ fitchprf{} { subproof{pline[1.]{((P liff Q) land (R liff Q))}[assumption for conditional derivation]}{ pline[2.]{(P liff Q)}[simplification, 1]\ pline[3.]{(R liff Q)}[simplification, 1]\ subproof{pline[4.]{P}[assumption for conditional derivation]}{ pline[5.]{Q}[equivalence, 2, 4]\ pline[6.]{R}[equivalence, 3, 5]\ } pline[7.]{(P lif R)}[conditional derivation, 4-6]\ subproof{pline[8.]{R}[assumption for conditional derivation]}{ pline[9.]{Q}[equivalence, 3, 8]\ pline[10.]{P}[equivalence, 2, 9]\ } pline[11.]{(R lif P)}[conditional derivation, 8-10]\ pline[12.]{(P liff R)}[bincondition, 7, 11]\ } pline[13.]{(((P liff Q) land (R liff Q)) lif (P liff R))}[conditional derivation 1-12]\ } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-85f65f4759edf54a63ebad5bd1144f9e_l3.png)
![Rendered by QuickLaTeX.com [ fitchprf{} { subproof{pline[1.]{lnot (P land Q)}[assumption for conditional derivation]}{ subproof{pline[2.]{lnot(lnot P lor lnot Q)}[assumption for indirect derivation]}{ subproof{pline[3.]{lnot P}[assumption for indirect derivation]}{ pline[4.]{(lnot P lor lnot Q)}[addition, 3]\ pline[5.]{lnot(lnot P lor lnot Q)}[repeat, 2]\ } pline[6.]{P}[indirect derivation, 3-5]\ subproof{pline[7.]{lnot Q}[assumption for indirect derivation]}{ pline[8.]{(lnot P lor lnot Q)}[addition, 7]\ pline[9.]{lnot(lnot P lor lnot Q)}[repeat, 2]\ } pline[10.]{Q}[indirect derivation, 6-9]\ pline[11.]{(P land Q)}[adjunction, 6, 10]\ pline[12.]{lnot (P land Q)}[repeat, 1]\ } pline[13.]{(lnot P lor lnot Q)}[indirect derivation, 2-12]\ } pline[14.]{(lnot (P land Q) lif (lnot P lor lnot Q))}[conditional derivation, 1-13]\ subproof{pline[15.]{(lnot P lor lnot Q)}[assumption for conditional derivation]}{ subproof{pline[16.]{lnot lnot (P land Q)}[assumption for indirect derivation]}{ pline[17.]{(P land Q)}[double negation 16]\ pline[18.]{P}[simplification, 17]\ pline[19.]{lnot lnot P}[double negation, 18]\ pline[20.]{lnot Q}[modus tollendo ponens, 15, 19]\ pline[21.]{Q}[simplification, 17]\ } pline[22.]{lnot (P land Q)}[indirect derivation 16-21]\ } pline[23.]{((lnot P lor lnot Q) lif lnot (P land Q))}[conditional derivation, 15-22]\ pline[24.]{(lnot (P land Q)liff (lnot P lor lnot Q) )}[bicondition,14, 23]\ } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-b956c0660fce60aa20a274357be16af7_l3.png)
![Rendered by QuickLaTeX.com [ fitchprf{pline[1.] {lnot (P lor Q)} [premise]\ }{ pline[2.]{(lnot (P lor Q) liff ( lnot P land lnot Q))}[theorem]\ pline[3.]{( lnot P land lnot Q)} [equivalence, 2, 1]\ pline[4.]{ lnot Q}[simplification, 3]\ } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-69afc45b765c65ae9dc5f341d2c33c34_l3.png)
![Rendered by QuickLaTeX.com [ fitchprf{pline[1.] {lnot ((P lif R) lor (Q lif S))} [premise]\ }{ pline[2.]{brokenform{(lnot ((P lif R) lor (Q lif S)) liff}{ formula{( lnot (P lif R) land lnot (Q lif S)))}}}[theorem T3]\ pline[3.]{( lnot (P lif R) land lnot (Q lif S))} [equivalence, 2, 1]\ pline[4.]{ lnot (Q lif S)}[simplification, 3]\ pline[5.]{( lnot (Q lif S) liff (Q land lnot S))} [theorem T2]\ pline[6.]{(Q land lnot S)}[equivalence, 5, 4]\ pline[7.]{lnot S}[simplification, 6] } ]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-c0140366d7466f6e3c20c506a6b03821_l3.png)