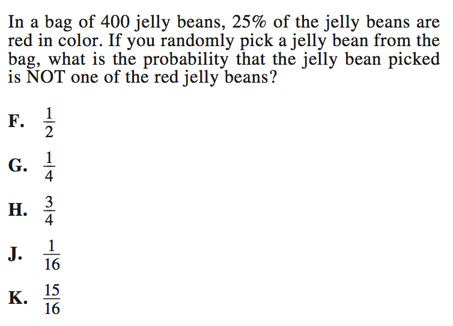Writing the phrase as an algebraic expression
Example
Write the phrase as an algebraic expression.
“Four less than twice ???x???”
The phrase “twice ???x???” means “???2??? times ???x???” which we know means to multiply, and so we can write it as ???2x???. Now we have
“Four less than ???2x???”
Less means subtraction, so we’ll subtract ???4??? from ???2x???.
???2x-4???
It may be tempting to write the ???4??? first and subtract ???2x???. Let’s use numbers to help us visualize this. When we say ???4??? less than ???10??? you know that you’d have to subtract ???4??? from ???10???, written out as ???10-4???. So ???4??? less than ???2x??? will be ???2x-4???.
Example
Find the value of the expression.
???frac{1}{4}??? of ???120???
In math, the word “of” (immediately after a proper or improper fraction) tells us to multiply. Therefore, the mathematical expression of the phrase will be
???frac{1}{4} cdot 120???
Because we were asked to actually find the value of the expression, we’ll perform the multiplication to get the simplified value.
???30???
Not only can we translate phrases into expressions, but we can write equations from some phrases as well.
For instance, suppose you wanted to use algebra to solve the following word problem:
John’s age is four less than twice Mary’s age. If Mary is ???18???, how old is John?
The first step in solving a word problem like this is to define the variables. What that means is to state the particular quantity that each variable stands for.
In this problem, we have two quantities: Mary’s age and John’s age. So we’ll define the variables by saying “Let ???x??? be Mary’s age, and let ???y??? be John’s age.” (We could use any letters of the alphabet for the variables, but people often use ???x??? for one of the variables, and if there are one or two additional variables, they tend to use ???y??? and ???z???, in that order.)
The next step in solving a word problem is to “translate” each word or phrase into mathematical symbols. Here, “John’s age” is translated as “???2x-4???.”
How about the word “is” (in “John’s age is four less than twice Mary’s age”)? Well, “is” is translated as an equals sign. To see this, it may help to think of the word “is” as having the same meaning (in math) as “is equal to.”
Combining all of these, we get the equation
???y=2x-4???
The third step in solving a word problem is to use the given data and solve the equation. Here, we’re given Mary’s age as ???18???, so we substitute ???18??? for ???x??? and then solve for ???y???.
???y=2(18)-4???
???y=36-4???
???y=32???
The final step is to answer the question that was asked. Here, we’re asked for John’s age. Since we defined ???y??? as John’s age, the answer is ???32???.
Suppose we’d been given the following word problem instead:
Currently, John’s age is four less than twice Mary’s age. If Mary is now ???18???, how old will John be seven years from now?
To solve this problem, it would be convenient to define ???x??? as Mary’s age now, and ???y??? as John’s age now, because we’re given a relationship between Mary’s age (now) and John’s age (now). Then in the last step (answering the question that was asked), we’d have to evaluate ???y+7??? (to get John’s age seven years from now), and our answer would be ???32+7=39???.
Get access to the complete Algebra 1 course
Teaching Students to Write Word Problems
I love word problems. There I said it, I really do. Anytime I can
squeeze in some extra practice for my kiddos, I do! I especially love
tasking my students with writing their own word problems. This
encourages them to think about word problems more critically than when
they simply read and solve a problem.
We recently started practicing this skill in my classroom. Typically, I start this much earlier in the school year, but we just weren’t ready to tackle this skill until recently. Some years are like that, right? Now that the skill has been introduced, we can practice it each week (and I’m pretty excited about that).
A Few Things You Need to Know
When I task my students with writing their own word problems there are two things you need to know.
1. I give them a starting point. Meaning, the activity isn’t totally open ended. I give them an answer, and it is their job to write a word problem to match.
2. I start out by keeping it simple because I want them to grasp the concept and feel successful with something new. I encourage the use of key words, and I encourage them to write straightforward problems without «extra» information. When the time is right, they will be encouraged to write tougher problems.
Procedures
So, to introduce the skill of writing word problems, I use this chart.
And, this mini book (or some variation of it….more on that in a moment).
Here’s a look at that chart again.
Keep in mind that these guidelines work for us because we write word problems based on a given answer.
Once we go over the chart, we write at least one word problem together, using the mini book from above and the chart to guide us. Then, I have the students work in pairs to write a second word problem. I check their stories as they finish. Finally, the students write one word problem independently. Again, I check it when they are finished writing because I like to help them make any necessary corrections/changes on the spot.
As we revisit the skill each week, the students will write one story at a time. Independently.
I keep it simple at first, encouraging them to use key words, and to stick to simple stories (two statements and a question) like the one shown below. Once they have these steps down, I will begin to
encourage them to add extra information to their problems.
I love using my What’s the Problem? mini books for practicing this skill (shown above, and below). I made an entire series of these mini books several years ago, and they are still a useful resource. Did I mention that they are a freebie? 
Frequency
As mentioned above, the first day that we practice this skill the students write three word problems. After that, they write just a few a week. We bring the book out as part of our math warm up, or at the end of our math lesson. They end up writing about two word problems a week. This gives them continued practice, but they also don’t get burned out as easily as they would if we did it every.single.day.
A Few Final Thoughts
It is always harder for students to write a word problem
than it is to solve one. And, they learn this pretty quickly. However,
they seem to enjoy the challenge of getting it right. As we say in my classroom, if you don’t challenge your brain, it won’t grow. So, bring on the challenge!
When you’re first starting out, you’ll notice that some
students «get it» very quickly, whereas others need repeated practice
with the skill before it begins to click. Some students will need more scaffolding than others, and some will need to be encouraged to write «tougher» problems. I’ve even changed some of the answers for students who needed to work with either bigger or smaller numbes. As always, do what’s best for your students and differentiate as needed.
Below are links to the What’s the Problem mini books that I’ve shared in the past. I hope you can use them. 
Have fun challenging your learners!
DON’T FORGET IT, PIN IT!
Share It:
Word problems are a great way for students to identify real world applications for the information they are learning in the classroom — while helping them develop critical thinking skills. To write a word problem, analyze the way you would solve it yourself, and decide on the best method for your students to use.
-
Introduce students to the concept of a word problem within the context of what they are learning. Doing a group example will help them better understand the material.
Identify the math skills you would like students to work on. For example, if you want students to focus on adding and using images to help solve problems, your focus will be on writing a paragraph that accomplishes that goal.
Choose a main character for your word problem. Pick the number of objects and type of object that he has. The best objects are easy visuals for children to identify and draw, if needed. For example, your first sentence can be «George has 6 red balloons.»
Choose a secondary character and identify the number of objects he possesses. For example, «Alexa has 7 purple balloons.»
Write a question at the end to the word problem. An example of end questions is the question, «What is the total number of balloons?» Use math vocabulary that is age-appropriate for the students.
Add further instructions to help students achieve the result you desire. For the sample problem, you would want to tell students to draw the balloons to help them solve it. Also, encourage students to write the number sentence that goes along with the problem.
Read through your word problem and try it. If you are not clear in your instructions or you decide that the problem is too complicated, revise it to suit your students.
Ask students to write their own word problems as an assignment to turn in. This will allow you to see if they grasp the concept. Use these student-created examples as practice problems in the future.
Tips
Related Pages
More Math Word Problems
Algebra Word Problems
How to write algebra word problems into systems of linear equations and solve systems of linear equations
using elimination and substitution methods?
Grade 8 Algebra Word Problems
How to solve algebra word problems using systems of linear equations?
Example:
Devon is going to make 3 shelves for her father. He has a piece of lumber 12 feet long.
She wants the top shelf to be half a foot shorter than the middle shelf, and the bottom
shelf to be half a foot shorter than twice the length of the top shelf. How long will
each shelf be if she uses the entire 12 feet of wood?
- Show Video Lesson
Grade 8 Algebra Word Problems — Line Segments
Example:
If JK = 7x + 9, JL = 114 and KL = 9x + 9. Find KL.
- Show Video Lesson
Grade 8 number word problems — common core
How to write word problems into systems of linear equations and solve systems of linear equations
using elimination and substitution methods?
Example 1:
The sum of two numbers is 361 and the difference between the two numbers is 173. What are the
two numbers?
Example 2:
There are 356 Grade 8 students at Euclid’s Middle School. Thirty-four more than four times the
number of girls is equal to half the number of boys. How many boys are in Grade 8 at Euclid’s
Middle School? How many girls?
Example 3:
A family member has some five-dollar bills and one-dollar bills in their wallet. Altogether
she has 18 bills and a total of $62. How many of each bill does she have?
Example 1:
A friend bought 2 boxes of pencils and 8 notebooks for school and it cost him $11. He went back
to the store the same day to buy school supplies for his younger brother. He spent $11.25 on 3
boxes of pencils and 5 notebooks. How much would notebooks cost?
Exercises:
- A farm raises cows and chickens. The farmer has a total of 42 animals. One day he counts the
legs of all of his animals and realizes he has a total of 114. How many cows does the farmer
have? How many chickens? - The length of a rectangle is 4 times the width. The perimeter of the rectangle is 45 inches.
What is the area of the rectangle? - The sum of the measures of angles x and y is 127″. If the measure of angle x is 34° more
than half the measure of angle y, what is the measure of each angle?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
If you really want your students to grow as a mathematician and have them succeed on standardized tests as an added bonus, incorporating more thought-provoking, relevant word problems can make a huge difference. By challenging them to read, write, think, and relate classroom lessons to their lives, you’ll both increase their ability and their investment in your classroom.
Before you can start, you have to know what not to do: don’t rely on questions from textbooks, released tests or state-issued material. You can use them if they fall into one of the categories below, but if you look at the examples you’ll see why they may not be as beneficial as you think.
Guidelines for Writing Better Word Problems
- Have them do something. Ask them to figure out something that would force them to get up and/or look around the room to find or get closer to an answer. This gets them involved and engaged immediately, because it’s not something they would be asked to do on a standardized test question.
- It’s all about them. As I’ve said many times, all teenagers have one thing in common: they want you to think about them. Sometimes this means demonstrating your keen awareness of them through the relevant questions you ask. This can take on many forms, but you can start with what their concerned about in their lives: school, cell phones, music, cars, movies, their boyfriend/girlfriend, other friends, etc.
- Spark a discussion. Don’t shy away from a challenging or controversial topic if it will get them thinking mathematically. That discussion might make your lesson one of the more memorable ones of the year, and that’s rarely a bad thing.
- Money, money, money. The easiest connection to make with most math topics is to money issues. Textbook and test makers rely on this as well, so its up to you to differentiate your questions from theirs by applying the other guidelines here.
- Connect math to the real world. Just keep in mind that their world and your world aren’t really the same thing, so think about things from their perspective (see #2). Make references to local people, places and things or situations they themselves or their family currently or will soon face.
Examples
Here are some examples that apply to some or all of the guidelines above, marked with the Algebra I topic they addressed.
Count the number of girls in this class right now. Then count the number of boys. Subtract the number of girls — the number of boys. Finally, subtract the number of boys — the number of girls. What’s the difference between the two answers? [adding and subtracting integers]
Juan makes $1200 a month working full time at Wal-Mart. If his bills are $400 for rent, $150 for electricity, $35 for water/garbage and $50 for his cell phone, how much does he have left for himself and his family? [solving one-step equations with adding and subtracting]
A new 19 inch TV costs about $200. At Rent-a-Center, you pay $12 a week for 78 weeks for the same TV. What’s the total cost at Rent-a-Center? [solving one-step equations with multiplication and division]
For every hour she works at Dollar General, Veronica makes 6 dollars. Make a table and a graph showing the hours she works and the money she makes (up to 8 hours). [creating and connecting tables and graphs of a relationship]
The cost of a Whataburger meal is $3.99 each. Write a function for the total cost, c, in terms of the number of meals you buy, m. Use your function to find out how much 8 meals would cost. [writing equations and functions]
A student has six weeks grades of 75 and 50. If you need at least 210 points to pass the semester, what grade does he or she need this six weeks? [measures of central tendency, inequalities]
The yearbook staff sells about $150 of snacks at lunch every day. How long would it take to raise at least $10,000? [inequalities]
Working as a waiter at the new Chili’s in Mission will earn you about $2 an hour plus tips. If you work 40 hours per week, at least how much do you need in tips to makes $250 a week? [inequalities]
A subscription to Netflix costs $18 per month for unlimited DVD rentals. If you rented DVDs from a local store, it would cost about $3.50 each. How many DVDs would you have to rent each month for you to SAVE money using Netflix? [systems of linear equations]
The population of Mission in the 2000 census was about 45,000. If the population is increasing by about 3,000 people a year, what should the population be by the end of this year? [rates, ratios, and proportions]
Verizon Wireless charges $0.49 per minute for calls to Mexico. Write an equation to find m, the number of minutes a person can call Mexico for $20. [writing equations and functions]
Mr. D walks 8 miles north and 3 miles west. How far is he from where he started? [Pythagorean theorem]
Mr. D stands on top of a building 250 meters tall. If he jumps off and falls at a rate of 9.8 meters per second, what equation could you use to show how long it will take him to hit the ground and DIE? [writing equations and functions]
Many of these questions led to relevant discussions, usually touched off by a student asking, «Is that true, sir?» More students were engaged in trying to figure out the problem than if I would have had them do something from the textbook or merely given them wordless problems to solve. They were used mostly as «Do Now» activities that would introduce the objective we would cover that day and hook students attention right away.
More Info
For more ideas like this, read my earlier article Reading and Writing in Math Through Journals. Click the literacy tag for even more.
Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/
We recommend reading any word problem at least three times. By the conclusion of the third reading, you should be magically whisked away to your home in Kansas.
Read it once…
…to get a general idea of what’s going on. Is the problem about money? Height and width? Distances? Money? Yeah, we already said money, but it’s important. Can you draw a picture in the margin that helps you visualize the problem?
Twice…
…to translate from English into math. Read the problem carefully this time, figuring out which pieces of information are important and which ones aren’t. Then ignore the unnecessary bits. This may sound a bit harsh, but they’re big boys. They’ll get over it.
Three times…
…a lady. Wait, that’s not it.
…to make sure you answered the right question. To be sure, read the question one last time before drawing a box around your final answer. Even if this method of double-checking saves you only once out of every 100 times, it’ll help you in the long run. One out of 100 is better than zero out of 100, but now we’re moving into some advanced mathematics.
Sample Problem
The local department store was having a sale. Holla! Gabe bought a pair of shoes for $21, although they would’ve been cheaper if he’d bought penny loafers. He also bought some shirts that were on sale for 25% off their normal retail price of $18 each. Gabe, always the bargain hunter, spent $75 total. How many shirts did he buy? Also, does he really think any of them will go with those shoes?
Read the problem:
Once…
…for a general idea of what’s going on: Gabe went shopping and spent money. Sounds like an old familiar story. Time for an intervention, friends of Gabe. Preferably before he maxes out his Diner’s Club card.
Now we need to figure out how many shirts he bought, so we read the problem:
Twice…
…to translate from English into math. Remember, we can translate a bit at a time, sort of like how Gabe pays for some of his major purchases when he has them on layaway. Sheesh, Gabe. Get a hold of yourself.
(total amount Gabe spent) = (amount he spent on shoes) + (amount he spent on shirts)
We know he spent $75 total, of which $21 was spent on shoes. This gives us the equation:
$75 = 21 + (amount he spent on shirts)
The problem has gotten smaller. It’s depressing when that happens with cake, but great when it happens to a word problem. Now all we need to do is come up with a symbolic expression for how much Gabe spent on shirts, or the cost per shirt times the number of shirts:
(amount he spent on shirts) = (cost per shirt)(number of shirts)
Since the shirts are 25% off their normal price of $18, they cost $18 – 0.25(18) = $13.50 each. What a deal, and real polyester, too!
We need to introduce a variable for the number of shirts; s will do the trick nicely.
(amount he spent on shirts) = 13.5s
When we plug this into the earlier equation, we find that:
75 = 21 + 13.5s
Finally, we’ve reduced this thing to a super-simple-looking equation! Good riddance, vestiges of language! Begone, nouns and verbs!
Things look much nicer now, right? No worrying about shirts or shoes or prices or Gabe’s uncontrollable shopping addiction. For the moment, we can forget about the word problem and solve the equation. The answer is s = 4, by the way. In case you were interested.
Three times…
…to make sure we’re answering the right question. We want to know how many shirts Gabe bought. Is that the answer we arrived at? We found that s = 4, and s was the number of shirts Gabe bought, so we’re all done. Four new shirts for Gabe, and three of them feature a Hawaiian pattern. Gabe, if you insist on buying far more clothes than you need, can’t you at least have a decent fashion sense?
When translating from English into math, some information can be ignored. We don’t care that «the local department store was having a sale.» Gabe might, but we certainly don’t. We care about statements that tell us numbers, and statements that tell us what the question is. Any extraneous information has been placed there simply as a decoy. We’re not going to fall for that. Wait a second…two for one? We’ll grab our jacket and meet you there.
Some people find it helpful to underline the important pieces of information in a word problem. You’re like an actor highlighting in a script the lines that are important for him to remember. Unlike an actor, however, you can always look back at the original problem if you draw a blank. Also, you don’t need to wear any stage makeup.
In the problem we just did, the important bits might look something like this:
The local department store was having a sale. Gabe bought a pair of shoes for $21 and some shirts that were on sale for 25% off their normal retail price of $18 each. If Gabe spent $75 total, how many shirts did he buy?
As you practice, you’ll become better at figuring out which parts of the word problem you can ignore and which parts are important.
Though the majority of ACT math problems use diagrams or simply ask you to solve given mathematical equations, you will also see approximately 15-18 word problems on any given ACT (between 25% and 30% of the total math section). This means that knowing how best to deal with word problems will help you significantly when taking the test. Though there are many different types of ACT word problems, most of them are not nearly as difficult or cumbersome as they may appear.
This post will be your complete guide to ACT word problems: how to translate your word problems into equations and diagrams, the different types of word problems you’ll see on the test, and how best to go about solving your word problems for test day.
What Are Word Problems?
A word problem is any problem that is based mostly or entirely on written description and does not provide you with an equation, diagram, or graph. You must use your reading skills to translate the words of the question into a workable math problem and then solve for your information.
Word problems will show up on the test for a variety of reasons. Most of the time, these types of questions act to test your reading and visualization skills, as well act as a medium to deliver questions that would otherwise be untestable. For instance, if you must determine the number of sides of an unknown polygon based on given information, a diagram would certainly give the game away!
Translating Word Problems Into Equations or Drawings
In order to translate your word problems into actionable math equations that you can solve, you’ll need to know and utilize some key math terms. Whenever you see these words, you can translate them into the proper action. For instance, the word “product” means “the value of two or more values that have been multiplied together,” so if you need to find “the product of a and b,” you’ll need to set up your equation with $a * b$.
|
Key Terms |
Mathematical Action |
|
Sum, increased by, added to, total of |
+ |
|
Difference, decreased by, subtracted from |
— |
|
Product, times |
* or x |
|
Divided by |
/ or ÷ |
|
Equals, is, are, equivalent, same |
= |
|
Is less than |
< |
|
Is greater than |
> |
|
Is less than or equal to |
≤ |
|
Is greater than or equal to |
≥ |
Let’s take a look at this in action with an example problem:
We have two different cable companies that each have different rates for installation and different monthly fees. We are asked to find out how many months it will take for the cost for each company to be the «same,» which means we must set the two rates equal.
Uptown Cable charges 120 dollars for installation plus 25 dollars a month. We do not know how many months we’re working with, so we will have:
$120 + 25x$
Downtown Cable charges 60 dollars for installation and 35 dollars per month. Again, we don’t know how many months we’re working with, but we know they will be the same, so we will have:
$60 + 35x$
And, again, because we are finding the amount of months when the cost is the «same,» we must set our rates equal.
$120 + 25x = 60 + 35x$
From here, we can solve for $x$, since it is a single variable equation.
[Note: the final answer is G, 6 months]
Learning the language of ACT word problems will help you to unravel much of the mystery of these types of questions.
Typical ACT Word Problems
ACT word problems can be grouped into two major categories: word problems where you must simply set up an equation and word problems in which you must solve for a specific piece of information.
Word Problem Type 1: Setting Up an Equation
This is the less common type of word problem on the test, but you’ll generally see it at least once or twice. You’ll also usually see this type of word problem first. For this type of question, you must use the given information to set up the equation, even though you don’t need to solve for the missing variable.
Almost always, you’ll see this type of question in the first ten questions on the test, meaning that the ACT test-makers consider them fairly “easy.” This is due to the fact that you only have to provide the set-up and not the execution.
We consider a “profit” to be any money that is gained, so we must always subtract our costs from our earnings. We know that Jones had to invest 10 million starting capital, so he is only making a profit if he has earned more than 10 million dollars. This means we can eliminate answer choices C, D, and E, as they do not account for this 10 million.
Now each boat costs Jones 7,000 dollars to make and he sells them for 20,000. This means that he earns a profit of:
$20,000 — 7,000$
$13,000$ per boat.
If $x$ represents our number of boats, then our final equation will be:
$13,000x — 10,000,000$
Our final answer is A, $13,000x — 10,000,000$
Word Problem Type 2: Solving for Your Information
Other than the few set-up word questions you’ll see, the rest of your ACT word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of ACT math topics, including averages, single variable equations, and probabilities, among others. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
This question is a rare example of a time in which not every piece of given information is needed to solve the problem. For most ACT word questions, all your given information will come into play at some point, but this is not the case here (though you can use all of your information, should you so choose).
For example, we are told that 25% of a given set of jelly beans are red. 25% translates to $1/4$ because 25% is the same as $25/100$ (or $1/4$). If we are being asked to find how many jelly beans are NOT red, then we know it would be $3/4$ because 100% is the same as 1, and 1 — $1/4$ = $3/4$.
So we didn’t need to know that there were 400 jellybeans to know that our final answer is H, $3/4$.
Alternatively, we could use all of our given information and find 25% of 400 in order to find the remaining jelly beans.
$400 * {1/4}$ or $400/4$
$100$
If 100 jellybeans are red, then 400 — 100 = 300 jelly beans are NOT red. This means that the not-red jelly beans make up,
$300/400$
$3/4$ of the total number of jelly beans.
Again, our final answer is H, $3/4$
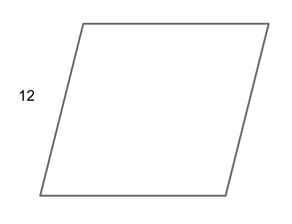
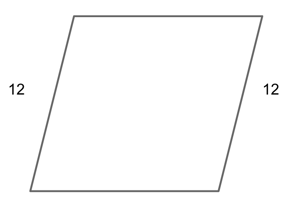
You might also be given a geometry problem as a word problem, which may or may not be set up with a scenario as well.
Geometry questions will be presented as word problems typically because the test-makers felt the problem would be too easy to solve had you been given a diagram.
The test-makers didn’t give us a diagram, so let’s make ourselves one and fill it in with what we know so far.
We know from our studies of parallelograms that opposite side pairs will be equal, so we know that the opposite side of our given will also be 12.
Now we can use this information to subtract from our total perimeter.
$72 — 12 — 12$
$48$
Again, opposite sides will be equal and we know that the sum of the two remaining sides will be 48. This means that each remaining side will be:
$48/2$
$24$
Now we have four sides in the pairings of 12 and 24.
Our final answer is C, 12, 12, 24, 24.
Now, how do we put our knowledge to its best effect? Let’s take a look.
ACT Math Strategies for Your Word Problems
Though you’ll see word problems on a myriad of different types of ACT math topics, there are still a few techniques you can apply to solve your word problems as a whole.
#1: Draw It Out
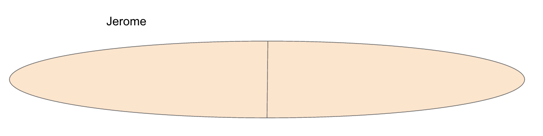
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what, exactly, you’re working with. For instance, let’s look at how a picture can help you solve a ratio/division problem:
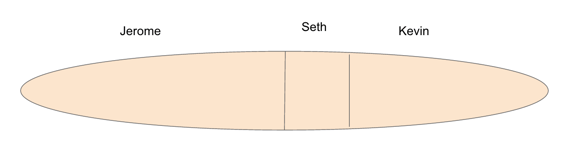
Let’s start by first drawing our sandwich and Jerome’s portion of it.
Now let’s divvy off Kevin’s portion and, by the remainder, Seth’s as well.
By seeing the problem visually, we can see that the ratio of Jerome’s share, to Kevin’s, to Seth’s will go in descending order of size. This let’s us eliminate answer choices A, B, and C, and leaves us with answer choices D and E.
Just by drawing it out and using process of elimination, and without knowing anything else about ratios, we have a 50-50 shot of guessing the right answer. And, again, without knowing anything else about fractions or ratios, we can make an educated guess between the two options. Since Jerome’s share doesn’t look twice as large as Kevin’s, our answer is probably not E.
This leaves us with our final answer D, 3:2:1.
[Note: for a breakdown on how to solve this problem using fractions and ratios instead of using a diagram and educated guessing, check out our guide to ACT fractions and ratios.]
As for geometry problems, remember—you’re often given a word problem as a word problem because it would be too simple to solve had you had a diagram to work with from the get-go. So take back the advantage and draw the picture yourself. Even a quick and dirty sketch can help you visualize the problem much easier than you can in your head and help keep all your information clear.
#2: Memorize Important Terms
If you’re not used to translating English words into mathematical equations, then ACT word problems can sound like so much nonsense and leave you floundering to set up the proper equation. Look to the chart and learn how to translate your keywords into their math equivalents. Doing so will help you to understand exactly what the problem is asking you to find.
There are free ACT math questions available online, so memorize your terms and then practice on real ACT word problems to make sure you’ve got your definitions down and can apply them to real problems.
#3: Underline and Write Out the Key Information
The key to solving a word problem is bringing together all the relevant pieces of given information and putting them in the right places. Make sure you write out all your givens on the diagram you’ve drawn (if the problem calls for a diagram) and that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline them in the problem and then write them out yourself before you set up your equation, so take a moment to perform this step.
#4: Pay Close Attention to Exactly What Is Being Asked of You
Little is more frustrating than solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of $x$ or $x + y$? Better to make sure before you start what you’re supposed to find than realize two minutes down the line that you have to solve the problem all over again.
#5: Brush Up on Any Specific Math Topic in Which You Feel Weak
You are likely to see both diagram/equation problems and word problems for any given ACT math topic on the test. Many of the topics can swing either way, which is why there are so many different types of word problems and why you’ll need to know the ins and outs of any particular math topic in order to solve its corresponding word problem. For example, if you don’t know how to properly set up a system of equations problem, you will have a difficult time of it when presented with a word problem on the topic.
So understand that solving a word problem is a two-step process: it requires you to both understand how word problems themselves work and to understand the math topic in question. If you have any areas of mathematical weakness, now is a good time to brush up on them, or else the word problem might be trickier than you were expecting.
All set? Time to shine!
Test Your Knowledge
Now to put your word problem know-how to the test with real ACT math problems.
Answers: K, C, A, E
Answer Explanations:
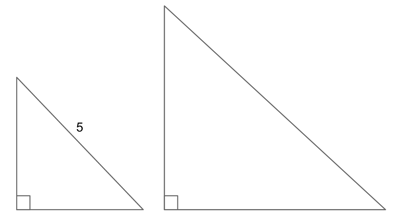
1) First, let us make a sketch of what we have, just so we can keep our measurements straight. We know we have two triangles, one smaller than the other, and the hypotenuse of the smaller triangle is 5.
Now our triangles are in a ratio of 2:5, so if the hypotenuse of the smaller triangle is 5, we can find the hypotenuse of the larger triangle by setting them up in a proportion.
$2/5 = 5/x$
$2x = 25$
$x = 12.5$
Our final answer is K, 12.5.
2) Because we are dealing with a hypothetical number that is increasing and decreasing based on percentage, we can solve this problem in one of two ways—by using algebra or by plugging in our own numbers.
Solving Method 1: Algebra
If we assign our hypothetical number as $x$, we can say that $x$ is increased by 25% by saying:
$x + 0.25x$
Which gives us:
$1.25x$
Now, we can decrease this value by 20% by saying:
$1.25x — (1.25x * 0.2)$
$1.25x — 0.25x$
This leaves us with:
$1x$ or 100% of our original number.
Our final answer is C, 100%.
Solving Method 2: Plugging in Numbers
Alternatively, we can use the same basic process, but make it a little simpler by using numbers instead of variables.
Let’s say our original number is 100. (Why 100? Why not! Our number can literally be anything and 100 is an easy number to work with.)
So if we need to increase 100 by 25%, we first need to find 25% of 100 and then add that to 100.
$100 + (0.25)100$
$100 + 25$
$125$
Now we need to decrease this value by 20%, so we would say:
$125 — (0.2)125$
$125 — 25$
$100$
We are left with the same number we started with, which means we are left with 100% of the number we started with.
Again, our final answer is C, 100%.
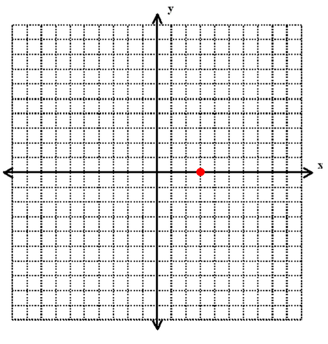
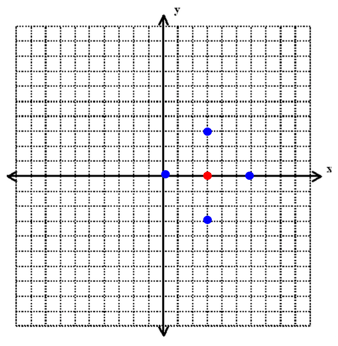
3) Let’s first begin by drawing a picture of our scene. We know that one vertex of the square is at (3, 0), so we can mark it on a coordinate plane.
Now, we are told that each side of the square is 3 cm long. To make life simple, we can start by marking all the possible vertexes attached to our known vertex at (3, 0) straight up, down, and side to side. If no answers match, we can then look to vertexes at different angles.
Our possible vertexes are:
(0, 0), (6, 0), 3, 3) and (3, -3)
One of our possible vertexes is at (6, 0 and this matches one of our answer choices, so we can stop here.
Our final answer is A, (6, 0).
4) We are told that Ms. Lopez throws out the lowest test score and then averages the remaining scores. Because Victor’s scores are already in ascending order, we can throw out the first score of 62.
Now to find the average of the remaining 4 scores, let us add them together and then divide by the number of scores.
$(78 + 83 + 84 + 93)/4$
$338/4$
$84.5$
Our final answer is E, 84.5.

Picture: John Morris/Flickr
The Take-Aways
Word problems comprise a significant portion of the ACT, so it’s a good idea to understand how they work and how to translate the words into a proper equation. But remember that translating your word problems is still only half the battle.
You must also supplement this knowledge of how to solve word problems with a solid understanding of the math topic in question. For example, it won’t do a lot of good if you can translate a probability word problem if you don’t understand exactly how probabilities work. So be sure to not only learn how to approach your word problems, but also hone your focus on any math topics you feel you need to improve upon. You can find links to all of our ACT math topic guides here to help your studies.
What’s Next?
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
SDI Productions / Getty Images
Updated on January 07, 2020
When you take a real-world situation and translate it into math, you are actually ‘expressing’ it; hence the mathematical term ‘expression’. Everything that is left of the equal sign is considered to be something you are expressing. Everything to the right of the equal sign (or inequality) is yet another expression. Simply stated, an expression is a combination of numbers, variables (letters) and operations. Expressions have a numerical value. Equations are sometimes confused with expressions. To keep these two terms separate, simply ask yourself if you can answer with a true/false. If so, you have an equation, not an expression that would have a numerical value. When simplifying equations, one often drops expressions such as 7-7 that equal 0.
A few samples:
| Word Expression | Algebraic Expression |
| x plus 5 10 times x y — 12 |
x 5 5x y — 12 |
Getting Started
Word problems consist of sentences. You will need to read the problem through carefully to ensure you have some understanding of what you are being asked to solve. Pay close attention to the problem to determine the key clues. Focus on the final question of the word problem. Read the problem again to make sure you understand what you’re being asked for. Then, jot down the expression.
Let’s get started:
1. On my last birthday, I weighed 125 pounds. One year later I have put on x pounds. Which expression gives my weight one year later?
a) x 125 b) 125 — x c) x 125 d) 125x
2. If you multiply the square of a number n by 6 and then added 3 to the product, the sum is equal to 57. One of the expressions equals 57, which one is it?
a) (6n)2 3 b) (n 3)2 c) 6(n2 3)d) 6n2 3
Answer for 1 is a) x 125
Answer for 2 is d) 6n2 3
Word Problems to Try
Sample 1
The price of a new radio is p dollars. The radio is on sale for 30% off. What expression will you write that will tell the savings that are being offered on the radio?
Answer: 0.p3
Sample 2
Your friend Doug has given you the following algebraic expression: «Subtract 15 times a number n from twice the square of the number. What is the expression that your friend is saying?
Answer: 2b2-15b
Sample 3
Jane and her three college friends are going to be sharing the cost of a 3 bedroom apartment. The cost of rent is n dollars. What expression can you write that will tell you what Jane’s share is?
Answer: n/5
Ultimately, becoming quite familiar with the use of algebraic expressions is an important skill for learning and conquering algebra.