We recommend reading any word problem at least three times. By the conclusion of the third reading, you should be magically whisked away to your home in Kansas.
Read it once…
…to get a general idea of what’s going on. Is the problem about money? Height and width? Distances? Money? Yeah, we already said money, but it’s important. Can you draw a picture in the margin that helps you visualize the problem?
Twice…
…to translate from English into math. Read the problem carefully this time, figuring out which pieces of information are important and which ones aren’t. Then ignore the unnecessary bits. This may sound a bit harsh, but they’re big boys. They’ll get over it.
Three times…
…a lady. Wait, that’s not it.
…to make sure you answered the right question. To be sure, read the question one last time before drawing a box around your final answer. Even if this method of double-checking saves you only once out of every 100 times, it’ll help you in the long run. One out of 100 is better than zero out of 100, but now we’re moving into some advanced mathematics.
Sample Problem
The local department store was having a sale. Holla! Gabe bought a pair of shoes for $21, although they would’ve been cheaper if he’d bought penny loafers. He also bought some shirts that were on sale for 25% off their normal retail price of $18 each. Gabe, always the bargain hunter, spent $75 total. How many shirts did he buy? Also, does he really think any of them will go with those shoes?
Read the problem:
Once…
…for a general idea of what’s going on: Gabe went shopping and spent money. Sounds like an old familiar story. Time for an intervention, friends of Gabe. Preferably before he maxes out his Diner’s Club card.
Now we need to figure out how many shirts he bought, so we read the problem:
Twice…
…to translate from English into math. Remember, we can translate a bit at a time, sort of like how Gabe pays for some of his major purchases when he has them on layaway. Sheesh, Gabe. Get a hold of yourself.
(total amount Gabe spent) = (amount he spent on shoes) + (amount he spent on shirts)
We know he spent $75 total, of which $21 was spent on shoes. This gives us the equation:
$75 = 21 + (amount he spent on shirts)
The problem has gotten smaller. It’s depressing when that happens with cake, but great when it happens to a word problem. Now all we need to do is come up with a symbolic expression for how much Gabe spent on shirts, or the cost per shirt times the number of shirts:
(amount he spent on shirts) = (cost per shirt)(number of shirts)
Since the shirts are 25% off their normal price of $18, they cost $18 – 0.25(18) = $13.50 each. What a deal, and real polyester, too!
We need to introduce a variable for the number of shirts; s will do the trick nicely.
(amount he spent on shirts) = 13.5s
When we plug this into the earlier equation, we find that:
75 = 21 + 13.5s
Finally, we’ve reduced this thing to a super-simple-looking equation! Good riddance, vestiges of language! Begone, nouns and verbs!
Things look much nicer now, right? No worrying about shirts or shoes or prices or Gabe’s uncontrollable shopping addiction. For the moment, we can forget about the word problem and solve the equation. The answer is s = 4, by the way. In case you were interested.
Three times…
…to make sure we’re answering the right question. We want to know how many shirts Gabe bought. Is that the answer we arrived at? We found that s = 4, and s was the number of shirts Gabe bought, so we’re all done. Four new shirts for Gabe, and three of them feature a Hawaiian pattern. Gabe, if you insist on buying far more clothes than you need, can’t you at least have a decent fashion sense?
When translating from English into math, some information can be ignored. We don’t care that «the local department store was having a sale.» Gabe might, but we certainly don’t. We care about statements that tell us numbers, and statements that tell us what the question is. Any extraneous information has been placed there simply as a decoy. We’re not going to fall for that. Wait a second…two for one? We’ll grab our jacket and meet you there.
Some people find it helpful to underline the important pieces of information in a word problem. You’re like an actor highlighting in a script the lines that are important for him to remember. Unlike an actor, however, you can always look back at the original problem if you draw a blank. Also, you don’t need to wear any stage makeup.
In the problem we just did, the important bits might look something like this:
The local department store was having a sale. Gabe bought a pair of shoes for $21 and some shirts that were on sale for 25% off their normal retail price of $18 each. If Gabe spent $75 total, how many shirts did he buy?
As you practice, you’ll become better at figuring out which parts of the word problem you can ignore and which parts are important.

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.
The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!
How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.
Here are the seven strategies I use to help students solve word problems.
1. Read the Entire Word Problem
Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.
2. Think About the Word Problem
Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.
Here are the questions:
A. What exactly is the question?
What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.
B. What do I need in order to find the answer?
Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.
This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better
Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.
One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.
If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?
This is where students will focus in on the numbers which will be used to solve the problem.
3. Write on the Word Problem
This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:
- Circle any numbers you’ll use.
- Lightly cross out any information you don’t need.
- Underline the phrase or sentence which tells exactly what you’ll need to find.
4. Draw a Simple Picture and Label It
Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.
For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!
5. Estimate the Answer Before Solving
Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.
6. Check Your Work When Done
This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable? I want students to do more than to be number crunchers but to really think about what those numbers mean.
Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.
7. Practice Word Problems Often
Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.
When students practice word problems, often several things happen. Word problems become less scary (no, really).
They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.
If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.
This 3rd Grade Math Task Cards Bundle has word problems in almost every one of its 30 task card sets.
There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.
CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.
CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.
CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?
3rd Grade: Rounding Whole Numbers Task Cards
4th Grade: Convert Fractions and Decimals Task Cards
5th Grade: Read, Write, and Compare Decimals Task Cards
Thanks so much for stopping by!

$begingroup$
High school students have a lot of trouble understanding word problems, and I don’t know how to help them.
It’s been too long since I’ve had trouble understanding usual word problems, so when I read the problem I automatically know what to do and how to do it. This, however, makes for terrible pedagogy.
What are good strategies to help them develop skill at solving these exercises?
asked Dec 4, 2014 at 6:42
Mark FantiniMark Fantini
2,9802 gold badges16 silver badges39 bronze badges
$endgroup$
4
$begingroup$
The answer provided by celeriko seems like it hits all of the main points. However, I have found in my experience teaching word problems with students that a few additional strategies are most effective for struggling students.
- Rewriting the important mathematical «givens» in a problem. By having students rewrite these ideas, they’re taking possession of these parts of the problem, and begin dissecting the problem from a «word problem» to a «regular problem». It is also helpful for them to have these pieces easily accessible and to not have to dig back into the paragraph of the word problem to use them. Writing things down is also helpful for students who are struggling because it gives them something to do. A common complaint I have heard from students is not knowing how to get started. This gives them something to start doing.
-
Decoding «buzz words» as celeriko mentions is key. There are other less common buzz words that I think are even more helpful than the ones listed in this other answer. Some of these other are:
- IS: This is usually translated into the mathematical symbol $=$ but is also used very often in common English grammar, so it is often glossed over.
- OF: Similar to IS, it needs to be emphasized in mathematics as multiplication.
- PER: Division, or fractions, with the word or words prior belonging to the numerator and the word(s) after belonging to the denominator.
- PERCENT: I discuss this with PER and break down the word into its two roots. PER meaning division, and CENT standing for 100. There are plenty of examples you can use to connect CENT to 100, such as cent or century.
- THAN: This is an interesting one since it doesn’t actually stand for any operation, but when paired with LESS, like «$5$ less than $9$» actually commutes the order of the elements when translating the word problem into a mathematical expression.
-
Creating a dialog and discussing problems with students in class is also important. This promotes a common method that many mathematicians use to solve their own problem, which is creating a dialog with themselves (I believe Polya mentioned this, but I could be wrong). In having these discussions, hopefully your students can glean from you some of your thought processes, and you may also discover how you actually think about these problems to enable you to break them down for your students.
answered Dec 5, 2014 at 6:52
$endgroup$
2
$begingroup$
I feel your angst, word problems are a consistent weakness across most grade/subject levels. Learning to decode and solve word problems is a learned skill and so it needs to be practiced. However, just giving students 50 word problems and telling them to solve them for homework wont help anyone. I’d suggest to focus on each of the following items individually, guiding students at first and then slowly letting them try on their own. Once they begin to pick them up, you can start having them combine the different techniques, again with guidance at first and gradual release.
- decoding «buzz words» (sum, difference, product, each, etc.)
- underline/highlight important words/numbers
- crossing out extraneous information
- draw a picture! (one of the most helpful skills in life)
- translating sentences into equations/expressions
- underline/highlight what the final question of the word problem is
- reading word problems (it sounds trivial, but many of my students have trouble even finishing reading certain word problems)
- make a plan (outline steps of what you need to do, sentence by sentence)
- make a table (for certain problems, this can really help visualize what is going on)
- smart solving (if you just spent the previous week calculating slope, there is a good chance the word problem today will have something to do with slope)
- working backwards (asking yourself «What do I know? What do I need to know? How can I know it?», one of the most difficult practices for students to develop)
Another area I would focus on, which is not necessarily used in the process of solving a WP, is the aspect of explaining an answer. If a student can explain their answer with words it proves a certain level of understanding. One idea is to give them a word problem, let them read through it, then present them with the work of someone else and see if they can explain what this other person did to solve the problem. In a similar vein, you can give them a worked through solution and have THEM write the word problem. This gives them a chance to be creative and also practice working backwards. I hope this helps!
answered Dec 4, 2014 at 16:25
celerikoceleriko
4,9002 gold badges17 silver badges56 bronze badges
$endgroup$
$begingroup$
Have you tried doing the reverse. Show them the solution and ask them to form a word problem (based on the solution). It would show you how students parse (break down) word problems in their minds.
Start easy for example: x + 2 = 8 form a word problem using slices of pizza. The way the children form sentences will show you the words they use to define a problem.
It would also allow you to reword some problems using words that the children use, since it looks more of a language problem than a math problem.
Don’t be strict in the child’s sentence construction, the point is you want an insight into their minds of how they form, break down, and express math word problems in their heads. You will probably see word problems looking like conversations instead of properly structured math word problems.
Once you have a common ground you can later show them what a properly structured word problem looks like — with emphasis on buzzwords as suggested by Andrew Sanfratello — allowing you to compare buzzwords to the words your students use.
answered Dec 16, 2014 at 5:23
$endgroup$
Why some kids struggle with math word problems
ByBob Cunningham, EdM
Quick tips to help kids with math problems
Word problems in math can be tricky. To get the right answer, kids have to be able to read the words, figure out what math operation to use, and then do the calculations correctly. A breakdown in any of these skills can cause trouble.
If kids seem to be good at math but struggle with word problems, here are possible reasons why:
Explore topics selected by our experts
Trouble with reading: To solve word problems, kids have to read well. So even if they usually do well with math, reading difficulties can make word problems hard.
Trouble understanding math phrases and concepts: Even if kids are strong readers, they may have trouble picking up on clues in word problems. These clues are phrases that help kids figure out what they need to do to solve the problem, like adding or subtracting. Kids then have to translate these phrases into a number sentence, like “two plus three equals five.”
Trouble with focus and self-control: Kids may get distracted by the words or get lost in their heads. Other kids struggle with self-control and rush through the problem. They may skip important parts or make simple calculation mistakes.
Dive deeper
Reading and word problems
Math concepts and word problems
Focus and word problems
Explore related topics
Tell us what interests you
Share
About the author
About the author
Bob Cunningham, EdM serves as executive director of learning development at Understood.
Copyright © 2014-2023 Understood For All Inc.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
When most people hear “word problems,” they often think of the popular example of trains traveling at different speeds, or unrealistic applications of math. However, word problems represent how most people use math in everyday life, and the SAT includes these problems to test students’ ability to reason logically and solve problems.
For many students, the hardest part of a word problem is figuring out exactly what the word problem is asking of you. Not all word problems are created the same though, so we’re going to break down what you need to know so that you feel confident solving them on the SAT.
Types of Math Word Problems on the SAT
You could divide math word problem in a few different ways. You could do it by topic, for example, such as using the SAT subscores as your guide. Or you could do it by the type of solution the problem requires of you. We’re going to focus on the second way, simply because trying to divide word problems by topic would mean we’d have to cover virtually every math topic the SAT covers, which is way more than we could fit in a single post.
Creating an equation or a formula. In these problems, you’ll be given some information about a scenario and asked to come up with an equation or formula that represents that scenario. In fact, looking for the word “represents” in the question might tip you off that you’re dealing with a problem of this type. These are almost exclusively found in the multiple-choice questions, with different equations or formulas listed as the answer choices.
Solving for a value. This is the most common form of word problem. Based on the information in the word problem, you’ll need to come up with at least one specific value that satisfies the requirements of the problem. Examples include finding “how much” or “how many” of something in the problem, or finding minimums and maximum values.
Defining or interpreting. For these problems, you are often asked to interpret what a variable or a constant means in the situation described, or you might be asked what kinds of conclusions can be drawn from a survey. These types of problems often have no “math” involved, and instead ask you to think logically about a situation.
Tip: Being able to identify problems by type on the SAT is a useful prep exercise and can help you on the day you take the test. You may want to use the Math section from a free practice SAT test and circle all of the word problems. Then, read each word problem and assign it to one of the types. Doing this will help you see the commonalities between different types of questions and will allow you to spend less time on the actual test wondering what type of question you’re dealing with!
How to Approach SAT Math Word Problems
For every SAT Math word problem, there are two things to consider. The first is what we discussed above, which is to figure out what type of problem you’re dealing with to best identify what you need to do. Once you know whether you need to provide a definition, write an equation, or solve for a value, you’ve taken the first step.
The next step will be to do the math that you’ve identified you need to do based on the type of word problem. Let’s take a look at each one:
Write an equation/formula. For problems of this type and for problems that ask you to solve for a specific value, you will often need to understand how to “translate” a word problem into an equation, diagram, or graph that you can work with. Luckily, the SAT is very particular about how it uses words in its word problems, so you can always be sure that certain words are meant to relate to specific mathematical concepts. Here are some of the common phrases used by test makers to clue you in to what kind of math you’re looking for:
| Word/phrase | Mathematical meaning/symbol |
| Is, will be, is equal to, is the same as | Equals, = |
| Plus, sum, increased by, added to, received | Addition, + |
| Minus, fewer, difference, decreased by | Subtraction, – |
| Times, product, multiplied by, of | Multiplication, x |
| Divided by, quotient, per, for | Division, ÷ |
| More than, greater than | Inequality, > |
| At least, minimum | Inequality, ≥ |
| Fewer than, less than | Inequality, < |
| At most, maximum | Inequality, ≤ |
| What, how many | Variable, x (or any other letter) |
Solve for a value. With these problems, you might be given an equation as part of your information, but most likely you have to write an equation or formula and solve for the answer. You may benefit from drawing a diagram on some of these questions, especially if the word problem refers to geometric shapes but doesn’t already include one. This can help you visualize the information you’re looking for (the measure of an angle, for example) and help you focus on the right concepts to find the solution.
When translating a word problem into a diagram, make sure you follow the set-up as described in the word problem to the best of your ability, and don’t be fooled by your own diagram. For example, a problem may mention a right triangle, so you draw one. You may end up drawing a diagram that looks like a 45-45-90 triangle, but the problem is actually dealing with a 30-60-90 triangle. By labeling all of the information on your diagram and making a mental note that your drawings aren’t to scale, you can quickly make sense of most problems.
Defining and interpreting. With these types of problems, you often have the equation or formula given to you, and you just need to explain how a part of it works. If you’re not sure, consider whether you’re being asked about a constant or a variable, and eliminate any choices that don’t correspond to the type of value you’re looking at. You can also test the equation with different numbers to see how the value in question influences the equation.
Some problems involve your knowledge of statistical topics, such as understanding how to draw conclusions from surveys, or what factors affect standard deviation. For many of these problems, you’ll need to review these concepts in order to form the correct conclusion.
Examples of SAT Math Word Problems
The following example problems come from the College Board’s free SAT practice tests.
Example of Creating an Equation/Formula
How to solve: We can tell we need to come up with our own formula based on the answer choices and the word “represents” in the problem’s question. We need to find the formula that represents what the original price of a laptop was in terms of p, what Alma paid for it.
Let’s make x the original price of the laptop. In this case, x would be multiplied by .8 to get to the sales price (representing the 20% discount). The sales prices would then be multiplied by 1.08 to account for sales tax. This means that p=(1.08)(0.8)(x). We need to isolate x, so we need to divide both sides by 1.08 and 0.8. That gives us D as the correct answer.
Alternate method: Many problems requiring you to create your own equation are not too difficult, but they can get tricky when there are several steps involved or several variables. You can substitute a number for the variable you’re solving for to find the solution that way. For example, you can set $100 to be the original price of the laptop. Multiply it by .8 to find the sales price, and then by 1.08 to find the price that Alma paid. Then plug the price Alma paid into the answer choices to find the correct answer.
Example of Solving for a Value
How to solve: The word “maximum” tips us off that we are looking for a specific value and that we’ll be dealing with an inequality (see above). Given the information in the problem, we can write this inequality to start: (weight of driver) + (weight of truck) + (14x, or the weight of the boxes) ≤ 6000.
Because we’re told that the weight of the driver and the truck equals 4,500, we can replace that part of the equation: 4500 + 14x ≤ 6000. Now, all we need to do is solve for x. Subtract 4500 from both sides to get 14x ≤ 1500. Then divide both sides by 14 to get x ≤ 107.14… The answer is thus 107.
Note: Pay close attention to how you need to round when working with inequalities. Although this particular decimal probably wouldn’t have made you think to round up, if the result of the division had been 107.9999 you should still round down in this case because the number you’re looking for needs to be less than that value.
Example of Defining/Interpreting
How to solve: Again, the use of the word “interpretation” lets us know what type of problem we’re dealing with. In this case, 12 is a coefficient for the variables n and h, which are the number of landscapers and the number of hours respectively. We can thus rule out choices B and D, since those answers define 12 as a constant in place of these variables.
Since this equation is used to calculate the price of a job, we can be sure 12 represents a dollar amount as reflected in choices A and C. To figure out how things are affected, we can substitute simple numbers for n and h. When both are equal to 1 (there is one landscaper who works for one hour), then 12nh=12(1)(1)=12. When we increase both of these numbers to two, then 12nh=12(2)(2)=48. We can thus rule out C, because the price increased by more than 12 when we added another hour. Choice A is the best interpretation.
How to solve: This is an interpretation problem dealing with statistical concepts rather than interpreting an equation. To be able to “solve” you’d need to know what factors contribute to a reliable conclusion and see what was missing from this survey set-up. In this case, the correct answer is D.
In order for reliable conclusions to be drawn, a sample must be selected at random from the population to ensure that the sample is representative of the population, which in this case is the entire town. By choosing people at the same restaurant on one day, the researcher is possibly biasing their results by narrowing their sample to “people who like this one restaurant.” Because the sample is not representative, choice D identifies the factor that makes the conclusion unreliable. The other choices are factors that, given what we know from the problem, don’t negatively impact the conclusion.
SAT Math Word Problems Tips
As you may have noticed in the last example, you’ll still need to be familiar with math concepts and understand how they might show up in different situations to really feel confident taking any problem on. Here are a couple of other tips worth mentioning:
For most problems, there is more than one way to solve it. We showed this with the first example, where we provided an alternate method for solving a problem. If you find yourself stumped on a problem (we’ve all been there!), then move on to other problems and return to the one that tripped you up later. You may find that you see what you need to do more clearly.
Read carefully. The SAT test makers put a lot of care into how they write math word problems. Be sure to carefully read the question so that you don’t misread something and solve for the wrong thing. (The test makers may even include the answers that result from these common misreadings in the choices!). It’s difficult to read a question correctly once you’ve misread it. If you’re a fast reader who tends to skip over things, try mouthing the words silently as you read. It will force you to slow down just enough that you won’t miss anything, but not so much that you won’t have time to finish the test.
In general, preparing for the SAT Math section requires a multi-faceted approach. You need to be able to identify the types of questions you’re dealing with, know mathematical concepts and how to use them, and deal with other testing issues like rushing through the end or dealing with test anxiety. To help you get started, check out our free SAT Guide that includes 8 of our best test prep tips!
For more information about preparing for the SAT, check out these posts below:
30 SAT Math Formulas You Need to Know
25 Tips and Tricks for the SAT
5 Common SAT Math Mistakes to Avoid
Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!
A Picture is Worth a Thousand Words
“Today, we are going to solve math word problems.” When students hear this from their math teacher, their faces drop, sweat starts to form on their foreheads and they refuse to make eye contact. As a math teacher, I understand. I understand the anxiety and want to make the learning process with word problems more enjoyable. This is where reading, writing and, math collide and the real world of math begins. Let’s talk about how to solve word problems with pictures.
When students struggle with word problems in school, they also have difficulty tackling them for homework. Most students want the “one-size-fits-all” formula for word problems but unfortunately, that does not exist. However, drawing a picture will help students visualize the problem and will start advancing their learning stage from the concrete to the abstract. Let’s take a look at how to solve a word problem using pictures:
Steps for Solving Word Problems using Pictures
- Read the entire problem: Get all the facts – Underline key word
- Answer the question: What am I looking for?
- Draw a picture or diagram: Visualize as a real world situation
- Solve the problem: Set up the equation and solve
- Check your solution: Is this answer reasonable?
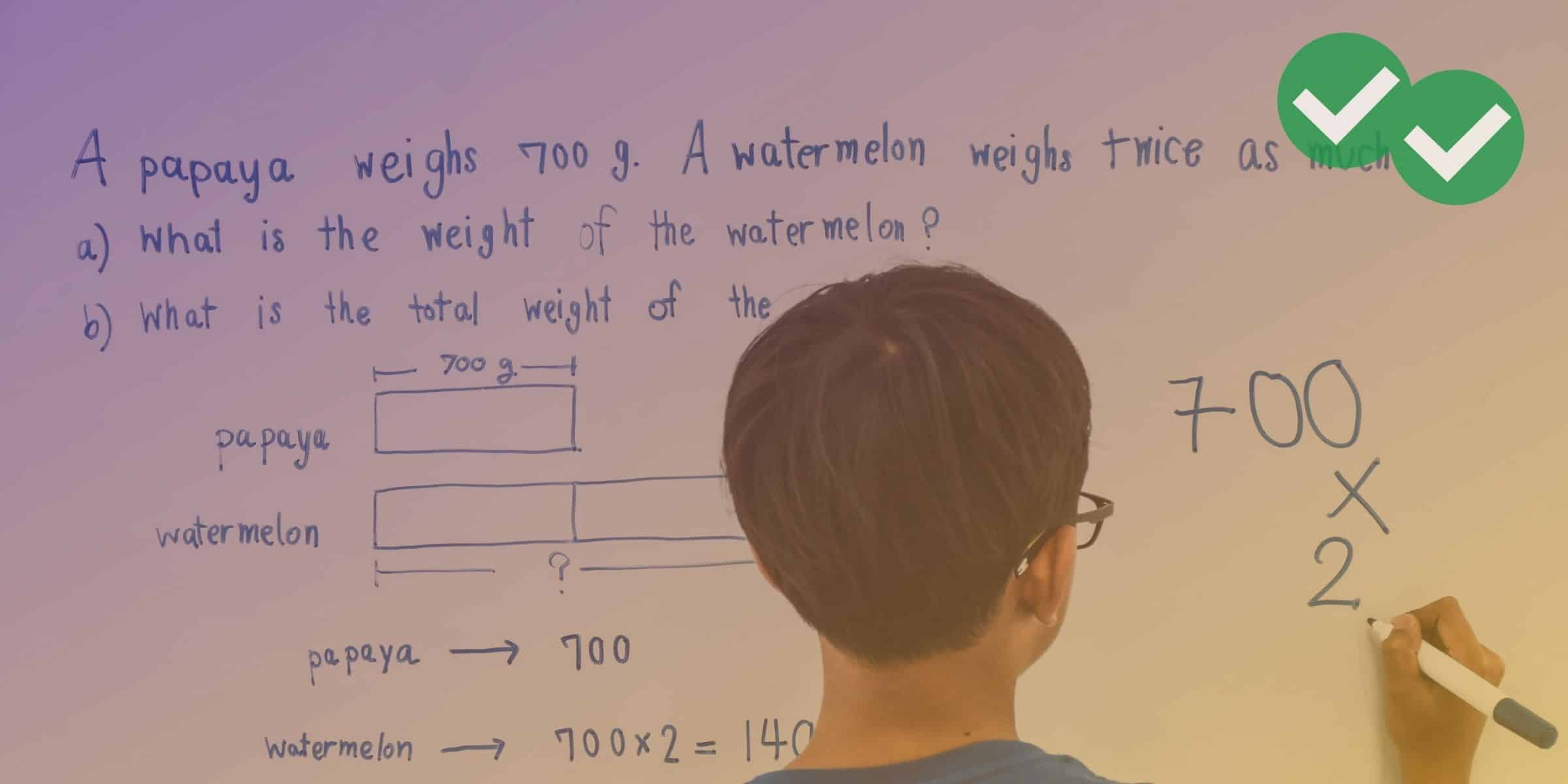
Word Problem Examples – Example A
Cody has 6 pencils on his desk, Jonah has 4 more than Cody and Vinny has three less pencils than Jonah. How many pencils are there in all?
- Read the entire problem √
- What am I looking for? How many pencils do Cody, Jonah and Vinny have altogether? √
- Draw a picture or diagram √
- Solve the problem √
6 + 10 + 7 = 23 pencils
- Check your solution √
This answer is reasonable
Example B
There are 3 fish tanks labeled X, Y, and Z. Y weighs 6 times as much as X and twice as much as Z. If Z is 36 lbs. heavier than X, find the total weight of X, Y and Z.
- Read the entire problem √
- What am I looking for? What is thetotal weight of fish tanks X, Y and Z? √
- Draw a picture or diagram √
- Solve the problem √
18 + 108 + 54 = 180 pounds
- Check your solution √
This answer is reasonable
Visualizing a word problem with pictures is a strategy that will help motivate many students to begin the process of solving them. This works especially for students that may become bored by the excess amount of words instead of numbers or for those students who become overwhelmed by the information and want to break it down into a simpler form. Another benefit of using pictures when solving word problems involves communicating the results. The pictures act as justification for answers, make the problems easier to understand and therefore, secure the learning process.
Meet our Guest Blogger: Jan Rowe
Jan is one of Educational Connections’ top tutors. She has twelve years of classroom teaching experience and holds a Virginia and Florida teaching license in middle school mathematics and elementary education. Jan has been with Educational Connections for over a year, working with over twenty students. Her tutoring goal is to help each student understand their learning style so they can improve the speed and quality of that learning. When she is not tutoring or teaching, Jan loves to play scrabble, go hiking and play Frisbee with her new puppy.
By on February 23, 2021 in SAT
If the phrase “word problems” makes you want to throw your SAT prep materials at the wall, know that you’re definitely not alone. Word problems are HARD if you’re not used to translating them into numbers. And the bad news? The SAT Math section LOOOVES their word problems — they comprise 25% of the Math section!
But wait, before you actually destroy your SAT prep book or, worse, your laptop, know that anyone can become an SAT word problem master with some practice. Even if you’re a pro at making mathematical equations out of word problems, this post will cover tactics to help you solve word problems in record time.
The Different Strategies for Tackling SAT Word Problems
As if word problems weren’t hard enough, not all word problems are created equal. Some want you to create an equation, some want you to pick an equation, and some are just bent on sounding like this: If the number of apples Mary has is twice the absolute value of chocolate, how many zebras on train B will travel to San Diego on shmoople zeeple heeple?
“Huh?” is right. It’s absolutely right.
To master SAT word problems, you need to become familiar with different types of SAT word problems and what strategy — or combination of strategies — is best for the problem and easiest for you. There are three main strategies for word problems: Active Reading, Process of Elimination, and Picking Numbers.
Active Reading: You have might have learned of the active reading strategy on the SAT, which is when you go through the reading comprehension passages while underlining or taking notes to better remember and make sense of the material. But this strategy also comes in pretty handy for SAT Math word problems and can easily be combined with the strategies below. Click here to see a few examples of active reading in practice.
Process of Elimination: Process of elimination is when you plug in answer choices in the context of the problem. Obviously, it only works when there are answer choices. If you feel like active reading is going to slow you down, definitely try process of elimination — click here for an example!
Picking Numbers: Sometimes word problems have equations in the question and answer choices. If this is the case, picking numbers and plugging them into given equations is a great strategy to speed things up. To see picking numbers in action, click here.
Active Reading and SAT Math
While it may feel like it takes longer than reading passively, active reading for the right kind of SAT word problem will actually save you a ton of time in the long run. Why? Because active reading forces you to work through problems as you’re reading them and by doing so, you often find yourself at or near the answer by the time you’re done reading the question.
Don’t believe me? Check out how active reading works in this problem:
Carrie invites some friends to a party. For every two friends who bring snacks, there are five who bring nothing with them. If the number of friends who bring nothing is 15 more than the number of friends who contribute snacks, how many friends in total arrive at the party?
Yikes, even I’m getting a headache looking at it and I’ve read it already. But before we get overwhelmed by all these words, understand that the key to approaching these types of problems is a two-step process:
Step 1. Draw your attention to the numbers and what they mean in the context of the problem.
Click here to review Step 1!
In other words, what kind of equation are these numbers making? The chart below can help you figure out how to translate key words into their equivalent operators.
| Words | Their equivalent operators |
|---|---|
| Total of, added to, increased, sum | + |
| Decreased by, subtracted from, difference | — |
| Times, product | x |
| Same, equivalent, equals, is | = |
| Less than | < |
| Greater than, more than | > |
| Greater than or equal to | ≥ |
| Less than or equal to | ≤ |
Step 2. Pay close attention to what you’re supposed to answer.
Click here to review Step 2!
When I was studying for the SAT (a century ago), I had spent a lot of time beating my head on the table because I picked the answer choice for x when I really was supposed to find x + 1, or that I solved for inches instead of feet. Underlining or circling what you’re supposed to find will save you headaches… Trust. Me.
Take a look at the question again and see if you can spot any words from the chart, and highlight what you need to solve.
Carrie invites some friends to a party. For every two friends who bring snacks, there are five who bring nothing with them. If the number of friends who bring nothing is 15 more than the number of friends who contribute snacks, how many friends in total arrive at the party?
Now check out the slides below to see an example of how active reading and annotations help you get to the answer. In this example, I used both underlining and notes in the margin. Both options are good if you’re new to active reading for SAT word problems, but I prefer just writing notes in the margin because it saves time while helping me create the equation that I need to solve.
Click here to review the slides
Drawing Word Problems
If you’re still not comfortable working with equations, there’s a different type of active reading strategy you can try: sketching the situation out. In fact, for most test-takers, drawing out the problem can be faster even if you are comfortable with equations.
Let’s try it out with the same question from above:
Carrie invites some friends to a party. For every two friends who bring snacks, there are five who bring nothing with them. If the number of friends who bring nothing is 15 more than the number of friends who contribute snacks, how many friends in total arrive at the party?
By just drawing some of Carrie’s crummy friends, we’ll get there faster. (Alright, so on the actual SAT, you won’t have the luxury or the time to create such a masterpiece. You’ll just draw some circles and squares, or something similar.)
It’s pretty clear on seeing this that 2/7 of the friends have snacks and 5/7 don’t. You can also see the difference is 3/7.
Click here for the rest of the explanation
So just do a little mental highlighting and copy-pasting of that picture.
How many groups of these guys will we need to get to 15? If there are 3 people in each group, we’ll need 5 groups. Five groups of seven people total? 35 friends arrived at the party.
The takeaway? It’s a lot easier to stay focused and get your foot in the door of SAT word problems if you start sketching out the situation like this. Even if you saw the mathematical relationship pretty quickly in this example, there will almost definitely be more difficult problems on the SAT that are best drawn, at least in the beginning. And if the math becomes clear soon after, then great — the picture has served its purpose.
Simplifying SAT Word Problems by Elimination
Because the SAT is mostly multiple-choice, you don’t really have to understand how to transform word problems into equations for a lot of the questions. You can use the answers to your advantage and totally circumvent it.
Not sure where to start on a question? Did drawing the situation fall flat?
Then take a look at the answer choices. If there are concrete numbers there (and not algebraic expressions), then you should try putting some of them through the process that the word problem describes. Like drawing, the process of elimination is often faster than straightforward math.
Below is a relatively basic example. Why don’t you give it a shot first using elimination?
At 8:00 a.m., there are exactly as many chocolate donuts as there are jelly donuts on a table in the teacher’s lounge. Within five minutes, 15 of the chocolate donuts are eaten, but nobody has eaten the jelly donuts. There are then four times as many jelly donuts as there are chocolate donuts on the table. How many jelly donuts are left?
A. 5
B. 10
C. 16
D. 20
E. 40
Click here for the answer and explanation!
Answer: 20
Explanation: So, where should you start? How about with (C)? After all, Neither (A) nor (B) is divisible by four, which the answer probably will be, since the number of jelly donuts is four times that of the chocolate. And (A) is definitely too small.
In (C), there are 16 jelly donuts left, which means there must be 4 chocolate. If there are 4 chocolate donuts after the five minutes are up, there must have been 19 at the start. 19 chocolate and 16 jelly don’t match up, so that’s no good.
Let’s try (D), then, so we’ll have more jelly donuts. 20 jelly means 5 chocolate left. 5 chocolate remaining means 20 chocolate at the start. 20 and 20 match up.
As you can see with the above example, we’re done just like that. Once you’re practiced with process of elimination, you’ll find that doing it in your head is even faster!
Word Problems and Picking Numbers
Our last SAT word problems strategy is picking numbers, which is pretty straightforward. The other easy thing about picking numbers for word problems is that this strategy only works when there is a real equation in either the question or answer choice.
Check out the problem below and pick some easy numbers for h and d.
Savannah is paid $5 for each hour she works and Enrique is paid $10 for each hour he works. Between them, Enrique and Savannah work for h hours, and Enrique earns d more dollars than Savannah. Which of the following expressions gives the number of hours for which Enrique worked?
A. (frac{5h+d}{15})
B. (frac{10h-d}{15})
C. (frac{10h+5d}{2})
D. (frac{5h+15d}{25})
Click here for the answer and explanation!
Takeaway: With Practice Comes Perfect
If we’ve done our job correctly with this SAT word problems post, I hope you’re feeling a little less “huh?” and a bit more zen and that you’re itching to put some of these strategies into practice. If you liked our practice questions, there’s more of that where that came from on our SAT web app, where we give you a 100-point guarantee or your money back.
While these strategies won’t help you become a word problem master overnight, they are a great starting point to building up your active reading, elimination, and picking numbers muscle, and pretty soon, you’ll be able to put your own spin on these techniques to get to solutions faster and best suited for your learning style. Happy studying!
Thanks to Lucas Fink for his contribution to this post, especially for his enviable MS Paint skills!
-
As one of Magoosh’s Blog Editors, Anika relies on her nearly 20 years in education and youth leadership spaces to produce empowering, student-centered content across Magoosh’s blogs. Anika has a BA from Grinnell College and an MPP from Harvard University. Her experience includes serving two years as a Fulbright English Teaching Assistant in Malaysia, an SAT tutor for Kaplan, and currently, as the Executive Director of Youth Activism Project, a nonprofit that she co-founded when she was 12 years old. Anika’s work has been featured in The Washington Post, The Boston Globe, and Yahoo! Money. She has also spoken at panels and given presentations at New York University and Harvard University. If you’d like to keep up with Anika, you can check out her LinkedIn, Instagram, Twitter, and personal website.
View all posts
By the way, Magoosh can help you study for both the SAT and ACT exams. Click here to learn more!
You are here: Home → Articles → How to set up an equation for a word problem
Students often have problems setting up an equation for a word problem in algebra. To do that, they need to see the RELATIONSHIP between the different quantities in the problem. This article explains some of those relationships.
I was asked,
I need an easy and helpful way to teach writing equations.
Example: Helen has 2 inches of hair cut off each time she goes to the hair salon. If h equals the length of hair before she cuts it and c equals the length of hair after she cuts it, which equation would you use to find the
length of Helen’s hair after she visit the hair salon?a) h = 2 − c c) c = h − 2
b) c = 2 − h d) h = c − 2Is there a single method to teaching students how to write algebraic equations? I need help.
The first thing I do when trying to figure out how to teach something is to analyze my own thinking. How do I think when solving this
problem? What are the steps and fine details? It is these details and steps that I may do automatically that I need to explain to students
to help them.
Seeing the quantities and their relationship instead of numbers
In this problem there is seemingly lots of information, but really it’s about recognizing quantities and the simple relationship between
them. This is of course the exact same task as translating a situation explained in words into a mathematical expression using symbols.
Children manifest the difficulty in this task when they read a simple word problem and then ask, «Do I go this times this, or do I divide?», just guessing the operation to perform with the different numbers given in the problem.
Students need to see the quantities and the RELATIONSHIP between them. They need to step out of the 5, 2, 10, 789, or any others numbers in the problem, and see the general quantities involved and how those are related to each other. In very simple word problems that relationship usually involves just one of the four basic operations. Then in algebra, there may be more quantities and more operations between them.
Examples of addition word problems
Example. Jenny has 7 marbles and Kenny has 5. How many do they have together?
The keyword together tells us that ADDITION is probably the operation needed. The quantities here are Jenny’s marbles, Kenny’s marbles, and total marbles. The relationship between the three is
Jenny’s marbles + Kenny’s marbles = Total marbles
From this general relationship between the quantities it is easy to write an equation for the problem, which solves it:
Relationship: Jenny’s marbles + Kenny’s marbles = Total marbles Equation: 7 + 5 = _____ I wrote ____ in the place of total marbles since that is what the problem is asking for (the unknown).
All of this may look oversimplified, but helping children to see the underlying relationship between the quantities is important. Consider now this problem:
Example: Jenny and Kenny together have 37 marbles, and Kenny has 15. How many does Jenny have?
Many teachers might try to explain this as a subtraction problem, but in the most fundamental level it is about addition! It still talks about two people having certain amount of marbles together. The relationship between the quantities is the SAME as above, so we still need to write an addition equation.
Relationship: Jenny’s marbles + Kenny’s marbles = Total marbles Equation: _____ + 15 = 37 Then, we can solve the equation ____ + 15 = 37 by
subtracting. Using this kind of approach in the elementary grades will help children to set up equations
in algebra story problems later.
Example: Jenny, Kenny, and Penny together have 51 marbles.
Kenny has double as many marbles as Jenny has, and Penny has 12. How many does Jenny have?The relationship between the quantities is the same, so it is solved the same way: by writing an addition equation. However, we need to denote the number of Jenny’s and Kenny’s marbles with something. Jenny’s marbles are unknown, so we can denote that with the variable n. Then Kenny has 2n marbles.
Relationship: Jenny’s marbles + Kenny’s marbles + Penny’s marbles = Total marbles Equation: n + 2n + 12 = 51
Example: Jane is on page 79 of her book. The book has 254 pages. How many pages does she still have to read?
This time the word «still» clues us in to an additive relationship where one of the addends is missing. You can initially write an empty line for what is not known, and later replace that with a variable.
pages already read + pages still to read = pages total + = This equation is of course is then solved by subtraction, but it is better if you view it as an addition situation and write an addition equation for it.
Example: The number of hours that were left in the day was one-third of the number of hours already passed. How many hours were left in the day?
(From Grade 5 word problems for kids)Can you see the general principle governing this problem? It talks about the hours of the day where some hours already passed and some hours left. This, of course, points to addition once again: we have one part of the day, another part, and a total.
The only quantity we know is the total hours for the day. We don’t know the hours already passed nor the hours left, so initially you can use two empty lines in the equation that shows the basic relationship between the quantities:
hours already passed + hours left = total hours = Then, the information in the first sentence gives us another relationship:
«The number of hours that were left in the day was one-third of the number of hours already passed.»
We don’t know the amount of hours passed nor the hours left. So let’s use the variable p for the hours passed. Then we can write an expression involving p for the hours left, because «hours left is one-third of the hours passed,» or
hours left = 1/3 p
Then writing 1/3p for the «hours left» in the first equation will give us:
hours already passed + hours left = total hours p + 1/3p = 24 This can be solved using basic algebra or by guess & check.
Subtraction word problems
One situation that indicates subtraction is difference or how many/much more. However, the presence of the word «more» can indicate either an addition or subtraction, so be careful.
Example: Ted read 17 pages today, and Fred read 28. How many more pages did Fred read?
The solution is of course 28 − 17 = 11, but it’s not enough to simply announce that – children need also to understand that difference is the result of a subtraction and tells the answer to how many more.
Relationship: Pages Fred read − pages Ted read = difference Equation: 28
− 17
= __
Example: Greg has 17 more marbles than Jack. Jack has
15. How many does Greg have?Here the word more has a different meaning. This
problem is not about the difference. The question asks how many does
Greg have – not what is the difference in the amounts of marbles. It simply states Greg has 17 more compared to Jack, so here the word more simply indicates addition: Greg has as many as Jack AND 17 more, so Greg has 15 + 17 marbles.
Example: The mass of the Great Pyramid is 557t greater than that of the Leaning Tower of Pisa. Stone Henge has a mass of 2695t which is 95t less than the Leaning Tower of Pisa. There once was a Greater Pyramid which had a mass twice that of the Great Pyramid. What was the mass of the Greater Pyramid?
(From Grade 5 word problems for kids)Each of the first three sentences give information that can be translated into an equation. The question is not about how many more so it’s not about difference. One thing being greater than another implies you add. One thing being less than another implies you subtract. And one thing being twice something indicates multiplying by 2.
When I read this problem, I could immediately see that I could write equations from the different sentences in the problem, but I couldn’t
see the answer right away. I figured that after writing the equations I would see some way forwad; probably one equation is solved and gives an answer to another equation.The first sentence says, «The mass of the Great Pyramid is 557t greater than that of the Leaning Tower of Pisa». What are the quantities and the relationship between them here?
mass of Great Pyramid = mass of the Leaning Tower of Pisa + 557t The second sentence says «Stonehenge has a mass of 2695t which is 95t less than the Leaning Tower of Pisa.»
Here it gives you a relationship similar to the one above, and it
actually spells out the mass of Stonehenge. It’s like two separate pieces
of information: «Stonehenge weighs 95t less than the tower.
Stonehenge weighs 2695t.» Less means you subtract. If you have
trouble deciding which is subtracted from which, you can think in your mind
which is heavier: Stonehenge or the tower?
either mass of Stonehenge = mass of tower − 95t or mass of tower = mass of Stonehenge − 95t Now since the mass of Stonehenge is given, you can solve this equation, and from that knowledge you
can solve the first equation, and from that go on to the mass of the «Greater Pyramid«.
If the teacher just jumps directly to the number sentences when solving word
problems, then the students won’t see the step that happens in the mind before
that. The quantities and the relationship between them have to be made
clear and written down before fiddling with the actual numbers. Finding
this relationship should be the most important part of the word problems.
One could even omit the actual calculations and concentrate just finding the
quantities and relationships.
Problem of Helen’s hair length
Problem. Helen has 2 inches of hair cut off each time she goes to the hair salon. If
h equals the length of hair before she cuts it and c equals the length of hair after she cuts it, which equation would you use to find the
length of Helen’s hair after she visit the hair salon?
a. h = 2 − c c. c = h − 2
b. c = 2 − h d. h = c − 2
Solution. Ignoring the letters c and h for now,
what are the quantities? What principle or relationship is there between
them? Which possibility of the ones listed below is right? Which do you take away from which?
| 1. | cut hair | − | hair length before cutting | = | hair length after cutting |
| 2. | cut hair | − | hair length after cutting | = | hair length before cutting |
| 3. | hair length before cutting | − | cut hair | = | hair length after cutting |
| 4. | hair length after cutting | − | cut hair | = | hair length before cutting |
SIMPLE, isn’t it?? In the original problem, the equations are given
with the help of h and c instead of the long phrases «hair length before
cutting» and «hair length after cutting». You can
substitute the c, h, and 2 into the relationships above, and then match the equations (1) — (4) with the equations (a) through (d).
Helping students to write the algebraic equations
One idea that came to mind is to go through the examples above, and more, based on the typical word problems in the math books, and then turn the whole thing around and have students do exercises such as:
- Write 3 different story problems where the solution is based on the relationship
money earned − money spent on this — money spent on that = money left
- Write 3 different story problems where the solution is based on the relationship
original price − discount percent x original price = discounted price
- Write 3 different story problems where the solution is based on the relationships
money earned each month − expenses/taxes each month = money to use each month AND
money to use each month × number of months = money to use over a period of time
- Write 3 different story problems where the solution is based on the relationships
speed × time = distance AND
distance from A to B + distance from B to C = distance from A to C
I’m sure you can think of more similar exercises.
See also:
Why are math word problems SO difficult for elementary school children?
Hint: it has to do with a «recipe» that many math lessons follow.
The do’s and don’ts of teaching problem solving in math
General advice on how you can teach problem solving in elementary, middle, and high school math.
How I Teach Word Problems by Andre Toom (PDF)
This article is written by a Russian who immigrated to US and noticed how COLLEGE LEVEL students have difficulties even with the simplest word problems! He describes his ideas on how to fill in the gap formed when students haven’t learned how to solve word problems in earlier education.
A list of websites focusing on word problems and problem solving
Use these sites to find good word problems to solve. Most are free!
Comments
When solving word problems, students must first decide what quantity represents x and then must write all the other quuantities in terms of x. I teach the students to set up arrows according to the language in the problem. All arrows point to x.
Example. Harry had 10 less toys than Mark. Sue has twice as many toys as Harry. Set up arrows: Sue— Harry—Mark Therefore Mark is x, Harry is x-10 and Sue is 2(x-10). Students find this very helpful.Sandy Denny
My idea is the math teacher might teach and understand the students at the same time and everyone would have a sense of humor. So I think she/he will know if the students are listening or not, when after the class, talk to the student and ask what is wrong. Don’t hurt the student’s feelings.
lorence