How to do regressions in excel

In Excel for the web, you can view the results of a regression analysis (in statistics, a way to predict and forecast trends), but you can’t create one because the Regression tool isn’t available.

You also won’t be able to use a statistical worksheet function such as LINEST to do a meaningful analysis because it requires you enter it as an array formula, which isn’t supported in Excel for the web.

If you have the Excel desktop application, you can use the Open in Excel button to open your workbook and use either the Analysis ToolPak’s Regression tool or statistical functions to perform a regression analysis there.

Click Open in Excel and perform a regression analysis.

For news about the latest Excel for the web updates, visit the Microsoft Excel blog.

For the full suite of Office applications and services, try or buy it at Office.com.

Regression is an Analysis Tool, which we use for analyzing large amounts of data and making forecasts and predictions in Microsoft Excel.

Want to predict the future? No, we are not going to learn astrology. We are into numbers and we will learn regression analysis in Excel today.

To predict future estimates, we will study:

• REGRESSION ANALYSIS USING EXCEL FUNCTIONS (MANUAL REGRESSION FINDING)

• REGRESSION ANALYSIS USING EXCEL’S ANALYSIS TOOLPAK ADD-IN

• REGRESSION CHART IN EXCEL

Let’s do it…

Scenario:

Let’s assume you sell soft drinks. How cool will it be if you can predict:

• How many soft drinks will be sold next year based on previous year’s data?
• Which fields need to be focused?
• And how can you increase your sales by changing your strategy?

It will be profitably awesome. Right?… I know. So let’s get started.

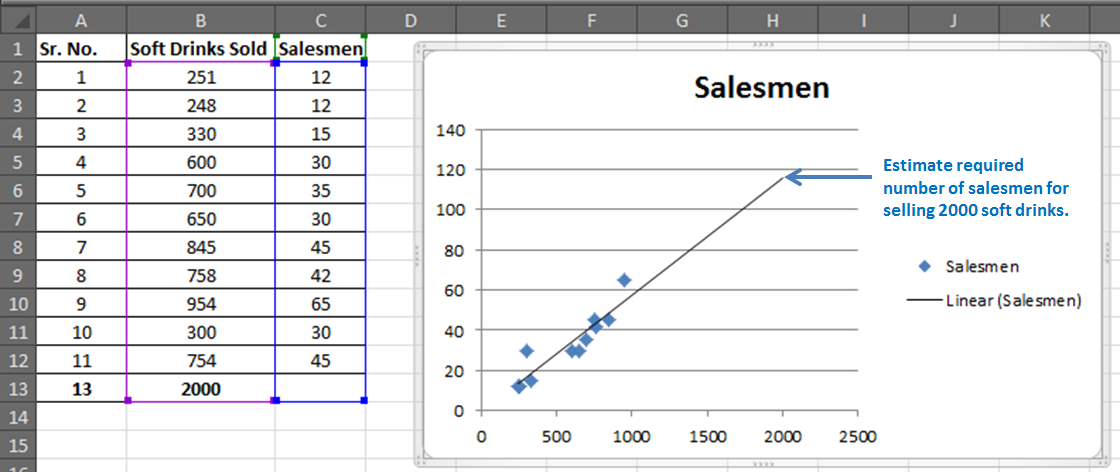
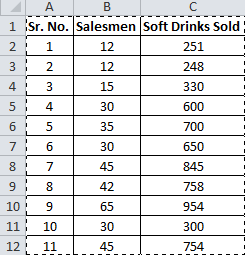
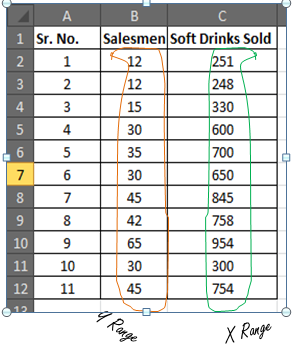
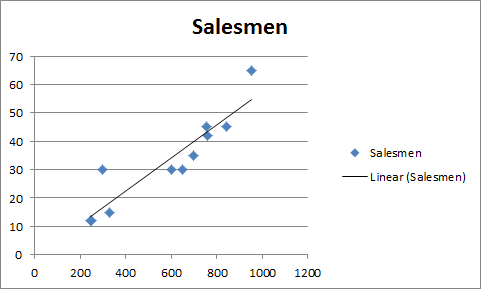
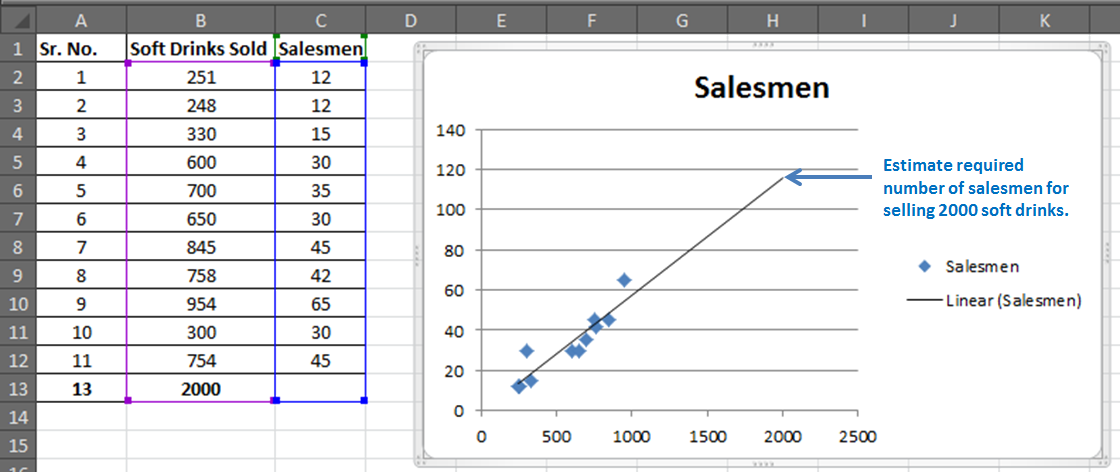
You have 11 records of salesmen and soft drinks sold.

Now based on this data you want to predict the number of salesmen required to achieve 2000 sales of soft drinks.

The regression equation is a tool to make such close estimates. To do so, we need to know Regression first.

REGRESSION ANALYSIS USING EXCEL FUNCTIONS (MANUAL REGRESSION FINDING)

This part will make you understand regression better than just telling excel regression procedure.

Introduction:

Simple Linear Regression: 

The study of the relationship between two variables is called Simple Linear Regression. Where one variable depends on the other independent variable. The dependent variable is often called by names such as Driven, Response, and Target variable. And the independent variable is often pronounced as a Driving, Predictor or simply Independent variable. These names clearly describe them.

Now let’s compare this with your scenario. You want to know the number of salesmen required to achieve 2000 sales. So here, the dependent variable is the number of salesmen and the independent variable is sold soft drinks.

The independent variable is mostly denoted as x and dependent variable as y.

In our case, soft drinks are sold x and the number of salesmen is y.

If we want to know how many soft drinks will be sold if we appoint 200 salesmen, then the scenario will be vice-versa.

Moving On.

The “Simple” Math of Linear Regression Equation:

Well, it’s not simple. But Excel made it simple to do.

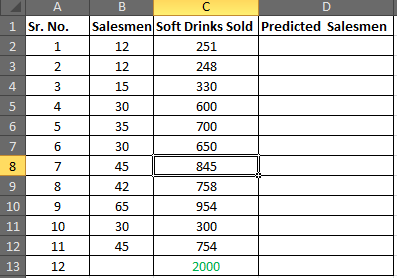
We need to predict the required number of salesmen for all 11 cases to get the 12th closest prediction.

Let’s say:

Soft Drink Sold is x

The number of Salesmen is y

The predicted y (number of salesmen) also called Regression Equation,  would be

Now you must be wondering where the stat will you get the slope and intercept. Don’t worry, excel has functions for them. You do not need to learn how to find the slope and intercept it manually.

If you want, I will prepare a separate tutorial for that. Let me know in the comments section. These are some important data analytics tools.

Now let’s step into our calculation:

Step1: Prepare this small table

Step 2: Find the slope of the regression line

Excel Function for slopes is

=SLOPE(known_y’s,known_x’s)

Your known_y’s are in range B2:B12 and known_x’s are in range C2:C12

In cell B16, write the formula below

(Note: Slope is also called coefficient of x in the regression equation)

You will get 0.058409. Round up to 2 decimal digits and you will get 0.06.

Step 3: Find the Intercept of Regression Line

Excel function for the intercept is

=INTERCEPT(known_y’s, known_x’s)

We know what our known x’s and y’s

In cell B17, write down this formula

=INTERCEPT(B2:B12, C2:C12)

You will get a value of -1.1118969. Roundup to 2 decimal digits. You will get -1.11.

Our Linear Regression Equation is = x*0.06 + (-1.11). Now we can predict possible y depending on the target x easily.

Step 4: In D2 write the formula below

=C2*$B$16+$B$17    (Regression Equation)

You will get a value of 13.55.

Select D2 to D13 and press CTRL+D to fill down the formula in the range D2:D13

In cell D13 you have your required number of salesmen.

Hence, to achieve the target of 2000 Soft Drink Sales, you need an estimate of 115.71 salesmen or say 116 since it is illegal to cut humans into pieces.

Now using this you can easily conduct What-If analysis in excel. Just change the number of sales and it will show you many salesmen will it take to get that sales target achieved.

Play around it to find out:

How much workforce do you need to increase sales?

How many sales will increase if you increase your salesmen?

Make Your Estimate More Reliable:

Now you know that you need 116 salesmen to get 2000 sales done.

In analytics, nothing is just said and believed. You must give a percentage of reliability on your estimate. It is like giving a certificate of your equation.

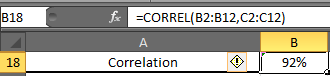
Correlation Coefficient Formula:

The next thing you will be asked is how much these two variables are related. In static terms, you need to tell the coefficient of correlation.

Excel function for correlation is

In your case, known_x’s and Know_y’s are array1 and array2 irrespectively.

In B18 enter this formula

You will have 0.919090. Formate cell B2 into the percentage. Now have 92% of correlation.

Now, what this 92% means. It means, there 92% of chances of sales increase if you increase the number of salesmen and 92% of sales decrease if you decrease the number of salesmen. It is called Positive Correlation Coefficient.

R Squire (R^2) :

R Squire value tells you, by what percentage your regression equation is not a fluke. How much it is accurate by the data provided.

The Excel function for R squire is RSQ.

RSQ(known_y’s, Known_x’s)

In our case, we will get R squire value in cell B19.

In B19 enter this formula

So we have 84% of r Square value. Which is a very good explanation of our regression. It says that 84% of our data is just not by chance. Y (number of salesmen) is very much dependent on X (sales of soft drinks).

There are many other tests we can do on this data to ensure our regression. But manually it will be a complex and lengthy procedure. That is why excel provides Analysis Toolpak. Using this tool we can do this regression analysis in seconds.

REGRESSION IN EXCEL USING EXCEL’S ANALYSIS TOOLPAK ADD-IN

If you already know what regression equations are, and you just want your results quickly then this part is for you. But if you want to understand regression equations easily then scroll up to REGRESSION ANALYSIS USING EXCEL FUNCTIONS (MANUAL REGRESSION FINDING).

Excel provides a whole bunch of tools for analysis in its Analysis Toolpak. By default, it is not available in the Data tab. You need to add it. So let’s add it first.

Adding Analysis Toolpak to Excel 2016

If you don’t know where is data analysis in excel follow these steps

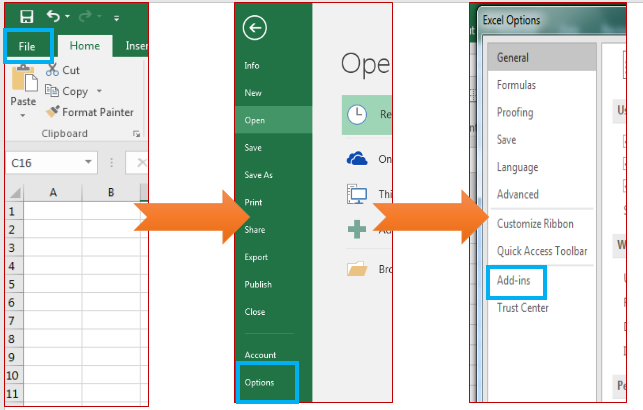
Step 1: Go to Excel Options: File? Options? Add-Ins

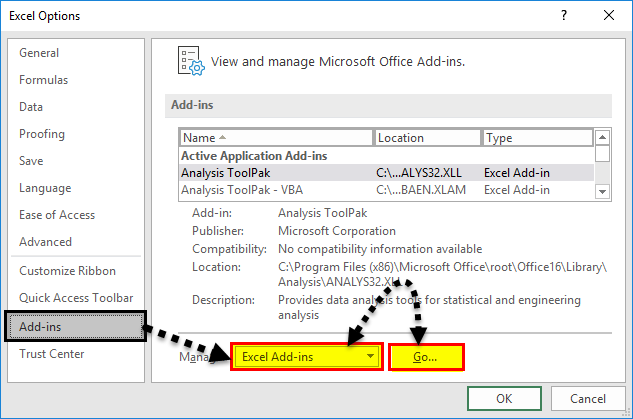
Step 2: Click on Add-Ins. You will see a list of available add-Ins.

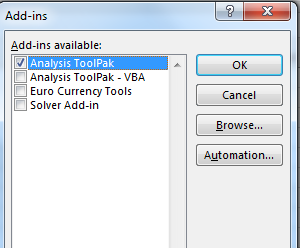
Select Analysis ToolPak and at the bottom of the window, find manage. In manage select Excel Add-Ins and Click on GO.

Add-ins window will open. Here, select Analysis ToolPak. Then click the ok button.

Now you can access all functions of data analysis ToolPak from Data Tab.

Using Analysis ToolPak for Regression

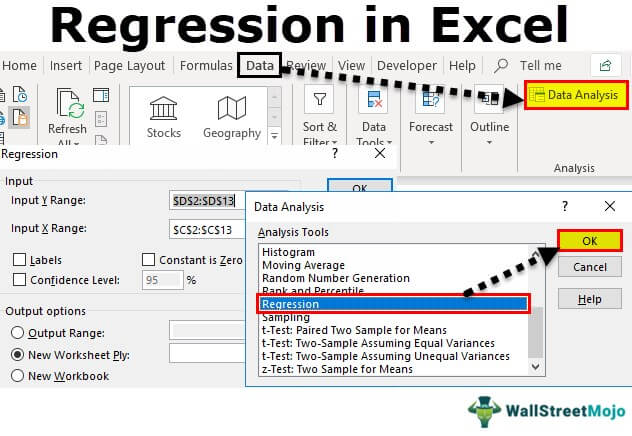
Step 1: Go to the Data tab, Locate Data Analysis. Then click on it.

A dialogue box will pop up.

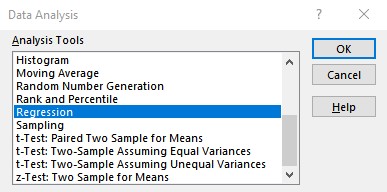
Step 2: Find ‘Regression’ in Analysis Tools list and hit the OK button.

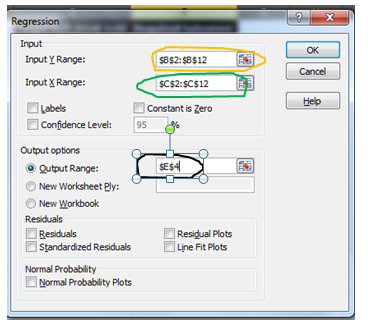
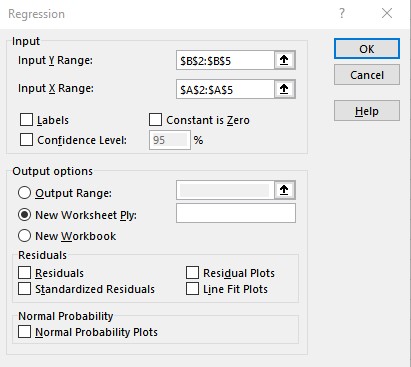
The regression input window will pop up. You will see a number of available input options. But for now, we will just concentrate on Y Range and X Range, leaving everything else to default.

Step 4: Provide Inputs:

No. of Salesmen is Y

Sales of soft drinks are X

Hence

• Y Range= B2:B11

And 

•  X Range = C2:C11

For the output range, I have selected E4 on the same sheet. You may select a new worksheet to get results on a new worksheet in the same workbook or a complete new workbook. When you are done with your inputs, hit the OK button.

Results:

You will be served with a variety of information from your data. Don’t get overwhelmed. You don’t need to consume all the dishes.

We will only deal with those results which will help us to estimate the required number of salesmen

Step 5: We know the regression equation for estimation of y, that is

x*Slope+Intercept

We just need to locate Slope and Intercept in results.

And here they are.

The intercept Coefficient is clearly mentioned.

The slope is written as ‘X Variable 1’, some times also mentioned as the coefficient of X. Round up them and we will get -1.11 as Intercept and 0.06 as Slope.

Step 6: From results, we can drive the Regression equation. And that would be

=x*(0.06) + (-1.11)

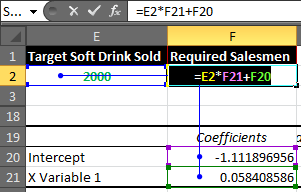
Prepare this table in excel.

For now, x is 2000, which is in cell E2.

In Cell F2 enter this formula

=E2*F21+F20

You will get a result of 115.7052757.

Rounding it up will give us 116 of Required Salesmen.

So we have learned how to form the regression equation manually and using Analysis ToolPak. How can you use this equation to estimate future stats?

Now let’s understand the regression output given by Analysis Toolpak.

Understanding the Regression Output:

There is no benefit, if you do regression analysis using analysis tool pack in excel and can’t interpret its meaning.

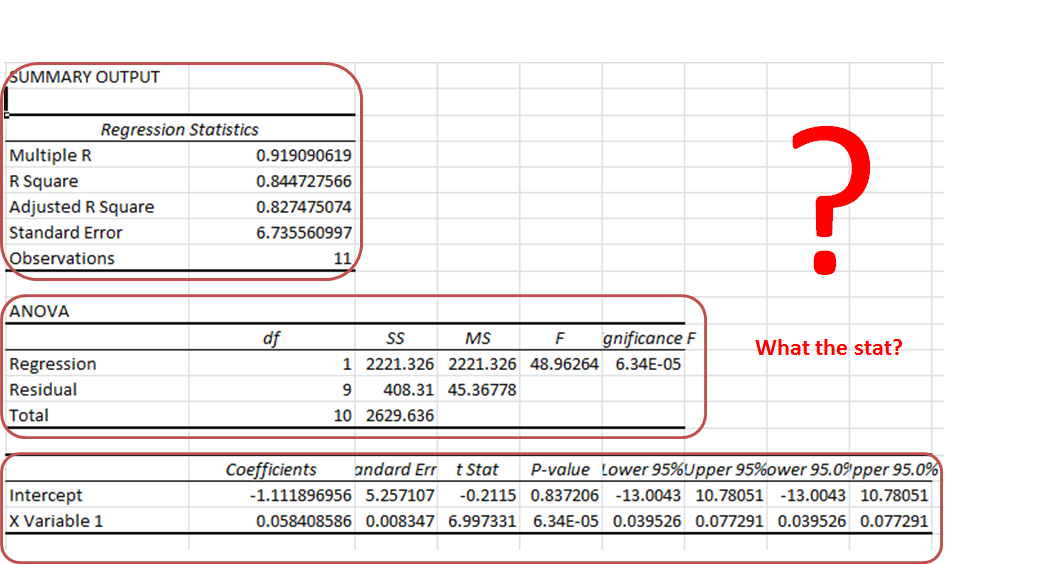
Summary Section:

As the name suggests, it is a summary of the data.

1. 1. Multiple R: It tells how fit the regression equation is to the data. It is also called the correlation coefficient. 

In our case, it is 0.919090619 or 0.92 (roundup). This means that there is a 92% chance of an increase in sales if we increase our salesmen count.

1. 1. R Square: It tells the reliability of found regression. It tells us how many observations are part of our line of regression. In our case, it is 0.844727566 or 0.85. It means that our regression is fit by 85%.
   2. Adjusted R Square: Theadjusted square is just a more testified version of R square. Mainly useful in Multiple Regression Analysis.
   3. Standard Error: While R. Squire tells you how many data points fall near the regression line, the standard error tells you how far a data point can go from the regression line. 

In our case, it is 6.74.

1. Observation: This is simply the number of observations, which is 11 in our example.

Anova Section:

This section is hardly used in linear regression.

1. df. It is a degree of freedom. It is used when calculating regression manually.
2. SS. Sum of squares. It is just a sum of squares of variances. Used to find R squire values.
3. MS. This means squared value.
4. And 5. F and Significance of F. If the significance of F (p-value of the slope) is less than the F test than you can discard the null hypothesis and prove your hypothesis. In simple language, you can conclude that there is some effect of x on y when changed. 

In our case, F is 48.96264 and Significance of F is 0.000063. It means our regression fits the data.

Regression Section:

In this section, we have the two most important values for our regression equation.

1. Intercept: We have an intercept here that tells where x-intercepts on Y. This is an important part of the regression equation. It is -1.11 in our case.
2. X variable 1 (Slope). Also called the coefficient of x. It defines the tangent of the regression line.

REGRESSION CHART IN EXCEL

In excel, it is easy to plot a regression chart. Just follow these steps. To add Regression Chart in Excel 2016, 2013, and 2010 follow these simple steps.

Step 1. Have your known x’s in the first column and know y’s in the second.

In our case, we know Known_ x’s are Soft Drinks Sold. And known_y’s are Salesmen.

Step 2. Select your known x’s and y’s range.

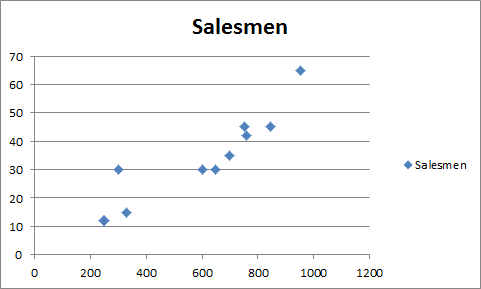
Step 3: Go to the Insert tab and click on the scatter chart.

You will have a chart that looks like this.

Step 4. Add the trend line: Goto layout and locate the trendline option in the analysis section.

Under the Trendline option, click on Linear Trendline.

You will have your graph looking like this.

This is your regression graph.

Now if you add the data below and extend the selected data. You will see a change in your graph.

For our example, we added 2000 to the Soft Drink Sold and left the Salesmen blank. And when we extend the range of the graph, this is what we will have.

It will give the required number of salesmen for doing 2000 sales of soft drinks in graphical form. Which is slightly below 120 in the graph. And from our regression equation, we know it is 116.

In this article, I tried to cover everything under Excel Regression Analysis. I explained regression in excel 2016. Regression in excel 2010 and excel 2013 is same as in excel 2016.

For any further query on this topic, use the comments section. Ask a question, give an opinion or just mention my grammatical mistakes. Everything is welcome. Just don’t hesitate to use the comment section.

Related Data:
How to Use STDEV Function in Excel

How To Calculate MODE function in Excel

How To Calculate Mean function in Excel

How to Create Standard Deviation Graph

Descriptive Statistics in Microsoft Excel 2016

How to Use Excel NORMDIST Function

How to use the Pareto Chart and Analysis

Popular Articles:

50 Excel Shortcut to Increase Your Productivity

How to use the VLOOKUP Function in Excel

How to use the COUNTIF function in Excel 2016

How to use the SUMIF Function in Excel

In this tutorial, you’ll learn how to perform Linear Regression in Excel. Linear regression is an approach to linear modeling the relationship between a dependent and an independent variable. Simple linear regression uses an independent variable to predict the outcome of the dependent variable.

The equation for linear regression is given by: y = a + bx, where x is the independent variable, y is the dependent variable and the coefficients are given by:

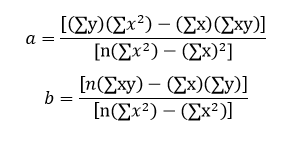
Our aim is to find coefficients a which is the intercept and b which is the slope to obtain the equation of the straight line which best fits our data by the least square method. There are two ways in Excel in which we can find the linear regression line which is discussed below for the following data set:

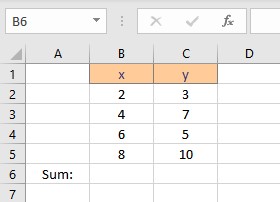
Calculate Linear Regression in Excel Using Its Formula

First, we need to calculate the parameters in the formula for coefficients a and b. The parameters are Σx, Σy, Σxy and Σx² . To calculate Σx follow these steps:

• Select the cell where you want to calculate and display the summation of x.
• Type =SUM(, select the cells containing the numbers and complete the formula with ).

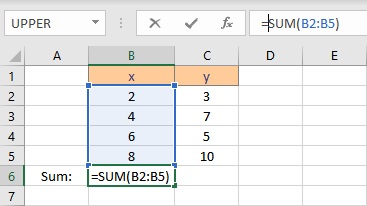
• Press the Enter key to display the result.

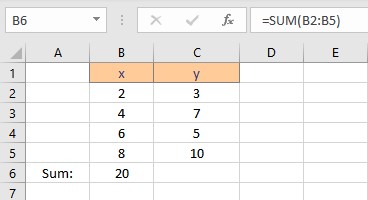
To calculate Σy follow these steps:

• Select the cell where you want to calculate and display the summation of y.
• Type =SUM(, select the cells containing the numbers and complete the formula with ).

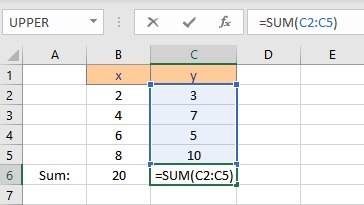
• Press the Enter key to display the result.

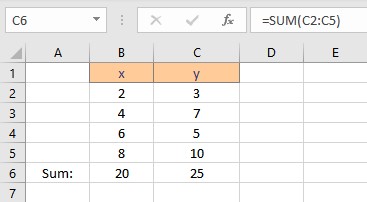
To calculate Σxy follow these steps:

• Select the cell where you want to calculate and display the product of a pair of x and y values.
• Type =B2*C2, as the first x and y values are in cells B2 and C2 respectively.

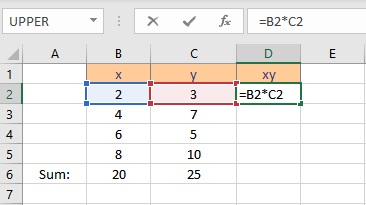
• Press the Enter key to display the result.

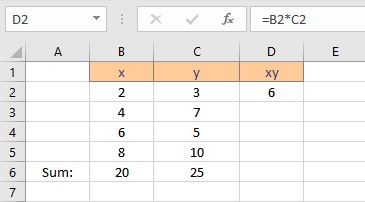
• Copy the formula for the calculation of product xy for the entire list by dragging down the fill handle.

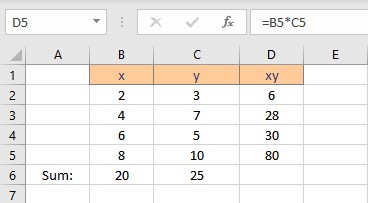
• Select the cell where you want to calculate and display the summation of xy.
• Type =SUM(, select the cells containing the numbers and complete the formula with ).

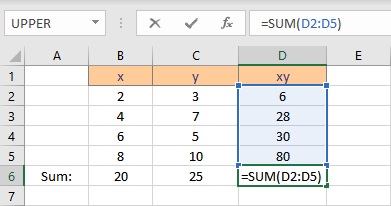
• Press the Enter key to display the result.

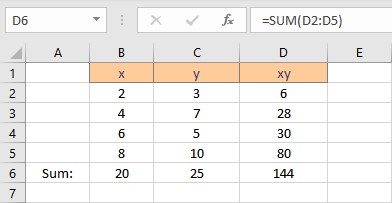
To calculate Σx² follow these steps:

• Select the cell where you want to calculate and display the square of the first x value.
• Type =B2^2, as the first x value, is in cell B2. The caret operator raises the number to the power written next to it.

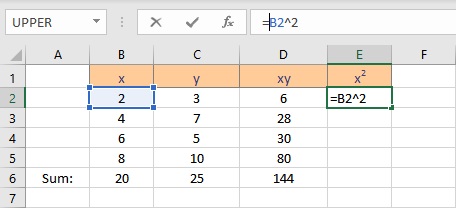
• Press the Enter key to display the result.

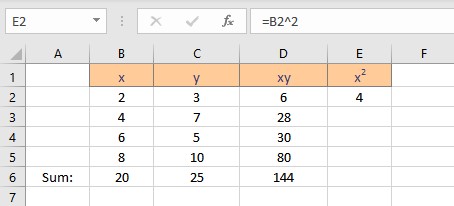
• Copy the formula for the calculation of squares of x for the entire list by dragging down the fill handle.

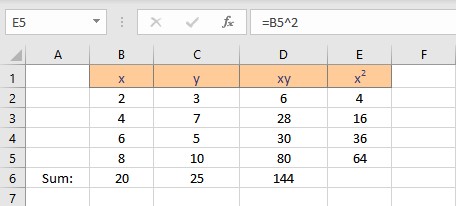
• Select the cell where you want to calculate and display the summation of x².
• Type =SUM(, select the cells containing the numbers and complete the formula with ).

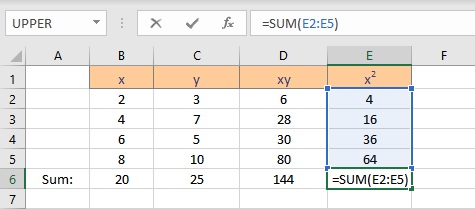
• Press the Enter key to display the result.

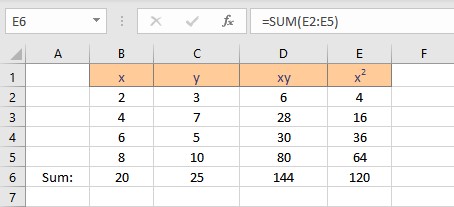
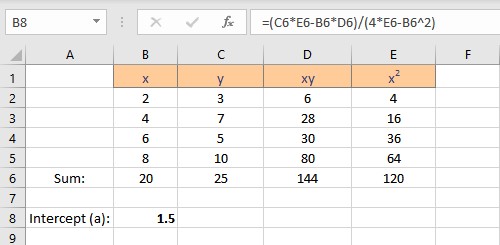
We now have the parameters essential for the calculation of coefficients intercept a and slope b. Follow the steps to calculate the intercept a:

• Select the cell where you want to display the value of the intercept.
• Type =(C6*E6-B6*D6)/(4*E6-B6^2), where C6 contains the value of Σy, E6 contains the value of Σx², B6 contains the value of Σx, D6 contains the value of Σxy and 4 is the number of data points in the data set.

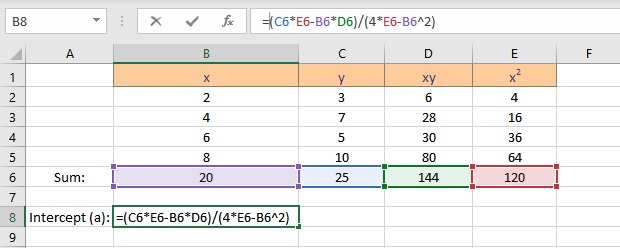
• Press the Enter key to display the result.

Follow the steps to calculate the slope b:

• Select the cell where you want to display the value of the slope.
• Type =(4*D6-B6*C6)/(4*E6-B6^2), where C6 contains the value of Σy, E6 contains the value of Σx², B6 contains the value of Σx, D6 contains the value of Σxy and 4 is the number of data points in the data set.

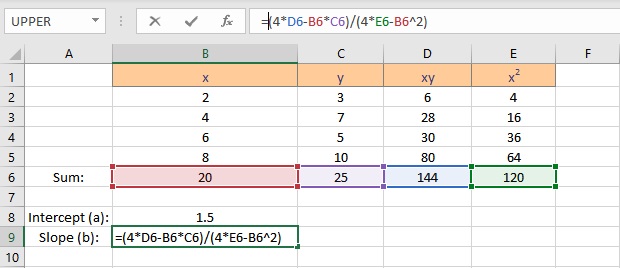
• Press the Enter key to display the result.

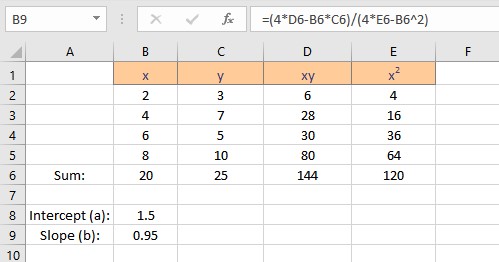
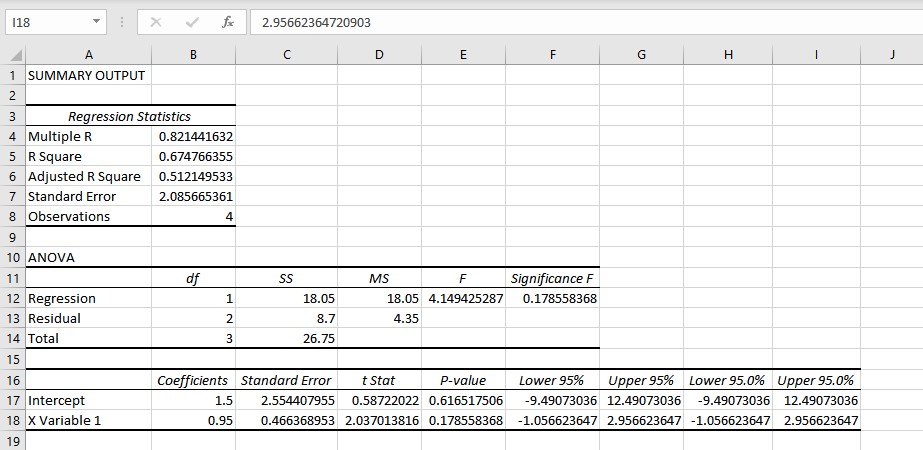
We have the values for the slope and intercept, the equation for the linear regression can be written as y = 1.5 + 0.95x. This equation can now be used to predict values of y for different values of x.

Linear Regression in Excel Using Data Analysis

To use the Data Analysis feature, you need to enable Analysis Toolpak in Excel. Follow these steps to manually enable the feature:

• Click on the File option present at the top left corner of the Excel window.
• From the menu that appears, click on Options to launch the Excel Options dialog box.
• Select the Add-ins option at the left side of the Excel Options dialog box.
• Select Excel Add-ins in the Manage box, and click Go.

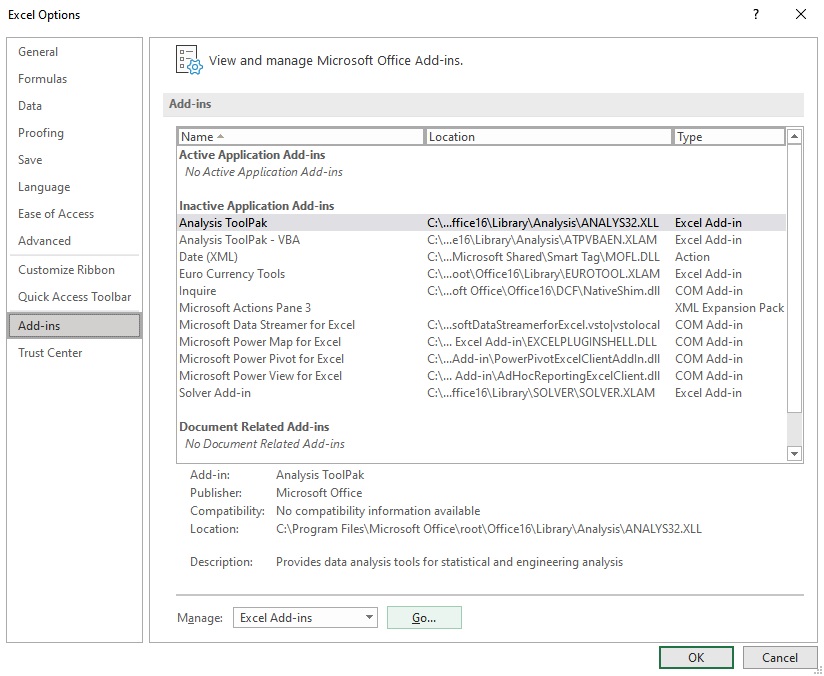
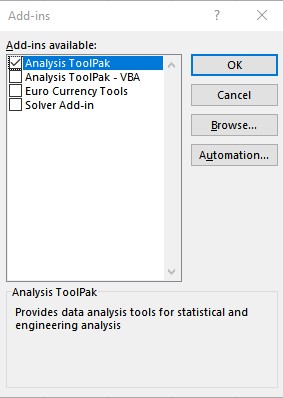
• In the Add-ins dialog box, check the Analysis Toolpak checkbox, and then click OK.

• The Data Analysis option now appears in the Analysis group on the Data tab.

Follow these steps to perform linear regression using Data Analysis:

• Click on Data Analysis present in the Analysis group on the Data tab.
• From the Data Analysis dialog box that appears, select Regression under the Analysis Tools and click on OK.

• Enter the cell ranges containing y values in the Input Y Range: text box and x values in the Input X Range: text box in the Regression dialog box and click OK.

• The results are displayed in a new worksheet. You can copy the intercept and slope coefficients to obtain an equation for the linear regression: y = 1.5 + 0.95x.

Conclusion

In this tutorial, we learned how to perform linear regression both using the formulas and Excel Add-ins.

References

• Load the Analysis ToolPak in Excel – Office Support (microsoft.com)

Is this article up to date?

How to do Linear Regression in Excel: Full Guide (2023)

How to do Linear Regression in Excel: Full Guide (2023)

Linear regression is an easy way of evaluating the relationship between two variables.

Previously, performing linear regression in Excel was nothing less than a complex task. But with advanced Excel data analysis tools, it is now only a matter of a few clicks.

The guide below will not only teach you how to perform linear regression in Excel but also how you may analyze a linear regression graph in Excel.

So, without further ado, let’s dive right in 👇

Download our free sample workbook here as you continue reading.

Linear regression equation

Simple linear regression draws the relationship between a dependent and an independent variable.

👉 The dependent variable is the variable that needs to be predicted (or whose value is to be found).

👉 The independent variable explains (or causes) the change in the dependent variable.

Simply put, the dependent variable depends upon the independent variable. And as the independent variable changes, the dependent variable changes too.

Mathematically, the linear relationship between these two variables is explained as follows:

Y= a + bx

Where,

Y = dependent variable

a = regression intercept term

b = regression slope coefficient

x = independent variable

“a” and “b” are also called regression coefficients. And Excel returns the predicted values of these regression coefficients too.

Kasper Langmann, Microsoft Office Specialist

How to do linear regression through a graph

Imagine a company that sells sweaters in a cold region. And the sale of sweaters is directly linked to the temperatures in that region.

The colder it is (low temperatures 🥶), the higher the sales of sweaters 🧣 go. This means sales (the dependent variable) depend upon the temperature (the independent variable).

Now, to predict the company’s sales for the future, you must analyze the sales trend in the past. This can be done by drawing a trendline.

Drawing this trendline between a dependent variable Y (the sales) and an independent variable X (the temperature) is called running linear regression.

So let’s do it!

The image above contains the historical data for both variables (temperatures and sales) for a few months.

To explain the relationship between these variables, we need to make a scatter plot.

To plot the above data in a scatter plot in Excel:

1. Select the data.
2. Go to the Insert Tab > Charts Group

1. Click on the scatterplot part icon.
2. Choose a scatter plot type from the drop-down menu.

Excel plots the data in a scatter plot.

Note that each dot in the scatter plot above is formed at the intersection of Variable X and Y.

For example, the first dot is plotted at the point where Y = 625 and X = 2.

Next, we must draw a trend line out of this scatter plot. To do so:

1. Click anywhere on the chart to select it.
2. Click on the “+” icon on the top right of the chart.

1. Hover your cursor over the option “Trendline”📈

A drop-down menu appears.

1. Select More Options. This will take you to the Format Trendline Pane.
2. Choose the linear trendline option to draw a trendline between the scatter points.

And there you go! Excel draws a linear trendline on the scatterplot.

The above image shows a downward regression line which represents a negative trend. But why is that?

To understand that, you must know how to analyze the results of a linear regression graph. And don’t worry – it’s only a section ahead.

Adding the equation and R-squared

We also want Excel to show the equation and R-squared for this graph. For that:

1. Scroll down the Task pane.
2. Check the option for “Equation” and “R-squared” on the graph.

And Excel will display the following regression statistics on the graph:

Equation: y= -19.622x + 612.77

R-squared= 0.7456

What are these? And what do they tell? We will discuss this shortly.

Pro Tip!

How to quickly interpret the relationship between two variables? By checking the sign of the x variable 💡

A positive sign means a positive relationship. And a negative sign means a negative relationship between the two variables.

Since our equation shows a “-19.622x”, the relation between our variables is negative.

Formatting the trendline

Do you also find the trendline a little overshadowed? Not to worry – You can always format it in Excel.

For example, to change the color of the trendline:

1. Select the trendline and right-click on it to launch the context menu.
2. Go to Format Trendline.
3. Under the Format Trendline pane, select “Fill & Line”.
4. To change the color of the trendline, choose a color as shown below.

Guess we will go with red for now 🚩 What do you think about it?

Trendline Style

Not only the color, but you can also change the style of the trendline.

Say, we want to change our dotted trendline to a solid one. To do so:

1. Select the trendline and right-click on it to launch the context menu.
2. Click on Format Trendline to launch the Format Trendline Pane.
3. Go to “Dash type” from the fill & line menu.
4. Select a solid line type.

This will change the style of the trendline from a dotted line to a perfectly solid line.

Chart Title

To enhance the readability of the graph, you may add graph titles and axes titles to it as follows:

1. Select the graph.
2. Go to Chart Elements > Chart Title > above chart.

1. Type in a Graph/Chart title as desired.

Axis titles

How about adding the Axis titles too?

To add a vertical title (for the Y-axis) to your chart:

1. Click Chart Elements > Axis Titles > Primary Vertical.

1. Type in a suitable title for the subject axis.

We have set the title for the Y-axis to “Sale of Sweaters”.

To add a horizontal Axis Title (for the X-axis):

1. Go to Chart elements > Axis Titles > Primary Horizontal.

1. Type in a suitable title for the subject axis.

We have set the title for the X-axis to “Avg. Temperature”

And that’s it. We’ve successfully run linear regression in Excel 🥳

How to analyze the linear regression graph

Good job with running linear regression in Excel.

Now is the time that we analyze the linear regression trendline formed above.

A linear trendline in Excel can take the following three shapes:

Positive trendline (upward facing)

If your trendline is upward facing (it elevates as it goes from left to right), it denotes a positive trend.

This means that there exists a positive relationship between both variables. An increase in the independent variable causes the dependent variable to increase.

This is how your graph will look with a positive trendline to it.

Negative trendline (downward sloping)

If your trendline is downward sloping (it slopes down as it goes from left to right), it denotes a negative trend.

A negative trendline means a negative relationship between both variables.

When there is a negative relationship between two variables, an increase in the independent variable causes the dependent variable to decrease.

This is how your graph will look with a negative trendline to it.

Jog down your memory lane to remember the trendline type in our example above. It was also a downward-sloping (negative) trendline.

That’s because there exists a negative relationship between sales and temperature. As the temperature falls, sales increase.

No trend

The two variables can also be independent of each other. In this case, movement in both variables is random with no relation to each other.

As there exists no relationship between them (neither positive nor negative), there is no particular slope for the trendline between them (neither upward facing nor downward sloping).

Such a trendline might look like this.

The trendline above is not exactly horizontal but very close to that. This is because there is no relation between the variables.

The slope of the graph

What if we want to know the percentage of change in Y caused by a change in X?

For example, for every 1% decrease in temperature, sales increase by what percentage?

The slope of the graph is an answer to this. Remember the linear regression equation?

Y = a + bx

In the above equation, the slope is represented by “b”. And the linear regression equation for our example turned out as follows:

Y= 612.77 – 19.622x

Here, the value for b is -19.622 and so is our slope. This means that a 1% change in the X variable (the temperature) causes a -19.622% change in the Y variable (the sales).

Also, as the sign with the value for b is a minus sign, this means that a 1% decrease in Variable X (temperature) causes a 19.622% increase in Variable Y (Sales).

Pro Tip!

An easy way to remember the slope is to remember Rise over Run. Rise means vertical axis. Run means horizontal axis. So the slope defines the change in variable Y caused by a change in variable X.

R-Squared

Another important output of our scatterplot is the R-squared value 👀

It tells us how much variation of the dependent variable comes from the change in the independent variable.

The R-squared for our example is 0.7456.

This tells that only 74.56% variation of Variable Y can be explained by Variable X.

Another statistical measure relevant to the linear regression model is the p value. However, it is totally opposite to the concept of R-squared.

Kasper Langmann, Microsoft Office Specialist

That’s it – Now what?

The above guide explains how to perform a linear regression analysis in Excel. And then, how to analyze the linear regression trendline and other relevant statistics.

👉 In addition to that, it also explains how you may format a trendline in Excel in different ways.

Performing linear regression in Excel through a scatter plot is super smart. But this is only one feature of Excel.

And there are many more smart functions in Excel. Like the VLOOKUP, SUMF, and IF functions.

Want to learn them already? Enroll in my 30-minute free email course that teaches you these and many more functions of Excel.

Other resources

Linear regression can be challenging to understand. But once you get a hold of it, you can run it for any possible dataset with sheer ease.

In addition to linear regression, Excel offers other forecasting functions too. Like the data analysis tools in Excel and the Excel FORECAST function.

Kasper Langmann2023-02-23T14:55:48+00:00

What Is Linear Regression?

Linear regression is a type of data analysis that considers the linear relationship between a dependent variable and one or more independent variables. It is typically used to visually show the strength of the relationship or correlation between various factors and the dispersion of results – all for the purpose of explaining the behavior of the dependent variable. The goal of a linear regression model is to estimate the magnitude of a relationship between variables and whether or not it is statistically significant.

Say we wanted to test the strength of the relationship between the amount of ice cream eaten and obesity. We would take the independent variable, the amount of ice cream, and relate it to the dependent variable, obesity, to see if there was a relationship. Given a regression is a graphical display of this relationship, the lower the variability in the data, the stronger the relationship and the tighter the fit to the regression line. 

In finance, linear regression is used to determine relationships between asset prices and economic data across a range of applications. For instance, it is used to determine the factor weights in the Fama-French Model and is the basis for determining the Beta of a stock in the capital asset pricing model (CAPM).

Here, we look at how to use data imported into Microsoft Excel to perform a linear regression and how to interpret the results.

Important Considerations

There are a few critical assumptions about your data set that must be true to proceed with a regression analysis. Otherwise, the results will be interpreted incorrectly or they will exhibit bias:

1. The variables must be truly independent (using a Chi-square test).
2. The data must not have different error variances (this is called heteroskedasticity (also spelled heteroscedasticity)).
3. The error terms of each variable must be uncorrelated. If not, it means the variables are serially correlated.

If those three points sound complicated, they can be. But the effect of one of those considerations not being true is a biased estimate. Essentially, you would misstate the relationship you are measuring.

Outputting a Regression in Excel

The first step in running regression analysis in Excel is to double-check that the free Excel plugin Data Analysis ToolPak is installed. This plugin makes calculating a range of statistics very easy. It is not required to chart a linear regression line, but it makes creating statistics tables simpler.  To verify if installed, select «Data» from the toolbar. If «Data Analysis» is an option, the feature is installed and ready to use. If not installed, you can request this option by clicking on the Office button and selecting «Excel options».

Using the Data Analysis ToolPak, creating a regression output is just a few clicks.

Given the S&P 500 returns, say we want to know if we can estimate the strength and relationship of Visa (V) stock returns. The Visa (V) stock returns data populates column 1 as the dependent variable. S&P 500 returns data populates column 2 as the independent variable.

1. Select «Data» from the toolbar. The «Data» menu displays.
2. Select «Data Analysis». The Data Analysis — Analysis Tools dialog box displays.
3. From the menu, select «Regression» and click «OK».
4. In the Regression dialog box, click the «Input Y Range» box and select the dependent variable data (Visa (V) stock returns).
5. Click the «Input X Range» box and select the independent variable data (S&P 500 returns).
6. Click «OK» to run the results.

[Note: If the table seems small, right-click the image and open in new tab for higher resolution.]

Interpret the Results

Using that data (the same from our R-squared article), we get the following table:

The R² value, also known as the coefficient of determination, measures the proportion of variation in the dependent variable explained by the independent variable or how well the regression model fits the data. The R² value ranges from 0 to 1, and a higher value indicates a better fit. The p-value, or probability value, also ranges from 0 to 1 and indicates if the test is significant. In contrast to the R² value, a smaller p-value is favorable as it indicates a correlation between the dependent and independent variables.

Charting a Regression in Excel

We can chart a regression in Excel by highlighting the data and charting it as a scatter plot. To add a regression line, choose «Add Chart Element» from the «Chart Design» menu. In the dialog box, select «Trendline» and then «Linear Trendline». To add the R² value, select «More Trendline Options» from the «Trendline menu. Lastly, select «Display R-squared value on chart». The visual result sums up the strength of the relationship, albeit at the expense of not providing as much detail as the table above. 

R Square | Significance F and P-Values | Coefficients | Residuals

This example teaches you how to run a linear regression analysis in Excel and how to interpret the Summary Output.

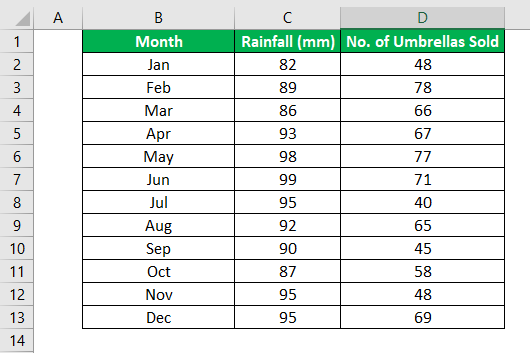
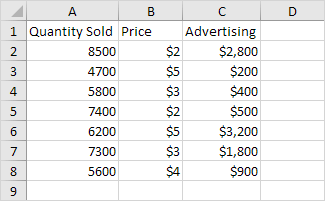
Below you can find our data. The big question is: is there a relation between Quantity Sold (Output) and Price and Advertising (Input). In other words: can we predict Quantity Sold if we know Price and Advertising?

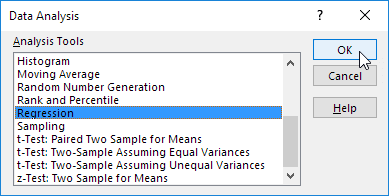
1. On the Data tab, in the Analysis group, click Data Analysis.

Note: can’t find the Data Analysis button? Click here to load the Analysis ToolPak add-in.

2. Select Regression and click OK.

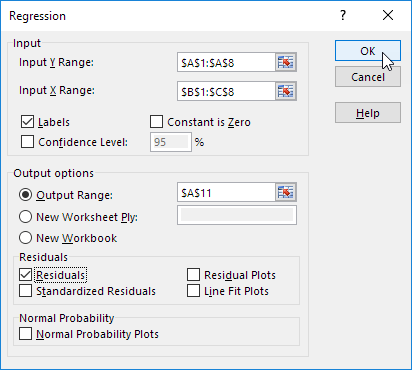
3. Select the Y Range (A1:A8). This is the predictor variable (also called dependent variable).

4. Select the X Range(B1:C8). These are the explanatory variables (also called independent variables). These columns must be adjacent to each other.

5. Check Labels.

6. Click in the Output Range box and select cell A11.

7. Check Residuals.

8. Click OK.

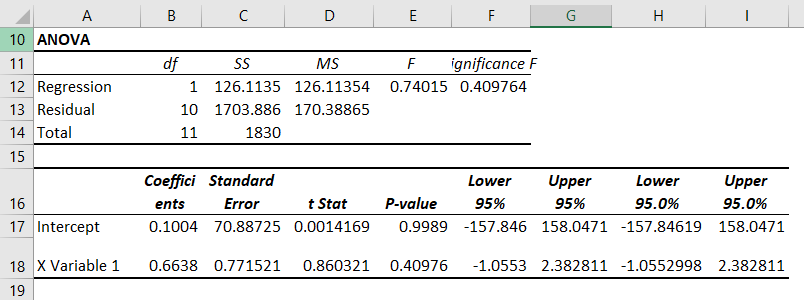
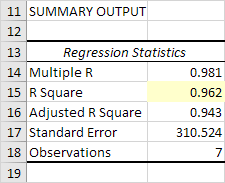
Excel produces the following Summary Output (rounded to 3 decimal places).

R Square

R Square equals 0.962, which is a very good fit. 96% of the variation in Quantity Sold is explained by the independent variables Price and Advertising. The closer to 1, the better the regression line (read on) fits the data.

Significance F and P-values

To check if your results are reliable (statistically significant), look at Significance F (0.001). If this value is less than 0.05, you’re OK. If Significance F is greater than 0.05, it’s probably better to stop using this set of independent variables. Delete a variable with a high P-value (greater than 0.05) and rerun the regression until Significance F drops below 0.05.

Most or all P-values should be below below 0.05. In our example this is the case. (0.000, 0.001 and 0.005).

Coefficients

The regression line is: y = Quantity Sold = 8536.214 -835.722 * Price + 0.592 * Advertising. In other words, for each unit increase in price, Quantity Sold decreases with 835.722 units. For each unit increase in Advertising, Quantity Sold increases with 0.592 units. This is valuable information.

You can also use these coefficients to do a forecast. For example, if price equals $4 and Advertising equals $3000, you might be able to achieve a Quantity Sold of 8536.214 -835.722 * 4 + 0.592 * 3000 = 6970.

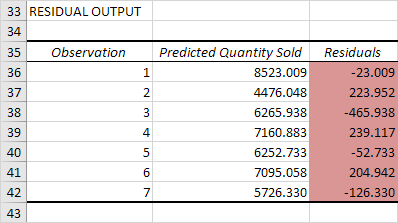
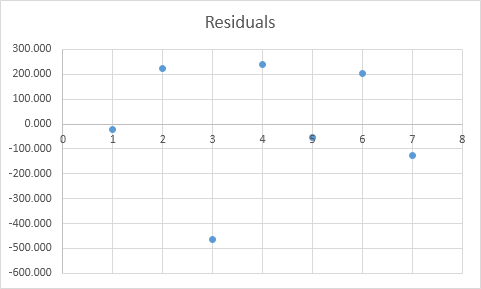
Residuals

The residuals show you how far away the actual data points are fom the predicted data points (using the equation). For example, the first data point equals 8500. Using the equation, the predicted data point equals 8536.214 -835.722 * 2 + 0.592 * 2800 = 8523.009, giving a residual of 8500 — 8523.009 = -23.009.

You can also create a scatter plot of these residuals.