How to calculate averages in excel

Download Article

Mathematically speaking, “average” is used by most people to mean “central tendency,” which refers to the centermost of a range of numbers. There are three common measures of central tendency: the (arithmetic) mean, the median, and the mode. Microsoft Excel has functions for all three measures, as well as the ability to determine a weighted average, which is useful for finding an average price when dealing with different quantities of items with different prices.

1
Enter the numbers you want to find the average of. To illustrate how each of the central tendency functions works, we’ll use a series of ten small numbers. (You won’t likely use actual numbers this small when you use the functions outside these examples.)
- Most of the time, you’ll enter numbers in columns, so for these examples, enter the numbers in cells A1 through A10 of the worksheet.
- The numbers to enter are 2, 3, 5, 5, 7, 7, 7, 9, 16, and 19.
- Although it isn’t necessary to do this, you can find the sum of the numbers by entering the formula “=SUM(A1:A10)” in cell A11. (Don’t include the quotation marks; they’re there to set off the formula from the rest of the text.)
2
Find the average of the numbers you entered. You do this by using the AVERAGE function. You can place the function in one of three ways:
- Click on an empty cell, such as A12, then type “=AVERAGE(A1:10)” (again, without the quotation marks) directly in the cell.
- Click on an empty cell, then click on the “f_x” symbol in the function bar above the worksheet. Select “AVERAGE” from the “Select a function:” list in the Insert Function dialog and click OK. Enter the range “A1:A10” in the Number 1 field of the Function Arguments dialog and click OK.
- Enter an equals sign (=) in the function bar to the right of the function symbol. Select the AVERAGE function from the Name box dropdown list to the left of the function symbol. Enter the range “A1:A10” in the Number 1 field of the Function Arguments dialog and click OK.
Advertisement
3
Observe the result in the cell you entered the formula in. The average, or arithmetic mean, is determined by finding the sum of the numbers in the cell range (80) and then dividing the sum by how many numbers make up the range (10), or 80 / 10 = 8.
- If you calculated the sum as suggested, you can verify this by entering “=A11/10” in any empty cell.
- The mean value is considered a good indicator of central tendency when the individual values in the sample range are fairly close together. It is not considered as good of an indicator in samples where there are a few values that differ widely from most of the other values.

1

Enter the numbers you want to find the median for. We’ll use the same range of ten numbers (2, 3, 5, 5, 7, 7, 7, 9, 16, and 19) as we used in the method for finding the mean value. Enter them in the cells from A1 to A10, if you haven’t already done so.
2
Find the median value of the numbers you entered. You do this by using the MEDIAN function. As with the AVERAGE function, you can enter it one of three ways:
- Click on an empty cell, such as A13, then type “=MEDIAN(A1:10)” (again, without the quotation marks) directly in the cell.
- Click on an empty cell, then click on the “f_x” symbol in the function bar above the worksheet. Select “MEDIAN” from the “Select a function:” list in the Insert Function dialog and click OK. Enter the range “A1:A10” in the Number 1 field of the Function Arguments dialog and click OK.
- Enter an equals sign (=) in the function bar to the right of the function symbol. Select the MEDIAN function from the Name box dropdown list to the left of the function symbol. Enter the range “A1:A10” in the Number 1 field of the Function Arguments dialog and click OK.
3

Observe the result in the cell you entered the function in. The median is the point where half the numbers in the sample have values higher than the median value and the other half have values lower than the median value. (In the case of our sample range, the median value is 7.) The median may be the same as one of the values in the sample range, or it may not.

1

Enter the numbers you want to find the mode for. We’ll use the same range of numbers (2, 3, 5, 5, 7, 7, 7, 9, 16, and 19) again, entered in cells from A1 through A10.
2
Find the mode value for the numbers you entered. Excel has different mode functions available, depending on which version of Excel you have.
- For Excel 2007 and earlier, there is a single MODE function. This function will find a single mode in a sample range of numbers.
- For Excel 2010 and later, you can use either the MODE function, which works the same as in earlier versions of Excel, or the MODE.SNGL function, which uses a supposedly more accurate algorithm to find the mode.^[1] (Another mode function, MODE.MULT returns multiple values if it finds multiple modes in a sample, but it is intended for use with arrays of numbers instead of a single list of values.^[2])
3
Enter the mode function you’ve chosen. As with the AVERAGE and MEDIAN functions, there are three ways to do this:
- Click on an empty cell, such as A14 then type “=MODE(A1:10)” (again, without the quotation marks) directly in the cell. (If you wish to use the MODE.SNGL function, type “MODE.SNGL” in place of “MODE” in the equation.)
- Click on an empty cell, then click on the “f_x” symbol in the function bar above the worksheet. Select “MODE” or “MODE.SNGL,” from the “Select a function:” list in the Insert Function dialog and click OK. Enter the range “A1:A10” in the Number 1 field of the Function Arguments dialog and click OK.
- Enter an equals sign (=) in the function bar to the right of the function symbol. Select the MODE or MODE.SNGL function from the Name box dropdown list to the left of the function symbol. Enter the range “A1:A10” in the Number 1 field of the Function Arguments dialog and click OK.
4
Observe the result in the cell you entered the function in. The mode is the value that occurs most often in the sample range. In the case of our sample range, the mode is 7, as 7 occurs three times in the list.
- If two numbers appear in the list the same number of times, the MODE or MODE.SNGL function will report the value that it encounters first. If you change the “3” in the sample list to a “5,” the mode will change from 7 to 5, because the 5 is encountered first. If, however, you change the list to have three 7s before three 5s, the mode will again be 7.

1
Enter the data you want to calculate a weighted average for. Unlike finding a single average, where we used a one-column list of numbers, to find a weighted average we need two sets of numbers. For the purpose of this example, we’ll assume the items are shipments of tonic, dealing with a number of cases and the price per case.
- For this example, we’ll include column labels. Enter the label “Price Per Case” in cell A1 and “Number of Cases” in cell B1.
- The first shipment was for 10 cases at $20 per case. Enter “$20” in cell A2 and “10” in cell B2.
- Demand for tonic increased, so the second shipment was for 40 cases. However, due to demand, the price of tonic went up to $30 per case. Enter “$30” in cell A3 and “40” in cell B3.
- Because the price went up, demand for tonic went down, so the third shipment was for only 20 cases. With the lower demand, the price per case went down to $25. Enter “$25” in cell A4 and “20” in cell B4.
2
Enter the formula you need to calculate the weighted average. Unlike figuring a single average, Excel doesn’t have a single function to figure a weighted average. Instead you’ll use two functions:
- SUMPRODUCT. The SUMPRODUCT function multiplies the numbers in each row together and adds them to the product of the numbers in each of the other rows. You specify the range of each column; since the values are in cells A2 to A4 and B2 to B4, you’d write this as “=SUMPRODUCT(A2:A4,B2:B4)”. The result is the total dollar value of all three shipments.
- SUM. The SUM function adds the numbers in a single row or column. Because we want to find an average for the price of a case of tonic, we’ll sum up the number of cases that were sold in all three shipments. If you wrote this part of the formula separately, it would read “=SUM(B2:B4)”.
3

Since an average is determined by dividing a sum of all numbers by the number of numbers, we can combine the two functions into a single formula, written as “=SUMPRODUCT(A2:A4,B2:B4)/ SUM(B2:B4)”.
4
Observe the result in the cell you entered the formula in. The average per-case price is the total value of the shipment divided by the total number of cases that were sold.
- The total value of the shipments is 20 x 10 + 30 x 40 + 25 x 20, or 200 + 1200 + 500, or $1900.
- The total number of cases sold is 10 + 40 + 20, or 70.
- The average per case price is 1900 / 70 = $27.14.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

wikiHow Video: How to Calculate Averages in Excel

You do not have to enter all the numbers in a continuous column or row, but you do have to make sure Excel understands which numbers you want to include and exclude. If you only wanted to average the first five numbers in our examples on mean, median, and mode and the last number, you’d enter the formula as “=AVERAGE(A1:A5,A10)”.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate averages in Excel, start by clicking on an empty cell. Then, type =AVERAGE followed by the range of cells you want to find the average of in parenthesis, like =AVERAGE(A1:A10). This will calculate the average of all of the numbers in that range of cells. It’s as easy as that! For step-by-step instructions with pictures, check out the full article below!

Did this summary help you?

Thanks to all authors for creating a page that has been read 185,303 times.

Is this article up to date?

Источник

Believe it or not, there are many different kinds of averages, and different ways to go about calculating them. The following methods are covered in this resource:

AVERAGE
AVERAGEA
AVERAGEIF
MEDIAN
MODE
Bonus: Nesting AVERAGE, LARGE and SMALL functions

AVERAGE

The most universally accepted average is the arithmetic mean, and Excel uses the AVERAGE function to find it. The Excel AVERAGE function is used to generate a number that represents a typical value from a range, distribution, or list of numbers. It is calculated by adding all the numbers in the list, then dividing the total by the number of values within the list.

Download your free average in Excel practice file!

Use this free average in Excel file to practice along with the tutorial.

Syntax

The AVERAGE function in Excel is straightforward. The syntax is:

=AVERAGE(number1, [number2],...)

Ranges or cell references may be used instead of explicit values.

The AVERAGE function can handle up to 255 arguments, each of which may be a value, cell reference, or range. Only one argument is required, but of course, if you’re using the AVERAGE function, it’s likely you have at least two.

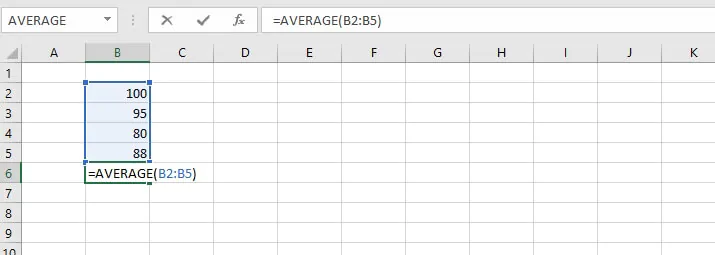
The formula below will calculate the average of the numbers 100, 95, and 80.

=AVERAGE(100,95,80)

To calculate the average of values in cells B2, B3, B4, and B5 enter:

=AVERAGE(B2:B5)

This can be typed directly into the cell or formula bar, or selected on the worksheet by selecting the first cell in the range, and dragging the mouse to the last cell in the range.

In order to calculate the average of non-contiguous (non-adjacent) cells, simply hold the Control key (or Command key — Mac users) while making the selections.

If typing the cell references directly into the cell or formula bar, non-contiguous references are separated by commas. For example:

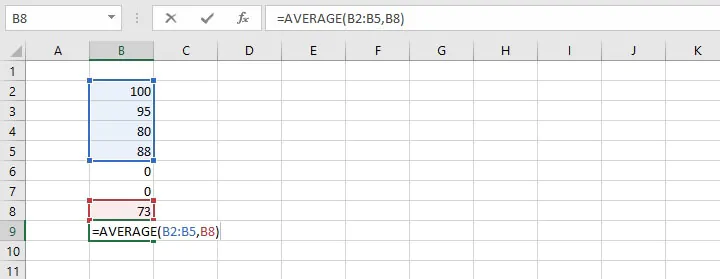
=AVERAGE(B2:B5,B8)

Remarks

When using the AVERAGE function, bear the following in mind.

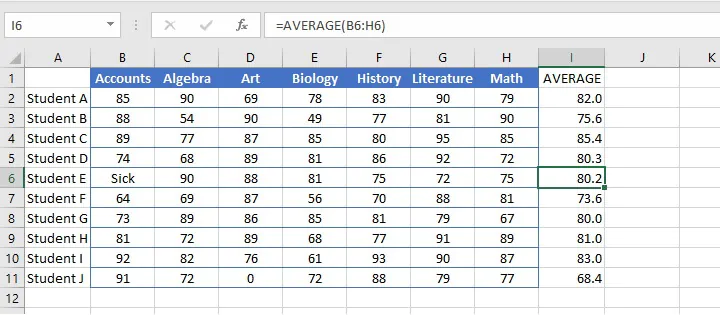
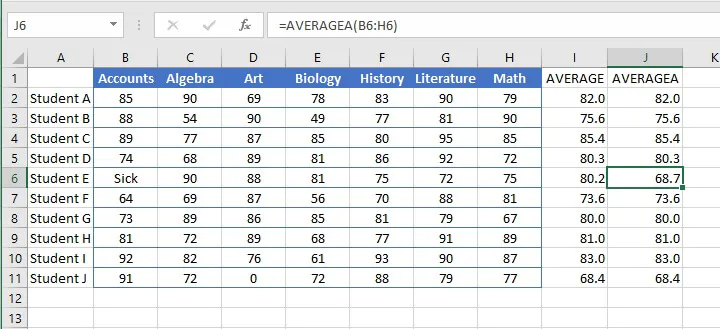
Text values and empty cells are ignored.

The word “Sick” in cell B6 (below) causes the AVERAGE function to ignore that cell altogether. This means that the average score in cell I6 was computed using the values in the range C8 to H8, and the total was divided by 6 subjects instead of 7.

Zero values are included.

When determining the number of values to divide the total by, zeros are considered valid amounts and will therefore reduce the overall average of the distribution. Notice that Student J’s average is quite different from Student E’s average, even though their grade totals were similar.

AVERAGEA

In order to eliminate this discrepancy, the AVERAGEA function may be used to include all values within a distribution, including text. The format is similar:

=AVERAGEA(value1, [value2],...)

A range or cell references may be used instead of explicit values.

AVERAGEA evaluates text values as zero, while the logical value TRUE is evaluated as 1. The logical value FALSE is considered a zero.

Compare the difference in results between using AVERAGE and AVERAGEA in the example below.

The averages for Student E and Student J are now similar when using the AVERAGEA function.

Check out the Microsoft Excel Basic & Advanced course

AVERAGEIF

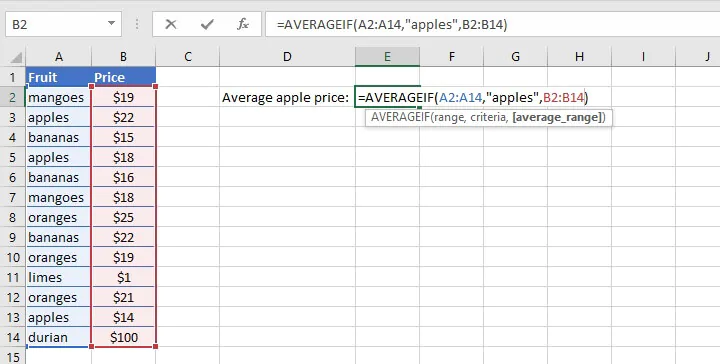
There are ways to find the average of only the numbers that satisfy certain criteria. With the AVERAGEIF function, Excel looks within the specified range for a stated condition, and then finds the arithmetic mean of the cells that meet that condition.

The syntax of the AVERAGEIF function is:

=AVERAGEIF(range,criteria,[average_range])

The range is the location where we can expect to find cells that meet the criteria.
The criteria are the value or expression that Excel should look for within the range.
Average_range is an optional argument. This is the range of cells where the values to be averaged are located. If the average_range is omitted, the range is used.

AVERAGEIF example 1

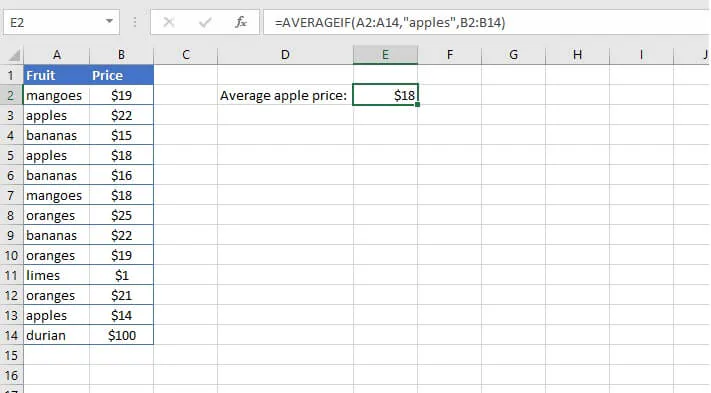
For example, from this list of various fruit prices, we can ask Excel to extract only the cells that say “apples” in column A, and find their average price from column B.

AVERAGEIF example 2

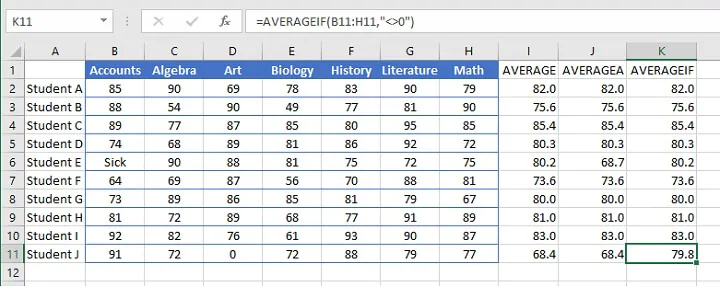
The criteria in an AVERAGEIF function may also be in the form of a logical expression, as in the example below:

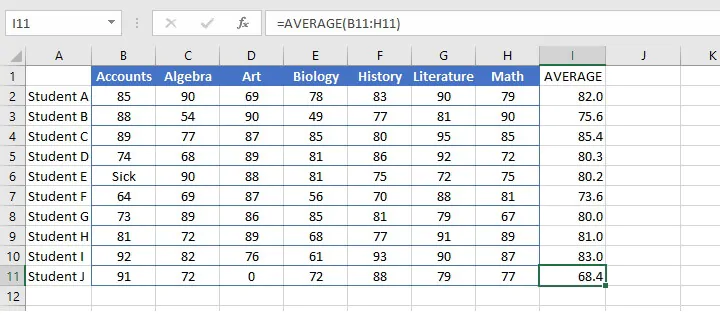
=AVERAGEIF(B4:H4,"<>0")

The above formula will find the average of the values in the range B4 to H4 that are not equal to zero. Note that the third (optional) argument is omitted, therefore the cells in the range are used to calculate the average.

Since cells that are evaluated as zeros are omitted due to our criteria, notice the difference in Student E and J’s results below when using the AVERAGEIF function.

In order to find the average of cells that satisfy multiple criteria, use the AVERAGEIFS function.

The arithmetic mean may be the most commonly-used method of finding the average, but it is by no means the only one. One outcome of using the arithmetic mean is that it allows very high or very low numbers to sway the outcome, thereby significantly altering the results.

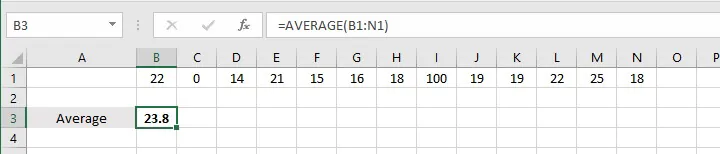
Take for example, the following list of numbers:

22, 1, 14, 21, 15, 16, 18, 100, 19, 19, 22, 25, 18

Finding the arithmetic mean would give a result of 23.8.

However, looking closely at the distribution of the numbers on the list, we would hardly say that 23.8 is the average value of those numbers. The problem, of course, is that the number 100 is an outlier and increased the sum of the numbers.

Therefore, in some situations, it is more desirable to use the MEDIAN function. This function determines the numerical order of the values being evaluated and uses the one in the middle as the average.

The syntax is:

=MEDIAN(number1, [number2], …)

A range or cell references may be used instead of explicit values.

In the above example, the numerical order would be:

1, 14, 15, 16, 18, 18, 19, 19, 21, 22, 22, 25, 100

There are 13 numbers in the distribution, making the seventh number the middle value. Therefore, the median would be 19.

If the number of values is an even number, the median would be determined by finding the average of the two numbers in the middle of the distribution. So, for the values 7,9,9,11,14,15 the median would be (9+11)/2=10.

The MEDIAN function ignores cells that contain text, logical values, or no value.

MODE

A third method for determining the average of a set of numbers is finding the mode, or the number that is repeated most often.

There are currently three “mode” functions within Excel. The classic, MODE, follows the syntax of:

=MODE(number1, [number2],...)

In this function, Excel evaluates the values within the list or range, and selects the most frequently occurring number as the average value of the group.

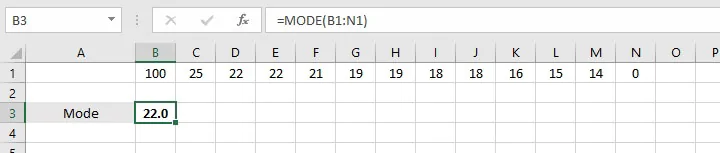
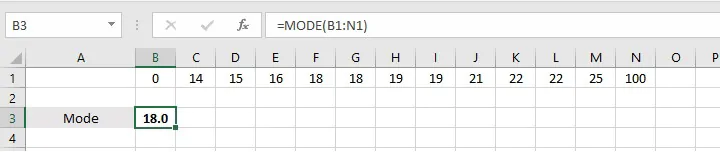
However, there are occasions when more than one number could be considered the mode. For example, consider the following list:

1, 14, 15, 16, 18, 18, 19, 19, 21, 22, 22, 25, 100

The numbers 18, 19, and 22 each appear two times. Which one is the mode? Microsoft chooses the first-appearing value as the mode — in the above case, 18.

If these same numbers were arranged in the reverse order, then 22 would be considered the mode.

If the numbers were arranged in a random order, then Excel would select from 18, 19, and 22 based on whichever number appeared in the distribution first.

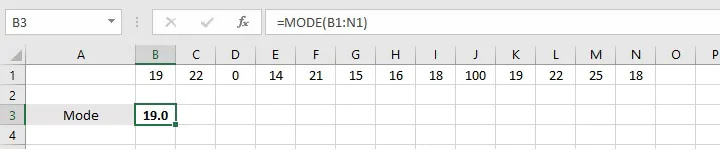
For example, in the list:

19, 22, 1, 14, 21, 15, 16, 18, 100, 19, 22, 25, 18

The MODE function considers 19 as the mode.

MODE.MULT

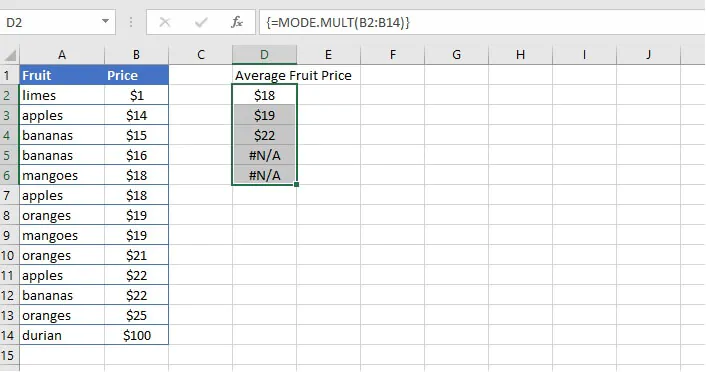
The MODE.MULT function is a solution to the discrepancies experienced in the above scenario. It allows us to anticipate and account for the possibility that there may be more than one mode within a group of numbers.

The syntax is:

=MODE.MULT(number1, [number2],...)

Since MODE.MULT is an array (CSE) function, these are the steps when using this function:

Select a vertical range for the output
Enter the MODE.MULT formula
Simultaneously select Control + Shift + Enter

Pressing Control + Shift + Enter (CSE) together will cause Excel to automatically place braces (curly brackets) around the formula, and will return a “spill” of results equal to the number of cells selected in Step 1. If there is more than one mode, they will be displayed vertically in the output cells. The MODE.MULT function will return the “#N/A” error if:

there are no duplicate values, or
there are no additional modes in the output range.

MODE.SNGL

Like the MODE.MULT function, the MODE.SNGL function was rolled out with Excel 2010. The syntax is:

=MODE.SNGL(number1, [number2],...]

The MODE.SNGL function behaves like the classic MODE function in determining the output.

Creative uses of the AVERAGE function

Top 3

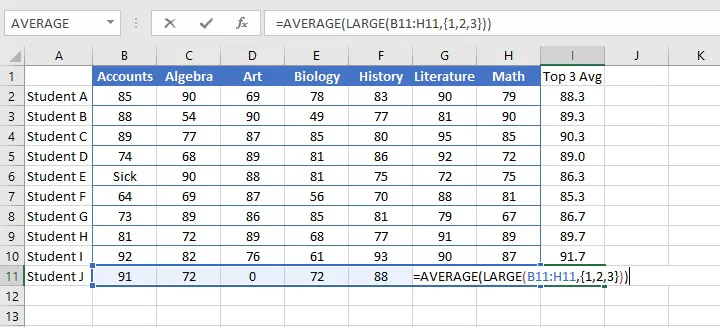
We can combine the AVERAGE function with the LARGE function to determine the average of the top “n” number of values.

The LARGE function extracts the n^t^h largest number from a range, using the format

=LARGE(array, k)

where k is the n^t^hnumber.

Using this format, we can display a number in the 1st, 2nd, 5th, or any rank.

In order to get the average of the three largest numbers in a range, we would nest the AVERAGE and LARGE functions as follows:

=AVERAGE(LARGE(array, {1,2,3}))

When we type braces around the k argument, Excel identifies the first, second, and third largest numbers in the array, and the AVERAGE function finds their average.

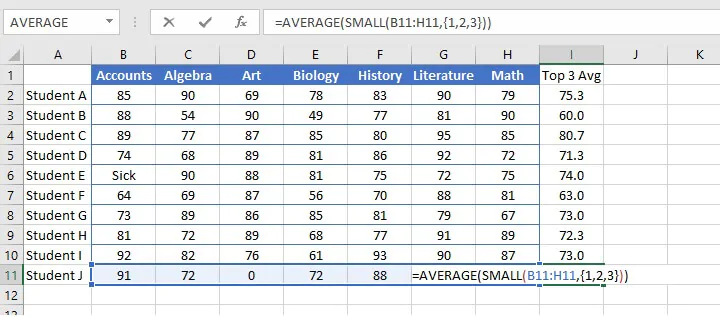
Bottom 3

We can use a similar logic to find the bottom 3 of a group of numbers using the SMALL function.

The following format will find the average of the three smallest numbers in the array.

=AVERAGE(SMALL(array, {1,2,3}))

The three main methods of finding the average within Excel are the AVERAGE (mean), MEDIAN (middle), and MODE (frequency) functions. They are all easy to use, so choose the one that’s right for your type of data and the questions you want to answer.

Learn more Excel formulas and functions

To learn more useful formulas, functions, and real-world Excel skills, try the GoSkills Basic and Advanced Excel course today.

Ready to become a certified Excel ninja?

Start learning for free with GoSkills courses

Start free trial

Источник

The AVERAGE function calculates the average of numbers provided as arguments. To calculate the average, Excel sums all numeric values and divides by the count of numeric values.

AVERAGE takes multiple arguments in the form number1, number2, number3, etc. up to 255 total. Arguments can include numbers, cell references, ranges, arrays, and constants. Empty cells, and cells that contain text or logical values are ignored. However, zero (0) values are included. You can ignore zero (0) values with the AVERAGEIFS function, as explained below.

The AVERAGE function will ignore logical values and numbers entered as text. If you need to include these values in the average, see the AVERAGEA function.

If the values given to AVERAGE contain errors, AVERAGE returns an error. You can use the AGGREGATE function to ignore errors.

Basic usage

A typical way to use the AVERAGE function is to provide a range, as seen below. The formula in F3, copied down, is:

=AVERAGE(C3:E3)

At each new row, AVERAGE calculates an average of the quiz scores for each person.

Blank cells

The AVERAGE function automatically ignores blank cells. In the screen below, notice cell C4 is empty, and AVERAGE simply ignores it and computes an average with B4 and D4 only:

However, note the zero (0) value in C5 is included in the average, since it is a valid numeric value. To exclude zero values, use AVERAGEIF or AVERAGEIFS instead. In the example below, AVERAGEIF is used to exclude zero values. Like the AVERAGE function, AVERAGEIF automatically excludes empty cells.

=AVERAGEIF(B3:D3,">0") // exclude zero

Mixed arguments

The numbers provided to AVERAGE can be a mix of references and constants:

=AVERAGE(A1,A2,4) // returns 3

Average with criteria

To calculate an average with criteria, use AVERAGEIF or AVERAGEIFS. In the example below, AVERAGEIFS is used to calculate the average score for Red and Blue groups:

=AVERAGEIFS(C5:C14,D5:D14,"red") // red average
=AVERAGEIFS(C5:C14,D5:D14,"blue") // blue average

The AVERAGEIFS function can also apply multiple criteria.

Average top 3

By combining the AVERAGE function with the LARGE function, you can calculate an average of top n values. In the example below, the formula in column I computes an average of the top 3 quiz scores in each row:

Detailed explanation here.

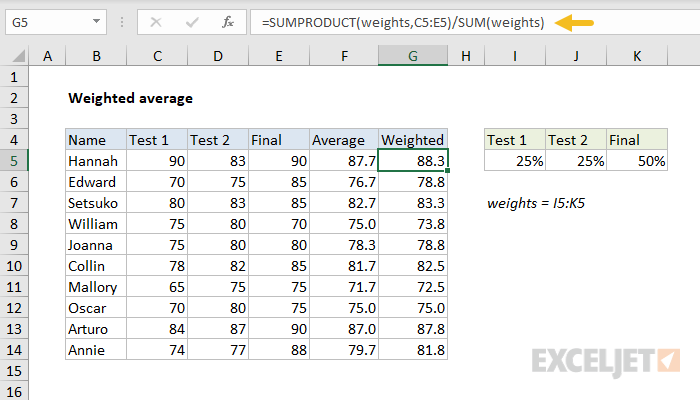
Weighted average

To calculate a weighted average, you’ll want to use the SUMPRODUCT function, as shown below:

Read a complete explanation here.

Average without #DIV/0!

The average function automatically ignores empty cells in a set of data. However, if the range contains no numeric values, AVERAGE will return a #DIV/0! error. To avoid this problem, you can check the count of values with the COUNT function and the IF function like this:

=IF(COUNT(range)>0,AVERAGE(range),"") // check count first

When the count of numeric values is zero, IF returns an empty string («»). When the count is greater than zero, AVERAGE returns the average. This example explains this idea in more detail.

Manual average

To calculate the average, AVERAGE sums all numeric values and divides by the count of numeric values. This behavior can be replicated with the SUM and COUNT functions manually like this:

=SUM(range)/COUNT(range) // manual average calculation

Notes

AVERAGE automatically ignores empty cells and cells with text values.
AVERAGE includes zero values. Use AVERAGEIF or AVERAGEIFS to ignore zero values.
Arguments can be supplied as constants, ranges, named ranges, or cell references.
AVERAGE can handle up to 255 total arguments.
To see a quick average without a formula, you can use the status bar.

Источник