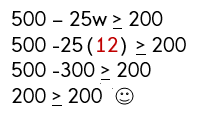The following diagrams show the three types of comparison word problems: Difference Unknown, Unknown Big Quantity, Unknown Small Quantity. Scroll down the page for examples and solutions.
Types of Comparison Word Problems
There are three main types of comparison word problems.
Difference Unknown
Connie has 15 red marbles and 28 blue marbles. How many more blue marbles than red marbles does Connie have?
This is a subtraction problem.
28 — 15 = 13
Unknown Big Quantity
Connie has 15 red marbles and some blue marbles. She has 13 more blue marbles than red ones. How many blue marbles does Connie have?
This is an addition problem.
15 + 13 = 28
Unknown Small Quantity
Connie has 28 blue marbles. She has 13 more blue marbles than red ones. How many red marbles does Connie have?
This is a subtraction problem.
28 -13 = 15
How to solve comparison word problems using Bar Models or Tape Diagrams?
This video explains how to use bar modeling in Singapore math to solve word problems that deal with comparing. This technique of using model drawings to solve word problems is recommended by the Common Core mathematics standards.
Example:
Adam has 11 fewer lollipops than Hope. If Adam has 16 lollipops, how may lollipops does Hope have?
- Show Video Lesson
Bar Model (Comparison)
This video employs a visual way to solve world problems using bar modeling. This type of word problem uses the comparison model. Because the part is missing, this is a subtraction problem.
Example:
Cayla did 88 sit-ups in the morning. Nekira did 32 sit-ups at night. How many more sit-ups did Cayla do than Nekira?
- Show Video Lesson
How to solve comparison word problems using Comparison Bars?
This is another strategy that we can use for story problems that involves comparison.
Examples:
- Bob has 14 crackers. Steve ate five fewer than Bob. How many did Steve eat?
- David has 5 marbles. Anna has 8 marbles. How many more does Anna have than David?
- Ellie has 9 goldfish. Laney has 5 more goldfish than Ellie. How many goldfish does Laney have?
- Mark earned $428 doing yard work. Troy earned $186. How much less did Troy earn?
- Billy has 679 gumballs. He has 278 more gumballs than Lee. How many gumballs does Lee have?
- Jake has 219 bottlecaps. Then, he found some more. Now he has 347 bottlecaps. How many bottlecaps did he find?
-
Show Video Lesson
Comparison Bars
Examples:
- Claire has 8 marbles. Sasha has 15 marbles. How many more marbles does Sasha have than Claire?
- Bill read 5 books. Beth read 2 more books than Bill. How many books did Beth read?
- Beth read 8 books. Bill read 3 fewer books than Beth. How many books did Bill read?
Example:
The Nature Center has a collection of snakes. The redbelly snake in the collection is 9 inches long. The eastern ribbon snake is 21 inches long. How much longer is the eastern ribbon snake than the redbelly snake?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Comparison word problems in elementary schools
Students may start solving comparison word problems as early as first
grade. Then, these problems get more and more challenging in 4th or 5th
grade. There are two types of comparison in math: additive and
multiplicative.
Next we show some examples commonly used in elementary schools.
Additive comparison
In additive comparison, the problem may have the following expressions where x can be a whole number.
- How much more?
- How much less?
- x more
- x less
Example #1
Darline has 6 candies. Sylvia has 5 more. How many candies does Sylvia have? Here is the model for this problem.
Sylvia has 6 + 5 candies or 11 candies.
Example #2
John has 15 books. Peter has 6 less. How many books does Peter have? Here is the model for this problem.
Peter has 15 — 6 or 9 books
Multiplicative comparison
In multiplicative comparison, the problem may have the following expressions where x can be a whole number.
- x times as many
- x times more … than
Example #3
Noemy has 3 times as many dolls as Tatiana. Tatiana has 2 dolls. How many dolls does Noemy have?
Step 1
Draw a model for this situation.
Step 2
Use the model to write an equation. Let n be the number of dolls Noemy has.
n = 3 x 2
Step 3
Solve the equation. n = 3. so Noemy has 6 dolls.
A challenging comparing word problem in elementary school.
Example #4
Kirk has 3 times as many baseball cards as Nancy. Together, they have 20 baseball cards. How many cards does Kirk have?
Step 1
Draw a box with the letter n in it to show that Nancy has an unknown number of cards. Kirk has 3 times as many cards as Nancy, so draw three identical boxes to represent Kirk’s cards.
Step 2
Use a model to write an equation. There are 4 equal boxes and each box has n cards.
To get the total numbers of cards, you need to do 4 x n. This amount must equal to 20 cards. So 4 x n = 20
Step 3
Solve the equation to find n.
4 times what number is equal to 20? Since 4 x 5 = 20, n = 5.
Nancy has 5 baseball cards.
Step 4
Find how many cards Kirk has. Kirk has 3 times as many as Nancy or 3 x 5.
Kirk has 15 cards.
Example #5
Kirk has 3 times as many baseball cards as Nancy. Together, they have 20 baseball cards. How many cards does Kirk have?
Recent Articles
-
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
-
#1
Which is correct:
A. How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
B. How many times more are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
I was going through a topic of probability in a textbook of elementary mathematics and found A… Think B is correct.
-
#2
You are correct. The than requires a comparative, in this case more.
-
#3
Sentence A begins:
A. How many times are the chances of getting …
This does not sound right because it has confused two different structures:
1/ What are the chances of getting (a red ball rather than a white ball?)
and
2/ How many times will we get (a red ball rather than a white ball?)
Only in structure 2 can we use «more»:
2b/ How many more times will we get (a red ball than a white ball?)
-
#4
Sentence A begins:
A. How many times are the chances of getting …
This does not sound right because it has confused two different structures:
1/ What are the chances of getting (a red ball rather than a white ball?)
and
2/ How many times will we get (a red ball rather than a white ball?)
Only in structure 2 can we use «more»:
2b/ How many more times will we get (a red ball than a white ball?)
I simply copied and pasted the sentence. It was a part of a long paragraph. Nevertheless, a sentence has to be complete in itself.
-
#5
I found the text here but I still think it is badly phrased and confusing. It is phrased as a question but does not end in a question mark:
It may be possible that the outcomes may not have equal chance of occuring unlike the cases of the coin and die. For example if a container has 5 red balls and 9 white balls and if a ball is pulled out without seeing, the chances of getting a red ball are much more. Can you see why? How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
If a comparative is to be used in your sentence it should be «less» because there are fewer red balls than white balls. There is a 5/14 chance of a red ball compared to a 9/14 chance of a white ball. Thus I would rephrase my previous suggestions:
How many less times will we get a red ball than a white ball?
or
How much less are the chances of getting a red ball than a white ball?
(answer = 4/14 = «four times out of fourteen less»)
Note: In the comparison to the previous reference (coins and dice) «more» is appropriate because each possibility on a coin is 1/2 and each possibility on a die is 1/6. The top number in both of these = 1 (ie. there is only one number 1, one number two… one heads, one tails) while there is more chance of selecting a red ball because there are five of them.
-
#6
How many less times will we get a red ball than a white ball?
We say «how many more times» not «how many much times». So, I wonder why «less» is used instead of «fewer»:
How many fewer times will we get a red ball than a white ball?
-
#7
Oh, do be careful here!
Let’s use five red balls and nine white balls. You might reasonably think that the question «how many times more are the chances of getting a white ball than a red ball?» is fine, and so it is, in a way.
You might be surprised to learn that the correct answer is «four fifths».
The problem lies in the use of «more». If A has five balls and B has six balls, few of us would argue with the person who says that B has 20% more balls than A.
If B has ten balls then he has 100% more balls than A.
If B has twenty balls then he has 300% more balls than A. 300% is the same as «three times» so B has three times more balls than A. But this sounds daft. B has twenty balls, A has five balls, and twenty is four times five, not three times five.
The problem lies in that little word «more». B has four times as many balls as A, but he has three times more balls than A.
I’ll leave you to work out for yourself how «less times» (or «times less») works out here (It is a trick question: it doesn’t)
Far better to avoid more or less in the question altogether.
What is the chance of getting a white ball compared with the chance of getting a red ball.
-
#8
Oh, do be careful here!
…
The problem lies in that little word «more». B has four times as many balls as A, but he has three times more balls than A.Far better to avoid more or less in the question altogether.
What is the chance of getting a white ball compared with the chance of getting a red ball.
This is a variation on a theme (The little word «more» is the comparative that the following thread suggests avoiding
three times longer than=three times as long as?
Last edited: Mar 14, 2018
-
#9
Thanks Unlce Jack and JulianStuart.
Let’s assume that for all my examples below there are 9 white balls and 5 red balls in the box.
______________________________________________
[Pw] — the chance of getting a white ball;
[Pr] — the chance of getting a red ball;
[Nw] — the number of white balls;
[Nr] — the number of red balls;
[A*] — how much more the chance of getting a white ball than a red ball is;
[B*] — how many times more the chance of getting a white ball than a red ball is;
[C*] — how many more times we will get a white ball than a red ball;
[Nw] = 9;
[Nr] = 5;
[Pw] = [Nw] / ([Nw] + [Nr]) = 9 / (9 + 5) = 9/14;
[Pr] = [Nr] / ([Nw] + [Nr]) = 5 / (9 + 5) = 5/14;
[A*] = [Pw] — [Pr] = 9/14 — 5/14 = 4/14;
[B*] = [A*] / [Pr] = (4/14) / (5/14) = 4/5;
[C*] = [Nw] — [Nr] = 9 — 5 = 4.
______________________________________________
You might be surprised to learn that the correct answer is «four fifths».
If I want the answer to be «four fourteenths», should I ask the question this way (the words in parentheses are optional):
1A. How much more is the chance of getting a white ball than (the chance of getting) a red ball? The answer is «four fourteenths».
2A. How much less is the chance of getting a red ball than (the chance of getting) a white ball? The answer is «four fourteenths».
1B. How much more are the chances of getting a white ball than (the chances of getting) a red ball? The answer is «four fourteenths».
2B. How much less are the chances of getting a red ball than (the chances of getting) a white ball? The answer is «four fourteenths».
How many fewer times will we get a red ball than a white ball?
Does the construction «how many fewer times»/»how many more times» make sense? For example, in these examples:
1C. If I keep taking one ball after the other until there’s nothing left in the box, then how many fewer times will I get a red ball than a white ball? The answer is «four».
2C. If I keep taking one ball after the other until there’s nothing left in the box, then how many more times will I get a white ball than a red ball? The answer is «four».
«less times» (or «times less»)
Is the word order essential?
1D. How many times more are the chances of getting a white ball than a red ball? The answer is «four fifths».
2D. How many more times are the chances of getting a white ball than a red ball? The answer is «four fifths».
1E. How many times less are the chances of getting a red ball than a white ball? The answer is «four fifths».
2E. How many less times are the chances of getting a red ball than a white ball? The answer is «four fifths».
-
#10
If I want the answer to be «four fourteenths», should I ask the question this way (the words in parentheses are optional):
1A. How much more is the chance of getting a white ball than (the chance of getting) a red ball? The answer is «four fourteenths».
2A. How much less is the chance of getting a red ball than (the chance of getting) a white ball? The answer is «four fourteenths».
1B. How much more are the chances of getting a white ball than (the chances of getting) a red ball? The answer is «four fourteenths».2B. How much less are the chances of getting a red ball than (the chances of getting) a white ball? The answer is «four fourteenths».
These all look fine to me (I see no distinction between chance and chances, though I would use the singular myself). You can also ask:
What is the difference in probability between getting a white ball and getting a red ball.
Does the construction «how many fewer times»/»how many more times» make sense? For example, in these examples:
1C. If I keep taking one ball after the other until there’s nothing left in the box, then how many fewer times will I get a red ball than a white ball? The answer is «four».
2C. If I keep taking one ball after the other until there’s nothing left in the box, then how many more times will I get a white ball than a red ball? The answer is «four».
That sounds very convoluted, and you have me puzzling over the tense of «get» and the use of «fewer», but I think both are justified and the sentences are correct.
Is the word order essential?
1D. How many times more are the chances of getting a white ball than a red ball? The answer is «four fifths».
2D. How many more times are the chances of getting a white ball than a red ball? The answer is «four fifths».
1E. How many times less are the chances of getting a red ball than a white ball? The answer is «four fifths».
2E. How many less times are the chances of getting a red ball than a white ball? The answer is «four fifths».
I would avoid all of these, to be honest. The word order doesn’t really matter («more times» and «times less» are most common, I think). The first question appears to want an answer of 1.8 and, although I said the correct answer was four fifths earlier because of the word «more», the word «times» really does confuse the issue. The second pair of questions in meaningless (though it does not stop people using the term «times less»). I would say the answer (if there is one) is «four ninths»; you have four fifths (I don’t know where you get that number from) and other people would say 1.8 (honestly!).
-
#11
The ‘more/less’, etc. complicates things unnecessarily, In My Opinion. Would you consider «What are my chances of getting a red ball rather than a white one?» as an alternative? «How much more likely am I to get a red ball than a white one?» is another alternative. Let your interlocutor figure out the mathematical odds!
Afterthought: «How much greater are my chances of getting a red ball than those of getting a white one?»
Last edited: Mar 16, 2018
-
#12
Thanks Uncle Jack and ain’ttranslationfun.
you have four fifths (I don’t know where you get that number from)
This is how I see it:
___________________________________________
Simple analogy:
___________________________________________
[A*] — the length of rope A;
[B*] — the length of rope B;
[A*] = 8;
[B*] = 2.
Rope A is [C*] times longer than rope B.
Rope B is [C*] times shorter than rope A.
[C*] = ([A*] — [B*]) / [B*] = (8 — 2) / 2 = 3.
Rope A is 3 times longer than rope B.
Rope B is 3 times shorter than rope A.
___________________________________________
Applying the above analogy to the example being discussed:
___________________________________________
[A*] — the probability of getting a white ball;
[B*] — the probability of getting a red ball;
[A*] = 9/14;
[B*] = 5/14.
The probability of getting a white ball is [C*] times more than the probability of getting a red ball.
The probability of getting a red ball is [C*] times less than the probability of getting a white ball.
[C*] = ([A*] — [B*]) / [B*] = (9/14 — 5/14) / (5/14) = (4/14) / (5/14) = 4/5.
The probability of getting a white ball is 4/5 times more than the probability of getting a red ball.
The probability of getting a red ball is 4/5 times less than the probability of getting a white ball.
___________________________________________
The first question appears to want an answer of 1.8
Would it be better to use the sentences below if I wanted either an answer of 1.8 or 0.(5)?
1F. How many times as much is the chance of getting a white ball as the chance of getting a red ball is? The answer is «nine fifths» or «1.8».
2F. How many times as much is the chance of getting a red ball as the chance of getting a white ball is? The answer is «five ninths» or «0.(5)».
1G. How many times is the chance of getting a white ball the chance of getting a red ball? The answer is «nine fifths» or «1.8».
2G. How many times is the chance of getting a red ball the chance of getting a white ball? The answer is «five ninths» or «0.(5)».
-
#13
This is how I see it:
___________________________________________
Simple analogy:
___________________________________________
[A*] — the length of rope A;
[B*] — the length of rope B;[A*] = 8;
[B*] = 2.Rope A is [C*] times longer than rope B.
Rope B is [C*] times shorter than rope A.[C*] = ([A*] — [B*]) / [B*] = (8 — 2) / 2 = 3.
Rope A is 3 times longer than rope B.
Rope B is 3 times shorter than rope A.
Which is why you really should not use «times shorter» (or «times less», as the case may be).
The difference is 6 (at least that is uncontroversial!)
A is 8 long, the difference 6 as a proportion of 8 is 75% (or three quarters or however you like to call it)
B is 75% shorter than A. This is correct English for expressing this relationship.
You might just about get away with saying that B is three-quarters times shorter than A, but this is inelegant and will leave people scratching their heads saying «why has he used ‘times’?».
What some people do say is that B is four times shorter than A. People say this, but I would never support such use. I don’t think anyone careless enough to use «times shorter» would ever consider that B was three times shorter than A, and would think you mad for saying so. They probably would not accept that A is three times longer than B, either, although this has rather more justification behind it, and would instead insist that A is four times longer than B.
This is why I say to be careful with «more» and «less» in this sort of mathematical comparison, and I recommend people avoid using any combination of «more» or «less» and «times».
Would it be better to use the sentences below if I wanted either an answer of 1.8 or 0.(5)?
1F. How many times as much is the chance of getting a white ball as the chance of getting a red ball is? The answer is «nine fifths» or «1.8».
2F. How many times as much is the chance of getting a red ball as the chance of getting a white ball is? The answer is «five ninths» or «0.(5)».
1G. How many times is the chance of getting a white ball the chance of getting a red ball? The answer is «nine fifths» or «1.8».
2G. How many times is the chance of getting a red ball the chance of getting a white ball? The answer is «five ninths» or «0.(5)».
These are horrible. Use something like «What is the ratio of the probabilities…» for the first pair. The second pair use the same construction as your sentence A at the top, which is wrong.
-
#14
Thanks Uncle Jack and ain’ttranslationfun.
This is how I see it:
…
The trouble is, a lot of people DON’T see it that way. You have been given a strong suggestion NOT to use a comparative with time or %.
This thread has vociferous arguments from both sides discussing
«Look at the following two sentences:
The rope is three times longer than that one.
The rope is three times as long as that one.
Do the two sentences mean the same?
So «X times longer than» or «X% shorter than» are seen differently by different people and if you wish to avoid ambiguity, you should avoid them. Feel free to join the discussion there
E.g., My piece of wood is three times as long as yours. If yours is 2 m long, mine is 6 m long. No ambiguity.
Same pieces of wood: My piece of wood is 4 m longer than yours. (No «times or % with comparative, just using units of measure) No ambiguity.
-
#15
Thanks Uncle Jack and JulianStuart.
The second pair use the same construction as your sentence A at the top, which is wrong.
It seems that I don’t understand what you mean. You said that my sentences 1A and 2A were good.
-
#16
It seems that I don’t understand what you mean. You said that my sentences 1A and 2A were good.
I was referring to sentence A in post #1.
-
#17
Now I see what you meant, Uncle Jack. Thanks for the clarification.
1F. How many times as much is the chance of getting a white ball as the chance of getting a red ball is? The answer is «nine fifths» or «1.8».
2F. How many times as much is the chance of getting a red ball as the chance of getting a white ball is? The answer is «five ninths» or «0.(5)».
When constructing sentences 1F and 2F, I wanted to apply the pattern of the sentence below:
How many times as many apples do I have as she does? (this link)
Can this pattern be applied somehow to the example in this thread?
1G. How many times is the chance of getting a white ball the chance of getting a red ball? The answer is «nine fifths» or «1.8».
2G. How many times is the chance of getting a red ball the chance of getting a white ball? The answer is «five ninths» or «0.(5)».
Here I wanted to use this pattern: «This house is three times the size of that house.» Can this be done?
My other attempt:
The chance of getting a white ball is 1.8 times the value of the chance of getting a red ball.
How many times is the chance of getting a white ball the value of the chance of getting a red ball?
-
#18
The trouble here is you are asking questions about probabilities, not apples or the sizes of houses, and whoever invented the English language really didn’t like probabilities, and failed to create the necessary vocabulary and syntax.
It is probably best to work backwards from a simple example. There are three red balls and one white ball.
Here are some statements that can be made about them :
- The probability of getting a red ball is 50% (or 0.5) higher than getting a white ball
- The probability of getting a white ball is 50% (or 0.5) lower than getting a red ball
- The probability of getting a red ball is three times the probability of getting a white ball
- The probability of getting a white ball is one third the probability of getting a red ball
You might also think, from all the discussion had above, that there are two other sentences that might be said:
5. The probability of getting a red ball is 200% more (or two times more) than getting a white ball
6. The probability of getting a white ball is 67% less (or two-thirds times less) than getting a white ball
but we cannot say these, because in English, «more» and «higher» are effectively synonymous (the prices in Finlay’s are 10% higher than the prices in Harrison’s), and so are «less» and «lower». Since the meanings have already been taken by (1) and (2), any attempt to try to use (5) and (6) are certain to be misunderstood. By all means replace «probability» with «chance» or «chances», but if we confine ourselves to simple English, I can think of no other valid comparison of the two probabilities than these four statements.
So, how do we ask a question to give each of the answers (1) to (4)?
A. How much higher is the probability of getting a red ball than a white ball?
Correct answers are (1) and (3)
B How much lower is the probability of getting a white ball than a red ball?
Correct answers are (2) and (4)
That might not be much help if you want to force the answer to be (1) or (2), but you could ask
C. What is the difference in probabilities between getting a red ball and getting a white ball?
In all honesty, I cannot think of a simple question which would unambiguously yield either (1) or (2) on its own, without allowing some other form of answer to be right. To force answer (3) or (4) you need to ask about the ratio of probabilities rather than the difference:
D. What is the ratio of probabilities between getting a red ball and getting a white ball?
-
#19
Thanks for the explanation, Uncle Jack.
The probability of getting a red ball is three times the probability of getting a white ball.
I wonder if I can form the following question based on the above quoted sentence:
How many times the probability of getting a red ball is the probability of getting a white ball?
-
#20
Thanks for the explanation, Uncle Jack.
I wonder if I can form the following question based on the above quoted sentence:
How many times the probability of getting a red ball is the probability of getting a white ball?
I though along those lines too, putting «is» before the first «the probability» but then could not think of a word to put where you have put the «is». You have managed to avoid this problem. Yes, it makes sense in English, but is difficult to read, and you yourself appear to have misread it, as the answer is one-third, my sentence (4), but you have quoted sentence (3).
-
#22
Which is correct:
A. How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
B. How many times more are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.I was going through a topic of probability in a textbook of elementary mathematics and found A… Think B is correct.
What you may be trying to say is:
How many times as great are the chances of getting a red ball as those of getting a white ball (probabilities for both being between 0 and 1)?
If this is the source of your sentence:
It may be possible that the outcomes may not have equal chance of occuring unlike the cases of the coin and die. For example if a container has 5 red balls and 9 white balls and if a ball is pulled out without seeing, the chances of getting a red ball are much more. Can you see why? How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
then no correction to the syntax or grammar of the sentence will fix the author’s error.
I wonder if I can form the following question based on the above quoted sentence:
How many times the probability of getting a red ball is the probability of getting a white ball?
This version means the same as mine.
Two more versions of the same thing:
How many times the probability of getting a red ball is that of getting a white ball?
How many times as likely is getting a red ball compared with getting a white one?
The answer to all of these, in the context of 5 red balls and 9 white ones, is 0.55555….
If the author meant 9 white and 5 red balls, the answer would be 1.8.
Last edited: Mar 17, 2018
-
#23
Thanks for the explanation, Forero.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
| Introduction to Systems | Distance Word Problem |
| Solving Systems by Graphing | Which Plumber Problem |
| Solving Systems with Substitution | Geometry Word Problem |
| Solving Systems with Linear Combination or Elimination | Work Problem |
| Types of Equations | Three Variable Word Problem |
| Systems with Three Equations | The “Candy” Problem |
| Algebra Word Problems with Systems: | Right Triangle Trigonometry Systems Problem |
| Investment Word Problem | Inequality Word Problem (in Linear Programming section) |
| Mixture Word Problems | More Practice |
Note that we solve Algebra Word Problems without Systems here, and we solve systems using matrices in the Matrices and Solving Systems with Matrices section here.
Introduction to Systems
“Systems of equations” just means that we are dealing with more than one equation and variable. So far, we’ve basically just played around with the equation for a line, which is (y=mx+b). Let’s say we have the following situation:
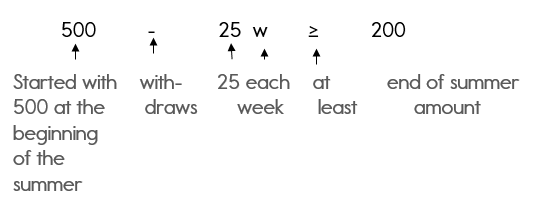
You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50. You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?
Now, you can always do “guess and check” to see what would work, but you might as well use algebra! It’s much better to learn the algebra way, because even though this problem is fairly simple to solve, the algebra way will let you solve any algebra problem – even the really complicated ones.
The first trick in problems like this is to figure out what we want to know. This will help us decide what variables (unknowns) to use. What we want to know is how many pairs of jeans we want to buy (let’s say “(j)”) and how many dresses we want to buy (let’s say “(d)”). Always write down what your variables will be:
Let (j=) the number of jeans you will buy
Let (d=) the number of dresses you’ll buy
Like we did before, let’s translate word-for-word from math to English:
|
English |
Math |
Explanation |
| “You really, really want to take home 6 items of clothing because you need that many.” |
(j+d=6) (Number of Items) |
If you add up the pairs of jeans and dresses, you want to come up with 6 items. |
| “… you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50.” |
(25j+50d=200) (Money) |
This one’s a little trickier. Use easier numbers if you need to: if you buy 2 pairs of jeans and 1 dress, you spend (left( {2times $25} right)+left( {1times $50} right)). Now you can put the variables in with their prices, and they have to add up to $200. |
Now we have the 2 equations as shown below. Notice that the (j) variable is just like the (x) variable and the (d) variable is just like the (y). It’s easier to put in (j) and (d) so we can remember what they stand for when we get the answers.
This is what we call a system, since we have to solve for more than one variable – we have to solve for 2 here. The cool thing is to solve for 2 variables, you typically need 2 equations, to solve for 3 variables, you need 3 equations, and so on. That’s easy to remember, right?
We need to get an answer that works in both equations; this is what we’re doing when we’re solving; this is called solving simultaneous systems, or solving system simultaneously. There are several ways to solve systems; we’ll talk about graphing first.
Solving Systems by Graphing
Remember that when you graph a line, you see all the different coordinates (or (x/y) combinations) that make the equation work. In systems, you have to make both equations work, so the intersection of the two lines shows the point that fits both equations (assuming the lines do in fact intersect; we’ll talk about that later). The points of intersections satisfy both equations simultaneously.
Put these equations into the (y=mx+b) ((d=mj+b)) format, by solving for the (d) (which is like the (y)):
(displaystyle j+d=6;text{ },text{ }text{solve for }d:text{ }d=-j+6text{ })
(displaystyle 25j+50d=200;text{ },,text{solve for }d:text{ }d=frac{{200-25j}}{{50}}=-frac{1}{2}j+4)
Now graph both lines:
|
Solving Systems using Graph |
Explanation |
 |
To graph, solve for the “(y)” value (“(d)” in our case) to use the slope-intercept method, or keep the equations as is and use the cover-up, or intercept method.
The easiest way to graph the second equation is the intercept method; when we put 0 in for “(d)”, we get 8 for the “(j)” intercept; when we put 0 in for “(j)”, we get 4 for the “(d)” intercept. We can do this for the first equation too, or just solve for “(d)” to see that the slope is (-1) and the (y)-intercept is (6). The two graphs intercept at the point ((4,2)). This means that the numbers that work for both equations are 4 pairs of jeans and 2 dresses! |
We can also use our graphing calculator to solve the systems of equations:
|
Graphing Calculator Instructions |
Screens |
|
(displaystyle begin{array}{c}j+d=6text{ }\25j+50d=200end{array}) Solve for (y,left( d right)) in both equations. Push (Y=) and enter the two equations in ({{Y}_{1}}=) and ({{Y}_{2}}=), respectively. Note that we don’t have to simplify the equations before we have to put them in the calculator. Push GRAPH. You may need to hit “ZOOM 6” (ZoomStandard) and/or “ZOOM 0” (ZoomFit) to make sure you see the lines crossing in the graph. (You can also use the WINDOW button to change the minimum and maximum values of your (x)- and (y)-values.) |
 |
| To get the point of intersection, push “2nd TRACE” (CALC), and then either push 5, or move cursor down to intersect. You should see “First curve?” at the bottom.
Then push ENTER. Now you should see “Second curve?” and then press ENTER again. Now you should see “Guess?”. Push ENTER one more time, and you will get the point of intersection on the bottom! Pretty cool! |
 |
Note that with non-linear equations, there will most likely be more than one intersection; an example of how to get more than one solution via the Graphing Calculator can be found in the Exponents and Radicals in Algebra section. Also, there are some examples of systems of inequality here in the Linear Inequalities section.
Solving Systems with Substitution
Substitution is the favorite way to solve for many students! It involves exactly what it says: substituting one variable in another equation so that you only have one variable in that equation. Here is the same problem:
You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50. You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?
Below are our two equations, and let’s solve for “(d)” in terms of “(j)” in the first equation. Then, let’s substitute what we got for “(d)” into the next equation. Even though it doesn’t matter which equation you start with, remember to always pick the “easiest” equation first (one that we can easily solve for a variable) to get a variable by itself.
|
Steps Using Substitution |
Notes |
| (displaystyle begin{array}{c}j+d=text{ }6;,,,,d=6-j\25j+50d=200end{array})
(displaystyle begin{array}{c}25j+50(6-j)=200\25j+300-50j=200\-25j=-100,,\j=4,\d=6-j=6-4=2end{array}) |
Solve for (d): (displaystyle d=6-j). Plug this in for (d) in the second equation and solve for (j).
When you get the answer for (j), plug this back in the easier equation to get (d): (displaystyle d=6-(4)=2). The solution is ((4,2)). |
We could buy 4 pairs of jeans and 2 dresses. Note that we could have also solved for “(j)” first; it really doesn’t matter. You’ll want to pick the variable that’s most easily solved for. Let’s try another substitution problem that’s a little bit different:
|
Steps Using Substitution |
Notes |
| (displaystyle begin{array}{c}color{#800000}{begin{array}{c}37x+4y=124,\x=4,end{array}}\\37(4)+4y=124\4y=124-148\4y=-24\y=-6end{array}) | This one is actually easier: we already know that (x=4).
Now plug in 4 for the second equation and solve for (y). The solution is ((4,-6)). |
Solving Systems with Linear Combination or Elimination
Probably the most useful way to solve systems is using linear combination, or linear elimination. The reason it’s most useful is that usually in real life we don’t have one variable in terms of another (in other words, a “(y=)” situation).
The main purpose of the linear combination method is to add or subtract the equations so that one variable is eliminated. We can add, subtract, or multiply both sides of equations by the same numbers – let’s use real numbers as shown below. We are using the Additive Property of Equality, Subtraction Property of Equality, Multiplicative Property of Equality, and/or Division Property of Equality that we saw here in the Types of Numbers and Algebraic Properties section:
| (displaystyle begin{array}{c},,,3,,=,,3\underline{{+4,,=,,4}}\,,,7,,=,,7end{array}) | (displaystyle begin{array}{l},,,12,=,12\,underline{{-8,,=,,,8}}\,,,,,4,,=,,4end{array}) | (displaystyle begin{array}{c}3,,=,,3\4times 3,,=,,4times 3\12,,=,,12end{array}) | (displaystyle begin{array}{c}12,,=,,12\frac{{12}}{3},,=,,frac{{12}}{3}\4,,=,,4end{array}) |
If we have a set of 2 equations with 2 unknowns, for example, we can manipulate them by adding, multiplying or subtracting (we usually prefer adding) so that we get one equation with one variable. Let’s use our previous problem:
| Linear Elimination Steps | Notes |
| (displaystyle begin{array}{c}color{#800000}{begin{array}{c}j+d=6text{ }\25j+50d=200end{array}}\\,left( {-25} right)left( {j+d} right)=left( {-25} right)6text{ }\,,,,-25j-25d,=-150,\,,,,,underline{{25j+50d,=,200}}text{ }\,,,0j+25d=,50\\25d,=,50\d=2\\d+j,,=,,6\,2+j=6\j=4end{array}) | Since we need to eliminate a variable, we can multiply the first equation by –25. Remember that we need to multiply every term (anything separated by a plus, minus, or (=) sign) by the –25.
Then we add the two equations to get “(0j)” and eliminate the “(j)” variable (thus, the name “linear elimination”). We then solve for “(d)”. Now that we get (d=2), we can plug in that value in the either original equation (use the easiest!) to get the other variable. The solution is ((4,2)): (j=4) and (d=2). |
We could buy 4 pairs of jeans and 2 dresses.
Here’s another example:
| Linear Elimination Steps | Notes |
|
(displaystyle begin{array}{l}color{#800000}{{2x+5y=-1}},,,,,,,text{multiply by –}3\color{#800000}{{7x+3y=11}}text{ },,,,,,,text{multiply by }5end{array}) (displaystyle begin{array}{l}-6x-15y=3,\,underline{{35x+15y=55}}text{ }\,29x,,,,,,,,,,,,,,,=58\,,,,,,,,,,,,,x=2\,,,,,,,,,,,,,,,\2(2)+5y=-1\,,,,,,4+5y=-1\,,,,,,,,,,,,,,,5y=-5\,,,,,,,,,,,,,,,,,y=-1end{array}) |
Since we need to eliminate a variable, we can multiply the first equation by –3 and the second one by 5. There are many ways to do this, but we want to make sure that either the (x) or (y) will be eliminated when adding the two equations. (We could have also picked multiplying the first by –7 and the second by 2).
We then get the second set of equations to add, and the (y)’s are eliminated. Solving for (x), we get (x=2). Now we can plug in that value in either original equation (use the easiest!) to get the other variable. The solution is ((2,-1)). |
Types of equations
In the example above, we found one unique solution to the set of equations. Sometimes, however, for a set of equations, there are no solutions (when lines are parallel) or an infinite number of solutions or infinitely many solutions (when the two lines are actually the same line, and one is just a “multiple” of the other).
When there is at least one solution, the equations are consistent equations, since they have a solution. When there is only one solution, the system is called independent, since they cross at only one point. When equations have infinite solutions, they are the same equation, are consistent, and are called dependent or coincident (think of one just sitting on top of the other).
When equations have no solutions, they are called inconsistent equations, since we can never get a solution.
Here are graphs of inconsistent and dependent equations that were created on a graphing calculator:
| Systems of Equations Calculator Screens | Notes |
 |
(displaystyle begin{array}{l}y=-x+4\y=-x-2end{array}) Notice that the slope of these two equations is the same, but the (y)-intercepts are different. In this situation, the lines are parallel, as we can see from the graph. These types of equations are called inconsistent, since there are no solutions. If we were to “solve” the two equations, we’d end up with “(4=-2)”; no matter what values we give to (x) or (y), (4) can never equal (-2). Thus, there are no solutions. The symbol (emptyset ) is sometimes used for no solutions; it is called the “empty set”. |
 |
(displaystyle x+y=6,,,,,,,text{or},,,,,,,y=-x+6) (displaystyle 2x+2y=12,,,,,,,text{or},,,,,,,y=frac{{-2x+12}}{2}=-x+6) Sometimes we have a situation where the system contains the same equations even though it may not be obvious. See how we may not know unless we actually graph, or simplify them? These types of equations are called dependent or coincident since they are one and the same equation and they have an infinite number of solutions, since one “sits on top of” the other. Since they have at least one solution, they are also consistent. If we were to “solve” the two equations, we’d end up with “(6=6)”, and no matter what values we give to (x) or (y), (6) always equals (6). Thus, there are an infinite number of solutions (infinitely many), but (y) always has to be equal to (-x+6). We can also write the solution as ((x,-x+6)). |
Systems with Three Equations
Let’s get a little more complicated with systems; in real life, we rarely just have two unknowns to solve for.
Let’s say at the same store, they also had pairs of shoes for $20 and we managed to get $60 more to spend! Now we have a new problem. To spend the even $260, how many pairs of jeans, dresses, and pairs of shoes should we get if want, for example, exactly 10 total items (Remember that jeans cost $25 each and dresses cost $50 each).
Let’s let (j=) the number of pair of jeans, (d=) the number of dresses, and (s=) the number of pairs of shoes we should buy. So far, we’ll have the following equations:
(displaystyle begin{array}{c}j+d+s=10text{ }\25j+text{ }50d+,20s=260end{array})
We’ll need another equation, since for three variables, we need three equations (otherwise, we theoretically might have infinite ways to solve the problem). In this type of problem, you would also need something like this: We want twice as many pairs of jeans as pairs of shoes. Now, since we have the same number of equations as variables, we can potentially get one solution for the system of equations. Here are the three equations:
| (displaystyle begin{array}{c}j+d+s=10text{ }\25j+50d+,20s=260\j=2send{array}) | Note that when we say “we have twice as many pairs of jeans as pair of shoes”, it doesn’t translate that well into math.
We can think in terms of real numbers, such as if we had 8 pairs of jeans, we’d have 4 pairs of shoes. Then it’s easier to put it in terms of the variables. |
We’ll learn later how to put these in our calculator to easily solve using matrices (see the Matrices and Solving Systems with Matrices section). For now, we can use two equations at a time to eliminate a variable (using substitution and/or elimination), and keep doing this until we’ve solved for all variables. These can get really difficult to solve, but remember that in “real life”, there are computers to do all this work!
Remember again, that if we ever get to a point where we end up with something like this, it means there are an infinite number of solutions: (4=4) (variables are gone and a number equals another number and they are the same). And if we up with something like this, it means there are no solutions: (5=2) (variables are gone and two numbers are left and they don’t equal each other).
And another note: equations with three variables are represented by planes, not lines (you’ll learn about this in Geometry). If all the planes crossed in only one point, there is one solution, and if, for example, any two were parallel, we’d have no solution, and if, for example, two or three of them crossed in a line, we’d have an infinite number of solutions.
Let’s solve our system: (displaystyle begin{array}{c}j+d+s=10text{ }\25j+text{ }50d+20s=260\j=2send{array}):
|
Solving Systems Steps |
Notes |
|
(displaystyle begin{array}{c}j+d+s=10text{ }\25j+50d+20s=260\j=2send{array}) (displaystyle begin{array}{c}2s+d+s=10,,,,,,,,,,Rightarrow ,,,,,,,,,,,,,,3s+d=10\25(2s)+50d+,20s=260,,,,,,Rightarrow ,,,,70s+50d=260end{array}) (displaystyle begin{array}{l}-150s-50d=-500\,,,,,underline{{,,70s+50d=,,,,260}}\,,-80s,,,,,,,,,,,,,,,,=-240\,,,,,,,,,,,,,,,,,,,s=3\\3(3)+d=10;,,,,,d=1,\j=2s=2(3);,,,,,,j=6end{array}) |
Use substitution since the last equation makes that easier. We’ll substitute (2s) for (j) in the other two equations and then we’ll have 2 equations and 2 unknowns.
We then multiply the first equation by –50 so we can add the two equations to get rid of the (d). We could have also used substitution again. First, we get that (s=3), so then we can substitute this in one of the 2 equations we’re working with. Now we know that (d=1), so we can plug in (d) and (s) in the original first equation to get (j=6). The solution is ((6,1,3)). |
We could buy 6 pairs of jeans, 1 dress, and 3 pairs of shoes.
Here’s one more example of a three-variable system of equations, where we’ll only use linear elimination:
(displaystyle begin{align}5x-6y-,7z,&=,7\6x-4y+10z&=,-34\2x+4y-,3z,&=,29end{align})
|
Solving Systems Steps |
Notes |
|
(displaystyle begin{array}{l}5x-6y-,7z,=,,7\6x-4y+10z=,-34\2x+4y-,3z,=,29,end{array}) (displaystyle begin{array}{l}6x-4y+10z=-34\underline{{2x+4y-,3z,=,29}}\8x,,,,,,,,,,,,,+7z=-5end{array}) (require{cancel} displaystyle begin{array}{l}cancel{{5x-6y-7z=7}},,,,,,,,,,,,,,20x-24y-28z,=,28,\cancel{{2x+4y-,3z,=29,,}},,,,,,,,underline{{12x+24y-18z=174}}\,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,32x,,,,,,,,,,,,,,-46z=202end{array}) (displaystyle begin{array}{l},,,cancel{{8x,,,+7z=,-5}},,,,,-32x,-28z=,20\32x,-46z=202,,,,,,,,,,,,underline{{,,32x,-46z=202}}\,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,-74z=222\,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,z=-3end{array}) (displaystyle begin{array}{l}32x-46(-3)=202,,,,,,,,,,,,,x=frac{{202-138}}{{32}}=frac{{64}}{{32}}=2\\5(2)-6y-7(-3)=7,,,,,,,,y=frac{{-10+-21+7}}{{-6}}=4end{array}) |
We first pick any 2 equations and eliminate a variable; we’ll use equations 2 and 3 since we can add them to eliminate the (y).
We then use 2 different equations (one will be the same!) to also eliminate the (y); we’ll use equations 1 and 3. To eliminate the (y), we can multiply the first by 4, and the second by 6. Now we use the 2 equations we’ve just created without the (y)’s and solve them just like a normal set of systems. We can multiply the first by –4 to eliminate the (x)’s to get the (z), which is –3. We can then get the (x) from either of the equations we just worked with. Since we have the (x) and the (z), we can use any of the original equations to get the (y). The solution is ((2,4,-3)). |
I know – this is really difficult stuff! But if you do it step-by-step and keep using the equations you need with the right variables, you can do it. Think of it like a puzzle – you may not know exactly where you’re going, but do what you can in baby steps, and you’ll get there (sort of like life sometimes, right?!). And we’ll learn much easier ways to do these types of problems.
Algebra Word Problems with Systems
Let’s do more word problems; you’ll notice that many of these are the same type that we did earlier in the Algebra Word Problems section, but now we can use more than one variable. This will actually make the problems easier! Again, when doing these word problems:
- If you’re wondering what the variables (or unknowns) should be when working on a word problem, look at what the problem is asking. These are usually (but not always) what your variables are!
- If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!
Here are some problems:
Investment Word Problem
| Investment Word Problem | Solution |
| Suppose Lindsay’s mom invests $10,000, part at 3%, and the rest at 2.5%, in interest bearing accounts.
The totally yearly investment income (interest) is $283. How much did Lindsay’s mom invest at each rate? |
Define a variable, and look at what the problem is asking. Use two variables: let (x=) the amount of money invested at 3%, and (y=) the amount of money invested at 2.5%.
The yearly investment income or interest is the amount that we get from the yearly percentages. (This is the amount of money that the bank gives us for keeping our money there.) To get the interest, multiply each percentage by the amount invested at that rate. Add these amounts up to get the total interest. We have two equations and two unknowns. The total amount ((x+y)) must equal $10000, and the interest ((.03x+.025y)) must equal $283: (displaystyle begin{array}{c}x,+,y=10000\.03x+.025y=283end{array}) (displaystyle begin{array}{c}y=10000-x\.03x+.025(10000-x)=283\,,,.03x,+,250,-.025x=283\,.005x=33;,,,,x=6600,,\,,y=10000-6600=3400end{array}) Turn the percentages into decimals: move the decimal point two places to the left. Substitution is the easiest way to solve. Lindsay’s mom invested $6600 at 3% and $3400 at 2.5%. |
We also could have set up this problem with a table:
| Amount | Turn % to decimal | Total | ||
| Amount at 3% | (x) | (.03) | (.03x) | Multiply across |
| Amount at 2.5% | (y) | (.025) | (.025y) | Multiply across |
| Total | (10000) | (283) | Do Nothing Here | |
| Add Down:
(x+y=10000) |
Do Nothing Here | Add Down: (.03x+.025y = 283) and solve the system |
Mixture Word Problems
Here’s a mixture word problem. With mixture problems, remember if the problem calls for a pure solution or concentrate, use 100% (if the percentage is that solution) or 0% (if the percentage is another solution).
| Mixture Word Problem | Solution | ||||||||||||||||||||||||
| Two types of milk, one that has 1% butterfat, and the other that has 3.5% of butterfat, are mixed.
How many liters of these two different kinds of milk are to be mixed together to produce 10 liters of low-fat milk, which has 2% butterfat? |
(Note that we did a similar mixture problem using only one variable here in the Algebra Word Problems section.)
First define variables for the number of liters of each type of milk. Let (x=) the number of liters of the 1% milk, and (y=) the number of liters of the 3.5% milk. Use a table again:
We can also set up mixture problems with the type of figure below. We add up the terms inside the box, and then multiply the amounts in the boxes by the percentages above the boxes, and then add across. This will give us the two equations. Let’s do the math (use substitution)! (displaystyle begin{array}{c}x,,+,,y=10\.01x+.035y=10(.02)end{array}) (displaystyle begin{array}{c},y=10-x\.01x+.035(10-x)=.2\.01x,+,.35,,-,.035x=.2\,-.025x=-.15;,,,,,x=6\,y=10-6=4end{array}) We would need 6 liters of the 1% milk, and 4 liters of the 3.5% milk. |
Here’s another mixture problem:
| Mixture Word Problem with Money | Solution | ||||||||||||||||||||||||
| A store sells two different types of coffee beans; the more expensive one sells for $8 per pound, and the cheaper one sells for $4 per pound.
The beans are mixed to provide a mixture of 50 pounds that sells for $6.40 per pound. How much of each type of coffee bean should be used to create 50 pounds of the mixture? |
First define variables for the number of pounds of each type of coffee bean. Let (x=) the number of pounds of the $8 coffee, and (y=) the number of pounds of the $4 coffee.
Use a table again:
Let’s do the math (use substitution)! (displaystyle begin{array}{c}x+y=50\8x+4y=50left( {6.4} right)end{array}) (displaystyle begin{array}{c}y=50-x\8x+4left( {50-x} right)=320\8x+200-4x=320\4x=120,;,,,,x=30\y=50-30=20\8x+4y=50(6.4)end{array}) We would need 30 pounds of the $8 coffee bean, and 20 pounds of the $4 coffee bean. See how similar this problem is to the one where we use percentages? |
Distance Word Problem:
Here’s a distance word problem using systems; distance problems have to do with an object’s speed, time, and distance. Note that, as well as the distance word problem here in the Algebra Word Problems section, there’s an example of a Parametric Distance Problem here in the Parametric Equations section.
| Distance Word Problem | Solution |
| Lia walks to the mall from her house at 5 mph. 10 minutes later, Lia’s sister Megan starts riding her bike at 15 mph (from the same house) to the mall to meet Lia. They arrive at the mall the same time.
How far is the mall from the sisters’ house? How long did it take Megan to get there? |
Remember always that (text{distance}=text{rate}times text{time}). It’s difficult to know how to define the variables, but usually in these types of distance problems, we want to set the variables to time, since we have rates, and we’ll want to set distances equal to each other in this case (the house is always the same distance from the mall). (Sometimes we’ll need to add the distances together instead of setting them equal to each other.)
Let (L) equal the how long (in hours) it will take Lia to get to the mall, and (M) equal to how long (in hours) it will take Megan to get to the mall. The rates of the Lia and Megan are 5 mph and 15 mph respectively. (Usually a rate is “something per something”). Lia’s time is Megan’s time plus (displaystyle frac{{10}}{{60}}=frac{1}{6},,,,(L=M+frac{1}{6})), since Lia left 10 minutes earlier than Megan (convert minutes to hours by dividing by 60 – try real numbers to see this). Use the distance formula for each of them separately, and then set their distances equal, since they are both traveling the same distance (house to mall). Then use substitution to solve the system for Megan’s time: after dividing both sides by 5, multiply both sides by 6 to get rid of the fractions.
Megan’s time is (displaystyle frac{1}{{12}}) of any hour, which is 5 minutes. The distance to the mall is rate times time, which is 1.25 miles. |
Which Plumber Problem
Many word problems you’ll have to solve have to do with an initial charge or setup charge, and a charge or rate per time period. In these cases, the initial charge will be the (boldsymbol {y})-intercept, and the rate will be the slope. Here is an example:
| “Which Plumber” Systems Word Problem | Solution |
| Michaela’s mom is trying to decide between two plumber companies to fix her sink.
The first company charges $50 for a service call, plus an additional $36 per hour for labor. The second company charges $35 for a service call, plus an additional $39 per hour of labor. At how many hours will the two companies charge the same amount of money? |
The money spent depends on the plumber’s set up charge and number of hours, so let (y=) the total cost of the plumber, and (x=) the number of hours of labor. Again, set up charges are typical (boldsymbol {y})-intercepts, and rates per hour are slopes. The total price of the plumber’s house call will be the initial or setup charge, plus the number of hours ((x)) at the house times the price per hour for labor.
To get the number of hours when the two companies charge the same amount of money, we just put the two (y)’s together and solve for (x) (substitution, right?): First plumber’s total price: (displaystyle y=50+36x) Second plumber’s total price: (displaystyle y=35+39x) (displaystyle 50+36x=35+39x;,,,,,,x=5) Here’s what a graph would look like: At 5 hours, the two plumbers will charge the same. At this time, the (y)-value is 230, so the total cost is $230. Note that, in the graph, before 5 hours, the first plumber will be more expensive (because of the higher setup charge), but after the first 5 hours, the second plumber will be more expensive. Thus, the plumber would be chosen based on how many hours Michaela’s mom thinks the plumber will be there. |
Geometry Word Problem:
Many times, we’ll have a geometry problem as an algebra word problem; these might involve perimeter, area, or sometimes angle measurements (so don’t forget these things!). Let’s do one involving angle measurements.
| Geometry Systems Word Problem | Solution |
| Two angles are supplementary. The measure of one angle is 30 degrees smaller than twice the other.
Find the measure of each angle. |
From Geometry, we know that two angles are supplementary if their angle measurements add up to 180 degrees (and remember also that two angles are complementary if their angle measurements add up to 90 degrees).
Define the variables and turn English into Math. Let (x=) the first angle, and (y=) the second angle. We really don’t need to worry at this point about which angle is bigger; the math will take care of itself. (x) plus (y) must equal 180 degrees by definition, and also (x=2y-30) (Remember the English-to-Math chart?) Solve, using substitution: (displaystyle begin{array}{c}x+y=180\x=2y-30end{array}) (displaystyle begin{array}{c}2y-30+y=180\3y=210;,,,,,,,,y=70\x=2left( {70} right)-30=110end{array}) The larger angle is 110°, and the smaller is 70°. Let’s check our work: The two angles do in fact add up to 180°, and the larger angle (110°) is 30° less than twice the smaller (70°). |
See – these are getting easier! Here’s one that’s a little tricky though:
Work Problem:
Let’s do a “work problem” that is typically seen when studying Rational Equations (fraction with variables in them) and can be found here in the Rational Functions, Equations and Inequalities section.
Note that there’s also a simpler version of this problem here in the Direct, Inverse, Joint and Combined Variation section.
| Work Word Problem
(Systems) |
Solution |
| 8 women and 12 girls can paint a large mural in 10 hours.
6 women and 8 girls can paint it in 14 hours. Find the time to paint the mural, by 1 woman alone, and 1 girl alone. |
Let’s let (w=) the part of the job by 1 woman in 1 hour, and (g=) the part of the job by 1 girl in 1 hour. We have 10 hours with 8 women and 12 girls that paint the mural (do 1 job), and 14 hours with 6 women and 8 girls that paint the mural (do 1 job).
Since (w=) the part of the job that is completed by 1 woman in 1 hour, then (8w=) the amount of the job that is completed by 8 women in 1 hour. Also, if (8w=) the amount of the job that is completed by 8 women in 1 hour, (10times 8w) is the amount of the job that is completed by 8 women in 10 hours. Similarly, (10times 12g) is the amount of the job that is completed by 12 girls in 10 hours. Add these two amounts and we get (displaystyle 10left( {8w+12g} right)), which will be the whole job. Use the same logic for the 6 women and 8 girls to paint the mural in 14 hours. The whole job is 1 (this is typical in work problems), and we can set up two equations that equal 1 to solve the system. Use linear elimination to solve the equations; it gets a little messy with the fractions, but we can get it! (displaystyle begin{array}{c}10left( {8w+12g} right)=1,text{ or }8w+12g=frac{1}{{10}}\,14left( {6w+8g} right)=1,text{ or },6w+8g=frac{1}{{14}}end{array}) (displaystyle begin{array}{c}text{Use elimination:}\left( {-6} right)left( {8w+12g} right)=frac{1}{{10}}left( {-6} right)\left( 8 right)left( {6w+8g} right)=frac{1}{{14}}left( 8 right)\cancel{{-48w}}-72g=-frac{3}{5}\cancel{{48w}}+64g=frac{4}{7},\,-8g=-frac{1}{{35}};,,,,,g=frac{1}{{280}}end{array}) (begin{array}{c}text{Substitute in first equation to get }w:\,10left( {8w+12cdot frac{1}{{280}}} right)=1\,80w+frac{{120}}{{280}}=1;,,,,,,w=frac{1}{{140}}\g=frac{1}{{280}};,,,,,,,,,,,w=frac{1}{{140}}end{array}) The answers we get is the part of the job that is completed by 1 woman or girl in 1 hour, so to get how long it would take them to do a whole job, we have to take the reciprocal. (Think about it; if we could complete (displaystyle frac{1}{3}) of a job in an hour, we could complete the whole job in 3 hours). Thus, it would take one of the women 140 hours to paint the mural by herself, and one of the girls 280 hours to paint the mural by herself. |
Three Variable Word Problem:
Let’s do one more with three equations and three unknowns:
| Three Variable Word Problem | Solution |
| A florist is making 5 identical bridesmaid bouquets for a wedding.
She has $610 to spend (including tax) and wants 24 flowers for each bouquet. Roses cost $6 each, tulips cost $4 each, and lilies cost $3 each. She wants to have twice as many roses as the other 2 flowers combined in each bouquet. How many roses, tulips, and lilies are in each bouquet? The trick is to put real numbers in to make sure you’re doing the problem correctly, and also make sure you’re answering what the question is asking! |
Look at the question being asked to define our variables: Let (r=) the number of roses, (t=) the number of tulips, and (l=) the number of lilies in each bouquet. Put the money terms together, and also the counting terms together:
(begin{array}{l}5left( {6r+4t+3l} right)=610,,,text{(price of each flower times number of flowers x }5text{ bouquets= total price)}\,,,,,,,,,r=2(t+l)text{ },,,,,,,,,,text{ (two times the sum of the other two flowers = number of roses)}\,,,,,,r+t+l=24text{ },,,,,,,,,text{(total number of flowers in each bouquet is }24text{)}end{array}) Use substitution and put (r) from the middle equation in the other equations. Then, use linear elimination to put those two equations together: multiply the second by –5 to eliminate the (l). We typically have to use two separate pairs of equations to get the three variables down to two! (begin{array}{c}6r+4t+3l=122\r=2left( {t+l} right)\,r+t+l=24\\6left( {2t+2l} right)+4t+3l=122\,12t+12l+4t+3l=122\16t+15l=122\\left( {2t+2l} right)+t+l=24\3t+3l=24end{array}) (displaystyle begin{array}{c},16t+15l=122\,,,,,,,,,cancel{{3t+3l=24}}\,,,,underline{{-15t-15l=-120}}\,,,,,t,,,,,,,,,,,,,,,,,=2\16left( 2 right)+15l=122;,,,,l=6\\r=2left( {2+6} right)=16\,,,,,,,,,,r=16,,,,t=2,,,,l=6end{array}) We get (t=2). Solve for (l) in this same system, and (r) by using the value we got for (t) and (l) (most easily in the second equation at the top). Thus, for one bouquet, we’ll have 16 roses, 2 tulips, and 6 lilies. If we had solved for the total number of flowers, we would have had to divide each number by 5. |
The “Candy” Problem
Sometimes we get lucky and can solve a system of equations where we have more unknowns (variables) then equations. (Actually, I think it’s not so much luck, but having good problem writers!) Here’s one like that:
| More Unknowns Than Variables Problem | Solution |
| Sarah buys 2 pounds of jelly beans and 4 pounds of chocolates for $4.00.
She then buys 1 pound of jelly beans and 4 pounds of caramels for $3.00. She also buys 1 pound of jelly beans, 3 pounds of licorice and 1 pound of caramels for $1.50. How much will it cost to buy 1 pound of each of the four candies? |
Look at the question being asked to define our variables: Let (j=) the cost of 1 pound of jelly beans, (o=) the cost of 1 pound of chocolates, (c=) the cost of 1 pound of caramels, and (l=) the cost of 1 pound of licorice. Here is the system of equations:
(begin{array}{c}2j+4o=4\j+4c=3\j+3l+1c=1.5\text{Want: }j+o+c+lend{array}) Wait! Something’s not right since we have 4 variables and 3 equations. But note that they are not asking for the cost of each candy, but the cost to buy all 4! Maybe the problem will just “work out” so we can solve it; let’s try and see. From our three equations above (using substitution), we get values for (o), (c) and (l) in terms of (j). (displaystyle begin{align}o=frac{{4-2j}}{4}=frac{{2-j}}{2},,,,,,,,,c=frac{{3-j}}{4},\j+3l+1left( {frac{{3-j}}{4}} right)=1.5\4j+12l+3-j=6\,l=frac{{6-3-3j}}{{12}}=frac{{3-3j}}{{12}}=frac{{1-j}}{4}end{align}) (require{cancel} displaystyle begin{align}j+o+c+l&=j+frac{{2-j}}{2}+frac{{3-j}}{4}+frac{{1-j}}{4}\&=cancel{j}+1-cancel{{frac{1}{2}j}}+frac{3}{4}cancel{{-frac{j}{4}}}+frac{1}{4}cancel{{-frac{j}{4}}}=2end{align}) When we substitute back in the sum (text{ }j+o+c+l), all in terms of (j), our (j)’s actually cancel out, which is very unusual! We can’t really solve for all the variables, since we don’t know what (j) is. But we can see that the total cost to buy 1 pound of each of the candies is $2. Pretty cool! |
There are more Systems Word Problems in the Matrices and Solving Systems with Matrices section, Linear Programming section, and Right Triangle Trigonometry section.
Understand these problems, and practice, practice, practice!
For Practice: Use the Mathway widget below to try a Systems of Equations problem. Click on Submit (the blue arrow to the right of the problem) and click on Solve by Substitution or Solve by Addition/Elimination to see the answer.
You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.
If you click on Tap to view steps, or Click Here, you can register at Mathway for a free trial, and then upgrade to a paid subscription at any time (to get any type of math problem solved!).
On to Algebraic Functions, including Domain and Range – you’re ready!
When most people hear “word problems,” they often think of the popular example of trains traveling at different speeds, or unrealistic applications of math. However, word problems represent how most people use math in everyday life, and the SAT includes these problems to test students’ ability to reason logically and solve problems.
For many students, the hardest part of a word problem is figuring out exactly what the word problem is asking of you. Not all word problems are created the same though, so we’re going to break down what you need to know so that you feel confident solving them on the SAT.
Types of Math Word Problems on the SAT
You could divide math word problem in a few different ways. You could do it by topic, for example, such as using the SAT subscores as your guide. Or you could do it by the type of solution the problem requires of you. We’re going to focus on the second way, simply because trying to divide word problems by topic would mean we’d have to cover virtually every math topic the SAT covers, which is way more than we could fit in a single post.
Creating an equation or a formula. In these problems, you’ll be given some information about a scenario and asked to come up with an equation or formula that represents that scenario. In fact, looking for the word “represents” in the question might tip you off that you’re dealing with a problem of this type. These are almost exclusively found in the multiple-choice questions, with different equations or formulas listed as the answer choices.
Solving for a value. This is the most common form of word problem. Based on the information in the word problem, you’ll need to come up with at least one specific value that satisfies the requirements of the problem. Examples include finding “how much” or “how many” of something in the problem, or finding minimums and maximum values.
Defining or interpreting. For these problems, you are often asked to interpret what a variable or a constant means in the situation described, or you might be asked what kinds of conclusions can be drawn from a survey. These types of problems often have no “math” involved, and instead ask you to think logically about a situation.
Tip: Being able to identify problems by type on the SAT is a useful prep exercise and can help you on the day you take the test. You may want to use the Math section from a free practice SAT test and circle all of the word problems. Then, read each word problem and assign it to one of the types. Doing this will help you see the commonalities between different types of questions and will allow you to spend less time on the actual test wondering what type of question you’re dealing with!
How to Approach SAT Math Word Problems
For every SAT Math word problem, there are two things to consider. The first is what we discussed above, which is to figure out what type of problem you’re dealing with to best identify what you need to do. Once you know whether you need to provide a definition, write an equation, or solve for a value, you’ve taken the first step.
The next step will be to do the math that you’ve identified you need to do based on the type of word problem. Let’s take a look at each one:
Write an equation/formula. For problems of this type and for problems that ask you to solve for a specific value, you will often need to understand how to “translate” a word problem into an equation, diagram, or graph that you can work with. Luckily, the SAT is very particular about how it uses words in its word problems, so you can always be sure that certain words are meant to relate to specific mathematical concepts. Here are some of the common phrases used by test makers to clue you in to what kind of math you’re looking for:
| Word/phrase | Mathematical meaning/symbol |
| Is, will be, is equal to, is the same as | Equals, = |
| Plus, sum, increased by, added to, received | Addition, + |
| Minus, fewer, difference, decreased by | Subtraction, – |
| Times, product, multiplied by, of | Multiplication, x |
| Divided by, quotient, per, for | Division, ÷ |
| More than, greater than | Inequality, > |
| At least, minimum | Inequality, ≥ |
| Fewer than, less than | Inequality, < |
| At most, maximum | Inequality, ≤ |
| What, how many | Variable, x (or any other letter) |
Solve for a value. With these problems, you might be given an equation as part of your information, but most likely you have to write an equation or formula and solve for the answer. You may benefit from drawing a diagram on some of these questions, especially if the word problem refers to geometric shapes but doesn’t already include one. This can help you visualize the information you’re looking for (the measure of an angle, for example) and help you focus on the right concepts to find the solution.
When translating a word problem into a diagram, make sure you follow the set-up as described in the word problem to the best of your ability, and don’t be fooled by your own diagram. For example, a problem may mention a right triangle, so you draw one. You may end up drawing a diagram that looks like a 45-45-90 triangle, but the problem is actually dealing with a 30-60-90 triangle. By labeling all of the information on your diagram and making a mental note that your drawings aren’t to scale, you can quickly make sense of most problems.
Defining and interpreting. With these types of problems, you often have the equation or formula given to you, and you just need to explain how a part of it works. If you’re not sure, consider whether you’re being asked about a constant or a variable, and eliminate any choices that don’t correspond to the type of value you’re looking at. You can also test the equation with different numbers to see how the value in question influences the equation.
Some problems involve your knowledge of statistical topics, such as understanding how to draw conclusions from surveys, or what factors affect standard deviation. For many of these problems, you’ll need to review these concepts in order to form the correct conclusion.
Examples of SAT Math Word Problems
The following example problems come from the College Board’s free SAT practice tests.
Example of Creating an Equation/Formula
How to solve: We can tell we need to come up with our own formula based on the answer choices and the word “represents” in the problem’s question. We need to find the formula that represents what the original price of a laptop was in terms of p, what Alma paid for it.
Let’s make x the original price of the laptop. In this case, x would be multiplied by .8 to get to the sales price (representing the 20% discount). The sales prices would then be multiplied by 1.08 to account for sales tax. This means that p=(1.08)(0.8)(x). We need to isolate x, so we need to divide both sides by 1.08 and 0.8. That gives us D as the correct answer.
Alternate method: Many problems requiring you to create your own equation are not too difficult, but they can get tricky when there are several steps involved or several variables. You can substitute a number for the variable you’re solving for to find the solution that way. For example, you can set $100 to be the original price of the laptop. Multiply it by .8 to find the sales price, and then by 1.08 to find the price that Alma paid. Then plug the price Alma paid into the answer choices to find the correct answer.
Example of Solving for a Value
How to solve: The word “maximum” tips us off that we are looking for a specific value and that we’ll be dealing with an inequality (see above). Given the information in the problem, we can write this inequality to start: (weight of driver) + (weight of truck) + (14x, or the weight of the boxes) ≤ 6000.
Because we’re told that the weight of the driver and the truck equals 4,500, we can replace that part of the equation: 4500 + 14x ≤ 6000. Now, all we need to do is solve for x. Subtract 4500 from both sides to get 14x ≤ 1500. Then divide both sides by 14 to get x ≤ 107.14… The answer is thus 107.
Note: Pay close attention to how you need to round when working with inequalities. Although this particular decimal probably wouldn’t have made you think to round up, if the result of the division had been 107.9999 you should still round down in this case because the number you’re looking for needs to be less than that value.
Example of Defining/Interpreting
How to solve: Again, the use of the word “interpretation” lets us know what type of problem we’re dealing with. In this case, 12 is a coefficient for the variables n and h, which are the number of landscapers and the number of hours respectively. We can thus rule out choices B and D, since those answers define 12 as a constant in place of these variables.
Since this equation is used to calculate the price of a job, we can be sure 12 represents a dollar amount as reflected in choices A and C. To figure out how things are affected, we can substitute simple numbers for n and h. When both are equal to 1 (there is one landscaper who works for one hour), then 12nh=12(1)(1)=12. When we increase both of these numbers to two, then 12nh=12(2)(2)=48. We can thus rule out C, because the price increased by more than 12 when we added another hour. Choice A is the best interpretation.
How to solve: This is an interpretation problem dealing with statistical concepts rather than interpreting an equation. To be able to “solve” you’d need to know what factors contribute to a reliable conclusion and see what was missing from this survey set-up. In this case, the correct answer is D.
In order for reliable conclusions to be drawn, a sample must be selected at random from the population to ensure that the sample is representative of the population, which in this case is the entire town. By choosing people at the same restaurant on one day, the researcher is possibly biasing their results by narrowing their sample to “people who like this one restaurant.” Because the sample is not representative, choice D identifies the factor that makes the conclusion unreliable. The other choices are factors that, given what we know from the problem, don’t negatively impact the conclusion.
SAT Math Word Problems Tips
As you may have noticed in the last example, you’ll still need to be familiar with math concepts and understand how they might show up in different situations to really feel confident taking any problem on. Here are a couple of other tips worth mentioning:
For most problems, there is more than one way to solve it. We showed this with the first example, where we provided an alternate method for solving a problem. If you find yourself stumped on a problem (we’ve all been there!), then move on to other problems and return to the one that tripped you up later. You may find that you see what you need to do more clearly.
Read carefully. The SAT test makers put a lot of care into how they write math word problems. Be sure to carefully read the question so that you don’t misread something and solve for the wrong thing. (The test makers may even include the answers that result from these common misreadings in the choices!). It’s difficult to read a question correctly once you’ve misread it. If you’re a fast reader who tends to skip over things, try mouthing the words silently as you read. It will force you to slow down just enough that you won’t miss anything, but not so much that you won’t have time to finish the test.
In general, preparing for the SAT Math section requires a multi-faceted approach. You need to be able to identify the types of questions you’re dealing with, know mathematical concepts and how to use them, and deal with other testing issues like rushing through the end or dealing with test anxiety. To help you get started, check out our free SAT Guide that includes 8 of our best test prep tips!
For more information about preparing for the SAT, check out these posts below:
30 SAT Math Formulas You Need to Know
25 Tips and Tricks for the SAT
5 Common SAT Math Mistakes to Avoid
Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!
About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.
This post will be your complete guide to SAT Math word problems. We’ll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.
Feature Image: Antonio Litterio/Wikimedia
What Are SAT Math Word Problems?
A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.
You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.
Secondly, these types of questions allow test makers to ask questions that’d be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it’d be difficult to demonstrate and ask this with only a diagram.
Translating Math Word Problems Into Equations or Drawings
In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.
For instance, the word «sum» means the value when two or more items are added together. So if you need to find the sum of a and b, you’ll need to set up your equation like this: a+b.
Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.
Here is a chart with all the key terms and symbols you should know for SAT Math word problems:
| Key Terms | Mathematical Action |
| Sum, increased by, added to, more than, total of | + |
| Difference, decreased by, less than, subtracted from | − |
| Product, times, __ times as much, __ times as many (a number, e.g., “three times as many”) | * or x |
| Divided by, per, __ as many, __ as much (a fraction, e.g., “one-third as much”) | / or ÷ |
| Equals, is, are, equivalent | = |
| Is less than | < |
| Is greater than | > |
| Is less than or equal to | ≤ |
| Is greater than or equal to | ≥ |
Now, let’s look at these math terms in action using a few official examples:
We can solve this problem by translating the information we’re given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let’s write this out in algebraic form.
We’ll say that the number of salads sold = S, and the number of drinks sold = D. The problem tells us that 209 salads and drinks have been sold, which we can think of as this:
S + D = 209
Finally, we’ve been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don’t know the exact numbers of S and D, but we do know how much each unit costs. Therefore, we can write this equation:
6.50S + 2D = 836.5
We now have two equations with the same variables (S and D). Since we want to know how many salads were sold, we’ll need to solve for D so that we can use this information to solve for S. The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S:
S + D = 209
Now, just subtract S from both sides to get what D equals:
D = 209 − S
Finally, plug this expression in for D into our other equation, and then solve for S:
6.50S + 2(209 − S) = 836.5
6.50S + 418 − 2S = 836.5
6.50S − 2S = 418.5
4.5S = 418.5
S = 93
The correct answer choice is (B) 93.
This word problem asks us to solve for one possible solution (it asks for «a possible amount»), so we know right away that there will be multiple correct answers.
Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.
If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.
Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.
Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.
Typical SAT Word Problems
Word problems on the SAT can be grouped into three major categories:
- Word problems for which you must simply set up an equation
- Word problems for which you must solve for a specific value
- Word problems for which you must define the meaning of a value or variable
Below, we look at each world problem type and give you examples.
Word Problem Type 1: Setting Up an Equation
This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You’ll also most likely see it first on the section.
For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.
Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.
To solve this problem, we’ll need to know both Armand’s and Tyrone’s situations, so let’s look at them separately:
Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m—the number of texts he sent per hour multiplied by the total number of hours he texted.
Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4p—the number of texts he sent per hour multiplied by the total number of hours he texted.
We now know that Armand’s situation can be written algebraically as 5m, and Tyrone’s can be written as 4p. Since we’re being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:
5m + 4p
The correct answer is choice (C) 5m + 4p
Word Problem Type 2: Solving for a Missing Value
The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics, such as averages, single-variable equations, and ratios. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
Let’s try to think about this problem in terms of x. If Type A trees produced 20% more pears than Type B did, we can write this as an expression:
x + 0.2x = 1.2x = # of pears produced by Type A
In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2x) to x, we get the number of pears produced by Type A trees.
The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2x is equal to the number of pears produced by Type A, we can write the following equation:
1.2x = 144
Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:
x = 144 / 1.2
x = 120
The correct answer choice is (B) 120.
You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math.)
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.
Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it’s the smallest integer larger than 55. Basically, it’s a safe bet!)
Now, because x = 56, the next angle in the triangle—2x—must measure the following:
56*2 = 112
Let’s make a rough (not to scale) sketch of what we know so far:
Now, we know that there are 180° in a triangle, so we can find the value of y by saying this:
y = 180 − 112 − 56
y = 12
One possible value for y is 12. (Other possible values are 3, 6, and 9.)
Word Problem Type 3: Explaining the Meaning of a Variable or Value
This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.
This question might sound tricky at first, but it’s actually quite simple.
We know that P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she’s worked 0 days (i.e., if we plug 0 into the equation), here’s what we get:
P = 108 − 23(0)
P = 108
This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.
To help juggle all the various SAT word problems, let’s look at the math strategies and tips at our disposal.
Ready to go beyond just reading about the SAT? Then you’ll love the free five-day trial for our SAT Complete Prep program. Designed and written by PrepScholar SAT experts, our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.
Click on the button below to try it out!
SAT Math Strategies for Word Problems
Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.
#1: Draw It Out
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you’re working with. For instance, let’s look at how a picture can help you solve a word problem about a circle (specifically, a pizza):
If you often have trouble visualizing problems such as these, draw it out. We know that we’re dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.
Because we’ll need to solve the weight of each slice in ounces, let’s first convert the total weight of our pizza from pounds into ounces. We’re given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:
3 * 16 = 48 ounces (for whole pizza)
Now, let’s draw a picture. First, the pizza is divided in half (not drawn to scale):
We now have two equal-sized pieces. Let’s continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):
This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:
48 / 6 = 8 ounces per piece
The correct answer choice is (C) 8.
As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.
#2: Memorize Key Terms
If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.
There are free SAT Math questions available online, so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.
#3: Underline and/or Write Out Important Information
The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.
#4: Pay Close Attention to What’s Being Asked
It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?
It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.
#5: Brush Up on Any Specific Math Topic You Feel Weak In
You’re likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.
For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!
Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now’s a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!
All set? Let’s go!
Test Your SAT Math Word Problem Knowledge
Finally, it’s time to test your word problem know-how against real SAT Math problems:
Word Problems
1. No Calculator
2. Calculator OK
3. Calculator OK
4. Calculator OK
Answers: C, B, A, 1160
Answer Explanations
1. For this problem, we have to use the information we’re given to set up an equation.
We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:
x + 1
Ken and Paul split the bill evenly. This means that we’ll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken’s sandwich cost x dollars and Paul’s cost x + 1, here’s what our equation looks like when we combine the two expressions:
x + x + 1
2x + 1
Now, we can divide this expression by 2 to get the price each person paid:
(2x + 1) / 2
x + 0.5
But we’re not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:
(x + 0.5) + 0.2(x + 0.5)
x + 0.5 + 0.2x + 0.1
1.2x + 0.6
The correct answer choice is (C) 1.2x + 0.6
2. You’ll have to be familiar with statistics in order to understand what this question is asking.
Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.
Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:
225 * 0.256 = 57.6
Since the question is asking «about how many students»—and since we obviously can’t have a fraction of a person!—we’ll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).
3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don’t be scared—it’s actually not as difficult as it appears!
First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here’s what happens to the equation when we plug in 0 for t:
h(0) = -16(0)2 + 110(0) + 72
h(0) = 0 + 0 + 72
h(0) = 72
As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).
4. You might be tempted to draw a diagram for this problem since it’s talking about a pool (rectangle), but it’s actually quicker to just look at the numbers given and work from there.
We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.
To find the amount of water in the pool now, we’ll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:
8 * 70 = 560 gallons
This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:
560 + 600 = 1160
The correct answer is 1160.
Aaaaaaaaaaand time for a nap.
Key Takeaways: Making Sense of SAT Math Word Problems
Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.
Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.
Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.
What’s Next?
Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math. From polygons and slopes to probabilities and sequences, we’ve got you covered!
Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score.
Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.
Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math, written by a perfect scorer.
Want to improve your SAT score by 160 points?
Check out our best-in-class online SAT prep program. We guarantee your money back if you don’t improve your SAT score by 160 points or more.
Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math strategy guide, you’ll love our program. Along with more detailed lessons, you’ll get thousands of practice problems organized by individual skills so you learn most effectively. We’ll also give you a step-by-step program to follow so you’ll never be confused about what to study next.
Check out our 5-day free trial:
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
Solving Word Problems in Algebra
Inequality Word Problems
How are you with solving word problems in Algebra? Are you ready to
dive into the «real world» of inequalities? I know that solving word
problems in Algebra is probably not your favorite, but there’s no point
in learning the skill if you don’t apply it.
I promise to make this as easy as possible. Pay close attention to
the key words given below, as this will help you to write the
inequality. Once the inequality is written, you can solve the
inequality using the skills you learned in our past lessons.
I’ve tried to provide you with examples that could pertain to your
life and come in handy one day. Think about others ways you might use
inequalities in real world problems. I’d love to hear about them if you do!
Before we look at the examples let’s go over some of the rules and
key words for solving word problems in Algebra (or any math class).
Word Problem Solving Strategies
- Read through the entire problem.
- Highlight the important information and key words that you need to solve the problem.
- Identify your variables.
- Write the equation or inequality.
- Solve.
- Write your answer in a complete sentence.
- Check or justify your answer.
I know it always helps too, if you have key words that help you to write
the equation or inequality. Here are a few key words that we associate
with inequalities! Keep these handy as a reference.
Inequality Key Words
- at least — means greater than or equal to
- no more than — means less than or equal to
- more than — means greater than
- less than — means less than
Ok… let’s put it into action and look at our examples.
Example 1: Inequality Word Problems
Keith has $500 in a savings account at the beginning of the summer. He wants to have at least $200 in the account by the end of the summer. He withdraws $25 each week for food, clothes, and movie tickets.
- Write an inequality that represents Keith’s situation.
- How many weeks can Keith withdraw money from his account? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: At least is a key word that notes that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know how many weeks.
Let w = the number of weeks
Step 3: Write your inequality.
500 — 25w > 200
I know you are saying, «How did you get that inequality?»
I know the «at least» part is tricky. You would probably think that at least means less than.
But… he wants the amount in his account to be at least $200 which means $200 or greater. So, we must use the greater than or equal to symbol.
Step 4: Solve the inequality.
The number of weeks that Keith can withdraw money from his account is 12 weeks or less.
Step 5: Justify (prove your answer mathematically).
I’m going to prove that the largest number of weeks is 12 by substituting 12 into the inequality for w. You could also substitute any number less than 12.
Since 200 is equal to 200, my answer is correct. Any more than 12 weeks and his account balance would be less than $200. Any number of weeks less than 12 and his account would stay above $200.
That wasn’t too bad, was it? Let’s take a look at another example.
Example 2: More Inequality Word Problems
Yellow Cab Taxi charges a $1.75 flat rate in addition to $0.65 per mile. Katie has no more than $10 to spend on a ride.
- Write an inequality that represents Katie’s situation.
- How many miles can Katie travel without exceeding her budget? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: No more than are key words that note that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know the number of miles Katie can travel.
Let m = the number of miles
Step 3: Write the inequality.
0.65m + 1.75 < 10
Are you thinking, «How did you write that inequality?»
The «no more than» can also be tricky. «No more than» means that you can’t have more than something, so that means you must have less than!
Step 4: Solve the inequality.
Since this is a real world problem and taxi’s usually charge by the mile, we can say that Katie can travel 12 miles or less before reaching her limit of $10.
Step 5: Justify (prove your answer mathematically).
Are you ready to try some on your own now? Yes… of course you are! Click here to move onto the word problem practice problems.
Take a look at the questions that other students have submitted:
- Home
- Inequalities
-
Inequality Word Problems
>
>
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/



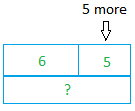
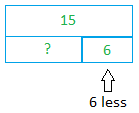
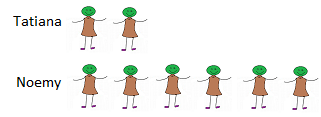
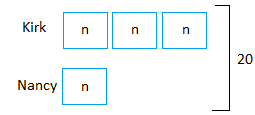
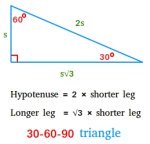
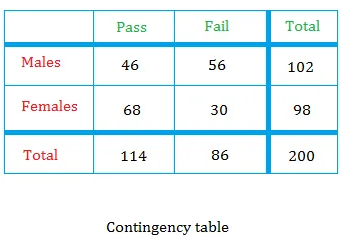


























 (begin{array}{c}L=M+frac{1}{6};,,,,,5L=15M\5left( {M+frac{1}{6}} right)=15M;,,,M+frac{1}{6}=3M,,\6M+1=18M;,,,12M=1;,,M,,=frac{1}{{12}},,text{hr}text{.}\D=15left( {frac{1}{{12}}} right)=1.25,,text{miles}end{array})
(begin{array}{c}L=M+frac{1}{6};,,,,,5L=15M\5left( {M+frac{1}{6}} right)=15M;,,,M+frac{1}{6}=3M,,\6M+1=18M;,,,12M=1;,,M,,=frac{1}{{12}},,text{hr}text{.}\D=15left( {frac{1}{{12}}} right)=1.25,,text{miles}end{array})