Help with math word problem

The Math Word Problems section is a recent addition to HelpingWithMath.com and it will be expanded over the next few months.

There is also a page on addition and subtraction word problems here. It covers the different types of addition and subtraction situations that students (especially around 1st Grade) might encounter.

There will be problems that include addition, subtraction, multiplication, division, fractions, measurement, and more. The links below are to the various mathematical word problems pages that have be added so far.

• Word Problems with Multiplication and Division
• Multi-step Word Problems
• Converting Metric Units of Measurement
• Money Word Problems

Your children’s reading ability may impact their understanding of the problem. Discuss with them any language or vocabulary they may be unfamiliar with. It is always good to have a dictionary handy.

Solving Math Word Problems

Solving word problems can be both a challenging and rewarding (like many things that are challenging!) activity. They help students to see math in the real world and they encourage and give reason for them to learn the underlying concepts and operations.

Below are some tips and techniques that can help with solving word problems.

• Read the question carefully. Depending on the complexity and length of the problem, it may require at least one re-reading.
• Take your time. This is perhaps easier to say than it is to do, especially if you are taking a test of being assessed against the clock. Nevertheless, time taken to fully understand a problem can made up by more quickly solving it.
• Highlight key words, language, and phrases. Underline or use a highlighter pen. Take notes in the margin.
• Ignore irrelevant information. Sometimes information that does not relate directly to the problem is included. Score out such information so it does not cause confusion.
• Complete all the steps. In some multi-step word problems there can be a temptation to stop before all the steps are complete. For example, with “..how much is left?” type questions, the hard part is finding how much has been used, and since it takes so long to work this out, the final subtraction from the original total step can be forgotten.
• Write your answer in full. For example, if the question is “How many runs did John score?”; answer “John scored 8 runs.” Do not just write “8”.
• Show your working. This will help when you check your answer and, even if you get the final solution wrong, you might get credit for your correct steps and calculations.
• Check to see if your answer makes sense. Ask yourself whether your answer should be bigger or smaller than the number you started with? Check that it is.

Related and Popular Resources on HelpingWithMath.com

Teaching math word problems without keywords? Yes, you can! In this blog post, I share how I use operation situations to help with math word problems.

“Who can tell me a word that tells us to add when we solve a word problem?” 

Fifteen hands shot into the air, some waving that oh-so-familiar “pick-me” wave. 

One by one, students shared their words . . . 

“in all”

“all together”

“increase”

“add”

“sum”

“total”

“plus”

“combine”

“join”

“together”

“both”

“Wow! You all came up with an amazing list of words, but what about subtraction? What words signal a subtraction problem?” 

The students raised their hands to respond.

“deduct”

“decrease”

“how many more”

“take away”

“how many less” 

“less than”

“minus”

“remain”

“difference”

Once the teacher recorded the words on chart paper, the students divided themselves into groups of two and completed a set of addition and subtraction task cards. 

—

While the students created an impressive list of words, I wondered if all the students would be able to remember them when solving word problems. 

I’m thinking, no! 😕

So, what’s wrong with using math keywords?

An Alternative To Keywords

If we can’t expect students to recognize these signal words to know what to do, how do we help with math word problems? 

Great question– I can answer it with two simple words– operation situations. 

Now, don’t get me wrong, I have been guilty of expecting my students to pick up on these keywords when solving problems too; however, a conference session I attended many years ago changed my way of thinking. 

At the time, I taught fourth grade and dedicated a portion of my math instruction to help my students develop word problem analysis skills with a word problem of the day program. 

As we read each day’s word problem, I noticed something interesting . . . each problem fell in a specific category for each operation.

I couldn’t believe it! It was like magic!

In the beginning, I referred to the set of operation situations I learned about at the summer conference session. 

They included: 

• Addition: part-part-whole, joining
• Subtraction: something leaves; comparing, missing part
• Multiplication: groups of something 
• Division: how many groups; how many in each group

Using Operation Situations To Help With Math Word Problems

Each time we encountered a new word problem, I asked the students to describe the event(s) happening in the word problem. From there, we discussed what action (operation) was taking place. 

From the beginning, most students could connect the picture they created in their heads with an operation. Then, I helped them connect the situation illustrated in the story problem with the more formal language of the corresponding operation situation. 

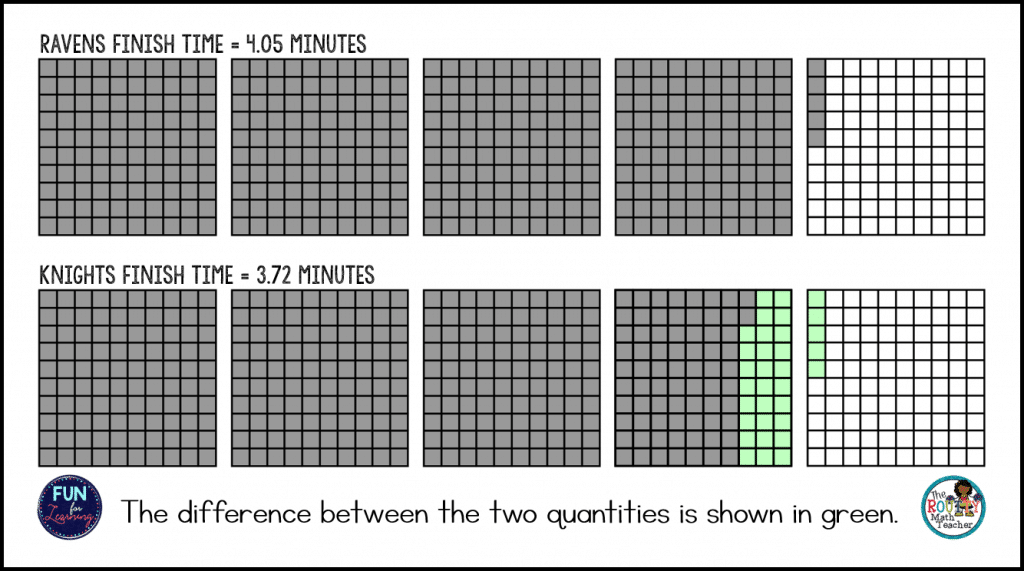
Example #1

Consider the following problem: 

The Lions finished the 400-meter freestyle relay race in 3.83 minutes. The Ravens finished in 3.72 minutes. The Knights finished in 4.05 minutes. What is the difference between the finish times for the first and third place teams?

For this problem, students might say we are looking for the difference between the finish time for the Ravens (first place) and the Knights (third place) relay race team. Students might also say we need to find out how much faster the first-place team (the Ravens) finished the race than the third-place team (the Knights). 

During this discussion, if not mentioned by a student, I would add we need to compare the Ravens time to the Knights time and state, “when we compare two numbers, we determine the difference between the two quantities”. I might even follow with a visual to help the students understand what it means to find the difference between two numbers.  (See the image below.)

Example #2

Okay. I know what you’re thinking . . . what about multiple-step problems?

That’s a great question. Let’s consider another problem. 

When Brandon and Kelly arrive at the BrightStar campground, they begin preparing dessert to eat after their campfire cookout. There are eight people on the camping trip. Brandon and Kelly prepare three smores for each person. Each smore has one marshmallow. If the bag of marshmallows they used had 4 dozen marshmallows, how many marshmallows are leftover?

For this problem, students will call it a subtraction situation because they need to determine the leftover amount. I would revoice their thinking and call this a “something leaves” situation because they started with a bag of 4 dozen marshmallows, then some left, and there is now a specific amount remaining.

The only missing piece of information from this situation is the quantity removed. So we go back to the problem to look for clues. 

Looking for Clues

When we return to the problem, we see there are eight people on the camping trip. We also know Brandon and Kelly prepare three smores for each person and each smore has one marshmallow. So, to determine how many marshmallows Brandon and Kelly need, we use the “groups of something” situation– which means to multiply 8 people x 3 smores (marshmallows). 

Hopefully, students will also notice the conversion. It’s not necessarily an operation situation we need to flesh out, but students need to acknowledge it. After working through the pieces of information needed to solve the problem, students can articulate they need to subtract the number of marshmallows used (8 groups of 3) from the total in the bag (4 dozen).  

Wait . . . there’s a keyword here.

Right now, you might be saying to yourself, “This problem has a keyword, so why is all of this necessary?” 

Because, this problem could have been written without the use of the word “leftover.” In fact, it could say, “If the bag of marshmallows they used had 4 dozen marshmallows, how many marshmallows were in the bag when Brandon and Kelly put the supplies away after dessert.” Notice there isn’t a keyword here, so some students might feel discouraged before even starting. 

The Bottom Line

We want our students to engage with story problems so they can see the story in their heads. Can you see Brandon, Kelly, Brenda, Dylan, Andrea, Steve, Donna, and David around the campfire after their high school graduation making smores? (Yes, you guessed it . . . I’m an 80s child and loved watching 90210!) 

When students can visualize the situation, they can make sense of the actions taking place, such as someone counting the number of marshmallows they need and removing them from the bag. After recognizing the action, we can easily determine the quantity remaining. 

More Operation Situations

I’m sure you’re wondering how I went from eight situations to the seventeen situations on the operation situations printable I shared in my keywords for math problems blog post.

During the first year I used this strategy to help my students with math word problems, my students and I noticed some situations didn’t quite fit, such as money situations where we know the amount spent and the change received but need to know the amount given to the cashier. 

These types of problems made me curious to look for more situations I could use to address all of the types of problems we encountered; however, these initial eight situations were a great starting place and helped my students become proficient at solving math word problems for a great number of years. 

Ready to use the operation situations to help with math word problems? Download a free set of posters using the form below!

Sound Off!

What strategies do you use to help with math word problems? Respond in the comments below.

Solving Word Problems in Mathematics

     Learn what word problems are and how to solve them in 7 easy steps.

     Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances. 
     As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem. 

     As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.

If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?

Steps of Solving a Word Problem

     To work through any word problem, students should do the following:

     1. Read the problem: first, students should read through the problem once.
     2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
     3. Visualize the problem: drawing a picture or creating a diagram can be helpful. 

     Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:

          – Addition: add, more, total, altogether, and, plus, combine, in all;

          – Subtraction: fewer, than, take away, subtract, left, difference;

          – Multiplication: times, twice, triple, in all, total, groups;

     These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems. 

     Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence. 
     6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
     7. Check the answer: finally, students should check their work to make sure that the answer is correct.

     These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that! 

     At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises! 

     Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience. 

     Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.

     From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes. 

     Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.  

     Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations. 

     Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams! 

To see the full exercise, follow this link.

     The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task. 

     Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language. 

Last Updated on May 31, 2022 by Thinkster

When I was a middle school teacher, I used to ask my students how their other classes were going and what they had learned that day. On the days they shared that their math lesson focused on word problems, the accompanying grumbles and groans were clear indicators that they were far from happy with that day’s lesson.

I used to wonder what it was that really irked my students about word problems. After all, the same students that grumbled and groaned were the ones that used procedural, analytical, and thinking skills in science, language arts, and social studies.

Not only did they use these skills in other classes, but many of these students used these skills incredibly well and successfully!

If my own students could easily write a response on the effects of colonialism in Latin America, something that requires them to use strong thinking skills, then why did they struggle to use similar thinking skills with math word problems? Or worse, why did they think it was hard to solve math word problems?

The trouble is that many students typically associate math with computational problems and ‘quick facts’. Some hold onto a perception that analytical and critical thinking skills should be saved for essays or lab reports.  

This is definitely not the case!

A strong math curriculum emphasizes developing analytical and conceptual thinking skills in students. These types of math problems require students to carefully plan, solve, and then check their work.

Students want to quickly work through their math problems, which often means that they make careless mistakes or struggle to understand what the problem is asking them to solve.

This can lead to massive frustration and why many students vehemently vocalize that they, “hate math word problems”.

There are two ways to combat this animosity and boost confidence when tackling math word problems. One, by ensuring your child knows different strategies and problem-solving tricks. Two, by having them practice different types of word problems frequently.

Thinkster Math tutors work with many students who struggle with math word problems. Together, we’ve compiled a list of our favorite tips and practice questions that you can use with your child.

Have your child organize their thinking

Before your child jumps in to try and solve a math word problem, they need to plan. This is often the step that students try and skip because they’re eager to finish their work quickly.

Not taking the time to carefully plan and dissect a word problem, though, can have your child feeling flustered when trying to solve it.

The planning process is incredibly important. It’s why authors take the time to outline and develop a plot before jumping in and writing a two hundred page novel. Planning allows for clarity and cohesive thoughts to develop.

This same planning process applies to math word problems.

As a first step, have your child identify what the problem is asking them to solve. Then, they should identify keywords and important details that are required to solve the problem. They can use highlighters, colored pencils, or even just a pen to underline or circle important information.

Identifying and understanding keywords and the order of operations in a word problem is a critical step!

Some kids also get confused by the different keywords and phrases used in word problems. In fact, some phrases might even have two meanings!

For example, using the words “increases by” could require using either addition or multiplication to solve the problem:

“There are 10 apples in a basket. The number of apples in the basket increases by 15. How many apples are there in all?”

“Johnny expects to pay $20 for his food, but the total bill increases by 7% because of tax. How much does Johnny need to pay?”

In the first word problem, your child simply adds 10 and 15 to get the answer. The second word problem requires multiplying $20 by 0.07, then adding that amount to $20.

These are two problems that use the same keyword, but require very different steps for solving!

This is why it’s great to practice keyword recognition with your child, and you can make flashcards for extra practice. For more helpful examples of keywords that your child should be able to identify, check out this link.

Encouraging your child to take the time to plan and organize their thinking by dissecting word problems helps them identify the details and operations required to solve. Finding this information helps your child as they start the next step of visualizing and illustrating the problem.

Solving math word problems with pictures

After your child identifies keywords within problems, the next step is to plan. There are many different types of strategies that your child can use. Creating illustrations, graphs, and diagrams are the most popular.

This is because many students are visual learners and benefit from using illustrations to help solve word problems. In fact, visual learners make up 65% of the students in a classroom.

Some math problems come with pictures or images for your child to refer to. For example:

This helps students learn and understand ways that they can organize their thinking to solve word problems.

Students also work with many word problems that do not come with any visuals or diagrams. This is why it’s a great idea to encourage your child to create their own images to help!

Here’s an example of how to use illustration to plan and solve a word problem:

There are 12 hens in a coop. Each hen lays 4 eggs a week. At the end of the week, Simon equally distributes and packs the eggs into 6 boxes. How many eggs are there in each box?

To solve this problem, your child will need to first calculate how many total eggs there are. Once they calculate 48 eggs (12 hens x 4 eggs each), they need to take this amount and divide it among 6 boxes. Your child can draw six boxes, then draw eggs into the boxes to visually represent how many eggs there are in each box.

Your child will develop strong problem-solving strategies as they grow accustomed to using charts and illustrations. This is also something that will help them as they tackle problems that involve patterns.

Solving math word problems with patterns

Another type of word problem that students encounter are problems with patterns.

For some students, these types of problems may seem difficult at first, especially if they are not taking the time to organize their thinking. But those that do take the time to use charts and visuals will find that there really is nothing to fear with pattern word problems!

Let’s try the following problem:

A bakery sells a different number of cakes each month. In March they sell 3 cakes, in April they sell 9 cakes, and in May they sell 27 cakes. If this pattern continues, how many cakes will they sell in July?

It’s not easy to try and figure out the answer mentally!  This is why creating a chart helps students organize their thinking to reach the correct answer.

Once this information is displayed carefully, your child should be able to spot that they actually need to do two calculations. The word problem requires them to determine the number of cakes sold in July, but they can’t reach the answer without first determining how many cakes are sold in June.  

Taking the time to carefully organize the data ensures that they do not miss this important step!

Here is another pattern word problem that you can have your child try to solve:

Robert adds chlorine tablets to a swimming pool every day to help keep it clean as more people come over to swim. On Monday he adds 3 tablets, on Tuesday he adds 5 tablets and on Wednesday he adds 7 tablets. If the pattern continues, how many chlorine tablets does he add on Thursday?

As your child solves the problem, make sure they underline keywords and important details, then organize their thinking with a chart! This is a great way to make sure they slow down when approaching the problem to minimize the risk of careless mistakes.

Solving math word problems with distractors

For students that try to sprint through solving word problems, distractors are often the reason they trip.

Which, quite honestly, is one of the reasons distractors are often thrown into word problems! They are meant to keep students on their toes and to ensure they are carefully reading what the problem is asking.

Distractors are words and information that are included in a problem, but really have nothing to do with it. It’s unnecessary information that students are expected to navigate around.

Thinkster Math CEO Raj Valli shares more on having students think on their feet with word problems that include distractors:

One tip that Thinkster tutors share with parents is to work on characterizing information and variables.

In the above video example, the problem requires students to determine how many fruits are in a basket. Characterizing all items in the basket and distinguishing between fruits and vegetables will ensure your child isn’t carelessly adding carrots into the final answer.

Here’s another example of a problem with a distractor that requires characterization:

A used car dealership has 91 cars and 29 trucks on the lot. Each day the dealership sells 13 cars. How many days would it take for all the cars to be sold?

A student that is rushing through the problem may add 91 and 29, then divide that amount by 13.

A student that takes the time to carefully dissect the problem will identify that there is a distractor.

As mentioned earlier, the first step is to understand what the word problem is answering. In this problem, your child needs to determine the number of days it takes to sell all cars at a dealership. By carefully characterizing the information, your child identifies that ‘29 trucks’ is information not needed to solve the problem.

Here is another word problem that you can have your child try solving:

Laura has invited 42 friends to her birthday. 18 friends are boys and 24 friends are girls. If she wants to give out 3 headbands to each of the girls, how many headbands will she have to buy?

Is your child able to pick out that “18 boys” is information not needed to solve the problem?

Having your child practice problems with distractors helps them spot this more quickly!

Get word problem practice and math help from an online math tutor

Along with following our tips and recommendations, one of the best ways for your child to grow more comfortable with solving word problems is by practicing.

A combination of exposure to different types of word problems along with frequent practice will help shift your child’s mentality when they tackle word problems. They should reach a point where they are no longer struggling, and instead have strong confidence when presented with a problem to solve.

While you can take the time to create your own word problems, there are online and digital tutoring programs, like Thinkster Math, that ensure your child is exposed to many different types of logical reasoning and critical thinking problems.

Thinkster Math’s world-class curriculum is packed with word problems!

We begin introducing word problems in our first-grade curriculum, which is on par with when students begin learning word problems in school. Introducing word problems at a young age ensures your child is developing strong problem-solving skills.

Thinkster also includes many real-world examples. Anchoring to real situations helps students understand and appreciate why they are solving word problems. It can also help them visualize what the problem is by asking them to solve it more easily.  

Conclusion

Whether your child is grumbling and groaning about word problems at school or at home, it’s time to squash any frustration and animosity toward math word problems!

There are a few things that you can do at home to help your child grow more comfortable with word problems. Have them organize their thinking by marking problems with highlighters and work on keyword recognition.

It’s important to also have your child try different types of word problems so that they feel more prepared and ready to tackle what they’ll be learning in school! Try problems with and without visuals, patterns, and distractors to give them balanced preparation.

And remember, daily practice with a program like Thinkster Math can help! The combination of practice, video tutorials, and customized feedback can have your child become more confident in their ability to use using problem-solving strategies, and you will see incredible learning improvements in less than three months.

You can explore our curriculum and try more sample problems similar to the ones shared in this blog.

If you’re looking for   to help your child, you can try Thinkster risk-free.

Thinkster provides a full-fledged  platform (driven by AI, behavioral, and data science), as well as supplemental ,   help, , and more. Our Parent Insights App allows you to monitor your ‘s work and  improvements at any time.

An elite,   and  system work together to help your  go beyond just   – we want them to master it.

Learn more about our curriculum and teaching style here.